Bistability regulates TNFR2-mediated survival and death of T-regulatory cells

Abstract

A subgroup of T cells called T-regulatory cells (Tregs) regulates the body’s immune responses to maintain homeostasis and self-tolerance. Tregs are crucial for preventing illnesses like cancer and autoimmunity. However, contrasting patterns of Treg frequency are observed in different autoimmune diseases. The commonality of tumour necrosis factor receptor 2 (TNFR2) defects and decrease in Treg frequency on the onset of autoimmunity demands an in-depth study of the TNFR2 pathway. To unravel this mystery, we need to study the mechanism of cell survival and death in Tregs. Here, we construct an ordinary differential equation (ODE)-based model to capture the mechanism of cell survival and apoptosis in Treg cells via TNFR2 signalling. The sensitivity analysis reveals that the input stimulus, the concentration of tumour necrosis factor (TNF), is the most sensitive parameter for the model system. The model shows that the cell goes into survival or apoptosis via bistable switching. Through hysteretic switching, the system tries to cope with the changing stimuli. In order to understand how stimulus strength and feedback strength influence cell survival and death, we compute bifurcation diagrams and obtain cell fate maps. Our results indicate that the elevated TNF concentration and increased c-Jun N-terminal kinase (JNK) phosphorylation are the major contributors to the death of T-regulatory cells. Biological evidence cements our hypothesis and can be controlled by reducing the TNF concentration. Finally, the system was studied under stochastic perturbation to see the effect of noise on the system’s dynamics. We observed that introducing random perturbations disrupts the bistability, reducing the system’s bistable region, which can affect the system’s normal functioning.

Introduction

A particular subpopulation of T cells known as T-regulatory cells (Tregs) suppresses immunological response to preserve homeostasis and self-tolerance. It has been demonstrated that Tregs can limit T cell expansion and cytokine production and are essential for avoiding autoimmunity [1]. On the other hand, in the case of cancer, Tregs infiltrate into several tumour tissues to suppress the effector functions of tumour-specific T cells [2]. Through direct and bystander inhibition, Tregs influence immunological tolerance. In direct suppression, Tregs act to specifically inhibit the target cell in response to an antigen. In contrast, in bystander suppression, Tregs specific for one antigen might inhibit immunological responses to other antigens in close proximity. Thus, immunological tolerance is restored, and these anti-inflammatory responses maintain immune homeostasis [3].

Conventionally, a decrease in the functional Treg number is often correlated with disease severity in autoimmune diseases [4]. However, a diverse pattern related to Treg frequency can be seen in the case of autoimmune diseases. A consistent decrease in Tregs number is observed in systemic lupus erythematosus (SLE) subjects [4], in the case of multiple sclerosis (MS), both an increase [5], and a decrease [6] in Tregs numbers were observed. Contrastingly, an increase in Tregs number was observed in rheumatoid arthritis (RA) and type 1 diabetes (T1D) patients [7, 8]. Although the number of Tregs in peripheral blood increases in the case of T1D but they have diminished functionality [9], a similar functional deficiency was also observed in the case of RA patients [10].

The contributing inflammatory responses that mark the pathogenesis of many autoimmune diseases begin with the up-regulation of tumour necrosis factor (TNF), which can bind to its two receptors, tumour necrosis factor receptor 1 (TNFR1) and tumour necrosis factor receptor 2 (TNFR2). Nearly every cell in the body expresses TNFR1. TNFR2 is expressed in more limited cells, which include T-regulatory cells (Tregs). Thus, TNFR2 becomes a more attractive molecular target than TNFR1 [11]. Exogenous TNF alone has a systemic harmful effect when TNFR1 is activated. TNFR2 offers better protective behaviour in diseases like autoimmunity, cardiac diseases, demyelinating, neurodegenerative disorders, and infectious diseases [11]. Several defects, including TNFR2 gene polymorphisms and TNFR2 receptor shedding, are present in many autoimmune disorders. These include graft versus host disease, Crohn’s disease, ulcerative colitis, and familial rheumatoid arthritis [11]. TNFR2 agonism has been a common strategy to destroy autoreactive T cells in various autoimmune diseases [11–15].

A highly complicated signalling network like TNF signalling frequently exhibits intricate dynamic regulation in response to perturbations. It has been established that mathematical modelling is a crucial method in the study of complex networks and dynamic systems in TNF signalling. Since mathematical modelling is important in molecular biology, it has been used to construct testable hypotheses and guide experimental design to maximise the information obtained [16–21]. These mathematical models can unravel complex mechanisms like bistability, demonstrating the all-or-none decision-making processes to determine the fate of cells [22, 23]. The mathematical model on bistability was also used to understand evolutionary reversibility by Kheir Gouda et al. [24]. These extremely complex signalling systems could be further influenced by the inherent noise present in the signalling network [25]. Low copy numbers of the chemical reactants and their diverse distribution inside the cell are the root causes of randomisation at the intracellular level [26]. Numerous intriguing effects of random fluctuations have recently been theorised and experimentally verified [27–31]. It has been seen that the bistability can be lost due to presence of randomness in the system [32]. Therefore, it is important to examine noise in these complicated systems.

The commonality of TNFR2 signalling abnormalities and the diverse patterns related to Treg frequency observed in autoimmune diseases motivated us to study the TNFR2 signalling pathway in Treg cells. TNF-mediated apoptosis is one of the intricate and carefully controlled cellular processes brought on by activating both pro- and anti-apoptotic signalling pathways. So, we are curious to understand the mechanism governing Treg cell survival and death that could facilitate targeted treatment for the disease. To capture the process of cell survival and death in Treg cells via TNFR2 signalling, an ordinary differential equation (ODE)-based model was developed and analysed. The model reveals the existence of bistability in the system. The system strives to adapt to changing stimuli through hysteretic switching. We compute bifurcation diagrams and create cell fate maps to analyse how stimulus strength and feedback strength affect cell survival and death. Our findings suggest that the main causes of the death of Tregs are an elevated level of TNF and enhanced JNK phosphorylation. Finally, the system was studied in the presence of random perturbations to capture the influence of noise in the observed bistability.

Construction of the deterministic model

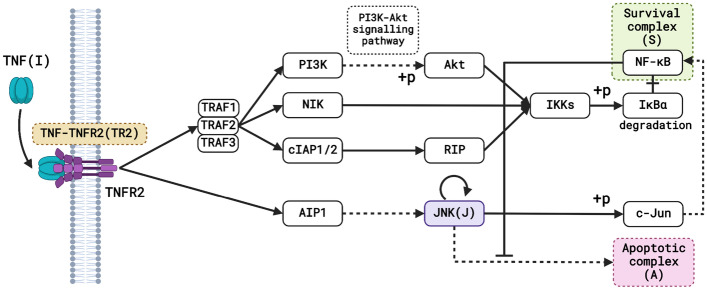
We proposed a simplified mathematical model of TNFR2 signalling in Treg cells to understand the underlying mechanism of TNF-mediated survival and death. To construct the mathematical model, we adopted the TNFR2 signalling pathway described in Fig. 1 from the Kyoto Encyclopedia of Genes and Genomes (KEGG) [33, 34] and literature [11, 35]. The model consists of the input stimuli TNF (I), which binds to its receptor TNFR2, forming the TNF-TNFR2 complex (TR2). After the initial trigger, we suppose that the signal moves towards the end irreversibly. The complex TR2 activates TNF receptor-associated factors 1, 2, 3 (TRAF1/2/3), which further activates the downstream signalling pathways. TRAF1/2/3 activates the IkB kinase (IKKs) via multiple signalling pathways through successive phosphorylation of the intermediate molecules like phosphoinositide 3 kinase (PI3K), protein kinase B (Akt), nuclear factor kappa B inducing kinase (NIK), cellular inhibitors of apoptosis proteins 1 and 2 (cIAP1/2) and receptor-interacting protein (RIP). Finally, IKKs activate nuclear factor kappa B (NF-$\kappa$B) by phosphorylating the inhibitor of NF-$\kappa$B (I$\kappa$B$\alpha$). The transcription factor NF-$\kappa$B ensures cell viability by dissociating from its cytoplasmic inhibitor protein IkB$\alpha$ and moving to the nucleus, where it activates target genes that are involved in cell survival [11]. So, we have considered the concentration of activated NF-$\kappa$B as the survival complex (S). TR2 also activates disabled homolog 2-interacting protein (AIP1), which further activates its downstream protein c-Jun N-terminal kinase (JNK (J)), which can promote cell survival by activating transcription factor Jun (c-Jun). Moreover, c-Jun promotes cell survival by activating the Akt survival pathway [36], which eventually activates NF-kB. Thus, we can consider the activation of the survival complex by JNK via an indirect link. Also, c-Jun can prevent apoptosis by cooperating with NF-$\kappa$B [37]. Apoptosis is triggered and carried out by caspase activation [35]. Thus, we have taken the concentration of caspase as the apoptotic complex (A), which is also the system’s output. Long-term JNK activation ‘breaks the brake’ on apoptosis by inactivating suppressors of the mitochondrial-dependent death cascade [35]. TNF activates NF-$\kappa$B, which prevents caspase activation and prevents TNF-induced apoptosis [35]. The additional downstream linkages and the cross-talks were not included to keep the mathematical model simple for analysis.

Fig. 1.

Map of the TNFR2 pathway. The figure depicts the schematic representation of the TNFR2 signalling pathway. The solid lines represent molecular interactions or relations, and the dashed lines represent indirect links. Furthermore, the arrow represents activation, and the line with the hammerhead denotes inhibition. The input TNF (I) and all the state variables used in the model system are written inside parentheses

The model’s equations describe the rates of loss and formation of the TNF-TNFR2 complex (TR2(t)), survival complex (S(t)), JNK (J(t)), and the apoptotic complex A(t) at time t. Here the input stimulus TNF, I, binds to the free TNFR2. Grell et al. [38] have shown that the formation of TNF-TNFR2 (TR2) has a saturation, so to replicate this behaviour, we have considered the Michaelis-Menten form of kinetics for TR2 formation. Similar enzymatic kinetics has been used to describe the interaction of TNF with its receptor [39]. The total number of TNFR2 in different cell types remains constant. For example, the number of TNFR2 in KYM-1 cells is approximately 30,000 per cell [38], and HeLa cells contain about 50,000 TNFR2 per cell [40]. Wang et al. [41] showed that the number of TNFR2 on the Treg cell surface is three times higher than the other T cell types, but their actual number is unknown. So, we have considered the total concentration of TNFR2 to be a constant and normalised to 1 [42]. So the concentration of free TNFR2 at the membrane is (1-[TR2]). Thus, the formation of TR2 can be given by $\frac{k_{1}I(1-[TR2])}{k_{m1}+(1-[TR2])}$, where $k_1$ is the maximum rate of TR2 formation and $k_{m1}$ is the half-saturation constant. The production of S depends on the number TR2 of TNF-TNFR2 complexes on the cell membrane, with a rate constant $k_2$ [17]. Also, the production of J depends on the number of TR2, with a rate constant of $k_4$. Similarly, the production of S and A depends on the number of J, with rate constant $k_3$ and $k_7$ respectively. So, a linear positive growth term is added to the respective equations. The cell survival pathway inhibits the apoptotic reactions in A with a rate $k_8$[S] [17]. Thus, a negative term is added to the apoptosis equation. Bagowski et al. [43] experimentally found that the steady-state response of the JNK cascade is highly ultrasensitive and exhibits switch-like responses to various stimuli. This ultra-sensitivity is due to strong positive feedback, which is given by the autocatalysis of the JNK activation [44]. The Hill equation can model this switch-like ultrasensitive response with a Hill coefficient greater than one [45]. Hence, we have added the term $\frac{k_5{[J]}^2}{k_6^2+{[J]}^2}$ for the autocatalysis to the equation of J considering the Hill coefficient to be equal to two. The ligand/receptor complexes TR2 can be degraded with a rate constant $d_1$. The activated JNK has a degradation with a rate constant of $d_3$. The processes described by the rate constants $d_2$ and $d_4$ respectively, represent the degradation of S and A by ubiquitination and proteasome cleavage and/or irreversibly inhibited by other molecular species [17]. All these assumptions lead to the following model:

$$\begin{array}{c}\hfill \begin{array}{c}\frac{d[TR2]}{\mathit{dt}}=\frac{k_{1}I(1-[TR2])}{k_{m1}+(1-[TR2])}-d_1[TR2]=F_1(TR2,S,J,A),\hfill \\ \frac{d[S]}{\mathit{dt}}=k_2[TR2]+k_3[J]-d_2[S]=F_2(TR2,S,J,A),\hfill \\ \frac{d[J]}{\mathit{dt}}=k_4[TR2]+\frac{k_5{[J]}^2}{k_6^2+{[J]}^2}-d_3[J]=F_3(TR2,S,J,A),\hfill \\ \frac{d[A]}{\mathit{dt}}=k_7[J]-k_8[S][A]-d_4[A]=F_4(TR2,S,J,A).\hfill \end{array}\end{array}$$ 1

with initial conditions

$$\begin{array}{c}\hfill TR2(0)=TR{2}_0>0,S(0)=S_0>0,J(0)=J_0>0,A(0)=A_0>0.\end{array}$$ 2

Analytical results

Positive invariance and boundedness of the solutions

• (i)All solutions of (1) satisfying the initial condition (2) are positively invariant. For proof see Appendix A.1.
• (ii)
  All solutions of system (1) with initial condition (2) are bounded within a region $\mathrm{\Gamma }$, where

  $$\begin{array}{cc}\hfill \mathrm{\Gamma }=& \{(TR2,S,J,A)ϵR_{+}^4:0<TR2(t)\le \frac{k_{1}I}{d_1},0<S(t)\le {\mathrm{\Omega }}_1,\hfill \\ \hfill & 0<J(t)\le \frac{1}{d_3}\left(k_4,\frac{k_{1}I}{d_1},+,k_5\right),0<A(t)\le \frac{k_7\left(k_4,\frac{k_{1}I}{d_1},+,k_5\right)}{d_3(d_4+k_8\alpha )}\},\hfill \end{array}$$

  ${\mathrm{\Omega }}_1=\frac{1}{d_2}\left\{k_2,\frac{k_{1}I}{d_1},+,\frac{k_3}{d_3},\left(k_4,\frac{k_{1}I}{d_1},+,k_5\right)\right\}$ and $\alpha$ is the minimum of S(t). For proof see Appendix A.2.

Equilibrium point and stability analysis

The system has no axial equilibrium points. The interior equilibrium point $E^{\ast }(TR{2}^{\ast },S^{\ast },J^{\ast },A^{\ast })$ of the system is obtained by solving the following algebraic equations:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \frac{k_{1}I(1-TR{2}^{\ast })}{k_{m1}+(1-TR{2}^{\ast })}-d_{1}TR{2}^{\ast }=0,\\ \hfill k_{2}TR{2}^{\ast }+k_3{J}^{\ast }-d_2{S}^{\ast }=0,\\ \hfill k_{4}TR{2}^{\ast }+\frac{k_5{(J^{\ast })}^2}{k_6^2+{(J^{\ast })}^2}-d_3{J}^{\ast }=0,\\ \hfill k_7{J}^{\ast }-k_8{S}^{\ast }{A}^{\ast }-d_4{A}^{\ast }=0.\end{array}\end{array}$$ 3

Solving the first equation we get a quadratic equation in $TR{2}^{\ast }$, given by

$$d_1{(TR{2}^{\ast })}^2-[d_1(k_{m1}+1)+k_{1}I]TR{2}^{\ast }+k_{1}I=0.$$

The discriminant (D) of this quadratic equation is given by $D={(d_1(k_{m1}-1)+k_{1}I)}^2+4d_1^2{k}_{m1}>0$. Thus, we get two distinct positive real roots $TR{2}^{\ast }$. So, $TR{2}^{\ast }$ is feasible when $0\le TR{2}^{\ast }\le 1$.

From the third equation of (3), we get $J^{\ast }$ in terms of $TR{2}^{\ast }$ which satisfies the cubic equation

$$\begin{array}{c}\hfill d_3{J}^{\ast 3}-(k_{4}TR{2}^{\ast }+k_5)J^{\ast 2}+d_3{k}_6^2{J}^{\ast }-k_4{k}_6^{2}TR{2}^{\ast }=0.\end{array}$$

From Descartes’ rule of signs, we can easily find that the $J^{\ast }$ have either one or three positive roots.

Next, by solving the second equation of (3) we get $S^{\ast }=\frac{1}{d_2}\left(k_2,T,R,2^{\ast },+,k_3,J^{\ast }\right)$ and from fourth equation we get $A^{\ast }=\frac{k_7{J}^{\ast }}{k_8{S}^{\ast }+d_4}$.

The Jacobian matrix evaluated at the interior equilibrium $E^{\ast }$ is given by

$$\begin{array}{cc}& V(TR{2}^{\ast },S^{\ast },J^{\ast },A^{\ast })=\hfill \\ \hfill & \left(\begin{array}{cccc}-d_1-\frac{k_1{k}_{m1}I}{{(k_{m1}+1-TR{2}^{\ast })}^2}& 0& 0& 0\\ k_2& -d_2& k_3& 0\\ k_4{J}^{\ast }& 0& -d_3+\frac{2k_5{k}_6^2{J}^{\ast }}{{(k_6^2+J^{\ast 2})}^2}& 0\\ 0& -k_8{A}^{\ast }& k_7& -k_8{S}^{\ast }-d_4\end{array}\right)\hfill \end{array}$$

The eigenvalues ${\lambda }_i(i=1,2,3,4)$ are the roots of the characteristic equation

$$\begin{array}{c}\hfill \begin{array}{c}\left(-,d_1,-,\frac{k_1{k}_{m1}I}{{(k_{m1}+1-TR{2}^{\ast })}^2},-,{\lambda }_1\right)(-d_2-{\lambda }_2)\hfill \\ \left(-,d_3,+,\frac{2k_5{k}_6^2{J}^{\ast }}{{(k_6^2+J^{\ast 2})}^2},-,{\lambda }_3\right)(-k_8{S}^{\ast }-d_4-{\lambda }_4)=0.\hfill \end{array}\end{array}$$ 4

Note that the three eigenvalues ${\lambda }_i(i=1,2,4)$ of (4) are always negative and the fourth eigenvalue ${\lambda }_3$ is negative iff $\frac{2k_5{k}_6^2{J}^{\ast }}{{(k_6^2+J^{\ast 2})}^2}<d_3$. Hence, the interior equilibrium point $E^{\ast }$ is locally asymptotically stable (LAS) iff $\frac{2k_5{k}_6^2{J}^{\ast }}{{(k_6^2+J^{\ast 2})}^2}<d_3$.

Construction of the stochastic model

Signalling systems are inherently noisy [32], so to study the effect of noise in the system we built a stochastic differential equation (SDE) model by incorporating random perturbation in the system (1). The random influences were viewed as systemic disturbances, and their effects were included in the model as multiplicative Gaussian white noise [46, 47]. Consequently, we added the stochastic perturbation terms to the equations relating to each state variable. The random fluctuations of the state variables around their steady-state values $E^{\ast }(TR{2}^{\ast },S^{\ast },J^{\ast },A^{\ast })$ are Gaussian white noise, and they are proportional to the distances of TR2,  S,  J and A from their steady-state values, respectively. In light of this, the stochastic model system that follows the deterministic model system (1) is as follows:

$$\begin{array}{c}\hfill \begin{array}{c}dTR2=F_1(TR2,S,J,A)dt+{\sigma }_1(TR2-TR{2}^{\ast })d{\xi }_t^1,\hfill \\ dS=F_2(TR2,S,J,A)dt+{\sigma }_2(S-S^{\ast })d{\xi }_t^2,\hfill \\ dJ=F_3(TR2,S,J,A)dt+{\sigma }_3(J-J^{\ast })d{\xi }_t^3,\hfill \\ dA=F_4(TR2,S,J,A)dt+{\sigma }_4(A-A^{\ast })d{\xi }_t^4.\hfill \end{array}\end{array}$$ 5

where ${\sigma }_i$ $(i=1,2,3,4)$ are real constants and known as the intensity of the fluctuations, ${\xi }_t^i={\xi }_i(t)$ $(i=1,2,3,4)$ are standard Wiener processes, independent of each other, and $F_i$ $(i=1,2,3,4)$ are defined in (1). We consider (5) as an Ito stochastic differential system of the type

$$\begin{array}{c}\hfill d{X}_t=F(t,X_t)dt+G(t,X_t)d{\xi }_t\end{array}$$ 6

where the solution ($X_t$, $t>0$) is an Ito process, F is the drift coefficient, G is the diffusion coefficient and ${\xi }_t$ is a four-dimensional stochastic process having scaler Wiener process components with increments $\mathrm{\Delta }{\xi }_t^j={\xi }_j(t+\mathrm{\Delta }t)-{\xi }_j(t)$ are independent Gaussian random variables $N(0,\mathrm{\Delta }t)$. In the case of the system (5),

$$\begin{array}{c}\hfill \begin{array}{c}\hfill X_t=\left[\begin{array}{c}TR2\\ S\\ J\\ A\end{array}\right],{\xi }_t=\left[\begin{array}{c}{\xi }_t^1\\ {\xi }_t^2\\ {\xi }_t^3\\ {\xi }_t^4\end{array}\right],F=\left[\begin{array}{c}{F}_1(TR2,S,J,A)\\ F_2(TR2,S,J,A)\\ F_3(TR2,S,J,A)\\ F_4(TR2,S,J,A)\end{array}\right],\\ \hfill G=\left[\begin{array}{cccc}{\sigma }_1(TR2-TR{2}^{\ast })& 0& 0& 0\\ 0& {\sigma }_2(S-S^{\ast })& 0& 0\\ 0& 0& {\sigma }_3(J-J^{\ast })& 0\\ 0& 0& 0& {\sigma }_4(A-A^{\ast })\end{array}\right].\end{array}\end{array}$$ 7

Since the diffusion matrix G depends upon the solution of $X_t$, the system (5) is said to have multiplicative noise.

Stochastic stability of the interior equilibrium point

The variables $U_1=TR2-TR{2}^{\ast }$, $U_2=S-S^{\ast }$, $U_3=J-J^{\ast }$, $U_4=A-A^{\ast }$ were introduced to centre the stochastic differential system (5) at its positive equilibrium points $E^{\ast }(TR{2}^{\ast },S^{\ast },J^{\ast },A^{\ast })$. To keep mathematical computations simple, we work with the stochastic differential equation created by linearising the vector function F (7) about the positive equilibrium point $E^{\ast }$. The linearised system of (6) around $E^{\ast }$ is given by

$$\begin{array}{c}\hfill dU(t)=f(U(t))dt+G(U(t))d\xi (t),\end{array}$$ 8

where

$$\begin{array}{c}\hfill \begin{array}{c}\hfill U(t)=\left[\begin{array}{c}{U}_1(t)\\ U_2(t)\\ U_3(t)\\ U_4(t)\end{array}\right],f(U(t))=\left[\begin{array}{c}-a_{11}{U}_1\\ k_2{U}_1-d_2{U}_2+k_3{U}_3\\ k_4{J}^{\ast }{U}_1-a_{33}{U}_3\\ -k_8{A}^{\ast }{U}_2+k_7{U}_3-a_{44}{U}_4\end{array}\right],\\ \hfill \\ \hfill G(U(t))=\left[\begin{array}{cccc}{\sigma }_1{U}_1& 0& 0& 0\\ 0& {\sigma }_2{U}_2& 0& 0\\ 0& 0& {\sigma }_3{U}_3& 0\\ 0& 0& 0& {\sigma }_4{U}_4\\ \end{array}\right],\end{array}\end{array}$$ 9

$$\begin{array}{c}\hfill a_{11}=d_1+\frac{k_1{k}_{m1}I}{{(k_{m1}+1-TR{2}^{\ast })}^2},a_{33}=d_3-\frac{2k_5{k}_6^2{J}^{\ast }}{{(k_6^2+J^{\ast 2})}^2},a_{44}=d_4+k_8{S}^{\ast }.\end{array}$$

Note that, in (8) the positive equilibrium $E^{\ast }$ corresponds to the trivial solution $(U_1,U_2,U_3,U_4)=(0,0,0,0)$. Let $\mathrm{\Omega }$ be the set defined by $\mathrm{\Omega }=\left[(t⩾t_0),\times ,{\mathrm{R}}^4,,,t_0,\in ,{\mathrm{R}}^{+}\right]$. To define stability following theorem [48] can be used,

Theorem 1

Suppose there exist a differentiable function $V(U,t)\in {\mathrm{C}}^4(\mathrm{\Omega })$ satisfying the inequalities

$$\begin{array}{c}\hfill K_1{|U|}^{\alpha }\le V(U,t)\le K_2{|U|}^{\alpha }\end{array}$$ 10

$$\begin{array}{c}\hfill LV(U,t)\le -K_3{|U|}^{\alpha },K_i>0,i=1,2,3,\alpha >0.\end{array}$$ 11

Then the trivial solution of (8) is exponentially $\alpha$ stable for all time $t\ge 0$.

Note that, if in (10), (11), $\alpha =2$, then the trivial solution of (8) is exponentially mean-square stable. Furthermore, the trivial solution of (8) is globally asymptotically stable in probability.

Here, following (8),

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill LV(t,U)=& \frac{\partial V(t,U(t))}{\partial t}+f^T(U(t))\frac{\partial V(t,U)}{\partial U}\hfill \\ \hfill & +\frac{1}{2}Tr\left[G^T,(U(t)),\frac{{\partial }^{2}V(t,U)}{\partial U^2},G,(U(t))\right]\hfill \end{array}\end{array}$$ 12

where

$$\begin{array}{c}\hfill \frac{\partial V}{\partial U}={\left(\begin{array}{cc}\frac{\partial V}{\partial U_1}& \frac{\partial V}{\partial U_2}\end{array}\right)}^T,\frac{{\partial }^{2}V(t,U)}{\partial U^2}={\left(\frac{{\partial }^{2}V}{\partial U_j\partial U_i}\right)}_{i,j=1,2}\end{array}$$

and T means transposition.

Using the above Theorem 1, we have calculated the critical value of noise (${\sigma }_c$), below which the system is stochastically stable. We can define and prove the following Theorem 2.

Theorem 2

Assume that for some positive real value ${\omega }_1$, ${\omega }_2$, ${\omega }_3$, ${\omega }_4$, and ${\omega }_5$ the following inequality holds:

$$\begin{array}{c}\hfill \left(2,a_{33},-,{{\sigma }_3}^2\right)\left(2,a_{44},-,{{\sigma }_4}^2\right)>\frac{k_7^2}{{\omega }_2}({\omega }_3+{\omega }_4+{\omega }_5)\end{array}$$ 13

then the zero solutions of the system (8) will be exponentially 2-stable if

$$\begin{array}{c}\hfill \begin{array}{c}{{\sigma }_1}^2<\frac{2P_{11}}{({\omega }_1+{\omega }_2+{\omega }_4)},{{\sigma }_2}^2<\frac{2P_{22}}{({\omega }_1+1)},{{\sigma }_3}^2<2a_{33},{{\sigma }_4}^2<2a_{44},\end{array}\end{array}$$ 14

where ${\omega }_1=\frac{P}{a_{11}+d_2-P}$, ${\omega }_2=\frac{k_3{\omega }_1+k_7{\omega }_4}{a_{11}-k_4{J}^{\ast }}$, ${\omega }_3=\frac{k_3}{k_7}(1+{\omega }_1)$, ${\omega }_4=\frac{a_{11}{\omega }_3}{a_{11}+a_{44}}$, ${\omega }_5=\left(\frac{a_{44}}{k_8{A}^{\ast }},-,1\right){\omega }_3-{\omega }_4$, $P=k_2-\frac{a_{11}{k}_3}{k_7}\left[1,+,\frac{k_8{A}^{\ast }}{a_{11}+a_{44}}\right]$, $P_{11}=a_{11}({\omega }_1+{\omega }_2+{\omega }_4)-k_2{\omega }_1-k_4{J}^{\ast }{\omega }_2$ and $P_{22}=d_2({\omega }_1+1)-k_8{A}^{\ast }{\omega }_3$.

For proof see Appendix B.

Numerical results

Model validation with experimental data

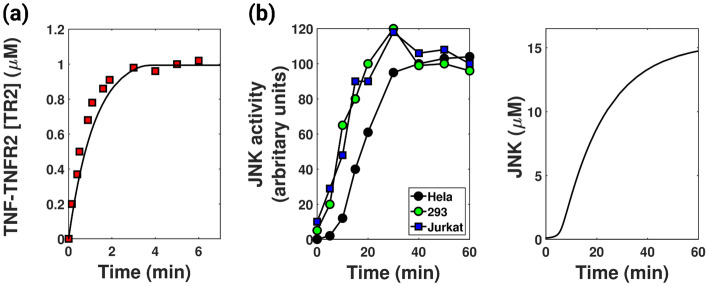
The model is first established by demonstrating certain key facets of the biological system. The model is observed to generate saturated TNF-TNFR2 formation [38] and sigmoidal JNK response [43, 44]. It is observed that the association of TNF with TNFR2 is very rapid [38]. Our model successfully depicts the saturation kinetics of TNF-TNFR2 formation (represented by the black line in Fig. 2a) in congruent with the experimental data (red dots in Fig. 2a) from Grell et al. [38]. The model also showed a sigmoidal JNK response (right panel in Fig. 2b) as reported by Bagowski et al. [43, 44] (left panel in Fig. 2b). The parameter values reported in Table 1 were required to generate these curves. Some of these values were taken from literature, and the rest were estimated. The output response (caspase concentration (A)) generated by this parameter set is in the scale of ${10}^{-5}$ $\mu$M, in agreement with the literature [23].

Fig. 2.

Model validation. a The figure depicts the time series of TNF-TNFR2 formation with parameters given in Table 1. Inconsistent with existing literature [38], the black curve shows saturation kinetics of TNF-TNFR2 formation. Here, the red boxes represent experimental data from Grell et al. [38]. (Details of the data curation are explained in Appendix C) b Left panel: Sigmoidal curve of JNK activity when HeLa, HEK 293 and Jurkat T cells were treated with sorbitol (data taken from literature [43]). Right panel: The figure shows the sigmoidal response of JNK similar to curves in the left panel. The parameters used are given in Table 1

Table 1.

Kinetic parameters involved in the system

Parameter	Description	Value	Reference
I	Concentration of free TNF acting	0.59 $\mu$M	Estimated
	as input stimulus
$k_1$	Association rate constant of TNF	1.49 min${}^{-1}$	[38]
	and TNFR2 giving TNF-TNFR2
$k_{m1}$	Half-saturation constant of	0.42 $\times$ ${10}^{-3}$ $\mu$M	[51]
	TNF-TNFR2 formation
$k_2$	Activation rate of survival complex	0.016 min${}^{-1}$	[17]
	by TNF-TNFR2 complex
$k_3$	Activation rate of survival complex	0.02 min${}^{-1}$	Estimated
	by JNK
$k_4$	Activation rate of JNK by	0.01 min${}^{-1}$	Estimated
	TNF-TNFR2 complex
$k_5$	Maximum expression level of JNK	0.9 $\mu$M min${}^{-1}$	Estimated
$k_6$	Half-saturation constant of JNK	0.5 $\mu$M	Estimated
$k_7$	Activation rate of death complex	0.9 min${}^{-1}$	Estimated
	by JNK
$k_8$	Caspase inhibition rate	2.2 $\times$ ${10}^3$ $\mu$M${}^{-1}$ min${}^{-1}$	[17]
$d_1$	Rate of degradation of	0.829 min${}^{-1}$	Estimated
	TNF-TNFR2 complex
$d_2$	Rate of degradation of survival	0.003 min${}^{-1}$	[17]
	complex
$d_3$	Rate of degradation of JNK	0.059 $\mu$M min${}^{-1}$	Estimated
$d_4$	Rate of degradation of death	0.003 min${}^{-1}$	[17]
	complex

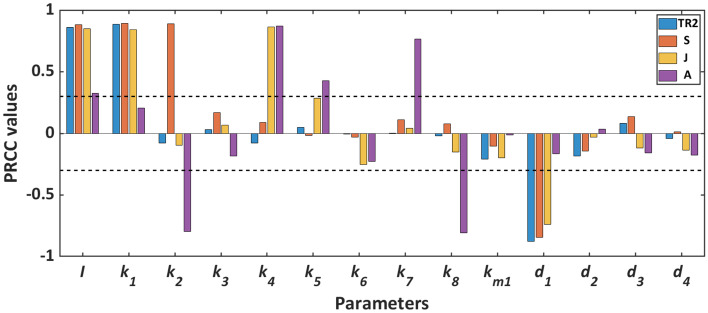
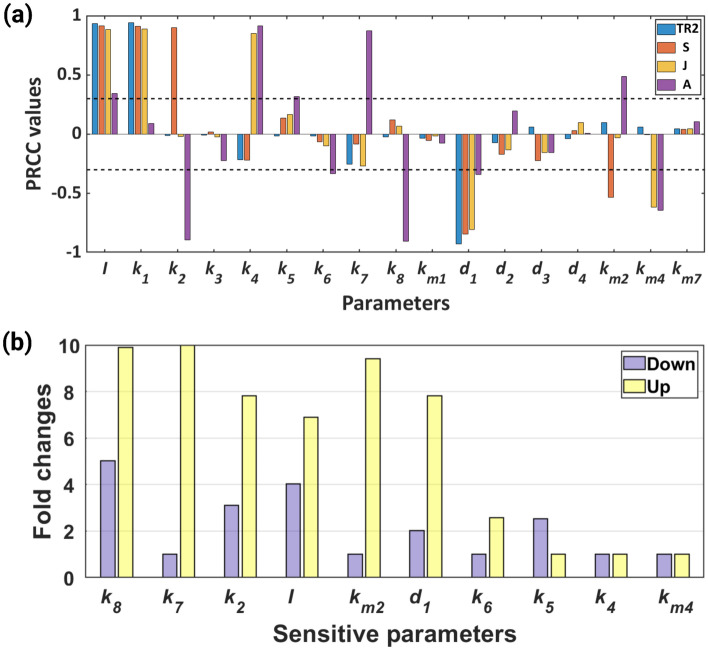
Global sensitivity analysis

We conducted global sensitivity analysis (GSA) using Latin Hypercube Sampling (LHS), and Partial Rank Correlation Coefficient (PRCC) analysis to evaluate the sensitivity of each parameter [49]. A parameter is considered sensitive if its PRCC value is equal to or larger than the predetermined threshold value of $\pm 0.3$ [32, 50]. The GSA reveals that the input parameter (I) is sensitive to all the state variables of the system. It is further observed that the output of the system (A) is sensitive to the parameters $k_2,k_4,k_5,k_7$ and $k_8$ (see Fig. 3).

Fig. 3.

Global sensitivity of the system parameters. Here, corresponding to every parameter, four different colour bars represent four state variables. And the sensitivity of each parameter is measured by the length of bars

Existence of bistability

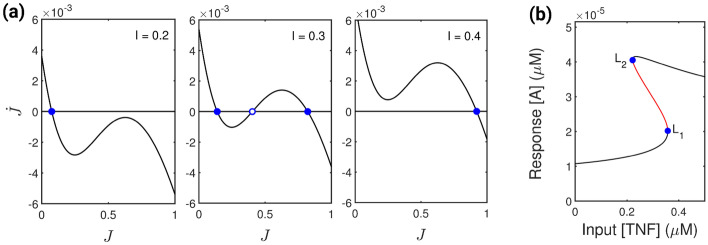
The presence of positive feedback on JNK production satisfies the necessary condition for the existence of bistability in the system [32]. In addition, Bagowski et al. [43, 44] reported that the JNK response is ultrasensitive, i.e. it can show abrupt response when subjected to different stimuli. These shreds of evidence suggest that with the change in feedback strength and the variation of input stimulus, the system may attain different characteristics of bistability [52]. Initially, the system exhibit bistability when we decrease the input concentration to 0.026 $\mu$M, and the rest of the parameter values are as in Table 1. We lower the feedback strength of the system to $k_5=0.075$ $\mu$M min${}^{-1}$ to examine different stability patterns of the system. For three different values of the input stimuli, viz. $I=0.2$ $\mu$M, $I=0.3$ $\mu$M and $I=0.4$ $\mu$M, the J vs $\dot{J}$ or $\frac{\mathit{dJ}}{\mathit{dt}}$ phase portrait display monostability, bistability and monostability respectively (see Fig. 4a). The system’s output response also shows saddle-node bifurcation at $L_1$ and $L_2$ (see Fig. 4b) in the process displaying bistability for a range of input stimuli.

Fig. 4.

Existence of bistability. a The figure depicts the phase portrait of $\dot{J}$ vs J (solid black line) for three distinct levels of the input stimulus, I. Blue dots with full and open centres denote stable and unstable fixed points. The units of J and I are in $\mu$M. b Single parameter saddle-node bifurcation diagram of response A showing stable (black line) and unstable (red lines) steady states. Bifurcations occurs at points $L_1$ and $L_2$. The feedback strength ($k_5$) used to generate figures (a) and (b) is 0.075 $\mu$M min${}^{-1}$ and the other parameters are given in Table 1

Robustness of bistability

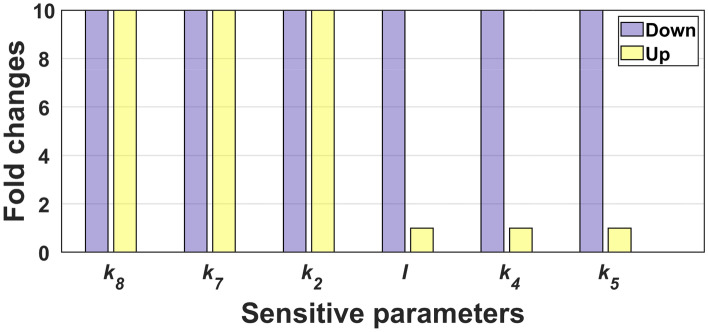
The observed bistability is robust if the sensitive parameters are varied and maintained bistability. So, to calculate the robustness of the bistability, we varied each sensitive parameter ten folds up and down from their basal values and evaluated their bistable region. The basal parameter values correspond to the parameters given in Table 1 with $I=0.026$ $\mu$M. We can see from Fig. 5, that the parameters $k_2,k_7,k_8$ can maintain bistability for the entire range of their variations. The other parameters $k_4,k_5$, and I retain bistability for the entire range when they are decreased. Thus, we could conclude that the bistability in the system is robust.

Fig. 5.

Robustness analysis. The figure shows the robustness of the sensitive parameters towards the maintenance of bistability. Each bar in this diagram indicates a parameter range in fold change from its basal values where the system is bistable. The basal value for I is 0.026 $\mu$M, and the rest of the parameters are given in Table 1

Bistability determines cell’s fate: survival or death

The robustness analysis of the sensitive parameters shows that the system exhibits bistability for a wide range of parameters. This motivates us to look for the significance of bistability. In the bistable region (shaded region in Fig. 6), the two stable steady states attained by the output of the system are termed as the lower steady state (LSS) for low value of A and an upper steady state (USS) for high value of A. That means in LSS, the apoptotic complex concentration or the caspase concentration is low, and the cell goes to survival. In USS, the caspase concentration is high, and the cell goes to apoptosis. Hence, LSS signifies cell survivability, and USS represents cell death (see Fig. 6). Similar considerations were also made by Bagci et al. [23]. Beyond this bistable range, the system is monostable, i.e. only one stable steady state exists. In this monostable range, the caspase concentration is either high or low. So, the cell can go only in one direction: survival or death.

Fig. 6.

Hysteresis: the hallmark of bistability. a The figure depicts the reversible hysteresis in the system. b Here the figure shows the irreversible hysteresis in the system. In both figures, the shaded region refers to the bistable region. The feedback parameter strength for reversible hysteresis (a) is $k_5$ = 0.075 $\mu$M min${}^{-1}$ and for irreversible hysteresis (b) is $k_5$ = 0.085 $\mu$M min${}^{-1}$. Table 1 gives all the other parameters

One of the hallmark of bistability is the existence of hysteresis, i.e. the system’s output becomes a loop rather than a curve [32]. This hysteresis can be of two types: reversible (see Fig. 6a) and irreversible (see Fig. 6b). In reversible hysteresis, the system can come back to its previous steady state only by changing the input stimulus (Fig. 6a), whereas in irreversible hysteresis, it can not (Fig. 6b) [32]. The nature of hysteresis depends on the strength of the feedback parameter [32, 53]. The change of qualitative behaviour of the response curve when we change the feedback strength is depicted in Fig. 7. With a low feedback strength ($k_5$ = 0.04 $\mu$M min${}^{-1}$) the response is a smooth curve. When $k_5$ is gradually raised to 0.06 $\mu$M min${}^{-1}$, it becomes sigmoidal (but still monostable). Upon further increasing the feedback strength to 0.07 $\mu$M min${}^{-1}$, the response splits into two curves and becomes bistable. And the system shows reversible hysteresis for $k_5$ = 0.07 $\mu$M min${}^{-1}$ and 0.08 $\mu$M min${}^{-1}$. Eventually, when the feedback becomes too large ($k_5$ = 0.09 $\mu$M min${}^{-1}$), the response shows irreversible hysteresis. The system can retain its current state through this hysteresis even when the input concentration is varied. Hence, this hysteresis makes the system robust against fluctuations in the input stimuli.

Fig. 7.

Response and feedback strength. The figure depicts the change of response curve upon changing the feedback strength ($k_5$). The response is a smooth curve when the feedback strength is low ($k_5$ = 0.04 $\mu$M min${}^{-1}$). It becomes sigmoidal when $k_5$ is increased slowly to 0.06 $\mu$M min${}^{-1}$ (but still monostable). Upon further increasing, the response curve splits into two curves and becomes bistable at $k_5$ = 0.07 $\mu$M min${}^{-1}$ and it shows reversible hysteresis for $k_5$ = 0.07 $\mu$M min${}^{-1}$ and 0.08 $\mu$M min${}^{-1}$. Eventually, the curve shows irreversible hysteresis when $k_5$ is 0.09 $\mu$M min${}^{-1}$. In this figure the blue line curves (with $k_5$ = 0.04 $\mu$M min${}^{-1}$) are included for comparison. Rest of the parameter values are given in Table 1

TNF concentration regulates cell death

The diverse pattern of Treg frequency observed in various autoimmune diseases may result from bistable caspase concentrations in the Treg system. That is, two systems with similar parametric conditions can attain opposite outputs. That means for equal concentrations of TNF, one system can achieve the survival state, whereas in the other case, it can go to apoptosis. To fully comprehend the mechanism, we have considered three different autoimmune diseases: inflammatory bowel disease (IBD), rheumatoid arthritis (RA) and systemic lupus erythematosus (SLE). In the case of IBD and SLE subjects, a decrease in Tregs number is observed in peripheral blood [4, 54]. However, in the case of RA, contradictory observations are reported that the number of Tregs in the peripheral blood increase, unchanged, or decreases [10]. However, a more precise analysis shows that the number of Tregs in peripheral blood decreases [10]. It suggests that the death of Tregs can mark the onset of the diseases. Thus, the USS in Fig. 6 could be defined as the disease state which marks the death of Tregs due to higher caspase concentrations. In the case of reversible hysteresis (Fig. 6a), the system will attain the USS when the TNF concentration is high, which means higher TNF concentration implies a high apoptosis rate of Tregs and can be reversed by reducing the TNF concentration. Similar observations are also reported in the literature that the serum TNF concentration is elevated in IBD [55], RA [56, 57] and SLE [58, 59] patients. The viability of the hypothesis can be examined by comparing the mathematical results with existing literature. Through our model, we observe that the system could be reversed, i.e. can change the stable steady states by reducing the TNF concentrations in the system. Veltkamp et al. [60] demonstrated that patients with active IBD showed more local CD4(+)Foxp3(+) Treg cell apoptosis in the inflamed mucosa than non-inflamed control colon tissue. In addition, there was a decrease in the frequency of Treg cells and an increase in their apoptosis, accompanied by increased caspase activity in the serum. They observed that anti-TNF therapy reduced Treg cell death with increased peripheral Treg cell numbers, in tandem with a decrease in caspase activation, and disease activity. These data suggest that the onset of IBD is marked by increased apoptosis of the Tregs and can be reversed by anti-TNF treatment, i.e. by reducing the TNF concentration, thus, validating our hypothesis. Similar kinds of narratives are reported in the literature for RA and SLE. When TNF antagonists were used to treat RA patients, they showed marked improvement of the disease symptoms [61]. In the case of SLE, an open-label reported that anti-TNF therapy suppresses the local tissue destruction [62]. These findings suggest that we can explain the complex mechanism of cell survival and death in Treg cells through bistable switching. Furthermore, by reducing TNF concentration, the system can be reversed.

A major factor that controls the nature of hysteresis is the feedback strength of the system. We can revert the system to its previous steady state if it is in reversible hysteresis. So, along with TNF concentration, we need to control the autoregulation of the JNK production to revert the system to the survival state. On the contrary, the increase in the feedback strength will make the system go to irreversible hysteresis. Then, even with the decrease in the TNF concentration, the disease state will persist. Thus, increased JNK activation will be associated with autoimmune patients. Related results have been reported that the increased JNK activation was associated with organ damage in SLE patients [63]. Similarly, increased phosphorylation of JNK was detected in inflamed joints of different animal models of RA and patients with autoimmune arthritis [64]. As JNK is autoregulated by its production [65]. Thus the inhibition of its activation can limit its rate. Administration of JNK specific inhibitors like SP600125 (anthra[1,9-cd]pyrazol-6(2H)-one), CC-930 improved symptoms related to autoimmune arthritis [64]. In our model, JNK is a function of TNF-TNFR2 concentration, which means a decrease in TNF indicates a decrease in TNF-TNFR2 formation, hence inferring a reduction in JNK production. Similar results were reported that in synovial samples from RA patients, immunological staining for JNK is reduced after anti-TNF therapy [64]. This evidence strongly suggests that the bistable mechanism of cell survival and apoptosis could be controlled. The system can be reverted to a survival state by reducing the TNF concentration.

Addition of randomness triggers loss of bistability

The effect of the inherent noise on the system’s bistability was studied through the stochastic model constructed on the deterministic system (1). The effect of stochasticity on the model system’s dynamics is depicted in Fig. 8. For a low value of noise, i.e. with the noise intensity ($\sigma$) below the critical value (${\sigma }_c$), the system shows slight deviation from its deterministic values, which means the system is stochastically stable (see left panel of Fig. 8a, b). With the noise intensity above the critical value, the time series shows significant deviations from its deterministic values, i.e., the system becomes stochastically unstable (see right panel of Fig. 8a, b).

Fig. 8.

Time evolution of TNF-TNFR2 and JNK in the presence of noise. At low noise intensity ($\sigma$ = 0.02), the time series of TR2 and JNK (see left panel of (a) and (b)) experience a little deviation from its deterministic curve (plotted in black). However, in case of high noise ($\sigma$ = 0.1), the system becomes stochastically unstable (see right panel of (a) and (b)). The parameters used are given in Table 1

It has been observed that the system may lose bistability in the presence of noise [32]. Thus, the system converges to one of the two stable steady states when noise intensity increases beyond the critical value [32]. In addition, the bistable properties of the model depend on the input parameter and the system’s feedback. So, to observe the effect of noise on the bistability of the system, we have calculated different stochastic stability regions when input is varied for different values of feedback strengths. In Fig. 9, the coloured regions of $\sigma -I$ plane depict the stochastically bistable (green), monostable (magenta) and unstable (yellow) regions. The system is stochastically bistable when the TNF concentration and noise intensity are low (the green region near the origin). However, with an increase in the noise value, the system becomes stochastically monostable (magenta). So, a deterministically bistable system may become monostable for high noise intensity. The system becomes stochastically unstable (yellow) with a further increase in the noise intensity, exceeding its critical value. When we gradually increase the value of TNF, the system shows a gradual decrease in $\sigma$ values for the stochastic bistable region. Beyond the bistable TNF concentration, the system attains stochastic monostability up to a certain $\sigma$ value, exceeding which, the system becomes stochastically unstable. This stochastic bistable region decreases as we gradually increase the feedback strength ($k_5$) of the system from 0.2 $\mu$M min${}^{-1}$ to 1 $\mu$M min${}^{-1}$. Thus, the bistable range of the input stimuli and the feedback parameter decreases when randomness is introduced to the system; hence the reversibility of the system is reduced.

Fig. 9.

Change of stochastic stability with variation in feedback strength: The figure depicts the change of stochastic stability of the equilibrium points with the variation of input stimulus (I) and the noise intensity ($\sigma$) for different values of feedback strength ($k_5$), as indicated in the plots. The unit of $k_5$ is $\mu$M min${}^{-1}$. The green, magenta and yellow coloured regions depict the stochastically bistable, monostable and unstable regions, respectively. The length of the X-axis in each figure refers to the deterministic bistability range of the input parameter for the feedback strength mentioned inside the figure. The rest of the calculation parameters are given in Table 1

Effect of saturated synthesis of S, J and A on model results

Although we have constructed a minimal model of the complex signalling system, which was further validated with experimental data and showed the emergence of complex behaviour like bistability, it would be interesting to check the change in the results with the introduction of additional non-linearity in the system. We used the saturated synthesis of S, J, and A. The new model also showed the existence of bistability. The new model and the parameter set are explained in Appendix D. GSA reveals similar results for the new and the old systems, see Fig. 10a. All the sensitive parameters of system (1) were also sensitive for system (17). In system (17) we obtained four additional sensitive parameters namely $k_6$, $d_1$, $k_{m2}$ and $k_{m4}$. The robustness of the sensitive parameters (see Fig. 10b) also remain same as observed for system (1), with the highly robust parameters remain highly robust and least robust parameters remain least robust. Thus, the addition of non-linearity to the system does not have a significant effect on the qualitative outcome of the study.

Fig. 10.

Global sensitivity analysis and robustness analysis. a The figure depicts the GSA of model parameters of model (17). Here, corresponding to every parameter, four different colour bars represent four state variables. And the sensitivity of each parameter is measured by the length of bars. b The figure shows the robustness of the sensitive parameters towards the maintenance of bistability. Each bar in this diagram indicates a parameter range in fold change from its basal value where the system is bistable. The basal values for the parameters are $T=0.026$, $k_5=0.075$, $k_{m2}=0.04$, $k_{m4}=0.6940$ and $k_{m7}=0.0053$ and the other parameters are mentioned in Table 1

Discussion

Immunological homeostasis of the body is maintained by a special subset of T cells known as Treg cells. They can influence immunological tolerance in an antigen-specific manner or by bystander suppression [3]. In bystander suppression of Tregs, TNF plays an important role, initiating the signalling by binding to its two receptors, TNFR1 and TNFR2. Generally, TNFR1 sends the signal for apoptosis, whereas TNFR2 signalling can lead to both survival and apoptosis [11]. Defects in TNFR2 signalling are prominent in many autoimmune diseases [11]. The contrasting patterns of Treg cell frequency have also been observed in different autoimmune diseases [4–8]. Thus, the similarity of TNFR2 signalling defects and abnormalities in Treg cell frequency in autoimmune diseases motivates us to study the mechanism of cell survival and cell death through TNFR2 signalling. To unravel the underlying mechanism of Treg cell survivability, we have constructed a theoretical model of TNFR2 signalling. We have formulated an ODE-based model to study the mechanism of cell survival and cell death in Treg cells. The proposed ODE model successfully reproduces the saturation kinetics for the TNF-TNFR2 formation as described by Grell et al. [38]. It also reproduces the sigmoidal JNK curve as reported by Bagowski et al. [43, 44]. It generates a response of apoptosis concentration in the ${10}^{-5}$ $\mu$M range as reported by Bagci et al. [23]. Thus, the model is validated by generating these important biological facets of the system.

The global sensitivity analysis reveals that six of fourteen model parameters are sensitive to the system’s output. Out of these six parameters, only the input parameter (I) is sensitive to all the state variables. The presence of feedback in the system satisfies the necessary condition for the existence of bistability [32]. JNK also exhibits graded responses for various stimuli [43, 44]. These pieces of evidence inspire us to study the present system for the existence of bistability. Initially, bistability is observed when we decrease the input TNF concentration. The robustness analysis of the sensitive parameters showed that the model could maintain this bistability for a wide range of parameter variations. Thus, the deterministic model can generate a graded response for significant variations of parameters. However, the system can exhibit different bistable behaviour when we alter the feedback strength of the system [52]. When the system’s feedback is modulated, the bistable curve becomes a loop called hysteresis [32]. Depending on the feedback strength, the system can have two types of hysteresis, reversible and irreversible [52]. In reversible hysteresis, the system can be reverted by reducing the input stimulus of the system, but not in the case of irreversible hysteresis [32]. Through this bistability, we can explain the complex behaviour of cell survival and cell death in Treg cells. Thus, the observed bistability can explain the diverse patterns related to Treg cell survivability observed in autoimmune diseases.

We have considered three different autoimmune diseases to understand the mechanism clearly: IBD, RA and SLE. These diseases are marked by the decrease in the number of the Tregs in the peripheral blood [4, 10, 54]. The death of Treg is characterised by high caspase concentration [23]. This evidence suggests that the increase of caspase is high in the autoimmune state. Our model reveals that the system can be reverted by reducing the TNF concentration in the system. This hypothesis is validated by the fact that the patients with these diseases have shown marked improvement with the anti-TNF therapy [60–62]. Thus, when the TNF concentration is reduced, the caspase concentration of the system can be decreased. Another factor that determines the output of the system is the feedback strength of the system. This feedback strength decides the type of hysteresis the system will show [52]. In reversible hysteresis, we can revert the system to its previous state [32]. Here, the feedback is defined by the autoregulation of the JNK; that is, it can enhance its production [65]. Thus, inhibition of JNK would limit its production. Similar observations were made when inhibitors of JNK were used to treat RA patients, and they showed marked improvements in the symptoms related to RA [64]. As JNK is a function of TNF-TNFR2, a reduction in the TNF would reduce the production of JNK. Similar stories were reported that anti-TNF therapy showed a decrease of JNK in synovial samples of RA patients [64]. This evidence cements our hypothesis that the bistability in the system regulates cell survival and apoptosis in Treg cells and can be controlled by reducing the TNF concentration.

Finally, our study incorporated inherent noise through a SDE-based model. We have shown that the presence of noise in the system can reduce the bistable parameter region of the system. Thus, the reversibility of the output is reduced due to the presence of randomness in the system. Before we wrap up the article, we would like to point out that the current study offers intriguing theories that may require more investigation. Although we did not include intermediate molecules in our model, this circuit quantitatively captured the realistic mechanism of TNFR2 signalling. We think the promise in the current work will also give experimental biologists some fresh ideas to investigate TNF treatment.

Appendix A. Proof of positive invariance and boundedness

A.1 Positive invariance

From the first equation of (1), we have

$$\begin{array}{cc}\hfill TR2(t)=& TR{2}_0{e}^{-d_{1}t}+\frac{k_{1}I}{d_1}\left[1,-,e^{-d_{1}t}\right]\hfill \\ \hfill & -k_1{k}_{m1}I{e}^{-d_{1}t}{\int }_0^t\left\{\frac{e^{d_{1}s}}{k_{m1}+1-TR2(s)}\right\}ds\hfill \end{array}$$

It implies that $TR2(t)\ge 0$ for all $t>0$ as $TR{2}_0>0$.

Similarly, from the third equation of (1)

$$\begin{array}{cc}\hfill J(t)=& J_0{e}^{-d_{3}t}+\frac{k_5}{d_3}\left[1,-,e^{-d_{3}t}\right]\hfill \\ \hfill & +e^{-d_{3}t}{\int }_0^t\left\{k_4,T,R,2,(s),-,\frac{k_5{k}_6^2}{k_6^2+J{(s)}^2}\right\}{e}^{d_{3}s}ds\hfill \end{array}$$

Since TR2(t) is positive, then J(t) remains non-negative for all $t>0$ provided $J_0>0$.

Also, we have

$$\begin{array}{c}\hfill S(t)=S_0{e}^{-d_{2}t}+e^{-d_{2}t}{\int }_0^t\left\{k_2,T,R,2,(s),+,k_3,J,(s)\right\}{e}^{d_{2}s}ds\end{array}$$

Since TR2(t) and J(t) both are positive, then S(t) remains non-negative for all $t>0$ provided $S_0>0$.

Following similar arguments, we have

$$\begin{array}{c}\hfill A(t)=A_0{e}^{-d_{4}t}+e^{-d_{4}t}{\int }_0^t\left\{k_7,J,(s),-,k_8,S,(s),A,(s)\right\}{e}^{d_{4}s}ds\end{array}$$

Since J(t) and S(t) both are positive, then A(t) remains non-negative for all $t>0$ provided $A_0>0$. Thus, all solutions of (1) satisfying the initial condition (2) are positively invariant. This completes the proof.

A.2 Boundedness

From the first equation of system (1), we can write

$$\begin{array}{c}\hfill \frac{dTR2}{\mathit{dt}}+d_{1}TR2\le k_{1}I\end{array}$$

where $k_{1}I$ is the maximum of $\frac{k_{1}I(1-TR2)}{k_{m1}+(1-TR2)}$. Thus, following [66], we have $TR2(t)\le \frac{k_{1}I}{d_1}$ as $t\to \infty$.

From the third equation of system (1), we can write

$$\begin{array}{c}\hfill \frac{\mathit{dJ}}{\mathit{dt}}+d_{3}J\le k_4\frac{k_{1}I}{d_1}+k_5\end{array}$$

where $\frac{k_{1}I}{d_1}$ is the maximum of TR2(t) and $k_5$ is the maximum of $\frac{k_5{J}^2}{k_6^2+J^2}$. Thus, following [66], we have $J(t)\le \frac{1}{d_3}\left(k_4,\frac{k_{1}I}{d_1},+,k_5\right)$ as $t\to \infty$.

Using the second equation, we have

$$\begin{array}{c}\hfill \frac{\mathit{dS}}{\mathit{dt}}+d_{2}S\le k_2\frac{k_{1}I}{d_1}+\frac{k_3}{d_3}\left(k_4,\frac{k_{1}I}{d_1},+,k_5\right)\end{array}$$

giving $S(t)\le \frac{1}{d_2}\left\{k_2,\frac{k_{1}I}{d_1},+,\frac{k_3}{d_3},\left(k_4,\frac{k_{1}I}{d_1},+,k_5\right)\right\}$ as $t\to \infty$.

From the fourth equation, we get

$$\begin{array}{c}\hfill \frac{\mathit{dA}}{\mathit{dt}}+(d_4+k_8\alpha )A\le \frac{k_7}{d_3}\left(k_4,\frac{k_{1}I}{d_1},+,k_5\right)\end{array}$$

where $\alpha$ is the minimum of S(t). Thus, following [66], we have $A(t)\le \frac{k_7}{d_3(d_4+k_8\alpha )}\left(k_4,\frac{k_{1}I}{d_1},+,k_5\right)$ as $t\to \infty$.

Hence all solutions of system (1) with initial condition (2) are ultimately bounded within the region $\mathrm{\Gamma }$, where

$$\begin{array}{c}\hfill \begin{array}{c}\mathrm{\Gamma }=\{(TR2,S,J,A)ϵR_{+}^4:0<TR2(t)\le \frac{k_{1}I}{d_1},0<S(t)\le {\mathrm{\Omega }}_1,\\ 0<J(t)\le \frac{1}{d_3}\left(k_4,\frac{k_{1}I}{d_1},+,k_5\right),0<A(t)\le \frac{k_7\left(k_4,\frac{k_{1}I}{d_1},+,k_5\right)}{d_3(d_4+k_8\alpha )}\},\end{array}\end{array}$$

${\mathrm{\Omega }}_1=\frac{1}{d_2}\left\{k_2,\frac{k_{1}I}{d_1},+,\frac{k_3}{d_3},\left(k_4,\frac{k_{1}I}{d_1},+,k_5\right)\right\}$ and $\alpha$ is the minimum of S(t). This completes the proof.

Appendix B. Proof of Theorem 2

Proof

Let us consider the Lyapunov function

$$\begin{array}{cc}\hfill V(U(t))=& \frac{1}{2}[{\omega }_1{(U_1+U_2)}^2+{U_2}^2+{\omega }_2{(U_1+U_3)}^2\hfill \\ \hfill & +{\omega }_3{(U_2-U_4)}^2+{\omega }_4{(U_1+U_4)}^2]\hfill \end{array}$$ 15

It is easy to check the inequalities in (10) are true for $\alpha =2$.

Next, using (9) and (12),

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill LV(U(t))=& \left(-,P_{11},+,\frac{1}{2},({\omega }_1+{\omega }_2+{\omega }_4),{{\sigma }_1}^2\right){U_1}^2+\left(-,P_{22},+,\frac{1}{2},({\omega }_1+1),{{\sigma }_2}^2\right){U_2}^2\hfill \\ \hfill & +\left(-,a_{33},+,\frac{1}{2},{{\sigma }_3}^2\right){\omega }_2{U_3}^2+\left(-,a_{44},+,\frac{1}{2},{{\sigma }_4}^2\right)({\omega }_3+{\omega }_4+{\omega }_5){U_4}^2\hfill \\ \hfill & +k_7\left({\omega }_3,+,{\omega }_4,+,{\omega }_5\right)U_3{U}_4\hfill \\ \hfill & =-U^{T}QU\hfill \end{array}\end{array}$$ 16

where

$$\begin{array}{c}\hfill Q=\left[\begin{array}{cccc}{H}_{11}& 0& 0& 0\\ 0& H_{22}& 0& 0\\ 0& 0& H_{33}& \frac{1}{2}{k}_7({\omega }_3+{\omega }_4+{\omega }_5)\\ 0& 0& \frac{1}{2}{k}_7({\omega }_3+{\omega }_4+{\omega }_5)& H_{44}\end{array}\right],\end{array}$$

and

$$\begin{array}{c}\hfill \begin{array}{c}{H}_{11}=P_{11}-\frac{1}{2}({\omega }_1+{\omega }_2+{\omega }_4){{\sigma }_1}^2,H_{22}=P_{22}-\frac{1}{2}({\omega }_1+1){{\sigma }_2}^2,\hfill \\ H_{33}=\left(a_{33},-,\frac{1}{2},{{\sigma }_3}^2\right){\omega }_2,H_{44}=\left(a_{44},-,\frac{1}{2},{{\sigma }_4}^2\right)({\omega }_3+{\omega }_4+{\omega }_5).\hfill \end{array}\end{array}$$

The relation (13) and (14) imply that Q is a real symmetric positive definite matrix and therefore all its eigenvalues ${\lambda }_i(Q)$, $i=1,2,3,4$ are positive real numbers. Let ${\lambda }_m=min\{{\lambda }_i(Q),i=1,2,3,4\},{\lambda }_m>0$. From (16), we get

$$\begin{array}{c}\hfill LV(U(t))\le -{\lambda }_m{|U(t)|}^2.\end{array}$$

If the conditions in Theorem 2 hold, then the zero solutions of the system (8) are exponentially mean-square stable.

Hence the proof.

Appendix C. Summary of parameter estimation and data collection from literature

TNF-TNFR2 association kinetics data:. Grell et al. [38] conducted their experiment using $4\times {10}^5$ KYM-1 cells in a volume of 150 $\mu$l. The average number of TNFR2 is approximately 30,000 per cell. Thus, the initial concentration of TNFR2 is $13.2\times {10}^{-5}$ $\mu$M.

Numerical value of $k_1$:. From Grell et al. [38], the association rate of TNF-TNFR2 is 1.49 min${}^{-1}$.

Numerical value of $k_{m1}$:. From Lang et al. [51], the half-saturation constant of TNF-TNFR2 formation is 0.42 $\times$ ${10}^{-3}$ $\mu$M.

Numerical values of $k_2,k_8,d_2$ and $d_4$:. From Chignola et al. [17], the activation rate of survival complex by TNF-TNFR2 complex ($k_2$) is between [0.016, 0.3] min${}^{-1}$, the caspase inhibition rate ($k_8$) is between [2.2 $\times$ ${10}^3$, 4.5 $\times$ ${10}^4$] $\mu$M${}^{-1}$min${}^{-1}$, the degradation rate of survival complex ($d_2$) and death complex ($d_4$) lie in the interval [0.0014, 0.003] min${}^{-1}$.

Appendix D. Model with saturated synthesis of S, J and A

Model formulation:. The mathematical model (1) was modified by considering non-linear synthesis of three state variables S, J, and A. In place of linear synthesis of S, J, and A in model (1), we have considered saturated synthesis of S, J, and A as we used for the formation of TR2. The modified mathematical model is given below:

$$\begin{array}{c}\hfill \begin{array}{c}\frac{d[TR2]}{\mathit{dt}}=\frac{k_{1}I(1-[TR2])}{k_{m1}+(1-[TR2])}-d_1[TR2],\hfill \\ \frac{d[S]}{\mathit{dt}}=\frac{k_2[TR2](1-[S])}{k_{m2}+(1-[S])}+k_3[J]-d_2[S],\hfill \\ \frac{d[J]}{\mathit{dt}}=\frac{k_4[TR2](1-[J])}{k_{m4}+(1-[J])}+\frac{k_5{[J]}^2}{k_6^2+{[J]}^2}-d_3[J],\hfill \\ \frac{d[A]}{\mathit{dt}}=\frac{k_7[J](1-[A])}{k_{m7}+(1-[A])}-k_8[S][A]-d_4[A],\hfill \end{array}\end{array}$$ 17

with initial conditions

$$\begin{array}{c}\hfill TR2(0)=TR{2}_0>0,S(0)=S_0>0,J(0)=J_0>0,A(0)=A_0>0.\end{array}$$ 18

We performed numerical analysis with the parameters from Table 1 and seek for bistability. Bistability was obtained for the parameters $T=0.026$, $k_5=0.075$, $k_{m2}=0.04$, $k_{m4}=0.6940$ and $k_{m7}=0.0053$ and the other parameters are mentioned in Table 1. The units of $k_{m2}$, $k_{m4}$ and $k_{m7}$ are in $\mu$M.

Author contribution

S.C. conceived the study. S.H. performed the analysis. S.H. and S.C. interpreted the results and wrote the manuscript.

Funding

The work is supported by SERB (Govt. of India) under MATRICS Scheme, Ref No. MTR/2018/000791. Research of SH is supported by CSIR (Govt. of India), File No.: 09/1049(0032)/2018-EMR-I.

Data availability

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.

Declarations

Ethical approval

This work is purely theoretical and does not require any ethical approval.

Informed consent

This work does not involve any human experimentation that would require informed consent.

Conflict of interest

The authors declare no competing interests.