Abstract
Background
The bidirectional brain-machine interfaces algorithms are machines that decode neural response in order to control the external device and encode position of artificial limb to proper electrical stimulation, so that the interface between brain and machine closes. Most BMI researchers typically consider four basic elements: recording technology to extract brain activity, decoding algorithm to translate brain activity to the predicted movement of the external device, external device (prosthetic limb such as a robotic arm), and encoding interface to convert the motion of the external machine to set of the electrical stimulation of the brain.
New method
In this paper, we develop a novel approach for bidirectional brain-machine interface (BMI). First, we propose a neural network model for sensory cortex (S1) connected to the neural network model of motor cortex (M1) considering the topographic mapping between S1 and M1. We use 4-box model in S1 and 4-box in M1 so that each box contains 500 neurons. Individual boxes include inhibitory and excitatory neurons and synapses. Next, we develop a new BMI algorithm based on neural activity. The main concept of this BMI algorithm is to close the loop between brain and mechaical external device.
Results
The sensory interface as encoding algorithm convert the location of the external device (artificial limb) into the electrical stimulation which excite the S1 model. The motor interface as decoding algorithm convert neural recordings from the M1 model into a force which causes the movement of the external device. We present the simulation results for the on line BMI which means that there is a real time information exchange between 9 boxes and 4 boxes of S1-M1 network model and the external device. Also, off line information exchange between brain of five anesthetized rats and externnal device was performed. The proposed BMI algorithm has succeeded in controlling the movement of the mechanical arm towards the target area on simulation and experimental data, so that the BMI algorithm shows acceptable WTPE and the average number of iterations of the algorithm in reaching artificial limb to the target region.
Comparison with existing methods and Conclusions: In order to confirm the simulation results the 9-box model of S1-M1 network was developed and the valid “spike train” algorithm, which has good results on real data, is used to compare the performance accuracy of the proposed BMI algorithm versus “spike train” algorithm on simulation and off line experimental data of anesthetized rats. Quantitative and qualitative results confirm the proper performance of the proposed algorithm compared to algorithm “spike train” on simulations and experimental data.
Keywords: Full closed loop brain machine interface, Neural activity, Encoding algorithm (sensory interface), Decoding algorithm (motor interface), LFP
1. Introduction
In recent years, researcher have been focused on the development of brain-machine interface algorithms, in most of these algorithms, the recorded activity from the motor cortical have been used to control the external object in human and non-human subjects [1]. BMIs are tools that have the potential to achieve two main goals by establishing a bidirectional interaction between the brain and world. The first goal is to restore movement ability or eliminate neurological disabilities in people who have lost them due to disease or injury. The second goal is to achieve a deeper understanding of the information processing approach in the nervous system [2,3]. The first realizations of BMIs simply decoded the recorded neural activity (e.g. from motor cortex) and translated it into commands for controlling an external device (e.g. a robotic arm). These decoding-based BMIs have the limitation that they require users to keep a constant focus of attention on the execution of a detailed motor command, and that they do not directly sense non-visual information relevant to the task (i.e. non-kinematic information, such as weight or rigidity of a manipulated object) [4,5]. These problems are boosting research towards bidirectional BMIs, which, in addition to decoding neural activity and translating it into a desired action, also provide the brain with external information relevant to the progress of the action in the form of electrical excitation of the neural tissue [[6], [7], [8]].
Neurophysiologists are still investigating the properties of neural recordings and are still carrying out basic research on the processing methods that are best suited for extracting information from the neural recordings [2]. In particular, the development of efficient decoding interfaces is crucial to interpret and execute actions expressed by activity of motor or pre-motor areas, whereas artificial sensory channels are crucial both to restore sensory function and to provide a real-time feedback which can replace the tactile or proprioceptive signals necessary for motor tasks. A more fundamental goal in restoring motor functions in people with paralysis requires establishing a real two way interaction between the brain and the artificial limb which implements both of these components that are necessary for essentially all tasks in everyday life. Moreover, work towards this goal will significantly increase our understanding of how the brain processes information, which is fundamental to all progress in clinical and basic neuroscience.
Approaches to record neural activity in recent years in brain-machine interface projects include implanting electrode arrays in the cortex, where spikes and local field potentials (LFP) are extracted from neurons. LFP is obtained by applying a low-pass filter with a cutoff frequency of less than 300 Hz on the extracellular potential, which represents the neural activity around the electrode [9].
The concept of bidirectional brain machine interfaces has been studied by Fetz [7,10,11]. Fig. 1 shows the bidirectional (full closed-loop) BMI.
Fig. 1.
The full closed-loop BMI. The motor interface decodes neural response into the desired force and sensory interface encode position of artificial limb to appropriate stimulation current.
The encoding part of the BMI algorithm translates the location of the external device into the stimulation applied to the sensory area. On the motor side, the decoding part converts the neural activity of motor cortex into the force which can direct the external device to the designated target. In fact, the motor interface transforms neural activity into a motive force used to drive the external system. In this study, it is assumed that a simple model and algorithm of the brain and BMI is enough to control the mechanical arm using neural signals, although the brain has complex dynamics and learning with the ability to change the force field. Here we propose a structure that creates a closed loop interaction between sensory and motor cortex in a procedure that follows the arbitrary force-fields (here is the control of the trajectories in a viscous medium toward a target region as center) through the calibration trials.
In this research, we address the full closed-loop BMI from a modeling and experimental point of view. We begin by simulating the primary somatosensory cortex (S1) and vibrissal motor cortex (M1) with a population of excitatory and inhibitory neurons ad synapses which model a local cortical population. The model used for both S1-M1 is a 4-box (9-box) model with a distant dependent connectivity among boxes. Individual box is composed of 400 pyramidal neurons and 100 interneurons. Then, by considering the topographic mapping, the S1-M1 spiking neural network is developed. In this way, it is supposed that one micro wire array delivers the micro stimulation to the S1 model and the second micro wire array records the neural signals from M1 model. Next, a novel LFP-based BMI algorithm based on computing the power spectrum in the gamma band (60–90 Hz) is introduced to control the motion state of a simulated trajectories in a viscous medium toward a target region. The results of model simulations and experimental data show that the proposed algorithm through the real time sensory interface and decoding the recorded neural activity can guide the artificial limb towards a desired path.
All equations have been solved with the Runge-Kutta algorithm with ms. S1-M1 network were simulated using Visual Studio software. Also, the simulations of BMI algorithms have been done in MATLAB software.
The different parts of the paper are organized in this way that Section 2 introduces the S1, M1 models to create a S1-M1 network. The BMI algorithm is explained in Section 3. The simulation results are discussed in Sections 4, 5 and Finally Section 7 concludes the paper.
2. Neural network model
In order to model the effect of stimulation of the sensory area and neural fluctuations of the motor area, a spiking network of neurons and excitatory and inhibitory synapses has been designed. In this Section, we first explain the network model that is used for Sensory cortex (S1), next the neural model of Motor cortex (M1) and then its connection to the S1 model are described.
2.1. The S1 network model
The S1 network model consists of spiking neurons with leaky integrate-and-fire model [12]. Fig. 2 (a) and Fig. 2 (b) show the main components and input of the network, respectively.
Fig. 2.
(a) The main components of the network which are interneurons, pyramidal neurons and excitatory and inhibitory synapses. (b) A time-varying rate of Poissonian spike trains as an input to network which average value is 1.2 spikes/ms.
The network model represents in a very simplified model of S1 and M1 cortex, and consists of spiking excitatory and inhibitory neurons with dynamical synapses. The connections of neurons in the network are formed randomly with a probability of 0.1. Synaptic activities are composed of AMPA currents (excitatory synaptic activities) and GABA currents (inhibitory synaptic activities). In order to simulate the activity from afferents, excitatory and inhibitory neural populations are excited using noisy external input.
We partition the S1 model into four boxes (2 by 2). Inside each box, there are 100 interneurons and 400 pyramidal neurons. So, the total number of neurons for 4-box model is 2000 neurons. The membrane potential of neuron k is formulated as follows:
| (1) |
where membrane time constant, excitatory (AMPA type) synaptic currents, and inhibitory (GABA-type) currents received by neuron k are denoted by τm (excitatory neurons = 20 ms, inhibitory neurons = 10 ms), IAk, IGk, respectively. In Eq. (1) the resting potential and threshold are considered zero and 18 mV, respectively (Mazzoni et al., 2008). Synaptic currents are obtained by subtracting the total activity of presynaptic excitatory neurons from activities of inhibitory neurons. The excitatory synaptic current as AMPA current () and inhibitory synaptic current as GABA current () are modeled using auxiliary equations xAk, xGk for AMPA and GABA current, respectively. The model of AMPA and GABA-type currents of neuron k formulate as follows:
| (2) |
| (3) |
| (4) |
| (5) |
All parameters are adapted from Ref. [12]. The external excitatory input by random Poisson spike trains (in the form of time varying rate) identically is fed to each excitatory and inhibitory neuron by the following equation:
| (6) |
Where the signal and noise are denoted by , and , respectively. A stochastic variable, n(t) based on Ornstein-Uhlenbeck process is defined in Eq. (7) as follows:
| (7) |
where is the noise standard deviation, and denotes a Gaussian white noise.
Individual boxes are connected with a function of the form: where K is a scaling factor and R is the distance between different boxes. The connectivity of the 2000 neurons (4-box model) and 4500 neurons (9-box model) is shown in Fig. 3(a) and (b), respectively.
Fig. 3.
The neuronal network which consists of population of pyramidal neurons and interneurons. Each box compos of 100 interneurons and 400 pyramidal neurons. The connectivity pattern creates by random connection between neurons with probability 0.1. The connectivity pattern among different boxes is a distant dependent function (a) 4-box model (b) 9-box model.
Because the firing activity of a single neuron is not regular, investigation of neural behavior is usually done with signals such as LFP, which represent the behavior of neurons population. Here, the absolute values of excitatory (AMPA) and inhibitory (GABA) current from pyramidal neurons are considered as LFP [13,14].
The structure of M1 network is similar to the S1 model and it is also composed of a population of interneurons and pyramidal neurons except that we slightly changed the parameters values to have two different models. For the 4-box S1 model, we developed the 4-box M1 model. Fig. 4 (a), (b) show the behavior of S1 network in the form of LFP in response to input stimulations 1.2 and 2 spikes/ms, respectively. Fig. 4 emphasizes that with the increase of the input spike rate, the level of network stimulation increases and a visible increase in the amplitude of the LFP signal is observed.
Fig. 4.
Dynamics of the box #3 of the 4-box S1 network with receiving different rates of the input signal (part a: 1.2 and part b: 2 spikes/ms). Each panel shows 400 ms simulation which is extracted from a 1 s time interval simulation.
2.2. The M1 network model
The M1 network model is similar to the S1 model and it is also composed of a population of interneurons and pyramidal neurons except that we slightly changed the parameters values to have two different models. Networks S1 and M1 should have similar behaviors but not exactly the same, because they are supposed to represent two different parts of the brain in the simulation. For this reason, different synaptic weights have been considered in network M1 than synaptic weights of network S1. While the time constants and other parameters of equations (1), (2), (3), (4), (5)) are the same for both networks.
For the 4-box S1 model, we developed the 4-box M1 model. Fig. 5 (a,b) shows the dynamics of the same box of Fig. 4 for the M1 network model.
Fig. 5.
Dynamics of the network in the form of LFP, box #3 of the 4-box M1 model with input signal rate of 1.2 spikes/ms (a) and 2 spikes/ms (b) that noise is added to the signal. The absolute values of excitatory (AMPA) and inhibitory (GABA) current from pyramidal neurons are considered as LFP.
2.3. S1-M1 network model
Some experimental observation proved that a focused activity in S1 causes similar activity in the same area as M1 [[15], [16], [17], [18]]. In order to simulate the similar situation, each box of the S1 is connected to the corresponding box of M1. This means that ith-box of S1 is connected to ith-box of M1. A connecting coefficient based on mean firing rate of pyramidal neurons of each box of S1 (K*<FR>PY) is added to the corresponding box of M1 as excitatory input. Therefore, Eq. (6) for ith-box of M1 is improved according to Eq. (8).
| (8) |
In the model, we assume that the excitation and recording electrodes have the same number and shape in the corresponding regions of S1 and M1. So that when a stimulus occurs in an area of S1, this stimulus is sensed at the corresponding recording electrode of M1, and this interaction is also observed in real data [16].
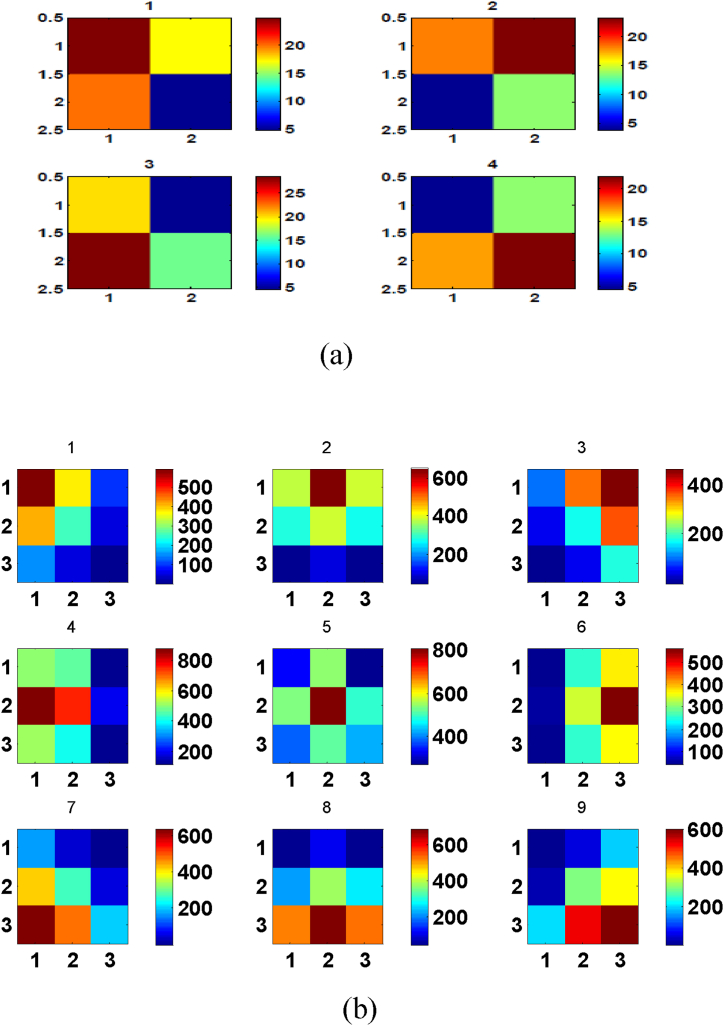
In the simulations, different scenarios of electrical stimuli were considered in encoding procedure of the sensory area. Different sets of stimulation are created by changing the location of the stimulation electrode between different boxes. It is assumed that both stimulating and recording electrodes are arranged in a 2*2 (9*9) grid. Due to a distant dependent connectivity among neurons in S1 and M1, stimulating 4 (9) different electrodes of S1, one by one, yields a gradient in the evoked spikes in M1.Considering Fig. 6 one can notify that the firing rate increases for that box of M1 corresponding to the stimulated box of S1 and there is a gradient in the recorded activities of M1 network for 4-box model (Fig. 6(a)) and 9-box model (Fig. 6(b)).
Fig. 6.
Topographical representation of the recorded spikes of 5 randomly selected neurons in individual boxes from M1 for one trial in the 4-box model (a) and 9-box model (b). The color plots show the average number of recorded spikes by recording electrodes in M1. Color scale represents the mean spike rate.
2.4. Model validation
To validate the S1-M1 network, we performed some in vivo experiments on anesthetized Long-Evans rats. We applied four different stimuli using array of electrodes placed on the S1 region, each of these stimuli applied 50 times separately, and then recorded the neural activities from the M1 using 16 electrodes arranged in 2*8 rectangular arrays. Since one electrode is a Reference electrode, we considered only the data from 15 electrodes. For individual trial, we compute the average neuronal firing rate () that is recorded by the 15 electrodes. Since each stimulus is repeated 50 times, we compute the and then compare this value with its counterpart of the S1-M1 network. It should be mentioned that since in real experiments we apply four different stimulus in S1, thus, in the S1-M1 network model, we use 4-box model for S1 and therefore 4-box model for M1. Then, we record 5 neurons from box 1, 4 neurons from box 2 and 3 neurons from box 3 and 4 neurons from box 4. Table 1 shows the comparison of the data recorded from the model and the experiments.
Table 1.
Comparison of the Experimental recorded data with the Model.
| Stimulus | Experimental data |
Model data |
||
|---|---|---|---|---|
| STD | STD | |||
| A | 1.1413 | 0.5487 | 1.0303 | 0.6007 |
| B | 0.6253 | 0.4058 | 0.7113 | 0.3638 |
| C | 0.2733 | 0.2459 | 0.3673 | 0.2944 |
| D | 0.9333 | 0.7742 | 0.9012 | 0.6034 |
Next, we perform two-sample t-test analysis. The results are summarized in Table 2. As Table 1, Table 2 show, the general behavior of the proposed S1-M1 network is similar to the recorded spiking activities.
Table 2.
The results of the t-test analysis for 50 trials of 4 different stimuli.
| Stimulus | two-sample t-test |
|
|---|---|---|
| H | P | |
| A | 0 | 0.4039 |
| B | 0 | 0.5854 |
| C | 0 | 0.3734 |
| D | 0 | 0.7702 |
This analysis show matching between real data and S1-M1 network data. Method is an approach to measure the difference in the average of two samples. Also, is a test to measure that two samples with unknown and equal standard deviations can have same mean. The result of this test is considered 1 in the case that hypothesis with alpha equal to 0.05 being rejected.
3. Basic of the full closed-loop BMI system
The full closed-loop BMI controls an external device using two way communication between motor and sensory interface. The encoding algorithm which called sensory interface encodes the position of the trajectories into the electrical stimulation to excite the S1 model. The motor interface as decoding algorithm uses the recorded LFP from the M1 model and decodes them into a force to move external device. Then the brain is aware of the new location of the artificial limb with the help of a sensory interface and produces a new motor response to guide the external device to the destination and the process continues until the artificial limb reaches the desired target.
The data used for calibration in the BMI algorithm is generated from a set of sensory cortex stimulation (S1 model) and the recorded LFP responses from the motor cortex (M1 model). These data are used to adjust the parameters of the sensory interface, and after the calibration is completed, the algorithm is tested by controlling external device based on the online information transfer between the S1-M1 network model and the external device through BMI algorithm. The algorithm calibrates the interface so that, the interface can follow a desired path through the desired force. The force field is a function, , expressing the desired force that will be applied to the external device when it is in position x. In this paper, we select the force field of Eq. (9).
| (9) |
This force field is shown in Fig. 7 and was designed to guide the external device toward a desired target position.
Fig. 7.
The force field in which can drive the mechanical system toward a goal (equilibrium state).
In fact Eq. (9) and Fig. 7 is the arbitrary force-fields, which the proposed full closed-loop BMI algorithm based on LFP through the calibration trials approximates this force.
The mechanical external system that its moving control by the interface can be simulated simply by a trajectory which moves towards the determined target location. This target location is considered as a region around the center of the field force balance. Each run of the system starts by placing the external device at location x0 with zero velocity. Then, the sensory interface calculates the appropriate electrical stimulation according to the position where the external device is located based on Eq. (10).
| (10) |
Where the center of the region of sensory and number of stimulus sets is denoted by and , respectively. Thus, sensory interface excites the S1 model by the stimulation current and the recorded neural response from M1 model decoded by the motor interface to produce force which causes the external device to move under the influence of this force and be placed in a new position x1. Again the loop continues. This loop continues until the external device reaches the designated target location or the number of repetition steps of the algorithm exceeds 70, which leads to the failure of the algorithm (non-convergent trajectory).
3.1. The LFP-based BMI algorithm
We assume that there is a set of electrical stimulus . From each of these M electrical stimulations, N neural response is recorded, which leads to the formation of the matrix with the dimensions of in Eq. (11).
| (11) |
Each response, is the LFP signal recorded from M1 in 600 ms time interval. Next, we compute LFP power spectrum and obtain the sum of the amplitude of power spectrum in the frequency range 60–90 Hz. In Fig. 8, we calculate statistical parameters mean and standard deviation of the “sum of the power spectrum amplitude of the recorded LFP in the gamma band” for 20 trials of stimulating S1 and recording M1 for the S1-M1 spiking network. For these simulations, we stimulate each box of S1 network 20 times with different noise realization and record LFP signal from individual boxes of M1 network of 4-box model (Fig. 8 (a)) and 9-box model (Fig. 8 (b)).
Fig. 8.
The sum of the amplitude of LFP power spectrum in the frequency range 60–90 Hz from individual boxes of M1 when we stimulate the S1-boxes one by one. It is observed the power spectrum of the recorded LFP of M1 for the same stimulated box of S1 has higher value.
In this way, we create an A matrix based on the LFP power spectrum in frequency interval 60–90 Hz based on Eq. (12).
| (12) |
Then, we compute the symmetric distance matrix by computing the Euclidean distances between each pair of observations in the -by- data matrix . Next, we apply multi-dimensional scaling (“mdscale” function in MATLAB) on the distance matrix, D (Eq. (13)), in order to create a set of two-dimensional points in the movement space of the artificial limb:
| (13) |
where change across the indexes of and , respectively. In order to set the movement space of the artificial limb in the desired dimensions, the obtained locations are multiplied by the factor according to Eq. (14).
| (14) |
Finally, to calculate the calibration center in each sensory region, we calculate the average spatial coordinates obtained for each area according to Eq. (15).
| (15) |
Utilizing, these M calibration centers and the nearest neighbor algorithm, we divide the movement space of the external device or the sensory interface into regions. Next, we utilize the LFP- based BMI algorithm to obtain the sensory region as shown in Fig. 9. Since we have 4 (9) stimuli and 20 trials, we will have 4 (9) sets (cluster of points) which contains 20 points which obtained by projecting the distance matrix, D, into in 2-dimensional space using MDS which is shown in Fig. 9(a) for 4-box model and Fig. 9(c) for 9-box model. Then, applying nearest neighbor algorithm, the sensory map is created which is shown in Fig. 9(b) for 4-box model and Fig. 9(d) for 9-box model. The calibration centers were showed as a square in data points and colored regions.
Fig. 9.
The obtained sensory region by using the proposed BMI algorithm. Here, we used a 4-box S1-M1 network (a–b) and 9-box S1-M1 (c–d) which each time we stimulated one box, 20 times with different noise realization and hence we get 4 (9) sets (cluster of points) which contains 20 points. (a,c) Projecting the distance matrix, D, into in 2-dimensional space using MDS and (b,d) show the obtained sensory regions based on nearest neighbor algorithm. The squares show the calibration centers.
In order to compare the sensory map created based on the proposed decoding algorithm (Fig. 9) with the valid decoding algorithm called “spike train” [2], the recorded data from S1-M1 model was calibrated and projected to the 2-dimensional space based on decoding algorithm “spike train” in Fig. 10 (a) for 4-box model and Fig. 10(c) for 9 box model. Also, the created sensory map for 4-box model and 9-box model is shown in Fig. 10(b)and (d), respectively.
Fig. 10.
The sensory map created by “spike train” decoding algorithm. (a,c) Represents projecting the distance matrix, D, into in 2-dimensional space for 4-box and 9-box model and (b,d) show the obtained sensory regions based on nearest neighbor algorithm for 4-box and 9-box model, respectively.
The within-class scatter matrix (SW) in Eq. (16) and between class scatter matrix (SB) in Eq. (17) define according to Eq. (18) which can show the effectiveness of the proposed algorithm in classifying data into separate classes.
| (16) |
| (17) |
| (18) |
The number of classes, number of samples in i-th class, the j-th sample in the i-th class, mean of samples in the i-th class and mean of all samples are denoted by c, ni, , mi, m, respectively.
In Table 3 we show CSM for simulation data. Large values of J are desirable because distance between-class is large and within-class is low.
Table 3.
CSM for simulation data.
| J for spike train Algorithm | J for LFP algorithm | |
|---|---|---|
| Simulation data with 4-box S1-M1 network | 0.972 | 2.1168 |
| Simulation data with 9-box S1-M1 network | 1.5074 | 2.044 |
3.2. The motor interface
The motor interface as decoding algorithm converts the recorded spike response from M1 into a force, which can drive the external device (mechanical arm) along the target region with the following dynamical equation.
| (19) |
Where, F is the force obtained from the neural response using motor interface, B = 13 N s/m is a force due to the viscosity, is the position of the trajectories as external device on a plane and M = 10 Kg is the device weight [2,3]. Eq. (19) was solved based on Runge-Kutta algorithm to calculate the new position x of external device after applying the force F.
To map current response into a force, we compute the distances of the recorded response from motor cortex (M1 model) with the neural response of the calibration experiments. These computed distances are placed in a matrix according to Eq. (20).
| (20) |
Following [2,3], we compute the average of the distances, , and then decode the stimulus in Eq. (21), whose the responses of calibration give the smallest mean of distance.
| (21) |
Finally, the force calculated to be applied to the artificial limb can be computed based on Eq. (22).
| (22) |
4. Results
As explained in the previous sections, we proposed 4-box and 9-box models for the S1-M1 network. Next, we explained the LFP BMI algorithm and also the sensory/motor interfaces (encoding/decoding parts) were described. Now, in this section, we want to use the BMI algorithm based on LFP to create the closed loop interaction between the external device and the S1-M1 network model.
As described, the motor interface decodes the recovered responses from the M1 model to the propulsive force of the external device, and the sensory interface encodes the new location of the mechanical arm to the stimulus applied to the S1 model. In this section, the online information exchange between S1-M1 network model and external device through the BMI algorithm is reported.
We test the BMI algorithm 16 times with 16 different starting points on the sensory plane. The external device is guided from the initial point x0 to the target area (white circle in Fig. 11) using the proposed BMI algorithm with the calibrated sensory interface of Fig. 8.
Fig. 11.
Performance of the on line BMI algorithms using LFP algorithm for 4-box model of S1-M1 network. Panel (a) shows trajectories generated by closed loop “LFP” algorithm and (b) indicates the step by step trajectories movement in the closed loop interaction between external device and S1-M1 network model.
The left panel of Fig. 11 shows the trajectories (denoted external device) of the system for the 4-box S1-M1 network model, starting from 16 different initial positions. The colored lines and black lines denoted trajectories generated by closed loop BMI algorithm and ideal trajectories, respectively. Also, the right panel of Fig. 11 indicates the step by step trajectories movement in the closed loop interaction between external device and S1-M1 network model. As it is evident, the BMI algorithm has succeeded in controlling the movement of the mechanical arm towards the target area. The simulation results presented in Fig. 11 have been repeated 10 times to show the robustness of the algorithm, and the results confirm the robustness of the closed loop BMI protocol. In order to quantify the performance accuracy of the algorithm in guiding the mechanical arm towards the target area, we introduced a criterion called Within-trajectory position error (WTPE) [3] which calculates the distance between ideal and actual trajectories in the left panel of Fig. 11. The WTPE parameter is obtained 3.9618 for 10 repetitions of BMI algorithm. Also, the average number of steps in reaching trajectories to the target region in 10 iterations of the algorithm is 26, which indicates the good performance of the closed loop BMI algorithm.
Also, In Fig. 12, the online information exchange between S1-M1 network model and external device through the “spike train” BMI algorithm is shown.
Fig. 12.
Performance of the on line BMI algorithms using the “spike train” algorithm for 4-box model of S1-M1 network.
The WTPE parameter is obtained 4.87 for 10 repetitions of “spike train” algorithm. Also, the average number of steps in reaching trajectories to the desired target area in 10 iterations of the algorithm is 34, which indicates the good performance of the LFP BMI algorithm compared to the valid BMI algorithm “spike train”. In order to compare the performance of the proposed BMI algorithm compared to “spike train” algorithm, the exchange of information to control the movement of the mechanical arm to the center using bidirectional interaction between the 9-box model of S1-M1 and the artificial arm is shown in Fig. 13 (a), (b) for “spike train” and “LFP” algorithms, respectively.
Fig. 13.
Performance of the on line BMI algorithms using the “spike train” (a) and “LFP” (b) algorithm for 9-box model of S1-M1 network.
It is evident that the proposed algorithm based on LFP was better than “spike train” algorithm in controlling an external device so that WTPE is 26 for “spike train” BMI algorithm and equal to 4.5 for “LFP” algorithm. Also, the average number of steps in reaching trajectories to the target region in 10 iterations of the “spike train” and “LFP” algorithms are equal to 31 and 23, respectively. Quantitative and qualitative results confirm the proper performance of the proposed algorithm compared to “spike train” algorithm, which is known as a validated algorithm on real data.
5. Discussion
The classical approach of the BMI algorithms includes recording electrodes to extract motor signal [19] and decoding neural response of motor in order to reveal moving target [20,21]. Although this approach has been successful [22], it does not consider sensory feedback in line with motor recording. In recent years, the creation of a closed loop between the brain and the external device to control its movement has received more attention [23]. Also, the possibility of using decoded signals from the motor cortex to directly stimulate the spinal cord in order to create movement in paralyzed limbs is one of the topics of interest in recent years [24]. Here, in order to establish a bridge between the two research paths, a non-linear and closed-loop approach of the brain-machine algorithm has been presented. The presented sensory and motor interface is based on two main points:
-
1
Two way communications of the brain and artificial limb is based on the decoding of information extracted from the motor cortex and converted into driving force, and then encoding the location of the external device to produce suitable sensory stimulation.
-
2
The simultaneous adjustment of the motor and sensor interface will lead to the production of the desired force field in arbitrary form.
In order to validate the performance and robustness of the “LFP” algorithm, in addition to comparing the performance of the proposed BMI approach with “spike train” algorithm which is a proven BMI algorithm, the results of the two algorithms have been tested and discussed on real data from anesthetized rats 1 to 5.
Next, we apply the proposed and “spike train” BMI algorithms on five experimental data sets. We applied 4 different stimuli (A,B,C,D) in each experiments. Five different experiments were done. For each experiment, we stimulated S1 region, 40 times with four different electrodes and then the spike response with 13 electrodes placed on M1 region has been recorded. Fig. 14 shows the results of the obtained sensory regions for the 40 trails of the five experiments. Because of applying four different stimuli, four sensory regions are also expected.
Fig. 14.
Show the sensory regions (panels a, b) and movement of the point mass (panel c) during off line running of the “spike train” algorithm (The first row of each Anesthetized rat) and LFP algorithm (The second row of each Anesthetized rat). The movement of point mass start from 16 different initial positions.
In Fig. 14, we run ten times the BMI systems (“LFP” and “spike train”) and show the results of running the BMI systems for the corresponding sensory regions. It should be pointed out that these results are offline. Indeed, we used 10 trials (besides to the 40 trails that were used to create the sensory regions) to test the performance the BMI systems.
Fig. 14 shows the sensory map and results of running BMI algorithms for experimental data of five anesthetized rats. It should be pointed out that these results are offline and we let the algorithm continue for a maximum of 80 iterations. Indeed, we divided the experimental data in two groups: one set to create the sensory map that have 40 trials or 160 tests and the second group is used to test the performance of the algorithm that have 10 trials (40 test).
In Table 4 CSM for five experimental data is denoted. As the results show, the LFP algorithm has been more successful than the spike train algorithm in separating the data classes.
Table 4.
CSM for five experimental data.
| J for spike train Algorithm | J for LFP algorithm | |
|---|---|---|
| Exprimental data 1 | 0.1001 | 0.1451 |
| Exprimental data 2 | 0.0947 | 0.0791 |
| Exprimental data 3 | 0.0859 | 0.1027 |
| Exprimental data 4 | 0.113 | 0.1125 |
| Exprimental data 5 | 0.1026 | 0.1066 |
Fig. 15 shows the robustness of algorithms based on wtpe parameter. As it is evident from the results of Fig. 15, the proposed algorithm has a better performance on real data compared to “spike train” algorithm.
Fig. 15.
Performance of the off line BMI algorithms (Alg.1: spike trains, Alg.2: the LFP) for anesthetized rat_1 (a) to anesthetized rat_5 (e) which has been indicated with wtpe parameter.
Also, the average steps to reach the target region in “spike train” and proposed BMI algorithm is shown in Table 5. The reported results in Table 5 also confirm the high computational ability of the proposed BMI algorithm.
Table 5.
The average step to reach the target region.
| Mean Number of step for Alg. Spike train | Mean Number of step for Alg. LFP | |
|---|---|---|
| Simulation data with 4-box S1-M1 network | 25 | 26 |
| Simulation data with 9-box S1-M1 network | 31 | 23 |
| Exprimental data 1 | 41 | 38 |
| Exprimental data 2 | 57 | 43 |
| Exprimental data 3 | 51 | 41 |
| Exprimental data 4 | 29 | 32 |
| Exprimental data 5 | 48 | 42 |
In general, although the full proof of the capability and potential of the proposed algorithm requires more tests on real data, the tests performed in this study confirm the computational capability of the proposed algorithm. Also, adding learning capability and STDP to the synapses of S1 and M1 networks can lead to improved performance of the proposed algorithm in approximating more complex force fields, which can be discussed in future studies.
6. Experimental set-up
In the process of experiment, 30 mg/kg and 5 mg/kg of Zoletil and Xylazine was used to anaesthetize rats, respectively. The experiment was done on male rats (Long-Evans) with weight of approximately 400 g. In order to minimize suffering of rats, supplementary doses of anesthetic was injected. The stereotaxic apparatus was used to place the anesthetized rats. A micro drill was placed on the primary sensory cortex (S1) and primary motor cortex (M1) to make a craniotomy. The stimulation array was placed in the parietal bone so that the barrel cortex could be visualized [[25], [26], [27]]. The stimulation arrays were placed vertically at a distance of 500 mm–900 mm from the pia and perpendicular to the cortex [[28], [29], [30]]. The recording array was placed in the frontal cortex so that the vibrissal representation could be visualized [26,[31], [32], [33], [34]]. Cathodic pulses with a pulse length of 200 ms with a minimum time interval of 2.5 s and a frequency of 300 Hz have been used to induce whisker twitches at a distance of 1.5 mm below the cortical surface. The intracortical microstimulation contained trains of 10 pulses with duration 100 ms with 150 mA amplitude and frequency of 333 Hz. The recording array was placed vertically in the cortex and the neural activity of the cells was recorded with a sampling frequency of 40 kHz in different channels. All experiments were followed the European Economic Community (EEC) in the field of animal protection (EEC Directive of 1986; 86/609/EEC) and Imam Reza Hospital Research Center approved the experiments of this study.
7. Conclusion
The last decade presented a significant increase in the development of brain-machine interfaces (BMIs) as assistive neural devices for paralysis patients. In the bidirectional BMI system, the motor interface as decoding algorithm translate recorded neural responses from the motor cortical to control an artificial limb. On the other hand, the sensory interface as encoding algorithm translates the location of artificial limb to electrical stimulation which excites the sensory region. In general, to implement a closed-loop BMI system in real world applications, an encoding, and decoding algorithm can be implemented by micro-stimulation techniques and neural activity recording, respectively. In this regard, we designed a bidirectional BMI by simultaneously controlling encoding and decoding interfaces. We modeled the primary somatosensory cortex (S1) and motor cortex (M1) as a population of inhibitory interneurons and excitatory pyramidal neurons with AMPA and GABA synapses. Next, these two networks were connected to create the S1-M1 network model and validated using experimental data. Then, the BMI algorithm based on LFP was proposed. In fact, the motor interface of BMI algorithm decoded the neural activity of the motor cortical (M1 model) into the motive force applied to the artificial limb in a viscous medium. The sensory interface encoded the location of the external mechanical device to the electrical stimulation that stimulates the somatosensory cortex (S1 model). Finally, we presented the results of applying the LFP algorithm, from the computational point of view, on the simulation data recorded from M1 in response to electrical stimulation of S1. In order to validate and confirm functional ability of “LFP” algorithm compared to the “spike train” algorithm as a proven BMI algorithm, in addition to 4-box and 9-box model of S1-M1 network, five experimental data sets also was considered in performance testing of BMI algorithms. Quantitative and qualitative results confirm the good performance of the proposed BMI algorithm compared to “spike train” algorithm, which is known as a validated algorithm on real data.
Author contribution statement
Masoud Amiri: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data.Amir Homayoun Jafari; Bahador Makkiabadi: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.Soheila Nazari: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability statement
Data will be made available on request.
Additional information
No additional information is available for this paper.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Contributor Information
Masoud Amiri, Email: masd.amiri@yahoo.com.
Soheila Nazari, Email: soheilanazari21@yahoo.com.
References
- 1.Tiwari N., Edla D.R., Dodia S., Bablani A. Brain computer interface: a comprehensive survey. Biologically inspired cognitive architectures. 2018;26:118–129. [Google Scholar]
- 2.Vato A., Semprini M., Maggiolini E., Szymanski F.D., Fadiga L., et al. Shaping the dynamics of a bidirectional neural interface. PLoS Comput. Biol. 2012;8:1–15. doi: 10.1371/journal.pcbi.1002578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Vato A., Szymanski F.D., Semprini M., Mussa-Ivaldi F.A., Panzeri S. vol. 9. 2014. pp. 1–20. (A Bidirectional Brain-Machine Interface Algorithm that Approximates Arbitrary Force-Fields PloS One). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gupta G., Pequito S., Bogdan P. ACM/IEEE 9th International Conference on Cyber-Physical Systems (ICCPS) IEEE; 2018. Re-thinking EEG-based non-invasive brain interfaces: modeling and analysis; pp. 275–286. 2018, April. [Google Scholar]
- 5.Gupta G., Pequito S., Bogdan P. 2019 American Control Conference (ACC) IEEE; 2019, July. Learning latent fractional dynamics with unknown unknowns; pp. 217–222. [Google Scholar]
- 6.Bonifazi P., Difato F., Massobrio P., Breschi G.L., Pasquale V., Levi T.…Chiappalone M. In vitro large-scale experimental and theoretical studies for the realization of bi-directional brain-prostheses. Front. Neural Circ. 2013;7 doi: 10.3389/fncir.2013.00040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jackson A., Fetz E.E. vol. 19. 2011. pp. 534–541. (Interfacing with the Computational Brain Neural Systems And Rehabilitation Engineering IEEE Transactions On). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Carmena J.M. vol. 11. 2013. pp. 1–4. (Advances in Neuroprosthetic Learning and Control PLoS Biology). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mehring C., Rickert J., Vaadia E., de Oliveira S.C., Aertsen A., Rotter S. Inference of hand movements from local field potentials in monkey motor cortex. Nat. Neurosci. 2003;6(12):1253–1254. doi: 10.1038/nn1158. [DOI] [PubMed] [Google Scholar]
- 10.Moritz C.T., Perlmutter S.I., Fetz E.E. Direct control of paralysed muscles by cortical neurons. Nature. 2008;456:639–642. doi: 10.1038/nature07418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mussa-Ivaldi F.A., Alford S.T., Chiappalone M., Fadiga L., Karniel A., Kositsky M.…Vato A. New perspectives on the dialogue between brains and machines. Front. Neurosci. 2010;4:44–52. doi: 10.3389/neuro.01.008.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mazzoni A., Panzeri S., Logothetis N.K., Brunel N. Encoding of naturalistic stimuli by local field potential spectra in networks of excitatory and inhibitory neurons. PLoS Comput. Biol. 2008;4:1–20. doi: 10.1371/journal.pcbi.1000239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.The underpinnings of the bold functional magnetic resonance imaging signal. J. Neurosci. 2003;23:3963–3971. doi: 10.1523/JNEUROSCI.23-10-03963.2003. Logothetis NK. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kamondi A., Acsadi L., Wang X.J., Buszaki G. 1998. Theta Oscillations in Somata and Dendrites of Hippocampal Pyramidal Cells in Vivo: Activity-dependent Phaseprecession of Action Potentials Hippocampus8 244–261. [DOI] [PubMed] [Google Scholar]
- 15.Fries P., Reynolds J.H., Rorie A.E., deSimone R. 2001. Modulation of Oscillatory Neuronal Synchronization by Selective Visual Attention Science291 1560; p. 1563. [DOI] [PubMed] [Google Scholar]
- 16.Geisler C., Brunel N., Wang X.J. Contributions of intrinsic membrane dynamics to fast network oscillations with irregular neuronal discharges. J. Neurophysiol. 2005;94:4344–4361. doi: 10.1152/jn.00510.2004. [DOI] [PubMed] [Google Scholar]
- 17.Gil Z., Amitai Y. Properties of convergent thalamocortical and intracortical synaptic potentials in single neurons of neocortex. J. Neurosci. 1996;16:6567–6578. doi: 10.1523/JNEUROSCI.16-20-06567.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li W., Li C., Xiang Y., Ji L., Hu H., Liu Y. 2019. Study of the Activation in Sensorimotor Cortex and Topological Properties of Functional Brain Network Following Focal Vibration on Healthy Subjects and Subacute Stroke Patients: an EEG Study Brain Research1722 146338. [DOI] [PubMed] [Google Scholar]
- 19.Grill W.M., Norman S.E., Bellamkonda R.V. Implanted neural interfaces: biochallenges and engineered solutions. Annu. Rev. Biomed. Eng. 2009;11:1–24. doi: 10.1146/annurev-bioeng-061008-124927. [DOI] [PubMed] [Google Scholar]
- 20.Wessberg J., Stambaugh C.R., Kralik J.D., Beck P.D., Laubach M., Chapin J.K.…Nicolelis M.A. Real-time prediction of hand trajectory by ensembles of cortical neurons in primates. Nature. 2000;408(6810):361–365. doi: 10.1038/35042582. [DOI] [PubMed] [Google Scholar]
- 21.Schwartz A.B. Useful signals from motor cortex. J. Physiol. 2007;579:581–601. doi: 10.1113/jphysiol.2006.126698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hochberg L.R., Bacher D., Jarosiewicz B., Masse N.Y., Simeral J.D., et al. Reach and grasp by people with tetraplegia using a neurally controlled robotic arm. Nature. 2012;485:372–375. doi: 10.1038/nature11076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pan H., Mi W., Lei X., Deng J. A closed-loop brain–machine interface framework design for motor rehabilitation. Biomed. Signal Process Control. 2020;58 [Google Scholar]
- 24.Bonizzato M., Pidpruzhnykova G., DiGiovanna J., Shkorbatova P., Pavlova N., Micera S., Courtine G. Brain-controlled modulation of spinal circuits improves recovery from spinal cord injury. Nat. Commun. 2018;9(1):1–14. doi: 10.1038/s41467-018-05282-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chapin J.K., Lin C.S. Mapping the body representation in the SI cortex of anesthetized and awake rats. J. Comp. Neurol. 1984;229:199–213. doi: 10.1002/cne.902290206. [DOI] [PubMed] [Google Scholar]
- 26.Hall R.D., Lindholm E.P. Organization of motor and somatosensory neocortex in the albino rat. Brain Res. 1974;66:23–38. [Google Scholar]
- 27.Paxinos G., Watson C. Academic press; 2007. The Rat Brain in Stereotaxic Coordinates. [DOI] [PubMed] [Google Scholar]
- 28.Brumberg J.C., Pinto D.J., Simons D.J. Cortical columnar processing in the rat whisker-to-barrel system. J. Neurophysiol. 1999;82:1808–1817. doi: 10.1152/jn.1999.82.4.1808. [DOI] [PubMed] [Google Scholar]
- 29.Simons D.J. Response properties of vibrissa units in rat SI somatosensory neocortex. J. Neurophysiol. 1978;41:798–820. doi: 10.1152/jn.1978.41.3.798. [DOI] [PubMed] [Google Scholar]
- 30.Woolsey T.A., Van der Loos H. The structural organization of layer IV in the somatosensory region (SI) of mouse cerebral cortex. The description of a cortical field composed of discrete cytoarchitectonic units. Brain Res. 1970;17:205–242. doi: 10.1016/0006-8993(70)90079-x. [DOI] [PubMed] [Google Scholar]
- 31.Donoghue J.P., Wise S.P. The motor cortex of the rat: cytoarchitecture and microstimulation mapping. J. Comp. Neurol. 1982;212:76–88. doi: 10.1002/cne.902120106. [DOI] [PubMed] [Google Scholar]
- 32.Franchi G. Reorganization of vibrissal motor representation following severing and repair of the facial nerve in adult rats. Exp. Brain Res. 2000;131:33–43. doi: 10.1007/s002219900297. [DOI] [PubMed] [Google Scholar]
- 33.Hoffer Z.S., Alloway K.D. Organization of corticostriatal projections from the vibrissal representations in the primary motor and somatosensory cortical areas of rodents. J. Comp. Neurol. 2001;439:87–103. doi: 10.1002/cne.1337. [DOI] [PubMed] [Google Scholar]
- 34.Neafsey E.J., Bold E.L., Haas G., Hurley-Gius K.M., Quirk G., et al. The organization of the rat motor cortex: a microstimulation mapping study. Brain Res. 1986;396:77–96. doi: 10.1016/s0006-8993(86)80191-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.