Quantifying organellar ultrastructure in cryo-electron tomography using a surface morphometrics pipeline

Barad and Medina et al. present a pipeline for quantifying the architecture of organellar membranes in cells visualized by cryo-electron tomography. They use this pipeline to detect changes in the membrane ultrastructure of fragmented and elongated mitochondria and identify statistically significant changes upon induction of ER stress.

Abstract

Cellular cryo-electron tomography (cryo-ET) enables three-dimensional reconstructions of organelles in their native cellular environment at subnanometer resolution. However, quantifying ultrastructural features of pleomorphic organelles in three dimensions is challenging, as is defining the significance of observed changes induced by specific cellular perturbations. To address this challenge, we established a semiautomated workflow to segment organellar membranes and reconstruct their underlying surface geometry in cryo-ET. To complement this workflow, we developed an open-source suite of ultrastructural quantifications, integrated into a single pipeline called the surface morphometrics pipeline. This pipeline enables rapid modeling of complex membrane structures and allows detailed mapping of inter- and intramembrane spacing, curvedness, and orientation onto reconstructed membrane meshes, highlighting subtle organellar features that are challenging to detect in three dimensions and allowing for statistical comparison across many organelles. To demonstrate the advantages of this approach, we combine cryo-ET with cryo-fluorescence microscopy to correlate bulk mitochondrial network morphology (i.e., elongated versus fragmented) with membrane ultrastructure of individual mitochondria in the presence and absence of endoplasmic reticulum (ER) stress. Using our pipeline, we demonstrate ER stress promotes adaptive remodeling of ultrastructural features of mitochondria including spacing between the inner and outer membranes, local curvedness of the inner membrane, and spacing between mitochondrial cristae. We show that differences in membrane ultrastructure correlate to mitochondrial network morphologies, suggesting that these two remodeling events are coupled. Our pipeline offers opportunities for quantifying changes in membrane ultrastructure on a single-cell level using cryo-ET, opening new opportunities to define changes in ultrastructural features induced by diverse types of cellular perturbations.

Introduction

Cellular cryo-electron tomography (cryo-ET) is a powerful technique that enables high-resolution, 3D views of protein and organellar structure in unfixed and fully hydrated conditions (Turk and Baumeister, 2020). By combining cryo-focused ion beam (cryo-FIB) milling with automated data collection schemes (Buckley et al., 2020; Schorb et al., 2019), it has become routine to collect large datasets of thin, cellular 3D reconstructions (tomograms) teeming with pristinely preserved proteins and organelles. Even as tremendous progress has been made in developing new algorithmic subtomogram averaging approaches to solve protein structures in cells (Tegunov et al., 2021; Himes and Zhang, 2018; Chen et al., 2019), it remains very challenging to quantitatively describe complex organellar membrane architectures (hereafter referred to as membrane ultrastructure) from cryo-tomograms. Organellar membrane remodeling plays a pivotal role in the cell’s ability to adapt and respond to various changes in the physiological state of the cell (e.g., of cellular stress), and is mediated through changes in the molecular interactions of proteins that reside within membrane compartments (Jiang et al., 2017; Schwarz and Blower, 2016). As such, an improved ability to quantify organellar architectures from cryo-tomograms would both enable contextualization of distinct protein structures revealed by subtomogram averaging and reveal subtle, yet functionally relevant, changes in organellar ultrastructures associated with distinct cellular physiologies.

Despite the inherent 3D nature of cryo-tomograms, the 2D virtual slices of cryo-tomograms are often used to quantify membrane ultrastructural parameters such as inter- and intramembrane distances through manual designation of membrane boundaries by locating distinct points along the membrane (Khanna et al., 2021; Ader et al., 2019; Tran et al., 2021; Mageswaran et al., 2021). Although this can serve as a proxy to quantify 3D ultrastructure, this analysis is time-intensive and prone to both user bias and inaccuracies in the precise location of membranes between 2D slices. Furthermore, the manual nature of this approach severely limits its applicability to perform ultrastructural quantification at a throughput and sample size sufficient to reveal substantial mechanistic insight. Toward a more accurate 3D representation, manual or automated (Martinez-Sanchez et al., 2014), voxel-based segmentation can be used to assign and label individual voxels within cryo-tomograms to specific cellular membranes (Chen et al., 2017). Although qualitatively informative, voxel-based segmentation methods do not encode for parameters defining membrane geometry (i.e. connectivity), a property essential for robust quantifications of ultrastructural features like membrane curvedness and spacing.

An alternative to using voxel segmentations to represent membranes is representing them as a meshwork of triangles. Triangle mesh surfaces represent the connectivity and implicit geometry of the membrane itself, enabling direct measurement of metrics like orientation and curvedness. A recently developed approach enables more accurate and robust estimation of each triangle’s geometry, improving quantification of local curvedness as well as the spatial relationship between individual triangles (i.e., membrane segments) both within the same (intra-) and between distinct (inter-) membrane compartments (Salfer et al., 2020). Despite these major advances, surface reconstructions using segmentations of membranes themselves (i.e., boundary segmentations) were not reliable due to the incomplete (open) nature of the membrane segmentations limiting the effectiveness of the reconstruction algorithm (Hoppe et al., 1992). In cryo-ET, even perfect segmentations will never show complete and closed membranes due to the substantial missing wedge (Lučič et al., 2013), making horizontal membranes invisible. To address these issues, quantifications using this new approach depended on using voxel segmentations that “fill” the entire internal volume encompassed within a membrane (i.e., compartment segmentations), which are not amenable to automation. Manual segmentation of filled membrane compartments is feasible for small and simple compartments, but the time-intensive process severely limits throughput and, thus, the ability to aggregate ultrastructural quantifications across large tomographic datasets. The low throughput is further exacerbated in the context of complex, highly variable organellar membranes, which can be very challenging to accurately fill in. Thus, new strategies are required to improve throughput, automation, and quantification of membrane ultrastructures for application to cryo-ET.

Mitochondria are an ideal target for the development of this approach. Mitochondria are highly pleomorphic organelles that function simultaneously as an interconnected network population and as discrete organellar units involved in energy production, ion homeostasis, cellular stress pathway integration, and innate immune signaling (Schirrmacher, 2020; West and Shadel, 2017; Wai and Langer, 2016). Their ability to perform these essential eukaryotic functions fundamentally depends on their dynamic remodeling both within the entire cellular mitochondrial network population (hereafter referred to as bulk mitochondrial morphology) and within their distinct outer and inner mitochondrial membranes (hereafter referred to as mitochondrial membrane ultrastructure; Chan, 2020). Changes to bulk mitochondrial morphology are mediated through the opposing processes of mitochondrial fusion and fission, and imbalances in these processes can promote interconnected (i.e., elongated) or disconnected (i.e., fragmented) networks that regulate prosurvival or proapoptotic mitochondrial functions (Sabouny and Shutt, 2020; Rambold et al., 2011). Within individual mitochondria, ultrastructures of both the outer and inner mitochondrial membranes (OMM and IMM, respectively) and the associations between these two membranes can exhibit dynamic remodeling to modulate metabolic and signaling functions (Nielsen et al., 2017).

In particular, the IMM contains functional membrane folds, called cristae, whose ultrastructure is intimately linked to nearly all aspects of mitochondrial function. The architecture of the cristae is maintained through the activity and localization of several proteins (termed “shaping” proteins), including components involved in cellular respiration such as ATP synthase, whose dimerization at the matrix-associated cristae “tip” regions induces membrane curvedness required for efficient mitochondrial respiration, (Colina-Tenorio et al., 2020; Siegmund et al., 2018; Blum et al., 2019). Cristae shape is also maintained through specialized regions called cristae junctions, formed by the interaction of mitochondrial contact site and cristae organizing system (MICOS) and Optic Atrophy 1 (OPA1), which act as dynamic molecular staples to compartmentalize the distinct internal cristae environments and associate IMM cristae with the OMM (Harner et al., 2011; Hu et al., 2020; Zhang et al., 2008). Alterations to the expression, localization, or activity of these shaping proteins disrupt mitochondrial respiration and can promote the induction of apoptotic signaling through the release of cytochrome C (Colina-Tenorio et al., 2020; Frezza et al., 2006). It is therefore important to understand the relationship between mitochondrial network morphology and membrane ultrastructure, and how they are altered in response to cellular perturbations.

Here, we sought to develop a correlative cryo-ET workflow that enables quantitative analysis of complex membrane ultrastructures across distinct mitochondrial network morphologies and cellular physiologies with throughputs sufficient for statistical hypothesis testing. Specifically, we combined cryo-fluorescence microscopy with cellular cryo-ET imaging to correlate distinct mitochondrial network morphologies (e.g., elongated versus fragmented) to mitochondrial membrane ultrastructure. We developed and implemented a robust, semiautomated workflow (Martinez-Sanchez et al., 2014) to segment cellular membranes present in cryo-tomograms and applied a screened Poisson reconstruction strategy (Kazhdan and Hoppe, 2013) to convert membrane voxel segmentations into implicit surface meshes that model complex cellular membrane geometries. To complement our surface generation workflow, we developed the surface morphometrics pipeline to measure several parameters of membrane shape including inter- and intramembrane spacing, curvedness, and orientation across several hundred square microns of mitochondrial membranes. We applied this workflow to cells experiencing acute levels of ER stress, a condition known to promote adaptive remodeling of mitochondrial networks (Lebeau et al., 2018), to explore how these changes influence membrane ultrastructure across distinct network morphologies. Our workflow for the first time allows us to distinguish statistically significant alterations in 3D ultrastructure in highly variable mitochondrial inner membranes.

Results

Correlative cryo-fluorescence microscopy and electron tomography enable association of bulk mitochondrial morphology with local membrane ultrastructure

We set out to understand the connection between the bulk morphology of the mitochondrial network within a single cell and the local membrane ultrastructure of the mitochondrial membranes within that same cell. We used cryo-fluorescence microscopy to image vitrified mouse embryonic fibroblasts whose mitochondria were labeled with a mitochondria-targeted GFP (MEF^mtGFP) such that the morphology of each cell’s mitochondrial network could be readily assessed (Fig. 1, A–C, and Fig. 2 A). We categorized cells for mitochondrial network morphology by blinded manual classification: Five researchers were given unlabeled fluorescence microscopy images of exemplar network morphologies (elongated and fragmented) as references to assign morphologies to the experimental fluorescence micrographs. We targeted cells with either fragmented or elongated mitochondrial networks for cryo-FIB milling to prepare thin (95–233 nm) lamellae (Fig. 1 D). We collected tilt series of the mitochondria within these lamellae to directly correlate the cell’s bulk mitochondrial morphology (Fig. 1 C) to the ultrastructure of mitochondrial membranes (Fig. 1, F–H). To further probe the connection between morphology and ultrastructure, we treated MEF^mtGFP cells with Thapsigargin (Tg), a small molecule that induces ER stress through inhibition of the sacro/ER Ca²⁺ ATPase and has been previously reported to promote mitochondrial elongation downstream of the ER stress-responsive kinase PERK through a process termed stress-induced mitochondrial hyperfusion (Lebeau et al., 2018). We applied our correlative approach to identify and target specific Tg-treated and vehicle (media with DMSO)-treated MEF^mtGFP cells with either elongated or fragmented mitochondrial network morphologies for cryo-FIB milling and cryo-ET data acquisition and reconstruction. Visual inspection of the mitochondrial membranes within tomograms revealed variability in IMM architecture between mitochondria from different network morphologies and treatment groups, but some overall trends were apparent in elongated and fragmented mitochondrial populations in response to Tg-induced ER stress (Fig. S1, S2, and S3). Notably, Tg treatment induced a shift toward regularly spaced disc-shaped (lamellar) cristae in the elongated population and toward a swollen tubular crista structure in the fragmented population. Due to the high degree of pleomorphism, with mixed populations in all conditions, we next established a workflow for ultrastructural quantification to determine the significance of these apparent changes.

Figure 1.

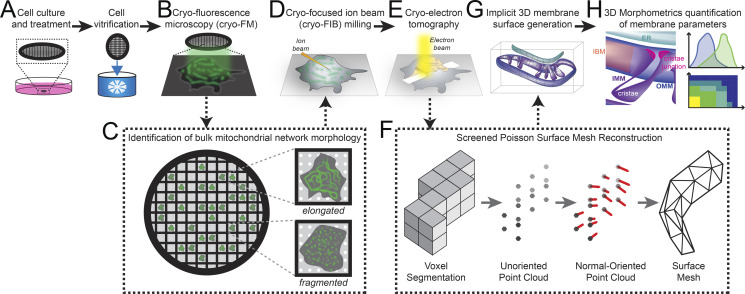
Correlative cellular cryo-ET workflow for robust quantitative analysis of membrane ultrastructures between distinct mitochondrial network morphologies and treatment conditions. (A) MEF^mtGFP cells were cultured on transmission EM grids (black mesh circle) and treated with vehicle or Tg (500 nM) for 8 h prior to vitrification via plunge freezing in ethane/propane mixture. (B) Vitrified MEF^mtGFP cells were imaged using cryo-fluorescence microscopy (cryo-FM). (C) Cryo-FM facilitated the identification of single cells with distinct elongated or fragmented bulk mitochondrial network morphologies. (D) These cells were targeted for cryo-FIB milling to generate thin sections (lamellae). (E) Lamella were imaged using standard cryo-ET imaging parameters to generate tilt series that were further reconstructed to generate 3D cryo-tomograms. (F) Voxel segmentations labeling distinct cellular membranes were generated using a semiautomated approach (Martinez-Sanchez et al., 2014) prior to conversion to point clouds. Next, a normal-oriented vector is estimated for each point (Cignoni et al., 2008). Normal-oriented point clouds were used to generate surface meshes using a novel application of a screened Poisson reconstruction method followed by masking to the original voxel segmentation (Kazhdan and Hoppe, 2013; Cignoni et al., 2008). (G) Surface meshes model the implicit 3D ultrastructure of distinct organellar membranes. Surface coloring: IMM, purple; OMM, blue; ER, teal. (H) Implicit geometries encoded within surface meshes are then used to perform 3D morphometrics to quantify several parameters that define membrane ultrastructure across mitochondria from distinct morphological and treatment conditions.

Figure 2.

Application of correlative workflow to visualize cellular membrane ultrastructures in elongated and fragmented mitochondrial networks in MEF^mtGFP cells. (A) Identification by cryo-FM of elongated (top; cyan outline) and fragmented (bottom; orange outline) mitochondrial morphologies from mixed populations of MEF^mtGFP cells. Cryo-FM images of bulk mitochondrial morphology are then used for targeted cryo-FIB milling to generate thin lamellae of 95–233 nm. MEF^mtGFP cell periphery is outlined in dashed white line. (B) Virtual slides of tomograms of MEF^mtGFP cells containing elongated (top) and fragmented (bottom) mitochondria are traced using the automated TomoSegMemTV program (Martinez-Sanchez et al., 2014), followed by manual cleanup using AMIRA software to generate 3D voxel segmentations. 3D voxel segmentations are then converted into implicit surface meshes using the screened Poisson mesh reconstruction. Scale bars = 100 nm. Surface coloring: IMM in pink, OMM in purple, ER in blue. (C) Detailed views of voxel (green) and triangle surface mesh (IMM: pink, OMM: purple, ER: blue) show the improved smoothness and hole-filling of surfaces generated with the screened Poisson mesh approach. Zoomed insets are rotated backward 20° to highlight features. Holes are outlined in red on the voxel segmentation.

Figure S1.

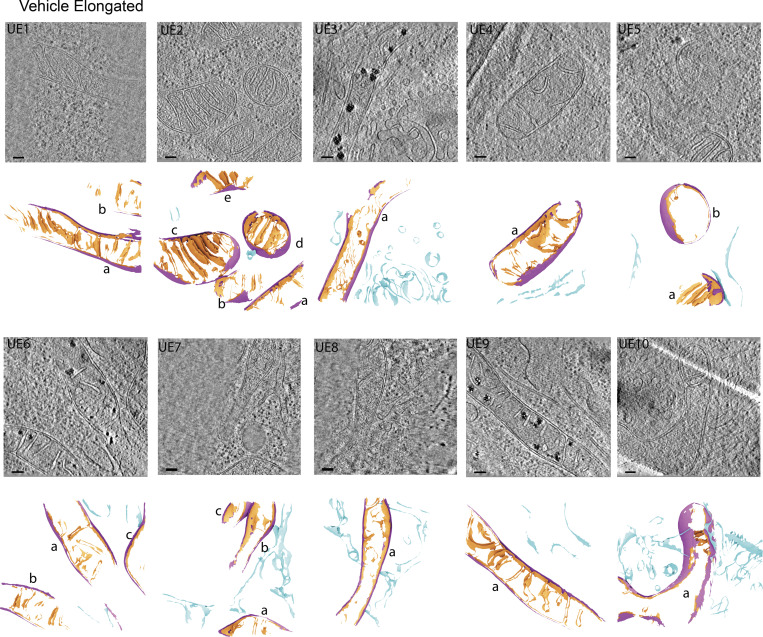
Gallery of cellular membranes used for downstream quantifications from cells with elongated mitochondrial networks in the absence of ER stress. Virtual slices of tomograms (upper panels) and corresponding reconstructed surface mesh models (lower panels) of mitochondrial membranes (IMM, orange; OMM, purple) and ER membranes (blue). The surfaces (lower panels) are labeled according to treatment conditions (U, untreated/vehicle-treated), mitochondrial morphology (E, elongated), and tomogram number. For example, “UE1” is untreated, elongated, tomogram 1. Individual mitochondria in the tomograms are labeled by letters (e.g., a, b, c). These labels correspond to the title labels of the histograms of individual mitochondria shown in Fig. S5. Meshes have been tilted backward by 20° for visualization. Scale bar = 100 nm. Vehicle-treated cells with elongated mitochondrial networks, n = 10 tomograms.

Figure S2.

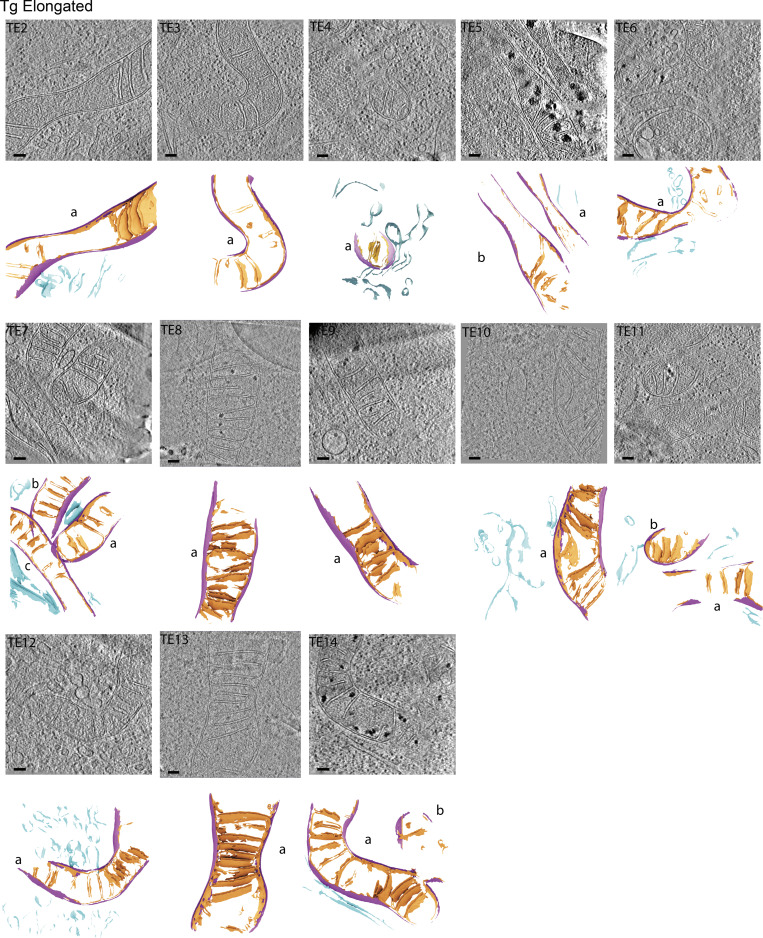
Gallery of cellular membranes used for downstream quantifications from cells with elongated mitochondrial networks in the presence of ER stress. Virtual slices of tomograms (upper panels) and corresponding reconstructed surface mesh models (lower panels) of mitochondrial membranes (IMM, orange; OMM, purple) and ER membranes (blue). The surfaces (lower panels) are labeled according to treatment conditions (U, untreated/vehicle-treated), mitochondrial morphology (E, elongated), and tomogram number. For example, “TE1” is Tg-treated, elongated, tomogram 1. Individual mitochondria in the tomograms are labeled by letters (e.g., a, b, c). These labels correspond to the title labels of the histograms of individual mitochondria shown in Fig. S5. Meshes have been tilted backward by 20° for visualization. Scale bar = 100 nm. Tg-treated cells  with elongated mitochondrial networks, n = 13 tomograms.

Figure S3.

Gallery of cellular membranes used for downstream quantifications from cells with fragmented mitochondrial networks in the absence and presence of ER stress. Virtual slices of tomograms (upper panels) and corresponding reconstructed surface mesh models (lower panels) of mitochondrial membranes (IMM, orange; OMM, purple) and ER membranes (blue). The surfaces (lower panels) are labeled according to treatment conditions (U, untreated/vehicle-treated), mitochondrial morphology (E, elongated), and tomogram number. For example, “TF1” is Tg-treated, fragmented, tomogram 1. Individual mitochondria in the tomograms are labeled by letters (e.g., a, b, c). These labels correspond to the title labels of the histograms of individual mitochondria shown in Fig. S5. Meshes have been tilted backward by 20° for visualization. Scale bar = 100 nm. Vehicle-treated cells with fragmented mitochondrial networks, n = 6 tomograms; and Tg-treated cells with fragmented mitochondrial networks, n = 5 tomograms.

Development of a framework to automate quantification of ultrastructural features of cellular membranes

In order to identify changes in different mitochondrial populations with and without induction of ER stress, we developed a semiautomated approach to quantify membrane features in three dimensions without the need for bias-prone manual measurements. We leveraged recent work (Salfer et al., 2020) that established a robust approach for estimating curvedness in membranes and developed a framework for additional quantifications using triangular mesh models of membranes. However, the generation of high-quality surface meshes has previously required labor-intensive manual segmentation approaches. These include manual contouring of membranes (Kremer et al., 1996; Navarro et al., 2018) and manual inpainting of entire compartments (Salfer et al., 2020), both of which are especially challenging with the complex and highly curved IMM and ER membrane. With these methods, it would be impractical to analyze a sufficient number of tomograms to overcome the variability between mitochondria observed in these distinct mitochondrial populations (elongated versus fragmented) and upon treatment (vehicle versus Tg). Instead, we developed a semiautomated workflow to enable analysis at higher throughput (Fig. 1 F). We used a segmentation strategy that takes advantage of the TomoSegMemTV program (Martinez-Sanchez et al., 2014), which identifies and enhances regions of the tomogram with membrane-like voxel values. This was followed by manual labeling of membranes into mitochondrial IMM and OMM, ER, and multilamellar membrane based on cellular context, as well as manual cleanup of individual membrane segmentation using AMIRA software (Thermo Fisher Scientific). With this strategy, we were able to segment 34 tomograms containing mitochondria, divided between the elongated and fragmented bulk morphology populations and the two treatment groups (Fig. 2 A, Fig. S1, S2, and S3). The segmentation output was fed into the fully automated surface morphometrics pipeline (Fig. 2 B). The voxel segmentation was converted to high-quality membrane surfaces using the screened Poisson algorithm (Kazhdan and Hoppe, 2013; Fig. S4 and Video 1). Next, these surfaces were converted into triangle graphs, and multiple membrane features were quantified including curvedness (estimated using pycurv¹⁵), distances within and between surfaces, and the relative orientations of different surfaces. Finally, the quantifications for each mitochondrion were combined into experiments to allow aggregate statistics and visualizations. Results were computed from 34 completed segmentations in a few hours using a cluster for parallelization (Table S1). This 3D surface morphometrics pipeline is configurable for any segmented membrane and is available at https://github.com/grotjahnlab/surface_morphometrics.

Figure S4.

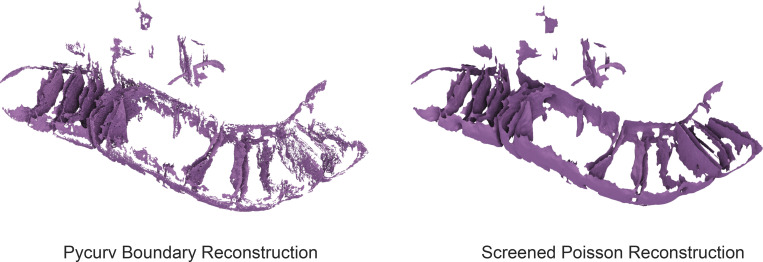
Comparison of surface reconstruction algorithms. The same IMM segmentation was subjected to the boundary segmentation surface reconstruction algorithm used in the pycurv software (Salfer et al., 2020; Hoppe et al., 1992; left) as well as our new reconstruction approach based on the screened Poisson algorithm (Kazhdan and Hoppe, 2013; right) show the improvements in smoothness and completeness enabled by the new surface reconstruction algorithm. While the left algorithm was made part of the pycurv software, it was not used for extensive analysis in the cited manuscript, in favor of algorithms using compartment segmentations.

Video 1.

Comparison of voxel segmentation vs. surface reconstruction. An example tomogram is shown with and without a completed voxel segmentation (green). A zoom in reveals voxel stepping artifacts that impact measurement precision, as well as small holes that result from automated segmentation. Switching to the reconstructed surface shows the smooth triangle mesh and the hole-filling properties of the surface reconstruction algorithm. Surface colors: IMM in pink, OMM in purple, ER in blue.

https://movie.rupress.org/media/by_doi/10.1083/jcb.202204093.v1/source

Bulk analysis and assessment of statistical significance based on surface quantifications

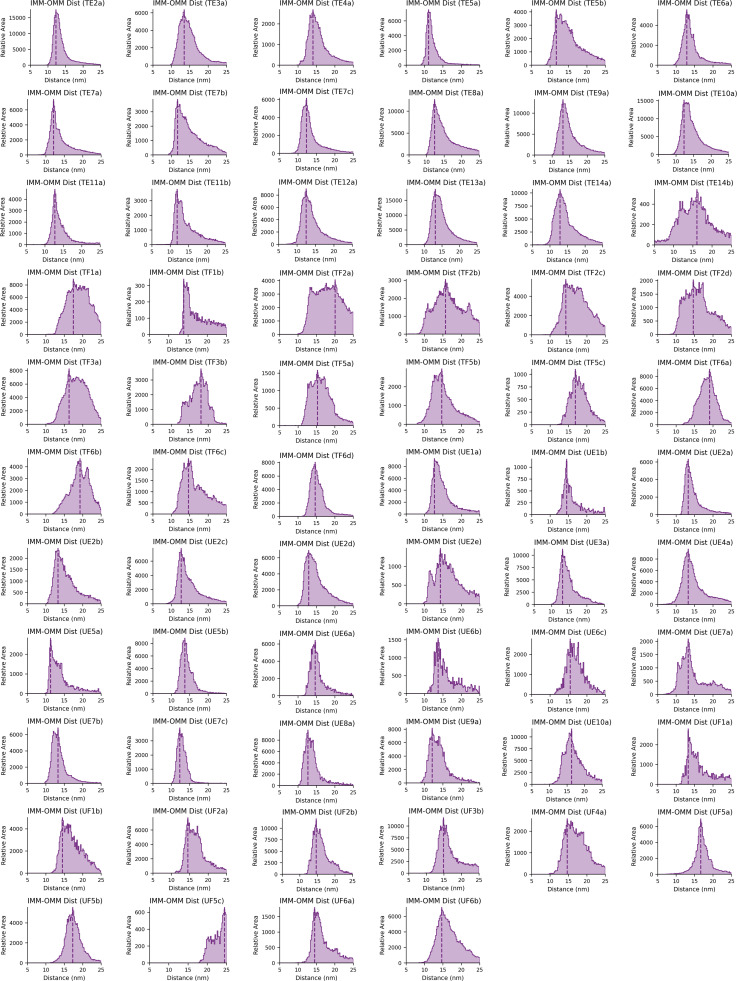
Our pipeline outputs multiple membrane feature quantifications (i.e., curvature, distance, and orientation) for each triangle, totaling ∼500,000 triangles per tomogram. We set out to determine an appropriate method for bulk quantitative and statistical analyses that would enable detection of subtle albeit potentially significant differences in membrane ultrastructure across different mitochondrial morphologies and treatment groups. We plotted the overall distributions of each membrane feature quantification using histograms of triangle values that are weighted by the area of each triangle, both for individual mitochondrion (Fig. S5) and for entire experiments. These histograms identify bulk differences in the membrane ultrastructure of mitochondria under different experimental conditions. For several membrane parameter quantifications, the observed histogram peak shifted visibly between conditions, suggesting potential differences between treatment and morphology groups. In order to test the statistical significance of these shifts, the weighted histogram peak for each membrane feature quantification for each individual mitochondrion was extracted and these peaks were used for statistical comparisons. In most cases, there was a statistically significant difference in the mean of the distributions, which was assessed via a non-parametric Mann-Whitney U test (Table S2). Differences in the variability of metrics between mitochondria within a given experimental condition were assessed with a two-sample Kolmogorov–Smirnoff test.

Figure S5.

Gallery of IMM–OMM distance histograms for individual mitochondria. The distribution of distances between the IMM and OMM was plotted for each mitochondrion individually for all Tg-treated, elongated (TE), Tg-treated, fragmented (TF), vehicle (i.e., untreated), elongated (UE), and vehicle (i.e., untreated), fragmented (UF). The peak position is plotted for each and is used for the violin plot in Fig. 3 D. The histograms are titled based on the measurement (i.e., IMM-IMM Dist) and correspond to the treatment conditions, morphologies, and individual mitochondria labels shown in Fig. S1 (e.g., “TE2a” corresponds to a Tg-treated [T], elongated [E], tomogram “2,” mitochondrion labeled “a”).

In some cases, there was an apparent change to the shape of distribution seen in quantification histograms rather than simply peak position. We primarily assessed the statistical significance of these changes by Mann–Whitney U tests and Kolmogorov–Smirnoff tests on the per-mitochondria standard deviation rather than histogram peak (Table S2). This metric captured changes to the variance of metrics. In order to quantify changes that combine variance and peak shifts, we used the two-sample Kolmogorov–Smirnoff test to test the statistical significance of changes to the distributions of mesh triangles in each condition. However, a major challenge of utilizing this statistical test for analysis of surface quantifications is assessing the true number of independent measurements being made. Triangles are highly correlated to their neighboring meshes, a correlation made even stronger by the vector voting approach employed by pycurv in order to better approximate a smooth membrane. When each triangle within a surface mesh is treated as an independent measurement (in some cases yielding sample sizes in the millions), even visibly identical distributions yield statistically significant P values. This is even further complicated because the number of triangles generated in a given surface mesh is arbitrary and not based on any physical constraint. In contrast, if each mitochondrion is treated as an independent measurement, the variance of features within the mitochondria is lost and there is essentially never statistical significance. We established a heuristic compromise based on the feature radius of 12 nm used in vector voting to optimally measure curvatures. The number of independent samples was assumed to be one per 452 nm² of membrane area, corresponding to the 12-nm feature size. In practice, this area corresponds to the area of a single crista tip or junction and yields results with P values that might be effectively used comparatively between different measurements. Altering the feature size to 9 or 15 nm changes the number of independent samples and absolute P values; however the relative P value differences across groups do not change, demonstrating that absolute value for assessing statistical significance is limited by the artificial selection of feature radius, but the choice of feature size does not affect the overall result of the comparative analyses across different membrane feature parameters (Table S2).

A challenge with using histogram peaks as a metric is determining the confidence interval associated with the metric. In order to assess the precision of the histogram peak measurements, we resampled each distribution using bootstrap sampling 1,000 times, and the histogram peak was extracted on each resampling. The 5th and 95th percentiles of these histogram peaks were used to represent the confidence interval of the histogram peak (Table S3).

Quantification of IMM–OMM spacing in mitochondria identifies ultrastructural differences in elongated and fragmented mitochondrial networks

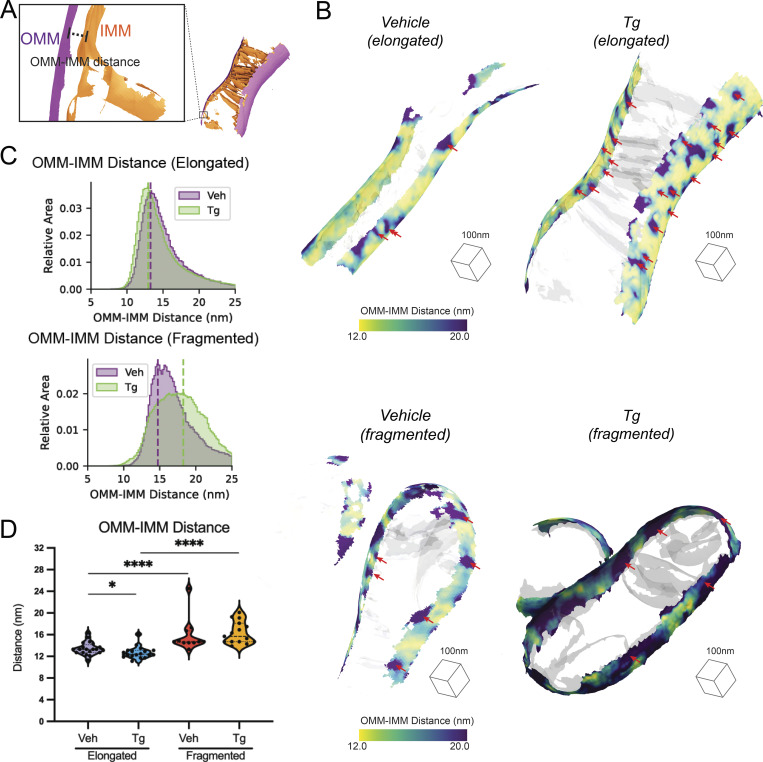
The most distinctive feature of mitochondria is the juxtaposed inner and outer mitochondrial membranes. Cryo-ET is uniquely able to reveal the details of the architecture of these two membranes in 3D, and we sought to use our tomograms to precisely measure their spacing. We measured the distance to the closest triangle on the IMM mesh for each triangle in the OMM mesh for each mitochondrion in our dataset (Fig. 3 A and Fig. S5). We then visualized the spatial distribution of these distances directly on the generated surface mesh reconstructions of the OMM of individual mitochondria visible within tomograms (Fig. 3 B). The resulting surface maps showed regions marked by the largest OMM–IMM distance representing the distribution of the crista junctions but also revealed general increases in distance in the fragmented over elongated mitochondria in both vehicle- and Tg-treated conditions (Fig. 3 B). In order to determine how consistent these effects were across all of the segmented mitochondria, we plotted a histogram of the combined distribution of distances for all surface mesh triangles within each condition (Fig. 3 C). This revealed an overall increase in intermembrane distance in fragmented mitochondria. Furthermore, we observed a subtle decrease in OMM–IMM distance after Tg-induced ER stress in elongated mitochondria, contrasted by a Tg-dependent increase in peak position and variability of distances in fragmented populations. We then assessed the peaks of the distance distribution for each mitochondrion as independent observations and identified statistically significant increases in spacing in cells with fragmented vs. elongated mitochondria by 2.4 nm in the vehicle-treated condition and by 3.6 nm in the Tg-treated condition. Additionally, we confirmed that the 0.8 nm decrease in distance between OMM and IMM of the elongated mitochondria after Tg treatment was statistically significant, while the increase in spacing in cells with fragmented mitochondria after Tg treatment was not significant (Fig. 3 D), demonstrating the power of our approach to quantify and test the significant differences across distinct bulk mitochondrial network morphologies.

Figure 3.

Distance between IMMs and OMMs is dependent on mitochondrial network morphology and presence or absence of ER stress. (A) Surface membrane reconstruction defining OMM (purple) and IMM (orange) distance measurement. (B) Representative membrane surface reconstructions of elongated (top) and fragmented (bottom) mitochondria in MEF^mtGFP cells treated with vehicle and Tg (500 nM, 8 h). The OMM surface is colored by outer-to-inner (OMM–IMM) membrane distance, and the IMM surface is shown in transparent gray. Red arrows indicate regions on OMM with large OMM–IMM distances that correspond to cristae junctions. (C) Combined histogram of OMM–IMM distances of elongated (top) and fragmented (bottom) mitochondria in MEF^mtGFP cells treated with vehicle and Tg. Dashed vertical lines correspond to peak histogram values of pooled data. (D) Quantification of peak histogram values from each mitochondrion within the indicated treatment and mitochondrial morphology class. Quantifications from vehicle elongated n = 20, Tg elongated n = 18, vehicle fragmented n = 11, and Tg fragmented n = 15 mitochondria are shown. P values from Mann–Whitney U test are indicated. *P < 0.05; ****P < 0.001.

Mitochondrial cristae and junction spacing in mitochondria are differentially impacted by Tg in elongated and fragmented mitochondrial networks

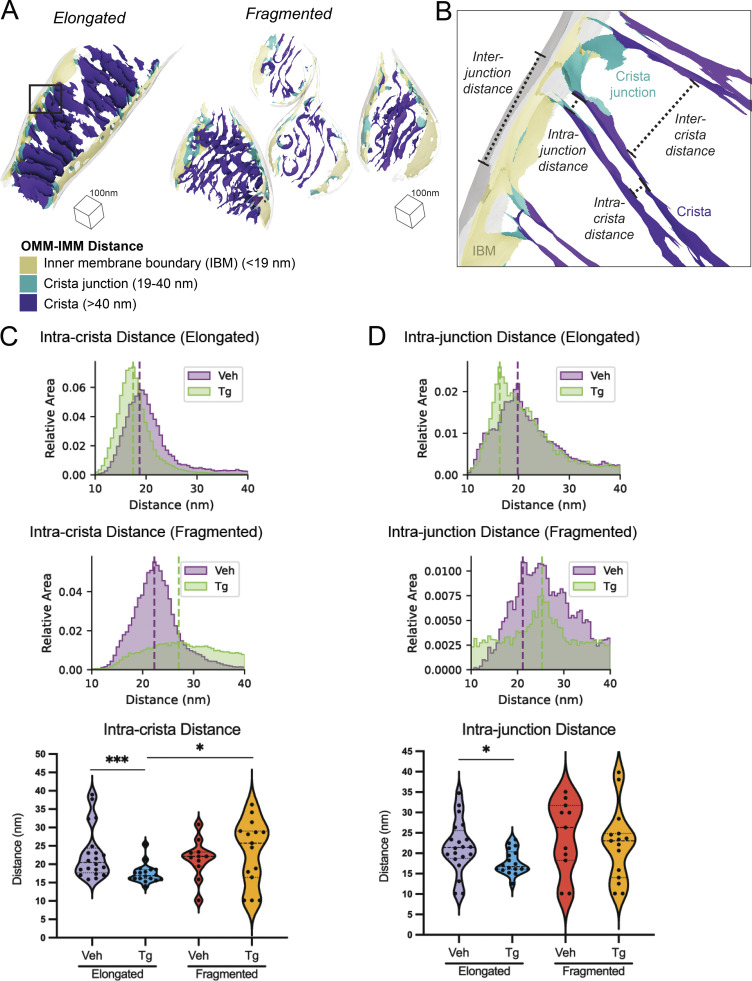
The IMM is divided between the inner boundary membrane (IBM), which is in close proximity to the OMM, and the invaginated mitochondrial cristae (Fig. 4 A), which are maintained as separate functional compartments by the organization of the MICOS complex and the protein OPA1 at crista junctions (Bohnert et al., 2012; Hu et al., 2020). We sought to understand how the organization of mitochondrial cristae and their junctions differed between fragmented and elongated mitochondria populations in the presence and absence of the ER stressor, Tg. We classified the IMM into three compartments (IBM, crista junctions, and crista bodies) based on their distance from the OMM such that quantifications could be performed based on the functional components of the membrane (Fig. 4 A). We then measured the distance between the membrane segments on either side of the crista bodies and junctions (intracrista and intrajunction distances, respectively), as well as the distance between adjacent crista bodies and junctions (intercrista and interjunction distances, respectively; Fig. 4 B and Fig. S6). We quantified these effects as combined histograms showing the change in different populations upon treatment with Tg, and as violin plots of the histogram peaks for each mitochondria (Fig. 4, C and D). Based on these distributions, we identified statistically significant but opposing changes in intracrista body spacing between the elongated and fragmented morphologies induced by Tg treatment. In elongated mitochondria, crista spacing was reduced by 5.3 nm upon Tg treatment, while in fragmented mitochondria the spacing increased by 1.8 nm upon Tg treatment. However, we did not observe significant changes in intercristae distance, intrajunction distance, or interjunction distance, with the exception of a 3.7 nm decrease in intrajunction spacing in the Tg-treated condition of elongated mitochondria relative to vehicle elongated mitochondria, suggesting that ER stress promotes rigidification of the junctions in elongated mitochondria.

Figure 4.

Spacing within and between mitochondrial cristae is differentially altered by Tg-induced ER stress in fragmented and elongated populations. (A) Representative membrane surface reconstructions of elongated (left) and fragmented (right) mitochondria in MEF^mtGFP cells treated with Tg (500 nM, 8 h) showing subdivision of IMM compartments (IBM, tan; junction, cyan; crista, purple) as defined by OMM–IMM distance. The OMM surface is represented as a transparent gray mesh. (B) Enlarged inset of boxed region in elongated example from A showing surface membrane reconstruction colored by inner membrane compartments defining intra- and intercrista and junction measurements. (C) Combined histogram of intracrista membrane distances of elongated (top) and fragmented (middle) mitochondria in MEF^mtGFP cells treated with vehicle and Tg. Dashed vertical lines correspond to peak histogram values of pooled data. Graph (bottom) showing peak histogram values from each mitochondrion within each corresponding treatment and mitochondrial morphology class. Quantifications from vehicle elongated n = 20, Tg elongated n = 18, vehicle fragmented n = 11, and Tg fragmented n = 15 mitochondria are shown. P values from Mann–Whitney U test are indicated. *P < 0.05; ***P < 0.005. (D) Combined histogram of intrajunction membrane distances of elongated (top) and fragmented (middle) mitochondria in MEF^mtGFP cells treated with vehicle and Tg. Dashed vertical lines correspond to peak histogram values of pooled data. Graph (bottom) showing peak histogram values from each mitochondrion within each corresponding treatment and mitochondrial morphology class. Quantifications from vehicle elongated n = 20, Tg elongated n = 18, vehicle fragmented n = 11, and Tg fragmented n = 15 mitochondria are shown. P values from Mann–Whitney U test are indicated. *P < 0.05.

Figure S6.

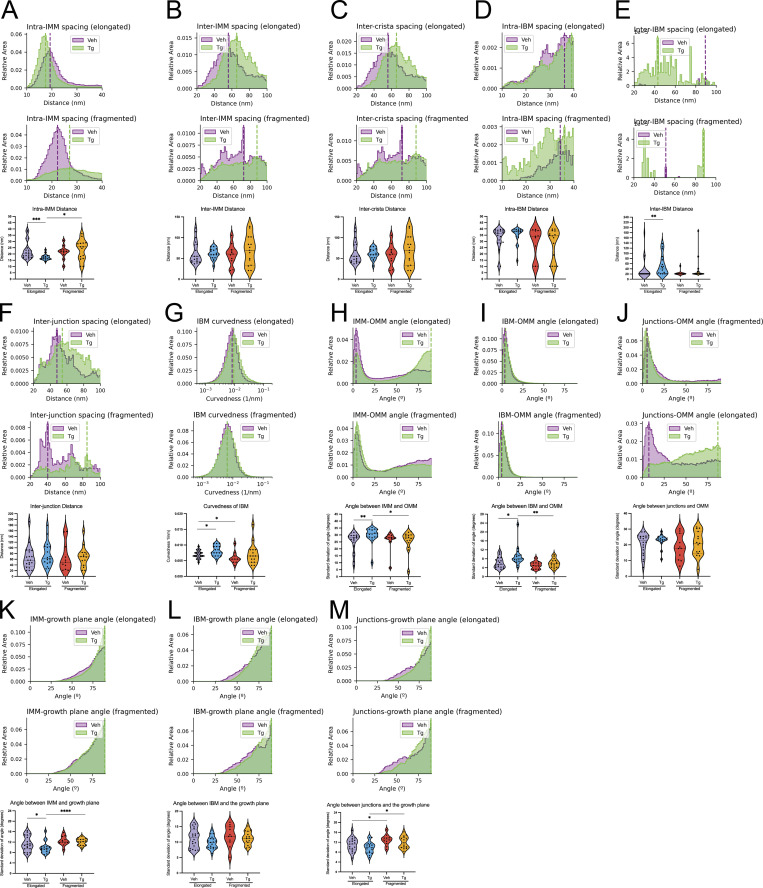
Additional quantifications of membrane ultrastructure. Additional quantifications output by the surface morphometrics pipeline, which showed non-significant changes or no apparent change. In all cases, quantifications from vehicle elongated n = 20, Tg elongated n = 18, vehicle fragmented n = 11, and Tg fragmented n = 15 mitochondria are shown. (A) Histograms and violin plot showing changes to spacing between closest neighbor segments of IMM. (B) Histograms and violin plot showing changes to spacing to the second nearest segments of IMM. (C) Histograms and violin plot showing changes to spacing between neighboring cristae. (D) Histograms and violin plot showing changes to spacing between closest neighbor segments of IBM. (E) Histograms and violin plot showing changes to spacing to the second nearest segments of IBM. (F) Histograms and violin plot showing changes to spacing between neighboring junctions. (G) Histograms and violin plot showing changes to curvedness of the IBM. (H) Histograms and violin plot showing changes to the angle between IMM and OMM. (I) Histograms and violin plot showing changes to the angle between IBM and OMM. (J) Histograms and violin plot showing changes to the angle between crista junctions and OMM. (K) Histograms and violin plot showing changes to the angle between IMM and the growth plane. (L) Histograms and violin plot showing changes to the angle between IBM and the growth plane. (M) Histograms and violin plot showing changes to the angle between crista junctions and the growth plane. *P < 0.05; **P < 0.01; ***P < 0.005; ****P < 0.001.

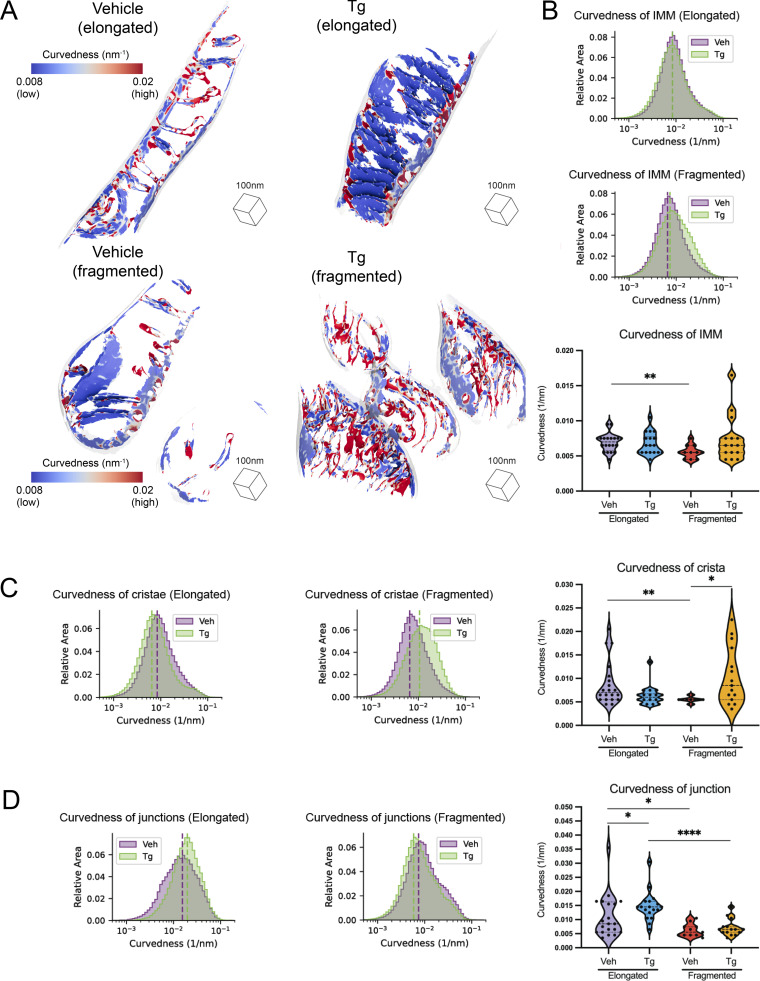
IMM curvedness is differentially sensitive to Tg treatment in elongated and fragmented mitochondrial networks

We next quantified the membrane curvedness locally at every mesh triangle position on each IMM surface to identify regions of local high and low curvedness (Fig. 5 A and Fig. S6; Salfer et al., 2020). Visual inspection of these surfaces suggested notable decreases in curvedness in the flat and lamellar cristae observed in the Tg-treated cells with elongated mitochondria, while in cells with fragmented mitochondria, Tg appeared to increase curvedness in the swollen and tubular cristae (Fig. 5 A). To understand the degree to which these effects differed across populations and not just within individual mitochondria, we quantified the total curvedness of the IMM across different mitochondrial network morphologies and treatment conditions (Fig. 5 B). A significant change was observed between the vehicle-elongated and vehicle-fragmented mitochondria, which established a basal distinction in curvedness among mitochondrial populations (Fig. 5 B). As visual inspection revealed local changes in curvedness in the cristae and junctions, rather than uniformly across the IMM, we broke down these quantifications into the IMM’s functional subcompartments (Fig. 5, C and D).

Figure 5.

The curvedness of mitochondrial cristae and crista junctions are dependent both on mitochondrial network morphology and Tg-induced ER stress. (A) Representative membrane surface reconstructions of elongated (top) and fragmented (bottom) mitochondria in MEF^mtGFP cells treated with vehicle and Tg (500 nM, 8 h). The IMM surface is colored by membrane curvedness and the OMM surface is represented as a transparent gray mesh. Curvedness is an unsigned combination of the two principal components of curvedness and is used because the surface normal vectors do not have canonical sign. (B) Combined histogram of total IMM curvedness of elongated (top) and fragmented (middle) mitochondria in MEF^mtGFP cells treated with vehicle and Tg. Dashed vertical lines correspond to peak histogram values of pooled data. Graph (bottom) showing peak histogram values from each mitochondrion within each corresponding treatment and mitochondrial morphology class. Quantifications from vehicle elongated n = 20, Tg elongated n = 18, vehicle fragmented n = 11, and Tg fragmented n = 15 mitochondria are shown. P values from Mann–Whitney U test are indicated. **P < 0.01. (C) Combined histogram of cristae curvedness of elongated (left) and fragmented (middle) mitochondria in MEF^mtGFP cells treated with vehicle and Tg. Dashed vertical lines correspond to peak histogram values of pooled data. Graph (right) showing peak histogram values from each mitochondrion within each corresponding treatment and mitochondrial morphology class. Quantifications from vehicle elongated n = 20, Tg elongated n = 18, vehicle fragmented n = 11, and Tg fragmented n = 15 mitochondria are shown. P values from Mann–Whitney U test are indicated. *P < 0.05; **P < 0.01. (D) Combined histogram of cristae junction curvedness of elongated (left) and fragmented (middle) mitochondria in MEF^mtGFP cells treated with vehicle and Tg. Dashed vertical lines correspond to peak histogram values of pooled data. Graph (right) showing peak histogram values from each mitochondrion within each corresponding treatment and mitochondrial morphology class. Quantifications from vehicle elongated n = 20, Tg elongated n = 18, vehicle fragmented n = 11, and Tg fragmented n = 15 mitochondria are shown. P values from Mann–Whitney U test are indicated. *P < 0.05; ****P < 0.001.

Larger changes in curvature were observed in cristae and crista junctions. The cristae of fragmented mitochondria were less curved than those of elongated mitochondria in the absence of ER stress. Interestingly, Tg treatment induced significant but opposing changes in fragmented and elongated mitochondria. In elongated mitochondria, curvedness of cristae decreased upon Tg treatment, while in fragmented mitochondria, curvedness increased upon Tg treatment. In crista junctions, the most notable difference was an increase in curvedness in Tg-treated cells with elongated mitochondria compared with both the vehicle-treated elongated mitochondria and the Tg-treated fragmented mitochondria. This reflects and confirms the visual observation of crista ordering upon Tg treatment in elongated mitochondria in the tomograms.

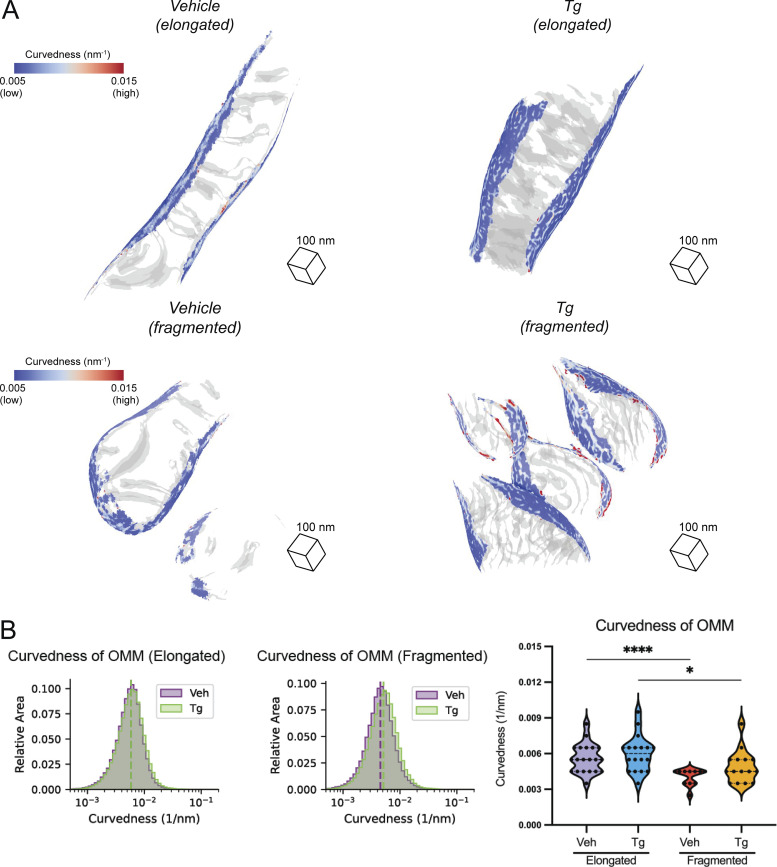
OMM curvedness is dependent on mitochondrial network morphology

In addition to the IMM, we calculated curvedness of the OMM for each mitochondrion. For both vehicle and Tg-treated cells, curvedness of the OMM is decreased in fragmented mitochondria relative to elongated networks (Fig. S7). This metric likely reports primarily on the radius of the mitochondria as a whole, suggesting that fragmented mitochondria are larger in radius despite their apparent shorter overall length.

Figure S7.

OMM curvature analysis. (A) Representative membrane surface reconstructions of elongated (top) and fragmented (bottom) mitochondria in MEF^mtGFP cells treated with vehicle and Tg (500 nM, 8 h). The OMM surface is colored by membrane curvedness and the IMM surface is represented as a transparent gray mesh. (B) Combined histogram of total OMM curvedness of elongated (left) and fragmented (middle) mitochondria in MEF^mtGFP cells treated with vehicle and Tg. Dashed vertical lines correspond to peak histogram values of pooled data. Graph (right) showing peak histogram values from each mitochondrion within each corresponding treatment and mitochondrial morphology class. Quantifications from vehicle elongated n = 20, Tg elongated n = 18, vehicle fragmented n = 11, and Tg fragmented n = 15 mitochondria are shown. *P < 0.05; ****P < 0.001.

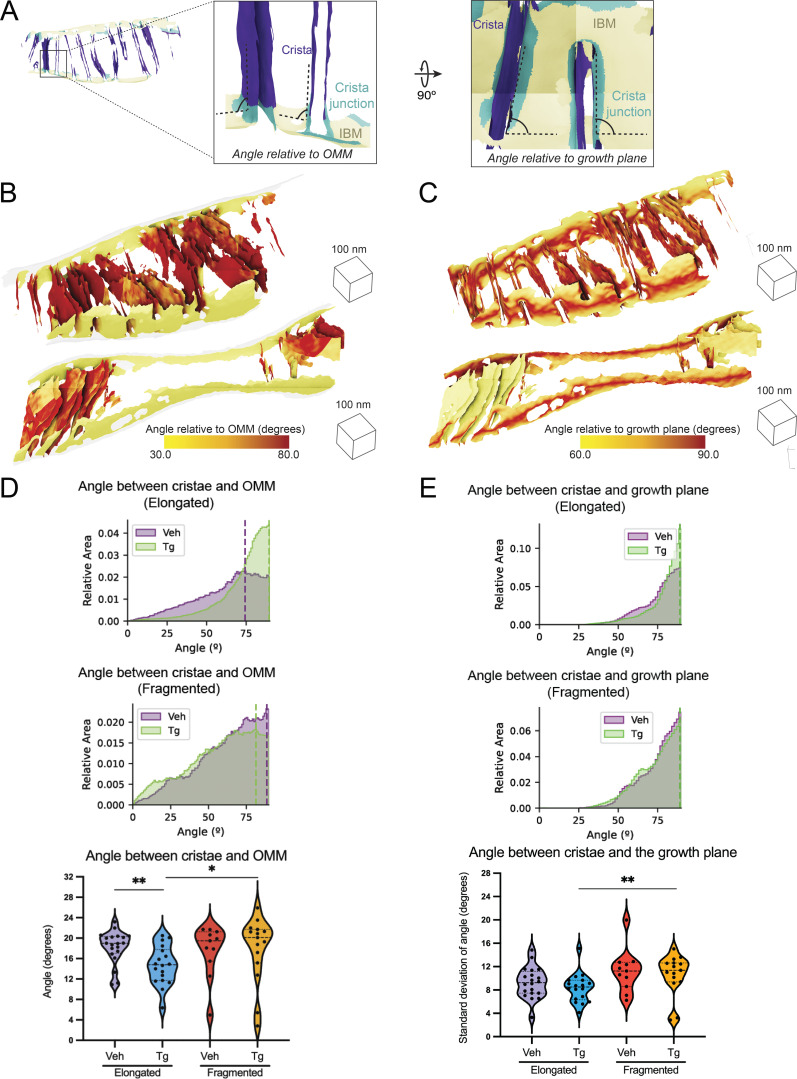
Membrane orientations in elongated and fragmented mitochondria differ upon Tg treatment

We next sought to understand to what degree the orientation of mitochondrial cristae was regulated and how they changed in different mitochondrial morphologies as well as in response to Tg-induced ER stress. We took advantage of the 3D nature of our surface reconstructions to measure the orientation of each triangle in the surface mesh relative to the nearest point on the OMM, as well as to the cell’s growth plane (the plane of the EM grid substrate on which the cells are grown; Fig. 6 A and Fig. S6). Visual inspection revealed that the highly organized lamellar phenotype that was typical of elongated mitochondria in Tg-treated cells was almost entirely held orthogonal to the OMM, forming the distinctive ladder-like phenotype (Fig. 6 B). Similarly, most but not all of these lamellar cristae were remarkably vertical relative to the growth plane of the cell (Fig. 6 C). We plotted the angles of the cristae and junctions relative to the OMM and the growth plane, revealing changes primarily in the variance of the angles rather than the peak position (Fig. 6 A and Fig. S6). Due to this, we quantified the standard deviation of these values for each mitochondrion in order to assess statistical significance of observed changes (Fig. 6, D and E). This revealed a significant decrease in the variability of the angle of the crista bodies relative to the OMM for elongated mitochondria in Tg-treated cells. Additionally, we observed a significant (based on the Mann–Whitney U test of standard deviations) increase in the variability of the angle of the cristae relative to the OMM for fragmented mitochondria in comparison with elongated mitochondria in Tg-treated cells (Fig. 6 and Table S2). We also identified a significant decrease in variability of the angle of the crista body relative to the growth plane in Tg-treated elongated relative to fragmented mitochondria (Fig. 6 E). In both cases, these differences corresponded to increased control over the orientation of the ladder-like lamellar cristae observed in the elongated Tg-treated condition. Despite the changes in crista orientation, no significant changes were observed in the angle of junctions relative to the OMM or the growth plane (Fig. S6).

Figure 6.

Tg-induced ER stress drives changes in crista orientation in elongated mitochondrial networks. (A) Surface membrane reconstruction colored by inner membrane compartments (IBM, tan; junction, cyan; crista, purple) defining angular measurements between the surface and the nearest OMM or to the growth plane of the cell. (B) Two representative membrane surface reconstructions of lamellar Tg-treated elongated mitochondria, colored by the angle of IMM relative to OMM. (C) Two representative membrane surface reconstructions of a less rigidly oriented Tg-treated elongated mitochondria, colored by an angle of IMM relative to the growth plane of the cell. (D) Combined histogram of the angle of cristae relative to OMM in elongated (top) and fragmented (middle) mitochondria in MEF^mtGFP cells treated with vehicle and Tg. Dashed vertical lines correspond to peak histogram values of pooled data. Graph (bottom) showing distribution of standard deviations within each corresponding treatment and mitochondrial morphology class. Quantifications from vehicle elongated n = 20, Tg elongated n = 18, vehicle fragmented n = 11, and Tg fragmented n = 15 mitochondria are shown. *P < 0.05; **P < 0.01. (E) Combined histogram of the angle of cristae relative to growth plane in elongated (top) and fragmented (middle) mitochondria in MEF^mtGFP cells treated with vehicle and Tg. Dashed vertical lines correspond to peak histogram values of pooled data. Graph (bottom) showing distribution of standard deviations within each corresponding treatment and mitochondrial morphology class. Quantifications from vehicle elongated n = 20, Tg elongated n = 18, vehicle fragmented n = 11, and Tg fragmented n = 15 mitochondria are shown. P values from Mann–Whitney U test are indicated. **P < 0.01.

Application of surface morphometrics and analysis to additional organellar membranes

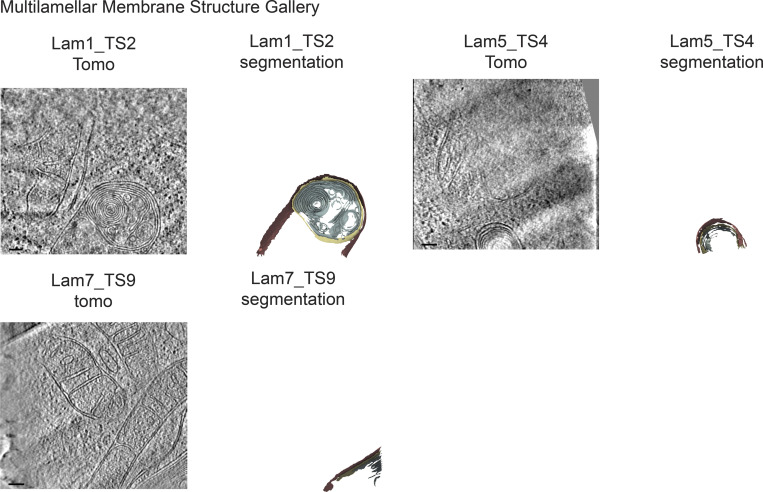
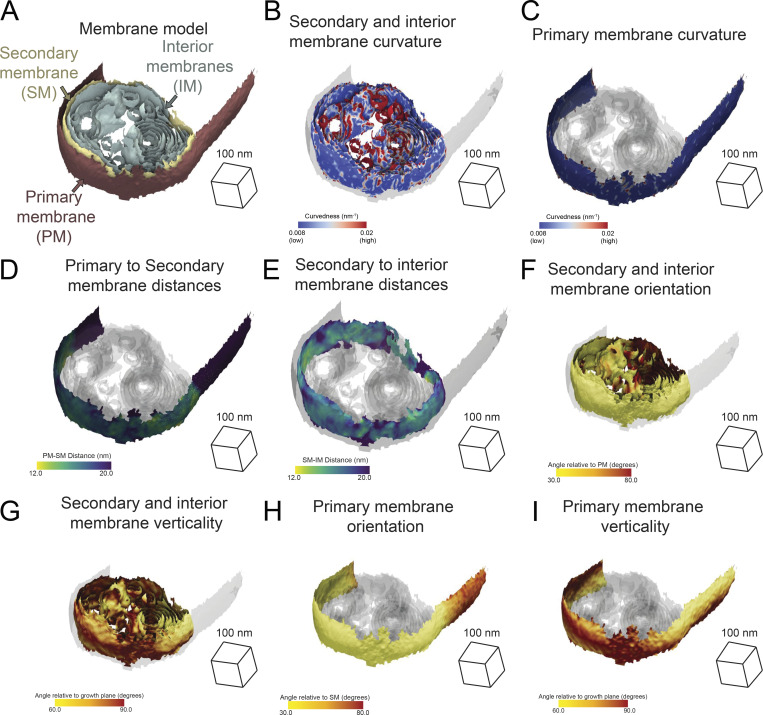
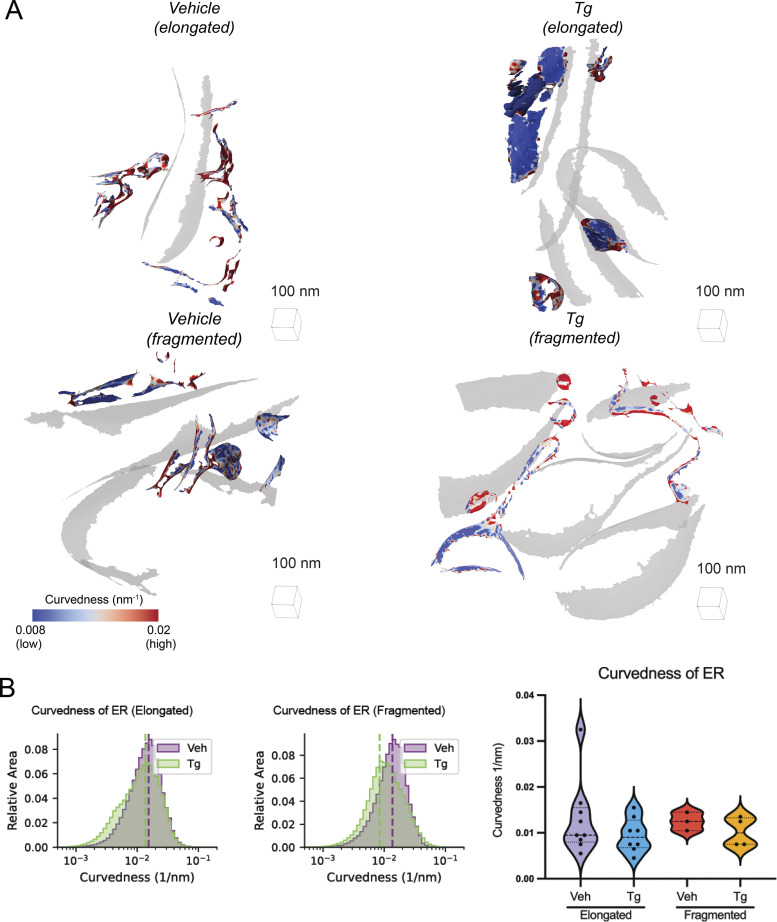
We further demonstrated the generality of this approach by generating mesh surfaces for membranes of other organelles present in our data: the ER (Figs. S1, S2, and S3) and observed multilamellar membrane structures (Fig. S8). We applied our morphometrics pipeline to quantify parameters of membrane architecture of these organelles. The observed multilamellar structures are comprised of multiple membranes (Bieber et al., 2022), including the primary membrane and the secondary membrane, as well as interior membranes (Fig. S9). We then visualized the spatial distributions of the curvatures, distances, and orientations of these distinct membranes on the generated surface reconstructions (Fig. S9). Additionally, we calculated the curvedness of ER membranes in cells with differing mitochondrial populations and observed no significant changes in any of the conditions (Fig. S10).

Figure S8.

Gallery of multilamellar membrane structures used for quantifications. Virtual slices of tomograms (left panels) and corresponding reconstructed surface mesh models (right panels) of multilamellar membrane structures. Primary membrane shown in red. Secondary membrane shown in yellow. Interior membranes shown in sage green. Meshes have been tilted 20° relative to tomography slice for visualization. Scale bar = 100 nm. n = 3 tomograms.

Figure S9.

Multilamellar membrane structure morphometric analysis. (A) Exemplar multilamellar membrane structure surfaces with membranes labeled. Primary membrane in red. Secondary membrane in yellow. Interior membranes in sage green. (B) Secondary and interior membrane surfaces colored by membrane curvedness; the primary membrane is represented as a transparent gray. (C) Primary surface is colored by membrane curvedness; the secondary and interior membranes are represented as a transparent gray. (D) Primary surface is colored by primary-to-secondary membrane distance; the secondary and interior membrane surfaces are shown in transparent gray. (E) Secondary surface colored by secondary to nearest interior (secondary–interior) membrane distance; the primary and interior membrane surfaces are shown in transparent gray. (F) Secondary and interior membranes surfaces are colored by angle relative to the primary membrane. Primary membrane surface is shown in transparent gray. (G) Secondary and interior membrane surfaces are colored by an angle relative to the growth plane of the cell. Primary membrane surface shown in transparent gray. (H) Primary membrane surface is colored by relative angle to the secondary membrane. Secondary and interior membrane surfaces are shown in transparent gray. (I) Primary membrane surface colored by relative angle to the growth plane of the cell. Secondary and interior membranes are shown in transparent gray.

Figure S10.

ER membrane curvature analysis. (A) Representative membrane surface reconstructions of the ER in MEF^mtGFP cells treated with vehicle and Tg (500 nM, 8 h) and associated with defined mitochondrial populations (elongated and fragmented). The ER surface is colored by membrane curvedness, and the OMM surface is represented as a transparent gray mesh. (B) Combined histograms of total ER curvedness of elongated (left) and fragmented (middle) mitochondria in MEF^mtGFP cells treated with vehicle and Tg. Dashed vertical lines correspond to peak histogram values of pooled data. Graph (right) showing peak histogram values from each ER membrane within each corresponding treatment and mitochondrial morphology class. Quantifications from vehicle elongated n = 9, Tg elongated n = 8, vehicle fragmented n = 3, and Tg fragmented n = 4 ER are shown.

Monitoring ER–mitochondrial contacts by surface morphometrics

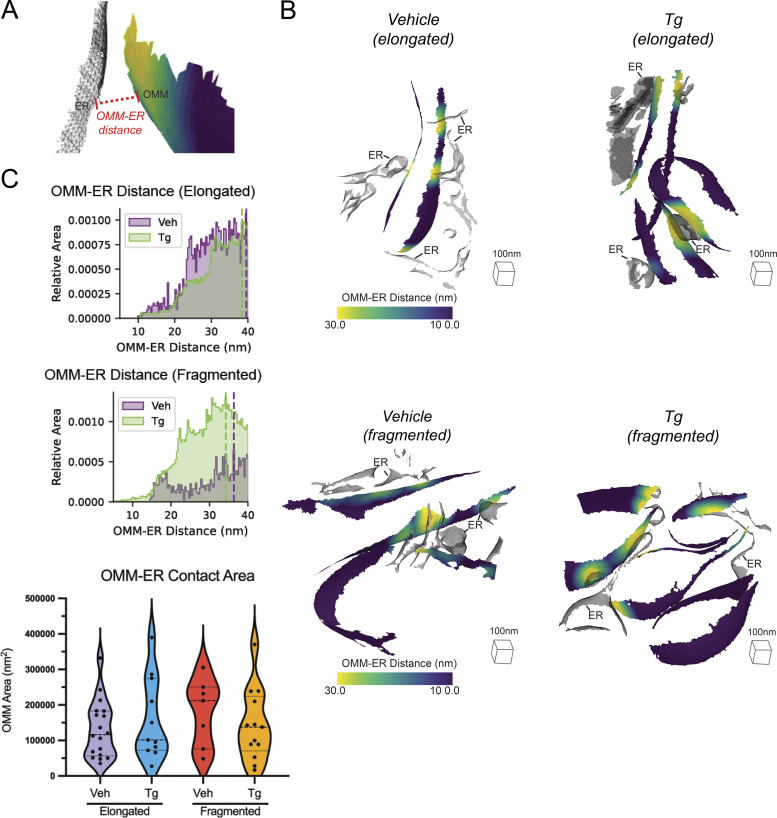
Mitochondria–ER contact sites are sites of significant exchange of lipids and proteins have been previously associated with a wide variety of critical regulatory functions for mitochondria, ranging from mitochondrial fission (Friedman et al., 2011) to autophagy (Bosc et al., 2020). To investigate whether the remodeling we observed in response to Tg-induced ER stress was correlated with alterations to the ultrastructure of these contact sites, we leveraged our 3D morphometrics workflow to quantify changes in ER-mitochondrial contacts in elongated vs. fragmented mitochondrial networks as well as in ER stress induced by Tg. Distances between different organelles can be as readily calculated as distances within mitochondria, with the only additional challenge that not all tomograms contained ER, and not all ER present was interacting with mitochondria. We measured the distance between the OMM and the nearest ER in all tomograms where the ER was present and visualized the contact sites on the surfaces of the OMM (Fig. S11, A and B). This showed detailed mapping of these functionally critical interactions in three dimensions. We also quantified the distribution of ER–OMM distances as a combined histogram (Fig. S11 C). None of the conditions were statistically significant, suggesting that changes in ER–mitochondrial contact distance or area at the imaged time point were not associated with the altered mitochondrial ultrastructure (Fig. S11 D).

Figure S11.

Surface analysis of mitochondria–ER contact sites. (A) Surface membrane reconstruction defining OMM (blue-yellow gradient) and ER (transparent mesh) distance measurement. (B) Representative membrane surface reconstructions of elongated (top) and fragmented (bottom) mitochondria in MEF^mtGFP cells treated with vehicle and Tg (500 nM) colored by OMM to ER (OMM–ER) membrane distance. (C) Combined histogram of OMM–ER distances of elongated (top) and fragmented (bottom) mitochondria in MEF^mtGFP cells treated with vehicle and Tg. Dashed vertical lines correspond to peak histogram values of pooled data. (D) Graph showing peak histogram values from each tomogram within each corresponding treatment and mitochondrial morphology class. Quantifications from vehicle elongated n = 18, Tg elongated n = 11, vehicle fragmented n = 7, Tg fragmented n = 13 mitochondria are shown.

Discussion

We describe a correlative cellular cryo-ET workflow for quantifying differences in membrane ultrastructure between distinct mitochondrial network morphologies and cellular conditions. Our approach takes advantage of the distinct capabilities of multiple imaging modalities (fluorescence microscopy and cryo-ET) to correlate single-cell, organellar network morphologies to single-organellar membrane ultrastructures in varying cellular conditions. To our knowledge, this is the first application of a correlative approach that directly assesses how distinct organellar morphologies (e.g., elongated versus fragmented mitochondria) and cellular stress states (e.g., presence or absence of Tg-induced ER stress) influence mitochondrial membrane remodeling at nanometer-scale resolution. Our workflow can be divided into two functional steps: (1) single-cell targeting and (2) 3D surface morphometrics analysis. The first step involves identifying cells that exhibit a particular mitochondrial network morphology by cryo-fluorescence microscopy, targeting these cells for sample thinning to generate cellular lamellae by cryo-FIB milling, and imaging these cellular lamellae by cryo-ET to reveal organellar membrane ultrastructures (Fig. 1, A–D, and Fig. 2 A). The second step involves adapting semiautomated segmentation and surface mesh reconstruction algorithms to cryo-ET data, thereby enabling unbiased quantification of several membrane parameters at high precision. We determined that the screened Poisson reconstruction approach (Kazhdan and Hoppe, 2013) provides a more accurate estimation of the implicit membrane geometry of complex membranes and can be used to model and quantify complex membranes such as the IMM.

To demonstrate proof-of-concept of our correlative workflow, we asked whether bulk changes in mitochondrial network morphologies were associated with ultrastructural remodeling of mitochondrial membranes, both in the presence and absence of ER stress. We identified cells with distinct mitochondrial morphologies (e.g., fragmented versus elongated) in both treatment conditions and quantified mitochondrial membrane parameters such as inter- and intramitochondrial membrane distances, curvedness, and orientation. We demonstrate that our approach can be used to identify changes to membrane ultrastructure in two ways. First, we can evaluate ultrastructural changes on an individual mitochondrion basis by overlaying values directly on individual triangles within our membrane surface maps. This enables contextualization of membrane quantifications based on the specific membrane microenvironment. Second, we combine ultrastructural quantifications across many mitochondria within specific morphological or cellular physiological groups, thereby enabling us to establish statistical criteria for identifying trends even in the context of mitochondrial pleomorphism across all conditions.

We first used our workflow to quantify the intermembrane distance between the inner and outer membranes of mitochondria (Fig. 3). These two membranes are mechanically linked by interactions between proteins on the two membranes (Bohnert et al., 2012; Callegari et al., 2019; Bauer et al., 2000), and in some instances, there are reports of inner membrane-bound proteins acting in trans on the outer membrane (Aaltonen et al., 2016). The uniquely high resolution and 3D information afforded by cryo-ET allowed us to visualize the fluctuations of distances between these membranes as well as to quantify changes in the overall distributions. We identified significant increases in the IMM–OMM spacing of mitochondria in fragmented networks over those in elongated networks. This increase in spacing may reduce the effectiveness of protein interactions across the two membranes, thereby increasing isolation of the IMM from external signals. In contrast, within the elongated population, Tg treatment reduced IMM–OMM spacing, suggesting tighter interactions that may be critical for the protective function of stress-induced mitochondrial hyperfusion (Lebeau et al., 2018). The difference in distance, from 13.5 to 12.7 nm between the centers of the membranes, is small, but correcting for the ∼7 nm thickness of mitochondrial membranes (Perkins et al., 1997) yields a change in intermembrane contact distance from 6.5 to 5.7 nm or a 12% reduction. This could have a significant effect on the potential for transmembrane activity of proteins, such as phosphatidylserine decarboxylase, an IMM protein previously suggested to act on the OMM (Aaltonen et al., 2016). The ability to consistently and robustly resolve such small but physiologically significant differences in intermembrane spacing opens new avenues for understanding how different perturbations may impact intermembrane communication in mitochondria. The spatially resolved high OMM–IMM distance proximal to crista junctions may also eventually prove to be an effective automated localization signal for particle picking and guided subtomogram averaging of proteins, such as the translocase of the OMM complex (Bohnert et al., 2012), which associate with the MICOS complex and may impact MICOS complex organization (Wollweber et al., 2017).

Mitochondrial inner membranes are functionally divided between the IBM and the mitochondrial cristae, with the cristae junctions that divide the two components organized by the MICOS complex (Wollweber et al., 2017). We were able to automatically classify our inner membrane surface into the IBM, cristae, and junctions based on distance from the OMM, and using this classification were able to quantify specific architectural changes in cristae and junctions in different mitochondrial populations in the presence or absence of Tg-induced ER stress. We measured the membrane spacing within and between cristae and junctions (Figs. 4 and S6), quantified the curvedness of the membranes (Figs. 5, S6, S7, S9, and S10), and measured their orientation relative to the OMM and the growth plane (Fig. S6 and 6). We observed consistent but opposing changes between fragmented and elongated mitochondrial populations when exposed to Tg. In elongated populations of cells treated with Tg, cristae became narrower, less curved, and more vertical lamellar structures that were highly orthogonal to the OMM. This is consistent with previous reports of ultrastructural changes induced in brown adipocytes subjected to cold stress (Latorre-Muro et al., 2021). In these conditions, modulations to the MICOS subunit Mic 19 remodels cristae architecture through the activity of the ER-stress responsive PERK kinase—a mechanism similar to that responsible for ER-stress-induced mitochondrial elongation (Lebeau et al., 2018). While future work is needed to determine whether cristae remodeling and mitochondrial elongation are regulated by the same mechanism, our results highlight that these two changes in mitochondrial shape are correlated in response to Tg-induced ER stress.

In contrast, cristae in fragmented populations became more swollen upon induction of ER stress, as measured by increases in intra-crista membrane spacing and crista curvedness. Of particular interest, our workflow will enable local analysis of individual cristae on the basis of their spacing, curvedness, and orientation to isolate different functional microenvironments that can be studied for differences in protein composition and conformation. Crista ultrastructure is largely controlled by MICOS (Harner et al., 2011), ATP synthase (Blum et al., 2019), and OPA1 (Hu et al., 2020), and we predict that the changes observed are driven by changes in composition, localization, or conformation of these proteins. Cryo-ET offers the unique combination of cellular and structural detail to pursue studies of how these proteins differ in distribution and conformation in different cristae even within the same mitochondrion, and how that is reflected in differences in mitochondrial architecture and function.

We demonstrated the general utility of our workflow beyond mitochondrial membranes and analyzed the curvedness, intermembrane distances, and orientation of cellular membranes of the ER and observed multilamellar membrane structures (Fig. S7, S9, S10, and S11). Although our results did not reveal any statistically significant differences in the architecture of these cellular membranes upon Tg-induced ER stress, we anticipate that our workflow will facilitate future studies on the critical importance of membrane remodeling of these organelles induced by different types of cellular perturbations.

A notable caveat of the methodology we have developed and presented is the potential for bias in which components of membrane are segmented and which are not. In addition to the components of membrane that are severed during the cryo-FIB-milling process, membranes fade and disappear when their normal vectors fall into the missing wedge of angles not collected in the tilt series (Turk and Baumeister, 2020), which can be seen in the lack of orientations less than 30° relative to the growth plane (Fig. 6). Additionally, the segmentation algorithm (Martinez-Sanchez et al., 2014) used in this study traces lower curved membranes more easily than high curved membranes, leading to limited segmentations of tight, high curved crista junctions and crista tips. We have mitigated these biases by comparing data collected in similar ways and processed identically across different populations, and we anticipate that improvements to both data collection and data processing will further reduce these biases in the future. The majority of these data were collected without the use of a post-column energy filter (Koning et al., 2018) or phase plate (Imhof et al., 2019), both of which improve contrast of visible features within tomograms. Additionally, there have been recent advances in algorithmic approaches to improve the quality and completeness of segmentations (Zhou et al., 2020 Preprint; Chen et al., 2017; Buchholz et al., 2018; Liu et al., 2021 Preprint). The flexibility of the screened Poisson surface reconstruction workflow will enable easy adaptation of these morphometric approaches to new segmentation tools.

Beyond incorporating new advances for ultrastructure, the automated surface reconstruction algorithm established in this paper for quantitative ultrastructural analysis presents additional potential for use in visual proteomics (Bäuerlein and Baumeister, 2021) and subtomogram averaging. Finding proteins in noisy tomograms is challenging, and membrane segmentations have proven effective guides for localizing protein density that would otherwise be difficult to detect with traditional template-matching approaches (Wietrzynski et al., 2020; Martinez-Sanchez et al., 2020). These approaches have in the past depended on voxel segmentations, but moving to high-quality meshes has the potential to improve particle picking further by constraining the orientation search to match the geometry of the membrane, as well as providing a more consistent central position than voxel segmentation, which might have variable thickness. Prior knowledge of orientation has proven to be valuable for achieving successful initial alignments for subtomogram averaging as well (Basanta et al., 2020). Membrane meshes have been used very successfully to guide subtomogram averaging in the past (Navarro et al., 2018; Burt et al., 2021 Preprint), but these have relied on manual segmentation and thus have been low throughput and restricted to relatively simple geometry. Surfaces generated automatically with our software have the potential to extend this guided approach to larger numbers of tomograms and much more complex biological environments.

There is tremendous potential for cryo-ET to enable better understanding of function and regulation by associating changes in protein conformation with the local cellular milieu (Erdmann et al., 2021; Wietrzynski et al., 2020; O’Reilly et al., 2020 Preprint; Siegmund et al., 2018; Guo et al., 2018; Jordan et al., 2018; Albert et al., 2020; Lin and Nicastro, 2018). Cryo-ET’s ability to reveal both 3D protein conformation and the cellular ultrastructures surrounding it allows connections between the two that cannot be determined any other way. By using correlative light microscopy approaches to incorporate knowledge of the physiological state of the cell in combination with detailed local membrane morphometrics, it will be possible to gain a much more detailed understanding of how both global cellular state and local membrane ultrastructure correlate to protein localization and conformation. Moving from qualitative association to quantification with the measurement of statistical significance, as outlined here, will improve the power of structure-context mapping to understand how protein structure and function impact complex cellular processes.

Materials and methods

Preparation of vitrified mouse embryonic fibroblasts on cryo-EM grids

Mouse embryonic fibroblasts with mitochondria-labeled GFP (MEF^mtGFP; Wang et al., 2012) were cultured in Dulbecco’s Modified Eagle Medium + GlutaMAX (Gibco) additionally supplemented with HiFBS (10%) and glutamine (4 mM) on fibronectin-treated (500 μg/ml; Corning) and UV-sterilized R ¼ Carbon 200-mesh gold EM grids (Quantifoil Micro Tools). After 15–18 h of culture, MEF^mtGFP cells were transferred to fresh media supplemented with DMSO in the vehicle treatment group or fresh media supplemented with Thapsigargin (500 nM; Thermo Fisher Scientific) in the Tg treatment group. After 8 h of incubation, samples were plunge-frozen in a liquid ethane/propane mixture using a Vitrobot Mark 4 (Thermo Fisher Scientific). The Vitrobot was set to 37°C and 100% relative humidity, and blotting was performed manually from the back side of grids using Whatman #1 filter paper strips through the Vitrobot humidity/temperature chamber side port. The Vitrobot settings used to disable automated blotting apparatus were as follows: Blot total: 0, 2; Blot force: 0, 3; Blot time: 0 s.

Cryo-fluorescence microscopy and mitochondria network morphology scoring

Fluorescence and bright-field tiled image maps (atlases) of EM grids containing vitrified cellular samples were acquired with a Leica CryoCLEM microscope (Leica) and collected using Leica LAS X software (25 um Z stacks with system optimized steps, GFP channel ex: 470, em: 525). Z stacks were stitched together in LAS X navigator to provide a single mosaic of maximum projections of the GFP signal, enabling rapid identification of the bulk mitochondrial morphology for each cell. For classification of mitochondrial network morphologies, max projections of individual tiles within fluorescence atlases of MEF^mtGFP cells were randomized and blinded. Five researchers classified the cells as containing primarily elongated or fragmented mitochondria (see Fig. 2 A for examples of scoring). Atlases were then exported from LAS X and loaded into MAPS (3.13; Thermo Fisher Scientific) for fluorescence-guided milling.

Fluorescence -guided milling

Cryo-FIB milling of lamellae was performed using an Aquilos dual-beam cryo-FIB/SEM instrument (Thermo Fisher Scientific). The fluorescence atlases were overlaid and aligned to SEM atlases of the same grid to target milling of MEF^mtGFP cells with distinct mitochondrial network morphologies, as determined during blind classification (described above). MEF^mtGFP cell targets were chosen based on their position within grid squares, the thickness of the ice in their vicinity, and their bulk morphology as assessed by the GFP fluorescence channel. Prior to milling, EM grids were first coated with a thin platinum sputter, then coated with an organometallic platinum layer using a gas injection system for 3–4 s using an automation script (Barad, 2023), followed by a third and final layer of platinum sputter. Targeted cells were milled manually (Schaffer et al., 2015) or using an automated cryo preparation workflow (Buckley et al., 2020), and both methods used xT software with MAPS (Thermo Fisher Scientific). Minimal SEM imaging for monitoring was done at 2 keV to ensure thin lamella generation while avoiding radiation damage. A total of six treated grids and eight untreated grids were milled for further tomography analysis.

Tilt series data collection

EM grids containing lamellae were transferred into a 300 keV Titan Krios microscope (Thermo Fisher Scientific) equipped with a K2 Summit direct electron detector camera (Gatan). A small subset of data was collected after the installation of a BioQuantum energy filter (Gatan). Individual lamellae were montaged with low dose (1 e⁻/Ų) at high magnification to localize cellular regions containing mitochondria, which were identified by their distinctive IMMs and OMMs. Data were collected to maximize the number of non-overlapping fields of view containing mitochondria, with no targeting of specific observed membrane ultrastructure. Tilt series were acquired using SerialEM software (Mastronarde and Held., 2017) with 2° steps between −60° and +60°. Data were collected with pixel sizes of 3.11 , 3.35 , or 3.55 Å, and a nominal defocus range between −5 and −10 µm. A subset of data was collected with dose fractionation, with 10 0.1 e/Ų frames collected per second. The total dose per tilt was 0.9–1.2 e/Ų and the total accumulated dose for the tilt series was under 70 e/Ų.

Tilt series processing and reconstruction

Dose-fractionated tilt series micrograph movies underwent contrast transfer function estimation and motion correction in Warp and combined into averaged tilt series for alignment. Both non-fractionated and fractionated tilt series were then aligned using patch tracking in etomo (Mastronarde and Held, 2017), with four times binning and 400 binned pixel patches. Resulting contours were manually curated to remove poorly aligning patches, and the remaining contours were used for alignment and reconstruction with weighted back projection into four times binned tomograms. Tomogram thicknesses ranged from 95 to 233 nm.

Semiautomated segmentation

Automated detection and enhancement of mitochondrial membranes were performed using the TomoSegMemTV software package (Martinez-Sanchez et al., 2014). Settings were optimized for individual tomograms to maximize the membrane quality. Typical parameters for membrane enhancement were as follows: scale_space -s 3; dtvoting -s 12; surfaceness -m 0.17 -s 0.8 -p 0.8; dtvoting -w -s 10; surfaceness -S -s 0.75 -p 0.75 -l 20; thresholding -l 0.01–2 30; global analysis −3 100.

The output correlation volumes containing high pixel intensity corresponding to membrane locations were imported into AMIRA (Thermo Fisher Scientific) for manual curation. Mitochondrial inner and outer membranes and ER were segmented and designated as separate labels in Amira using 3D threshold-based selection and the 3D magic wand tool, and very small gaps in segmentation were filled in manually using a paint tool.

Software workflow

The surface morphometrics pipeline is a python-scripted workflow with requirements that can be installed as a conda environment contained in an “environment.yml” file. The workflow is fully scripted and configurable with a “config.yml” file and is run in three fully pipelined steps, with statistical analysis and visualization as an optional fourth step. First, a segmentation MRC file is converted automatically to a series of surface meshes formatted in the VTP file format. Second, for each mesh, the surface is converted to a graph (tg format) and curvature is estimated using pycurv. Third, orientations and distances between and within surfaces are calculated using the resulting graphs, and a CSV with quantifications as well as a final VTP surface file is output with all quantifications built in. Fourth, the outputs from multiple tomograms are combined for visualization and statistical analysis. Times and computational requirements are shown in Table S1.

Automated surface reconstruction

The process for conversion of voxel segmentations into smooth open surfaces fit for quantification was fully automated using python and pymeshlab (Muntoni and Cignoni, 2021). First, the individual classes in each segmentation volume were converted into unoriented point clouds, with a single point at the center of each segmented voxel. Next, the normal vectors for each point in the point cloud were estimated based on 120 neighbors with a single smoothing iteration. A surface mesh was calculated from the oriented point cloud using the screened Poisson algorithm (Kazhdan and Hoppe, 2013), with a reconstruction depth of 9, an interpolation weight of 0.7, and a minimum number of samples of 1.5. These settings were chosen to maximize correspondence to the data rather than smoothness. The resulting surface extended beyond the segmented region, so triangles more than 1.5 nm away from the point cloud were deleted. Interpolation weight (point_weight) and the mask distance (extrapolation_distance) are both configurable in the surface morphometrics pipeline if more aggressive smoothing and hole filling are desirable. The resulting mesh was simplified with quadric edge collapse decimation to produce a surface that represented the membrane with 150,000 triangles or fewer. This process was accomplished with the “segmentation_to_meshes.py” script.

Refinement of surface orientation and estimation of surface curvedness using pycurv

Output surfaces were processed with pycurv to remove extraneous and poorly modeled regions and to refine surface normals using an area-weighted tensor voting approach (Salfer et al., 2020). This vector voting process also resulted in robust estimation of curvature metrics. As the open surfaces generated from membrane segmentations do not have a meaningful inside or outside, signed metrics of curvature are not appropriate for analysis; instead, the unsigned curvedness metric (Eq. 1) provides a single positive readout that can be used for quantification. Pycurv output triangle graph files containing the refined normal angles and curvedness metrics, which enabled efficient computation of additional morphometric features, and the pycurv library was used as a base for the remaining quantifications in the manuscript. Pycurv calculations were done in the “run_pycurv.py” script.

$$curvedness=\sqrt{\frac{{\kappa }_1^2+{\kappa }_2^2}{2}}\text{.}$$ (1)

Calculation of distances between individual surfaces

For calculations of distances between respective surface meshes, the minimum distance from each triangle on one surface to the nearest triangle on the other surface was calculated using a k-dimensional tree. Both the distance and identifier of the nearest triangle on the neighboring surface are recorded in the triangle to enable further analysis. This analysis is accomplished as part of the “measure_distances_orientations.py” script.

Automated subclassification of the IMM

In order to understand how different components of the IMM vary with bulk morphology, triangles from inner membrane surfaces were classified into IBM, crista junction, or crista body based on their distance from the OMM. Triangles falling within 19 nm of the OMM are classified as IBM, those between 19 and 40 nm from the OMM as crista junction, and those >40 nm from the OMM are classified as crista body. The IBM distance was chosen as the smallest integer value above the peak OMM–IMM distance for all tomograms, while the crista body distance was selected based on visual inspection and to ensure enough triangles were assigned to the crista junctions for robust calculations.

Calculation of distances between components within the inner membrane surface

As all-to-all distance measurements within the same surface would trivially yield the spacing between neighboring triangles on the graph rather than true distances between neighboring segments of membrane, measurements of distances within individual surfaces are made based on intersections along the normal vector of each triangle, similar to approaches used previously (Collado et al., 2019). To modify this approach for measuring distances on surfaces without canonical normal directions, the first intersecting triangle was measured both along the normal vector and its inverse, and those distances were sorted into shorter and longer distances. For cristae and junctions, the shorter distances were interpreted as the spacing between membranes within a crista or junction, whereas the longer distance of the two was interpreted as the distance between individual cristae or junctions. Normal-vector-based distance measurements are sensitive to the completeness of the segmentation, and not all triangles have a normal-vector-based neighbor. Those triangles were filtered out before any further quantifications. These measurements are made in the “measure_distances_orientations.py” script.

Calculation of relative orientations with the growth plane and neighboring regions

The smoothed normal vectors for each triangle, as estimated by pycurv, were used to estimate the orientation of mitochondrial membranes relative to each other and the growth plane. Angles considered ranged only from 0° to 90° in the absence of canonical normal angle directions. For comparisons to the growth plane, the relative angle was calculated as follows (Eq. 2):

$$verticality=\mathit{arccos}\left(\left|norma{l}_z\right|\right)\text{.}$$ (2)

Comparisons of orientations between membranes were made by comparison of the pycurv-smoothed normal vector between each triangle on a surface to the normal vector to its nearest neighbor as determined previously. The angle between these two vectors was calculated as follows (Eq. 3):

$$relative\_angle=\mathit{arccos}\left(|self·neighbor|\right)\mathit{.}$$ (3)

Both orientation calculations are determined in the ”measure_distances_orientations.py“ script.

Visualization and aggregate quantification of data and assessment of statistical significance

The per-triangle measurements are stored within the pycurv triangle graph file as well as being output both as surface meshes using the visualization pipeline “vtp” (Schroeder et al., 2006) format as well as in csv files using existing pycurv functions. Visualizations were generated using the vtp files in paraview (Ahrens et al., 2005). Aggregate histograms and empirical continuous distribution plots were plotted in matplotlib after aggregating all triangles across all tomograms within a condition and morphology group and weighting each triangle by its area (Hunter, 2007). Violin plots were generated by generating triangle-area weighted histograms for each tomogram with 100 bins and identifying the value of the most populated bin, followed by aggregation of peak values. Statistics were similarly calculated using Mann–Whitney U tests (Mann and Whitney, 1947) on the peak values calculated for each tomogram to identify statistically significant differences in peak positions. For quantifying differences in distribution shape, a Mann–Whitney U test was applied to the standard deviations of each tomogram rather than the histogram peak. Statistical testing based on distributions, rather than peaks, is complicated by unbiased assessment of the number of independent samples in each tomogram. Aggregation, statistics, and visualization are accomplished by the “morphometrics_stats.py” classes and functions, and the mitochondria-specific statistics and visualizations are generated by the “mitochondria_statistics.py” script. The complete output of the per mitochondrion analyses for every measurement is available at https://zenodo.org/record/7510830.

Online supplemental material

Figs. S1, S2, and S3 are a gallery of cellular membranes used for downstream quantifications from cells with elongated mitochondrial networks in the absence of ER stress, cells with elongated mitochondrial networks in the presence of ER stress, and cells with fragmented mitochondrial networks in the presence and absence of ER stress, respectively. Fig. S4 shows a comparison of different surface reconstruction algorithms. Fig. S5 is a gallery of histograms showing the distribution of IMM–OMM distances for each individual mitochondrion. Fig. S6 presents additional quantifications that do not show statistically significant differences. Fig. S7 shows analysis of changes to OMM curvature. Fig. S8 shows a gallery of multilamellar membrane bodies observed in the data and their segmentations. Fig. S9 shows a gallery of surface morphometrics pipeline quantifications mapped onto the multilamellar membrane bodies. Fig. S10 shows analysis of changes to ER curvature. Fig. S11 shows quantification of mitochondria–ER contact sites. Table S1 shows typical computational requirements and time required for each step of the surface morphometrics pipeline. Table S2 shows additional statistical assessments for each quantification and each condition. Table S3 shows the confidence intervals derived from bootstrap analysis of each quantification. Video 1 shows a comparison of voxel segmentation and implicit surface reconstruction.

Supplementary Material

Table S1

shows the approximate time for each step of the surface morphometrics workflow.

Table S2

shows the statistical analyses of peaks and standard deviations.

Table S3

shows the confidence intervals of quantifications with bootstrap analysis.

Data availability

All scripts used for surface reconstruction, ultrastructure quantifications, and plotting and statistical significance testing are available at https://github.com/grotjahnlab/surface_morphometrics. Installation is simplified with a conda environment and a pip requirements file. Scripts are licensed under the GNU Public License version 3 (GPLv3). All tilt series, reconstructed tomograms, voxel segmentations, and reconstructed mesh surfaces used for quantifications were deposited in the Electron Microscopy Public Image Archive under accession code EMPIAR-11370.