Significance
Many engineering applications request soft materials to maintain tough under monotonic loads, and fatigue-resistant under cyclic loads. While fracture toughness of a soft material can be enhanced by orders of magnitude, its fatigue threshold remains insusceptible. Here we demonstrate a crack tip softening (CTS) concept to break this dilemma. Experiments show that the CTS concept enhances both toughness and threshold of polyacrylamide hydrogels by about four times. This simultaneous enhancement comes from stress de-concentration and elastic shielding at the crack tip. The CTS concept is generic to many material systems, geometrical singularity regions, and external loads. Our paper provides a crack retardation method during material application.
Keywords: crack tip softening (CTS), toughness, fatigue threshold, stress de-concentration, elastic shielding
Abstract
Soft materials fail by crack propagation under external loads. While fracture toughness of a soft material can be enhanced by orders of magnitude, its fatigue threshold remains insusceptible. In this work, we demonstrate a crack tip softening (CTS) concept to simultaneously improve the toughness and threshold of a single polymeric network. Polyacrylamide hydrogels have been selected as a model material. The polymer network is cured by two kinds of crosslinkers: a normal crosslinker and a light-degradable crosslinker. We characterize the pristine sample and light-treated sample by shear modulus, fracture toughness, fatigue threshold, and fractocohesive length. Notably, we apply light at the crack tip of a sample so that the light-sensitive crosslinkers degrade, resulting in a CTS sample with a softer and elastic crack tip. The pristine sample has a fracture toughness of 748.3 ± 15.19 J/m2 and a fatigue threshold of 9.3 J/m2. By comparison, the CTS sample has a fracture toughness of 2,774.6 ± 127.14 J/m2 and a fatigue threshold of 33.8 J/m2. Both fracture toughness and fatigue threshold have been enhanced by about four times. We attribute this simultaneous enhancement to stress de-concentration and elastic shielding at the crack tip. Different from the “fiber/matrix composite” concept and the “crystallization at the crack tip” concept, the CTS concept in the present work provides another option to simultaneously enhance the toughness and threshold, which improves the reliability of soft devices during applications.
Soft materials have been extensively studied for applications in various fields. Examples include adhesives (1, 2), coatings (3–5), optical devices (6–8), ionotronics (9–11), and soft machines (12–14). These applications often require soft materials to work under monotonic or cyclic loads during their lifetimes. When a crack or flaw exists in a soft material, the external load may cause the crack growth and final failure of the sample. The ability of a material to resist crack growth is characterized by fracture toughness under a monotonic load and fatigue threshold under a cyclic load.
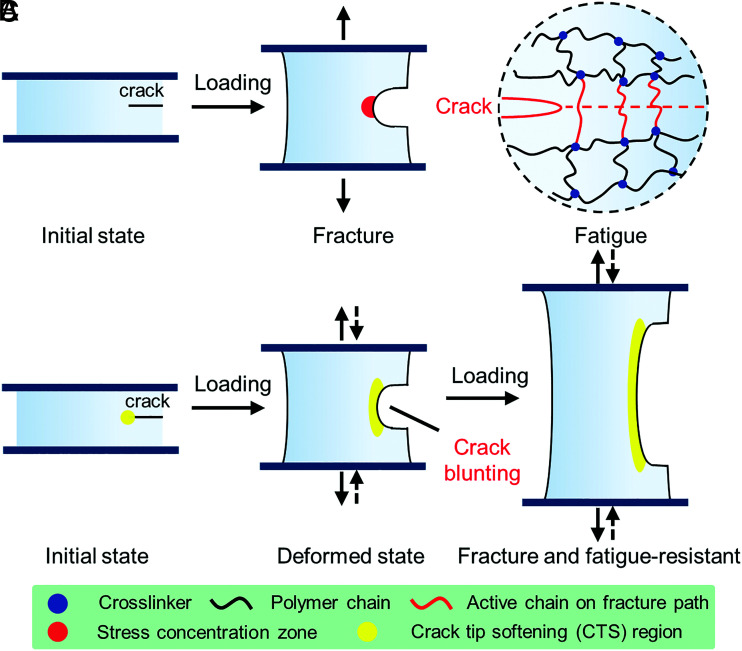
In Fig. 1 A and B, we depict the fracture and fatigue of a polymer network by schematics. When a notched sample is stretched by a monotonic load, stress concentrates in the red region around the crack tip (Fig. 1A). Polymer chains inside this region suffer substantial damage and lead to final rupture. Typically, the fracture toughness of a pure single polymeric network has a value in the range of tens to hundreds J/m2, which is significantly lower than that of metals (~tens of thousands J/m2). One needs dissipation in the material to make it tough. Methods have been developed in the last two decades by introducing sacrificial bonds, such as covalent bonds (15), noncovalent complexes (16, 17), and inorganic fillers (18). Nowadays, the fracture toughness of a soft material can be enhanced by orders of magnitude, easily reaching 10,000 J/m2. However, those materials still suffer from fatigue fracture under cyclic loads (19–21). The resistance to fatigue crack propagation is caused only by the energy required to break a single layer of polymer chains and is not affected by the dissipation mechanisms described above (22, 23) (Fig. 1B). For example, the fracture toughness of polyacrylamide-alginate hydrogels is 3,375 J/m2, but its fatigue threshold is poorly 35 J/m2 (24). This publicizes a great challenge: simultaneously increasing the toughness and threshold in a polymeric network.
Fig. 1.
(A) Schematic illustration of a single-edge notched sample subjected to an external load. Stress concentration exists near the crack tip and leads to the ultimate break of polymer networks. (B) The classical Lake-Thomas model assumes that a crack propagates by breaking only a single layer of active chains across the crack plane. The fatigue threshold is equal to the covalent energy stored in a layer of polymer chains per unit area. (C) CTS makes the crack blunt and resists the crack propagation under both monotonic load and cyclic load.
Several strategies have tried to enhance both the toughness and fatigue threshold of soft materials. One is the “fiber/matrix composite” concept (25–28). Stiff and stretchable fibers are embedded inside a soft matrix during sample preparation. The matrix and the fibers have high modulus contrast and are tightly bonded. When loaded, extensive shear deformation of the soft matrix alleviates the stress concentration in the hard fibers at the crack front, and the crack is blocked by the stiff fibers. Both fracture and fatigue need to break the front fiber, which releases all the elastic energy in the fiber around the crack tip (25, 29). By this design, a threshold above 1,000 J/m2 of elastomer-hydrogel composite has been achieved, which is comparable to its toughness ~ 4,000 J/m2 (27). Another way is the “crystallization at the crack tip” concept (30–33). Crystallinity in hydrogels is introduced by freeze-thawing, mechanical training, or other methods. High densities of crystalline domains effectively retard fatigue cracks. Much higher energy is required to fracture the aligned nanofibrils in the crystalline domain than that of the corresponding amorphous polymer chains. The threshold of PVA gel can exceed 1,000 J/m2 by this method (30, 31). The above-mentioned methods are limited to either specific production process or type of polymers.
Here we propose a crack tip softening (CTS) concept which simultaneously improves the toughness and the fatigue threshold of a single polymeric network (Fig. 1C). The crack tip is softened by an external stimulus. On the one hand, the soft region blunts under both monotonic loads and cyclic loads, endowing a high stretch of the sample. On the other hand, the soft region is more elastic than the bulk material, providing an elastic shielding to the bulk material. These two factors enhance the toughness and threshold simultaneously. To demonstrate our hypothesis, polyacrylamide hydrogels have been selected as a model material. The polymer network is cured by two kinds of crosslinkers: a normal crosslinker and a light-degradable crosslinker. Light treatment can be applied locally in the vicinity of the crack tip to soften the hydrogel network. The samples are then loaded monotonically or cyclically. Experiment shows that CTS makes the crack blunt and resists the crack propagation under both monotonic load and cyclic load.
Results
Mechanical Properties of Light-Softened Hydrogel.
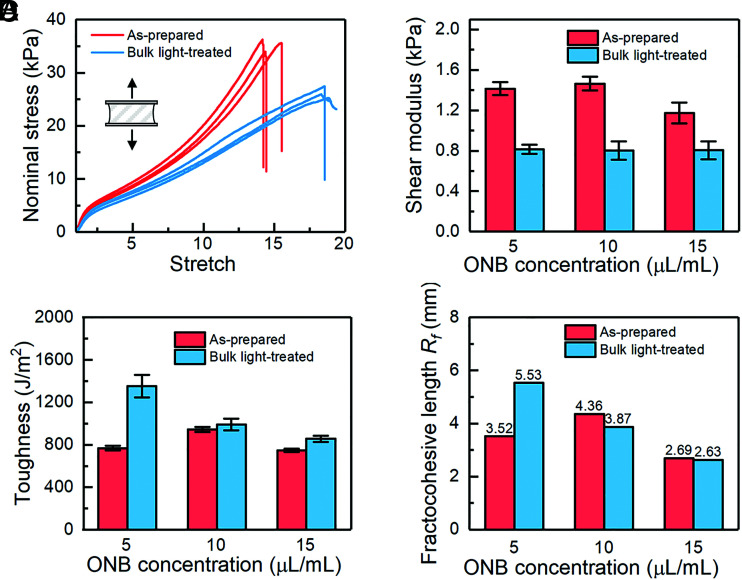
We characterize the mechanical properties of the hydrogels before and after Ultraviolet (UV) light treatment. We first load unnotched samples. Fig. 2A shows the typical stress–stretch curves of the samples with an ONB crosslinker concentration of 10 μL/mL. Two groups of unnotched samples are compared: one is the as-prepared samples and the other is the UV light-treated samples. After UV light treatment, the measured stress is lower for the same stretch, and the ultimate extensibility is higher compared with the un-treated samples, which confirms the light-induced softening of the hydrogels. The softening is due to the alteration of the network by the break of crosslinker ONB moiety (34). When the crosslink density is reduced, the average chain length of the polymer network is increased, resulting in a lower shear modulus and a higher ultimate extensibility. Samples with different concentrations of ONB crosslinkers are also tested (Fig. 2B). With the increase of ONB concentration, the shear modulus of the as-prepared hydrogels increases in the low concentration range but decreases at a relatively high concentration. The ONB molecule is a macromolecule with a molecular weight greater than 5,000. Long polymer chains would affect the polymerization process of small monomers. Specifically, increased ONB chains lead to the higher viscosity of the precursor and consequently reduce the kinetic energy of the monomers and the polymerization opportunity.
Fig. 2.
Mechanical properties of the hydrogels. (A) Stress–stretch curves of hydrogel with the ONB crosslinker concentration of 10 μL/mL. (B) Shear modulus as a function of the ONB concentration for the as-prepared samples and the light-treated samples. (C) Toughness as a function of the ONB concentration. (D) Fractocohesive length as a function of the ONB concentration.
We also measured the toughness using notched samples. The sample with an edge cut is easier to stretch to fracture, and the critical stretch is usually much lower than the ultimate stretch of unnotched samples. For the as-prepared samples we tested, the toughness falls in the range of 750 to 1,000 J/m2 (Fig. 2C), which is comparable but a little higher than the previously reported values (29, 35) for the single crosslinker polyacrylamide hydrogels. The toughness increase might be associated with the dispersion of chain length in the double crosslinker polyacrylamide hydrogels. After being treated with UV light, the toughness is higher than that of the as-prepared one. In the light-treated polymer network, chains crosslinked by ONB molecules degrade, which increases the average chain length and the density of dangling chain. A hydrogel with a lower modulus usually has a higher toughness (36).
The fractocohesive length, defined as Γ/Wf, is a critical physical length, below which the ultimate material properties, such as ultimate energy density, ultimate stretch, and strength, are independent of crack length (35, 37). As the work of fracture Wf is nearly constant, the fractocohesive length follows the same trend as the toughness, ranging from 2.63 to 5.6 mm (Fig. 2D).
Enhanced Fracture Toughness under Monotonic Loads.
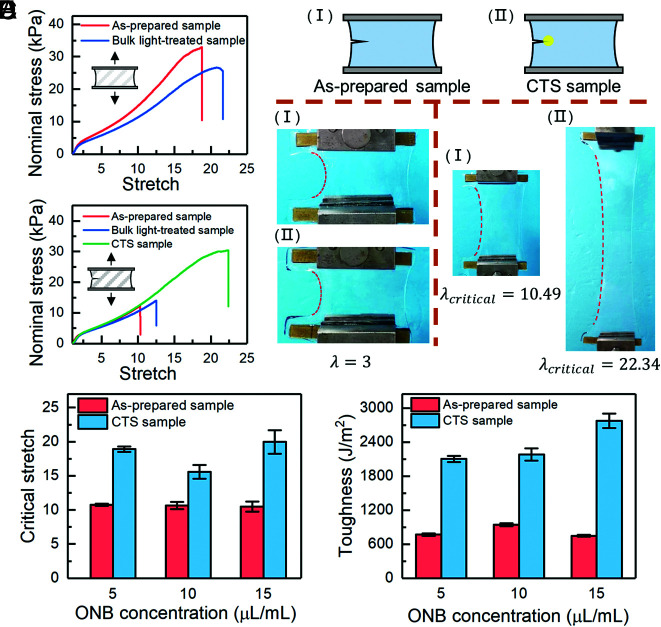
This section demonstrates that CTS retards crack propagation under monotonic loads. Fig. 3 A and B show the typical stress–stretch curves for the samples with an ONB crosslinker concentration of 15 μL/mL. Unnotched samples before and after bulk UV light treatment are tested in Fig. 3A. Three kinds of notched samples are tested in Fig. 3B: the as-prepared one, the bulk UV-treated one, and the crack tip UV-treated one. With light treatment at the crack tip, the critical stretch of the notched sample is substantially increased, which is even slightly larger than the ultimate stretch of the as-prepared unnotched samples. The local softening removes the notch sensitivity, and the locally enhanced extensibility promotes the overall stretchability. The profiles of the cracks are shown in Fig. 3C for samples without (I) and with (II) UV light treatment. At the same stretch (λ = 3), the radius of curvature at the crack front becomes larger for the light-treated sample (Fig. 3 C, Left). At the critical fracture state, the stretch for the light-treated cracked sample is much larger (Fig. 3 C, Right). The profile corresponding to the original crack surface is also similar to the right side which has no edge crack, indicating the notch effect has been attenuated.
Fig. 3.
CTS makes crack blunting under monotonic load. (A) Stress–stretch curves of the unnotched samples. (B) Stress–stretch curves of the notched samples. (C) Images of crack blunting in the as-prepared and CTS hydrogel samples. (D) Critical stretch as a function of the ONB concentration. (E) Toughness as a function of the ONB concentration.
This phenomenon is quite repeatable. We have tested hydrogel samples made from different recipes, and the phenomenon remains the same. Fig. 3D shows the comparison of the critical stretch for the groups with and without CTS. All the light-treated cracked samples reach the maximum stretch of the unnotched samples. The breakage of the samples did not occur at the crack front, but at the boundary between the hydrogel ends and the clamps. The toughness comparison between the as-prepared group and the CTS group is given in Fig. 3E. For the recipe where the ONB crosslinker concentration is 15 μL/mL, the toughness has been improved from 748.3 ± 15.19 J/m2 to 2,774.6 ± 127.14 J/m2, nearly four folds.
We conduct finite-element simulation (ABAQUS/Explicit, a commercial finite-element software) to investigate the stress field around the crack for the as-prepared and CTS samples. The hydrogel is modeled as an elastic Neo-Hookean material, using the material properties measured from experiments. The as-prepared region has a shear modulus of 1.4 kPa, while the CTS region with a radius of 2 mm has a shear modulus of 0.7 kPa. The element type is an eight-node biquadratic plane stress quadrilateral with reduced integration (CPS8R). The bottom boundary is fixed and top boundary is stretched upward by six times of the original height. SI Appendix, Fig. S3 shows the Mises stress fields for the as-prepared samples (SI Appendix, Fig. S3A) and the CTS sample (SI Appendix, Fig. S3B). Clearly, the stress concentration is relieved for the CTS group (SI Appendix, Fig. S3C). The energy release rate in SI Appendix, Fig. S3D indicates that the driving force of CTS sample is greatly reduced.
To conclude this section, experimental and finite-element simulation results show that the CTS concept enhances fracture toughness by increasing the stretchability of the crack tip and reducing the driving force at the crack tip.
Enhanced Fatigue Threshold under Cyclic Loads.
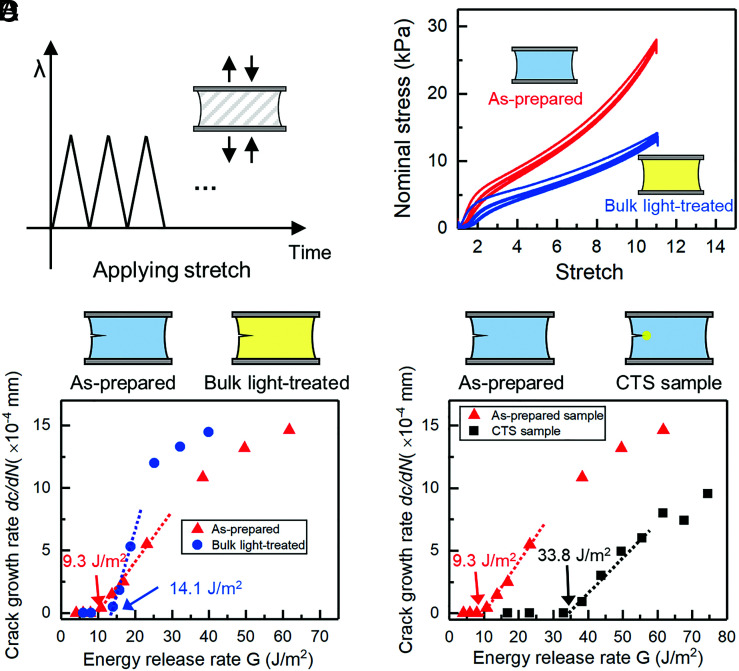
This section demonstrates that CTS retards crack propagation under cyclic loads. The fatigue resistance of the hydrogels before and after UV light treatment is studied. Unnotched samples are loaded cyclically (Fig. 4A), and the stress–stretch curves are obtained. The difference between the consecutive loading loops reflects the damage and internal structure change of the hydrogel network. A hysteresis curve shows the energy dissipation in each cycle. The damage to the hydrogel network and the energy dissipation is the greatest in the first cycle and becomes diminished in the subsequent cycles (Fig. 4B). These findings agree with the data for the polyacrylamide hydrogel reported in the previous work (35).
Fig. 4.
Fatigue test of the hydrogel. (A) Schematic of the cyclic test. The unnotched sample is stretched from λ = 1 to λ = 11 and applied repeatedly for the calculation of the energy release rate G. Loading frequency is fixed at 1 Hz. (B) Nominal stress as a function of stretch for the hydrogels before and after UV light treatment. (C) G-dc/dN curves for as-prepared samples and samples with bulk UV treatment. (D) G-dc/dN curves for the as-prepared samples and the CTS samples.
Notched samples are also tested to obtain the fatigue threshold of hydrogels. We first compare the fatigue threshold for as-prepared samples and samples with bulk UV treatment (Fig. 4C). The threshold for the as-prepared group is 9.3 J/m2, which is comparable with the previously reported values of 5 to 10 J/m2 for polyacrylamide hydrogels (19–21). After being treated with UV light over the whole body, the threshold of the hydrogel increases to 14.1 J/m2, due to the alteration of the hydrogel network. Based on the Lake-Tomas model (22), fatigue crack growth breaks only one layer of chains and the threshold is estimated by , where is the volume fraction of the polymer chains, is the chemical bond energy, is the volume of a monomer, is the monomer length, and n is the number of monomers per chain. It is also known that in polymer physics, i.e., the volume fraction of the polymer chains is proportional to the product of the number of monomers per chain n and the number of molecular chains per unit volume N. As a result, the fatigue threshold can be written as . Clearly, both N and n affect the threshold, but the exponent of n (3/2) is greater than that of N (1). Hence, n has a greater effect compared with N. This finding is confirmed by our experimental results that the threshold of light-treated sample (14.1 J/m2) is larger than that of as-prepared sample (9.3 J/m2) and is also confirmed in other works (21, 38, 39).
Next, the same cyclic tests are performed on CTS samples. Fig. 4D compares the G-dc/dN curves of the as-prepared notched samples and the CTS samples. The fatigue threshold is 33.8 J/m2 for the CTS samples, which is even higher than that of the bulk UV-treated ones, indicating superior fatigue resistance property. During application, materials are required to work reliably under certain environments and conditions for a certain designed time. We fix the energy release rate G = 31.6 J/m2 at the crack tip and apply given loading cycles on the as-prepared samples and CTS samples. The recorded crack front is given in SI Appendix, Fig. S7. Crack grows obviously in the as-prepared sample when the loading cycle is 10,000, but remains stable in the CTS sample even the loading cycle reaches 20,000.
We repeat the experiments in Fig. 4 B and D using polyacrylamide hydrogels with a higher crosslink density (SI Appendix, Fig. S8). The fatigue threshold of the as-prepared sample with a higher crosslink density is 7.5 J/m2, which is reasonably lower than that of the sparsely crosslinked one. By comparison, the fatigue threshold of the CTS sample is 16.2 J/m2: Nearly twice enhancement on the fatigue threshold is confirmed.
To conclude this section, experimental results show that the CTS samples have a higher fatigue threshold when compared with the as-prepared samples and bulk UV-treated samples.
Discussion
The degradation of ONB molecules reduces the crosslink density around the crack tip. Consequently, the crack tip has a lower shear modulus compared with the bulk material. Also, the crack tip becomes more stretchable than the bulk as the extensibility is approximately proportional to , where n can be regarded as the chain length. These two effects make the crack blunt under both monotonic and cyclic loads. The degradation of ONB molecules at the crack tip would also cause chain entanglement and further affects the fracture and fatigue of polymers (38, 40, 41). In order to investigate the effects of chain entanglement in our polyacrylamide hydrogels, we perform three kinds of experiments: 1) monotonic tension tests at various stretch rates, 2) rheology experiments at various shear rates, and 3) swelling experiments of three kinds of hydrogel samples. Details can be found in SI Appendix, Figs. S4–S6. The experimental results show that the polyacrylamide hydrogels used in this work are stretch rate-independent, shear rate-independent, and swelling-consistent. The effect of entanglement on the enhancement of fracture toughness and fatigue threshold is minimized.
The CTS concept bears two mechanisms for fracture and fatigue: stress de-concentration and elastic shielding. The crack tip becomes softer and tougher after light treatment. A soft crack tip becomes blunt under external load, re-distributing the stress along a large amount of material. A tough crack tip raises the crack growth resistance. Consequently, the barrier between the driving force and resistance at the crack tip becomes greater, and the bulk material becomes fracture resistant under a monotonic load.
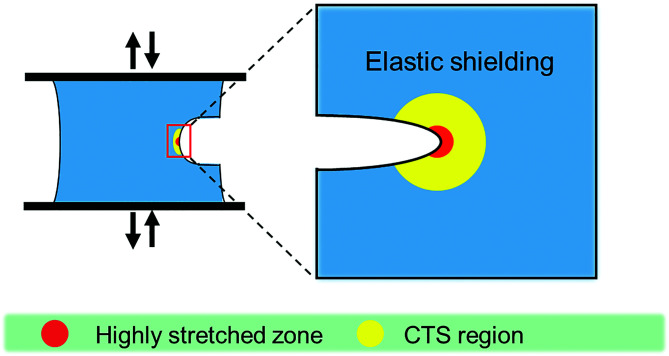
The fatigue threshold of a CTS sample is much larger than that of a pristine sample. A crack will not grow under cyclic load in a CTS sample even when the energy release is great than the threshold of a pristine sample. This can be explained in Fig. 5. The yellow region in the figure represents a treated region where the material is softer and possesses longer chains. This region becomes nearly elastic after treatment. Under cyclic load, only the small red region becomes higher stretched than the bulk. However, this stretch is not high enough to cause any damage around the crack tip due to stress de-concentration, and the material behaves elastically. In other words, the light-treated material acts as an elastic shielding under cyclic load, and the material becomes fatigue-resistant. The concept of elastic shielding is similar to the overload protection concept in hard materials like metals (42–44). However, when the cyclic load increases further, a crack extends by breaking one layer of chains based on the Lake-Thomas model. The light treatment introduces chain scission and increases the average chain length at the crack tip region. When the crack extends, each chain acts as an elastic dissipater (25, 29), releases the energy along the whole chain, and contributes to the threshold. As a result, the CTS concept also enhances the threshold.
Fig. 5.
Schematic of elastic shielding makes the sample more fatigue-resistant. Softening makes the materials in the yellow region softer and more fatigue-resistant. This region could provide an elastic shield to retard the crack propagation under cyclic loads.
A limiting case in the CTS concept is that the crack tip region has zero moduli, i.e., the material at the crack tip vanishes after light treatment. In this case, the crack tip has a finite radius. The geometric singularity is greatly avoided, and the material behaves approximately the same as an unnotched one. Our experiments show that the stretchability and strength of a notched sample with CTS treatment (Fig. 3B, green curve) are comparable with that of an unnotched sample (Fig. 3A, red curve). By employing the CTS concept, the effect of crack is minimized. In this sense, the CTS concept is analogous to drilling a stop hole at the crack tip in hard materials to arrest crack propagation (45–47).
There are two representative concepts to improve both the toughness and threshold of a polymer network. One is the fiber/matrix composite concept (25, 27, 48, 49). In this concept, the crack is arrested by a macroscopic fiber, which is fabricated vertically to the crack propagation direction during sample preparation and has a characteristic length of sample size. When the crack extends to the fiber/matrix interface, stress de-concentration is accomplished by the blocking of crack tip by the stiff fiber. To further grow the crack under a monotonic load or cyclic load, the fiber needs to be broken. The fiber acts as an elastic dissipater and a giant “polymer chain,” which releases a large amount of energy upon crack growth and contributes to both the toughness and fatigue threshold. The other way to improve the toughness and threshold is the crystallization concept (30, 31). In this concept, the material is trained by a certain method, e.g., mechanically cyclic load, to introduce hard crystallization in a soft matrix. The hard phase can block crack growth. The characteristic length of the crystalline grain is much larger than that of a chain length. Similarly, crack propagation needs to break this crystallization phase. The energy stored in this hard phase contributes to the toughness and fatigue threshold.
The CTS concept is fundamentally different from the above-mentioned approaches. One major difference is that both approaches toughen a material by a hard phase, while the CTS method employs a soft phase at the crack tip. The other difference is that both approaches need a material to be modified or designed before any application, either during fabrication or training after fabrication. On the other hand, the CTS concept allows a material during application to be toughened. In this sense, the CTS concept has a more realistic practice meaning.
The CTS concept is generic to many material systems, geometrical singularity regions, and external loads. This paper uses polyacrylamide hydrogels as model materials. In fact, most polymer networks are imperfect (35). Short chains and long chains co-exist in the network. Short chains at the crack tip can always be broken by external loads to achieve softening. In this sense, the CTS concept is generic to most polymer systems. The CTS concept can be applied to stress concentration regions, not necessarily the crack tip. For example, notches, holes, grooves, and soft/rigid boundaries can be softened to prevent crack growth. We fabricate a hydrogel membrane and perform punctuation tests using a metal bar (SI Appendix, Fig. S9). The as-prepared membrane fails when the loading displacement reaches 80 mm. By comparison, the central-softened sample sustains a load over 100 mm. In this test, stress concentration occurs in a metal-hydrogel contact region instead of a crack.
In the present work, we demonstrate the CTS concept by using a light-degradable crosslinker. This softening method is non-contact, benefiting various practical applications. Light is an economic, easy-to-control, and readily available resource. Other stimuli such as thermal heat, electric, or mechanical load can be used to achieve CTS in practice. For example, as we demonstrated in a previous work (50), a dielectric elastomer membrane with a hole can sustain more mechanical stretch when the hole edge is softened by an electric field. All these examples prove that CTS concept makes a structure strong under external loads.
In engineering applications, one does not need to clearly locate or predict the region where stress concentration occurs. A possible practice is to regard these defects as a black box and apply a load higher than the designed value on the sample for certain cycles. During this overload, the stress concentration region becomes softer and the material becomes more fatigue-resistant when the external load recovers to the designed value. These materials, geometries, and load aspects deserve further study.
Conclusion
In this work, we demonstrate a CTS concept to simultaneously improve the toughness and fatigue threshold of a single polymeric network. We applied monotonic loads and cyclic loads to polyacrylamide hydrogels and characterized the mechanical properties of pristine samples and CTS samples. A light-treated hydrogel is softer and more elastic than an un-treated one. Experimental results demonstrate that the CTS concept enhances both the toughness and fatigue threshold of polyacrylamide hydrogels by about four times. We attribute this enhancement to stress de-concentration and elastic shielding at the crack tip. The CTS concept is generic to many material systems, applicable to different geometrical singularity regions, and to various external loads (monotonic or cyclic). This paper provides a crack retardation method during material application.
Materials and Methods
Chemistry of Light-Soften Hydrogel.
Following the work (34), two kinds of crosslinkers are used to cure the hydrogel network (SI Appendix, Fig. S1A). One is the commonly used crosslinker (N,N′-methylene diacrylamide, MBAA), and the other one is a light-degradable crosslinker (PEG 4000 4-(3-(1-acryloyloxyethyl)-4-nitrophenoxy) butanoate, ONB). The acrylamide monomers (AAms) and crosslinkers are polymerized into a network by a thermal initiator ammonium persulphate (APS) and a catalyst N,N,N′,N′-tetramethylethylenediamine (TEMED). An ONB crosslinker contains a light-cleavable moiety and is capped by acrylate functional groups (SI Appendix, Fig. S1C). Under a UV light, it breaks into two parts, while the MBAA molecules remain crosslinked. As a result, the crosslink density of the network is reduced, and the material becomes softer than the pristine one (SI Appendix, Fig. S1B).
Preparations of Polyacrylamide Hydrogel Samples.
Polyacrylamide hydrogels have been selected as model materials to demonstrate the CTS concept (SI Appendix, Fig. S2). AAm, MBAA, APS, and TEMED are purchased from Sigma Aldrich. ONB crosslinkers are commercially available from Lianyungang Tengfa Bio-Tech Co. Ltd. We add 14 g AAm in 100 mL of deionized water. Both MBAA and ONB powders are dissolved into water to form a 0.1 M solution. The thermal initiator APS solution was 0.15 M. For every 1 mL of monomer solution, 1.5 μL of APS solution, 0.5 μL of TEMED solution, and 5 μL of MBAA solution are added. The amount of ONB solution is changeable to form networks of various crosslink densities. The mixed precursor is poured into a glass mold and cured at room temperature for 1 d. During cure, the AAms formed polyacrylamide chains and the polyacrylamide chains are crosslinked by both MBAA and ONB molecules to form a network. After cure, we disassemble the glass mold, and light-degradable polyacrylamide hydrogels with various crosslink densities are obtained.
To obtain the mechanical properties of the hydrogels before and after UV light treatment, two kinds of samples are prepared (SI Appendix, Fig. S2A). For pristine samples, hydrogels are stored in a sealed bag for 1 d before use. For light-treated samples, hydrogels are exposed to a UV lamp (15 W, 365 nm, UVPXX-15L) at a distance of 10 cm for 2 h and then stored for 1 d before use. During this light treatment process, the samples are sealed in a transparent bag to prevent any water loss.
To verify that CTS samples resist crack propagation under loads, two kinds of notched samples are prepared (SI Appendix, Fig. S2B). For pristine samples, hydrogels are first cut with a razor blade to introduce an edge crack of 15 mm and then stored in a sealed bag for 1 d. For light-treated samples, the same edge crack is introduced and only the crack tip region is exposed to a point UV source (5 W, 365 nm) for 2 h. During this process, a mask with a hole of radius of 2 mm is used to make sure that the UV light is precisely applied at the crack tip, while the other bulk regions remain untreated. During this light treatment process, the samples are sealed in a transparent bag to prevent any water loss.
Mechanical Measurement.
Mechanical properties of polyacrylamides hydrogels are measured by a mechanical tester (Instron 5944) in a pure shear configuration. The deformable sample size for pure shear tests is 80 mm × 10 mm × 2 mm. All specimens are loaded to fracture at a velocity of 60 mm/min. The nominal stress–stretch curve can be calculated from the recorded force-displacement data. The nominal stress is the measured force divided by the initial cross-sectional area of the sample (sample width times thickness), and the stretch is the current sample height divided by its initial height. Work of fracture Wf is the area underneath the stress–stretch curve. Shear modulus is 1/4 the initial slope of the stress–stretch curve. For notched specimens, the stress–stretch curves are also measured, and the critical stretch at the rupture is determined. The toughness is calculated by integrating the stress–stretch curve of the unnotched sample from to the critical stretch to get W(), and then multiplied by the initial sample height H, i.e., , (16, 51). At least four specimens were used for each set of testing conditions. For all the tests, a humidifier was used to prevent the hydrogel from losing water.
The sample size for the fatigue cyclic tests is the same as that of monotonic tests. For each applied stretch range, we conduct cyclic tests for both unnotched samples and notched samples. The stress–stretch curves of unnotched samples are used to calculate the energy release rate , where W() is the integration of the steady stress–stretch curve and is the applied stretch on the notch sample. The crack growth process of the notched sample is recorded by a digital camera, and the crack length c and the loading cycles N are obtained. That finally leads to a G-dc/dN curve.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
This work is supported by the National Natural Science Foundation of China (No. 12132014), and the 111 Project (No. B21034).
Author contributions
B.L., T.Y., S.Q., and W.Y. designed research; B.L., T.Y., J.Z., D.Z., and S.Q. performed research; B.L., T.Y., and H.Y. analyzed data; and B.L., T.Y., H.Y., S.Q., and W.Y. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission.
Data, Materials, and Software Availability
All study data are included in the article and/or SI Appendix.
Supporting Information
References
- 1.Chen X., Yuk H., Wu J., Nabzdyk C. S., Zhao X., Instant tough bioadhesive with triggerable benign detachment. Proc. Natl. Acad. Sci. U.S.A. 117, 15497–15503 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Deng J., et al. , Electrical bioadhesive interface for bioelectronics. Nat. Mater. 20, 229–236 (2021). [DOI] [PubMed] [Google Scholar]
- 3.Yao X., et al. , Hydrogel paint. Adv. Mater. 31, 1903062 (2019). [DOI] [PubMed] [Google Scholar]
- 4.Liu J., Qu S., Suo Z., Yang W., Functional hydrogel coatings. Natl. Sci. Rev. 8, nwaa254 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yin T., Lavoie S. R., Qu S., Suo Z., Photoinitiator-grafted polymer chains for integrating hydrogels with various materials. Cell Rep. Phys. Sci. 2, 100463 (2021). [Google Scholar]
- 6.Yin T., et al. , Soft display using photonic crystals on dielectric elastomers. ACS Appl. Mater. Interfaces 10, 24758–24766 (2018). [DOI] [PubMed] [Google Scholar]
- 7.Yin T. H., et al. , Ultrastretchable and conductive core/sheath hydrogel fibers with multifunctionality. J. Polym. Sci. Part B-Polym. Phys. 57, 272–280 (2019). [Google Scholar]
- 8.Liu B., et al. , Hydrogel coating enabling mechanically friendly, step-index, functionalized optical fiber. Adv. Opt. Mater. 9, 2101036 (2021). [Google Scholar]
- 9.Yang C., Suo Z., Hydrogel ionotronics. Nat. Rev. Mater. 3, 125–142 (2018). [Google Scholar]
- 10.Yuk H., Lu B., Zhao X., Hydrogel bioelectronics. Chem. Soc. Rev. 48, 1642–1667 (2019). [DOI] [PubMed] [Google Scholar]
- 11.Zhu H., Hu X., Liu B., Chen Z., Qu S., 3D printing of conductive hydrogel-elastomer hybrids for stretchable electronics. ACS Appl. Mater. Interfaces 13, 59243–59251 (2021). [DOI] [PubMed] [Google Scholar]
- 12.Liu X., Liu J., Lin S., Zhao X., Hydrogel machines. Mater. Today 36, 102–124 (2020). [Google Scholar]
- 13.Chen Z., et al. , 3D printing of multifunctional hydrogels. Adv. Funct. Mater. 29, 1900971 (2019). [Google Scholar]
- 14.Ge Q., et al. , 3D printing of highly stretchable hydrogel with diverse UV curable polymers. Sci. Adv. 7, eaba4261 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gong J. P., Katsuyama Y., Kurokawa T., Osada Y., Double-network hydrogels with extremely high mechanical strength. Adv. Mater. 15, 1155–1158 (2003). [Google Scholar]
- 16.Sun J. Y., et al. , Highly stretchable and tough hydrogels. Nature 489, 133–136 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Han Z., et al. , A versatile hydrogel network–repairing strategy achieved by the covalent-like hydrogen bond interaction. Sci. Adv. 8, eabl5066 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhao X., Multi-scale multi-mechanism design of tough hydrogels: Building dissipation into stretchy networks. Soft Matter 10, 672–687 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tang J., Li J., Vlassak J. J., Suo Z., Fatigue fracture of hydrogels. Extreme Mech. Lett. 10, 24–31 (2017). [Google Scholar]
- 20.Zhang E., Bai R., Morelle X. P., Suo Z., Fatigue fracture of nearly elastic hydrogels. Soft Matter 14, 3563–3571 (2018). [DOI] [PubMed] [Google Scholar]
- 21.Bai R., Yang J., Suo Z., Fatigue of hydrogels. Eur. J. Mech.-A/Solids 74, 337–370 (2019). [Google Scholar]
- 22.Lake G., Thomas A., The strength of highly elastic materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 300, 108–119 (1967). [Google Scholar]
- 23.Yin T., Wu T., Liu J., Qu S., Yang W., Essential work of fracture of soft elastomers. J. Mech. Phys. Solids 156, 104616 (2021). [Google Scholar]
- 24.Zhang W., et al. , Fracture toughness and fatigue threshold of tough hydrogels. ACS Macro Lett. 8, 17–23 (2018). [DOI] [PubMed] [Google Scholar]
- 25.Wang Z., et al. , Stretchable materials of high toughness and low hysteresis. Proc. Natl. Acad. Sci. U.S.A. 116, 5967–5972 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Li C., Yang H., Suo Z., Tang J., Fatigue-resistant elastomers. J. Mech. Phys. Solids 134, 103751 (2020). [Google Scholar]
- 27.Xiang C., et al. , Stretchable and fatigue-resistant materials. Mater. Today 34, 7–16 (2020). [Google Scholar]
- 28.Yang H., et al. , Fabricating hydrogels to mimic biological tissues of complex shapes and high fatigue resistance. Matter 4, 1935–1946 (2021). [Google Scholar]
- 29.Liu J., et al. , Polyacrylamide hydrogels. II. Elastic dissipater. J. Mech. Phys. Solids 133, 103737 (2019). [Google Scholar]
- 30.Lin S., et al. , Anti-fatigue-fracture hydrogels. Sci. Adv. 5, eaau8528 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lin S., Liu J., Liu X., Zhao X., Muscle-like fatigue-resistant hydrogels by mechanical training. Proc. Natl. Acad. Sci. U.S.A. 116, 10244–10249 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Liu J., et al. , Fatigue-resistant adhesion of hydrogels. Nat. Commun. 11, 1–9 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hua M., et al. , Strong tough hydrogels via the synergy of freeze-casting and salting out. Nature 590, 594–599 (2021). [DOI] [PubMed] [Google Scholar]
- 34.Raman R., et al. , Light-degradable hydrogels as dynamic triggers for gastrointestinal applications. Sci. Adv. 6, eaay0065 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Yang C., Yin T., Suo Z., Polyacrylamide hydrogels., I. Network imperfection. J. Mech. Phys. Solids 131, 43–55 (2019). [Google Scholar]
- 36.Zhou Y., et al. , The stiffness-threshold conflict in polymer networks and a resolution. J. Appl. Mech. 87, 031002 (2020). [Google Scholar]
- 37.Chen C., Wang Z., Suo Z., Flaw sensitivity of highly stretchable materials. Extreme Mech. Lett. 10, 50–57 (2017). [Google Scholar]
- 38.Zheng D., Lin S., Ni J., Zhao X., Fracture and fatigue of entangled and unentangled polymer networks. Extreme Mech. Lett. 51, 101608 (2022). [Google Scholar]
- 39.Zhang W., Gao Y., Yang H., Suo Z., Lu T., Fatigue-resistant adhesion I. Long-chain polymers as elastic dissipaters. Extreme Mech. Lett. 39, 100813 (2020). [Google Scholar]
- 40.Kim J., Zhang G., Shi M., Suo Z., Fracture, fatigue, and friction of polymers in which entanglements greatly outnumber cross-links. Science 374, 212–216 (2021). [DOI] [PubMed] [Google Scholar]
- 41.Kim J., Yin T., Suo Z., Polyacrylamide hydrogels. V., Some strands in a polymer network bear loads, but all strands contribute to swelling. J. Mech. Phys. Solids 168, 105017 (2022). [Google Scholar]
- 42.Gray T., Gallagher J., Predicting fatigue crack retardation following a single overload using a modi. ASTM Spec. Tech. Publ. 331 (1976). [Google Scholar]
- 43.Alzos W., Hillberry B., Skat A., Effect of Single Overload/underload Cycles on Fatigue Crack Propagation (ASTM International, 1976). [Google Scholar]
- 44.Lu Y.-C., Yang F.-P., Chen T., Effect of single overload on fatigue crack growth in QSTE340TM steel and retardation model modification. Eng. Fract. Mech. 212, 81–94 (2019). [Google Scholar]
- 45.Goto M., Miyagawa H., Nisitani H., Crack growth arresting property of a hole and Brinell-type dimple. Fatigue Fract. Eng. Mater. Struct. 19, 39–49 (1996). [Google Scholar]
- 46.Fanni M., Fouda N., Shabara M., Awad M., New crack stop hole shape using structural optimizing technique. Ain Shams Eng. J. 6, 987–999 (2015). [Google Scholar]
- 47.Makabe C., Murdani A., Kuniyoshi K., Irei Y., Saimoto A., Crack-growth arrest by redirecting crack growth by drilling stop holes and inserting pins into them. Eng. Fail. Anal. 16, 475–483 (2009). [Google Scholar]
- 48.Zhang G., Yin T., Nian G., Suo Z., Fatigue-resistant polyurethane elastomer composites. Extreme Mech. Lett. 48, 101434 (2021). [Google Scholar]
- 49.Gao Y., et al. , Hydrogel–mesh composite for wound closure. Proc. Natl. Acad. Sci. U.S.A. 118, e2103457118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Yin T., Wang P., Yu H., Qu S., Failure of soft dielectric membrane with a hole subjected to mechanical and electric loads. Int. J. Non Linear Mech. 117, 103243 (2019). [Google Scholar]
- 51.Rivlin R., Thomas A. G., Rupture of rubber. I. Characteristic energy for tearing. J. Polym. Sci. 10, 291–318 (1953). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
All study data are included in the article and/or SI Appendix.