Unraveling the molecular mechanism of collagen flexibility during physiological warmup using molecular dynamics simulation and machine learning

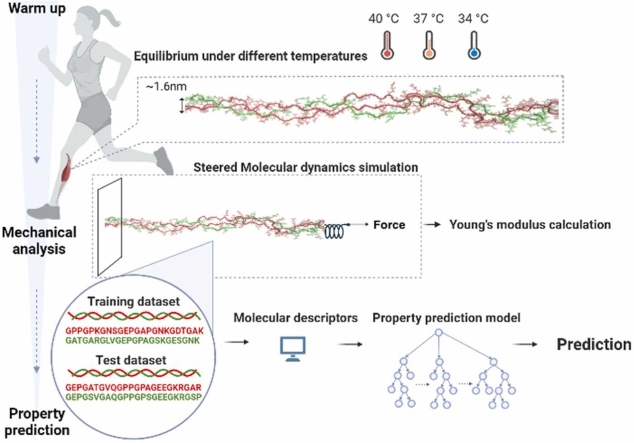
Abstract

Physiological warmup plays an important role in reducing the injury risk in different sports. In response to the associated temperature increase, the muscle and tendon soften and become easily stretched. In this study, we focused on type I collagen, the main component of the Achilles tendon, to unveil the molecular mechanism of collagen flexibility upon slight heating and to develop a model to predict the strain of collagen sequences. We used molecular dynamics approaches to simulate the molecular structures and mechanical behavior of the gap and overlap regions in type I collagen at 307 K, 310 K, and 313 K. The results showed that the molecular model in the overlap region is more sensitive to temperature increases. Upon increasing the temperature by 3 degrees Celsius, the end-to-end distance and Young’s modulus of the overlap region decreased by 5% and 29.4%, respectively. The overlap region became more flexible than the gap region at higher temperatures. GAP-GPA and GNK-GSK triplets are critical for providing molecular flexibility upon heating. A machine learning model developed from the molecular dynamics simulation results showed good performance in predicting the strain of collagen sequences at a physiological warmup temperature. The strain-predictive model could be applied to future collagen designs to obtain desirable temperature-dependent mechanical properties.

Graphical Abstract

Highlights

• •The molecular structure can exhibit up to 0.02 strain during physiological warmup.
• •Only specific regions of collagen molecules are temperature sensitive.
• •The overlap region is more sensitive to temperature increases.
• •GAP-GPA and GNK-GSK triplets are critical for molecular flexibility upon heating.
• •The strain-predictive machine learning model can be used in future designs.

1. Introduction

With the rising sports population, the relationship between sports and injury has attracted public attention. According to a National Health Interview Survey encompassing 2011–2014, 8.6 million sports-related injuries occurred annually [1]. Tendon injuries are the most common sports-related injuries, often occurring in long-term running and badminton [2], [3], [4], [5]. The Achilles tendon stores elastic energy in humans as a muscle-tendon unit [6], [7], [8]. Sports experiments showed that physiological warmup decreases the risk of Achilles tendon injuries by increasing the temperature by 2.5 °C [9], [10]. Once the muscle–tendon units are stretched, the tensile strength of the Achilles tendon rises [11], [12]. This diminishes the tension on muscle-tendon junctions and the incidence of injury [11], [13], [14], [15].

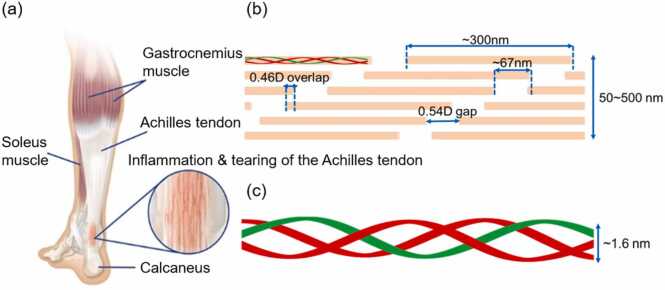
The Achilles tendon is mainly composed of water, type I collagen, and proteoglycans [16], [17], [18]. Among its composition, the type I collagen molecule is a heterotrimer composed of two polypeptide chains termed α1 chains and one termed the α2 chain. These chains coil around each other in a triple-helical configuration with a width of 1.6 nm. The length of the type I collagen molecule is approximately 300 nm. It aligns axially as a type I collagen fibril with a 67 nm-staggered repeat (D-period) [19], [20], [21]. The gap region and the overlap region included in the fibril structure are 0.54D and 0.46D, respectively. The width of type I collagen fibrils is in the range of 50–500 nm.

A previous study used various methods to investigate the mechanical behavior of collagen tissues, including atomic force microscopy [23], [24], [25], [26], [27], X-ray diffraction [28], [29], and MEMS stretching [30], [31]. With improvements in computer power, molecular dynamics (MD) has been used to study the mechanical properties of collagen tissues at the molecular level. This is a computational method for interatomic force calculations that simulates atom trajectories by predicting atom positions, velocities and accelerations [32]. Recent MD studies have uncovered a relationship between the mechanical properties of type I collagen and its structure. The mechanical properties of type I collagen are influenced by molecular mutations and cross-links [33], [34]. Moreover, the stability is altered by the application of force [35]. Studies have found heterogeneity in collagen with respect to its structure and mechanical properties along the longitudinal axis [36], [37]. A prominent difference was found between the gap region and the overlap region in collagen [38], [39], [40].

Type I collagen was experimentally found to be thermally unstable at 37 °C [41]. It was found that the melting temperature of triple helical monomers can be changed by adjusting the collagen hydroxyproline content, which determines the strength and elasticity of fibers. A previous MD simulation study also showed that certain mechanical properties decreased with increasing temperature from 24 °C to 40 °C and at 70 °C, the supraphysiological temperature [42]. Recently, machine learning (ML) models have been provided to predict the molecular properties of collagens [43], [44]. However, few studies have discussed the effect of physiological warmup, which increases the temperature by only 3 degrees, and it remains unclear how a slight increase in temperature could reduce the injury risk.

In this study, we aimed to uncover the molecular mechanism of the temperature effect on the structure and mechanical properties of type I collagen. Molecular dynamics simulation was used to study the gap region and the overlap region in type I collagen at 307 K (34 °C), 310 K (37 °C), and 313 K (40 °C). The simulation results were further applied to the development of the strain-predictive model based on ML approaches. We predicted the strain of unknown combinations of amino acid sequences at 313 K in type I collagen through this model. This study could expand the existing knowledge of collagen temperature-dependent mechanical properties from known to unknown combinations of amino acid sequences and further apply to the design of collagen in the future.

2. Materials and methods

2.1. Collagen molecule models

To study the behavior of gap and overlap regions in collagen during physiological warmup, two molecular models were constructed from the equilibrated fibril model by a two stage simulation approach. First, a full-length type I tropocollagen fibril model was built of real sequences of two type I α1(I) chains (version AAH50014.1) and one type I α2(I) chain (version NP_031769.2) of Mus musculus (+/+ mouse) adopted from the NCBI protein database. Side chains were added to the backbone of the chains to consist of the 1014 residues in the type I tropocollagen prototype [45]. According to a previous study [19], [20], we built a collagen fibril model with the following lattice constants: a≈ 40.0 Å, b≈ 27.0 Å, c≈ 678 Å, α ≈ 89.2°, β ≈ 94.6°, and γ ≈ 105.6° as shown in Fig. S1 (a). We used LAMMPS software to equilibrate the fibril model and applied the small stress by the NPT ensemble. The CHARMM22 force field [19] was used to describe the interaction between atoms. We applied 60 MPa to the longitudinal axis (x-axis) and 1 atmosphere to the other axes (y- and z-axes). We ran the simulation for 5 ns and used the final structure to build the initial molecular models for the gap and overlap regions. Next, the D-period and the molecule length were used to divide the gap region and the overlap region from the fibril model. Secondly, two representative models were constructed. For the gap model, the triplet number ranged from 118 to 142, and for the overlap model, the triplet number ranged from 79 to 103. We also considered a relatively stable glycine-proline-hydroxyproline (Gly-Pro-Hyp, GPO) model [46], which comprised 24 GPO triplets, as a control group to compare the behavior of the gap and overlap models in this study. The sequences for the overlap model were.

α1-GPSGPQGPSGPPGPKGNSGEPGAPGNKGDTGAKGEPGATGVQGPPGPAGEEGKRGARGEPGPSGLPGPPGER and.

α2-GIPGPAGAAGATGARGLVGEPGPAGSKGESGNKGEPGSVGAQGPPGPSGEEGKRGSPGEAGSAGPAGPPGLR.

The sequences for the gap model were.

α1- GLPGAKGLTGSPGSPGPDGKTGPPGPAGQDGRPGPAGPPGARGQAGVMGFPGPKGTAGEPGKAGERGLPGPP and.

α2-

GLMGPRGLPGSPGNVGPSGKEGPVGLPGIDGRPGPIGPAGPRGEAGNIGFPGPKGPSGDPGKPGERGHPGLA.

2.2. Equilibrium of collagen molecules

We equilibrated the molecular structures of the gap model and the overlap model separately, which was carried out by nanoscale molecular dynamics (NAMD) [47]. Visual molecular dynamics (VMD) [48] was used to calculate the end-to-end distance and the number of hydrogen bonds and visualize 3D graphical molecules. The equilibrated molecular structures adopted from the fibril model for the gap model and the overlap model are shown in Fig. S1 (b). Electrical charges in the system were neutralized by adding ions into the water box. We defined 310 K as the baseline temperature [49], 307 K as the cooling temperature [50], and 313 K as the heating temperature [51], [52], [53], [54]. The gap, overlap, and GPO models were run for 20 ns at the three temperatures. Three independent simulations are performed for the gap and overlap models for each temperature to enhance the sampling. The following analysis results are averaged from the trajectories of the last 5 ns.

2.3. Steered molecular dynamics (SMD) simulation

To investigate the differences in the mechanical properties for the three models at different temperatures, SMD simulation was applied. A dummy atom was attached to the 66th atom counted from the front end of each model through a harmonic spring with a constant of 7 kcal/mol/Ų and moved in space under a constant velocity of 10 Å/ns for eight ns. Strain was calculated as the displacement divided by the original length, and stress was calculated as the force divided by the cross-sectional area of the collagen, which is $1.76\times {10}^{-18}{m}^2$ [21]. The stress—strain curve was fitted by the worm-like chain model [55],

$$F=\frac{k_{B}T}{4L_p}\left[{\left(1-\frac{x}{L_c}\right)}^{-2}+\frac{4x}{L_c}-1\right],$$

where $F$ is the pulling force acting on the end of the collagen molecule, $L_p$ is the persistence length, $L_c$ is the contour length, $k_B$ is the Boltzmann constant, and $T$ is the temperature. The worm-like chain model was further applied to calculate the Young's modulus. The Young’s modulus was calculated by the slope of the worm-like chain model at 0.5 GPa.

2.4. Structural analysis

The end-to-end distance was calculated by the following equation:

$$\sum _{i=15}^{20}\frac{‖\left(P_{66i}^A+P_{66i}^B+P_{66i}^C\right)-(P_{8i}^A+P_{8i}^B+P_{8i}^C)‖}{3\times 5},$$

where i is the last five ns in equilibrium. $P_{66i}^A$, $P_{66i}^B$, and $P_{66i}^C$stand for the positions of the 66th atom counted from the front end of each model in chains A, B, and C, respectively. $P_{8i}^A$, $P_{8i}^B$, and $P_{8i}^C$ represent the positions of the eighth atom counted from the front end of each model in chains A, B, and C, respectively. Use of the calculation average suppressed the influence of random peaks. The strain per unit height was calculated by the equation in reference [34], [45]:

$\mathrm{Strain}\mathrm{of}\mathrm{unit}height=\frac{\mathrm{||}{\overline{P}}_{i+1}-{\overline{P}}_i{\mathrm{||}}_{\mathit{SMD},313K}-\mathrm{||}{\overline{P}}_{i+1}-{\overline{P}}_i{\mathrm{||}}_{\mathrm{equilibrium},313\mathrm{K}}}{\mathrm{||}{\overline{P}}_{i+1}-{\overline{P}}_i{\mathrm{||}}_{\mathrm{equilibrium},310\mathrm{K}}}$

$${\stackrel{\circledR }{P}}_i=\sum _{i=4}^{22}\frac{P_i^A+P_i^B+P_i^C}{3},$$

where $P_i^A,P_i^B{\mathit{and\; P}}_i^C$ are the positions in chains A, B, and C. $\stackrel{\circledR }{P_i}$ is the position of the C_α atom of the i^th Gly calculated by the average of $P_i^A,P_i^B{\mathit{and\; P}}_i^C$. The unit height was the distance between the position of continuous Cα atoms, ${\stackrel{\circledR }{P}}_{i+1}$and $P_i$, as shown in S1(c). The strain of unit height was calculated with the unit height during SMD simulation and that during equilibrium. We calculated the strain per unit height for the overlap region to study the mechanical properties of amino acid sequences. The number of hydrogen bonds was calculated under the geometric criteria of donor-acceptor distance 3.5 Å and donor-hydrogen-acceptor angle 30°.

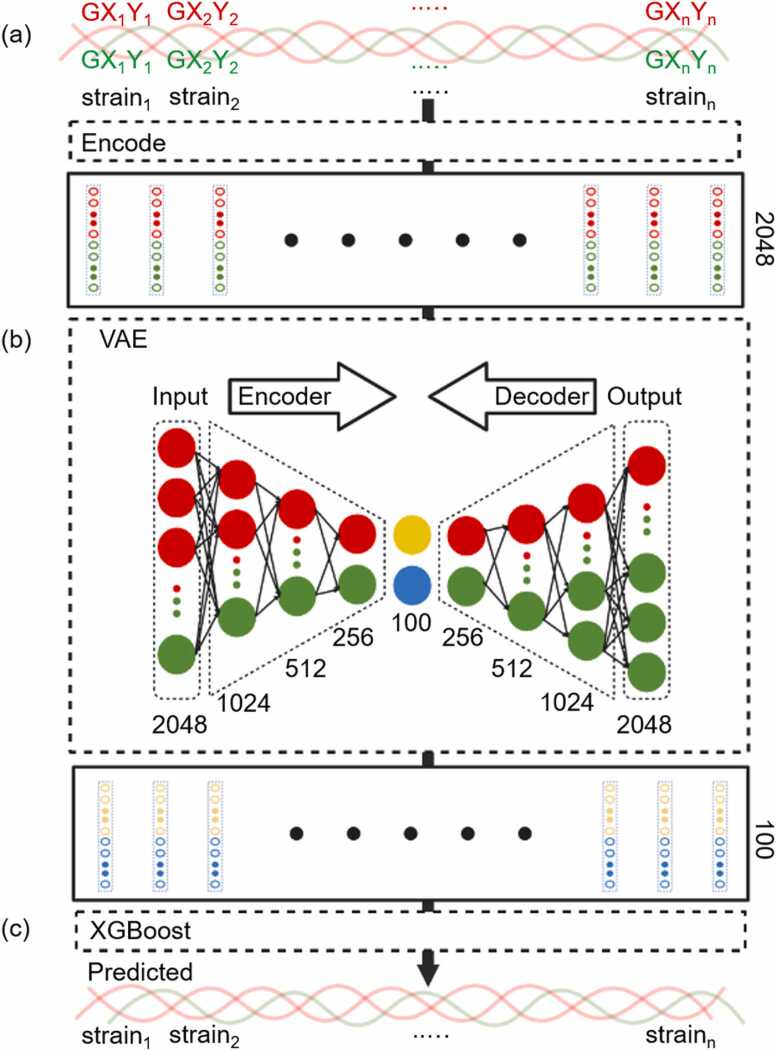
2.5. Development of the strain-predictive model

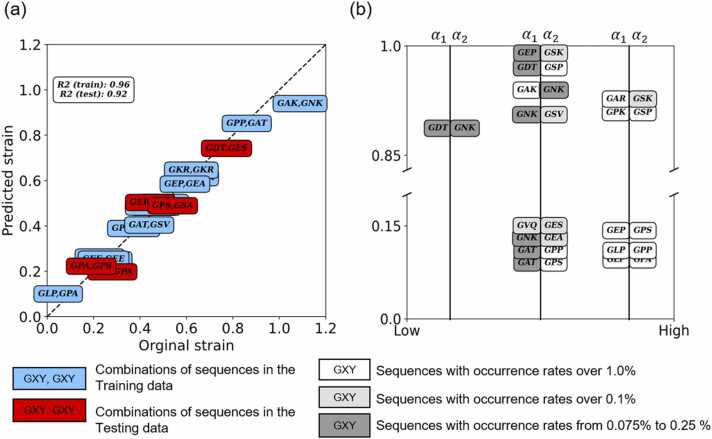
The 19 sequences in the middle of the overlap model with 16 nonrepetitive amino acids in the α1 chain and 17 nonrepetitive amino acids in the α2 chain were randomly distributed into a training set and testing set at a ratio of 4:1. Every three amino acid sequences, GXY, in the α1 chain and α2 chain were transformed into 1024 vector embedding [56], as shown in Fig. 2(a). The vector embedding from the α1 chain and α2 chain were connected as a 2048 vector embedding and were input into the variational autoencoder (VAE) model [57] in Fig. 2(b). The vector embedding went through an encoding process with dense layers of shapes 1024, 512, 256, and 100 and a decoding process with dense layers of the shapes in reverse. We took the rectified linear unit (ReLU) [58] as the activation function in the first 6 dense layers and the hyperbolic tangent activation function (TanH) [59] in the last dense layer. Stochastic gradient descent (SGD) was the optimizer, and the mean squared error was the loss function in the VAE model. The process underwent 45 epochs with a learning rate of 10⁻² and batch sizes of 8. The output was the encoded 100 vector embedding of each sequence, whose dimensionality was reduced from 2048 vector embedding. The encoded 100 vector embedding of each sequence was used as the input features of the strain-predictive model shown in Fig. 2(c). The strain-predictive model was trained on extreme gradient boosting (XGBoost) [60]. For the overlap case, the learning rate was 0.38, and the number of gradient-boosted trees was 60. The subsample ratio of the training instance was 0.53, and the subsample ratio of columns when constructing each tree was 0.70. The L1 regularization was 0.18, and the L2 regularization was 0.14. The ground truth was the strain per unit height of the 19 sequences obtained after SMD simulation, and the output was the predicted strain per unit height. More detail is shown in Tables S2 and S3.

Fig. 2.

Diagram of the machine learning framework. (a) Every three amino acids, GXY, of the two red α1 chains and one green α2 chain was transformed into the 2048 vector embedding by the encoder model. (b) The 2048 vector embeddings of the sequences in red and green were encoded into a 100 vector embedding of the sequence in yellow and blue by the variational autoencoder model. (c) The strain-predictive model was trained based on XGBoost with the input, 100 vector embeddings of sequences and output of the predicted strain of each combination of sequences.

3. Results and discussion

3.1. Effect of temperature on the molecular structure of collagen molecules

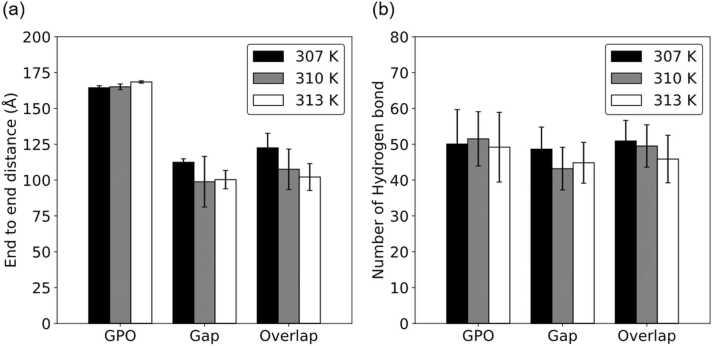
We first analyzed the structures of three models, GPO, gap and overlap models, at different temperatures. Fig. 3 shows the end-to-end distance of the molecular structure and the number of intramolecular hydrogen bonds in the GPO model, gap model and overlap model. No notable difference was observed in the end-to-end distance (307 K: 164.4 Å; 310 K: 165.1 Å; 313 K: 168.5 Å) or the number of intramolecular hydrogen bonds (307 K: 50.1; 310 K: 51.5; 313 K: 49.2) of the GPO model at the three temperatures, showing that GPO has the highest thermal stability and thus is not sensitive to temperature changes. For the gap model, the end-to-end distance was the shortest at 310 K (98.1 Å), and the number of intramolecular hydrogen bonds at this temperature (43.65) was the lowest. The end-to-end distance was 112.47 Å at 307 K and 100.34 Å at 313 K. The number of intramolecular hydrogen bonds was 48.64 at 307 K and 44.84 at 313 K. For the overlap model, its end-to-end distance (307 K: 122.5 Å; 310 K: 107.54 Å; 313 K: 102.16 Å) and the number of intramolecular hydrogen bonds (307 K: 50.92; 310 K: 49.50; 313 K: 45.88) decreased while the temperature increased from 307 K to 313 K. In summary, while increasing the temperature of the overlap region in the collagen by 3 °C, the end-to-end distance decreased by 5.38 Å. The result showed that the overlap model was more sensitive to temperature change than the gap model. We believe that this is due to the breaking of unstable hydrogen bonds after warmup. For the gap model, we found that the end-to-end distance at 310 K is close to 313 K, but the number of the hydrogen bonds is lower than 313 K and the standard deviation of the end-to-end distance at 310 K is higher than 313 K. We believe that the collagen molecule of the gap model is unstable at both 310 K and 313 K.

Fig. 3.

(a) End-to-end distances and (b) number of intramolecular hydrogen bonds of the GPO, gap, and overlap models after equilibrium at 307 K, 310 K, and 313 K.

3.2. Effect of temperature on the mechanical properties of collagen molecules

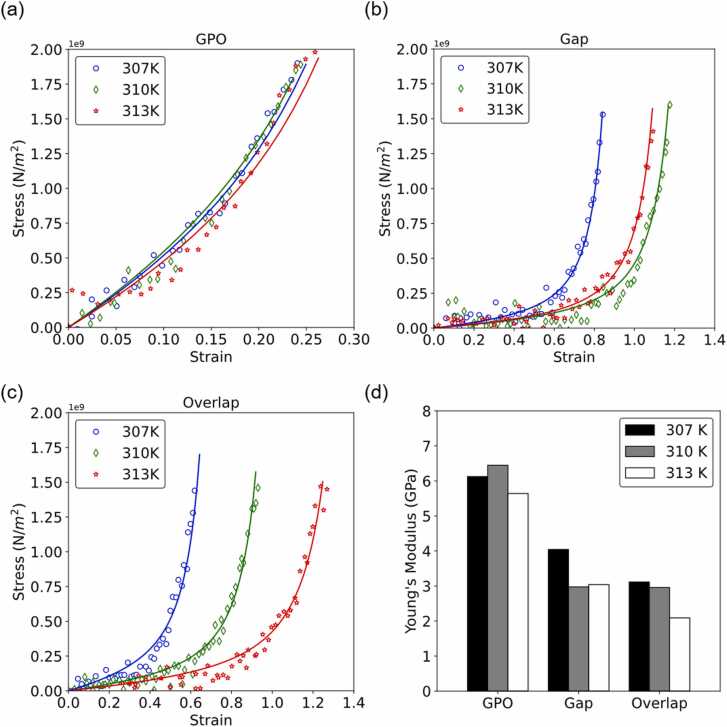
We performed SMD simulations on three models at different temperatures and further analyzed their mechanical properties. Fig. 4(a) to (c) show the stress—strain curves of the GPO, gap and overlap models, and the mechanics of collagen molecules can be described by the worm-like chain model. We observed a similar trend in the stress—strain curves of the GPO model at different temperatures. The stress—strain curve of the gap model at 310 K showed that under the same stress, the model had a relatively larger strain than the model at 307 and 313 K.

Fig. 4.

Analysis diagram after SMD simulation at 307 K, 310 K, and 313 K. The stress—strain curves of the (a) GPO model, (b) gap model and (c) overlap model. (d) Young’s modulus of the GPO, gap, and overlap models.

For the overlap model, the material softened while the temperature rose from 307 K to 313 K. Young's modulus was calculated from the worm-like chain model shown in Fig. 4(d). The results of the Young’s modulus are consistent with previous studies [28], [61], [62], [63], [64], [65]. The GPO model had a similar Young’s modulus at different temperatures. While increasing the temperature of the overlap model by 3 °C, Young’s modulus decreased by 29.4%. The overlap model was more deformable than the gap model. The behavior of the overlap model was consistent with the observation at the macroscale, in which the muscle softens and easily stretches when the temperature increases. Therefore, we further focused on the overlap region and studied its structural characteristic change along the sequence between 310 K and 313 K.

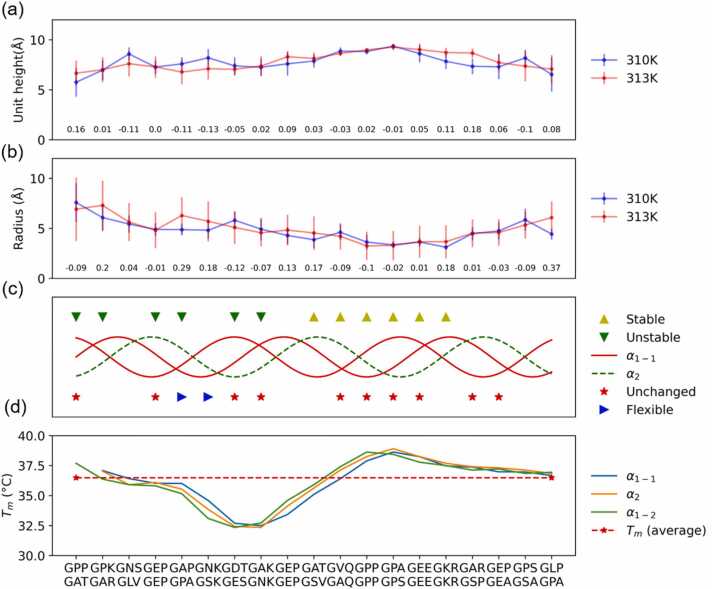
We analyzed the unit height and radius for the overlap model at different temperatures, as shown in Fig. 5(a) and (b). Blue represents the model at 310 K, and red represents the model at 313 K. We further defined a unit height higher than the average of the sample and a radius lower than the average of the sample as “stable.” In contrast, it is defined as “unstable.” The instability means that the structure would unfold at 310 K. In addition, we defined a change in unit height and radius below 10% as “unchanged” region. The change in unit height decreases by 10%, and the radius increases by 10% as “flexible” region. “Flexible” means that the structure would “become unfolding” when the temperature increased. The results are shown in Fig. 5(c). The unstable regions included the sequences of GPP-GAP, GPK-GAR, GEP-GEP, GAP-GPA, GDT-GES, and GAK-GNK. The stable regions included the sequence of GAT-GSV, GVQ-GAQ, GPP-GPP, GPA-GPS, GEE-GEE, and GKR-GKR. The flexible regions included the sequence of GAP-GPA and GNK-GSK, which had the most significant changes in both unit height and radius. The unchanged regions included the sequence of GPP-GAT, GEP-GEP, GDT-GES, GAK-GNK, GVQ-GAQ, GPP-GPP, GPA-GPS, GEE-GEE, GAR-GSP, and GEP-GEA.

Fig. 5.

Structural analysis for the overlap region between 310 K and 313 K. (a) Distribution of the unit height and (b) radius in the overlap region at 310 K and 313 K. (c) Stable region, unstable region, unchanged region, and flexible region in the overlap region. (d) Predicted melting temperature (T_m) along the overlap model sequence. T_m was predicted from the THeBuScr builder [66].

In particular, the adjacent sequences of GAT-GSV, GVQ-GAQ, GPP-GPP, GPA-GPS, GEE-GEE, and GKR-GKR formed a region to stabilize the triple-helix structure. We used the Triple-Helical collagen Building Script tool (THeBuScr) to predict the melting temperatures (T_m) from the sequence [66]. A predicted T_m higher than the average value represented higher thermal stability, and a T_m lower than the average T_m indicated weaker thermal stability.

The results show that the predicted melting temperatures have a similar tendency to our result. The unstable regions GPP-GAP, GPK-GAR, GEP-GEP, GAP-GPA, GDT-GES, and GAK-GNK are located in the region with a lower T_m, and the stable regions GAT-GSV, GVQ-GAQ, GPP-GPP, GPA-GPS, GEE-GEE, and GKR-GKR are located in the region with a higher T_m. In addition, GAP-GPA and GNK-GSK are the most temperature-sensitive regions from 310 K to 313 K.

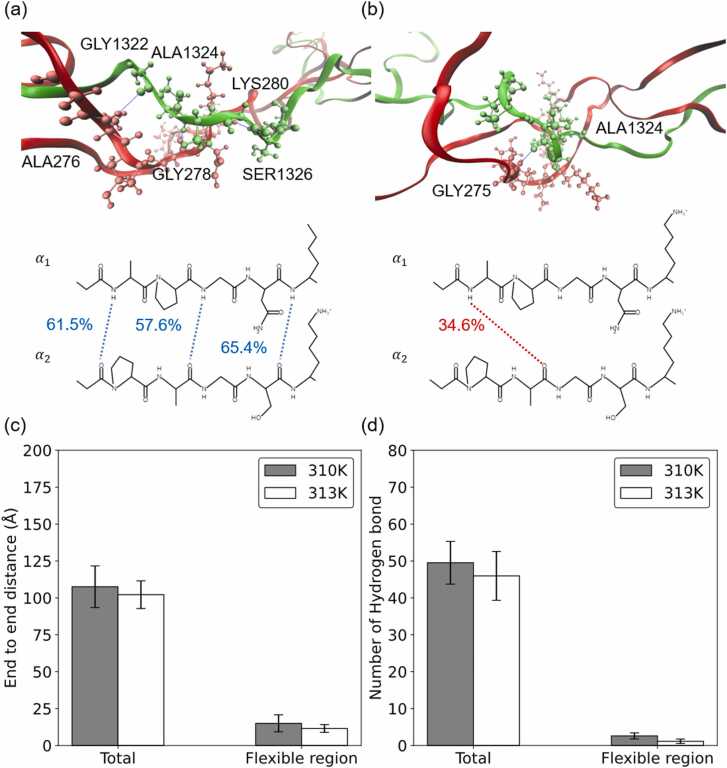
Snapshots of the molecular structures of the overlap models at 310 K and 313 K are shown in Fig. 6(a) and (b). The figure shows that the flexible region in the overlap model folds at 313 K, and the region exhibits a more stretched structure at 310 K. The flexible region is defined as the sequence of GAP-GPA and GNK-GSK in Fig. 5(d). The end-to-end distance in the flexible region is 15.02 ± 5.76 Å at 310 K and 11.5 ± 2.62 Å at 313 K. The results agree with the longer end-to-end distance of overlap at 313 K shown in Fig. 6(c). Interestingly, we also found that the end-to-end distance of the flexible region is close to the end-to-end distance of the whole molecule which means the flexible region controls whole molecule stiffness from 310 K to 313 K. To explore the influence of temperature on hydrogen bonding, we analyzed hydrogen bonding in the flexible region at 310 K and 313 K, as shown in Fig. 6(c). The number of hydrogen bonds in the flexible region is 2.59 ± 0.82 at 310 K and 1.13 ± 0.59 at 313 K. The results show that the number of interchain hydrogen bonds in the flexible region decreases with increasing temperature. We further compare with the interchain hydrogen bond in the overlap model. The main decrease in hydrogen bonds in the overlap region comes from the decrease in hydrogen bonds in the flexible region. In Fig. 6, the flexible region at 310 K has more hydrogen bonds than the flexible region at 313 K, and we also found that the flexible region has a larger interchain distance increase at 313 K resulting from the changes in the nonbonding interaction energies, as shown in Figs. S4 to S6. The overlap region exhibits more sensitivity to the thermal effect than the gap region, forming a folded structure and fewer hydrogen bonds at a higher temperature.

Fig. 6.

Snapshot of the molecular structure of the overlap model and the distribution of interchain hydrogen bonds in the overlap model at (a) 310 K and (b) 313 K. The alpha1 and alpha2 chains are represented as ribbons and colored red and green, respectively. The molecular structures of the flexible region are plotted as CPK in VMD and colored by atom type. Hydrogen bonds with high occupancy (above 40%) are highlighted by blue dashed lines. (c) The end-to-end distance in the overlap model and in the flexible region at 310 K and 313 K. (d) Number of total hydrogen bonds in the overlap model and in the flexible region at 310 K and 313 K.

3.3. Evaluation of the strain-predictive model

Considering the consistency of the mechanical behavior of the overlap model and muscle at the macroscale, the strain-predictive model was developed from the strains of the unit height of the overlap region sequence in MD simulations. The coefficient of determination (R2) of the strain-predictive model was 0.92, showing the credibility of the strain-predictive model. Fig. 7(a) shows the relationship between the original and the predicted strain of the known combinations of sequences. The closer the combination of sequences is to the diagonal, the lower its validation loss is. We predicted the strain of the 272 combinations of sequences that came from the permutations of the sequences in the overlap region with the model. Those with predicted strains over 0.85 and those with predicted strains under 0.15 are shown in Fig. 7(b). The results of the remaining sequences are shown in Fig. S7. In Fig. 7, the color illustration and the occurrence rates of combinations of sequences are applied according to a previous study [67]. Among the sequences with higher predicted strains, GAR-GSK and GPK-GSP were the most common combinations in collagens. Other combinations, such as GEP-GSK, GDT-GSP, GAK-GNK, and GNK-GSV, were also predicted to have high strain, although they were less common than the mentioned combinations in collagens. Our model also found high strain from the combination of GDT-GNK, which was seldom observed in the collagens. In addition to the group of high predicted strains, we found common combinations in the collagens, including GEP-GPS, GLP-GPP, and GLP-GPA, in the group of low predicted strains. Combinations such as GVQ-GES, GNK-GEA, GAT-GPP, and GAT-GPS were less common in the collagens, but their predicted strains were low as well. Based on the high performance of the strain-predictive model, the temperature-dependent mechanical properties of unknown sequence combinations could be uncovered. This approach can be applied to collagen designs in the future.

Fig. 7.

(a) Linear regression with the strain from the MD simulation and the predicted strain. Blue: Combinations of sequences in the training data. Red: Combinations of sequences in the testing data. (b) Combinations of sequences with predictive strain over 0.85 and lower than 0.15. Sequences with occurrence rates from 0.075% to 0.25% are in dark gray. Those with occurrence rates over 0.1% were in light gray, and occurrence rates over 1.0% were in white. The color illustration approach was described in a previous study [67]. The combinations of sequences on the right-hand side were more common in collagens than those on the left-hand side.

4. Conclusion

In this study, we applied molecular dynamics simulation to study the molecular mechanism of collagen molecules during physiological warmup. The equilibrated collagen models showed that the overlap model was more sensitive to temperature change than the gap model and the GPO model. During the mechanical test, we found that the Young’s modulus of the overlap region decreased upon a temperature increase from 310 K to 313 K. The overlap region was found to be more flexible than the gap region, and the mechanical behavior of the former was consistent with observations at the macroscale, in which the tendon becomes softened and easily stretched at a higher temperature. The detailed structural analysis showed that the flexible region in the overlap model formed a more folded conformation and fewer hydrogen bonds, causing weaker mechanical behavior in this model. A strain-predictive model was developed based on the MD simulation to predict the deformation of collagen amino acid sequences. The prediction of the strain of unknown combinations of amino acid sequences showed their different mechanical properties during physiological warmup. The model could be applied to future collagen designs to obtain desirable temperature-dependent mechanical properties.

CRediT authorship contribution statement

Wei-Han Hui: Data curation, Formal analysis, Writing – original draft, Revising the manuscript critically for important intellectual content. Pei-Hsin Chiu: Data curation, Formal analysis, Writing – original draft. Ian-Ian Ng: Investigation, Writing – original draft. Shu-Wei Chang: Conceptualization, Methodology, Hardware, Writing – review & editing, Supervision. Chia-Ching Chou: Conceptualization, Hardware, Writing – review & editing, Supervision. Hsiang-Ho Chen: Conceptualization, Writing – review & editing, Supervision.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. Supplementary material

Supplementary material.

.