Occult Regions of Suppressed Coherence in Liver B-Mode Images

Abstract

Ultrasound is an essential tool for diagnosing and monitoring diseases, but it can be limited by poor image quality. Lag-one coherence (LOC) is an image quality metric that can be related to signal to noise ratio (SNR) and contrast to noise ratio (CNR). In this study, we examine matched LOC and B-mode images of the liver to discern patterns of low image quality, as indicated by lower LOC values, occurring beneath the abdominal wall, near out-of-plane vessels, and adjacent to hyperechoic targets such the liver capsule. These regions of suppressed coherence are often occult; they present as temporally stable uniform speckle on B-mode images, but the LOC measurements in these regions suggest substantially degraded image quality. Quantitative characterization of the coherence suppression beneath the abdominal wall shows a consistent pattern both in simulations and in vivo; sharp drops in coherence occurring beneath the abdominal wall asymptotically recover to a stable coherence at depth. Simulation studies suggest that abdominal wall reverberation clutter contributes to the initial drop in coherence but does not influence the asymptotic LOC value. Clinical implications are considered for contrast loss in B-mode imaging and estimation errors for elastography and Doppler imaging.

Introduction

Liver disease represents a large global health burden that is projected to increase due to rising rates of obesity and metabolic diseases (Estes et al., 2018). An estimated 25% of the global population has non-alcoholic fatty liver disease (Cotter and Rinella, 2020) and 3.5% of deaths worldwide are attributed to cirrhosis and liver cancer (Asrani et al., 2019). Ultrasound is an indispensable tool for diagnosing and managing chronic liver diseases (Gerstenmaier and Gibson, 2014). Conventional B-mode imaging is used for detecting fatty liver disease based on liver echogenicity (Ozturk et al., 2018) and cirrhosis based on the nodularity of the liver (Filly et al., 2002). Lesions associated with hepatocellular carcinoma (HCC) can be identified on the B-mode image (Singal et al., 2009) or by using contrast enhanced ultrasound (CEUS) (Dietrich et al., 2020). Doppler ultrasound is used to monitor portal vein hypertension, a common complication of liver cirrhosis (Robinson et al., 2009). Elastography is an emerging area of ultrasound imaging which uses the estimated stiffness of liver tissue to predict liver fibrosis grading; it has been applied to the clinical management of fatty liver disease, chronic hepatitis, and HCC (Dietrich et al., 2017). Research in quantitative ultrasound shows promise for the continued development of robust diagnostic metrics for chronic liver diseases (Berzigotti et al., 2018). Ultrasound’s versatility in liver screening and the development of robust quantitative diagnostic metrics suggest that ultrasound will continue to play a central role in managing these endemic chronic liver diseases.

While liver ultrasound screening increases the likelihood of early disease detection and improves treatment outcomes (Singal et al., 2014), it often fails to produce diagnostically useful data. Ultrasound images are primarily degraded by sources of noise originating in the tissue, collectively referred to as acoustic ‘clutter.’ Clutter is a temporally stable random noise pattern superimposed on the image with a similar visual appearance to speckle. Clutter is often worse in obese patients; previous work has shown the signal to clutter ratio can be as low as 0 dB (Lediju et al., 2008a). Clutter substantially reduces image quality and resolution, resulting in poor target conspicuity and reduced clinical performance (Lediju et al., 2008a; Dahl and Sheth, 2014; Pinton et al., 2011). A recent study found that the detection rate for HCC lesions was just 33% (Esfeh et al., 2020). In obese patients, a population much more likely to develop HCC (Marengo et al., 2016), the detection rate was 21% (Esfeh et al., 2020). Another study found that 20% of ultrasound scans had inadequate image quality for HCC surveillance in patients with cirrhosis, with even lower performance for obese patients (Simmons et al., 2017).

Clutter has been attributed to three major sources: reverberation, aberration, and off-axis scattering (Pinton et al., 2011, 2014). Reverberation clutter occurs when sound reflects multiple times between structures or scatterers, such as tissue layers in the abdominal wall, before returning to the transducer (Dahl and Sheth, 2014; Fatemi et al., 2019). These reverberant echoes present on B-mode images as a diffuse haze overlaid on the regions beneath the reverberation source (Dahl and Sheth, 2014; Pinton et al., 2011; Lediju et al., 2008b; Fatemi et al., 2019). Aberration clutter is caused by sound speed inhomogeneities between different tissue types, resulting in focusing errors during beamforming (Pinton et al., 2011; Hinkelman et al., 1998; Mast et al., 1998; O’Donnell and Flax, 1988). Off-axis scattering clutter is generated when beam sidelobes reflect from off-target structures, reducing resolution and contrast by decreasing the relative amount of received energy in the focused main lobe (Lediju et al., 2008a; Pinton et al., 2014; Fatemi et al., 2019). Thick abdominal walls in obese patients generate high levels of reverberation and aberration, due to thick bands of tissue layers and the relatively lower sound speed associated with fat (Lediju et al., 2008a; Dahl and Sheth, 2014; O’Donnell and Flax, 1988; Hinkelman et al., 1998). Poor image quality results from the reductions in contrast and resolution associated with clutter (Lediju et al., 2008a; Pinton et al., 2011; Dahl and Sheth, 2014; Pinton et al., 2014).

Clutter can be directly observed as a diffuse haze, particularly in anechoic or hypoechoic structures such as the bladder, blood vessels, and amniotic fluid (Lediju et al., 2008b). Clutter can be indirectly measured using spatial coherence, which is calculated as the average correlation between pairs of radio-frequency (RF) channel data signals. The separation of the paired elements is known as the ‘lag.’ The van Cittert-Zernike theorem describes the theoretical spatial coherence as a function of lag, and reductions in spatial coherence relative to theoretical expectations can be attributed to noise (Mallart and Fink, 1991). While spatial coherence measurements are sensitive to both temporally variable electronic noise and temporally stable clutter noise, they can be distinguished by measuring temporal coherence. Temporal coherence can be estimated from the average correlation in channel data across repeated A-lines at a fixed position. High temporal coherence suggests low levels of electronic noise, so changes in spatial coherence can be attributed to clutter in high temporal coherence environments (Long et al., 2018). Spatial coherence is a well-validated measure of clutter and has seen use in image quality improvement for a wide range of applications (Pinton et al., 2014; Li and Li, 2003; Bamber et al., 2002; Long et al., 2020a; Nguyen and Prager, 2018; Lediju et al., 2011; Dahl et al., 2017; Nock et al., 1989; Vienneau et al., 2019; Ozgun et al., 2019; Matrone et al., 2014). The spatial coherence of neighboring element pairs, known as lag-one coherence (LOC), can be directly related to signal to noise ratio (SNR) and contrast to noise ratio (CNR) (Long et al., 2018); it correspondingly has been shown to be a reliable indicator of image quality on B-mode images. Most applications of LOC have focused on using LOC values in a small region of interest (ROI) at the focus as a feedback parameter for image optimization (Flint et al., 2020; Bottenus et al., 2018). A recent application used LOC to restore contrast in B-mode images by estimating and removing pixel brightness associated with clutter (Long et al., 2020b). Coherence is also related to imaging performance in elastography and Doppler imaging, which both rely on the quality of correlations between received echoes (Dietrich et al., 2017; Jensen, 1996).

In the present study, we compare images of pixel-wise LOC estimates with matched B-mode liver images in order to describe patterns in regional image quality. We describe simulation and in vivo methods for collecting RF channel data and characterizing image quality using LOC. In the qualitative results section, we show patterns in the suppression of LOC values beneath the abdominal wall and near the liver capsule, as well as suppression of coherence without a readily observable pattern or cause in the B-mode image. These regions of suppressed coherence have a generally high temporal coherence and appear as uniform liver tissue on the B-mode image, indicating that the reductions in LOC are caused by clutter (i.e. reverberation, aberration, and off-axis scattering) rather than temporally varying random noise. In the quantitative results section, we show consistent quantitative patterns in coherence in the regions beneath the abdominal wall in vivo and in simulations. Manipulating simulation conditions allows for isolating the effects of aberration and reverberation on the pattern of coherence seen beneath the abdominal wall. We discuss the clinical implications of these suppressed coherence regions that are undetectable on B-mode images but whose coherence suggests that image quality is impaired.

Materials and Methods

Lag One Coherence Clutter Mapping

The spatial coherence of RF channel data is calculated as the average coherence between signals received by pairs of transducer elements with an element separation distance referred to as the ‘lag.’ Formally, this can be expressed as

$$\widehat{R}[m]=\langle \frac{1}{M-m}\sum _{i=1}^{M-m}\frac{{\sum }_{n=n_1}^{n_2}{s}_i[n]s_{i+m}[n]}{\sqrt{{\sum }_{n=n_1}^{n_2}{s}_i^2[n]{\sum }_{n=n_1}^{n_2}{s}_{i+m}^2[n]}}\rangle$$ (1)

where $\widehat{R}$ is the spatial coherence, ⟨⟩ indicate an ensemble average, m is the lag separating channel pairs, M is the total number of elements in the active aperture, S_i and s_i+m are the signals received by elements i and i + m respectively, n is the sample number, and n₁ and n₂ represent the axial range for the kernel (Mallart and Fink, 1991). A 5λ axial kernel was used to calculate LOC values for each pixel in the B-mode image.

To calculate LOC, one simply substitutes m=1 into equation 1, i.e.

$$LOC=\widehat{R}[1]$$ (2)

The presence of clutter in the received RF signals will decrease LOC below its theoretical value for a noise-free environment. At the focal depth, the theoretical noise-free LOC in uniform speckle can be calculated analytically as (M − 1)/M (Mallart and Fink, 1991). Outside of the focal depth, noise-free coherence measurements are altered by focal effects, particularly in the near-field (Bottenus et al., 2013). In order to determine the noise-free LOC for any given pixel on the image, an LOC image for each transmit condition was created using a large uniform phantom. To ensure there was minimal electronic noise, only phantom images with temporal coherence greater than 0.98 for depths from 0 - 10 cm were used. Temporal coherence was calculated as the normalized cross-correlation between these successive A-line pulses at a given position. With a high temporal coherence and through observations consistent between spatial coherence as a function of lag and predictions from the van Cittert-Zernike theorem for a noise-free measurement, these LOC images were validated. Coherence suppression in vivo, denoted ΔLOC, was calculated as the difference between the LOC image for a given subject and the noise-free LOC image, i.e.

$$\Delta LOC=LO{C}_{\text{subject}}-LO{C}_{\text{phantom}}$$ (3)

In vivo Liver Imaging

Ten healthy volunteers were recruited with informed consent under a Duke Institutional Review Board-approved protocol. For each volunteer, channel data from three subcostal and three intercostal acoustic windows were collected by an experienced radiologist using a C5-2v curvilinear probe on a Verasonics Vantage imaging system (Verasonics, Kirkland, WA). Each acoustic window was unique, i.e. the probe was placed in a new position for each acquisition. The acquisition sequence used 2.36 MHz phase inverted transmit pulses to sweep focal depths every centimeter between 4 and 9 cm with an F/2 aperture configuration. Harmonic channel data were generated by summing echos from the inverted pulses and filtering over 80% fractional bandwidth centered around 4.72 MHz. For each transmit condition, 91 scan lines of channel data were collected over a 45 degree sector scan with 12 cm of radial depth. For each condition, there were also 3 sets of 5 repeated A-line pulses spread evenly through the 45 degree sector. These repeat A-lines were used for temporal coherence calculation.

Fullwave Simulations

Fullwave is a numerical non-linear acoustic simulation tool which uses the Westerveldt equation to simulate wave propagation based on input maps for density, sound speed, attenuation, and non-linearity (Pinton et al., 2009). It can accommodate harmonic generation, reverberation, and aberration, and has been well validated for modelling pulse-echo ultrasound (Pinton et al., 2011; Pinton, 2017; Pinton et al., 2014; Dahl and Sheth, 2014; Bottenus et al., 2019). In this study, two-dimensional Fullwave simulations were performed, collecting RF channel data in the axial-lateral plane of a linear array transducer model. The transducer element pitch was selected to match the Verasonics C5-2v transducer used for the in vivo studies. The acquisition sequence used 2 MHz inverted transmit pulses with an F/2 aperture focused at 4 cm to collect 45 A-lines over a 0.8 cm lateral range with 10 cm of axial depth and a grid pixel size of 8.8 μm. Harmonic channel data were generated by summing the inverted pulses and filtering over a 100% fractional bandwidth centered around 4 MHz. Speckle was generated by randomly changing the sound speed of 50 pixels per resolution cell to Gaussian random values with a mean corresponding to the original sound speed and a standard deviation of ±5% (Pinton et al., 2009). Six abdominal walls were created using tissue labeled histological slides from the Diagnostic Research Laboratory at the University of Rochester (Mast et al., 1997). Acoustic properties used for fat, muscle, connective tissue, and liver tissue are shown in Table 1. They were selected based on reference values in the literature (Goss et al., 1978, 1980; Hamilton et al., 1998).

Table 1:

TISSUE ACOUSTIC PARAMETERS USED FOR SIMULATIONS

	B/A	α (dB/MHz/cm)	C0 (m/s)	ρ0 (gm/cm3)
Fat	9.6	0.4	1478	0.937
Connective	8	0.5	1613	1.120
Muscle	5.5	1	1566	1.070
Liver	7.6	0.5	1570	1.064

Table 2 summarizes the simulation conditions and expected clutter types for each case. There were three basic types of simulations used in this study. Uniform (U) simulations consisted of uniform speckle with liver tissue acoustic parameters. Uniform + Wall (UW) simulations consisted of one of six abdominal wall models, with appropriate tissue parameters based on histological labelling, placed above a region with uniform liver speckle. Wall (W) simulations consisted of only the abdominal wall model above an anechoic (i.e. no speckle-generating scatterers) liver region. Since W simulations had no scattering beneath the abdominal wall, RF signal received distal to the abdominal wall may be attributed to reverberant echos from the abdominal wall.

Table 2:

SIMULATION CONDITIONS AND EXPECTED CLUTTER TYPES

Simulation Type	Description	Expected Clutter
Uniform (U)	Uniform liver with speckle	None
Uniform + Wall (UW)	Abdominal wall over uniform liver w/ speckle	Reverberation, aberration
Wall (W)	Abdominal wall over anechoic liver (no speckle)	Reverberation
Isoimpedance	UW − W RF data; subtracts reverberation clutter	Aberration
Scaled Reverberation Clutter	UW + N×W RF data; adds additional reverberation clutter	Aberration, (1+N) × original reverberation

Reverberation clutter levels were manipulated to distinguish the effects of reverberation and aberration. Isoimpedance (i.e. no reverberation) simulation data was generated by subtracting the RF data from the W simulations from the UW simulation RF data. This removes reverberation clutter in the RF data, thereby isolating the effects of aberration (Pinton et al., 2011). To assess the effects of adding reverberation clutter, ‘scaled clutter’ simulation data was generated by adding RF data from W simulations to the UW simulation RF data with varying multiplicative scaling factors (1, 2, or 5).

Qualitative Results

Liver Capsule Coherence Suppression

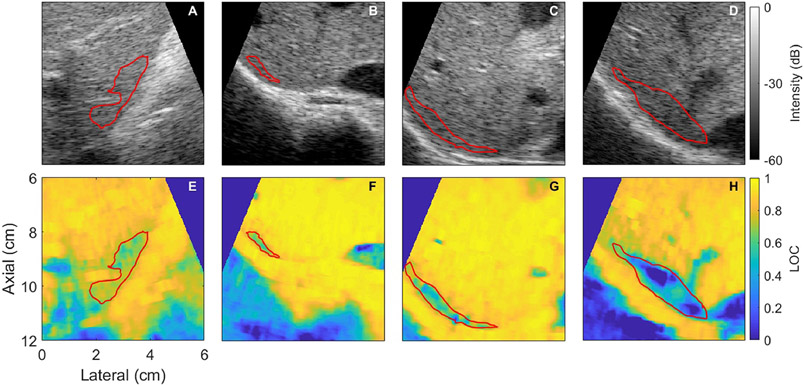
Figure 1 shows representative examples demonstrating suppression of coherence in the regions adjacent to the hyperechoic liver capsule at depth. LOC values in these regions range from 0.32 to 0.70 for these examples. These regions of suppressed coherence present visually as uniform speckle. All of these examples have a temporal coherence greater than 0.95, corresponding to an SNR of 25 dB, except 1C, which has a temporal coherence of 0.8 (SNR = 12 dB) in the ROI.

Figure 1:

Representative examples showing suppressed coherence near the liver capsule comparing B-mode (top) and LOC (bottom) images for each subject (columns). The average LOC within the red region of interest for E-F is 0.70, 0.68, 0.62, 0.32 respectively. The corresponding regions on the B-mode image (shown in red) appear as uniform speckle. All images are focused at 9 cm.

Suppression of Coherence from Unknown Sources

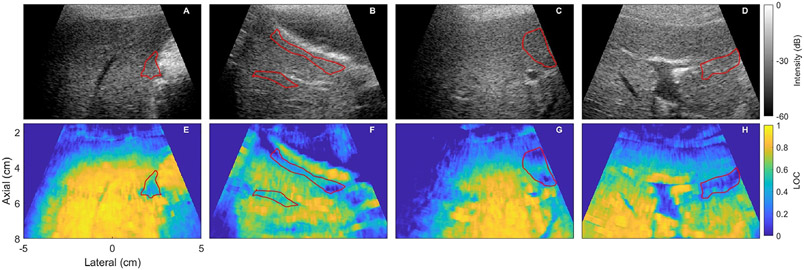
In numerous images, there were regions of suppressed coherence that could not be readily explained by features in the B-mode image. Representative examples of these phenomena are shown in Figure 2. The average LOC in these regions ranges from 0.21 to 0.52. The temporal coherence in these regions is greater than 0.95 for all examples. Some of these regions appear to be related to a nearby hyperechoic structure or slightly out-of-plane vessels. Similar to the liver capsule coherence suppression examples, these regions present as uniform speckle on the matched B-mode image.

Figure 2:

Images showing cases where there is a region of suppressed coherence that cannot be obviously explained by the capsule or abdominal wall. B-mode (top) and lag one coherence (LOC) (bottom) images are shown with the region of suppressed coherence shown in red. The mean LOC values in the region of interest are 0.52, 0.41, 0.27, and 0.21 for E-F respectively. As with the capsule and abdominal wall coherence suppression, the B-mode images do not give any obvious indicators that there is a low SNR in the region in of suppressed coherence; it appears as uniform speckle. All images are focused at 6 cm.

Abdominal Wall Coherence Suppression

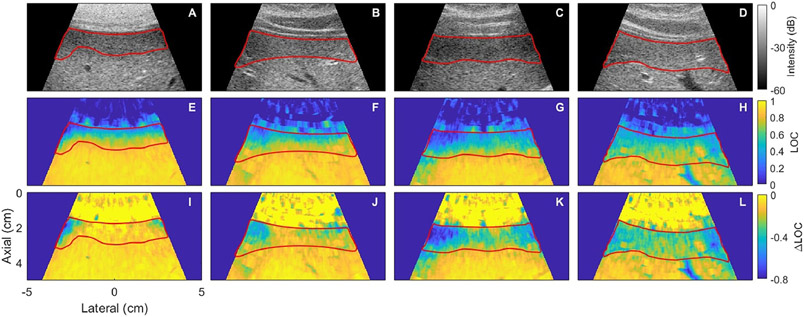
Figure 3 shows representative examples of suppressed coherence beneath the abdominal wall. The amount of suppression and the length of the suppressed region varied considerably among subjects. The coherence generally recovered to a stable, relatively high asymptotic value at depth in the liver. The length of the suppressed region ranged from 0.5 cm to 2.5 cm. A more robust quantitative characterization of this pattern in coherence beneath the abdominal wall is described in the following section. The ΔLOC images are also shown to make the region of suppressed coherence relative to a uniform phantom more clear in the near-field.

Figure 3:

Representative images showing suppression of coherence beneath the abdominal wall comparing B-mode (top), lag one coherence (LOC) (middle), and ΔLOC (bottom) images for each subject (columns) with the region of suppressed coherence highlighted in red. All images are focused at 4 cm. The average and range of LOC and ΔLOC values for each image column is shown in table 3.

Quantitative Results

In vivo Liver

LOC as a function of depth was quantified by manually drawing ROIs in regions of the liver that visually appeared uniform on both the B-mode and LOC images. ROIs varied in length based on the length of a continuous uniform region for a given acquisition. Acquisitions were excluded if the presence of vessels, artifacts, or other structures prohibited drawing a continuous ROI in a uniform region with a minimum width of 0.5 cm and a minimum length of 6 cm in depth. Once uniform regions were isolated, lateral averaging across the uniform ROI extracted trends in coherence as a function of depth. Figure 4 demonstrates this process. The uniform phantom LOC map (A) was subtracted from the LOC map observed in a liver acquisition (B) to yield a ΔLOC map (C). Laterally averaging the spatially uniform regions of phantom LOC, liver LOC, and ΔLOC maps yielded the traces displayed in Figure 4D.

Figure 4:

ΔLOC calculation demonstration for a 4 cm focal depth acquisition. The measured LOC field in a uniform phantom (A) was subtracted from the LOC map formed from a matched in vivo liver acquisition (B). This yielded the ΔLOC map shown in (C). Frame D displays the laterally averaged coherence information as a function of depth in approximately uniform tissue regions in the phantom, liver, and ΔLOC maps.

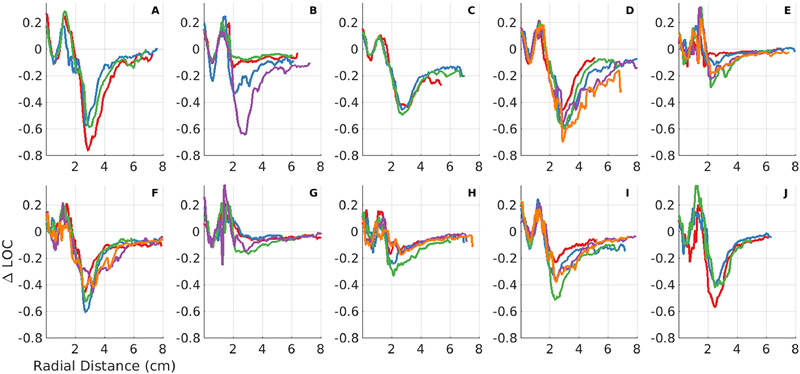
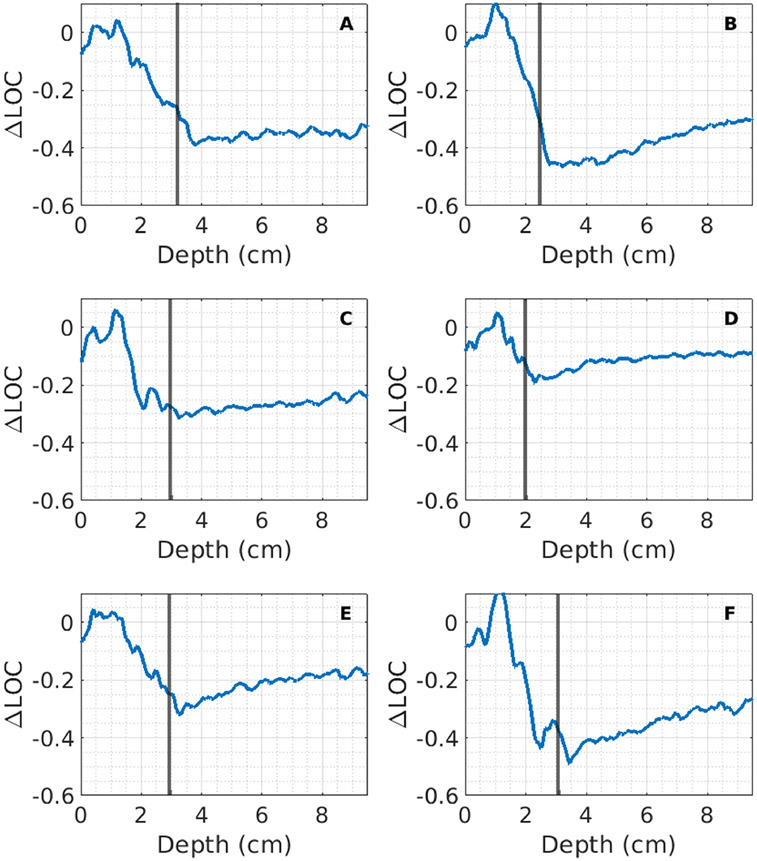
Figure 5 shows the ΔLOC as a function of depth in repeat acquisitions for all 10 volunteers. There is a pattern of erratic ΔLOC values in the near-field. This is likely caused by a combination of focusing errors due to the shallow depth and coherent hyper-echoic bands separating tissue layers in the abdominal wall. There is considerable variability in values for the minimum ΔLOC and the asymptotic ΔLOC across subjects. Some subjects had substantially decreased LOC compared to a uniform phantom, with ΔLOC as low as −0.75. Others showed very little reduction in coherence compared to a uniform phantom, with ΔLOC values around −0.1, indicating nearly ideal image quality with very little acoustic clutter. The asymptotic ΔLOC value also varies considerably; some make almost a complete recovery, reaching ΔLOC values as high as −0.05, whereas others only reach asymptotic values of −0.2 to −0.3. Between acquisitions with unique acoustic windows for a given subject, there is often a consistent pattern in axial LOC. Some subjects show variability within acquisitions, suggesting that that different acoustic windows have different local clutter levels. For example, in Figure 5B, one acquisition has a minimum ΔLOC of approximately −0.65 and an asymptotic ΔLOC of approximately −0.15, while a different acoustic window has a minimum ΔLOC of −0.08 and an asymptotic ΔLOC of −0.04.

Figure 5:

ΔLOC vs axial depth in manually drawn ROIs in regions of uniform speckle that do not contain lag one coherence (LOC) suppression associated with out-of-plane structures and the liver capsule shown in the previous section. Each plot represents acquisitions for a given subject. Each colored line is a unique acquisition. Acquisitions for some subjects were excluded if a continuous uniform ROI could not be drawn. Note the consistent pattern of erratic coherence in the near-field, a region of suppressed coherence beneath the abdominal wall, and a region of relatively high, asymptotic coherence at depth.

Fullwave Simulations

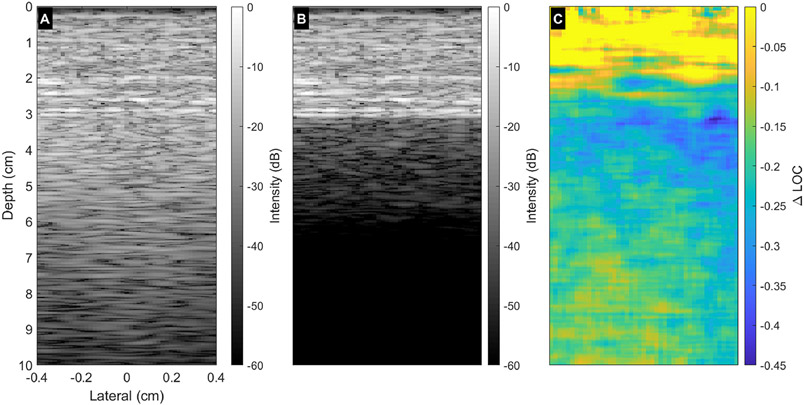
Figure 6 shows representative examples of the B-mode images for (A) the wall over a uniform speckle region, (B) the wall over an anechoic region with reverberation ringdown beneath the wall, and (C) the ΔLOC image for the UW B-mode image shown in (A). Figure 6B shows the significant reverberation clutter in the region below the abdominal wall that is not visible in the B-mode image shown in (A). The length of the suppressed coherence region shown in (C) correlates with the magnitude of clutter visible in the B-mode image shown in (B). The ringdown clutter shown in (B) is analogous to the clutter that has been observed in vivo in anechoic structures such as the bladder, blood vessels, and amniotic fluid.

Figure 6:

Representative images showing (A) the B-mode image of the wall over uniform tissue, (B) an image of the wall over an anechoic region and (C) an image of the Δ LOC values for (A). (B) shows the expected reverberation in (A). Note the distinct region of suppressed coherence occurring after the abdominal wall at roughly 3 cm, followed by a recovery as the clutter levels shown in Figure (B) attenuate.

Figure 7 shows ΔLOC as a function of axial depth for six simulated abdominal walls. There is a consistent pattern of erratic coherence in the near-field and suppression of coherence beginning after the abdominal wall (denoted by the black vertical line). The region of suppressed coherence visually presents as isoechoic uniform speckle. The sharp drop in ΔLOC values generally occurs near the end of the abdominal wall. Walls shown in 7B, 7D-F show a recovery to an asymptotic value at depth, similar to what has been observed in vivo, while walls 7A and 7C generally remain flat at the initial suppressed ΔLOC value. The wall shown in 7D almost completely recovers, reaching a ΔLOC value of just −0.1. In contrast, the one shown in 7A makes little recovery and has a constant ΔLOC value of approximately −0.35 beneath the abdominal wall. Similar to in vivo conditions, there is considerable variability in the amount of initial suppression and the asymptotic value.

Figure 7:

ΔLOC values as a function of depth for six different abdominal wall models, averaged laterally over a 1 cm region. The end of each abdominal wall is denoted by the black vertical line shown on each plot. Note the similarities to the in vivo curves, with most walls showing a consistent pattern of suppressed coherence followed by recovery to an asymptotic value.

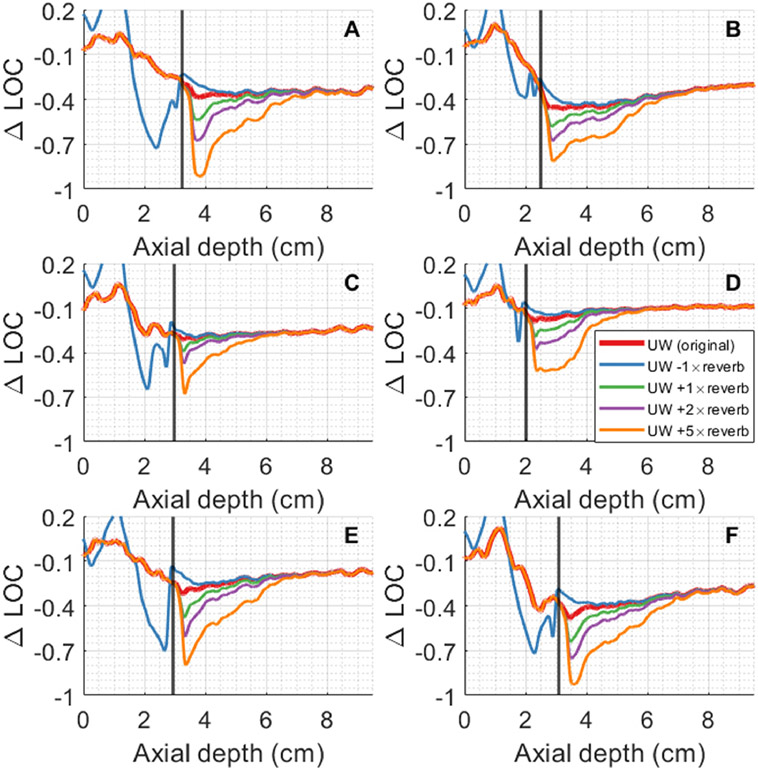
Figure 8 shows the effects of adding and subtracting reverberation clutter in the W simulation from the RF data in the UW simulation. The end of each abdominal wall is denoted by a vertical black line. Removing reverberation clutter to isolate the effects of aberration nearly eliminates the initial suppression of coherence; the coherence after the abdominal wall is roughly the same as the asymptotic value at depth. Increasing the magnitude of reverberation clutter has the effect of increasing the amount of initial suppression in coherence and increases the distance required to reach an asymptotic ΔLOC value. Altering the amount of reverberation clutter does not change the asymptotic ΔLOC value for a given simulation.

Figure 8:

ΔLOC vs depth with varying magnitudes of reverberation clutter. ‘UW − W’ indicates subtraction of W RF data from the UW RF data, thereby removing reverberation clutter. ‘UW + N×W’ indicates addition of W RF data multiplied by a factor of N to the UW RF data, which increases the amount of reverberation clutter. Adding or subtracting reverberation clutter respectively increases or decreases the initial levels of coherence suppression but does not change the asymptotic value.

Discussion

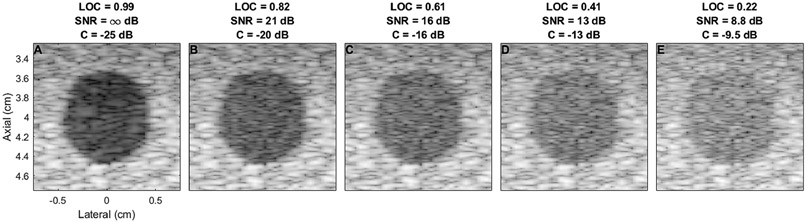
There is some previously reported evidence for clinical observations of poor image quality in the region beneath the abdominal wall. In B-mode imaging, assessment of liver surface nodularity for detection of liver cirrhosis is significantly worse on the surface immediately below the abdominal wall compared to deep surfaces, with a sensitivity of 53% and 86% respectively (Filly et al., 2002). In echocardiography, reverberation from fat and muscle tissue in the chest has been shown to reduce visibility of the heart walls and intraventricular contrast (Fatemi et al., 2019). Intraventricular reverberation clutter can also present as a blood clot, potentially resulting in misdiagnosis (De Vos et al., 2020). Our results showing coherence suppression beneath the abdominal wall are consistent with these clinical observations, given the known relationships between LOC and image quality. For example, the average coherence outlined in the regions of interest shown in Figures 1-3 ranges from 0.21 to 0.8. Based on theory developed by Long et al., this coherence corresponds to a beamformed SNR of approximately 8.5 dB to 20 dB (Long et al., 2018). Lediju et al. estimates the contrast loss for this range of clutter levels in a 24 dB lesion would be between 15 dB and 4 dB, meaning a 24 dB lesion would only have an observed contrast of 9 dB to 21 dB (Lediju et al., 2008a). This is shown visually in Figure 9. More subtle lesions would likely be rendered undetectable in these regions.

Figure 9:

Visualization of lesion contrast for different signal to noise ratios. (A) shows a 24 dB contrast lesion with no added noise. (B)-(E) add increasing amounts of noise to the image shown in (A), with the contrast decreasing from −20 dB to −9.1 dB as the amount of noise decreases. This simulation was performed in Field II using a probe matching the geometry of a the C5-2v and focused at 4 cm.

Stiffness estimation in elastography has also been shown to be compromised below the abdominal wall. One study found that the success rate of shear wave speed measurements was significantly reduced in the 1-2 cm region immediately below the liver capsule (Wang et al., 2014). Clinical guidelines consistently advise against performing measurements in this region (Dietrich et al., 2017). The SNRs associated with the regions of suppressed coherence observed in this study also suggest that elastography methods would be compromised with high local clutter levels. Pinton et al. (2006) quantifies the relationship between displacement tracking accuracy and SNR for stationary noise. The results of this work suggest that for a beamformed SNR of 8 dB (the lower end of SNRs for the regions of suppressed coherence), there would be a downward bias of 0.5 μm for a 4.8 μm displacement. This downward bias would affect ARFI and other elastography methods directly relating estimated displacement to stiffness. A region with suppressed coherence gives rise to a downward bias in displacement estimation, causing this region to appear stiffer. Shear wave elastography (SWE) would be less sensitive to this displacement bias because it relies on shear wave arrival times rather than displacement magnitudes. However, if clutter levels are very high, SWE measurements would have a lower success rate because the stationary echoes associated with clutter would overshadow the echoes from moving tissue. Similar problems may occur in Doppler imaging, in that high levels of stationary clutter would give rise to higher performance requirements for wall filters to remove those stationary echoes.

These findings suggest that clinicians should be wary of imaging performance immediately beneath the abdominal wall and near the liver capsule. Given the variable and somewhat unpredictable nature of suppressed coherence, designers of ultrasound systems may consider incorporating a tool which displays a matched LOC or ΔLOC image alongside B-mode images. This would allow clinicians to be more confident about which regions of a given image are trustworthy and could help guide elastography measurement locations. This LOC display tool could also inform acoustic window selection. Figure 5 shows that there is variability in the amount of coherence suppression between acquisitions for some subjects. Sonographers currently use heuristics for finding a good acoustic window, but a tool which shows the quality of the acoustic window using LOC may allow for more robust acoustic window optimization.

The effects of adding and subtracting pure reverberation clutter from the UW RF data suggest that higher levels of abdominal wall reverberation clutter correspond to lower post-wall minimum LOC values and longer recovery times, but do not impact the asymptotic LOC value. Other clutter sources, namely aberration and multiple-scattering reverberation from beyond the abdominal wall, must then be the basis for the asymptotic LOC value. These findings are consistent with previous results that spatially locate where different clutter types are present (Pinton et al., 2011; Long et al., 2020a; Lambert et al., 2020), as well as the physical principles of aberration and reverberation. Reverberation clutter attenuates during propagation, so reverberation from the abdominal wall will decrease with depth. In contrast, aberration introduced by the abdominal wall will persist even as distance from the abdominal wall increases, though the effect of speed of sound errors introduced by the abdominal wall may diminish with depth as the error relative to the propagation distance will decrease. Multiple-scattering reverberation not introduced by the abdominal wall can occur at any depth, but through uniform regions of liver would likely have a relatively consistent effect on image quality. The distribution of different clutter sources observed here has implications for clutter removal algorithms in abdominal imaging; it suggests that image quality near the abdominal wall is most impaired by substantial reverberation clutter from the abdomen, whereas image quality at depth in the liver will be most improved by correcting for aberration or persistent multiple-scattering reverberations.

The in vivo coherence beneath the abdominal wall shows a consistent pattern of coherence suppression followed by recovery to an asymptotic ΔLOC value. The simulation results followed this pattern in four of the six walls, with two walls showing suppression without substantial recovery. There are a number of limitations in the simulation studies which may explain this discrepancy. Firstly, the exact acoustic parameters for different tissue types may not have sufficient fidelity to the true properties in vivo; the literature offers a wide range of estimates for these parameters, indicating the difficulty associated with getting precise and accurate measurements (Goss et al., 1978, 1980). Secondly, the digitization of the abdominal walls results in sharper tissue boundaries than what may be observed in vivo. This may amplify the overall amount of reverberation noise seen in simulation. A blur filter was applied to the wall maps to mitigate this effect, but it is difficult to calibrate the filter’s kernel size to precisely match in vivo conditions. Thirdly, the pattern of clutter generated by the abdominal wall could be influenced by subtle structural details not captured by the tissue maps used in simulation.

Some of the regions of suppressed coherence appear hypoechoic compared to the surrounding uniform liver tissue. For example, in Figure 3E, the tissue in the region immediately beneath the abdominal wall appears darker. This phenomenon is inconsistent; in Figure 3G, for example, the tissue does not appear darker in the suppressed coherence region. It is unclear what is causing this phenomenon and whether or not it is related to the suppressed coherence. A number of factors can cause tissue to appear hypoechoic, such as the settings on the time gain control, focal effects, and out-of-plane anechoic structures. More investigation across a larger sample size would be required to determine the cause of these slightly darker regions and their relationship, if any, to suppressed coherence.

Conclusions

We have presented evidence for hidden patterns of reduced image quality revealed using LOC. These regions of low image quality are temporally stable and not readily apparent on conventional B-mode imaging. These regions of suppressed coherence occur with a high level of consistency beneath the abdominal wall and adjacent to the liver capsule. Coherence is occasionally suppressed in the central region of the liver, seemingly near out-of-plane vessels or hyper-echoic structures. The suppressed coherence beneath the abdominal wall shows a pattern of a sharp drop in LOC followed by recovery to an asymptotic LOC value at depth in the liver. Simulation studies with models of the abdominal wall support this pattern. The addition and subtraction of reverberation clutter in simulation experiments suggest that reverberation from the abdominal wall determines the initial amount of suppression and rate of recovery, but does not determine the asymptotic LOC value. The clinical implications of these occult regions of low image quality could be substantial; lesion detectability and displacement tracking are both considerably impaired in these regions in a way that is not discernible from the B-mode image, and this may limit clinical tasks such as lesion detection, stiffness estimation, and blood velocity measurements.

Table 3:

LOC AND ΔLOC VALUES WITHIN ROI ON FIGURE 3

	LOC		Delta LOC
	Range	Average Value	Range	Average Value
Column 1	[0.078, 0.84]	0.57	[−0.32, −0.11]	−0.15
Column 2	[0.16, 0.82]	0.61	[−0.42, −0.14]	−0.24
Column 3	[0.15, 0.73]	0.47	[−0.54, −0.24]	−0.38
Column 4	[0.28, 0.70]	0.56	[−0.45, −0.22]	−0.34