Coherence of output gaps in the euro area: The impact of the COVID-19 shock

Abstract

Using the measures proposed by Mink et al. (2012), we reexamine the coherence of business cycles in the euro area using a long sample period. We also analyze the impact of the COVID-19 pandemic on business cycle coherence and examine whether our measures for business cycle coherence indicate a core versus periphery within EMU. Our results suggest that business cycle coherence did not increase monotonically. The COVID-19 pandemic made that the signs of the output gaps of euro area countries became more similar, but we find large differences in the amplitude of the output gaps across countries.

1. Introduction

With the creation of the European Economic and Monetary Union (EMU), member states gave up domestic monetary and exchange rate policies which they could use to respond to idiosyncratic shocks. Whereas common shocks hit all member states (although their transmission may be asymmetric as the COVID-19 pandemic has illustrated), idiosyncratic shocks are asymmetric in nature. In other words, not all members of the monetary union are affected by those shocks. Under normal circumstances, common shocks in the euro area can be countered by the monetary policy of the European Central Bank (ECB), while national fiscal policy could be used to stabilize idiosyncratic shocks and the asymmetric effects of common shocks.

Before the start of EMU, many academics questioned the viability of a monetary union comprised of many countries. In their seminal paper, Bayoumi and Eichengreen (1993) show that before the start of EMU there was a core of countries where economic shocks were highly synchronized, and a periphery where synchronization was significantly lower. In their update of the Bayoumi–Eichengreen study, Campos and Macchiarelli (2016) reach more optimistic conclusions. Using a similar estimation methodology and the same sample of countries and time period, these authors study the 1989–2015 period and conclude that the core–periphery pattern has weakened. Updating their previous study, Bayoumi and Eichengreen (2017) even report that Portugal, Ireland, Italy, Spain, and Greece belong to the core of the euro area, where the core is defined as countries whose aggregate supply and demand shocks are relatively highly correlated with those of Germany.1 Rathke et al. (2020) estimate common euro area shocks and calculate impulse responses to these shocks at the country-sector level. They report varying degrees of heterogeneity across member countries’ responses to common shocks. The level of heterogeneity was most pronounced during the financial crisis. Finally, Campos and Macchiarelli (2021) use a new dynamic framework to study convergence dynamics and find that Ireland, Portugal, and Finland are persistently classified as periphery countries. Spain is moving towards the core, while Greece moves away from the core.2

A more direct way to examine whether the common monetary policy is equally optimal for all countries in the euro area is to analyze the coherence (or, as it is often called, the synchronization) of business cycles. Business cycles reflect shocks, amplification channels, and channels of adjustments.3 The more business cycles differ, the less the ECB’s policies will benefit all countries equally. For instance, whereas countries with a negative output gap would prefer an expansionary monetary policy, countries with a positive output gap would prefer a more restrictive policy stance. Still, even if output gaps would have the same sign, cross-country differences in the amplitude of the output gap can hamper the implementation of a common monetary policy as well. Countries with large swings in their output gaps would prefer larger interest rate steps than countries with moderate output gap amplitudes.4 So divergent business cycles may lead to political-economy tensions among EMU member states and to political pressure on the ECB, notably if these differences in business cycle coherence turn out to be persistent.5

There is a large literature examining (the drivers of) business cycle coherence (see de Haan et al. (2008) and Gaechter and Riedl (2014) for reviews). Most of this literature uses the correlation of output gaps to measure business cycle coherence. However, as shown by Mink et al. (2012), the correlation coefficient of output gaps does not properly take into account that output gaps can have different signs and/or different amplitudes. For instance, two output gap series may have very different amplitudes while the correlation between both series equals one. These authors propose two simple measures to analyze output gap coherence that can be used as an alternative for the correlation coefficient. These measures examine whether countries’ output gaps have the same sign (output gap synchronicity), and whether these output gaps have the same amplitude (which is taken into account by their measure of output gap similarity).6 Mink et al. (2012) show that output gaps in the US are less coherent than output gaps in the euro area, even though the US has been a monetary union for much longer and is generally believed to be more integrated than the euro area.

This paper employs the methodology of Mink et al. (2012) in order to examine business cycle coherence in the euro area. Several alternative methods have been used to analyze business cycle coherence, such as network analysis (cf. Matesanz Gomez et al. (2017)) or fuzzy clustering (cf. Alhborn and Wortmann (2018)). One of the advantages of the method used in this paper is that it provides measures for businesses cycle coherence for each time period in the sample, so that we can zoom in on differences between the period before the COVID-19 crisis hit Europe and the COVID-19 crisis period. Another advantage of this method is that it takes differences between the amplitudes of business cycles into account. This is important, as Belke et al. (2017) report that there are large differences in the amplitudes of national business cycles in the euro area.

Our paper contributes to the literature as follows. First, we reexamine coherence of business cycles in the euro area using a long sample period. Although it has received a lot of attention in the past, recent research on this issue is scant. Second, we analyze the impact of the COVID-19 pandemic on business cycle coherence in the euro area. Although the COVID-19 crisis is generally considered as a common shock, it seems that not all countries in the euro area were equally affected. Furthermore, in terms of timing and diffusion as well as effect there was quite some heterogeneity across countries (both due to ex ante health system capacity as well as ex post containment measures). Crises may affect business cycle coherence. Previous research suggests, for instance, that the financial crisis had a major impact on business cycle coherence (cf. Gaechter et al. (2012)). Likewise, Belke et al. (2017) report that the output co-movement between core and peripheral countries in the euro area decreased markedly in the wake of the financial crisis. Interestingly, they also report that core countries saw rising coherence of output during both the financial crisis and the subsequent sovereign debt crisis. Third, we examine whether our measures for business cycle coherence suggest a core versus periphery classification within EMU and whether COVID-19 has led to changes therein.

The rest of the paper is structured as follows. Section 2 outlines the method. Section 3 describes the data, while Section 4 offers the results. Section 5 presents a robustness analysis. The final section concludes.

2. Method

As explained in the previous section, we focus on output gaps, i.e., deviations of real GDP from its trend value.7 Such output gaps play a central role in the monetary policy maker’s reaction function, either because the policy maker explicitly aims at stabilizing output fluctuations, or because the output gap is used as an indicator of future inflationary pressures.

2.1. Computation of output gaps

Our real GDP data suffer from structural breaks towards the end of the sample due to the COVID-19 shock. This makes the computation of output gaps more difficult. We cannot use the band-pass filter of Baxter and King (1999) because it implies dropping observations at both the beginning and end of the sample. The Christiano and Fitzgerald (2003) filter can also not be used, because it generates symmetric cycles in the middle of the sample but asymmetric cycles towards both ends of the sample.

An alternative would have been the often-used (Hodrick and Prescott, 1997) filter. However, Hamilton (2018) heavily criticizes the HP filter for several reasons. Therefore, we use the Hamilton filter, which estimates:

$$y_{t+h}=\alpha +{\beta }_0{y}_t+{\beta }_1{y}_{t-1}+\cdots +{\beta }_p{y}_{t-p}+v_{t+h},$$

where $h$ is the time lag, $p$ is the number of lags used and the estimated ${\hat{v}}_{t+h}$ is the cyclical component. We have used $h=8$ and $p=4$ as advised by Hamilton for quarterly data.

2.2. Synchronicity

Our first coherence measure, which we call output gap synchronicity, captures for a region of $n$ countries whether positive and negative output gaps coincide, regardless of their amplitudes. Denoting the output gap of country $i$ at time $t$ by $g_i\left(t\right)$ and the reference output gap for the region at time $t$ by $g_r\left(t\right)$, we calculate synchronicity between an individual country $i$ and the reference in period $t$ as

$${\varphi }_{it}=\frac{g_i\left(t\right)g_r\left(t\right)}{\left|g_i\left(t\right)g_r\left(t\right)\right|}.$$ (1)

For now, we assume the reference is the output gap of one country $r$ out of the $n$ countries in the region, but below we propose an alternative way to define the region’s reference output gap. The synchronicity measure is either -1 or 1, where a value of 1 indicates that output gap $i$ has the same sign as the reference, while a value of −1 indicates that both output gaps have opposite signs.

The synchronicity measure can be used to evaluate overall synchronicity of the $n$ countries in the region with the reference output gap. To this end we calculate

$${\varphi }_{it}=\frac{1}{n}\sum _{i=1}^n\frac{g_i\left(t\right)g_r\left(t\right)}{\left|g_i\left(t\right)g_r\left(t\right)\right|},$$ (2)

where $g_i\left(t\right)$ is the output gap of country $i$ at time $t$ and $g_r\left(t\right)$ is the reference output gap for the region at time $t$. It is defined on a $[-1+2/n,1]$ scale, where a value of 1 indicates that the output gaps of all countries have the same sign as the reference. When all output gaps (other than the reference) have a different sign than the reference output gap, it follows that the measure equals $-1+2/n$, which for large $n$ is about equal to −1.8

2.3. Similarity

While output gap correlations do not accurately reflect to what extent output gaps have the same sign, they also do not consider whether output gaps have the same amplitude. The correlation between two series can be equal to one even when both series have different standard deviations. Perfect correlation between the output gaps of countries forming a currency union thus does not mean that the common monetary policy suits all these countries equally well.

To take amplitude differences between output gaps for a region of $n$ countries into account, we measure output gap similarity between country $i$ and the reference output gap $r$ as

$${\theta }_{it}=1-\frac{|g_i\left(t\right)-g_r\left(t\right)|}{\sum _{i=1}^n\left|g_i\left(t\right)\right|/n}$$ (3)

Similarity thus subtracts the absolute difference between both output gaps as a share of the average of all output gaps in the region from one. Through scaling by the average absolute output gap, the similarity measure becomes scale invariant.9 Similarity is defined on a $[1-n,1]$ scale, where a value of one indicates that both output gaps are perfectly synchronous and have identical amplitudes. A value of $1-n$ occurs when $i$ and $r$ have opposite signs and all other output gaps are equal to zero.

Overall similarity of the $n$ countries with the reference is calculated by “averaging” the measure in Eq. (3) over all countries, which yields

$${\theta }_{it}=1-\frac{\sum _{i=1}^n|g_i\left(t\right)-g_r\left(t\right)|}{\sum _{i=1}^n\left|g_i\left(t\right)\right|}.$$ (4)

This measure is defined on a $[2-n,1]$ scale. Similarity equals one when all output gaps are identical; the lower boundary is reached when all output gaps are equal to zero, except the reference output gap.10

2.4. Reference output gap

Having defined our output gap synchronicity and similarity measures, we need to specify the region’s reference output gap. We adopt a statistical approach here and select the reference that maximizes synchronicity in Eq. (2) and similarity in Eq. (4) simultaneously.11 This implies that the reference gap $g_r\left(t\right)$ should be set to the median of the output gaps of all individual countries observed at time $t$. This minimizes the numerator of Eq. (2) and thus maximizes output gap similarity in the sample of countries (see Joag-Dev, 1989), while it simultaneously maximizes overall synchronicity, since the median output gap has by definition the same sign as the majority of the observed output gaps.12

This reference gap time series maximizes synchronicity and similarity not only for the full sample period for which it is calculated, but also for all possible sub-samples. This property reflects the fact that the reference output gap and the synchronicity and similarity measures are calculated on a per-observation basis without being affected by output gaps observed at earlier or later dates.

Defining the reference as the median output gap rather than as the output gap of a particular country (or as the weighted output gap of a group of countries as we do in the robustness analysis) implies that the minimum values that synchronicity and similarity in the region as a whole can attain are now equal to zero. The synchronicity measure equals zero if half of the countries have a positive output gap and half have a negative output gap. The similarity measure equals zero if the reference output gap is equal to zero. For all other values of the reference output gap, the measure is larger than zero. This result follows from the fact that the sum of the difference between output gaps and their median, i.e., the numerator of Eq. (4), is always smaller than the sum of the difference between these output gaps and zero, i.e., the denominator of the equation. Similarity only attains its minimum (maximum) value when synchronicity is at its minimum (maximum) value as well.

3. Data

To analyze the coherence of output gaps, we estimate the synchronicity and similarity of the output gap for all countries that have been part of the euro area for a long time (except for Luxembourg). More specifically, our country set consists of Austria, Belgium, Finland, France, Germany, Greece, Ireland, Italy, the Netherlands, Portugal, and Spain. Countries that joined the euro area later have not been included as the time series for their output gaps are rather short. Our data set contains time series for quarterly real GDP (with reference year 2010) for each country. The data source is the IMF’s International Financial Statistics. The period 2000 Q1 until 2022 Q2 is used in the analysis so that the global financial crisis (GFC) and the COVID-19 crisis are included. Figure A.1 in Appendix A presents the data used.

4. Results

4.1. Synchronicity and similarity: full sample

Fig. 1 shows the synchronicity measures for each country in our sample. The graph in the bottom right panel in this figure summarizes the outcomes by showing for each year the number of countries having a synchronicity measure of one. During the GFC in 2007–2009 the average number of countries with a synchronicity equal to $1$ is higher than in other years. Also before and during the COVID-19 crisis, this number of countries is relatively high.

Fig. 1.

Output gap synchronicity for each country based on output gaps obtained by the Hamilton (2018) filter. Note: The graph in the bottom right panel in this figure summarizes the outcomes by showing for each year the number of countries having a synchronicity measure of one.

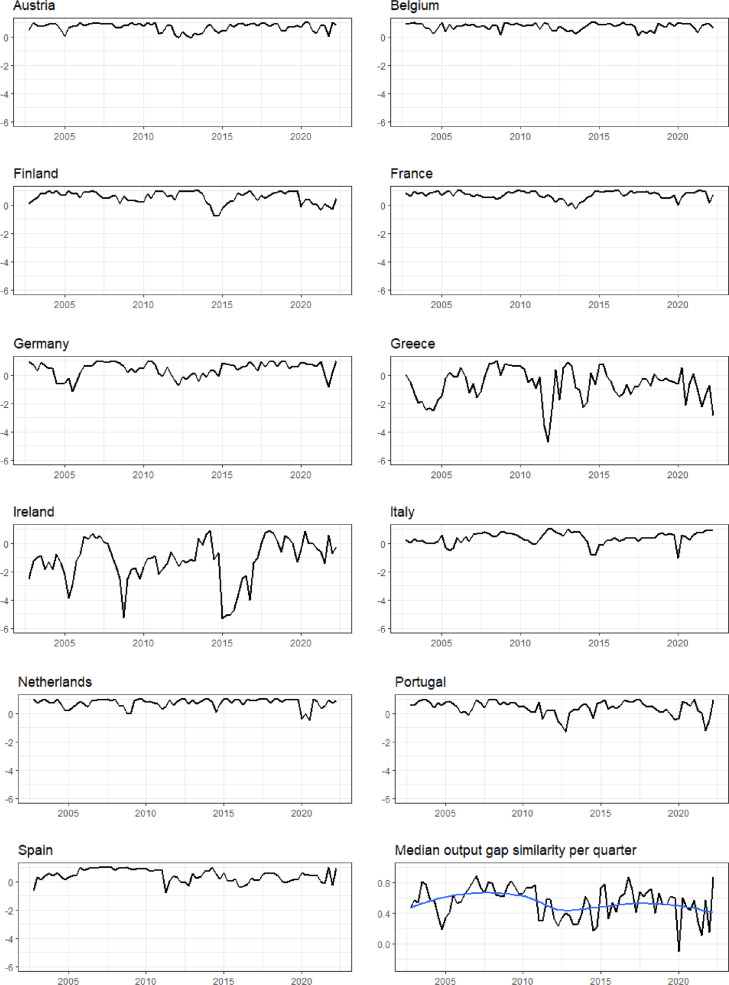
Fig. 2 shows the similarity measure for individual euro area countries. The graph in the bottom right panel in Fig. 2 shows for each year the median value of the synchronicity measure and the LOESS curve.13 The blue line represents the LOESS curve.

Fig. 2.

Output gap similarity for each country based on output gaps obtained by the Hamilton (2018) filter. Note: The graph in the bottom right panel in Fig. 2 shows for each year the median value of the synchronicity measure and the LOESS curve. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Both synchronicity and similarity fluctuate over time and differ across countries; especially Greece and Ireland deviate from the rest. The graphs suggest that business cycle coherence in the euro area follows a non-linear pattern. Notably during crises, business cycle coherence seems to increase.

Since we also want to examine the impact of the (common) COVID-19 shock on the coherence of output gaps in the euro area, the period 2019 Q2 until 2021 Q1 is singled out. This period covers the four quarters before the COVID-19 crisis, and the first four quarters of the crisis. Table 1 shows the average synchronicity and similarity measures during the last four quarters before the COVID-19 crisis and the four quarters of the COVID-19 crisis. The second and third column of the table show that overall synchronicity increased from 0.59 before the crisis to 0.77 during the crisis. The most notable increases occurred in Greece, Portugal, and Spain, while synchronicity decreased in Finland. Although the COVID-19 pandemic was a common shock, these results suggest that countries were not hit with the same intensity. This is also shown in the time series of the original GDP data and the output gap based on the Hamilton filter, as shown in Figures A.1 and A.2 in Appendix A, respectively.

Table 1.

Mean output gap synchronicity and similarity before and during COVID-19 shock.

Period	Synchronicity		Similarity
	2019Q2–2020Q1	2020Q2–2021Q1	2019Q2–2020Q1	2020Q2–2021Q1
Austria	1.00	1.00	0.74	0.68
Belgium	1.00	1.00	0.86	0.89
Finland	0.50	0.00	0.71	0.25
France	1.00	1.00	0.42	0.80
Germany	1.00	1.00	0.65	0.75
Greece	−0.50	1.00	−0.44	−0.53
Ireland	0.00	0.00	−0.36	0.15
Italy	1.00	1.00	0.21	0.47
Netherlands	0.50	0.50	0.65	0.33
Portugal	0.50	1.00	−0.12	0.79
Spain	0.50	1.00	0.24	0.45
Overall	0.59	0.77	0.33	0.46

Note: Numbers shown refer to four quarters before the COVID-19 pandemic and four quarters during the COVID-19 pandemic. The last row shows the mean of all 11 countries per period.

One popular narrative was that COVID-19 increased solidarity among European Union (EU) countries, especially to the extent that intra-union transfers and collective risk-sharing became more politically feasible, as reflected in the agreement on Next Generation EU (NGEU), a package to support Member States to recover from the COVID-19 pandemic. This package of EUR 750 billion was adopted on 14 December 2020 and will operate from 2021 to 2026. Our finding that synchronicity and similarity increased during the pandemic is consistent with this narrative. However, it is possible that even without the NGEU programme, business cycle coherence may have increased as the COVID-19 shock hit all euro area Member States.

The two right-hand side columns of Table 1 show average similarity just before and during the COVID-19 crisis. Average similarity also increased, from 0.33 just before the crisis to 0.46 during the crisis. However, we see a much more diverse pattern than for synchronicity. In fact, in some countries (e.g. Austria, Finland, and the Netherlands) similarity dropped, while in others (e.g. France, Ireland, Italy, Portugal, and Spain) it increased. This suggests that the impact of the COVID-19 pandemic on the output gap in these countries differs from that in other countries in the euro area. So despite the fact that the COVID-19 crisis was a common shock, countries have been affected differently.

4.2. Core versus periphery

We can use our findings to shed light on the discussion of core versus periphery countries. Table 2 shows the average number of times a particular country has synchronicity equal to $1$ per year. The average output gap synchronicity as shown in the last row of Table 2 suggests a clear demarcation. Most countries are pretty close to each other. They have an average synchronicity above 0.80 and can therefore be considered core countries, except for Greece and Ireland. This is good news for the ECB as it implies that the sign of the output gap in most countries in the euro area is very often the same. In other words, the direction of the stance of monetary policy required was the same for most countries in the euro area. This also holds also for countries that were previously frequently identified as periphery countries, like Italy and Spain.

Table 2.

The average number of times per year the output gap of a particular country has the same sign as the reference.

Year	Austria	Belgium	Finland	France	Germany	Greece	Ireland	Italy	Netherlands	Portugal	Spain	Average number of countries
												with a synchronicity equal to 1
2002	1.00	1.00	1.00	1.00	1.00	0.00	0.00	0.00	1.00	1.00	1.00	8.00
2003	1.00	1.00	1.00	1.00	1.00	0.00	0.00	0.75	1.00	1.00	1.00	8.75
2004	1.00	0.50	0.75	1.00	1.00	0.00	0.00	0.00	1.00	1.00	1.00	7.25
2005	0.75	0.75	1.00	0.75	0.25	0.75	0.75	0.75	0.75	0.75	0.50	7.75
2006	1.00	1.00	1.00	1.00	0.75	1.00	1.00	1.00	1.00	0.50	1.00	10.25
2007	1.00	1.00	1.00	1.00	1.00	1.00	0.75	1.00	1.00	1.00	1.00	10.75
2008	1.00	0.75	1.00	0.75	0.75	1.00	0.00	1.00	1.00	1.00	1.00	9.25
2009	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.75	1.00	1.00	10.75
2010	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.50	1.00	0.75	1.00	10.25
2011	0.75	0.75	0.75	0.50	0.75	0.25	0.25	0.75	0.75	0.75	0.75	7.00
2012	0.00	0.50	0.75	0.00	0.00	0.75	1.00	1.00	1.00	1.00	1.00	7.00
2013	0.75	1.00	1.00	0.50	0.75	0.50	1.00	1.00	1.00	1.00	1.00	9.50
2014	1.00	1.00	1.00	0.75	0.25	0.00	0.50	1.00	1.00	1.00	0.50	8.00
2015	0.25	1.00	0.00	1.00	1.00	0.50	1.00	0.00	1.00	0.50	1.00	7.25
2016	1.00	1.00	1.00	1.00	1.00	0.00	1.00	0.00	1.00	0.50	1.00	8.50
2017	1.00	1.00	1.00	1.00	1.00	0.00	0.50	1.00	1.00	1.00	1.00	9.50
2018	1.00	1.00	1.00	1.00	1.00	0.25	0.75	1.00	1.00	1.00	1.00	10.00
2019	1.00	1.00	1.00	1.00	1.00	0.00	0.50	1.00	1.00	1.00	1.00	9.50
2020	1.00	1.00	0.50	1.00	1.00	1.00	0.75	1.00	0.50	0.75	0.75	9.25
2021	0.75	1.00	0.50	1.00	0.50	0.50	0.50	1.00	0.75	0.75	0.75	8.00
2022	1.00	1.00	1.00	0.50	0.50	1.00	1.00	1.00	1.00	1.00	0.50	9.50
Average	0.87	0.92	0.87	0.85	0.79	0.50	0.63	0.75	0.93	0.87	0.89	8.86

Note: The final row presents the overall average number of times the output gap of a particular country has the same sign as the reference, whereas the final column shows the average number of countries per year with a synchronicity equal to 1.

However, the results for the output gap similarity given in Table 3 not only suggest that Greece and Ireland deviate but also that the magnitude of the amplitude of the business cycle in Italy deviates quite substantially from the reference as well. To some extent, this also holds for Portugal and Spain. Quite remarkably, Table 3 suggests that also the business cycle amplitude of Germany deviates substantially from the reference. The difference between the mean and median similarity measure as well as the minimum similarity for Germany suggests that this may reflect that in some particular years Germany deviated a lot. So whereas Germany is often considered as the most important core country, our results suggest differently.14 These findings imply that the policies of the ECB have often not been consistent with the German business cycle, which may have undermined support for EMU in Germany. However, before drawing definite conclusions about this issue, we check in Section 5.1 whether Germany’s position changes if we take a GDP-weighted output gap as reference.

Table 3.

Summary statistics of output gap similarity for the period 2002 Q3 until 2022 Q2.

	Mean	St.dev	Median	Min	Max
Austria	0.70	0.30	0.81	−0.08	1.00
Belgium	0.74	0.24	0.81	0.07	1.00
Finland	0.56	0.42	0.67	−0.78	1.00
France	0.72	0.28	0.80	−0.27	1.00
Germany	0.44	0.52	0.61	−1.14	1.00
Greece	−0.67	1.14	−0.49	−4.72	1.00
Ireland	−1.20	1.52	−1.10	−5.31	0.90
Italy	0.39	0.42	0.44	−1.06	1.00
Netherlands	0.75	0.33	0.88	−0.50	1.00
Portugal	0.43	0.50	0.54	−1.32	1.00
Spain	0.45	0.43	0.45	−0.79	1.00

So overall these results suggest that the sign of the output gap in countries in the euro area indicate that only a few countries would be considered periphery countries. However, once the amplitude of the business cycle is taken into account, the outcome is less optimistic: for many countries the ECB policies are not in line with their domestic economic situation. This even holds for countries that are generally considered as core country, notably Germany. Of course, one may object that this conclusion is based on an analysis in which we define the reference in a way that deviates from what the ECB does, namely focusing on the output gap in the euro area as a whole. In the robustness section, we will therefore re-examine this issue using the GDP-weighted average output gap in the euro area as benchmark instead of the median output gap.

5. Robustness analysis

5.1. Weighted reference

As pointed out in Section 2.4, the ECB focuses on the economic situation in the euro area as a whole, which can be proxied by using GDP-weighted output gaps. If we take this series as reference instead of the median output gap, the results are remarkably similar. The graphs on the left-hand side of Fig. 3 show the median output gap similarity measures using the median reference (upper part) and the GDP-weighted reference (lower part).

Fig. 3.

Descriptive figures of the median reference and weighted reference. Note: The graphs in the left panels show the median value of the similarity measure for each year and the LOESS curve.

Although the similarity measure based on the weighted reference is more volatile and slightly lower, it shows a very similar pattern as the similarity measure constructed with the median output gap as reference. The synchronicity measures as shown in the right-hand side part of Fig. 3 are also very similar. This suggests that our main conclusions are not driven by using the median output gap as reference.

Table 4 replicates Table 3 using the GDP-weighted reference instead of the median. The table suggests that business cycles in Greece, Ireland, Italy, and Portugal deviate quite substantially from the reference and these countries can therefore be considered as periphery countries, thus confirming our previous finding. However, the results for Germany are better than previously, although its output gap similarity is still lower than that of other countries widely considered as core countries, like Belgium, France, and the Netherlands.

Table 4.

Summary statistics of output gap similarity with weighted reference for the period 2002 Q3 until 2021 Q1.

	Mean	St.dev	Median	Min	Max
Austria	0.69	0.24	0.75	−0.12	0.99
Belgium	0.72	0.22	0.77	0.03	1.00
Finland	0.44	0.46	0.56	−0.89	0.98
France	0.73	0.17	0.74	0.19	0.99
Germany	0.55	0.40	0.65	−0.83	1.00
Greece	−0.68	1.11	−0.49	−4.78	0.94
Ireland	−1.23	1.47	−1.13	−5.22	0.97
Italy	0.31	0.39	0.37	−0.96	0.94
Netherlands	0.67	0.35	0.80	−0.83	1.00
Portugal	0.31	0.57	0.39	−1.75	0.99
Spain	0.42	0.40	0.45	−0.70	1.00

Finally, Table 5 replicates Table 1 to examine whether our results for the impact of the COVID-19 pandemic on business cycle coherence change if we use the GDP-weighted reference instead of the median. As before, we find that overall synchronicity and similarity increased during the COVID-19 pandemic (as shown in the final column of Table 5). However, these averages mask cross-country heterogeneity. For instance, in Finland synchronicity and similarity dropped, while similarity also declined in the Netherlands. Overall, the results concerning the impact of the COVID-19 pandemic as reported previously are thus confirmed when we use the GDP-weighted output gap as reference instead of the median output gap.

Table 5.

Mean output gap synchronicity and similarity before and during COVID-19 shock.

Period	Synchronicity		Similarity
	2019Q2–2020Q1	2020Q2–2021Q1	2019Q2–2020Q1	2020Q2–2021Q1
Austria	1.00	1.00	0.60	0.66
Belgium	1.00	1.00	0.73	0.73
Finland	0.50	0.00	0.58	0.08
France	1.00	1.00	0.51	0.68
Germany	1.00	1.00	0.61	0.78
Greece	−0.50	1.00	−0.30	−0.36
Ireland	0.00	0.00	−0.22	0.06
Italy	1.00	1.00	0.35	0.64
Netherlands	0.50	0.50	0.50	0.31
Portugal	0.50	1.00	−0.25	0.67
Spain	0.50	1.00	0.11	0.62
Overall	0.59	0.77	0.29	0.44

Note: Numbers shown refer to four quarters before the COVID-19 pandemic and four quarters during the COVID-19 pandemic. The last row is the mean of all 11 countries per period.

5.2. The European sovereign debt crisis

Next to the COVID-19 period, the European debt crisis is another interesting period for analyzing the coherence of business cycles during a crisis. The debt crisis began in the late 2009 in Greece, then spread primarily to Portugal, Italy, Ireland, and Spain. The crisis peaked between 2010 and 2012. We take Draghi’s ‘whatever it takes’ speech as the end, as following this speech interest rates in vulnerable countries dropped sharply.

Table 6 shows the average synchronicity and similarity before and during the European sovereign debt crisis. The results suggest that the coherence of business cycles seems to decrease during the European debt crisis. This can be explained by the fact that not all European several countries were hit during the European sovereign debt crisis. If the shock hits most of the European countries, the coherence between the business cycles seems to increase, as shown during the COVID-19 period, while this is not the case if the crisis affects only a few countries. This illustrates that the COVID-19 period is a different type of crisis than the European debt crisis.

Table 6.

Mean output gap synchronicity and similarity before and during the European sovereign debt crisis.

Period	Synchronicity		Similarity
	2007Q1–2009Q3	2009Q4–2012Q1	2007Q1–2009Q3	2009Q4–2012Q1
Austria	1.00	0.45	0.86	0.63
Belgium	0.82	0.45	0.75	0.77
Finland	1.00	0.64	0.51	0.65
France	0.82	0.27	0.66	0.78
Germany	0.82	0.45	0.75	0.30
Greece	1.00	0.45	0.13	−0.94
Ireland	0.09	0.45	−1.40	−1.45
Italy	1.00	0.45	0.68	0.47
Netherlands	0.82	0.82	0.72	0.76
Portugal	1.00	0.64	0.79	0.20
Spain	1.00	0.82	0.95	0.45
Overall	0.85	0.54	0.49	0.24

Note: Numbers shown refer to ten quarters before the European debt crisis and ten quarters during the European debt crisis. The last row is the mean of all 11 countries per period.

5.3. Using modified gross national income of Ireland

One criticism that can be raised about our conclusions for Ireland is that they are based on Irish GDP data. The credibility of GDP statistics in Ireland was strained when the Central Statistics Office (CSO) announced that GDP grew 26.3 percent in 2015. This reflected that a number of large multinational corporations relocated their economic activities, and more specifically their underlying intellectual property, to Ireland. As a result, sales (production) generated from the use of intellectual property now contribute to Irish GDP rather than to other countries’ GDP. CSO provides an alternative, namely Modified Gross National Income (GNI). This measure is only available at the annual frequency, which is why we did not use it in our main analysis. Fig. 4 shows that using this alternative proxy for Irish output makes a difference. The graphs in the bottom left panel of Fig. 4 show that notably for the years around 2015 output gap similarity based on modified GNI is higher. In general, output gap synchronicity is not clearly higher if modified GNI is used instead of real GDP (bottom right panel).

Fig. 4.

Outcomes for Ireland using annual modified GNI and real GDP. Note: Black and purple line represent real GDP and Modified GNI, respectively.

Table 7 shows summary statistics of output gap similarity for Ireland using annual modified GNI and annual GDP, respectively. In line with Fig. 4, the summary statistics suggest that the output gap similarity measure is closer to zero if the modified real GNI is used instead of the real GDP, but Ireland is still considered as a periphery country for both time-series due to the low mean and median.

Table 7.

Summary statistics of output gap similarity with median reference for the period 2002 Q3 until 2021 Q1 using annual modified GNI and annual GDP.

	Mean	St.dev	Median	Min	Max
Ireland modified GNI	−0.68	1.36	−0.19	−3.39	0.87
Ireland GDP	−1.35	1.85	−0.95	−5.60	1.00

6. Conclusion

Using the measures proposed by Mink et al. (2012), we have reexamined the coherence of business cycles in the euro area over the 2002–2021 period. We have also analyzed the impact of the COVID-19 pandemic on business cycle coherence. Finally, we have examined whether our measures for business cycle coherence indicate a core versus periphery within EMU.

To apply our preferred measures for business cycle coherence, we need to construct output gap measures. For this purpose, we have applied the Hamilton (2018) filter. As pointed out by Schueler (2018), this filter yields more robust cycle estimates at the end of the sample than the Hodrick–Prescott (H–P) filter. As one of the aims of our research is to examine the impact of the COVID-19 pandemic on business cycle coherence in the euro area, we therefore opted for the Hamilton filter. Of course, potential output is non-observable. Thus, our study, like other studies in this line of research, amounts to a test of a joint hypothesis (of the output gap estimate alongside business cycle coherence).

Our results suggest that although business cycle coherence in the euro area increased, it did not rise monotonically. This non-linearity is not consistent with the view of Frankel and Rose (1998) that increased trade intensity in the currency union will lead to increasing business cycle coherence. At the same time, the trade links between the countries that our analysis identifies as having low business cycle coherence with the euro area and other countries in the euro area are low. The non-linearity we have found is consistent with the view of De Grauwe and Ji (2017) who argue that bilateral trade integration explains only a small fraction of the variation in the bilateral business cycle correlations. They suggest that business cycle synchronization reflects “animal spirits”, i.e., waves of optimism and pessimism, that get correlated internationally. The authors argue that this propagation occurs even with relatively low levels of trade integration. In addition, once a particular level of trade integration is reached further integration does not increase the synchronization of business cycles anymore.

Our results suggest that notably during crisis periods which hit all euro area Member States, such as the crisis due to COVID-19 pandemic, business cycle coherence increased. During this period, the signs of the output gaps of euro area countries became more similar. During the sovereign debt crisis business cycle coherence did not clearly increase in contrast to the crisis due to the COVID-19 pandemic. Our results thus illustrate that the COVID-19 period is a different type of crisis than the European debt crisis. This reflects that a shock hitting most of the European countries leads to an increase in business cycle coherence, as shown during the COVID-19 period. However, the European debt crisis affected only a few European countries. But even during the COVID-19 pandemic, we find large differences in the amplitudes of the output gaps across countries.

Our results suggest that the ECB’s attempts to counter financial fragmentation in the euro area may have contributed to more business cycle coherence. After 2010, financial fragmentation in the euro area increased significantly, as highlighted by the significant increases in interest rate spreads. However, the introduction of Outright Monetary Transactions after Draghi’s famous ‘whatever it takes’ speech reduced these spreads significantly. Likewise, the introduction of the Pandemic Emergency Purchase Programme led to lower spreads (De Grauwe and Ji, 2022). This is important as arguably persistently high spreads would have contributed to business cycle divergence.

Our results also shed light on the classification of euro area member states as core or periphery countries. Our results suggest that notably Greece, Ireland, Italy, Finland, and Portugal have business cycles that are very different from business cycles in other euro area countries. This makes that the ECB monetary policies will not be optimal for all countries in the euro area.

An interesting topic for future research is to examine to what extent support for the euro in Member States depends on the coherence of the business cycles in individual Member States and the euro area. It seems that support for the euro according to the latest Eurobarometer survey is not lower in countries that we identify as peripheral.15 For instance, support for the euro in Ireland is among the highest in the euro area. Likewise, in Portugal and Spain support for the euro is also very high. On the other hand, in Greece support for the euro is rather low. So, further analysis seems warranted.

Another suggestion for future research is to use alternative filters, like the H–P filter, the modified H–P filter as proposed by Phillips and Shi (2021), or the Beveridge and Nelson (1981) decomposition to determine the output gap. The HP filter is often criticized for weaknesses at the end points, which is why we opted for the Hamilton filter, but it does a decent job when sufficiently in-sample. It would be interesting to analyze whether using these different filters affect our conclusions about business cycle coherence in the euro area.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary material related to this article.

Data availability

Data will be made available on request.