Abstract

Upconversion processes effectively convert two or more low energy photons into one higher energy photon, and they have diverse prospective applications in photovoltaics and biomedicine. We focus on two specific mechanisms for photochemical upconversion in solution: triplet–triplet annihilation (TTA) and singlet oxygen mediated energy transfer (SOMET). TTA is spin-selective, whereas SOMET is not, so the interplay between these two upconversion mechanisms can be examined via their different magnetic field responses. A kinetic model is developed and applied to explain the different photoluminescence profiles of oxygenated versus deoxygenated systems. From the magnetic field response, the triplet–triplet annihilation rate constant is estimated. The conditions required to maximize upconversion photoluminescence intensity in oxygenated solution are determined, providing a set of design principles to guide molecule choices for robust and air-stable upconversion systems in the future.
Introduction
In photochemical upconversion, the energy of two incident photons is pooled together and emitted as a single, higher energy photon. In photovoltaic applications, upconversion could enable solar cell efficiencies beyond the 33.7% maximum single threshold solar cell limit1 by harvesting incoming solar energy below the silicon bandgap. In biological applications, upconversion can be used in photodynamic therapy where the skin is transparent to infrared light, but higher energy light is required in situ to sensitize drug-release or facilitate imaging.2,3
Delayed fluorescence in solution through upconversion has been studied in a range of systems, both deoxygenated4−8 and oxygenated.9−14 Upconversion from below the silicon bandgap was recently demonstrated in solution.15 In that system, contrary to the usual expectation, the presence of oxygen (i) increased the upconverted photoluminescence intensity and (ii) suppressed the signature triplet–triplet annihilation magnetic field response.
These counterintuitive findings are explained here through a kinetic model incorporating two different upconversion mechanisms: (1) triplet–triplet annihilation and (2) singlet-oxygen mediated energy transfer (see Figure 1).
Figure 1.
Comparison of upconversion processes: triplet–triplet annihilation (TTA) left, and singlet oxygen mediated energy transfer (SOMET) right between sensitizer (S) and acceptor (A) species. Triplet levels are indicated by pale lines. In both TTA and SOMET, the sensitizer absorbs a photon (1) and undergoes intersystem crossing to a near-lying triplet state (2). In TTA the triplet energy of the sensitizer is transferred to the acceptor, promoting it to its triplet state (3). Two acceptor triplets pool their energy to produce an excited acceptor singlet (4) and a ground state acceptor singlet. Finally the excited singlet fluoresces and emits light (5). In SOMET, steps 3 and 4 of TTA are replaced by steps 6–8: rather than triplet energy transfer directly from the sensitizer to the acceptor, energy is first transferred to ground state oxygen, producing 1O2* (6). The excited singlet oxygen then transfers energy to a ground state acceptor promoting it to its triplet state (7). Another excited singlet oxygen molecule interacts with the triplet acceptor to promote it to its excited singlet state (8).
Theory
Deoxygenated Upconversion
In triplet–triplet annihilation (TTA), a molecular sensitizer (S) species absorbs a photon (1) and undergoes intersystem crossing to a near-lying triplet state (2). The triplet energy of the sensitizer is transferred to a molecular acceptor (A) species, promoting the acceptor to its triplet state (3). Two acceptor triplets pool their energy to produce an excited acceptor singlet (4) and a ground state acceptor singlet. Finally the excited singlet fluoresces and emits light (5).
These processes are described by the TTA Reaction Scheme of eqs 1–5, along with the deleterious processes of triplet decay eq 6 and internal conversion eq 7. See Table 1 for the rate constant abbreviations for each process.
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
Table 1. Rate Constant Abbreviations.
| kabs | absorption |
|---|---|
| kisc | intersystem crossing |
| kset | sensitizer energy transfer to acceptor |
| ktta | triplet–triplet annihilation |
| kf | fluorescence |
| kt | triplet decay |
| kic | internal conversion |
| ksetO2 | sensitizer energy transfer to O2(3Σ) |
| ketΔ | energy transfer by O2(1Δ) |
| kqp | quenching of phosphorescence by O2(3Σ) |
| kqf | quenching of fluorescence by O2(3Σ) |
Upconversion requires a sensitizer molecule with a high absorption cross-section at the excitation wavelength, fast and efficient intersystem crossing to a near-lying triplet state, and a triplet lifetime long enough to allow energy transfer to an acceptor molecule.8,16 For efficient energy transfer, the emitting acceptor molecule ought to have a triplet energy level below that of the sensitizer. (Triplet energy transfer to an acceptor with a slightly higher triplet energy level is also possible, if sensitizer and acceptor concentrations are chosen so that the reaction is entropically driven.17) The acceptor triplet state must be adequately long-lived to facilitate interaction with another triplet acceptor molecule and eventual annihilation. And finally the acceptor species must have a high quantum yield of fluorescence at a desirable wavelength. To avoid reabsorption by the sensitizer, the emission spectrum of the acceptor should not overlap with absorption spectrum of the sensitizer. Hence the triplet and singlet energy levels of the sensitizer must lie between those of the acceptor,8Figure 1.
Sensitizer energy transfer eq 3 and TTA eq 4 formally occur via Dexter transfer mediated by electron exchange, and they require a physical collision to occur. The rate of collision in solution is diffusion-limited ∼109–1010 M–1 s–1.18
As an additional limitation, TTA is a spin-statistical process so only a fraction of triplet pairs have singlet-character and successfully annihilate.8 A long acceptor triplet lifetime is essential to increase the triplet encounter probability facilitating TTA.
Oxygenated Upconversion
Oxygen is a renowned quencher of molecular triplet states.19−22 As upconversion by triplet–triplet annihilation requires long-lived triplet species, oxygen quenching is detrimental to typical upconversion systems. Due to oxygen’s atmospheric presence, any air-saturated solution is prone to oxygen quenching. This imposes a practical requirement of deaeration upon triplet–triplet annihilation-based upconversion systems.
The unique electronic structure of oxygen with its triplet ground state 3O2, and singlet excited state 1O2*, renders interactions with both singlet and triplet state hydrocarbon molecules (M) spin-allowed.22 This enhances chromophore intersystem crossing, promoting quenching of both molecular phosphorescence through 3M* →1M deactivation (eq 8), and also fluorescence via 1M* →3M* (eq 9).
| 8 |
| 9 |
The energy difference
between molecular oxygen’s ground
and first excited states is 0.98 eV. As this is smaller than the triplet
level 3M* of most hydrocarbons (i.e., DPA 1.73 eV and perylene
1.52 eV8), deactivation of 3M* by 3O2 quenching transfers enough energy
to oxygen to sensitize production of 1O2*. 3O2 can
also quench fluorescence, because the energy difference between 1M* and 3M* for most hydrocarbons, while smaller
than 3M* to 1M (i.e., for DPA 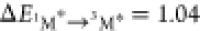 eV and for perylene
eV and for perylene 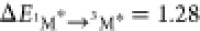 eV8), is still
larger than molecular oxygen’s
eV8), is still
larger than molecular oxygen’s  of 0.98 eV.
of 0.98 eV.
However, not all hydrocarbons are susceptible to fluorescence
quenching by oxygen: β-carotene is a notable, well-studied exception22 due to its importance in photosynthesis. With 3M* at 0.94 eV, β-carotene cannot be quenched by 3O2. But the reverse reaction, energy transfer to
the β-carotene ground state by 1O2* to sensitize production of the
triplet state is possible. Indeed, β-carotene protects plants
by quenching 1O2. Thus, for any molecule with 3M*
< 0.98 eV, the reverse of eq 8 can occur, namely triplet sensitization by energy transfer
from 1O2*. Similarly, when 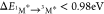 (for example in fluorescein), the reverse
of eq 9 can occur: singlet
sensitization by energy transfer from 1O2.
(for example in fluorescein), the reverse
of eq 9 can occur: singlet
sensitization by energy transfer from 1O2.
Due to the different multiplicity of molecular oxygen’s ground and excited states, 1O2* is long-lived (with a lifetime of 30.5 μs in air-saturated toluene solution at room temperature23). This long lifetime in combination with oxygen’s fast diffusion and capacity to promote intersystem crossing makes it a perfect mediator of energy-transfer between sensitizers with 3M* > 0.98 eV (for sensitization of 1O2) and acceptors with 3M* < 0.98 eV. As a mediator of energy-transfer, 1O2* does not deteriorate the acceptor species in oxygenated upconversion,14 and while organic sensitizer species are still susceptible to degradation by oxygen, the quenching action of the acceptor has been shown to reduce sensitizer photodegradation.14 The stability of quantum dot sensitizers in oxygenated environments is largely ligand-dependent,24 with ligands typically used in upconversion systems passivating and promoting triplet energy transfer.25,26 For practical utility, these ligands must also be stable in oxygenated environments.
A Reaction Scheme for Oxygen-Mediated Energy Transfer (SOMET) is outlined in eqs 10–14. Rate constant abbreviations are summarized in Table 1.
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
Results and Discussion
We apply this model the results of Gholizadeh et al.15 and find excellent agreement for both the photoluminescence and magnetic field response. To understand the relative contribution of the various processes, we develop a kinetic model which incorporates both TTA and SOMET.
The Kinetic Model
The Reaction Scheme of Eqs. 3 to (7) and Eqs. 10 to (14), is converted into a system of coupled differential equations, Eqs. 15 to (21), and solved numerically using a finite difference method.
| 15 |
 |
16 |
| 17 |
| 18 |
| 19 |
| 20 |
| 21 |
As triplet energy transfer processes,
occurring on a time scale of microseconds, are orders of magnitude
slower than absorption and ISC, the kinetic model begins at the sensitizer
energy transfer step. Fluorescence quenching is omitted (kqf = 0 M–1 s–1) because
V79’s  is less than the 0.98 eV required to sensitize
singlet oxygen, so quenching of the fluorescent singlet state by 3O2 cannot occur in this system. Model input parameters
are listed in Table 2 and based on the upconversion system of Gholizadeh et al.,15 with sensitizer species TIPS-tetracene-carboxylic-acid
(TTCA) ligated PbS quantum dots, and acceptor violanthrone-79 (V79)
in toluene solution at room temperature. These parameters are typical
of photochemical processes in solution, which have well-known and
narrow ranges.29 While a specific example15 is used here for illustrative purposes, the
kinetic model is stable over physical values, and provides general
insights to optimize upconversion. Toluene is a commonly employed,
nonpolar solvent. Note that polar solvents would introduce charge
transfer states, altering the energy transfer pathways of these mechanisms,23,30 and solvent viscosity would affect the efficiency of the diffusional
energy transfer.31
is less than the 0.98 eV required to sensitize
singlet oxygen, so quenching of the fluorescent singlet state by 3O2 cannot occur in this system. Model input parameters
are listed in Table 2 and based on the upconversion system of Gholizadeh et al.,15 with sensitizer species TIPS-tetracene-carboxylic-acid
(TTCA) ligated PbS quantum dots, and acceptor violanthrone-79 (V79)
in toluene solution at room temperature. These parameters are typical
of photochemical processes in solution, which have well-known and
narrow ranges.29 While a specific example15 is used here for illustrative purposes, the
kinetic model is stable over physical values, and provides general
insights to optimize upconversion. Toluene is a commonly employed,
nonpolar solvent. Note that polar solvents would introduce charge
transfer states, altering the energy transfer pathways of these mechanisms,23,30 and solvent viscosity would affect the efficiency of the diffusional
energy transfer.31
Table 2. Kinetic Model Parameters.
| [3S*]i | 2.4 μMa |
| τt | 18 nsb |
| τs | 6.7 nsc |
| Φf | ∼0.25a |
| kf | Φf/τs |
| kic | (1 – Φf)/τs |
| kt | 1/τt |
| ktta | 9.5 × 108 M–1 s–1 d |
| kset | 1.7 × 107 M–1 s–1 a |
| ksetO2 | 1.0 × 107 M–1 s–1 b |
| ketΔ | 1.2 × 1010 M–1 s–1 e |
| kqp | 1.3 × 109 M–1 s–1 f |
| kqf | 0 M–1 s–1 g |
| [3O2]i | 8.69 mMh |
Modeling Photoluminescence Profiles
The photoluminescence (PL) profile of any upconversion system is a direct indicator of the relative excited singlet acceptor concentration, [1A*]. The proportion of the excited singlet state population that decays radiatively to fluoresce is described by the fluorescence quantum yield Φf for the species.
The modeled fluorescent acceptor state concentration [1A*] for typical initial ground-state acceptor concentrations [1A]i is shown in Figure 2 for both deoxygenated and oxygenated systems. For initial acceptor concentrations above 10 mM, aggregation becomes increasingly likely. In practice, aggregation leads to fluorescence quenching,32 and it is not accounted for in this model.
Figure 2.

Evolution of fluorescent acceptor state concentration [1A*] with time as predicted by the kinetic model for various initial acceptor concentrations [1A]i. The solid line shows the oxygenated system with upconversion by SOMET and TTA; the dotted line the deoxygenated system with TTA only.
These concentration profiles serve as a proxy for photoluminescence intensity and show three notable features: contrary to expectation in typical TTA-based upconversion systems, the oxygenated system enhances photoluminescence rather than quenching it; there is a “sweet spot” in initial acceptor concentration to produce maximum fluorescence in oxygenated upconversion; and the rise and decay kinetics are faster with increasing initial acceptor concentration.
Considering the deoxygenated system (dotted lines of Figure 2), as initial acceptor concentration is increased (left to right), the concentration of 1A* generated through TTA alone increases. This follows from eq 3 for sensitizer energy transfer. The initial excitation concentration [3S*]i is fixed by the excitation intensity and is constant in this model, so increasing the initial acceptor concentration [1A]i promotes formation of acceptor triplets 3A*, the necessary precursors to upconversion by TTA.
The enhancement
of photoluminescence in the oxygenated case is
an example of upconversion through singlet-oxygen mediated energy
transfer (SOMET). In Gholizadeh et al.15 the sensitizer (TTCA) and acceptor (V79) triplet levels sandwich
the 0.98 eV of the 1O2* excited state appropriately to accommodate
SOMET (see Figure 1). After absorbing the excitation pulse, the sensitizer TTCA ligands
undergo intersystem crossing to their triplet state, 3S*,
and transfer energy to ground state oxygen, generating 1O2 (eq 10), which is in turn quenched
by the ground state acceptor species V79 to produce triplets, 3A* (eq 11).
For V79, 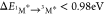 , so a second energy transfer from another 1O2* to 3A* can produce the fluorescent singlet state 1A*
(as in eq 12) via SOMET.
While SOMET explains the much higher fluorescent 1A* state
concentrations for initial acceptor concentrations of 0.10 to 10 mM
in the oxygenated relative to deoxygenated systems (Figure 2), it is important to remember
that TTA can still occur, and it is indeed a competing process.
, so a second energy transfer from another 1O2* to 3A* can produce the fluorescent singlet state 1A*
(as in eq 12) via SOMET.
While SOMET explains the much higher fluorescent 1A* state
concentrations for initial acceptor concentrations of 0.10 to 10 mM
in the oxygenated relative to deoxygenated systems (Figure 2), it is important to remember
that TTA can still occur, and it is indeed a competing process.
This competition between the two different upconversion processes explains the “sweet spot” in oxygenated 1A* concentration and the faster kinetics with increase of initial acceptor concentration.
In air-saturated solution, the initial concentration of ground state molecular oxygen 3O2 is fixed. In this model, the initial excitation concentration is also fixed (through the initial triplet sensitizer concentration [3S*]i). In the presence of oxygen, the initial sensitizer 3S* excitation is distributed between energy transfer to two species: (i) ground state acceptor molecules to produce 3A* and (ii) ground-state oxygen to produce 1O2*.
Once produced, 1O2* generates 3A* through quenching by 1A. As the rate of 1O2 energy transfer ketΔ is diffusion-limited, this process is orders of magnitude faster than generation of 3A* via sensitizer energy transfer. Hence SOMET produces 3A* much more effectively through energy transfer by 1O2*, than occurs directly from the sensitizer alone in TTA.
As the initial acceptor concentration is increased, a smaller proportion of the available excitation is transferred to oxygen. This leads to less 1O2* overall and has two important consequences: (i) the increase in [3A*] through 1O2 energy transfer is less pronounced, and (ii) the proportion of 1A* reached by TTA rather than SOMET increases with increasing initial acceptor concentration. So changes to initial acceptor concentration increase the proportion of sensitizer energy transfer to the acceptor, relative to that to oxygen.
These competing processes result in a sweet spot for maximum 1A* generation through both upconversion mechanisms, TTA and SOMET. Figure 3 shows a color plot of fluorescent singlet concentration 1A* with time for initial acceptor concentrations from 0.1 mM to 10 mM. Maximum photoluminescence intensity occurs for an initial acceptor concentration of 0.69 mM. The contour lines clearly show the faster kinetics for increasing initial acceptor concentration.
Figure 3.

Oxygenated upconversion: color plot of fluorescent acceptor state concentration [1A*] with time for initial acceptor concentrations [1A]i ranging from 0.1 to 10 mM.
Predicting Magnetic Field Response
The competition between whether the fluorescing 1A* state is reached via (i) TTA between two excited acceptor triplets or (ii) 1O2* energy transfer to an acceptor triplet can be experimentally examined though the magnetic field effect. The magnetic field effect is defined as the ratio of the change in photoluminescence intensity (PL) with the magnetic field B, to the photoluminescence intensity at no magnetic field, eq 22.
| 22 |
TTA is a spin-selective process4 because the intermediate triplet pair state may have singlet, triplet or quintet multiplicity. As the applied magnetic field is increased, the singlet character of the intermediate triplet pair state is spread over fewer eigenstates, resulting in a decrease in photoluminescence intensity with increasing magnetic field strength.5 Atkins and Evans33 incorporated diffusional motion and decoherent relaxation to describe the change in photoluminescence intensity (PL) with magnetic field that occurs in TTA in solution. Fitting Atkins and Evans’ theory to the deoxygenated V79 photoluminescence of Gholizadeh et al.15 shows the typical decreasing magnetic field effect with field strength (Figure 4, lower).
Figure 4.

Magnetic field response of upconversion in oxygenated and deoxygenated solutions of 0.5 mM V79, data reproduced from Gholizadeh et al.15 The deoxygenated system (dark green) displays the typical magnetic field response due to triplet–triplet annihilation, and is fit by the theory of Atkins and Evans33 with parameters translational correlation time, τa = 486 ± 21 ps and proportion of upconverted triplet–triplet encounters, λ = 0.28 ± 0.01. The oxygenated data is fit by scaling the deoxygenated MFE by a factor of (3.9 ± 1.4)%. Shaded regions show 95% confidence intervals for the fits.
In contrast to TTA, SOMET occurs through electron exchange between a singlet and triplet state. This is not a spin-selective process (because the intermediate pair state always has triplet multiplicity), so has no magnetic field dependence, resulting in zero MFE.
Upconversion in the oxygenated system occurs mainly via SOMET, but there is still a contribution from spin-selective TTA. The extent of the contribution of TTA in the oxygenated system can be deduced from the reduction in the magnetic field effect relative to the deoxygenated case. Indeed, scaling the deoxygenated Atkins and Evans MFE by a factor of (3.9 ± 1.4)% fits the oxygenated MFE (Figure 4). This indicates that around 1 in 25 of the fluorescing acceptor singlets 1A* was reached through upconversion by TTA.
In fact, the measured reduction in MFE can be used to determine the proportion of upconversion occurring via TTA and accordingly estimate the TTA reaction rate, ktta. Figure 5 shows how the proportion of fluorescing 1A* generated via TTA varies with ktta for initial acceptor concentrations between 0.1 and 10 mM. The TTA reaction rate is not always well-characterized for less common acceptor species (such as V79), but it may be calculated from the observed reduction in MFE. For example, for the V79 MFE data in Gholizadeh et al.,15 shown in Figure 4, the oxygenated MFE is 4% of the deoxygenated MFE for an acceptor concentration of 0.5 mM, indicating from Figure 5 that ktta = (9.5 ± 3.5) × 108 M–1 s–1 for acceptor V79. This estimate is consistent with typical TTA reaction rates.29
Figure 5.
Proportion of fluorescing acceptor singlets 1A1* generated through TTA with ktta, for initial acceptor concentrations from 0.1 mM through 10 mM. The dashed vertical line shows the diffusion-limited rate of singlet oxygen energy transfer, ketΔ = 1.2 × 1010 M–1 s–1, and practical upper limit for ktta.
Conclusions
Using a kinetic model approach, we have modeled the interplay of triplet–triplet annihilation and singlet oxygen mediated energy transfer in photochemical upconversion in solution. With this approach, we can explain the experimental results of Gholizadeh et al.,15 concerning upconversion in the presence of oxygen and the resulting magnetic field response.
The feasibility of SOMET as an alternative pathway to TTA depends strongly on the relative energy levels of the molecules involved. Upconversion through SOMET has advantages over TTA. Most obviously, the photoluminescence intensity at typical initial acceptor concentrations is significantly higher. The energy transfer to the acceptor is faster, competing more effectively triplet decay. Acceptor triplets are used twice as efficiently to reach the fluorescent singlet state.
There are also drawbacks. The energy-level requirement of the sensitizer and acceptor triplet levels sandwiching that of 1O2* limits the combinations of suitable chromophores, and also imposes an upper bound of 0.98 eV on the overall upconversion anti-Stokes energy shift that can be achieved.
The minimum (theoretical) emission wavelength that can be achieved is 630 nm, so SOMET is only suitable for applications requiring upconversion to the red to infrared regions of the spectrum. Unfortunately red-emitting molecules are more prone to nonradiative decay due to the Energy Gap Law,34 and accordingly have low quantum yields (Φf = 0.13 to 0.2835).
In an air-saturated toluene solution, the initial concentration of oxygen and the rate of diffusion will be constant for any combination of sensitizer and acceptor molecule. The upconversion efficiency of the modeled system is limited by the slow sensitizer energy transfer from the TTCA-ligated PbS QD to both the acceptor species and O2, on a time scale competing with the sensitizer triplet lifetime. In practice, degradation of the sensitizer by oxygen must also be considered and addressed.
Upconversion through SOMET relies on the diffusion of oxygen through the solution to propagate energy transfer, but ultimately, for device applications, it is essential to move from solution to the solid-state. The much slower diffusion in the solid-state would render the energy transfer time-scale slower than that of triplet decay. This problem would need to be overcome for successful application of SOMET to device technologies.
Acknowledgments
This work was supported by the Australian Research Council (Grant Number CE170100026) and the National Computational Infrastructure (NCI), which is supported by the Australian Government.
The authors declare no competing financial interest.
References
- Tayebjee M. J. Y.; Gray-Weale A. A.; Schmidt T. W. Thermodynamic Limit of Exciton Fission Solar Cell Efficiency. J. Phys. Chem. Lett. 2012, 3, 2749–2754. 10.1021/jz301069u. [DOI] [Google Scholar]
- Liang G.; Wang H.; Shi H.; Wang H.; Zhu M.; Jing A.; Li J.; Li G. Recent Progress in the Development of Upconversion Nanomaterials in Bioimaging and Disease Treatment. J. Nanobiotechnol. 2020, 18, 154. 10.1186/s12951-020-00713-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bharmoria P.; Bildirir H.; Moth-Poulsen K. Triplet-Triplet Annihilation Based Near Infrared to Visible Molecular Photon Upconversion. Chem. Soc. Rev. 2020, 49, 6529–6554. 10.1039/D0CS00257G. [DOI] [PubMed] [Google Scholar]
- Johnson R. C.; Merrifield R. E.; Avakian P.; Flippen R. B. Effects of Magnetic Fields on the Mutual Annihilation of Triplet Excitons in Molecular Crystals. Phys. Rev. Lett. 1967, 19, 285–287. 10.1103/PhysRevLett.19.285. [DOI] [Google Scholar]
- Merrifield R. E. Theory of Magnetic Field Effects on the Mutual Annihilation of Triplet Excitons. J. Chem. Phys. 1968, 48, 4318–4319. 10.1063/1.1669777. [DOI] [Google Scholar]
- Avakian P.; Groff R.; Kellogg R.; Merrifield R.; Suna A. In Organic Scintillators and Scintillation Counting; Horrocks D. L., Peng C.-T., Eds.; Academic Press: New York, 1971; pp 499–510. [Google Scholar]
- Minaev B. F. Theoretical Model of Triplet-Triplet Annihilation. Russ. Phys. J. 1978, 21, 1120–1124. 10.1007/BF00894558. [DOI] [Google Scholar]
- Singh-Rachford T. N.; Castellano F. N. Photon Upconversion Based on Sensitized Triplet-Triplet Annihilation. Coord. Chem. Rev. 2010, 254, 2560–2573. 10.1016/j.ccr.2010.01.003. [DOI] [Google Scholar]
- Arnold S. J.; Finlayson N.; Ogryzlo E. A. Some Novel Energy-Pooling Processes Involving O2(1Δg). J. Chem. Phys. 1966, 44, 2529–2530. 10.1063/1.1727077. [DOI] [Google Scholar]
- Ogryzlo E. A.; Pearson A. E. Excitation of Violanthrone by Singlet Oxygen. A Chemiluminescence Mechanism. J. Phys. Chem. 1968, 72, 2913–2916. 10.1021/j100854a039. [DOI] [Google Scholar]
- Abbott S. R.; Ness S.; Hercules D. M. Chemiluminescence from Peroxide Decomposition Reactions. The Role of Energy Transfer. J. Am. Chem. Soc. 1970, 92, 1128–1136. 10.1021/ja00708a005. [DOI] [Google Scholar]
- Murphy S. T.; Kondo K.; Foote C. S. Singlet-Oxygen-Sensitized Delayed Fluorescence: Direct Detection of Triplet Phthalocyanine as an Intermediate. J. Am. Chem. Soc. 1999, 121, 3751–3755. 10.1021/ja974293g. [DOI] [Google Scholar]
- Krasnovsky A. A.; Stremedlovskaya V. S. Singlet-Oxygen-Sensitized Delayed Fluorescence of Phthalocyanines Caused by Photosensitized and Direct Excitation of Dissolved Oxygen by Laser Radiation. J. Porphyrins Phthalocyanines 2008, 12, 1194–1200. 10.1142/S1088424608000571. [DOI] [Google Scholar]
- Fückel B.; Roberts D. A.; Cheng Y. Y.; Clady R. G. C. R.; Piper R. B.; Ekins-Daukes N. J.; Crossley M. J.; Schmidt T. W. Singlet Oxygen Mediated Photochemical Upconversion of NIR Light. J. Phys. Chem. Lett. 2011, 2, 966–971. 10.1021/jz200270w. [DOI] [Google Scholar]
- Gholizadeh E. M.; Prasad S. K. K.; Teh Z. L.; Ishwara T.; Norman S.; Petty A. J.; Cole J. H.; Cheong S.; Tilley R. D.; Anthony J. E.; et al. Photochemical Upconversion of Near-Infrared Light from Below the Silicon Bandgap. Nat. Photonics 2020, 14, 585–590. 10.1038/s41566-020-0664-3. [DOI] [Google Scholar]
- Schmidt T. W.; Castellano F. N. Photochemical Upconversion: The Primacy of Kinetics. J. Phys. Chem. Lett. 2014, 5, 4062–4072. 10.1021/jz501799m. [DOI] [PubMed] [Google Scholar]
- Cheng Y. Y.; Fückel B.; Khoury T.; Clady R. G. C. R.; Ekins-Daukes N. J.; Crossley M. J.; Schmidt T. W. Entropically Driven Photochemical Upconversion. J. Phys. Chem. A 2011, 115, 1047–1053. 10.1021/jp108839g. [DOI] [PubMed] [Google Scholar]
- Atkins P. W.; de Paula J.; Keeler J.. Atkins’ Physical Chemistry, 11th ed.; Oxford University Press: London, England, 2018. [Google Scholar]
- Adamczyk A.; Wilkinson F. In Organic Scintillators and Scintillation Counting; Horrocks D. L., Peng C.-T., Eds.; Academic Press: New York, 1971; pp 223–238. [Google Scholar]
- Gijzeman O. L. J.; Kaufman F.; Porter G. Oxygen Quenching of Aromatic Triplet States in Solution. Part 1. J. Chem. Soc., Faraday Trans. 2 1973, 69, 708. 10.1039/f29736900708. [DOI] [Google Scholar]
- Gijzeman O. L. J.; Kaufman F. Oxygen Quenching of Aromatic Triplet States in Solution. Part 2. J. Chem. Soc., Faraday Trans. 2 1973, 69, 721. 10.1039/f29736900721. [DOI] [Google Scholar]
- Schweitzer C.; Schmidt R. Physical Mechanisms of Generation and Deactivation of Singlet Oxygen. Chem. Rev. 2003, 103, 1685–1758. 10.1021/cr010371d. [DOI] [PubMed] [Google Scholar]
- Bregnhøj M.; Westberg M.; Minaev B. F.; Ogilby P. R. Singlet Oxygen Photophysics in Liquid Solvents: Converging on a Unified Picture. Acc. Chem. Res. 2017, 50, 1920–1927. 10.1021/acs.accounts.7b00169. [DOI] [PubMed] [Google Scholar]
- Becker-Koch D.; Albaladejo-Siguan M.; Lami V.; Paulus F.; Xiang H.; Chen Z.; Vaynzof Y. Ligand Dependent Oxidation Dictates the Performance Evolution of High Efficiency PbS Quantum Dot Solar Cells. Sustainable Energy Fuels 2020, 4, 108–115. 10.1039/C9SE00602H. [DOI] [Google Scholar]
- Kroupa D. M.; Arias D. H.; Blackburn J. L.; Carroll G. M.; Granger D. B.; Anthony J. E.; Beard M. C.; Johnson J. C. Control of Energy Flow Dynamics between Tetracene Ligands and PbS Quantum Dots by Size Tuning and Ligand Coverage. Nano Lett. 2018, 18, 865–873. 10.1021/acs.nanolett.7b04144. [DOI] [PubMed] [Google Scholar]
- Liao J.; Guo W.; Luo X. Triplet Energy Transfer Between Inorganic Nanocrystals and Organic Molecules. J. Photochem. Photobiol. 2022, 11, 100128. 10.1016/j.jpap.2022.100128. [DOI] [Google Scholar]
- Gholizadeh E. M.; Prasad S. K. K.; Gillan L. V.; Nielsen M. P.; Ekins-Daukes N. J.; McCamey D. R.; Tayebjee M. J. Y.; Schmidt T. W. Singlet and Triplet Exciton Dynamics of Violanthrone. J. Phys. Chem. C 2021, 125, 22464–22471. 10.1021/acs.jpcc.1c06848. [DOI] [Google Scholar]
- Field L. R.; Wilhelm E.; Battino R. The Solubility of Gases in Liquids 6. Solubility of N2, O2, CO, CO2, CH4, and CF4 in Methylcyclohexane and Toluene at 283 to 313 K. J. Chem. Thermodyn 1974, 6, 237–243. 10.1016/0021-9614(74)90175-X. [DOI] [Google Scholar]
- Turro N. J.; Ramamurthy V.; Scaiano J.. Modern Molecular Photochemistry of Organic Molecules; University Science Books: Mill Valley, CA, 2010. [Google Scholar]
- Tachikawa H.; Bard A. J. Magnetic Field Effects on Oxygen Quenching of Delayed Fluorescence of Anthracene and Pyrene in Fluid Solution. J. Am. Chem. Soc. 1973, 95, 1672–1673. 10.1021/ja00786a059. [DOI] [Google Scholar]
- Yokoyama K.; Wakikawa Y.; Miura T.; Fujimori J.-I.; Ito F.; Ikoma T. Solvent Viscosity Effect on Triplet-Triplet Pair in Triplet Fusion. J. Phys. Chem. B 2015, 119, 15901–15908. 10.1021/acs.jpcb.5b11208. [DOI] [PubMed] [Google Scholar]
- Dvořák M.; Prasad S. K. K.; Dover C. B.; Forest C. R.; Kaleem A.; MacQueen R. W.; Petty A. J.; Forecast R.; Beves J. E.; Anthony J. E.; et al. Singlet Fission in Concentrated TIPS-Pentacene Solutions: The Role of Excimers and Aggregates. J. Am. Chem. Soc. 2021, 143, 13749–13758. 10.1021/jacs.1c05767. [DOI] [PubMed] [Google Scholar]
- Atkins P.; Evans G. Magnetic Field Effects on Chemiluminescent Fluid Solutions. Mol. Phys. 1975, 29, 921–935. 10.1080/00268977500100801. [DOI] [Google Scholar]
- Siebrand W. Radiationless Transitions in Polyatomic Molecules. I. Calculation of Franck-Condon Factors. J. Chem. Phys. 1967, 46, 440–447. 10.1063/1.1840685. [DOI] [Google Scholar]
- Rurack K.; Spieles M. Fluorescence Quantum Yields of a Series of Red and Near-Infrared Dyes Emitting at 600–1000 nm. Anal. Chem. 2011, 83, 1232–1242. 10.1021/ac101329h. [DOI] [PubMed] [Google Scholar]




