Abstract
Purpose
Automated perimetry is relied on for functional assessment of patients with glaucoma, but questions remain about its effective dynamic range and its utility for quantifying rates of progression at different stages of the disease. This study aims to identify the bounds within which estimates of rate are most reliable.
Methods
Pointwise longitudinal signal-to-noise ratios (LSNR), defined as the rate of change divided by the standard error of the trend line, were calculated for 542 eyes of 273 patients with glaucoma/suspects. The relations between the mean sensitivity within each series and lower percentiles of the distribution of LSNRs (representing progressing series) were analyzed by quantile regression, with 95% confidence intervals derived by bootstrapping.
Results
The 5th and 10th percentiles of LSNRs reached a minimum at sensitivities 17 to 21 dB. Below this, estimates of rate became more variable, making LSNRs of progressing series less negative. A significant step change in these percentiles also occurred at approximately 31 dB, above which LSNRs of progressing locations became less negative.
Conclusions
The lower bound of maximum utility for perimetry was ∼17 to 21dB, coinciding with previous results suggesting that below this point, retinal ganglion cell responses saturate and noise overwhelms remaining signal. The upper bound was ∼30 to 31 dB, coinciding with previous results suggesting that above this point, the size III stimulus used is larger than Ricco's area of complete spatial summation.
Translational Relevance
These results quantify the impact of these two factors on the ability to monitor progression and provide quantifiable targets for attempts to improve perimetry.
Keywords: automated perimetry, glaucoma, progression, data analysis
Introduction
Functional testing, in the form of visual field tests from static standard automated perimetry, remains an essential part of clinical care in glaucoma.1 In particular, the limited dynamic range of structural tests, such as ocular coherence tomography,2 means that perimetry is relied on to monitor eyes with moderate or severe damage. However, we have previously suggested that the effective dynamic range of automated perimetry is much narrower than often assumed.3 Test–retest variability increases as sensitivities decline,4,5 until it becomes so large that it swamps any remaining signal on a single test when sensitivities reach around 15 to 19 dB,3 and so event analyses of change can no longer be relied upon. Most current perimetric testing algorithms report sensitivities down to 0 dB, which is defined as the most intense stimulus that the hardware is capable of producing, but censoring those sensitivities by assigning them a value of 15 dB or even 20 dB does not appear to harm the ability to detect progression.6,7
However, those previous studies have focused on the ability to detect change—that is, whether a location has reached some predetermined criterion for “progressing” versus “stable.” In reality, the rate of deterioration exists on a continuum, and assessing the rate of change at a location is both more robust and more relevant to clinical care than simplifying to whether the location reaches an arbitrary cutoff such as P < 0.05.8 One way to assess methods of monitoring the rate of change is by examining the longitudinal signal-to-noise ratio (LSNR).9,10 This technique expresses the observed rate of change as a proportion of the variability in that particular series. A more negative LSNR indicates high confidence that significant reduction in sensitivity is occurring and that the rate of change is being estimated reliably. Not all locations of all eyes are rapidly progressing, but by looking at the lower tail of the distribution of LSNRs within a population, it is possible to test how reliably the rate of change can be determined at those locations that are deteriorating fastest. By performing this exercise among groups of locations with similar sensitivity, we can assess the ability to monitor progression at different levels of functional loss and determine whether this ability is hampered below some cutoff.
While it is important to identify the cutoff below which perimetry may no longer be reliable, it is also of great interest to look at the ability to monitor progression in less damaged regions. There is ongoing debate about the best stimulus size to use for automated perimetry. Current clinical perimeters mostly use a size III stimulus (0.43° diameter) at all locations and all contrasts. Some groups have advocated for using a larger size V stimulus, which increases sensitivities, reducing variability11,12 (since variability is strongly correlated with sensitivity13) and allowing testing at more severely damaged locations7,14 (because the lower cutoff of ∼15–19 dB is unchanged13). Others have advocated using stimuli smaller than Ricco's area of complete spatial summation,15 which expands in regions of glaucomatous loss.16 A given stimulus size is larger than Ricco's area, and hence operating under partial spatial summation, when sensitivity is above ∼30 to 31 dB (as is the case for both size III and size V stimuli in healthy observers, especially centrally).17 The same stimulus size is smaller than Ricco's area at locations whose sensitivity is below ∼30 to 31 dB, causing a greater change in sensitivity for the same amount of cell loss18–20 and hence potentially improving the signal-to-noise ratio.15 Other groups have posited that the differences between stimulus sizes, in particular being above versus below Ricco's area, are too minor to be of clinical significance. Importantly, properties of sensitivity estimates such as variability and dynamic range appear to be determined primarily by sensitivity. If one location is tested using a size III stimulus, while another is tested with a size V stimulus, and both have sensitivity 27 dB for their respective stimulus sizes, then they will also have almost exactly the same test–retest variability.13 Thus, by looking at the LSNR above versus below 30 to 31 dB, we can learn about the ability to monitor change using stimuli larger than versus smaller than Ricco's area, without the confound of having to actually use different-sized stimuli and hence be inconsistent in the retinal ganglion cells being stimulated.
In this study, we calculate the LSNRs of clinical pointwise sensitivity estimates in a large, well-controlled population of glaucoma suspects and cases. By grouping locations according to their sensitivity, we can assess the ability to detect change across the range of severities of glaucomatous loss, including above versus below 31 dB (to learn about the utility of different stimulus sizes) and above versus below 18 dB (to learn about the extent of the dynamic range of perimetry).
Methods
Data for this analysis were taken from the Portland Progression Project, an ongoing longitudinal study of glaucomatous progression.21,22 Patients had a diagnosis of either “glaucoma” or “glaucoma suspect.” Exclusion criteria were comorbidities or medications likely to affect the visual field, including severe cataract, diabetic retinopathy, or macular degeneration, or an inability to reliably perform visual field testing. Determination of all inclusion and exclusion criteria was at the discretion of the participant's clinician. Both eyes were tested, on the basis that a diagnosis in one eye makes the other eye more likely to also develop glaucoma, unless the fellow eye failed the exclusion criteria. Participants were tested once every 6 months. For the purposes of this analysis, the most recent six visual fields per eye were used, covering at least 2.5 years, in order to capture instances of rapid progression. All testing was approved by the local institutional review board and adhered to the tenets of the Declaration of Helsinki.
Visual field testing was carried out on a Humphrey Field Analyzer IIi (Carl Zeiss Meditec, Inc., Dublin, CA, USA), using the Swedish Interactive Testing Algorithm (SITA Standard).23 In light of results suggesting that the instrument's reliability indices are not closely related to actual test performance,24–28 tests were not excluded on this basis; instead, the technician performing the test monitored fixation on the instrument's monitor and discarded and repeated the test in the event of excessive fixation instability, inattention, and/or obvious artifacts in the results such as a lens rim artifact.29–31
The LSNR is defined in this study as the rate of change from ordinary least squares linear regression over time in dB/y (the longitudinal signal) divided by the standard error of the slope estimate from that regression line in dB (the noise). It is therefore expressed in units of y−1. A more negative LSNR indicates a decreasing sensitivity that is less likely to be due to noise. Thus, the LSNR is conceptually similar to a one-tail P value reflecting whether the sensitivity is increasing or decreasing over time. LSNR was calculated for each of the 52 nonblindspot locations in the 24-2 visual field, together with the minimum, maximum, and mean sensitivity within that series. All analysis were performed in R version 4.0.3.32
For visualization, the pointwise series were split into bins according to the mean sensitivity within that series. Bins were 1 dB wide, spanning 0 dB < mean ≤ 1dB, 1 dB < mean ≤ 2 dB, and so on, except between 3 and 11 dB, where bins were 2 dB wide (i.e., 3 dB < mean ≤ 5 dB, etc.) to ensure there were at least 50 series within each of those bins. Series with mean sensitivity ≤0 dB were excluded since change cannot be measured at such locations. Within each bin, the 5th, 10th, and 20th percentiles of the LSNR distribution were calculated. These are chosen to reflect the typical LSNR at progressing locations; looking only at the mean or median LSNR would dilute any effect since the majority of locations will only be progressing slowly in a population under clinical management. A secondary visualization was performed excluding any series that contained one or more sensitivities of 0 dB or <0 dB, to remove the floor effect caused by hardware limitations.
Quantile regression analyses were performed to formally determine whether the 5th, 10th, 20th, and/or 90th percentiles of the LSNR distribution varied with mean sensitivity across subsets of sensitivities chosen to test the specific hypotheses that the signal-to-noise ratio may differ above/below 17 dB (due to reaching the lower limit of the effective dynamic range somewhere between 15 and 19 dB3,6,7) and also above/below 31 dB (due to the stimulus being larger/smaller than Ricco's area15). To avoid problematic distributional assumptions (in particular, to avoid having to assume that the within-eye and between-eye distributions of LSNR are homoscedastic), a semiparametric nested bootstrap approach was used. A sample of 542 eyes were randomly selected, with replacement, from the 542 available eyes. For each of those eyes, N eligible locations were randomly selected, with replacement, from the N locations whose mean sensitivity within the series was within the subset being analyzed (hence N varied between eyes). Linear quantile regression models were then used to derive the change in each of the chosen percentiles with sensitivity. One thousand such bootstrap samples were generated, and the 2.5th and 97.5th percentiles define a 95% confidence interval (CI) for the change in sensitivity. Analyses were performed using the quantreg package for R.33
Results
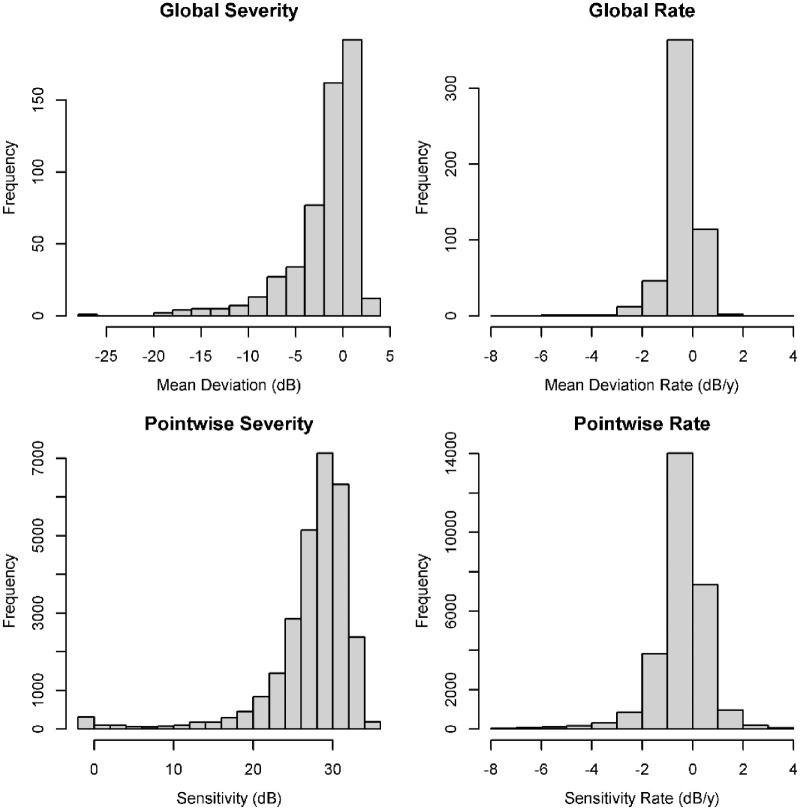
Series of six visual fields were taken from 542 eyes of 273 patients. The average mean deviation in the series was −1.8 dB (range, −26.3 to +2.5 dB), changing at average rate of −0.38 dB/y (range, −5.9 to +1.3dB/y). Figure 1 shows histograms of the severities (averaged across each series) and rates of change, both for global mean deviation and for pointwise sensitivities. The median pointwise LSNR across the entire data set was −0.58 y−1, ranging from −18.5 to +19.8 y−1.
Figure 1.
Histograms of the severities (left, averaged across the series of six visual fields for each eye) and rates of change (right, from linear regression against time), for global metric mean deviation (top) and for the 52 pointwise sensitivities per eye (bottom).
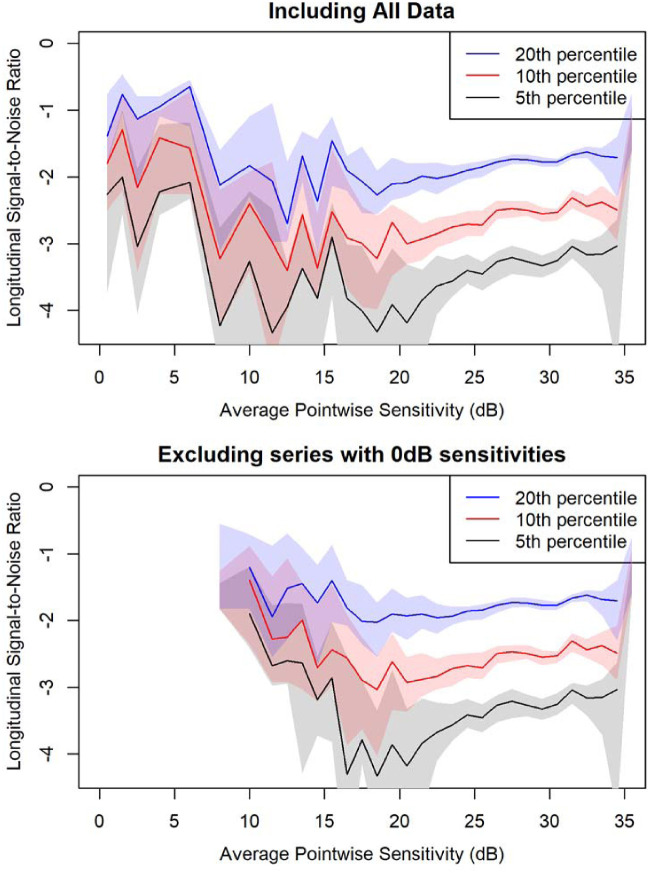
Figure 2 shows the 5th, 10th, and 20th percentiles of the LSNR distribution within bins defined by the average sensitivity within the series. Three things are noticeable here. First, the LSNRs reach a minimum between approximately 17 and 21 dB. This is consistent with the idea that sensitivities become much noisier below this point,3 making the LSNRs closer to zero. The further minima in the 7- to 9-dB and 11- to 12-dB bins are based on a much smaller sample of just 67 and 51 series, respectively, and do not appear to be consistent with neighboring bins on either side, so are likely a chance finding. The 20th percentile of LSNRs was lower between 17 and 21 dB than between 13 and 17 dB (95% CI for the difference, −0.491 to −0.032 y−1), although this difference was not statistically significant for the 10th percentile (−0.570 to +0.345 y−1) or the 5th percentile (−0.928 to +0.211 y−1). The minimum is particularly clear in the bottom panel of Figure 2, which excludes series containing sensitivities ≤0 dB, whose variability is artifactually low due to the imposed floor effect; the LSNR again reaches an apparent minimum between 17 and 21 dB. When excluding those series with ≤0-dB sensitivities, the 20th percentile of LSNRs was again significantly lower between 17 and 21 dB than between 13 and 17 dB (95% CI for the difference, −0.581 to −0.058 y−1). Supplementary Figure S1 shows the equivalent plots when binning series according to the initial or final sensitivities in the series.
Figure 2.
Quantiles of the distribution of LSNRs, defined as the rate of change from linear regression divided by the standard error of that regression line, in series of six visual fields, among locations with similar mean sensitivity across that series. The 20th, 10th, and 5th percentiles are shown for locations in bins of width 1 dB, except between 3 and 11 dB, where 2-dB-wide bins were used to ensure adequate sample size. The top plot includes all such series. The bottom plot excludes series that contained one or more sensitivities ≤0 dB; only bins including at least 20 series are shown to ensure that the 5th percentile is well defined. The shaded area around each line represents the 95% confidence interval for that line, derived by 1000 bootstrap resamplings of the data in that bin.
Second, within the range from 20 to 29 dB that is largely unaffected by the hypothesized effects of dynamic range or Ricco's area, the LSNRs appear to improve (become more negative) as sensitivity decreases, even though the test–retest variability (the denominator in the LSNR calculation) increases.5 This trend was statistically significant for the 5th percentile of LSNRs (95% CI, −0.039 to −0.120 y−1 per 1-dB reduction in sensitivity), the 10th percentile (−0.037 to −0.092 y−1), and the 20th percentile (−0.026 to −0.062 y−1).
Third, the LSNRs appear to be worse (less negative) above 31 dB than below. The 5th percentile of LSNRs was significantly worse (less negative) between 31 and 35 dB than between 27 and 31 dB (95% CI for the difference, +0.018 to +0.288 y−1). This increase was also statistically significant for the 10th percentile (difference +0.036 to +0.240 y−1) and the 20th percentile (difference +0.036 to +0.152 y−1). Even after adjusting for the trend discussed in the previous paragraph—that is, using a model of the form Quantile = Intercept + A × Sensitivity + B × (Sensitivity >31)—when analyzing all locations with sensitivity 20 to 35 dB, the coefficient B indicating a step change in the quantiles when crossing that cutoff was statistically significant for the 5th percentile (+0.055 to +0.250 y−1), the 10th percentile (+0.032 to +0.167 y−1), and the 20th percentile (+0.043 to +0.121 y−1).
The cutoffs chosen for the two breakpoints were based on the literature but are also supported by the results above, in particular Figure 2. After adjusting for the overall trend as in the previous paragraph, there was no significant breakpoint at 30 dB for any percentile; a breakpoint at 32 dB was significant for the 20th percentile (+0.027 to +0.124 y−1) but not for the 5th or 10th percentiles.
The 90th percentile of the LSNR distribution was almost constant. It did not differ between 13 and 17 dB versus 17 and 21 dB (95% CI for difference, −0.343 to +0.311 y−1) or between 27 and 31 dB versus 31 and 35 dB (difference −0.056 to +0.099 y−1). This supports the supposition that the apparent trends in the lower percentiles of the LSNR distribution are not purely due to changes in variability but instead reflect the ability to monitor progressing locations.
Discussion
In this study, we found that pointwise LSNRs from progressing locations were more negative, indicating greater ease of identifying progression, at locations with sensitivities between approximately 17 and 31 dB than at locations with sensitivities above or below that range. Clinically, the implication is that automated perimetry is indeed most useful for monitoring progression in the range of severities at which it is most relied upon diagnostically. For the purposes of improving our understanding of perimetry and using that to improve functional testing, the lower and upper limits of that range have differing explanations and implications.
The lower bound, below which perimetry starts to become less useful for monitoring progression, was around 17 to 21 dB. We deliberately state this as a range rather than a single value to emphasize that it is a gradual reduction in utility rather than a hard cutoff, and the cutoff may vary between individuals. Since it is a gradual reduction, it can be partially overcome by more frequent testing, and hence the cutoff would be lower for trend analyses than for event analyses that rely on just two data points. However, continuing to increase tested frequency does bring diminishing returns and is subject to the bounds of patient acceptability. Another way to extend the dynamic range is by averaging locations, which comes at the cost of losing spatial resolution. We have previously shown evidence that this cutoff is due to the responses of remaining retinal ganglion cells becoming saturated, such that further increasing contrast has very little impact on the firing rates of those cells and hence very little impact on the probability that the patient detects the stimulus3,34; that explanation has been questioned,35 but the existence of such a limit is supported by studies showing that censoring at that sensitivity does not decrease clinical utility.6,7 Notably, the cutoff of 17 to 21 dB found in this analysis is very similar to previous estimates based on different data and different techniques.3,6,7,36
The upper bound, above which there was an apparent step change worsening the signal-to-noise ratio, was around 31 dB. For clinical care, the regions of most interest for monitoring progression are locations with sensitivity below this point. The implications are related more to methods for improving on current clinical perimetry, since this cutoff occurs at the approximate point at which Ricco's area of complete spatial summation equals the area of the size III stimulus used. There is ongoing debate over whether it is better to increase the stimulus size (most likely from size III to size V),7,37 which would greatly increase the proportion of locations that are above this cutoff,13 or to decrease the stimulus size (to ensure it stays within Ricco's area),15,38 which would ensure that all locations were below this cutoff,17 or whether the difference is too small to be of clinical relevance. The results of the above analyses may prove to be a Rorschach test for each point of view. Proponents of using stimuli smaller than Ricco's area might point to evidence in Figure 2 and the subsequent quantile regression analyses that the signal-to-noise ratio, in the form of the LSNR, was indeed better below the cutoff. Proponents of using stimuli that are larger than Ricco's area in healthy observers, in order to increase sensitivities, might point out that there are sufficient caveats with these results that they do not disprove the benefits of larger stimuli. Our results could be caused by the distribution of rates of loss, not by any inherent upper limit on the optimal dynamic range. There are likely to be a lower proportion of locations that are truly progressing (and hence have more negative LSNR) at sensitivities 31 to 35 dB than at 27 to 31 dB; this caveat is reduced by looking at the 5th, 10th, and 20th percentiles of the distribution but is not eliminated entirely. Further, significant step changes in LSNR were not found when using cutoffs of 30 dB or 32 dB, which could be taken as evidence that the results are not robust or could be taken as evidence that the 31-dB cutoff is indeed appropriate and optimal given its agreement with previous literature.17 Finally, it should be pointed out that Ricco's area enlarges in glaucoma, and so in regions of advanced damage, a larger stimulus might extend the effective dynamic range while remaining within Ricco's area.16 Meanwhile, the relatively small difference in LSNR above/below the cutoff (the 10th percentile in Figure 2 was −2.53 y−1 for locations with sensitivity 30–31 dB versus −2.31 y−1 for locations with sensitivity 31–32 dB) could be taken as evidence that the difference is too small to be clinically relevant, and hence that practical factors such as patient experience should take precedence,39 although it should be noted that this difference is diluted by the fact that most locations whose mean sensitivity is near 31 dB will have been above the cutoff on some visits and below on others. A useful next step would be to perform LSNR analysis on series of fields acquired with different stimulus sizes on the same days. If staying below Ricco's area is indeed beneficial, we would predict that the LSNR at progressing locations would be more negative for size III than size V when the location is below 31 dB for size III but above 31 dB for size V but approximately equal otherwise. If using larger stimuli is indeed beneficial, we would predict that the LSNR at progressing locations would be more negative for size V than size III across the range.
It is perhaps surprising that percentiles of the LSNR distribution appeared to become more negative with increasing damage (until reaching the cutoff at 17–21 dB), despite the fact that test–retest variability is known to increase.5 However, rates of change are also correlated with severity of loss.40 Glaucomatous eyes are of course more likely to deteriorate than suspect eyes, but also, the logarithmic dB scale means that a constant rate of ganglion cell loss correlates with more rapid functional loss in dB/y when sensitivities are reduced.41,42 Counteracting this is the fact that the data set comes from patients under clinical management, and eyes with more severe damage will be treated more aggressively to reduce progression. Importantly, though, the percentiles did not appear to decrease as sensitivity reduced from 31 to 27 dB (see Figure 2), and so this caveat seems unlikely to have driven any of the primary conclusions drawn from the results.
The data set used for these analyses was drawn from the Portland Progression Project. In this study, patients are aimed to be tested on a regular schedule, once every 6 months. In practice, the intervals between visits are not completely uniform, due to factors such as patient availability and the temporary pause in testing during the early months of the COVID-19 pandemic. Importantly, though, the interval between visits is independent of both glaucoma severity and the rate of progression. This contrasts with clinical data sets, where patients are seen more frequently if they are progressing rapidly. More frequent testing makes estimates of the rate of change over a fixed number of visits more variable, for a given magnitude of test–retest variability. This will increase the standard error of the trend line and hence reduce the magnitude of the LSNR. Therefore, in a clinical data set, the magnitude of LSNRs from progressing eyes would be artifactually reduced compared with those from stable eyes that are seen less frequently when using a fixed number of visits. By contrast, more frequent testing would decrease the standard error of the trend line and hence increase the magnitude of the LSNR when using a fixed number of years of series duration. Using a consistent series duration and interval between tests helps ensure that the lower 10% of LSNRs does indeed reflect the series undergoing more rapid progression.
Series of six visual fields were used for this study. This is designed to represent the most relevant clinical scenario, where a clinician wishes to assess the recent rate of disease progression. Longer series can mask periods of more rapid progression,43 not least because these patients were managed at their clinicians’ discretion, and so after a few years of rapid progression, an eye would be prescribed more aggressive treatment. The relatively short series length does mean that estimates of the rate of change are noisier, especially when using pointwise data. In particular, the extreme tails of the distribution of slopes are more likely to represent noise than to represent true rates of change. This effect is reduced but not eliminated by looking instead at the distribution of LSNRs. Only 0.13% of series had an LSNR <−5 y−1, and 0.01% had an LSNR >5 y−1, which would be considered implausible. This is why the primary results are based on the 5th, 10th, and 20th percentiles of the distribution, rather than smaller percentiles.
A further caveat is that data came from patients with or at risk of developing glaucoma. It is unknown whether the same cutoffs would apply in individuals with other pathologies. For example, if the lower bound of 17 to 21 dB is caused by the responses of remaining retinal ganglion cells becoming saturated, then this may not apply in diseases characterized by loss of photoreceptors instead of loss of ganglion cells. It should be noted, though, that imposing a cutoff of 17 to 20 dB has been shown to aid detection of change in eyes with retinitis pigmentosa.44 The cutoffs may also be higher in individuals with media opacities that reduce the effective contrast on the retina.
In summary, the longitudinal signal-to-noise ratio was generally more negative at progressing locations with sensitivities between approximately 17 and 31 dB than at locations below that range (beyond the effective dynamic range of standard automated perimetry) or above that range (at which the size III stimulus used is smaller than Ricco's area of complete spatial summation). This is reassuring for the use of current clinical perimetry between those cutoffs while also providing essential further guidance for any attempts to improve perimetry and extend its effective dynamic range.
Supplementary Material
Acknowledgments
Supported by NEI R01 EY020922, NEI R01 EY031686, and Good Samaritan Foundation.
Disclosure: S.K. Gardiner, None
References
- 1. Stagg BC, Stein JD, Medeiros FA, et al.. The frequency of visual field testing in a US nationwide cohort of individuals with open angle glaucoma. Ophthalmol Glaucoma. 2022; 5(6): 587–593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Moghimi S, Bowd C, Zangwill LM, et al.. Measurement floors and dynamic ranges of OCT and OCT angiography in glaucoma. Ophthalmology. 2019; 126(7): 980–988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Gardiner SK, Swanson WH, Goren D, Mansberger SL, Demirel S.. Assessment of the reliability of standard automated perimetry in regions of glaucomatous damage. Ophthalmology. 2014; 121(7): 1359–1369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Heijl A, Lindgren A, Lindgren G.. Test-retest variability in glaucomatous visual fields. Am J Ophthalmol. 1989; 108(2): 130–135. [DOI] [PubMed] [Google Scholar]
- 5. Artes PH, Iwase A, Ohno Y, Kitazawa Y, Chauhan BC.. Properties of perimetric threshold estimates from Full Threshold, SITA Standard, and SITA Fast strategies. Invest Ophthalmol Vis Sci. 2002; 43(8): 2654–2659. [PubMed] [Google Scholar]
- 6. Gardiner SK, Swanson WH, Demirel S.. The effect of limiting the range of perimetric sensitivities on pointwise assessment of visual field progression in glaucoma. Invest Ophthalmol Vis Sci. 2016; 57(1): 288–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Wall M, Zamba GKD, Artes PH.. The effective dynamic ranges for glaucomatous visual field progression with standard automated perimetry and stimulus sizes III and V. Invest Ophthalmol Vis Sci. 2018; 59(1): 439–445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Caprioli J. The importance of rates in glaucoma. Am J Ophthalmol. 2008; 145(2): 191–192. [DOI] [PubMed] [Google Scholar]
- 9. Gardiner SK, Fortune B, Demirel S.. Signal-to-noise ratios for structural and functional tests in glaucoma. Transl Vis Sci Technol. 2013; 2(6): 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Gardiner SK, Boey PY, Yang H, Fortune B, Burgoyne CF, Demirel S.. Structural measurements for monitoring change in glaucoma: comparing retinal nerve fiber layer thickness with minimum rim width and area. Invest Ophthalmol Vis Sci. 2015; 56(11): 6886–6891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Wall M, Kutzko K, Chauhan B.. Variability in patients with glaucomatous visual field damage is reduced using size V stimuli. Invest Ophthalmol Vis Sci. 1997; 38(2): 426–435. [PubMed] [Google Scholar]
- 12. Wall M, Woodward KR, Doyle CK, Artes PH.. Repeatability of automated perimetry: a comparison between standard automated perimetry with stimulus size III and V, matrix, and motion perimetry. Invest Ophthalmol Vis Sci. 2009; 50(2): 974–979. [DOI] [PubMed] [Google Scholar]
- 13. Gardiner SK, Demirel S, Goren D, Mansberger SL, Swanson WH.. The effect of stimulus size on the reliable stimulus range of perimetry. Transl Vis Sci Technol. 2015; 4(2): 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Wall M, Woodward KR, Doyle CK, Zamba G.. The effective dynamic ranges of standard automated perimetry sizes III and V and motion and matrix perimetry. Arch Ophthalmol. 2010; 128(5): 570–576. [DOI] [PubMed] [Google Scholar]
- 15. Rountree L, Mulholland PJ, Anderson RS, Garway-Heath DF, Morgan JE, Redmond T.. Optimising the glaucoma signal/noise ratio by mapping changes in spatial summation with area-modulated perimetric stimuli. Sci Rep. 2018; 8: 2172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Redmond T, Garway-Heath DF, Zlatkova MB, Anderson RS.. Sensitivity loss in early glaucoma can be mapped to an enlargement of the area of complete spatial summation. Invest Ophthalmol Vis Sci. 2010; 51(12): 6540–6548. [DOI] [PubMed] [Google Scholar]
- 17. Phu J, Khuu SK, Zangerl B, Kalloniatis M.. A comparison of Goldmann III, V and spatially equated test stimuli in visual field testing: the importance of complete and partial spatial summation. Ophthalmic Physiol Opt. 2017; 37(2): 160–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Khuu SK, Kalloniatis M.. Standard automated perimetry: determining spatial summation and its effect on contrast sensitivity across the visual field. Invest Ophthalmol Vis Sci. 2015; 56(6): 3565–3576. [DOI] [PubMed] [Google Scholar]
- 19. Choi AYJ, Nivison-Smith L, Khuu SK, Kalloniatis M.. Determining spatial summation and its effect on contrast sensitivity across the central 20 degrees of visual field. PLoS ONE. 2016; 11(7): e0158263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Gardiner SK. Differences in the relation between perimetric sensitivity and variability between locations across the visual field. Invest Ophthalmol Vis Sci. 2018; 59(8): 3667–3674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Gardiner SK, Johnson CA, Demirel S.. Factors predicting the rate of functional progression in early and suspected glaucoma. Invest Ophthalmol Vis Sci. 2012; 53(7): 3598–3604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Gardiner SK, Mansberger SL, Fortune B.. Time lag between functional change and loss of retinal nerve fiber layer in glaucoma. Invest Ophthalmol Vis Sci. 2020; 61(13): 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Bengtsson B, Olsson J, Heijl A, Rootzen H.. A new generation of algorithms for computerized threshold perimetry, SITA. Acta Ophthalmol Scand. 1997; 75(4): 368–375. [DOI] [PubMed] [Google Scholar]
- 24. Bengtsson B, Heijl A.. False-negative responses in glaucoma perimetry: indicators of patient performance or test reliability? Invest Ophthalmol Vis Sci. 2000; 41(8): 2201–2204. [PubMed] [Google Scholar]
- 25. Newkirk MR, Gardiner SK, Demirel S, Johnson CA.. Assessment of false positives with the Humphrey Field Analyzer II perimeter with the SITA Algorithm. Invest Ophthalmol Vis Sci. 2006; 47(10): 4632–4637. [DOI] [PubMed] [Google Scholar]
- 26. Heijl A, Patella VM, Flanagan JG, et al.. False positive responses in standard automated perimetry. Am J Ophthalmol. 2022; 233: 180–188. [DOI] [PubMed] [Google Scholar]
- 27. Demirel S, Vingrys AJ.. Eye movements during perimetry and the effect that fixational instability has on perimetric outcomes. J Glaucoma. 1994; 3(1): 28–35. [PubMed] [Google Scholar]
- 28. Sanabria O, Feuer WJ, Anderson DR.. Pseudo-loss of fixation in automated perimetry. Ophthalmology. 1991; 98(1): 76–78. [DOI] [PubMed] [Google Scholar]
- 29. Zalta AH. Lens rim artifact in automated threshold perimetry. Ophthalmology. 1989; 96(9): 1302–1311. [DOI] [PubMed] [Google Scholar]
- 30. Tan NYQ, Tham YC, Koh V, et al.. The effect of testing reliability on visual field sensitivity in normal eyes: the Singapore Chinese Eye Study. Ophthalmology. 2018; 125(1): 15–21. [DOI] [PubMed] [Google Scholar]
- 31. Yohannan J, Wang J, Brown J, et al.. Evidence-based criteria for assessment of visual field reliability. Ophthalmology. 2017; 124(11): 1612–1620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. R Development Core Team. R: A Language and Environment for Statistical Computing. 4.0.0 ed. Vienna, Austria: R Foundation for Statistical Computing; 2020. [Google Scholar]
- 33. Koenker R. Computational methods for quantile regression. In: Koenker R, Chernozhukov V, He X, Peng L, eds. Handbook of Quantile Regression. Boca Raton, FL: Chapman and Hall/CRC; 2017: 55–67. [Google Scholar]
- 34. Swanson WH, Sun H, Lee BB, Cao D.. Responses of primate retinal ganglion cells to perimetric stimuli. Invest Ophthalmol Vis Sci. 2011; 52(2): 764–771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Anderson AJ, McKendrick AM, Turpin A.. Do intense perimetric stimuli saturate the healthy visual system? Invest Ophthalmol Vis Sci. 2016; 57(14): 6397–6404. [DOI] [PubMed] [Google Scholar]
- 36. Pathak M, Demirel S, Gardiner SK.. Reducing variability of perimetric global indices from eyes with progressive glaucoma by censoring unreliable sensitivity data. Transl Vis Sci Technol. 2017; 6(4): 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Wall M, Kutzko KE, Chauhan BC.. Variability in patients with glaucomatous visual field damage is reduced using size V stimuli. Invest Ophthalmol Vis Sci. 1997; 38(2): 426–435. [PubMed] [Google Scholar]
- 38. Rountree L, Mulholland PJ, Anderson RS, Morgan JE, Garway-Heath D, Redmond T.. Quantifying the signal/noise ratio with perimetric stimuli optimised to probe changing spatial summation in glaucoma. Invest Ophthalmol Vis Sci. 2017; 58(8): 2852.28570737 [Google Scholar]
- 39. Gardiner SK, Demirel S.. Assessment of patient opinions of different clinical tests used in the management of glaucoma. Ophthalmology. 2008; 115(12): 2127–2131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Gardiner SK, Demirel S, Johnson CA.. Perimetric indices as predictors of future glaucomatous functional change. Optom Vis Sci. 2011; 88(1): 56–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Hood DC, Kardon RH.. A framework for comparing structural and functional measures of glaucomatous damage. Prog Retin Eye Res. 2007; 26(6): 688–710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Harwerth RS, Carter-Dawson L, Smith EL III, Barnes G, Holt WF, Crawford ML.. Neural losses correlated with visual losses in clinical perimetry. Invest Ophthalmol Vis Sci. 2004; 45(9): 3152–3160. [DOI] [PubMed] [Google Scholar]
- 43. Gardiner SK, Demirel S, De Moraes CG, et al.. Series length used during trend analysis affects sensitivity to changes in progression rate in the ocular hypertension treatment study. Invest Ophthalmol Vis Sci. 2013; 54(2): 1252–1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Bittner AK, Mistry A, Nehmad L, Khan R, Dagnelie G.. Improvements in test–retest variability of static automated perimetry by censoring results with low sensitivity in retinitis pigmentosa. Transl Vis Sci Technol. 2020; 9(12): 26. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.