Fast, Optimal, and Targeted Predictions using Parametrized Decision Analysis

Abstract

Prediction is critical for decision-making under uncertainty and lends validity to statistical inference. With targeted prediction, the goal is to optimize predictions for specific decision tasks of interest, which we represent via functionals. Although classical decision analysis extracts predictions from a Bayesian model, these predictions are often difficult to interpret and slow to compute. Instead, we design a class of parametrized actions for Bayesian decision analysis that produce optimal, scalable, and simple targeted predictions. For a wide variety of action parametrizations and loss functions—including linear actions with sparsity constraints for targeted variable selection—we derive a convenient representation of the optimal targeted prediction that yields efficient and interpretable solutions. Customized out-of-sample predictive metrics are developed to evaluate and compare among targeted predictors. Through careful use of the posterior predictive distribution, we introduce a procedure that identifies a set of near-optimal, or acceptable targeted predictors, which provide unique insights into the features and level of complexity needed for accurate targeted prediction. Simulations demonstrate excellent prediction, estimation, and variable selection capabilities. Targeted predictions are constructed for physical activity data from the National Health and Nutrition Examination Survey (NHANES) to better predict and understand the characteristics of intraday physical activity.

1. Introduction

Prediction is a cornerstone of statistical analysis: it is essential for decision-making under uncertainty and provides validation for inference (Geisser, 1993). Predictive evaluations are crucial for model comparisons and selections (Gelfand et al., 1992) and offer diagnostic capabilities for detecting model misspecification (Gelman et al., 1996). More subtly, predictions provide an access point for model interpretability: namely, via identification of the model characteristics or variables which matter most for accuracy. However, the demands of many datasets—which can be high-dimensional, high-resolution, and multi-faceted—often necessitate sophisticated and complex models. Even when such models predict well, they can be cumbersome to deploy and difficult to summarize or interpret.

Our focus is targeted prediction, where predictions are customized for the decision tasks of interest. The translation of models into actionable decisions requires predictive quantities in the form of functionals of future or unobserved data. Predictions should be optimized for these decision tasks—and targeted to the relevant functionals. The target is fundamental for defining the correct (predictive) likelihood (Bjornstad, 1990). Absent specific functionals of interest, targeted prediction offers a path for interpretable statistical learning: the functionals probe the data-generating process to uncover the predictability of distinct attributes.

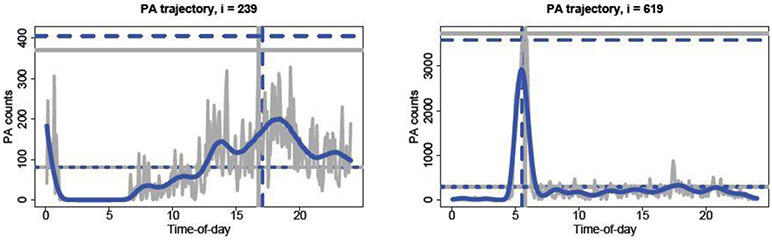
To illustrate these points, we display wearable device data from the National Health and Nutrition Examination Survey (NHANES) in Figure 1. Physical activity (PA) trajectories are modeled as functional data and accompanied by subject-specific covariates; descriptions of the data and the model are in Section 5. Scientific interest does not reside exclusively with these intraday profiles: we are also interested in functionals of the trajectories. Figure 1 shows several such functionals: the average activity (avg), the peak activity level (max), and the time of peak activity (argmax). These functionals summarize daily PA and describe clear sources of variability in PA among the individuals. Other features are discernible, such as sedentary behavior and periods of absolute inactivity, and are investigated in Section 5. However, Bayesian model-based point predictions alone do not explain what drives the variability among individuals and can be slow to compute out-of-sample.

Fig. 1.

Intraday physical activity (gray line) and fitted values (blue line) for two subjects under model $\mathcal{M}$ in (6)-(8). The lines denote the empirical (solid gray) and predictive expected value (dashed blue) of avg (lower horizontal), max (upper horizontal), and argmax (vertical).

Our goal is construct targeted predictions that improve accuracy, streamline decision making, and highlight the model attributes and covariates that matter most for prediction—which notably may differ among functionals. Building upon classical decision analysis, we introduce parametrized actions that extract optimal, simple, and fast predictions under any Bayesian model $\mathcal{M}$. The parameterizations exploit familiar model structures, such as linear, tree, and additive forms, while the actions minimize a posterior predictive expected loss that is customized for each functional. For a broad class of parametrized actions and loss functions, we derive a convenient representation of the optimal targeted prediction that yields efficient and interpretable solutions. These solutions can be computed using existing software packages for penalized regression, which allows for widespread and immediate deployment of the proposed techniques. The targeted predictions are constructed simultaneously for multiple functionals based on a single $\mathcal{M}$, which avoids the need to re-fit a Bayesian model for each functional. While intrinsically useful for prediction, the elicitation of multiple targeted predictors is also informative for understanding and summarizing the model $\mathcal{M}$ posterior.

A key feature of our approach is the use of the model $\mathcal{M}$ predictive distribution to provide uncertainty quantification for out-of-sample predictive evaluation. We design a procedure to identify not only the most accurate targeted predictor, but also any predictor that performs nearly as well with some nonnegligible predictive probability. This strategy emerges as a Bayesian representation of the Rashomon effect, which observes that there often exists a multitude of acceptably accurate predictors (Breiman, 2001). The set of acceptable predictors is informative: it describes the shared characteristics and level of complexity needed for near-optimal targeted prediction. We do not require any re-fitting of $\mathcal{M}$ and instead design an efficient algorithm to approximate the relevant out-of-sample predictive quantities for each functional. The proposed methods are applied to both simulated and real data and demonstrate excellent prediction, estimation, and selection capabilities.

There is a rich literature on the use of decision analysis to extract information from a Bayesian model. Bernardo and Smith (2009) provide foundational elements, while Vehtari and Ojanen (2012) give a prediction-centric survey. MacEachern (2001) and Gutiérrez-Peña and Walker (2006) use decision analysis to summarize Bayesian nonparametric models. The proposed methods expand upon a line of research for posterior summarization, most commonly for Bayesian variable selection, advocated by Lindley (1968) and rekindled by Hahn and Carvalho (2015). These techniques have been adapted for seemingly unrelated regressions (Puelz et al., 2017), graphical models (Bashir et al., 2019), nonlinear regressions (Woody et al., 2020), functional regression (Kowal and Bourgeois, 2020), and time-varying parameter models (Huber et al., 2020). Alternative approaches combine linear variable selection with Kullback-Leibler distributional approximations (Goutis and Robert, 1998; Nott and Leng, 2010; Tran et al., 2012; Crawford et al., 2019; Piironen et al., 2020). In general, these methods focus on global summarizations of a particular model $\mathcal{M}$ posterior distribution. By comparison, our emphasis on predictive functionals adds specificity and a direct link to the observables, which provides a solid foundation for (out-of-sample) predictive evaluations and broadens applicability among Bayesian models with different parameterizations.

The remainder of the paper is organized as follows. Section 2 introduces predictive decision analysis for optimal targeted prediction. Section 3 develops the methods and algorithms for predictive evaluations and comparisons. A simulation study is in Section 4. The PA data are analyzed in Section 5. Section 6 concludes. Online supplementary material includes methodological generalizations and further examples, computational details, additional results for the simulated and PA data, proofs, and R code to reproduce the analyses.

2. Targeted point prediction

Consider the paired data $\{{\mathit{x}}_i,{\mathit{y}}_i{\}}_{i=1}^n$ with p-dimensional covariates x_i and m-dimensional response y_i. The response variables y_i may be univariate (m = 1), multivariate (m > 1), or functional data with y_i =(y_i(τ₁,),…,y_i(τ_m))′ observed on a domain $\mathcal{T}\subset {\mathbb{R}}^d$. Suppose we have a satisfactory Bayesian model $\mathcal{M}$ parametrized by θ with posterior $p_{{}_{\mathcal{M}}}(\theta \mid \mathit{y})$. The requisite notion of “satisfactory” is made clear below, but fundamentally $\mathcal{M}$ should encapsulate the modeler’s beliefs about the data-generating process and demonstrate empirically the ability to capture the essential features of the data. Although these criteria are standard for Bayesian modeling, they often demand highly complex and computationally intensive models. There is broad interest in extracting simple, accurate, and computationally efficient representations or summaries of $\mathcal{M}$, especially for prediction.

Our approach builds upon Bayesian decision analysis. First, we target the predictive functionals $h_1(\tilde{\mathit{y}}),\dots ,h_J(\tilde{\mathit{y}})$, where each h_j is a functional of interest and $\tilde{\mathit{y}}\sim p_{{}_{\mathcal{M}}}(\tilde{\mathit{y}}\mid \mathit{y})$ is the predictive distribution of unobserved data at covariate value $\tilde{\mathit{x}}$ and conditional on observed data. Each h_j reflects a prediction task: often the data (x, y) are an input to a system h_j, which inherits predictive uncertainty when y has not yet been observed. Alternatively, the functionals {h_j} can be selected to provide distinct summaries of the model $\mathcal{M}$. Next, we introduce a parametrized action $g(\tilde{\mathit{x}};\delta )$, which is a point prediction of $h(\tilde{\mathit{y}})$ at $\tilde{\mathit{x}}$ with unknown parameters δ. The role of g is to produce interpretable, fast, and accurate predictions targeted to h. Examples include linear, tree, and additive forms, but g is not required to match the structure of $\mathcal{M}$. The targeted predictions are not burdened by the complexity required to capture the global distributional features of $p_{{}_{\mathcal{M}}}(\theta \mid \mathit{y})\mathsf{or}{p}_{{}_{\mathcal{M}}}(\tilde{\mathit{y}}\mid \mathit{y})$—which may be mostly irrelevant for predicting any particular $h_j(\tilde{\mathit{y}})$—yet use the full posterior distribution under $\mathcal{M}$ to incorporate all available data. Lastly, we leverage the model $\mathcal{M}$ predictive distribution to quantify and compare the out-of-sample predictive accuracy of each parametrized action. Using this information, we assemble a collection of near-optimal, or acceptable targeted predictors, which offers unique insights into the predictability of $h_j(\tilde{\mathit{y}})$.

For any functional h_j = h, predictive accuracy is measured by a loss function ${\mathcal{L}}_0\{h(\tilde{\mathit{y}}),g(\tilde{\mathit{x}};\delta )\}$, which determines the loss from predicting $g(\tilde{\mathit{x}};\delta )$ when $h(\tilde{\mathit{y}})$ is realized. To incorporate multiple covariate values $\tilde{\mathcal{X}}≔\{{\tilde{\mathit{x}}}_i{\}}_{i=1}^{\tilde{n}}$, we introduce an aggregate loss function

$${\overline{\mathcal{L}}}_0\left[\{h({\tilde{\mathit{y}}}_i),g({\tilde{\mathit{x}}}_i;\delta ){\}}_{i=1}^{\tilde{n}}\right]≔{\tilde{n}}^{-1}\sum _{i=1}^{\tilde{n}}{\mathcal{L}}_0\{h({\tilde{\mathit{y}}}_i),g({\tilde{\mathit{x}}}_i;\delta )\},$$

where each ${\tilde{\mathit{y}}}_i$ is the predictive variable at ${\tilde{\mathit{x}}}_i$ under model $\mathcal{M}$. The choice of $\tilde{\mathcal{X}}$ can be distinct from the original covariates $\{{\mathit{x}}_i{\}}_{i=1}^n$, for example to customize predictions for specific designs or subpopulations of interest, yet still leverages the full posterior distribution under model $\mathcal{M}$. We augment the aggregate loss with a complexity penalty $\mathcal{P}$ on the unknown parameters δ:

$${\overline{\mathcal{L}}}_{\lambda }\left[\{h({\tilde{\mathit{y}}}_i),g({\tilde{\mathit{x}}}_i;\delta ){\}}_{i=1}^{\tilde{n}}\right]≔{\overline{\mathcal{L}}}_0\left[\{h({\tilde{\mathit{y}}}_i),g({\tilde{\mathit{x}}}_i;\delta ){\}}_{i=1}^{\tilde{n}}\right]+\lambda \mathcal{P}(\delta ),$$

where λ ≥ 0 indexes a path of parameterized actions and determines the tradeoff between predictive accuracy $({\overline{\mathcal{L}}}_0)$ and complexity $(\mathcal{P})$.

Since ${\overline{\mathcal{L}}}_{\lambda }$ depends on a random quantities $\{{\tilde{\mathit{y}}}_i{\}}_{i=1}^{\tilde{n}}$, Bayesian decision analysis proceeds by optimizing for δ over the joint posterior predictive distribution $p_{{}_{\mathcal{M}}}({\tilde{\mathit{y}}}_1,\dots ,{\tilde{\mathit{y}}}_{\tilde{n}}\mid \mathit{y})$:

$${\widehat{\delta }}_{\mathcal{A}}≔\text{arg}\underset{\delta }{\text{min}}{\mathbb{E}}_{[{\tilde{y}}_1,\dots ,{\tilde{y}}_{\tilde{n}}\mid y]}{\overline{\mathcal{L}}}_{\lambda }\left[\{h({\tilde{\mathit{y}}}_i),g({\tilde{\mathit{x}}}_i;\delta ){\}}_{i=1}^{\tilde{n}}\right].$$ (1)

This operation averages the predictive loss over the joint distribution of future or unobserved values $\{h({\tilde{\mathit{y}}}_i){\}}_{i=1}^n$ at $\tilde{\mathcal{X}}$ under model $\mathcal{M}$, and then selects parameters ${\widehat{\delta }}_{\mathcal{A}}$ that minimize this quantity. We define the parametrized action $\mathcal{A}≔(g,\mathcal{P},\lambda )$ as a triple consisting of the targeted predictor g, the complexity penalty $\mathcal{P}$, and the complexity parameter λ. Since we typically compare among parametrized actions for the same functional h, design points $\tilde{\mathcal{X}}$, and Bayesian model $\mathcal{M}$, we suppress notational dependence on these terms.

The challenge is to produce optimal point prediction parameters ${\widehat{\delta }}_{\mathcal{A}}$ for distinct parametrized actions $\mathcal{A}$, and subsequently to evaluate and compare the resulting point predictions. A schematic is presented in Figure 2: given data $\{{\mathit{x}}_i,{\mathit{y}}_i{\}}_{i=1}^n$, a Bayesian model $\mathcal{M}$ is constructed; for each functional h, one or more parametrized actions $\mathcal{A}$ are optimized for prediction; point predictions $g(\tilde{\mathit{x}};{\widehat{\delta }}_{\mathcal{A}})$ are computed for $h(\tilde{\mathit{y}})$ at $\tilde{\mathit{x}}$. The optimal parameters ${\widehat{\delta }}_{\mathcal{A}}$ offer a summary of the posterior (predictive) distribution of model $\mathcal{M}$—akin to posterior expectations, standard deviations, and credible intervals—but specifically targeted to h.

Fig. 2.

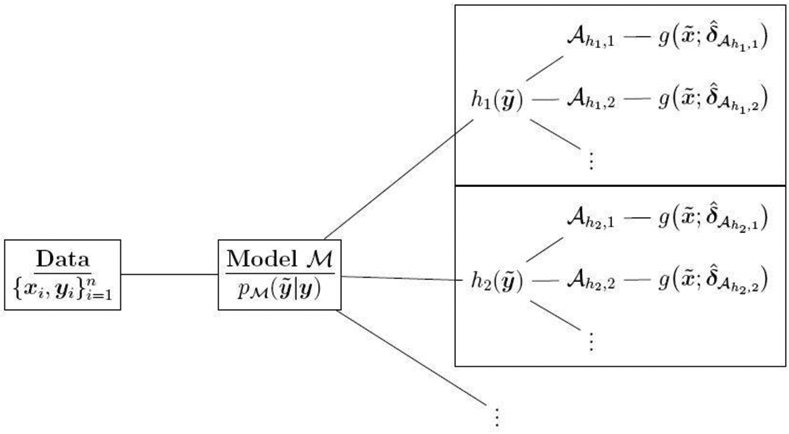
Given data $\{{\mathit{x}}_i,{\mathit{y}}_i{\}}_{i=1}^n$, a Bayesian model $\mathcal{M}$ is constructed. For each functional $h(\tilde{\mathit{y}})$ and using model $\mathcal{M}$, multiple parametrized actions $\mathcal{A}$ are optimized, evaluated, and compared. The optimal parameters ${\widehat{\delta }}_{\mathcal{A}}$ are used to compute point predictions $g(\tilde{\mathit{x}};{\widehat{\delta }}_{\mathcal{A}})$ of $h(\tilde{\mathit{y}})$ at $\tilde{\mathit{x}}$.

By design, the optimal parameters ${\widehat{\delta }}_{\mathcal{A}}$ depend on the loss function ${\mathcal{L}}_0$. Generality of ${\mathcal{L}}_0$ is desirable, but tractability is essential for practical use. A natural starting point is squared error loss ${\mathcal{L}}_0\{h(\tilde{\mathit{y}}),g(\tilde{\mathit{x}};\delta )\}=\Vert h(\tilde{\mathit{y}})-g(\tilde{\mathit{x}};\delta ){\Vert }_2^2$ with generalizations considered below. In this setting, we identify a representation of the requisite optimization problem (1) that admits fast and interpretable solutions for a broad class of parametrized actions:

Theorem 1. When ${\mathbb{E}}_{[{\tilde{\mathit{y}}}_i\mid \mathit{y}]}\Vert h({\tilde{\mathit{y}}}_i){\Vert }_2^2<\infty$ at each ${\tilde{\mathit{x}}}_i\in \mathcal{X},i=1,\dots ,\tilde{n}$, the optimal point prediction parameters in (1) under squared error loss are

$${\widehat{\delta }}_{\mathcal{A}}=\text{arg}\underset{\delta }{\text{min}}\left[{\tilde{n}}^{-1}\sum _{i=1}^{\tilde{n}}\Vert {\overline{h}}_i-g({\tilde{\mathit{x}}}_i;\delta ){\Vert }_2^2+\lambda \mathcal{P}(\delta )\right\}$$ (2)

where ${\overline{h}}_i≔{\mathbb{E}}_{[{\tilde{\mathit{y}}}_i\mid \mathit{y}]}h({\tilde{\mathit{y}}}_i)$ is the posterior predictive expectation of $h({\tilde{\mathit{y}}}_i)$ at ${\tilde{\mathit{x}}}_i$ under model $\mathcal{M}$.

Theorem 1 establishes an equivalence between the solution to the posterior predictive expected loss (1) and a penalized least squares criterion, with important computational implications. First, estimation of ${\overline{h}}_i$ is a standard Bayesian exercise, for example using posterior predictive samples: ${\overline{h}}_i\approx S^{-1}\sum _{s=1}^{S}h({\tilde{\mathit{y}}}_i^s)$ for ${\tilde{\mathit{y}}}_i^s\sim p_{{}_{\mathcal{M}}}({\tilde{\mathit{y}}}_i\mid \mathit{y})$ at ${\tilde{\mathit{x}}}_i$. Most commonly, posterior predictive samples are generated by iteratively drawing ${\theta }^s\sim p_{{}_{\mathcal{M}}}(\theta \mid \mathit{y})$ from the posterior and ${\tilde{\mathit{y}}}_i^s\sim p_{{}_{\mathcal{M}}}({\tilde{\mathit{y}}}_i\mid {\theta }^s)$ from the sampling distribution. Second, the penalized least squares representation in (2) implies that the optimal point prediction parameters ${\widehat{\delta }}_{\mathcal{A}}$ can be computed easily and efficiently for many choices of $\mathcal{A}$ using existing algorithms and software. Third, the optimal parametrized actions produce fast out-of-sample targeted predictions: the prediction of $h(\tilde{\mathit{y}})$ at any $\tilde{\mathit{x}}$ is $g(\tilde{\mathit{x}};{\widehat{\delta }}_{\mathcal{A}})$, which is quick to compute for many choices of g. Lastly, the optimal parameters from (2) can be computed simultaneously for many parametrized actions $\mathcal{A}$ and distinct functionals h—all based on a single Bayesian model $\mathcal{M}$.

Remark. Certain choices of h, such as binary functionals $h(\tilde{\mathit{y}})\in \{0,1\}$, are incompatible with squared error loss. In the supplementary material, we discuss generalizations to deviance-based loss functions. Importantly, the core attributes of the proposed approach are maintained: computational speed, ease of implementation, and interpretability.

We illustrate the utility of this framework with the following examples; an additional example with $h(\tilde{\mathit{y}})\in \{0,1\}$ is presented in the supplementary material.

Example 1 (Linear contrasts). Consider a (multivariate) regression model ${\mathbb{E}}_{[{\mathit{y}}_i\mid \theta ]}{\mathit{y}}_i=f_{\theta }({\mathit{x}}_i)$ for y_i = (y_i,1,…, y_i,m)′. The linear contrast $h(\tilde{\mathit{y}})=\mathit{C}\tilde{\mathit{y}}$ is often of interest: the matrix C can extract specific components of $\tilde{\mathit{y}}$, evaluate differences between components of $\tilde{\mathit{y}}$, and apply a linear weighting scheme to $\tilde{\mathit{y}}$. For functional data with y_i,j = y_i(τ_j), the linear contrast can target subdomains $\mathit{C}\tilde{\mathit{y}}=\{\tilde{y}(\tau ){\}}_{\tau \in \mathcal{S}}$ for $\mathcal{S}\subset \mathcal{T}$ and evaluate derivatives of $\tilde{y}(\tau )$. In this setting, the predictive target simplifies to the posterior expectation $\overline{h}={\mathbb{E}}_{[\theta \mid \mathit{y}]}\{\mathit{C}{f}_{\theta }(\tilde{\mathit{x}})\}=\mathit{C}{\mathbb{E}}_{[\theta \mid \mathit{y}]}{f}_{\theta }(\tilde{\mathit{x}})$. Given an estimate ${\widehat{f}}_{\theta }(\tilde{\mathit{x}})$ of the posterior expectation of the regression function at $\tilde{\mathit{x}}$, the response variable ${\overline{h}}_i\approx \mathit{C}{\widehat{f}}_{\theta }({\tilde{\mathit{x}}}_i)$ needed for (2) is easily computable for many choices of C. Notably, the predictive expected contrast $\mathit{C}{\widehat{f}}_{\theta }({\mathit{x}}_i)$ is distinct from the empirical contrast h(y_i) = Cy_i: the former can incorporate shrinkage, smoothness, and other regularization of the regression function f_θ under $\mathcal{M}$. From a single Bayesian model $\mathcal{M}$, multiple parametrized actions $\mathcal{A}$ can be optimized for each contrast C.

Example 2 (Functional data summaries). Suppose h is a scalar summary of a curve $\{y(\tau ){\}}_{\tau \in \mathcal{T}}$, such as the maximum $h(\tilde{\mathit{y}})={\max }_{\tau }\tilde{y}(\tau )$ or the point at which the maximum occurs $h(\tilde{\mathit{y}})=\text{arg}{\max }_{\tau }\tilde{y}(\tau )$, and let $\mathcal{M}$ be a Bayesian functional data model (Section 5 provides a detailed example). To select variables for optimal linear prediction of $h(\tilde{\mathit{y}})$, we apply Theorem 1 with $g(\tilde{\mathit{x}};\delta )={\tilde{\mathit{x}}}^{\prime }\delta$ and an ℓ₁-penalty, $\mathcal{P}(\delta )=\Vert \delta {\Vert }_1=\sum _{j=1}^p\mid {\delta }_j\mid$:

$${\widehat{\delta }}_{\mathcal{A}}=\text{arg}\underset{\delta }{\text{min}}\left\{{\tilde{n}}^{-1}\sum _{i=1}^{\tilde{n}}\Vert {\overline{h}}_i-{\tilde{\mathit{x}}}_i^{\prime }\delta {\Vert }_2^2+\lambda \Vert \delta {\Vert }_1\right\},$$ (3)

for example using the observed covariates $\tilde{\mathcal{X}}=\{{\mathit{x}}_i{\}}_{i=1}^n$. The optimal parameters ${\widehat{\delta }}_{\mathcal{A}}$ are readily computable using existing software, such as glmnet in R (Friedman et al., 2010).

In practice, we apply an adaptive variant of the ℓ₁-penalty. Motivated by the adaptive lasso (Zou, 2006), Kowal et al. (2020) introduce the penalty $\mathcal{P}(\delta ,\theta )=\sum _{j=1}^p{\omega }_j\mid {\delta }_j\mid$, where ω_j =∣ β_j ∣⁻¹ and β_j are the regression coefficients in a Gaussian linear model $\mathcal{M}$. For nonlinear or non-Gaussian models $\mathcal{M}$ and targeted predictions, we use the generalized weights $\omega =\mid {\tilde{\delta }}_0{\mid }^{-1}$, where ${\tilde{\delta }}_0$ is the ℓ₂-projection of the predictive variables $h({\tilde{\mathit{y}}}_i)$ onto the predictor g. Bayesian decision analysis requires integration over the unknown θ, so the requisite penalty in (2) becomes the posterior expectation $\overline{\mathcal{P}(\delta )}≔{\mathbb{E}}_{[\tilde{\mathit{y}}\mid \mathit{y}]}\mathcal{P}(\delta ,\theta )=\sum _{j=1}^p{\widehat{\omega }}_j\mid {\delta }_j\mid$ for $\widehat{\omega }={\mathbb{E}}_{[\tilde{\mathit{y}}\mid \mathit{y}]}(\mid {\tilde{\delta }}_0{\mid }^{-1})$, which is estimable using posterior predictive samples.

The parameterized and targeted decision analysis from (1) features connections with classical decision analysis. Targeted prediction arises in classical decision analysis through the Bayes estimator ${\overline{h}}_i={\mathbb{E}}_{[{\tilde{\mathit{y}}}_i\mid \mathit{y}]}h({\tilde{\mathit{y}}}_i)$, which is obtained from Theorem 1 as a special case:

Corollary 1. Let ${\mathcal{A}}_{{}_B}=(g(\tilde{\mathit{x}};\delta )=\delta (\tilde{\mathit{x}}),\lambda =0)$ denote an unrestricted and unpenalized action. The optimal point predictor parameters are $\widehat{\delta }({\tilde{\mathit{x}}}_i)={\overline{h}}_i$.

However, action parametrization and penalization are valuable tools: they lend interpretability to the targeted prediction, highlight the balance between accuracy and simplicity, and often produce faster—and more accurate—out-of-sample predictions via $g(\tilde{\mathit{x}};{\widehat{\delta }}_{\mathcal{A}})$.

In some cases, the optimal actions ${\widehat{\delta }}_{\mathcal{A}}$ can be linked to the underlying model parameters θ, such as when the parameterization $\mathcal{A}$ matches the form of $\mathcal{M}$ and both are linear:

Corollary 2. Let ${\mathcal{A}}_L=(g(\tilde{\mathit{x}};\delta )={\tilde{\mathit{x}}}^{\prime }\delta ,\lambda =0)$ denote a linear and unpenalized action. For a model $\mathcal{M}$ with ${\mathbb{E}}_{[{\tilde{\mathit{y}}}_i\mid \theta ]}h({\tilde{\mathit{y}}}_i)={\tilde{\mathit{x}}}_i^{\prime }\theta$ and using the observed design points $\tilde{\mathcal{X}}=\{{\mathit{x}}_i{\}}_{i=1}^n$, the optimal point predictor parameters are ${\widehat{\delta }}_{{\mathcal{A}}_L}={\mathbb{E}}_{\theta \mid \mathit{y}}\theta$.

Corollary 2 is most familiar when $\mathcal{M}$ is a linear model and h is the identity. By further allowing λ > 0 with a sparsity penalty $\mathcal{P}$, we recover the decoupling shrinkage and selection approach for Bayesian linear variable selection (Hahn and Carvalho, 2015). Similar links to Woody et al. (2020) can be established for nonlinear regression.

Despite the potential connections to θ in certain cases, the parametrized actions are not bound by the parametrization of model $\mathcal{M}$. The full benefits of Theorem 1 are realized by the simultaneous generality of the model $\mathcal{M}$, the functionals h, and the parametrized actions $\mathcal{A}$. Of course, we can shift the emphasis from prediction toward posterior summarization by replacing the predictive functional $h(\tilde{\mathit{y}})$ with a posterior functional h(θ), such as $h(\theta )=h\left({\mathbb{E}}_{[\tilde{\mathit{y}}\mid \theta ]}\tilde{\mathit{y}}\right)$. However, we prefer the predictive functionals: they correspond to concrete observables that are comparable across Bayesian models (Geisser, 1993).

3. Predictive inference for model determination

Decision analysis extracts an optimal ${\widehat{\delta }}_{\mathcal{A}}$ by minimizing a posterior (predictive) expected loss function. However, this optimality is obtained only for a given parametrized action $\mathcal{A}$. The key implication of Theorem 1 is that optimal point predictions can be computed easily and efficiently for many $\mathcal{A}$ (see Figure 2). To fully exploit these benefits, additional tools are needed to evaluate, compare, and select among the parametrized actions.

We proceed to evaluate predictive performance out-of-sample, which best encapsulates the task of predicting new data. The Bayesian model $\mathcal{M}$ provides predictive uncertainty quantification for all evaluations and comparisons. These out-of-sample predictive comparisons serve to identify not only the best targeted predictor, but also those targeted predictors that achieve an acceptable level of accuracy for out-of-sample prediction. The collection of acceptable targeted predictors illuminates the shared characteristics of near-optimal models, such as the important covariates, the forms of g and $\mathcal{P}$, and the level of complexity needed for accurate prediction of $h(\tilde{\mathit{y}})$. This approach only requires a Bayesian model $\mathcal{M}$, an evaluative loss function L, and the design points at which to evaluate the predictions under some g.

3.1. Predictive model evaluation

The path toward model comparisons and selection begins with evaluation of a single targeted predictor. We proceed nominally using $g(\tilde{\mathit{x}};{\widehat{\delta }}_{\mathcal{A}})$, but note that any point predictor of $h(\tilde{\mathit{y}})$ at $\tilde{\mathit{x}}$ can be used. Let $L(\mathit{z},\widehat{\mathit{z}})$ denote the loss associated with a prediction $\widehat{\mathit{z}}$ when z has occurred. We consider both empirical and predictive versions of the loss: the former uses empirical functionals z = h(y) and relies exclusively on the observed data, while the latter uses predictive functionals $\mathit{z}=h(\tilde{\mathit{y}})$ and inherits a predictive distribution under $\mathcal{M}$.

Out-of-sample evaluation necessitates a division of the data into training and validation sets: model-fitting and optimization are restricted to the training data, while predictive evaluations are conducted on the validation data. Dependence on any particular data split is reduced by repeating this procedure for K randomly-selected splits akin to K-fold cross-validation; we use K = 10. Let ${\mathcal{I}}_k\subset \{1,\dots ,n\}$ denote the kth validation set, where each data point appears in (at least) one validation set, ${\cup }_{k=1}^K{\mathcal{I}}_k=\{1,\dots ,n\}$. We prefer validation sets that are equally-sized, mutually exclusive, and selected randomly from (1,…, n}, although other designs are compatible. Importantly, we do not require re-fitting of the Bayesian model $\mathcal{M}$ on each training set, and instead use computationally efficient approximation techniques based on a single fit of $\mathcal{M}$ to the full data (see Section 3.3).

For each data split k, the out-of-sample empirical and predictive losses are

$${\mathbb{L}}_{\mathcal{A}}^{out}(k)≔\frac{1}{\mid {\mathcal{I}}_k\mid }\sum _{i\in {\mathcal{I}}_k}L\left\{h({\mathit{y}}_i),g({\mathit{x}}_i;{\widehat{\delta }}_{\mathcal{A}}^{-{\mathcal{I}}_k})\right\},{\mathbb{L}}_{\mathcal{A}}^{out}(k)≔\frac{1}{\mid {\mathcal{I}}_k\mid }\sum _{i\in {\mathcal{I}}_k}L\left\{h({\tilde{\mathit{y}}}_i^{-{\mathcal{I}}_k}),g({\mathit{x}}_i;{\widehat{\delta }}_{\mathcal{A}}^{-{\mathcal{I}}_k})\right\}$$ (4)

respectively, where ${\widehat{\delta }}_{\mathcal{A}}^{-{\mathcal{I}}_k}≔\text{arg}{\text{min}}_{\delta }{\mathbb{E}}_{[\tilde{\mathit{y}}\mid {\mathit{y}}^{-{\mathcal{I}}_k}]}{\overline{\mathcal{L}}}_{\lambda }\left[\{h({\tilde{\mathit{y}}}_i),g({\tilde{\mathit{x}}}_i;\delta ){\}}_{i\notin {\mathcal{I}}_k}\right]$ is optimized only using the training data ${\mathit{y}}^{-{\mathcal{I}}_k}≔\{{\mathit{y}}_i{\}}_{i\notin {\mathcal{I}}_k}$, and similarly ${\tilde{\mathit{y}}}_i^{-{\mathcal{I}}_k}\sim p_{{}_{\mathcal{M}}}({\tilde{\mathit{y}}}_i\mid {\mathit{y}}^{-{\mathcal{I}}_k})$ is the predictive variate at x_i conditional only on the training data. Although in-sample versions are available, there is an important distinction between the out-of-sample predictive distribution, $p_{{}_{\mathcal{M}}}({\tilde{\mathit{y}}}_i\mid {\mathit{y}}^{-{\mathcal{I}}_k})$, and the in-sample predictive distribution, $p_{{}_{\mathcal{M}}}({\tilde{\mathit{y}}}_i\mid \mathit{y})$. The in-sample version conditions on both the training data ${\mathit{y}}^{-{\mathcal{I}}_k}$ and the validation data ${\mathit{y}}^{{\mathcal{I}}_k}≔\{{\mathit{y}}_i{\}}_{i\in {\mathcal{I}}_k}$, which overstates the accuracy and understates the uncertainty for a validation point $i\in {\mathcal{I}}_k$. The out-of-sample version avoids these issues and more closely resembles most practical prediction problems.

Evaluation of $\mathcal{A}$ is based on the averages of (4) across all data splits,

$${\mathbb{L}}_{\mathcal{A}}^{out}≔K^{-1}\sum _{k=1}^K{\mathbb{L}}_{\mathcal{A}}^{out}(k),{\mathbb{L}}_{\mathcal{A}}^{out}≔K^{-1}\sum _{k=1}^K{\mathbb{L}}_{\mathcal{A}}^{out}(k).$$

The K-fold aggregation averages over two sources of variability in (4): variability in the training sets $\{{\mathit{x}}_i,{\mathit{y}}_i{\}}_{i\notin {\mathcal{I}}_k}$, each of which results in a distinct estimate of the coefficients ${\widehat{\delta }}_{\mathcal{A}}^{-{\mathcal{I}}_k}$, and variability in the validation sets $\{{\mathit{x}}_i,{\mathit{y}}_i{\}}_{i\in {\mathcal{I}}_k}$, which evaluates predictions only at the validation design points $\{{\mathit{x}}_i{\}}_{i\in {\mathcal{I}}_k}$. The contrast between ${\mathbb{L}}_{\mathcal{A}}^{out}$ and ${\mathbb{L}}_{\mathcal{A}}^{out}$ is important: ${\mathbb{L}}_{\mathcal{A}}^{out}$ is a point estimate of the risk under predictions from $\mathcal{A}$, while ${\mathbb{L}}_{\mathcal{A}}^{out}$ provides the distribution of out-of-sample loss under different realizations of the predictive variables $h({\tilde{\mathit{y}}}_i)$. Specifically, each h(y_i) for $i\in {\mathcal{I}}_k$ represents one possible realization of the out-of-sample target variable at x_i; the predictive variable $h({\tilde{\mathit{y}}}_i^{-{\mathcal{I}}_k})$ for ${\tilde{\mathit{y}}}_i^{-{\mathcal{I}}_k}\sim p_{{}_{\mathcal{M}}}({\tilde{\mathit{y}}}_i\mid {\mathit{y}}^{-{\mathcal{I}}_k})$ expresses the distribution of possible realizations according to $\mathcal{M}$. The predictive loss ${\mathbb{L}}_{\mathcal{A}}^{out}$ incorporates this distributional information for out-of-sample predictive uncertainty quantification.

3.2. Predictive model selection

The out-of-sample empirical and predictive losses, ${\mathbb{L}}_{\mathcal{A}}^{out}$ and ${\mathbb{L}}_{\mathcal{A}}^{{}^{out}}$, respectively, provide the ingredients needed to compare and select among targeted predictors. Predictive quantities have proven useful for Bayesian model selection; see Vehtari and Ojanen (2012) for a thorough review. Our goal is not only to identify the most accurate predictor, but also to gather those targeted predictors that achieve an acceptable level of accuracy. In doing so, we introduce a Bayesian representation of the Rashomon effect, which observes that for many practical applications, many approaches can achieve adequate predictive accuracy (Breiman, 2001).

The proposed notion of “acceptable” accuracy is defined relative to the most accurate targeted predictor, ${\mathcal{A}}_{min}≔\text{arg}{\text{min}}_{\mathcal{A}\in \mathbb{A}}{\mathbb{L}}_{\mathcal{A}}^{out}$, which minimizes out-of-sample empirical loss as in classical K-fold cross-validation. The set $\mathbb{A}$ may include different forms for g and $\mathcal{P}$ and usually will include a path of λ values for each (g, $\mathcal{P}$) pair. We prefer relative rather than absolute accuracy because it directly references an empirically attainable accuracy level.

For any two actions $\mathcal{A},{\mathcal{A}}^{\prime }\in \mathbb{A}$, let ${\mathbb{D}}_{\mathcal{A},{\mathcal{A}}^{\prime }}^{{}^{out}}≔100\times ({\mathbb{L}}_{\mathcal{A}}^{{}^{out}}-{\mathbb{L}}_{{\mathcal{A}}^{\prime }}^{{}^{out}})∕{\mathbb{L}}_{{\mathcal{A}}^{\prime }}^{{}^{out}}$ be the percent increase in out-of-sample predictive loss from ${\mathcal{A}}^{\prime }$ to $\mathcal{A}$. We seek all parametrized actions $\mathcal{A}$ that perform within a margin η ≥ 0% of the best model, ${\mathbb{D}}_{\mathcal{A},{\mathcal{A}}_{min}}^{{}^{out}}<\eta \%$, with probability at least ε ∈[0,1]. The margin η acknowledges that near-optimal performance—especially for simple models—is often sufficient, while the probability level Ɛ incorporates predictive uncertainty. In concert, η and Ɛ provide domain-specific and model-informed leniency for admission into a set of acceptable predictors. We formally define the set of acceptable predictors as follows:

Definition 1. The set of acceptable predictors is

$${\Lambda }_{\eta ,\epsilon }≔\left\{\mathcal{A}\in \mathbb{A}:{\mathbb{P}}_{\mathcal{M}}({\mathbb{D}}_{\mathcal{A},{\mathcal{A}}_{min}}^{out}<\eta )\ge \epsilon \right\},where{\mathbb{D}}_{\mathcal{A},{\mathcal{A}}_{min}}^{out}≔100\times ({\mathbb{L}}_{\mathcal{A}}^{out}-{\mathbb{L}}_{{\mathcal{A}}_{min}}^{out})∕{\mathbb{L}}_{{\mathcal{A}}_{min}}^{out}.$$

The probability ${\mathbb{P}}_{{}_{\mathcal{M}}}$ is estimated using out-of-sample predictive draws under model $\mathcal{M}$ (see Section 3.3). Each set Λ_η,ε is nonempty, since ${\mathcal{A}}_{min}\in {\Lambda }_{\eta ,\epsilon }$ for all η, ε, and nested: Λ_η,ε ⊆ Λ_η′,ε′, for any η′ ≥ η or ε′ ≤ ε, so increasing η or decreasing Ɛ can expand the set of acceptable predictors. The special case of sparse Bayesian linear regression was considered in Kowal et al. (2020). With similar intentions, Tulabandhula and Rudin (2013) and Semenova and Rudin (2019) define a Rashomon set of predictors for which the in-sample empirical loss is within a margin η of the best predictor. By comparison, Λ_η,ε uses out-of-sample criteria for evaluation and incorporates predictive uncertainty via the Bayesian model $\mathcal{M}$.

The set of acceptable predictors also can be constructed using prediction intervals:

Lemma 1. A predictor $\mathcal{A}$ is acceptable, $\mathcal{A}\in {\Lambda }_{\eta ,\epsilon }$, if and only if there exists a lower (1 − ε) posterior prediction interval for ${\mathbb{D}}_{\mathcal{A},{\mathcal{A}}_{min}}^{{}^{out}}$ that includes η.

Viewed another way, $\mathcal{A}$ is not acceptable if the lower 1 − ε predictive interval for ${\mathbb{D}}_{\mathcal{A},{\mathcal{A}}_{min}}^{{}^{out}}$ excludes η. From this perspective, unacceptable predictors are those $\mathcal{A}$ for which there is insufficient predictive probability (under $\mathcal{M}$) that the out-of-sample accuracy of $\mathcal{A}$ is within a certain margin of the best predictor. This definition is similar to the confidence sets of Lei (2019), which exclude any $\mathcal{A}$ for which the null hypothesis that $\mathcal{A}$ produces best predictive risk is rejected. Lei (2019) relies on a customized bootstrap procedure, which adds substantial computational burden to the model-fitting and cross-validation procedures. By comparison, acceptable predictor sets are derived entirely from the predictive distribution of $\mathcal{M}$ and accompanied by fast and accurate approximation algorithms (see Section 3.3).

Among acceptable predictors, we highlight the simplest one. For fixed (g, $\mathcal{P}$), the simplest predictor has the largest complexity penalty: ${\lambda }_{\eta ,\epsilon }≔\max \{\lambda :(g,\mathcal{P},\lambda )\in {\Lambda }_{\eta ,\epsilon }\}$. When $\mathcal{P}$ is a sparsity penalty such as (3), the simplest acceptable predictor contains the smallest set of covariates needed to (nearly) match the predictive accuracy of the best predictor—which may itself be ${\mathcal{A}}_{min}$. Selection based on λ_η,ε resembles the one-standard-error rule (e.g., Hastie et al., 2009), which selects the simplest predictor for which the out-of-sample empirical loss is within one standard error of the best predictor. Instead, λ_η,ε uses the out-of-sample predictive loss with posterior uncertainty quantification inherited from $\mathcal{M}$.

3.3. Fast approximations for out-of-sample predictive evaluation

The primary hurdle for out-of-sample predictive evaluations is computational: they require computing ${\widehat{\delta }}_{\mathcal{A}}^{-{\mathcal{I}}_k}$ and sampling ${\tilde{\mathit{y}}}_i^{-{\mathcal{I}}_k}\sim p_{{}_{\mathcal{M}}}({\tilde{\mathit{y}}}_i\mid {\mathit{y}}^{-{\mathcal{I}}_k})$ for each data split k = 1,…, K. Re-fitting $\mathcal{M}$ on each training set $\{{\mathit{x}}_i,{\mathit{y}}_i{\}}_{i\notin {\mathcal{I}}_k}$ is impractical and in many cases computationally infeasible. To address these challenges, we develop efficient approximations that require only a single fit of the Bayesian model $\mathcal{M}$ to the data—which is already necessary for standard posterior inference. Specifically, we use a sampling-importance resampling (SIR) algorithm with the full posterior predictive distribution as a proposal for the relevant out-of-sample predictive distributions. The subsequent results focus on squared error loss, but adaptations to other loss functions are straightforward.

To obtain ${\widehat{\delta }}_{\mathcal{A}}^{-{\mathcal{I}}_k}$, we equivalently represent the optimal action as in Theorem 1:

$${\widehat{\delta }}_{\mathcal{A}}^{-{\mathcal{I}}_k}=\text{arg}\underset{\delta }{\text{min}}\left\{(n-\mid {\mathcal{I}}_k\mid {)}^{-1}\sum _{j\notin {\mathcal{I}}_k}\Vert {\overline{h}}_j^{-{\mathcal{I}}_k}-g({\mathit{x}}_j;\delta ){\Vert }_2^2+\lambda \mathcal{P}(\delta )\right\}$$ (5)

where ${\overline{h}}_j^{-{\mathcal{I}}_k}={\mathbb{E}}_{[{\tilde{\mathit{y}}}_j\mid {\mathit{y}}^{-{\mathcal{I}}_k}]}h({\tilde{\mathit{y}}}_j)$ is the out-of-sample point prediction at x_j. As such, (5) is easily solvable for many choices of $\mathcal{A}$ : all that is required is an estimate of ${\overline{h}}_j^{-{\mathcal{I}}_k}$ for each $j\notin {\mathcal{I}}_k$ in the training set. We estimate this quantity using importance sampling. Proposals $\{{\tilde{\mathit{y}}}_j^s{\}}_{s=1}^S\sim p_{{}_{\mathcal{M}}}({\tilde{\mathit{y}}}_j\mid \mathit{y})$ are generated from the full predictive distribution by sampling $\{{\theta }^s{\}}_{s=1}^S\sim p_{{}_{\mathcal{M}}}(\theta \mid \mathit{y})$ from the full posterior and $\{{\tilde{\mathit{y}}}_j^s{\}}_{s=1}^S\sim p_{{}_{\mathcal{M}}}({\tilde{\mathit{y}}}_j\mid {\theta }^s)$ from the likelihood. The full data posterior $p_{{}_{\mathcal{M}}}(\theta \mid \mathit{y})$ serves as a proposal for the training data posterior $p_{{}_{\mathcal{M}}}(\theta \mid {\mathit{y}}^{-{\mathcal{I}}_k})$ with importance weights $w_k^s\propto 1∕p({\mathit{y}}^{{\mathcal{I}}_k}\mid {\theta }^s)$, with further factorization under conditional independence. The target can be estimated using ${\overline{h}}_j^{-{\mathcal{I}}_k}\approx \sum _{s=1}^S{w}_k^{s}h({\tilde{\mathit{y}}}_j^s)$ or based on SIR sampling. In some cases, it is beneficial to regularize the importance weights (Ionides, 2008; Vehtari et al., 2015), but our empirical results remain unchanged with or without regularization. Successful variants of this approach exist for Bayesian model selection (Gelfand et al., 1992) and evaluating prediction distributions (Vehtari and Ojanen, 2012).

SIR provides a mechanism for sampling ${\tilde{\mathit{y}}}_i^{-{\mathcal{I}}_k}\sim p_{\mathcal{M}}({\tilde{\mathit{y}}}_i\mid {\mathit{y}}^{-{\mathcal{I}}_k})$ using the importance weights $\{w_k^s{\}}_{s=1}^S$, which in turn provides out-of-sample predictive draws of ${\mathbb{L}}_{\mathcal{A}}^{{}^{out}}$ and ${\mathbb{D}}_{\mathcal{A},{\mathcal{A}}^{\prime }}^{{}^{out}}$, for any actions $\mathcal{A},{\mathcal{A}}^{\prime }\in \mathbb{A}$. The idea is to obtain the proposal samples $\{{\tilde{\mathit{y}}}_j^s{\}}_{s=1}^S\sim p_{{}_{\mathcal{M}}}({\tilde{\mathit{y}}}_j\mid \mathit{y})$ from the full posterior distribution and then subsample from $\{{\tilde{\mathit{y}}}_j^s{\}}_{s=1}^S$ without replacement based on the corresponding importance weights $\{w_k^s{\}}_{s=1}^S$. The full SIR algorithm details are provided in the supplementary material.

4. Simulation study

We evaluate the selection capabilities and predictive accuracy of the proposed techniques using synthetic data. For targeted prediction, these evaluations must be directed toward a particular functional of the response variable. Specifically, we generate functional data $\{Y_{{}_i}^{{}^{\ast }}(\tau ):\tau \in [0,1]\}$ such that the argmax of each function, ${\tau }_{{}_i}^{{}^{\ast }}≔\text{arg}{\max }_{\tau }{Y}_{{}_i}^{{}^{\ast }}(\tau )=h(Y_{{}_i}^{{}^{\ast }})$, is linearly associated with a subset of covariates, ${\tau }_{{}_i}^{{}^{\ast }}={\mathit{x}}_i^{\prime }{\beta }^{{}^{\ast }}$. The covariates are correlated and mixed continuous and discrete: we draw x_i,j from marginal standard normal distributions with Cor(x_i,j,x_i,j′) = (0.75)^{∣j−j′∣} and binarize half of these p variables, $x_{i,j}\leftarrow \mathbb{I}\{x_{i,j}\ge 0\}$. The continuous covariates are centered and scaled to sample standard deviation 0.5. For the true coefficients $\{{\beta }_j^{\ast }{\}}_{j=1}^p$, we randomly select 5% for ${\beta }_{{}_j}^{{}^{\ast }}=1$, 5% for ${\beta }_{{}_j}^{{}^{\ast }}=-1$, and leave the remaining values at zero with the exception of the intercept, ${\beta }_{{}_0}^{{}^{\ast }}=1$. The coefficients $\{{\beta }_j^{\ast }{\}}_{j=0}^p$ are rescaled such that ${\tau }_{{}_i}^{{}^{\ast }}={\mathit{x}}_i^{\prime }{\beta }^{{}^{\ast }}\in [0.2,0.8]$ to ensure that the argmax occurs away from the boundary; see the supplementary material. The true functions are computed as $Y_{{}_i}^{{}^{\ast }}(\tau )=a_{0,i}+a_{1,i}\tau -(a_{1,i}+a_{2,i})(\tau -{\tau }_{{}_i}^{{}^{\ast }}{)}_{+}$, where $a_{0,i}\stackrel{iid}{\sim }N(0,1),a_{1,i},a_{2,i}\stackrel{iid}{\sim }{\chi }_5^2$, and $(x{)}_{+}≔x\mathbb{I}\{x\ge 0\}$. By construction, $Y_{{}_i}^{{}^{\ast }}$ is piecewise linear and concave with a single breakpoint, ${\tau }_{{}_i}^{{}^{\ast }}=\text{arg}{\max }_{\tau }{Y}_{{}_i}^{{}^{\ast }}(\tau )$, and therefore $h(Y_{{}_i}^{{}^{\ast }})={\mathit{x}}_i^{\prime }{\beta }^{{}^{\ast }}$. Finally, the observed data y_i are generated by adding Gaussian noise to $Y_{{}_i}^{{}^{\ast }}(\tau )$ at m equally-spaced points with a root signal-to-noise ratio of 5. Example figures are provided in the supplementary material.

The synthetic data-generating process is repeated 100 times for p = 50 covariates, m = 200 observation points, and varying sample sizes n ∈{75, 100, 500}. For each simulated dataset $\{{\mathit{x}}_i,{\mathit{y}}_i{\}}_{i=1}^n$, we compute the posterior and predictive distributions under the Bayesian function-on-scalars regression model of Kowal and Bourgeois (2020), which models a linear association between the functional data response and the scalar covariates. We emphasize that this model $\mathcal{M}$ does not reflect the true data-generating process, yet our targeted predictions are derived from the predictive distribution under $\mathcal{M}$. We consider linear actions $g(\tilde{\mathit{x}};\delta )={\tilde{\mathit{x}}}^{\prime }\delta$ with the adaptive ℓ₁-penalty from Example 2 and computed using glmnet in R (Friedman et al., 2010). In this case, the set of parametrized actions $\mathbb{A}$ is determined by the path of λ values, which control the sparsity of the linear action δ. For benchmark comparisons, we use the adaptive lasso (Zou, 2006) and projection predictive feature selection (Piironen et al., 2020) on the empirical functionals $\{{\mathit{x}}_i,h({\mathit{y}}_i){\}}_{i=1}^n$. Model sizes were selected using 10-fold cross-validation. Implementation of Piironen et al. (2020) uses the projpred package in R; for the requisite Bayesian linear model, we assume double exponential priors for the linear coefficients, but results are unchanged for Gaussian and t-priors.

To validate the proposed definition of acceptable predictor sets, we investigate a simple yet important question: does the true model belong to Λ_η,ε ? Specifically, we determine whether the true set of active variables $\{j:{\beta }_{{}_j}^{{}^{\ast }}\ne 0\}$ matches the set of active variables for any acceptable predictor $\mathcal{A}\in {\Lambda }_{\eta ,\epsilon }$. This task is challenging: we do not assume knowledge of the active variables, so the true model only belongs to Λ_η,ε when it is both correctly identified along the λ path and correctly evaluated by ${\mathbb{D}}_{\mathcal{A},{\mathcal{A}}^{\prime }}^{{}^{out}}$. Correct identification is only satisfied when all and only the true active variables $\{j:{\beta }_{{}_j}^{{}^{\ast }}\ne 0\}$ are nonzero according to $\mathcal{A}$.

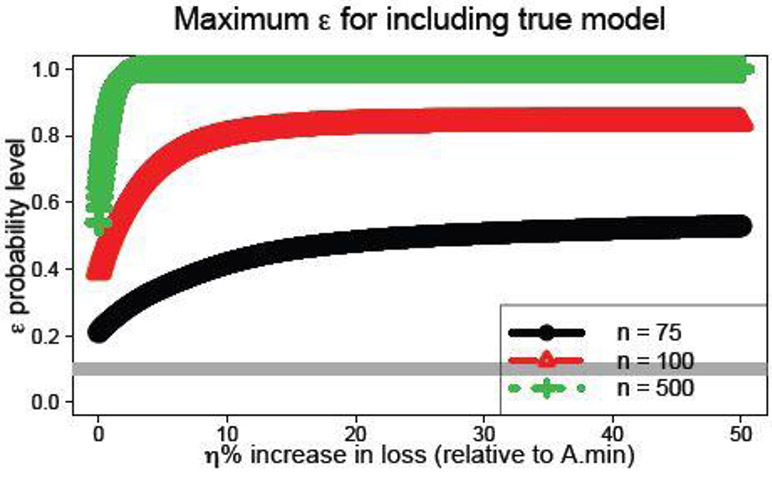
For this task, we compute ${\epsilon }_{max}(\eta )≔{\mathbb{P}}_{{}_{\mathcal{M}}}\left({\mathbb{D}}_{{\mathcal{A}}^{\ast },{\mathcal{A}}_{min}}^{{}^{out}}<\eta \right)$, which is the maximum probability level for which the true model ${\mathcal{A}}^{{}^{\ast }}$ is acceptable. The margin η corresponds to the percent increase in loss relative to ${\mathcal{A}}_{min}$. By design, ${\mathcal{A}}^{{}^{\ast }}\in {\Lambda }_{\eta ,{\epsilon }^{\prime }}$, remains acceptable for any smaller probability level ε′ ≤ ε_max(η). Most important, we set ε_max(η) = 0 if ${\mathcal{A}}^{{}^{\ast }}$ is not on the λ path. For each simulated dataset, we compute ε_max(η) for a grid of η% values. The results averaged across 100 simulations are in Figure 3. Naturally, ε_max(η) uniformly increases with the sample size for each value of η. When η = 0, the average maximum probability levels are ε_max(0) ∈{0.21, 0.39, 0.54} for n ∈{75, 100, 500}, respectively, which suggests that a cutoff of ε = 0.1 is capable of capturing the true model even when zero margin is allowed. Notably, ε_max(η) does not converge to one as η increases for the smaller sample sizes n ∈{75, 100}. The reason is simple: if ${\mathcal{A}}^{{}^{\ast }}$ is not discovered along the λ path, then ε_max(η) = 0 by definition—regardless of the choice of η. This result demonstrates the importance of the set of predictors under consideration $\mathbb{A}$, which here is determined entirely by the selected variables in the glmnet solution path.

Fig. 3.

The maximum probability level ε_max(η) for which the true model is acceptable, ${\mathcal{A}}^{{}^{\ast }}\in {\Lambda }_{\eta ,\epsilon }$, across values of η. For any smaller probability level ${\epsilon }^{\prime }\le {\epsilon }_{max}({\mathcal{A}}^{{}^{\ast }})$, the true model remains acceptable: ${\mathcal{A}}^{{}^{\ast }}\in {\Lambda }_{\eta ,{\epsilon }^{\prime }}$. The horizontal gray line is ε = 0.1.

Next, we evaluate point predictions of $h(Y_{{}_i}^{{}^{\ast }})$ and estimates of β* using root mean squared errors (RMSEs). The parametrized actions ${\widehat{\delta }}_{\lambda }$ and point predictions $g(\tilde{\mathit{x}};{\widehat{\delta }}_{\lambda })={\tilde{\mathit{x}}}^{\prime }{\widehat{\delta }}_{\lambda }$ are computed for multiple choices of λ: the simplest acceptable predictor λ = λ_η,ε with η = 0 and ε = 0.1 (proposed(out)); the analogous choice of λ based on in-sample evaluations (proposed(in)); and the unpenalized linear action with λ = 0 (proposed(full)). For comparisons, we include the aforementioned adaptive lasso and projpred, the point predictions ${\overline{h}}_i$ under model $\mathcal{M}$ (h_bar; see Corollary 1), and the empirical functionals h(y_i) (h(y)). The results are in Figure 4. In summary, clear improvements in targeted prediction are obtained by (i) fitting to $h({\tilde{\mathit{y}}}_i)(\mathsf{via}{\overline{h}}_i)$ rather than h(y_i), (ii) including covariate information, (iii) incorporating penalization or variable selection, and (iv) selecting the complexity λ based on out-of-sample criteria. The targeted actions $\mathcal{A}$ vastly outperform the model $\mathcal{M}$ predictions—even though each $\mathcal{A}$ is based entirely on the predictive distribution from $\mathcal{M}$. Lastly, the accurate estimation of the linear coefficients is important: the estimates ${\widehat{\delta }}_{\lambda }$ describe the partial linear effects of each x_j on targeted prediction of $h(\tilde{\mathit{y}})$.

Fig. 4.

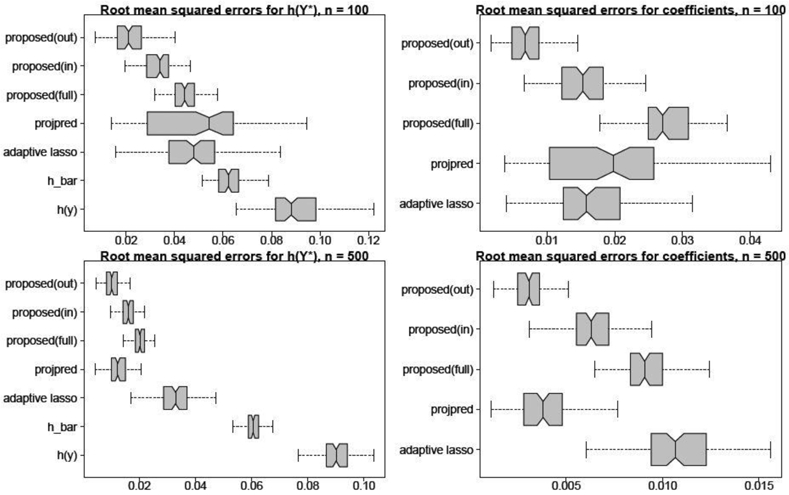
RMSEs for the true functionals h(Y*) (left) and the true regression coefficients β* (right) for n = 100 (top) and n = 500 (bottom) across 100 simulated datasets. Non-overlapping notches indicate significant differences between medians. The parametrized actions with out-of-sample selection are most accurate for prediction and estimation.

The supplementary material includes additional comparisons. Marginal variable selection is evaluated based on true positive and negative rates, with proposed(out) offering the best performance among these methods. Results for high dimensional data with p > n(n = 200, p = 500 and n = 100, p = 200) confirm the prediction and estimation advantages of the proposed approach. Sensitivity to ε ∈{0.05, 0.10, 0.20, 0.50} is also studied for prediction, estimation, and selection. Lastly, we evaluate the robustness in predictive accuracy among these methods. Specifically, we consider the setting in which the distribution of the covariates differs significantly between the training and validation datasets. The parametrized actions offer superior targeted predictions, especially for small to moderate sample sizes.

5. Physical activity data analysis

We apply targeted prediction to study physical activity (PA) data from the National Health and Nutrition Examination Survey (NHANES). NHANES is a large survey conducted by the Centers for Disease Control to study the health and wellness of the U.S. population. We analyze data from the 2005-2006 cohort, which features minute-by-minute PA data measured by hip-worn accelerometers (see Figure 1). To date, the 2005-2006 cohort is the most recent publicly available NHANES PA data. These data are high-resolution and empirical measurements of PA, and offer an opportunity to study intraday activity profiles.

PA has been linked to all-cause mortality not only in total daily activity (Schmid et al., 2015) but also via other functionals that describe activity behaviors (Fishman et al., 2016; Smirnova et al., 2019). Our goal is to construct targeted predictions that more accurately predict and explain the defining characteristics of PA. Specifically, we consider the following functionals $h(\tilde{\mathit{y}})$ for intraday PA $\tilde{\mathit{y}}=(\tilde{y}({\tau }_1),\dots ,\tilde{y}({\tau }_m){)}^{\prime }$ at times-of-day τ₁,…, τ_m:

$$\begin{array}{c}\hfill \text{avg}\hfill \\ \hfill \int \tilde{y}(\tau )d\tau \hfill \end{array}\begin{array}{c}\hfill \mathrm{t}\mathrm{l}\mathrm{a}\mathrm{c}\hfill \\ \hfill \int \log \{\tilde{y}(\tau )+1\}d\tau \hfill \end{array}\begin{array}{c}\hfill \text{sd}\hfill \\ \hfill \Vert \tilde{y}-\int \tilde{y}(\tau )d\tau {\Vert }_{L^2}\hfill \end{array}\begin{array}{c}\hfill \text{sedentary}\hfill \\ \hfill \int \mathbb{I}\{\tilde{y}(\tau )\le 100\}d\tau \hfill \end{array}\begin{array}{c}\hfill \max \hfill \\ \hfill {\max }_{\tau }\tilde{y}(\tau )\hfill \end{array}\begin{array}{c}\hfill \text{argmax}\hfill \\ \hfill \text{arg}{\max }_{\tau }\tilde{y}(\tau )\hfill \end{array}$$

where avg captures average daily activity, tlac is the total log activity count and measures moderate activity (Wolff-Hughes et al., 2018), sd targets the intraday variability in PA, sedentary computes the amount of time below a low activity threshold, max is the peak activity level, and argmax is the time of peak activity. In addition, we include a binary indicator of absolute inactivity during sleeping hours: $\text{zeros(1am}-\text{5am)}≔\mathbb{I}\{\tilde{y}(\tau )=0$ for all τ ∈[1am,5am]}. Individuals with zeros(1am-5am) = 1 likely removed the accelerometer during sleep in accordance with the NHANES instructions. Since we omit subjects with insufficient accelerometer wear time (< 10 hours), individuals with zeros(1am-5am) = 1 are active at other times of the day.

The PA data are accompanied by demographic variables (age, gender, body mass index (BMI), race, and education level), behavioral attributes (smoking status and alcohol consumption), self-reported comorbidity factors (diabetes, coronary heart disease (CHD), congestive heart failure, cancer, and stroke), and lab measurements (total cholesterol, HDL cholesterol, systolic blood pressure). Data pre-processing generally follows Leroux et al. (2019) using the R package rnhanesdata. We consider individuals aged 50-85 without mobility problems and without missing covariates. The continuous covariates are centered and scaled to sample standard deviation 0.5.

In accordance with the schematic in Figure 2, targeted predictive decision analysis begins with a Bayesian model $\mathcal{M}$. Since the PA data are intraday activity counts, we use a count-valued functional regression model based on the simultaneous transformation and rounding (STAR) framework of Kowal and Canale (2020). STAR formalizes the popular approach of transforming count data prior to applying Gaussian models, but includes a latent rounding layer to produce a valid count-valued data-generating process. STAR models can capture zero-inflation, over- and under-dispersion, and boundedness or censoring, and provide a path for adapting continuous data models and algorithms to the count data setting.

For each individual, we aggregate PA across all available days (at least three and at most seven days per subject) in five-minute bins. Let y_i,j and $y_{i,j}^{tot}$ and denote the average and total PA, respectively, for subject i at time τ_j, where i = 1,…, n = 1012 and j = 1,…, m = 288. Total PA is count-valued and will serve as the input for the STAR model, while all subsequent functionals and predictive distributions use average PA. Model $\mathcal{M}$ is the following:

$$y_{i,j}^{tot}=\text{round}(y_{i,j}^{\ast }),z_{i,j}^{\ast }=\text{transform}(y_{i,j}^{\ast })$$ (6)

$$z_{i,j}^{\ast }={\mathit{b}}^{\prime }({\tau }_j){\theta }_i+{\sigma }_{ϵ}{ϵ}_i,{ϵ}_i\stackrel{iid}{\sim }{t}_v(0,1)$$ (7)

$${\theta }_{i,\ell }={\mathit{x}}_i^{\prime }{\alpha }_{\ell }+{\sigma }_{{\gamma }_i}{\gamma }_{i,\ell },{\gamma }_{i,\ell }\stackrel{iid}{\sim }N(0,1)$$ (8)

with ${\alpha }_{\ell ,j}\stackrel{indep}{\sim }N(0,{\sigma }_{{\alpha }_j}^2)$ and ${\sigma }_{ϵ}^{-2},{\sigma }_{{\gamma }_i}^{-2},{\sigma }_{{\alpha }_j}^{-2}\stackrel{iid}{\sim }\text{Gamma}(0.01,0.01)$. In (6), round maps the latent continuous data $y_{i,j}^{{}^{\ast }}$ to {0,1,…, ∞}, while transform maps $y_{i,j}^{{}^{\ast }}$ to $\mathbb{R}$ for continuous data modeling. We use round(t) = ⌊t⌋ for t > 0 and round(t) = 0 for t ≤ 0, so $y_{{}_{i,j}}^{{}^{tot}}=0$ whenever $y_{{}_{i,j}}^{{}^{\ast }}<0$, and set $\text{transform}(t)=2(\sqrt{t}-1)$ in the Box-Cox family. In the functional regression levels (7)-(8), b is a vector of spline basis functions with basis coefficients θ_i for subject i and a_ℓ is the vector of regression coefficients for each basis coefficient ℓ. The spline basis is reparametrized to orthogonalize b and diagonalize the prior variance of the basis coefficients, which justifies the assumption of independence across basis coefficients in (8). Heavy-tailed innovations (v = 3) are introduced to model large spikes in PA.

Posterior inference is conducted based on 5000 samples from a Gibbs sampler after discarding a burn-in of 5000 iterations; the algorithm is detailed in the supplementary material. Posterior predictive diagnostics (see the supplementary material) demonstrate adequacy of $\mathcal{M}$ for the functionals of interest. These results are insensitive to v, but alternative choices of transform (e.g., logt) or b (e.g., wavelets) produce inferior results.

Targeted predictions for each functional were constructed using a linear action $g(\tilde{\mathit{x}};\delta )={\tilde{\mathit{x}}}^{\prime }\delta$ with an adaptive ℓ₁-penalty (see Example 2). Trees were also considered but were not competitive. The set of parametrized actions $\mathbb{A}$ is given by the path of λ values computed using glmnet in R (Friedman et al., 2010): we highlight the simplest acceptable action λ = λ_0,0.1 (proposed(out)) and the unpenalized linear action λ = 0 (proposed(full)). For comparison, we fit an adaptive lasso to $\{{\mathit{x}}_i,h({\mathit{y}}_i){\}}_{i=1}^n$ for each h. Squared error loss is used for all but zeros(1am-5am) which uses cross-entropy. In the supplementary material, we consider quadratic effects for age and BMI and pairwise interactions for each of age and BMI with race, gender, the behavioral attributes, and the self-reported comorbidity factors.

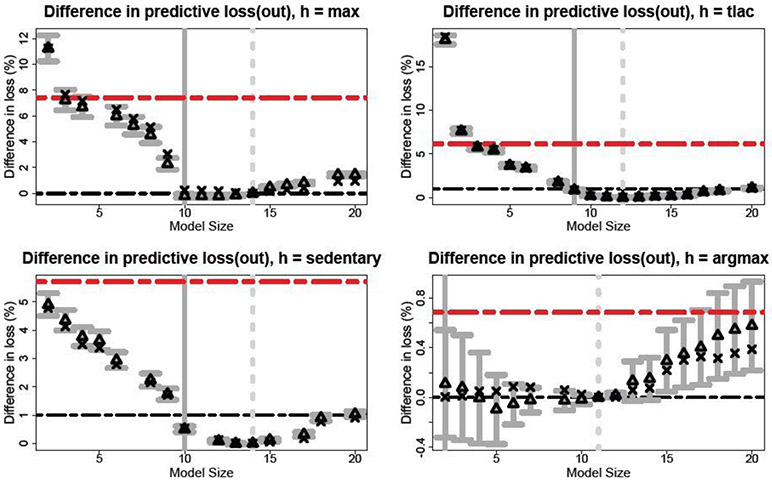
The targeted predictions are evaluated out-of-sample using the approximations from Section 3.3. For each functional h and complexity λ—which indexes the number of nonzero elements in ${\widehat{\delta }}_{\mathcal{A}}$ —Figure 5 presents the percent increase in predictive and empirical loss relative to the best predictor ${\mathcal{A}}_{min}$. The measures of vigorous PA (avg, sd, and max) produce nearly identical results, so we only include max here; avg and sd are in the supplement. The predictive expectations align closely with the empirical values, which suggests that model $\mathcal{M}$ is adequate for these predictive metrics.

Fig. 5.

Approximate out-of-sample squared error loss for sparse linear actions targeted to each functional. Results are presented for each size as a percent increase in loss relative to ${\mathcal{A}}_{min}$. The predictive expectations (triangles) and 80% intervals (gray bars) are included with the empirical relative loss for each model size (x-marks) and the adaptive lasso (red lines). The horizontal black lines denote the choices of η and the vertical lines denote λ_η,0.1 (solid) and ${\mathcal{A}}_{min}$ (dashed).

For each functional, we obtain optimal or near-optimal predictions with only about 10 covariates with better accuracy than the adaptive lasso. Many of the selected covariates are shared among functionals: age, BMI, gender, race, HDL cholesterol, and CHD are selected for all but argmax, while smoking status (avg, sd, max), diabetes (avg, sd, sedentary, max), and total cholesterol (tlac, sedentary) appear as well. The functionals measuring vigorous PA agree on the selected variables, including negative effects for diabetes and smoking. Most distinct is argmax: while ${\mathcal{A}}_{min}$ includes 11 covariates, the predictive uncertainty quantification from ${\mathbb{D}}_{\mathcal{A},{\mathcal{A}}_{min}}^{{}^{out}}$ indicates that linear predictors with as few as one covariate (race) are acceptable. These covariates are simply not linearly predictive of argmax: the difference between ${\mathcal{A}}_{min}$ and any other $\mathcal{A}\in \mathbb{A}$ is less than 1%. Details on the selected covariates and the direction of the estimated effects are provided in the supplement.

Robustness to the choice of η is also illustrated in Figure 5. We select η = 0% for max and argmax and η = 1% for tlac and sedentary, which highlights the purpose of η: by allowing η > 0, we can obtain targeted predictors with fewer covariates. By comparison, increasing the margin to η = 1% for max and argmax does not change the smallest acceptable predictor.

To validate the approximations in Figure 5, we augment the analysis with a truly out-of-sample prediction evaluation. For each of 20 training/validation splits, model $\mathcal{M}$ and the adaptive lasso are fit to the training data and sparse linear actions are targeted to each h. We emphasize that this exercise is computationally intensive: the MCMC for model $\mathcal{M}$ requires about 30 minutes per 10000 iterations (using R on a MacBook Pro, 2.8 GHz Intel Core i7), so repeating the model-fitting process 20 times is extremely slow. Comparatively, the approximations used for Figure 5 compute in under two seconds.

Point predictions were generated for the validation data using $\overline{h}$ under $\mathcal{M}$ (h_bar), the adaptive lasso, and sparse linear actions with λ = λ_0,0.1 (proposed(out)), λ = 0 (proposed(full)), and ${\mathcal{A}}_{min}$. Since ${\mathcal{A}}_{min}$ is also the unique acceptable predictor when ε = 1, η = 0, it provides information about robustness to Ɛ and η. The point predictions under $\mathcal{M}$ are highly inaccurate—and so excluded from Figure 6—and slow to compute: we draw $\tilde{\mathit{y}}\sim p_{{}_{\mathcal{M}}}(\tilde{\mathit{y}}\mid \mathit{y})$ at each validation point $\tilde{\mathit{x}}$ and then average $h(\tilde{\mathit{y}})$ over these draws. The targeted actions simply evaluate $g(\tilde{\mathit{x}};{\widehat{\delta }}_{\mathcal{A}})={\tilde{\mathit{x}}}^{\prime }{\widehat{\delta }}_{\mathcal{A}}$, which is faster, simpler, less susceptible to Monte Carlo error, and empirically more accurate. Predictions were evaluated on the empirical functionals h(y_i) in the validation data using mean squared prediction error.

Fig. 6.

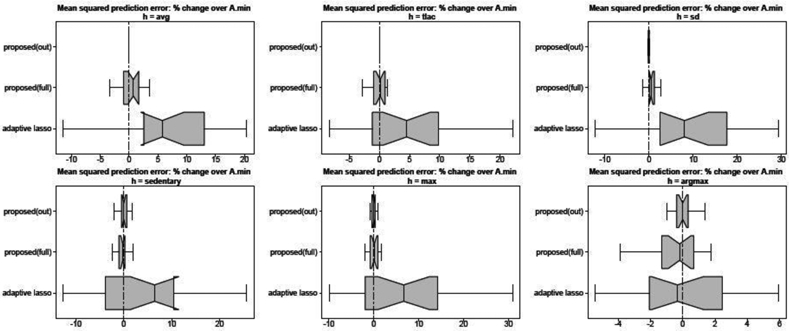
Mean squared prediction error for each functional across 20 training/validation splits. Results are presented as a percent increase relative to ${\mathcal{A}}_{min}$; values below zero (vertical line) indicate improvement over ${\mathcal{A}}_{min}$. Non-overlapping notches indicate significant differences between medians. Point predictions from $\mathcal{M}$ (h_bar) are noncompetitive and omitted. Both proposed(out) proposed(full) improve upon adaptive lasso and h_bar, while proposed(out) is most accurate and performs almost identical to ${\mathcal{A}}_{min}$ despite using fewer covariates.

The results from the out-of-sample prediction exercise are in Figure 6. The smallest acceptable predictor proposed(out) performs almost identical to the best predictor ${\mathcal{A}}_{min}$ despite using fewer covariates—which is precisely the goal of the acceptable predictor sets and the out-of-sample approximations in Figure 5. Both proposed(out) and proposed(full) outperform the adaptive lasso, in some cases by a large margin. The strength of this result is remarkable: the predictions are evaluated on the empirical functionals h(y_i), which are used for training the adaptive lasso but not for the proposed methods. Instead, the parametrized actions are trained using ${\overline{h}}_i$—which is itself a poor out-of-sample predictor. However, the targeted actions only rely on the in-sample adequacy of ${\overline{h}}_i$ and, unlike models trained to the empirical functionals, leverage both the model-based regularization and the uncertainty quantification provided by $\mathcal{M}$. In summary, the targeted predictors improve upon both the empirical predictor and the model-based predictor from which they were derived. Lastly, we note that the performance comparisons in Figure 6 confirm those in Figure 5, which validates the accuracy of the out-of-sample approximations from Section 3.3.

Since NHANES data are collected using a stratified multistage probability sampling design, it is natural to question the absence of survey weights from this analysis. Although it is straightforward to incorporate the survey weights into an aggregate loss function to mimic a design-based approach (e.g., Rao, 2011), the unweighted approach has its merits. By design, NHANES oversamples certain subpopulations to ensure representation in the dataset. So although our out-of-sample predictions are not evaluated on a representative sample of the U.S. population, they are evaluated on a carefully-curated sample that includes key demographic, income, and age groups within the U.S. population.

6. Discussion

Using predictive decision analysis, we constructed optimal, simple, and efficient predictions from Bayesian models. These predictions were targeted to specific functionals and provide new avenues for model summarization. Out-of-sample predictive evaluations were computed using fast approximation algorithms and accompanied by predictive uncertainty quantification. Simulation studies demonstrated the prediction, estimation, and model selection capabilities of the proposed approach. The methods were applied to a large physical activity dataset, for which we built a count-valued functional regression model. Using targeted prediction with sparse linear actions, we identified 10 covariates that provide near-optimal out-of-sample predictions for important and descriptive PA functionals, with substantial gains in accuracy over both Bayesian and non-Bayesian predictors.

A core attribute of the proposed approach is that only a single Bayesian model $\mathcal{M}$ is required. The model $\mathcal{M}$ is used to construct, evaluate, and compare among targeted predictors for each functional h, and is the vessel for all subsequent uncertainty quantification. Although it is practically impossible for $\mathcal{M}$ to be adequate for every functional, many well-designed models are capable of describing multiple functionals. We only require that $\mathcal{M}$ provides a sufficiently accurate predictive distribution for each $h(\tilde{\mathit{y}})$, which is empirically verifiable through standard posterior predictive diagnostics (Gelman et al., 1996). When the predictive distribution of $\mathcal{M}$ is intractable or computationally prohibitive, the proposed methods remain compatible with any approximation algorithm for $p_{{}_{\mathcal{M}}}\{h(\tilde{\mathit{y}})\mid \mathit{y}\}$.

Future work will establish uncertainty quantification for the optimal point prediction parameters ${\widehat{\delta }}_{\mathcal{A}}$. This task is nontrivial: frequentist uncertainty estimates for penalized regression are generally not valid, since the data have already been used to obtain the posterior (predictive) distribution under model $\mathcal{M}$. A promising alternative is to project the predictive targets $h(\tilde{\mathit{y}})$ onto $g(\tilde{\mathit{x}};\delta )$, which induces a predictive distribution for the resulting parameter δ. Similar posterior projections have proven useful for linear variable selection (Woody et al., 2020) with growing theoretical justification (Patra and Dunson, 2018).