A Simplified Model for Whole-body Angular Momentum Calculation

Abstract

The capability to monitor gait stability during everyday life could provide key information to guide clinical intervention to patients with lower limb disabilities. Whole body angular momentum (L_body) is a convenient stability indicator for wearable motion capture systems. However, L_body is costly to estimate, because it requires monitoring all major body segment using expensive sensor elements. In this study, we developed a simplified rigid body model by merging connected body segments to reduce the number of body segments, which need to be monitored. We demonstrated that the L_body could be estimated by a seven-segment model accurately for both people with and without lower extremity amputation.

Introduction

Gait stability is referred to as the capacity of continuous locomotion tasks in the presence of disturbances, such as new terrains, additional cognitive tasks, and contacts with the environment [1, 2]. Impaired gait stability is regarded as a contributor to life quality degradation and associated with underlying disease development, increased fall risk, and mobility loss [3]. Evaluation of gait stability is critical to track the impact of disease and quantify the effectiveness of rehabilitation [4, 5]. Although various clinical approaches [6] are available to evaluate gait stability through motor performance tests or specially designed questionnaires, these clinic-based assessments cannot represent the actual observed gait stability in daily life; as an example these stability indicators are not well correlated with the number of falls.[1]. One of the major speculations is that the clinical evaluation does not represent the everyday tasks well enough, so both clinicians and researchers are seeking gait stability metrics that are feasible to be monitored beyond clinics. However, making a gait stability monitor requires careful selection of stability indicators and effective system integration.

Wearable biomechanics sensors

The development of wearable sensors enables measurements of gait variables at a relatively low cost in a variety of environments. The most commonly adopted mechanical sensors include, accelerometers, inertial measurement units (IMU), force sensors, and pressure sensors [7]. Some wearable sensors are commercially available and used for daily step counting and fall detection, such as the Apple watch (Apple Inc., CA, US) and MOBILITY LAB (APDM wearable technologies Inc. OR, US).

IMU (often includes accelerometers, gyroscopes, and magnetometers) is the most adopted wearable sensor [8]. Despite its popularity, IMUs have their own limitations: 1) IMU only generates orientation, acceleration, angular velocity of a body segment. Repeated calibration is necessary for accurate position measurements to compensate sensor drifts or integration errors [9]; 2) IMUs have difficulty in detecting gait events accurately. Despite extensive efforts, there is still no reliable solution for detecting both heel strike and toe-off [10] for all populations; 3) although trivial compared with camera-based systems, the cost of each IMU block is still around $1,000 for gait analysis based on authors’ current knowledge; and 4) IMU sensors have to be calibrated at a known reference posture to avoid orientation bias between the IMU’s coordinates and the coordinates of human body.

Gait stability indicators

Existing gait stability indicators [1] are based on 1) practical measurements, 2) dynamic system theories, and 3) margin to unstable gait status. Practical measurements, such as walking speed, step length, and cadence, are easy to calculate and their correlation to gait stability are well documented [11, 12]. These practical gait measures, however, are evaluated on a step-by-step basis and therefore rely on accurate gait event detection. Furthermore, because these indicators do not reflect gait stability directly, it is not reliable to infer stability solely based on these measures.

Indicators from dynamic system theories quantify the capability of human to maintain stable status (continuous walking in most cases) under disturbances. Although these indicators, such as maximum Lyapunov exponent [13] and maximum Floquet multiplier [14], are theoretically sound, they can only be estimated reliably based on data collected from a continuous-consistent locomotion (often over 100 steps, seldom seen outside a lab) [14].

Another way to define stability is to find the minimum margin between the current status and an unstable status. By defining the event, when the centre of mass (COM) is out of the base of support (BOS), as unstable, margin of stability (MOS) is measured as the distance between the velocity adjusted COM and the boundary of the BOS [15]. MOS also relies on accurate gait event detection and foot location measurements.

Based on the observation that L_body is well regulated during locomotion, whole-body angular momentum (L_body) is also used as a practical measurement of stability; and its deviation from the usual/nominal values indicates unstable [16]. The L_body has following advantages: 1) it does not rely on accurate gait event detection or foot position measurements, and 2) it can provide continuous information and has been used to a) extract information about behaviour of people with/without disability [17, 18] in walking and more challenging tasks, such as stair ambulating [19], turning [20], sloped walking [21], and coping with perturbation [22, 23], and b) guide the development of assistive devices to restore efficient walking behaviour during daily life [24, 25]. All these features make L_body a good option for IMU based stability monitoring.

Challenges

Despite advantages of L_body, the cost to measurement is relatively high. To calculate the L_body, we need to estimate the angular momentum (L_s) for each major body segment. Because one IMU can only track one segment, a lot of IMU sensors are needed (for an example, the MVN Awinda system from Xsens includes 17 sensors). It is still too costly for a home device. Additionally, more sensors also mean higher demands on data transfer, processing, and storage, which increases the required computational resources. A high number of sensors can also be cumbersome to don and doff.

A straightforward way to reduce the number of IMU sensors is to reduce the number of monitored segments. However, removing segments from L_body may reduce accuracy. One practical approach is to generate a simplified body model, which 1) includes fewer segments, and 2) reserve the inertial properties needed for L_body calculation. However, no related studies are available.

Our solution

Here we developed a simplified model to calculate L_body through segment merging. We estimated the key merging parameters on kinematic data collected from 10 able-bodied subjects through optimization. The merged model was also validated on data collected from three transfemoral amputees. The results demonstrate that a simplified model can be used to calculate the L_body reliably on various subjects.

Methods

Merging of body segments

Because motions of adjacent segments are often correlated, it is reasonable to assume that some of the segments can be represented by a dominant one. A straightforward solution is to 1) merge a proximal segment and a distal segment, which are physically connected and 2) define the orientation of the merged segment in the reference posture. We expect that the L_S of the merged segment equal the sum of L_S of the two segments before merging.

A 12-segment rigid body model was used as the standard model, which includes: head, torso, right/left upper arms, right/left front arms, right/left thighs, right/left shanks, and right/left feet. The model is calibrated using the anatomical position as the reference posture.

Some rational assumptions were made to simplify the merging procedure. 1) the merged segment is connected to the adjacent body using the same joint as the original proximal segment, 2) angular velocity of the merged segment is the same as the original proximal segment, and 3) the merging procedure does not affect the mass distribution of the two merged segments. Based on these assumptions, we can claim that there is a constant bias between the merged segment and the original proximal segment (BMO); and we can use an IMU attached on the original proximal segment to track the merged segment after we remove the bias by adjusting the adopted reference posture.

To calculate L_S of the merged segment, following information is needed: 1) COM of the merged segment $d_m^r$ (a 3X1 vector) and 2) the moment of inertia of the merged segment, I_m (a 3X3 matrix). Because it is impractical to get $d_m^r$ and I_m through optimization directly, further simplifications are needed. Here, we assumed that 1) the merging is conducted by fixing the joint angle, which connects the two segments; and 2) the orientation BMO is limited in the sagittal plane. These assumptions 1) made it easy to calculate $d_m^r$ and I_m using known properties of the body segments, and 2) permitted the model to be optimized for the sagittal plane component of L_body, which has the largest amplitude among its three dimensions.

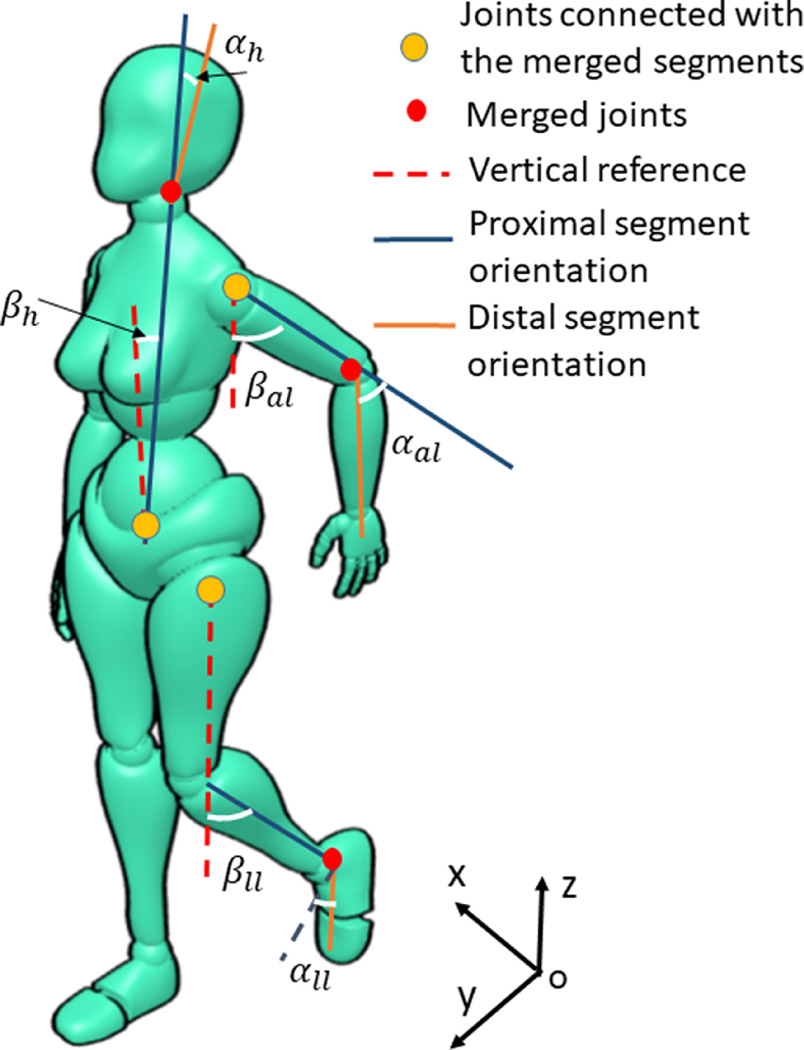
The Fig. 1 provided an illustrative example of the merging. The segments on the right side of the body remained in its anatomical position, and the segments on the left side were merged, as were the head and torso. Following the above discussion, the merging procedure was conducted using two steps. Step 1: defining a merged segment by fixing the joint between the two segments (a distal one and a proximal one) at a fixed angle$\angle \alpha$, which is defined as the merging angle. Step 2: selecting an incline angle, $\angle \beta$, which can represent the BMO. This incline angle was materialized by rotating the merged segment on the reference posture around its proximal joint in the sagittal plane. Although two angles are both defined in the sagittal plane, compared with the$\angle \alpha$, which is defined between two segments, the $\angle \beta$ is defined between the proximal-distal axis of the proximal segment and the z axis. The coordinate system is also shown in Fig. 1.

Figure 1:

the merging procedure and definition of the merging parameters on the left side of the body and on the trunk and head.

Here, we developed the simplified model by merging forearms and upper arms, feet and shanks, and head and torso. The list of merging angles, incline angles, and their related segments are shown in Table 1. We will address the potential of further merging in the discussion.

Table 1:

the list of merging angles and incline angles used in the merging procedure.

Merging Angle	Incline Angle	Proximal Segment	Distal Segment
$\angle {\alpha }_{la}$	$\angle {\beta }_{la}$	Left upper arm	Left forearm
$\angle {\alpha }_{ra}$	$\angle {\beta }_{ra}$	Right upper arm	Right forearm
$\angle {\alpha }_{ll}$	$\angle {\beta }_{ll}$	Left shank	Left foot
$\angle {\alpha }_{rl}$	$\angle {\beta }_{rl}$	Right shank	Right foot
$\angle {\alpha }_h$	$\angle {\beta }_h$	Trunk	Head

Calculate variables related to the merged segment

To adopt the simplified model, we 1) calculated the COM location and moments of inertia of the merged segments in the reference posture using the defined $\angle \alpha$ and$\angle \beta$; 2) calculated the L_s of the merged segments. Merging of forearm and upper arm is detailed in the supplementary file as an example.

Optimize the merging procedure based on experimental data

To decide the five merging and five incline angles, which are key parameters, we conducted an optimization based on data collected from able-bodied subjects using a brutal force optimization (see supplementary materials for details). The root mean square of the error compared with the reference L_body, which was averaged for each stride, was used as the cost function. To reduce calculation burden, we made a further simplification that merging was conducted symmetrically by forcing:

$$\angle {\alpha }_{la}=\angle {\alpha }_{ra},\angle {\alpha }_{ll}=\angle {\alpha }_{rl},\angle {\beta }_{la}=\angle {\beta }_{ra},\angle {\beta }_{ll}=\angle {\beta }_{rl}$$ Eq. (1)

To understand the influence of inter-subject variation, we also calculate subject-specific optimal merging parameters. The impact of inter-subject variation was quantified by the ratio of the increased cost function, which is defined as:$f_j=\frac{C_j^G-C_j}{C_j}$, where C_j is the cost function for the subject j using that subject’s optimal merging parameters, and the $C_j^G$ as the cost function for the subject j using the merging parameters in Table 1. A model, which yields low f_i for all participants, can be treated as a genetic model.

Human subjects and the experimental procedure

Following approved IRB protocols, the simplified model is constructed based on data collected from ten subjects without disabilities, who walked through a 15-meter walkway in three self-selected walking speeds, normal, slow, and fast. The simplified model was also validated using data collected from three transfemoral amputees, who wore a powered knee prosthesis. These participants underwent a similar protocol although they walked 1) on a 7m long walkway, 2) only at self-selected normal speed, and 3) with fall protection from an overhead rail. The demographic information about the participants and experimental procedure can be found in the supplementary materials.

Results

The optimal merging parameters were identified from data collected from all subjects without disabilities and shown in Table 2. For all the subjects without disabilities, f_j is 0.07(mean) ± 0.06(standard diviation), which indicated that inter-subject variation had a limited impact.

Table 2:

optimized merging parameters based on data collected from able-body subjects.

Merge Parameter	$\angle {\alpha }_{la}=\angle a_{ra}$	$\angle {\beta }_{la}=\angle {\beta }_{ra}$	$\angle {\alpha }_{ll}=\angle {\alpha }_{rl}$	$\left|\angle {\beta }_{ll}=\angle {\beta }_{rl}\right|$	$\angle {\alpha }_h$	$\angle {\beta }_h$
Optimal Value (°)	50	0	10	0	170	9

The L_body was also calculated for three transfemoral amputees. Although these participants wore a powered prosthetic knee, which was much heavier than their everyday prosthetic legs, the simplified model performed well with both subject-specific optimized merging parameter sets, and the merging parameters represented in Table 2. The ratio of the increased cost function was 0.04, 0.08, and 0.03 for the TF01, TF02, and TF03, respectively. The subject specific optimized parameters are included in the supplementary materials.

Discussion and Conclusion

This work focused on developing a simplified model, so fewer IMU sensors would be needed to measure whole-body angular momentum, L_body, a gait stability indicator. The concept stemmed from the observation that the motion of adjacent segments is correlated, suggesting that a proxy of their combined contribution could accurately provide L_body from the merged segments. Indeed, we demonstrated that L_body could be calculated using a 7-segment model incorporating optimal merging parameters.

Although Eq. 1 puts additional limitation on the merging procedure, its impacts on the L_s are expected to be limited, due to the facts 1) the asymmetry inertial properties of the segments are considered when the rigid mode was defined before merging; and 2) the two thighs and shanks contribute a large portion of the L_body and their kinematics are represented accurately in the simplified model. Because amputees’ uses a fixed ankle prosthesis, the amputees’ merging angles at the ankle shows a large variation (see the supplementary material), however, this variation’s impact is limited due to 1) inertia of the foot is much lower compared with the shank and 2) the foot motion follows the shank in most of the gait cycle. Good merging results on amputees, who showed an asymmetry gait, is aligned with our expectation.

We assessed the feasibility of further simplifying the model by considering: 1) merging the two arms with the torso/head 2) merging the feet, shanks, and thighs. Although the torso/head have a much larger inertial, the quick movement of the arms generates a significant L_s along the z-axis. This component could not be preserved after merging, so merging of the arm and torso/head should only be considered when the L_body along the z-axis can be ignored.

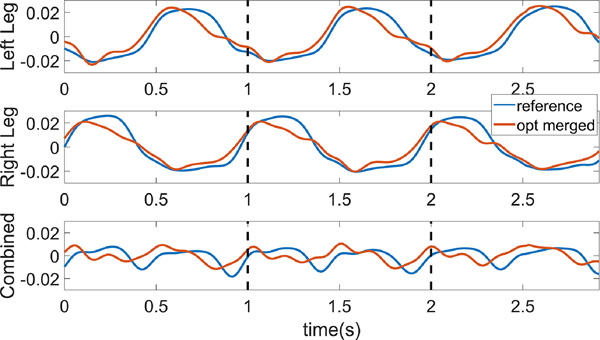
Finally, we merged segments within the legs (e.g., thigh, shank, and foot) as shown in Fig. 3. Although the L_s of the full leg segments, merged at the knee and ankle, still shared the general trends, the sum of the two legs deviated substantially from the reference. We were unable to overcome this problem, even with eliminating the symmetry limitation at the knee and hip, as posed in Eq. 1. Considering that the legs contribute about 70% of the L_body, the current merging approach failed to generate a merged leg segment.

Figure 3:

The angular momentum of the left leg, right leg, and both legs in the sagittal plane. The blue line is from the reference model, the red line is from the optimized model with the thigh, shank, and foot merged together for each leg. The optimization is conducted for each leg separately.

The limitations of this research include a limited number of subjects and relies on an existing motion capture system to calculate all kinematic variables. In our future study, we plan to build a customized IMU system for L_body calculation and test on more subjects with various age and level of disabilities.

In summary, our findings suggest that we were able to accurately calculate L_body from a reduced number of segments. Through careful merging of adjacent segments, with optimized genetic parameters (i.e., merging and incline angles), we were able to accurately calculate L_body with only a 7-segment model.

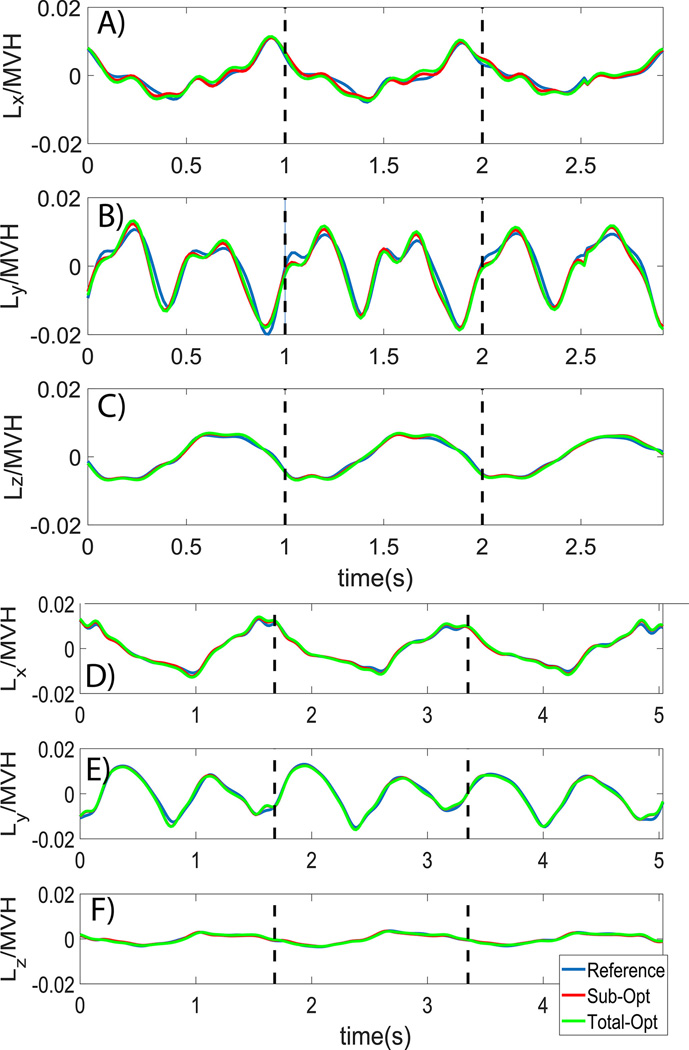
Figure 2.

A), B), and C) The normalized L_body of AB05. Fig. D), E), and F) The normalized L_body of TF01. The L_body calculated from the reference model (blue line), simplified model with the subject-specific optimal merging parameters (red line), and simplified model with the merging parameters shown in Table 2. The steps started from the right heel strike and the dash black lines show the second and the third right heel strike. MVH is an abbreviation of body mass, walking velocity, and body height.

Highlights:

• A simplified rigid body model to calculation of full body angular momentum

• Only 7 IMU sensors are needed to calculate the full body angular momentum using this simplified model

• The model was validated on both able-bodied subjects and transfemoral amputees