Abstract
Developing a ligand with high affinity for a specific protein target is essential for drug design, and water molecules are well known to play a key role in protein–drug recognition. However, predicting the role of particularly ordered water molecules in drug binding remains challenging. Furthermore, hydration free energy contributed from the water network, including the second shell of water molecules, is far from being well studied. In this research we focused on these aspects to accurately and efficiently evaluate water effects in protein–ligand binding affinity. We developed a new strategy using a free-energy calculation method, VM2. We successfully predicted the stable ordered water molecules in a number of protein systems: PDE 10a, HSP90, tryptophan synthase (TRPS), CDK2 and Factor Xa. In some of these, the second shell of water molecules appeared to be critical in protein–ligand binding. We also applied the strategy to largely improve binding free energy calculation using the MM/PBSA method. When applying MM/PBSA alone for two systems, CDK2 and Factor Xa, the computed binding free energy resulted in poor to moderate R2 values with experimental data. However, including water free energy correction greatly improved the free energy calculation. Furthermore, our work helped to explain how xk263 is a 1000-times faster binder to HIVp than ritonavir, a potentially useful tool for investigating binding kinetics. Our studies reveal the importance of fully considering water effects in therapeutic developments in pharmaceutical and biotechnology industries and for fundamental research in protein–ligand recognition.
Keywords: water analysis, binding thermodynamics, drug discovery, implicit solvent model, computer-aided drug design
Graphical Abstract
Uncovering Water Effects in Protein–Ligand Recognition: Importance in the Second Hydration Shell and Binding Kinetics
INTRODUCTION
Accurately predicting protein–ligand binding affinity and binding kinetics in computer-aided drug discovery requires careful examination of bridging water molecules[1–6]. A survey of structures in the protein data bank (PDB) showed that more than 85% of complexes had one or more water molecules bridging a protein and ligand, with a mean of 3.5 molecules per complex [7,8]. Ligands have to compete with water for binding to the protein cavity. Depending on the context, water molecules will be replaced, retained, or displaced to favor or oppose ligand binding[9]. This occurs through displacement of poorly ordered water molecules or the formation of newly ordered water networks during binding. Implicit solvent theories successfully model the effect of bulk water[10–28]; however, these continuum solvent models have difficulty computing important explicit water–ligand and water–protein interactions. Because the water–ligand interactions are highly system-specific and various water molecules may be displaced by ligand binding, identifying and predicting bridging water molecules and their roles in ligand binding remains challenging[29]. Furthermore, the range of effects mediated by water is huge but far from being fully understood. Water stabilizes ligand interactions and also frequently plays a biological role. The possible contribution of water free energy to ligand binding barriers has been recognized for some specific protein–ligand systems[30–33].
Water sites can be predicted by running molecular dynamics (MD) or Monte Carlo (MC) simulations with an explicit water model and averaging over water-molecule locations from the MD or MC trajectories. One method is inhomogeneous fluid solvation theory (IFST), popularized by Lazaridis[34–37]. IFST forms the basis of the WaterMap program. The grid-based MC method JAWS[38] is another well-known method. These MD or MC techniques can also include entropic effects in the prediction. However, a major problem with the methods is that moving water molecules in and out of cavities at the protein interface, especially with buried cavities, can be excessively slow.
Comparatively rigorous free energy perturbation (FEP) and thermodynamic integration methods[39–41] can be used to compute the absolute binding free energy of a water molecule at a putative location. These approaches are based on sound theories, but the main obstacle is the excessive simulation time. Therefore, the challenge is handling a system that considers multiple water molecules in the protein-binding site.
Fast solvation methods have been pursued for a number of years[42–45]. Also, an open-source software MobyWat[46] showed good performance for 344 interfacial water molecules in various complexes of peptide and protein ligands[47]. A geometry-based method, WarPP[48], applies an iterative shifting-clustering algorithm, with a success rate similar to the above dynamic methods. Other research groups developed new static approaches, such as HydraMap[49] and Splash’Em[50]. The common weakness of these methods is that they lack the entropy contribution when evaluating the water–protein and/or water–ligand interactions, which play a critical role in drug binding.
Overall, these methods often lack the balanced accuracy and efficiency required in practice, especially in early-stage drug design. More importantly, the methods do not cover the kinetics of protein–ligand interactions that govern the drug residence time. This work aims to account for these deficiencies.
We integrated the free energy calculation method, the VM2 program[51–53], into our new water analysis strategy to achieve more accurate and efficient calculations for predicting locations of stable water molecules and the free energy of removing them for ligand binding. Molecular docking and scoring are popular fast methods used by the pharmaceutical and biotechnology industries and academia for lead identification. Because a binding pocket of an apo-protein is always filled by water molecules, approximating a penalty when tightly bound water molecule(s) are displaced can improve ligand-binding affinity calculations[54–63]. The net effect of displacing a water molecule depends on the balance between the free energy of transferring water molecules to the bulk solvent and new interactions formed by a ligand. In addition, removing water molecules from a hydrophobic region, or “dewetting”, is directly associated with water molecules, a ligand and a protein[64–68]. Water molecules compete with or facilitate ligand binding/unbinding from a binding site, which may contribute significantly to the ligand binding free energy landscape, such as creating a kinetic barrier during ligand binding and unbinding[69–72]. Therefore, by more accurately capturing the water–ligand/protein interactions, we can improve the accuracy of molecular docking and scoring methods, thermodynamic end-states analysis and drug binding kinetics analysis. In this paper, we discuss the results of carefully investigating water effects using our new strategy on multiple protein systems and their implications for the field of drug discovery.
METHODS
We created three novel approaches with the VM2 program to accurately and efficiently probe interfacial water molecules: 1) a hydration sites-locating algorithm to determine the location of water molecules in protein–ligand interfaces; 2) a water-removal algorithm to evaluate the free energy of moving water molecules from their binding sites to bulk; and 3) extending the water-removal algorithm to handle multiple water molecules.
1. VM2 free energy calculation
VM2 is a rigorous statistical thermodynamics method. It belongs to a class of methods that focus on the most stable conformations of the molecules, so they are sometimes called predominant states methods. They compute the standard chemical potential of the protein–ligand complex and the free ligand and protein and use the difference to obtain the standard free energy of binding,
| (1) |
The standard chemical potential of each molecular species (i.e., complex, protein and ligand) is obtained by finding its N most stable conformations ( j = 1, N), integrating the Boltzmann factor within each energy well j to obtain a local configurational integral zj and combining these local configuration integrals according to the following formula, where X = complex, protein, or ligand:
| (2) |
Here C0 is the standard concentration, which, combined with the factor of 8π2, accounts for the positional and orientational mobility of the free molecule at standard concentration, and the second form of the summation is given in terms of the chemical potentials of the individual conformations. The probability of the energy well j can be approximated on the basis of zj, and then the mean potential energy <U> or solvation energy <W> can be obtained. The configurational entropy at the standard concentration can be computed as . The configurational entropy includes both a conformational part, which reflects the number of energy wells (conformations), and a vibrational part, which reflects the average width of the energy wells. 〈U + W 〉 implicitly includes the change in solvent entropy via the implicit solvent model. As a consequence, the configurational entropy values reported here should not be directly compared with experimental entropy changes of binding for these systems.
The VM2 calculations are moderately fast, in part because they use implicit solvent models, which are widely accepted as computationally efficient alternatives to more detailed solvent models, and in part because for large systems such as protein–ligand complexes, only a subset of atoms (~500–5000, depending on the nature of the active site) are treated as flexible.
2. Hydration sites-locating algorithm
We developed an algorithm to accurately predict hydration sites for a ligand-binding pocket of a protein. Although water molecules may be observed in crystal structures, they cannot reveal whether a water molecule is stable there or not. In addition, the data may not be reliable because of an artificial environment during protein crystallization and low resolution, or in many cases such as homology modeling, water molecules are missing in the structures.
In this algorithm, a crystal structure for the protein–ligand complex is used as the reference structure, and all water molecules, cofactors, metal ions, etc. are removed from it. If more than one crystal structure is available, the complex of the target protein and a ligand with the highest experimental binding affinities (measured by the lowest Ki or IC50) in a series is selected as the reference structure. The protein is then parameterized with AMBER force fields[73]. A grid box with 0.2-Å spacing is centered on the ligand in the complex. The residues within the cut-off distance of 12 Å from the ligand are identified. The minimum and maximum of the Cartesian coordinates of the α-carbons of these residues are used to define the 8 corners of the grid box. Then the vacant grid points in the grid box that define the binding site are identified and counted (Ngrid). All Ngrid binding-site points are then probed with a water probe as described in the GRID[42] and ConCept[74,75] methods. The interaction between the water probe and the protein at binding-site point i is estimated as follows:
| (3) |
| (4) |
| (5) |
| (6) |
where EiNP is the energy of non-polar interactions, EiES is the energy of Coulombic interactions and EiHB is the energy of hydrogen bonding interactions for binding-site point i. Nprot is the total number of protein atoms and rij is the distance between binding-site point i and protein atom j in equations (4) and (5). In equation (6), rij is the distance from the binding-site point i to a hydrogen-bond donor or acceptor j, and θ is the angle among a protein donor atom, a hydrogen, and the probe. The whole term is set to zero when θ ≤ 90°. If the probe group donates a bond, the probe is assumed to orient itself to form the most effective hydrogen-bond interaction with the acceptor atom of the protein, and the cosθ term is set to unity.
The average grid energy is then computed as , and each binding-site point with energy below 〈E〉 is marked as a candidate interaction point, where Ngrid is the total number of vacant interaction grid points in the grid box of a system. By this way, we discard the grid points with energies above average (in other words, weak interactions with the protein). Then each candidate interaction point is checked for the number of its neighbors, where a neighbor is another candidate interaction point within a distance of 3 Å. Points with below-average neighbor counts are discarded; those that remain are classified as interaction points. In addition, interaction points with neighbor counts in the top 15th percentile are clustered by a distance cutoff of 3 Å, and a hydration site with a radius of 1 Å is placed at the mean coordinates of each of the resulting clusters.
The hydration sites identified in the above procedure are the first layer that has direct interactions with the protein (and the ligand, if any). The water probes are placed at these hydration sites and the search procedure is repeated, except that now the water probe also interacts with the hydration sites. The hydration sites found in the second search are called the second layer, and those in the third search, the third layer etc. This iterative search runs until no new hydration sites can be found in the binding site.
3. Water-removal algorithm
Consider the free energy for moving a bound water molecule from a protein into bulk solution, leaving just an empty cavity with the same shape as that of the water, and no other changes, as illustrated in Scheme 1. Thus, the water removal free energy is computed as follows:
| (7) |
where is the standard (Co = 1M) chemical potential of a protein–ligand–water complex, is the standard chemical potential of the protein–ligand complex without the water (but with the water-shaped cavity), and is the standard chemical potential of the water in gas phase (no GB or PB solvation). and are calculated with VM2 for the protein–ligand–water complex and the protein–ligand complex, respectively. Notably, the non-polar term of solvation free energy Gnp is included in free energy , which approximates the free energy contribution of cavity formation. The chemical potential of gas-phase TIP3P water at standard concentration of 1M is calculated as −5.1 kcal/mol with VM2.
Scheme 1:
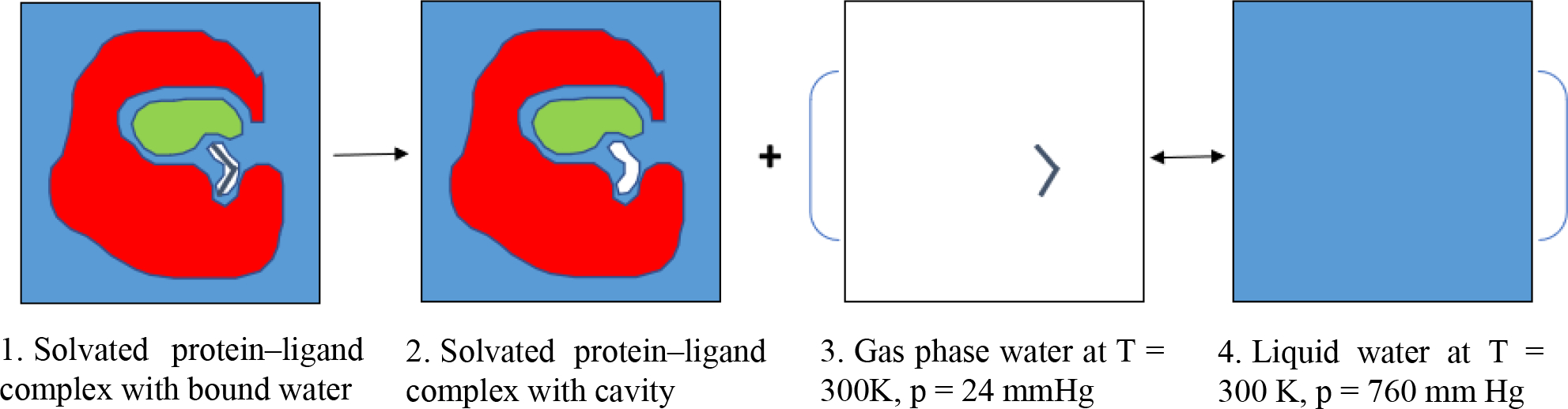
Illustration of water removal, where red, green, white with two blue lines, white and blue background represent the protein, the ligand, a water molecule, a cavity and the continuum aqueous solution, respectively. A bound water molecule is removed from a protein-ligand complex (1) into bulk solution (3, 4), leaving just an empty cavity with the same shape as that of the water (2).
Equation (7) tells us about the free energy of taking the water molecule out of the protein–ligand complex and putting it into the gas phase at 1M. However, what we want is the free energy of putting it into liquid phase. We correct this by adding the gas-to-liquid transfer free energy of the water, ΔGgl. Hence:
| (8) |
| (9) |
The entropy changes while removing the water, ΔS°wr-liquid, is computed in equation (9) with the same notation for each species shown in equation (8). The vapor pressure of water at 300 K is 24 mm Hg, so the chemical potential of water at 24 mm Hg is equal to that of liquid water. Hence, free energy of gas–liquid transfer ΔGgl is the free energy change from the initial gas-phase concentration C in moles/liter to a new concentration corresponding to an ideal gas at 24 mm Hg. An amount of 1 mol ideal gas at 1 atm occupies 22.4 l, so its concentration is 0.0446 (mol/l-atm). Therefore, the concentration equals [24 mm Hg/760 mm Hg/atm] [0.0446 mol/l-atm] = 0.00141 M. Thus, the free energy change is
| (10) |
where T is the temperature, R is the Boltzmann’s constant and C is the concentration. The overall process of entropy change involves adjusting 300-K gaseous water at concentration C to 373 K and 1 atm pressure (boiling point) by using a literature value for the entropy change of condensation at the boiling point, then cooling the now-liquid water to 300 K.
| (11) |
The partial molar enthalpy at T=300K can be calculated as follows:
| (12) |
In this water-removal implementation, when a water molecule needs to be removed from the system, leaving an empty cavity, this is implemented by simply setting the following parameters to zero: the partial charges and van der Waals parameter Emin of its atoms, force constants of its bonds, and force constant of its angle. The live set, which defines the mobile atoms in calculations, includes only water molecules. Also, flat-bottom energy well constraints, as expressed in the following equation where k is the force constant of the restraint, r is the location of the restrained atom, r0 is the center of the flat-bottomed well Rrestraint is the radius of the restraint region and p is a parameter controlling the hardness of the energy wall around the energy well, are applied to all of the water oxygen atoms. The values of k, Rrestraint and p were set to 5.0 kcal/mol, 1.0 Å and 12, respectively, for all calculations presented here.
| (13) |
4. Water-removal algorithm handling multiple water molecules
This approach aims to calculate the free energy for the system with all water molecules present, then break the free energy into contributions from individual water molecules and their pairwise cross-terms, or their interactions. The locations and orientations of the water molecules are sampled with the protein kept rigid and a flat-bottomed energy well constraint (see Equation 13) applied to the oxygen atoms of the water molecules.
Scheme 2 shows an example of energy decomposition with two water molecules, W1 and W2, and the protein. In this matrix-like representation, the water removal free energy will be attributed to a change from the water molecule itself GW2, along with the water–protein interaction GProtein–W2 and the water–water interaction GW1–W2, as demonstrated in the shaded area for W2. All intrinsic or “self” terms are on the diagonal, the interaction terms are on the off-diagonal, and the matrix is symmetric. The interactions are Boltzmann-averaged if multiple conformations are available. The water removal free energy for W2 can be expressed as follows:
| (14) |
Scheme 2:
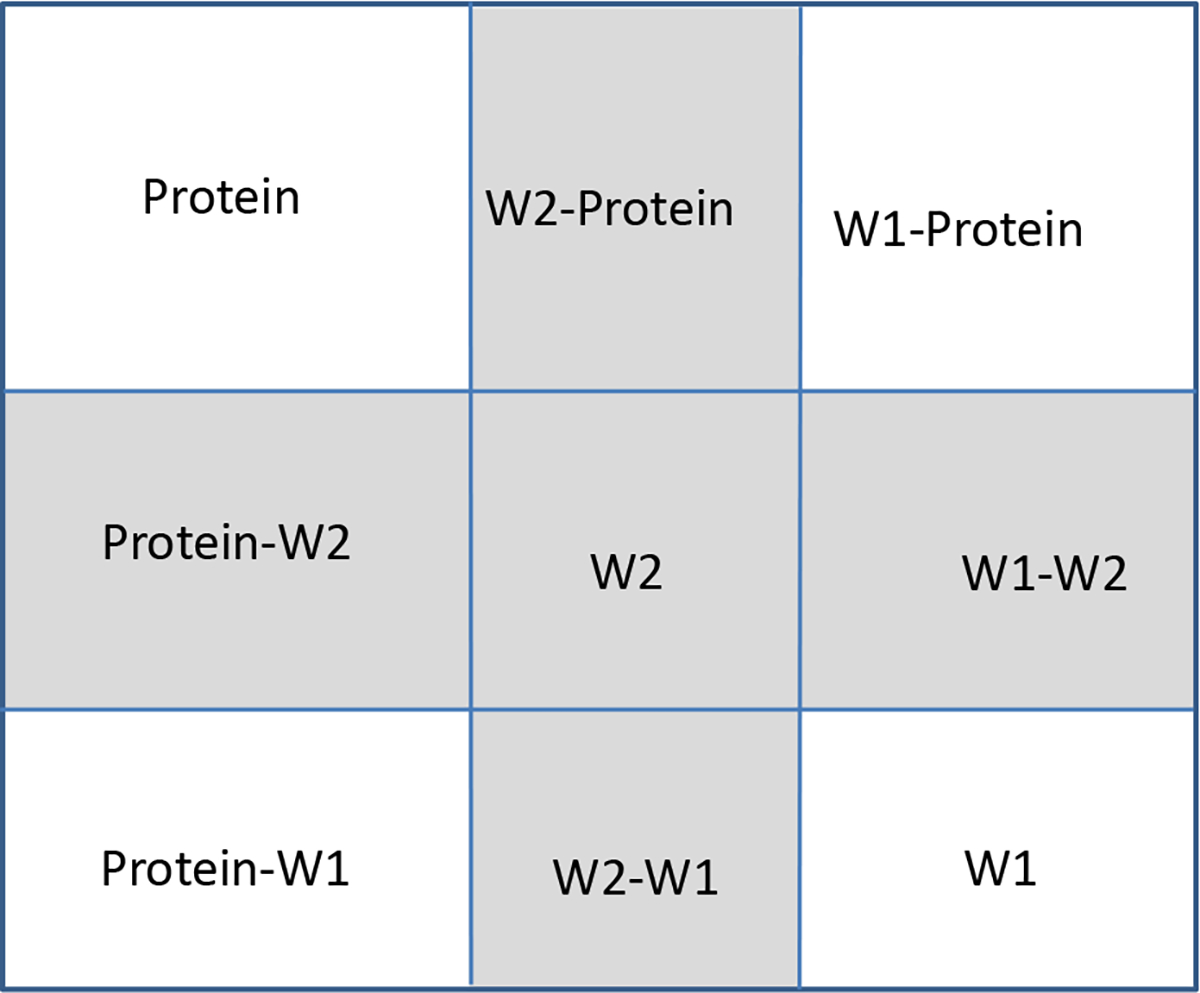
The free energy of a system of a protein and two water molecules, W1 and W2, can be decomposed into several energy components as shown in the matrix below. As an example, the shaded area has the components from the water molecule itself GW2, along with the water–protein interaction GProtein–W2, and the water–water interaction GW1–W2, and all together, they contribute to the water removal energy for W2.
In the same way, the water removal free energy can be obtained for combinations. For instance, removing both W1 and W2 is expressed as follows:
| (15) |
5. MM/PBSA calculation and water-analysis correction
We used the MM/PBSA method[76] to evaluate the inter-molecular interactions between a ligand and a protein, then compared its results with those from the water-analysis correction. The method computes the energy (EMM/PBSA) of a system from the protein (Eprotein), ligand (Eligand) and complex (Ecomplex), with the interaction energy computed as
| (16) |
where 〈E〉 denotes the computed ensemble average energy from a given trajectory. In this study, our trajectories were generated by the VM2 program where multiple protein conformations were obtained from conformation search, not from MD runs. The energy of each species, including protein, ligand and complex, was computed as
| (17) |
where Ebonded is the bonded energy, Eelec and EvdW are electrostatic and vdW energy, GPB is the solvation energy computed by solving the Poisson Boltzmann (PB) equation, and Gnp is the nonpolar energy estimated from the solvent-accessible surface area. The ensemble average energy is calculated with the Boltzmann weight of each conformation in the trajectory.
| (18) |
where kB is the Boltzmann constant, T is the temperature, and Ei is the energy calculated with equation 17 for conformation i in the trajectory. Although the same trajectory for the bound state is used for all three species, the Boltzmann weights of each frame for the complex (the bound state), the protein (the free state after the ligand is removed) and the ligand (the free state after being removed from the complex) are not necessarily same. As a result, their ensemble average energies 〈Ecomplex〉, 〈Eprotein〉 and 〈Eligand〉 have to be calculated separately. The MM/PBSA calculations were implemented with the VM2 program.
In the water-analysis correction, the conformation of the complex with the lowest energy Ecomplex was selected as the reference structure. Then the ligand was removed from the reference structure and the water-analysis calculation was performed on the protein binding site. After the hydration sites and their corresponding removal free energies were obtained, the MD frames used in the MM/PBSA calculation were superimposed on the reference structure. The hydration sites that were displaced by the ligands and the corresponding removal free energies () were determined by the degree of overlap between the ligand heavy atoms and the hydration sites. The MM/PBSA energy corrected with water removal energies is calculated as follows:
| (19) |
A hydration site is completely displaced and its removal free energy is fully counted when the distance between the hydration site center and the ligand heavy atom approaches zero. The removal free energy of hydration site displacement decreases linearly to zero when the distance between them is equal to 80% of the sum of their vdW radii, beyond which there is no displacement. Multiple ligand atoms may contribute to the displacement of the same hydration site. These contributions cease once total displacement is achieved.
The input files and files for the molecular systems tested here are available in the supplementary information.
RESULTS AND DISCUSSION
1. Water removal free energy
(1). Phosphodiesterase 10a
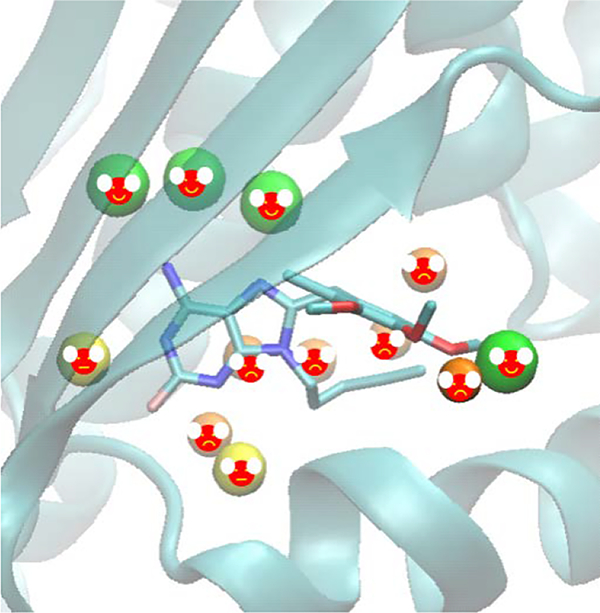
We used our new strategy to calculate the removal free energy of key water molecules from Phosphodiesterase 10a (PDE 10a). The purpose was to assess whether considering the water networks with multiple solvation shells can help predict which crystallographic water molecules are tightly bound and which can profitably be replaced. The application to PDE 10a in particular was motivated by the published observations from Pfizer[77] and Roche[78] indicating that there are two tightly bound structural water molecules in the binding pocket of PDE 10a. We started from the crystal structure PDB ID 3HR1, which provides the coordinates of the complex of PDE 10a and Compound 9 of reference 77 and water molecules, as shown in Figure 1. We identified two key water molecules, W16 and W84. W16 forms an almost ideal tetrahedral hydrogen bonding coordination with residues GLN716, TYR720, TRP752 and W84. W84 forms hydrogen bonds with residues THR675 and THR678, and its hydrogen bond with Compound 9 is considered critical to the potency of this compound[77]. As a comparison, we also studied Compound 18 in reference 77, which forms no hydrogen bond with the key water molecules.
Figure 1.
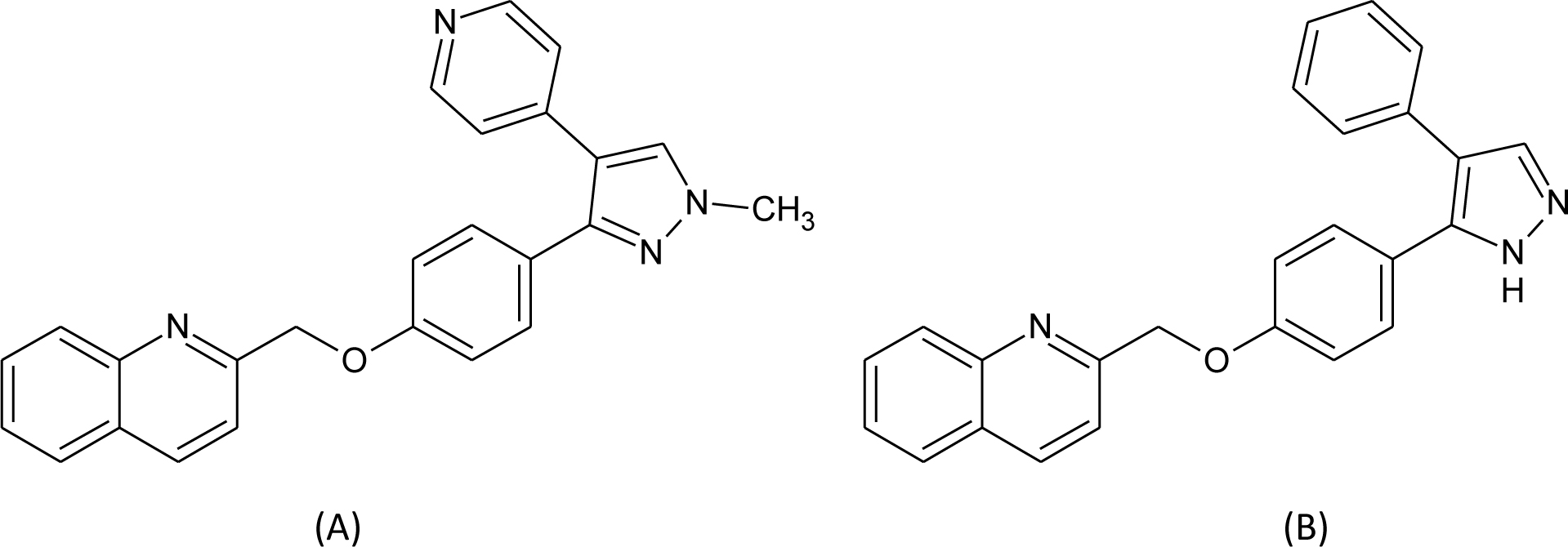
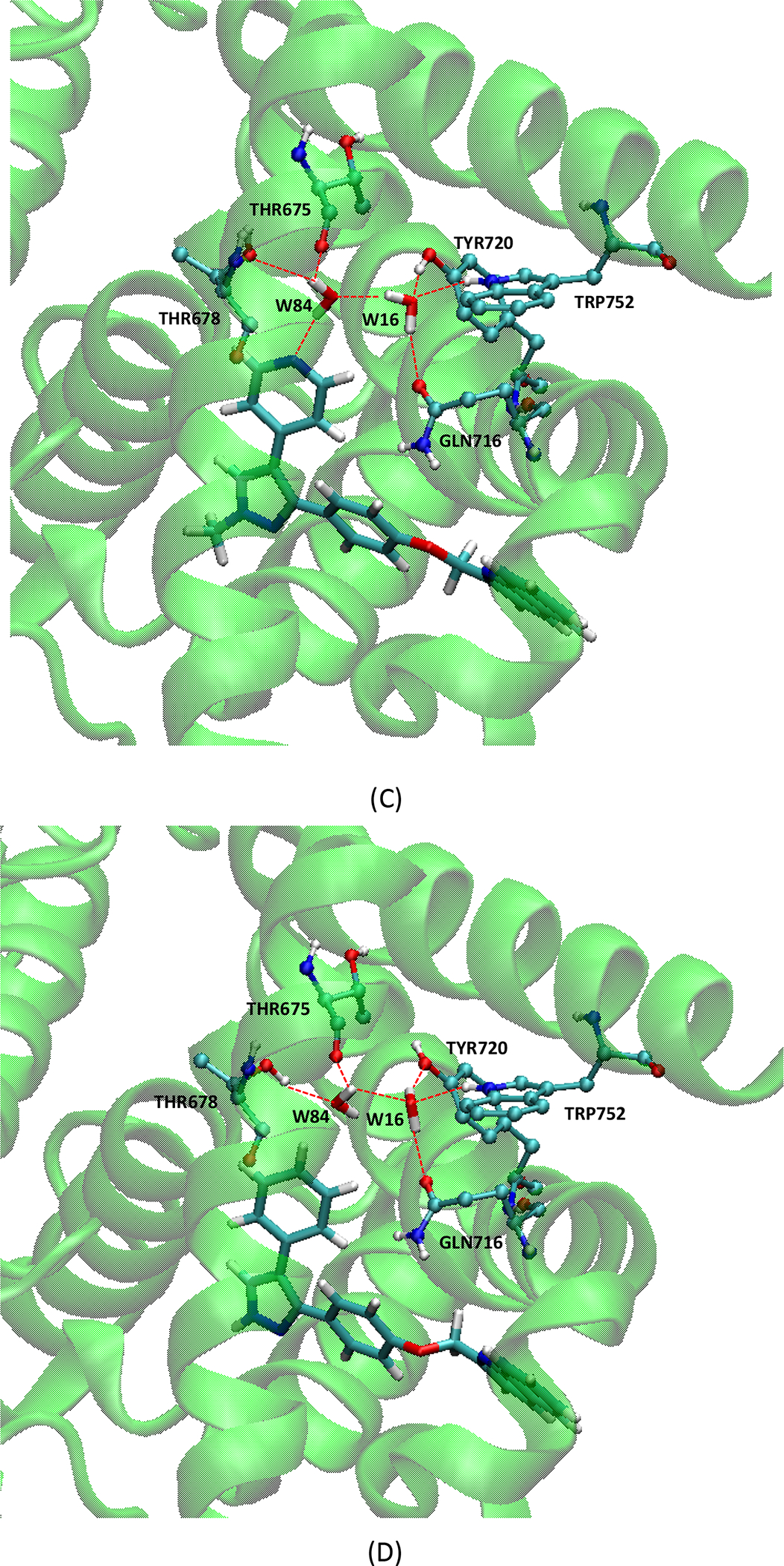
(A) Molecular structure of compound 9; (B) molecular structure of compound 18; (C) interactions in the complex of PDE 10a and Compound 9; (D) interactions in the complex of PDE 10a and Compound 18. In (C) and (D), the protein residues involved in hydrogen bonds are in ball-and-stick, and ligands and water molecules are in licorice.
Here, following theory and methods described above, we obtained water removal free energies (kcal/mol), in the presence of Compound 9 or Compound 18[77] (Table 1). With both compounds, removal of either water is predicted to be thermodynamically unfavorable. Consistent with the medicinal chemistry experience[78], the more buried W16 is particularly tightly held. The table decomposes these data into energetic and entropic terms. Not surprisingly, release of these water molecules yields a consistently favorable entropy change but a more unfavorable energy change.
Table 1.
Removal free energies of water molecules W16 and W84 in the binding site of PDE 10a, with or without the presence of selected ligands. Unit: kcal/mol.
| W16 | W84 | |||||
|---|---|---|---|---|---|---|
| ΔG | ΔE | -TΔS | ΔG | ΔE | -TΔS | |
| with Compound 9 | 5.5 | 15.5 | −10.0 | 1.0 | 10.7 | −9.7 |
| without Compound 9 | 3.3 | 13.3 | −10.0 | −0.5 | 7.7 | −8.2 |
| with Compound 18 | 2.7 | 12.4 | −9.7 | 1.5 | 10.5 | −9.0 |
| without Compound 18 | 2.3 | 12.1 | −9.8 | 1.5 | 10.4 | −8.9 |
We also performed the same calculations with the bound ligands removed without re-optimizing the water conformations and protein. In this case, we can examine the contribution from compounds 9 or 18 to the water removal free energies. As shown in Table 1, when compound 9 is absent, both water molecules are remarkably easier to be removed, with 2.2 and 1.5 kcal/mol smaller free energy cost to remove W16 and W84, respectively, as compared with the presence of compound 9. We think this is because compound 9 has a nitrogen positioned to accept an H-bond from W84, and the conformation of both the water molecules and their protein environment adjust to take advantage of this opportunity. As a consequence, removing compound 9 leaves the water molecules in a non-optimal state. In particular, W84 is trying to form an H-bond with the N-atom of compound 9, which is no longer present. This further disrupts the hydrogen bond network with W16 and thus affects the removal energy for W16 as well. In contrast, compound 18 does not H-bond with W84 (Figure 1), so the water molecules and protein are already optimized for stability almost as if no ligand were bound. Thus, removing compound 18 has less effect on water stability than removing compound 9.
(2). Heat shock protein 90
When several water molecules are present in a protein pocket, they may form an energetically favorable hydrogen bonding network including the second shell of water molecules in the binding pocket. The chaperone protein heat shock protein 90 (HSP90) is a potential target for cancer treatment. Wright et al. provided the crystal structure (PDB ID: 1UYF) of the HSP90alpha N-terminal domain complexed with a purine-based inhibitor, PU1, in which many water molecules were found in the vicinity of this ligand in the binding pocket[79]. For this specific protein–ligand system, we tried to identify the tightly bound water molecules and analyze the removal free energies for them. Besides the three water molecules that sit in the channel running from the ATP binding site behind the helix and out to solvent, making hydrogen bonds with two methoxy groups of the PU1 ligand and TYR139[79], we found another trio that correspond to water molecules W2063, W2146, W2277 in the 1UYF crystal structure. W2063 sits in the middle of the three water molecules and interacts with the amine group of PU1, SER52 and the other two water molecules; W2146 interacts with ILE91 and ASP93 and W2063; W2277 interacts with the purine ring of PU1, ASN51 and W2063 (Figure 2).
Figure 2.
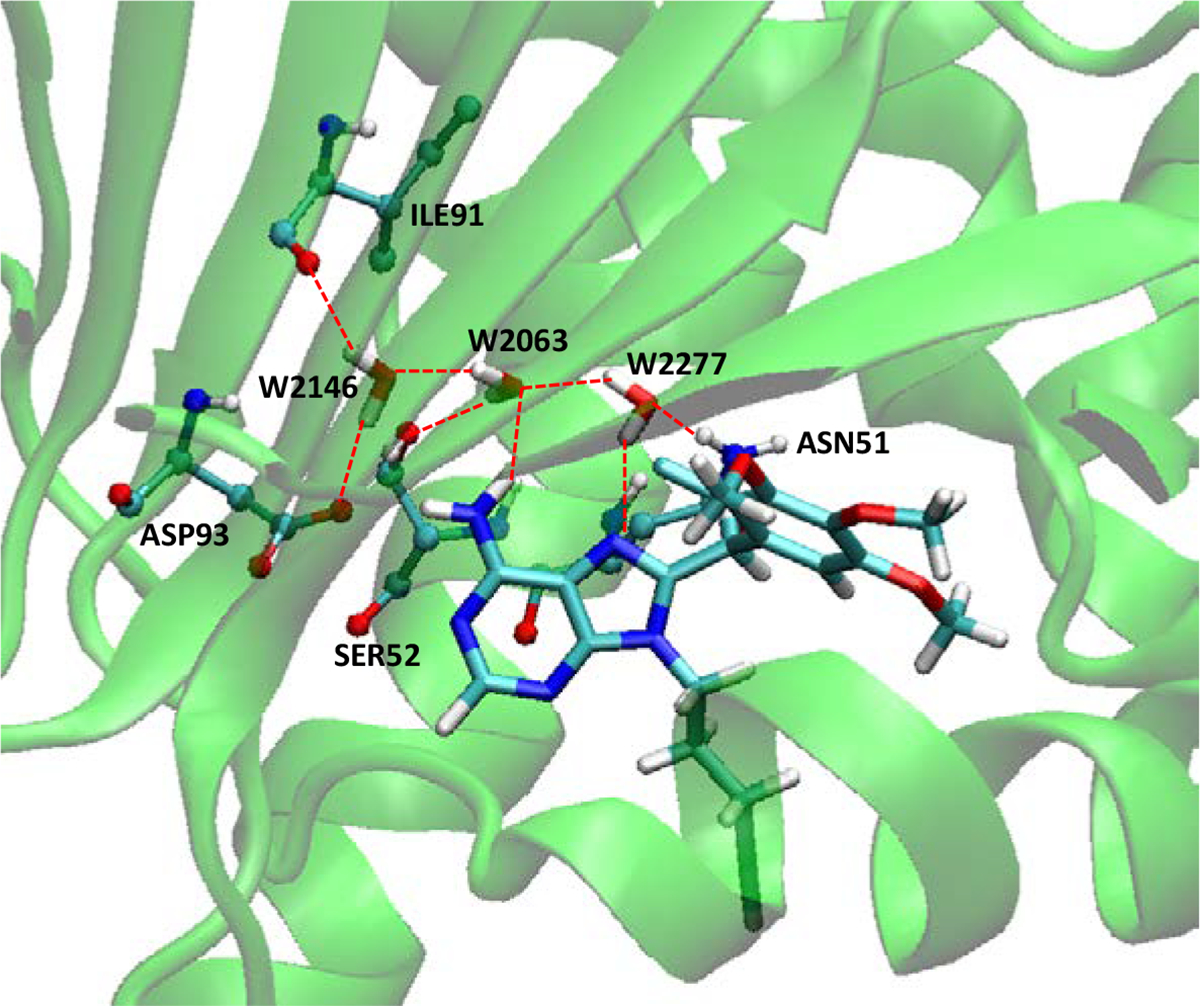
The hydrogen bonding network among HSP90, PU1 and three water molecules. Molecule representations are the same as in Figure 1.
The calculated water removal free energies are listed in Table 2. All three of these water molecules are stably bound in the presence of the crystallographic ligand, with W2277 most weakly bound and W2063 most strongly bound. Combined removal of multiple water molecules tends to cost a little less free energy (ΔG= 11.9 kcal/mol) than the sum of individual removals (sum ΔG = 12.8 kcal/mol), which indicates some cooperation in the binding of these water molecules to the protein–ligand complex. The computed energy (ΔE) and entropy (−TΔS) changes further elucidate the cooperation of these water molecules; ΔE and -TΔS values in removing all the three water molecules (ΔE = 36.9 and -TΔS= −25.0 kcal/mol) are significantly different from the simple sum of individuals (sum ΔE = 46.9 and sum -TΔS= −34.1 kcal/mol). Our study suggests that these three water molecules should all be considered for better results in molecular docking and scoring practices.
Table 2.
Removal free energies of three water molecules in the binding site of HSP90 with the presence of PU1, removed individually, or pairwise, or all together. Unit: kcal/mol.
| Water(s) Removed | ΔG | ΔE | -TΔS |
|---|---|---|---|
| W2146 | 4.5 | 16.9 | −12.4 |
| W2063 | 6.3 | 17.8 | −11.5 |
| W2277 | 2.0 | 12.2 | −10.2 |
| W2146,W2277 | 6.4 | 26.1 | −19.7 |
| W2063,W2277 | 8.3 | 26.6 | −18.3 |
| W2146,W2063 | 10.6 | 28.6 | −18.0 |
| All of three | 11.9 | 36.9 | −25.0 |
(3). Tryptophan synthase
A protein binding site may exist deeply buried or in small compact cavities for water molecules; these positions bring challenges to a modeling program used to predict these hydration sites. To further examine whether considering detailed water effects could successfully predict stable ordered water molecules in a compact space, we used tryptophan synthase (TRPS) with an intermediate 2-aminophenol quinonoid (PDB ID: 4HPJ)[80] as a model system. TRPS is typically found as an α2β2 tetramer. In this specific crystal structure, TRPS binds F9 in its α-subunit and 2-aminophenol quinonoid in its β-subunit. We analyzed the β-subunit with the bound intermediate. Because the water molecules locate in a small space in this substrate-bound catalytic site, it is challenging to catch the hydration sites. With our strategy, we found two water molecules, corresponding to W525 and W593 in 4HPJ, within 5 Å of the ligand and reasonable results: removal free energies of −12.97 and −2.28 kcal/mol for W525 and W593, respectively, which indicates that W525 is much more stable than W593. W525 interacts with the phosphate group of the intermediate and plays an important role in the binding (Figure 3). W593 lingers around, forming no major interactions with TRPS or the ligand. It is an “unhappy” water molecule and could be displaced, providing a way to improve the potency of the ligand.
Figure 3.
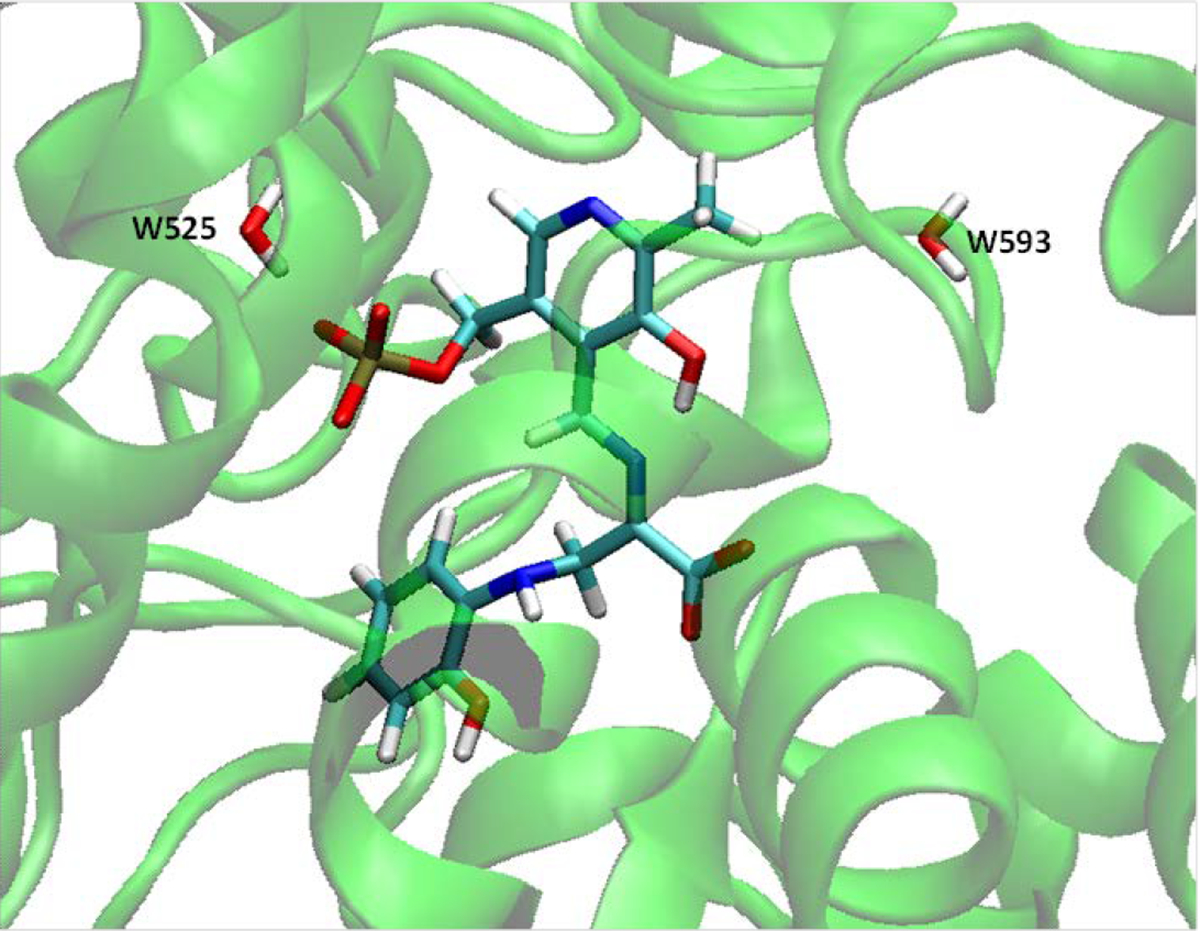
Intermediate 2-aminophenol quinonoid in the catalytic site of TRPS β-subunit, together with two water molecules nearby.
2. Correction of MM/PBSA calculation results
Guimaraes and Mathiowetz reported the first attempt to use WaterMap as a correction term to replace the protein desolvation term in the generalized-born (GB) model for improving MM/GBSA rescoring[81]. In WaterMap, protein and ligand entropic changes and intramolecular strain upon binding as well as ligand–solvent and protein–ligand interaction energies are excluded from the free energy calculations. In contrast, the MM/GBSA method includes most of the terms. However, WaterMap includes the loss of protein–solvent interactions when the cavity is created in the binding site, a term that is not reliably computed by the continuum solvation model. Therefore, WaterMap and MM/GBSA are complementary and could be used together and give promising results by the examination of a series of CKD2 and fXa inhibitors. Inspired by this idea, we strictly followed this strategy to score the same series of CDK2 and Factor Xa inhibitors. In our calculations, Amber force-field parameters were assigned to both the proteins and the ligands, and a Poisson-Boltzmann (PB) model was used to estimate the solvation energies.
In total, 29 CDK2 inhibitors and 19 Factor Xa inhibitors were used in this calculation. These congeneric series contain a reasonable number of compounds as well as activity data (Ki values for factor Xa series and IC50 values for CDK2 series) covering three orders of magnitude. The calculated MM/PBSA energies and the experimental data for these two series of inhibitors are plotted in Figure 4. MM/PBSA calculations neglect configurational entropy term, which acts as the penalty to the free energy and cancels most of the enthalpy term, thus leading to much more negative values in MM/PBSA energies than those of experimental ones. Use of MM/PBSA alone calculations for two systems, CDK2 and Factor Xa, resulted in only poor to moderate R2 values as in Figure 4A and Figure 4C, but the improvement with water energy correction is remarkable, for improved overall effectiveness and accuracy. Of note, in the MM/PBSA calculations (both alone and with water correction), the trajectories for the bound state are used to calculate the energies for the complex, the protein and the ligand. Also, the trajectories are not relaxed after the ligand removal for the protein energy calculations, which might account for the poorer performance of our MM/PBSA alone calculations as compared with the MM/GBSA calculations for the same series of proteins and inhibitors[81].
Figure 4.
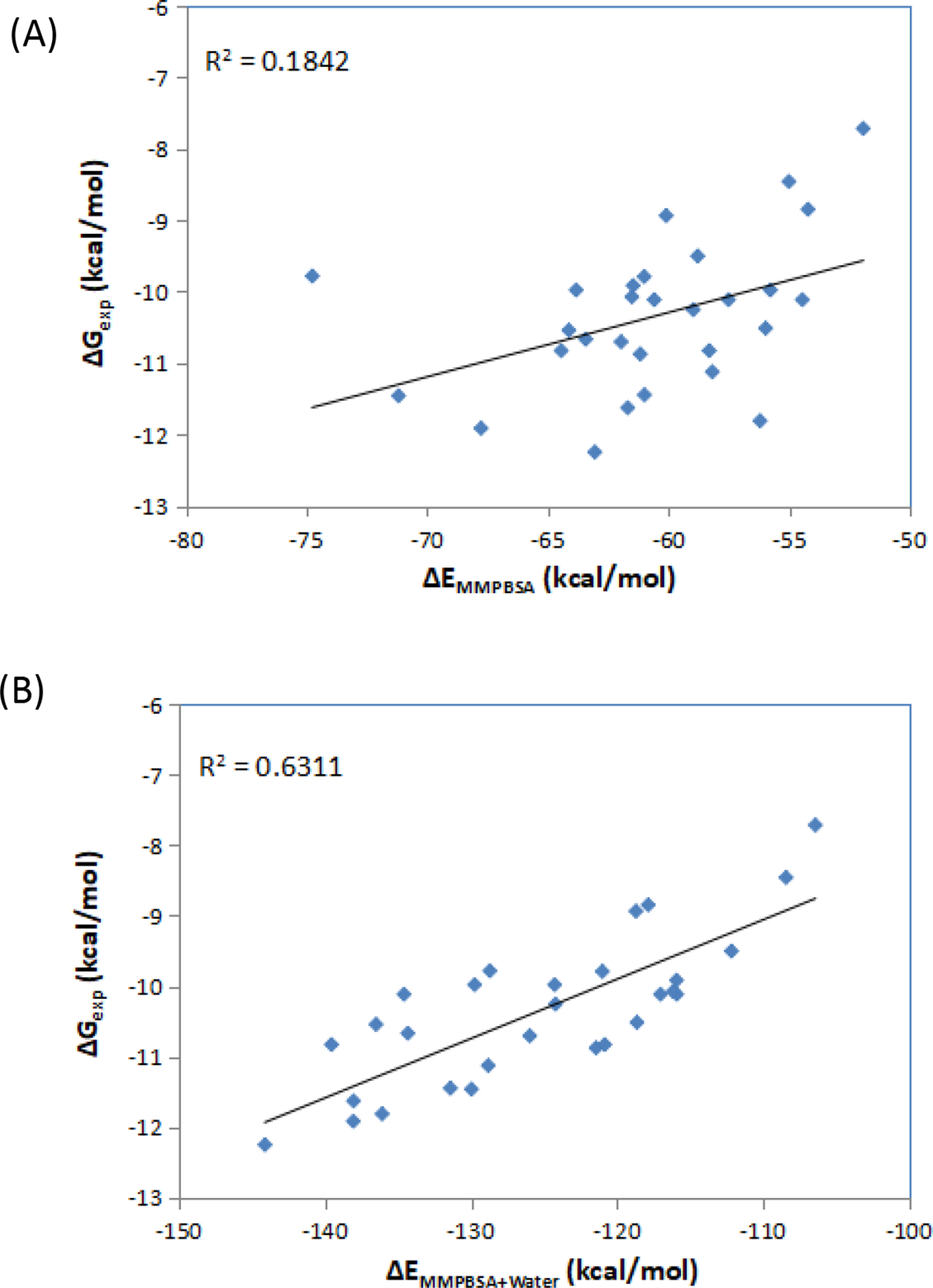
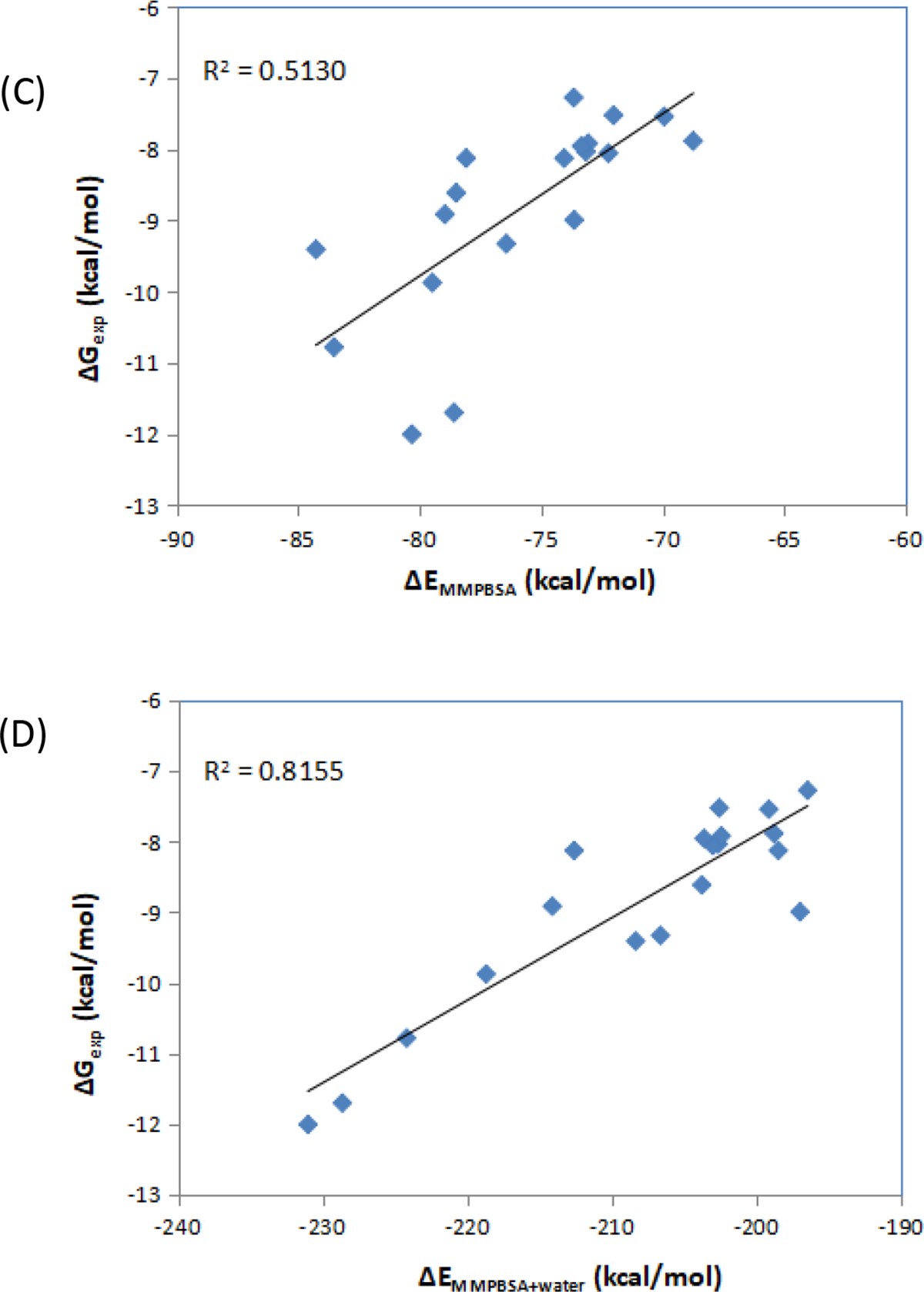
Correlation between the experimental free energies and MM/PBSA results. (A) MM/PBSA alone for CDK2 inhibitors; (B) MM/PBSA with water energy correction for CDK2 inhibitors; (C) MM/PBSA alone for factor Xa inhibitors; (D) MM/PBSA with water energy correction for factor Xa inhibitors.
3. Water analysis in the protein–ligand association process
Because drug binding kinetics, such as the residence time, largely correlate with the drug’s efficacy in many protein systems, understanding a ligand’s binding kinetics and optimizing its kinetic profile can be advantageous for drug development. However, so far, little is known about the factors that govern the quantitative structure–kinetics relationship (QSKR). We used our water analysis strategy to investigate how water molecules may affect the binding kinetics of Ritonavir and xk263 to HIV protease (HIVp), a slow and a fast binder. The thorough presentation of this work has been published elsewhere[82]. In this paper, we focus on the water removal analysis and implications for drug kinetics.
We performed more than 50 classical MD simulations ranging from 200 ns to 14 μs to examine the binding processes of xk263 and ritonavir. The fast binder xk263 preferentially binds to HIVp with a semiopen-flap conformation, which reflects the induced-fit mechanism. This binding is accomplished by the dehydration of surrounding water molecules, thereby allowing xk263 to directly interact with the protein and induce flap motion to allow xk263 access to the active site. The slower binder ritonavir successfully binds to HIVp with an open-flap conformation, which reflects the conformation selection mechanism. Because of the more polar features of ritonavir, the hydration shell surrounding it weakens ritonavir’s ability to directly interact with the protease and induce flap motion; thus, ritonavir must wait for HIVp to sample an open conformation for favorable binding. However, computed interactions of HIVp and the ligand could not explain why xk263 is a 1000-times faster binder than ritonavir. We then focused on the transient bridging water molecules that stayed between the protein and ligand for >100 ps. We selected conformations while a drug was approaching the protein to perform several 100-ps MD simulations. A frame was saved every 5 ps in the short MD runs, so we computed the removal free energy for 21 frames from each MD. The calculated removal energies fluctuate. For xk263, the water molecules we studied have removal energies of 1.5 to 2.0 kcal/mol, showing their loose binding capability to the HIVp–xk263 system. In fact, most transient bridging water molecules in the HIVp–xk263 system stayed for a considerably short period of time (i.e., 15 ± 5 ps). A closer inspection of the conformations reveals that water molecules have to form a network to bridge the ligand and the protein, and such a network appears to be vulnerable in the 100-ps MD run. In contrast, a water molecule between HIVp and ritonavir has an average removal energy of ~5.0 kcal/mol. This stable water molecule directly bridges the thiazole moiety of ritonavir and residues of HIVp (Figure 5) and seems very stable in the 100-ps MD run. The tight bridging water contributes longer intermediate states and slower binding processes for HIVp–ritonavir than HIVp–xk263. Compared with xk263, ritonavir has more polar functional groups that may contribute to the larger FE and longer dwell time of the transient bridging water molecules in the HIVp−ritonavir intermediate states. These polar functional groups provide more opportunities to form a hydrogen bonding network with the surrounding water molecules. This result sheds light on controlling binding kinetics by transient water molecules.
Figure 5.
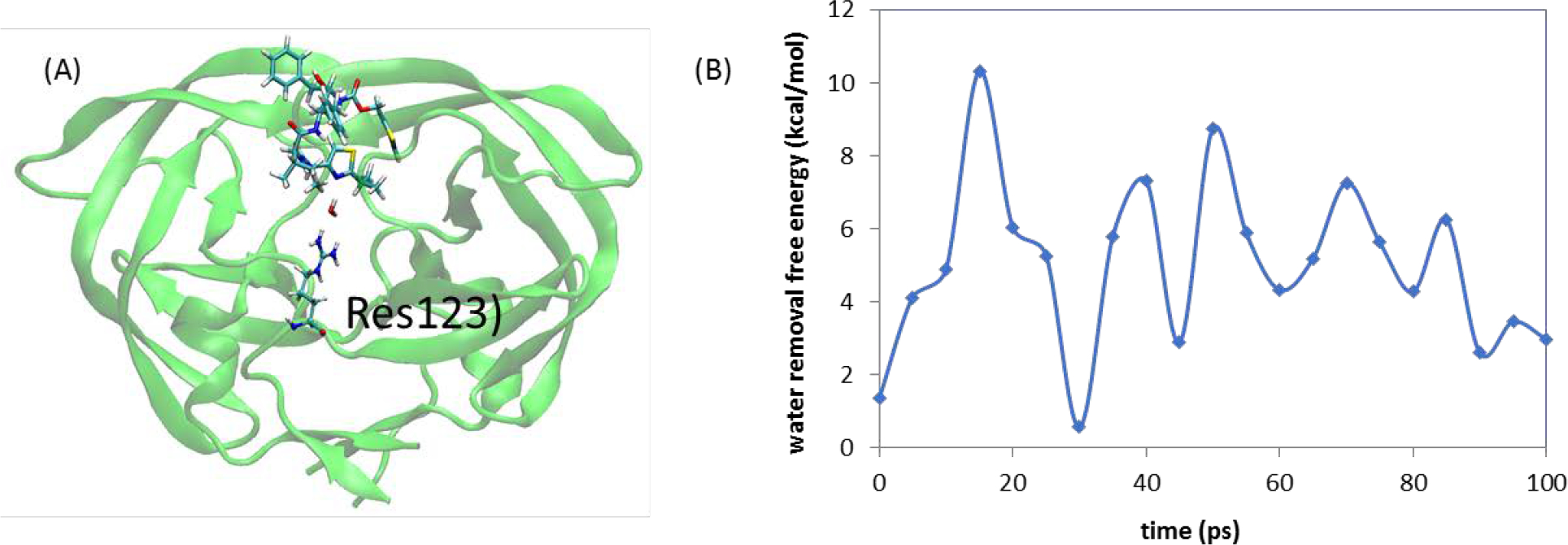
Free energy needed to remove a specific water molecule during ritonavir dissociation. (A) A bridging water molecule was found between ARG8 of HIVP and ritonavir; (B) computed water removal free energy for this transient bridging water molecule with > 100-ps dwell time. An average removal free energy is ~5 kcal/mol.
CONCLUSION
Water molecules in a binding pocket of a target protein should be considered in de novo drug design. Methods that accurately capture the effects with these water molecules improve protein–ligand docking and scoring. The improved methods also result in accurately predicting binding affinity and advancing the estimation of ligand binding kinetics. As discussed, our water analysis strategy can capture the key bridging water molecules and estimate their stability through removal free energy calculation in multiple protein–ligand systems. With the aid of our strategy, computations should save time and cost in drug discovery. It will guide docking programs to consider bridging water molecules explicitly and accurately help re-score the docked results, which will improve the results in the lead identification stage. Our strategies also allow for rigorous thermodynamic end-state analysis to dissect changes in enthalpy and entropy of water molecules in the free and bound state of a protein system, to assist in drug modification. We also demonstrated use of the strategy to post-analyze molecular dynamics simulation results and consider free energy contributions from crucial water molecules for estimating ligand association and dissociation energy barriers, which is linked to the drug-target residence time. Such knowledge could be advantageous in the context of lead optimization.
Supplementary Material
ACKNOWLEDGEMENT
The VM2 software package was provided by VeraChem LLC and is available free for academic use at www.verachem.com.
FUNDING SOURCES
This study was supported by the US National Institutes of Health (NIH, GM-109045).
Footnotes
CONFLICTS OF INTEREST
There are no conflicts to declare.
DATA AVAILABILITY
The data that support the findings of this study are available on request from the corresponding authors.
REFERENCES
- [1].Hayashi T Water at Interfaces: Its Behavior and Roles in Interfacial Phenomena. Chemistry Letters, 2021, 50(6): 1173–1180. [Google Scholar]
- [2].Maurer M, Oostenbrink C Water in protein hydration and ligand recognition. Journal of Molecular Recognition, 2019, 32(12): e2810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Wong S; Lightstone FC Accounting for water molecules in drug design. Expert Opinion on Drug Discovery 2011, 6, 65–74. [DOI] [PubMed] [Google Scholar]
- [4].Ge Y; Wych DC; Samways ML; Wall ME; Essex JW; and Mobley DL Enhancing Sampling of Water Rehydration on Ligand Binding: A Comparison of Techniques. Journal of Chemical Theory and Computation, 2022, 18(3): 1359–1381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Fu H; Chen H; Blazhynska M; de Lacam EGC; Szczepaniak F; Pavlova A; Shao X; Gumbart JC; Dehez F; Roux B; Cai WS; Chipot C Accurate determination of protein: ligand standard binding free energies from molecular dynamics simulations. Nature Protocols, 2022: 1–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Zsidó BZ; Hetényi C The role of water in ligand binding. Current Opinion in Structural Biology, 2021, 67: 1–8. [DOI] [PubMed] [Google Scholar]
- [7].Ross GA; Morris GM; Biggin PC Rapid and Accurate Prediction and Scoring of Water Molecules in Protein Binding Sites. PLoS ONE 2012, 7(3): e32036. doi: 10.1371/journal.pone.0032036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Huang N; Shoichet BK Exploiting ordered waters in molecular docking. J. Med. Chem, 2008, 51 (16), 4862–4865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Spyrakis F; Ahmed MH; Bayden AS; Cozzini P; Mozzarelli A; Kellogg GE The Roles of Water in the Protein Matrix: A Largely Untapped Resource for Drug Discovery. J. Med. Chem. 2017, 60 (16), 6781–6827. [DOI] [PubMed] [Google Scholar]
- [10].Gilson M; Honig B Calculation of the total electrostatic energy of a macromolecular system: solvation energies, binding energies, and conformational analysis. Prot. Struct. Func. Gen. 1988, 4, 7–18. [DOI] [PubMed] [Google Scholar]
- [11].Sitkoff D; Sharp KA; Honig B Accurate calculation of hydration free energies using macroscopic continuum models. J. Phys. Chem. 1994, 98, 1978–1988. [Google Scholar]
- [12].Gilson MK; Honig B The inclusion of electrostatic hydration energies in molecular mechanics calculations. J. Comput. Aided. Mol. Des. 1991, 5, 5–20. [DOI] [PubMed] [Google Scholar]
- [13].Qiu D; Shenkin P; Hollinger F; Still WC The GB/SA continuum model for solvation. A fast analytical method for the calculation of approximate Born radii. J. Phys. Chem. A 1997, 101, 3005–3014. [Google Scholar]
- [14].Schaefer M; Karplus M A comprehensive analytical treatment of continuum electrostatics. J. Phys. Chem. 1996, 100, 1578–1599. [Google Scholar]
- [15].Sitkoff D; Sharp K; Honig B Accurate calculation of hydration free energies using macroscopic solvent models. J. Phys. Chem. 1994, 98, 1978–1988. [Google Scholar]
- [16].Onufriev AV; Case DA Generalized Born implicit solvent models for biomolecules. Annual review of biophysics, 2019, 48: 275–296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Zhou S; Weiß RG; Cheng LT; Cheng Li-Tien, Dzubiella J; McCammon JA; Li B Variational implicit-solvent predictions of the dry–wet transition pathways for ligand–receptor binding and unbinding kinetics. Proceedings of the National Academy of Sciences, 2019, 116(30): 14989–14994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Chakravorty A; Panday S; Pahari S; Zhao S; and Alexov E Capturing the Effects of Explicit Waters in Implicit Electrostatics Modeling: Qualitative Justification of Gaussian-Based Dielectric Models in DelPhi. Journal of chemical information and modeling, 2020, 60(4), 2229–2246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Okiyama Y; Watanabe C; Fukuzawa K; Mochizuki Y; Nakano T; Tanaka S Fragment molecular orbital calculations with implicit solvent based on the Poisson–Boltzmann equation: II. Protein and its ligand-binding system studies. The Journal of Physical Chemistry B, 2018, 123(5): 957–973. [DOI] [PubMed] [Google Scholar]
- [20].Herbert JM Dielectric continuum methods for quantum chemistry. Wiley Interdisciplinary Reviews: Computational Molecular Science, 2021, 11(4): e1519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Izadi S; Harris RC; Fenley MO; Onufriev AV Accuracy comparison of generalized Born models in the calculation of electrostatic binding free energies. Journal of chemical theory and computation, 2018, 14(3): 1656–1670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Mahmoud SSM; Esposito G; Serra G; Fogolari F Generalized Born radii computation using linear models and neural networks. Bioinformatics, 2020, 36(6): 1757–1764. [DOI] [PubMed] [Google Scholar]
- [23].Tolokh IS; Thomas DG; Onufriev AV Explicit ions/implicit water generalized Born model for nucleic acids. The Journal of Chemical Physics, 2018, 148(19): 195101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Dong L; Qu X; Zhao Y; Wang BJ Prediction of Binding Free Energy of Protein–Ligand Complexes with a Hybrid Molecular Mechanics/Generalized Born Surface Area and Machine Learning Method. ACS omega, 2021, 6(48): 32938–32947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Wei H; Luo A; Qiu T; Luo R; Qi RX Improved Poisson–Boltzmann Methods for High-Performance Computing. Journal of chemical theory and computation, 2019, 15(11): 6190–6202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Pearlman DA Evaluating the molecular mechanics Poisson-Boltzmann surface area free energy method using a congeneric series of ligands to p38 MAP kinase. J. Med. Chem. 2005, 48, 7796–7807. [DOI] [PubMed] [Google Scholar]
- [27].Chen J; Brooks CL 3rd; Khandogin J Recent advances in implicit solvent based methods for biomolecular simulations. Curr. Opin. Struct. Biol 2008, 18, 140–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Gallicchio E; Paris K; Levy RM The AGBNP2 Implicit Solvent Model. J Chem. Theory Comput. 2009, 5, 2544–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Geschwindner S; Ulander J The current impact of water thermodynamics for small-molecule drug discovery. Expert Opinion on Drug Discovery, 2019, 14(12): 1221–1225. [DOI] [PubMed] [Google Scholar]
- [30].Limongelli V Ligand binding free energy and kinetics calculation in 2020. Wiley Interdisciplinary Reviews: Computational Molecular Science, 2020, 10(4): e1455. [Google Scholar]
- [31].Bruce NJ; Ganotra GK; Kokh DB; Sadiq SK; Wade RC New approaches for computing ligand–receptor binding kinetics. Current opinion in structural biology, 2018, 49: 1–10. [DOI] [PubMed] [Google Scholar]
- [32].Schiebel J; Gaspari R; Wulsdorf T; Ngo K; Sohn C; Schrader TE; Cavalli A; Ostermann A; Heine A; Klebe G Intriguing role of water in protein-ligand binding studied by neutron crystallography on trypsin complexes. Nature communications, 2018, 9(1): 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Dror RO; Pan AC; Arlow DH; Shaw DE Pathway and mechanism of drug binding to G-protein-coupled receptors. Proc. Natl. Acad. Sci. USA 2011, 108(32), 13118–13123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Lazaridis T Inhomogeneous fluid approach to solvation thermodynamics. I. Theory. The Journal of Physical Chemistry B 1998, 102, 3531–3541. [Google Scholar]
- [35].Li Z; Lazaridis T Computing the thermodynamic contributions of interfacial water. Methods Mol. Biol. 2012, 819, 393–404.. [DOI] [PubMed] [Google Scholar]
- [36].Nguyen CN; Kurtzman Young T; Gilson MK Grid inhomogeneous solvation theory: hydration structure and thermodynamics of the miniature receptor cucurbit[7]uril. The Journal of chemical physics, 2012, 137(4): 044101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Chen L; Cruz A; Roe DR; Simmonett AC; Wickstrom L; Deng N; Kurtzman T Thermodynamic decomposition of solvation free energies with particle mesh Ewald and long-range Lennard-Jones interactions in Grid Inhomogeneous Solvation Theory. Journal of Chemical Theory and Computation, 2021, 17(5): 2714–2724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Michel J; Tirado-Rives J; Jorgensen WL Prediction of the water content in protein binding sites. J. Phys. Chem. B 2009, 113(40), 13337–13346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Hamelberg D; McCammon JA Standard free energy of releasing a localized water molecule from the binding pockets of proteins: double-decoupling method. J. Am. Chem. Soc. 2004, 126, 7683–7689. [DOI] [PubMed] [Google Scholar]
- [40].Bayden AS; Moustakas DT; Joseph-McCarthy D; Lamb ML Evaluating free energies of binding and conservation of crystallographic waters using SZMAP[J]. Journal of chemical information and modeling, 2015, 55(8): 1552–1565.. [DOI] [PubMed] [Google Scholar]
- [41].Samways ML; Taylor RD; Macdonald HEB; Essex JW Water molecules at protein–drug interfaces: computational prediction and analysis methods. Chemical Society Reviews, 2021. [DOI] [PubMed] [Google Scholar]
- [42].Goodford PJ A computational procedure for determining energetically favorable binding sites on biologically important macromolecules. J. Med. Chem. 1985, 28(7), 849–857. [DOI] [PubMed] [Google Scholar]
- [43].Xiao W; He Z; Sun M; Li S; Li H Statistical analysis, investigation, and prediction of the water positions in the binding sites of proteins. J. Chem. Inf. Model. 2017, 57 (7), 1517–1528. [DOI] [PubMed] [Google Scholar]
- [44].Patel H; Grüning BA; Günther S; Merfort I PyWATER: A PyMOL plug-in to find conserved water molecules in proteins by clustering. Bioinformatics 2014, 30 (20), 2978–2980. [DOI] [PubMed] [Google Scholar]
- [45].Morozenko A; Stuchebrukhov AA Dowser++, a new method of hydrating protein structures. Proteins: Struct., Funct., Genet. 2016, 84 (10), 1347–1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].JeszenÅi N; Horváth I; Bálint M; van der Spoel D; Hetényi C Mobility-based prediction of hydration structures of protein surfaces. Bioinformatics 2015, 31:1959–1965. [DOI] [PubMed] [Google Scholar]
- [47].JeszenÅi N; Bálint M; Horváth I; van der Spoel D; Hetényi C Exploration of interfacial hydration networks of target-ligand complexes. J Chem Inf Model 2016, 56:148–158. [DOI] [PubMed] [Google Scholar]
- [48].Nittinger E; Flachsenberg F; Bietz S; Lange G; Klein R; Rarey M Placement of water molecules in protein structures: from large-scale evaluations to single-case examples. J Chem Inf Model 2018, 58:1625–1637. [DOI] [PubMed] [Google Scholar]
- [49].Li Y; Gao YD; Holloway MK; Wang R Prediction of the favorable hydration sites in a protein binding pocket and its application to scoring function formulation. J Chem Inf Model 2020. 10.1021/acs.jcim.9b00619. [DOI] [PubMed] [Google Scholar]
- [50].Wei W; Luo J; Waldispühl J; Moitessier N Predicting positions of bridging water molecules in nucleic acid-ligand complexes. J Chem Inf Model 2019, 59:2941–2951. [DOI] [PubMed] [Google Scholar]
- [51].Chen W; Gilson MK; Webb SP; Potter MJ Modeling Protein-Ligand Binding by Mining Minima, J Chem Theory Comput, 2010, 6(11): 3540–3557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Chen W; Ren X; Chang CE Discovery of New CDK8/CycC ligands with a Novel Virtual Screening Tool, ChemMedChem, 2019, 14(1):107–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Huang YM; Chen W; Potter MJ; Chang CE Insights from Free-Energy Calculations: Protein Conformational Equilibrium, Driving Forces, and Ligand-Binding Modes, Biophysical Journal, 2012, 103(2):342–351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Roberts BC; Mancera RL Ligand-protein docking with water molecules. J. Chem. Inf. Model. 2008, 48, 397–408. [DOI] [PubMed] [Google Scholar]
- [55].Thilagavathi R; Mancera RL Ligand-protein cross docking with water molecules. J. Chem. Inf. Model. 2010, 50, 415–421. [DOI] [PubMed] [Google Scholar]
- [56].Matricon P; Suresh RR; Gao ZG; Panel N; Jacobson KA; Carlsson J Ligand design by targeting a binding site water. Chemical science, 2021, 12(3): 960–968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Wahl J; Smiesko M Assessing the predictive power of relative binding free energy calculations for test cases involving displacement of binding site water molecules. Journal of chemical information and modeling, 2019, 59(2): 754–765. [DOI] [PubMed] [Google Scholar]
- [58].Verdonk ML; Chessari G; Cole JC; Hartshorn MJ; Murray CW; Nissink JWM; Taylor RD; Taylor R Modeling water molecules in protein-ligand docking using GOLD. J. Med. Chem. 2005, 48(20), 6504–6515. [DOI] [PubMed] [Google Scholar]
- [59].Darby JF; Hopkins AP; Shimizu S; Roberts SM; Brannigan JA; Turkenburg JP; Thomas GH; Hubbard RE; Fischer M Water networks can determine the affinity of ligand binding to proteins. Journal of the American Chemical Society, 2019, 141(40): 15818–15826. [DOI] [PubMed] [Google Scholar]
- [60].Chen D; Li Y; Zhao M; Tan W; Li X; Savidge T; Guo W; Fan XL Effective lead optimization targeting the displacement of bridging receptor–ligand water molecules. Physical Chemistry Chemical Physics, 2018, 20(37): 24399–24407. [DOI] [PubMed] [Google Scholar]
- [61].Ben-Shalom IY; Lin Z; Radak BK; Lin C; Sherman W; Gilson MK Accounting for the central role of interfacial water in protein–ligand binding free energy calculations. Journal of Chemical Theory and Computation, 2020, 16(12): 7883–7894.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Liu C; Wrobleski ST; Lin J; Ahmed G; Metzger A; Wityak J; Gillooly KM; Shuster DJ; McIntyre KW; Pitt S; Shen DR; Zhang RF; Zhang HJ; Doweyko AM; Diller D; Henderson I; Barrish JC; Dodd JH; Schieven GL; Leftheris K 5-Cyanopyrimidine derivatives as a novel class of potent, selective, and orally active inhibitors of p38-alpha MAP kinase. J. Med. Chem. 2005, 48(20), 6261–6270. [DOI] [PubMed] [Google Scholar]
- [63].Wahl J; Smieško M Thermodynamic insight into the effects of water displacement and rearrangement upon ligand modifications using molecular dynamics simulations. ChemMedChem, 2018, 13(13): 1325–1335. [DOI] [PubMed] [Google Scholar]
- [64].Chandler D Interfaces and the driving force of hydrophobic assembly. Nature 2005, 437(7059), 640–647. [DOI] [PubMed] [Google Scholar]
- [65].Berne BJ; Weeks JD; Zhou R Dewetting and hydrophobic interaction in physical and biological systems. Annu. Rev. Phys. Chem. 2009, 60, 85–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Rasaiah JC; Garde S; Hummer G Water in nonpolar confinement: from nanotubes to proteins and beyond. Annu. Rev. Phys. Chem. 2008, 59, 713–740. [DOI] [PubMed] [Google Scholar]
- [67].Jamadagni SN; Godawat R; Garde S Hydrophobicity of proteins and interfaces: Insights from density fluctuations. Annu. Rev. Chem. Biomol. Eng. 2011, 2, 147–171. [DOI] [PubMed] [Google Scholar]
- [68].Patel AJ Varilly P; Jamadagni SN; Hagan MF; Chandler D; Garde S Sitting at the Edge: How Biomolecules use Hydrophobicity to Tune Their Interactions and Function. J. Phys. Chem. B 2012, 116(8), 2498–2503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Tiwary P; Mondal J; Morrone JA, Berne BJ Role of water and steric constraints in the kinetics of cavity–ligand unbinding. Proceedings of the National Academy of Sciences, 2015, 112(39): 12015–12019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Bortolato A; Deflorian F; Weiss DR; Mason JS Decoding the role of water dynamics in ligand–protein unbinding: CRF1R as a test case. Journal of Chemical Information and Modeling, 2015, 55(9): 1857–1866. [DOI] [PubMed] [Google Scholar]
- [71].Wang L; Berne BJ; Friesner RA Ligand binding to protein-binding pockets with wet and dry regions. Proc. Natl. Acad. Sci. USA 2011, 108(4), 1326–1330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Tiwary P; Limongelli V; Salvalaglio M; Parrinello M Kinetics of protein–ligand unbinding: Predicting pathways, rates, and rate-limiting steps. Proceedings of the National Academy of Sciences, 2015, 112(5): E386–E391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Tian C; Kasavajhala K; Belfon KAA; Raguette L; Huang H; Migues AN; Bickel J; Wang Y; Pincay J; Wu Q; Simmerling C ff19SB: Amino-Acid-Specific Protein Backbone Paramters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2019, 16, 528–552. [DOI] [PubMed] [Google Scholar]
- [74].Chen W; Gilson MK ConCept: de Novo Design of Synthetic Receptors for Targeted Ligands. J. Chem. Inf. Model. 2007, 47, 425–434. [DOI] [PubMed] [Google Scholar]
- [75].Chen W; Chang CE; Gilson MK Concepts in Receptor Optimization: Targeting the RGD Peptide. J. Am. Chem. Soc. 2006, 128, 4675–4684. [DOI] [PubMed] [Google Scholar]
- [76].Tuccinardi T What is the current value of MM/PBSA and MM/GBSA methods in drug discovery?. Expert Opinion on Drug Discovery, 2021, 16(11): 1233–1237. [DOI] [PubMed] [Google Scholar]
- [77].Verhoest PR; Chapin DS; Corman M; Fonseca K; Harms JF; Hou XJ; Marr ES; Menniti FS; Nelson F; O’Connor R; Pandit J; Proulx-LaFrance C; Schmidt AW; Schmidt CJ; Suiciak JA; Liras S Discovery of a novel class of phosphodiesterase 10A inhibitors and identification of clinical candidate 2-[4-(1-methyl-4-pyridin-4-yl-1H-pyrazol-3-yl)-phenoxymethyl]-quinoline (PF-2545920) for the treatment of schizophrenia. Journal of medicinal chemistry, 2009, 52(16): 5188–5196. [DOI] [PubMed] [Google Scholar]
- [78].Bissantz C; Kuhn B; Stahl MA Medicinal chemist’s guide to molecular interactions. Journal of medicinal chemistry, 2010, 53(14): 5061–5084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Wright L; Barril X; Dymock B; Sheridan L; Surgenor A; Beswick M; Drysdale M; Collier A; Massey A; Davies N; Fink A; Fromont C; Aherne W; Boxall K; Sharp S; Workman P; Hubbard RE Structure-activity relationships in purine-based inhibitor binding to HSP90 isoforms. Chemistry & biology, 2004, 11(6): 775–785. [DOI] [PubMed] [Google Scholar]
- [80].Niks D; Hilario E; Dierkers A; Ngo H; Borchardt D; Neubauer TJ; Fan L; Mueller LJ; Dunn MF Allostery and substrate channeling in the tryptophan synthase bienzyme complex: evidence for two subunit conformations and four quaternary states. Biochemistry 2006, 52, 6396–6411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Guimaraes CRW; Mathiowetz AM Addressing Limitations with the MM-GB/SA Scoring Procedure using the WaterMap Method and Free Energy Perturbation Calculations. J. Chem. Inf. Model.2010, 50, 547–559. [DOI] [PubMed] [Google Scholar]
- [82].Huang YM; Raymundo MAV; Chen W; and Chang CE Mechanism of the association pathways for a pair of fast and slow binding ligands of HIV-1 protease, Biochemistry, 56(9):1311–1323, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding authors.


