Development of a new personalized staff-scheduling method with a work-life balance perspective: case of a hospital

Abstract

Burnout rates and dissatisfaction among healthcare workers remain high due to long working hours. One possible solution to this problem is to let them choose their weekly working hours and starting times in order to achieve a work-life balance. Moreover, a scheduling process that responds to changing healthcare demands at different times of the day should increase work efficiency in hospitals. In this study, a methodology and software were developed to schedule hospital personnel, taking into account their preferences regarding working hours and starting time. The software also allows the hospital management to determine the number of staff needed at different times of the day. Three methods and five working-time scenarios characterized by different divisions of working time are proposed to solve the scheduling problem. The Seniority score Priority assignment Method appoints personnel prioritizing seniority, whereas the newly developed Balanced and Fair assignment Method and Genetic Algorithm Method aim for a more nuanced distribution. The methods proposed were applied to physicians in the internal diseases department in a specific hospital. Weekly/monthly scheduling of all employees was carried out with the software. The results of scheduling factoring in work-life balance, and the performances of algorithms are shown for the hospital where the application was trialled.

Introduction

Healthcare staff (e.g., doctors, nurses, and technicians) are expected to carry out their jobs (i.e., diagnostic and treatment care) calmly and carefully and be responsive to patient needs. This requires workload balance taking account of social and family life. Efficient scheduling for the staff should aim to increase job satisfaction, reduce burnout, and help them focus on their work.

Personnel efficiency and job satisfaction will also be improved by scheduling weekly working and daily starting hours appropriate to their needs and requests. Physicians are the most expensive and scarcest group of hospital employees and need to be carefully managed. To maintain the stability of staffing, the job satisfaction of physicians is essential (Hinami et al., 2012). Personal preferences, qualifications, and many other criteria must be taken into account to do appropriate planning. This makes it necessary to utilize state-of-the-art digital solutions to overcome inefficiency. Moreover, making appropriate plans for allocating personnel will increase productivity and better provide for patients’ needs (Topaloglu & Özkarahan, 2004).

Work-life balance (WLB) is recognized as a crucial issue to tackle. Personnel inefficiency sometimes arises from unbalanced work and social/family life. WLB can be briefly described as a situation where the work and personal-life demands on an individual are in balance (Lockwood, 2003); or where employees are able to fulfil their family and work responsibilities simultaneously without any problems. This balance can be achieved by harmonizing the demands, purposes, and goals arising from the individual’s work area and family and personal needs (Pichler, 2008). As a result of employees experiencing work-family conflict, employee job dissatisfaction may arise, as well as increased staff turnover and absenteeism, lower job performance and increased job stress (Rose et al., 2007). In another study, 27% of employees in the EU perceived that they spent too much time at work; 28% thought they spent too little time with their family; 36% thought they did not have enough time for friends and other social relationships; 51% believed that they did not have enough time for their hobbies and interests (Kotowska et al., 2010). Yildirim and Aycan (2008) found that academic and clinical nurses’ work demands (i.e., excessive workload, irregular work schedules, long working hours) were significantly correlated with work-family conflict. The job and life satisfaction of nurses were also negatively affected by work-family conflict. Moreover, it is indicated by exploratory analyses that social support influences work-family conflict and job satisfaction. The study suggested that improved work conditions (reduced workload and regular work schedule) could assist in improving the well-being of nurses.

The problem in work-life balance stems from disproportionate time-sharing between work, family, or individual needs. The ability to choose daily working times and starting times on a weekly basis will go a long way toward solving this problem. With the aim of achieving better work-life balance, doctors and nurses working at the hospital can be provided with a software tool to choose their weekly uptimes and start times according to their preferences. For this purpose, a methodology and specially designed software tool are extensively studied. The developed software tool provides a personalized weekly/monthly work-time list aimed at optimizing working hours and starting times to improve the employees’ work-life balance.

The main aim of the developed tool—WLB-Tool henceforth—is to provide a work-life balance in which the hospital staff can indicate their weekly uptime and start time preferences. For the purposes of this study, a group of doctors in the internal medicine department within a university hospital was used. The physicians were organized with different methods and scenarios taking account of work-life balance and scheduled by the proposed WLB-Tool. The results of personnel scheduling and the percentage correlation with each staff member’s requests are given for comparison.

While the literature abounds with studies on related problems and solution methods, none of them approach the work-life balance problems with a perspective focusing on personnel preferences in terms of their weekly working and starting times. In this study, the daily timetable on a weekly basis was further divided into chunks in order to better meet staff preferences. The case study mentioned above was applied, and a suggestion was made to the hospital management to divide a day into desired working periods and apply the desired methodology, and to the workers to state scheduling preferences (on weekly working and starting times). The WLB-Tool, in this study, provided hospital management and workers with output lists that indicated each staff member’s working days and hours and the group of personnel working together for each period.

The novelty of this study lies in focusing on work-life balance and considering the preferences of working staff in order to optimize personal timetables. To the best of our knowledge, there is no study in the scientific literature that attempts to improve workers’ work-life balance with a scheduling system into which the workers can register their preferences for both weekly working hours and starting times. In contrast, the software and algorithms developed in this study ensure that the employees can indicate their preferences for weekly working times and the time periods they can work. The result is a timetable that best meets the needs and preferences of staff.

Although many studies have been conducted to address the problem using various optimization approaches such as genetic algorithms, no scheduling study has been found that gives staff preferences the highest priority, as does this study. It has become evident that personnel enabled to choose weekly working and starting hours themselves will solve this problem to a large extent. With the aim of achieving work-life balance, doctors and nurses at the hospital can be provided with access to the WLB-Tool to choose their own weekly uptimes and start times based on their needs and preferences. This has been demonstrated in the case study of doctors and nurses in the internal medicine department of a university hospital. The results obtained suggest that the success of the algorithms can be determined from the highest correlation rate with the physicians’ own preferences.

The remainder of this paper is organized as follows: In Sect. 2, the related literature and contributions of the present paper are discussed, while in Sect. 3, the structure and features of the developed work-life balance methodology, scheduling methods and mathematical models are explained. In Sect. 4, a case study of scheduling scenarios related to improving the current situation of staff in a hospital and starting work in accordance with the new work-life balance and weekly working time are explained. In Sect. 5, the results of the work-life balance scenarios and the scheduling algorithms applied in the developed methodology, i.e., the extent to which the requests of the personnel were met, or the success of the algorithms in assigning personnel requests, are given and discussed. Some numerical results are presented. The evaluation of the results and the optimal solution are provided. In Sect. 6, the conclusions and future adjustments to the developed methodology are presented.

Background and the related literature

A survey was conducted to organize the working hours of the employees in the university hospital. A total of 138 doctors and nurses participated in the initial survey. Employees’ satisfaction and its effects were investigated in terms of flexible working hours or varied working hours and start times. When the survey was evaluated, it was understood that 13.8% of the employees were not satisfied with the current working hours and their positions; 41.3% of the employees did not have a problem with their families due to their current positions, and 29.7% of them had difficulties in family and business life due to their positions. Furthermore, 66% of the employees stated that they did not have any ideas or suggestions for determining working hours. Regarding the questions about the appropriateness of working hours, 30% of the employees replied that they found them appropriate, while 38.4% replied that they did not. The remaining 40.6% said that they were “partially satisfied” with the programmed working hours. Therefore, it was understood from the survey results that a significant proportion of employees was not satisfied with the duration of work and the work schedule, and that they would be more satisfied with a flexible work schedule in which they could determine the working and start time (Koruca & Boşgelmez, 2018).

Allowed flexibilities in operational research methodology, work-rest scheduling, and shift scheduling for fatigue prevention or alleviation are discussed in the study. Scientific applications in manufacturing, construction, transportation, hospitals, and services are examined, and it is shown in this study that different scientific studies contribute many effective algorithms and heuristic solution procedures to work-related fatigue reduction and work-rest scheduling issues (Xu & Hall, 2021).

Unbalanced working hours of employees in the hospital might cause prolongation of treatment and diagnosis that eventually decreases service quality. Traditional longer working shifts in hospitals also reduce the motivation of physicians, nurses, and caregivers, thereby causing fatal medical errors (Gratias, 2002). To prevent such problems, daily working time can be divided into segments to provide more efficient arrangements depending on patient numbers and the availability of staff. Flexible, innovative, and self-directed working time models can be used to make hospitals more efficient (Gamber & Börkircher, 2008). Likewise, flexible and staff-oriented working-time models to improve staff work-life balance may provide effective timetabling of employees that can also be profitable for the hospital administration (Hornberger & Knauth, 2000).

Harris et al. (2010) studied the flexibility of working implementation and strategy on nursing work-life balance in managerial policy, and Harris et al. (2015) also studied the impact of 12-h shift patterns in nursing within five themes: ‘risks to patients’, ‘patient experience’, ‘risks to staff’, ‘staff experience’ and ‘impact on the organization of work’. Their paper was a guided study for non-nursing-related industries. Similarly, studies have been done on the effects of 12-h shifts on nursing perceptions (Saville, 2020), irregular shift work (Karhula et al., 2020), the impact of moving 12-h shift patterns (Suter et al., 2020), and the development of a participatory working time scheduling software on sickness absence (Turunen et al., 2020).

In the studies of Haar (2013), and Çalışkan and Sungur (2009), quantitative models were used to examine work-life balance. In the studies, married and single employees were investigated. Based on the differing expectations and conditions of both groups, an analytical scale was developed to measure work-life balance. It was observed that work-life balance has a positive effect on work motivation and increases both work and life satisfaction. Li et al. (2007) proposed an integrated staff-sizing system for staff planning and staff scheduling by applying Multiple Objective Linear Programming (MOLP) in order to iteratively revise unsatisfactory staff-scheduling. Their study was conducted with a nurse sizing model on managerial insights. Zülch et al. (2011) classified employees based on lifestyles and social roles. Lifestyles with predefined features were modelled for 12 different working systems; full-time and part-time, as well as fixed and flexible working systems, and the organizational model of existing employees was simulated for 12 alternative scenarios without personnel exchange. Their simulation study measured capacity utilization rate, physical stress, time stress, service rate, cost of capacity used, and service time. In order to provide efficient and effective management of nursing personnel, a new integrative long-term nurse staffing and shift scheduling approach was applied, considering working conditions and quality in a real-life environment (Maenhout & Vanhoucke, 2013). Similarly, nurses’ schedules and satisfaction improved in several units in a hospital by reducing overtime. Furthermore, the results showed that the number of undesirable shifts improved by approximately 34%, and overtime was reduced by approximately 80% while simultaneously reducing costs by just under 11% using the proposed centralized decision pooling model (Wright & Mahar, 2013).

Rerkjirattikal et al. (2020), in their study, developed a goal-programming approach to nurse planning that simultaneously considered workload fairness and individual preferences in shift and leave assignments. The case study of an operating room in an Australian hospital was used to demonstrate model capabilities to solve a real nurse scheduling problem. Job satisfaction factors identified in an interview and survey questionnaire were integrated into the model. Compared with manual scheduling results, more appropriate charts were obtained to improve the nurses’ perception of justice and preference satisfaction. The main contribution of this case study to the scientific literature is a Goal Programming Approach to nurse planning enabling the analysis of equitable and multiple individual preferences.

Goli et al. (2021) designed a fuzzy mixed-integer linear programming model to improve the scheduling and formation of parts within cells in a cellular manufacturing system (CMS) using automated guided vehicles (AGVs). They developed a hybrid genetic algorithm and a whale optimization algorithm, which were found to have better performance than other known algorithms (CPLEX, particle swarm optimization and ant colony optimization) in terms of computational efficiency and accuracy. Again, with similar optimization algorithms, Tirkolaee et al. (2020a) proposed a novel bi-objective MILP model for Pollution-Routing Problem with Cross-dock Selection (PRP-CDS) aimed at minimizing the total cost, including pollution and routing costs, and maximizing supply reliability. They used Multi-Objective Simulated-Annealing Algorithm (MOSA) and Non-dominated Sorting Genetic Algorithm II (NSGA-II) to provide efficient Pareto solutions and evaluated NSGA-II as the most efficient tool for optimal route planning.

Doulabi and Khalilpourazari (2022) applied a two-stage stochastic method to minimize the sum of the fixed opening cost of operating theatres and expected overtime costs in their study of the weekly planning problem. They proposed a state variable model which has fewer number of variables and constraints compared to an equivalent scenario-based stochastic programming model. The results showed that their proposed model could find optimal solutions.

Similarly, in the glass industry, Rocha et al. (2014) offered a constructive heuristic approach for staff planning by comparing it with a Mixed Integer Programming (MILP) model. Computational times and solutions obtained for the problem were selected as performance indicators. Results were more effective than the MILP model on the problem in the glass industry as well as problems with different features. Van der Veen et al. (2016) presented an approach for creating feasible schedules that included schedules proposed by employees as input. Then they investigated how computational results and scheduling performance were affected by the various model parameters. Again, with a similar method, Tirkolaee et al. (2020c) developed a bi-objective Mixed Integer Programming (MILP) model for flow shop scheduling considering outsourcing option and Just-In-Time (JIT) delivery simultaneously, using Self-Adaptive Artificial Fish Swarm Algorithm (SAAFSA) and Multi-Objective Fuzzy Mathematical Programming (MOFMP) to obtain effective solutions with Pareto optimal solutions, using CPLEX.

Subsequently, mathematical models have been constructed to ensure patient care quality and help physicians maintain work/life balance, and harmonize their priorities with hospital requirements. As the number of equalization constraints increases, the optimization of physician scheduling becomes more complex, and a new class of valid inequalities and a polynomial separation algorithm are derived from being used with a branch-and-cut algorithm. Results have been presented for many different specialties and hospitals on the design of schedules (Damcı-Kurt et al., 2019). Abadi et al. (2021) took into account some new factors related to the appointment of nursing staff during the COVID-19 period. Appropriate scheduling of nursing staff and optimal appointment of nurses can significantly affect the quality of clinical facilities. Unlike routine nurse assignment problems, during the COVID-19 pandemic, nurses were often asked to leave, take breaks, and change environments while caring for patients. Considering this situation, typical scheduling scenarios were taken into account, and a new model of Hybrid Salp Herd Algorithm and Genetic Algorithm (HSSAGA) was proposed to optimize the scheduling and assignment of nurses. It is maintained that this proposed algorithm outperforms the most advanced approaches. Lan et al. (2019) examined the scheduling problem of physicians and healthcare personnel working in the polyclinics of large multi-branch hospitals. In order to increase the working efficiency of physicians, a health professional would be present for each physician during working hours. Also, their study examined the demand and available resources of the hospital, the workload of physicians and health personnel. Based on these constraints, their study aimed to minimize the dissatisfaction and cost of physicians, and the frequency of travel for physicians working in multiple clinics. A hybrid meta-heuristic SCA-VNS was proposed, combining the Sine Cosine Algorithm (SCA) and Variable Neighbourhood Search (VNS) based on the Hungarian iterative algorithm, which was included to improve the assignments of health professionals (Lan et al., 2019).

Cildoz et al. (2021) presented a solution to a long-term physician-scheduling problem in a mathematical model to allocate workdays and shift types among all physicians in an emergency department. The mathematical model was built using the actual calendar, including holidays, without simplifications. This eliminated the possibility of circular type solutions and involved a variety of constraints (demand, workload, ergonomics, fairness, etc.). A mathematical model was formulated for the problem of planning emergency physicians’ working times by including a hybrid algorithm combining continuous linear programming with the Greedy Randomized Adaptive Search Procedure (GRASP). Finally, the model created according to the Integer Linear Programming method, inspired by a natural environment, was applied as a module in a software program to create the charts of doctors in a local emergency service for a year.

In the study of Tsai and Li (2009), a staff scheduling system was developed. This system consisted of two phases, including hospital management requirements, government regulations, and nursing staff’s shift preferences. Among the nurses, the Genetic algorithm (GA) method was applied to prevent scheduling injustice. In the second stage, the nurse list program was organized, and the GA was also adopted to solve the optimal program. The results obtained from the solution with GA showed that the GA could be an effective tool to solve the nurse scheduling problem.

Simulation and GA methods were applied for the scheduling of nurses and additional staff assignment in order to reduce the queue of patients coming to the emergency department and to improve service quality. The simulation model simulated the entire flow from the emergency room for the patients to a near-optimal nurse-scheduling aiming to minimize the queue time of the patients (Yeh & Lin, 2007).

Similarly, many studies have also been conducted using meta-heuristics algorithms recently. On the problem of airline crew pairing, first, a novel search space was obtained by an improved dynamic-based genetic algorithm, a deadhead-minimizing pairing search and a partial solution approach (Demirel & Deveci, 2017). Then, the memetic and hill climbing-based GAM methodologies were used for optimizing airline crew pairing subject to formation and matching problems (Deveci & Demirel, 2018). As a popular research theme, the interval-valued fuzzy set multi-criteria decision-making approach improved by Simulated Annealing was applied to the problem of optimal location of electric charging stations (Turk et al., 2021), and the improved WASPAS method to determine the most suitable electric vehicle supply equipment (Erdogan et al., 2021).

Breuer et al. (2022) developed two robust optimization models to help determine the number of beds and nurses in hospital units/clinics and to plan for patient admissions, length of stay and staff number uncertainties, all of which are stochastic in practice. In the models, a case study involving different patient types and levels of care yielded results where resource sharing reduced costs, reducing the number of untreated patients by 85% for the budget model and up to 100% for the data-driven model. As a result, important implications were obtained about how uncertainty clusters are formed when applying robust optimization to health problems. Furthermore, with robust optimization in scheduling, Golpîra and Tirkolaee (2019) proposed a bi-objective Robust Optimization (RO) concept for maintenance and repair tasks scheduling problem to concurrently minimize total expected maintenance cost and maximize the total float of tasks under uncertain conditions. Using a similar method in another study, Tirkolaee et al. (2020b) proposed a novel bi-objective MILP model for allocating and scheduling disaster rescue units considering the learning effect, which has similarities with unrelated parallel machine scheduling (UPMS) problem and travelling salesman problem (TSP). They used an uncertainty-set-based robust optimization technique and multi-choice goal programming (MCGP) with utility functions to obtain effective solutions for the high-complexity problem.

The literature and related work scanned and reviewed above makes it evident that the work-life balance problem has not been studied to the extent that staff-preference driven timetables have been implemented. Optimization to maximize the staff experience and well-being while minimizing staff shortage and gaps in service delivery has not been addressed. The study presented in this work is the first-ever study to tackle this issue and resolve work-life conflicts.

Proposed methodology: implemented in work-life balance tool (WLB-Tool)

In order to show the feasibility of the method we developed and proposed, we created probable work-life balance scenarios based on the internal medicine clinic of a real university hospital in Turkey (Süleyman Demirel University Hospital), in line with the wishes of the doctors working in that unit. Then, using the WLB-Tool according to these scenarios, we scheduled the doctors’ work time, taking into account their weekly working hours and starting time preferences. The results and success of each scheduling method are also presented.

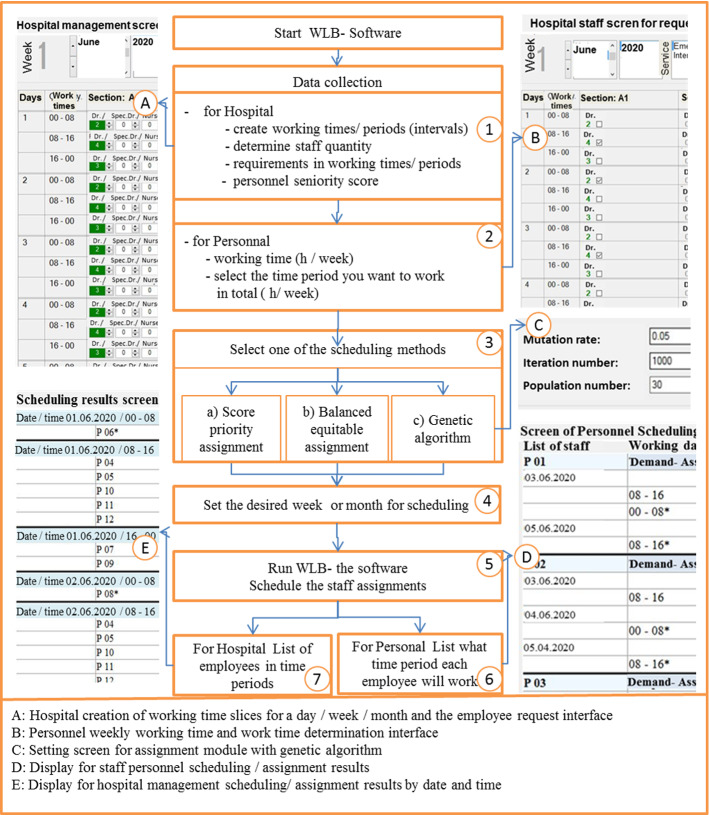
In this study, a flexible WLB-Tool was developed with C# programming. Figure 1 shows the general features, structural connections, input data, usage, workflow, and scheduling results of the software. This research aimed to schedule weekly or monthly shifts or working periods for hospital staff with the help of software developed for this study. The weekly working hours and starting times of staff were adjusted based on their requests, and the following steps were considered for the development of the methods:

1. Hospital administration must record the number of staff required at different hours of the day (Fig. 1(1)).

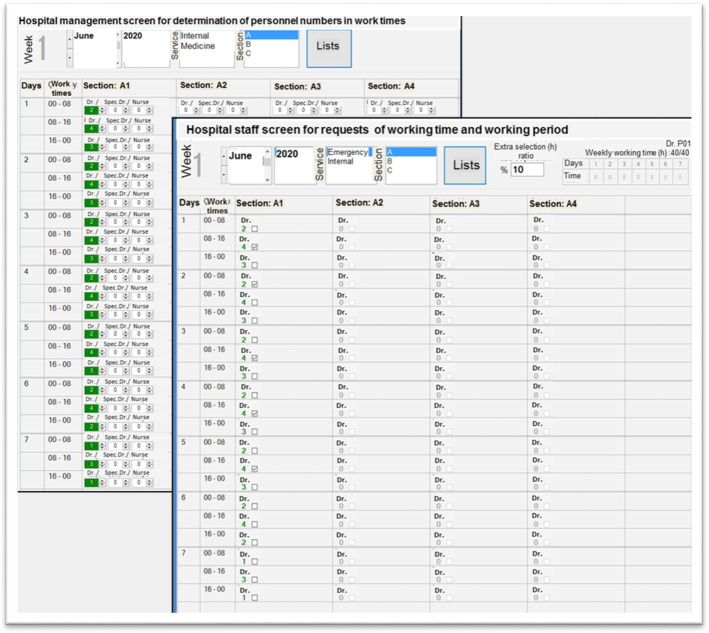
2. Ranking scores for seniority obtained from the parameters such as years of work experience, certificates, and medical capabilities of the hospital staff (doctors, nurses, and technicians), were recorded on the software’s database. In addition, this information was included in the assignment if the method that prioritized seniority scores was used in scheduling (Fig. 1(1)-(A), and Fig. 2).

3. Each person registered in the database must manually enter their preferred number of weekly working hours into the software database. They also needed to select the working time periods (starting and ending hours) they preferred, predefined by the hospital management (Fig. 1(2)-(B), Fig. 2).

4. Finally, hospital management must decide which of the following scheduling methods to apply (Fig. 1(3)). If the hospital management preferred to prioritize the seniority of their workers (experience, years of service, certificates or qualities personnel possess) in scheduling, Seniority score Priority assignment Method (SPM) was used. However, if the management aimed for fair and balanced assignment of personnel according to the employee’s preferences, the Balanced Fair assignment Method (BFM) ought to be used. SPM and BFM are important methods first developed in this study. Additionally, alongside the two methods indicated above, we have included the widely known and applied heuristic Genetic Algorithm Method (GAM) among our options since we desired to comparatively evaluate the scheduling results of an optimization algorithm with those of BFM.

Fig. 1.

Data flow diagram of the Work-Life Balance Tool (WLB-Tool) for hospital management

Fig. 2.

The interface to determine the number of staff for hospital management and requests of staff

The implemented scheduling methods in this study are as follows(Fig. 1(3)):

1. Seniority score Priority assignment Method (SPM): It assigned staff by including their scores in the appointments considering their year of employment, seniority, or qualifications. These factors vary from person to person and are required to calculate points for staff and must be saved in the database. A higher score provides priority/advantage in the appointment of staff. This information can only be applied in the Seniority score Priority assignment Method (SPM).

2. Balanced Fair assignment Method (BFM): This method is an optimization method developed particularly for this study. It is an equitable method for personnel that aims to meet each employee’s demands at the highest rate, focusing on equality and balance in meeting the demands among employees at the same time.

3. Genetic Algorithm Method (GAM): Genetic algorithms are frequently used optimization procedures based on natural selection and genetics. Therefore, genetic algorithms scan a vast territory of possible problems, and appropriate solutions are obtained quickly. Genetic algorithms were used in the study to meet the requests of all employees at the highest rate.

Mutation rate, iteration number, and population number must be entered before running this method. The basic operations used in the simple genetic algorithm are breeding, crossover, and mutation. After breeding, the crossover process is applied initially by selecting two individuals from the mating pool created during the breeding process. The next step is that a random crossover location is chosen over the design vector length. Finally, the mutation operator is applied to new sequences at a certain probability level. A randomly selected integer value replaces one or more values of a design vector in a mutation. In the mutation process, a random integer value between the upper and lower limits happens at a random place in the sequence. Finally, new sequences from crossover and mutation processes are replaced with the old sequences in the newly formed population.

Structure and features of work-life balance tool (WLB- Tool)

This paper focused on implementing personalized scheduling of hospital staff in C# programming language with the help of different methods/algorithms. Figure 1 shows the program flow, data collections, and scheduling outputs. This software aims to organize the weekly working hours and starting times of the personnel individually, considering both the requirements of the hospital and the requests of the personnel.

The software developed features saving the daily, weekly, and monthly required numbers of doctors and/or nurses in the units and shows them in the database. Hence, the hospital management can assign shifts by choosing any of the scheduling methods presented above. Hospital management creates working shifts by dividing one day (24 h) into several parts (3, 4, 5, or 6 parts) or periods of 3, 4, 5, 6, or 8 h to allow the staff to choose the time they prefer to work (Table 1). The numbers of personnel needed during the working periods or time intervals are recorded in the database with the help of the developed interface (Fig. 1(A), Fig. 2).

Table 1.

Result of Scenarios: (a) (A0-1) (A0-2) and (b) (S1, S2, S3)

(a) Scenarios (A0-1), (A0-2), personnel preferences’ rate of return (%) and fair assignation (a) results
HP: Hospital staff P1f:PersonalNoFemale P6m: PersonalNoMale SS: Seniority score NP: Number of preferences SPM, BFM, GAM (%): Satisfaction rate of preferences			A0-1: 3 periods (8 h, 8 h, 8 h) The work start time is selectable The working hours is fixed (40 h/W)					A0-2: 3 periods (8 h, 8 h, 8 h) The start time is selectable The Working hours is determinable (from 24 h/W to 56 h/W)
			Weekly work time					Weekly work time
HP	Age	SS	(h/W)	NP	SPM (%)	BFM (%)	GAM (%)	(h/w)	NP	SPM (%)	BFM (%)	GAM (%)
P1f	25–29	50	40	5	60	80	75	24	3	0	33	33
P2f	25–29	50	40	5	25	80	60	24	3	0	33	67
P3f	30–34	55	40	5	60	80	75	24	3	0	33	67
P4f	35–39	60	40	5	80	80	60	32	4	75	75	100
P5f	40–50	65	40	5	80	60	60	32	4	75	75	50
P6m	25–29	50	40	5	50	75	60	40	5	25	60	20
P7m	25–29	50	40	5	20	80	80	48	6	20	60	50
P8m	30–34	55	40	5	80	60	80	40	5	80	50	75
P9m	35–39	60	40	5	80	60	60	48	6	100	60	80
P10m	40–45	75	40	5	80	60	60	32	4	75	75	100
P11m	45–55	80	40	5	80	60	80	32	4	75	75	67
P12m	55–65	80	40	5	80	75	60	32	4	75	75	75
$\overline{\text{x}}$					64.6	70.8	67.5			50	58.7	65.3
$\mathrm{\sigma }$					22.3	9.7	9.4			37.6	17.6	24.1

(b) Scenarios (S1, S2, S3), personnel preferences' rate of return (%) and fair assignation (a) results
HP: Hospital staff SS: Seniority score WWT: Weekly working time (h/W) NP: Number of preferences SPM, BFM, GAM (%): Satisfaction rate of preferences				S1: 4 periods (6 h, 6 h, 6 h, 6 h) The work start time is selectable The Working hours is determinable (from 24 h/W to 56 h/W)				S2: 5 periods (8 h, 5 h, 4 h, 3 h, 4 h) The work start time is selectable The Working hours is determinable (from 24 h/W to 56 h/W)				S3: 6 period (4 h, 4 h, 4 h, 4 h, 4 h, 4 h) The work start time is selectable The Working hours is determinable (from 24 h/W to 56 h/W)
HP	Age	SS	(h/W)	NP	SPM (%)	BFM (%)	GAM (%)	NP	SPM (%)	BFM (%)	GAM (%)	NP	SPM (%)	BFM (%)	GAM (%)
P1f	25–29	50	24	4	25	75	75	5	50	80	50	6	0	67	40
P2f	25–29	50	24	4	0	50	100	5	17	60	40	6	0	50	50
P3f	30–34	55	24	4	75	50	50	5	40	60	80	6	83	50	60
P4f	35–39	60	32	5	100	80	40	7	86	71	100	8	88	63	50
P5f	40–50	65	32	5	100	80	80	7	86	50	71	8	88	63	50
P6m	25–29	50	40	7	43	57	71	10	55	89	78	10	44	60	60
P7m	25–29	50	45	8	50	63	86	10	20	78	67	11	55	64	92
P8m	30–34	55	40	7	71	71	71	9	67	60	44	10	90	78	67
P9m	35–39	60	45	8	100	100	100	10	100	100	73	11	100	100	92
P10m	40–45	75	32	5	100	80	40	7	86	43	43	8	88	88	88
P11m	45–55	80	32	5	100	80	80	7	100	50	63	8	88	88	88
P12m	55–65	80	32	5	100	60	60	7	86	57	63	8	88	88	88
X					72	70.5	71.1		66.1	66.5	64.3		67.7	71.6	68.8
a					34.9	14.9	20.4		24.9	17.3	17.8		35.3	16.4	19.6

For instance, explanations of the status of the personnel;

P1f: P1 Personnel No, f: Female; P6m: P6 Personnel No, m: Male

Seniority score(SS) (P1:50; The score 50 is a new worker or lowest in seniority, and 100 highest in seniority) (P1: 25 to 29 years) and weekly work time requests (WWT)

Staff Female: P1f, P2f, P3f, P4f, P5f, and Staff Male: P6m, P7m, P8m, P9m, P10m, P11m, P12m

12 staff are working in the hospital in total

$\overline{\text{x}}$ : The arithmetic mean; $\mathrm{\sigma }$ : the standard deviation

The daily, weekly or monthly report generation option and “Assign” button on this interface are common to all methods. However, unlike the other methods, in the genetic algorithm application, mutation rate, iteration number, and population number are registered as variable inputs into the program. The software lists the assignment results on its interface and generates report output if desired. The setup interface is provided in Fig. 1(3)-(C) to execute the assignments by the genetic algorithm.

One may note that parameter optimization is an essential issue for any parametric algorithm solving NP-hard problems. However, this situation is easier for the most commonly used optimization algorithms, such as Genetic Algorithms, Simulated Annealing, etc. In this paper, we use Genetic Algorithms with the parameters of the population size as ten chromosomes, crossover rate as 1.0 (fully crossover 100%), mutation rate as 5%, and iteration number as 1000 (Fig. 1(3)-(C)). These values were determined by examining a GA scheduling study (Aydemir & Koruca, 2015).

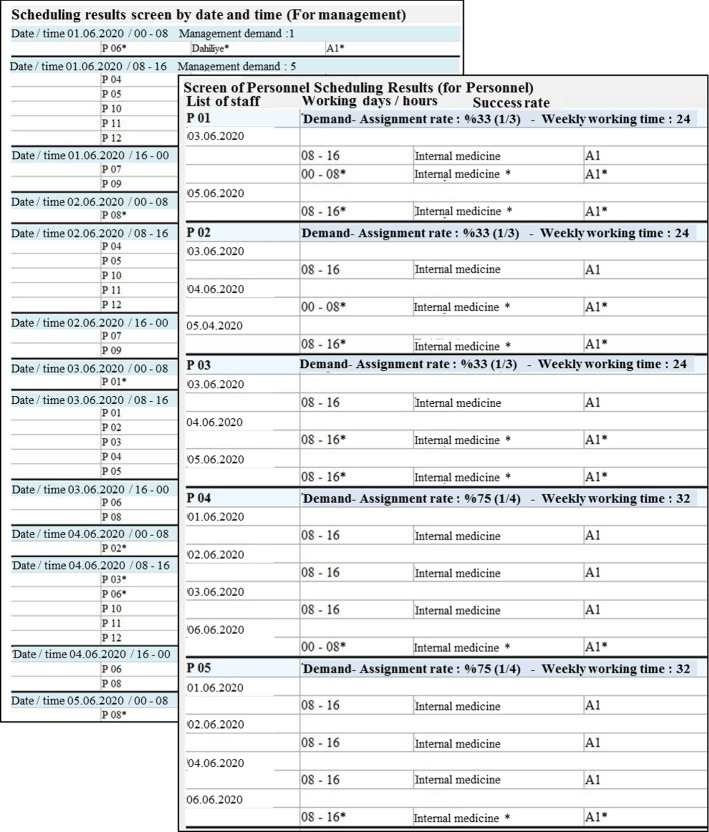
After entering into the database the numbers of personnel required for each working period and the selections made by the staff, the assignment/scheduling was started with the “Assign” button at the end of the selected adjustments for each method (Fig. 1(5)). As a result of the assignment procedures, (a) lists of working days and hours for each employee (Fig. 1(6)-(D)); (b) and lists of groups of working personnel for each period (Fig. 1(7)-(E), Fig. 3) were given. The work schedule can be edited weekly or monthly. In these lists, the percentages at which personnel choices were met and the number of weekly working hours for each person are also shown. The assignments marked with “A1*” in Fig. 3. (Results for personal) indicate that those assignments by the software were made from necessity rather than personnel request to ensure that management needs were fulfilled. Other assignments were made according to staff preferences.

Fig. 3.

Scheduling results for hospital management and staff (obtained from the WLB- Tool software)

Scheduling methods and properties

The software can meet the work-life balance expectations of the staff while appointing the number of personnel requested by the hospital management in all shift periods. Three scheduling algorithms have been developed in the software that will operate considering the number of personnel in shift periods determined according to management and personnel preferences, and the related processing methods are described below.

As aforementioned, the software can list all personnel work schedules according to Seniority Score Priority Assignment Method (SPM), or Balanced Fair Assignment Method (BFM), or Genetic Algorithm Method (GAM). In addition, the list of assignments and the rate of meeting the demands of the personnel are also given. The methods are described below, and the workflow is presented in (Fig. 1(3)).

1. Scheduling with Seniority Score Priority Assignment Method (SPM)

   The software allows hospital management to consider the seniority scores of the staff. The method prioritizes the staff with higher scores in assignments. The hospital management enters a score for each employee by evaluating and calculating the number of essential factors such as the number of certificates owned by the staff, hierarchical orders or ranking in terms of their years in service, and the satisfaction rate of the patients (as seen in Fig. 1 (1)). In Table 1, the personnel’s scores on a scale of 0–100 are recorded in the database. In this method, employees with higher scores are given priority in assigning the working periods they prefer.

2. Scheduling with Balanced/fair Assignment Method (BFM)

   Schedule appointments are assigned so that the periods they prefer are fairly apportioned among all personnel. It is aimed that the rate of meeting the demands of each staff member is equal or close to each other.

3. Scheduling with Genetic Algorithm Method (GAM)

   Optimization of the Genetic Algorithm Method uses factors such as chromosome, gene, population, crossover, selection, mutation, and iteration. Like the other two methods, it is a method that works by scheduling personnel assignments, optimizing all employees’ requests after the numbers of personnel required have been entered by the hospital management, and personnel working time preferences have been recorded in the system.

Problem description and mathematical modelling

In the above section, the features of the software and scheduling methods were explained. In this section, the applied/used constraints, parameters, decision variables, objective functions and mathematical models of the problem are discussed. Each scheduling method has its own prioritized constraints, decision variables and mathematical model that are given.

With the software prepared, the fact that the total working hours included in Damci’s 2018 study comply with labour law was added as a constraint. The first model was prepared with assignment conditions balanced among personnel (Damci, 2019). In this model, the aim is that the total working hours of the personnel are close to each other. In the second assignment model, a mathematical model based on seniority was prepared. In this model, the seniority score was defined for the personnel, and the seniority score was used as a constraint in the assignment. In addition to these two models, a mathematical model was developed using the genetic algorithm included in the Abadi 2021 study. The model developed for the heuristic algorithm used is intuitively related to the employee’s preferences and managerial appointment requests. In this study, the following parameters were used to develop the multi-objective mathematical model of the problem:

Notation

$i$	Number of personnel that is to enter assignment request to the software {1, …, n}
$j$	Number of shifts that can be preferred by the staff in the software (determined by the manager) {1, …, m}
$k$	Number of personnel assignment requests entered into the software {1, …, b}
$t$	The shift hour to be assigned in the software {1, …, s}
$l$	Number of units to work in the department {1, … r}
$\mathit{TST}$	Total staff working time
Additional different parameters in scheduling according to seniority score (SPM)
$T_i$	Total working time of $i$th personnel
$u$	Seniority score {0, …, 100}
Additional different parameters in scheduling personnel assignment percentages, being the most equitable/balanced and closest to each other (BFM)
$u_i$	Total working time of $i$th staff
$u_{\mathit{max}}$	Maximum seniority score in the software
$a$	Percentage of staff assignment
$\mathit{TPT}$	Total personnel working hours
Additional different parameters in genetic algorithm scheduling (GAM)
$h$	Mutation rate within the range of [0, 1]
$g$	Mutation rate entered into the software within the range of [0, 1]
$p$	Number of shifts in the software {1, …, c}
$P_i$	Objective function for maximum satisfaction of employee demands

The parameters used in the algorithms were adjusted in accordance with the problem in question, and the mathematical model created was defined in the Notation section. The number of employees in the software was defined by $i$th. The number of assignment requests entered by the management was defined by $j$th. After the constraints needed in solving the problem were determined, the functions were prepared for the main constraints in solving the problem. In addition, the functions were determined in accordance with the special constraints for the three algorithms used. The purpose functions were defined specifically for the algorithms in accordance with the determined functions.

Decision variables

In the prepared software, the hospital manager determines how many time zones (3, 4, 5, or 6 shifts) (as in Table 1) a day will be divided into, and the number of personnel to work in these time zones in the interface. Physicians first determine the weekly working hours and choose the appropriate working time zones for themselves from the time zones determined by the manager.

Any shift $n$ in which a staff member enters an assignment request is controlled by $x_{\mathit{ip}}$.

$$x_{\mathit{ip}}=\left\{\begin{array}{cc}1\hfill & iththenumberofpthshiftchosenbythepersonnel\\ 0\hfill & \mathit{otherwise}\end{array}\right)$$

In the personnel shift selection process, regardless of the number of personnel required by the manager, the relevant personnel are requested to assign the relevant shift to the active shifts. When all personnel complete shift’s request entry, the total number of requests entered by the personnel for a shift opened the manager is followed by the $\left(z_{\mathit{ik}}\right)$ variable.

$$z_{\mathit{ik}}=\left\{\begin{array}{cc}1\hfill & kthpersonnelrequestnumberenteredinithpersonnel\\ 0\hfill & \mathit{otherwise}\end{array}\right)$$

• $y_{\mathit{ikj}}$: $\mathit{jth}$ request number of $k$ requests entered by $\mathit{ith}$ personnel

  All requests entered by each personnel are transferred from the interface to the database. The traceability of the manager assignment request, which is appropriate in the mathematical model used, and the assignment request selected by the personnel are provided with the ${(y}_{\mathit{ikj}})$ variable.

• $w_{\mathit{ipl}}:$ $l^{\mathit{th}}$ section number of $i^{\mathit{th}}$ personnel in $p^{\mathit{th}}$ shift

  While entering their assignment request, the employee chooses the departments where he/she can work. They can make an assignment request to more than one department during their assignment request selection period for the relevant shift, but since the person will only work in one department during a shift, the variable ($w_{\mathit{ipl}})$ checked that the employee is assigned a task in only one department in the related shift with the ($w_{\mathit{ipl}})$ variable.

• $d_{\mathit{ikt}}:t$ hour working time of $k$ requests of $i^{\mathit{th}}$ personnel

  The working hours of the personnel are determined according to labour law and contracts. Controlling the total working time is monitored with the ($d_{\mathit{ikt}}$) variable, the assignment will be made relevant personnel’s working time in labour contract according to the demands entered.

• $e_{\mathit{uik}}:k^{\mathit{th}}$ assignment number of $i^{\mathit{th}}$ personnel with maximum $u$ seniority points

  In the seniority-based assignment algorithm used in the prepared software, a seniority score between 0 and 100 is assigned to the personnel according to their seniority years. Considering this seniority score, the assignment process is followed with the ${(e}_{\mathit{uik}}$) variable in cases where more than one personnel request for the same shift.

• $v_{\mathit{ikh}}:h\mathrm{is}\mathrm{mutation}\mathrm{rate}\mathrm{of}{i}^{\mathit{th}}{\mathrm{personnel}}^{{}^{\prime }}\mathrm{s}{k}^{\mathit{th}}\mathrm{is}\mathrm{assignment}\mathrm{number}$

  For $k^{\mathit{th}}$ assignment number, the mutation rate determined by the software for the request is monitored by $v_{\mathit{ikh}}$.

Constraints

1. A staff member can only work in one place at the same time. In other words, personnel cannot be assigned to more than one place at the same time.

2. No fewer or more personnel can be assigned than the number on the day and time-period determined by the management. In other words, the personnel needs must be met in line with the demands of the management.

Objective functions

Fulfilment of manager’s requests

For the basic constraints of the software, the first objective function was prepared according to the $f\left(x,,,y,,,\mathrm{w}\right)$ variables; in other words, the manager’s assignment demands are $\left(100,\%\right)$ paramount (1). For all personnel, the number of personnel entering the system, the total number of requests and the shift duration must be equal to the number of assignment requests entered by the manager and the total assignment request-period entered.

$$f\left(x,y,\text{w}\right)=\sum _{i=1}^s\sum _{k=1}^b\sum _{p=1}^c\sum _{i=1}^n(X_{\mathit{ip}}{w}_{\mathit{ipl}}t)=\sum _{i=1}^n\sum _{k=1}^b\sum _{j=1}^m\sum _{t=1}^s(y_{\mathit{ipj}}t)$$ 1

One staff member working in one shift and only in one department

The variable ($y)$ in the software gives the assignment requests entered by the manager. The variable ($z)$ gives the number of requests employees can enter. The variable ($y)$ gives the maximum number of requests that can be entered by employees. Also, the variable ($w)$ controls that an employee is assigned to only one department during the same shift. The Function $f\left(x,,,y,,,\mathrm{w}\right)$ is prepared according to the variables $x,y,w$ as follows (2):

$$f\left(w,y,z\right)=\sum _{i=1}^n\sum _{j=1}^m\sum _{k=1}^b\frac{y_{\mathit{ikj}}}{max(z_{\mathit{ik}})}=\sum _{l=1}^r\sum _{i=1}^n\sum _{p=1}^c{w}_{\mathit{ipl}}=1$$ 2

The total working time of a staff is equal to the assignment time

The total number of assignment requests and shift working times of the personnel assigned with the $f\left(d,,,x\right)$ variables should be equal to the total shift time entered into the software by the manager (3). At the same time, it should be equal to the total personnel working hours determined in accordance with labour law and contracts.

$$f\left(d,\text{x}\right)=\sum _{k=1}^b\sum _{t=1}^s\sum _{p=1}^n{d}_{\mathit{ikt}}=\sum _{t=1}^s\sum _{i=1}^n\sum _{p=1}^c{X}_{\mathit{ip}}t=TPT$$ 3

1. Scheduling with Seniority Score Priority Assignment Method (SPM)

   The $f\left(x,,,y,,,e\right)$ function (4) ensures that if one or more personnel are selected for the shifts for which the manager’s assignment request is entered, personnel using $\left(u_{\mathit{max}}\right)$ $u$ are assigned. Here, Eq. (4) runs with $u_{\mathit{max}}$ for staff $i$, $i=1,\cdots ,n$.

   $$f\left(x,y,\text{e}\right)=\sum _{k=1}^b\sum _{i=1}^n\sum _{p=1}^c\sum _{u=0}^{100}(e_{\mathit{uik}}{x}_{\mathit{ip}})>\sum _{k=1}^b\sum _{j=1}^m\sum _{i=1}^n\sum _{u=0}^{100}(y_{\mathit{ikj}}/e_{\mathit{uik}})$$ 4
   It is calculated according to the $f\left(x,,,y,,,z\right),f\left(w,,,y,,,z\right),f\left(d,,,x\right)$ functions prepared in accordance with the main constraints used in the solution of the problem in question. With the $f\left(x,,,y,,,e\right)$ function prepared for the Seniority Score Priority Assignment Method (SPM), a special function has been added to the algorithm used in the objective function. In the prepared objective function, the manager assignment requests are fulfilled with the $f\left(x,,,y,,,z\right)$ function. The $f\left(x,,,y,,,e\right)$ function is aimed at meeting the demands of the employees with the maximum seniority score. Maximum satisfaction of employee requests, which is the secondary main constraint of the problem under consideration, is provided by the objective function $P_i$ (5). It is ensured that each employee’s assignment requests are assigned at the maximum rate by running the objective function for each staff member $i$.

   $$P_i=max\left[f\left(x,y,z\right),f\left(w,y,z\right),f\left(d,x\right),f\left(x,y,e\right)\right]$$ 5

2. Scheduling with Balanced/fair Assignment Method (BFM)

   The difference of the algorithm prepared for the Balanced Fair assignment method from those of the two other methods is that the assignment success rate in this algorithm is similar for each employee. For the control of this structure, it is expected that the standard deviation of the assignments made with the software will be close to the standard deviation of the sum of the shift times of the employees. Likewise, the ratio of the number of assignment requests entered by all employees and the ratio of shift times to the total manager assignment requests is expected to be close to the total shift time. Constraint 7 in the $P_i(\text{.})$ function checks that the assignment percentage is maximum for each ith employee.

   The Balanced Fair Appointment Method (BFM) aims to ensure that each employee reaches the average assignment percentage. In this context, the $f\left(x,,,z,,,d\right)$ function has been developed (6). In addition, it is included in the $f\left(w,,,d,,,y\right)$ function as a condition that the requests made by the manager for the departments and the assignment made to an employee are approximately equal (7). With the main constraints, two functions developed specifically for this algorithm were included in the objective function, and the $P\left(i\right)$ function was formed (8). It is ensured that each employee’s assignment requests are assigned at the maximum rate by running the objective function for each staff member$i$.

   $$f\left(x,z,d\right)=SS\left(AVERAGE\left(\sum _{i=1}^n\sum _{k=1}^b\sum _{P=1}^c\left(x_{\mathit{ip}}{z}_{\mathit{ik}}{d}_{\mathit{ikt}}\right)\right)\right)\cong SS\left(a\right)\text{for all}i\in n$$ 6

   $$f\left(w,d,y\right)=\sum _{i=0}^n\sum _{k=1}^b\sum _{l=0}^r\sum _{j=1}^m\frac{\left(w_{\mathit{ipl}}{d}_{\mathit{ikt}}\right)}{y_{\mathit{ikj}}}\cong a_{\mathit{max}}\text{for all}i\in n$$ 7

   $$P_i=max\left[f\left(x,y,z\right)f\left(w,y,z\right),f\left(d,x\right),f\left(x,z,d\right),f\left(w,d,y\right)\right]$$ 8

3. Scheduling with Genetic Algorithm Method (GAM)

   The mutation rate in the natural population is quite low. The size of the mutation rate affects the performance of the GA (Engin and Fığlalı, 2002). Accordingly, the above objective function has been prepared so that the one with the minimum mutation rate can be preferred in assignment processes.

   The $\left(v\right)$ variable assigns a mutation rate to the personnel who make an assignment request for the relevant shift. After working algorithm then the obtained mutation rate is expected to be smaller than the mutation rate in the system. With this approach in the genetic algorithm, the mutation rate in all personnel assignment requests should be lower than the number of assignment requests entered into the system by the administrator and the mutation rate determined without running the software.

   In the algorithm customized for the assignment process with the Genetic Algorithm Method (GAM), the mutation rate assigned to the employees and the mutation rate of the system were compared, and the suitability for the assignment was sought. This fitness condition is included in the objective function with the $f\left(v,,,y\right)$ function (9). Purpose function $P_i$ is prepared by adding the main constraints $f\left(x,,,y,,,z\right),f\left(w,,,y,,,z\right),f\left(d,,,x\right)$ of the problem under consideration and the special constraints needed with the GAM (10). It is ensured that each employee’s assignment requests are fulfilled at the maximum rate by running the objective function for each staff member $i$.

   $$f\left(v,\text{y}\right)=\sum _{h=0}^1\sum _{k=1}^b\sum _{i=1}^n{v}_{\mathit{ikh}}<\sum _{i=1}^n\sum _{k=1}^b\sum _{j=1}^m{y}_{\mathit{ikj}}g$$ 9

   $$P_i=max\left[f\left(x,y,z\right),f\left(w,y,z\right),f\left(d,x\right),f\left(v,y\right)\right]$$ 10

Case study

Considering a hospital’s personnel structure and qualities, besides the scenarios derived from the initial situation (A0), S1, S2, and S3 scenarios were developed for the doctors in an internal medicine department according to the work-life balance approach. With the help of the developed software, three previously introduced methods were used for scheduling five working scenarios (A0-1, A0-2, S1, S2, S3). In these scenarios, personnel needs could be determined in the working time periods by considering the daily patient numbers. In case of a need for more staff on specific days and time periods, the number of personnel could be increased. The results of the scenarios and methods were measured. and the operation ability of the software was demonstrated.

Initial situation (A0): personnel working times in hospital

Usually, the daily working time in hospitals is eight hours.

A0 In total 12 physicians of different genders and various ages are currently working in the internal medicine department of the university hospital. The weekly official working time of the personnel in the enterprises is assumed as 40 h. One day is divided into three equal (8 h) periods. The starting time of the staff changes every week. In the initial state (A0), according to labour law, all personnel in the working system operate 40 h per week.

The scenario of work-life balance

The study’s primary goal was to obtain a new personnel schedule structure that provided a fair and balanced schedule for each employee working in a team. The scenario for introducing work-life balance into the existing scheduling system was as follows: Hospital management divided its employees into three shifts (8 h a day) and provided weekly schedules for the shifts. Initially, the preferences of the employees were not taken into consideration. Subsequently, the WLB-Tool allowed hospital management to determine the duration of working periods and the number of staff needed within that period. It further enabled the employees to determine which period or start time and weekly working time they would like.

Scenarios derived from the initial (A0) situation: (A0-1) and (A0-2)

Scenario (A0-1) In this scenario derived from the initial state (A0), employees could choose the starting time, but the weekly work-time remained unchanged for 40 h. The number of doctors needed by the hospital in the working periods remained unchanged as in the initial situation (A0) (Table 1). Therefore, the staff could select the start time.

Scenario (A0-2) The difference between this scenario and the previous one (A0-1) is that the staff can determine how many hours they prefer to work in a week as well as choosing starting times. The total work hours for each employee in this scenario decreased compared to the total work hours in the initial situation (A0-1), as the hospital management determined the number of personnel needed in 8-h periods according to patient numbers (Table 1). Staff could request their weekly working and starting times ((Table 1a) (A0-1) and (A0-2)). Thus, the employees could select 3 to 7 working time periods based on their weekly choices. Staff information, ratings appropriate to their seniority, the success of assigning/scheduling algorithms, and (A0-1) and (A0-2) scenario results are given in Table 1.

Alternative work-life balance scenarios: (S1), (S2), (S3)

• Scenario (S1) This is a scenario in which four time periods (6 h + 6 h + 6 h + 6 h) are generated. In the scenario, a day is divided into four equal time period. The employees determine their weekly working time (weekly working hours and start time) by selecting these periods.

• Scenario (S2) This working time scenario consists of five time periods (8 h + 5 h + 4 h + 3 h + 4 h). Thus, a day (24 h) is divided into five parts, and it is designed to provide the employees with a more comprehensive selection opportunity.

• Scenario (S3) This working time scenario consists of six time periods (4 h + 4 h + 4 h + 4 h + 4 h + 4 h). As a day is divided into six equal time zones, it is more flexible and gives better freedom of selection. ((Table 1b) (S1, S2, S3)).

Experimental results

The Performances of the work-life balance scenarios

1. From the Initial Scenarios

   Scenario (A0-1) The SPM-algorithm prioritizes the preferences of staff with high seniority scores (P4f, P5f, P8m, P9m, P10m, P11m, P12m), giving them a success of 80%. On the other hand, personnel with low seniority scores (P2f, P7m) are assigned to their preferences at the level of 20 to 25%. On the other hand, the BFM-algorithm tries to assign the personnel as equally as possible. Thus with the latter, the difference in meeting the personnel’s requests is reduced, and a certain amount of justice is provided in meeting employees’ wishes. The GAM algorithm also provided a similar assignment success to the BFM.

   Scenario (A0-2) In the SPM-algorithm, the preferences of the personnel with low seniority points (P1f, P2f, P3f) were not considered, and the success of meeting their requests was 0%, whereas the preferences of the personnel with high seniority score (P9m, P10m, P11m, P12m) were met with 75% to 100% success. In the results of the SPM-algorithm, the average of the percentages of meeting the requests of all personnel was 50.0%. The BFM-algorithm met personnel requests from 33 to 75 percent, and the average for all staff was 58.7%. The GAM algorithm was observed to meet from 20 to 100% of personnel requests, and the average for all staff was 65.3% (Table 1, Result of Scenarios a) (A0-1), (A0-2)).

2. Alternative work-life balance scenarios

   Scenario (S1) The preference of personnel with a high score (e.g., P4f, P5f, P9m, P10m, P11m, P12m) in the Seniority Priority (SPM) algorithm is seen as having a high designation success (100%). However, personnel with low scores (e.g., P1f, P2f) did not seem to be assigned according to their preferences (25% and 0%). The Balanced Fair Assignment (BFM) algorithm varied from 50 to 100% in terms of assigning personnel to their preferences. When the assignment of personnel according to their preferences is examined, it is observed that, using the BFM algorithm, a certain degree of justice is provided to the appropriate level of 14.9 in standard deviation (σ). The genetic algorithm (GAM) shows that a relatively higher level of personnel requests is achieved, and a moderate and fair assignment is provided compared to other algorithms (Table 1).

   Scenario (S2) In the Seniority Priority Method (SPM), the lowest success in assigning personnel to the desired period was P2f and P7m at 17% and 20%, and the highest appointment success was achieved for P9m at 100%. In the Balanced Fair assignment the success of assigning personnel was lowest at 43% for P10m and highest at 100% for P9m. The lowest success with the genetic algorithm (GAM) was 43% for P10m and highest at 100% for P4f.

   Scenario (S3) Seniority Priority Method (SPM) prioritizes personnel with a high seniority score, with the success of meeting personnel requests at 100% for P9m and 90% for P8m while it was 0% for the personnel with a low seniority score (P1f and P2f). The requests of these two latter groups were not met at all. With the Balanced Fair assignment Method (BFM), the lowest demand assignment success was 50%, and the highest assignment success was 100%. In the Genetic Algorithm (GAM) Method, the lowest success was 40% for P1f, and the highest achievement was 92% for P9m (Table 1, Result of Scenarios b) (S1, S2, S3)).

The success of algorithms in personnel scheduling

In the Seniority score Priority assignment (SPM) algorithm, the success of assigning personnel to their requests varied between 0 and 100%. The assignment rates for P4f, P5f, P8m, P9m, P10m, P11m, P12m achieved over 60%. On the other hand, the success of assigning the wishes of the employees with a low score (that is 50–55 age) was from 0 to 60% and considered low. These results were expected, as the seniority scores were prioritised.

The success of assigning personnel to their wishes in the Balanced Fair assignment Method (BFM) ranged from 60 to 80% in (A0-1) and from 33 to 75% in (A0-2). In the Genetic Algorithm Method (GAM), the success of assigning personnel according to their wishes varied between 60 and 80% for (A0-1) and between 33 and 100% for (A0-2).Among the scenarios derived from the initial state, the highest personnel request ratio (x̄) was obtained at 70.8% with the Balanced Fair assignment algorithm (BFM) in the scenario (A0-1) (Table 1, Fig. 4).

Fig. 4.

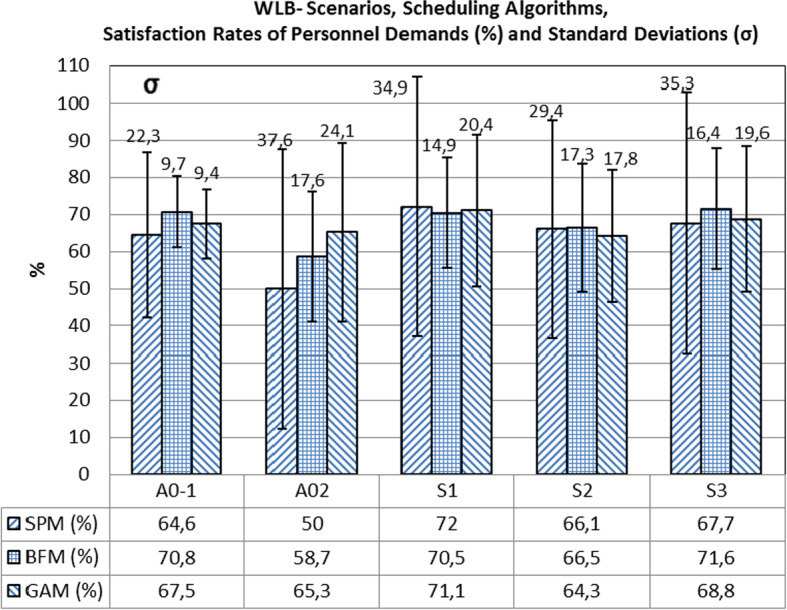
The satisfaction rates of the personnel demand of the algorithms developed for the scenarios (%), and the standard deviations (σ)

The standard deviation (σ) of the same scenario and algorithm was at the level of 9.7. The standard deviation (σ) obtained from the assignment with the Seniority Priority algorithm for the scenario (A0-1) was at the level of 22.3. The high standard deviation means that injustice increased in assignment of personnel.

Among the alternative scenarios, the Balanced Fair assignment algorithm (BFM) achieved the highest personnel preferences at 71.6% in scenario (S3), while the standard deviation (σ) was at 16.4. In this scenario, a day was divided into six equal pieces with 4 h of work. It was, therefore, possible for personnel to choose their preferred starting times. From that perspective, it can be claimed that scenario (S3) is the most appropriate scenario for achieving work-life balance. Furthermore, in this method (BFM), scenario (S3) had the highest satisfaction rate of personnel preferences; and in scenario (S3), the method (BFM) had the lowest standard deviation (namely the fairest scheduling).

With scenarios (A0-1, A02, S1, S2, S3) of the developed algorithms, the Balanced Fair assignment Method results had the highest average ratio of 67.6% in meeting personnel requests, while the standard deviation was 15,2. The Genetic Algorithm with 67.4% was in second place in meeting personnel requests, with a standard deviation of 18.26. It is possible to obtain better solutions by changing the Genetic Algorithm’s mutation rate, iteration number, and population number. It is observed that the success rate increases when the iteration value is increased to 2000 by keeping the population number and mutation rate constant. However, working with very high iteration values results in a solution that takes longer to produce similar results. Therefore it is necessary to balance the time required to reach the solution and the quality of the solution, and to run the software according to the best input parameters. These values may vary depending on the particulars of the problem (Table 1, Fig. 4).

Conclusion and future work

Constantly changing numbers of patients visit hospitals at different times of the day. It is necessary to have an adequate number of doctors available, and certain demands must be met. Therefore, scheduling doctors and nurses according to the number of patients directly affects the efficiency of the hospital and patient satisfaction. In traditional staff scheduling processes in hospitals, it is difficult to take personnel requests into account and meet these while making balanced and fair scheduling of assignments with simple tools, manual charts, or computers. Therefore, the use of a scheduling tool is necessary to factor in the plurality of possibilities for personnel assignment and to exploit the flexibility of human resources. This study aimed to schedule personnel assignments using three different methods with five working time scenarios.

A methodology and applied software (WLB-Tool) were developed using work-life balance methods to solve the scheduling problem. Firstly, a systematic optimization approach using the SPM was applied. The superiority of this method is that the seniority of staff and their certificates are scored, and the needs of those with higher scores are prioritized in scheduling. The Balanced Fair assignment Method (BFM), on the other hand, is an optimization method developed especially within the scope of this study in order to provide fair scheduling.

This equitable method provided for allocating personnel based on meeting the requests of each employee at the highest rate, taking into account equal treatment and balancing the employees’ requests. On the other hand, using genetic algorithms, a vast territory of possible solutions was examined for the problems, and appropriate solutions were obtained quickly. The Genetic Algorithms Method (GAM) was employed in the study to maximize the satisfaction of all employees’ requests.

Two different scenarios were derived from the current situation (A0) in a hospital, in which a day (24 h) was divided into three shifts (each 8 h). In the first scenario (A0-1), the employees must work 40 h a week, while in the second scenario (A0-2), the weekly working time could be determined according to the employees’ wishes. In both scenarios, the employees could give preferences on their starting times. Apart from these two scenarios, S1, S2, and S3 scenarios were based on a day (24 h) divided into 4, 5, and 6 shifts respectively. These arrangements were made to consider the work-life balance of employees because the shorter working periods were more able to be assigned according to their preferences. The scheduling results of the scenarios obtained from the software, and the rates of meeting individual requests are shown comparatively in this study.

The main contribution of this study is that the scheduling models allow for both working time and starting time requests and those individual requests can be taken on board in each planning period. This means that individual requests can be considered for scheduling even if they change on weekly basis. This advantage means that the hospital management can respond to personal requests more easily, quickly, justly, and according to the time shifts following hospital policy.

For future studies, new scenarios considered in different time periods in larger hospitals with larger numbers of staff and new heuristic algorithms can be developed. Moreover, a new optimization module can be added to the WLB-Tool software, and the scheduling results of all algorithms, the degree of fulfilment of individual requests, and the success rates of the algorithms can be comparatively presented.

Author contribution

HİK: Conceptualization, Methodology, Software Design, Data curation, Writing—original draft. MSE and EG: Methodology, Formal analysis, Software design, Data curation.

Declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.