Abstract
A crucial necessity in integrated water resource management is flood forecasting. Climate forecasts, specifically flood prediction, comprise multifaceted tasks as they are dependant on several parameters for predicting the dependant variable, which varies from time to time. Calculation of these parameters also changes with geographical location. From the time when Artificial Intelligence was first introduced to the field of hydrological modelling and prediction, it has produced enormous attention in research aspects for additional developments to hydrology. This study investigates the usability of support vector machine (SVM), back propagation neural network (BPNN), and integration of SVM with particle swarm optimization (PSO-SVM) models for flood forecasting. Performance of SVM solely depends on correct assortment of parameters. So, PSO method is employed in selecting SVM parameters. Monthly river flow discharge for a period of 1969 - 2018 of BP ghat and Fulertal gauging sites from Barak River flowing through Barak valley in Assam, India were used. For obtaining optimum results, different input combinations of Precipitation (Pt), temperature (Tt), solar radiation (Sr), humidity (Ht), evapotranspiration loss (El) were assessed. The model results were compared utilizing coefficient of determination (R2) root mean squared error (RMSE), and Nash–Sutcliffe coefficient (NSE). The most important results are highlighted below.
-
•
First, the inclusion of five meteorological parameters improved the forecasting accuracy of the hybrid model.
-
•
Second, model comparison specifies that hybrid PSO-SVM model executed superior performance with RMSE- 0.04962 and NSE- 0.99334 compared to BPNN and SVM models for monthly flood discharge forecasting.
-
•
Third, applied optimization algorithm has easy implementation, simple theory, and high computational efficacy.
Results revealed that PSO-SVM could be utilised as an improved alternate method for flood forecasting as it provided a higher degree of reliability and accurateness.
Keywords: Bpnn, Svm, Pso-svm, Flood
Method name: PSO-SVM
Graphical abstract
Specifications table
| Subject area: | Engineering |
| More specific subject area: | Geology and Hydrology, Flood |
| Name of your method: | PSO-SVM |
| Name and reference of original method: | C Zhou, K Yin, Y Cao, B Ahmed, (2016) Application of time series analysis and PSO–SVM model in predicting the Bazimen landslide in the Three Gorges Reservoir, China. Engineering Geology, 204, 108–120 |
| Resource availability: | MATLAB (validation and Methodology), Origin pro-2020 (Results and graphical analysis), GIS (Study Area) |
Introduction
Floods are responsible for significant destruction of social and economic amenities and also loss of human life. Flooding possess a potential threat to heavily inhabited regions positioned downstream of and next to major river bodies. Precise flood flow forecasting is a necessity to reduce flooding risk and is significant for water resources planning and management. But, precise river discharge forecasting is a challenging issue as analysis of river flood level is a multifaceted, dynamic procedure categorized by temporal and spatial variations. Many prediction methods, which entail a huge volume of data to forecast, have been suggested for mitigating or preventing impact of flood conditions. Due to changes in global climatic conditions, there is a rise in occurrence of flood extremes around the world [10,18] in rural catchments, increasing sternness of flood hazards.
In India, many destructive flooding occurred recently, like the 2008 Bihar flood in River Kosi, 2005 Mumbai flood in River Mithi, cloudburst in Uttarakhand in 2013, Chennai flood in 2015 and Assam in 2022. Therefore, a reliable flood forecasting method is needed and very essential for helping the local and high-level government in reducing the damage and loss of life and property. Different ANN (artificial neural network) models provide good forecasting results for various problems. Prediction of flood discharge is done using ANNs at different gauging stations [1,28,29]. Yet, these models were subjected to slow learning and local convergence. Hence, they could not achieve agreeable performance while resolving complicated hydrological processes. In recent times, SVM model has emerged as an efficacious computational approach as it overcomes several of ANN's shortcomings and is therefore found in many applications for various areas of engineering and science [17,18,46]. Even in the field of hydrological modelling, investigators have extensively applied SVM.
Han et al. [14] described applicability of SVM over Bird Creek watershed, USA. They addressed a few significant problems on development and usability of SVM to forecast flood events considering an optimum number of input parameters and combinations. Study results showed that SVM can be a reliable technique used for different rainfall inputs and performed well under different evaluation criteria. Nikam and Insom et al. [17] applied a novel method to develop an improved SVM model based on particle filter to estimate suitable model parameters for enhanced flood classification system. Based on obtained results proposed method provided a more accurate analysis and performed superior to standard SVM model. Latt and Wittenberg [21] examined performance of stepwise-MLP (multi-layer perceptron) and ANN models for multi-step flood forecasts of Chindwin River in north Myanmar. ANN models performed superiorly compared to SMLP models. Liu et al. [23] proposed combined stacked auto-encoders (SAE) with BPNN for stream flow prediction and compared with SVM, RBFN, BPNN, and ELM (extreme learning machine) models. Outcomes showed that projected hybridised model performed much better than other models. Macharyulu et al. [52] applied CNN and MLP models for developing a flood prediction model considering hydrological data from Subarnarekha river basin. Various artificial intelligence approaches are applied to predict different climatic indices at various watersheds in India ([31], [32], [33]). In several case studies, SVM generates better estimations than ANN and other traditional approaches.
With an increasing number of applications in forecasting flood events, SVM is a dependable technique for computing extensive non-linear time-series data [15,19]. SVM's performance mainly depends on hyperparameter and kernel function choices [25]. Most frequently utilised kernel function is RBF kernel which is used to develop SVM models (Raghavendra and [8]). However, there are certain drawbacks related to SVM; while determining these parameters, sufferings from dimensionality and large time consumption are experienced during data analysis [53]. To overcome such drawbacks, scientists have developed several evolutionary optimisation algorithms inspired by nature which include ACO (ant colony optimisation), GA (genetic algorithm), PSO, ABC (artificial bee colony), DE (differential evolution), etc. Integrated models have been developed utilising metaheuristic algorithms for determining parameters of techniques like ANFIS (adaptive neuro-fuzzy inference system), SVM, MLP, etc. Hence, in this study, PSO algorithm is applied to determine optimum SVM parameters in an SVM-based (PSO-SVM) flood forecasting model.
Wang et al. [45] used a combination of SVM with PSO (SVM-PSO) model to forecast annual reservoir inflow of Fengtan reservoir situated downstream of Yuan river basin. Obtained results were compared with ANN model which discovered that SVM-PSO model showed better forecasting performance. Guo et al. [13] applied SVM-PSO for monthly stream flow estimation of Changjiang River basin and compared obtained results with ANN and traditional SVM model. Findings verified that developed SVM model had a better ability to generalize and higher prediction accurateness. Wang et al. [44] applied simple SVM and hybrid PSO-SVM models to forecast monthly runoff of Dahuofang reservoir. Results revealed that hybrid model produced more accurate predictions compared to simple SVM model at proposed study area. Ch et al. [5] explored efficiency of hybrid SVM model combined with quantum-behaved PSO (SVM-QPSO) to predict monthly streamflows of Polavaram and Vijayawada stations of Andhra Pradesh, India. Based on evaluation measures proposed SVM-QPSO model performed better compared to other conventional models with better accuracy. Li et al. [22] developed SVM model based on boosting algorithm and kernel PCA for forecasting flood occurrences of Wangjiaba station at River Huaihe. Results revealed that developed ensemble model enhanced flood forecasting precision efficiently. Ebtehaj et al. [9] evaluated average stream velocity below sediment deposition constraints in partly occupied rounded storm sewers utilising SVM model combined with FFA (firefly algorithm). Enactment of hybrid tool was contrasted with those of SVM, genetic programming (GP), and ANN models, and findings indicate that SVM-FFA predicted dens metric particle Froude number at settlement limit very precisely.
Zaini et al. [47] applied a conjoint SVM model combined with PSO for forecasting short-term daily river flow at Upper Bertam watershed. Obtained results were compared against simple SVM model, which revealed that hybridized SVM-PSO model outperformed the simple SVM model and provided more accurate results. Zaini et al. [48] investigated potential of two hybrid models, namely bat algorithm integrated with BPNN (Bat-BPNN) and SVM-PSO, for forecasting monthly stream flow at River Kuantan situated in Malaysia and compared with traditional BPNN and SVM models. Outcomes specified that hybrid Bat-BPNN and SVM-PSO produced better performance than regular BPNN and SVM models, respectively, in stream flow forecasting. Chen et al. [7] proposed an improved GA combined with BPNN (IGA-BPNN) to predict water levels at middle and lower stretches of River Han, China. The performance of IGA-BPNN model was compared with traditional artificial intelligence models which revealed that IGA-BPNN improved prediction accuracy and model stability for desired study area. Robati and Iranmanesh [50] developed a model for studying the inflation rate in Iran using ANFIS-PSO model. Applied method was found to be effective and reliable based on the statistical measures. Kao et al. [54] applied Long Short-Term Memory and feed forward neural network combined with Encoder-Decoder (FFNN-ED and LSTM-ED) models for forecasting multi-step ahead flood using hydrological data from Shihmen Reservoir, Taiwan. Results revealed that LSTM-ED produced more accurate and reliable flood forecasting compared to FFNN-ED. Adikari et al. [55] compared potential of LSTM, Convolutional Neural Network (CNN), and Wavelet-ANFIS in forecasting flooding and drought events. They found that CNN showed best performance in forecasting flood whereas WANFIS in forecasting drought, irrespective of the climatic condition of the study region. Xiujia et al. [51] investigated the efficiency of SVM, BPNN, Wavelet Neural Network (WNN), SVM-PSO, BPNN-PSO, and WNN-PSO for calculating Crop Water Deficit Index (CWDI) to predict drought of regional crops in Fuxin City, China. Compared outcomes indicated that WNN-PSO model performed superior compared to all other models. Kamali and Asghari [56] applied SVM-SPO model to investigate impact of droughts on groundwater storage and measure the effect of impending drought occurrences on Najafabad aquifer in Iran based on variations in climatic conditions. Agnihotri et al. [1] proposed ANFIS combined with ACO algorithm for flood prediction at Matijuri gauging site of Barak basin, India. Outcomes revealed that proposed optimization algorithm had good ability of enhancing accuracy of standard ANFIS. Aswad et al. [57] applied Random Forest, Decision Tree (DT), and Decision Jungle for predicting flood process. Their research findings show that DT provided highest accuracy amongst the three algorithms.
In this work, a hybrid optimisation technique known as PSO-SVM is introduced to predict flood discharge and performance of the model is evaluated based on quantitative statistical measures. Also, a comparison is made between the hybrid and conventional approaches. Here two conventional techniques BPNN and SVM are applied to predict flow and compared with the results of PSO-SVM algorithm. PSO algorithm being a robust technique discovers out search space in a proficient way and helps in finding out optimal set of SVM parameters. The novelty in this research lies in the inclusion of evapotranspiration loss parameters for flood forecasting. Though this parameter had a little impact on flood, however, it was observed that addition of evapotranspiration loss improved model accuracy and prediction results. In literature survey, it was found that there was no inclusion of evapotranspiration loss in flood forecasting studies. Also, the importance of this work lies in the identified study region. Since Assam receives major flooding every year because of glaciers melting in summer that accords with monsoon rainfall resulting in an escalation of downstream, causing the annual floods. There is no previous study conducted in the particular area which can be a flood sensitive region because of its location.
Study area
Barak River is a 900 km river that flows through Nagaland, Assam, Mizoram, and Manipur states of India and via Bangladesh into Bay of Bengal. It originates from its source at Village Liyai Kullen situated in Manipur. Out of the total length, 524 km flows through India, 31 km on Indo-Bangladesh boundary, and rest through Bangladesh. River Barak lies in the southern portion of Assam (Fig. 1). It falls between 24°8′ to 25°8′ N latitudes and 92,015′ to 93,015′ E longitudes and is the second largest river in North-East India. Average annual precipitation in this valley is around 2400–4100 mm, with 80–85% from April to the middle of October. Two gauging stations BP ghat and Fulertal are considered in this study.
Fig. 1.
Study area map (Barak Valley).
Methodology
BPNN
BPNN was first introduced to the field of neural networks (NNs) by Rumelhart and McClelland [27]. It is a multi-layer FFNN trained by error BP algorithm and is one of the most extensively utilized ANN models [6,12,31,34]. Learning rule involved in BPNN is to utilize steepest descent technique and repetitively adjust biases and weights of network using reverse iteration to minimize summation of squared errors [4,35].
Elementary training procedure comprises of two approaches. First approach involves forward propagation, while the second is error back propagation. In forward propagation, computation of error output is executed from input to output. Here, input data affects output node via a hidden layer, and output is produced by non-linear conversion. If actual output does not relate with simulated output, then error is back propagated for eliminating as much of it as conceivable. This is utilized for passing output error via hidden nodes, layer by layer, utilizing error signals acquired from every layer as a source to adjust weights, hence allocating error to every node in each layer. Adjustment of bias and joint strength amidst layers, error gets diminished alongside direction of gradient, and after repetitive learning preparation, network constraints are found for satisfying minimal error. BPNN utilized in present study is specified by following equation:
| (1) |
where is self-regulating training and testing input variables, is output variable, is weight from input to hidden; is weight from hidden to output; and is bias for output and hidden layers, in respective order; and are transfer functions for output and hidden layers. Architecture and flowchart of BPNN are presented in Fig. 2a and b.
Fig. 2.
Architecture of BPNN.
SVM
Vapnik [42] proposed SVM for the first time for solving regression and classification kind of problems. It is a very capable method for data regression and classification [38,39]. Conventional machine learning techniques involve numerous difficulties, such as local minima; low convergence rate, demand for various training data, and under fitting/over fitting [24], [30]. Operating based on structural risk minimisation (SRM), SVM incapacitates these problems. SVM's output function is given by:
| (2) |
where specifies Lagrange factors, is inner product core function described according to Mercer theorem and is bias value.
SVM is a computer-based algorithm that learns using examples to find preeminent function of classifier or hyperplane for splitting two classes in input space [36], [37]. Fig. 3a and b demonstrate the architecture and flowchart of SVM model.
Fig. 3.
Architecture of SVM.
PSO
Kennedy and Eberhart [20] were the first to introduce PSO algorithm in 1995. PSO is employed in this study as a prevalent optimization tool. It is a swarm intelligence where birds cooperate in a swarm for searching an optimum place to obtain food. Predominantly it is based on inspiration from social movement of bird flocks and then recognized as a basic model on basis of birds probing for foodstuff. A population in a D-dimensional target search space is formed by a bird flock whose amount is m and known as “particle”. If solution space of optimisation problem is D dimensions, space vector is presented as -th element, where is location of -th element, and also a conceivable explanation. It is being broadly used for solving variable optimization problems as it is very easy to understand and has great convergence rapidity [11], [16], [43], [49]. In addition to SVM, PSO is presented for obtaining optimum constraints in SVM.
Velocity and position of particles are iterated for finding subsequent equations:
| (3) |
| (4) |
where is -th particle velocity, and is ideal location of this element. Optimal swarm location is . Under -th particle condition at -th iteration, and are -th position and constituent of speed. Positive coefficient,, and - random numbers ranging between 0 and 1; is inertial PSO algorithm weight. It supports multiple points search and can pact with continuous optimization problems. Therefore, we consider PSO algorithm for finding constraints of SVM to improve its performance. Flowchart of hybrid PSO-SVM structure is revealed in Fig. 4.
Fig. 4.
Flowchart of hybrid PSO-SVM.
PSO technique in selecting SVM parameters
Performance of SVM depends on kernel function parameter and regularization parameter. Hence and must be selected carefully for increasing classification accurateness. PSO-based SVM model in learning stage is trained on basis of SRM for minimizing training error. When there is an improvement in training error, and are controlled using PSO. Most suitable parameters are the controlled parameters having the least error. Accordingly, optimum parameters are to be found. After finding optimised parameters of SVM, it is utilized in the retraining of SVM model. SVM classifier is now prepared for identification of new samples in testing period after passing the training period. Through the above feature selection from original dataset, a testing set is also selected. Then, imputation of testing patterns is done to the trained multi-layer SVM classifier. Following are the overall steps involved in parameter optimization of SVM model.
Step 1
Initialising parameters of particle swarm, comprising learning factors, particle number, weighting coefficient, particle velocity, and particle position.
Step 2
Encoding and of SVM as the location of particles.
Step 3
Training SVM model with 50 training samples. Along with flying of particles, there is a variation in parameter pairs (, ).
Step 4
Calculating and assessing the particle's fitness value. Fitness value is utilised for evaluating validity of flood forecasting model with parameter combination and . A lesser fitness value specifies greater flood forecasting accuracy.
Step 5
Terminating iteration procedure and obtaining optimum parameters of SVM if preferred accurateness is received, or continue to iterative computation.
Steps 6
and 7: Updating particle best, global best, of parameter and updating particle velocity with particle position.
Step 8
Validating SVM model with attained combinations of optimal parameter and . The pseudo-code of PSO algorithm is presented below.

Preparation of data set
Precipitation (Pt), solar radiation (Sr), temperature (Tt), humidity (Ht), and evapotranspiration loss (Et) data (1969–2018 of monsoon months) are collected from Indian meteorological department. Data collected from 1969 to 2003 are applied for training, and from 2004 to 2018 are employed for testing. Following arrangements are considered as inputs:
| Model | Input parameter | BPNN | SVM | PSO-SVM |
|---|---|---|---|---|
| M!1 | Pt | BPNN1 | SVM1 | PSO-SVM1 |
| M!2 | Pt, Tt | BPNN2 | SVM2 | PSO-SVM2 |
| M!3 | Pt, Tt, Sr | BPNN3 | SVM3 | PSO-SVM3 |
| M!4 | Pt, Tt, Sr, Ht | BPNN4 | SVM4 | PSO-SVM4 |
| M!5 | Pt, Tt, Sr, Ht, Et | BPNN5 | SVM5 | PSO-SVM5 |
Evaluating criteria
RMSE, NSE, and are statistical assessment factors for finding best performing model. For the perfect model in this study, condition is RMSE must be least and (and NSE must be highest. The values of RMSE lies between 0 - , R2 between 0 - 1.0 and NSE between -∞ - 1.0.
(Samantaray et al. 2022a, b)
| (5) |
| (6) |
RMSE ([60], Samantaray et al. 2022c)
| (7) |
Where
= Predicted data
= Collected data
=Mean predicted data
= Mean collected data
Results and discussion
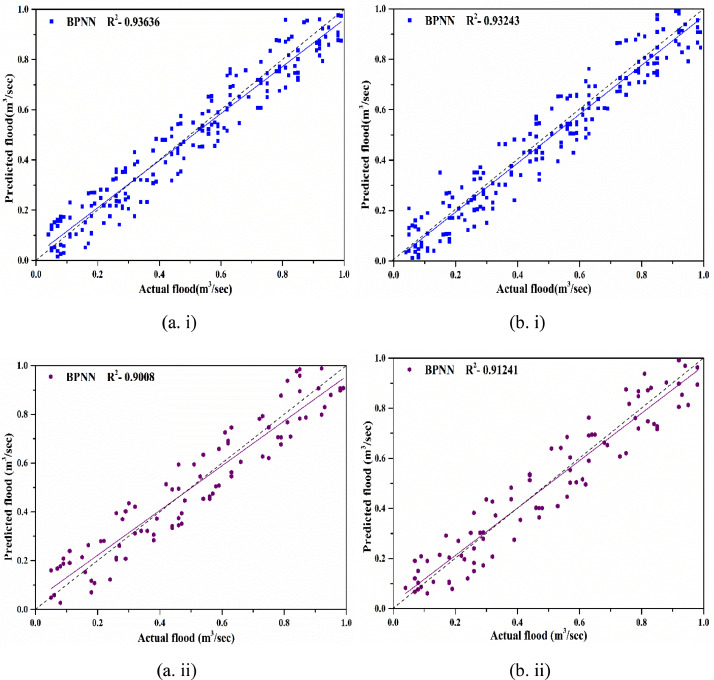
Three different techniques BPNN, SVM, PSO-SVM are employed here to assess their performance in flood discharge prediction. Several input scenarios are applied through BPNN algorithms to evaluate performance of model (Table 2). For assessing model performance, different constraints like R2, RMSE, and MSE are considered. Five types of input scenarios in context to one output are applied to develop the model. Detail model performances of both gauge stations are specified in Table 2. Model BPNN:5 gives the preeminent value of performance amongst all the models. The paramount values of R2 are 0.91241 and 0.9008 for BP Ghat, Fulertal gauge stations when model BPNN:5 is considered as input scenario during testing phase. Consistently for same input condition, excellent values of R2 are 0.93636 and 0.93243 for BP Ghat, Fulertal gauge station while considering training phases. Actual predicted graph for both stations is revealed in Fig. 5.
Table 2.
Consequences of BPNN.
| Station | Model | Architecture | NSE |
RMSE |
R2 |
|||
|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | |||
|
BP Ghat |
M!1 | 1–2–1 | 0.90582 | 0.88731 | 0.07752 | 0.03937 | 0.89965 | 0.88114 |
| M!2 | 2–6–1 | 0.91705 | 0.89425 | 0.07590 | 0.03831 | 0.91002 | 0.88782 | |
| M!3 | 3–9–1 | 0.9218 | 0.89803 | 0.07354 | 0.03394 | 0.91774 | 0.89265 | |
| M!4 | 4–5–1 | 0.92839 | 0.91007 | 0.07268 | 0.03262 | 0.92386 | 0.90563 | |
| M!5 | 5–7–1 | 0.94001 | 0.91844 | 0.07201 | 0.03084 | 0.93636 | 0.91241 | |
|
Fulertal |
M!1 | 1–8–1 | 0.89534 | 0.88234 | 0.07576 | 0.03782 | 0.89012 | 0.87663 |
| M!2 | 2–3–1 | 0.90492 | 0.88936 | 0.07464 | 0.03673 | 0.89965 | 0.88119 | |
| M!3 | 3–2–1 | 0.91837 | 0.89197 | 0.07331 | 0.03374 | 0.91487 | 0.88465 | |
| M!4 | 4–7–1 | 0.9266 | 0.90562 | 0.07244 | 0.03129 | 0.92161 | 0.89923 | |
| M!5 | 5–4–1 | 0.93809 | 0.90865 | 0.07193 | 0.02325 | 0.93243 | 0.9008 | |
Fig. 5.
Actual verses predicted graph for (a) BP Ghat, (b) Fulertal gauge station using BPNN during (i) training, and (ii) testing phases.
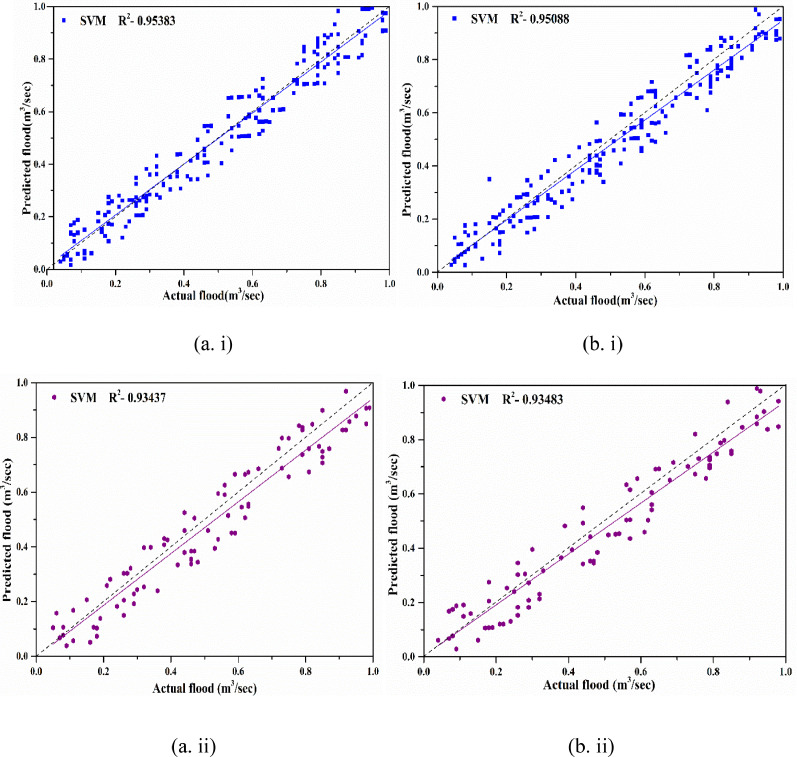
Similarly, SVM techniques are applied with several combination of input scenarios for BP Ghat, Fulertal gauge station are specified in Table 3. On a similar way model, 5 found best models while considering SVM algorithms for both stations. Excellent values of R2 are 0.93483, and 0.93437 for BP Ghat, Fulertal gauge station during testing phase. Consistently in case of training phase paramount value of R2 for BP Ghat, Fulertal gauge stations are 0.95383, 0.95088 while P, T, Sr, H, El is considered as input scenario. Actual versus predicted graph for both stations is presented in Fig. 6.
Table 3.
Consequences of SVM.
| Station | Input | NSE |
RMSE |
R2 |
|||
|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | ||
|
BP Ghat |
M!1 | 0.92763 | 0.90498 | 0.06809 | 0.02232 | 0.92227 | 0.89968 |
| M!2 | 0.93927 | 0.90825 | 0.06794 | 0.02209 | 0.93382 | 0.90021 | |
| M!3 | 0.94506 | 0.9143 | 0.06742 | 0.02175 | 0.93812 | 0.90827 | |
| M!4 | 0.94772 | 0.92106 | 0.06601 | 0.02157 | 0.94065 | 0.91658 | |
| M!5 | 0.95984 | 0.93991 | 0.06082 | 0.02134 | 0.95383 | 0.93483 | |
|
Fulertal |
M!1 | 0.92406 | 0.90435 | 0.06788 | 0.02203 | 0.91887 | 0.89113 |
| M!2 | 0.92943 | 0.90861 | 0.06782 | 0.02199 | 0.92215 | 0.90002 | |
| M!3 | 0.9401 | 0.91437 | 0.06689 | 0.02168 | 0.93763 | 0.90773 | |
| M!4 | 0.94847 | 0.92246 | 0.06462 | 0.02144 | 0.94001 | 0.91553 | |
| M!5 | 0.95669 | 0.9389 | 0.05981 | 0.02035 | 0.95088 | 0.93437 | |
Fig. 6.
Actual verses predicted graph for (a) BP Ghat, (b) Fulertal gauge station using SVM during (i) training and (ii) testing phases.
Fig. 7 shows Actual verses predicted plots for PSO-SVM model of BP Ghat and Fulertal station. Results show that model PSO-SVM:5 gives the prominent result amongst all the scenarios for both the gauge station. The best value of R2 for BP Ghat and Fulertal station is 0.98918 and 0.98762 during training phase. Similarly, during testing phase, the best R2 value is 0.9638 and 0.96204 for station BP Ghat and Fulertal, respectively. Detailed performance results of PSO-SVM techniques are given below (Table 4).
Fig. 7.
Actual versus predicted graph for (a) BP Ghat, (b) Fulertal gauge station using PSO-SVM during (i) training and (ii) testing phases.
Table 4.
Consequences of PSO-SVM.
| Station | Input | NSE |
RMSE |
R2 |
|||
|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | ||
|
BP Ghat |
M!1 | 0.96735 | 0.94721 | 0.05706 | 0.01805 | 0.96113 | 0.94114 |
| M!2 | 0.9746 | 0.95227 | 0.05599 | 0.01679 | 0.96882 | 0.94688 | |
| M!3 | 0.97861 | 0.95936 | 0.05395 | 0.01425 | 0.97021 | 0.95325 | |
| M!4 | 0.98408 | 0.96405 | 0.05261 | 0.01308 | 0.97774 | 0.95887 | |
| M!5 | 0.99334 | 0.96998 | 0.04973 | 0.01069 | 0.98918 | 0.9638 | |
|
Fulertal |
M!1 | 0.96736 | 0.94435 | 0.05556 | 0.01637 | 0.96002 | 0.93899 |
| M!2 | 0.9698 | 0.94902 | 0.05539 | 0.0161 | 0.96229 | 0.94365 | |
| M!3 | 0.97623 | 0.95537 | 0.05344 | 0.01378 | 0.96997 | 0.94991 | |
| M!4 | 0.98164 | 0.96113 | 0.05092 | 0.01162 | 0.97556 | 0.95532 | |
| M!5 | 0.98996 | 0.96849 | 0.04962 | 0.01039 | 0.98762 | 0.96204 | |
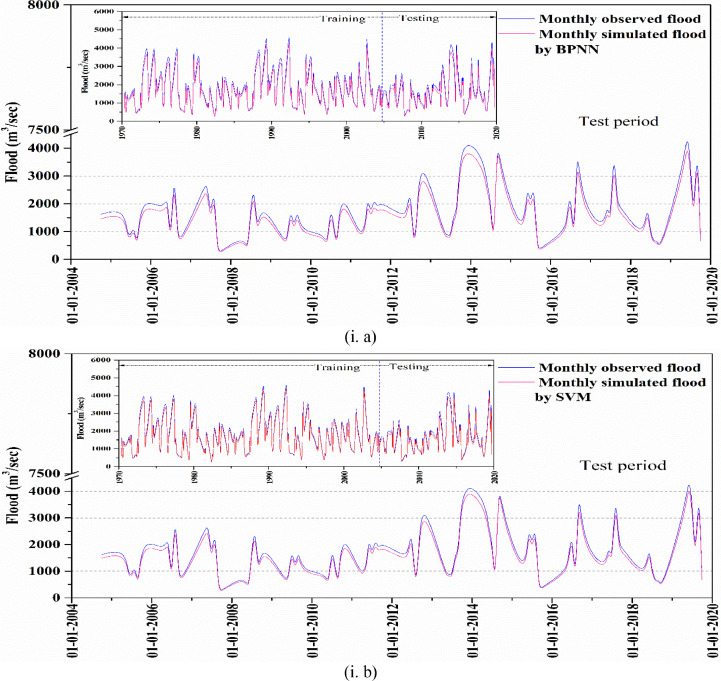
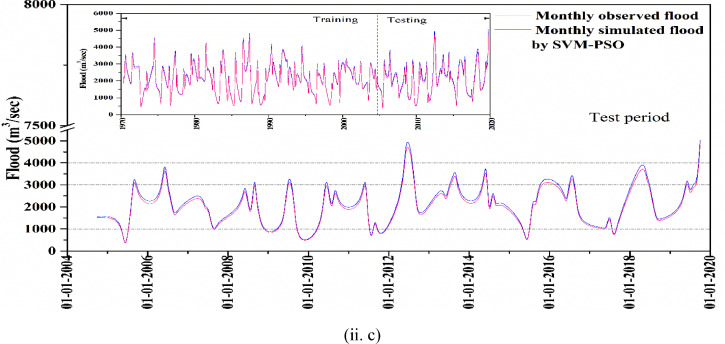
Linear scale plots of actual vs. predicted floods for BP Ghat and Fulertal locations are shown in Fig. 8. Outcomes demonstrate that predictable peak flood discharge is 5054.36m3/S, 5163.94m3/S, 5328.58m3/S for BPNN, SVM, and PSO-SVM against actual peak 5451.79m3/S for the station BP Ghat. The approximated peak discharge is 5423.92m3/S, 5540.9m3/S, and 5717.55m3/S for BPNN, SVM, and PSO-SVM adjacent to actual peak 5849.15m3/S for Fulaertal division.
Fig. 8.
Linear scale graph for (i) BP Ghat, (ii) Fulertal gauge station using (a) BPNN, (b) SVM and (c) PSO-SVM.
Using a boxplot spread of observed and predicted flood water levels have been demonstrated in Fig. 9. Boxplot using respective quartile values signifies degree of spread in predicted dataset. Quartile Q1 (25th percentile) represents the lower end of plot, and quartile Q3 (75th percentile) represents upper end. Median of data is denoted by second quartile Q2 (50th percentile) shown by a vertical line. It is observed that median of observed and estimated flood of hybrid PSO-SVM model was nearly identical for both the stations. However, whiskers prolong to slightly different values for each instance.
Fig. 9.
Box plot representation of actual v. predicted data for (i) BP Ghat, (ii) Fulertal gauge station.
Fig. 10 presents the histogram chart with 12 bins for the test and training, in BPNN, SVM, PSO-SVM modelling. The shape of histogram bears a resemblance to that of a normal distribution curve. The deviations of the PSO-SVM model in relation to observed flood values are very low as compared to simple SVM and BPNN models. The histogram plot also resembles the effective predictions by the PSO-SVM model.
Fig. 10.
Histogram chart of proposed prediction models for (i) BP Ghat, (ii) Fulertal gauge station.
Comparison of BPNN, SVM, and PSO-SVM models
Performances of modelling flood flow data are compared utilizing three methods namely BPNN, SVM, and PSO-SVM. Performance measure values are provided in Table 5, which specifies that performance of all models in predicting river discharge is satisfactory and these methods are appropriate to model river discharge data. Best R2 values of two stations for BPNN models are 0.93636, 0.91241, and 0.93243, 0.9008 during training and testing phases respectively. Similarly, PSO-SVM models of two stations have R2 values of 0.98318, 0.98098 and 0.9638, and 0.96204 for training and testing phases. Consequently, a comparison of R2 values of flood forecasting models revealed that results of the PSO-SVM model are better than BPNN and SVM models.
Table 5.
Comparison of results for proposed station.
| Station | Techniques | NSE |
RMSE |
R2 |
|||
|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | ||
| BPNN | 0.94001 | 0.91844 | 0.07201 | 0.03084 | 0.93636 | 0.91241 | |
| BP Ghat | SVM | 0.95984 | 0.93991 | 0.06082 | 0.02134 | 0.95383 | 0.93483 |
| PSO-SVM | 0.99334 | 0.96998 | 0.04973 | 0.01069 | 0.98918 | 0.9638 | |
| BPNN | 0.93809 | 0.90865 | 0.07193 | 0.02325 | 0.93243 | 0.9008 | |
| Fulertal | SVM | 0.95669 | 0.9389 | 0.05981 | 0.02035 | 0.95088 | 0.93437 |
| PSO-SVM | 0.98996 | 0.96849 | 0.04962 | 0.01039 | 0.98762 | 0.96204 | |
Moreover, SVM performed slightly better than BPNN in monthly flood prediction. This is in accordance with Bafitlhile and Li [3]. Findings of present study revealed that proposed PSO-SVM model performed more accurately and consistently than other applied models considered in different studies [2], [26], [40], [41]. Hence, it can be practically concluded that PSO-SVM showed better prediction performance than other models since it is a robust hybrid machine learning approach that efficiently predicts natural hazards or other environmental constituents. Fig. 11 clearly indicates that performance of SVM-PSO in terms of NSE value (testing phase) is best compared to BPNN and SVM models.
Fig. 11.
Comparison of applied models.
Discussion
Obtained results from the present study revealed that developed models could analyse data with fewer parameters, lesser calculation time, and good performance. Developed hybrid model can be an alternate time-consuming and cost-effective technique for predicting floods with relatively high efficacy. There are some limitations related to capturing, understanding, and analysing full-scale flood risks by just utilizing remotely sensed data and radar-based images. Moreover, floods cause substantial destruction to critical infrastructures, damaging roads, telecommunication networks, and bridges, making it challenging to reach people trapped in submerged zones. For minimizing effects of such destructions in the future, there is a vital requirement for strengthening early flood warning systems sustained by well-distributed fluvial discharge stations and hydro-meteorological networks. Development of flood prediction models and monitoring are influential methods to mitigate flood damage. The continuous improvement of ML techniques over the past decades, together with the accessibility of long-term hydrological constraints like temperature, streamflow, and precipitation, has presented a great level of potential for predicting flood magnitude. The performance of ML models certainly has higher accuracy than physical and conventional statistical models. Errors in the datasets may partly explain the study's findings: limitations existing in geospatial floods archive may not be entirely correct because of digitisation errors or may not show the maximum extent of the floods at all times. Naturally, these shortcomings will also impact the performance of methods that are based on mechanistic models. The data limitations specify the requirement for continued reliable monitoring of flood events.
Conclusion
Performances of three modelling methods are investigated in present research for providing suggestions regarding suitable methods for monthly flood forecasting. The studied techniques comprise BPNN, SVM, and PSO-SVM. An amalgam model on basis of integration of SVM and PSO is developed in this study for improving forecasting performances. PSO-SVM model was acquired by combining two new techniques SVM and PSO. Combination of SVM with PSO where PSO algorithm was utilized to select optimal parameters for SVM model. This resulted in better performance by the hybrid model than other conventional models applied in this study. Model comparison stipulates that hybrid PSO-SVM model achieved higher performance with RMSE- 0.04962, R2 - 0.98918 and NSE- 0.99334 considering both the stations for monthly flood discharge forecasting. Monthly flow discharge data of two gauge sites, i.e. BP ghat and Fulertal from Barak River over a period of 50 years (1969–2018), were utilized.
Moreover, this research concludes that projected PSO-SVM provides a legitimate substitute for applicability in different hydrological modelling scenarios. The study shows that proposed models can be successfully applied for flood forecasting in selected area of study. However, based on performance evaluation measures used in present study, it is observed that robust PSO-SVM model performed better than BPNN, SVM models. This knowledge of hybrid modelling technique can be utilized in different areas like weather, sediment concentration, water table depth and runoff forecasts for checking applicability of proposed model.
Table 1.
Parameters used in PSO model.
| Parameters | Value |
|---|---|
| Acceleration constants () | (2, 2) |
| Inertia weight | Varied linearly |
| Population size | 50 |
| Minimum error gradient | 10−8 |
CRediT authorship contribution statement
Sandeep Samantaray: Conceptualization, Methodology, Software, Writing – original draft. Abinash Sahoo: Conceptualization, Methodology, Software, Writing – original draft. Ankita Agnihotri: Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Contributor Information
Sandeep Samantaray, Email: samantaraysandeep963@gmail.com.
Abinash Sahoo, Email: abinash_rs@civil.nits.ac.in.
Data availability
Data will be made available on request.
References
- 1.Agnihotri A., Sahoo A., Diwakar M.K. Springer; Singapore: 2022. Flood Prediction Using Hybrid ANFIS-ACO Model: A Case Study, In Inventive Computation and Information Technologies; pp. 169–180. [Google Scholar]
- 2.Anupam S., Pani P. Flood forecasting using a hybrid extreme learning machine-particle swarm optimization algorithm (ELM-PSO) model. Modeling Earth Systems and Environment. 2020;6(1):341–347. [Google Scholar]
- 3.Bafitlhile T.M., Li Z. Applicability of ε-support vector machine and artificial neural network for flood forecasting in humid, Semi-Humid and Semi-Arid Basins in China. Water (Basel) 2019;11(1):85. [Google Scholar]
- 4.Buscema M. Back propagation neural networks. Subst Use Misuse. 1998;33:233–270. doi: 10.3109/10826089809115863. [DOI] [PubMed] [Google Scholar]
- 5.Ch S., Anand N., Panigrahi B.K., Mathur S. Streamflow forecasting by SVM with quantum behaved particle swarm optimization. Neurocomputing. 2013;101:18–23. [Google Scholar]
- 6.Chen F.C. Back-propagation neural networks for non-linear self-tuning adaptive control. IEEE Control Syst Mag. 1990;10:44–48. [Google Scholar]
- 7.Chen N., Xiong C., Du W., Wang C., Lin X., Chen Z. An Improved Genetic Algorithm Coupling a Back-Propagation Neural Network Model (IGA-BPNN) for Water-Level Predictions. Water (Basel) 2019;11:1795. [Google Scholar]
- 8.Deka P.C. Support vector machine applications in the field of hydrology: a review. Appl Soft Comput. 2014;19:372–386. [Google Scholar]
- 9.Ebtehaj I., Bonakdari H., Shamshirband S., Ismail Z., Hashim R. New approach to estimate velocity at limit of deposition in storm sewers using vector machine coupled with firefly algorithm. J Pipeline Syst Eng Pract. 2017;8 [Google Scholar]
- 10.Ezer T., Atkinson L.P. Accelerated flooding along the US East Coast: on the impact of sea-level rise, tides, storms, the Gulf Stream, and the North Atlantic Oscillations. Earth's Futur. 2014;2:362–382. [Google Scholar]
- 11.Feng H.M., Chen C.Y., Ye F. Evolutionary fuzzy particle swarm optimization vector quantization learning scheme in image compression. Expert Syst Appl. 2007;32:213–222. [Google Scholar]
- 12.Goh A.T.C. Back-propagation neural networks for modeling complex systems. Artif Intell Eng. 1995;9:143–151. [Google Scholar]
- 13.Guo J., Zhou J., Qin H., Zou Q., Li Q. Monthly streamflow forecasting based on improved support vector machine model. Expert Syst Appl. 2011;38:13073–13081. [Google Scholar]
- 14.Han D., Chan L., Zhu N. Flood forecasting using support vector machines. J hydroinformatics. 2007;9:267–276. [Google Scholar]
- 15.He Z., Wen X., Liu H., Du J. A comparative study of artificial neural network, adaptive neuro fuzzy inference system and support vector machine for forecasting river flow in the semiarid mountain region. J Hydrol (Amst) 2014;509:379–386. [Google Scholar]
- 16.Huang T.C., Huang Y.M., Cheng S.C. Automatic and interactive e-learning auxiliary material generation utilizing particle swarm optimization. Expert Syst Appl. 2008;35:2113–2122. [Google Scholar]
- 17.Insom P., Cao C., Boonsrimuang P., Liu D., Saokarn A., Yomwan P., Xu Y. A support vector machine-based particle filter method for improved flooding classification. IEEE Geosci Remote Sens Lett. 2015;12:1943–1947. [Google Scholar]
- 18.Jena P.P., Chatterjee C., Pradhan G., Mishra A. Are recent frequent high floods in Mahanadi basin in eastern India due to increase in extreme rainfalls? J Hydrol. 2014;517:847–862. [Google Scholar]
- 19.Kalra A., Ahmad S., Nayak A. Increasing streamflow forecast lead time for snowmelt-driven catchment based on large-scale climate patterns. Adv Water Resour. 2013;53:150–162. [Google Scholar]
- 20.Kennedy J., Eberhart R. Proceedings of ICNN’95-International Conference on Neural Networks IEEE. 1995. Particle swarm optimization; pp. 1942–1948. [Google Scholar]
- 21.Latt Z.Z., Wittenberg H. Improving flood forecasting in a developing country: a comparative study of stepwise multiple linear regression and artificial neural network. Water Resour Manag. 2014;28:2109–2128. [Google Scholar]
- 22.Li S., Ma K., Jin Z., Zhu Y. 2016 IEEE Congress on Evolutionary Computation (CEC) IEEE. 2016. A new flood forecasting model based on SVM and boosting learning algorithms; pp. 1343–1348. [Google Scholar]
- 23.Liu F., Xu F., Yang S. 2017 IEEE third International conference on multimedia big data (BigMM) IEEE. 2017. A flood forecasting model based on deep learning algorithm via integrating stacked autoencoders with BP neural network; pp. 58–61. [Google Scholar]
- 24.Lu W., Wang W., Leung A.Y., Lo S.M., Yuen R.K., Xu Z., Fan H. Proceedings of the 2002 International Joint Conference on Neural Networks IJCNN’02 (Cat. No. 02CH37290) IEEE; 2002. Air pollutant parameter forecasting using support vector machines; pp. 630–635. [Google Scholar]
- 25.Nieto P.G., García-Gonzalo E., Fernández J.A., Muñiz C.D. Hybrid PSO–SVM-based method for long-term forecasting of turbidity in the Nalón river basin: a case study in Northern Spain. Ecol Eng. 2014;73:192–200. [Google Scholar]
- 26.Rezaeianzadeh M., Tabari H., Yazdi A., Isik S., Kalin L. Flood flow forecasting using ANN, ANFIS and regression models. Neural Computing and Applications. 2014;25(1):25–37. [Google Scholar]
- 27.Rumelhart D.E., Hinton G.E., Williams R.J. Learning representations by back-propagating errors. Nature. 1986;323:533–536. [Google Scholar]
- 28.Sahoo A., Samantaray S., Bankuru S., Ghose D.K. Smart Intelligent Computing and Applications. Springer; Singapore: 2020. Prediction of Flood Using Adaptive Neuro-Fuzzy Inference Systems: a Case Study; pp. 733–739. [Google Scholar]
- 29.Sahoo A., Samantaray S., Ghose D.K. Stream flow forecasting in mahanadi river basin using artificial neural networks. Procedia Comput Sci. 2019;157:168–174. [Google Scholar]
- 30.Salat R., Osowski S. Accurate fault location in the power transmission line using support vector machine approach. IEEE Trans power Syst. 2004;19:979–986. [Google Scholar]
- 31.Samantaray S., Sahoo A., Ghose D.K. ICT Analysis and Applications. Springer; Singapore: 2020. Prediction of Sedimentation in an Arid Watershed Using BPNN and ANFIS; pp. 295–302. a. [Google Scholar]
- 32.Samantaray S., Sahoo A., Ghose D.K. Smart Intelligent Computing and Applications. Springer; Singapore: 2020. Infiltration Loss Affects Toward Groundwater Fluctuation Through CANFIS in Arid Watershed: a Case Study; pp. 781–789. b. [Google Scholar]
- 33.Samantaray S., Sahoo A., Ghose D.K. International Conference on Intelligent Computing and Communication. Springer; 2019. Assessment of Groundwater Potential Using Neural Network: a Case Study; pp. 655–664. a. [Google Scholar]
- 34.Samantaray S., Sahoo A., Ghose D.K. Assessment of runoff via precipitation using neural networks: watershed modelling for developing environment in arid region. Pertanika J Sci Technol. 2019;27(4):2245–2263. b. [Google Scholar]
- 35.Samantaray S., Sahoo A. Frontiers in Intelligent Computing: Theory and Applications. Springer; Singapore: 2020. Appraisal of Runoff Through BPNN, RNN, and RBFN in Tentulikhunti Watershed: a Case Study; pp. 258–267. a. [Google Scholar]
- 36.Samantaray S., Tripathy O., Sahoo A., Ghose D.K. Smart Intelligent Computing and Applications. Springer; IndiaSingapore: 2020. Rainfall Forecasting Through ANN and SVM in Bolangir Watershed; pp. 767–774. c. [Google Scholar]
- 37.Samantaray S., Sahoo A., Ghose D.K. Assessment of Sediment Load Concentration Using SVM, SVM-FFA and PSR-SVM-FFA in Arid Watershed, India: a Case Study. KSCE J Civ Eng. 2020;24(6):1944–1957. d. [Google Scholar]
- 38.Samantaray S., Sahoo A. Frontiers in Intelligent Computing: Theory and Applications. Springer; Singapore: 2020. Estimation of Runoff Through BPNN and SVM in Agalpur Watershed; pp. 268–275. [Google Scholar]
- 39.Samantaray S., Sahoo A. Smart Intelligent Computing and Applications. Springer; Singapore: 2020. Assessment of Sediment Concentration Through RBNN and SVM-FFA in Arid Watershed, India; pp. 701–709. [Google Scholar]
- 40.Sudheer C., Maheswaran R., Panigrahi B.K., Mathur S. A hybrid SVM-PSO model for forecasting monthly streamflow. Neural Comput Appl. 2014;24:1381–1389. [Google Scholar]
- 41.Tsakiri K., Marsellos A., Kapetanakis S. Vol. 10. New York, Water; 2018. p. 1158. (Artificial Neural Network and Multiple Linear Regression For Flood Prediction in Mohawk River). [Google Scholar]
- 42.Vapnik V. Springer New York google scholar; New York: 1995. The Nature of Statistical Learning Theory. [Google Scholar]
- 43.Vlachogiannis J.G., Lee K.Y. Multi-objective based on parallel vector evaluated particle swarm optimization for optimal steady-state performance of power systems. Expert Syst Appl. 2009;36:10802–10808. [Google Scholar]
- 44.Wang L.X., Wang L.N., Li G.F., Luan C., Sun F.F. Applied Mechanics and Materials Trans Tech Publ; 2012. Application Research of Support Vector Machine Based On Particle Swarm Optimization in Runoff Forecasting; pp. 2303–2307. [Google Scholar]
- 45.Wang W., Nie X., Qiu L. 2010 International Conference on Artificial Intelligence and Computational Intelligence. IEEE; 2010. Support vector machine with particle swarm optimization for reservoir annual inflow forecasting; pp. 184–188. b. [Google Scholar]
- 46.Xie J.X., Cheng C.T., Chau K.W., Pei Y.Z. A hybrid adaptive time-delay neural network model for multi-step-ahead prediction of sunspot activity. Int J Environ Pollut. 2006;28:364–381. [Google Scholar]
- 47.Zaini N., Malek M.A., Yusoff M., Mardi N.H., Norhisham S. IOP Conference Series: Earth and Environmental Science. IOP Publishing Ltd.; 2018. Daily river flow forecasting with hybrid support vector machine–particle swarm optimization; pp. 1315–1755. a. [Google Scholar]
- 48.Zaini N., Malek M.A., Yusoff M., Osmi S.F.C., Mardi N.H., Norhisham S. Support vector machine and neural network based model for monthly stream flow forecasting. Int J Eng Technol. 2018;7:683–688. b. [Google Scholar]
- 49.Zhao L., Yang Y. PSO-based single multiplicative neuron model for time series prediction. Expert Syst Appl. 2009;36:2805–2812. [Google Scholar]
- 50.Robati F.N., Iranmanesh S. Inflation rate modeling: adaptive neuro-fuzzy inference system approach and particle swarm optimization algorithm (ANFIS-PSO) MethodsX. 2020;7 doi: 10.1016/j.mex.2020.101062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Xiujia C., Guanghua Y., Jian G., Ningning M., Zihao W. Application of WNN-PSO model in drought prediction at crop growth stages: a case study of spring maize in semi-arid regions of northern China. Computers and Electronics in Agriculture. 2022;199 [Google Scholar]
- 52.Macharyulu I.S., Satapathy D.P., Sahoo A., Samantaray S., Mohanta N.R., Ray A. Intelligent System Design: Proceedings of INDIA 2022. Springer Nature Singapore; Singapore: 2022. Performance Evaluation of MLP and CNN Models for Flood Prediction; pp. 273–281. [Google Scholar]
- 53.Lin G.F., Chou Y.C., Wu M.C. Typhoon flood forecasting using integrated two-stage support vector machine approach. Journal of Hydrology. 2013;486:334–342. [Google Scholar]
- 54.Kao I.F., Zhou Y., Chang L.C., Chang F.J. Exploring a Long Short-Term Memory based Encoder-Decoder framework for multi-step-ahead flood forecasting. Journal of Hydrology. 2020;583 [Google Scholar]
- 55.Adikari K.E., Shrestha S., Ratnayake D.T., Budhathoki A., Mohanasundaram S., Dailey M.N. Evaluation of artificial intelligence models for flood and drought forecasting in arid and tropical regions. Environmental Modelling & Software. 2021;144 [Google Scholar]
- 56.Kamali S., Asghari K. The effect of meteorological and hydrological drought on groundwater storage under climate change scenarios. Water Resources Management. 2022:1–19. [Google Scholar]
- 57.Aswad F.M., Kareem A.N., Khudhur A.M., Khalaf B.A., Mostafa S.A. Tree-based machine learning algorithms in the Internet of Things environment for multivariate flood status prediction. Journal of Intelligent Systems. 2022;31(1):1–14. [Google Scholar]
- 58.Satapathy D.P., Swain H., Sahoo A., Samantaray S., Satapathy S.C. Intelligent System Design: Proceedings of INDIA 2022. Springer Nature Singapore; Singapore: 2022. Application of a Combined GRNNFOA Model for Monthly Rainfall Forecasting in Northern Odisha, India; pp. 355–364. [Google Scholar]
- 59.Mishra A., Sahoo A., Samantaray S., Satapathy D.P., Satapathy S.C. Intelligent System Design: Proceedings of INDIA 2022. Springer Nature Singapore; Singapore: 2022. Monthly Runoff Prediction by Support Vector Machine Based on Whale Optimisation Algorithm; pp. 329–338. [Google Scholar]
- 60.Kumar N.M., Saikrishnamacharyulu I., Sahoo A., Samantaray S., Kumar M.H., Naik A., Sahoo S. Intelligent System Design: Proceedings of INDIA 2022. Springer Nature Singapore; Singapore: 2022. Improving Streamflow Prediction Using Hybrid BPNN Model Combined with Particle Swarm Optimization; pp. 299–308. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.