Mechanics of neurulation: from classical to current perspectives on the physical mechanics that shape, fold, and form the neural tube

Abstract

Neural tube defects arise from mechanical failures in the process of neurulation. At the most fundamental level, formation of the neural tube relies on coordinated, complex tissue movements that mechanically transform the flat neural epithelium into a lumenized epithelial tube (Davidson, 2012). The nature of this mechanical transformation has mystified embryologists, geneticists, and clinicians for more than 100 years. Early embryologists pondered the physical mechanisms that guide this transformation. Detailed observations of cell and tissue movements as well as experimental embryological manipulations allowed researchers to generate and test elementary hypotheses of the intrinsic and extrinsic forces acting on the neural tissue. Current research has turned towards understanding the molecular mechanisms underlying neurulation. Genetic and molecular perturbation have identified a multitude of subcellular components that correlate with cell behaviors and tissue movements during neural tube formation. In this review, we focus on methods and conceptual frameworks that have been applied to the study of amphibian neurulation that can be used to determine how molecular and physical mechanisms are integrated and responsible for neurulation. We will describe how qualitative descriptions and quantitative measurements of strain, force generation and tissue material properties as well as simulations can be used to understand how embryos use morphogenetic programs to drive neurulation.

Developmental biologists have long debated the physical mechanisms driving neurulation. Early embryologists applied physical analog models to understand the basic mechanical processes that could cause the buckling and folding of a flat epithelial sheet into a tube and then sought to identify the intrinsic and extrinsic sources of force in those processes. In recent years, research has focused more on the genetic and molecular processes that guide neurulation. This latter effort has been successful in identifying numerous cell biological processes essential to neurulation and genes associated with neural tube defects but has struggled to connect these molecular mechanisms to the physical mechanics that directly shapes the neural tube. Both molecular-genetic dissection and physical mechanical exploration have yielded valuable insights into the complexity of neurulation and we are now at a time where molecular and biophysical approaches can be integrated to build a more complete understanding of how neurulation proceeds and how neural tube defects arise. This review will first briefly establish historical perspectives on the mechanical basis of neurulation and then describe modern approaches to synthesizing our current molecular understanding of neurulation with biomechanical analysis.

Tracing the historical formulations and refutation of hypothetical morphogenetic mechanisms provides a valuable perspective on the evolution of ideas as physical descriptions were supplemented with the molecular descriptions of this process. His’ descriptions of the different stages of neurulation and experimentation with physical analogs showing how different material sheets buckled led him to propose that pushing forces generated by the epidermis tissue along the lateral edges of the neural plate could drive neural plate invagination (His, 1874). However, this theory lost favor when Roux separated the neural plate from adjacent tissue and saw that folds still formed (Roux, 1885). Later embryologists proposed more intrinsic mechanisms that would drive folding through cell shape and volume change (Glaser, 1916). While a causative role of intrinsic cell shape change was accepted, theories proposing volume change were refuted (Brown et al., 1941). In 1947, the focus on active physical mechanisms driving neurulation turned to the apical domains of neural epithelial cell sheets when Lewis created a physical analog of the 2D transection of an epithelial sheet with rubber bands and brass bars representing tension bearing apical gel layer (Lewis, 1947). Lewis' physical analog models reproduced tissue invagination well and showed how previously observed flask-shaped cells, e.g. apically constricted cells might contribute to neurulation. By the 1960s, electron microscopy revealed the presence of unique subcellular structures, including newly visualized cytoskeletal elements and intracellular vesicles, which were correlated with cell shape changes and patterned within the neural epithelium during neurulation. Together with newly discovered small molecule inhibitors of the cytoskeleton, EM revealed the involvement of F-actin and microtubule cytoskeletal arrays in neurulation (Baker and Schroeder, 1967; Brun and Garson, 1983; Karfunkel, 1971; 1972; Schoenwolf and Powers, 1987). Live time-lapse, or cine-microscopy enabled detailed kinematic analysis of tissue shape change during the early phases of neurulation (Burnside and Jacobson, 1968; Jacobson and Gordon, 1976). These last studies lie at the foundation of modern studies on the physical and molecular mechanisms of morphogenesis and represent a productive methodology that continues today.

Associating actomyosin localization with cell shape change gave credence to the concept that epithelial tissues like the neural plate could autonomously deform through active apical constriction. Lewis’ models provided a physical demonstration of the potential role of apical constriction, the concept of apical constriction actively driving epithelial deformation was proposed as early as 1902 (Rhumbler, 1902). Apical constriction has since been observed in many cases of epithelial deformation including cell ingression and invagination during gastrulation as well as optic and otic placode formation (Ettensohn, 1985). These experimental models of epithelial morphogenesis have enabled the identification of a number of molecular regulators of apical constriction (Sawyer et al., 2010) and have suggested other concurrent, potentially redundant mechanisms driving epithelial folding such as basal expansion. These apical constriction independent mechanisms still result in a correlation between apical shape change and tissue folding. In order to understand the contribution of both apical constriction and alternative mechanisms of force generation to epithelial morphogenesis in general and neurulation in specific, a biomechanical framework of analysis is needed.

In 1990, Koehl reviewed the then current understanding of the physical basis for neural tube formation (Koehl, 1990). The methodical approach, based on approaches to studying functional morphology (Wainwright et al., 1976) and comparative biomechanics (Vogel, 2003), offers an excellent introduction to the engineering definitions of mechanics and how biomechanical approaches can further our understanding of tissue morphogenesis (Shawky and Davidson, 2015). The goal of this current work is to review efforts to expose the biomechanics of neurulation over the last 25 years and where future efforts are needed.

The 1990 Koehl paper identified five stages of a biomechanical analysis of a morphogenetic process. #1) Qualitative description of the process and qualitative statement of physical mechanisms involved. #2) Qualitative experiments where components of the physical mechanisms are removed or altered (e.g. removal of structural elements or altered mechanical boundary conditions). #3) Quantitative analysis of the process involving (a) morphometric analysis, (b) kinematic analysis, and (c) dynamic force measurements, and (d) measurement of mechanical properties, #4) Quantitative statement of theories, and #5) Empirical tests of model predictions. In addition to an update on progress in biomechanical analyses of neurulation we add a brief review of molecular pathways, how they may be used to formulate possible physical mechanisms, and how they may relate to the mechanics of neurulation.

Qualitative description of phenomena and empirical evidence

Primary neurulation can be broken into a series of deformations and tissue movements that convert the flat ectodermal sheet of tissue on the embryo’s surface into an internalized tube. Many studies have described and proposed potential mechanical events leading to neurulation and we refer readers to elegant reviews of chick and mouse neurulation (Colas and Schoenwolf, 2001; Jacobson, 1978; Schoenwolf and Smith, 1990). In this review we will describe the tissue movements in amphibians and correlate those movements with cell behaviors observed in both amphibians and other models. These correlations do not necessarily imply causation since cell shape changes and movements can occur in response to forces generated in different tissues or cells. During the earliest step, known as plate shaping, the neural plate thickens in the dorsal-ventral axis, which is perpendicular to the anterior-posterior and medio-lateral axis of the embryo, and is accompanied by apical-basal height increases within the neural ectodermal cells that are thought to drive this process. At this same time, the lateral edges of the plate begin converging towards the dorsal midline while elongating in the anterior-posterior direction. This convergence and extension of the neural plate is accompanied by mediolateral cell intercalation. Intercalation can occur via polarized junctional remodeling as demonstrated within the mouse and chick epithelium (Nishimura et al., 2012; Williams et al., 2014) or through polarized protrusive activity, such as observed in deep mesenchymal cells of the Xenopus neural plate as well as in the basolateral surfaces of the mouse epithelium (Davidson and Keller, 1999; Elul et al., 1997; Keller et al., 1992; Williams et al., 2014).

In the next phase of neurulation, neural plate bending, a medial hinge point forms at the dorsal midline and lateral edges of the folds rise and are brought into apposition. The medial hingepoint is marked by wedge shaped midline cells adjacent to non-constricted cells (Schroeder, 1970); apical constriction of these cells is thought to provide motive bending forces. Wedging at the midline is coincident with the elevation of lateral edges of the neural plate to produce neural folds. In chick and Xenopus, fold formation relies on adjacent non-neural ectoderm (Alvarez and Schoenwolf, 1992; Morita et al., 2012). Throughout this period, the neural plate continues to converge and extend, bringing the folds closer towards apposition as the neural groove deepens. Fold apposition may rely on the formation of dorsolateral hinge points, a line of wedge-shaped cells midway between the medial notoplate and lateral margins of the neural epithelium that may contribute to bringing folds towards the dorsal midline. Whereas medial hinge points are common in vertebrate species, the formation of dorsolateral hinge points varies between species as well as its precise location within the neural plate. For instance, initial sites of closure at the level of the mesencephalic fold in the chick do not involve dorsolateral hinge points but instead appear to bring folds into apposition progressing ventral to dorsal (Van Straaten et al., 1996). Differences in fold apposition between locations in the same embryo and between species suggest developmental programs of mechanics have evolved distinct mechanical solutions to the same problem, operating within a diverse set of physical constraints will still ensuring success of this key step in neurulation.

Shape changes at hinge points and throughout the neural plate and neural groove as the folds rise are accompanied by changes in the cytoskeleton and a rearrangement of intracellular structures. Notable among these changes is the accumulation of actin and myosin along apical cell-cell junctions and within the medioapical cortex of neural epithelial cells. Such an accumulation of actomyosin apical and the narrowing of apical surfaces is collectively referred to as apical constriction (Ettensohn, 1985) and has been described in a wide range of epithelial folding events in development and organogenesis (Sawyer et al., 2010). Within the Xenopus neural epithelium there are additional reductions in apical intermediate filaments and increases in basal-to-apical microtubule arrays (Baker and Schroeder, 1967). Beyond cytoskeletal reorganization there is a movement of nuclei from apical domains to basal (Glaser, 1914). This last movement, termed interkinetic nuclear migration (Messier, 1978), has been observed in avian (Schoenwolf and Franks, 1984) and amphibian neurulation (Lofberg, 1974) and accompanies many other cases of epithelial folding such as the Drosophila ventral furrow (Leptin and Grunewald, 1990). Contractile actomyosin networks are often considered the main source of force production within the neural plate but little is known about the contribution of other cytoskeletal networks or the role of coordinating movement of intracellular organelles such as nuclei.

Once neural folds are apposed new cell-cell adhesions are formed between the apical surfaces of contacting cells in a process known as fusion. Little is known about this process but fusion must involve a carefully choreographed release of neural epithelial cells from their neighboring non-neural ectoderm. Both neural and non-neural ectoderm cells must exchange 'dis-like' neighbors for 'like' cells from the apposing fold, establishing a contiguous sheet of epithelial cells over the dorsal midline of the embryo and a contiguous neural tube beneath the epithelium. It is unclear how the two sides of apposed neural folds are aligned but in some species, fusion is initiated at stereotypical locations and cell adhesions are remodeled in a progressive manner known as zippering. Zippering of the neural folds can occur in both anterior-to-posterior or posterior-to-anterior directions. Where it has been observed in time-lapse or with high resolution imaging in mouse, zippering is accompanied by apical protrusions and membrane ruffles (Pyrgaki et al., 2010; Rolo et al., 2016) that may ensure correct positioning of contacts between apposed folds. By establishing new contacts between the left to right sides of the embryo, cells in the epidermis and neural epithelium appear to resolve into new shapes with a new set of cell-cell contacts after the folds fuse.

Self-assembly of the vertebrate neural tube can proceed via two distinctly different mechanisms; primary neurulation, the process described above, involves bending and rolling of a sheet of cells contiguously into a tube whereas secondary neurulation involves neural lumen formation within of a solid cylindrical mass of cells (Lowery and Sive, 2004). The extent to which these two modes of formation occur is species dependent. Teleosts appear to rely solely on the secondary form (Compagnon and Heisenberg, 2013) whereas tetrapods appear to use primary neurulation in the brain and anterior spinal cord, and secondary neurulation in posterior regions of the spinal cord (Criley, 1969). The two modes of neurulation are compatible to the extent that different regions of the neural tube, e.g. dorsal or ventral may rely on secondary- or primary-like modes combined at the same anterior-posterior location (Costanzo et al., 1982; Schoenwolf, 1984). Such a state might occur during neurulation in the spinal region of Xenopus where both rolling and intercalation contribute to the formation of the definitive neural tube lumen (Davidson and Keller, 1999). The physical mechanics of these two processes are likely to differ substantially. This review will focus on primary neurulation mechanisms, but a general biomechanical approach could be applied to understand secondary neurulation as well.

Qualitative experiments where components are removed or altered.

There are strong correlations between lesions in specific molecular pathways and neural tube defects. Just as physical isolation and microsurgical ablation experiments were able to reveal tissues that might contribute to neurulation, removing and altering these pathways using genetic ablation, knock-out, knock-down, dominant-active or dominant-negative overexpression have also informed our hypotheses on the mechanics of neural tube closure. We direct interested readers to a number of excellent recent reviews of genetic and molecular pathways and their involvement in neurulation (Copp and Greene, 2013; Wallingford et al., 2013) and note that many of these pathways regulate the cell structural components and force generating machinery (Suzuki et al., 2012). Furthermore, a surprising number of mutations linked to cranial and caudal neural tube defects lie in actomyosin regulators such as cofilin (Escuin et al., 2015; Grego-Bessa et al., 2015), Rac1 (Rolo et al., 2016), RhoA/ROCK (Kinoshita et al., 2008; Nishimura et al., 2012), ENA/VASP (Roffers-Agarwal et al., 2008), and Shroom (Haigo et al., 2003; Hildebrand and Soriano, 1999; Lee et al., 2007; McGreevy et al., 2015). Since neurulation relies on polarized cell deformation, both planar cell polarity (Wallingford and Harland, 2002) as well as apicobasal polarity pathways (Eom et al., 2012), which lie upstream of actomyosin or microtubule dependent processes, are also involved in neurulation (Sokol, 2016). The next challenges in these efforts involve understanding how genetic changes alter spatial and temporal protein activities, and how these pathways respond to mechanical cues as well as how they direct cell and tissue mechanics during neurulation.

Integrating quantitative description of kinematics and morphometrics with molecular analysis

To understand the role of mechanics requires both morphometric and kinematic analyses of neurulation. Morphometric analysis is the quantification of static geometric features of cells and tissue in neurulation. Kinematic analysis is the quantification of the direction, magnitude and rates of movement. In combination, morphometric and kinematic analyses are particularly useful to understand the effects of molecular perturbations on tissue shape change. Together they can be used to describe strain occurring in the neural plate at both cell and tissue levels. In a simplified definition, strain is described as the change in length of an object with respect to a reference length.

Generally, when morphological defects are observed after molecular or genetic perturbation, researchers have quantified tissue level morphometrics such as distance between neural folds or width of neural plates as well as changes in overall tissue thickness (Escuin et al., 2015; Grego-Bessa et al., 2015; Itoh et al., 2014; Massarwa and Niswander, 2013; McGreevy et al., 2015; McShane et al., 2015; Roffers-Agarwal et al., 2008; Wallingford and Harland, 2002). A number of these studies have gone on to quantify differences in cell level morphological properties to determine any associations between cell level behaviors and tissue level morphologies. Researchers use transverse sections through the neural plate of fixed embryos to measure ratios between apical to basal width or between apical width and cell height in order to quantify degree of apical constriction between different treatment or conditions (Eom et al., 2012; Itoh et al., 2014; Lee et al., 2007; Suzuki et al., 2010). Cell height changes and nuclear positioning can also be derived from transverse views (Eom et al., 2012; Lee et al., 2007). En face views of cells allow researchers to determine planar cell elongation and apical area (Christodoulou and Skourides, 2015; Elul et al., 1997; Grego-Bessa et al., 2015; Lee et al., 2007; McGreevy et al., 2015; Morita et al., 2012). Techniques to visualize en face views of the neural plate in live embryos have been developed and allow researchers to track both cell morphological features such as apical area or cell junction length and tissue level morphology changes over time, providing morphometric and kinematic analyses of both normal as well as perturbed neurulation (Christodoulou and Skourides, 2015; Elul et al., 1997; Massarwa and Niswander, 2013; Morita et al., 2012; Williams et al., 2014).

Fixed embryos allow correlation between measured morphometric aspects of the neural plate and surrounding tissues such as cell height with markers that delineate cell identities, patterns of gene expression or protein activity. However, key dynamic or kinematic analyses of neurulation such as the determination of tissue or cell strain or strain rates cannot be measured from fixed samples; without a recording of the trajectory of earlier movement a static analysis provides no initial reference point for the tissue. Differences in static cell shapes and embryo morphology may reflect variability between embryos or variation across a field of cells. Alternatively, live imaging allows direct measurement of strain and strain rates by recording cell or tissues morphology through time. The following examples describe the utility of live imaging for building mechanics-based hypotheses and exploring the subtle differences between molecular and physical manipulations.

Static and dynamic analysis of neurulation are key elements of both qualitative and quantitative biomechanical analyses. "End point analyses" of neurulation and neural tube defects, e.g. the static description of cell shapes and protein localization or activity at late stages of neurulation, can be useful when correlating phenotypes with different treatments. Extending quantitative analysis to the kinematics and morphometrics as the embryo passes through earlier stages can reveal multiple concurrent mechanisms contributing to the tissue deformation. A recent study of mouse neural plate convergent-extension highlights the utility of this approach (Williams et al., 2014). During tissue convergent extension, wild type cells display both polarized junctional remodeling apically and basally as well as directed basolateral protrusive activity. Mutations in Vangl2 and Ptk7, both a part of the planar cell polarity pathway, impair tissue level convergent-extension with Ptk7 mutants generating a larger defect. Morphometric analysis revealed each mutant alters different behaviors within the neural epithelial cells. Whereas Ptk7 mutants lose all polarized behaviors both apically and basally, they maintain the ability to undergo unpolarized neighbor exchanges; by contrast, Vangl2 deficient cells are unable to undergo proper neighbor exchange due to impaired apical junctional remodeling.

The forces driving neurulation cannot be inferred from analyses of tissue movements alone. A kinematic description of movement, i.e. characterizing tissue or cell deformation over time, is not sufficient to quantify driving forces, however, such an analysis can form the basis of mechanistic hypotheses for how and where these forces may be generated. Such mechanistic hypotheses can also take into account experimental embryological and biomechanical observations. For example, analysis using distortion diagrams that describe local patterns of tissue strain in Xenopus laevis neural deep cell tissue explants revealed that regions surrounding the midline of the neural plate had high strain rates of both convergence and extension (Elul et al., 1997). Subsequently, smaller explants including less lateral tissues showed an increased rate of convergence indicating medial tissues make a major contribution to convergent extension and that lateral tissues may inhibit this process. Further analysis of cell shape within medial tissues indicated cells would periodically become elongated in the mediolateral direction, perpendicular to the direction of tissue level elongation, indicating that cells were not simply passively stretched in the direction of tissue deformation. Together with quantitative descriptions of tissue movements in whole embryos the observations of episodic elongation in cell shape accompanied by polarized protrusive activity suggested that directed cell intercalation drives convergence and extension in the neural plate (Elul et al., 1998).

Improvements in live imaging and recent advances in semi-automated image analysis techniques enable analysis of cell and tissue dynamics simultaneously during tissue morphogenesis. By tracking cells and tissues through time, it is possible to calculate strain, which is defined as change in dimensions of an object with respect to a reference. The "tissue tectonics" approach is an ideal platform through which events at the cell-scale can be correlated with global tissue level strain changes (Blanchard et al., 2009). This approach involves tracking of local domains of cells through time and space and de-composition of those movements into invariant components of strain and strain rate produced by different cell behaviors, such as cell division, cell intercalation, cell shape change, and rearrangement. Tectonic analysis can reveal subtle patterns in morphology and kinematics that are easily overlooked by end-point or static analyses that focus on localized regions within the neural plate at specific time points. In Drosophila, this and similar techniques, have shown how specific cell behaviors dominate various phases of tissue deformation and how tissue boundary conditions influence cell behaviors (Butler et al., 2009; Etournay et al., 2015). Recently, this approach was used to show differences between cell elongation behaviors of the lateral ectoderm versus the early neural plate (Yamashita et al., 2016). Such techniques increase the sensitivity of perturbation and ablation studies and will be useful in parsing the contribution of individual cell mechanisms in both wild-type and mutant cases of neurulation. A list of select image analysis software are described in Table 1 which are needed to begin these types of analyses.

Table 1: Useful image analysis software to measure cell and tissue morphological changes.

Many software packages allow researchers to quantifiy kinematic and morphometric data from live images. This table describes advantages and disadvantages of specific software used for general quantitative image analysis and software with specific uses for cell segmentation which allows data for individual cells to be derived in semi-automated or automated fashion and typically used with confocal images of apical cell surfaces. To our knowledge no single method is completely error-free and must therefore allow the user to manually correct erroneously segmented cells.

Program	Usage
ImageJ/FIJI (Eliceiri et al., 2012) (Schneider et al., 2012)	General image analysis software	Java based Established image analysis software used in biological research Free Built in graphical user interface (GUI) Extensive documentation Provides built in plugins for a number of analysis algorithms Custom macros or plugins
SeedWater Segmenter (Mashburn et al., 2012)	Watershed Algorithm Cell Segmentation Software	Python based Built in GUI Semi-automated- allows for user correction of boundaries Outputs data on select morphological parameters Tracks cells through time stack Open Source Currently provides only 2D analysis Can be slow with larger image files
MorphoGraphX (Barbier de Reuille et al., 2015)	Watershed Algorithm Cell Segmentation Software	C++ Cuda based Built in GUI 2.5D Visualization and segmentation program Recreates image surfaces based on 3D stack information Open Source Requires linux based operating system and special graphics card
TissueAnalyzer (formerly Packing Analyzer) (Aigouy et al., 2010)	Watershed Algorithm Cell Segmentation Software	Java based Semi-automated segmentation method- Allows some user correction Built-in GUI Easy to install Works with FIJI Not open source
TissueMiner (Etournay et al., 2016)	Cell shape analysis toolkit	R and Python based Used in conjunction with TissueAnalyzer Provides database structure for morphology information derived from segmented images Has built in analysis tool to derive multiscale analyses of deformation and cell tracking Provides graphical data visualization capabilities Allows user to create personalized data analysis algorithms to be added to analysis library (require programming knowledge) Provides 2D analysis Not fully open source
EpiTools (Heller et al., 2016)	Watershed Algorithm Cell Segmentation Software	Semi-automated segmentation – allows some user correction Built-in GUI Provides analysis of cell junctions Outputs data on select morphological parameters Interfaces with ImageJ Accounts for surface curvature Matlab based GUI
SIESTA (Fernandez-Gonzalez and Zallen, 2011)	Watershed Algorithm Cell Segmentation Software	Semi-automated segmentation- allows some user correction Built-in GUI Outputs data on select morphological parameters Accounts for surface curvature Matlab, DIPImage ToolBox based Provides 2D analysis Not open-source
MEDUSA (Zulueta-Coarasa et al., 2014)	Active Contour Snake-Based Cell Segmentation Software	Semi-automated segmentation – allows some user correction Provides analysis of cell junctions Outputs data on select morphological parameters Accounts for surface curvature Provides 3D segmentation Matlab, DIPImage ToolBox based Not open source
Matlab (Mathworks), Mathematica (Wolfram)	Numerical	Programmable Many built in functions Good handling of matrix operations Faster debugging rates Good Documentation Slow compared to other programming languages programming knowledge required Expensive
ITK library	C++ based Bioimaging library for image analysis data processing	Many algorithms available for image segmentation, registration, stitching, and more Can be wrapped in other languages (Python, Java) Programming knowledge required

Measurement of forces and material properties

Embryonic tissues, like any material, deform under externally or internally applied loads or forces. The amount and manner in which a tissue or material deforms under a load depends on its material properties such as elastic stiffness and viscosity. Thus, to understand how tissue deformations during neurulation are physically driven one must characterize the forces acting upon and within the neural plate as well as the material properties of the neural plate and surrounding tissues. Given the important role of these properties during neurulation it remains surprising that few studies have quantitatively analyzed the material properties of and forces produced by cells and tissues during neurulation. Currently, most of our knowledge on the mechanics of neurulation comes from experimental mechanical studies on amphibian embryos (Benko and Brodland, 2007; Selman, 1955; 1958; Wiebe and Brodland, 2005; Zhou et al., 2009; Zhou et al., 2010; Zhou et al., 2015). This is likely due to the large size and relatively simple culture conditions of these embryos making them ideal for physical manipulation and direct mechanical testing. While there are detailed descriptions of morphological changes during neurulation in a few species of amniotes and anamniotes very little is known about the process in human embryos or about the physical mechanics of neurulation in these animal model systems (Araya et al., 2016; Colas and Schoenwolf, 2001). Recently, descriptions of static stages have been supplemented with descriptions of phenotypic changes in mutants and live cell dynamics in mouse mutants. For example, cell morphological and phenotypic changes in cofilin mutants (Grego-Bessa et al., 2015) have been described, as well as Shroom3 and PCP mutants (McGreevy et al., 2015) and Rho GTPase mutants (Rolo et al., 2016). Live imaging have described apical protrusion dynamics during fold fusion (Massarwa and Niswander, 2013; Pyrgaki et al., 2010 ) as well as dynamic cellular behaviors during tissue convergent extension (Williams et al., 2014). Certainly mechanics must play an important role in these events but there have been no comparative studies that shed light on differences in the mechanical processes operating in these groups. To understand the comparative mechanics of neurulation in different animal model systems, researchers must develop novel techniques to manipulate and measure forces and tissue material properties of these tissues.

Measurement of Material Properties

Tension within the neural plate of the axolotl, Ambystoma mexicanum, were measured with force-calibrated wires afixed to the apical surfaces of both neural and non-neural ectoderm (Wiebe and Brodland, 2005). These tissues were then microsurgically isolated from the embryo and pulled apart while tissue deformations were tracked. A stiffness modulus could then be calculated (as the slope of the force resultant versus strain curve) and compared between different stage samples as well as between different tissue types (ie. neural vs epidermal ectoderm). The stiffness modulus measured in these studies depends on tissue geometry. To translate the geometry-dependent stiffness modulus to a geometry-independent Young's modulus requires measurement of the cross-sectional area. Assuming a constant tissue thickness, the Young's modulus of neural tissue was estimated at 20 Pa. These studies demonstrated the existence of material anisotropy, regional differences, and stage-dependent differences in stiffness modulus based on tissue location within the anterior posterior axis but could not separate stiffness changes from positional or stage-dependent shape changes within the neural plate.

The mechanical properties of the neural plate and dorsal tissues of the African claw-toed frog, Xenopus laevis, were measured with an unconfined uniaxial compression test (also known as a creep or stress-relaxation test (Findley et al., 1989); (Zhou et al., 2009)). This method yields a measurement of the geometry-independent Young's modulus of dorsal tissue explants that contain all three germ-layers including the neural plate. This study revealed a stage-wise increase in axial tissue modulus (e.g. residual modulus). Furthermore, perturbation of actin and myosin through acute drug treatment revealed the role of the cytoskeleton in establishing a tissue's Young's modulus; however, disruption of actomyosin reduced the modulus but only 50% indicating actomyosin accounts for some but not all of the ability of a neural stage embryo to resist mechanical tension and compression. In these tests the stiffness of the neural plate was estimated to be 40 to 60 Pa, similar to that of the underlying notochord. With these and other studies (Rolo et al., 2009; von Dassow et al., 2010; Zhou et al., 2010) revealing the dependence of neurula mechanical properties on F-actin and myosin, it is highly likely that many of the upstream regulators of actin and myosin affect tissue mechanical properties.

Measurement of Force Production and Stresses within the Neural plate

In the 1950s, Selman measured the force of neural fold convergence using magnetic dumb-bells that were placed against the inside of folds of the alpine newt Ichthyosaura alpestris, and the axolotl (Selman, 1955; 1958). By creating magnetic repulsion between the dumb bells, Selman could estimate the force needed to stall fold convergence. These forces were variable but Selman found neural folds could produce 0.40 to 0.45 μN (40 to 45 x 10⁻³ dynes) in the newt and 0.8 to 1.1 μN (80 to 110 x 10⁻³ dynes) in the axolotl. In both species, Selman noted that the force needed to stall convergence increased over time.

Most recently, extensional stresses produced during neurulation were measured for Xenopus laevis tissues (Zhou et al., 2015). This approach utilized a gel based stress sensor in which dorsal tissue explants were embedded in an agarose gel. As the explant converges and extends, it pushes against the gel, generating stress within and causing deformation of the gel. Gel deformations tracked by observing the movements of microbeads embedded within the gel were converted into displacement and strain. Using the known material properties of the gel, the mean stress generated along the anterior-posterior axis of the extending tissue was found to be ~ 5 Pa, or roughly 0.6 μN of force distributed over the transverse cross-sectional area of a dorsal tissue. Inhibiting rho-kinase (ROCK)-mediated myosin activity reduced stress production of these tissues. Surprisingly, no changes in the rates of tissue convergence and extension could be observed in ROCK-inhibited explants cultured outside the gel. In the absence of a mechanical 'phenotype' a conventional genetic interpretation would suggest ROCK is not involved. However, biomechanical analysis allowed the separation and quantification of two physical mechanical properties of the embryo, e.g. force production and mechanical resistance. Each of these mechanical aspects of convergent extension are coaffected and that their interaction after ROCK inhibition does not generate an obvious changes in neurulation. These studies also revealed that isolated neural plate isolates alone could generate extensional stresses similar to those produced by dorsal explants containing all three germ layers.

Estimating the mechanical status of contractile epithelia using microdissection via microsurgery or laser ablation.

Microsurgery has long been used qualitatively to distinguish active generation of forces from passive tissue deformation during morphogenesis (e.g. Keller and Jansa, 1992; Schechtman, 1942; Townes and Holtfreter, 1955) but has been adapted recently for more quantitative analyses. Stress resultants within the early neural plate of axolotl embryos were measured using a force-calibrated set of steel wires (Benko and Brodland, 2007). After affixing steel wires, the neural ectoderm was dissected from the remainder of the embryo and the position of the wires adjusted to minimize changes in shape of the newly released neural plate. This approach was used to estimate the tension exerted by the plate in vivo. Using a finite element model analogous to a spherical pressure vessel, the authors estimated that non-neural ectoderm was under isotropic tension and that interior of the embryo during neurulation was under 1100 Pa pressure.

In animal models where physical manipulations are not possible, laser ablation can be used to probe tension within the embryonic epithelium. Laser ablation provides a semi-quantitative platform to understand stresses acting within tissue sheets. This method is analogous to early experiments involving cutting tissues to observe tissue recoil (Beloussov et al., 1975; Jacobson and Gordon, 1976). The advantage of the laser ablation technology in combination with modern imaging techniques is that one can accurately control where cuts are made and allow analysis of recoil within the first few seconds which reduces the confounding influence of wound healing. Recoil in the first few seconds reflect the degree of tissue strain which is a function of both tissue tension and tissue stiffness (Ma et al., 2009). Laser ablation can reveal differences in directional strain along boundaries and within the cortex of cells. Although absolute values for tension cannot be measured, most studies assume constant tissue stiffness and rely on instantaneous recoil velocity as an index of tension. These experiments are particularly useful in describing local and directional differences in strain within cell junctions or the cortex. However, it should be noted changes in recoil velocity might alternatively reflect changes in material properties of the cells. Though laser ablation has not yet been used in studying tensions within early neural ectodermal cells, it has been used to interrogate the mechanical status of the epidermis during processive neural fold fusion in Ciona intestinalis ascidian embryos (Hashimoto et al., 2015); ascidian neurulation appears similar to vertebrate neurulation and offers a unique comparative model for neural fold fusion.

Simulating Neural tube formation

Physical Analog Models of Neurulation

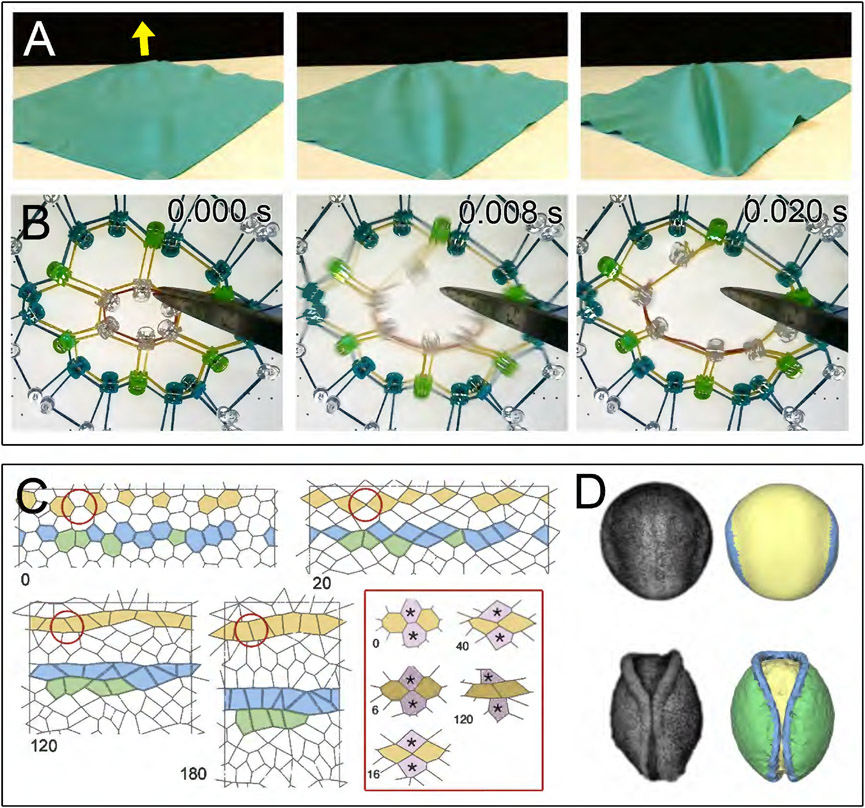
Where mechanical testing of embryonic tissues may not be possible, physical analogs can provide a way to recreate the deformations seen in the neural ectoderm using materials of known material properties that could approximate the properties of embryonic tissues. Embryologists have mainly used physical analog models to test the plausibility of biomechanical theories on the origin of a particular deformation or what type of material properties cells and tissues might be an important factor in these deformations. Physical analog models can be built to represent tissue mechanics at different scales. Wilhelm His proposed compressive forces exerted by the lateral ectoderm could neural plate invagination similarly to how laminate sheets buckle under lateral compression. In this case, His viewed the neural plate as a contiguous material (His, 1874). Lewis was one of the earliest investigators to consider the discrete cell mechanics of neural folding and invagination using brass bars and rubber bands representing individual cells and specific compartments in the neural plate (Lewis, 1947). Rubber bands exerted a contractile force in the “apical” compartment of the model causing the system to become concave. This model demonstrated how differential contractility in the apical compartment could drive an entire epithelial sheet to buckle. Another model demonstrated how tissue extension may be sufficient to cause buckling by demonstrating the formation and convergence of ridges after pulling on a rubber sheet (Jacobson, 1978). The simplicity of physical analog models remain attractive and can easily demonstrate biomechanical processes of folding (Fig. 3A). Scaled physical models can also be used to test different assumptions of experiments that test cell and tissue properties; for instance, a rubber band-connected model of a multicellular array can be dissected with "laser" ablation and provide intuition about anisotropic conditions of tension and stiffness exposed by biophysical and embryological manipulations of embryonic epithelial sheets (Fig. 3B).

Figure 3: Simulating the mechanics of neurulation with physical analogs and computational models.

A) Physical analog model of fold formation in an elastic sheet. Tensile force is applied (yellow arrow) causing lateral buckling and fold formation. B) Physical analog model of laser ablation. Cells boundaries represented by network of elastic rubber bands under differential tension and with differential elasticity. When a single rubber band is cut, tension is released and network recoils. The instantaneous velocity of recoil reflects both the tension and mechanical properties of cell sheets in laser ablation experiments. C) Computational vertex-model of cell rearrangement during neural plate shaping in the chick. Patterns of cell-cell adhesion are predicted to produce aligned rows through directed cell rearrangement (modified from Fig. 2 in Nishimura et al., 2012; with authors' permission). D) Continuum model of axolotl neurulation. Finite element model based on image-acquired 3D geometry (modified from Figure 9 in Chen and Brodland, 2008; with authors' permission).

Whereas researchers have increasingly turned towards computational simulations to model biological processes, physical analogs can still play an important role in building the mechanical intuition needed to implement more complex computer simulations. Physical analogs can inform the biologist about the process of building models, the roles of implicit constraints such as boundary and initial conditions, and how models might be used with experiment. Recently, this approach proved to be illuminating in understanding the mechanical behavior of the curled embryonic gut (Savin et al., 2011). Early exploratory work with a physical model, where there are few obstacles to model development and modification, should be more broadly adopted in biomechanical studies of development in general and of neurulation in specific.

Computational Models of Neurulation

Just as physical analog models guided early embryologists current biomechanical analysis of epithelial morphogenesis is informed by computational models. Like physical analogs, these models can be constructed to test the roles of specific mechanical assumptions or theories of force-generation. A wide range of biomechanical and computational models have been developed to study epithelial morphogenesis and these can be broken down into several categories based on the level of detail at the cell and tissue levels (Davidson et al., 2010). Two-dimensional models of the apical face of the neural plate or transverse sections across the neural plate can be assembled by connecting vertices representing cell-cell junctions by springs and dashpots (vertex-models; (Nishimura et al., 2012)). Vertex-models combined with material conservation laws can be constructed to recapitulate the complex elastic and plastic behavior of epithelial tissues and mimic the appearance and dynamic behaviors of living epithelial sheets. Few models have been developed to represent species specific mechanics of neurulation and have instead taken the form of more generic tests of convergence and extension (Brodland and Veldhuis, 2006; Weliky et al., 1991; Zajac et al., 2003) and epithelial folding (Chen and Brodland, 2008; Davidson et al., 1995; Odell et al., 1981). Vertex-models (Fletcher et al., 2014) have been particularly useful in testing biomechanical hypotheses of "in-plane" movements, e.g. two-dimensional epithelial morphogenesis (Farhadifar et al., 2007), and the methodology has recently been extended to three-dimensional cases of morphogenesis (Murisic et al., 2015).

Extending computational models to explore the complex dynamics of 3D tissue movements in complex composite tissues has proven challenging. For instance, vertex-models use spring-like struts (incorporating contractility and adhesion) to represent structures such as adherens junctions in 2D models but do not represent sheet-structures that compose basolateral cell-cell contacts, dispersed point-like desmosomes, or extracellular matrix found along the basal surface of most epithelial sheets. To side-step these difficulties two different modeling strategies have been taken: 1) particle based 3D models in which each cell in a tissue can be represented by a set of self-interacting particles or discrete virtual cells (Palm and Merks, 2015; Sandersius et al., 2011), or 2) continuum 3D models in which cell-cell interfaces and internal structures are lumped within finite element models (Taber, 1995).

Both continuum- and vertex-models have been useful tools to extend experimental intuition concerning mechanics-based hypotheses of neurulation. The cellular focus of vertex-models has been most compatible with cell-focused analyses of morphogenesis. By contrast, continuum-methods are more robust in representing large-deformations and complex nonlinear materials that compose the embryo. Ideally, future modeling approaches will need to incorporate hybrid formulations combining continuum methods with discrete representation of cells, complex extracellular interfaces, and extracellular matrix. Such hybrid models would be more flexible and able to predict the roles of intracellular programs of force generation and their impact on macroscopic processes of force transmission and collective tissue movement involved in neurulation.

Mechanics as component in the signaling networks of neurulation

Ongoing studies in mechanobiology suggest a complex interplay between mechanics, cell and subcellular protein activity, and subsequent tissue deformation (Heisenberg and Bellaiche, 2013; Sasai, 2013; von Dassow and Davidson, 2011). Not only do cell behaviors drive mechanical events within tissues, but mechanics can feedback to cell signaling pathways and influence cell behaviors both passively and actively. Growing evidence supports the role for mechanics as a patterning cue during development (Heller and Fuchs, 2015). Central to the patterning function of mechanical cues is the establishment of anisotropic tissue strain fields that can orient cell divisions, initiate shape change, and guide protrusive activity (Aigouy et al., 2010; Campinho et al., 2013; Chien et al., 2015; Etournay et al., 2015; Lau et al., 2015; Weber et al., 2012). Recent work in both fly and frog suggests anisotropic tissue strain can directly regulate planar tissue polarity via non-canonical WNT or PCP signaling pathways. Cells isolated from wing hinge contraction in the drosophila pupal wing can prevent the endogenous reorientation of PCP complexes needed to instruct polarized cell behaviors (Aigouy et al., 2010). More recently, studies using Xenopus skin ectoderm showed that isolating early gastrula ectoderm from large scale movements in the embryo prevents efficient PCP polarity stabilization at later stages (Chien et al., 2015). This defect can be rescued with the application of exogenous strains onto tissue explants showing that strain may orient PCP components in a timely manner. The authors suggest that, in vivo, strains generated by gastrulation guide this process. Such studies set a precedent for exploring how mechanics may influence signaling networks that control PCP or apico-basal polarized cell behaviors in neural tube morphogenesis. As planar cell polarity genetic mutations are found in neural tube defects, our understanding of how these genetic defects are manifested may benefit from evaluating the mechanical background against which they act and vice versa. Should mechanical regulation operate during neurulation, an important question is how these mechanical cues are transduced to affect cell behaviors. Cell culture studies have identified a number of mechanosensitive proteins including those associated with cell adhesion and mechanically gated ion channels that could allow cells to sense mechanical cues and use these cues to direct morphogenetic processes (Miller and Davidson, 2013).

Biomechanics of neurulation, neural tube defects, and robust development.

The ultimate goal of building a mechanical description of neurulation is to understand the origins of human neural tube defects. Since all neural tube defects are mechanical in nature, an understanding of neurulation mechanics should allow us to attribute these defects to specific cell biological sources that result in defects in tissue mechanical properties, cell force generation, or patterning. Over the last 125 years, the plausibility of many hypotheses on the mechanical processes contributing to neurulation have been demonstrated in physical analogs, computational models, or through qualitative embryological manipulation, however, little is known about contribution of specific biomechanical processes to maintaining robust neurulation. Biomechanical lesions underlying birth defects, either through genetic or environmental perturbations, remain unknown. To understand the incidence of birth defects will require a quantitative understanding of how phenotypic changes in neurulation vary with genotypic and environmental perturbations. Forging this linkage between genetics, mechanics, and functional morphology remains a major challenge to understanding developmental biomechanics (von Dassow and Davidson, 2011). With the broader availability of experimental biomechanical tools, advanced cell biological methods, and predictive conceptual frameworks we anticipate the predictive power of computational simulations of neurulation will be combined with experiment biomechanical analyses to build more complete understanding of the mechanics of neurulation and the origin of neural tube defects.

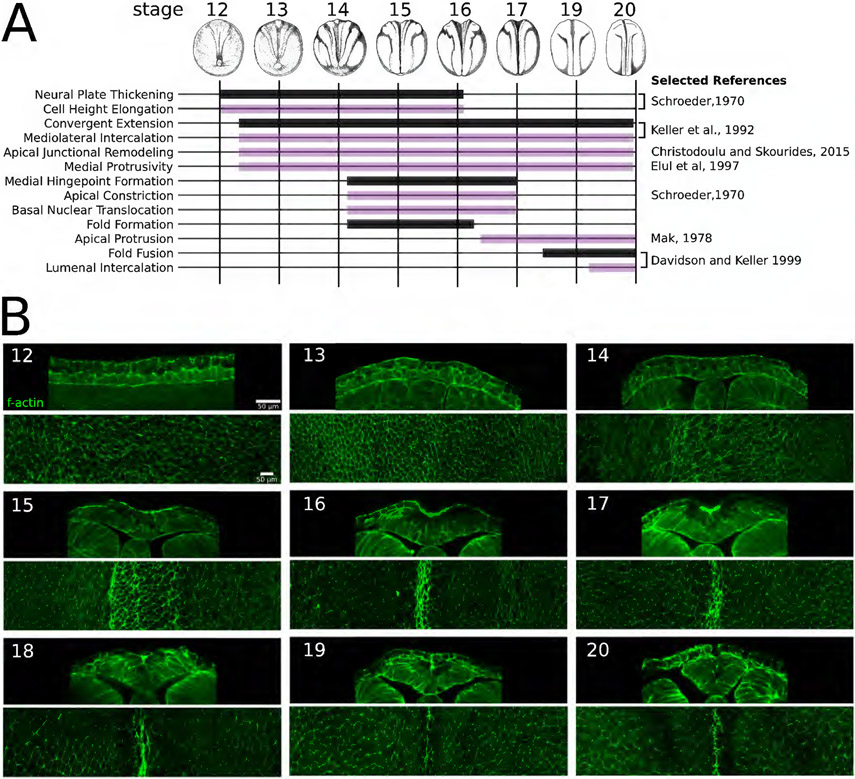
Figure 1: Concurrent mechanical processes shape the neural tube in Xenopus laevis.

A) Stage-dependency of specific tissue deforming processes (black bars) and cell behaviors (purple bars) that accompany the different phases of neurulation in Xenopus laevis. We refer interested readers to a similar diagram describing tissue movements and cell behaviors during stages of chick neurulation (Schoenwolf and Smith, 1990). B) Transverse sections and maximally z-projected en face sections of F-actin stained cell outlines of the posterior neural and non-neural dorsal ectoderm in fixed Xenopus laevis embryos showing cell and tissue morphological changes at each stage of neurulation.

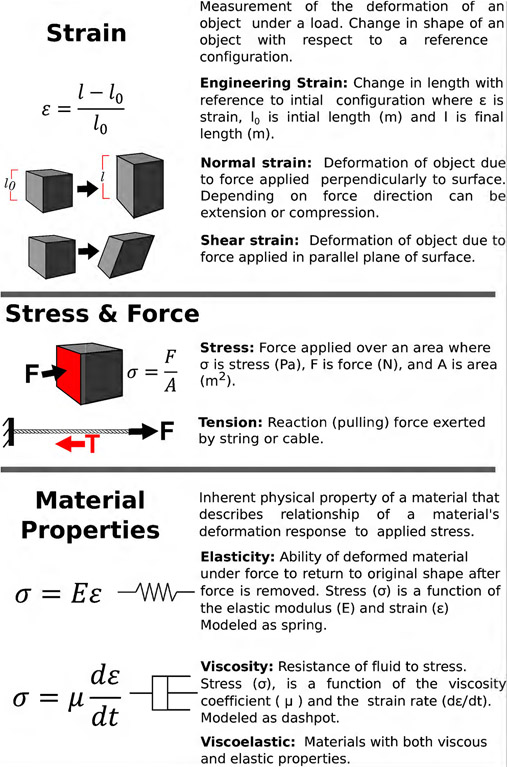
Figure 2: Formal definitions of mechanical terminology.

Engineering provides specific terms to create mechanical descriptions of biological processes. Provided are commonly used definitions that demonstrate the relationship between strain, stress and material properties.