Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Feb 2;8(2):704–711. doi: 10.1021/acssensors.2c02218

Tension Gauge Tethers as Tension Threshold and Duration Sensors

Jingzhun Liu †, Shimin Le ‡, Mingxi Yao §, Wenmao Huang ∥, Zhikai Tio ⊥, Yu Zhou †, Jie Yan †,∥,*
PMCID: PMC9973368  PMID: 36731861

Abstract

graphic file with name se2c02218_0007.jpg

Mechanotransduction, the process by which cells respond to tension transmitted through various supramolecular linkages, is important for understanding cellular behavior. Tension gauge tethers (TGTs), short fragments of double-stranded DNA that irreversibly break under shear-stretch conditions, have been used in live cell experiments to study mechanotransduction. However, our current understanding of TGTs’ mechanical responses is limited, which limits the information that can be gleaned from experimental observations. In this study, we quantified the tension-dependent lifetime of TGTs to better understand their mechanical stability under various physiologically relevant stretching conditions. This work has broad applications for using TGTs as tension threshold and duration sensors and also suggests the need to revisit previous interpretations of experimental observations.

Keywords: mechanosensing and mechanotransduction, focal adhesion, adherence junction, magnetic tweezers, DNA tension sensor, tension gauge tether (TGT)

Cells in tissues are connected to the extracellular matrix (ECM) and neighboring cells through focal adhesions (FAs) for cell–matrix connection and adherence junctions (AJs) for cell–cell connection.1−5 These connections allow cells to transmit dynamic tension generated by actomyosin contraction or external perturbations. By responding to this tension, cells are able to sense and respond to mechanical cues in their local environment through mechanotransduction, which plays a crucial role in regulating various cell behaviors such as cell spreading, migration, and differentiation.1−10

The way in which cells translate mechanical signals into biochemical responses, known as mechanotransduction, relies on the mechanical properties of supramolecular linkages that transmit tension.1 Different mechanical stresses applied to cells lead to varying dynamic tensions, causing tension-dependent conformational changes in mechanosensing protein domains. These changes result in tension-dependent interactions with binding factors, effectively converting mechanical cues into a series of biochemical reactions.11−18 Evidence suggests that mechanical unfolding of mechanosensing protein domains is a key mechanism in revealing hidden binding sites for signaling proteins. The critical tension Fc, the tension associated with equal probabilities of unfolding and folding of a structural domain, is typically in the range of a few piconewtons (pN).16−20

The conformational transitions and interactions of protein domains that are dependent on tension can take a significant amount of time. Therefore, both the level of tension and the duration of tension are important factors. Recently developed tension sensors, such as short peptides or small biomolecular structures that undergo reversible conformational changes based on tension, have allowed for the investigation of tension ranges in various tension-transmission linkages.21−28 These tensions, which are typically in the range of a few pN and are relevant to physiological processes,21,23,25,28 have been found to coincide with the tensions needed to unfold mechanosensing protein domains in these linkages.12,15,17

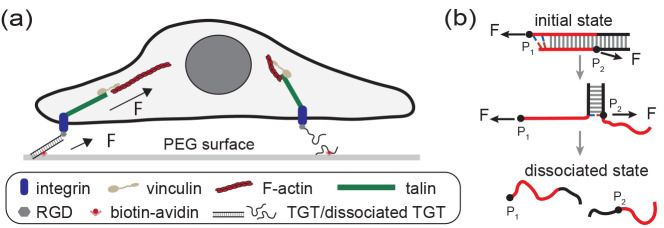
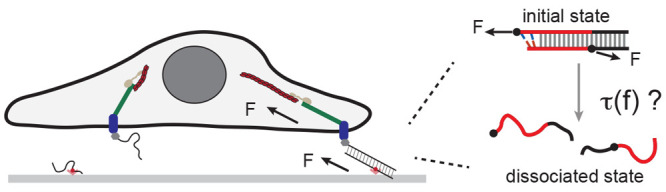
Tension gauge tethers (TGTs) are short, double-stranded DNA segments29 that have been inserted into tension–transmission linkages on the exterior of FAs (Figure 1a) and AJs to study the mechanical responses of cells. In experiments, a TGT is inserted into a tension–transmission linkage at two points, P1 on the end of one strand and P2 on a position on the complementary strand separated from P1 by M base pairs (Figure 1b). The mechanical stability of the TGT can be adjusted by changing the number of base pairs between P1 and P2. When the DNA strands in a TGT are dissociated, the corresponding tension–transmission linkage is disconnected. Unlike reversible tension sensors, TGTs undergo irreversible tension-dependent strand dissociation, which is referred to as the rupturing of TGTs.

Figure 1.

Figure 1

Open in a new tab

Illustration of TGTs and their applications in cell studies. (a) Schematic illustrating a cell adhered to a surface through integrins binding to RGD-labeled TGTs tethered to the surface. When the two strands in a TGT dissociate, the tension transmission pathway disappears. (b) Illustration depicting the tension-dependent strand-dissociation pathway of a TGT through strand-peeling from the ends.30 The force attachment points, indicated by the black dots on the DNA strands, are labeled as P1 and P2.

Cell behavior has been shown to significantly change in response to changes in the stability of TGTs inserted at FAs.29 This suggests that the mechanical stability of TGTs has a direct impact on the mechanotransduction process occurring in the tension–transmission linkages from integrin to the cytoskeleton. Additionally, the mechanical stability of TGTs has been found to strongly impact mechanotransduction activities involved in cell–cell connection26 and T-cell activation.31,32 While these observations are interesting, it is still unclear what insights can be derived from them.

TGTs were originally developed as extracellular tension sensors to report whether tension exceeds a threshold termed tension tolerance that is defined as the average tension needed for TGTs’ rupturing within two seconds.29 However, as a TGT can rupture at any tension with a tension-dependent lifetime, without prior knowledge of the time scale of tension duration, it is not straightforward to use TGTs to gauge the tension level.33 Indeed, the tension levels estimated with TGTs often appear significantly higher than those reported by reversible DNA hairpin tension sensors.23,24 To decode the information from the complex dependence of the cell’s mechanotransduction on the mechanical stabilities of TGTs, a comprehensive understanding of the mechanical stabilities of TGTs is needed.

Our current understanding of the mechanical stability of TGTs is not very clear. One reason for this is that the tension tolerance values of TGTs have not been accurately determined through experiments. Instead, they have been estimated using a formula developed by de Gennes that is based on the static analysis of the elastic energy of DNA.34 This formula does not take into account the effects of temperature or the specific sequence of the TGTs. Additionally, the concept of tension tolerance, which is used to quantify mechanical stability, is only a crude description. It only provides a qualitative comparison of the stability of different TGTs: the higher the value of the tension tolerance, the greater the mechanical stability. A more complete understanding of the mechanical stability of TGTs is needed in order to extract additional information from experimental observations.

In this study, we carried out experimental calibration of several TGTs for their tension-dependent lifetimes τ(f) at a temperature of 37 °C. This measurement gives us a detailed understanding of the mechanical stability of TGTs and allows us to determine the tensions at which the TGTs rupture or their lifetimes under various stretching conditions. This information is useful for a wide range of applications of TGTs as tension threshold or duration sensors. Based on our results, we also revisited previous cell studies to reassess their interpretations.

Experimental Section

Materials

All DNA oligos used in this study were custom synthesized by Integrated DNA Technologies (Coralville, IA, USA) as shown in Supporting Information Table SI. The DNA-based detector, with two dsDNA handles and a hairpin region, was synthesized following the standard PCR, digestion, annealing, ligation, and purification protocols.

Magnetic Tweezer-Based Single-Molecule Manipulation

The single-molecule manipulation experiments were conducted using an in-house-made backscattered vertical magnetic tweezers with a spatial resolution of 1 nm and temporal resolution of 200 Hz. A DNA-based detector was tethered to the coverslip through biotin/traptavidin linkage, while the other end of the detector was linked to a superparamagnetic bead through thiol/epoxy reaction. This system was performed in a laminar flow channel. The extension change of the tethered DNA was measured based on the height change of the superparamagnetic bead tethered to the DNA-based detector under force. The details of the force calibration and control for the single-molecule magnetic tweezers experiments have been described in previous works.20,35

Experiments were performed in a standard solution containing the following: 1 × PBS and 1% BSA at multiple temperatures (23 °C (room temperature), 30, and 37 °C). To achieve temperatures higher than room temperature, a non-magnetic nanocarbon-based thermal film (ultrathin flexible heater, Pelonis Technologies) was applied on the top of the sample channel.

Data Analysis

Bootstrap is a resampling method that generates groups of independent sample data from an existing sample data with the same data size. From our approach, we obtained Nr, which is the number of cycles that a TGT ruptured corresponding to a bead height change at constant target force, F, during a certain time interval, Δt, after repeating force jump cycles for N times. Thus, 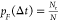Inline graphic.

The resampling procedure is as follows: Assuming that the data pool contains Nr rupturing events and N – Nr non-rupturing events (N events in total), we randomly chose one event from N events, determined whether it was a rupturing event or a non-rupturing event, and then put it back to the data pool. Following this step and choosing N times, we obtained a group of N resampled data with Nrb rupturing events, resulting in a resampled probability 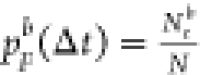Inline graphic. Repeating this resampling process for 100 times, we generated 100 groups of resampled data and thus have 100 independent 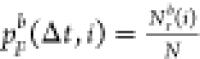Inline graphic (i = 1, 2, ..., 100). The mean value and the standard deviation of the rupturing probability under a certain condition (F, T, Δt) can be calculated from pF(Δt,i) (i = 1, 2, ..., 100). Then, with resampled pFb(Δt,i) of a range of Δt and fitting with the single-exponential-decay function, the average lifetime, τ(F), and its standard error can be found.

Structural-Elastic Model of Force-Dependent Unfolding Rate

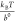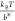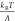At low force, the differential force-dependent entropic extension fluctuation between the native and the transition states leads to the force dependence of the transition rate. This is related to the differential structural-elastic properties of molecules between their native state and the transition state.36 At forces larger than Inline graphic, Inline graphic, and Inline graphic, this rate has a simple asymptotic expression: 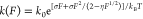Inline graphic, which contains a kinetic parameter k0 and three model parameters

graphic file with name se2c02218_m008.jpg

referring to Figure S5.

In the case of the force-dependent strand dissociation of TGTs, γ0 = γ* ∈ (1000, 1500) pN37 are the stretching rigidity of dsDNA, which makes the term αF2/2 negligible compared with the other two terms. 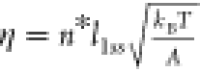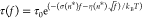As the two remaining model parameters σ and η are determined by the transition state, they can be described by a single parameter n*, which is the number of ruptured base pairs at the transition state: σ = n*(l1ss – l1ds) and Inline graphic, where l1ss = 0.7 nm and l1ds = 0.34 nm are the contour lengths per ssDNA nucleotide and dsDNA base pair, respectively, and A = 0.7 nm is the bending persistence length of ssDNA in 150 mM KCl.36,38 It can be shown that Inline graphic. By fitting the measured data with this model, the transition states (n*) of these TGTs under shearing tension geometry can be obtained.

Results and Discussion

Experimental Design

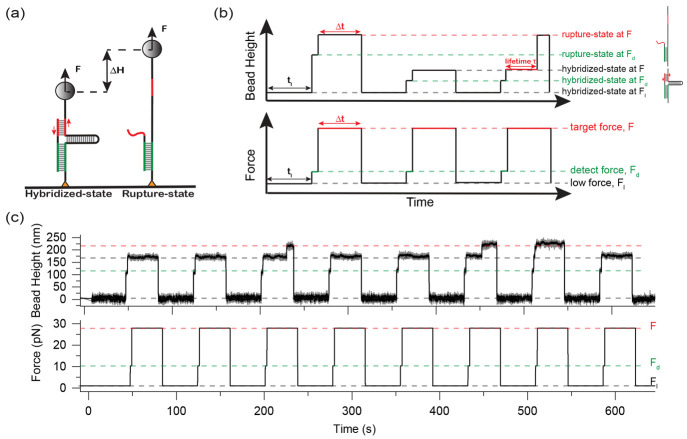
We designed a single-molecule detector (Figure 2a), consisting of a DNA hairpin spanned between two single-stranded DNA (ssDNA) handles, and an ssDNA oligo complementary to regions of both ssDNA handles adjacent to the fork of the hairpin marked by green and red. At tension below the threshold destabilizing tension of the hairpin (Fhairpin = 7.0 ± 0.7 pN at 37 °C), the hairpin remains stable so that the green and red regions of the ssDNA oligo can hybridize with the corresponding regions of both ssDNA handles. The technical details of the magnetic tweezers used for the single-molecule study can be found in our previous publications.20,35 Further details on the manipulation of the single-molecule detector can be found in Supporting Information Sections I–IV.39

Figure 2.

Figure 2

Open in a new tab

Single-molecule experimental design to quantify the mechanical stability of a TGT. (a) Schematic of the designed DNA detector tethered between a glass surface and a superparamagnetic bead. The TGT is shown in red. The green DNA duplex is to anchor the ssDNA on the detector for higher experimental throughput. (b) Schematics of tension–jump cycles applied to measure the tension-dependent lifetime of TGTs. The hybridized or ruptured state of the TGT is determined based on the bead height. (c) Representative experimental data for a 15-bp TGT at 37 °C. For each tension–jump cycle, the target force F = 28 pN and Δt = 35 s. Three rupture events are observed during the eight tension–jump cycles.

The red duplex corresponding to the region between P1 and P2 in a TGT is the target to be measured for its mechanical stability. At a tension F, the opening of the last base pair in the red duplex will place the hairpin under tension in an unzipping force geometry. This mimics an actual TGT, where the opening of the base pair at the P2 position will render the remaining duplex in the same unzipping force geometry. When F is greater than Fhairpin, the opening of the last base pair in the red duplex is followed by immediate unzipping of the hairpin. Hence, the transition state of the designed construct is the same as TGTs (Figure 1b, Supporting Information Sections V and VI).

The rupturing of the red duplex leads to a large stepwise increase in the bead height that can be detected by our in-house-constructed magnetic tweezers.20,35 The green duplex is made much longer than the red duplex to ensure that the rupturing only occurs on the red duplex (Supporting Information Section VII(39)). After rupturing the red duplex, the ssDNA oligo remains bound to the detector via the green duplex (Figure 2a, right), allowing the red duplex to re-form when tension is reduced to below Fhairpin. This way, many data points can be obtained from one detector.

Determination of τ(f) for TGTs

We quantified the tension-dependent rupturing probability of the red duplex over a time interval Δt at a constant tension F, pF(Δt). The average lifetime of the red duplex τ(f) was obtained by fitting the pF(Δt) data with a single-exponential function 1 – e(−Δt/τ). The pF(Δt) data were obtained by applying tension–jump cycles described in Figure 2b. Each cycle starts with a tension Fl at which the hairpin is stable, for 1 min to allow the formation of the red duplex. Then, tension was jumped to Fd slightly higher than the hairpin unzipping threshold tension, for two seconds to check whether the red duplex is formed. The two states of the red strand, hybridized or ruptured, can be unambiguously determined by their large extension difference (Figure 2a). Finally, the tension was jumped to a target tension F, for a holding time of Δt, during which the red duplex may or may not rupture. Repeating the cycles for N times, pF(Δt) is calculated by pF(Δt) = Nr/N, where Nr is the number of cycles where the red duplex is ruptured.

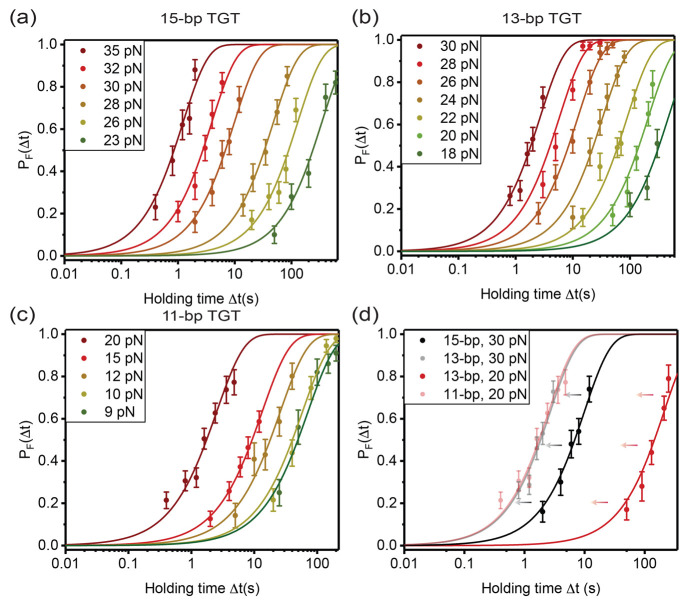
Most cell studies have been performed at 37 °C.29,40−48 As τ(f) of a TGT is sensitive to temperature (Supporting Information Section VIII(39)), we quantified τ(f) of four TGTs (Table 1) at 37 °C, including three (7-bp, 11-bp, and 15-bp) widely used in previous studies and one modified (13-bp) from the 15-bp TGT. For each TGT, the pF(Δt) data were determined from at least 50 cycles for each holding time from multiple tethers (Supporting Information Section IX(39)). Panels a–c of Figure 3 show pF(Δt) from a 15-bp TGT and an 11-bp TGT used in previous cell studies,29 as well as a 13-bp TGT generated by deleting the last two base pairs of the 15-bp TGT. The pF(Δt) curves obtained at the same forces shift left as the lengths of TGTs decrease (Figure 3d), suggesting decreased mechanical stability of shorter TGTs.

Table 1. Sequences of TGTs29.

Length (bp) Sequence (5′ → 3′)
7 GTG TCG T
11 GTG TCG TGC CT
13 GTG TCG TGC CTC C (truncated from no. 15)
15 GTG TCG TGC CTC CGT
Open in a new tab

Figure 3.

Figure 3

Open in a new tab

Tension-dependent lifetimes of three TGTs in Table 1 at 37 °C. Rupturing probabilities of 15-bp TGT (a), 13-bp truncated TGT (b), and 11-bp TGT (c) within different holding times detected over a certain tension range. (d) Comparison of pF(Δt) curves of 15-bp and 13-bp TGTs at 30 pN (dark and light black lines) and 13-bp and 11-bp TGTs at 20 pN (dark and light red lines) (mean ± standard error).

For each TGT, the best-fitted τ(f) was obtained over a certain tension range (Figure 4; Supporting Information Section X(39)), with the errors obtained by bootstrap analysis (Supporting Information Section XI(39)). τ(f) is extrapolated (solid line, Figure 4) from the measured τ(f) data to tensions outside the range of measurement based on an expression derived from Arrhenius law of tension-dependent transition kinetics, 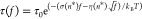Inline graphic, where σ = n*(l1ss – l1ds) and 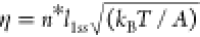Inline graphic (Supporting Information Section XII(39)). Here, l1ss = 0.7 nm and l1ds = 0.34 nm are the contour lengths of one nucleotide step of ssDNA and one base pair step of dsDNA, respectively, and A = 0.7 nm is the bending persistence length of ssDNA in 150 mM KCl.36,38 This model can be applied at tensions greater than a few pN where the worm-like chain polymer model of ssDNA is valid.49,50

Figure 4.

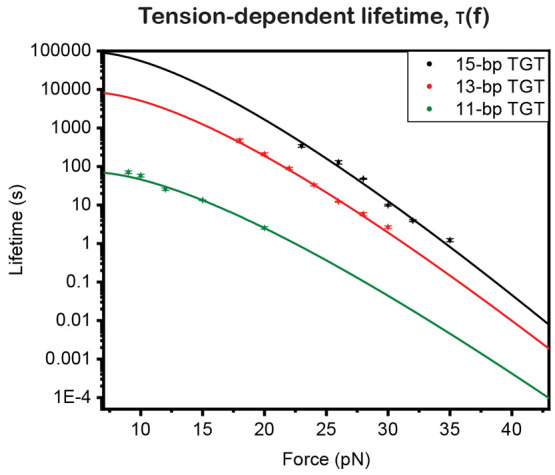
Figure 4

Open in a new tab

Mechanical stabilities of TGTs in Table 1. For the tension-dependent lifetime, τ(F), data are obtained from exponential fitting of measured pF(Δt) and are further extrapolated to tensions above a few pN using the structural-elastic model (Supporting Information Section XII(39)).

Applications

TGTs as Tension Threshold Sensors

TGTs were originally developed to determine whether tension exceeds a certain threshold based on 2 s tension tolerance values. However, our results (as shown in Figure 4 with the dashed line) reveal that, at a lifetime of 2 s, the average rupturing tensions for 11-bp, 13-bp, and 15-bp TGTs are approximately 21, 30, and 33 pN, respectively. These values are unexpectedly about 20 pN lower than the previously estimated values based on de Gennes’ formula,34 which requires significant adjustments to the previously reported 2 s tension tolerance values for TGTs. The knowledge of τ(f) can be used to define the tension tolerance at a wide range of time scales and can be applied to various processes that involve constant tensions of different durations. It should be noted that the use of tension tolerance requires processes with nearly constant tension over a known duration.

In principle, based on τ(f), TGTs could also report whether tension exceeds a threshold for processes involving dynamic tensions that increase with time, based on the peak rupturing tension of a TGT subjected to a time-varying tension predicted based on τ(f). For example, if the tension is increasing at a constant rate r and is given by f(t) = rt, the TGT’s rupturing tension distribution is 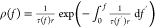Inline graphic.51 For the 11-bp TGT that provides the minimal stability to support the formation of nascent FAs,29,48 the TGT’s peak rupturing tension is in the range from 20 to 26 pN for loading rates in the order of a few pN/s (Figure 5a, middle panel, Supporting Information Section XIII(39)) that are physiologically relevant (see below).

Figure 5.

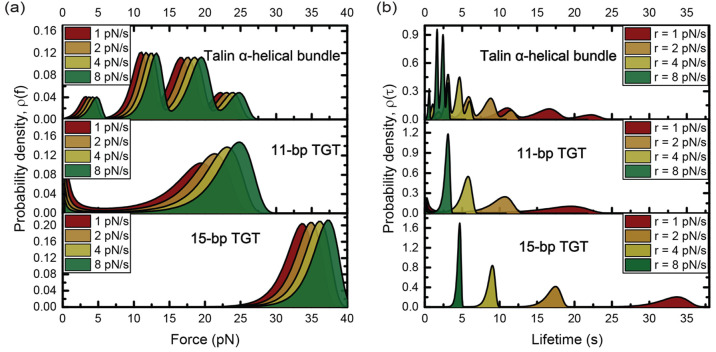
Figure 5

Open in a new tab

Comparison of the mechanical stabilities of talin α-helical bundles, 11-bp TGT, and 15-bp TGT. Rupturing tension probability densities (a) and lifetime probability densities (b) of α-helical bundles in talin rod (top panel), the 11-bp TGT (middle panel), and the 15-bp TGT (bottom panel) under increasing tension with different loading rates: 1, 2, 4, and 8 pN/s.

TGTs as Tension Duration Sensors

The quantity τ(f) directly provides the average lifetime of a TGT under a near-constant tension. For example, it was determined that the average lifetimes of 15-bp TGTs, 13-bp TGTs, and 11-bp TGTs were between 103 and 104 s, between 102 and 103 s, and between 101 and 102 s, respectively, over a tension range of 10–15 pN. When the tension varies over time at a certain rate, the most probable lifetime of the TGT can be obtained from the distribution density function 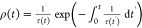Inline graphic, where τ–1(t) is the time-varying rupturing rate of the TGT caused by a time-varying tension f(t). Therefore, when the tension dynamics are known, TGTs can serve as sensors for the average tension duration. This property can be used to determine the threshold duration of tension needed for mechanotransduction.

The process of transitioning from nascent to matured focal adhesions involves the use of talin and vinculin-mediated rigidity sensing. This process involves the mechanical unfolding of helical bundles in talin under tension and the binding and activation of vinculin.15,16,18,52−55 Research has shown that newly assembled talin-mediated linkages are subjected to increasing tension due to the retrograde flow of actin.56 Although there is no direct measurement of the force loading rate for integrins, estimates can be made based on the rate of retrograde actin flow (in the order of 10 nm/s57,58), the magnitude of tensions involved in the unfolding of protein domains (from a few to tens of pN for talin domains18), and the extension range over which the unfolding of protein domains can occur (200–300 nm for talin rod18). Based on these estimates, it is reasonable to approximate the loading rates for such linkages to be in the order of pN/s.

In Figure 5b, we compare the lifetime distribution of talin’s 13 tension-bearing helical bundles in the rod domain, based on the tension-dependent unfolding rates measured in our previous study,18 to the lifetimes of the 11-bp and 15-bp TGTs at the same loading rates of r = 1, 2, 4, and 8 pN/s. The 11-bp and 15-bp TGTs are known to provide minimal stability for the formation of nascent and matured FAs, respectively.29,48 Our results show that the 11-bp TGT has a longer lifetime than the majority of talin’s α-helical bundles and the 15-bp TGT has a longer lifetime than all of talin’s α-helical bundles at the corresponding loading rates. Therefore, both TGTs are able to support the mechanical unfolding of talin’s α-helical bundles.

Since the 11-bp TGT cannot support the transition from nascent to matured FAs,29,48 it is likely that the tension duration it provides might not be sufficiently long to support the downstream mechanotransduction that requires recruiting and activating vinculin. A more stable TGT, such as the 15-bp TGT that was reported able to support the formation of matured FAs,48 is needed to provide a longer tension duration (Figure 5b) for the downstream mechanotransduction steps. Indeed, over the loading rate range, the lifetimes (5—35 s) of the 15-bp TGT are significantly longer than those (3—20 s) of the 11-bp TGT. Moreover, for other downstream process like YAP translocation from cytoplasm to nucleus driven by mechanical cues, cells on even more stable 18-bp TGT showed a dramatic enrichment of YAP nuclear localization than 11-bp and 15-bp TGTs.48 This observation can be similarly expained based on a longer tension duration needed for mechanotransduction that leads to YAP translocation into the nucleus, which requires a more stable TGT than the 15-bp TGT. Overall, the knowledge of τ(f) offers new insights into previous cell studies from a novel perspective of tension duration.

Having knowledge of τ(f) significantly expands the range of uses for TGTs as a tension threshold or tension duration reporter, enabling us to gain valuable insights into the mechanotransduction activities occurring on the tension–transmission linkage where the TGT is inserted.

Conclusion

In summary, we have examined the τ(f) of several TGTs at 37 °C over a range of time scales that are relevant to physiological processes. Our findings reveal a complete picture of the mechanical stability of TGTs. We discovered that previously reported two-second tension tolerance values for TGTs are significantly overestimated and that τ(f) can be used to determine tension tolerance for TGTs over a wide range of time scales when used as a tension threshold sensor in situations with near-constant, known tension durations. Additionally, we found that TGTs can also serve as a tension threshold sensor in situations where tension varies over time, based on the peak rupturing tension of the distribution density function of rupturing tensions that can be calculated from τ(f). Our results also highlight the potential use of TGTs as a tension duration sensor in situations where the dynamics of tension are known, which can provide information on the minimal tension duration required for specific mechanotransduction activities on tension–transmitting supramolecular linkages. Overall, our findings provide a foundation for using TGTs as a tension threshold or duration sensor in a wide range of situations depending on the available knowledge of the experimental system.

One limitation of this study is that it only considers the TGTs in the shear-stretching mode, which means that the transition state structure corresponds to the last base pair in the shear-mode part of the duplex being ruptured. This means that the tensions must be higher than the base-pair-destabilizing threshold under the unzipping geometry (greater than 10 pN) for this model to be applicable to the remaining part of the DNA. The unzip-mode part of TGTs is expected to significantly increase the TGT’s lifetime at tensions below 10 pN, where the unzip-mode part is mechanically stable. It is important to have a complete understanding of the tension-dependent lifetime of TGTs, including the lower tension range (below 10 pN), which is a current project in our group.

Acknowledgments

The authors thank Alexander Bershadsky and Pakorn Tony Kanchanawong for critical reading of the manuscript. The research was funded by the Singapore Ministry of Education Academic Research Funds Tier 2 (MOE2019-T2-1-099, MOE-T2EP50220-0015) and the Ministry of Education under the Research Centres of Excellence programme.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acssensors.2c02218.

  • Single-molecule constructs and manipulation methods; superparamagnetic microbead force calibration; bead height change; TGTs’ design, stretching geometry, and strand-dissociation transition pathways; detector and actual TGT energy landscapes; negligible rupturing possibility, TGTs’ mechanical stability; individual tethers data; limited experimental force range; bootstrap sampling methods; unfolding rate structural-elastic model; TGT’s rupturing tension distribution (PDF)

Author Contributions

J.L. and J.Y. designed the research, interpreted the experimental data, and wrote the manuscript. J.L. and Z.T. carried out the single-molecule experiments and performed data analysis. J.L., S.L., M.Y., Y.Z., and W.H. contributed to the design and synthesized the DNA detector for single-molecule experiments. J.Y. supervised the research.

The authors declare no competing financial interest.

Supplementary Material

se2c02218_si_001.pdf (2MB, pdf)

References

  1. Iskratsch T.; Wolfenson H.; Sheetz M. P. Appreciating force and shape—the rise of mechanotransduction in cell biology. Nat. Rev. Mol. Cell Biol. 2014, 15, 825–833. 10.1038/nrm3903. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Uhler C.; Shivashankar G. Regulation of genome organization and gene expression by nuclear mechanotransduction. Nat. Rev. Mol. Cell Biol. 2017, 18, 717–727. 10.1038/nrm.2017.101. [DOI] [PubMed] [Google Scholar]
  3. Vining K. H.; Mooney D. J. Mechanical forces direct stem cell behaviour in development and regeneration. Nat. Rev. Mol. Cell Biol. 2017, 18, 728–742. 10.1038/nrm.2017.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Panciera T.; Azzolin L.; Cordenonsi M.; Piccolo S. Mechanobiology of YAP and TAZ in physiology and disease. Nat. Rev. Mol. Cell Biol. 2017, 18, 758–770. 10.1038/nrm.2017.87. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Ladoux B.; Mège R.-M. Mechanobiology of collective cell behaviours. Nat. Rev. Mol. Cell Biol. 2017, 18, 743–757. 10.1038/nrm.2017.98. [DOI] [PubMed] [Google Scholar]
  6. Schoen I.; Pruitt B. L.; Vogel V. The Yin-Yang of rigidity sensing: how forces and mechanical properties regulate the cellular response to materials. Annu. Rev. Mater. Res. 2013, 43, 589–618. 10.1146/annurev-matsci-062910-100407. [DOI] [Google Scholar]
  7. Sun Z.; Guo S. S.; Fässler R. Integrin-mediated mechanotransduction. J. Cell Biol. 2016, 215, 445–456. 10.1083/jcb.201609037. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Martino F.; Perestrelo A. R.; Vinarskỳ V.; Pagliari S.; Forte G. Cellular mechanotransduction: from tension to function. Front. Physiol. 2018, 9, 824. 10.3389/fphys.2018.00824. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Angulo-Urarte A.; van der Wal T.; Huveneers S. Cell-cell junctions as sensors and transducers of mechanical forces. Biochimica et Biophysica Acta (BBA)-Biomembranes 2020, 1862, 183316. 10.1016/j.bbamem.2020.183316. [DOI] [PubMed] [Google Scholar]
  10. Michael M.; Parsons M. New perspectives on integrin-dependent adhesions. Curr. Opin. Cell Biol. 2020, 63, 31–37. 10.1016/j.ceb.2019.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Nakamura F.; Osborn T. M.; Hartemink C. A.; Hartwig J. H.; Stossel T. P. Structural basis of filamin A functions. J. Cell Biol. 2007, 179, 1011–1025. 10.1083/jcb.200707073. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Pang S. M.; Le S.; Kwiatkowski A. V.; Yan J. Mechanical stability of αT-catenin and its activation by force for vinculin binding. Molecular biology of the cell 2019, 30, 1930–1937. 10.1091/mbc.E19-02-0102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Wang Y.; Yan J.; Goult B. T. Force-dependent binding constants. Biochemistry 2019, 58, 4696–4709. 10.1021/acs.biochem.9b00453. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Goult B. T.; Brown N. H.; Schwartz M. A. Talin in mechanotransduction and mechanomemory at a glance. J. Cell Sci. 2021, 134, jcs258749. 10.1242/jcs.258749. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Yao M.; Goult B. T.; Chen H.; Cong P.; Sheetz M. P.; Yan J. Mechanical activation of vinculin binding to talin locks talin in an unfolded conformation. Sci. Rep. 2014, 4, 4610. 10.1038/srep04610. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Del Rio A.; Perez-Jimenez R.; Liu R.; Roca-Cusachs P.; Fernandez J. M.; Sheetz M. P. Stretching single talin rod molecules activates vinculin binding. Science 2009, 323, 638–641. 10.1126/science.1162912. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Yao M.; Qiu W.; Liu R.; Efremov A. K.; Cong P.; Seddiki R.; Payre M.; Lim C. T.; Ladoux B.; Mege R.-M.; et al. Force-dependent conformational switch of α-catenin controls vinculin binding. Nat. Commun. 2014, 5, 4525. 10.1038/ncomms5525. [DOI] [PubMed] [Google Scholar]
  18. Yao M.; Goult B. T.; Klapholz B.; Hu X.; Toseland C. P.; Guo Y.; Cong P.; Sheetz M. P.; Yan J. The mechanical response of talin. Nat. Commun. 2016, 7, 11966. 10.1038/ncomms11966. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Schlierf M.; Berkemeier F.; Rief M. Direct observation of active protein folding using lock-in force spectroscopy. Biophysical journal 2007, 93, 3989–3998. 10.1529/biophysj.107.114397. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Chen H.; Fu H.; Zhu X.; Cong P.; Nakamura F.; Yan J. Improved High-Force Magnetic Tweezers for Stretching and Refolding of Proteins and Short DNA. Biophys. J. 2011, 100, 517–523. 10.1016/j.bpj.2010.12.3700. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Grashoff C.; Hoffman B. D.; Brenner M. D.; Zhou R.; Parsons M.; Yang M. T.; McLean M. A.; Sligar S. G.; Chen C. S.; Ha T.; et al. Measuring mechanical tension across vinculin reveals regulation of focal adhesion dynamics. Nature 2010, 466, 263–266. 10.1038/nature09198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Morimatsu M.; Mekhdjian A. H.; Adhikari A. S.; Dunn A. R. Molecular tension sensors report forces generated by single integrin molecules in living cells. Nano Lett. 2013, 13, 3985–3989. 10.1021/nl4005145. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Blakely B. L.; Dumelin C. E.; Trappmann B.; McGregor L. M.; Choi C. K.; Anthony P. C.; Duesterberg V. K.; Baker B. M.; Block S. M.; Liu D. R.; et al. A DNA-based molecular probe for optically reporting cellular traction forces. Nat. Methods 2014, 11, 1229–1232. 10.1038/nmeth.3145. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Zhang Y.; Ge C.; Zhu C.; Salaita K. DNA-based digital tension probes reveal integrin forces during early cell adhesion. Nat. Commun. 2014, 5, 5167. 10.1038/ncomms6167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kim T.-J.; Zheng S.; Sun J.; Muhamed I.; Wu J.; Lei L.; Kong X.; Leckband D. E.; Wang Y. Dynamic visualization of α-catenin reveals rapid, reversible conformation switching between tension states. Current biology 2015, 25, 218–224. 10.1016/j.cub.2014.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Wang X.; Rahil Z.; Li I. T.; Chowdhury F.; Leckband D. E.; Chemla Y. R.; Ha T. Constructing modular and universal single molecule tension sensor using protein G to study mechano-sensitive receptors. Sci. Rep. 2016, 6, 21584. 10.1038/srep21584. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Roca-Cusachs P.; Conte V.; Trepat X. Quantifying forces in cell biology. Nature cell biology 2017, 19, 742–751. 10.1038/ncb3564. [DOI] [PubMed] [Google Scholar]
  28. Ringer P.; Weißl A.; Cost A.-L.; Freikamp A.; Sabass B.; Mehlich A.; Tramier M.; Rief M.; Grashoff C. Multiplexing molecular tension sensors reveals piconewton force gradient across talin-1. Nat. Methods 2017, 14, 1090–1096. 10.1038/nmeth.4431. [DOI] [PubMed] [Google Scholar]
  29. Wang X.; Ha T. Defining single molecular forces required to activate integrin and notch signaling. Science 2013, 340, 991–994. 10.1126/science.1231041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Cocco S.; Yan J.; Léger J.-F.; Chatenay D.; Marko J. F. Overstretching and force-driven strand separation of double-helix DNA. Phys. Rev. E 2004, 70, 011910. 10.1103/PhysRevE.70.011910. [DOI] [PubMed] [Google Scholar]
  31. Liu Y.; Blanchfield L.; Ma V. P.-Y.; Andargachew R.; Galior K.; Liu Z.; Evavold B.; Salaita K. DNA-based nanoparticle tension sensors reveal that T-cell receptors transmit defined pN forces to their antigens for enhanced fidelity. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 5610–5615. 10.1073/pnas.1600163113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Ma V. P.-Y.; Hu Y.; Kellner A. V.; Brockman J. M.; Velusamy A.; Blanchard A. T.; Evavold B. D.; Alon R.; Salaita K. The magnitude of LFA-1/ICAM-1 forces fine-tune TCR-triggered T cell activation. Sci. Adv. 2022, 8, eabg4485 10.1126/sciadv.abg4485. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Mosayebi M.; Louis A. A.; Doye J. P.; Ouldridge T. E. Force-induced rupture of a DNA duplex: from fundamentals to force sensors. ACS Nano 2015, 9, 11993–12003. 10.1021/acsnano.5b04726. [DOI] [PubMed] [Google Scholar]
  34. de Gennes P.-G. Maximum pull out force on DNA hybrids. C. R. Acad. Sci., Ser. IV: Phys., Astrophys. 2001, 2, 1505–1508. 10.1016/S1296-2147(01)01287-2. [DOI] [Google Scholar]
  35. Zhao X.; Zeng X.; Lu C.; Yan J. Studying the mechanical responses of proteins using magnetic tweezers. Nanotechnology 2017, 28, 414002. 10.1088/1361-6528/aa837e. [DOI] [PubMed] [Google Scholar]
  36. Guo S.; Tang Q.; Yao M.; You H.; Le S.; Chen H.; Yan J. Structural-elastic determination of the force-dependent transition rate of biomolecules. Chem. Sci. 2018, 9, 5871–5882. 10.1039/C8SC01319E. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Wenner J. R.; Williams M. C.; Rouzina I.; Bloomfield V. A. Salt dependence of the elasticity and overstretching transition of single DNA molecules. Biophysical journal 2002, 82, 3160–3169. 10.1016/S0006-3495(02)75658-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Zhang X.; Chen H.; Le S.; Rouzina I.; Doyle P. S.; Yan J. Revealing the competition between peeled ssDNA, melting bubbles, and S-DNA during DNA overstretching by single-molecule calorimetry. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 3865–3870. 10.1073/pnas.1213740110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. See the Supporting Information for detailed information of magnetic-tweezer experiment, base-pair-destablizing tension, temperature-sensitive mechanical stability of TGTs, bootstrap sampling methods, structural-elastic model, and the physiologically relevant tension range.
  40. Chowdhury F.; Li I. T.; Leslie B. J.; Doğanay S.; Singh R.; Wang X.; Seong J.; Lee S.-H.; Park S.; Wang N.; et al. Single molecular force across single integrins dictates cell spreading. Integrative Biology 2015, 7, 1265–1271. 10.1039/C5IB00080G. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Jo M. H.; Cottle W. T.; Ha T. Real-time measurement of molecular tension during cell adhesion and migration using multiplexed differential analysis of tension gauge tethers. ACS Biomaterials Science & Engineering 2019, 5, 3856–3863. 10.1021/acsbiomaterials.8b01216. [DOI] [PubMed] [Google Scholar]
  42. Zhang Y.; Qiu Y.; Blanchard A. T.; Chang Y.; Brockman J. M.; Ma V. P.-Y.; Lam W. A.; Salaita K. Platelet integrins exhibit anisotropic mechanosensing and harness piconewton forces to mediate platelet aggregation. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, 325–330. 10.1073/pnas.1710828115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Zhao Y.; Sarkar A.; Wang X. Peptide nucleic acid based tension sensor for cellular force imaging with strong DNase resistance. Biosens. Bioelectron. 2020, 150, 111959. 10.1016/j.bios.2019.111959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Zhao Y.; Wang Y.; Sarkar A.; Wang X. Keratocytes generate high integrin tension at the trailing edge to mediate rear De-adhesion during rapid cell migration. Iscience 2018, 9, 502–512. 10.1016/j.isci.2018.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zhao Y.; Pal K.; Tu Y.; Wang X. Cellular force nanoscopy with 50 nm resolution based on integrin molecular tension imaging and localization. J. Am. Chem. Soc. 2020, 142, 6930–6934. 10.1021/jacs.0c01722. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Hu Y.; Ma V. P.-Y.; Ma R.; Chen W.; Duan Y.; Glazier R.; Petrich B. G.; Li R.; Salaita K. DNA-Based Microparticle Tension Sensors (μTS) for Measuring Cell Mechanics in Non-planar Geometries and for High-Throughput Quantification. Angew. Chem. 2021, 133, 18192–18198. 10.1002/ange.202102206. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Li H.; Zhang C.; Hu Y.; Liu P.; Sun F.; Chen W.; Zhang X.; Ma J.; Wang W.; Wang L.; et al. A reversible shearing DNA probe for visualizing mechanically strong receptors in living cells. Nat. Cell Biol. 2021, 23, 642–651. 10.1038/s41556-021-00691-0. [DOI] [PubMed] [Google Scholar]
  48. Chang Chien C.-Y.; Chou S.-H.; Lee H.-H. Integrin molecular tension required for focal adhesion maturation and YAP nuclear translocation. Biochem. Biophys. Rep. 2022, 31, 101287. 10.1016/j.bbrep.2022.101287. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Fu H.; Le S.; Chen H.; Muniyappa K.; Yan J. Force and ATP hydrolysis dependent regulation of RecA nucleoprotein filament by single-stranded DNA binding protein. Nucleic Acids Res. 2013, 41, 924–932. 10.1093/nar/gks1162. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Bosco A.; Camunas-Soler J.; Ritort F. Elastic properties and secondary structure formation of single-stranded DNA at monovalent and divalent salt conditions. Nucleic Acids Res. 2014, 42, 2064. 10.1093/nar/gkt1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Dudko O. K.; Hummer G.; Szabo A. Intrinsic rates and activation free energies from single-molecule pulling experiments. Physical review letters 2006, 96, 108101. 10.1103/PhysRevLett.96.108101. [DOI] [PubMed] [Google Scholar]
  52. Wang Y.; Yao M.; Baker K. B.; Gough R. E.; Le S.; Goult B. T.; Yan J. Force-dependent interactions between talin and full-length vinculin. J. Am. Chem. Soc. 2021, 143, 14726–14737. 10.1021/jacs.1c06223. [DOI] [PubMed] [Google Scholar]
  53. Kanchanawong P.; Shtengel G.; Pasapera A. M.; Ramko E. B.; Davidson M. W.; Hess H. F.; Waterman C. M. Nanoscale architecture of integrin-based cell adhesions. Nature 2010, 468, 580–584. 10.1038/nature09621. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Thievessen I.; Thompson P. M.; Berlemont S.; Plevock K. M.; Plotnikov S. V.; Zemljic-Harpf A.; Ross R. S.; Davidson M. W.; Danuser G.; Campbell S. L.; et al. Vinculin–actin interaction couples actin retrograde flow to focal adhesions, but is dispensable for focal adhesion growth. J. Cell Biol. 2013, 202, 163–177. 10.1083/jcb.201303129. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Bays J. L.; DeMali K. A. Vinculin in cell–cell and cell–matrix adhesions. Cell. Mol. Life Sci. 2017, 74, 2999–3009. 10.1007/s00018-017-2511-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Andreu I.; Falcones B.; Hurst S.; Chahare N.; Quiroga X.; Le Roux A.-L.; Kechagia Z.; Beedle A. E.; Elosegui-Artola A.; Trepat X.; et al. The force loading rate drives cell mechanosensing through both reinforcement and cytoskeletal softening. Nat. Commun. 2021, 12, 4229. 10.1038/s41467-021-24383-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Alexandrova A. Y.; Arnold K.; Schaub S.; Vasiliev J. M.; Meister J.-J.; Bershadsky A. D.; Verkhovsky A. B. Comparative dynamics of retrograde actin flow and focal adhesions: formation of nascent adhesions triggers transition from fast to slow flow. PloS one 2008, 3, e3234 10.1371/journal.pone.0003234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Swaminathan V.; Kalappurakkal J. M.; Mehta S. B.; Nordenfelt P.; Moore T. I.; Koga N.; Baker D. A.; Oldenbourg R.; Tani T.; Mayor S.; et al. Actin retrograde flow actively aligns and orients ligand-engaged integrins in focal adhesions. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 10648–10653. 10.1073/pnas.1701136114. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

se2c02218_si_001.pdf (2MB, pdf)

Articles from ACS Sensors are provided here courtesy of American Chemical Society

RESOURCES