Magnetic Resonance Imaging‐Derived Microvascular Perfusion Modeling to Assess Peripheral Artery Disease

Abstract

Background

Computational fluid dynamics has shown good agreement with contrast‐enhanced magnetic resonance imaging measurements in cardiovascular disease applications. We have developed a biomechanical model of microvascular perfusion using contrast‐enhanced magnetic resonance imaging signal intensities derived from skeletal calf muscles to study peripheral artery disease (PAD).

Methods and Results

The computational microvascular model was used to study skeletal calf muscle perfusion in 56 individuals (36 patients with PAD, 20 matched controls). The recruited participants underwent contrast‐enhanced magnetic resonance imaging and ankle‐brachial index testing at rest and after 6‐minute treadmill walking. We have determined associations of microvascular model parameters including the transfer rate constant, a measure of vascular leakiness; the interstitial permeability to fluid flow which reflects the permeability of the microvasculature; porosity, a measure of the fraction of the extracellular space; the outflow filtration coefficient; and the microvascular pressure with known markers of patients with PAD. Transfer rate constant, interstitial permeability to fluid flow, and microvascular pressure were higher, whereas porosity and outflow filtration coefficient were lower in patients with PAD than those in matched controls (all P values ≤0.014). In pooled analyses of all participants, the model parameters (transfer rate constant, interstitial permeability to fluid flow, porosity, outflow filtration coefficient, microvascular pressure) were significantly associated with the resting and exercise ankle‐brachial indexes, claudication onset time, and peak walking time (all P values ≤0.013). Among patients with PAD, interstitial permeability to fluid flow, and microvascular pressure were higher, while porosity and outflow filtration coefficient were lower in treadmill noncompleters compared with treadmill completers (all P values ≤0.001).

Conclusions

Computational microvascular model parameters differed significantly between patients with PAD and matched controls. Thus, computational microvascular modeling could be of interest in studying lower extremity ischemia.

Nonstandard Abbreviations and Acronyms

ρ_v

microvascular pressure

AM

anterior muscle group

DM

deep posterior muscle group

GBCA

gadolinium‐based contrast agent

GM

gastrocnemius muscle

k^t

transfer rate constant

K_tissue

interstitial permeability to fluid flow

LM

lateral muscle group

OFC

outflow filtration coefficient

SM

soleus muscle

φ

porosity

Clinical Perspective.

What Is New?

• Computational microvascular model parameters differed significantly between patients with peripheral artery disease and matched controls.

• Computational microvascular modeling could be of interest in studying lower extremity ischemia.

What Are the Clinical Implications?

• This work adds to the growing body of evidence on the importance of the microcirculation in peripheral artery disease, and the presented computational microvascular model provides a potential tool to elucidate associations between the microcirculation and peripheral artery disease symptoms.

Peripheral artery disease (PAD) is a vascular disease accompanied by atherosclerotic lesions and is associated with an increased risk of cardiovascular events and mortality. ¹ , ² PAD is characterized by impaired muscle function, and diabetes is common in individuals with lower extremity ischemia. ³ , ⁴ Improving microvascular perfusion of the leg muscles and alleviating intermittent claudication remain a challenge in patients with PAD, as present surgical and therapeutic treatments are not successful in relieving symptoms in all patients with lower extremity ischemia. ⁵ , ⁶ , ⁷ , ⁸ A previous report ¹ showed that contrast‐enhanced magnetic resonance imaging (CE‐MRI) permits studying microvascular muscle perfusion in patients with PAD and could be of clinical interest in assessing PAD severity. Computational fluid dynamics has shown good agreement with CE‐MRI measurements in cardiovascular disease applications ⁹ , ¹⁰ , ¹¹ and could be an important tool for studying tissue perfusion. ¹² , ¹³ , ¹⁴ A biomechanical model of microvascular perfusion in patients with PAD ¹⁵ was developed using CE‐MRI signal intensities derived from 5 distinct calf muscle regions, including the anterior muscle group (AM), lateral muscle group (LM), deep posterior muscle group (DM), soleus muscle (SM), and gastrocnemius muscle (GM). The model was robust and can be used to estimate microvascular transport properties in the calf muscles. The present study aimed to determine tissue perfusion parameters and compare tissue transport properties between patients with PAD and matched controls, along with estimates of changes in tissue transport properties depending on disease severity or concomitant diabetes. The primary purpose of this study was to investigate whether parameters from a biomechanical model of microvascular perfusion based on CE‐MRI are associated with known markers of PAD and can be used to differentiate between patients with PAD and matched controls. In addition, we sought to determine whether the parameters from the biomechanical model of microvascular perfusion can differentiate between PAD treadmill‐completers and noncompleters.

METHODS

In accordance with the American Heart Association journals' implementation of the Transparency and Openness Promotion Guidelines, the data supporting the findings of this study are available from the corresponding author upon reasonable request. Study participants provided informed consent, and the study obtained approval from the local institutional review board. Patients with PAD and controls were recruited from the Houston Methodist Hospital and the Michael E. DeBakey Veterans Affairs Medical Center, Houston, TX, as described previously. ¹ , ¹⁶ The study details and baseline characteristics of the same participants have been reported previously. ¹⁶ Briefly, adults with a resting ankle‐brachial index (ABI) <0.9, a lifestyle‐limiting intermittent claudication, and an estimated glomerular filtration rate >40 mL/min per 1.73 m² but without contraindications to magnetic resonance imaging (MRI) were included in this study. Controls without PAD were matched for age, sex, and body mass index. To achieve balanced enrollment, we periodically performed statistical testing of the matching variables (age, sex, body mass index) between the patients with PAD and controls using an independent sample Student t‐test or a Chi‐square test. Study participants underwent ABI measurements at rest and after a 6‐minute graded treadmill walking test, as reported previously. ¹⁶

Magnetic Resonance Imaging

A 3.0‐T system (Siemens Magnetom Trio, or Verio, Erlangen, Germany) with a 36‐element bilateral lower extremity coil was used for CE‐MRI with a gadolinium‐based contrast agent (GBCA). After initial localizers, muscle perfusion imaging was performed at the midcalf level, as described previously. ¹ Briefly, a reactive hyperemia protocol was implemented by using MRI compatible bilateral blood‐pressure cuffs that were placed above the knee and inflated to supra‐systolic pressure levels (170 mm Hg) for 3.5 minutes. Following rapid cuff deflation and the GBCA administration, perfusion imaging was performed immediately using a high‐resolution saturation recovery gradient echo pulse sequence (repetition time/echo time=2.7/1.23 ms; field of view=17.5×35.0 cm; slice thickness=10 mm, temporal resolution (perfusion imaging frame rate)=409 ms).

Image Analysis

The acquired CE‐MRI data sets saved in DICOM format had a slice thickness of 10 mm and a temporal resolution of 409 ms. The MRI scans were anonymized before analysis. Calf muscle domains, including AM, LM, DM, SM, and GM were semi‐automatically segmented using an in‐house graphical user interface developed in MATLAB (MathWorks Natick, MA). The arterial lumen of the posterior tibialis, anterior tibialis and peroneal arteries were segmented with Sante DICOM Editor Version 3.0 (Santesoft LTD, Greece). Additional details about the segmentation algorithm were previously described. ¹ , ¹⁶ The peak arterial signal, the minimum post‐peak enhancement, and the level of arterial signal enhancement were extracted for each of the 3 main arteries (posterior tibialis, anterior tibialis, and peroneal arteries), and the cross‐sectional leg muscle area was measured, as described previously. ¹

Biomechanical Modeling: Computational Microvascular Model

The validated biomechanical model for calf muscle microvascular perfusion was reported previously. ¹⁵ Briefly, the ANSYS SpaceClaim application within the ANSYS Workbench (Ansys, Inc, v. 18.2) was used for creating 3‐dimensional volumes of leg segments with a thickness of 10 mm to maintain continuity and clinical relevance (same thickness as CE‐MRI scans). The 2‐compartment Tofts‐Kermode model ¹⁷ of plasma and tissue was taken as the basis of our computational microvascular model, which was used to describe the CE‐MR signal enhancement by GBCA as a reaction term in the tissue regions. The convection‐diffusion and reaction models were adopted to simulate 3‐dimensional convection‐enhanced delivery in the tissue regions. ¹⁸ The skeletal muscle tissue was modeled as a porous media using the user‐defined model of elastic solid tissue with a porosity of 20% to 80% (Figure).

Figure 1. Contrast‐enhanced magnetic resonance imaging and corresponding simulated signal intensities from the computational microvascular model for a matched‐control, a treadmill completer with peripheral artery disease, and a treadmill noncompleter with peripheral artery disease.

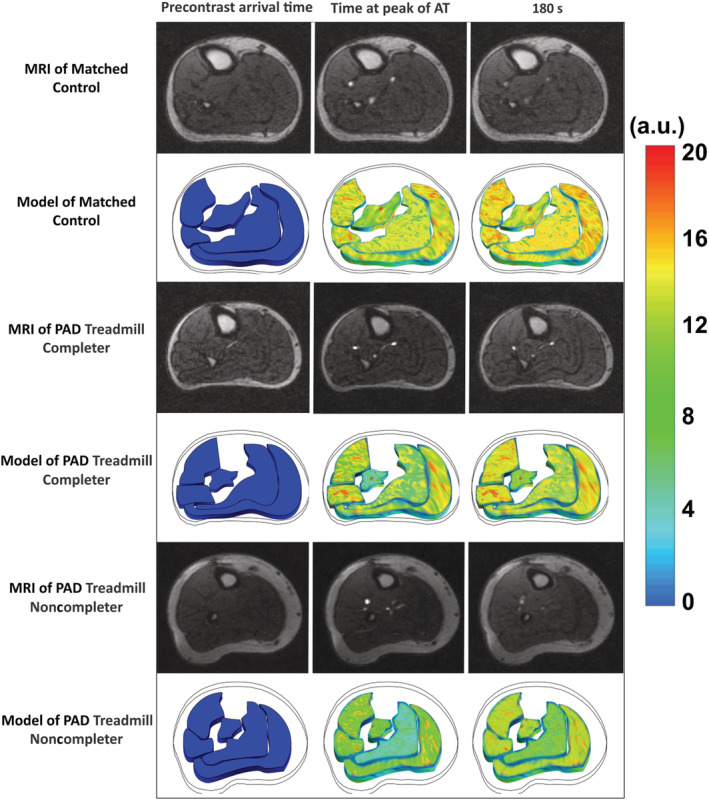
Specific time points are shown including before contrast arrival, peak arterial enhancement of the anterior tibial artery, and after 180 seconds. The panels of the computational microvascular model include 5 distinct skeletal calf muscle compartments (anterior muscle, lateral muscle, deep posterior muscle, soleus muscle, and the gastrocnemius muscle). A.U. indicates arbitrary units; AT, anterior tibial artery; MRI, magnetic resonance imaging; and PAD, peripheral artery disease.

The primary microvascular model parameters include the transfer rate constant (k ^t ), ¹⁵ , ¹⁹ , ²⁰ a measure of vascular leakiness; the interstitial permeability to fluid flow (K _tissue) ¹⁵ , ¹⁹ , ²⁰ which reflects the permeability of the microvasculature that is modeled as a porous medium ²⁰ ; porosity (φ), ¹⁵ , ²⁰ , ²¹ a measure of the fraction of the extracellular space or tissue porosity; the outflow filtration coefficient (OFC) ¹⁵ , ²⁰ ; and the microvascular pressure ($p_{\upsilon }$). ¹⁵ , ²⁰ , ²² The OFC is the product of the vessel permeability and the microvascular surface area per unit volume. ¹⁵ , ²⁰ Further details of the computational microvascular model were reported previously. ¹⁵

Parameters of the finite element model were calculated using the programming method implemented in the ANSYS software (v. 18.2). The developed full porous model is a generalization of the Navier–Stokes equations and Darcy law commonly used for flows in porous regions. Blood perfusion velocity and pressure were determined and described for each muscle domain. Blood perfusion was assumed to be transient, incompressible flow. On the boundaries, mass sources were applied to introduce additional fluid into the simulation. The arterial input function corresponding to the signal intensity of the contrast agent in the blood plasma was obtained from CE‐MRI scans ¹ and applied as a boundary condition for the suggested biomechanical model. Furthermore, a relative static pressure of zero was specified over the outlet boundary, and the flow velocity at the wall boundary was also set to zero. Full information about model parameters is available in our previous publication. ¹⁵ The grid test and transient time step sensitivity tests were performed to check the quality of the model and for solution convergence. Mean square and mean absolute percentage errors were calculated to estimate the best agreement between simulated and CE‐MRI signal intensities. Intrarater and interrater (for 3 patients with PAD and 5 controls) reproducibility for simulated mean signal intensity over all time steps was excellent for all muscle groups, as reported previously. ¹⁵

Statistical Analysis

Statistical analyses were performed with Stata IC 13.1 (College Station, Texas, StataCorp LP). All variables were expressed as means, or medians along with a measure of variability (SD, interquartile range, frequencies, or percentages). The Shapiro–Wilk test was used to check for variable normality. An independent sample Student t test was used for continuous variables, and the Mann–Whitney‐Wilcoxon test was used for non‐normal variables. Pearson correlation analyses were performed, and the strength of the correlation was described as weak (r<0.3), medium (0.3≤r<0.5), or strong (r≥0.5). Associations between computational microvascular model parameters and markers of PAD were determined using linear regression analysis. The chi‐square or Fisher exact test was used to analyze group differences in categorical variables. Variables were compared between patients with PAD and matched controls, PAD treadmill completers and PAD noncompleters, and diabetic and nondiabetic study participants. All tests were 2‐sided, and a P value <0.05 was considered statistically significant.

RESULTS

Baseline Characteristics

A total of 66 participants were enrolled, and 61 patients completed the baseline MRI visit. Five patients were excluded because of incomplete MRI due to poor image quality (n=4), or incomplete ABI data (n=1). In the final analysis, 56 participants were included (36 PAD, 20 controls). The baseline characteristics of the same participants have been reported previously and are summarized here next. ¹⁶ There were no differences in age, sex, race, or body mass index between patients with PAD and matched controls (Table 1). Compared with controls, patients with PAD were more likely to be diabetic (47% versus 15%, P=0.021), hypertensive (92% versus 60%, P=0.011), hyperlipidemic (94% versus 60%, P=0.002), and on lipid‐lowering therapy (89% versus 45%, P=0.001). Furthermore, more patients with PAD had a history of lower extremity revascularization (61% versus 0%, P=0.001) and were smokers (89% versus 40%, P<0.001) than controls.

Table 1.

Baseline Patient Characteristics

Variable	Patients with PAD (n=36)	Controls (n=20)	P value
Age, y	69±9.0	65±6.7	0.10
Men, %	27 (75%)	12 (60%)	0.36
Race, % Black	12 (33%)	4 (20%)	0.36
Body mass index, kg/m2	27±4.9	29±5.3	0.19
Resting ABI, A.U.	0.75±0.2	1.17±0.1	<0.001
Post‐treadmill ABI, A.U.	0.60 (0.5–0.7)	1.19 (1.1–1.2)	<0.001
Smoker, %	32 (89%)	8 (40%)	<0.001
Diabetes, %	17 (47%)	3 (15%)	0.021
Hypertension, %	33 (92%)	12 (60%)	0.011
Hyperlipidemia, %	34 (94%)	12 (60%)	0.002
Heart rate, bpm	78±19	71±10	0.13
Hematocrit, %	41 (39–42)	412 (40–44)	0.46
eGFR, ml/min per 1.73 m2	78±22	78±18	0.95
ACE inhibitor, %	17 (47%)	5 (25%)	0.15
Beta‐blocker, %	18 (50%)	7 (35%)	0.40
Claudication onset time, s	222 (180–264)	353 (346–360)	<0.001
Peak walking time, s	282 (248–317)	353 (346–360)	0.002
Complete 6‐min treadmill, %	19 (53%)	19 (95%)	0.002
Cholesterol‐lowering drug use, %	32 (89%)	9 (45%)	0.001
Coronary artery disease, %	15 (42%)	5 (25%)	0.26
Lower extremity revascularization history, %	22 (61%)	0 (0%)	0.001
Family history of coronary heart disease, %	14 (39%)	8 (40%)	0.07

Values are reported as mean±SD, median (interquartile range), and number (percentage). Hematocrit controls: n=15; post‐treadmill ankle‐brachial index patients with peripheral artery disease: n=35; claudication onset time patients with peripheral artery disease: n=35; peak walking time patients with peripheral artery disease: n=35. The baseline characteristics of the same participants have been reported previously. ¹⁶ ABI indicates ankle‐brachial index; A.U., arbitrary units; eGFR, estimated glomerular filtration rate; and PAD, peripheral artery disease.

Please note that the same findings about the ABIs and the treadmill walking parameters have been reported before and are summarized below. ¹⁶ Resting ABIs were significantly lower (0.75±0.2 versus 1.17±0.1, P<0.001), wheras the peak walking time (PWT) was shorter (282 [248–317] seconds versus 353 [346–360] seconds, P=0.002) for patients with PAD than those for matched controls (Table 1). The ABIs decreased significantly post‐treadmill walking in patients with PAD but not in controls, as expected (P<0.001 versus P=0.50, Table 1).

In a subgroup analysis, patients with PAD were divided into 2 groups: (1) those who completed the 6‐minute treadmill walking test, and (2) those who did not, as reported previously (treadmill completers, n=19; treadmill noncompleters, n=17). ¹⁶ Treadmill completers had lower resting ABIs (0.65±0.2 versus 0.84±0.2, P=0.011), a shorter PWT (190 [148–232] seconds versus 360 [360–360] seconds, P<0.001), and a shorter claudication onset time (122 [80–164] seconds versus 232 [163–301] seconds, P=0.005), when compared with noncompleters, as reported before. ¹⁶

Computational Microvascular Model Parameters

Averaged over all muscle groups, k ^t , K _tissue, and $p_{\upsilon }$ were higher in patients with PAD than in controls (all P values <0.001, Table 2). Porosity and the OFC averaged over all muscle groups were lower in patients with PAD than in controls (all P values <0.015, Table 2).

Table 2.

Computational Microvascular Model Parameters for Matched Controls and Patients With PAD

Variable	Control	PAD	Pooled	P value
k t , 1/s	2.45 (2.28–2.62)	7.09 (5.86–8.31)	5.43 (4.45–6.41)	<0.001
K tissue, m2	1.81 (1.81–1.81)	4.31 (4.03–4.60)	3.42 (3.05–3.79)	<0.001
φ	0.67 (0.65–0.69)	0.47 (0.44–0.49)	0.54 (0.51–0.57)	<0.001
OFC, 1/Pa s	13.37 (12.16–14.58)	11.10 (9.92–12.28)	11.91 (11.01–12.81)	0.014
$p_{\upsilon }$, mm Hg	49.21 (48.74–49.67)	52.53 (51.65–53.41)	51.34 (50.64–52.06)	<0.001

All values are expressed as median (interquartile range). P values were calculated with the Kruskal–Wallis rank test. Control group: n=20; peripheral artery disease group: n=36. Pooled: includes both patients with PAD and controls. k ^t indicates transfer rate constant; K _tissue, interstitial permeability; OFC, outflow filtration coefficient; PAD, peripheral artery disease; $p_{\upsilon }$, microvascular pressure; and φ, porosity (values in the range from 0 to 1).

Modeling parameters were heterogeneous across individual calf muscle groups. Compared with controls, patients with PAD had significantly higher k ^t and K _tissue values in all 5 muscle groups (Table S1 through S3). Similarly, $p_{\upsilon }$ was significantly higher in the LM (P=0.006), DM (P<0.001), and GM (P=0.005) of patients with PAD than that in the corresponding muscle groups of the controls but was similar in the AM and SM. Furthermore, φ was significantly lower in patients with PAD than in controls in all 5 muscle groups (P<0.001). The OFC was significantly lower in the AM of patients with PAD than in the AM of controls (P=0.001) but not in other muscle groups.

Correlation of Patient Characteristics With Computational Microvascular Model Parameters

There were no significant correlations between age, BMI, and the eGFR with the computational microvascular model parameters (Table 3).

Table 3.

Correlation Analyses of Markers of PAD With Computational Microvascular Modeling Parameters

Variable	Group		Obs	k t	K tissue	φ	OFC	$p_{\upsilon }$
Age	Control	r	20	0.32	0.19	0.10	−0.22	0.10
		P value		0.17	0.42	0.68	0.35	0.67
	PAD	r	36	−0.05	0.14	−0.13	−0.03	0.01
		P value		0.77	0.43	0.46	0.86	0.95
	Pooled	r	56	0.11	0.25	−0.23	0.14	0.15
		P value		0.42	0.06	0.08	0.30	0.27
Body mass index	Control	r	20	−0.10	0.01	0.10	0.24	−0.20
		P value		0.67	0.95	0.67	0.32	0.39
	PAD	r	36	−0.13	0.02	0.03	−0.01	0.11
		P value		0.47	0.90	0.88	0.96	0.52
	Pooled	r	56	−0.19	−0.15	0.17	0.12	−0.07
		P value		0.16	0.28	0.21	0.39	0.62
eGFR	Control	r	20	0.24	−0.09	−0.03	−0.09	0.02
		P value		0.30	0.70	0.91	0.71	0.94
	PAD	r	36	−0.02	0.24	0.02	−0.08	0.16
		P value		0.92	0.17	0.93	0.66	0.36
	Pooled	r	56	<0.01	0.11	<0.01	−0.08	0.11
		P value		1.00	0.43	0.99	0.58	0.41

Pooled, includes both patients with peripheral artery disease and controls. eGFR indicates estimated glomerular filtration rate; k ^t , transfer rate constant; K _tissue, interstitial permeability; Obs, number of observations; OFC, outflow filtration coefficient; PAD, peripheral artery disease; $p_{\upsilon }$, microvascular pressure; and φ, porosity.

Associations of Computational Microvascular Model Parameters With Markers of PAD

The parameters k ^t , K _tissue, φ, OFC, and $p_{\upsilon }$ were significantly associated with the resting ABI, post‐treadmill ABI, claudication onset time, and PWT in the pooled analysis comprising all study participants (all P values ≤0.013, Table 4). K _tissue and φ were significantly associated with the difference in the ABI (P=0.006; P=0.010) of the pooled analysis. In separate analyses, only among patients with PAD, but not among controls, K _tissue , φ, OFC, and $p_{\upsilon }$ were significantly associated with claudication onset time and PWT (Table 5). Conversely, k ^t was associated with the post‐treadmill ABI, and the OFC was associated with the resting ABI in controls but not in patients with PAD (Table 6).

Table 4.

Associations of Computational Microvascular Modeling Parameters With Markers of PAD

Variable	Independent variable	Obs	β	SE	R 2	Adjusted r 2	P value
k t	Resting ABI	56	−0.032	0.0093	0.18	0.16	0.001
	Post‐treadmill ABI	55	−0.043	0.0120	0.20	0.18	0.001
	Δ of ABI	55	−0.012	0.0069	0.05	0.03	0.10
	Claudication onset time, s	55	−16.67	3.7337	0.27	0.26	<0.001
	Peak walking time, s	55	−8.258	3.0860	0.12	0.10	0.010
K tissue	Resting ABI	56	−0.129	0.0205	0.42	0.41	<0.001
	Post‐treadmill ABI	55	−0.178	0.0259	0.47	0.46	<0.001
	Δ of ABI	55	−0.050	0.0177	0.13	0.12	0.006
	Claudication onset time, s	55	−54.93	8.8906	0.42	0.41	<0.001
	Peak walking time, s	55	−43.75	6.3649	0.47	0.46	<0.001
φ	Resting ABI	56	1.634	0.2235	0.50	0.49	<0.001
	Post‐treadmill ABI	55	2.185	0.2918	0.51	0.50	<0.001
	Δ of ABI	55	0.560	0.2097	0.12	0.10	0.010
	Claudication onset time, s	55	776.8	86.325	0.60	0.60	<0.001
	Peak walking time, s	55	542.6	71.138	0.52	0.51	<0.001
OFC	Resting ABI	56	0.027	0.0105	0.11	0.09	0.013
	Post‐treadmill ABI	55	0.037	0.0137	0.12	0.10	0.009
	Δ of ABI	55	0.011	0.0077	0.04	0.02	0.15
	Claudication onset time, s	55	18.33	4.0849	0.28	0.26	<0.001
	Peak walking time, s	55	16.64	2.7839	0.40	0.39	<0.001
$p_{\upsilon }$	Resting ABI	56	−0.049	0.0122	0.23	0.22	<0.001
	Post‐treadmill ABI	55	−0.056	0.0164	0.18	0.17	0.001
	Δ of ABI	55	−0.008	0.0096	0.01	−0.01	0.43
	Claudication onset time, s	55	−28.65	4.4608	0.44	0.43	<0.001
	Peak walking time, s	55	−18.72	3.6501	0.33	0.32	<0.001

Linear regression analyses were performed for all included individuals (pooled). ABI indicates ankle‐brachial index; k ^t , transfer rate constant; K _tissue, interstitial permeability; Obs, number of observations; OFC, outflow filtration coefficient; PAD, peripheral artery disease; $p_{\upsilon }$, microvascular pressure; Δ of ABI, difference between resting ankle‐brachial index and post‐treadmill ankle‐brachial index; and φ, porosity.

Table 5.

Associations of Computational Microvascular Modeling Parameters From Patients With PAD With Markers of PAD

Variables	Independent variable	Obs	Β	SE	R 2	Adjusted r 2	P value
k t	Resting ABI	36	0.002	0.0107	0.00	−0.03	0.82
	Post‐treadmill ABI	35	0.006	0.0124	0.01	−0.02	0.64
	Δ of ABI	35	0.004	0.0091	0.00	−0.03	0.70
	Claudication onset time, s	35	−9.431	5.5899	0.08	0.05	0.10
	Peak walking time, s	35	−3.712	4.7367	0.02	−0.01	0.44
K tissue	Resting ABI	36	−0.012	0.0459	0.00	−0.03	0.79
	Post‐treadmill ABI	35	0.010	0.0537	0.00	−0.03	0.86
	Δ of ABI	35	0.018	0.0393	0.01	−0.02	0.65
	Claudication onset time, s	35	−59.01	22.883	0.17	0.14	0.015
	Peak walking time, s	35	−89.50	13.448	0.57	0.56	<0.001
φ	Resting ABI	36	0.940	0.4563	0.11	0.08	0.047
	Post‐treadmill ABI	35	0.761	0.5579	0.05	0.02	0.18
	Δ of ABI	35	−0.145	0.4199	0.00	−0.03	0.73
	Claudication onset time, s	35	1116.3	184.08	0.53	0.51	<0.001
	Peak walking time, s	35	1014.7	130.53	0.65	0.64	<0.001
OFC	Resting ABI	36	0.004	0.0111	0.00	−0.02	0.70
	Post‐treadmill ABI	35	0.009	0.0129	0.01	−0.02	0.49
	Δ of ABI	35	0.006	0.0095	0.01	−0.02	0.57
	Claudication onset time, s	35	17.40	5.2504	0.25	0.23	0.002
	Peak walking time, s	35	18.98	3.7169	0.44	0.42	<0.001
$p_{\upsilon }$	Resting ABI	36	−0.007	0.0148	0.01	−0.02	0.66
	Post‐treadmill ABI	35	0.013	0.0172	0.02	−0.01	0.47
	Δ of ABI	35	0.019	0.0122	0.07	0.04	0.12
	Claudication onset time, s	35	−24.09	6.9062	0.27	0.25	0.001
	Peak walking time, s	35	−18.23	5.8204	0.23	0.21	0.004

Linear regression analyses were performed for patients with PAD. ABI indicates ankle‐brachial index; k ^t , transfer rate constant; K _tissue, interstitial permeability; Obs, number of observations; OFC, outflow filtration coefficient; PAD, peripheral artery disease; $p_{\upsilon }$, microvascular pressure; Δ of ABI, difference between resting ankle‐brachial index and post‐treadmill ankle‐brachial index; and φ, porosity.

Table 6.

Associations of Computational Microvascular Modeling Parameters From Controls With Markers of PAD

Variable	Independent variable	Obs	β	SE	R 2	Adjusted r 2	P value
k t	Resting ABI	20	0.042	0.0591	0.03	−0.03	0.48
	Post‐treadmill ABI	20	0.149	0.0557	0.29	0.25	0.015
	Δ of ABI	20	0.107	0.0783	0.09	0.04	0.19
	Claudication onset time, s	20	−9.855	12.786	0.03	−0.02	0.45
	Peak walking time, s	20	−9.855	12.786	0.03	−0.02	0.45
φ	Resting ABI	20	−0.967	0.5799	0.13	0.09	0.11
	Post‐treadmill ABI	20	−1.097	0.6353	0.14	0.09	0.10
	Δ of ABI	20	−0.129	0.8550	0.00	−0.05	0.88
	Claudication onset time, s	20	−19.22	135.13	0.00	−0.05	0.89
	Peak walking time, s	20	−19.22	135.13	0.00	−0.05	0.89
OFC	Resting ABI	20	0.022	0.0067	0.37	0.33	0.005
	Post‐treadmill ABI	20	0.017	0.0084	0.19	0.15	0.05
	Δ of ABI	20	−0.004	0.0116	0.01	−0.05	0.71
	Claudication onset time, s	20	0.777	1.8260	0.01	−0.05	0.68
	Peak walking time, s	20	0.777	1.8260	0.01	−0.05	0.68
$p_{\upsilon }$	Resting ABI	20	−0.014	0.0218	0.02	−0.03	0.51
	Post‐treadmill ABI	20	−0.020	0.0238	0.04	−0.02	0.41
	Δ of ABI	20	−0.006	0.0302	0.00	−0.05	0.85
	Claudication onset time, s	20	−0.303	4.7780	0.00	−0.06	0.95
	Peak walking time, s	20	−0.303	4.7780	0.00	−0.06	0.95

Linear regression analyses were performed for controls. K _tissue is a constant for controls. ABI indicates ankle‐brachial index; k ^t , transfer rate constant; K _tissue, interstitial permeability; Obs, number of observations; OFC, outflow filtration coefficient; PAD, peripheral artery disease; $p_{\upsilon }$, microvascular pressure; Δ of ABI, difference between resting ankle‐brachial index and post‐treadmill ankle‐brachial index; and φ, porosity.

Computational Microvascular Model Parameters in Subgroup Analysis

Averaged over all muscle groups, K _tissue and $p_{\upsilon }$ were higher in patients with diabetes and PAD than in patients with PAD without diabetes (Table 7). k _tissue was significantly higher in the AM (P=0.005), LM (P=0.009), DM (P=0.009), and SM (P=0.023) of patients with diabetes and PAD compared with the corresponding muscles of those without diabetes. $p_{\upsilon }$ was significantly higher in patients with PAD and diabetes than in patients without diabetes for the DM (P=0.005) but not for the other muscle groups. Parameter φ was significantly lower in the GM of patients with diabetes and PAD than in patients with PAD without diabetes (P=0.026) but not in other muscle groups (Table S2).

Table 7.

Computational Microvascular Model Parameters for Nondiabetic And Diabetic Patients With PAD

Variable	Nondiabetic group	Diabetic group	P value
k t , 1/s	5.40 (3.97–6.83)	5.49 (4.37–6.60)	0.93
K tissue, m2	3.10 (2.62–3.57)	4.00 (3.44–4.56)	0.017
φ	0.55 (0.51–0.60)	0.51 (0.46–0.56)	0.21
OFC, 1/Pa s	11.82 (10.84–12.81)	12.07 (10.14–14.00)	0.79
$p_{\upsilon }$, mm Hg	50.78 (49.92–51.64)	52.36 (51.09–53.64)	0.034

All values are expressed as median (interquartile range). P values were calculated with the Kruskal–Wallis rank test. Nondiabetic group: n=36; diabetic group: n=20. k ^t indicates transfer rate constant; K _tissue, interstitial permeability; OFC, outflow filtration coefficient; PAD, peripheral artery disease; $p_{\upsilon }$, microvascular pressure; and φ, porosity (values in the range from 0 to 1).

K _tissue and $p_{\upsilon }$ were significantly higher in treadmill noncompleters than in treadmill completers when averaged over all muscle groups (both P values <0.001, Table 8). Averaged over all muscle groups, φ and the OFC were significantly lower in treadmill noncompleters versus treadmill completers (both P values <0.001, Table 8). Compared with treadmill completers, treadmill noncompleters had significantly higher k ^t values in the DM (P<0.001) and SM (P<0.001); however, no differences in k ^t were found for the AM, LM, and GM (Table S3). K _tissue was significantly higher in the AM (P=0.005), LM (P=0.004), SM (P=0.009), and GM (P<0.001) of treadmill noncompleters compared with the corresponding values of treadmill completers but was not different for the DM. Similarly, treadmill noncompleters had a significantly higher $p_{\upsilon }$ in the DM (P=0.007) and GM (P=0.002) than treadmill completers but not in the AM, LM, and SM. Furthermore, φ was significantly lower in all 5 muscle groups in treadmill noncompleters compared with treadmill completers. The OFC was significantly lower in the LM (P=0.008), DM (P=0.033), SM (P<0.001), and GM (P<0.001) of treadmill noncompleters compared with that of treadmill completers but did not differ in the AM for both groups.

Table 8.

Computational Microvascular Model Parameters for PAD Treadmill Completers and Noncompleters

Variable	Completers	Noncompleters	P value
k t , 1/s	6.15 (4.39–7.91)	8.13 (6.41–9.85)	0.10
K tissue, m2	3.72 (3.44–4.00)	4.98 (4.70–5.25)	<0.001
φ	0.53 (0.51–0.56)	0.40 (0.38–0.41)	<0.001
OFC, 1/Pa s	12.97 (12.00–13.94)	9.01 (7.14–10.88)	<0.001
$p_{\upsilon }$, mm Hg	51.15 (49.78–52.52)	54.07 (53.60–54.55)	<0.001

All values are expressed as median (interquartile range). P values were calculated with the Kruskal–Wallis rank test. Completers PAD group: n= 19; noncompleters PAD group: n=17. k ^t indicates transfer rate constant; K _tissue, interstitial permeability; OFC, outflow filtration coefficient; PAD, peripheral artery disease; $p_{\upsilon }$, microvascular pressure; and φ, porosity (values in the range from 0 to 1).

DISCUSSION

Using numerical modeling based on CE‐MRI signal intensities, we determined muscle perfusion properties depending on PAD severity and concomitant diabetes. There were 5 main findings in this study. First, averaged over all muscle groups, k ^t , K _tissue, and $p_{\upsilon }$ were significantly higher while φ and the OFC were significantly lower in patients with PAD compared with the corresponding parameters in matched controls. Second, tissue permeability was significantly higher across distinct muscle regions in patients with PAD than in controls, and φ was heterogeneous across muscle groups. Third, K _tissue and $p_{\upsilon }$ were significantly higher in patients with diabetes and PAD than in patients with PAD without diabetes. Fourth, K _tissue and $p_{\upsilon }$ were significantly higher, whereas φ and the OFC were significantly lower in treadmill noncompleters than in treadmill completers. Fifth, muscle perfusion parameters of the biomechanical model were significantly associated with the resting ABI, post‐treadmill ABI, claudication onset time, and PWT in the pooled analysis comprising all study participants.

Conventional techniques to evaluate PAD are of limited ability to estimate diffuse or small vessel disease, or microvascular dysfunction, which are fundamental aspects of the pathophysiology of PAD. ²³ Clinical studies have shown that perfusion imaging can evaluate PAD severity. ²⁴ In a study of patients with PAD, perfusion deficits in the calf muscles and disease severity were determined by contrast‐enhanced ultrasound. ²⁵ A previous study showed that patients with PAD with intermittent claudication compared with controls had lower peak exercise perfusion and lower limb perfusion. ²³ Moreover, patients with PAD and diabetes were found to have poor tissue perfusion and flow impairment attributable to microvascular dysfunction. Perfusion imaging by contrast‐enhanced ultrasound showed patients with diabetes with microvascular complications had reduced capillary volume recruitment. ²³ , ²⁶ Muscle microvascular blood flow, oxygenation, and pH can act as surrogate markers for perfusion pressure. Previous studies showed that increased intramuscular pressure is associated with a significant decrease in muscle microvascular blood flow, oxygenation, pH, and perfusion pressure in the leg. ²⁷ Hence, modeling parameters of microvascular perfusion could be useful to define disease severity including the influence of diabetes on lower extremity ischemia, as reported in this study. Meneses et al demonstrated a strong correlation between impaired muscle perfusion and disease severity in patients with PAD during postocclusion hyperemia. ²⁸

Duscha et al showed an association of capillary density with claudication times and anaerobic threshold in patients with PAD. ²⁹ Robbins et al ³⁰ reported that leg muscle capillary density is associated with peak hyperemic blood flow in patients with lower extremity ischemia. These data indicate that microcirculatory changes contribute to functional impairment, which agrees with our findings.

Wu et al ³¹ reported that differences in the composition of muscle fibers across various skeletal muscle compartments and connective tissue could cause inhomogeneous muscle perfusion in healthy adults. We have also observed heterogeneous patterns of the modeling parameters across skeletal calf muscle compartments.

The estimation of capillary permeability allows for defining the inflammatory response and regenerative processes following muscle injury. ³² Inflammation increased capillary permeability. ³³ Shimotsu et al ³⁴ showed that endothelial cell swelling corresponds to enhanced microvascular permeability which aligns with our finding that capillary permeability was higher in patients with PAD than in matched controls. We further observed that capillary permeability and microvascular pressure were also higher in diabetes compared with patients with PAD without diabetes.

This study adds to the growing body of evidence on the importance of the microcirculation in PAD. Future work will need to further elucidate associations between the microcirculation and typical PAD symptoms, and to understand whether therapeutic interventions can sustainably alter microvascular blood flow in the lower extremities.

This study has limitations including a limited sample size. Patients with a contraindication to MRI or GBCAs were excluded from this study. Chronic kidney disease is significantly and independently associated with PAD, limiting the use of GBCA during MR imaging. The finite element model of muscle perfusion has limitations. Blood was assumed as a Newtonian fluid, and we did not include nonlinear reactions. However, we have previously reported that using a non‐Newtonian model does not significantly affect the results. ¹⁵ We have not tested interaction terms between clinical variables and the computational microvascular model parameters which will need to be investigated in larger future studies.

In conclusion, computational microvascular model parameters differed significantly between patients with PAD and matched controls. Thus, computational microvascular modeling could be of interest in studying lower extremity ischemia.

Sources of Funding

This work was supported by funding from the National Institutes of Health (R01HL137763 and K25HL121149 both to GB) and the American Heart Association (13BGIA16720014 to GB).

Disclosures

None.

Supporting information

Tables S1–S3