Spatial structure and benefits to hosts allow plasmids with and without post-segregational killing systems to coexist

Abstract

To persist, a plasmid relies on being passed on to a daughter cell, but this does not always occur. Plasmids with post-segregational killing (PSK) systems kill a daughter cell if the plasmid has not been passed on. By killing the host, it also kills competing plasmids in the same host, something competing plasmids without a similar system cannot do. Accordingly, plasmids with PSK systems can displace other plasmids. In nature, plasmids with and without PSK systems coexist and prior theory has suggested this is expected to be very rare or unstable, such that one or the other type of plasmid eventually takes over. Here, we show that if there is spatial structure and plasmids confer benefits to hosts, coexistence of plasmids occurs broadly. Often plasmids confer benefits (even ones with a PSK system) and bacteria are often spatially structured. So, our results may be generally applicable.

1. Introduction

Conjugative plasmids are an important driving force of bacterial adaptation and diversification; by providing accessory genes that would not already be found on the bacterial chromosome, plasmids can improve the fitness of the host bacteria [1,2]. But it is also the case that plasmids are their own entities, with some carrying genes that kill daughter cells who did not inherit a particular plasmid from its parent. Plasmids of this type have what is called a post-segregational killing (PSK) system [3].

PSK systems include a gene for a toxin and a complementary gene for an antitoxin. If a cell has the plasmid, then expression of the antitoxin neutralizes the toxin. But, if upon cell division a daughter cell by chance does not inherit a copy of the plasmid, then the antitoxin is not transcribed and expressed. Lingering in the daughter cell's cytoplasm is the toxin and the daughter cell either dies or its fitness is reduced. All else being equal, conjugative plasmids encoding a PSK system (PSK+) are expected to outcompete conjugative plasmids from a different incompatibility group that do not encode for one (PSK−). The reason for this is because a daughter cell that inherits a PSK− plasmid is expected to die or have reduced fitness, if that daughter cell is derived from a parent that also had a PSK+ plasmid. By contrast, if a daughter cell inherits a PSK+ plasmid, but not the PSK− plasmid from its parent, then it will not be killed by the PSK system. Accordingly, there is a difference in fitness between PSK+ and PSK− plasmids in cases when one type of plasmid is passed to a daughter cell and the other is not from a parent that houses both [4]. In line with this principle, PSK systems seem to be fairly successful since they are present in nearly every species of bacteria [5]. Nevertheless, the expectation that PSK+ overtakes PSK− makes it hard to reconcile the coexistence between PSK+ and PSK− in nature [6].

Early theory showed for a PSK+ plasmid to invade a PSK− population, PSK+ requires a high initial density and that it is difficult for a PSK− plasmid to invade an established PSK+ population [7]. Generally, the conditions for coexistence appeared to be very rare. More recent theory noted that with spatial structure either PSK+ or PSK− can be locally abundant and this may facilitate invasion of a plasmid [8]. The authors derived a spatial model, based on an approximation of a two-dimensional lattice using a pair approximation approach [9,10]. The authors found conditions where PSK+ invades at lower initial densities. Nevertheless, when PSK+ and PSK− were in competition they found either one exists at the exclusion of the other. This later work did not include the plasmidless state, and it is not clear from their work whether plasmids conferred an overall beneficial or deleterious effect relative to the plasmidless state.

Here we propose that beneficial effects of plasmids combined with spatial structure support coexistence. Spatial structure has been found to help promote the persistence of coexistence in other contexts [11]. Spatial structure is likely important since many bacteria are found within biofilms. Furthermore, beneficial effects of plasmids may also be important since antibiotic resistance is linked with PSK systems [12]. Results of this study suggest beneficial effects combined with spatial structure leads to coexistence because beneficial effects allow for PSK− and PSK+ plasmids to out compete plasmidless bacteria and spatial structure may lead to the coexistence of all three because of local density effects combined with conjugation and segregation.

Plasmids co-occur with chromosomes in a host cell and certain combinations of plasmid–chromosome pairs can be specialized to one another in a multi-strain system, or at least have co-evolved in such a way that compensatory evolution has led to higher fitness when paired together versus when apart [13]. Accordingly, we test the idea that beneficial effects and spatial structure support the coexistence in a two-strain system with specialization of plasmids to hosts, as well as a single-strain system without specialization. Together, the single- and two-strain systems offer points of comparison, and the single-strain system is directly comparable to prior work [7,8].

2. Material and methods

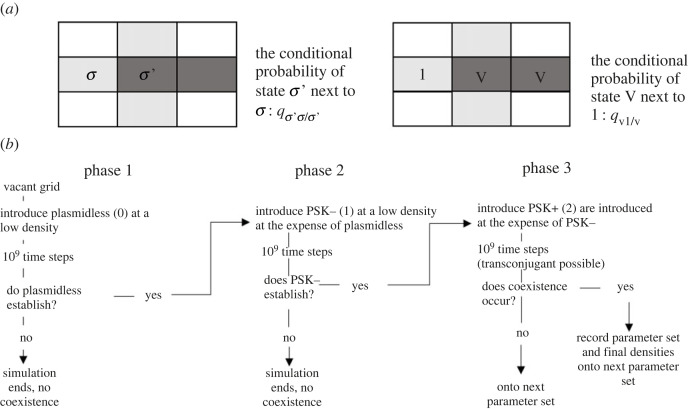
Theoretically, spatial structure is captured using a doublet approach [8,10]. A doublet is two adjacent sites on an infinite plane (figure 1a). In the single-strain model there are five different states of a site: vacant (v), occupied by a plasmidless bacteria (0), a bacterium that contains a plasmid that is PSK− (1), a bacterium that contains a plasmid that is PSK+ (2), and a bacterium that contains both a PSK− and a PSK+ plasmid otherwise known as a transconjugant (3). Each cell contains up to one copy of the plasmid. The number of doublets given n states is n(n + 1)/2. Thus, the five states at individual sites result in 15 doublets. We assume PSK+ confers a greater cost or a weaker benefit than PSK− otherwise it is expected to spread by conjugation and segregation alone. In the two-strain model with specialization the strains of bacteria are an A genotype and a B genotype. The PSK− and the PSK+ plasmids have different fitnesses in the host strains due to the plasmids being more specialized in one strain versus the other. In particular, the PSK− plasmid is less costly or even beneficial in the A genotype compared to the B genotype, while the PSK+ plasmid is less costly or even beneficial in the B genotype compared to the A genotype. A plasmid can conjugate into any of the bacterial strains and therefore come from different incompatibility groups. In this model, a strain is associated with a plasmid state, such that the state space of sites is {v, A0, A1, A2, A3, B0, B1, B2, B3}. These nine states give rise to 45 doublets. Spatial structure is captured by accounting for the conditional probability a particular state is in a particular doublet (figure 1a).

Figure 1.

Illustrates the principle of a doublet in a spatial lattice (a), as well as the procedure used to identify points of coexistence (b). A doublet is two adjacent sites in a lattice. For example, σ′σ forms a doublet where σ and σ′ are possible states (i.e. σ = 1 and σ′ = v). The quantity q_{σ′σ/σ′}, captures spatial structure and is the conditional probability that given a site is in state σ′ it is adjacent to a site in state σ. For example, given a site is in state v, the probability it is in a doublet v1 is q_v1/v. (b) outlines the three-phase approach to finding points of coexistence.

The continuous-time dynamic of a doublet for both single- and two-strain systems is captured by the following conceptual model,

$${\displaystyle \frac{\mathrm{d}{\rho }_{{\sigma }^{\mathrm{\prime }}{\sigma }^{\mathrm{\prime }\mathrm{\prime }}}}{\mathrm{d}t}=\mathrm{\Delta }\mathrm{birth}+\mathrm{\Delta }\mathrm{conjugation}+\mathrm{\Delta }\mathrm{segregation}+\mathrm{\Delta }\mathrm{death},}$$

where ${\rho }_{{\sigma }^{\mathrm{\prime }}{\sigma }^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}}$ is the density of a doublet of type σ′σ″, Δbirth and Δdeath are the instantaneous rates of change in density due to birth and death, whereas Δconjugation and Δsegregation are rates of change due to conjugative transfer and segregational loss of a plasmid. Electronic supplementary materials S1 provides a complete summary of the systems of ordinary differential equations, which model the dynamics of single- and two-strain systems. A list of variables and parameters in the model is provided in table 1, with citations in support of ranges of values that are studied. Note the effect of a plasmid is modelled in terms of ‘cost’ [8], such that a positive cost is deleterious and a negative cost beneficial.

Table 1.

A summary of variables and parameters used in this study.

variable or parameter	definition	values
ρi	the density of a bacteria cell or doublet of type i	0–1
V	a vacant site	—
0	a plasmidless bacteria	—
1	a bacteria that has a PSK− plasmid	—
2	a bacteria that has a PSK+ plasmid	—
3	a bacteria that contains both a PSK− plasmid and PSK+ plasmid (transconjugant)	—
A	strain A bacteria	—
B	strain B bacteria	—
m	the rate of conjugation per plasmid (h−1) [6,14–18]	10−7–10−4
δ	the rate of segregational loss per plasmid (h−1) [6,13,19,20]	5 × 10−4–5 × 10−3
b	the rate of birth of a bacterial cell (h−1) [20–24]	0.04–0.8
d	the rate of death of a bacteria (h−1) [6,25,26]	0.009 – 3/4b
ci	the cost of carrying a plasmid for a bacteria of type i [6,13,19]	see electronic supplementary material S1

Due to the systems of equations for both the single-strain and two-strain models being high-dimensional, analytical and numerical approximation of equilibria were not possible. To find equilibria we randomly and uniformly generated parameter values, with a constraint on costs. A parameter set was subject to the phased introduction of first bacteria, then PSK− plasmids and then PSK+ plasmids (figure 1b). Any parameter set that resulted in both PSK− and PSK+ plasmids persisting at the end of phase 3 was considered to have resulted in coexistence. Illustrative examples of trajectories of frequencies of PSK− and PSK+ that result in coexistence after phase 3 are provided in electronic supplementary material, figure S1. These examples indicate long-term stable coexistence between PSK− and PSK+ plasmids.

3. Results

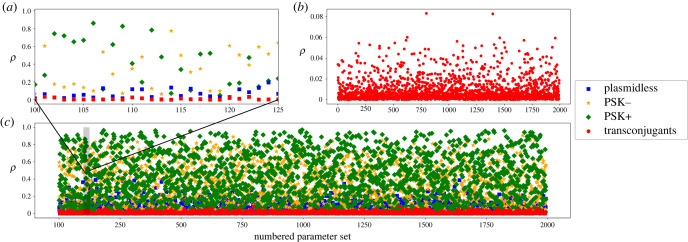
Spatial structure combined with beneficial effects of plasmids support the coexistence of PSK− and PSK+ plasmids in a single-strain system (figure 2). At coexistence points, PSK− and PSK+ plasmid densities can be at moderate frequencies simultaneously. Parameters that support coexistence occur across the full breadth of the parameter space (electronic supplementary material S2), except for costs. All ‘costs’ that support coexistence confer a fitness benefit to the host bacteria for the range of parameters in table 1, and despite the allowance for deleterious costs. We also find coexistence points when both PSK− and PSK+ confer deleterious costs, but these required marginally high conjugation rates and rates of segregation to be lower than rates of conjugation, which is not consistent with known values (electronic supplementary material S2). An examination of relationships among parameters indicate combinations of birth, death, conjugation and costs result in overall positive growth, as well as certain combinations of parameters occurring at higher densities than others (electronic supplementary material S3).

Figure 2.

Equilibrium frequencies when coexistence occurs for the single-strain model. There are 1994 points of coexistence across 100 000 random parameter sets. In (a), the frequencies of plasmidless bacteria, PSK−, and PSK+ bacteria for parameter sets 100 to 125. In (b), transconjugant frequencies. In (c), frequencies for all states.

Although points of coexistence occur broadly across parameter space, only 2% of random parameters sets resulted in coexistence, and it is not clear if these points of coexistence are isolated from each other. To test for whether coexistence points are connected, we performed several parameter walks. In particular, each walk started with the same parameter set that resulted in a point of coexistence between PSK− and PSK+. From this starting point parameters m and δ were randomly perturbed in a biased manner in four directions, which is reflected in the plot (electronic supplementary material, figure S3). Importantly, the other parameters were also simultaneously and randomly perturbed, but in an unbiased manner. Results indicate that coexistence points occur and are connected by small steps in parameters in all four directions.

The two-strain model with specialization also supports coexistence of PSK− and PSK+ plasmids (electronic supplementary material, figure S4). The parameters that result in coexistence of PSK− and PSK+ plasmids are found throughout most of the parameter range (electronic supplementary material, figure S5), except that plasmids confer benefits as opposed to costs to their hosts, like the single-strain model. An examination of parameter relationships indicates some differences relative to the single-strain model, such as a higher density of points for low birth and high segregation, as well as low conjugation and high segregation rates (electronic supplementary material S3). The specialization model resulted in fewer points of coexistence than the single strain model. This is probably due to the larger number of parameters being randomized. However, parameter walks produce connected points of coexistence (electronic supplementary material, figure S6).

4. Discussion

Our theoretical analysis supports the idea that spatial structure combined with beneficial effects of plasmids is sufficient for the coexistence of PSK− and PSK+ across a broad set of birth and death rates, and for conjugation and segregation rates consistent with published values. In a model that lacked spatial structure, the conditions for coexistence of PSK− and PSK+ appeared to be rare [7]. In a subsequent model with spatial structure, a narrow band of coexistence occurred, but required much higher conjugation rates compared to our results [8]. Furthermore, they did not allow for the plasmidless state, such that it was not clear whether the narrow band of coexistence would occur in its presence. Our work does not conclusively demonstrate that spatial structure and benefits are necessary conditions for coexistence. For example, our two-strain model with benefits may lead to coexistence in absence of spatial structure. We leave this possibility for future work.

In our analysis, points of coexistence are sparse, but it is also the case that they are connected by small perturbations in parameters and are therefore accessible to one another. In both the single-strain model and two-strain model with specialization, coexistence can be quite strong, such that both PSK− and PSK+ plasmids were found at upwards of 40% of the population (figure 2). Coexistence arises despite low initial densities of PSK− and PSK+, unlike early work [7].

Our approach expands the region of coexistence despite using more restrictive, but realistic conditions. In particular, we included the plasmidless state of a bacteria. By contrast, when the plasmidless state is allowed, the plasmidless state may prove superior to either PSK− or PSK+, or both. Nevertheless, we find that with beneficial effects of PSK− and PSK+ coexistence occurs across all three states.

We also found coexistence across all three states when PSK− and PSK+ were deleterious, but this required high conjugation rates, as well as segregation rates that were lower than conjugation rates (electronic supplementary material S2). This combination does not occur in nature based on our current state of knowledge (table 1).

We studied coexistence once PSK+ is fully formed and in competition with a PSK− plasmid from different incompatibility groups. A model of the stepwise evolutionary origin and establishment of a PSK+ system is an open question [27]. The co-occurrence of a PSK− and PSK+ plasmid within the same incompatibility group may increase the rate of segregation and therefore decrease the frequency of transconjugants. There is also a lack of research on plasmid coexistence especially in terms of different life strategies since most models assume competing plasmids are the same except in terms of costs or transfer rates [6,8,28]. Lastly, our model did not include for the uptake of the antitoxin to a chromosome [28–30]; it is not clear how this may affect coexistence. Here, we demonstrated that coexistence between PSK− and PSK+ plasmids is possible with spatial structure, and when plasmids are both unspecialized and specialized with a beneficial effect on a bacterial strain.

Data accessibility

Python code and data are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.sf7m0cgb1 [31].

Data is available as part of the electronic supplementary material [32].

Authors' contributions

W.V.: conceptualization, data curation, formal analysis, investigation, methodology, software, visualization, writing—original draft, writing—review and editing; C.K.G.: project administration, supervision, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

We received no funding for this study.