Motor recalibration of visual and saccadic maps

Abstract

How does the brain maintain an accurate visual representation of external space? Movement errors following saccade execution provide sufficient information to recalibrate motor and visual space. Here, we asked whether spatial information for vision and saccades is processed in shared or in separate resources. We used saccade adaptation to modify both, saccade amplitudes and visual mislocalization. After saccade adaptation was induced, we compared participants' saccadic and perceptual localization before and after we inserted ‘no error’ trials. In these trials, we clamped the post-saccadic error online to the predicted endpoints of saccades. In separate experiments, we either annulled the retinal or the prediction error. We also varied the number of ‘no error’ trials across conditions. In all conditions, we found that saccade adaptation remained undisturbed by the insertion of ‘no error’ trials. However, mislocalization decreased as a function of the number of trials in which zero retinal error was displayed. When the prediction error was clamped to zero, no mislocalization was observed at all. The results demonstrate the post-saccadic error is used separately to recalibrate visual and saccadic space.

1. Introduction

Successful interaction with our environment requires that sensory input is organized into a representation of the external world that accurately encodes spatial relations. Neurons representing objects of interest in a perceptual map must convey information to corresponding neurons in motor maps such that precise actions can be generated. The success of each action is implicitly measured in the errors of movement production. Any deviation from a desired movement trajectory will be corrected by a modification of the following movement [1,2]. Minimization of movement errors thus recalibrates space in the motor map. The perceptual spatial map demands for a likewise recalibration. This process would require feedback about the actual state of the external world and a frequent occurrence in order to guarantee maintenance of precision.

Saccade eye movements are the prime candidate to satisfy the urgent need to recalibrate internal spatial maps for action and perception. They are the movements we perform most often per day (about three times per second) and their errors reveal mismatches between internal and external space. Saccades bring the fovea onto objects of interest, although they usually undershoot intended objects and land short of the target [3,4]. A corrective saccade will compensate for the undershoot such that the eye fixates the target [4]. The undershoot has been linked to the magnification factor in the superior colliculus [5]. Research has suggested that this inaccuracy does not reflect motor execution noise but a strategy of saccade control [6–8]. Saccade planning generates a prediction of where the eye will land and the sensed post-saccadic error, i.e. the distance of the fovea to the position of the target, will be compared against the prediction [9–11]. Prediction errors can become effective only after the movement has been completed since saccades are too fast to be adjusted online by visual feedback. Any deviation between the predicted landing error and the actual post-saccadic error will shape the amplitude of the following saccade such as to re-establish the predicted saccade landing. Laboratory experiments in previous research have presented an artificial post-saccade error of the same direction and size after execution of the same saccade amplitude (for a review see [12]). In these experiments, saccade adaptation gradually increases or decreases saccade amplitudes across trials until it reaches an adaptation steady state. The functional role of saccade adaptation has been seen in a compensation of eye muscle fatigue or damage. However, it has repeatedly been shown that adaptive modifications can be found on single saccades [13–16] and on top-down task-relevant information even in the absence of bottom-up visual error [17].

We have recently demonstrated that post-saccadic errors from single saccades recalibrate, in a serially dependent manner, saccade and visual space [18]. Post-saccadic errors might provide the signal that recalibrates the spatial metric not only in motor but also in visual maps (figure 1a). The crosstalk between action and perception gives rise to a fundamental question about how space is processed in the brain: Is there one resource of space, shared between perception and action, or are spatial coordinates for action and perception processed separately?

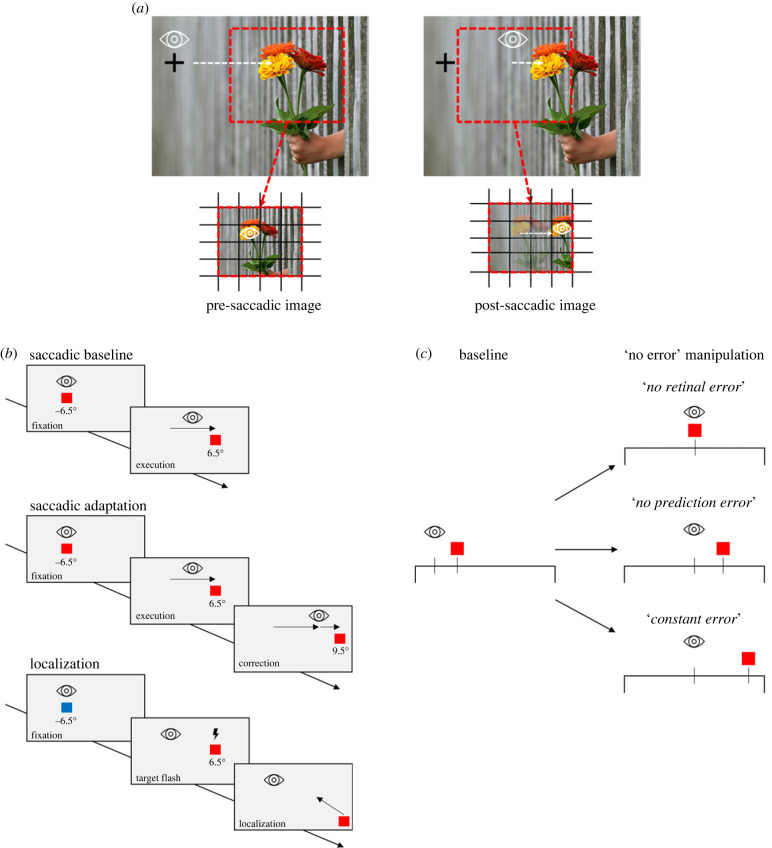
Figure 1.

(a) Illustration of visual recalibration by the post-saccadic error. When making a saccade toward the flower on the right, its retinal projection travels from a peripheral location (pre-saccadic image) to a foveal location (post-saccadic image). Any error in foveate the predicted position of the object (i.e. saccade falling shorter on the flower) will be corrected by a modification of the following movement. (b) Saccade and localization task. Saccade baseline: subjects perform a saccade from a fixation square (–6.5°) to a target square (+6.5°), as soon as the fixation target disappears. Saccade adaptation: subjects saccade to the target, which is displaced 3° outwards from its pre-saccadic position, as soon as the saccade has been detected. Localization: subjects fixate a blue fixation square (–6.5°). After pressing the space bar, fixation disappears and a red target flash for 24 ms at the same position of the saccade target (+6.5°). Subjects indicate the perceived target position via mouse click. Background's colour during the experiment was dark. (c) Examples of the ‘no error’ manipulation applied. The initial saccade target is always at 13° (filled red square). In baseline (the same for all ‘no error’ manipulations), the eye undershoots the intended target position (saccade amplitude of 12°), which correspond to a retinal and prediction error. In the ‘no error’ manipulations (right panels), we predicted the saccade endpoint to apply different ‘no error’ trials. To obtain a retinal error of zero (no retinal error), the target had to be stepped to the predicted saccade landing position (red square). In the second example (no prediction error), the baseline prediction error of each subject has been added to the predicted eye landing position. Therefore, the prediction error is set to zero while the retinal error still occurs. ‘Constant error’ example: eye's landing position was predicted, and the target was displaced by adding a constant error of 3° to this prediction.

On one perspective, motor actions might produce necessary error signals to recalibrate internal spatial estimates to external space, such that both, action and perception, rely on a shared resource. In this view, any change in the motor adaptation must be reflected in visual space. Electrophysiological studies have suggested that the detection of the post-saccadic error is a function of the cerebellum [19]. Although adaptive modifications of saccade amplitudes are computed within the cerebellum, cortical processing of the post-saccadic error has been reported [20]. Neurons in posterior parietal cortex with persistent pre- and post-saccadic responses reflect the intended saccade landing based on efference copy information, whereas neurons with late post-saccadic responses represent the actual saccade ending position. Brain imaging studies in humans suggested that the parietal cortex is one of the sites where saccade adaptation takes place [21]. The parietal cortex represents a likely candidate to host a shared resource for action and perception, given its functional role as a hub for spatial coordinates [22]. The parietal cortex might alternatively relay error signals further into visual areas in order to recalibrate spatial maps separately. This route might serve the purpose of visual recalibration via post-saccadic errors.

A straightforward strategy to address how space is processed in the brain consists in an attempt to drive motor space and visual space in different directions. A singular shared resource would not allow such a dissociation. If motor and visual coordinates can be manipulated such as to shift in opposite directions, neural resources of space must be separate. Studies have shown that saccade adaptation is accompanied by a comparable shift in spatial perception (e.g. [23–26]) and in pointing movements [27].

In our experiments, we adapted saccade amplitudes. After adaptation, we applied trials in which we predicted saccade landing during the execution of the eye movement, in order to present the saccade target such that no error signal is ensued. In our previous study, we found that in the absence of motor errors, visual localization shifts in direction of the fovea [18]. In the current study we varied the number of trials in which the sensorimotor system received ‘no error’ information and wondered whether we would find concomitant or different shifts in localization between action and perception. Concomitant shifts would reinforce claims of a shared resource whereas different shifts would present clear evidence to the contrary.

2. Methods

(a) . Participants

Nine subjects (mean age 25.78 years, s.d. = 4.79 years; 5 women) participated in the ‘no retinal error’ experiment (experiment 1). Four of them plus five additional (mean age = 22.43 years, s.d. = 5.13 years; 6 women) were tested on a second experiment (‘no prediction error’ experiment). Finally, four subjects (who also participated in the previous two experiments) plus three new subjects (mean age = 23.89 years, s.d. = 6.83 years; 5 women) took part in a third experiment (‘constant error’ experiment). Subjects were all German native speakers with no neurological or psychiatric diseases. Participants either reported to have normal vision or they wore lenses during their acquisition. All participants were recruited through the Heinrich-Heine University Düsseldorf and received either course credit or payment of 10 euros per hour.

(b) . Setup

Stimuli were generated under Matlab R2016b (v. 7.10.0; The MathWorks, Natick, MA, United States) using PsychToolbox routines (v. 3.0.17 [28]) run by a Mac Mini, 2014 and presented on screen (CRT, 12.9 inches, Diamond Pro 2070) with a resolution of 800 × 600 pixel and a refresh rate of 120 Hz, placed at 57 cm from the observer. To avoid the potentially confounding influence of any visual references the room was completely dark (except for the EyeLink IR illuminator which emitted some diffuse light that could be potentially used as visual reference. However, the adaptation and mislocalization effects reported in the present study are comparable to the ones reported in literature [29,30]). A transparent foil reduced the luminance of the monitor by 2 log units and prevented the visibility of the monitor borders. Subjects were stabilized in a chin rest to prevent head movements. Before the experiment started subjects were dark adapted for 3 min. The background colour of the screen was dark (0.01 cd m⁻²) to reduce illumination.

Eye movements were recorded by a desktop-mounted eye tracker (EyeLink 1000 Plus), sampling eye position at 1000 Hz. Subjects performed the task binocular but only the left eye was used for eye movement recording. At the beginning of the experiment a standard 9 points calibration routine was run. A standard keyboard and mouse were used to collect participants responses.

(c) . Experimental procedure

Figure 1b shows the trial structure. Each trial began with a fixation square (0.55 × 0.55°) presented 6.5° left of the screen centre. Its colour indicated whether subjects were required to perform a saccade (red, saccade trials) or to keep fixation on the fixation point (blue, localization trials). The protocol consisted of the following blocks of trials: baseline localization and baseline saccades (baseline), adaptation followed by visual localization (post-adaptation), one block of ‘no error’ trials followed by visual localization (post no error trials early), a second block of ‘no error’ trials followed by visual localization (post no error trials late) and saccade de-adaptation (de-adapt). A condition started with 20 baseline localization trials and 20 baseline saccade trials. These were followed by 100 saccade adaptation trials in which the saccade target was displaced outward by 3° as soon as saccade execution was detected. In the next 20 trials, localization performance was measured (post-adaptation). Then, in the ‘no error’ trials (‘post no error trials early’ and ‘post no error trials late’), we manipulated the size of the post-saccadic error systematically in separate experiments (figure 1c for an example of error modifications applied). To this end, we predicted the saccade landing position online and stepped the target according to the post-saccadic error provided. In separate conditions, we varied the number of ‘no error’ trials: in condition ‘short’ 12 ‘no error’ trials, in condition ‘medium’ 25 ‘no error’ trials and in condition ‘long’ 50 ‘no error’ trials were presented. After these, 20 localization trials were tested. Blocks with ‘no error’ trials and localization trials blocks alternated two times. At the end of the session, 20 de-adaptation trials were applied. These trials were identical to the saccadic baseline block and were performed to cancel out the adaptation.

Each condition lasted for around 20 min. A minimum of 15 min break between each condition was conducted to ensure no saccadic adaptation transfer from one condition to the other. The short condition (12 ‘no error’ trials) resulted in a total trial length of 244 trials, the medium condition (25 ‘no error’ trials) resulted in 270 trials and the long condition (50 ‘no error’ trials) resulted in 320 trials. The order of the conditions was randomized within participants.

(d) . Saccadic baseline

At trial onset, a red fixation square (0.55 × 0.55°) was presented horizontally 6.5° left from the screen centre. The vertical position for all targets was always centred. A trial was initiated by disappearance of the fixation target if the subject had fixated it for a randomly selected time interval drawn from a uniform distribution between 500 and 1200 ms. After this time, a red target square (T1) of the same size as the fixation square was presented 6.5° right from the screen centre for 1200 ms. Subjects were instructed to perform a saccade toward the saccade target as soon as it appears. The next trial started with a new fixation square. One trial lasted around 3000 ms (figure 1b, saccadic baseline).

(e) . Saccadic adaptation

After completing 20 trials of baseline, saccadic adaptation was induced (figure 1b, saccadic adaptation). The trial structure was identical to saccadic baseline, except that the target was displaced during execution of the saccade. Eye velocity was calculated online and the target then stepped 3° to the right (T2) as soon as the eye reached a velocity bigger than 30° s^–1 in 5 consecutive samples. A new fixation square then appeared after the saccade was completed and the second target was extinguished (1200 ms after saccade completion).

(f) . Localization trials

A blue fixation square (0.55 × 0.55°; presented 6.5° left from the centre) indicated a localization trial (figure 1b, localization task). Subjects were instructed to fixate the fixation square during the whole trial to prevent motor influences. Subjects started the trial by pressing the spacebar. A red target with the same physical characteristics and the same screen coordinates as in saccade trials was flashed for 24 ms. Simultaneously to the disappearance of the target, a red square with the same physical properties as the target appeared in the lower right screen corner. Subjects were instructed to match the location of the mouse target with the location of the flashed target and confirm their answer via mouse click. A localization trial lasted around 3000 ms.

(g) . ‘No retinal error’ experiment (experiment 1)

The ‘no retinal error’ trials started as the saccadic adaptation trials. Instead of displacing the saccade target outwards, we predicted the eye landing position online and presented the target at the predicted position (see [31]; figure 1c, upper panel). Saccade velocity was calculated online. When saccade velocity fell below 30° s^–1 in three consecutive samples, we selected the current gaze position as the prediction of the saccadic landing point. The mean error between the predicted landing position and the actual landing position resulted over all trials and subjects in 0.19° (s.d. = 0.32°). As described before, ‘no retinal error’ trials were intermingled with localization trials every 12, 25 or 50 trials depending on the session tested.

(h) . ‘No prediction error’ experiment (experiment 2)

The ‘no prediction error’ experiment is identical to the ‘no retinal error’ experiment (experiment 1), except that instead of setting the post-saccadic retinal error to zero, we mimicked the retinal error observed in the baseline trials. We used the mean error of each subject in their baseline saccade trials (difference between the saccade landing position and actual target position) and added this error to the predicted gaze landing position (see [31]; figure 1c, middle panel). Prediction errors contain a certain variance since motor execution noise cannot be precisely foreseen by the sensorimotor system. However, on average this noise should cancel out. The mean baseline prediction error over all conditions was 2.03° (s.d. = 0.44°), while the mean error between prediction and actual landing was 0.19° (s.d. = 0.15°). As for the ‘no retinal error’ experiment (experiment 1), 20 localization trials were intermingled with 12, 25 or 50 ‘no prediction error’ trials, depending on the condition.

(i) . ‘Constant error’ experiment (experiment 3)

In ‘constant error’ trials, we used a target displacement that was clamped to the end point of the eye movement [31]. The saccade landing position was predicted online (see section ‘no retinal error’ trials), and the saccade target was displaced 3° to the right of the predicted saccade landing position (figure 1c, lower panel). The trial structure was the same as in the previous two experiments, but only one condition (long error trials) was tested. ‘Constant error’ trials were intermingled with localization trials after saccade trials were completed. Over all subjects, the mean error between prediction and actual landing was 0.19° (s.d. = 0.17°).

(j) . Target displacements

We checked the timing of the target displacement relative to saccade performance in an offline analysis. Independent of the condition, displacements were presented well within the period of saccade execution: over all blocks, displacements took place on average 45.6 ms (± 3.4) after the saccade onset (on average saccades lasted approximatively 54.1 ms (± 5.9)) in experiment 1; 39.7 ms (± 4.3) after the saccade onset (on average saccades lasted 51.1 ms (± 2.4)) in experiment 2 and 42.1 ms (± 3.8) after the saccade onset (on average saccades lasted approximatively 49.2 (± 2.1)) in Exp 3. Moreover, participants were asked to report after the conclusion of the experiment whether they saw a displacement of the target during the session. None of the participants tested reported to have noticed the target moving.

(k) . Data analyses

For all three experiments we excluded saccade trials in which the subject blinked during saccade execution or if a saccade was initiated before the fixation target disappeared (anticipatory saccades). In order to check for saccades occurring soon after the disappearance of the target, saccade latency was calculated as time from target offset to saccade onset: in less than 1.5% of the valid trials, saccade latencies were shorter than 80 ms. Since their very rare occurrence, these trials were not excluded from the analyses. We excluded trials in which the saccade landing position was smaller than 3.5° or bigger than 9.5°. For the localization trials, trials were excluded in which a perceived localization was smaller than 3.5° or bigger than 9.5°. Additionally, we investigated if the subject fixated during the localization task. If they dissolved fixation during the target flash or during their response of the perceived localization, these trials were excluded from the data analyses. On average, a participant was included in the analyses if at least the 60% of trials was considered valid. Saccadic gain, expressed as the ratio of the saccade landing position over the target position, was calculated for each trial, as well as localization gain (cursor position divided by target position). To compare localization changes over the course of conditions, we calculated the deviation of each localization block from the pre-adaptation baseline trials as the difference between mean localization in the baseline trials and mean localization in each of the three blocks of visual localization. Saccadic landing position changes were obtained, similarly, by computing the difference between subjects' performance in baseline trials and the last 10 valid trials of each adaptation blocks, in order to reduce the temporal offset between saccade and localization. In both cases, positive values indicate an outward shift, while values that fall close to zero indicate no effect of adaptation.

We calculated non-parametric repeated-measures ANOVAs, entailing aligned rank transforms for nonparametric factorial data (ARTool [32]; version 2.1.2) for both, the ‘no retinal error’ experiment (experiment 1) and the ‘no prediction error’ experiment (experiment 2).

First, we analysed if saccade landing positions or target localization adapted outward. We, therefore, performed a 2 × 3 non-parametric repeated-measures ANOVA with factors ‘block’ (baseline, manipulation) and ‘condition’ (short, medium, long) on either saccade landing positions or target localizations.

Second, we analysed if saccade and visual localization performance differ from each other. We performed a 2 × 3 non-parametric repeated-measures ANOVA with factors ‘task’ (saccade, localization) and ‘condition’ (short, medium, long) on the mean saccade adaptation effect (saccade landing positions in the current block minus saccade baseline) and the mean localization adaptation effect (target localization in the current block minus target localization baseline).

Students t-tests against zero on the mean saccade and localization adaptation effect were conducted for the ‘constant error’ experiment (experiment 3).

3. Results

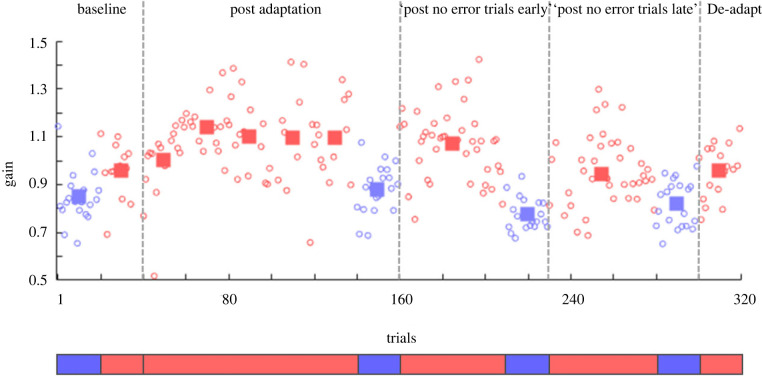
To investigate if visual and saccadic space is processed by shared or separate resources, we inserted ‘no error’ trials and observed how those affected saccade adaptation and visual mislocalization. Figure 2 shows saccadic and target localization data for one example participant, tested in the long ‘no retinal error’ experiment (experiment 1). Saccade gain (red dots) changed from 0.96 (± 0.12) in the pre-adaptation baseline trials to 1.08 (± 0.16) over the course of the adaptation period. However, saccadic gain did not remain stationary. Rather, it slowly decayed starting from the ‘post no error trials early’ (1.07 ± 0.15) to the ‘post no error trials late’ (0.95 ± 0.16) up to the very last block (0.95 ± 0.11), where the participant was brought back to its initial de-adapted state.

Figure 2.

Saccadic and localization gain as a function of trial number for one subject in the long ‘no retinal error’ condition (experiment 1). A gain of 1 indicates no difference between the eye/mouse position and the target. Circles represent single data points (saccade in red, localization in blue). Rectangles in baseline, adaptation and de-adaptation symbolize the mean over 20 trials, with the exception of red rectangles in ‘post no error trials early’ and ‘post no error trials late’ which are the mean over the trial length of the condition (here: bins of 50 trials). The subject first performed 20 trials of baseline localization, followed by 20 saccade baseline trials (baseline). Hundred trials of saccadic adaptation then started, followed by a localization block of 20 trials (post-adaptation). Thereafter, 50 ‘no retinal error’ trials and 20 localization trials were conducted (post no error trials early). This was followed by another block of 50 ‘no retinal error’ and 20 localization trials (post no error trials late). Lastly, 20 de-adaptation trials were performed (de-adapt).

After completing each block of saccade adaptation, participants localized with the screen cursor the position of a brief flashed target presented at 6.5° to the right of the centre of the screen. Similar to saccades, mean localization gain (blue dots) changed from 0.85 in baseline trials (± 0.11) to 0.88 (± 0.10) after the post-adaptation, and from 0.78 (± 0.07) to 0.82 (± 0.08) respectively after saccade blocks of ‘post no error trials early’ and ‘post no error trials late’.

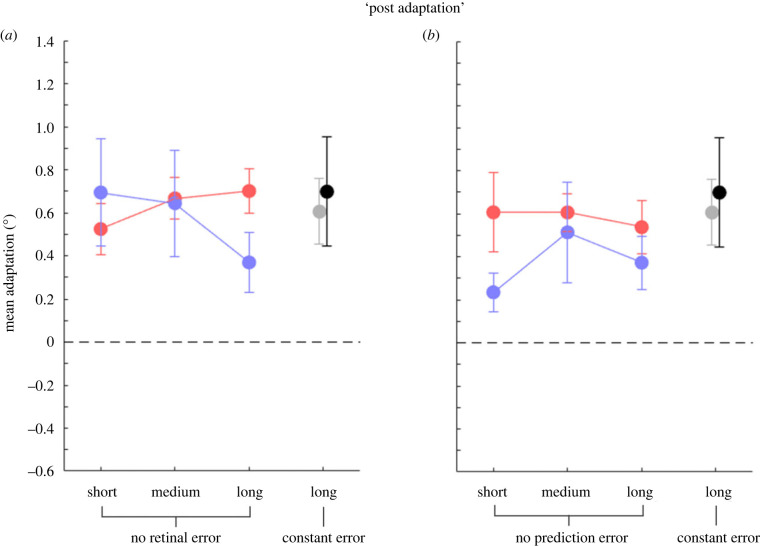
Saccade adaptation was elicited in post-adaptation by an intrasaccadic target displacement paradigm: Participants performed saccades to a target which was presented at 6.5° to the right of the centre of the screen and always displaced by 3° outward (to 9.5°) once a saccade has been detected. Figure 3 plots the amount of adaptation (difference in saccade landing position relative to the baseline landing position, red dots) and the amount of mislocalization (difference in localization position relative to the baseline localization position, blue dots) averaged over subjects for the three condition types, separately for the ‘no retinal error’ experiment (experiment 1), the ‘no prediction error’ experiment (experiment 2) and the ‘constant error’ experiment (experiment 3). Short (12 trials), medium (25 trials) and long (50 trials) labels in figure 3 refer to the number of trials in which the motor system received an error; however, data shown in figure 3 are relative to the trials before this manipulation was applied.

Figure 3.

Mean adaptation (°) for saccade (red) and the following localization trials (blue) over subjects in the post-adaptation trials, before the ‘no error trials’ were performed: (a) ‘no retinal error’ trials; (b) ‘no prediction error’ trials. Mean saccade adaptation in the ‘constant error’ condition (experiment 3) is shown in grey, corresponding localization trials in black. The dotted line indicates a null effect of adaptation. Positive values indicate an outward shift. Error bars are standard errors of the mean. Modification of saccade amplitudes via saccade adaptation resulted in a positive shift in the direction of the target displacement, which was followed by visual localization.

Modification of saccadic amplitudes with this adaptation method produced a clear shift in gaze positions. In all three experiments, a 2 × 3 non-parametric repeated-measures ANOVA with the factors ‘block’ (baseline, manipulation) and ‘condition’ (short, medium, long) on the saccade landing positions revealed a main effect of factor ‘block’ (‘no retinal error’ experiment [experiment 1]: F_1,8 = 69.16, p < 0.001 ; ‘no prediction error’ experiment [experiment 2]: F_1,8 = 43.39, p < 0.001). Therefore, we found large changes in saccade vectors for the ‘post-adaptation’ block. For the ‘constant error’ experiment (experiment 3), on which 7 subjects were tested, a Student's t-test against zero on the saccade landing positions also revealed increased saccade vectors, t₆ = 4.26, p = 0.005.

Moreover, saccadic adaptation affected visual localization, leading to an outward shift of the perceived target position in space, as revealed by a 2 × 3 non-parametric repeated-measures ANOVA with the factors ‘block’ (baseline, manipulation) and ‘condition’ (short, medium, long); (‘no retinal error’ experiment [experiment 1]: F_1,8 = 20.51, p = 0.002; ‘no prediction error’ experiment [experiment 2]: F_1,8 = 13.86, p = 0.006).

Again, for the ‘constant error’ experiment (experiment 3), a Student's t-test against zero on the target localization revealed outward shifted perceived localization, t₆ = 3.25, p = 0.018).

These results show that modifications of saccadic amplitude by saccadic adaptation are paralleled by associated changes in visual localization, consistent with the idea of a common manipulation of motor and perception [23–26].

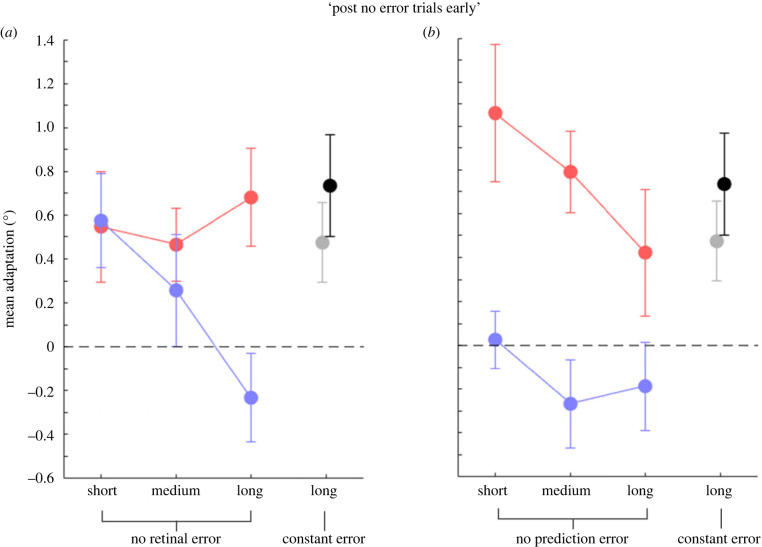
A key question for our study is how the adapted state of saccades and of the following mislocalization develops when no post-saccadic error is provided anymore. Figure 4 plots the mean adaptation magnitude for trials following the ‘no error’ trials (post no error trials early), for modified saccade vectors (in red) and target localization (in blue), as a function of the saccade trials length. In both experiments, a 2 × 3 non-parametric repeated-measures ANOVA with the factors ‘block’ (baseline, manipulation) and ‘condition’ (short, medium, long) on the saccade landing positions revealed that saccades stayed adapted, irrespective of the trial length and of the error variations applied (significant main effect of factor ‘block’; ‘No retinal error’ experiment [experiment 1]: F_1,8 = 14.87, p = 0.005; ‘No prediction error’ experiment [experiment 2]: F_1,8 = 23.31, p = 0.001).

Figure 4.

Mean saccade and localization adaptation (°) for ‘post no error trials early’ in the three conditions tested. (a) Mean saccade (red dots) adaptation and visual localization (blue dots) in the ‘no retinal error’ trials experiment (experiment 1). (b) The same convention as in (a), for trials in the ‘no prediction error’ experiment (experiment 2). Grey and black circles represent the mean saccade adaptation and visual localization, respectively. Error bars are standard errors of the mean. The dotted line indicates a null effect of adaptation.

Moreover, a 2 × 3 non-parametric repeated-measures ANOVA with the factors ‘task’ (saccade, localization) and ‘condition’ (short, medium, long) on the mean saccade or localization adaptation effect revealed that, after performing saccades without a retinal error (experiment 1; figure 4a), mislocalization shifts occur as a function of the number of ‘no error’ trials (significant interaction between factor ‘task’ and ‘condition’), F_2,16 = 4.51, p = 0.028. Indeed, applying 50 ‘no error’ trials, a shift of localization in foveal direction was found, confirming previous results [18].

Visual mislocalization performance in the ‘no prediction error’ experiment (experiment 2; figure 4b), however, diverged from saccade adaptation, irrespective of the condition tested (F_1,8 = 25.80, p = 0.001), as a significant main effect of factor ‘task’ in a 2 × 3 non-parametric repeated-measures ANOVA with the factors ‘task’ (saccade, localization) and ‘condition’ (short, medium, long) on the mean saccade or localization adaptation effect revealed. This result shows no significant localization shifts in the direction of the adapted saccades, independently of the condition (no significant main effect of factor ‘condition’; F_2,16 = 1.34, p = 0.287; 2 × 3 non-parametric repeated-measures ANOVA with the factors ‘block’ (baseline, manipulation) and ‘condition’ (short, medium, long) on the target localization).

Moreover, when a constant error was provided (experiment 3; long ‘constant error’ condition) visual mislocalization (black dot) developed very similar to saccade adaptation (grey dot): the constant post-saccadic error method succeeded in inducing saccade adaptation (t₆ = 2.81, p = 0.031), which was accompanied by mislocalization in favour of an outward displacement (t₆ = 3.40, p = 0.015).

We additionally compared the amount of mislocalization evoked by the ‘post no error trials early’ in the ‘no retinal error’ experiment (experiment 1) and the ‘no prediction error’ experiment (experiment 2). Shifts in localization depended on the nature of the error signal. Indeed, a 2 × 3 non-parametric between-subjects ANOVA with the factors ‘experiment’ (no retinal error, no prediction error) and ‘condition’ (short, medium, long) on the mean localization adaptation effect showed a main effect of factor ‘experiment’ (F_1,8 = 7.35, p = 0.027). The absence of retinal error during saccade execution led, therefore, to a higher recalibration of visual space compared to when ‘no prediction error’ was provided. Moreover, the absence of prediction error caused a decay in visual localization just after 12 no prediction error trials. Therefore, both errors were equally effective in inducing shifts in saccade amplitudes but it appears that annulling the retinal error was more powerful in evoking visual perception changes, which remained significant up to 50 trials no error trials.

In order to quantify how the ‘no error’ trials affected visual localization, we calculated the difference between localization in the ‘post-adaptation’ trials and ‘post no error trials early’ for all three experiments and all conditions (short, medium, long). A 2 × 3 non-parametric repeated-measure ANOVA with the factors ‘experiment’ (no retinal error, no prediction error) and ‘condition’ (short, medium, long) revealed a significant main effect for the factor ‘condition’ (F_2,16 =7.44, p = 0.005) and no significant main effect of factor ‘experiment’ (F_1,8 = 0.59, p = 0.466) nor a significant interaction (F_2,16 = 1.47, p = 0.26). In experiment 3, where a constant post-saccadic error is applied, the difference in localization did not differ significantly from zero (t₆ = 0.71, p = 0.506), indicating that in both blocks, localizations in the ‘constant error’ experiment were outward adapted.

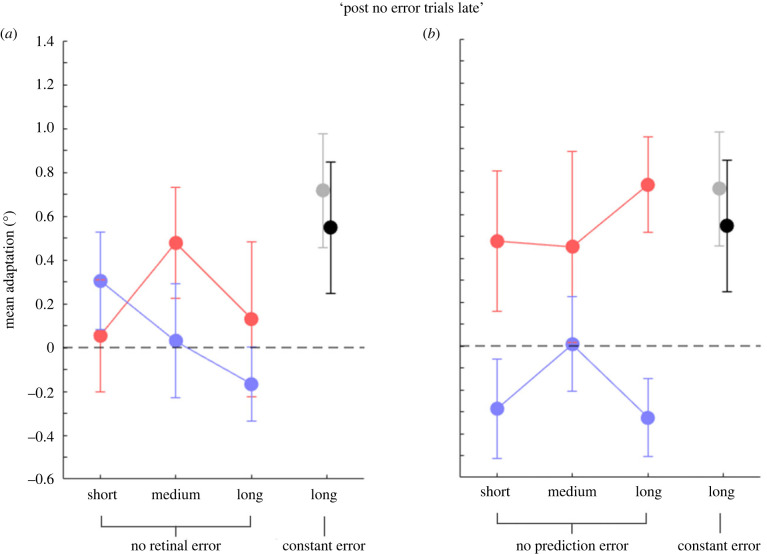
We then investigated mean adaptation magnitude for trials at the very end of the condition (‘post no error trials late’; figure 5). A 2 × 3 non-parametric repeated-measure ANOVA with the factors ‘block’ (baseline, manipulation) and condition (short, medium, long) revealed no significant saccade or localization adaptation anymore (no significant factor ‘block’) in the ‘no retinal error’ condition (experiment 1; figure 5a; saccades: F_1,8 = 2.09, p = 0.187; localization: F_1,8 = 0.87, p = 0.374) but only adapted saccades in the ‘no prediction error’ condition (saccades: F_1,8 = 16.93, p = 0.003; localization: F_1,8 = 1.14, p = 0.317) and a significant difference in the saccade and localization landing positions in experiment 2 (figure 5b; F_1,8 = 10.41, p = 0.012). Applying a constant post-saccadic error modified saccade vectors (t₆ = 2.98, p = 0.025) while localization vectors showed no outward modification anymore (t₆ = 1.97, p = 0.097).

Figure 5.

Mean saccade and localization adaptation (°) for ‘post no error trials late’ in the three conditions tested. (a) Mean saccade (red dots) adaptation and visual localization (blue dots) in the ‘no retinal error’ experiment (experiment 1). (b) Same convention as in (a), for trials in the ‘no prediction error’ experiment (experiment 2). Grey and black circles represent the mean saccade adaptation and visual localization, respectively, of experiment 3. Error bars are standard errors of the mean. The dotted line indicates a null effect of adaptation, while dots falling below the dotted lines indicates a shift in the opposite direction on the target.

4. Discussion

In the present study, we present evidence that saccade adaptation modifies saccadic and visual space separately. In our experiments, various amounts of saccadic error-clamp trials, in which we artificially abolished the post-saccadic error, were followed by trials in which participants localized a visual target while maintaining ocular fixation. While saccade adaptation remained at a steady state level across, visual mislocalization decreased to the baseline level.

The established model of saccade generation involves a motor control architecture in which an inverse model computes the saccade plan and a forward model predicts the sensory consequences following saccade execution. Several studies have reported that consistent with this scheme, saccade amplitudes adapt when the sensorimotor system detects a spatial mismatch between the predicted and the actual saccade landing [9–11]. In a laboratory setting, which usually reduces the visual scene to a saccade target, the prediction of the sensory consequences following a saccade consists in the spatial location of the post-saccadic target. In our baseline trials we confirmed the well-known undershoot in saccade landing positions (e.g. [3–5]). Our target displacement in outward direction increased this undershoot, thus urging the sensorimotor system into an adaptive increase of saccade amplitudes.

Many studies have shown that saccade adaptation changes space perception [23–26]. Motor signals are thus involved in the construction of visual space. In the shared resource model, the metric of visual space could derive directly from motor structures, such that both, action and perception, rely on same spatial coordinates. In this view, any change in the motor adaptation must be likewise reflected in visual space. Alternatively, resources for saccade and visual space might be recalibrated by the same post-saccadic error signal but processed in separate areas in the brain.

In order to decide between the two models, we applied two major manipulations. First, before measuring visual localization, we varied the number of trials with either no retinal or no prediction error. In our previous study [18], we found that visual space compresses toward the fovea if deprived of recalibration by post-saccadic errors. If visual localization would reveal compression to the fovea following the ‘no error’ trials while saccades maintain adaptation, clear evidence for a dissociation between saccade and visual space would be found. Such a dissociation would rule out the shared resource model and favour the model involving separate resources for visual and motor space. Second, we contrasted the influence of the two different sources of error information on visual localization, i.e. the retinal error (distance between the saccade landing position and the visual target), and the prediction error (difference between the predicted post-saccadic retinal error and the observed post-saccadic retinal error).

Our data clearly speak in favour of the model positing separate resources for saccade and visual space. In all conditions, we found significant changes in visual localization when measured directly after saccade adaptation trials. However, when we measured localization after ‘no error’ trials had been presented, we found that mislocalization strength depended on the persistence (i.e. the number of ‘no error’ trials): while a small number of ‘no error’ trials did not change mislocalization magnitude, increasing the number led to a disappearance of mislocalization. In conditions with the highest number of ‘no error’ trials we even found that localization drifted toward the fovea, in agreement with previous results [18]. These changes in localization demonstrate a dissociation between motor and visual targeting because saccade adaptation remained unchanged by the insertion of the ‘no error’ trials. In line with this dissociation, a recent study found significant mislocalization even though subjects, following the instructions, successfully inhibited saccade adaptation [29]. Moreover, evidence of a dissociation between motor and visual targeting have been shown also for saccade directed to moving targets (instead of static targets as in this study), in which the difference between perception and action is suggested to rely on an accumulation of position error over the temporal integration window of motion and position signals, which is much reduced in the motor system [33,34].

Electrophysiological work has demonstrated that the parietal cortex contains a representation of post-saccadic error [20]. It is thus likely that the parietal cortex processes the post-saccadic error in order to recalibrate both, saccade and visual space. The involvement of the parietal cortex in the construction of visual space [22] and in saccade generation [35] and adaptation [21] is well documented. Our data exclude that visual recalibration by the post-saccadic error occurs in early visual areas. If visual recalibration would occur in early visual areas, the changes in saccade amplitudes that we observed would actually be visual in nature. Since the magnitude of visual and saccadic adaptation was identical, it would be impossible under this model that visual mislocalization decays while saccadic adaptation remains stable. However, the latter scenario describes exactly what we found in the present study.

Multiple processes contribute to learning in motor adaptation [36]. Studies suggest that at least two components control learning: an initial process that learns fast and decays quickly and a more gradual process that adapts slow and has a long retention [37,38]. Summing learning from both components yields the final adaptation magnitude. In our study, visual recalibration decayed more quickly than motor recalibration. Since faster adaptive learning is connected to a shorter retention (i.e. a quicker decay), it would be interesting to find out if also recalibration learning is faster for vision than for motor. However, it is unlikely that our data are due to separate components of a single learning process. Since visual and motor changes are of equal strength, when measured immediately after adaptation, the only option remains that saccadic adaptation would be purely visual. However, as argued above, this interpretation must be rejected because motor adaptation was observed when visual mislocalization returned to the baseline level.

In conclusion, our data suggest that resources of motor and visual space are separate and that the post-saccadic error recalibrates the metric of both, saccades and visual localization.

Ethics

Participants gave informed consent prior to participation. Experimental procedures were approved by the local ethics committee of the mathematics and natural sciences faculty of the Heinrich-Heine University Düsseldorf (ethics approval number: ZI01-2021-01). Written informed consent was obtained prior to the experiments in accordance with the declaration of Helsinki.

Data accessibility

Data used for this publication have been deposited into the Dryad Digital Repository: https://doi.org/10.5061/dryad.rbnzs7hft [39].

Authors' contributions

S.T.: conceptualization, formal analysis, investigation, methodology, visualization, writing—original draft; A.P.: conceptualization, formal analysis, funding acquisition, investigation, methodology, supervision, validation, visualization, writing—review and editing; E.Z.: conceptualization, funding acquisition, investigation, methodology, project administration, resources, supervision, validation, visualization, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

This research has received funding from the German Research Foundation (Deutsche Forschungsgemeinschaft; DFG; grant agreement number ZI 1456/6-1) to E.Z., from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programs (grant agreement number 757184–moreSense) to E.Z. and from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie (grant agreement number 101029574– APPROVE ‘Autistic Perception and the predictive role of visual experience’) to A.P.