Reactive mixing performance for a nanoparticle precipitation in a swirling vortex flow reactor

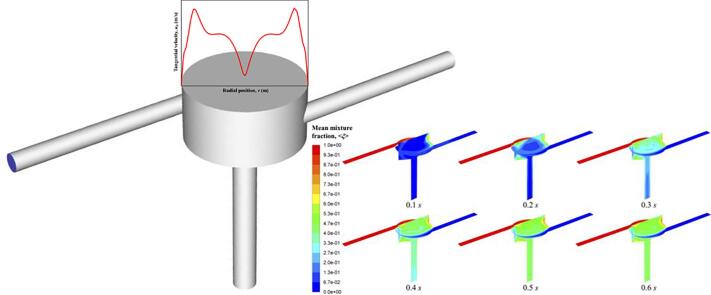
Graphic abstract

Highlights

• •Mixing performance at both a macroscale and microscale was assessed by CFD method.
• •Simulation of turbulent reacting flow was realized by using DQMOM-IEM model.
• •The adoption of ultrasound can improve both the global and local mixing.
• •Effective mixing still exists even under a laminar flow condition.

Abstract

Mixing performance for a consecutive competing reaction system has been investigated in a swirling vortex flow reactor (SVFR). The direct quadrature method of moments combined with the interaction by exchange with the mean (DQMOM-IEM) method was employed to model such reacting flows. This type of reactors is able to generate a strong swirling flow with a great shear gradient in the radial direction. Firstly, mixing at both macroscale and microscale was assessed by mean mixture fraction and its variance, respectively. It is found that macromixing can be rapidly achieved throughout the whole reactor chamber due to its swirling feature. However, micromixing estimated by Bachelor length scale is sensitive to turbulence. Moreover, the additional introduction of ultrasound irradiation can significantly improve the mixing uniformity, namely, free of any stagnant zone presented in the reactor chamber on a macroscale, and little variance deviating from the mean environment value can be observed on a microscale. Secondly, reaction progress variable and the reactant conversion serve as indicators for the occurrence of side reaction. It is found that strong turbulence and a relatively fast micromixing process compared to chemical reaction can greatly reduce the presence of by-product, which will then provide homogenous environment for particle precipitation. Moreover, due to the generation of cavitation bubbles and their subsequent collapse, ultrasound irradiation can further intensify turbulence, creating rather even environment for chemical reactions. Low conversion rate was observed and little by-products were generated consequently. Therefore, it is suggested that the SVFR especially intensified by ultrasound irradiation has the ability to provide efficient mixing performance for the fine-particle synthesis process.

Nomenclature

A_i

cross-section area of inlet tubes, m³

c

species concentration, mol/m³

Da

Damköhler number

Dc

chamber diameter, m

d

inlet diameter, m

F

flow ratio

f_Φ

probability distribution function

f

pressure frequency, s⁻¹

g

gravity, m/s²

I_us

ultrasound power per unit area, W/m²

k

turbulent kinetic energy, m²/s²

k₁, k₂

chemical reaction rate constant, m³/(mol·s)

P

ultrasound pressure, Pa

P_a

pressure amplitude, Pa

p

static pressure, Pa

p_n

probability

Q_i

inlet flow rate, m³/s

R

mechanical-to-scalar time scale ratio

R_v

vortex characteristic length

Re_v

chamber Reynolds number

Re_v

vortex Reynolds number

S

chemical reaction source term

Sc

Schmidt number

Sc_T

turbulent Schmidt number

t_m

micromixing time, s

t_r

chemical reaction time, s

u_i

fluid velocity, m/s

V_s

sound velocity in fluid, m/s

X

DMP conversion

Y

reaction progress variable

Greek letters

γ

micromixing rate, s⁻¹

ε

turbulent energy dissipation rate, m²/s³

μ

viscosity, kg/(m·s)

$\nu$

kinematic viscosity, m²/s

ρ

density, kg/m³

$\xi$

mixture fraction

${\xi \prime }^2$

mixture fraction variance

ω_i

rotational speed of the inner cylinder, rad/s

Γ_T

turbulent diffusivity, m/s

η

Kolmogorov length scale, m

η_B

Bachelor length scale, m

1. Introduction

Advanced functional nanoparticles have wide applications in the fields of pharmaceuticals [1], drug delivery [2], energy storage [3], dyes [4], and cosmetics [5]. Many preparation techniques have been developed to control particle size and its distribution, among which flash nanoprecipitation can be seen as a promising approach. Flash nanoprecipitation was firstly proposed by Johnson and Prud’homme [6], and it requires an extremely fast mixing to quickly create high supersaturation, while high supersaturation enables the formation of numerous crystal nuclei, and thus small uniform particles [7]. Therefore, it can be suggested that a well-controlled synthesis of nanoparticles requires deep understanding and investigation of the mixing mechanism.

Turbulent mixing is an important unit operation in chemical engineering. Especially for those processes involved fast chemical reactions, micromixing plays an important role, as it can directly affect chemical reactions. Micromixing often refers to the process of the viscous-convective deformation of turbulent fluid elements, followed by the molecular diffusion in order to finally achieve homogeneity [8]. Various microscale devices have been developed to meet the requirement of a rapid and homogenous mixing, such as the confined impinging jet reactor [6], [9], T-mixers [10], [11], micro-fluidic channel [12]. In our previous study [13], a swirling vortex flow reactor (SVFR) was proposed for the preparation of mesoporous silicon dioxide (SiO₂) nanoparticles with flexible operating modes. The synthesized particles presented spherical morphology with narrow size distribution, especially with the assistance of ultrasound irradiation.

Swirling flow is defined by an angular motion imposed to the main axial movement of a fluid [14]. It has the feature of a “Rankine vortex-like” flow in the core region, surrounded by a free vortex flow [15]. Turbulent swirling flow is commonly observed in nature and industrial processes [16]. Such a fluid flow has long been used in the fields of oil, mineral, water treatment, and combustion industries due to its distinct features, such as simple realization, easy maintenance, reduced pressure in the central part, and good mixing performance [14], [17]. In Liu et al.’s study [18], they indicated that swirling flow has the ability to significantly enhance mixing. Swirling flow with a sudden expansion in the chamber can lead to the generation of various scales of swirl, and the mixing on these scales is suggested to be equally fast. Furthermore, the intensity of turbulent fluctuations can be enhanced by vortex wandering motion in the centre region, and mixing is improved, consequently [19].

Acoustic effect has been employed in many studies for the intensification of mixing due to its non-invasive nature and cavitation. As micro bubbles collapse, local micro perturbation and turbulence will be induced subsequently [20]. Such small or tiny scale bubbles have the ability to directly affect chemical reactions at a molecular level [21]. In Rahimi et al.’s study [22], they experimentally demonstrated the effect of ultrasound wave on micromixing segregation index in a T-shaped micromixer, which decreased up to 20 %. Parvizian et al. [23] developed a sonochemical reactor, which had a more efficient mixing compared to the traditional stirred tank reactor. Zhang et al. [21] also suggested an improved mixing performance with the acoustic excitation. Two main enhancement mechanisms could be the entrance effect and the interactive vortices. Also, they firstly revealed the interaction existing between the main flow and the acoustic streaming through the simulated streamlines.

Following our previous work [13], mixing in the swirling vortex flow reactor (SVFR) is investigated in the current study. Such a reactor composes of two tangential inlet tubes connected by a round swirling chamber, where the chemical reactions occur. Its configuration is the same as the one used in our previous study, and the operating conditions also keep consistent during simulation. Different from experimental method, numerical modelling can provide more information based on grid resolution. The commonly used modelling method is to couple concentration equations with fluid flow dynamics [24]. Most works often used the transport of a passive scalar (i.e., species concentration) to characterize turbulent mixing effect. However, this approach is far from precise, as mixing always involves a wide range of scales (i.e., macromixing, mesomixing, and micromixing). Especially for turbulent reactive flow, the smallest eddies are often down to the Batchelor scale, much smaller than the Kolmogorov scale. Therefore, a much more fine-scale grid resolution is necessary for the simulation of turbulent mixing effect on chemical reactions, but direct numerical simulation (DNS) is generally too expensive and time-consuming for industrial applications [18]. To this end, in order to describe the molecular reaction on a rather coarse grid scale, a micromixing model is required.

Computational flow dynamics (CFD) combined with the probability density function (PDF) method is widely used for the prediction of turbulent reactive systems, by which chemical source term under the sub-grid scale can be closed [25]. The two-environment DQMOM-IEM (direct quadrature method of moments combining with the interaction by exchange with the mean) micromixing model used in current study is a presumed PDF method, where the correction term is calculated by DQMOM, and the molecular diffusion term is closed by IEM model [26]. To the best of our knowledge, few research works have been conducted concerning the micromixing modelling by the DOMOM-IEM approach in the SVFR, especially with the intensification of ultrasound irradiation. To this end, this paper aims to evaluate the mixing performance by using the DQMOM-IEM model under the same operating conditions as our previous particle synthesis experiments in the SVFR. Coupling of the ultrasound irradiation effect in the modelling has been introduced in this paper. By the aid of the computational approach, the “experiment-free” design and scale-up of the SVFR could be possible.

2. Mathematical model

2.1. Reaction kinetics

As micromixing refers to the process from the viscous-convective deformation to molecular diffusion, its performance can be characterized by chemical reaction probes. The principle of chemical reaction probes lies in the measurement of the yield of by-product produced by the relatively slow reaction. A high concentration of the by-product serves as an indicator for poor micromixing [27]. The consecutive competing reaction scheme developed by Bourne et al. [28] is widely used as such a probe by setting two chemical reactions with great difference in reaction rate [6], [29]. Due to the stable reactants and the easy detection method of product concentration, such a reaction system is employed in current work, as follows,

$$H^{+}+{\mathit{OH}}^{-}\stackrel{k_1}{\to }{H}_{2}O$$ (1)

$${H^{+}+CH}_{3}C{\left(OC{H}_3\right)}_{2}C{H}_3(DMP)\left(+H_{2}O\right)\stackrel{k_2}{\to }{H}^{+}+C{H}_{3}COC{H}_3+2C{H}_{3}OH$$ (2)

Reaction (1) is a fast neutralization reaction between acid and sodium hydroxide with a second order reaction rate constant, $k_1=1.4\times {10}^8{m}^3/(mol\bullet s)$. Reaction (2) is the acid catalysed hydrolysis of 2,2-dimethoxypropane (DMP), where H⁺ serving as a catalyst appears in both sides of the chemical reaction formula. Therefore, there is no consumption of acid. For such a competing reaction scheme, the reaction rate of Reaction (2) is much slower than Reaction (1). The rate constant for Reaction (2) can be estimated by $k_2=7.32\times {10}^7\mathrm{e}\mathrm{x}\mathrm{p}(-556/T)10^{(0.05434+7.07\times 10^{-5}{C}_s)}{m}^3/(mol\bullet s)$, where C_s is the concentration of sodium chloride in the initial feed stream [6].

Such a reaction system is micromixing sensitive. Reaction (1) is extremely faster than the micromixing occurring in the reaction-flow coupling process, and the rate constants k₁ and k₂ are different by many orders of magnitude, thus Reaction (2) can be seen as a limiting step. H⁺ in Reaction (2) serves as both the reactant and product, so its concentration changes little. The characteristic reaction time of such a reaction system can be expressed as a pseudo first-order time constant of the slow reaction [6], as follows:

$$t_r=\frac{1}{k_2{c}_{\mathit{DMP},0}/(1+F)}$$ (3)

The reactants are separately injected into the reactor from two or more flow streams. c_DMP,0 is the initial DMP concentration at one inlet, and F is the flow ratio of H⁺ stream to DMP stream. Therefore, $c_{\mathit{DMP},0}/(1+F)$ can be seen as the average concentration in the chamber after mixing as if there is no chemical reaction occurring. If micromixing is much faster than Reaction (2), the local environment will be homogenous and well-mixed. H⁺ will be completely consumed by Reaction (1), so that Reaction (2) will not occur. On the contrary, if the micromixing time t_m is comparable to the characteristic reaction time t_r, DMP has the opportunity to diffuse to the local excessive H⁺, resulting in the creation of by-product. Therefore, the conversion of DMP can be seen as an indicator for micromixing performance, defined as

$$X=1-\frac{c_{\mathit{DMP}}}{c_{\mathit{DMP},0}/(1+F)}$$ (4)

2.2. DQMOM-IEM micromixing model

Turbulent reacting flows in current study are solved by using CFD method, thus a micromixing model is necessary to describe the interaction between turbulent mixing and chemical reactions. In this work, the two-environment DQMOM-IEM model is applied to simulate the aforementioned consecutive competing reaction scheme. This model is based on the idea that the joint composition PDF is the summation of Ne weighted multi-dimensional Dirac delta functions [30]:

$$f_{\mathrm{\Phi }}\left(\mathbf{\Psi };\mathit{x},t\right)=\sum _{n=1}^{N_e}{p}_n\left(x,t\right)\prod _{\alpha =1}^{N_s}\delta \left[{\mathrm{\Psi }}_{\alpha }-<{\mathrm{\Phi }}_{\alpha }{>}_n\left(x,t\right)\right]$$ (5)

where Φ is the composition vector; Ψ is its state-space counterpart; N_e is the number of environments; p_n is the probability or weight of environment n; N_s is the number of scalars in the composition vector. The application of Equation (5) is based on some assumptions [30], [31]. Firstly, such a presumed PDF method is expressed by a joint-composition PDF. Secondly, the mean value can be reconstructed by a finite number of environments. Thirdly, all composition scalars are independent, and they have the same f_Φ in each computational cell.

Based on the above theory, variables including probability p, mixture fraction $\xi$, and reaction progress variable Y, in each environment are used to reconstruct the joint composition PDF. Thus, Equation (5) can be written in the following format:

$$f_{\xi ;Y}\left(\zeta ,y;\mathit{x},t\right)=\sum _{n=1}^{N_e}{p}_n(x,t)\delta [\zeta -{\xi }_n(x,t)]\delta [y-Y_n\left(x,t\right)]$$ (6)

For a mixing system with finite-rate, each species concentration can be expressed as a linear combination of the mixture fraction $\xi$ and reaction progress variable Y:

$$\frac{c_{H^{+}}}{c_{H^{+},0}}=\left(1-\xi \right)-\left(1-{\xi }_{s1}\right)Y_1;\frac{c_{{\mathit{OH}}^{-}}}{c_{{\mathit{OH}}^{-},0}}=\xi -{\xi }_{s1}{Y}_1;\frac{c_{\mathit{DMP}}}{c_{\mathit{DMP},0}}=\xi -{\xi }_{s2}{Y}_2$$ (7)

where ${\xi }_{s1}$ and ${\xi }_{s2}$ are the stoichiometric mixture fraction for Reactions (1), (2), respectively.

$${\xi }_{s1}=\frac{c_{H^{+},0}}{c_{H^{+},0}+c_{{\mathit{OH}}^{-},0}};{\xi }_{s2}=\frac{c_{H^{+},0}}{c_{H^{+},0}+c_{\mathit{DMP},0}}$$ (8)

Five transport equations for this two-environment model are set as follows,

$$\frac{\partial p_1}{\partial t}+\overline{u_j}\frac{\partial p_1}{\partial x_j}-\frac{\partial }{\partial x_j}\left({\mathrm{\Gamma }}_T\frac{\partial p_1}{\partial x_j}\right)=0$$ (9)

$$\frac{\partial p_1{\xi }_1}{\partial t}+\overline{u_j}\frac{\partial p_1{\xi }_1}{\partial x_j}-\frac{\partial }{\partial x_j}\left({\mathrm{\Gamma }}_T\frac{\partial p_1{\xi }_1}{\partial x_j}\right)=\gamma p_1{p}_2\left({\xi }_2-{\xi }_1\right)+\frac{{\mathrm{\Gamma }}_T}{{\xi }_1-{\xi }_2}\left(p_1\frac{\partial {\xi }_1}{x_j}\frac{\partial {\xi }_1}{x_j}+p_2\frac{\partial {\xi }_2}{x_j}\frac{\partial {\xi }_2}{x_j}\right)$$ (10)

$$\frac{\partial p_2{\xi }_2}{\partial t}+\overline{u_j}\frac{\partial p_2{\xi }_2}{\partial x_j}-\frac{\partial }{\partial x_j}\left({\mathrm{\Gamma }}_T\frac{\partial p_2{\xi }_2}{\partial x_j}\right)=\gamma p_1{p}_2\left({\xi }_1-{\xi }_2\right)+\frac{{\mathrm{\Gamma }}_T}{{\xi }_2-{\xi }_1}\left(p_1\frac{\partial {\xi }_1}{x_j}\frac{\partial {\xi }_1}{x_j}+p_2\frac{\partial {\xi }_2}{x_j}\frac{\partial {\xi }_2}{x_j}\right)$$ (11)

$$\frac{\partial p_1{Y}_{21}}{\partial t}+\overline{u_j}\frac{\partial p_1{Y}_{21}}{\partial x_j}-\frac{\partial }{\partial x_j}\left({\mathrm{\Gamma }}_T\frac{\partial p_1{Y}_{21}}{\partial x_j}\right)=\gamma p_1{p}_2\left(Y_{22}-Y_{21}\right)+\frac{{\mathrm{\Gamma }}_T}{Y_{21}-Y_{22}}\left(p_1\frac{\partial Y_{21}}{x_j}\frac{\partial Y_{21}}{x_j}+p_2\frac{\partial Y_{22}}{x_j}\frac{\partial Y_{22}}{x_j}\right)+p_1{S}_{2\infty }\left({\xi }_1,Y_{21}\right)$$ (12)

$$\frac{\partial p_2{Y}_{22}}{\partial t}+\overline{u_j}\frac{\partial p_2{Y}_{22}}{\partial x_j}-\frac{\partial }{\partial x_j}\left({\mathrm{\Gamma }}_T\frac{\partial p_2{Y}_{22}}{\partial x_j}\right)=\gamma p_1{p}_2\left(Y_{21}-Y_{22}\right)+\frac{{\mathrm{\Gamma }}_T}{Y_{22}-Y_{21}}\left(p_1\frac{\partial Y_{21}}{x_j}\frac{\partial Y_{21}}{x_j}+p_2\frac{\partial Y_{22}}{x_j}\frac{\partial Y_{22}}{x_j}\right)+p_2{S}_{2\infty }\left({\xi }_2,Y_{22}\right)$$ (13)

As the sum of probability equals to unity ($p_1+p_2=1$), there is no need to solve p₂.

Turbulent diffusivity, Γ_T can be evaluated based on the Boussinesq hypothesis

$${\mathrm{\Gamma }}_T=\frac{C_{\mu }}{{\mathit{Sc}}_T}\frac{k^2}{\epsilon }$$ (14)

where C_μ is a constant, C_μ = 0.09, and Sc_T is the turbulent Schmidt number, Sc_T = 0.7.

In Eqs. (10), (11), (12), (13), the first two terms are micromixing term and correction term, respectively. γ is the exchange coefficient, also called the micromixing rate. It can be modelled by

$$\gamma =R\frac{\epsilon }{2k}$$ (15)

R is the mechanical-to-scalar time scale ratio, which is extracted from a scalar energy spectrum [30]. Generally, for a high Reynolds number, R takes a value of 2.0. ε is the turbulent energy dissipation rate and k is the turbulent kinetic energy, and. In addition, the characteristic micromixing time t_m for sub-scale segregation can be estimated by γ:

$$t_m=\frac{1}{2\gamma }$$ (16)

The last term in Eqs. (12), (13) is the chemical reaction source term for Reaction (2), given by

$$S_2\left(\xi ,Y_1,Y_2\right)=\frac{k_2{c}_{H^{+}}{c}_{\mathit{DMP}}}{c_{\mathit{DMP},0}{\xi }_{s2}}=\frac{k_2{c}_{H^{+},0}\left[\left(1-\xi \right)-\left(1-{\xi }_{s1}\right)Y_1\right]c_{\mathit{DMP},0}\left(\xi -{\xi }_{s2}{Y}_2\right)}{c_{\mathit{DMP},0}{\xi }_{s2}}={c_{{\mathit{OH}}^{-},0}\xi }_{s1}{k}_2\left(\frac{1-\xi }{1-{\xi }_{s1}}-Y_1\right)\left(\frac{\xi }{{\xi }_{s2}}-Y_2\right)$$ (17)

Note that there is no need to solve Y₁ for Reaction (1), as it can be obtained by the limiting case. Reaction (1) is an instantaneous chemical reaction, which means H⁺ and OH^– cannot co-exist at any point in the flow. Thus, either $c_{H^{+}}$ or $c_{{\mathit{OH}}^{-}}$ should be zero. In other words, Y₁ is limited by

$$Y_{1\infty }=\min \left(\frac{1-\xi }{1-{\xi }_{s1}},\frac{\xi }{{\xi }_{s1}}\right)$$ (18)

Under the condition that Reaction (2) occurs, $Y_{1\infty }$ should take the value of $\xi /{\xi }_{s1}$. Accordingly, Equation (17) can be written as

$$S_{2\infty }\left(\xi ,Y_2\right)={c_{{\mathit{OH}}^{-},0}\xi }_{s1}{k}_2\left(\frac{1-\xi }{1-{\xi }_{s1}}-\frac{\xi }{{\xi }_{s1}}\right)\left(\frac{\xi }{{\xi }_{s2}}-Y_2\right)={c_{H^{+},0}k}_2\left(1-\frac{\xi }{{\xi }_{s1}}\right)\left(\frac{\xi }{{\xi }_{s2}}-Y_2\right)$$ (19)

Note that chemical reaction source term should be nonzero, so that $\xi$ and Y₂ are limited by $0\le \xi \le {\xi }_{s1}$ and $0\le Y_2\le {\xi }_{s2}$.

Once the mixture fraction and reaction progress variable are known in each environment, each species concentration can be calculated consequently.

$$\frac{{c_{H^{+}}}_n}{c_{H^{+},0}}=\left(1-{\xi }_n\right)-\left(1-{\xi }_{s1}\right)Y_{1n};\frac{{c_{{\mathit{OH}}^{-}}}_n}{c_{{\mathit{OH}}^{-},0}}={\xi }_n-{\xi }_{s1}{Y}_{1n};\frac{{c_{\mathit{DMP}}}_n}{c_{\mathit{DMP},0}}={\xi }_n-{\xi }_{s2}{Y}_{2n}$$ (20)

Mean mixture fraction and mean concentrations can thus be estimated by:

$$<\xi >={\int }_0^1{\int }_0^1{f}_{\xi ;Y_2}\left(\zeta ,y;\mathit{x},t\right)d\zeta d{y}_2\approx p_1{\xi }_1+p_2{\xi }_2$$ (21)

$${<c}_{H^{+}}>\approx p_1{c_{H^{+}}}_1+p_2{c_{H^{+}}}_2;{<c}_{{\mathit{OH}}^{-}}>\approx p_1{c_{{\mathit{OH}}^{-}}}_1+p_2{c_{{\mathit{OH}}^{-}}}_2;{<c}_{\mathit{DMP}}>\approx p_1{c_{\mathit{DMP}}}_1+p_2{c_{\mathit{DMP}}}_2$$ (22)

By using Equation (22) and the numerical results, the conversion of DMP in Equation (4) can be written in the following format:

$$X=1-\frac{\overline{{<c}_{\mathit{DMP}}>}}{c_{\mathit{DMP},0}\overline{<\xi >}}$$ (23)

3. Operating conditions

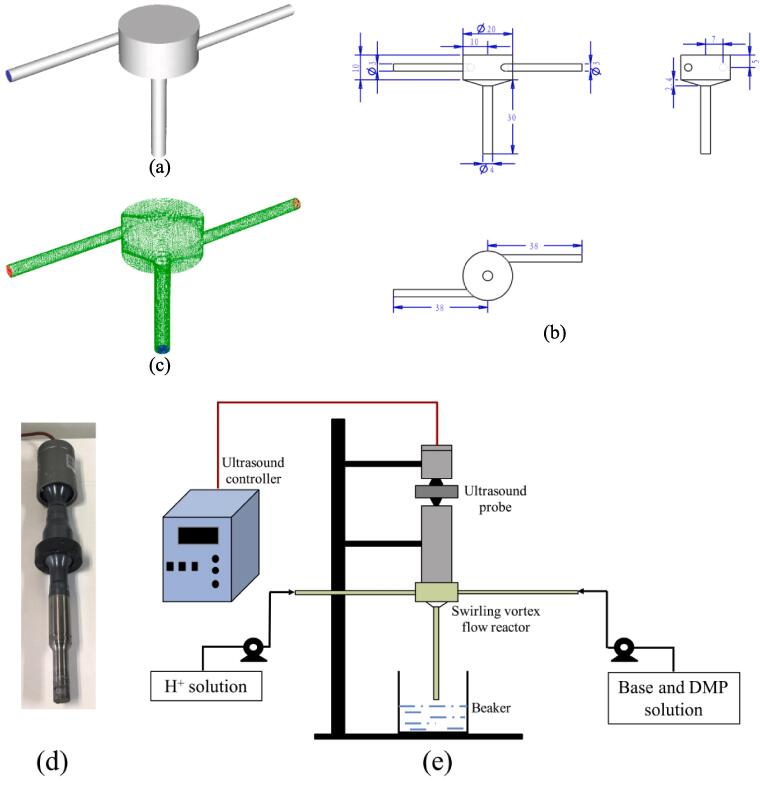
The configuration of the SVFR is shown in Fig. 1(a), which is the same as the one used in our previous work [13]. The reactor chamber is cylindrical in shape with a diameter of 20 mm and height of 10 mm. The diameter for both inlets is 3 mm, and for the outlet is 4 mm. Additionally, the ultrasound probe is located on the top of the reactor with a diameter of 20 mm and compact sealing, shown in Fig. 1(d). Detailed geometric parameters are shown in Fig. 1(b). Acid solution was injected into the chamber from one inlet, while the base and DMP mixture was injected from the other one. Flow rate in the current study was also set the same as the one employed in the previous study. The equal flow rates are 1.92 ml/s, 3.83 ml/s, 5.75 ml/s, 7.66 ml/s, and 9.58 ml/s. An ultrasound power of 240 W was imposed to the reactor chamber for the intensification of the turbulence. A schematic diagram to illustrate the simulated consecutive competing reaction system is shown in Fig. 1(e).

Fig. 1.

(a) Schematic diagram of the SVFR; (b) Dimensions of the SVFR; (c) Mesh setup for the SVFR; (d) Ultrasound probe; (e) Schematic diagram of the simulated consecutive competing reaction system.

Reactant concentration adopted the experimental data in Johnson and Prud’homme’s work [6]. The initial inlet concentration for acid solution is $c_{H^{+},0}=9.373mol/m^3$, and for base and DMP solution is $c_{{\mathit{OH}}^{-},0}=9.842mol/m^3$, $c_{\mathit{DMP},0}=9.373mol/m^3$ to satisfy the molar ratio of 1:1.05:1. Moreover, in order to investigate the effect of the competition between the mixing and reaction, the initial reactant concentration was changed from 9.373 mol/m³ to 177.92 mol/m³, corresponding to the characteristic reaction time from 317 ms to 16.7 ms. All operating parameters are listed in Table 1.

Table 1.

Operating conditions.

Experimental No.	Flow rate of both inlets (ml/s)	Vortex Reynolds number, Rev	Ultrasound power (W)	H+ inlet concentration (mol/m3)	Characteristic reaction time (ms)
R1	1.92	2,553	–	9.373	317
R2	3.83	5,106	–	9.373	317
R3	5.75	7,659	–	9.373	317
R4	7.66	10,212	–	9.373	317
R5	9.58	12,766	–	9.373	317
R6	5.75	7,659	–	16.42	181
R7	5.75	7,659	–	48.72	61
R8	5.75	7,659	–	106.12	28
R9	5.75	7,659	–	177.92	16.7
R10	5.75	7,659	240	9.373	317

4. CFD modelling

4.1. Governing equations

A widely used chamber Reynolds number, Re_c in the SVFR is defined by the sum of all inlet channels:

$${\mathit{Re}}_c=\sum _{i=1}^n\frac{\rho Q_i{D}_c}{A_i\mu }$$ (24-1)

where D_c is the diameter of the reactor chamber, Q_i is the inlet flow rate in each channel with cross-section area of A_i, n is the number of inlet channels. Additionally, based on the features of the SVFR, we also define a vortex Reynolds number based on the characteristic parameters of vortex core, given by

$${\mathit{Re}}_v=\sum _{i=1}^n\frac{2{\omega }_i{R_v}^2}{\nu }$$ (24-2)

where ω_i is the angular velocity calculated from each inlet channel, ν is the kinematic viscosity, and R_v is the vortex characteristic length, estimated by $R_v=(D_c-2d)/2$. Here, d is the diameter of the inlet channel. For all operating conditions, Re_v is listed in Table 1. In current study, the minimum inlet flow rate is 1.92 ml/s, corresponding to an inlet velocity of 0.27 m/s, and a minimum Re_c of 5,210 and Re_v of 2,553. Based on these two Reynolds numbers, flow in the SVFR can be judged as turbulent flow, and its simulation was realized by using Reynolds Average Navier-Stokes equations (RANS) coupled with Reynolds stress model (RSM). RSM takes anisotropic Reynolds stresses into consideration, which is rather appropriate for those swirling dominated flows [32], [33].

The governing equations are set as follows,

Continuity equation:

$$\frac{\partial \overline{u_i}}{\partial x_i}=0$$ (25)

Momentum conservation equation:

$$\frac{\partial \rho \overline{u_i}}{\partial t}+\frac{\partial \rho \overline{u_j}\overline{u_i}}{\partial x_j}=-\frac{\partial \overline{p}}{\partial x_i}+\frac{\partial }{\partial x_j}\left(2\mu S_{\mathit{ij}}-\rho \overline{{u_i}^{\prime }{u_j}^{\prime }}\right)+\rho g_i$$ (26)

where ρ is the fluid density, $\overline{u_i}$ is the Reynolds-averaged velocity in x_i direction, p is the static pressure, μ is the fluid viscosity, g is the gravity, and S_ij is the mean shear strain rate, taking the form of $S_{\mathit{ij}}=\frac{1}{2}(\frac{\partial \overline{u_i}}{\partial x_j}+\frac{\partial \overline{u_j}}{\partial x_i})$. Reynolds stresses, $\rho \overline{{u_i}^{\prime }{u_j}^{\prime }}$ were modelled by RSM to close the above equations. For our system, the transport equations of Reynolds stresses without the effect of buoyancy and system rotation are expressed as follows,

$$\frac{\partial \rho \overline{{u_i}^{\prime }{u_j}^{\prime }}}{\partial t}+\frac{\partial \rho \overline{u_k}\overline{{u_i}^{\prime }{u_j}^{\prime }}}{\partial x_k}=\frac{\partial }{\partial x_k}\left(\frac{{\mu }_T}{{\sigma }_k}\frac{\partial \overline{{u_i}^{\prime }{u_j}^{\prime }}}{\partial x_k}+\mu \frac{\partial \overline{{u_i}^{\prime }{u_j}^{\prime }}}{\partial x_k}\right)-{\rho \left(\overline{{u_i}^{\prime }{u_k}^{\prime }}\frac{\partial \overline{u_j}}{\partial x_k}+\overline{{u_j}^{\prime }{u_k}^{\prime }}\frac{\partial \overline{u_i}}{\partial x_k}\right)+\mathrm{\Phi }}_{\mathit{ij}}-\frac{2}{3}\rho \epsilon {\delta }_{\mathit{ij}}$$ (27)

The terms on the right hand side represent diffusion, stress production, pressure strain, and dissipation, respectively. μ_T is the turbulent viscosity and is assumed to take the form of ${\mu }_T=\rho C_{\mu }\frac{k^2}{\epsilon }$, where $C_{\mu }=0.09$. μ is the molecular viscosity. σ_k is the turbulent Prandtl number, taking a value of 0.82. Φ_ij is the pressure strain. Details of these terms and parameters can refer to Versteeg and Malalasekera’s book [34]. The additional equations for k and ε are given as follows,

$$k=\frac{1}{2}\overline{{u_i}^{\prime }{u_j}^{\prime }}$$ (28)

$$\frac{\partial \rho \epsilon }{\partial t}+\frac{\partial \rho \epsilon \overline{u_i}}{\partial x_i}=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_T}{{\sigma }_{\epsilon }}\right)\frac{\partial \epsilon }{\partial x_j}\right]+2C_{1\epsilon }\frac{\epsilon }{k}{{\mu }_{T}S}_{\mathit{ij}}{\bullet S}_{\mathit{ij}}-C_{2\epsilon }\rho \frac{{\epsilon }^2}{k}$$ (29)

σ_ε is the turbulent Prandtl number, taking a value of 1.0. C_1ε and C_2ε are constants, taking values of 1.44 and 1.92, respectively. More details of these terms and parameters can refer to Launder and Spalding’s work [35].

In addition, the effect of ultrasound irradiation imposed to the SVFR was realised by a cyclic sound pressure as a boundary condition during simulation. Two assumptions were made here: firstly, only the effect of acoustic streaming generated by ultrasound wave propagation is considered; secondly, the ultrasound pressure distribution is expressed in the form of a sinusoidal pressure wave [20], [36].

The pressure is evaluated by

$${P=P}_a\cos \left(2\pi ft\right)+\frac{1}{2}\rho U^2$$ (30)

where P_a is the pressure amplitude, given by

$$P_a=\sqrt{2I_{\mathit{us}}\rho V_s}$$ (31)

where I_us is the ultrasound power per unit area, v_s is the sound velocity in the fluid, and f is the frequency. Here we set a fixed frequency of f = 20 kHz. U is the velocity magnitude due to the propagation of ultrasound waves.

4.2. Numerical simulation

Both inlets have an aspect ratio of $l/d=31/3\approx 10.3$. It is suggested by previous studies that the ratio of length to diameter should be larger than 8 to ensure a stable and fully developed flow [6], [29], [37]. The reactor geometry was firstly created by ANSYS DesignModeler, and then the mesh was generated by ANSYS ICEM, shown in Fig. 1 (c). The total meshes in the computational domain have around 461,000 control cells. The trial simulation on mesh independence check was conducted to confirm the feasibility of such mesh setup.

Flow filed information was obtained by solving governing equations using the commercial software, ANSYS Fluent 19.0. RSM was employed to capture the turbulence features. Second-order upwind scheme was applied for the spatial discretisation of the convective terms, and the pressure–velocity coupling was realised by SIMPLE algorithm. A maximum number of iteration was set to 100 at each time step. The convergence criteria for the simulation were set at 10^-5, and the time step size was set at 10^-4 s for temporal discretisation. Boundary conditions at both inlets and outlet were set as velocity inlet and pressure outlet, respectively. In addition, the effect of ultrasound irradiation was implemented into the simulation as a boundary condition by user defined function (UDF). The density and viscosity of all flow streams were 962.5 kg/m³ and 0.001995 kg/(m·s), respectively, keeping consistency with another experimental work [6].

Two-environment DQMOM-IEM model was implemented by the user defined scalar (UDS) to predict the turbulent reacting flow. Five independent scalars are:

$$X_0=p_1,X_1=p_1{\xi }_1,X_2=p_2{{\xi }_2,X}_3=p_1{Y_1,X}_4=p_2{Y}_2$$ (32)

The inlet boundary conditions for the H⁺ stream are:$X_0=1$ and $X_1=X_2=X_3=X_4=0$; and for the OH^– and DMP stream are:$X_0=X_1=X_3=X_4=0$ and $X_2=1$. All scalars were solved with a second-order upwind scheme, and the convergence criteria were set at 10^-4. After the turbulent flow field had been obtained, scalars’ transport equations were activated. Additionally, in order to ensure the DQMOM-IEM model to be able to characterize mixing and chemical reactions, model validation has been performed in advance by the comparison with Liu and Fox’s data in a confined impinging jet reactor [29], shown in Fig. S1. Details are provided in the Supplementary Material.

5. Results and discussion

5.1. Mesh independence check

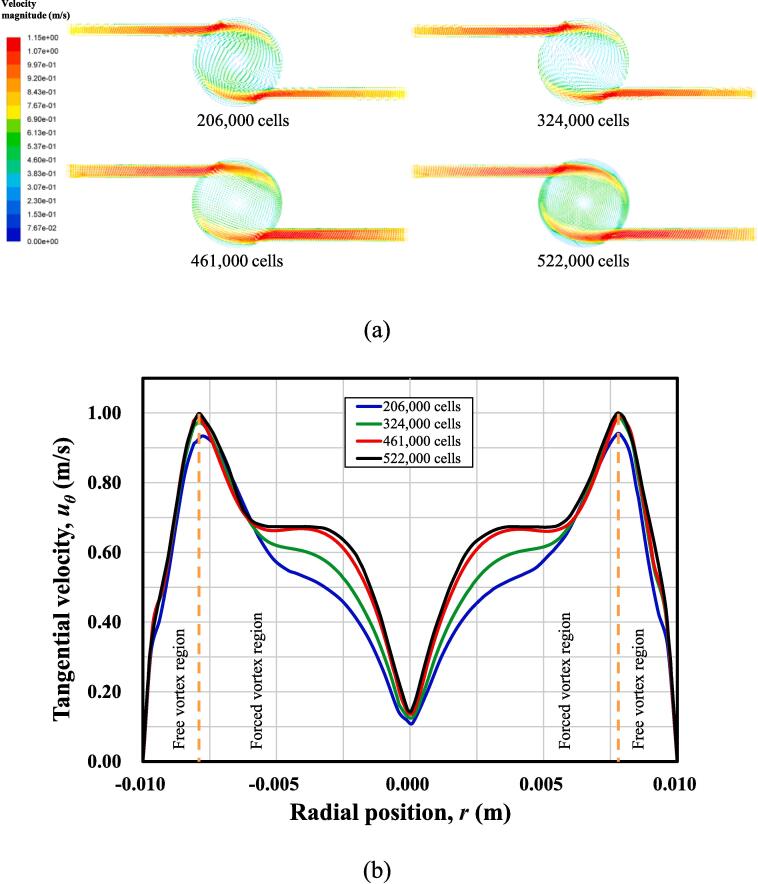
To confirm the CFD modelling results on the flow in the reactor chamber to be independent of mesh size, the simulations with different mesh sizes (i.e., 206,000 cells, 324,000 cells, 461,000 cells, 522,000 cells) were performed. Firstly, in order for the main flow features in the SVFR to be fully captured, the velocity distribution in the horizontal cutting plane of inlet tubes is depicted in Fig. 2(a). It can be seen from the figure that inlet tubes are long enough to ensure a fully developed flow for these four different mesh sizes, and swirling flow patterns are well formed in the reactor chamber.

Fig. 2.

(a) Velocity vector in the horizontal cutting plane of the SVFR; (b) Tangential velocity profiles along the horizontal middle plane of the SVFR.

Secondly, an approximate model to characterize such swirling flow in the SVFR is the Rankine vortex model, which includes both a forced vortex region and a free vortex region. The forced vortex flow can be seen as a type of rotational flow, while the free vortex flow is categorized as an irrotational flow [16]. For a quantitative observation, Fig. 2(b) shows the tangential velocity profiles along the chamber horizontal middle plane. Four mesh setups can capture the main vortex features in the chamber, marked in the figure. However, two obvious transition regions are observed in the last two finer mesh cases. This may be due to the increased mesh size near the vortex core, thus more refined flow structures can be identified. Also, the last two cases present almost coincided tangential velocity, and the most refined 522,000 cells only leads to a slight improvement.

The simulation results for the flow in the reactor chamber clearly indicate that the use of 461,000 mesh size is sufficient to obtain the mesh independent results, and further refined mesh has negligible impact. Therefore, mesh size with 461,000 control cells was finally adopted in current work for further CFD modelling.

5.2. Effect of flow rate and ultrasound on mixing

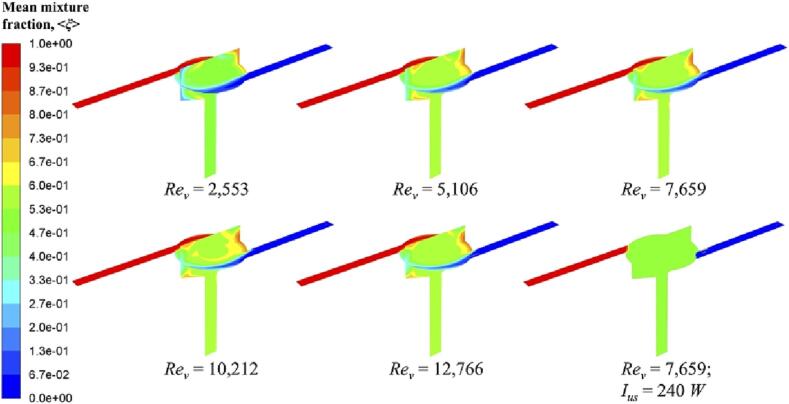
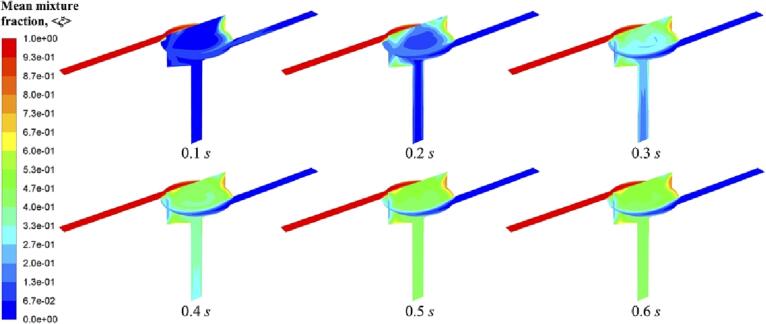
As described in Equation (24–2), flow rate determines Reynolds number. Firstly, macromixing is characterized by a grid-scale variable, mean mixture fraction, <ξ >. It can be seen from its contour distribution in Fig. 3, the mean mixture fraction profiles do not change much when increasing Re_v, which means effective macromixing conditions in the SVFR chamber and the following outlet can be achieved under all turbulent conditions investigated. This can be interpreted by such a process that a tracer is injected into the reactor from one inlet, and then fluid plumes carrying such a tracer are spread and mixed. One should be mentioned here, at a low Re_v of 2,553, mean mixture fraction seems to be rather close to 0.5, which indicates a complete mixing. The reason could be that the tracer injected with a low flow rate is easy to be quickly dispersed throughout the whole system. Additionally, there are few stagnant zones can be observed in Fig. 3 through two orthogonal cutting planes of the SVFR. The major area of the reactor chamber is well mixed, only small amount of segregation occurs in the free vortex regions. This indicates that fluid injected from different inlet streams will not completely mix until it reaches the chamber centre. Such process can be confirmed by observing the variation of mean mixture fraction at different flow times. Here we only show a representative condition with an inlet flow rate at 0.81 m/s for an example in Fig. 4. The unmixed fluid is stretched into thin layers in the free vortex region, and then spirally spreads to the forced vortex region. It is suggested by the previous study that the centre of the swirling flow is unsteady, presenting a random or precession wondering motion [15]. Due to such a wondering motion in the forced vortex region, turbulence can be enhanced, and thus mixing will be improved. For a successive observation, a video record is provided.

Fig. 3.

Mean mixture fraction < ξ > at different operating conditions.

Fig. 4.

Mean mixture fraction < ξ > contour at different flow times at Re_v = 7,659.

When imposing ultrasound irradiation on the reactor chamber, almost all regions except for the both inlets can achieve a good mixing condition, as shown in the last image of Fig. 3. As expected, mean mixture fraction approaches 0.5. This could be resulted from the acoustic cavitation effect, which can trigger the generation of a large number of bubbles. These bubbles will further oscillate and collapse into rather small micro-bubbles. In Zhao’s study [38], they observed that when the ultrasound intensity increases to a certain level, cavitation bubbles will be presented with a large size. Another study also suggested that there is a competition between interfacial tension and acoustic pressure [39]. Once the acoustic pressure is large enough, the interfacial tension can no longer provide sufficient resilience to maintain the shape of large bubbles. Accordingly, they will collapse into small bubbles. It can be deduced that the operating condition of 240 W in our study has the potential to create large cavitation bubbles, then collapsing into small bubbles, which will finally result in an efficient dispersion of the tracer throughout the whole reactor.

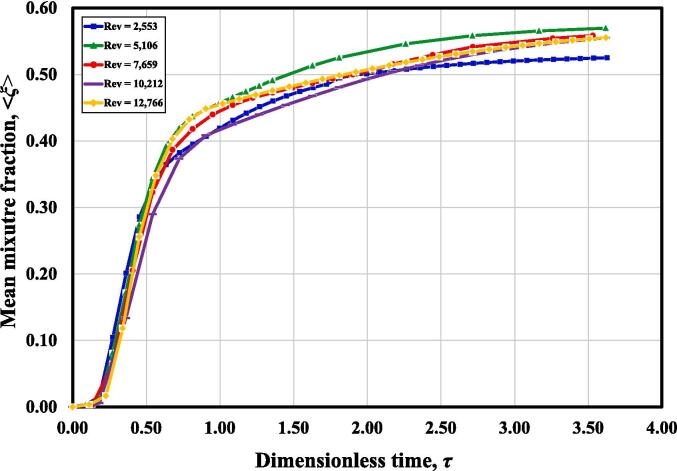
Quantitatively, the time required to achieve a perfect mixing condition on a macroscale is also investigated. In order to save the computational time and avoid numerical divergence, and also given that enormous power in the reactor chamber could lead to the backflow of reactant streams, the ultrasound irradiation was imposed on the reactor after the turbulent flow field and scalar fields had been obtained during CFD simulation. Therefore, the time required to build up a good mixing condition on a macroscale is not the real time required under this condition. Here, we only take the effect of inlet flow rate into consideration, and introduce a dimensionless time τ, defined as the ratio of current time to the mean residence time, $\tau =t/t_r$. Fig. 5 shows the variation of the mean mixture fraction with time at outlet. It can be seen that after about 2.5 times of the mean residence time, the tracer can be perfectly mixed with the other fluid plumes throughout the whole reactor on a macroscale. In full range of Reynolds numbers investigated, such a time interval (i.e.,$\tau =2.5$) is almost unchanged, indicating that the change of vortex Reynolds number has little impact on reactor macromixing. This result is in an agreement with Liu et al.’s work [40], where they suggested that macromixing is mainly controlled by reactor geometry, which can be hardly affected by turbulence level once the flow field is fully developed.

Fig. 5.

Mean mixture fraction < ξ > change with time.

Secondly, as an index to evaluate micromixing performance in the SVFR, mixture fraction variance ${{<\xi }^{\prime }}^2>$ is suggested to be used, referring to the deviation from the mean value.

$${{<\xi }^{\prime }}^2>=p_1{{\xi }_1}^2+p_2{{\xi }_2}^2-{<\xi >}^2$$ (33)

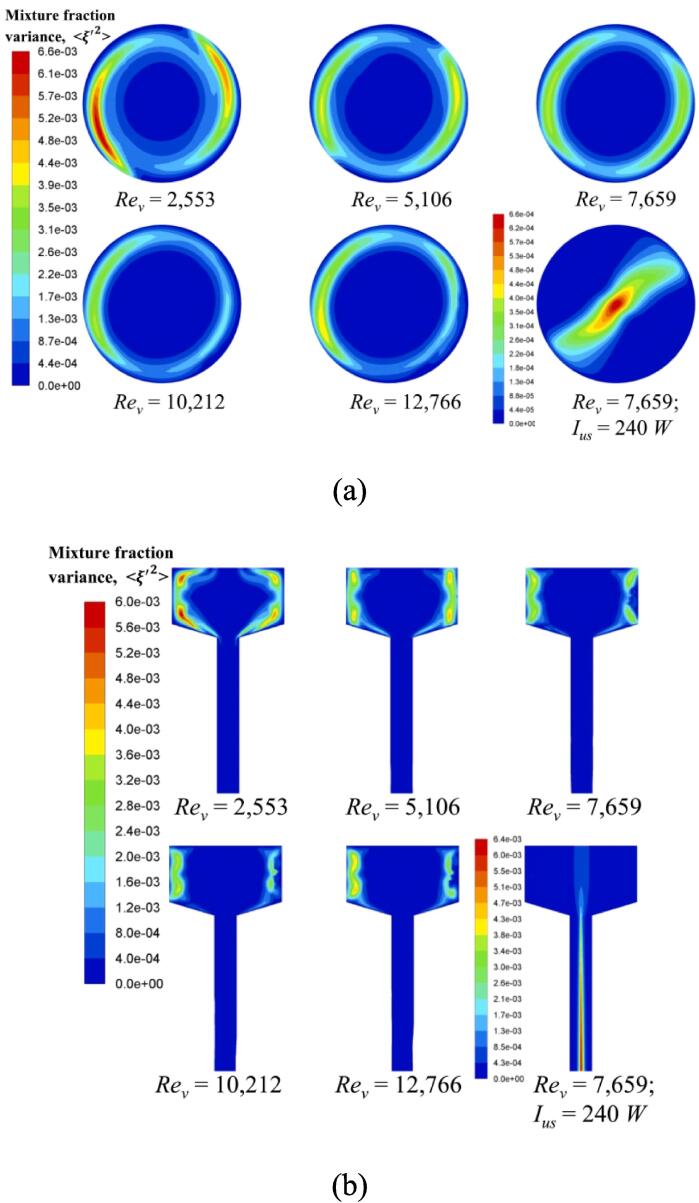
Fig. 6 shows the contour of mixture fraction variance ${{<\xi }^{\prime }}^2>$ at different Re_v (i.e., different inlet flow rates). In order to avoid significantly large values in both inlet regions, we only depict the region in the reactor chamber. Different from the mean mixture fraction contour, its variance shows an almost symmetric structure around the centre of the swirling flow. The great variance is observed in the free vortex region, while the small value appears in the forced vortex region. This result suggests that micromixing performance is improved as the flow approaches the chamber centre. It is interesting to notice on bottom right of Fig. 6(a) and (b) that the application of ultrasound irradiation leads to a totally opposite effect, where the mixture fraction variance shows its maximum value in the swirling centre, but with a low order of magnitude. For a general swirling flow, the lowest pressure appears in the vortex centre due to the centrifugal force. However, the effect of ultrasound irradiation in our study was exerted by introducing a cyclic sound pressure, which was much higher than its original hydrodynamic pressure. Thus, the original forced vortex region loses its rotational feature like a rigid body. A large number of cavitation bubbles tend to move to the centre through a spiral motion. The expansion and collapse of these bubbles will subsequently create considerable micro-bubbles in the surroundings. Consequently, turbulence is intensified by these micro-bubbles with local induced small eddies. This could finally result in the creation of rather good micromixing environment away from the swirling centre when imposing ultrasound irradiation.

Fig. 6.

Mixture fraction variance ${{<\xi }^{\prime }}^2>$ contour in the reactor chamber at different operating conditions in: (a) horizontal cutting plane; (b) vertical cutting plane.

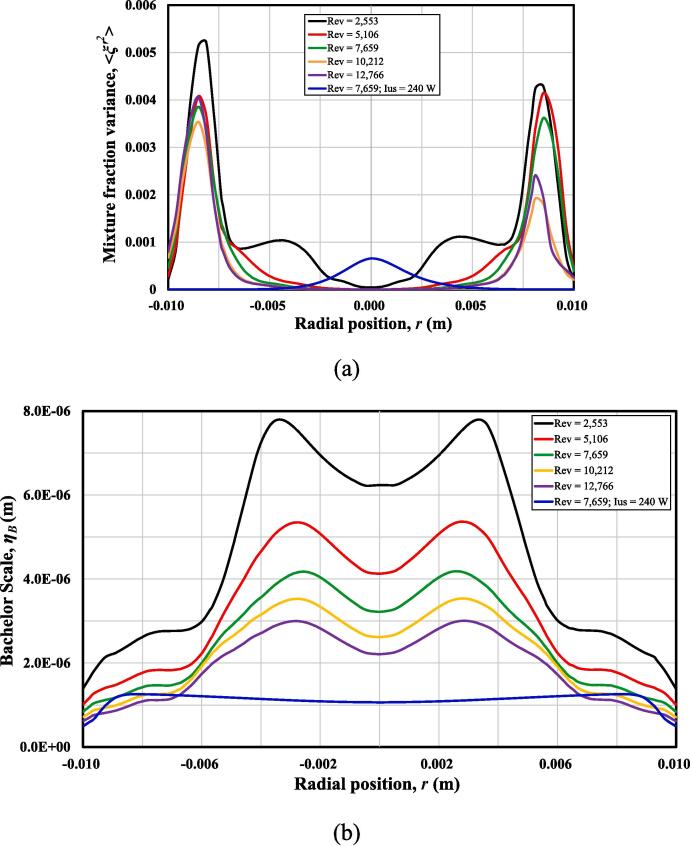
Quantitatively, Fig. 7(a) shows the comparison of the mean mixture variance, ${{<\xi }^{\prime }}^2>$ at different Re_v (i.e., different inlet flow rates) by extracting data along the centre line of the horizontal plane. It can be seen that a small Reynolds number often leads to a poor mixing. When the inlet flow rate is larger than 1.08 m/s, corresponding to a Re_v of 10,212, little difference can be observed in terms of the mixture fraction variance. This indicates that further increasing Reynolds number cannot improve the micromixing performance of the SVFR significantly. It has been suggested that the smallest turbulent mixing scale can be estimated by Bachelor scale, ${\eta }_B=\eta /\sqrt{\mathit{Sc}}$, where η is the Kolmogorov scale, and Sc is the Schmidt number [18]. It can be seen from Fig. 7(b) that the length difference of turbulence eddies is reduced when increasing turbulence level. As the eddy size cannot keep decreasing, the micromixing efficiency will also demonstrate a limit.

Fig. 7.

(a) Mixture fraction variance ${{<\xi }^{\prime }}^2>$; (b) Bachelor length scale η_B change along the radial direction at different operating conditions.

It is worth mentioning that our previous SiO₂ nano-particle synthesis result shows similar particle size and distribution with Re_v at 10,212 and 12,766. The correlation coefficient between turbulent shear rate and reactant consumption rate also changes little under these two conditions. It is suggested that particle property is mixing dependent, while mixing in the SVFR is controlled by both macromixing and micromixing. As mentioned before, macromixing is mainly controlled by the reactor configuration and geometry. At a relatively low Re_v, mixing is mainly controlled by micromixing, while macromixing becomes dominant when Re_v increases up to 10,212. A similar trend was also obtained in Liu’s work [18], where they found that mixing efficiency will not be improved when Reynolds number is larger than a certain value.

Additionally, the magnitude of the mean mixture fraction variance with the employment of ultrasound irradiation is much smaller than that without it, shown in Fig. 7(a). Due to the collapse of the cavitation bubbles, many micro-bubbles are created, and turbulence is thus intensified. The smallest Bachelor scale is observed with the treatment of ultrasound irradiation in Fig. 7(b). Therefore, the micromixing performance is improved significantly.

5.3. Effect of flow rate and ultrasound on chemical reactions

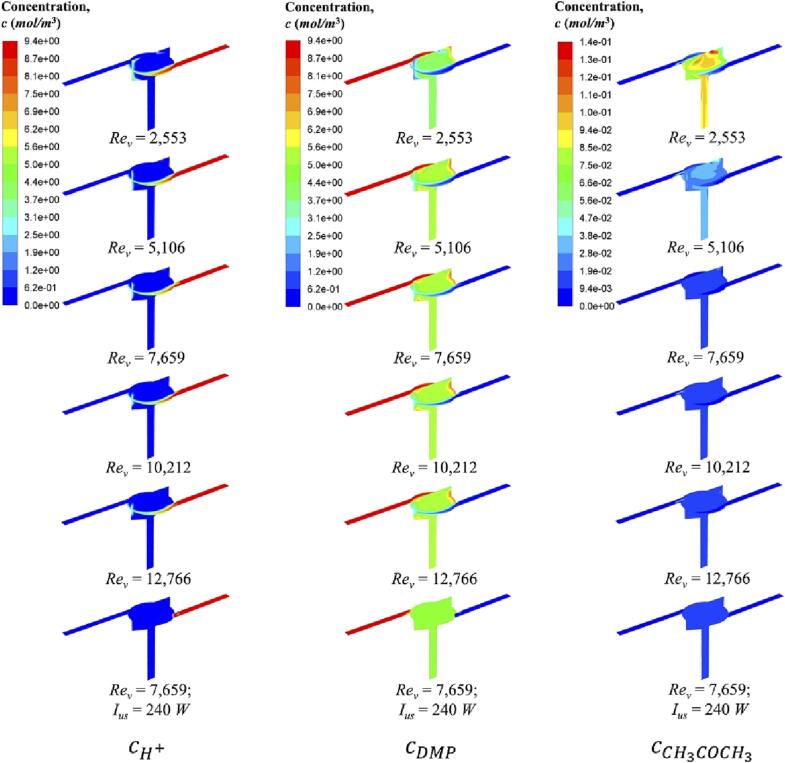
As the acid solution was injected into the reactor from one inlet, and the premixed sodium hydroxide and DMP solution was injected from the other side, they encountered with each other in the reactor chamber along with the swirling flow. This means that chemical reactions almost took place in the chamber as both inlets were only filled with reactants. Fig. 8 demonstrates the species concentration of Reaction (2) at different Re_v (i.e., different inlet flow rates). It can be clearly seen that as soon as acid solution enters the reactor, it is quickly consumed by either Reaction (1) or Reaction (2). As mentioned before, the degree of the occurrence of Reaction (2) is determined by the micromixing efficiency. For a poor micromixing condition, local excessive acid will react with DMP to produce by-product, CH₃COCH₃. Firstly, it is reasonable that the poor mixing appears near the wall region. However, in this SVFR, such stagnant regions are not remarkable even in low turbulence. Secondly, other poor mixing regions can be judged from the concentration contour of CH₃COCH₃ produced by Reaction (2), shown in the last column of Fig. 8. With the increase of Re_v, its concentration is obviously reduced.

Fig. 8.

Species concentration at different operating conditions.

Moreover, the introduction of ultrasound irradiation leads to a low possibility of Reaction (2). After mixing of two flow streams, DMP concentration approaches half of its initial concentration. This indicates little consumption of DMP, and thus the production of CH₃COCH₃ is almost none. When DMP was injected into the reactor, it was dispersed evenly within a short time interval with the assistance of ultrasound irradiation. Both perfect macromixing and micromixing are achieved. Therefore, chemical reaction with low reaction rate can hardly occur.

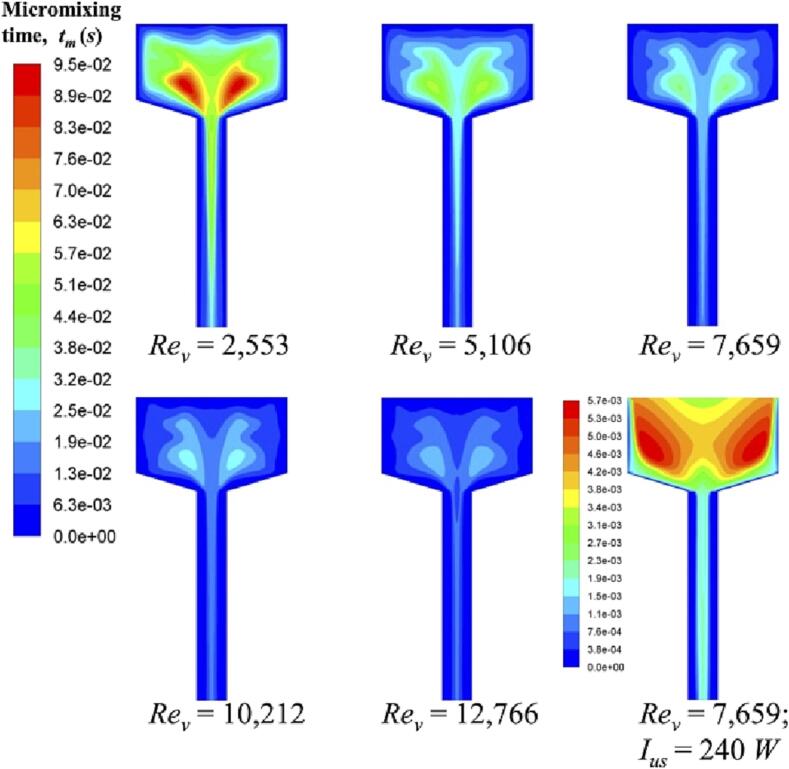
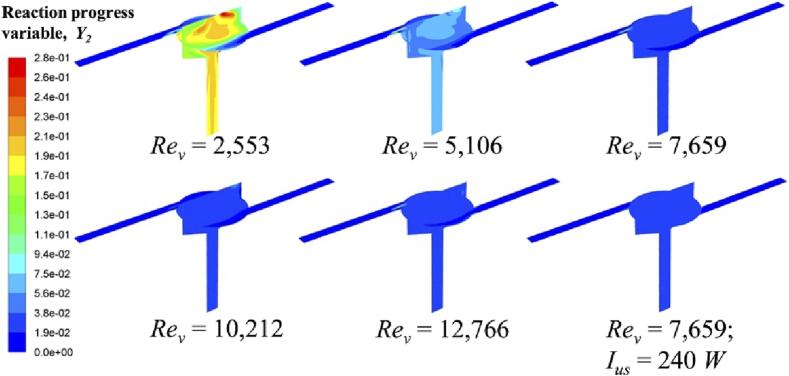
In addition, we can also estimate the degree of chemical reactions from the observation of micromixing time t_m and reaction progress variable Y₂, shown in Fig. 9, Fig. 10, respectively. As there is no mixing occurring in both inlets, we only demonstrate the micromixing time in the reactor chamber. At a low Re_v, micromixing time is longer than or comparable to the characteristic reaction time of slow reaction (i.e., Reaction (2)). Thus, reactants carried by fluid plume cannot be dispersed evenly within a short time interval, and the local excess of acid will lead to the possibility for acid and DMP to react. Different from mixture fraction, reaction progress variable is a chemical reaction related parameter. Y₂ denotes the occurrence of Reaction (2). When Re_v increases, mixing on a microscale is improved. According to the reaction rate constant, under a good micromixing condition, the fast reaction (i.e., Reaction (1)) is favourable to occur with respect to the slow reaction (i.e., Reaction (2)). In fact, the maximum value of Y₂ is sensibly reduced from 0.28 to 0.13 when Re_v increases from 2,553 to 12,766.

Fig. 9.

Micromixing time t_m in the vertical cutting plane of the reactor chamber at different operating conditions.

Fig. 10.

Reaction progress variable Y₂ at different operating conditions.

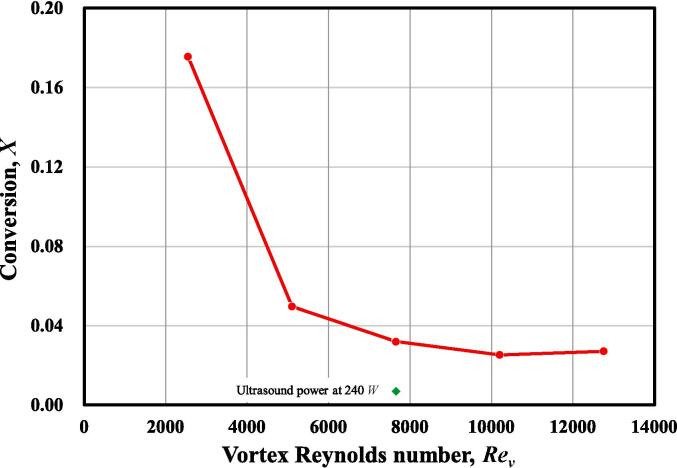
For a quantitative observation, Fig. 11 shows the conversion of DMP at reactor outlet, calculated by Equation (23). Such conversion denotes the consumption of DMP by Reaction (2), which is significantly reduced with the increased Re_v. Furthermore, the ultrasound irradiation results in a rather low DMP conversion. A perfect micromixing condition is achieved with the assistant of ultrasound irradiation, thus Reaction (1) is favourable to occur, and no acid is left to react with DMP.

Fig. 11.

DMP conversion at reactor outlet at different operating conditions.

5.4. Effect of reactant concentration on chemical reaction

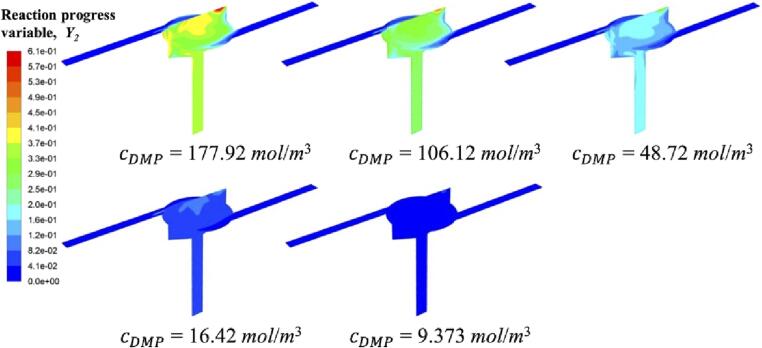
From chemical reaction kinetics, we know that reaction rate is determined by both rate constant and reactant concentration. Therefore, change of reactant concentration can result in the change of characteristic reaction time, as described by Equation (3). In order to investigate the competition between chemical reaction and micromixing, reactant concentration was set at five levels, corresponding to five reaction times. Fig. 12 shows the contour of reaction progress variable for Reaction (2). It is obvious that at a high reactant concentration, more DMP molecules exist in the reaction system, and thus chemical reaction rate is increased. Such large number of molecules are hard to be dispersed quickly at a given flow condition. Their local accumulation will finally lead to the reaction between DMP and acid. In fact, the maximum value of reaction progress variable reaches 0.63, indicating a high reaction degree of Reaction (2). However, this value decreases to 0.14 when DMP concentration is reduced.

Fig. 12.

Reaction progress variable Y₂ contour at different initial DMP concentrations.

Damköhler number is often employed to identify the dominant factor for a given chemical reaction and flow coupling process. It is defined as the ratio of mixing timescale to reaction timescale.

$$\mathit{Da}=\frac{t_m}{t_r}$$ (34)

A small Da number indicates the dominance of the chemical reaction while a large Da number represents a fast mixing. Thus, Da can serve as an indicator for the reactant conversion. In fact, Johnson and Prud’homme [6] suggested a power relationship between conversion and Da. Fig. 13 shows that DMP conversion increases with the increase of Da. A fitting curve with a function of $X=0.57{\mathit{Da}}^{0.76}$ and $R^2=0.9857$ is obtained in our study.

Fig. 13.

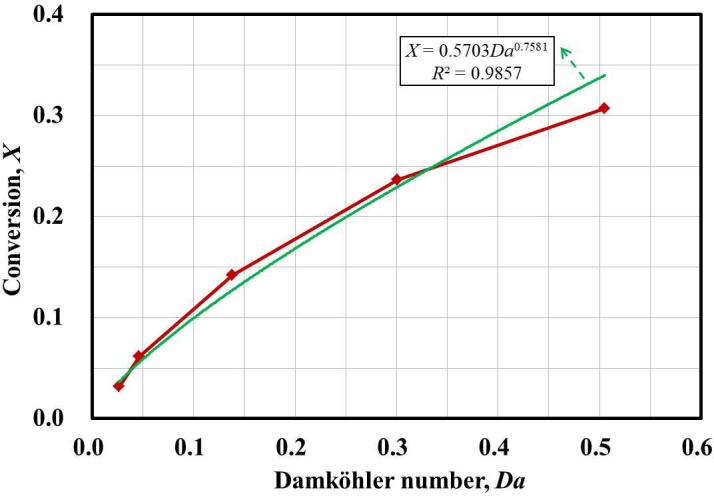
The relationship between DMP conversion X with Damköhler number Da.

5.5. Mixing performance under a laminar flow condition

All of our particle synthesis experiments were conducted under turbulent flow conditions as characterized by using Eqs. (24-1) and (24-2). However, in order to show that the proposed SVFR has its distinctive advantages, we also carried out mixing simulation under a laminar flow condition. The inlet velocity was set at 0.034 m/s, corresponding to a vortex Reynolds number of 321. Fig. 14(a) shows the velocity field in two orthogonal cutting planes. From the magnified picture in the vertical cutting plane of the reactor chamber, it can be clearly seen that two pairs of vortex are generated. The mixture fraction in Fig. 14(b) shows that two flow streams can still be mixed in the reactor chamber as the value of the mean mixture fraction in major regions is close to 0.5. Also, even a relatively good mixing condition can be achieved at the outlet. The poor mixing mainly appears in the middle outflow regions of the chamber. This result indicates that even under such a laminar flow condition, the SVFR can still provide a good mixing environment. This could be due to its swirling feature. Thus, it is suggested that such reactor has potential to be used in particle preparation processes, especially for those flash nanoparticle synthesis and mixing sensitive chemical reactions.

Fig. 14.

(a) Velocity field in two orthogonal cutting planes under a laminar flow condition in the SVFR; (b) Mean mixture fraction contour.

6. Conclusions

Mixing performance evaluation of the turbulent reacting flow in the SVFR has been carried out by CFD simulation. Sub-grid mixing is modelled by a two-environment DQMOM-IEM method. The effects of flow rate, reactant concentration, and ultrasound irradiation were investigated. The main conclusions reached as the outcomes of the present study are summarized as follows:

• Turbulent condition has little effect on macromixing, confirmed by the mean mixture fraction at different vortex Reynolds numbers. The time interval to reach a complete mixing on a macroscale is about 2.5 times of the mean residence time. Micromixing is significantly affected by turbulent eddies. Mixture fraction variance is reduced when increasing vortex Reynolds number. By introducing ultrasound irradiation, mixing on both macroscale and microscale is greatly improved. This could be due to the generation of cavitation bubbles and their subsequent collapse to small micro-bubbles. The effect of acoustic cavitation needs to be verified in future study.

• Turbulent reacting flow was investigated by employing a consecutive competing reaction scheme. The maximum value of the reaction progress variable is reduced from 0.28 to 0.13, and DMP conversion is reduced from 0.18 to 0.03 when Re_v increases from 2,553 to 12,766, especially with the treatment of ultrasound irradiation. This indicates that a local homogenous condition can be created in strong turbulent flows, and there is no excess of reactant left for the slow reaction to occur.

• The competition between chemical reaction and micromixing was investigated by changing reactant concentration. A fitting function between DMP conversion and Damköhler number was obtained in current study, suggesting that compared to chemical reaction, a relatively fast micromixing rate is beneficial for the reduction of by-products.

• Additionally, even in a laminar flow condition, the SVFR can still have a good mixing performance due to its swirling flow feature. Such a reactor has a great potential to be used in particle synthesis process.

CRediT authorship contribution statement

Lu Liu: Data curation, Methodology, Writing – original draft, Funding acquisition. Xiaogang Yang: Conceptualization, Writing – review & editing. Yanqing Guo: Investigation. Bin Li: Data curation. Lian-Ping Wang: Supervision, Writing – review & editing, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: