Multi-Technique Experimental Benchmarking of the Local Magnetic Anisotropy of a Cobalt(II) Single-Ion Magnet

Abstract

A comprehensive understanding of the ligand field and its influence on the degeneracy and population of d-orbitals in a specific coordination environment are crucial for the rational design and enhancement of magnetic anisotropy of single-ion magnets (SIMs). Herein, we report the synthesis and comprehensive magnetic characterization of a highly anisotropic Co^II SIM, [L₂Co](TBA)₂ (L is an N,N′-chelating oxanilido ligand), that is stable under ambient conditions. Dynamic magnetization measurements show that this SIM exhibits a large energy barrier to spin reversal U_eff > 300 K and magnetic blocking up to 3.5 K, and the property is retained in a frozen solution. Low-temperature single-crystal synchrotron X-ray diffraction used to determine the experimental electron density gave access to Co d-orbital populations and a derived U_eff, 261 cm^–1, when the coupling between the d_{x² – y²} and d_xy orbitals is taken into account, in very good agreement with ab initio calculations and superconducting quantum interference device results. Powder and single-crystal polarized neutron diffraction (PNPD, PND) have been used to quantify the magnetic anisotropy via the atomic susceptibility tensor, revealing that the easy axis of magnetization is pointing along the N–Co–N′ bisectors of the N,N′-chelating ligands (3.4° offset), close to the molecular axis, in good agreement with complete active space self-consistent field/N-electron valence perturbation theory to second order ab initio calculations. This study provides benchmarking for two methods, PNPD and single-crystal PND, on the same 3d SIM, and key benchmarking for current theoretical methods to determine local magnetic anisotropy parameters.

Introduction

The rapid growth of the digital ecosystem in recent decades has made the need for powerful processors and high-density data storage systems more apparent, and single-molecule magnets (SMMs) are considered as having great potential in this regard.¹⁻⁶ The last three decades have seen tremendous progress in this field, both on the synthetic side as well as in the development of computational methods and new advanced spectroscopic techniques that provide a direct correlation between experimental findings and theoretical models.⁷⁻¹⁵ In recent years, some excellent high-performance 3d- and 4f-ion-based SMMs have been reported that possess a very high effective energy barrier for magnetization reversal (U_eff) and blocking temperature (T_B).¹⁶⁻²⁵ In the case of SMMs based on 3d metal ions, magnetic bistability originates from an energy barrier (U_eff) that in turn results from the zero-field splitting (ZFS) of the ground spin multiplet. Current synthetic strategies thus target systems that minimize quenching of the angular momentum L, usually via ligand field design that preserves degeneracy of the (d_{x² – y²}, d_xy) and/or (d_xz, d_yz) orbital pairs. Even in the case of largely quenched orbital angular momentum, however, sizable ZFS may result from spin–orbit coupling (SOC). Here, the axial ZFS parameter (D) and the total ground spin-state (S) define the energy barrier for a 3d SMM with U_eff = |D|S² or U_eff = |D|(S² – 0.25) for integer and non-integer spin systems, respectively.

Among the 3d transition metals, Co^II ions are particularly exploited for the development of single-ion magnets (SIMs).²⁶⁻²⁸ The main emphasis is to increase the effect of SOC to enhance ZFS by designing systems with a defined geometry and coordination environment to achieve quasi-degenerate sets of orbitals.²⁶ Prominent examples are two-coordinate nearly linear d₇ complexes such as [Fe^I(C(SiMe₃)₃)₂]⁻ and [(sIPr)Co^IINDmp] which feature a large orbital angular momentum contribution or the linear dialkyl complex Co^II(C(SiMe₂ONaph)₃)₂ exhibiting a limiting magnetic anisotropy for a Co^II ion with a non-Aufbau ground state L = 3.¹⁶⁻¹⁸ However, the highly reactive nature and low stability of these complexes render them impractical for, e.g., anchoring on surfaces and for any device fabrication process. On the other hand, some four, six, and eight coordinate Co^II complexes have been shown to serve as rugged and air-stable SIMs with moderate and high energy barriers;^19,29−41 however, only a few of these Co^II SIMs have been reported to exhibit slow relaxation dynamics in the absence of an applied magnetic field (see Table S5), the first reported one being the highly air-sensitive complex (Ph₄P)₂[Co(SPh)₄].⁴²

While beneficial design guidelines for conceiving SIMs with higher operating temperatures have emerged, further progress is still hampered by the difficulty of experimentally accessing the molecular magnetic susceptibility tensor, and by a limited understanding of the effects of local molecular and lattice vibrations and hyperfine coupling effects, etc., on the dynamics of the relaxation mechanism.^43,44 Common theoretical methods still have their limitations as they mostly exclude various intermolecular interactions and packing effects in the crystalline state to avoid overparameterization, whereas experimental parameters obtained from superconducting quantum interference device (SQUID) magnetometry include the entirety of effects operative in the solid state. To obtain more precise local magnetic anisotropy parameters, sophisticated techniques such as low-temperature high-field high-frequency electron paramagnetic resonance (EPR), X-band EPR, variable field far-infrared (IR) spectroscopy, nuclear magnetic resonance (NMR) paramagnetic shift, and torque magnetometry have been used.^9,11,13 These techniques not only enable direct estimation of the magnitude and sign of D but simultaneously allow for cross-verification of the theoretical models used.

In addition to the above-mentioned spectroscopic techniques, low-temperature single-crystal synchrotron X-ray diffraction has been employed to model an atom-centered experimental electron density (EED).⁷ EED studies have been recently applied in the field of molecular magnetism to obtain the experimental d-orbital population in SMMs.^7,45 The d-orbital populations not only give an idea about the ligand field splitting but also a direct estimation of the ZFS. The strengths of the EED approach have also recently been exploited to quantify the oblateness of the 4f-valence EED in a Dy^III SIM, and thus the magnetic easy axis as well as an estimate of the M_J-composition of the electronic ground state.⁸ In addition to EED studies, polarized neutron diffraction (PND) provides local atomic magnetic susceptibility tensors and the direction of the easy-axis or easy-plane with respect to the local coordination environment. This has been utilized in a few cases to study the correlation of magnetic anisotropy with the local coordination structure.^12,46−50 The major drawback of this method is the requirement of +1 mm³ single crystals suitable for diffraction. However, it has recently been shown by some of us that the atomic susceptibility tensor can also be obtained reliably from powder PND measurements,^46,51,52 substantially advancing this method as it is now pertinent to nearly all materials. These experimentally observable parameters also give confidence and reliability to the results obtained from theoretical calculations that are crucial for making significant progress toward the realization of high-performance SMMs. In particular, the magnetic easy axes derived from interpreting low-temperaturehigh-resolution synchrotron X-ray diffraction in two Dy^III SIMs were found to deviate by only 13.1 and 8.7° compared to those obtained by ab initio calculations.⁸

In this report, we introduce an air-stable dianionic Co^II complex derived from an N,N′-chelating bis(4-chlorophenyl)oxanilido ligand (H₂L),⁵³ [L₂Co](TBA)₂ (1), which exhibits a very high energy barrier for magnetization reversal under zero magnetic field and displays magnetic blocking up to 3.5 K. This new complex has been magnetically characterized both in solid state and frozen solution by direct current (dc) and alternating current (ac) magnetometry. A bouquet of advanced experimental and computational techniques including low-temperature single-crystal synchrotron X-ray diffraction with multipole refinement of the electron density (ED), powder PND, single-crystal PND, and ab initio calculations have then been applied to interrogate the signatures and the origin of the large magnetic anisotropy of 1. This study demonstrates that polarized neutron powder diffraction can be very useful to benchmark the local magnetic anisotropy of a Co^II SIM, opening a way to bypass the requirement of large single crystals.

Results and Discussion

Synthesis, Characterization, and Molecular Structure

The Co^II complex [L₂Co](TBA)₂ (1) and its Zn^II analogue [L₂Zn](TBA)₂ (2) were synthesized by the reaction of anhydrous CoCl₂ or ZnCl₂, respectively, with the dipotassium salt of the ligand (H₂L) under inert dinitrogen atmosphere and subsequent cation exchange with tetrabutylammonium bromide (TBABr; Scheme S1). Large block-shaped crystals were grown by slow diffusion of diethyl ether into MeCN solutions of the products. Complexes 1 and 2 were found to be stable under ambient aerobic conditions in the solid state for months without any significant decomposition.

After initial structure elucidation by standard single-crystal X-ray diffraction (see the SI for details), low-temperature high-resolution single-crystal X-ray synchrotron diffraction data of complex 1 were recorded at 25 K. 1 crystallizes in the triclinic space group P1̅ with the Co^II ion in a distorted tetrahedral {N₄} coordination environment with two dianionic ligands close to an orthogonal arrangement (Figure 1). The charge of the [L₂Co]^2– dianion is balanced by two TBA cations. The Co–N bond lengths lie in the narrow range 1.9766(4)–1.9969(5) Å. The N(1)–Co–N(2) and N(3)–Co–N(4) bite angles of the chelating oxanilido ligands [83.88(2) and 83.63(2)°] are considerably smaller than the other four N–Co–N angles [120.23(2)–129.50(2)°], thus giving rise to an approximate D_2d symmetry or elongated tetrahedron (τ₄ = 0.756, Table S9).⁵⁴ The dihedral angle between the chelating N–Co–N planes is 87.88°, close to an orthogonal situation (Figure 1). The nearest metal ions in the lattice are separated by 11.82 Å. The isomorphous Zn^II complex (2) displays similar structural features as complex 1 (see the SI for details). Selected bond lengths and angles of complexes 1 and 2 are listed in Table S10.

Figure 1.

Molecular structure of the anion of 1 at 25 K (90% probability ellipsoids); hydrogen atoms, disordered parts, and cations have been omitted for clarity. The inset shows the nearly orthogonal arrangement of the Co-NCCN metallacycles.

The Vis–NIR spectrum of solid 1 reveals apparent absorption bands at 529 and 566 nm as well as a broad absorption extending from 800 to 1600 nm, centered around 1120 nm (Figure S8). In an environment of ideal T_d symmetry, Co^II ions with a⁴A ground state feature three spin-allowed transitions to the ⁴T₂, ⁴T₁(⁴F), and ⁴T₁(⁴P) excited states. However, as evident from the crystal structure (Figure 1 inset and Table S9), the {N₄} coordination sphere of the Co^II ion in 1 is tetragonally elongated away from T_d toward D_2d symmetry, giving rise to multiple transitions that lead to broad absorption bands.³² The Vis–NIR spectrum of 1 in MeCN (Figure S9) shows similar bands at 530 and 568 as well as the broad feature centered around 1130 nm, indicating that the molecular structure is retained in solution. Rather low extinction coefficients (ε < 800 M^–1 cm^–1) corroborate that the absorption bands in the visible and NIR region originate from d–d transitions.

Magnetic Properties of 1

The static magnetic properties of complex 1 have been studied using a polycrystalline powdered sample covered with low-viscosity inert oil to prevent any torquing in the magnetic field. At 200 K, the χ_MT value of 3.16 cm³ K mol^–1 is higher than the spin-only value of one isolated Co^II ion (S = 3/2, g = 2.0; χ_MT = 1.875 cm³ K mol^–1), evidencing significant orbital contributions to the magnetic moment (Figure 2). The χ_MT value decreases slowly upon lowering the temperature before decreasing more sharply below 6 K to finally reach a value of 2.32 cm³ K mol^–1 at 2 K; the latter decrease indicates the presence of substantial magnetic anisotropy. The magnetization of 1 at 2.0 K rises steeply with magnetic fields up to 1.5 T before showing a more gradual further increase until 7.0 T, finally reaching 2.31 μ_B without complete saturation (Figure S15). This value is well below the expected M_sat value of 3.0 μ_B for an isolated isotropic S = 3/2 system.

Figure 2.

Temperature dependence of χ_MT for 1 measured under an applied dc field of 0.5 T. The black solid line is the best fit to the spin Hamiltonian in eq 1. Inset: Zero field-cooled (ZFC) and field-cooled (FC) magnetic susceptibility measurements showing clear blocking at ca. 3.5 K for 1. The solid lines are only a guide to the eye.

To gain further insight, the magnetic susceptibility and variable-temperature variable-field magnetization data (Figure S14) were simultaneously simulated with the program julX_2s⁵⁵ using the spin Hamiltonian in eq 1

1

The best fit was obtained for D = −113.0 cm^–1, g_x = g_y = 2.25, and g_z = 3.01. The large negative D indicates the presence of an easy axis of magnetic anisotropy and suggests an energy separation of ca. 226 cm^–1 (325 K, |2D|) between the ground state m_S = ±3/2 Kramers doublet (KD) and the excited state m_S = ±1/2 KD. An ab initio theoretical calculation performed with the complete active space self-consistent field (CASSCF)/N-electron valence perturbation theory to second order (NEVPT2) method and def2-TZVP basis-sets using ORCA software^56,57 and crystallographic atom coordinates give values of D = −118.1 cm^–1 (E/D = 0.002) and g_x = 1.94, g_y = 1.95, g_z = 3.3, in excellent agreement with experiment (only the anion [L₂Co]^2– and the major fraction of its disordered part was included in the calculations; details are provided in the SI). To explore the magnetization relaxation dynamics, zero field-cooled (ZFC) and field-cooled (FC) magnetic susceptibility measurements were carried out at a sweep rate of 2 K/min, revealing a blocking temperature (T_B) of 3.5 K (Figure 2 inset). Temperature-dependent hysteresis measurements carried out at a sweep rate of 30 Oe/s show a butterfly-shaped open hysteresis loop up to 3.5 K, albeit with low coercivity (Figure S16). The sudden collapse of the hysteresis loop near zero-field can be attributed to quantum tunneling of magnetization (QTM), which is a common phenomenon in mononuclear Co^II SMMs.^16,19

Ac susceptibility measurements were performed in the frequency range 0.1–1000 Hz to quantify the dynamics of the slow relaxation of magnetization. Maxima in the frequency-dependent out-of-phase (χ_M″) component were observed from 4.5 to 20.0 K in the absence of any external dc field (Figure 3a). Cole–Cole plots of the ac susceptibilities show two merging semi-circular curves, indicating the existence of two distinct relaxation processes with one dominating at a lower temperature (Figure 3b). The χ_M″ versus χ_M′ curves were fitted with a generalized Debye function, and the relaxation rates (τ^–1) for the fast and slow relaxation processes (FRP and SRP) were extracted (Table S1). Insight into the mechanism of magnetic relaxation was obtained by fitting the relaxation rates (τ^–1) using the following function,

2

where the first term represents magnetic relaxation through QTM, the second and third terms correspond to relaxation via direct and Raman processes, and the last term accounts for relaxation through the Orbach mechanism. The fast relaxation process exhibits temperature-independent relaxation rates at lower temperatures indicating the presence of QTM (Figure S18). Fitting the relaxation rates of the FRP over the entire temperature range with a combination of Raman and QTM processes yields n = 4.73 ± 0.18 and C = 1.36 ± 0.07 × 10^–2 s^–1 K^–n and τ_QTM = 2.04 ± 0.24 × 10^–3 s (Figure S18d). Multiple attempts were made to fit the relaxation rates of the SRP using a combination of different relaxation processes, but a complete fit could not be obtained at lower temperatures. It is interesting to note that the relaxation rates obtained under zero dc field for a frozen dimethylformamide (DMF) solution of complex 1 could be satisfactorily fitted with a combination of Orbach and Raman relaxation pathways (vide infra, Figure 3d). A reasonable fit was obtained by treating the relaxation rates of the SRP with a combination of Orbach and Raman processes [U_eff = 325 K (fixed to |2D|)] with τ₀ = 1.46 ± 0.13 × 10^–10 s, n = 4.54 ± 0.04, and C = 4.92 ± 0.59 × 10^–3 s^–1 K^–n. The inclusion of a QTM process did not influence the quality of the fit. The best-fit parameters obtained are comparable with those reported in the literature for Co^II SIMs.^{16,18,19,35,58,59} Complex 1 displays a bite angle and dihedral angle close to those of highly anisotropic four-coordinate Co^II SIMs reported in the literature (see Table S5). The application of an optimum dc field of 2000 Oe quenches the FRP, and only one relaxation process is evident from the Cole–Cole plots (Figure S19). The relaxation rates obtained under a dc field of 2000 Oe are comparable to the relaxation rates obtained (SRP) under a zero-dc field (Figure S30 and Table S2). As in the previous case, the relaxation rates could be fitted assuming a combination of Orbach and Raman mechanisms, yielding U_eff = 325 K (fixed to |2D|) with τ₀ = 3.62 ± 0.08 × 10^–11 s, n = 4.98 ± 0.05, and C = 1.47 ± 0.21 × 10^–3 s^–1 K^–n (Figure S19d).

Figure 3.

(a) Out-of-phase (χ_M″) component of the frequency-dependent ac susceptibility measured in an oscillating ac field of 3.0 Oe and zero applied dc field for 1. (b) Cole–Cole plots for 1 under zero dc field revealing two relaxation processes. (c) Cole–Cole plots for the frozen DMF solution of 1 under zero dc field revealing a single relaxation process. (d) Plot of the relaxation rate τ^–1 (logarithmic scale) versus T for 1 for the SRP (green circles) and for the frozen DMF solution of 1 under zero applied dc field. The solid blue line corresponds to the best fit including Orbach and Raman mechanisms.

To establish the intrinsic relaxation dynamics of 1 in the absence of intermolecular dipolar interactions, we prepared magnetically diluted samples containing ca. 5% (1′) or 2% (1″) of Co^II complex 1 in the isomorphous diamagnetic matrix of Zn^II complex 2. In contrast to the zero-field ac susceptibility measurements for the crystalline sample of pure 1, interestingly only a single relaxation process was observed for magnetically diluted 1′ throughout the whole temperature range (Figure S20, Table S3), similar to the ac susceptibility signature found for 1 upon application of a 2000 Oe dc field. Best-fit parameters are U_eff = 325 K (fixed to |2D|), τ₀ = 1.37 ± 0.07 × 10^–10 s, n = 4.75 ± 0.04, and C = 2.61 ± 0.29 × 10^–3 s^–1 K^–n (Figure S20d). Overall, the relaxation rates (SRP) extracted for pure 1 and magnetically diluted 1′ are comparable over the entire temperature range (Figure S30 and Table S3). Temperature-dependent hysteresis measurements for 1″ (Figures S24 and S25) show slightly larger hysteresis loops with a minimal increase in coercivity compared to pure 1. In addition, ZFC and FC magnetic susceptibility measurements reveal no major change in the blocking temperature (T_B) of 3.5 K (Figure S26), confirming the molecular origin of the SIM behavior.

Magnetic properties in solution have been reported only for a few SMMs,^{17,20,21,60−64} though it is a prerequisite for many potential SMM applications that they preserve their slow relaxation signatures as isolated molecules outside a crystal lattice. The lack of lattice solvent molecules facilitates a comparison of the magnetic properties of 1 in the solid state/powder and in solution. The high solubility of complex 1 prompted us to investigate a frozen 100 mM DMF solution of 1 (Figure S29), which indeed exhibits relaxation dynamics and hysteretic behavior very similar to the pristine solid sample of 1, though only a single relaxation is observed (Figure 3c). This corroborates that the relaxation dynamics observed for the solid material reflect an intrinsic property of the complex. The relaxation rates are comparable to those observed in the solid state (Figure S30 and Table S4) and could be fitted by a combination of Orbach and Raman relaxation mechanisms over the entire temperature range (Figure 3d); the best-fit parameters are U_eff = 325 K (fixed to |2D|) with τ₀ = 7.38 ± 0.27 × 10^–10 s, n = 4.13 ± 0.03, and C = 1.93 ± 0.20 × 10^–2 s^–1 K^–n.

Experimental Electron Density

We have recently shown how the ED, and more specifically the d-orbital populations derived from it, can be exploited to extract the energy barrier for magnetic relaxation⁷ and facilitate a comparison with the values obtained using magnetization measurements. Therefore, the low-temperature high-resolution single-crystal X-ray synchrotron diffraction data⁶⁵ of complex 1 in the ground electronic state have been used to refine a multipole model (MM) of the EED. A detailed account of the data collection and model refinement is given in the SI. We note that one of the cations is strongly disordered, even at this low temperature (25 K). However, the largest residual density features around the cations (∼1.3 eÅ^–3) are much higher than those found near the [L₂Co]^2– dianion (∼0.6 eÅ^–3), which gives confidence in the extracted d-orbital populations for the central Co ion.

It is well-known that for a metal ion in an elongated tetrahedral coordination sphere with the unique axis along the elongation axis, the d-orbital energies are ordered as follows: d_z² < d_{x² – y²} < d_xy < d_xz, d_yz.⁷ From the MM, d-orbital populations for 1 were extracted as shown in Table 1. This table highlights two conspicuous points. First, when the total population in the d-orbitals is taken into account, all orbitals show significant deviation from integer populations. For d_{x² – y²} and d_xy, this clearly indicates strong mixing of the ground (d_xy¹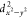) and excited state (d_xy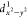) via SOC, while the deviations for the other three orbitals are the results of ligand-to-metal charge transfer. The second point is the asymmetry in the d_xz and d_yz orbital populations, which are expected to be nearly degenerate. Table 1 also provides the d-orbital populations resulting from a theoretical MM (theoretical electron density, TED; for details, see the SI). The overall distribution is similar but does not replicate the variations in d_xz and d_yz, seen in the experimental populations. Note that the absolute values for the d-orbital populations are slightly higher in the EED than the TED due to the higher total d-electron count in the former. This discrepancy is likely caused by experimental uncertainties; omission of the highly disordered countercations in the theoretical calculation and thereby in the TED may also contribute to the discrepancies between the two models.

Table 1. d-Orbital Populations on Co^II in 1 from Various Methods^a.

d-orbital	idealized	MM-experimental	MM-theoretical	ab initio (KD1)	ab initio (KD2)
dxz	1	1.05 (13.6%)	1.14 (15.4%)	1.000	1.000
dyz	1	1.38 (17.9%)	1.14 (15.4%)	1.000	1.000
dxy	1	1.47 (19.1%)	1.33 (17.9%)	1.282	1.089
dx2 – y2	2	1.97 (25.5%)	1.75 (23.6%)	1.715	1.903
dz2	2	1.84 (23.8%)	2.06 (27.7%)	2.000	2.000
total	7	7.71	7.43	6.997	6.992

^aFor ab initio, the d-orbital populations have been obtained by directly taking the weights of (1) and (2) as the face value of d_xy and d_{x² – y²}. This has been done both for KD1 and KD2. For MM, this is the conversion from refined multipole parameters on Co^II. See text for more details.

The procedure that allows us to calculate the energy difference between the two lowest KDs from the (experimental) d-orbital populations in an elongated tetrahedral coordination geometry has been described by Damgaard-Møller et al.⁷Scheme 1 shows the electronic structure of Co^II obtained from the theoretical calculation. We exploit the nearly single Slater-determinant nature of the two lowest-lying and energetically isolated states, (1) and (2), prior to SOC. This paves the way to directly quantify the effect of SOC from the contribution, or weight, of (2) in the ground state, KD1. In addition, clearly given the discernible d-orbital distribution of (1) and (2), this weight is easily retrieved from the experimental d-orbital populations. We note that the experimental temperature of 25 K ensures that we have probed the ED of KD1 exclusively, with no contamination from KD2. The final step, converting the d-orbital distribution to an energy barrier involves an existing linear correlation between the energy barrier and weight of (2), see Scheme 1.

Scheme 1. Scheme Showing the Two Lowest-Lying CASSCF States and the Kramers Doublets Appearing Due to Spin–Orbit Coupling^a.

Dashed lines show which CASSCF states contribute to the Kramers doublets (KDs). The dashed line between (2) and KD1 is colored as a guide for the eye due to the linear relation between this weight and the energy barrier, Δ_K.

While the MM gives access to the d-orbital populations through the refined multipole parameters, both from the theoretical (TED) and the EED, the theoretical calculations lead directly to the weight of (2) in the ground state KD1, which is 0.282 (see the SI for more details). The d-orbital population from the ab initio calculation, the TED, and EED are summarized in Table 1.

We note that the weight of 0.282 of (2) in KD1 found for the theoretical calculation leads to an energy barrier of Δ_K = 236.3 cm^–1, in perfect accordance with the calculated D value of −118.1 cm^–1 (vide supra). This confirms the accuracy of the linear relationship between Δ_K and the weight of (2). The significant coupling between d_{x² – y²} and d_xy orbitals is clearly reflected in the populations, both from the ab initio calculation (1.715 and 1.282, respectively) and experimentally (1.967 and 1.472, respectively). The d_z² orbital is significantly depopulated in the EED relative to the expected 2.0 electrons, while the d_yz, on the other hand, deviates from the expected population of 1e^– with a higher value. All these deviations are signs of the mixing of states.

We use two different approaches for calculating the value of the energy barrier, Δ_K, from the experimental d-orbital population. In the first approach (A), the population in the d_{x² – y²} orbital (1.967) is used to represent the weight (0.967) of the ground state, (1), followed by a remaining contribution (0.033) which is the weight of the first excited state. This leads to the following wave function for the ground state: GS(A) : 0.967|(1), ± 3/2⟩ + 0.033|(2), ± 3/2⟩. With this composition, Δ_K is calculated to be only 30.8 cm^–1. In the second approach (B), we posit that the populations of d_{x² – y²} and d_xy represent the weights of the ground and first excited states, respectively. This leads to the wave function 0.967|(1), ± 3/2⟩ + 0.472|(2), ± 3/2⟩, which after normalization gives GS(B) : 0.672|(1), ± 3/2⟩ + 0.328|(2), ± 3/2⟩. This composition gives a Δ_K value of 261 cm^–1. In the first approach (A), where the wave function is based solely on the population of the d_{x² – y²} orbital, the contribution to the first excited state is very low, which underestimates the energy barrier, Δ_K. The reason is the large total d-electron count, making this approach less reliable. In the second approach (B), where populations of both the d_{x² – y²} and d_xy orbitals are taken into account, the effect of the total d-electron count is removed and leads to a more realistic value compared to magnetic measurements and theoretical calculations. This shows that the coupling of the two orbitals is important to consider when the energy barrier is estimated from the EED.

Polarized Neutron Diffraction

While the EED approach can estimate the energy barrier with good precision, it assumes the existence of a magnetic anisotropy axis as the d-orbitals are defined according to a coordinate system in which the z axis is along the elongation direction and the x,y axes point in-between ligands. Indeed, information on these axes is not directly accessible via the EED. In contrast, the local magnetic anisotropy in paramagnetic compounds can be quantified using PND via the site susceptibility model.⁶⁶ The method has been successfully used to determine the atomic susceptibility tensors in several SMMs.^{12,46,48,51,67−69} Recently, the applicability of the method was extended to powder samples (polarized neutron powder diffraction, PNPD),⁵⁰ alleviating the demanding need for large single-crystals and time-consuming measurements at multiple crystal orientations. However, this remarkable progress has so far only been exploited on a single occasion to study the atomic susceptibility tensor,⁵¹ without independent verification from the single-crystal method. Importantly, the present work thus includes benchmarking the two methods, PNPD and single crystal PND, on the same compound. PNPD data of 1 were collected at the D20 diffractometer of ILL^200,70 using neutrons of a 2.41 Å wavelength at 2 K and an applied field of 1 T. Single-crystal PND data of 1 were collected at the HB-3A/DEMAND⁷¹ diffractometer of Oak Ridge National Laboratory (ORNL), high flux isotope reactor (HFIR) using neutrons of a 1.5424 Å wavelength at 4 K and an applied field of 0.48 T. Susceptibility tensors were refined using the Python-package Cryspy (0.5.9)/Cryspy_Editor (1.6.0).⁵⁰ The synchrotron X-ray structure discussed earlier was used to simulate the nuclear structure factors. Describing the tensor required the refinement of six independent susceptibility parameters due to the site symmetry of the Co^II ion (for details see the SI). In Figure 4, the refined susceptibility tensor for the Co site in 1 is visualized as an ellipsoid overlaid on the molecular structure, in a manner similar to depicting atomic displacement parameters.

Figure 4.

Magnetic susceptibility tensor for 1 derived from (a) PNPD and (b) joint PND/PNPD refinement. Negative eigenvalues are shown as positive. Ellipsoid is scaled arbitrarily, with the relative magnitudes corresponding to the relative eigenvalues in μ_BT^–1. Counterions and hydrogen atoms are omitted for clarity. Thermal ellipsoids are drawn with a 50% probability.

For the PNPD model, the 2θ range 7.6–32.1° was used. Background, shape parameters, asymmetry parameters, scale factor, and beam offset were refined using the sum and difference patterns. These parameters were then fixed, and the susceptibility parameters were modeled using only the difference pattern. The obtained susceptibility tensor leads to a prolate surface and thus a clearly discernible easy axis anisotropy of 1. The eigenvector corresponding to the most magnetically susceptible direction nearly bisects the bridging C–C bond of the amides of the oxanilido ligand, thus lying close to the molecular axis (3.8° offset to the N1–N2 midpoint). The eigenvalues of the susceptibility tensor [3.35(17), −0.12(15), 0.56(18) μ_BT^–1] indicate a strong axial magnetic anisotropy of 1. These results agree with the magnetization data and ab initio calculations, which also suggest easy-axis anisotropy. We find a close agreement (7.3° deviation) between the easy-axis directions from CASSCF calculations and PNPD, Figure 5. As the PNPD measurements were performed in the linear region of the magnetization curve, the powder-averaged magnetization can be estimated using the expression 1/3(χ_x + χ_y + χ_z)H, resulting in a value of 1.3(1) μ_B. This value is somewhat lower than the expected value of ∼1.65 μ_B at 2 K and 1 T obtained from the bulk magnetization curve shown in Figure S15. It should be noted that the crystal structure coordinates used in the refining of the PND data were based on an X-ray synchrotron diffraction experiment, which may explain the discrepancy of the estimated powder averaged magnetization using local anisotropy parameters with the expected value. Indeed, it is well known that neutrons are more sensitive to the hydrogen position than X-rays. Thus, since the polarized signal is proportional to the product of nuclear and magnetic structure factors, uncertainty in the estimation of the former can cause a systematic error in the calculation of the atomic susceptibility tensor.

Figure 5.

Visualization of the magnetic easy axis of 1 from CASSCF calculations (blue), PNPD (red), and joint PND/PNPD refinement (green). Counterions and hydrogen atoms are omitted for clarity.

A refinement model using only single-crystal PND data was not possible, as we could only extract flipping ratios from one magnetic field direction for the single-crystal PND experiment. This was because the crystal broke during the multiple heating and cooling cycles. However, it has been possible to refine a joint PND/PNPD model using the 38 extracted flipping ratios together with the PNPD data. From this, a similar susceptibility ellipsoid was found, Figure 4 (bottom), as well as a similar g_z direction, Figure 5 (10.1° offset to PNPD easy axis). The found discrepancies between easy axis directions from ab initio calculations and PND/PNPD measurements are of similar magnitudes to those found by other studies.^12,51

Conclusions

In summary, we have employed a set of sophisticated techniques, including static and dynamic magnetometry, EED based on high-quality, low-temperature synchrotron diffraction data, powder and single-crystal PND, and ab initio electronic structure analysis to decipher the origin and quantify the large magnetic anisotropy of a new Co^II based SIM. This Co^II SIM with two chelating diamido ligands and strongly distorted local tetrahedral geometry around Co^II features a large energy separation of over 300 K between the ground and excited-state KDs and shows magnetic hysteresis up to 3.5 K. The slow relaxation dynamics are preserved upon magnetic dilution and in frozen solution, indicating that it is an intrinsic molecular property of 1. From the EED, we were able to extract d-orbital populations for the Co^II ion, which show a clear coupling between the d_{x² – y²} and d_xy orbitals. Calculations of the energy barrier between the two lowest Kramers’ doublets were performed based on results from the EED. When this coupling is taken into account, the resulting energy barrier is 261 cm^–1, which correlates well with both magnetic measurements and theoretical calculations. Results from PNPD and PND allow experimental determination of the magnetic susceptibility tensor, showing clear easy axis anisotropy for 1; the direction of the easy axis being in good agreement with the ab initio results. The present fundamental study demonstrates the unique strengths of combining a complete magnetic characterization with advanced diffraction methods, in particular single-crystal synchrotron X-ray diffraction and PNPD, in the assessment of SMMs.

Experimental and Computational Methods

Materials

All solvents employed in the syntheses were dried and distilled before use according to standard procedures. Syntheses of the complexes were carried out under a dry and inert nitrogen atmosphere. Unless otherwise stated, all chemicals were purchased from commercial sources and used as received. The proligand H₂L, N,N′-bis(4-chlorophenyl)oxanilide, was synthesized following a previously reported procedure.⁵³ Complexes 1 and 2 were found to be stable under ambient atmospheric conditions.

Instruments for Spectroscopic and Analytical Characterization

¹H NMR and ¹³C NMR spectra were recorded on Bruker Avance 400 spectrometers at room temperature. Chemical shifts are reported in parts per million (ppm) relative to residual proton and carbon signals of the solvent. IR spectra were recorded on a Cary 630 FTIR spectrometer equipped with Dial Path Technology and analyzed by FTIR MicroLab software. Vis–NIR (visible–near-IR) spectra of solutions and solid material were recorded with a Varian Cary 5000 spectrophotometer. ESI mass spectra were collected using a Bruker HCT ultra spectrometer. Elemental analyses were performed by the analytical laboratory of the Institute of Inorganic Chemistry at the University of Göttingen using an Elementar Vario EL III instrument.

Synthesis Protocols

[L₂Co](TBA)₂ (1)

H₂L (309 mg, 1.0 mmol) was dissolved in dry THF (20.0 mL) and KH (80.0 mg, 2.0 mmol) was added, leading to the evolution of dihydrogen. The solution was stirred overnight and solid anhydrous CoCl₂ (65 mg, 0.5 mmol) was then added. The reaction mixture was stirred at room temperature for 24 h. Tetrabutylammonium bromide (354 mg, 1.1 mmol) was added and stirring continued for a further 24 h. The red solution was allowed to settle and then filtered. The volume of the filtrate was reduced under vacuum to around 4.0 mL. Diffusion of diethyl ether into the solution led to the formation of reddish pink blocked-shaped crystals (Figure S1) within a few days. Yield: (475 mg, 82% based on Co). Elemental analysis calculated for C₆₀H₈₈Cl₄CoN₆O₄ C 62.23; H 7.66; N 7.26. Found C 61.99; H 7.72; N 7.28. FTIR (cm^–1) 2961 (w), 2934 (w), 2874 (w), 1646 (w), 1604 (s), 1582 (s), 1561 (m), 1480 (s), 1458 (m), 1403 (w), 1373 (m), 1302 (s), 1291 (s), 1265 (s), 1211 (w), 1164 (w),1101 (w), 1087 (m), 1031 (w), 1008 (w), 974 (w), 940(w), 919 (m), 881 (w), 857 (w), 831 (s), 801 (m), 738 (w), 706 (w), 677 (w), 589 (w), 522 (w), 502 (m), 471 (m). ESI-MS (negative ion mode, CH₃CN): m/z 915.1 [M-TBA]⁻, 336.3 [M-2TBA]^2–. Vis–NIR (in CH₃CN, λ_max in nm [ε in M^–1 cm^–1]) 530 [318], 568 [797], 1130 [101]. Vis–NIR (solid state, λ_max in nm) 529, 566, 1120.

[L₂Zn](TBA)₂ (1)

H₂L (309 mg, 1.0 mmol) was dissolved in dry THF (20.0 mL), and KH (80.0 mg, 2.0 mmol) was added, leading to the evolution of dihydrogen. The solution was stirred overnight and solid anhydrous ZnCl₂ (68 mg, 0.5 mmol) was then added. The reaction mixture was stirred at room temperature for 24 h. Tetrabutylammonium bromide (354 mg, 1.1 mmol) was added and stirring continued for 24 h. The colorless solution was allowed to settle and then filtered. The volume of the reaction mixture was reduced under vacuum to around 4.0 mL. Diffusion of diethyl ether into the solution led to the formation of colorless blocked-shaped crystals within a few days. Yield: (490 mg, 84% based on Zn). Elemental analysis calculated for C₆₀H₈₈Cl₄N₆O₄Zn C 61.88; H 7.62; N 7.22. Found C 62.21; H 7.71; N 7.16. ¹H NMR (400 MHz, CD₃CN) δ 7.75–7.67 (m, 1H), 7.09–7.01 (m, 1H), 3.13–3.04 (m, 2H), 1.58 (p, J = 7.8 Hz, 2H), 1.32 (h, J = 7.4 Hz, 2H), 0.94 (t, J = 7.3 Hz, 3H) ppm. ¹³C NMR (100 MHz, CD₃CN) δ 167.6, 149.0, 128.8, 125.4, 125.2, 59.3, 24.3, 20.3, 13.8 ppm. FTIR (cm^–1) 2962 (w), 2935 (w), 2874 (w), 1650 (w), 1603 (s), 1582 (s), 1560 (m), 1481 (s), 1460 (m), 1404 (w), 1374 (m), 1307 (s), 1293 (s), 1265 (s), 1212 (w), 1168 (w),1102 (w), 1087 (m), 1031 (w), 1008 (w), 972 (w), 939 (w), 921 (m), 881 (w), 858 (w), 831 (s), 802 (m), 737 (w), 706 (w), 676 (w), 627 (w), 590 (w), 520 (w), 502 (m), 481 (w), 468 (m). ESI-MS (negative ion mode, in CH₃CN): m/z 922.0 [M-TBA]⁻, 338.8 [M-2TBA]^2–.

Preparation of the Magnetically Diluted Samples [L₂Co_0.05Zn_0.95](TBA)₂ (1′) and [L₂Co_0.02Zn_0.98](TBA)₂ (1″)

Appropriately weighed amounts of complexes 1 and 2 (by molar ratio) were dissolved in a minimum amount of MeCN, and the solution was stirred for 1 h. Diethyl ether was allowed to diffuse into the solution, leading to the near quantitative isolation of bright light pink crystals within a week.

Magnetic Measurements

Magnetic measurements were carried out with a Quantum-Design MPMS3 SQUID magnetometer equipped with a 7 T magnet. dc magnetic susceptibility measurements were performed under an applied dc field of 0.5 T with powdered polycrystalline samples in the range from 200.0 to 2.0 K. The powdered samples were packed in a polycarbonate or gelatine capsule and covered with low-viscosity perfluoropolyether-based inert oil Fomblin Y45 in a non-magnetic sample holder. Each raw data for the measured magnetic moment was corrected for the diamagnetic contribution of the capsules (including the inert oil) according to M_dia(capsule) = χ_g·m·H, with an experimentally obtained gram susceptibility of the capsules including the inert oil. The diamagnetic contribution of the compounds was corrected using Pascal’s constants. Magnetic measurements of frozen solutions were carried out by dissolving the sample in DMF in an NMR tube and sealing the tube under a vacuum to exclude dioxygen. Experimental data were modeled using a fitting procedure to the spin Hamiltonian:

Full-matrix diagonalization of the spin Hamiltonian for ZFS and Zeeman splitting was performed with the julX_2s program.⁵⁵ ac susceptibility measurements were carried out in an oscillating ac field of 3.0 Oe and frequencies ranging from 0.1 to 1000 Hz.

Single-Crystal Structure Determination

In-house X-ray data were collected on an STOE IPDS II diffractometer (graphite monochromated Mo-Kα radiation, λ = 0.71073 Å) by use of ω scans at −140 °C. To obtain high-quality data necessary for modeling the ED of 1, single crystal X-ray diffraction was measured at BL02B1 at the SPring-8 synchrotron. ω scans were performed from 0 to 180° in steps of 0.1°, with fixed χ assuming values of 0, 20, and 40°, respectively, and 2θ at 0 and −20°, resulting in 6 scans in total with 1800 frames in each. The scan time was 0.44 s per frame and the diffracted data was collected with a PILATUS3 X 1M CdTe detector. The crystal was cooled to 25 K and a wavelength of 0.24830 Å was employed. Further experimental details as well as details of the structure solutions are provided in the Supporting Information. CCDC 2212249 (1, STOE IPDS), 2212250 (2, STOE IPDS), and 2212086 (1, SPring-8 synchrotron) contain the supplementary crystallographic data for this paper. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif, by emailing data_request@ccdc.cam.ac.uk, or by contacting The Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033.

Electron Density Modeling

The ED was modeled based on the synchrotron data with the program XD2016⁷² using the Hansen–Coppens MM formalism. The z axis for Co was chosen to point in-between N(1) and N(2), and the x-axis in-between N(1) and N(3). Hydrogen atoms have been positioned using tabulated bond distances and described with isotropic ADPs. Hexadecapolar angular functions were used to describe the ED for all non-H atoms, while selected quadropoles were used for hydrogen atoms. Core expansion/contraction parameters were included based on the results of multipole modeling from theoretical structure factors.

Polarized Neutron Diffraction

PNPD data were collected at the high-flux powder diffractometer D20 of the Institut Laue-Langevin (ILL)⁷⁰ on a powdered sample of 1. Data were measured at 2 K and an applied magnetic field of 1 T, with neutrons of a 2.41 Å wavelength, using the angular range 2θ = 7.6–32.1°. The flipping difference pattern was used to model the atomic site susceptibility tensor for Co using the Python-package Cryspy (v. 0.5.9) through Cryspy_Editor (v. 1.6.0).⁵⁰ Single-crystal PND data were measured at the ORNL HFIR four-circle single-crystal neutron diffractometer HB-3A/DEMAND.⁷¹ Data were measured with a 1.5424 Å wavelength at 4 K and a field of 0.48 T. Only one crystal orientation provided data of sufficient quality, and a joint PND/PNPD model was refined.

Theoretical Calculations

Ab initio calculations were performed in ORCA software,^56,57,73 using the atom positions obtained from the EED. Prior to the calculation, the two counterions were removed from the structure, so the calculation is only performed on the [L₂Co]^2– dianion. Furthermore, the disorder within the anion was removed, that is, one of the peripheral 4-Cl-phenyl groups (see Figure S33a) was removed and the occupancy of the other group was set to 1. The CASSCF method was used in the calculation with the seven d-electrons in the Co^II ion in five active orbitals, together with the NEVPT2 method. In the calculations, all 10 S = 3/2 states and 40 S = 1/2 states were included, and the def2-TZVP basis set was used. The alignment of the molecule was performed according to the pseudo-D_2d symmetry with the z axis for Co between the N(1) and N(2) atoms, and the x axis for Co between the N(1) and N(3) atoms.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.2c00575.

• Further spectroscopic and analytical data, crystallographic information, magnetic characterization, and details of theoretical calculations (PDF)

• ORCA output file from theoretical calculation (TXT)

Author Contributions

S.K.G. carried out the synthesis, spectroscopic characterization and magnetic measurements and their analyses. H.H.N. carried out the synchrotron X-ray data collection, theoretical calculation and ED modeling. A.M.T. collected and analyzed PNPD and PND data, with contributions from E.A.K. E.F. and H.B.C. helped collect PND data. T.C.H., E.L.B., and A.G. helped collect PNPD data. I.K. assisted with the PNPD analysis. S.D. and S.D. helped with the in-house single-crystal X-ray data and magnetic data collection and analysis. J.O. and F.M. conceived the study and supervised the experiments and analyses. The manuscript was written through the contributions of all authors. All authors have approved the final version of the manuscript. S.K.G., H.H.N., and A.M.T. contributed equally. CRediT: Sandeep K. Gupta data curation, formal analysis, investigation, visualization, writing-original draft; Hannah Hedegaard Nielsen data curation, formal analysis, investigation, visualization, writing-original draft; Andreas Munch Thiel data curation, formal analysis, investigation, visualization, writing-original daft; Emil Andreasen Klahn data curation, formal analysis; Erxi Feng data curation, investigation; Huibo B. Cao data curation, investigation; Thomas Christian Hansen data curation, investigation; Eddy Lelièvre-Berna data curation, investigation; Arsen Gukasov data curation, investigation; Iurii Kibalin data curation, formal analysis, investigation, validation, writing-review & editing; Sebastian Dechert data curation, investigation; Serhiy Demeshko data curation, formal analysis, investigation; Jacob Overgaard conceptualization, funding acquisition, supervision, writing-original draft; Franc Meyer conceptualization, funding acquisition, resources, supervision, writing-review & editing.

The authors declare no competing financial interest.