Statistical methods for design and testing of 3D-printed polymers

Abstract

Different statistical methods are used in various fields to qualify processes and products, especially in emerging technologies like Additive Manufacturing (AM) or 3D printing. Since several statistical methods are being employed to ensure quality production of the 3D-printed parts, an overview of these methods used in 3D printing for different purposes is presented in this paper. The advantages and challenges, to understanding the importance it brings for design and testing optimization of 3D-printed parts are also discussed. The application of different metrology methods is also summarized to guide future researchers in producing dimensionally-accurate and good-quality 3D-printed parts. This review paper shows that the Taguchi Methodology is the commonly-used statistical tool in optimizing mechanical properties of the 3D-printed parts, followed by Weibull Analysis and Factorial Design. In addition, key areas such as Artificial Intelligence (AI), Machine Learning (ML), Finite Element Analysis (FEA), and Simulation require more research for improved 3D-printed part qualities for specific purposes. Future perspectives are also discussed, including other methods that can help further improve the overall quality of the 3D printing process from designing to manufacturing.

Graphical abstract

Introduction

Statistics as a branch of science is mainly concerned with collecting, organizing, summarizing, and analyzing data and generating conclusions, making the data set more understandable. It also aids in making intelligent judgments and informed decisions in any uncertainty and variation.^[1] With this, the widespread use of different statistical methods has been practiced in various fields such as medicine,^[2,3] aerospace,^[4] automotive.^[5] Statistical methods are also essential in planning, designing, processing, testing, and assessing projects in the abovementioned fields, especially for research and development purposes. Emerging technologies also rely upon the results of the applied statistical methods.^[6] Additive Manufacturing or 3D printing is one of the production technology that needs to employ various statistical methods to ensure the production of quality products.^[2–12] This technology creates a 3D-printed object from a digital 3D model by adding materials layer-by-layer.^[8–12] Over the years, different statistical methods such as Design of Experiment (DOE), Taguchi methodology,^[7,11,13] and Weibull^[14–21] were also applied in numerous studies concerning the designing, pre-processing, post-processing, and testing of the 3D-printed polymer parts.

Because many research studies use statistical methods and analyses in 3D printing optimization, choosing which statistical tool to utilize for a certain application has become challenging. This study, therefore, aims to collect, summarize and synthesize relevant literature regarding the use of different statistical methods in assessing the quality of 3D-printed polymer parts. Moreover, this study also aims to identify which statistical methods are being employed for the qualification of 3D-printed parts, the advantages, and disadvantages of using different statistical methods and to understand the importance of using other statistical methods in designing and testing 3D-printed parts. This paper only briefly discusses simple statistical treatments and those rarely found in the literature. This study also explores the possibility of applying advanced statistical methods and simulation models in data analysis to design and test 3D-printed polymer parts.

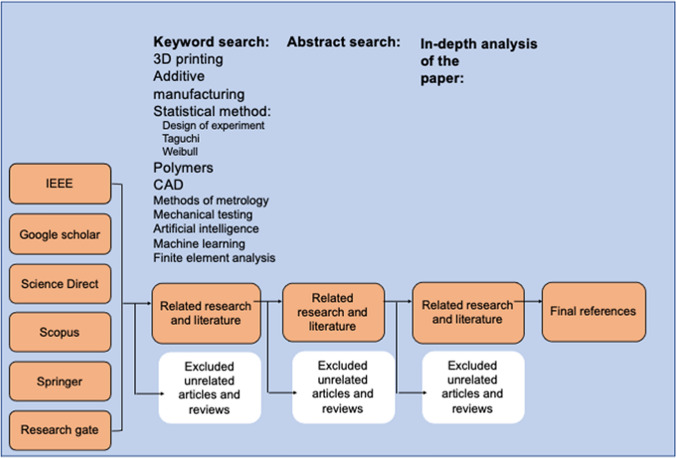
The gathering of relevant information related to the statistical methods used in 3D printing polymer materials was done. A keyword search was used in scientific journal databases and other online sources. The following keywords were used for the examination as [3D printing OR AM AND statistical methods (DOE, Taguchi Methodology, Weibull) AND polymers], [3D printing OR AM AND statistical methods AND CAD], [3D printing OR AM AND statistical methods AND methods of metrology], [3D printing OR AM AND statistical methods AND mechanical testing AND polymer], [3D printing OR AM AND Artificial Intelligence AND Machine Learning], and [3D printing OR AM AND Finite Element Analysis]. Other more specific keywords were used. Initial scanning of obtained references was performed. Only relevant papers related to the statistical methods, tools, and techniques that can help design and test the 3D-printed polymer materials were included, and irrelevant documents were excluded. Lastly, selected papers were analyzed and synthesized. A detailed process flowchart of the literature search is shown in Fig. 1 below.

Figure 1.

Process flow of the literature search.

Methods of statistical analysis

DOE (Factorial Design and Taguchi Methodology)

DOE or Factorial Design was introduced by R.A. Fisher in the 1920s as a powerful statistical technique to study the effect of multiple variables simultaneously. This includes different factorial levels, such as three-level, four-level, full factorial, and fractional factorial. Early applications include finding out the amount of sunshine, fertilizer, water, necessary to harvest the best crop. Eventually, further development for this statistical technique has taken place in the academic setting, but it also aided the advancement of various applications in production. Genichi Taguchi, a Japanese researcher, further studied the DOE techniques. He made this experimental technique more user-friendly, and its application improved the quality of a manufactured product. This standardized technique or method, known as the Taguchi Method or Taguchi Approach, was introduced in the early 1980s in the USA. Engineers and researchers consider this the most effective quality building tool in all manufacturing activities. In addition, this method is economical as it significantly minimizes the time to conduct experimental investigations. DOE using the Taguchi approach is highly effective for optimizing product and process designs and studying the effects of multiple factors based on performance. The influence of the individual elements on each performance can also be checked using this technique.^[1,22]

Meticulous preparation, thorough experiment layout, and skilled interpretation of the results are necessary for applying the DOE. Genichi Taguchi's years of investigation and testing have led to this conclusion and developed the standardized methodologies for each of the DOE application steps outlined below. As a result, DOE using Taguchi Approach has become a far more appealing tool for engineers and scientists.^[22]

• Experiment planning and problem formulation depend on modern work practices that emphasize teamwork. Projects are more successful when everyone agrees on the experimental aims and parameters.

• The number of samples to be evaluated and the experiment guidelines are defined. The experiment layout's size is standardized for a given number of factors and levels, emphasizing the cost and magnitude of the tests. To limit variation, uncontrollable factors are explicitly treated.

• Data Analysis uses standardized steps for analysis and a standard procedure for determining the optimum, and significance test and pooling guidelines are defined.

• The term "error" is defined clearly in the interpretation of results. There is a discrete indicator regarding confirmation of the results and the ability to put a monetary value on improvements.

• The overall advantage of using Taguchi in DOE aims to increase quality, which can be defined as performance consistency and reduction of variation in results. This can be accomplished by bringing the average performance closer to the target and minimizing variations around the mark. The traditional DOE does not precisely address quality. The Taguchi experiment design technique is primarily motivated by reducing variation. As a result, this technique focuses on achieving the desired quality targets.

The standardized technique of DOE using the Taguchi Approach can be applied to various applications such as analytical simulation in the early stages of design, development testing, process development, manufacturing, and problem-solving in all areas of manufacturing and production.^[1,22–30]

Additive Manufacturing (AM), also known as 3D printing, is a technology that builds a 3D-printed object layer-by-layer from a 3D-printed model. Nowadays, different types of 3D printing technologies are available in the market, creating a wide range of opportunities to make customizable and flexible production of various 3D-printed objects.^[4,5] One factor that needs to be considered is the quality in achieving the desired property of each 3D-printed object. To ensure this, other research groups have carefully studied different variables in printing parameters. DOE and Taguchi Methods are two of the various statistical techniques used to identify the optimum 3D printing parameters in different types of 3D printing technologies following the desired property for 3D-printed products.

In a study by Khalid et al., they used Taguchi's DOE to investigate the printing parameters of AM technology for sustainability to minimize process energy and material consumption. Using the Fused Deposition Modelling (FDM) technology, they also identified the printing parameters as printing layer height, the number of shells, material infilling percentage, infilling type, and building orientation.^[31]

Furthermore, Durão et al. investigated and optimized the AM technology's material consumption, manufacturing time, and dimensional accuracy using DOE. They identified that the print speed and the number of contours were the critical factors for a good quality 3D-printed part^[32] (Fig. 2). Using Taguchi L25 orthogonal array, Fotovvati et al. analyzed the significance and contribution of the processing parameters for a Laser-Based Powder Bed Fusion (L-PBF) process. A fractional factorial DOE was also used for the response surface method (RSM), optimizing the L-PBF processing parameters.^[33]

Figure 2.

Response surface plots of each two-parameter combination for different properties using Factorial Design.^[32]

Fused Filament Fabrication (FFF) is a type of AM technology widely used to produce complex geometry parts. The Taguchi methodology was used to design the experiment by Shakeri et al. to investigate the effect of the different printing parameters, such as chamber temperature, printing temperature, layer thickness, and print speed. They used ANOVA and Taguchi's S/N ratio to identify the optimal printing parameters to improve the geometrical accuracy and mechanical behavior of an FFF 3D-printed part.^[34] The Taguchi S/N ratio was employed by Shakeri et al. to optimize the FFF process parameters to improve shape deviations, cylindricity, and circularity of 3D-printed items. Their study concluded that the optimal FFF process parameters for the shape deviations should have a hexagonal infill pattern, 5 mm thickness, a wall layer of 2, and a layer height of 1.125 mm^[35] (Fig. 3).

Figure 3.

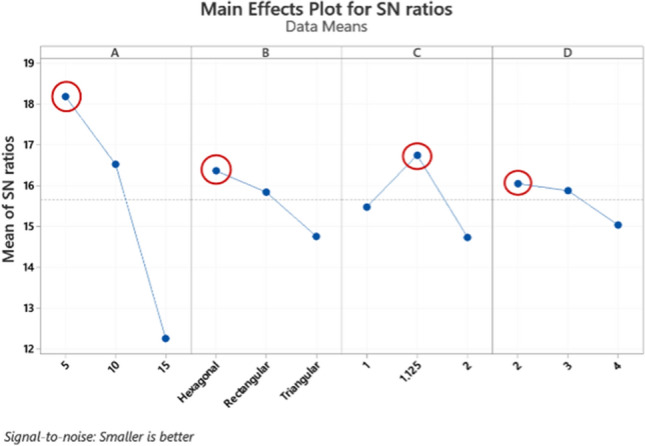
Signal-to-noise ratio of cylindricity of polyamide 6 3D-printed parts.^[35]

Weibull

The Weibull distribution is a continuous probability distribution named after Waloddi Weibull. It is generally used to model failure times, analyze life data, and assess product reliability.^[21] It is also being used to describe the variability in the strength of materials. Moreover, it is commonly used to measure ceramic materials' probability of failure or mechanical reliability. The Weibull modulus could indicate a material's stability and structural homogeneity.^[19,35] A higher value of the Weibull modulus indicates a narrower strength distribution and may be concluded to be a more reliable material.^[36]

The probability of failure (reliability) occurring from critical flaws in ceramic materials may be quantified by the Weibull probability function given as a cumulative distribution equation^[36]:

$$P_f\left(\sigma \right)=1-exp\left[\frac{-{\left(\sigma -{\sigma }_{\text{t}}\right)}^m}{{\sigma }_0}\right]$$

where P_f(σ)—probability of failure at stress (σ), σ_o—Weibull scale parameter—the stress value where the probability of failure is at a certain percentage, σ_t—threshold stress—no failure occurs in the material below this value, maybe zero for ceramics, m—Weibull modulus.

Weibull distribution is widely used to analyze the mechanical properties of conventionally manufactured parts. For example, Da Costa et al. investigated the dependence of the tensile strength of culm-stripped bamboo fibers on their diameter using Weibull analysis. Results showed that the strength is inversely correlated with the fiber diameter, i.e., the fibers with smaller diameters have more significant tensile strengths.^[17] Schilling et al. evaluated the mechanical properties of soy protein that were molded by compression with different concentrations of glycerin plasticizer. Based on Weibull statistics analysis, the samples demonstrated stiff and brittle behavior and good tensile strength reliability.^[37] Boyce et al. tested over 1000 identical tensile bars. Results showed substantial variability in mechanical properties within a single build and more significant variability between builds. They noted that these findings on variability might not be possible by testing only a few samples, and a probabilistic (or worst-case threshold) may be needed to prevent unexpected failures during the service of parts.^[38]

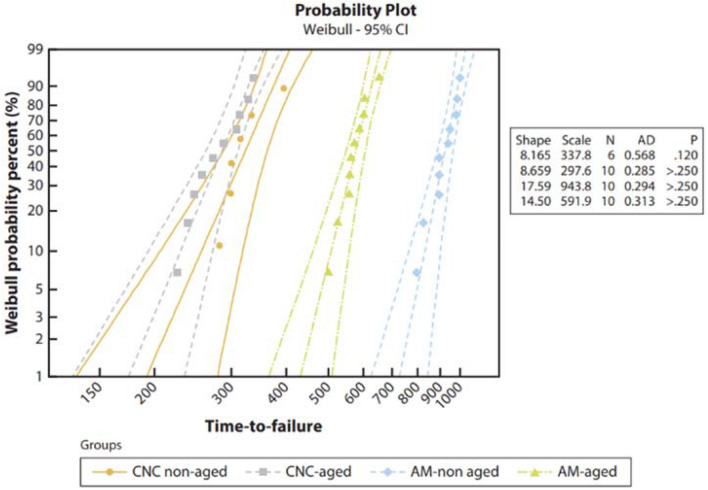
Juhar et al., via the Weibull distribution, studied the plastic deformation of fibrous polymers (polypropylene fibers, pan-based carbon fibers, and Kevlar fibers). They observed that the strength, Young’s modulus, and strain at break of the tested fibers showed dependence on the size effect. They further concluded that the Weibull model is appropriate for statistically representing fibrous polymers.^[14] (Fig. 4) Additionally, Naito investigated the tensile behavior, fracture behavior, and Weibull Modulus of High-Performance Polymer Fibers, including Polyethylene, Polyacrylate, and Polylactic acid (PLA). He found that the Weibull modulus decreases with increasing tensile strength, tensile modulus, and inverse of the failure strain.^[16] Ouamomar et al. investigated the mechanical properties of industrial polymers via Weibull statistical analysis to extract Weibull elements and define the reliability theory. Their insights regarding Weibull parameters, such as the Weibull modulus, may determine the material's homogeneity/heterogeneity of defect distribution. Moreover, the Weibull distribution defines the survival probability and damage and thus may be used for timely predictive maintenance of parts.^[18]

Figure 4.

Weibull moduli of CNC and AM Groups.^[14]

In 3D printing, the Weibull analysis is also employed in different engineering materials. Revilla-León et al. compared the flexural strength and Weibull characteristics of SLA 3D-printed and milled zirconia using 3-point flexural tests. They calculated the two-parameter Weibull distribution values, including the Weibull modulus, scale, and shape. The manufacturing and mastication simulation (aging procedures) significantly affected the measured flexural strength and the interaction between these two procedures. Moreover, the mastication simulation significantly reduces the flexural strength obtained for 3D printing and subtractive manufacturing. Lastly, the Weibull modulus showed considerably higher values for the milled specimens than those produced via 3D printing.^[15] Byun et al. studied the mechanical properties of Silicon Carbide (SiC) created using binder jetting. Samples with two or three orientations were subjected to mechanical loading and obtained the equiaxial flexural failure strength and elastic constants. Similar flexural failure strength results were observed from Weibull distributions regardless of different orientations.^[39] Feilden et al. explored the use of Robocasting in the production of structural parts. The authors formulated hydrogel-based inks for the robocasting of ceramic materials. Specifically, they investigated 3D-printed Aluminum Oxide (Al₂O₃) and Silicon Carbide (SiC) parts. Robocasting is a process where “green” objects are produced by extruding a paste (ink) through a nozzle/extruder controlled by the 3D printing software based on the CAD model, and the parts are built layer-by-layer, similar to FFF. But unlike FFF, where the fusion of layers results from solidification, the extruded material in robocasting impinges on the preceding layer and merges with it because of surface tension. They observed anisotropic values in strength and Weibull modulus due to defects from the printing process, limiting the strength of the parts depending on the printing orientation.^[40]

Hu et al. investigated carbon fiber damage during FDM 3D printing of polymer matrix laminates. They specifically studied the two-parameter Weibull strength distribution of the carbon fiber in its original and printed conditions. They investigated the damage caused to the continuous carbon fibers during the 3D printing process to understand the reason for the decay and found that the FDM process significantly degrades the strength of the carbon fibers.^[41] Additionally, Wang et al. investigated the material stiffness of fiber-reinforced composites produced via Large Area Additive Manufacturing (LAAM). They incorporated the fiber aspect ratio distribution to predict the elastic properties of LAAM-produced polymer composite beads. The fiber length distribution of carbon fiber-reinforced ABS composite beads has been measured using high-resolution optical microscopy. Weibull distribution was used to describe the measured data statistically. To calculate the variability of the elastic properties of the composite bead, the fitted probability density function was incorporated into a fiber orientation homogenization process. The elastic modulus was calculated using their proposed homogenization approach, and the measured fiber aspect ratio distribution was similar to previous reports.^[42]

Moreover, Weibull analysis was also employed in investigating 3D-printed materials intended for medical purposes. Lu et al. used Digital Light Processing (DLP) as a fabrication technique for zirconia-based dental restorations. They studied the flexural strength of Yttria-stabilized Tetragonal Zirconia Polycrystal (Y-TZP) produced via DLP SLA 3D printing and subtractive manufacturing. They employed uniaxial (3-point bending) and biaxial (ring on a ring) tests and evaluated the results using Weibull distribution. They observed that the flexural strength of DLP-fabricated samples was close to those of Y-TZP produced via subtractive manufacturing. However, they observed that the Weibull modulus of samples produced via DLP was lower than those made via subtractive manufacturing.^[19] Roohani-Esfahani et al. designed and fabricated 3D-printed scaffolds that are highly porous, anisotropic, glass–ceramic scaffolds with hexagonal architecture to repair bone defects. These scaffold designs may treat bone defects in maxillofacial, dental, and orthopedic applications. Under cyclic compression and flexural tests, the scaffold was observed to exhibit high fatigue resistance, relatively high flexural strength, and failure reliability compared with those scaffolds produced with conventional architecture. They used Weibull analysis to obtain the Weibull modulus and Weibull scale parameter.^[36] Farzadi et al. investigated the effect of layer printing delay of 50 ms, 100 ms, 300 ms, and 500 ms on the dimensional accuracy and mechanical properties of 3D-printed porous parts for bone tissue engineering. The researchers used Calcium Sulfate based powders to fabricate porous scaffolds (printing orientation: x-direction). A depowdering step followed the printing. Results show that the toughness, compressive strength, and tangent modulus of samples printed with a delay of 300 ms have the highest values compared with other samples and have the highest dimensional accuracy. The calculated Weibull modulus of four samples is, correspondingly, S50 (1.262), S100 (1.117), S300 (1.738), and S500 (1.505). They concluded that higher values of the Weibull modulus mean that the material is more consistent and that defects are uniformly distributed throughout the entire volume.^[43]

In food 3D printing applications, De Rossi et al. used Weibull analysis to model microbial inactivation, microbial growth, and other degradation reactions. They investigated the effects of two (2) printing variables, namely flow level and print speed, on the printability of fruit-based formulation for the 3D-printed customized snacks. They observed that a higher amount of deposited materials (by increasing the flow level) increased the part's total weight, volume, and side length and reduced its porosity fraction. Further, increasing the flow also increased the distribution of filament thickness. On the other hand, the print speed and flow may affect the pore diameter distribution. Additionally, the print speed affected the samples' growth rate (in height), and the print speed and flow level affected the deposition rate of the formulation. Generally, the results demonstrated that the Weibull distribution model fits the experimental results.^[44] At the same time, Huang 3D-printed two (2) hydrocolloids, namely xanthan gum and modified starch. He used a syringe extrusion system for this extrusion-based room-temperature 3D printing. The Weibull distribution function was used to fit the obtained data from experimental and steady-state extrusion rates and the time required to reach steady-state.^[45]

Computer-aided design vs. 3D printing parameters

Computer-Aided Design (CAD) and Computer-Aided Manufacturing (CAM) were considered one field of specialization until these broke out into different names and manufacturing systems later in the 1950s.^[46] That was during the era of traditional manufacturing that involved milling and other subtractive and integrated manufacturing methods. CAD became a necessary design tool in many areas, such as in-network,^[47] mechanical, and manufacturing designs,^[48] requiring careful consideration of both the design model and the design outcomes based on that model. In other words, CAD is the most critical pre-manufacturing process that defines the model before its actual manufacturing, factoring in the geometry of the parts, orientations, and composition tuned around the specific parameters of the utilized manufacturing technology.^[48]

CAD is a vital product design process in 3D printing, regardless of the 3D printing technology. Although 3D models can be designed through any CAD software that can produce a Standard Tessellation Language or STL, such as SolidWorks, many technologies only allow the use of their proprietary software bundled alongside the 3D printer itself that can optimize the generic 3D model design centered on the 3D-printer-specific parameters.^[49–53] However, unlike traditionally-manufactured products where 3D models made in SolidWorks can take on simulations based on specific material properties, 3D models used for 3D printing can only take on the geometry of the design. The CAD is a design process that can only be optimized through the 3D model's shape, orientations, and the number of parts for a particular 3D printing technology but not in terms of a CAD design containing material characteristics. It is because 3D printing requires a layer-by-layer manufacturing process. Hence additive manufacturing is contrary to traditional manufacturing, which fabricates from and produces a monolith of a material.^[48] Thus, material characteristics matter and can only be embedded as relevant CAD properties for specific conventional manufacturing processes. With this challenge, 3D printing requires CAD methodologies from the geometrical design down to the material-level design considerations.

Several other challenges were articulated by Oropallo and Piegl (see Table I) that are implicated in CAD and 3D manufacturing processes, such as shape optimization, designing, pre-processing, printing methodology, part orientation, and slicing (see Fig. 5), and multi-material printing. The effects of these challenges need to be accounted for in CAD and 3D printing parameters.^[48]

Table I.

Summary of computer-aided design vs. 3D printing parameter challenges.^[48]

Challenge	CAD considerations	Print parameter
Shape optimization (cell structure and topological optimization)	CAD systems have issues with the geometric modeling of thousands of elements and may be computationally expensive	Infill geometry and density (to optimize design space)
Design for 3D printing (hierarchical structure and multiple parts)	In the context of 3D printing, CAD has no way of directly representing the model physically. CAD bottlenecks in processing multiple elements and geometries	Object properties (part size, layers, parts, and orientations)
Pre-processing (CAD and supports)	STL limits the accuracy of the curved surfaces because there is no other manufacturing information but only the boundary information for which the layers are created from slicing the model	Layer thickness, print speed (or feed rate), and type of support structure
Printing methodology (layered manufacturing)	Only 2.5 dimensions of the supposed 3D model are created due to the losses in the curves caused by layers Digitalization of 3D models in 3D printing can involve using the 3D equivalent of pixels called voxels. This unit (specific to 3D printing technology) is tessellated against the 3D model to provide representations of the object in the 3D printing manufacturing process	Parameters specific to 3D printing technologies (e.g., filament and nozzle size, bed and melting temperature, layer thickness, etc.)
Part orientation (changing the part orientation to cater to manufacturing considerations)	Optimizations can be done via CAD. But changing the orientation affects other build properties that cannot be addressed by changing the model design through CAD	Build time, part quality, and support structure (may result in curling, shrinkage, distortion, etc.)
Slicing	3D printing requires slicing the CAD model into fixed layer thickness throughout (uniform slicing). The containment issue lies when the layer may be inside or outside the CAD model, which needs to be consistently decided upon for the whole process	Affects layer thickness, nozzle, and filament size
Multi-material printing	CAD is not designed to model heterogeneous objects fabricated through 3D printing. CAD should be combined with other systems to achieve this	Object properties (multiple parts, orientations, etc.)

Figure 5.

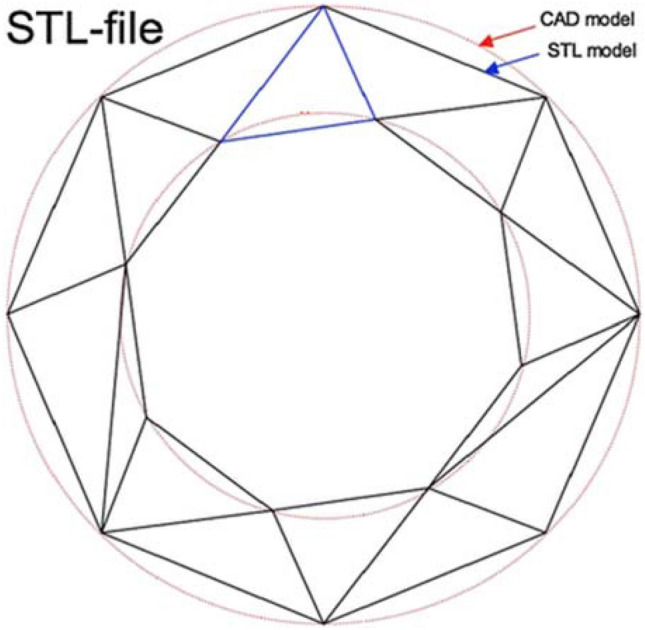
STL model vs CAD model.^[48]

These challenges commonly manifest in the dimensional accuracy and mechanical properties of the 3D-printed parts. Thus, creating a 3D model with an accurate dimension the same as the CAD model must be emphasized, as well as ensuring good quality 3D-printed parts thru testing its mechanical properties.

Methods of metrology

Creating some highly complex components and even assemblies is now possible with 3D printing. With infinite design freedom in 3D printing comes infinitely complex shapes to measure. Hence, there is often a big question about the dimensional accuracy and qualities of these components and assemblies. Therefore, it puts new demands on how measurements and application of metrology are carried to components manufactured by 3D printing. Metrology involves establishing units, developing measurement protocols, and producing artifacts that act as measurement standards to allow traceability and measurement analysis on uncertainties and accuracies.^[54,55] Metrology is used to gauge a part's fit-for-purpose, which is determined by considering tolerance and functionality. It allows the manufacturing of complex parts while avoiding unnecessary scrap material and redundant processing time, improves energy efficiency and gives customers confidence in the product.

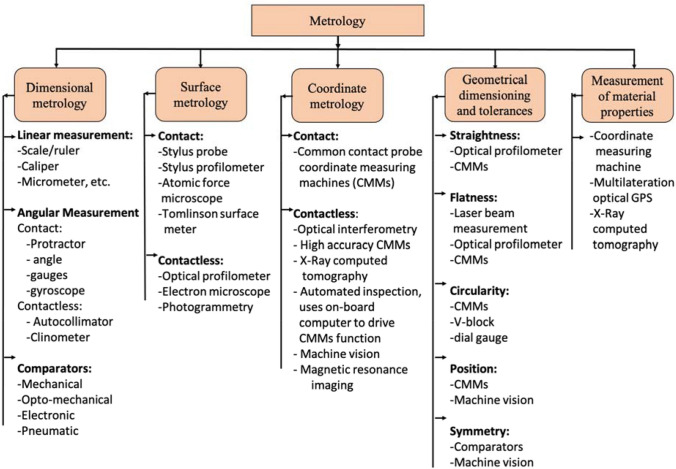
Figure 6 shows current metrology methods applied to 3D-printed polymers. These methods have specific advantages and disadvantages; therefore, thorough consideration is required before choosing which will be adopted. With so many developments coupled with an array of equipment manufacturers' claims, it is often difficult to choose the optimum measuring instrument for a user. However, the non-destructive, contactless, real-time, in situ measurements and accurate, less time- and cost-consuming methods that are consistent and facilitate process control are more favorable.^[54] The following sections discuss some of these state-of-the-art metrology methods.

Figure 6.

Current method of metrology used in additive manufacturing.

Measurement of physical properties of 3D-printed polymers

Dimensional metrology was defined by Vora et al. as concerned with geometric features, particularly in the measurement of size, distance, angle, form, or coordinates. Furthermore, they emphasized its critical role in monitoring and controlling manufacturing processes where contacts between mechanical components create drifts in geometry. They considered linear, angular, and comparators under this method. The dimensional metrology method is selected or utilized based on accuracy, precision of measurements, quickness, and ease of use. See Fig. 6 for some examples of each measurement method.

When assembling parts, the properties of their mating surfaces significantly impact the successful manufacturing of the whole system in terms of friction, stress, corrosion, aesthetics, reliability, etc. Therefore, the application of Surface metrology or measurement of the variation within the surface between two points on the same surface, surface characteristics such as surface finish, topography, or roughness, is essential. Surface irregularities such as roughness, waviness, lay, flaws, surface texture, and form error describe surface metrology. When these surface irregularities are measured, they are assigned a numerical value. Some of the popular representations of surface roughness are the 10-point height average (Rz), centerline average (Ra), and Root Mean square (Rq) value. See Fig. 6 for examples of surface metrology methods.

On the other hand, Coordinate metrology is the most advanced method to measure three-dimensional coordinate information.^[54–56] The coordinates, location, or position information is essential for three-dimensional measurements. The current ability to manufacture parts with the highest precision is only possible due to Coordinate metrology instruments. Advancements in electronics, mechanics, mechatronics, optics, and computer science have directly contributed to the development of coordinate metrology systems that use dimensional, optical, and imaging metrology based on modern contact or contactless systems (visual) and modern multi-sensor systems. Contactless coordinate metrology generally provides high precision and accuracy in measurements, but the systems are more expensive, and measurements are time-consuming. Optical or contactless coordinate metrology is becoming more popular, offering fast measurements that are inaccurate. Coordinate metrology techniques and equipment involving Coordinate measuring machines (CMMs), multilateration optical GPS, X-ray computed tomography, automated inspections, machine visions, and magnetic resonance imaging.

Geometrical dimensioning and tolerances (GD&T) refer to the information on manufacturing variables or characteristics such as straightness, flatness, squareness, roundness, parallelism, cylindricity, and runout to evaluate parts and process capabilities.^[54] Dimensional, surface, and coordinate metrology techniques and equipment previously introduced can all be used to assess the geometrical dimensioning and tolerances. However, it is common to encounter coordinate metrology, especially when using coordinate measuring machines in GD&T characterization.

One of the significant challenges in AM technology is the dimensional accuracy of the 3D-printed polymer materials since it is a clear indicator of how exactly a 3D-printed part was manufactured and processed regarding the 3D CAD model. Along with dimension accuracy, tolerance is also essential due to the application of parts in assemblies.^[57,58] Even though FDM has various advantages, only limited studies have been conducted about the dimensional accuracy of FDM/FFF printed parts and the impact of slicing parameters on them.^[59–62] Here are some researches that studied the dimensional metrology of 3D-printed parts. It was observed by Ali et al. that the accuracy of the measured dimension between ABS and PLA 3D-printed parts has no significant difference.^[63] In addition, Dardzinska et al. used computed tomography (CT) and a 3D scanner to measure the dimensional accuracy of 3D-printed parts. They compared various 3D printing processes, including Polyjet, FDM, and others.^[64]

Some researchers have also used more complex measurement techniques. In a study conducted by Wang et al., surface metrology was considered. They created a process tool for changing the effects of parameters. The post-processing procedure shows a varying Surface quality result, with these variations attributed to manual or chemical changes in the material.^[65,66] Chohan et al. employed a study using the Taguchi L9 orthogonal array; here, the specimen used is an Acrylonitrile Butadiene Styrene (ABS) FDM 3D-printed part. The parameters considered to study the surface roughness were infill pattern, nozzle temperature (°C), thickness measurement, and printing speed (mm/s). The Taguchi method helped determine that the print speed is the most influential printing parameter considering the surface roughness.^[67] Other researchers evaluated 3D-printed parts using coordinate metrology. Yankov et al. used an SLA 3D printer to create micro-squares. They used a Carl-Zeiss optical microscope to determine the coordinates of the items. The micrographs were used to calculate the object's microgrid deviations. Depending on the object's placement on the build plate, they found more significant and irregular deviations from CAD values.^[68]

On the other hand, Kacmarcik et al. used a coordinate measuring machine (CMM) to study the shape, size, orientation, and location accuracy of FDM 3D-printed items. They found that industrial 3D printers are more accurate than 3D printers manufactured at home.^[69] Furthermore, geometrical dimensioning and tolerances were utilized by Mahesh et al. to investigate geometries using free-form surfaces and reported deviations from the set dimension ranging from 5 to 15%.^[66] According to Jadayel et al., the three-dimensional metrology feedback and mesh morphing enhanced accuracy in eliminating systematic deviations. They employed a 3D geometric compensation method that morphed the object's original surface mesh model using the inverse of the systematic deviations. They scanned many sacrificial 3D-printed items to measure systematic deviations and then computed the average deviation vector throughout the model.^[70] Although many factors must be considered while analyzing the dimensional accuracy of parts, the size of the specimen or samples has been overlooked. It has been discovered that the specimen's mechanical properties are influenced by its size, also known as the 'size effect'.^[71] They recently employed a factorial design in determining the best combinations of different sizes, layer thickness, and infill density for dimensional accuracy in 3D-printed items.^[7,13]

Measurement of mechanical properties of 3D-printed polymers

Material properties are best evaluated using common mechanical testing methods such as non-destructive tests, tension tests, impact tests. Also, in situ metrology methods using thermocouples, high-speed cameras, thermal cameras, pyrometers, X-Ray Diffraction, etc. are being employed. Using a high-speed optical scanning system integrated with an FDM 3D printer, McGuan et al. developed a method for layer-by-layer mapping of 3D-printed items. This setup might scan the object throughout the printing process to validate and conduct in situ adjustments of 3D printing parameters in real-time.^[72]

A 3D-printed material is usually highly anisotropic; hence, it exhibits a highly complicated material behavior. Several printing parameters influence these behaviors, such as filament material, temperature, printing speed, and print orientation. Different mechanical tests may be employed together with statistical test methods to understand the relationship between these printing parameters. Mechanical testing of 3D-printed materials generally involves tensile, compression, flexure, impact, creep, and fatigue tests. In addition, ASTM and ISO standards for the mechanical testing of polymers have already been developed. Standard test methods must govern the determination of the mechanical properties of the polymer, including specifications, guides, and practices, to have a reliable result.

The mechanical properties of a 3D-printed part cannot be known or approximated before its printing and material testing. Hence, Sagias et al. showed that the influence of a printing parameter is directly related to the mechanical properties of an ABS 3D-printed part. They used the Taguchi methodology as the optimization tool to obtain improved mechanical properties of a 3D-printed part before its printing.^[73] The tensile test is one of the most common mechanical tests used to determine and analyze several mechanical properties of materials that are vital in design.^[74] Therefore, the mechanical behavior of some 3D-printed materials have been widely studied by many researchers under tensile tests with the help of statistical testing techniques. Auffray and his group explored the influence of several printing parameters on the tensile properties of FFF 3D-printed PLA specimens using the L27 Taguchi orthogonal array supplemented by a two-level fractional factorial design with four factors (24–1). Their methodology helped them find that the infill density, raster pattern, printing orientation, and printing velocity are the most influential parameters. In contrast, layer height, extruder temperature, and outline overlap have no significant influence on Young's modulus and yield strength.^[75] Similar materials were investigated by Mena et al. However, they only investigated the effect of the filling percentage on the tensile strength of 3D-printed PLA specimens for different printing patterns, using an ANOVA and a DOE with a single factor to obtain appropriate filling percentages for printing parts according to the desired filling pattern.^[76] Sukindar et al. employed Taguchi's 3³ factorial design and ANOVA to analyze the impact process parameters on the tensile strength of 3D-printed PLA material using 3D print Repetier-Host software.^[77] Hikmat et al. also used the Taguchi methodology and ANOVA in their research. Their group studied the effect of various printing parameters such as build orientation, raster orientation, nozzle diameter, temperature, infill density, shell number, and extrusion speed on the tensile strength of FDM 3D-printed PLA materials. They used Taguchi's mixed model fractional factorial design to determine the number of experiments. The ANOVA was used to indicate the significant parameters and their effect on the tensile strength of the materials. Further, they also used the Signal-to-Noise ratio (S/N) to select the optimal combination of the parameters. Using their method, they developed a linear regression model to predict the tensile strength of the 3D-printed part.^[78] Ouhsti et al. used the central composite design (CCD) to develop an empirical model relating to response and process parameters. The ANOVA was used to test the validity of determining the desired mechanical properties. They studied the effect of printing parameters such as deposition angle, extruder temperature, and printing speed on the tensile strength and elastic modulus of FDM 3D-printed PLA parts.^[79] The central composite design (CCD) was also used by Godec et al. for optimization processes of 3D printing parameters, such as extrusion temperature, flow rate multiplier, and layer thickness, to obtain the maximum tensile strength of the FFF 3D-printed 17-4PH Stainless Steel. The ANOVA and response surface models were used to explore the relationship between the adjustable printing parameters and their tensile properties.^[80] The ANOVA was also used by Pernica et al. to investigate the effect of different temperature nozzles on the tensile strength of 3D-printed PLA, PETG, and ABS materials. They also include the Tukey test in their statistical evaluation.^[81] On the other hand, Eguren et al. demonstrated the effectiveness of applying DOE techniques in improving the 3D printing process to obtain high-quality 3D-printed parts. They used composite material and investigated its mechanical properties under tensile test.^[82] Jiang et al. conducted a study utilizing an L9 orthogonal array of Taguchi experimental design, which helps to compare the tensile strength and porosity of the Polyetheretherketone (PEEK) FDM 3D-printed part. The optimal printing parameters were 5 mm/s print speed, 0.1 mm layer thickness, 395°C printing temperature, and 0.44 mm extrusion strand. The 3D-printed part underwent an annealing process; the tensile strength increased from 91.48 to 98.85 MPa, while the porosity decreased from 3.9 to 0.3%. Hence, the study concluded that using the optimal printing parameters in a low-cost FDM machine is appropriate since it can produce PEEK 3D-printed parts with high tensile strength and good crystallinity.^[83] Keles et al. performed tensile tests on 3D-printed ABS samples with and without a hole (in the center) to investigate the effect of build orientation on the mechanical reliability of 3D-printed ABS parts. Seven (7) sets of ~ 30 samples were printed with different orientations (XY, XZ, and C + 45). Weibull distribution was used to quantify the variation in tensile strength, and the analysis showed that the reliability of 3D-printed ABS could be low, similar to advanced ceramics. The XZ printing orientation showed the highest average fracture strength for both sample configurations with and without a hole. The C + 45 orientation demonstrated the lowest strength. They further claimed that since the Weibull distribution can be used to relate the probability of failure to the applied stress, the Weibull analysis proves to be a practical design approach in determining the reliability of 3D-printed parts.^[84]

Aside from the tensile test, other mechanical tests, such as compressive and flexural tests, were also used along with statistical testing techniques to characterize the material behavior of 3D-printed materials. Compression tests are essential for measuring brittle or low-ductility materials' elastic and compressive fracture properties.^[74] On the other hand, the flexural tests measure the force required to bend a beam of plastic material and determine the resistance to a material's flexing (stiffness).

Under compressive and flexural tests, Calvo et al. evaluated the mechanical properties of continuous fiber fabrication (CFF) 3D print technology. They used the DOE as a statistical method in investigating the effect of reinforcement pattern, reinforcement distribution, print orientation, and percentage of fiber on compressive and flexural properties of polyamide 6 (PA6) reinforced with carbon fiber.^[85] Additionally, Mamo et al. conducted a study that analyzes flexural strength using the fuzzy logic (FL) technique to develop a prediction model for an FDM 3D-printed ABS part. They used the Taguchi L18 orthogonal design technique to organize the tests. In addition, they also studied the relationship between layer thickness, raster width, raster angle, orientation angle, and the flexural strength of the ABS 3D-printed components using ANOVA.^[86] An almost similar approach was employed by Kumar et al., which used the Taguchi L9 experimental method to analyze the effects of print speed, infill density, and layer height on flexural strength, tensile strength, and hardness of FDM 3D-printed carbon fiber-reinforced PETG thermoplastics for optimization. They also analyzed the ANOVA to determine the link between print speed, infill density, and layer height.^[87]

The requirements of the orthogonal arrays are met by considering different experimental factors.^[11] Espino et al. used the Taguchi methodology in identifying the optimum 3D printing configuration based on the indentation hardness properties of SLA 3D-printed parts. Arifin et al. used the Taguchi method to improve the dimensional changes in 3D printing. They identified the major molding parameters, such as layer height, print speed, and temperature. Results show that the optimal parameters from a Brinell Hardness number are 0.10 mm layer height, 20 mm/s print speed, and 205°C print temperature.^[88] A material’s hardness is determined through the hardness test method, which investigates the resistance of a material to penetration using various indenters.^[89] Hardness testing is a non-destructive test and is easy to perform. Unlike another material testing, hardness testing can be carried out directly on the material without making a significant adjustment.

Furthermore, most of the equipment used for hardness tests is more inexpensive than the other types of material testing equipment. These tests have been very beneficial for material evaluation and ensuring quality control.^[90] The earlier mechanical tests discussed in this paper are quasi-static tests because they are conducted at a low strain rate. However, since many materials fail suddenly under the high strain rate condition, material behavior must be investigated using the impact test method when subjected to impact loading. The impact test is used to investigate the fracture mechanics of the material by measuring the energy the material can absorb during a collision. Moreover, this test can generate essential values such as toughness, impact strength, fracture resistance, impact resistance, or fracture resistance of the material, which are critical in material selection in applications that involve shock loading properly.^[9] Using this experimental test and the Taguchi methodology, Atakok and his group conducted a statistical investigation to understand the effects of different layer thicknesses, occupancy rates, and filling structures on the impact strength of 3D-printed PLA and recycled PLA (Re-PLA) parts. They also investigated the effect of the mentioned parameters on the tensile strength and three-point bending strength of PLA and recycled PLA (Re-PLA) parts.^[91] Kananathan et al. also performed a statistical analysis investigating the effects of infill percentage and infill pattern on the impact properties of coconut wood-filled PLA composites 3D-printed parts. They also developed a mathematical model that can predict the energy absorbed and the impact energy of the 3D-printed components. The ANOVA was used to validate the experimental data, and a mathematical model was then developed.^[92] Recently, Mazen et al. used a DOE method like Fractional factorial experiments to study the effect of print orientation, layer height, extrusion width, nozzle diameter, and filament temperature on the impact toughness and ultimate tensile strength of the 3D-printed samples. The test results were analyzed with a normal probability plot complimented with ANOVA. Also, an adopted regression equations model was used to predict the ultimate tensile strength and the impact toughness as a function of the print orientation.^[93] The various research studies that employed statistical methods in 3D printing are shown in the Table II. Graphical results representing various statistical methods applied in some research studies mentioned earlier are shown in Figs. 2 and 3.

Table II.

Statistical methods used in various studies.

Research study	Statistical tool/technique used
	Design of experiment		Weibull	Other(s)
	Factorial design	Taguchi methodology
Juhar et al.[14]			✓
Revilla-León et al.[15]			✓
Naito[16]			✓
Da Costa et al.[17]			✓
Ouamomar et al.[18]			✓
Khalid et al.[31]		✓
Durão et al.[32]		✓
Fotovvati et al.[33]	✓
Shakeri et al.[34]		✓
Shakeri et al.[35]		✓
Roohani-Esfahani et al.[36]			✓
Schilling et al.[37]			✓
Boyce et al.[38]			✓
Byun et al.[39]			✓
Feilden et al.[40]			✓
Hu et al.[41]			✓
Wang et al.[42]			✓
Lu et al.[19]			✓
Farzadi et al.[43]			✓
De Rossi et al.[44]			✓
Huang et al.[45]			✓
Chohan et al.[67]		✓
Sagias et al.[73]		✓
Auffray et al.[75]		✓
Mena et al.[76]	✓
Sukindar et al.[77]	✓	✓
Hikmat et al.[78]	✓	✓		Regression Analysis
Ouhsti et al.[79]		✓		Central Composite Design (CCD)
Godec et al.[80]		✓		Central Composite Design (CCD)
Pernica et al.[81]		✓
Eguren et al.[82]		✓
Jiang et al.[83]		✓
Keles et al.[84]			✓
Calvo et al.[85]		✓
Mamo et al.[86]		✓		Fuzzy Logic (FL)
Kumar et al.[87]		✓
Espino et al.[90]		✓
Arifin et al.[88]		✓
Atakok et al.[91]		✓
Kananathan et al.[92]		✓
Mazen et al.[93]	✓	✓		Regression Analysis

Artificial intelligence and machine learning (AI/ML)

From the humble beginnings of image processing and recognition, artificial intelligence (AI) has become a very sophisticated technology that involves, at its core, a barrage of computers processing information in unprecedented ways. The applications for AI may be found in robotics, medical diagnosis, face recognition, internet applications, data mining, and other industries.^[94] Among the application location for Deep Learning technology or AI are Chatbots or Conversational agents developed just to emulate conversations but to answer questions that use these environments.^[95] AI is finding its way into becoming the supra-intelligence^[96] while serving in various situations, such as the COVID-19 pandemic.^[97] AI is steadily finding its way into surpassing human cognitive abilities.^[98]

Early machine learning (ML) technologies used the logistic regression algorithm.^[99] Logistic regression takes a data set of N examples known as training sets corresponding to outcome Y. The labels or tags describe these training sets' image (outcome Y). The eventual task is to predict Y given data X. The data X is coupled with another parameter that changes the data X into a sample Z. The interesting portion in this exciting likelihood or the probability of the given data X into the Z. The point of interest shifts to the probability of the outcome Y. This certain probability is changed into a sigma function that shows a certain probability of occurrence. This sigma variable is later turned into a sigmoid function that results in an infinite positive value from zero (0) to one (1). Complex prediction requirements developed into the multilayer perceptron (MP) model, basically a multiple layer of the logistic regression.^[99]

The MP is considered the start of Deep Learning technology. This is where the primary result of the simple logistic regression is layered and transformed into another layer of the data set, providing depth of information. Feature maps of the characteristics of the basic images are stacked and layered by creating more data sets and leading to features that distinguish them from other images of the same category. The features become the information that relates to the characteristics of people or users. This forms Convolutional Neural Networks (CNN), which became the natural extension of MP. This is accomplished by passing the primary image filter across the sample layer. The various degree of similarity of the features is recorded into data matrices that describe the probability of similarity. One can see that these are layered logistic regression models, which are now called MP or CNN.

The learning process described above is built upon statistical approaches either in the simple logistic regression or the deep learning convolutional neural networks. The methods are just repetitions of the same steps as an attempt to build the features of the image in contrast with a set of filters passed and compared to the data set. These filters are constructed with vast quantities of data and information. The computational requirements of deep learning have become very big because of the stacks of features and information. Machine learning takes the overall probabilities of a decision most likely taken by a human doing the same task. However, Machine Learning does not rely on the highest probability only. Instead, it also takes on the lowest possible comparison error.^[100]

In sophisticated machine learning tools such as Silas, machine learning is fused with logical reasoning: formal verification of the prediction model against user specifications, training correct-by-construction models, and explaining the decision-making of predictions.^[101] In these setups, real-life problems are solved using artificial intelligence. This incorporates Automatic AI—a hybrid approach to selecting algorithms and hyperparameter tuning.^[102] Technologies like autonomous driving cars are applications of deep learning algorithms which require vast amounts of data for processing and learning directly from input data.^[100]

Deep learning continues to evolve to drive industry 4.0. Machine learning systems also help educational systems with data retention and recognition of requirements based on survey answers.^[103] Personalized learning and data retentions through the identification of attributes become key learning validation processes. Intelligent technologies and AI have also started finding ways for home energy management systems.^[104]

The study provided proof of concept for the importance of data availability and speed of access requirements for AI-enabled systems. Among other requirements, perhaps the most important would be the data required for reliable AI. As mentioned, even the basic logistic regression algorithm requires vast amounts of data for learning. The samples or training sets need to be pre-labeled by humans and stored in databases that are readily accessible to the system. The delay or shortage of information could lead to loss of lives; such are cases for augmented reality and predictive systems that provide notifications for impending danger.^[105]

Quality assurance in additive manufacturing (AM) continues to benefit from ML with various algorithms that check sensor data to evaluate the conditions of the manufacturing classification processes.^[106] Among the trend-setting innovations is 3D printing in construction, where value-adding activities are moved once again to the site in the form of one-off construction projects or customized designs specific to particular sections of the project. Or, at the time, modular construction enables the contractor to build the sections elsewhere and bring them to the site later. This maximizes the efficiency and productivity of manpower and resources.^[107]

The quality of 3D-printed products also plays an essential role in the acceptance of AM. A study on one of the market's most popular 3D printing technologies is known as FDM, which incorporates several parameters for the optimization of the process. Investigating the effects of the process parameters on FDM products requires the DOE methods. Characteristics of the PLA material, namely in terms of tensile characteristics of 3D-printed products, have been studied using the Taguchi Optimization Methodology and ANOVA.^[108] Analyzing such factors and features also require ML and other statistical analysis.

Future perspectives

Information-rich metrology for 3D printing optimization

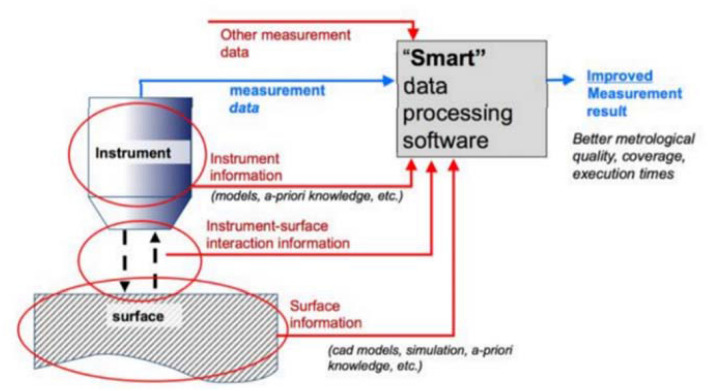
Senin et al. introduced the term information-rich metrology to refer to any additional information to improve measurement processes. Information may be obtained from knowledge of the manufacturing process, the object to be measured, and an understanding of the physical interactions and principles underlying the measurement. Information may come from "priori" information such as CAD, models, course measurement data. If optical equipment is used and a priori manufacturing data is combined with decent modeling, this can significantly enhance measurements, Fig. 7.^[109]

Figure 7.

Additional information sources and information flow change from conventional metrology to the IRM,^[109] (Fig. 6b).

Prediction models for 3D printing optimization

AM is an enabling technology that needs to have standards and standardized testing for translation to various fabrication formats and highly reliable performance. AM-produced parts can be of higher design complexity but require high tolerance, accuracy, and precision for their intended application. In dimensional stability, layer-by-layer fabrication requires unique process development compared to bulk formative manufacturing or net-shaped subtractive manufacturing. More than anything else, the type of materials properties, coefficient of thermal expansion (CTE), melting point, heat deflection temperatures (HDT), tensile modulus, etc., will determine the expected failure properties that need to be predicted or empirically tested. There should be a focus on utilizing simulation and finite element analysis (FEA) methods as a predictive procedure and helping define structure-composition-property relationships. The development of in situ, real-time testing and inspection methods can be used as data point harvesting modes to implement Artificial Intelligence and Machine learning (AI/ML) projects to improve the materials and fabrication process and even define better metrology tools. There will be advantages in coupling AI/ML methods with testing and metrology for digital manufacturing methods such as AM because of the ability to optimize properties rapidly. However, there are still multiple challenges to overcome to enable these new technologies to become reliable manufacturing capabilities. Some of these future directions are as follows:

AI/ML materials development and optimization

There is high potential in AI/ML-driven materials optimization. Starting with Bayesian and straightforward artificial neural network (ANN)-based methods, it is possible to focus on a more automated design and discovery protocol for future materials and materials properties. This differs from the conventional approach based on intuition (experience), trial-and-error-based optimization approaches, or improved DOE methods. A data-enabled route results in efficient and targeted approaches to complete the feedback loop much closer to the hypothesis-driven scientific method. By building data gathering and algorithm development during materials development, characterization, and testing, this informatics-based method enables one to connect and iterate through different steps. The materials design and optimization process can be cost and time-sensitive in any project, including AM. It is possible to accelerate optimized materials discovery and AM methods by focusing on hypothesis generation, prediction, AI-driven synthesis, characterization, and testing.

FEA and simulation

The Finite Element Analysis (FEA) application with 3D printing (AM) is almost a story of parallel development since both are based on digital design and refinement methods with CAD. Therefore, FEA and AM should be combined as much as possible to enable a parallel understanding of materials' properties or failure with design. The importance of predicting materials property primarily generated by anisotropy and lack of predicted thermo-mechanical values with new and more complex topologies provides FEA significant leverage to evaluate and reduce product development time. This means it is possible to construct unique designs and enable complex process development protocols to achieve optimum properties in the shortest amount of time. For FDM printing, the strengthening in particular axes (anisotropy) is not easily avoided due to the nature of the XYZ CNS Movement. It only becomes more complex with 5 or 6-axis fabrication. For lightweighting, reducing parts and simplifying the design and strength can take advantage of FEA (or other similar methods). It can also help better design aesthetics, quality control, lower cost, and reduce fabrication time. A typical FEA method involves solving multiple static implicit steps with sets of finite elements added stepwise until failure is initiated. The discretization of the 3D model can involve voxelization to approximate the 3D shape. Another consists in defining the toolpath and constructing finite elements by sweeping them along the path. Thus, FEA-based models can effectively simulate complex prints with various material properties and recommend a better print strategy to save time and cost. Some recently published works used FEA in dealing with the effects of input parameters and material types for predicting fracture load, dynamic and static load, and estimation of mixed-mode load bearing on load carrying capacity and integrity of 3D-printed parts.^[110–113]

3D printing with bio-inspired mechanics and metrology

Digital 3D and 4D printing will enable the capture of design from nature. With a bioinspired design, it is possible to derive a new function that draws inspiration from various biomechanics applications and new structure-composition-property relationships inspired by nature. There will be a need to develop unique characterization and metrology tools that accommodate these new designs very different from bulk properties. Examples include the lotus leaf hierarchy of roughness, the nacre structure, structures of diatomaceous organisms, and the exoskeleton of several crustaceans and marine animals, which requires a shift in the conventional ring and evaluation of properties. 4D printing enables other transformative and metamorphic features to give new functions. Usually, the properties have origins in stimuli-responsive elements or properties that produce a cause-and-effect shift in the targeted properties. It can pose challenges in characterization and testing due to the new design and materials concepts never before reported, much less developed standards.

Summary and conclusion

This paper presented and studied the application of various statistical methods used to analyze and interpret data sets in Additive Manufacturing (AM) or 3D printing. Some statistical methods were applied to ensure the quality of a 3D-printed part, starting from designing, pre-processing, post-processing, and up to testing, such as Taguchi Methodology, Factorial Design, and Weibull analysis. Also, numerous studies that show the importance and advantages of utilizing these statistical methods in designing and testing 3D-printed parts were covered in this paper. It includes applying the statistical approach in solving the variation between the 3D CAD model and 3D-printed parts brought by the effects of different 3D printing parameters. These have been combined with varying metrology methods in optimizing the physical and mechanical properties of 3D-printed parts.

In conclusion, employing various statistical methods significantly helped AM in the creation of higher-quality 3D-printed parts. However, there is still a wide range of available methods that can potentially help improve AM technology that needs to be studied further. The paper also discussed the following possibilities: (1) AM can produce the more complex design of 3D-printed parts by utilizing Simulation and Finite Element Analysis (FEA) methods, and (2) application of Artificial Intelligence and Machine Learning (AI/ML) as a tool in improving the materials and manufacturing process, and helping to define better metrology methods or tools to be used in 3D printing.

Funding

Funding was provided by Bataan Peninsula State University and Department of Energy, Basic Energy Sciences.

Data availability

Additional data is available with the supplementary information file that will be made accessible with publication. In addition, more data and inquiry are possible through communication with the authors.

Declarations

Conflict of interest

The authors have no conflict of interest to declare.