Structure of a 28.5 kDa duplex-embedded G-quadruplex system resolved to 7.4 Å resolution with cryo-EM

Abstract

Genomic regions with high guanine content can fold into non-B form DNA four-stranded structures known as G-quadruplexes (G4s). Extensive in vivo investigations have revealed that promoter G4s are transcriptional regulators. Little structural information exists for these G4s embedded within duplexes, their presumed genomic environment. Here, we report the 7.4 Å resolution structure and dynamics of a 28.5 kDa duplex-G4-duplex (DGD) model system using cryo-EM, molecular dynamics, and small-angle X-ray scattering (SAXS) studies. The DGD cryo-EM refined model features a 53° bend induced by a stacked duplex-G4 interaction at the 5’ G-tetrad interface with a persistently unstacked 3’ duplex. The surrogate complement poly dT loop preferably stacks onto the 3’ G-tetrad interface resulting in occlusion of both 5’ and 3’ tetrad interfaces. Structural analysis shows that the DGD model is quantifiably more druggable than the monomeric G4 structure alone and represents a new structural drug target. Our results illustrate how the integration of cryo-EM, MD, and SAXS can reveal complementary detailed static and dynamic structural information on DNA G4 systems.

INTRODUCTION

Regions of the genome that are guanine rich can fold into non-B form DNA structures known as G-quadruplexes. G-quadruplexes (G4) are four-stranded nucleic acid tertiary structures composed of two or more stacked guanine tetrads (‘G-tetrads’). G-tetrads form through the association of four guanines in a square planar arrangement stabilized by Hoogsteen hydrogen bonding, stacking, and coordinating cations (1,2). The traditional G4 motif [G_≥3-L_1–7-G_≥3-L_1–7-G_≥3-L_1–7-G_≥3] has four runs of three or more guanines, separated by 1–7 loop nucleotides. G4 motifs are conserved (3), and are located at regulatory sites such as telomeres (4,5), promoters (6–8), immunoglobulin switch regions (7), and replication origins (8). G4 motifs are enriched in the promoters of many proto-oncogenes (9) and directly act as recruitment sites for transcription factors (10). From a therapeutic standpoint, promoter G4s are attractive targets since they might inhibit expression of ‘undruggable’ oncogene proteins (9). G4 structural diversity and the low G4 copy number in the cell provide potentially selective targetable features (11). Promoter G4s, their regulation, and targeting have been recently reviewed (12).

The architecture of promoter G4s within their duplex context is not well defined. Early electron microscopy (EM) investigations using RNA to invade and displace the G-rich strand in plasmids (known as ‘R-loop’ formation) showed that stable ‘G-loops’ formed on the non-template strand in a co-transcriptional manner (13). The estimated resolution of this study was ∼150 bp and no fine structural detail was reported. A later study, using atomic force microscopy (AFM) and similar R-loop trapping method, revealed that the G-rich strand forms small, asymmetric protrusions with an approximate height of a four-stranded DNA structure (14). That study also revealed that G4s disappear after RNaseH treatment, implying that sequestration of the reverse complement C-rich strand is necessary to permit G4 formation. Neither EM nor AFM study could achieve the resolution necessary to infer atomic structural insight. In recent studies of the potentially unique interaction interfaces of duplex-G4 junctions, the Phan lab has reported several NMR structures of unimolecular quadruplexes with hairpin-G4 junctions (15,16). The authors established that direct duplex-G-quartet stacking interactions can be stabilizing overall, but are not necessary for a duplex-G4 tertiary arrangement (15). Altogether, these studies reveal a gap in our understanding of promoter G4 structure and behavior at the atomic level. We believe this gap exists for many reasons, but none more so than the inherent difficulty in studying extended, flexible or polymorphic, DNA sequences by traditional structural biology methods such as NMR and X-ray crystallography.

Recent advances in cryo-EM imaging capabilities and data processing (17) permit the characterization of small (<50 kDa) nucleic acid structures with resolutions on the order of 3–8 Å (18). At resolutions of 3–5 Å it is possible to determine base-pairing interactions (19), and in the range of 5–9 Å duplex grooves and tertiary arrangements can be assigned (20). Two recent studies by Zhang et al. demonstrate the applicability of cryo-EM single particle analysis (SPA) on small RNA systems. In the first report, a 40 kDa apo- and S-adenosylmethionine (SAM)-bound SAM-IV riboswitch RNA was refined to resolutions of 3.7 and 4.1 Å, respectively (19). The latter reconstruction was of sufficient resolution to assign the SAM binding site. In a second study, Zhang et al. reported on the 6.9 Å map of a ∼28 kDa COVID-19 frameshift stimulation element (FSE) RNA using a nanostructure tagging method (20). These recent RNA studies (18) motivated us to use cryo-EM, for the first time, to characterize a DNA duplex-G4-duplex (DGD) model promoter bubble.

A previous nonstructural investigation of a DGD model was done by Tuntiwechapikul and Salazar (21), who devised and validated a model of a duplex-flanked telomere G4 sequence with a short poly-dT surrogate-complement incorporated to prevent duplex competition. Inspired by their work, we created our DGD system with a poly dT surrogate-complement of the same length as our G4 insert to better mimic the length of an actual displaced complement loop. Our DGD model with an unstructured non-complementary loop was used for practicality and is also appropriate, since G4 and i-motif formation are reported to be mutually exclusive in vitro (22) and interdependent in vivo (23). The duplex ‘handle’ sequences were designed with the intention of preventing formation of alternative forms of DNA other than duplex. For the G4, we chose a promoter-derived sequence from the MYC NHEIII (nuclease-hypersensitive element III), known by its PDB identifier 1XAV (24). The 1XAV G4 is an ideal structure for our purposes because it is parallel (the most common promoter G4 topology (11)), it retains the unidirectionality of the backbone when folded (i.e. the 5’ and 3’ ends are not facing the same direction), and it has high thermodynamic and kinetic stability in physiological potassium buffers (24,25).

We used an integrative structural biology (ISB) approach, combining cryo-EM, small-angle X-ray scattering (SAXS), analytical ultracentrifugation, circular dichroism, 1D-NMR, molecular dynamics (MD) and modelling tools, to characterize the DGD structure. Cryo-EM reveals three distinct maps with nominal resolutions of 8.1, 7.4 and 6.2 Å. Each map has distinguishing bend angle, length, and apparent poly dT loop organization. Three-dimensional variability analysis (3DVA) of the combined particle stacks reveals stretching, bending, and coiling motions that are in good agreement with MD simulations. Cryo-EM, MD and SAXS data mutually agree that there is a stable stacking at the 5’ G-tetrad-duplex interface and a persistently unstacked 3’ duplex handle region, resulting in bend angles of 49–67° and particle flexibility. A significant outcome is that, within the duplex context, the G4 structure is much more occluded than would be expected based on the commonly used schematic renderings of promoter G4s (see (12) for example). Binding site analysis of the DGD model system reveals that it has a quantitatively more druggable binding site located at the duplex-G4 junctional region than any binding site on the 1XAV G4 alone. Collectively, this work presents the first medium-resolution model of a promoter G4 bubble and demonstrates that the combination of cryo-EM, MD, and SAXS is a powerful combination for studying higher-order DNA G4 systems.

MATERIALS AND METHODS

Sample preparation

DNA oligonucleotides were purchased from IDT (Coralville, IA). The DGD construct was prepared in the following way. First, the 46 nt G-quadruplex strand (5’- CTATGTATACAAAGAGGGTGGGTAGGGTGGGTTTAATGCGGCACGC) was diluted to 10 μM in 100 mL of BPEK buffer (8 mM sodium phosphate buffer supplemented with 185 mM KCl, pH 7.2, with 1 mM sodium EDTA to inhibit DNase). The sample was then heated to 99.9°C for 20 min before slow cooling overnight in a 2 L water bath. The sample was then concentrated to approximately 1 mM and mixed with the 46 nt surrogate-complement strand (5’- GCGTGCCGCATTAATTTTTTTTTTTTTTTTTTTTTTGTATACATAG) at a 1:1 ratio. The sample was then incubated overnight at 4°C to allow for annealing of the duplex regions. The sample was subsequently filtered through 0.2 μm filters and purified by size-exclusion chromatography (SEC) using a Superdex 75 16/600 SEC column (GE Healthcare 28-9893-33) running at 0.5 ml/min with fractions collected every 2 min. The purified aliquots were then concentrated with Pierce protein concentrators (ThermoFisher, #88515) and stored at 4°C until use.

Circular dichroism (CD)

CD spectra were acquired in a Jasco J710 spectropolarimeter in 1 cm path length quartz cuvettes at 20.0°C as outlined previously (26). Collection parameters were: 1.0 nm step size, 200 nm/min. scan rate, 1.0 nm bandwidth, 2 s integration time and 4 scan accumulation. Spectra were corrected for buffer background and normalized by strand concentration using the following formula:

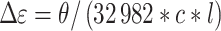(1)

where θ is ellipticity in millidegrees, c is molar DNA concentration, and l is path length.

Analytical ultracentrifugation sedimentation velocity (AUC-SV)

Experiments were performed in a Beckman Coulter ProteomeLab XL-A analytical ultracentrifuge at 20.0°C and 40k rpm in standard 2-sector cells using either an An60Ti or An50Ti rotor. Samples were equilibrated for >1 h. at 20.0°C prior to data acquisition. For each experiment, 100 scans were collected over an approximately 8-h period. Analysis was performed in SEDFIT (27) using the continuous C(s) model with resolution of 100 and partial specific volume of 0.55 ml/g for DNA.

Proton nuclear magnetic resonance spectroscopy (¹H-NMR)

1D proton NMR was performed on a Bruker Avance Neo 600-Mhz instrument with nitrogen-cooled prodigy TCI cryoprobe. Each measurement was conducted at 20.0°C using 3-mm NMR tubes. Water signal was minimized using a water flip-back pulse sequence. For each measurement, 1024 complex points were collected with an acquisition time of 86 ms. In total, 256 scans were collected for the DGD complex.

Cryo-EM data collection and image processing

The DGD sample was diluted to 2.5 mg/ml (or 87.7 μM) in BPEK buffer and 3 μl was applied to glow-discharged 300-mesh R1.2/1.3 UltrAufoil (lot #191113) grids. The grids were blotted for 4 s at 100% humidity and 5°C using a Vitrobot Mark IV (ThermoFisher) prior to vitrification in liquid ethane. The grids were screened using a Glacios cryo-electron microscope (ThermoFisher) operated at 200 kV to verify that particles of the approximate size were observed and had an optimal dispersion and density. High-resolution imaging was performed using a Titan Krios cryo-electron microscope (ThermoFisher) operated at 300 kV with a Falcon4 camera and at 96 000× nominal magnification. The calibrated pixel size of 0.8330 Å was used for processing. Cryo-EM movies were collected using Leginon (28) at a dose rate of 7.88 e⁻/Ų/s with a total exposure of 8.70 seconds, for an accumulated dose of 68.54 e⁻/Ų. Movie frames were recorded every 0.174 seconds for a total of 50 frames per micrograph. A total of 12 175 images were collected at a nominal defocus range of 0.8–2.7 μm. Appion (29) was used for monitoring data collection and experimental parameters.

Micrographs were corrected for beam-induced motion and dose-weighted using MotionCor2 (30). Corrected micrographs were imported into cryoSPARC (31) and contrast transfer function (CTF) estimations were performed using patch CTF estimation. In total, 9045 micrographs were used in the analysis after curation for CTF fit resolution, ice thickness, astigmatism, and defocus. Particles were first picked using a blob picker with min. diameter of 70 Å and max. diameter 130 Å (roughly based on the D_max value from SEC-SAXS), elliptical shape, and a min. separation distance of 0.75. Particles were inspected, extracted with a 256-pixel box size, and 2.9 million particles were used in an initial 2D classification with 150 2D classes (with max. resolution of 8 Å and initial classification uncertainty factor of 3). Six 2D classes were selected with 1.75 million particles and subsequently used to generate an ab initio model for template generation for a second round of particle picking using cryoSPARC’s template picker and separation distance of 0.75. Particles were again inspected and extracted resulting in a final of 4.65 million particles. These particles were used in 2D classification with 100 classes, max. resolution of 6 Å, an initial classification uncertainty factor of 5, force max over poses/shifts set to true, number of online-EM iterations set to 60, and 200 batch size per class. From this, 10 classes were selected with 666 328 particles. An initial 3D ab initio with three classes (max. resolution 5 Å, initial resolution 30 Å, class similarity 0.1) and subsequent heterogeneous refinement resulted in two ‘junk’ classes and one good class with 303,928 particles (46%) of the expected size and shape. Here, a ‘junk’ class refers to a 2D class that contains either poorly resolved particles or artifacts from ice or carbon edges that are not useful for particle reconstruction. Non-uniform refinement of the good class resulted in a map with GSFSC estimated resolution of 6.9 Å, however, the map had no discernible features apart from two regions that could be assigned to duplex arms. Subsequent 3DVA using this particle stack and volume revealed stretching, bending, and coiling movements. Therefore, to classify the particle stack into representative conformational states, we used another round of ab initio classification with 3 classes and similarity set to 0.8. The three resulting class volumes (class_0, class_1, class_2) were then used in another round of heterogeneous refinement with the same 303,928 particles and subsequently passed to non-uniform refinement jobs with max. align resolution of 6 Å, initial lowpass resolution of 20 Å, and non-uniform AWF set to 1.5. The resulting class refinements had GSFSC resolutions of 8.1 Å (class_0), 7.4 Å (class_1) and 6.2 Å (class_2) and had discernable secondary structural features, such as duplex grooves, a density ‘hole’ where the loop region is, and a flat region where the 3’ G-tetrad is expected. A diagram of the workflow and breakdown of the three non-uniform refinement results is shown in Figure S2-5. Map segmentation and coloring was done in UCSF Chimera v1.12 using the Segger (32) module.

Model building and refinement

Initially, a duplex-G4-duplex system was created that lacked the poly dT loop region. Duplex regions were built as B-form DNA using the structure editor function of UCSF Chimera v1.12. The G-quadruplex portion was built using atomic coordinates from parallel G4 structure 1XAV from the PDB. The three DNA regions were pieced together in Schrodinger's Maestro (Schrodinger Inc., https://www.schrodinger.com/) with potassium ions added and minimized between the G-tetrad stacks of the G4 using Maestro's minimization function with OPLS3e (33,34) force field and VSGB (35) (Generalized Born continuum solvent) model. Minimization was performed with 2 iterations, 65 steps per iteration, and an RMS gradient for convergence of 0.01 kcal/mol/Å. This loop-less model was simulated for 100 ns using the OL15 (36) DNA force field with TIP3P (37) waters (‘OL15-TIP3P’) which has worked well in the past for modeling the solution structures of higher-order DNA G4s (11,38). The resulting lowest energy model was chosen from the trajectory and used as starting coordinates for building in the poly dT loop region by systematically ‘growing’ each dT residue from 5’ to 3’ using Maestro's place fragment function. As each fragment was placed, slight manual adjustments to sugar-phosphate backbone were made to generate a reasonable loop topology to attached to the 5’ of the opposite duplex handle region. The dT loop was subsequently minimized twice using Prime (as above) while holding the duplex and G4 regions rigid. This model was subsequently used to generate two ‘bent’ models, one in which the 5’ duplex region was unstacked (‘5’ unstacked model’) and one with the 3’ duplex unstacked (‘3’ unstacked model’). In both cases the poly dT loop region was minimized using Prime (as above), prior to 100 ns simulations using the OL15-TIP3P and Joung and Cheatham (39) potassium ion parameters.

Model refinement against class_1 EM map

The closest fitting 3’ unstacked DGD model was identified by comparing the class_1 map to frames across the 100 ns trajectory using UCSF Chimera's map correlation function. Fitting of the 3’ unstacked model to the class_1 cryo-EM map was accomplished using a self-guided Langevin dynamics (SGLD) approach with AMBER’s EMAP restraint option (a.k.a. SGLD-EMAP) (40). The SGLD-EMAP refinement was performed in two steps in implicit solvent with the OL15 (36) DNA force field. In the first 25 ps, weak restraints of 1.0 kcal/mol/Å were placed on the duplex handle residues and G4 with tempsg = 400, sgft = 0.1, tsgavg = 0.2 and EMAP fcons = 0.1 and resolution = 50 Å. During the second 25 ps, the duplex and G4 restraints were removed and tempsg was reduced to 300. Convergence to an optimal map fit took ∼50 ps and was judged based on the calculated Chimera map fit value (the first model was chosen as the fit approached 1.0). This model was used as the starting configuration of all subsequent molecular dynamic simulations.

Molecular dynamics (MD) and trajectory analysis

MD simulations were conducted using the class_1 refined model as starting coordinates with two K⁺ ions manually placed in the central channel of the G-quartets of the G4. These ions were subjected to energy minimization in Schrodinger's Maestro (with OPLS3e (33,34) force field and VSGB (35) implicit solvent, 2 iterations, 65 steps per iteration and an RMS gradient for convergence of 0.01 kcal/mol/Å.) prior to simulation. Two separate 100 ns simulations were initially conducted with different force field and water combinations. The first implemented the OL15 (36) DNA force field with TIP3P (37) waters (OL15-TIP3P), which has worked well in the past for modeling the solution structures of higher-order DNA G4s (11,38). The second used a combination of parmbsc1 (41) DNA force field and SPC/E (42) waters (BSC1-SPCE). It has recently been shown that SPC/E waters yield satisfactory results in modeling G4 loop dynamics (43). In all cases, Joung and Cheatham (39) potassium ion parameters were implemented as they have been shown to behave best with G4 systems (44). To investigate system convergence, 500 ns simulations were conducted in duplicate using the BSC1-SPCE parameter set.

Systems were constructed by neutralizing the additional net negative charges with potassium ions prior to solvating in a water box with 12 Å distance between the solute and the edge of the periodic box using AMBER20’s LeaP (45) package. The systems were minimized and equilibrated to 300 K and 1 atm in five steps: (i) minimization of water and ions with weak restraints (10.0 kcal/mol/Å) on all nucleic acid residues (2000 cycles of minimization, 500 steepest decent before switching to conjugate gradient) with a 10 Å cutoff distance for non-bonded interactions; (ii) heating from 0 to 100 K over 20 ps with moderate restraints (50.0 kcal/mol/Å) on all nucleic acid residues; (iii) minimization of the entire system without restraints (2500 cycles, 1000 steepest decent before switching to conjugate gradient) with a 10.0 Å cutoff for non-bonded interactions; (iv) heating from 100 to 300 K over 20 ps with weak restraints (10.0 kcal/mol/Å) on nucleic acid residues and; (v) equilibration at 1 atm for 100 ps with weak restraints (10.0 kcal/mol/Å) on all nucleic acid residues. The output of equilibration was then used as input for unrestrained production simulations. MD simulations were performed using GPU accelerated pmemd code in the isothermal isobaric ensemble (300 K with friction coefficient of 1 ps⁻¹ and 1 atm) with periodic boundary conditions and Particle-Mesh Ewald (PME) for long-ranged, slow decay potentials. The SHAKE (46) algorithm was used to constrain bonds involving hydrogen atoms. Temperature was controlled using the Langevin thermostat (47) (ntt = 3) and pressure using the Berendsen barostat (48) (ntp = 1). A 12 Å cutoff distance for non-bonded interactions was used in all production simulation runs.

For SAXS modeling, an initial 100 ns simulation was conducted with restraints on all residues aside from the poly dT loop of the class_1 refined model to allow for a conformational search. As the resulting models were still too compact relative to what was measured by SAXS, we next conducted three independent 100 ns accelerated MD (aMD) (49) simulations with the OL15-TIP3P parameters to investigate the possibility of short-lived or high energy conformational states that may only be observable on much longer timescales. Our past observations have shown that aMD is an optimal technique for generating lowly populated expanded conformational states useful in modeling flexible ensembles (38). Production aMD simulations were performed by boosting the whole potential as well as extra to torsions (iamd = 3) using values calculated from the last 10 ns of the first 100 ns OL15-TIP3P simulation: Ethreshd = 3072.75, Ethreshp = –328 528, alphad = 64.4, alphap = 18733.32.

The program CPPTRAJ from the AmberTools20 (45) software package was used to calculate heavy atom RMSDs, anhydrous radius of gyration, and to perform principle component analysis (PCA) from each trajectory. Clustering was performed using the DBSCAN method (minpoints = 10, epsilon = 2.2, sieve 10, rms residues 47–92@P,O3',O5',C3',C4',5'). Solvent accessible surface area (SASA) calculations were done using the program NACCESS v2.1.1 (http://www.bioinf.manchester.ac.uk/naccess/), which implements the method of Lee and Richards (50), using the default probe size of 1.4 Å.

SEC-SAXS analysis and modeling

Size-exclusion chromatography-resolved small-angle X-ray scattering analysis was performed at the BioCAT beamline (18-ID) at the Advanced Photon Source in Chicago, IL. The sample was spun down prior to injecting onto an equilibrated Superdex 75 10/300 Increase GL column (Cytiva) maintained at a flow rate of 0.6 mL/min. using an AKTA pure FPLC (GE Healthcare Life Sciences). The eluate was directed through a 1 mm ID quartz capillary cell with 20 μm walls. A co-flowing buffer sheath was used to reduce radiation damage and keep the sample separated from the capillary walls (51). Scattering intensity was recorded on a Pilatus3X1M detector (Dectris) at a distance of 3.642 m from the sample, giving access to a q-range of 0.003–0.35 Å⁻¹. A continuous series of 0.5 s exposures were collected during elution and the data was reduced using the software BioXTAS RAW v2.1.3 (52). Creation of the buffer corrected I (q) vs. q curve was done by creating buffer blanks derived from averaging of regions flanking the elution peak and using these to subtract from the exposures selected within the sample peak. Deconvolution of the scattering vs. elution profile was performed in BioXTAS RAW v2.1.3 using the evolving factor analysis (EFA) functionality (see https://bioxtas-raw.readthedocs.io/en/latest/tutorial/s2_efa.html and (53)). SAXS data collection, reduction, analysis, and presentation have been done in accordance with published guidelines (54). The elution versus time data, Guinier analysis, Kratky analysis, P(r) distribution and tabulated results are given in Figures S8, S9, and Table S1. SAXS data and models have been deposited in the SASBDB (https://www.sasbdb.org/).

Generation of the DAMMIF ab initio model was done using DAMMIF (55) in slow mode with 15 reconstructions and no anisometry assumption followed by averaging using DAMAVER (56). Output from DAMAVER was subsequently used as the input for a final refinement in the program DAMMIN (57). Model resolution was estimated using SASRES (58). Results are in Table S1.

Modeling against the SAXS data was performed by directly comparing the cryo-EM refined or MD generated models directly to the scattering curve using CRYSOL v2.8.3 (59) with solvent density increased slightly to 0.3368 e/Å⁻³ to account for buffer components, 30 harmonics, 201 points and max q of 0.35 Å⁻¹. Models were generated from each simulation (with the two G4 channel K⁺ retained) using the CPPTRAJ (60) module of AMBER20. The results from each analysis are tabulated in Table S1. CRYSOL v2.8.3 calculates and attempts to minimize the following function when fitting:

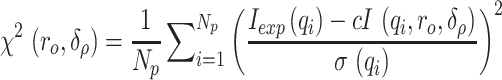(2)

where I_exp(q) is the experimental scattering, I(q) is the calculated scattering, σ(q) is the experimental scattering error, N_p is the number of points in the profile, r_o and δ_o are the effective atomic radius and hydration layer density, respectively.

To investigate how models compare to the experimental data with water explicitly accounted for, selected models from CRYSOL were submitted to the WAXSiS server (61,62). The WAXSiS server automatically computes small- and wide-angle X-ray scattering profiles of macromolecules using explicit solvent MD simulations, allowing for scattering profile calculations that account for the structure and density of the solvation layer (obviating fitting for such parameters). In this way, WAXSiS is a more rigorous, albeit very computationally expensive, method of assessing model fits.

SiteMap analysis

Two models were used in SiteMap binding site analysis: the DGD model with its poly dT loop converted to its full reverse complement (a.k.a. ‘G-DNA’ model) and the G4 alone (PDB ID 1XAV) used as-is. The G-DNA was created by mutating each respective base in the cryo-EM class_1 DGD model using the ‘swapna’ command in Chimera. This model was then simulated for 20 ns in explicit solvent with K⁺ neutralization and the OL15-TIP3P parameters. A representative model was generated by clustering over the entire 20 ns production simulation using sugar phosphate backbone heavy atoms and 10 clusters. The representative model of the largest cluster was used in SiteMap evaluation. SiteMap analysis reports a druggability, or Dscore, for each putative binding site identified. It is calculated as follows:

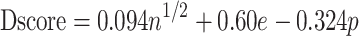(3)

where n is the number of site points at the identified site (max 100), e is the degree of enclosure, and p is the hydrophilic component. The average Dscore values from protein test cases were 0.631 for ‘undruggable,’ 0.871 for ‘difficult’ sites, and 1.108 for ‘druggable’ sites. The authors designate druggability classification in the following way: undruggable < 0.83; 0.83 < difficult < 0.98; 0.98 < druggable (63).

RESULTS

An overview of the DGD integrative structural biology (ISB) approach

The DGD system is complex due to its flexibility, asymmetry, partial disorder, and multiple DNA structural domains (single-, double- and tetra-stranded). For these reasons, no single technique is suitable for structural determination and, instead, an integrative approach is required (64). Instead of relying on a single method to describe the DGD system, the ISB approach allows for a more complete description, both of structure and dynamics, by incorporating all available biophysical information into a single consensus depiction. We characterized the DGD system in the following way: (i) we first obtain secondary structure information using CD and NMR spectra, which inform on the types of DNA topologies in the particle; (ii) we gather low resolution information, such as hydrodynamic size and shape from AUC-SV analysis and SAXS, results that provide model building constraints; (iii) we combine the topological and low-resolution shape information with nucleic acid geometries from deposited NMR or X-ray crystal structures (where applicable) to create an atomic model for MD simulation; (iv) we refine the system using a low resolution cryoEM map to obtain a final model; (v) we then use the cryoEM refined model to answer questions about the solution behavior and dynamics using more extensive MD simulation. The final DGD model is a more complete description of the system than any one technique alone can provide.

DGD forms stable duplex and parallel G4 features

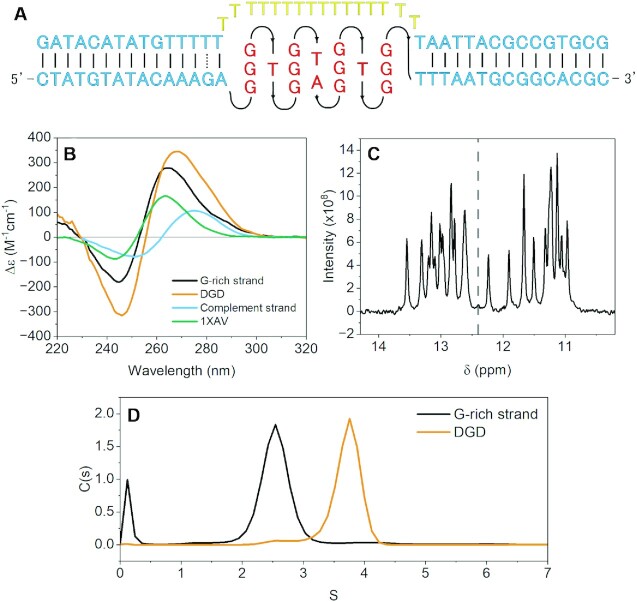
A schematic representation of the duplex-G4-duplex (DGD) construct is shown in Figure 1A. Prior to cryo-EM and SAXS analyses we confirmed that the G-rich strand of the DGD sequence forms a parallel G4, that G4 formation does not impede binding of the complement strand to form duplex handles, and that the G4 remains intact after complement binding. The CD spectrum of the G-rich strand shows a classically parallel signature with trough at 240 nm and peak at 264, similar to, but greater in magnitude than the 1XAV sequence, confirming a parallel conformation (Figure 1B). The addition of the poly dT surrogate-complement results in a peak shift from 264 to 270 nm, consistent with the additive CD signal from formation of B-form duplex handles. Duplex and G4 formation of the SEC-purified DGD complex was confirmed using ¹H NMR (Figure 1C), which shows both Watson–Crick and Hoogsteen hydrogen bonding chemical shifts. There are ∼12 partially overlapped G4 imino peaks, confirming the formation of a three-tetrad G-quadruplex (65). Lastly, sedimentation velocity experiments show unequivocally that the presence of the G4 does not inhibit complement strand binding, evidenced by a doubling of MW and substantial increase in S_20,w (Figure 1D) when the two strands are mixed.

Figure 1.

Schematic and preliminary secondary structure analysis of DGD. (A) Schematic of the DGD system with surrogate poly dT complement strand (top) and G-rich strand (bottom). (B) Normalized circular dichroism spectra of 1XAV, the DGD complex, and each of the DGD constituent strands by themselves. (C) ¹H NMR spectrum of the imino proton region of the purified DGD complex with dashed line visually denoting Watson–Crick (>12.4 ppm) and Hoogsteen (<12.4 ppm) regions. (d) AUC-SV sedimentation distributions of the G-rich strand alone or in complex with the complement strand to form the DGD construct.

DGD is a flexible bent particle with duplex features flanking a central globular density

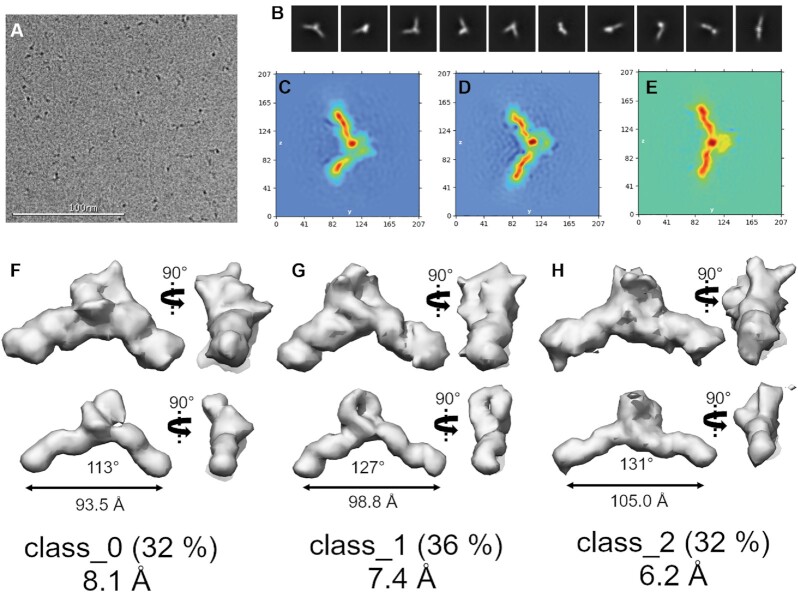
We next collected cryoEM data on the DGD system using a Titan Krios operated at 300 kV. In total, 12 175 images were collected and, after manual curation for CTF fit resolution, ice thickness, astigmatism and defocus, 9045 micrographs were used in final processing. Figure 2A shows a representative motion corrected micrograph, showing black specks that range in shape from globular (viewing down the duplex axis) to elongated and V-like with longest dimensions of 110–130 Å. Figure 2B shows the reference-free 2D class averages of 666 328 particles identified from particle picking. These classifications show that the DGD particle is V-shaped and exhibits a bulky, globular central density flanked by two thinner rod-like regions, consistent with a G4 flanked by two duplex arms.

Figure 2.

Cryo-EM single particle analysis of DGD. (A) Representative motion corrected and dose weighted micrograph. (B) cryoSPARC reference-free 2D class averages. (C–E) cryoSPARC real-space heat map slices showing slices through each of the three distinct conformations derived from 3D ab initio reconstructions. (F–H) Final 3D reconstructions with low (top row) and high (bottom row) thresholds. The real-space heat maps correspond to the 3D reconstructions (C with F, D with G, and E with H). Distance and angle measurements are derived from the high threshold maps. Below each map is the GSFSC resolution at 0.143. See Figures S1–S4 for more detailed workflow and non-homogenous refinement outputs.

We next performed a 3D ab initio reconstruction from the various views to assign the placement of the G4 within the central globular density. Initially, all the good particles identified from 2D classification were pooled to generate a final map with nominal Gold Standard Fourier Shell Correlation (GSFSC) resolution of 6.81 Å. However, this map had no distinguishable features, such as the anticipated duplex grooves or features within the central density. We found empirically that the best map resolutions were achieved by splitting the particle stack into three classes, and that no recombination of particle stacks (e.g. class_0 & class_2, class_1 & class_2, class_ 0 & class_1) improved the maps. See Supplementary Figure S1 for full workflow. Heat maps derived from the three 3D class refinements are shown in Figure 2C–E. Like the 2D class averages, features from the duplex helix are evident and a distinct globular density is centered between each duplex handle. The cryoSPARC heat maps themselves are compelling, as they appear to reveal a dynamic asymmetric stacking and unstacking or bending in and out of the Z–Y plane. The final 3D reconstructions of each class are shown in Figure 2F–H (see also Supplementary Figures S2–S4 for non-uniform refinement output). To further investigate particle dynamics, we also conducted a 3D variability analysis (66) (3DVA) of the combined particles from each of the three classes. 3DVA reveals that the first, second, and third principal components of movement are 5’ to 3’ stretching (101–123 Å end-to-end), twisting, and wagging, respectively, with each movement linked to density alterations among the poly dT fulcrum region (see Supplementary Figure S5 and supplemental videos 1–3).

The nominal GSFSC resolutions of the refined, final maps are 8.1, 7.4 and 6.2 Å. In each case, high and low thresholding reveals that the duplex handles and a central, globular density are evident. Only class_1, at 7.4 Å, has features that are interpretable for model refinement. Class_1 has well-defined right-handed B-form duplex features, a wide flat density consistent with the tetrad face of the G4, and loop density features that imbue the map with a handedness. At high thresholding, class_1 maintains the G4 central globular density and reveals a ‘hole’ between the G4 and dT loop region (Figure 2) that is consistent with the dT loop protruding away from the duplex/G4 axis. Classes 0 and 2 are too ambiguous for use in modeling but are interesting in that they show two extremes in the bending/flexing distribution of DGD, consistent with 3DVA and MD analyses (below). Altogether, the results from cryoEM single particle analysis reveal that the DGD system is flexible, with the poly dT protruding outward from the duplex axis and the G4 situated at the fulcrum point between the two duplex handles.

Molecular dynamics reveals that the DGD G4 preferentially stacks onto the 5’ duplex handle and exhibits significant flexibility because of a persistently unstacked 3’ handle

As there are no deposited atomic coordinates to model the DGD system against, aside from the G4 component 1XAV (24), we manually constructed junctions between G4 and B-form duplex regions. An initial DGD model was created using 1XAV and two B-DNA duplex handles in which the handles were stacked coaxially onto the G4s at both G-tetrad interfaces (Supplementary Figure S6). Initially, the poly dT loop was absent, and this loopless DGD system was simulated extensively to achieve a low energy conformation. Interfacial stacking was maintained throughout the loopless DGD simulations. The poly dT surrogate loop was then added by building in each residue one by one from 5’ to 3’ with manual backbone torsion adjustment to join the two complement duplex handle regions. The poly dT loop was subsequently minimized for multiple rounds while keeping the duplex and G4 regions restrained. This model was used as the starting point for subsequent MD investigations and rationalization of the cryo-EM class_1 map.

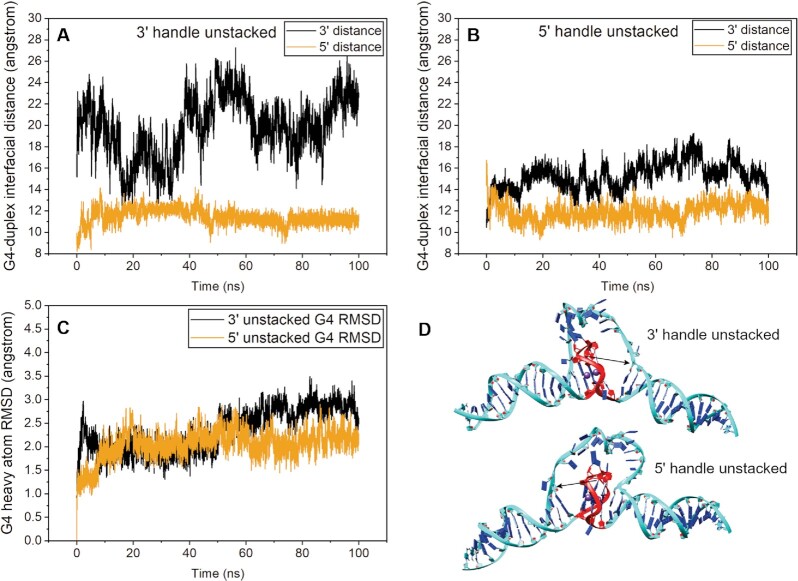
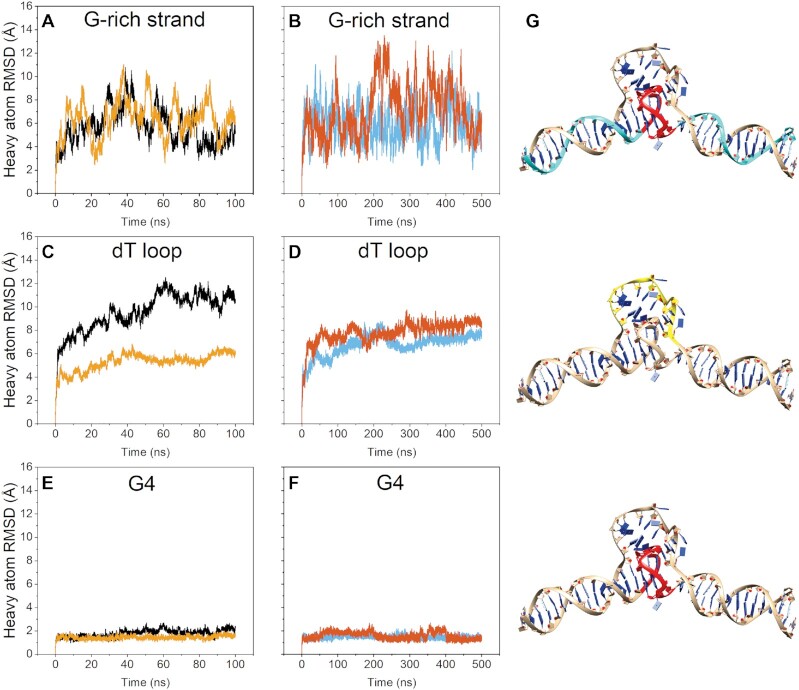
The cryo-EM heatmap slices revealed that the duplex arms range from stacked, to ‘unstacked,’ to bent slightly out of plane (Figure 2C–E). Due to the limited resolution of the class_1 map, it is difficult to say which handle should be modeled as unstacked. To investigate this, we constructed both systems, ‘5’ handle unstacked’ and ‘3’ handle unstacked’, by manually adjusting the handles at angles such that they are in approximate agreement with the bend angle observed for the class_1 map. In each case, the poly dT surrogate loop was minimized to account for any strain or geometry violations induced from moving the duplex arms. Figure 3D shows plots of the distances between the central G-tetrad and corresponding thymine residue at both 5’ and 3’ duplex stacking interfaces over the course of 100 ns of simulation. In both cases, the simulations start with an ∼16 Å distance between central G-tetrad and corresponding thymine (Figure 3A, B). The 3’ handle never returned to the stacked conformation, owing to the non-complementary dT-dT base pair (Figure 3a black line). Conversely, within about 3 ns the 5’ handle re-stacks onto the G4 and maintains this interaction throughout the simulation (Figure 3B, gold line). The relative instability of the 3’ handle (in the case when the 5’ handle is unstacked) is also evidenced by its fluctuation in distance over time (Figure 3B, black line). Figure 3C shows that there is little change in G4 conformation throughout both simulations, confirming that it remains stable and intact. Collectively, these simulations show that the 5’ stacking interface is preferential to the 3’ interface for the DGD system.

Figure 3.

Molecular dynamics analysis of DGD starting from 5’ or 3’ duplex handles ‘unstacked’ from G-tetrad interface. (A and B) Plots of residue-residue distances for the 3’ handle unstacked (A) and the 5’ handle unstacked (B) simulations. In each case the distances plotted are between the central G-tetrad of the G-quadruplex and complement thymine residues of the base pair closest to the stacking interface. (C) G4 residue RMSD plots of heavy atoms. (D) starting models for each simulation with red indicating the G4 residues and black arrows indicating the distance being measured in each case.

CryoEM class_1 map refinement reveals a persistent poly dT loop interaction at the 3’ G-tetrad interface

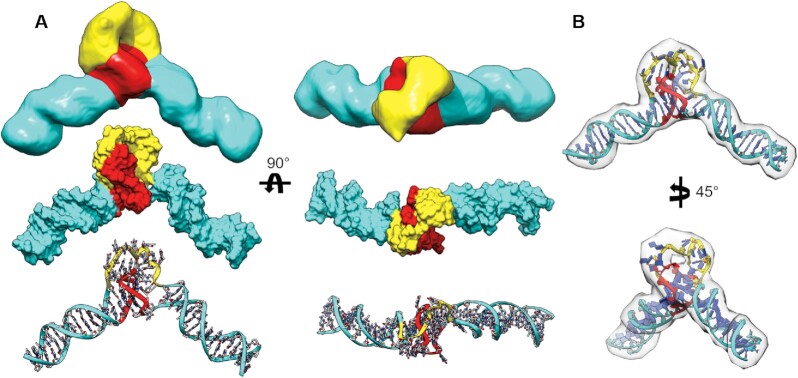
The class_1 EM map is not of sufficient resolution for atomic-level structural refinement. However, multiple techniques, such as normal mode analysis, geometric simulation, and molecular dynamics, have been developed over the years to aid in flexible structural refinement into low resolution maps (67). Molecular dynamics-based approaches offer the distinct advantage of using contemporary nucleic acid force fields to flexibly refine models, which is essential for our purposes of fitting a single-stranded poly dT loop. To this end we used a self-guided Langevin dynamics (MapSGLD) (40) with AMBER EMAP (SGLD-EMAP) simulation (see Supplemental Video 4), which uses the cryoEM class_1 map as a restraint for conformational searching. Figure 4 shows the results of refinement using the 3’ handle unstacked model as input. A comparison of the 3’ unstacked model in Figure 3 with that of the final refined model in Figure 4 shows that only subtle conformational adjustments took place in the 5’ handle/G4 region, whereas the poly dT loop conformation changed dramatically as it was guided into the map, creating an interaction interface with the 3’ G-tetrad.

Figure 4.

Structural comparison of the class_1 EM map with SGLD-EMAP MD-refined model. (A) Comparison of the cryo-EM map (top) segmented and colored by putative domains with the EMAP-refined model in space-filling (middle) and atoms and ribbons representations (bottom). Domains are colored based on duplex (cyan), poly dT loop (yellow), and G4 (red) regions. (B) The EMAP-refined DGD model docked into its map density at a ‘medium’ threshold to emphasize fit of poly dT loop.

As an independent, unbiased, method of assessing the structural domains of the class_1 map and validity of our map-refined model, we employed the program Segger (32). Segger attempts to identify distinct regions of EM maps that correspond to separate subunits or domains. Reinforcing our structural analysis, the program identified the duplex handles, G4, and poly dT regions in the EM map as separate domains, colored in cyan, red and yellow, respectively (Figure 4). The red region has orthogonal protrusions relative to the duplex handle axis with a very flat, partially exposed region that we presume to be the G4 propeller loops and 3’ G-tetrad face, respectively. At high threshold, the cavity between the red and yellow regions reveals a hole between the dT loop and G4 regions (Figure 4B), which is consistent with the yellow region being attributed to a flexible loop rather than the G4. We note that due to the low resolution of the map, and in part the lack of understanding of how single-stranded DNA behaves under vitrification conditions, the dT loop appears to be ‘stuffed’ into the map by the SGLD-EMAP refinement procedure. This is possibly a result of a reduced dT loop density due to its presumed flexibility. Regardless, the MapSGLD fitting procedure allowed us to build a representative atomic model with confidence in the arrangement of duplex handles and G4.

MD simulation of the class_1 map refined DGD recapitulates flexing motions inferred from heat map slices and 3DVA

We next conducted more extensive MD simulation to probe the overall conformational stability and dynamics of the class_1 refined DGD model. We previously observed good agreement between experimental SAXS data and higher-order DNA G4s when using the OL15-TIP3P parameter set (11,38). However, recent long time-scale simulations have shown that the parmbsc1 (41) DNA force field and SPC/E (42) (‘BSC1-SPCE’) yield good results with standard B-form (68) and G-quadruplex loop dynamics (43), respectively. It is important to show that both sets of force field parameters yield similar conformations and dynamics across their trajectories, as the DGD system is exceptional in that it contains three distinct topologies of DNA (single-stranded, double-stranded, and tetra-stranded). We began by conducting 100 ns simulations using both OL15-TIP3P and BSC1-SPCE parameter sets (Figure 5A, C, E). In both cases, the G4 remained stable and intact (Figure 5E) with the bulk of the movement derived from bending and coiling movements that span the duplex-G4-duplex axis (as shown by the magnitude of RMSD fluctuations in Figure 5A). The two simulations were consistent in that that thymine residues of the poly dT loop remain stacked at the 3’ interface of the G-quadruplex. To verify that we were not missing any major conformational dynamics we also conducted triplicate accelerated MD (aMD) simulations of 100 ns using the OL15-TIP3P parameters (Supplementary Figure S7), as well as duplicate 500 ns simulations using the BSC1-SPCE parameters (Figure 5B, D, F). In all cases the structural features were maintained (i.e. the duplex handles and G4 maintained their structure and H-bonding interactions) and the partially disordered poly dT loop remained persistently stacked at the 3’ G-tetrad interface. The two G4 coordinated potassium ions were retained in all simulations (without the use of restraints) and are displayed as part of the model. However, they were not experimentally verified or observed directly in the cryo-EM map density. We note that the poly dT loop residues sample a larger conformational space in the aMD simulations but remained persistently stacked against the 3’ G-tetrad in all cases (Supplementary Figure S7).

Figure 5.

Molecular dynamics of the class_1 EM refined DGD model. Data in (A), (C) and (E) are from OL15-TIP3P simulation (black) and BSC1-SPCE simulation (yellow). Data in (B), (D) and (F) are duplicate 500 ns BSC1-SPCE simulations. (A, B) heavy atom RMSDs of the G-rich strand residues only. (C, D) heavy atom RMSDs of the poly dT loop residues only. (E, F) heavy atom RMSDs of the G-quadruplex residues only. (G) most representative model from clustering across the duplicate BSC1-SPCE trajectories (B, D and F) showing the residues used in calculating the RMSDs in panels A–F in cyan, yellow and red.

Lastly, we wanted to investigate the major modes of DGD movement across the simulations to see how they compare with the cryoEM 3DVA and heat map slices in Figure 2. As the system appeared converged, based on significant overlap of frames during clustering of the two 500 ns BSC1-SPCE trajectories, we used the combined trajectories in a principal component analysis (PCA). Consistent with observations from cryoEM, the first three major components of motion, which are given in Supplemental Videos 5–7, show ‘fulcrum’ bending motions that arise from concerted poly dT loop sliding and 3’ handle bend and twist movements. Collectively, the combined MD and cryoEM results reveal a highly stable 5’ duplex-G4 interaction interface with a highly dynamic, unstacked 3’ duplex handle and poly dT surrogate complement loop region.

Size-exclusion chromatography-resolved small-angle X-ray scattering (SEC-SAXS) confirms the DGD 5’ duplex-G4 stacking preference and suggests a highly expanded poly dT loop exists in solution

Considering that highly dynamic and/or disordered regions are often poorly resolved or entirely lost in cryoEM reconstructions, we next sought to investigate how our refined DGD model compares with its SAXS scattering. SAXS is highly sensitive to the sugar-phosphate backbone of nucleic acids, making it well suited for studying the solution behavior of single-stranded DNA (69). SAXS scattering was collected continuously as a function of elution from an SEC column with co-flowing buffer sheath to mitigate radiation damage (51). The elution profile exhibited minor leading and lagging peaks which were due to minor aggregation and non-complexed single strand, respectively, based on estimated sizes. We attempted to overcome this by using an evolving factor analysis (EFA) (53) to deconvolute the DGD scattering from contaminants (Supplementary Figure S8). The resulting DGD scattering curve proceeds horizontally to the Y-axis and has normally distributed residuals by Guinier analysis (Supplementary Figure S9b, c), indicating that the DGD scattering profile is free of interparticle interactions.

After confirming that the SAXS data quality is sufficient for interpretation, we assessed its size and shape. The Guinier R_g for DGD is 32.49 ± 0.09 Å. Conversion of the scattering to a dimensionless Kratky plot reveals that DGD is an elongated and flexible particle, as indicated by a plateau region from ∼2.4–5 qR_g, consistent with our former cryoEM and MD analyses. The P(r) distribution shows that DGD has an R_g = 33.23 ± 0.06 Å and D_max = 133 Å (See Supplementary Table S1 for tabulated results). The latter is in good agreement with the maximum stretch motions observed in the first component of cryoSPARC 3DVA. Qualitatively, the P(r) distribution has a poorly defined maximum and skew at high values of r, which suggests a multi-domain flexible particle (70) and is consistent with an unstacked duplex handle region. A representative ab initio dummy atom model (DAM) is shown in Supplementary Figure S10. The model is in good agreement with the overall architecture of the class_1 EM refined DGD model.

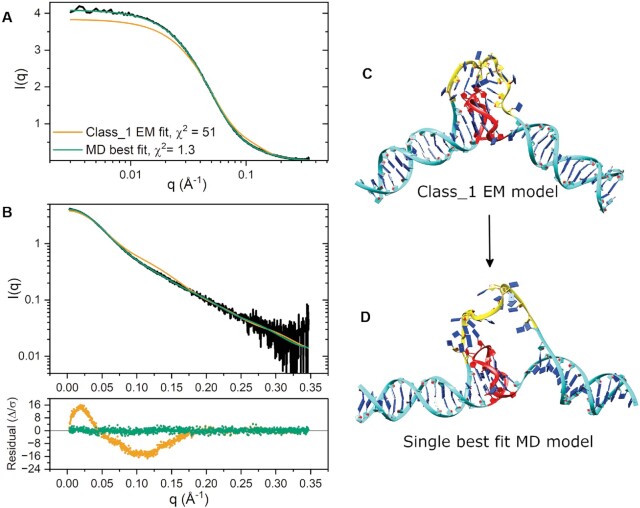
To determine how the class_1 refined DGD model compared with our SAXS data, we employed CRYSOL v2.8.3 (59) to evaluate its scattering. The calculated fit is shown in Figure 6A, B and model in Figure 6C. The class_1 refined model has a poor fit in the low- to mid-q regime, as shown by the magnitude and shape of residuals and χ² values. The EM model is also 4.7% smaller than measured by SAXS, with R_{g,class_1} = 31.68 Å (versus R_g,exp. = 33.23 ± 0.06 Å). We reasoned that the fit discrepancies could arise from differences in poly dT loop behavior in vitreous versus solution conditions, as a highly flexible and extended poly dT region could result in smaller apparent cryo-EM map volumes. To investigate this, we used CRYSOL to calculate the fits of models from across all MD simulations (including the 5’ and 3’ unstacked models). The single best fit model was identified from the 3’ unstacked trajectory (Figure 6D), which exhibits a nearly maximized extension of the poly dT loop region and significant out of plane bending of the 3’ duplex region. The calculated fit to the model is in excellent agreement with the SAXS scattering as judged by its normally distributed residuals and a low χ² = 1.3. Further, the calculated radius of gyration is in general agreement with both the Guinier and P(r) values (R_g,model = 32.82 Å versus R_g,Guinier = 32.49 Å and R_g,P(r) = 33.23 Å). However, one of the two fitted parameters (δ_o), which corresponds to hydration layer electron density (71), was maximized, possibly indicating over-fitting. To investigate this discrepancy, we examined this DGD best fit model with the WAXSiS server (61), which explicitly accounts for the hydration layer. WAXSiS analysis indicates excellent agreement between model and experimental scattering with χ² = 1.4 (Supplementary Table S1). The two model conformations in Figure 6C and D are visually in agreement with the class_1 and class_0 cryo-EM heat map slices shown in Figure 2, respectively. Further, the conformational change required to shift between these two models is consistent with flex or out-of-plane wag motions observed by 3DVA. We note that the best fit model exhibits H-bonding across the G4 propeller loop and poly dT loop that appear to lock the 5’ duplex handle and G4 into a stacked configuration, possibly contributing to the preference for 5’ stacking. Overall, the SAXS results support the cryo-EM analysis and the preferential 3’ handle unstacking and suggest that a more expanded poly dT loop species may exist in the non-vitreous state.

Figure 6.

CRYSOL fits to SAXS scattering. (A) SAXS scattering and model fits shown on a linear-log scale to emphasize differences in scattering at very small angles. (B) SAXS scattering and model fits shown on a log-linear scale with corresponding residual plot. (C) class_1 refined DGD model. (D) Best fit class_1 loop MD DGD model. (D) Single best fit explicit solvent MD DGD model.

Although EFA deconvolution is usually quite robust, in this case similar choices of ranges for components yielded curves with similar shapes but R_gs that varied by ∼5%, so there is some inherent uncertainty in the true size of the macromolecule in solution. We believe this is primarily due to the overlap of a small amounts of aggregated species within the analyte peak, which is evident in the SEC-SAXS elution profile (Supplementary Figure S8 and S9). Because of this limitation, more robust modeling methods for flexible systems, such as the ensemble optimization method (EOM) (70), were not pursued. Instead, we draw conclusions from the collective SAXS results which qualitatively support a flexible system and validate the overall architecture of the cryo-EM derived models.

SiteMap assessment of the ‘G-DNA’ model shows that the duplex-G4 junction is quantifiably more druggable than the 1XAV G4

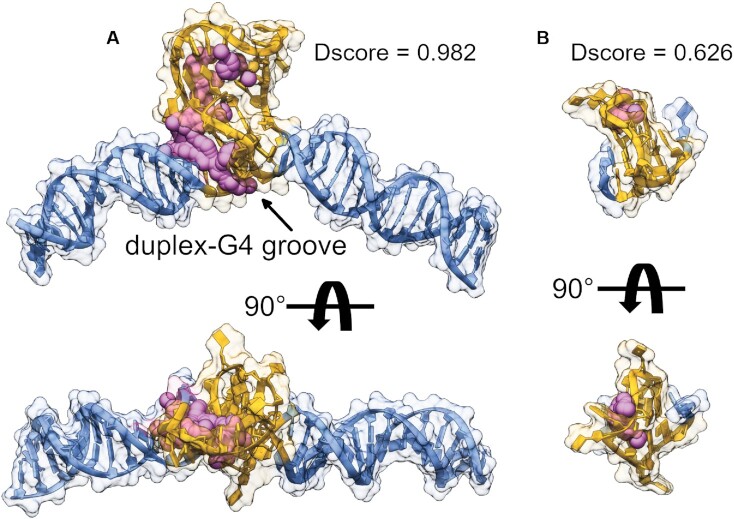
With the first medium-resolution structure of a duplex-embedded G4 model, we next wanted to see how it fares as a target relative to an isolated monomeric G4. To do this, we used the DGD (class_1) model to generate a more biologically relevant ‘G-DNA’ by swapping the poly dT loop for the reverse complement sequence and performing a short MD simulation to allow the new loop to adjust. We also included the NMR structure of 1XAV in the analysis to contrast the differences in targeting a single small G4 versus a higher-order G4-duplex promoter system. To identify putative drug binding sites and quantitatively assess their respective druggability, we employed the program SiteMap (63,72). The output from SiteMap analysis is a druggability score, or ‘Dscore,’ which incorporates the number of SitePoints (size of the contiguous pocket), isolation from solvent, and a penalty for high hydrophilicity (Eq. 2). It was empirically determined that binding sites with Dscores below 0.83 are ‘undruggable’, sites above 0.98 as ‘druggable’, and those in between as ‘difficult’ (63). Figure 7 shows the Dscores of the highest scoring binding sites identified by SiteMap analysis. The G-DNA model has a binding site with ‘druggable’ Dscore of 0.982 that traces the groove located between the duplex–G4 junction and spans into the region of the G4 propeller loop and C-rich complement loop interaction site. Note that the G·C and A·T base pairs preceding the 5’ G-tetrad that make up the bulk of the binding groove are consistent with the wild-type MYC NHIII promoter (24). In contrast to the G-DNA model, the isolated 1XAV G4 is predicted to be ‘undruggable’ with a Dscore of 0.626. The 1XAV loop binding site is predicted to have many comparable characteristics to the G-DNA site but is hampered by its smaller volume (86% smaller) and fewer predicted hydrogen bond donors and acceptors (Supplementary Table S2). No major differences were observed between the G-tetrad stems of the G-DNA and 1XAV structures aside from the propeller loop, which differs by 6.8 Å RMSD due to C-rich loop H-bonding interactions (Supplementary Figure S11). The G-DNA site offers the distinct advantages of a unique sequence composition coupled with the tertiary arrangement of duplex, G4, and the milieu of the complement loop/G4 propeller loop interactions. Collectively, these results indicate that the higher-order G4 is a more selective DNA target than a simple monomeric form.

Figure 7.

SiteMap potential receptor binding site identification and quantification. (A) The G-DNA system built from cryo-EM class_1 refined DGD coordinates, (B) the parallel G4 1XAV from NMR investigations. Magenta spheres and surface regions are 3D representation of the SiteMap sites and 5 Å zones surrounding the identified pocket. Orange regions encompass the G4 and its reverse complement (where applicable) and blue regions correspond to the duplex (non-G4 forming) regions. Models in (A) and (B) are to scale. The results of SiteMap analysis are tabulated in Supplementary Table S2.

DISCUSSION

It is estimated that 40% or more of human gene promoters harbor G4 motifs (73), and these motifs share extensive overlap with transcription factor (TF) regulatory sites (i.e. within 100 bases of the TSS) (74,75). G4-ChIP-seq and transcriptional profiling studies have revealed that TF recognition can be both structure and sequence driven (10). Promoter G4s have emerged as a new layer of epigenetic transcriptional control that influence both cell-type (76) and cell-state (77). For these reasons it is important that we gain a structural understanding of G4s within their natural duplex context.

Since a cartoon model of G4 formation within a duplex promoter sequence was published as Scheme 2 in (78), that model has become a meme for representing possible drug binding to G4 promoters. In contrast to such arbitrary schematic representations of promoter G-quadruplexes, where the G4 is depicted as protruding away from the helical axis and is entirely exposed (12), we show here that the duplex-embedded G4 is in fact occluded. Our DGD system shows a definite preference for coaxial stacking of the duplex at the 5’ end of the G4. The preference for stacking at the 5’ G-tetrad of parallel G4s is well established. Multiple crystal structures of parallel G4s have been resolved with a 5’-5’ stacking preference (79–81). Solution NMR dimerization studies have also confirmed a preference for 5’-5’ stacking over alternative modes (3’–3’, 5’–3’, 3’–5’) using model G4 sequences (80). Stacking of hairpin duplex base pairs (15–16,81) and unpaired bases (24,82) (such as terminal bases or loops) against G-tetrads has also been reported, although 5’ and 3’ preferences have not been directly tested. However, the thermodynamics of base stacking and mismatched hydrogen bonding are well established (83). In our DGD system, the 5’ duplex handle meets the G-tetrad interface with an A·T base pair in which the adenine maintains a B-form type sugar-phosphate backbone geometry (83,84) and stacks against the subsequent guanine in the 5’ G-tetrad face. In contrast to this, the 3’ handle meets the 3’ G-tetrad with a mismatched T·T base pair. The A→G type stacking and A·T base pairing interactions are thermodynamically more stable than G→T stacking and T·T hydrogen bonding interactions (83), which provides a rationale for the preferential 5’ stacking interaction model. Based on the SAXS modeling analysis, it is also apparent that the poly dT loop may influence the 5’ stacking preference by H-bonding with the propellor loops of the G4 moiety. Mutations to the surrogate poly dT region could feasibly change the stacking preference if, for instance, the T·T were mutated to an A·T Watson–Crick base pair.

Our cryo-EM map-refined models, MD simulations, and SAXS models all indicate that the poly dT loop interacts with the G4’s propeller loop nucleotides and preferentially stacks against the 3’ G-tetrad face (Figures 4 and 5). Our ‘G-DNA’ model, which has the poly dT loop region mutated into the G4-region complement, maintains these interactions, supporting the notion that the G4 is occluded in a more natural sequence environment (Figure 7). In fact, solvent accessible surface area (SASA) calculations show that the G-DNA model G4 is 16% less exposed than the single-strand flanked 1XAV G4 (Supplementary Table S3). The difference increases to 34% when only non-polar surfaces are considered. This is important given that the majority of high affinity G4 ligands target the G-tetrad faces through an end-pasting binding mode (i.e. π–π stacking interactions) (85). Targeting the small, isolated promoter G4 structures may be unproductive if, in situ, these G4 tetrad faces are inaccessible. However, DGD is highly flexible, owing to its loop and displaced 3’ handle region. Therefore it remains possible that the static occluded conformation is not the ideal structural target for drug discovery efforts (86).

In contrast to the work of Tuntiwechapikul and Salazar (21), who modeled their duplex-embedded G4 with a shortened poly dT surrogate-complement, we chose to use a full-length sequence to mimic the actual backbone length of a promoter bubble. The cryo-EM classes identified present bend angles relative to the duplex axis by as much as 70°. As confirmed by MD simulations, this bending behavior persisted throughout all simulations conducted. Solution SAXS measurements indicate that the poly dT could exhibit a ‘maximized’ conformation, rather than interfacial stacking, with frequent H-bonding of the propeller loops. Taken together with the observed molecular dynamics of the poly dT region, this suggests that the poly dT loop allows for significant flexibility, possibly imposing strain on the system. In the absence of stabilizing interactions, such as base-pairing and stacking, single-stranded DNA behavior is strongly influenced by counterion concentration (87). Indeed, at 200 mM cation, single-stranded DNA has a persistence length on the order of 15–30 Å (88,89), which is longer than the 15 Å distance required for stacking at both ends of the DGD G4 (measuring O3’ to O5’ of the poly dT gap in Supplementary Figure S6). The biological implications of such a stressed loop are manifold (e.g. G4s in non-template strands facilitating transcriptional progression (90)). It is reasonable to assume that the actual C-rich complementary strand would behave similarly under physiological circumstances.

The DGD model, with its bent, hinge-like feature, fits well into the overall scheme of G4-promoter regulation as we currently understand it. Duplex DNA is extremely rigid, with a persistence length on the order of 500 Å (or 150 bp, ∼3× the length of DGD) (91). Transcription often requires multiprotein complexes that act in cis on promoter elements from distant binding motifs. It follows that energy must be expended to bend or twist the DNA to facilitate transcriptional protein-protein interactions (requiring about 17–19 kcal/mol of energy) (92). Recently, Shen and colleagues (93) established that promoter G-quadruplexes exist independently of transcription and are controlled by the local chromatin state, suggesting that they act to recruit the transcription machinery rather than form as the result thereof. This mechanism is in line with the G4 ‘binding hub’ hypothesis of Spiegel et al. (10), where G4s function as general recruitment centers for transcription factors. Direct evidence for promoter G4s acting as DNA hinge sites was shown using the G4 binding transcription factors Yin and Yang 1 (YY1), where the authors used a HiChIP-seq method to verify that YY1 modulates DNA looping in a G4-dependent manner (94). Altogether, these studies point to a possible mechanical role for G4s in promoters where quadruplex formation facilitates the sharp bending necessary for transcriptional activation by energetically relieving bend-induced strain (for reference, 1XAV has a free energy of folding on the order of –11 kcal/mol (25)).

An ongoing challenge in the EM field is the atomic-level interpretation of low resolution (>>4 Å) maps—a problem that is compounded by flexibility. There are many excellent approaches for interpreting EM maps, such as rigid fitting, flexible fitting, machine learning, and de novo approaches (reviewed in ref (67)). Unfortunately, many of these tools, such as de novo and machine learning approaches, are protein-centric, and are often not applicable to DNA G-quadruplex systems. Further, in the case of the DGD system, although the duplex handle regions and G4 could be treated as separate rigid domains, there remains the problem of allowing the poly dT loop to probe conformational space while accounting for local geometry, torsional stress, and physiochemical interactions. Fortunately, flexible fitting molecular dynamics approaches, such as the SGLD-EMAP (40) approach implemented here, have been developed that allow for the incorporation of contemporary MD force fields with EM maps of virtually any resolution to refine atomistic models against experimental EM data. To our knowledge, this is the first application of SGLD-EMAP to an all-DNA system.

A possible point of concern is the comparatively poorer fit of the cryo-EM map-refined DGD models with their solution-based SAXS scattering data (Figure 6). This could result from multiple sources, both technical and practical. Technically, it is possible that an expanded poly dT loop (such as in Figure 6D) would not be captured by cryo-EM due to its inherent plasticity. Consistent with this, we observe little to no loop density in the heat maps in Figure 1 and the general conformation of the expanded poly dT loop conformation visually agrees with the class_0 heat map (Figure 2C). Practically, minor amounts of aggregated species that may not be fully deconvoluted from the DGD scattering profile were evident in the SEC-SAXS profile (Supplementary Figures S8 and S9). Due to this inherent uncertainty in the final SAXS scattering curve, no further refinement (such as EOM (70)) against this data was carried out. The model in Figure 6D agrees with what was observed by cryo-EM and MD; however, it may also be a façade, or ‘averaged’ conformation (e.g. of an ensemble of dT loop configurations) which soaks up errors in the fit by the many parameters of the CRYSOL fit function (Eq. 2). Although we did not observe substantial conformational expansions of the poly dT loop in simulations of the class_1 refined model, it is possible that these events occur on a longer time scale (ms or s) or that the MD force fields used are deficient. Regardless of these potential shortcomings, the collective results show that models derived from the two methods with dissimilar sample environments offer complementary information necessary for rationalizing the complexities of dynamic higher-order DNA systems.

Structural characterization of higher-order DNA G-quadruplex systems is challenging by traditional high-resolution methods (NMR, X-ray diffraction), as evident by the dearth of structures available. We have recently shown that tens of thousands of gene promoters, many of which are from proto-oncogenes, have the capacity of forming complex higher-order G4 assemblies (e.g. duplex–G4, G4–G4, G4–hairpin–G4) with unique loop, groove and junctional sites (11,95). As their biological importance grows, so does the need for methods that can capture their tertiary folds and dynamics with sufficient resolution. Here we have shown that an integrative structural approach combining SAXS, MD and cryo-EM, can resolve structural features and dynamics of higher-order DNA G4 systems. Further, at a nominal resolution of 7.4 Å, our DGD model reveals a tertiary arrangement with sufficient detail to gain actionable structural insight to facilitate drug targeting.

DATA AVAILABILITY

The supporting data for this manuscript are available from the corresponding authors upon reasonable request. Cryo-EM and SAXS structures and atomic models, where applicable, have been deposited to their respective data banks: EMDB accession code EMD-27726, PDB accession code 8DUT, SASBDB accession code SASDPU6.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institute of Health [GM077422]. Funding for open access charge: UofL Health Brown Cancer Center.

Conflict of interest statement. None declared.