Shear shock waves mediate haptic holography via focused ultrasound

Abstract

Emerging holographic haptic interfaces focus ultrasound in air to enable their users to touch, feel, and manipulate three-dimensional virtual objects. However, current holographic haptic systems furnish tactile sensations that are diffuse and faint, with apparent spatial resolutions that are far coarser than would be theoretically predicted from acoustic focusing. Here, we show how the effective spatial resolution and dynamic range of holographic haptic displays are determined by ultrasound-driven elastic wave transport in soft tissues. Using time-resolved optical imaging and numerical simulations, we show that ultrasound-based holographic displays excite shear shock wave patterns in the skin. The spatial dimensions of these wave patterns can exceed nominal focal dimensions by more than an order of magnitude. Analyses of data from behavioral and vibrometry experiments indicate that shock formation diminishes perceptual acuity. For holographic haptic displays to attain their potential, techniques for circumventing shock wave artifacts, or for exploiting these phenomena, are needed.

The spatial resolution and dynamic range of holographic haptic displays are determined by shear shock wave formation in the skin.

INTRODUCTION

A longstanding goal in the engineering of haptic systems for telepresence, teleoperation, and virtual reality has been to create technologies that allow their users to touch, feel, and interact with virtual three-dimensional (3D) objects or environments in midair, where no physical object is present. Emerging 3D holographic haptic displays can supply such tactile feedback in midair by focusing ultrasound emitted from phased arrays of transducers. Nonlinear acoustic radiation forces generated by incident ultrasound impart small deformations to the skin (1, 2). Similar phenomena and technologies have also been exploited for acoustic particle manipulation (3). Holographic haptic displays rapidly scan ultrasound focal points along trajectories on the skin to enable users to feel 3D objects (4), patterns (5, 6), contact-like impulses (7), or textures (8). Among existing haptic technologies, such holographic systems are unique in their ability to enable users to interact with palpable virtual objects in midair, where no physical device or interface is present. Consequently, there is tremendous current interest in holographic interface technologies for telepresence, telerobotics, augmented and virtual reality, computer-aided design, and other areas (9).

Although promising, current holographic haptic display techniques yield tactile sensations that are faint and diffuse. Users describe them as feeling like a “breeze” or “puff of air” or like touching lightweight material, such as thin, muslin fabric (10). Practical displays can readily focus ultrasound in air with resolutions of a few millimeters (11, 12), but tactile sensations felt by users are far less localized, as reflected in thresholds for two-point discrimination (>3 cm) and line angle discrimination (18°) (2, 13). While prior numerical and experimental studies have demonstrated that holographic haptic feedback excites distributed vibrations in the skin (14–16), the acoustic-elastic phenomena involved have not been characterized, and no mechanistic explanation for the disparity between perceptual acuity and acoustic focusing has yet been advanced.

Here, we show how the effective spatial resolution and dynamic range of holographic haptic displays are determined by effects of viscoelastic wave transport in the skin, including the formation of ultrasound-driven shear shock wave patterns whose spatial dimensions can exceed acoustic focal dimensions by an order of magnitude. These shock wave phenomena arise from the use in holographic haptic systems of a technique (termed spatiotemporal modulation) of rapidly scanning a focused ultrasound source along a geometric path on the skin (4, 17, 18). This technique yields sensations that are more easily felt because ultrasound intensity is held at a constant, maximum level at all times (17). Furthermore, the rapid source motion excites skin oscillations at elevated frequencies (100 to 300 Hz) that drive responses in the multitudes of vibration-sensitive receptors in the skin, including Meissner and Pacinian corpuscle sensory afferents (19, 20). However, rapid source motion is also theoretically associated with ancillary wave effects, including shear shock formation, that have not been contemplated, described, or characterized in prior research on haptic holography. Notably, commonly used scanning speeds, v = 3 to 22 m/s (15, 17, 18, 21), can readily exceed the propagation speed, c = 1 to 10 m/s, of shear waves, which transport most energy in soft tissues within the range of tactile frequencies (22–24). Scanning speeds can be further elevated because of effects such as grazing incidence. When the scanning speed, v, is greater than or equal to the shear wave speed, c, the excited shear waves constructively interfere along a prominent shock front—the Mach cone—that confines most energy within a trailing conical region whose apex angle, θ = sin⁻¹(1/M), becomes more acute with increasing Mach number M = v/c. Similar shear shock wave processes arise in medical ultrasound radiology, as in the supersonic shear imaging technique (25).

RESULTS

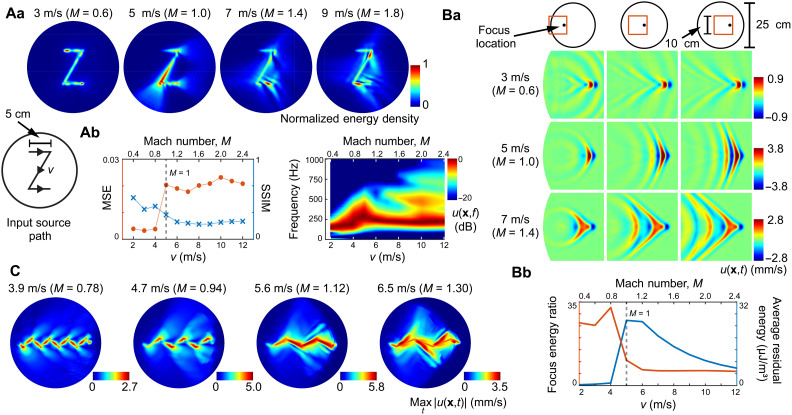
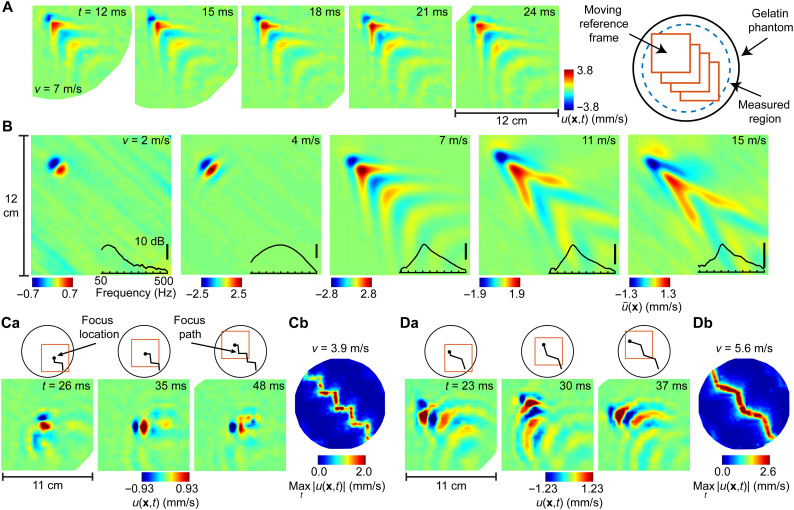
We first numerically simulated ultrasound-elicited mechanical responses in a viscoelastic tissue slab with material properties approximating human skin (see Materials and Methods). Constant-intensity focused ultrasound sources (focal diameter, 0.6 cm) scanned geometric trajectories across the surface of the tissue, exciting prominent shear wave oscillations. Consistent with theoretical predictions, the scanning ultrasound sources excited viscoelastic wake patterns that trailed the source (Fig. 1), extending up to 10 cm or more behind the instantaneous source location (Fig. 1Ba). Energy imparted to the medium was distributed over a region whose surface area (10 to 50 cm²) was far larger than the ultrasound focal area (0.28 cm²). At transonic (M = 1) and supersonic (M = 1.4) scanning speeds, shear shock fronts formed Mach cones with apex angles that became more acute with increasing Mach number M = v/c (Fig. 1, A and B). Amplitudes were largest near M = 1. This is the speed at which waves excited at prior times coherently superimpose at the focal location. Similar shock wave patterns formed even when the motion path was coarsely discretized by updating the focus location at sample rates that were as slow as, or slower than, those used in existing holographic haptic devices (Fig. 2). Lower scanning speeds (M = 0.6) not only yielded the most localized wave patterns but also produced the smallest-amplitude oscillations because the excited waves propagated more isotropically and did not combine along a Mach cone. Rapid (M ≥ 1) scanning speeds impaired focusing, decreasing the focal energy ratio (a measure of contrast) by as much as 85% and increasing the average residual energy (ARE; an error measure) by 2500% (Fig. 1Bb). Shock waves resulted in prominent artifacts where the scanning trajectory changed direction in a manner that caused propagating wavefronts to overlap, yielding constructive and destructive interference (Figs. 1C and 3).

Fig. 1. Shear shock wave formation during focused ultrasound stimulation of numerically simulated tissue.

(Aa) Energy density of surface waves as an ultrasound focal point scanned a trajectory at subsonic (v = 3 m/s, M = 0.6) and supersonic (M ≥ 1) speeds. (Ab) Supersonic scanning excited shock waves, increasing the mean-squared error (MSE) and reducing structural similarity (SSIM) between the designed and elicited feedback patterns. Supersonic scanning excited higher-frequency oscillations. (Ba) Shear shock waves formed at higher scanning speeds [instantaneous normal oscillation velocity u(x, t) is shown]. Mach cones trailed the focus location by more than 9 cm. (Bb) Shock formation diminished focal energy and increased residual (error) energy density. (C) Wave patterns elicited by lateral modulation of the scanning trajectory [scanning velocity v = (v_x, v_y), v_x = 3,4,5,6 m/s, v_y = ± 2.5 m/s]. Shock formation yielded prominent corner artifacts along the zigzag scanning trajectory.

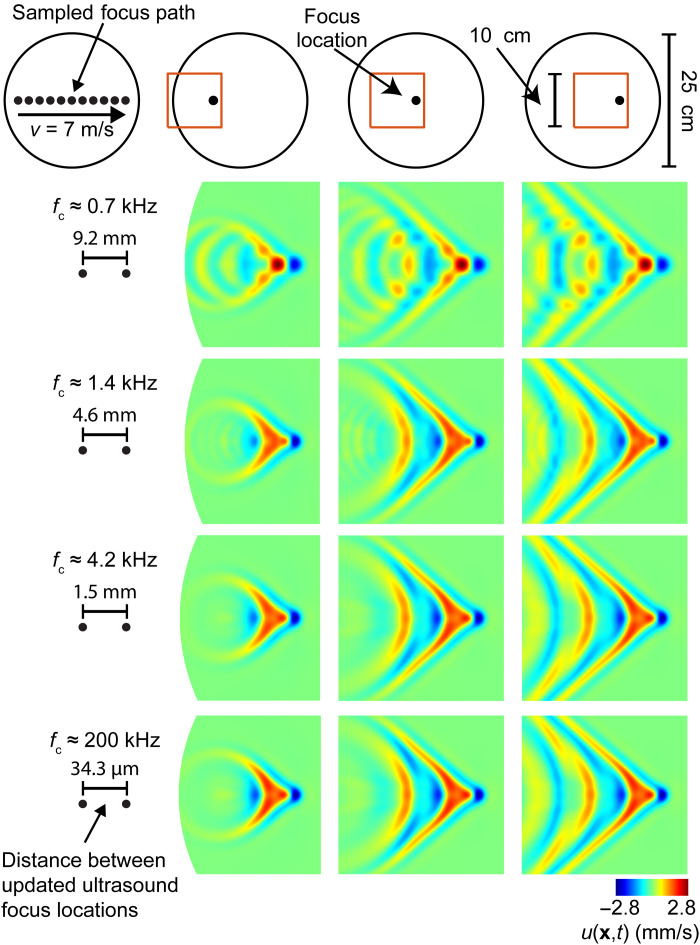
Fig. 2. Shear shock wave characteristics are robust to variations in focus control sample rate.

Shear shock wave patterns formed as an ultrasound focal point scanned a linear trajectory with supersonic speed [v = 7 m/s, M = 1.4; oscillation velocity u(x, t) is shown]. The focal location was updated at control sample rates of f_c = 0.7, 1.4, 4.2, and 200 kHz, yielding respective spatial sample periods of 9.2, 4.6, 1.5, and 0.03 mm along the scanning trajectory. Shear shock wave characteristics, including Mach cone formation, were conserved as the focus control rate was varied. Modest sampling artifacts occur at the lowest control rate of 0.7 kHz, which is far less rapid (less than 5%) than the rates used in commercially produced devices. At all higher control rates, shock wave pattern characteristics were nearly indistinguishable (numerical results presented in Figs. 1, 3, and 4 and fig. S1 were obtained with f_c = 200 kHz).

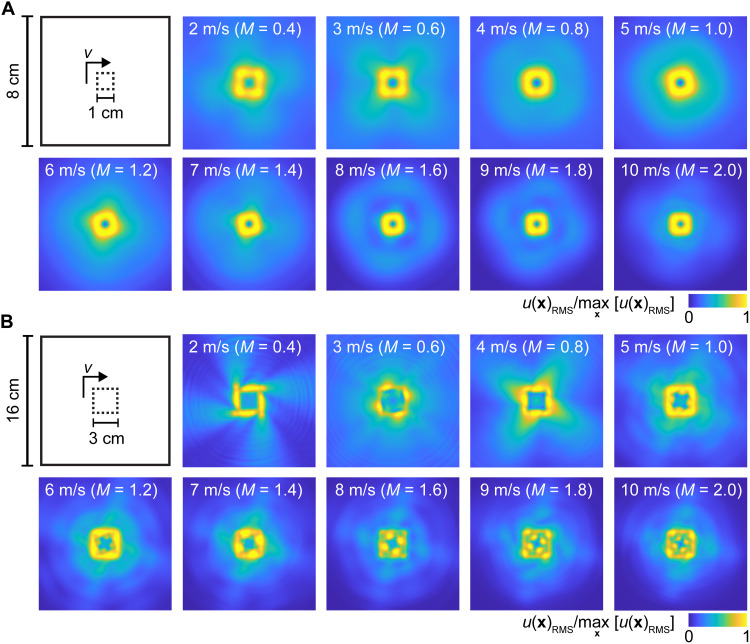
Fig. 3. Complex shock wave artifacts produced during display of simple geometric forms at different scanning velocities.

(A) Time-averaged wave patterns elicited via scanning stimulation of numerically simulated tissue along small square trajectories [normalized root mean square (RMS) oscillation velocity is shown]. Here, the shape dimensions (1 cm) are comparable in size to the wavelengths excited in the medium, yielding wave patterns that are smoothed and distorted, with substantial residual energy in central and peripheral regions at all scanning speeds. (B) Larger (3-cm) squares exhibited complex artifacts arising from constructive interference. At high speeds, global (v = 8 m/s) or local (v = 9, 10 m/s) maxima of the oscillation amplitude occur near discrete points interior to the scanning path.

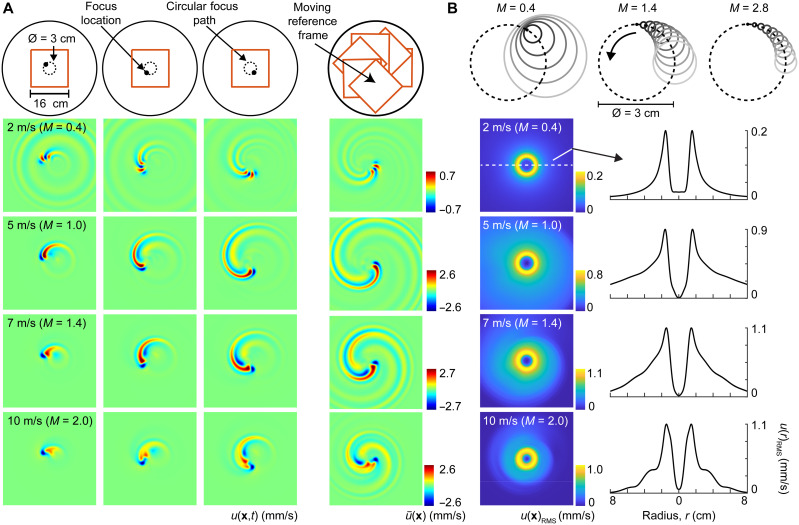
Complex shock wave artifacts also affected the display of closed geometric figures, including squares and circles (Figs. 3 and 4 and fig. S1). Focused ultrasound delivered along circular scanning paths excited extended wave patterns whose Mach cones formed distorted spiral wakes that became longer with increasing Mach number (Fig. 4A), consistent with theory (26). Wake lengths also reflected effects of viscous damping. Constructive interference in the interior of the circular scanning path resulted in oscillations whose energy was distributed over a range of radial distances that contracted toward the center of the circle with increasing Mach number, causing an apparent shrinking of the displayed shape (fig. S1). It is possible that such phenomena could be exploited to improve focusing resolution. Minimal wave energy was delivered to the center of the circular scanning paths (Fig. 4B), consistent with prior theoretical predictions for the confinement of spiral wave energy in the exterior of a central disc that is delimited by the terminal loci of constant-phase spiral wave crests (26).

Fig. 4. Shear shock wave formation in numerically simulated tissue during scanning along closed circular trajectories.

(A) Wake patterns trailed the scanning focus location. Because of shock formation, wakes were longest at higher scanning speeds v ≥ 5 m/s, corresponding to Mach numbers M ≥ 1 [oscillation velocity u(x, t) is shown]. Right column: Temporal compositing in the moving reference frame of the source, $\overline{u}(\mathbf{x})$, revealed spiral wake patterns. (B) Time-averaged wave fields; RMS oscillation velocity is shown. For Mach numbers M ≥ 1, waves radiated outward from the circular scanning trajectory. Constructive interference in the region circumscribed by the scanning trajectory yielded the greatest wave amplitude along a smaller circle whose radius decreased as M increased. Wave oscillations were greatly attenuated throughout a central quiescent disc, consistent with theoretical predictions (see also fig. S1) (26).

We confirmed these findings using laboratory vibrometry experiments that measured wave patterns elicited during focused ultrasound stimulation of a tissue phantom and human hands (Fig. 5). We captured spatially and temporally resolved optical vibrometry measurements of surface oscillations as a tissue phantom with skin-like mechanical properties was stimulated via constant-intensity focused ultrasound (see Materials and Methods and movies S1 and S2). Consistent with wave mechanics and consistent with findings from our numerical simulations, large-amplitude shear shock wave patterns, with acute, speed-dependent wake angles, were elicited when an ultrasound source scanned across the surface at transonic to supersonic speeds (Fig. 6, A and B). These shear shock patterns lagged behind the focus location and formed rapidly, over the course of milliseconds. The surface area (10 to 50 cm²) of their wake region was orders of magnitude larger than the effective acoustic focal area [0.36 cm², based on prior characterizations (2)]. Thus, the effective focusing resolution was dominated by shock wave formation rather than by ultrasound focusing. Wave energy trailed the focus location within a wake 10 cm or more in length and also extended several centimeters in directions perpendicular to the scanning path. Complex artifacts were generated at even moderate scanning speeds when additional lateral modulation was applied to the linear path (forming a zigzag pattern) (Fig. 6, C and D) due to the increase in instantaneous scanning speed and to coherent self-interference of the trailing Mach cone (see movie S3). Lower scanning speeds (v = 2 m/s) yielded wave patterns that were concentrated near the focal location due, in part, to viscous damping. However, these waves were smaller in amplitude and lower in frequency and thus would be felt only faintly by the skin (Fig. 6B) (27).

Fig. 5. Time-resolved optical vibrometry characterizations were obtained during focused ultrasound stimulation of a tissue phantom and human hands.

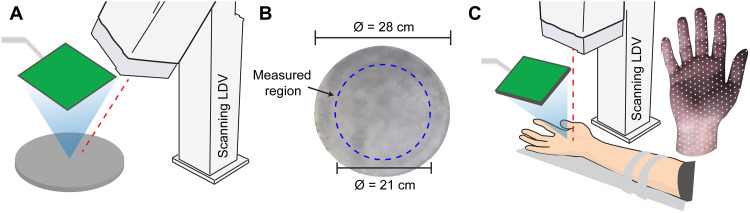
(A) A scanning laser Doppler vibrometer (LDV) captured surface oscillations elicited as a tissue phantom with mechanical properties emulating those of human skin was stimulated via focused ultrasound delivered from a phased array of ultrasound transducers (shown in green). (B) Time-resolved vibrometry measurements were captured with high spatial resolution (5-mm resolution and 1200 locations) uniformly distributed throughout a central region of the tissue phantom. (C) In vivo vibrometry measurements were captured from human hands at more than 300 measurement locations (right).

Fig. 6. Shear shock wave formation in a tissue phantom excited via focused ultrasound.

(A) Time-resolved wave patterns observed via scanning optical vibrometry [oscillation velocity u(x, t) is shown]. Time averaging in the moving reference frame of the source, $\overline{u}(\mathbf{x})$, revealed coherent wake structures (B). (B) Coherent structure in waves excited via source scanning. Supersonic scanning (M > 1) excited trailing wake patterns with lengths (≥ 12 cm) that were large, relative to the source dimensions (focal width δ < 1 cm). In contrast, low-speed scanning (v = 2 m/s, M < 1) excited wave patterns that remained confined near the focus location. Inset: Frequency content in excited wave patterns. As Mach number increased, a broader range of higher frequencies was excited. (C and D) Wave patterns excited via scanning along a zigzag path at subsonic (Ca and Cb) and supersonic (Da and Db) speeds.

We obtained similar findings from further analyses of in vivo measurements of human hands. The analyzed data were collected in an earlier study by the authors (Fig. 7A and fig. S2; see Materials and Methods) (14). Ultrasound scanning paths extended along an axis of the volar hand surface, from the wrist to the tip of the index finger. The linear paths were laterally modulated transverse to the motion direction (yielding zigzag path shapes) because such modulation has been found to elicit stronger sensations (18). Because of viscoelasticity, shear waves in tissues are dispersive, propagating with frequency-dependent wave speeds. However, the lowest and highest scanning speeds (v_l = 1 and 11 m/s) were, respectively, within the subsonic and supersonic regimes over the range of frequencies excited here (Fig. 7D) (22). Consistent with theory and findings from our numerical simulations and phantom tissue experiments, low scanning speeds (v_l = 1 m/s) excited shear wave patterns that extended outward from the instantaneous focal location (Fig. 7A). At higher scanning speeds (v_l > 4 m/s), the patterns formed wakes that trailed the motion by 10 cm or more (Fig. 7, A and B). The length of these wave patterns exceeded the approximate focal width (0.6 cm) by more than an order of magnitude. At the lowest scanning speed, time-averaged frequency content was concentrated near harmonic multiples of 125 Hz (twice the modulation speed), because the constant-pressure focal region crossed the axis of symmetry of the trajectory twice every 16 ms (Fig. 7D). At high speeds, the motion path was approximately linear, and a broadly distributed range of higher frequencies was excited because of the shorter total duration of the stimulus and the shorter duration of the transient pressure increase that was imparted to each skin location on the path when it was traversed by the focus. Frequency content at low and high speeds also reflected effects of frequency-dependent damping that, due to viscoelasticity, caused greater attenuation at higher frequencies (28).

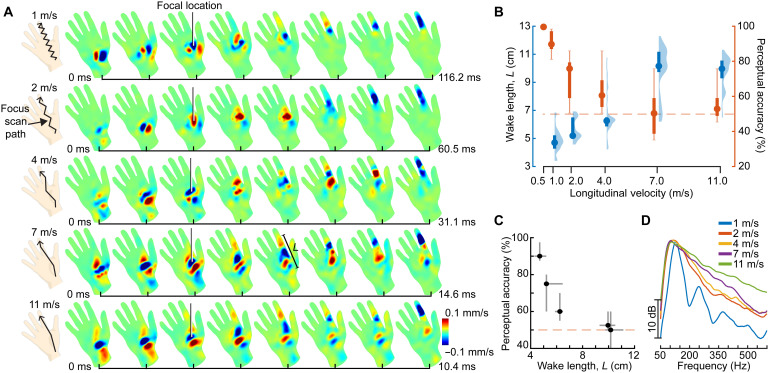
Fig. 7. Shear shock formation diminishes the perception of haptic feedback via focused ultrasound.

(A) Viscoelastic wave patterns excited via focused ultrasound stimulation of the volar hand surface revealed with optical vibrometry [oscillation velocity u(x, t) is shown]. Low scanning speeds yielded wave patterns that radiated outward from the focal location. High speeds elicited trailing wake patterns with lengths of 10 cm or more. (B) Wake length increased with increasing scanning speed (blue: median, interquartile range, and violin plot). Accuracy of tactile motion perception followed an opposite trend (red: median, interquartile range, and extrema). (C) As wake length increased, perceptual accuracy decreased monotonically (median and interquartile range are shown). (D) As scanning speed increased, energy was distributed over a broader and higher range of frequencies.

We confirmed that these phenomena are reflected in human haptic perception by comparing results of these analyses of the in vivo vibrometry data (Fig. 7B, blue) with behavioral data that were obtained via an experiment on tactile motion perception (Fig. 7B, red) (14). Conditions in the perception experiment mirrored those used in the vibrometry experiment (see Materials and Methods). During each trial, participants felt a focused ultrasound stimulus that scanned from the wrist to the tip of digit 2 or vice versa; they reported the direction of scanning motion. Perceptual accuracy was greater for lower scanning speeds (P < 0.0001) and declined to chance levels at the three highest scanning speeds (v_l = 4, 7, and 11 m/s), which produced the most elongated wakes (Fig. 7B, blue). An integrative analysis comparing data from the perception and vibrometry experiments revealed that perceptual accuracy declined monotonically with increasing wake length (Fig. 7C).

Thus, a prominent decline in perceptual accuracy was associated with supersonic scanning speeds. Supersonic scanning excited shear shock wave patterns with wake lengths that were nearly as long as the entire motion path (Fig. 7, B and C). This decline in perceptual accuracy occurred despite the fact that skin oscillation velocities were far greater at high than at low scanning speeds (Fig. 7A), indicating that the decline is due to the increase in spatial extent of skin oscillations. Moderately supersonic scanning speeds elicited oscillations in larger surface areas and delivered greater total energy to the skin. Such rapid scanning allows sensations delivered by holographic haptic displays to be more easily detected via touch (17), but our results show that this benefit is accompanied by a prominent spatial spreading of the stimulus. The perception of such holographic haptic stimuli also reflects the neural processing of spatiotemporal tactile stimuli in somatosensory brain areas (29). Today, these processes are not fully understood. Furthermore, neuroscience research may be required to fully clarify the effects of neural processing on such perceptual responses, which are, nonetheless, consistent with observations from our vibrometry experiments.

DISCUSSION

In summary, we report several lines of evidence that show how the spatial resolution and dynamic range of holographic haptic feedback supplied via focused ultrasound are effectively determined by ultrasound-driven elastic wave transport in soft tissues. Theoretical considerations, results from numerical simulations, and optical vibrometry measurements—with both phantom tissue and human hands—show that dynamic stimulation via focused ultrasound excites widespread ancillary vibrations in the skin. The most prominent of such artifacts are large-amplitude shear shock waves, which are efficiently generated whenever dynamic ultrasound feedback is supplied via scanning at transonic or supersonic speeds, irrespective of the scanning trajectory. Complex patterns of skin oscillation are produced for scanning trajectories that cause wake regions to overlap, because of constructive interference (Figs. 1C, 3B, and 6, C and D). The dimensions of the ensuing wave artifacts can exceed the aeroacoustic focal dimensions by more than an order of magnitude. Thus, when shear shock waves are present, they determine the effective spatial resolution and dynamic range of holographic haptic displays.

Ultrasound source variations that are sufficiently dynamic to drive shock wave formation arise frequently in practice (9), such as in the following instances: when feedback is supplied via rapid source scanning along a geometric path, as is commonly done to compensate for dynamic range limitations; when a scanning path is rapidly modulated; when a dynamically varying feedback pattern, or a scene containing moving virtual objects, is displayed; when a sufficiently oblique angle of ultrasound incidence arises because of hand or array inclination, resulting in elevated scanning phase velocities; or when a user’s hand reaches into an object, yielding oblique incidence near the periphery of the hand. Thus, the phenomena reported here are likely commonplace in current practice.

As we have demonstrated, shear shock waves can markedly alter the spatiotemporal characteristics of holographic haptic feedback supplied to the skin. We also confirmed that the accuracy of motion perception decreases monotonically as wake length increases, which occurs at increasingly supersonic scanning speeds. These perceptual findings, in concert with our theoretical, numerical, and experimental vibrometry characterizations, indicate that the perceptual fidelity of feedback supplied via holographic haptics is substantially determined by elastic wave transport processes. Although our results are generally consistent with prior investigations (15, 17), some caution is required in extrapolating from these findings connecting mechanics and perception. The stimulus set used in the behavioral experiment facilitated comparison with the vibrometry results; however, the diversity of the stimuli was limited. The scanning trajectories traversed the entire length of the hand with different scanning speeds, which could raise concerns about the confounding effects of duration. However, in further experiments, we confirmed that the findings from the perceptual study were conserved when duration was held constant by cyclically repeating the stimuli (see Supplementary Text and fig. S3). Furthermore, in our main study, differences in stimulus duration were compensated by the fact that participants repeated stimuli at higher speeds considerably more often than at lower speeds (fig. S3B). More generally, extant methods provide incomplete insight into the complex neural and perceptual processes through which mechanical oscillations of the skin are transduced, by multitudes of heterogeneous tactile sensory receptors (19), into neural information that is subsequently processed via somatosensory networks in the brain. Notwithstanding recent progress (30–32), theoretical and methodological advances are needed to elucidate the effects of elastic wave transport in the skin on tactile perception.

The phenomena that we report are salient for contemporary efforts to engineer holographic haptic interfaces for virtual reality, robotic teleoperation, and other areas. Our findings show how holographic haptic feedback is mediated by viscoelastic wave transport in the skin, including shear shock formation. Shock formation is associated with many display configurations that match those in current practice. These phenomena may explain why the sensations elicited by holographic haptic displays are described by users as feeling diffuse (10), despite the fine resolution [<5 mm (11, 33)] with which practical displays can focus ultrasound in air. Additional knowledge and techniques for leveraging ultrasound-elicited wave transport in the skin could enable high-fidelity holographic haptic systems that allow their users to touch, feel, and interact with otherwise intangible remote or virtual worlds.

MATERIALS AND METHODS

Focused ultrasound–based holographic haptic display

The holographic haptic display (UHEV1, Ultrahaptics Ltd.) comprised a planar array of N ultrasound emitters. Such a display focuses sound in air by applying a phase delay to each transducer signal. Constructive interference yields localized regions of high differential pressure, sufficient to impart time-varying displacements to the skin (1, 2). The differential acoustic pressure field may be described by

$$p(\mathbf{x},t)={\displaystyle \sum _{n-1}^N}\frac{1}{4\mathrm{\pi }{r}_n}{a}_n\exp [j({kr}_n-\mathrm{\omega }t-{\mathrm{\varphi }}_n)]$$ (1) (1)

where x is a position within the Fresnel zone of the array, a_n is the amplitude of the acoustic pressure wave emitted from transducer n, k = ω/c is the wave number, f = ω/(2π) = 40 kHz is the ultrasound carrier frequency, c is the speed of sound, r_n = ‖x − x_n‖ is the distance from x to the location x_n of transducer n, and ϕ_n is the corresponding phase delay. Focusing at a location x_f is achieved by matching the phase delays, ϕ_n, to the propagation time for a wavefront to reach the focus ϕ_n = ω‖x_f − x_n‖/c, thus yielding constructive interference. The focal width, δ, satisfies a Rayleigh diffraction limit, with δ ⪆ c/(2f).

Ultrasound frequency oscillations cannot be directly felt via touch. In haptic holography, palpable low-frequency mechanical signals are produced via a nonlinear phenomenon known as acoustic radiation pressure. Neglecting viscosity, the Langevin acoustic radiation force F_L imparted to an object (here, the skin) at a focus location is, to second order, given by

$${\mathbf{F}}_L=-{\iint }_{S}dS(⟨p_2⟩\mathbf{I}+{\mathrm{\rho }}_0⟨{\mathbf{u}}_1\otimes {\mathbf{u}}_1⟩)\cdot \mathbf{n}$$ (2) (2)

where p, ρ, and u are the fluid pressure, density, and velocity fields. The angular brackets denote time-averaged quantities, n is the surface normal, I is the unit tensor, and S is a surface region containing the focus location. Subscripts 0, 1, and 2 refer to successive terms in a perturbation expansion about a quiescent fluid configuration (33–36). Applying the same expansion to the Navier-Stokes equation yields an expression for 〈p₂〉 in terms of lower-order quantities

$$⟨p_2⟩=\frac{1}{2}\frac{1}{{\mathrm{\rho }}_0{c}_0^2}⟨p_1^2⟩-\frac{1}{2}{\mathrm{\rho }}_0⟨{\mid {\mathbf{u}}_1\mid }^2⟩$$ (3) (3)

Averaged over 1 cycle of oscillation, only the quadratic terms are nonzero. Together, they yield a nonvanishing, low-frequency force F_L(x, t) that elicits vibrations in the skin (see Supplementary Text). The time evolution of these vibrations is governed by a driven elastic wave equation

$${\mathbf{F}}_L(\mathbf{x},t)=\{-m\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{t}^2}+\mathrm{\mu }{\mathrm{\nabla }}^2+[(K+\mathrm{\mu }/3)\mathrm{\nabla }]\mathrm{\nabla }\cdot \}\mathrm{\xi }(\mathbf{x},t)$$ (4) (4)

Here, ξ(x, t) is tissue displacement, and m, μ, and K are the mass density, shear modulus, and bulk modulus, respectively. Plane wave solutions, $\mathrm{\xi }(\mathbf{x},t)=A\hat{\mathbf{r}}{e}^{j(\mathbf{k}\cdot \mathbf{x}-\mathrm{\omega }t)}$, describe oscillations along polarization directions $\hat{\mathbf{r}}$. Because of the low-frequency content of the acoustic radiation force and high propagation speed of compression waves, most acoustic energy is transferred to shear (transverse) wave components, $\hat{\mathbf{k}}\cdot \hat{\mathbf{r}}=0$. For skin or soft tissues, shear wave speeds, $c=\sqrt{\mathrm{\mu }/m}$, are frequency dependent and can range from 1 to 10 m/s at the tactile frequencies applicable to this study (22, 23). Because of viscoelasticity, wave amplitudes are also attenuated in a frequency-dependent manner with increasing propagation distance (30).

Elastic wave simulations

We used the pseudo-spectral numerical method [software package k-Wave (37)] to simulate ultrasound-elicited shear viscoelastic waves in a cylindrical slab of tissue-like material (diameter, 25 cm; thickness, 1 cm; mass density, 923.5 kg/m³; absorption, 300,000 dB/MHz² cm; and shear wave speed, 5 m/s). The simulation used a pseudo-spectral, time-domain method, with viscoelasticity captured via a Kelvin-Voigt model. The simulations modeled mechanical responses in the slab that were elicited via a focused acoustic source with a Gaussian spatial profile [full width at half maximum (FWHM) δ ≈ 6 mm] that was 28% larger than the focusing limit implied by Rayleigh diffraction. A constant-intensity acoustic source scanned designated geometric trajectories at specified speeds, which ranged from 2 to 20 m/s. The analyzed results consisted of the normal component of velocity of vibration at the surface of the material under each condition.

We assessed focusing quality via the focus energy ratio, the ratio of the total wave field energy located within the FWHM along the source scanning path to all energy imparted to other locations. We also computed the ARE, or mean energy outside the scanning path; the mean-squared error, computed as a point-wise loss between the normalized energy density of the acoustic radiation force source pattern (in our case, a “Z”) and the normalized energy density of the medium response; and the structural similarity index, a widely used error measure that accounts for spatial correlations between nearby data points. Further details can be found in Supplementary Text.

Vibrometry measurements with elastomer plate

We fabricated an elastomer plate with dimensions and properties matching those used in the simulations. The plate was composed of synthetic medical gelatin (Gelatin #2, Humimic, USA; mass density, 923.5 kg/m³). The planar array of 256 ultrasound transducers was programmed to furnish a scanning ultrasound source localized at the surface of the elastomer. The source parameters approximated those used in the simulations. We acquired temporally and spatially resolved oscillations normal to the surface of the elastomer using a scanning laser Doppler vibrometer (Ometron, model 8330) (Fig. 5, A and B). We varied the scanning path and the instantaneous scanning speed, which ranged from 2 to 15 m/s, during the experiments. As in the simulations, the source intensity was held constant, and both the scanning path and speed were varied for each experimental configuration. Further details are provided in Supplementary Text.

Human hand: Wave patterns and perception

We examined the relationship between wake formation and tactile motion perception by analyzing a human hand vibrometry dataset and a behavioral dataset that were captured in a previous study by the authors (14). In all of the human participant studies, before data collection, written informed consent was gathered for all participants. The experiments were conducted according to the protocol approved by the human participants committee of our institution. The vibrometry experiment measured ultrasound-elicited skin vibrations in the direction normal to the volar (palmar) surface of a human hand using a scanning laser vibrometer (PSV-500, Polytec; sampling rate, 125 kHz). The focused ultrasound haptic display was used in the same manner as in the elastomer experiments. The hand was fixed to a vibration-isolated table in an open posture using 3D-printed brackets affixed to the fingernails via an adhesive, with the arm positioned in a relaxed posture (Fig. 5C). A constant-intensity source scanned along a 16-cm path to or from the base of the thenar eminence to the tip of digit 2. To facilitate comparison with the perception experiment, we modulated the scanning path in a similar manner to what is commonly used in haptic holography. Thus, the scan path consisted of a zigzag pattern with a 2-cm path width. The focus traversed the nominal motion path (along the path of the finger) at scan speeds v_l = 1,2,4,7,11 m/s and was laterally modulated transverse to this primary motion axis, in alternating directions, with velocity v_mod = ± 2.5 m/s (see Supplementary Text). For each speed, we analyzed the wake length, or spatial extent of skin vibrations along the motion axis, defined as the length in which vibration amplitude was at least 10% of maximum.

Behavioral data were captured in an experiment on tactile motion perception in which participants reported the direction of scanning via a two-alternative forced choice task. The stimuli were identical to those used in the vibrometry experiment but included an additional low-speed stimulus, v_l = 0.5 m/s, whose motion direction could be easily perceived. Scanning stimuli were block-randomized over scanning speed and direction. Each of 12 participants completed 120 trials (10 repetitions for each of 12 stimuli). Participants could elect to repeat the stimuli one or more times. We computed per-participant summary statistics of the response data (Fig. 7B) and performed statistical analyses using generalized linear mixed modeling with a logistic link function (n = 12; significance of fixed effect coefficients assessed using two-tailed tests). We analyzed combined data from the vibrometry and behavioral experiments to determine the relationship between perception accuracy and wake length (Fig. 7C).

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S3

Legends for movies S1 to S3

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S3