Long-range functional connections mirror and link microarchitectural and cognitive hierarchies in the human brain

Abstract

Background

Higher-order cognition is hypothesized to be implemented via distributed cortical networks that are linked via long-range connections. However, it is unknown how computational advantages of long-range connections reflect cortical microstructure and microcircuitry.

Methods

We investigated this question by (i) profiling long-range cortical connectivity using resting-state functional magnetic resonance imaging (MRI) and cortico-cortical geodesic distance mapping, (ii) assessing how long-range connections reflect local brain microarchitecture, and (iii) examining the microarchitectural similarity of regions connected through long-range connections.

Results

Analysis of 2 independent datasets indicated that sensory/motor areas had more clustered short-range connections, while transmodal association systems hosted distributed, long-range connections. Meta-analytical decoding suggested that this topographical difference mirrored shifts in cognitive function, from perception/action towards emotional/social processing. Analysis of myelin-sensitive in vivo MRI as well as postmortem histology and transcriptomics datasets established that gradients in functional connectivity distance are paralleled by those present in cortical microarchitecture. Notably, long-range connections were found to link spatially remote regions of association cortex with an unexpectedly similar microarchitecture.

Conclusions

By mapping covarying topographies of long-range functional connections and cortical microcircuits, the current work provides insights into structure-function relations in human neocortex.

Introduction

In the mammalian brain, the distance between cortical regions largely determines the extent to which they are interconnected (Ercsey-Ravasz et al. 2013; Roberts et al. 2016). Although most cortico-cortical connections are local and link mainly nearby regions (Markov et al. 2011), it is hypothesized that long-range connectivity patterns likely play a key role in organizing human brain structure and function (Oligschläger et al. 2017; Deco et al. 2021). Long-range connections may help integrate distributed functional communities facilitating more complex computation, thereby improving the efficiency of brain network communication (Bassett and Bullmore 2006; Kaiser and Hilgetag 2006; Achard and Bullmore 2007; Bullmore and Sporns 2012; Collin et al. 2014). Long-range connections, however, are neither evenly nor randomly distributed across the cortical mantle but appear concentrated in transmodal association cortex, regions that host networks that engage in increasingly abstract and self-generated cognition (Sepulcre et al. 2010; Amft et al. 2015; Poerio et al. 2017; Schacter et al. 2017). Conversely, long-range connections are less frequently found in sensory and motor regions that interact more closely with the here and now (Mesulam 1990; Sepulcre et al. 2010; Buckner and Krienen 2013; Krienen and Buckner 2020). Despite the widely held view that long-range connectivity holds functional importance to human brain organization, the specific layout and neural underpinnings of long-range connections remain incompletely characterized.

The study of human brain connectivity has increasingly benefitted from the analysis of brain signals during task-free, or “resting-state” functional magnetic resonance imaging (fMRI) acquisitions (Greicius et al. 2003; Biswal et al. 2010). In these paradigms, inter-regional signal correlations are often used to infer functional connections (Biswal et al. 2010; Friston 2011; Smith et al. 2013). Resting-state fMRI (rs-fMRI) probes multiple functional networks within a single acquisition (Fox et al. 2005; Shehzad et al. 2009; Smith et al. 2009; Biswal et al. 2010; Castellanos et al. 2013), and rs-fMRI networks have been shown to be both reproducible and reliable (Damoiseaux et al. 2006). Prior research has underscored the value of rs-fMRI in profiling connectivity patterns of specific areas (Margulies et al. 2007; Kelly et al. 2012; Eickhoff et al. 2018; Vos de Wael et al. 2018) and of delineating large-scale networks, which often correspond to systems engaged during cognitive states (Smith et al. 2009). To understand distance effects on cortical connectivity, prior studies combined rs-fMRI analysis with cortico-cortical distance profiling (Sepulcre et al. 2010; Oligschläger et al. 2017), suggesting that sensory/motor networks have a locally clustered connectivity profile while transmodal association cortices show rather long-range connections. Here, we combined functional connectivity analysis with assessments of cortical topology by analytically differentiating regions involved in long- versus short-range functional networks.

Converging evidence has indicated that resting-state functional connectivity patterns follow similar spatial axes as microstructural variations, but that these two modalities become increasingly dissociated in transmodal default mode and frontoparietal networks (Mesulam 1998; Huntenburg et al. 2017; Paquola et al. 2019). Spatial gradients that differentiate sensory and motor systems from transmodal association cortices have been reported at the level of cortical microstructure captured using myelin-sensitive in vivo MRI as well as postmortem 3D histology (Paquola et al. 2020). Such sensory-fugal spatial trends have also been indicated when assessing cortical gene expression, including recent data based on postmortem microarray transcriptomics showing regionally varying cortical microcircuit organization (Fornito et al. 2019). Notably, these gradients align with gradients obtained from functional connectivity analysis differentiating sensory/motor systems from transmodal networks in terms of intrinsic connectivity patterns (Margulies, Ghosh, et al. 2016b; Huntenburg et al. 2018), suggesting correspondence between functional hierarchies and microcircuit patterns (Huntenburg et al. 2017; Paquola et al. 2019; Valk et al. 2021; Bernhardt et al. 2022). Here, we built on this emerging literature, by performing systematic spatial association analyses between functional connectivity distance topographies as well as cortical microarchitecture derived from myelin-sensitive in vivo MRI in the same participants, as well as postmortem 3D histology and transcriptomics.

In addition to examining spatial covariation of function and structure across the cortical mantle, combined structure–function assessment can clarify the role of long-range connectivity in the global cortical landscape. In general, cortical regions that are closer to one another are more likely to be connected and will have a more similar microstructural context. Conversely, there is generally an overall reduction in the microstructural similarity and functional connectivity of different areas with increasing spatial distance between them (Barbas 2015; Huntenburg et al. 2017). However, the human brain seems to also incorporate exceptions to this rule (Barbas 2015; Krienen and Buckner 2020; Deco et al. 2021). For example, transmodal association cortices show an increased clustering of (otherwise relatively rare) long-range cortico-cortical connections, and distributed association networks are also more likely to be connected than expected based on their sometimes-large distance. By studying the similarity of cortical functional networks in terms of their microstructure and gene expression profiles, we furthermore aimed at testing whether long-range connectivity patterns serve a special role in an expanded human cortex, allowing to connect microstructurally similar cortices across a large cortical distance.

The current work mapped cortical topographies of functional connectivity distance in the human brain and examined associations to underlying microstructure. We profiled the extent to which each cortical region participates in long- versus short-range functional networks based on a combination of rs-fMRI connectivity and cortex-wide geodesic distance mapping (Oligschläger et al. 2017; Lariviere et al. 2020). A first set of analyses contextualized the topography of long-range connections with respect to other established motifs of macroscale cortical organization. We assessed associations to the participation in macroscale community as a measure of integrative brain function (Guimerà and Nunes Amaral 2005) and the principal functional gradient as a proxy for sensory-transmodal functional hierarchy (Margulies, Ghosh, et al. 2016b). In both cases, we hypothesized that long-range connectivity will be more likely in transmodal areas with more integrative functions. We furthermore examined spatial associations to meta-analytical data of task-based fMRI studies (Yarkoni et al. 2011) and again expected an association of long-range connections to higher-order functions. The intrinsic and task-related functional association analysis was complemented by an exploration of associations to cortical microarchitecture, combining analysis of myelin-sensitive in vivo MRI in the same participants together with analysis of microscale features based on postmortem histology and gene expression (Hawrylycz et al. 2012; Amunts et al. 2013). These microarchitectural properties similarly reflect cortical hierarchical organization, with transmodal regions showing a distinct microarchitectural markup than primary sensory and motor areas. We anticipated clear associations between those features and long-range connectivity as well, which would speak to a hypothesized confluence of microarchitectural and functional topographies in the human brain. Several sensitivity analyses assessed robustness of our findings with respect to different analytic choices, and we replicated all in vivo findings in an independent dataset.

Materials and methods

Participants

Our study was based on two independent human neuroimaging datasets, MICA-MICs and Human Connectome Project (HCP).

For our main analysis, we studied imaging and phenotypic data of 50 unrelated healthy adults (age: 29.82 ± 5.73 years, 21 females), based on MICA-MICs (Royer et al. 2021). Data were collected between April 2018 and March 2020, and all participants denied a history of neurological illness. All participants had quality-controlled multimodal MRI data available (see below). The Ethics Committee of the Montreal Neurological Institute and Hospital approved the study. Written informed consent was obtained from all participants.

To verify the reproducibility of our findings, we repeated the main analyses on an independent validation dataset from the HCP (Van Essen et al. 2013), including 200 unrelated healthy young adults (28.68 ± 3.69 years, 119 females).

MRI acquisition

MICA-MICs

Scans were acquired using a 3T Siemens Magnetom Prisma-Fit equipped with a 64-channel head coil at the McConnell Brain Imaging Centre of the Montreal Neurological Institute. All participants underwent T1-weighted (T1w) structural MRI, multiband rs-fMRI, and quantitative T1 (qT1) imaging.

Two T1w scans with identical parameters were acquired with a 3D magnetization-prepared rapid gradient echo (MPRAGE) sequence (0.8 mm isovoxels, matrix = 320 × 320, 224 sagittal slices, repetition time (TR) = 2,300 ms, echo time (TE) = 3.14 ms, inversion time (TI) = 900 ms, flip angle = 9°, integrated Parallel Acquisition Techniques (iPAT) factor = 2). Scans were visually examined to ensure minimal head motion and repeated if necessary. qT1 relaxometry data were acquired using a 3D-MP2RAGE sequence (0.8 mm isovoxels, 240 sagittal slices, TR = 5,000 ms, TE = 2.9 ms, TI 1 = 940 ms, T1 2 = 2830 ms, flip angle 1 = 4°, flip angle 2 = 5°, iPAT = 3, bandwidth = 270 Hz/px, echo spacing = 7.2 ms, partial Fourier = 6/8). Both inversion images were combined for qT1 mapping to minimize sensitivity to B1 inhomogeneities and optimize intra- and intersubject reliability (Marques et al. 2010; Haast et al. 2016).

A 7-min rs-fMRI scan was acquired using multiband accelerated 2D-blood oxygenation level-dependent echo-planar imaging [TR = 600 ms, TE = 30 ms, 3 mm isovoxels, flip angle = 52°, field of view (FOV) = 240 × 240 mm², slice thickness = 3 mm, mb factor = 6, echo spacing = 0.54 ms]. Participants were instructed to keep their eyes open, not fall asleep, and look at a fixation cross. Two spin-echo images with reverse phase encoding were also included for distortion correction of the rs-fMRI scans (phase encoding = AP/PA, 3 mm isovoxels, FOV = 240 × 240 mm², slice thickness = 3 mm, TR = 4,029 ms, TE = 48 ms, flip angle = 90°, echo spacing = 0.54 ms, bandwidth = 2,084 Hz/Px).

Human Connectome Project

T1-weighted, T2-weighted, and rs-fMRI data were obtained using a Siemens Skyra 3T at Washington University (Van Essen et al. 2013). The T1-weighted images were acquired using a MPRAGE sequence (TR = 2,400 ms; TE = 2.14 ms; FOV = 224 × 224 mm²; voxel size = 0.7 mm³; and number of slices = 256). T2-weighted data were obtained with a T2-SPACE sequence, and acquisition parameters were aligned to those of the T1-weighted data except for TR (3,200 ms) and TE (565 ms). The rs-fMRI data were collected using gradient-echo echo-planar imaging (TR = 720 ms; TE = 33.1 ms; FOV = 208 × 180 mm²; voxel size = 2 mm³; number of slices = 72; and number of volumes = 1,200 per time series). During the rs-fMRI scan, participants were instructed to keep their eyes open looking at a fixation cross. Two sessions of rs-fMRI data were acquired; each of them contained data of left-to-right and right-to-left phase-encoded directions, providing up to four time series per participant.

Data preprocessing

MICA-MICs

Raw DICOMS were sorted using custom scripts and converted to NIfTI using dcm2niix (https://github.com/rordenlab/dcm2niix) (Li et al. 2016), renamed, and assigned to their respective subject-specific BIDS directories (Gorgolewski et al. 2016). The BIDS validator (https://bids-standard.github.io/bids-validator/) ensured agreement to BIDS standards. Preprocessing was based on an open-source pipeline (Rodriguez-Cruces et al. 2022) (http://github.com/MICA-MNI/micapipe).

T1w scans were deobliqued and reoriented, linearly co-registered, averaged, and corrected for intensity nonuniformity. Resulting volumes were skull stripped using FSL FIRST (Jenkinson et al. 2012). We used FreeSurfer 6.0 (Dale et al. 1999; Fischl, Sereno, and Dale 1999a) to generate cortical surface models from native T1w scans. Surface extractions were visually inspected and corrected for any segmentation errors with the placement of control points and manual edits (Royer et al. 2021; Rodriguez-Cruces et al. 2022). Then, 14 equivolumetric surfaces were constructed for each participant between pial and white matter interfaces. These surfaces were used to systematically sample qT1 intensity profiles to construct individual microstructural profile similarity matrices.

The rs-fMRI data were preprocessed using AFNI (Cox 1996) and FSL (Jenkinson et al. 2012) tools. The first five volumes were discarded to ensure magnetic field saturation. Volumes were reoriented, followed by motion and distortion correction. Nuisance signal was removed using FMRIB’s ICA-based X-noiseifier (ICA-FIX) (Salimi-Khorshidi et al. 2014) and by performing spike regression, which regressed out timepoints with large motion spikes (Lemieux et al. 2007; Satterthwaite et al. 2013). Volume timeseries were registered to FreeSurfer space using boundary-based registration (Greve and Fischl 2009). This procedure was visually verified, also using automated quality control procedures (Royer et al. 2021; Rodriguez-Cruces et al. 2022). Surface-mapped timeseries were registered to Conte69, a template that has 32k vertices per hemisphere, and smoothed using a surface-based diffusion kernel (full width at half maximum = 10 mm).

Human Connectome Project

HCP minimal preprocessing was performed using FSL, FreeSurfer, and Workbench (Fischl 2012; Jenkinson et al. 2012; Glasser et al. 2013). T1- and T2-weighted data were corrected for gradient nonlinearity and b0 distortions and then were co-registered using a rigid body transformation. White and pial surfaces were approximated using FreeSurfer (Dale et al. 1999; Fischl, Sereno, and Dale 1999a; Fischl, Sereno, Tootell, et al. 1999b). A midthickness surface was generated by averaging white and pial surfaces and used to generate the inflated surface that was registered to the Conte69 template (Van Essen et al. 2012) using MSMAll (Glasser et al. 2016) and downsampled to a 32k vertex mesh. HCP provides a myelin-sensitive proxy based on the ratio of the T1- and T2-weighted contrast (Glasser and Van Essen 2011; Glasser et al. 2014). Then, rs-fMRI data were corrected for distortions and head motion and were registered to the T1-weighted data and subsequently to MNI152 space. Magnetic field bias correction, skull removal, and intensity normalization were performed. Noise components were removed using ICA-FIX (Salimi-Khorshidi et al. 2014). Time series were mapped to the standard grayordinate space, with a cortical ribbon-constrained volume-to-surface mapping algorithm.

Connectivity distance coefficient computation

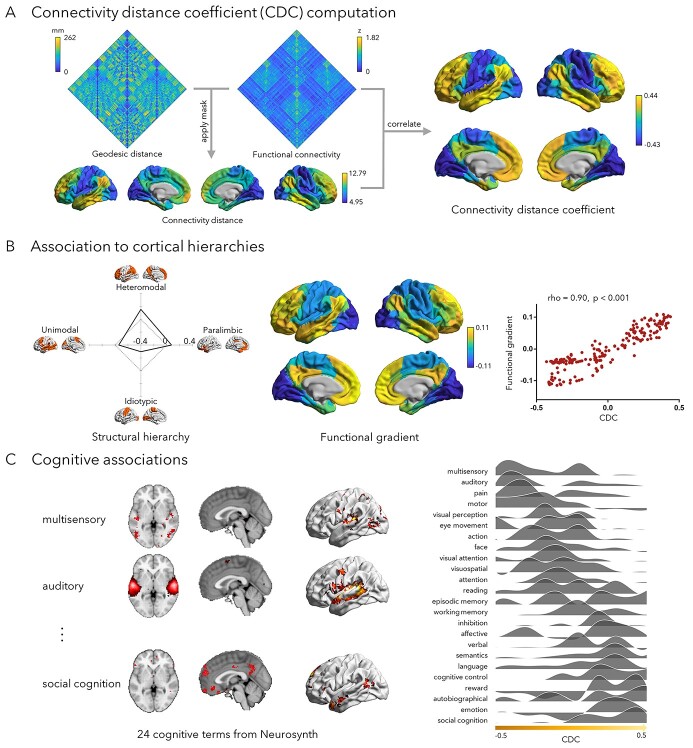
Functional connectomes were generated by correlating preprocessed rs-fMRI averaged from 200 functionally defined cortical parcels (Schaefer et al. 2018). Correlation matrices underwent Fisher's R-to-Z transformations. Individual geodesic distance matrices were calculated from the native pial surface using Surfdist (https://github.com/NeuroanatomyAndConnectivity/surfdist) (Margulies, Falkiewicz, et al. 2016a). Within each hemisphere, geodesic distance between cortical parcels was estimated by avoiding non-cortical paths through the medial wall, mapped to the native cortical surface, and averaged within nodes. Interhemispheric geodesic distance was represented by the average of geodesic distance matrix of 2 hemispheres. Connectivity distance was estimated to describe each region’s average distance to its functionally connected regions. For each region, we retained the top 10% functional connections and averaged their geodesic distance to the seed. Since strong functional connections in the cortex are generally short-range, we used region-wise thresholding to avoid penalizing long-range connections. With this approach of ensuring the same number of top connections for each region, we generated a cortex-wide connectivity distance map in line with prior work (Lariviere et al. 2020). For each region, the connectivity distance coefficient (CDC) was defined as the spatial correlation between the region’s unthresholded functional connectivity map and the connectivity distance map (Fig. 1A). Positive values indicate that region’s connectivity profile increasingly maps to regions with long-range connections, while negative values indicate that it increasingly maps to those regions with short-range connections. Subject-level data were averaged to generate group-level estimates. For a stratification of geodesic distances with respect to CDC, please see Supplementary Fig. S1. In addition to surface mapping, we stratified CDC according to intrinsic functional communities (Yeo et al. 2011) and an atlas of functional zones (Mesulam 2000; Paquola et al. 2019), i.e. idiotypic/primary, unimodal, heteromodal, or paralimbic. The latter was manually mapped to cortical surfaces in a previous study (Paquola et al. 2020), where it was furthermore shown that it strongly captured microstructural differentiation based on BigBrain and in vivo myelin gradients, as well as functional connectivity gradients derived from rs-fMRI (Fig. 1B, Supplementary Fig. S2). To verify robustness of the CDC metric with respect to analysis parameter variations, we constructed it using different thresholds of functional connectivity (5%, 15%, 20%, 25%), as well as functional data processed with additional global signal regression (Supplementary Fig. S3). We furthermore evaluated interindividual variations of CDC and corresponding functional associations (Supplementary Fig. S4).

Fig. 1.

Cortex-wide mapping of the connectivity distance coefficient (CDC). A) For each region, we retained its top 10% functional connections. The seed region’s geodesic distance to these regions was averaged resulting in its connectivity distance. For each region, the correlation between its unthresholded functional connectivity and the connectivity distance map was defined as its CDC. B) Stratification relative to an atlas of functional zones (Mesulam 2000; Paquola et al. 2019) and a data driven gradient of rs-fMRI connectivity (Margulies et al. 2016; Vos de Wael et al. 2020). The correlation between CDC and functional gradient was estimated using Spearman’s rank correlation, and P-value was corrected using spin test. C) Cognitive associations based on task-fMRI meta-analysis using Neurosynth (Yarkoni et al. 2011).

Functional and microarchitectural contextualization

A series of analyses assessed spatial associations between CDC and different features of neural organization. All spatial correlations in this study were estimated using Spearman’s rank correlation, while 1,000 nonparametric spin tests (Alexander-Bloch et al. 2018) controlled for spatial autocorrelations. Unless otherwise specified, 1,000 nonparametric spin tests (Alexander-Bloch et al. 2018) assessed spatial associations while controlling for spatial autocorrelation.

Functional contextualization

We first assessed the spatial correlation between CDC and the functional participation coefficient (Guimerà and Nunes Amaral 2005), a graph theoretical index of connectional diversity (Supplementary Fig. S2). The participation coefficient was computed at both group and individual levels, where each brain region was assigned to one of seven predefined functional communities (Yeo et al. 2011). For a given region, its participation coefficient will be 0 if its connections are entirely restricted to one given community, which estimated by intrinsic functional connectivity (Yeo et al. 2011). In contrast, the participation coefficient will approach 1 if the region’s connections are evenly distributed among all communities. We also assessed associations between CDC and the principal functional gradient (Margulies, Ghosh, et al. 2016b). Functional gradients were calculated using BrainSpace (https://github.com/MICA-MNI/BrainSpace) (Vos de Wael et al. 2020). In brief, an individual’s resting-state functional connectome was thresholded to retain the top 10% connectivity per region, and this connectome was converted into a normalized angle matrix. The principal functional gradient was identified using diffusion map embedding (Coifman et al. 2005), an efficient nonlinear dimensionality reduction technique that is robust to noise (Tenenbaum et al. 2000; von Luxburg 2007). It is controlled by 2 parameters α and t, where α controls influence of the density of sampling points on the manifold (α = 1, no influence; α = 0, maximal influence), and t controls the scale of eigenvalues of the diffusion operator. We set α = 0.5 and t = 0 to retain the global relations between data points in the embedded space (Margulies, Ghosh, et al. 2016b; Paquola et al. 2019; Vos de Wael et al. 2020; Park et al. 2021). Individual-level manifolds were aligned to a template manifold obtained from the HCP dataset via Procrustes alignment (Langs et al. 2015) and averaged to generate a group-level manifold (Fig. 1B).

Meta-analysis on cognitive functions

To assess which cognitive faculties are related to long- and short-range connectivity, we analyzed meta-analytic maps from Neurosynth (http://www.neurosynth.org) (Yarkoni et al. 2011). Neurosynth combines meta-analysis and text mining techniques to generate probabilistic mappings between cognitive terms and spatial brain patterns. We analyzed meta-analytic z-statistics maps of 24 terms (Margulies, Ghosh, et al. 2016b; Paquola et al. 2019) covering a wide range of cognitive functions (Fig. 1C). The vertex-level z-statistic was mapped to the Schaefer atlas (Schaefer et al. 2018) with 200 regions and averaged within each region. We divided the CDC into 10 percentile bins and calculated the mean z-statistic of per term within each bin. This resulted in overall z-activations of each cognitive term with respect to functional connectivity distance. Findings were replicated in the HCP dataset (Supplementary Fig. S5).

Microarchitectural contextualization

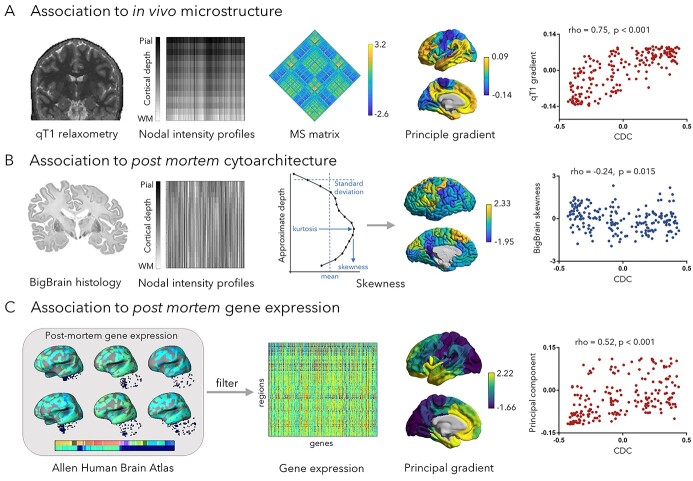
We assessed spatial associations to in vivo qT1 measures in the same subjects, as well as postmortem histology and gene expression (Fig. 2).

Fig. 2.

Associations to cortical microarchitecture. A) Association to an in vivo microstructural gradient derived from qT1 relaxometry mapping in the same participants. B) Association to post mortem cytoarchitecture measures (intracortical profile skewness) derived from the BigBrain dataset (Amunts et al. 2013). C) Association to post mortem gene expression data derived from the Allen human brain atlas (Hawrylycz et al. 2012). Gene expression data were filtered across six donors, and a CGE matrix was constructed followed by principal component analysis. All correlations between CDC and microarchitectural properties were estimated using Spearman’s rank correlation, and P-values were corrected using spin test. MS, microstructural similarity.

Quantitative T1

Consistent with prior work (Waehnert et al. 2014; Paquola et al. 2019; Royer et al. 2021), we constructed 14 equivolumetric intracortical surfaces to sample qT1 intensities across cortical depths. Specifically, we systematically constructed 14 equivolumetric surfaces between the outer and inner cortical interfaces (Wagstyl et al. 2018; Paquola et al. 2019). The equivolumetric model compensates for cortical folding by varying the Euclidean distance ρ between pairs of intracortical surfaces throughout the cortex to preserve the fractional volume between surfaces (Waehnert et al. 2014). Here, ρ was calculated as follows for each surface:

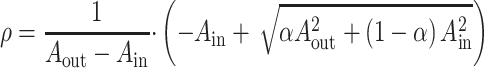(1)

where α represents fraction of the total volume of the segment accounted for by the surface, while A_out and A_in represent the surface area of the outer and inner cortical surfaces, respectively. Next, vertex-wise microstructure profiles were estimated by sampling intensities along linked vertices from the outer to the inner surface across the whole cortex. Data sampled from surfaces closest to the pial and white matter boundaries were removed to mitigate partial volume effects. The fsaverage5 surface-mapped Schaefer atlas with 200 parcels (Schaefer et al. 2018) was interpolated to the native surface in each individual, and vertex-wise intensity profiles were averaged within parcels. The registration was visually verified (Royer et al. 2021; Rodriguez-Cruces et al. 2022). Nodal microstructural profiles were cross-correlated across the cortical mantle using partial correlations, while controlling for the average cortex-wide intensity profile. The resulting matrix was thresholded and log-transformed. This matrix captures the similarity in intracortical microstructural profiles across the cortex. In line with prior work and the functional analyses (Margulies, Ghosh, et al. 2016b; Vos de Wael et al. 2018; Paquola et al. 2019), we thresholded the microstructural similarity matrix, converted it into a normalized angle matrix, and derived microarchitectural gradients using diffusion map embedding. Individual-level gradients were aligned to the template manifold obtained from the group-level microstructural similarity matrix and averaged to generate a group-level microstructural gradient (Vos de Wael et al. 2020). The association between CDC and the principal microarchitectural gradient derived from qT1 measures was examined both at the group and individual levels (Fig. 2A; Supplementary Fig. S6). Analyses were repeated in the HCP dataset (Supplementary Fig. S7), which uses T1w/T2w imaging ratio as an alternative microstructural index. We also assessed skewness of microstructural profiles across cortical layers and averaged them across all participants to contrast relative properties of deep and superficial cortical layers. The latter feature is a critical dimension of laminar differentiation that relates to architectural complexity (Zilles et al. 2002) and cortical hierarchy (Mesulam 1998). Correlations between CDC and qT1 skewness were examined on the individual level and group level (Supplementary Fig. S6).

BigBrain

BigBrain is an ultra-high-resolution 3D volumetric histological reconstruction of a postmortem human brain (https://bigbrain-ftp.loris.ca/) (Amunts et al. 2013). For analysis of BigBrain-derived cytoarchitecture, a similar procedure was performed for BigBrain as for qT1. We constructed 16 equivolumetric intracortical surfaces with 163,842 matched vertices per hemisphere to sample intensities across cortical depths (Waehnert et al. 2014), yielding intensity profiles reflecting microstructural composition of each cortical vertex. Data sampled from surfaces closest to the pial and white matter boundaries were discarded to mitigate partial volume effects. Using SurfStat for Matlab(http://math.mcgill.ca/worsley/surfstat) (Worsley et al. 2009), we constructed surface-based linear models and controlled the midsurface y coordinate to account for an anterior–posterior increase in intensity values across the BigBrain due to coronal slicing and reconstruction (Paquola et al. 2019). Vertex-wise intensity profiles were subsequently averaged within 200 functionally defined parcels (Schaefer et al. 2018). To index intracortical laminar differentiation based on cytoarchitecture (Mesulam 1998; Zilles et al. 2002), as a complement to the above in vivo analysis, we estimated skewness as the third moment of these intensity profiles and assessed the association to CDC (Fig. 2B). In prior work, we found that in particular skewness helps differentiating allocortical and isocortical regions in the mesiotemporal lobe (Paquola et al. 2020). We then estimated skewness of intensity profiles, to index intracortical microstructural differentiation (Mesulam 1998; Zilles et al. 2002), and assessed the association to CDC (Fig. 2B).

Gene expression

We examined microarray gene expression data provided by the Allen Human Brain Atlas (AHBA) (Hawrylycz et al. 2012). Among all genes from AHBA, we downsampled the expression data to a nodal level and selected only those genes that were consistently expressed across the six AHBA donors using the abagen toolbox (https://github.com/rmarkello/abagen) (Markello et al. 2021). For the four donors in whom only the left hemisphere was available, their left hemisphere data were flipped to the right hemisphere. For each gene, the whole-brain gene expression maps between all pairs of donors were correlated, while genes with an average inter-donor r ≤ 0.5 were discarded (Fig. 2C). We then constructed a correlated gene expression (CGE) matrix by cross-correlating these genes and estimated the first component of CGE using principal component analysis, a linear dimensionality reduction technique. Next, we correlated the first principal component to the CDC map, controlling for spatial autocorrelation. These selected genes were spatially correlated with the CDC map [false discovery rate (FDR) correction] (Benjamini and Hochberg 1995), to further investigate genes whose expression correlated to CDC (FDR < 0.05). To highlight common and distinct spatial trends across the different measures of cortical organization across modalities, we analytically integrated them as well, similar to a prior study investigating spatial gradients in mouse cortex (Fulcher and Fornito 2016). Visualization of multimodal properties of cortical regions was achieved similar to a previous approach (Fulcher and Fornito 2016). Specifically, we constructed a n_regions × n_properties matrix, shown in Supplementary Fig. S9. We calculated z-scores for each column, f(x) = [(x - mean)/SD] to ensure zero mean and unit standard deviation. The first eigenvector was estimated using principal component analysis, which was used to order regions along a sensory-transmodal direction. We only focused on genes that were positively correlated to longer functional connectivity distance. To investigate cell type-specific gene enrichment, we compared these genes to cell type-specific genes, including excitatory and inhibitory neurons as well as microglia, endothelial cells, pericytes, astrocytes, as well as oligodendrocytes and precursor cells (Lake et al. 2016; Lake et al. 2018). To assess the distribution of genes in each cell type, we calculated the overlap ratio (Supplementary Fig. S8). Here, FDR and spin tests were used again to correct findings for multiple comparisons, spatial autocorrelation, and influence caused by inflated false-positive rates due to a violation of independence assumptions (Wei et al. 2021).

Distance-based stratification of microarchitectural similarity

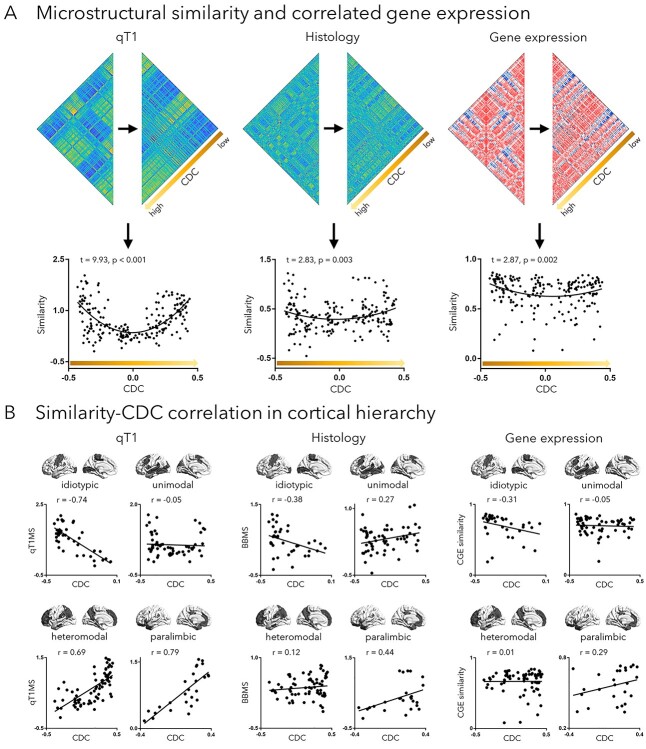
For each cortical parcel, we retained the top 10% of edges in the group averaged functional connectivity matrix and averaged the microarchitectural similarity of this network (based on qT1, BigBrain, CGE; Fig. 3A). Parcels were sorted relative to functional connectivity distance, and we fitted linear and quadratic functions to model this relationship (Supplementary Fig. S10). In addition to assessing distance effects on a single metric, we also built a mixed effects model that assesses distance effects on the microarchitectural similarity based on qT1, BigBrain, and gene expression. Analyses were carried out across the whole cortex and repeated in specific functional communities and cortical hierarchy levels (Fig. 3B, Supplementary Fig. S11). We repeated the main analyses in the HCP dataset and found consistent findings (Supplementary Fig. S12).

Fig. 3.

Long-range connections bypass distance-dependent wiring in the human brain. A) The microstructural similarity (MS) matrices (derived from qT1 and BigBrain) and CGE matrix were sorted by CDC and averaged in the predefined functional connectivity configuration to generate the microstructural and genetic similarity map. These maps were then fitted to CDC using quadratic function. B) The correlation between microstructural/genetic similarity and CDC was further examined in cortical hierarchy. qT1MS, microstructural similarity derived from qT1; BBMS, microstructural similarity derived from BigBrain.

Results

Our main analyses were based on a sample of 50 healthy young adults (29.82 ± 5.73 years, 21 females) evaluated in our institute who had high definition functional and microstructural in vivo MRI data available (Royer et al. 2021). Replication analysis was based on an independent dataset of 200 unrelated healthy young adults from the HCP dataset (Van Essen et al. 2013) (28.68 ± 3.69 years, 119 females).

Gradients of functional connectivity distance

We defined a region’s CDC as the spatial correlation between its unthresholded functional connectivity map and the cortex-wide connectivity distance map. Specifically, we calculated for each region the correlation between its connectivity distance, which is the average geodesic distance of its functionally connected brain regions, and functional connectivity (see Methods). We observed highest CDC in transmodal association networks and lowest CDC in sensory/motor cortices (Fig. 1A). When stratifying CDC according to an atlas of functional zones (Mesulam 1998), we identified peak values in heteromodal and paralimbic cortices, the transmodal apex of the sensory-fugal hierarchy, while lowest values were observed in primary cortices (Fig. 1B).Higher cognitive processes relate to a dynamic interplay between distributed cortical regions linked by long-range connections. We, thus, contextualized the topography of CDC relative to several established characteristics of macroscale cortical organization, using spatial correlations while controlling for spatial autocorrelations (Alexander-Bloch et al. 2018). To explore the potential role of long-range connections in functional hierarchy, we examined associations between CDC and the principal functional gradient, which was approximated via nonlinear dimensionality reduction applied to rs-fMRI connectivity data (Coifman et al. 2005; Margulies, Ghosh, et al. 2016b). The principal gradient was found to closely resemble the CDC topography (rho = 0.90, P_spin < 0.001). Similar findings were observed when stratifying CDC according to intrinsic functional communities (Yeo et al. 2011), (Supplementary Fig. S2). We then correlated CDC to participation coefficient, a graph theoretical measure that taps into how diverse/integrative the connectivity of a given region is (Guimerà and Nunes Amaral 2005; Hwang et al. 2017). High participation coefficient indicates that a region is communicating to multiple macroscale communities, whereas low participation coefficient indicates that a region is communicating to only few communities. We observed a low-to-moderate positive correlation between CDC and the participation coefficient (rho = 0.29, P_spin < 0.001), suggesting that areas with higher CDC generally also showed more integrative connectivity profiles.

Confirmatory meta-analysis using the Neurosynth (Yarkoni et al. 2011) database of previous task-fMRI studies estimated spatial associations to activation patterns across cognitive terms (Margulies, Ghosh, et al. 2016b). Resulting spatial associations were stratified from low to high CDC (Fig. 1C). Terms associated with long-range connectivity involved social/emotional functions, such as “social cognition” and “emotion,” while short-range connections were more common in processes related to sensory functions, such as “multisensory” and “auditory.”

We evaluated robustness of the CDC findings against variations in preprocessing and analysis choices (i.e. functional connectome thresholding and use of global mean signal regression during preprocessing) and obtained similar results (Supplementary Fig. S3). We also estimated the CDC by using the top 10% absolute functional connections, which was almost identical to the original one (rho = 0.99, P_spin < 0.001). Functional findings were also relatively stable at the individual participant level (Supplementary Fig. S4). Moreover, functional findings were similar when analyzing the independent HCP dataset (Supplementary Fig. S5).

Associations to local cortical microarchitecture

In addition, we systematically examined the relationship between CDC and cortical microarchitecture (Paquola et al. 2019). In particular, building upon an emerging literature assessing structure–function relations in the cortex, we examined associations to features sensitive to microstructural differentiation based on MRI-derived proxies of cortical myelination, histology-derived cytoarchitecture, and microarray-derived gene expression. Prior work has shown cortex-wide variations in these microscale features, in particular between sensory and motor systems and transmodal association cortex (Huntenburg et al. 2017; Burt et al. 2018; Paquola et al. 2019). Firstly, we sampled intracortical in vivo qT1 relaxometry MRI profiles (Bock et al. 2013; Dinse et al. 2013) in all cortical parcels in the same participants. We then cross-correlated qT1 intensity profiles between parcels to generate a microstructural similarity matrix (Fig. 2A) and generated a cortex-wide microstructural gradient (Coifman et al. 2005; Paquola et al. 2019), running from primary towards paralimbic areas. CDC correlated strongly with this gradient (rho = 0.75, P_spin < 0.001; Fig. 2A). Correlations remained stable at the individual level (Supplementary Fig. S6). We confirmed that structure–function relations were similar in the HCP dataset (Supplementary Fig. S7), which uses T1w/T2w imaging ratio as an alternative microstructural index (Glasser and Van Essen 2011).

In a separate analysis, we sampled intracortical intensity profiles from BigBrain (Amunts et al. 2013; Paquola et al. 2019), a 3D postmortem histological reconstruction of a human brain. We estimated skewness measures (Goulas et al. 2018) of intensity profiles to represent microstructural differentiation (Mesulam 1998; Zilles et al. 2002) and obtained significant correlations with CDC (skewness: rho = −0.24, P_spin = 0.015; Fig. 2B). We also assessed skewness of qT1 intensity profile and obtained significant correlations with CDC at a group and individual level (rho = −0.74, P_spin < 0.001; Supplementary Fig. S6).

We leveraged the AHBA (Hawrylycz et al. 2012) to assess transcriptomic correlates of connectivity distance. We selected only genes consistently expressed across the six donors (r > 0.5; 1,050/20,647, i.e. 5.09%) genes (Fig. 2C). Based on those 1,050 genes, we identified the first principal component of gene expression (explaining 71.58% of co-expression variance) and found that this component correlated to CDC (rho = 0.52, P_spin < 0.001, Fig. 2C). We then performed cell type-specific gene enrichment (Lake et al. 2016; Lake et al. 2018) analysis and calculated overlap ratios in gene expression between the 508 positively distance-related genes and cell type-specific genes using 1,000 permutation tests. These genes showed a significant overlap with genes expressed in excitatory and inhibitory neurons in both supragranular and infragranular layers, as well as astrocytes and oligodendrocyte progenitor cells (FDR < 0.05; Supplementary Fig. S8). Therefore, CDC was found paralleling cortical microarchitectural gradients derived from myeloarchitecture, cytoarchitecture, and gene expression. We combined representative measurements from each data type: CDC, functional gradient, participation coefficient, microstructural gradients derived from qT1 imaging, the principal gradient of cortical gene expression, and skewness of laminar differentiation derived from 3D histology. These properties were visualized together (Supplementary Fig. S9). We furthermore estimated the first principal component of these diverse measurements, which ordered regions from primary somatosensory to transmodal areas.

Long-range functional connectivity links distant but microarchitecturally similar cortical regions

In the human brain, microarchitectural similarity of cortical regions generally declines with increasing spatial distance (Huntenburg et al. 2017; Wei et al. 2019). Here, we verified this relationship and assessed the role of long-range connections in such distance-dependent microarchitectural associations. We quantified microstructural similarity as above using qT1, BigBrain, and CGE of cortico-cortical functional networks and reordered similarity according to CDC (Fig. 3A). Interestingly, we observed a quadratic relationship between microstructural similarity and CDC for qT1 (t = 9.93, P < 0.001), BigBrain (t = 2.83, P = 0.003), and gene expression similarity (t = 2.87, P = 0.002). In all cases, a quadratic model provided a better model fit than a linear model (F > 8.03, P < 0.001), suggesting that regions with high connectivity distance express and unexpectedly high microarchitectural similarity given their distance (Supplementary Fig. S10). An overarching mixed effects model, aggregating qT1, BigBrain, and gene expression confirmed a strong quadratic effect (t = 9.04, P < 0.001). When assessing distance effects stratified for different levels of the cortical hierarchy levels, negative effects of distance on microstructural/genetic similarity were found in primary and unimodal association networks, while transmodal areas (i.e. heteromodal and paralimbic networks) showed positive relations (Fig. 3B). Similar findings were seen for different intrinsic functional communities (Supplementary Fig. S11). Moreover, findings were robust in the HCP dataset (Supplementary Fig. S12).

Discussion

Long-distance connections likely facilitate distributed human brain function due to their contributions to increased global communication efficiency (Bassett and Bullmore 2006; Kaiser and Hilgetag 2006; Achard and Bullmore 2007; Bullmore and Sporns 2012; Collin et al. 2014; Deco et al. 2021). The present study integrated rs-fMRI connectivity analysis and cortex-wide geodesic distance mapping and differentiated sensory and motor networks from transmodal regions which were more involved in long-range subgraphs. The CDC indexes spatial similarity between a region’s functional connectivity profile and a connectivity distance map that was based on a previous approach (Lariviere et al. 2020). If a region shows mainly connections to regions with long-range connections, the CDC will approach 1 and if a region shows mainly connections to regions with short-range connections, it will approach −1. Increases in CDC were found to reflect increasingly integrative connectivity patterns, as suggested by small-to-moderate associations with the participation coefficient (Guimerà and Nunes Amaral 2005). Even more strongly, CDC was highly associated with a previously demonstrated sensory-transmodal gradient of resting-state connectivity, suggesting that high CDC regions were primarily localized in the transmodal apex of this gradient (Margulies, Ghosh, et al. 2016b; Huntenburg et al. 2018; Paquola et al. 2019). Confirmatory meta-analysis of previous task-fMRI findings based on Neurosynth (Yarkoni et al. 2011) demonstrated that these regions are engaged in more affective and higher-order social processes. In contrast, regions involved in sensory and motor functions were mainly characterized by more localized, short-range cortico-cortical connections. Capitalizing on in vivo myelin-sensitive MRI obtained in the same participants, as well as postmortem 3D histology and transcriptomics datasets (Hawrylycz et al. 2012; Amunts et al. 2013), we determined that the topography of CDC converged with sensory-fugal gradients in cortical microarchitecture. Critically, long-range connections were found to link spatially remote regions of transmodal association cortices with relatively high microarchitectural similarity. Establishing topographic associations between long-range connections and cortical microarchitecture showed that long-range connections partially counteract the overall distance-dependent decline in inter-areal similarity, thus providing a possible substrate for integrative and parallel function in human association cortex.

Our CDC measure that quantified participation of a region in short- versus long-range functional subnetworks complements prior studies that have explored cortical connectivity distance variations in human and nonhuman brains. Using a discrete Euclidean distance thresholding (set at 14 mm) of resting-state fMRI connectivity patterns, a prior study categorized areas into those with local versus distant connections (Sepulcre et al. 2010). Parallel graph theoretical assessment revealed that regions with short-range connections more frequently contributed to localized network clustering, while long-range connections ensure global efficiency increases (Sepulcre et al. 2010). Follow-up studies in humans and nonhuman primates combined rs-fMRI and surface-based geodesic distance mapping and suggested dissociations between sensory and transmodal regions in terms of wiring distance (Oligschläger et al. 2017; Oligschläger et al. 2019). In the current work, distances between cortical areas were measured using a geodesic distance mapping that runs through the cortical mantle. This approach was utilized previously to show that transmodal systems such as the default mode network are maximally remote from sensory/motor systems (Margulies, Ghosh, et al. 2016b) and suggested to assess cortical geometry and wiring cost (Ecker et al. 2013; Hong et al. 2017; Oligschläger et al. 2017). It needs to be acknowledged, however, that cortico-cortical anatomical distances are not solely determined by geodesic associations within the gray matter. Instead, they may additionally depend on short- as well as long-range white matter fibers, which become increasingly detectable by techniques such as diffusion MRI tractography. Here, we expanded these previous methods by computing the similarity of a region’s functional connectivity profile to the cortex-wide connectivity distance topography, to quantify in how far a region participates in long- versus short-range functional networks. This approach markedly segregated transmodal areas from unimodal and sensory systems, in line with work suggesting that midline regions in paralimbic and default mode networks have a high-density and long-range embedding, an architecture also referred to as the “rich-club” (van den Heuvel and Sporns 2011). In the current work, we mapped the mean CDC across different areas as a compact descriptor of the connectivity distance distribution. Our understanding of region-to-region variations in connectivity distance may benefit from additional parametrization of these distributions, for example with respect to higher-order statistical moments such as variance, skew, and kurtosis. In our study, we confirmed that long-range connectivity directly contributes to integrative brain function by showing spatial correlations between connectivity distance and the participation coefficient, a graph theoretical index of the connectional diversity of a given region (Guimerà and Nunes Amaral 2005). Diverse connectivity profiles likely play a role in network stability, along with the maintenance of whole-brain communication (Allegra et al. 2020). We also noted robust correlations to the principal functional connectivity gradient (Margulies, Ghosh, et al. 2016b), a data-driven approximation of sensory-transmodal hierarchy in the primate brain (Mesulam 1998; Margulies, Ghosh, et al. 2016b; Paquola et al. 2019). Our results, thus, support that CDC variations reflect established motifs of macroscale cortical organization. Confirmatory meta-analysis based on Neurosynth (Yarkoni et al. 2011) revealed that connectivity distance variations mirrored, in part, putative cognitive hierarchies, running from sensory and motor processes towards higher-order affective and socio-cognitive functions (Paquola et al. 2019). Uni- and heteromodal association cortices underwent a disproportionate enlargement during human evolution (Kaas 2006; Van Essen and Dierker 2007; Buckner and Krienen 2013; Mueller et al. 2013), and long-range connections may, in turn, ensure their continued ability to communicate across a wide cortical territory. This may, overall, provide increased ability to integrate diverse information and thus allowed for a greater degree of cognitive flexibility and adaptability of these networks.

A mounting literature emphasizes that cortical functional organization likely reflects cortical microarchitecture (Whitaker et al. 2016; Burt et al. 2018; Huntenburg et al. 2018). Using myelin-sensitive in vivo MRI in the same participants (Schmierer et al. 2007; Bock et al. 2009; Geyer et al. 2011; Sereno et al. 2013), we could show that the sensory-fugal connectivity distance patterns follow gradients that distinguish sensory and motor regions from transmodal cortices on the basis of intracortical microstructure (Glasser et al. 2016; Margulies, Ghosh, et al. 2016b; Huntenburg et al. 2017; Burt et al. 2018). The specific microstructural context of transmodal versus sensory/motor cortices may show different neurodevelopmental trajectories and diverging potential for experience-driven plasticity (García-Cabezas et al. 2017; Vainik et al. 2020), a finding likely related to regional variations in activity-dependent myelination (Miller et al. 2012) and synaptic pruning (Mesulam 1998; Petanjek et al. 2011). Associations to intracortical microstructure, in particular cytoarchitectonic measures of laminar differentiation, were also seen when examining associations on a postmortem 3D reconstruction of a human brain, the BigBrain dataset (Amunts et al. 2013). Our approach furthermore showed transcriptomic co-variations with shifts in functional connectivity distance (Hawrylycz et al. 2012). A congruence was globally seen when studying associations to the principal component of cortical CGE, echoing prior findings on transcriptomic substrates of functional imaging measures (Fornito et al. 2019; Shafiei et al. 2020; Arnatkeviciute et al. 2021). Paralleling the myelo- and cytoarchitectural underpinnings of neuronal function, the transcriptional and functional architecture of human cortex likely share a common axis, where gradients of microscale properties ultimately contribute to macroscale functional specialization (Burt et al. 2018). Gene enrichment analysis could identify associations to genes expressed in excitatory and inhibitory neurons in both supragranular and infragranular compartments, together with astrocytes. Overall, this finding points to a rather diverse microcircuit layout of transmodal regions harboring long-range connections. A recent study reported genes enriched in supragranular cortical layers in humans relative to mice (Zeng et al. 2012), molecular innovations that may have contributed to the evolution of long-range cortico-cortical projections. Another study systematically identified long-range projecting markers by aligning temporal variation in gene expression and structure, reporting a set of genes identifying long-range projecting neurons in both upper and deeper layers (Charvet et al. 2021). Neuronal as well as non-neuronal contributions to microcircuit organization, for example through astrocytes, may play important roles in neuronal activity (Fiacco and McCarthy 2004; Jourdain et al. 2007) and plasticity (De Pittà and Brunel 2016) at both excitatory and inhibitory synapses (Perea and Araque 2007; Benedetti et al. 2011). Notably, by acting through transmitter-dependent and transmitter-independent mechanisms (Jalonen et al. 1997; Chever et al. 2010; Schipke et al. 2011; Larsen et al. 2014; Sibille et al. 2015; Stoica et al. 2017), astrocytes can serve as modulators of short- as well as long-range cortico-cortical communication (Pacholko et al. 2020).

Generative connectome models seek to identify the rules governing cortical wiring (Betzel et al. 2016), and model performance was previously found to be improved by also incorpoating inter-regional transcriptional or microstructural similarity (Oldham et al. 2021). Studies show that a combination of geometric constraints, including a distance penalty, as well as a homophilic wiring mechanism can reproduce key topological characteristics of the human connectome (Vértes et al. 2012; Betzel et al. 2016). Distance dependence implicates that proximal regions are more likely to be connected (Vértes et al. 2012). Similarly, findings in many species indicate that areas with similar microstructural and neurobiological features are more likely to be wired to one another (Barbas 1986; Barbas and Rempel-Clower 1997; Barbas 2015; Richiardi et al. 2015). Moreover, a previously formulated “structural model” of connectivity posits that similarities in overall laminar organization could help explain the presence, variation, and patterns of cortical connections (Hilgetag et al. 2016; García-Cabezas et al. 2019). Our work adds to this literature, suggesting an interplay of both distance dependence and homophilic wiring, underscored by the observed u-shaped association between microarchitectural similarity and connectivity distance. This confirms, on the one hand, the notion that adjacent regions with short-range connections have similar gene expression and microstructure, potentially underpinning their segregated functions. On the other hand, it also shows that transmodal cortices that participate in the long-range functional subnetworks have an unexpected increase in their microarchitectural similarity. The long-range connections that are mainly present in transmodal association cortices appear to allow for distant communication of microstructurally and transcriptionally similar territories, bypassing a general distance-dependent decline in homophily of brain wiring. Long-range connections, thus, likely allow for integrative communication across remote cortical regions (Sporns and Zwi 2004; van den Heuvel and Sporns 2011). Thereby, communication pathways formed by long connections may exhibit redundancies that promote network robustness and complexity and potentially enable parallel information processing across different cortical zones (Betzel and Bassett 2018).

A battery of sensitivity analyses confirmed that our findings were relatively robust across different analysis parameters, and we replicated our findings in an independent data set and showed consistency at both group and single participant levels. Overall, these results support a sensory-fugal topography of functional connectivity distance variations and show spatially covarying microarchitectural axes. Long-range connections may allow for integration of spatially remote, yet microarchitecturally similar areas of association cortex. These results suggest that long-range connections may facilitate integrative communication in an expanded cerebral cortex, potentially contributing to parallel and higher-order information processing that is central to human cognition.

Funding

BP was funded by the National Research Foundation of Korea (NRF-2021R1F1A1052303), Institute for Information and Communications Technology Planning and Evaluation (IITP) funded by the Korea Government (MSIT) (2020-0-01389, Artificial Intelligence Convergence Research Center, Inha University; 2021-0-02068, Artificial Intelligence Innovation Hub; 2022-0-00448), and Institute for Basic Science (IBS-R015-D1). SL was funded by CIHR and a Richard and Ann Sievers award. RVdW was funded by studentships from the Savoy Foundation for Epilepsy and a Richard and Ann Sievers award. CP was funded through a postdoctoral fellowship of the FRQ-S. SV was funded by the Max Planck Institute. BCB furthermore acknowledges research support from the National Science and Engineering Research Council of Canada (NSERC Discovery-1304413), the Canadian Institutes of Health Research (CIHR FDN-154298), SickKids Foundation (NI17-039), Azrieli Center for Autism Research (ACAR-TACC), BrainCanada (Future-Leaders), and the Tier-2 Canada Research Chairs (CRC) program. Data were provided, in part, by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research and by the McDonnell Center for Systems Neuroscience at Washington University. YW, ACE, and BCB were supported by the Helmholtz International BigBrain Analytics and Learning Laboratory (HiBALL). JR was supported by a Canadian Open Neuroscience Platform (CONP) fellowship and the Canadian Institute of Health Research (CIHR).

Conflict of interest statement: No author declares competing interests.

Data availability

Data from the locally studied dataset are openly available on CONP (https://portal.conp.ca/dataset?id=projects/mica-mics); processing pipelines are openly available on http://github.com/MICA-MNI/micapipe documented on http://micapipe.readthedocs.io. Analysis code for the main analysis is openly available on https://github.com/MICA-MNI/micaopen/tree/master/CDC.