Bayesian inference of chemical exposures from NHANES urine biomonitoring data

Abstract

BACKGROUND:

Knowing which environmental chemicals contribute to metabolites observed in humans is necessary for meaningful estimates of exposure and risk from biomonitoring data.

OBJECTIVE:

Employ a modeling approach that combines biomonitoring data with chemical metabolism information to produce chemical exposure intake rate estimates with well-quantified uncertainty.

METHODS:

Bayesian methodology was used to infer ranges of exposure for parent chemicals of biomarkers measured in urine samples from the U.S population by the National Health and Nutrition Examination Survey (NHANES). Metabolites were probabilistically linked to parent chemicals using the NHANES reports and text mining of PubMed abstracts.

RESULTS:

Chemical exposures were estimated for various population groups and translated to risk-based prioritization using toxicokinetic (TK) modeling and experimental data. Exposure estimates were investigated more closely for children aged 3 to 5 years, a population group that debuted with the 2015–2016 NHANES cohort.

SIGNIFICANCE:

The methods described here have been compiled into an R package, bayesmarker, and made publicly available on GitHub. These inferred exposures, when coupled with predicted toxic doses via high throughput TK, can help aid in the identification of public health priority chemicals via risk-based bioactivity-to-exposure ratios.

INTRODUCTION

There are more than 10,000 chemicals currently in commercial use in the US, and hundreds more are introduced every year [1]. Due to the extensive time and resources needed to experimentally assess the risk of a chemical, approaches are needed to prioritize these chemicals for in-depth exposure and hazard characterization. For chemicals with dose-response high-throughput screening (HTS) in vitro toxicity data, methods are available to first identify biological targets of chemicals [2] and then estimate an equivalent dose in humans [3]. However, as risk is a function of both hazard and exposure, identification of potential hazards by HTS must be accompanied by complementary rapid exposure screening tools [4–8]. While some chemicals may be data rich or have a variety of different types of data, the majority of chemicals currently lack sufficient exposure data [3, 4], and thus, computational exposure screening methods that are efficient, easily applied, and high-throughput are being developed.

Exposure predictions for large numbers of chemicals are not meaningful without reliable estimates of uncertainty and variability. To obtain such information for high-throughput exposure (HTE) predictions, “actual exposure” data must be available for model evaluation, for instance via biological monitoring. Biomonitoring data is an important component of chemical risk assessment and has started to play an increasing role in the development of high-throughput exposure models as focus moves from a per-chemical basis to the larger exposure landscape as a whole (see reviews [9, 10]). However, collecting such data is expensive and labor intensive [11, 12]. Therefore, our ability to construct accurate models for different exposure pathways (the path from a chemical source to a human receptor) is often limited, mainly due to a lack of proper data for evaluation. Two broad classes of exposure pathways can be defined: near-field (that is, indoor, proximate sources) and far-field (for example, industrial releases) sources, both of which need to be addressed with limited monitoring data [13, 14].

Unfortunately for exposure scientists, the actual exposure events for an individual are both difficult to monitor and confounded by the inherent complexities of human behavior. However, we can obtain data that could be used to characterize potential sources upstream of exposure, such as composition of consumer products, characterization of environmental releases, or measurements in environmental media. There have been a number of exposure models using such data to estimate exposure by different pathways [8, 15–19] We can also obtain exposure indicator data (that is, downstream), particularly biomarkers of exposure (for example, chemical concentrations in urine or plasma) [20]. Since the exposure event itself can be difficult to observe, we develop models to either estimate exposure from upstream sources (forward modeling) or infer exposure from downstream sources (reverse modeling) [10]. Both forward and reverse modeling have drawbacks (for example, it can require many accurate forward models to get an idea of aggregate exposures while biomonitoring data can struggle to capture acute or intermittent exposures, exposure to chemicals with short half-lives, or high clearance rates), and recent advances have been made to compare the results of both approaches to establish model effectiveness—that is, the predictive ability of models for chemicals covered by biological and environmental monitoring data [14].

Biomonitoring data reflect aggregate human exposures across all pathways for the general population [9, 21]. A forward modeling approach unintentionally may omit important exposure pathways for certain chemicals. The Systematic Empirical Evaluation of Models (SEEM) framework is a consensus model of multiple forward exposure model predictions (referenced in the previous paragraph; and other data such as national production volume) intended to provide a more complete and accurate estimate of both potential exposure and its inherent uncertainty [22]. SEEM calibrates the statistical weight associated with each model predictor across a range of chemicals for which data are available (for example, median intake rate estimates inferred from biomonitoring data). The residual chemical-to-chemical variability in exposure that is unexplained by the predictors provides an estimate of model uncertainty. SEEM can be used to estimate a range of possible exposures using both its consensus model of calibrated predictors and the empirically estimated uncertainty for the hundreds of thousands of chemicals lacking evaluation data.

For this work, biomonitoring data were obtained from the National Health and Nutrition Examination Survey (NHANES) [23]. NHANES is an elaborate study conducted by the Centers for Disease Control and Prevention (CDC) at multiple locations throughout the United States. Starting with 1999–2000, NHANES is conducted in cohorts over 2-year cycles. Data from a cycle can take years to be completed and released publicly; the most recent data used in this work is from 2015–2016. The study is designed to have sufficient statistical power to characterize key biometrics for the general United States population as well as various sub-populations of interest. The surveys include household interviews, collection of medical histories, standardized physical examinations, and collection of biological specimens. One result of analyzing these specimens is a regular report on “Human Exposure to Environmental Chemicals” [24, 25]. NHANES data are reported for various demographics (for example, gender, race, age) at selected percentiles (for example 50th, 95th) as well as a geometric mean. For this analysis, quantiles of the total population were used, as calculated from the CDC NHANES data files [23, 26].

Dozens of studies have utilized the NHANES data to look at exposure (see review [10]), however, a large majority of them are limited in scope, usually focusing on a small subset of urine biomarkers or staying within the area of comparing biomarker concentrations. As exposure science moves to be more high-throughput and assess larger numbers of chemicals, there is a lack of well-documented approaches to use biomonitoring studies on this larger scale. Several studies, focusing in on individual or small numbers of related chemicals, employ urine metabolite concentration data with some procedure involving survey population quantiles, adjustment by creatinine excretion, bodyweight, etc., and occasionally chemical-specific exposure routes to estimate exposure as an intake dose [27–30]. While these studies provide valuable insights and may be more accurate as they can be specific to certain chemicals and their exposure routes, there are hundreds of chemicals with biomonitoring data in NHANES alone. Furthermore, as mentioned previously, there are many forward exposure models to predict chemical intake doses, but assessment of their accuracy is highly limited due to a lack of validation data. Providing a well-designed and publicly available method to estimate exposure intake rates for hundreds of chemicals based on biomonitoring data can fill a major gap in exposure and risk assessment research.

In this paper, we outline a reverse modeling approach to infer ranges of chemical exposures (intake rates in mg/kg/day) for parent chemicals of biomarkers measured in urine samples from the U.S. population by the National Health and Nutrition Examination Survey (NHANES) [23]. The approach uses Bayesian methodology to appropriately incorporate the inherent uncertainties associated with limit of detection issues in the biomonitoring data and the complexities of chemical metabolism. Exposure reconstruction from biomonitoring data [27, 29, 31, 32], including Bayesian methods [28], has been used elsewhere for individual chemicals. Here we refined (see methods subsection Bayesmarker Package for details) a multichemical method originally described in Wambaugh et al. (2013) and made it publicly available on GitHub as an R package called bayesmarker (https://github.com/USEPA/CompTox-HumanExposure-bayesmarker), which is intended to be applicable generally to urine biomonitoring datasets. We illustrated the application of bayesmarker using updated data from NHANES and additional parent-product metabolism relationships identified through an informatics-led literature review. Exposure estimates were obtained for 179 parent chemicals, which were then prioritized using a risk-based metric calculated using high-throughput toxicokinetics. The exposure estimates of chemicals not in the initial SEEM calibration set were also compared to SEEM predictions to assess consistency between forward and reverse modeling approaches. Lastly, exposure estimates were investigated more closely for children aged 3–5 years, a population group that was introduced in the 2015–2016 NHANES cohort. These inferred intake rates, when coupled with predicted toxic doses via high throughput toxicokinetics, allowed for the identification of public health priority chemicals via risk-based bioactivity:exposure ratios (BER) and provided an evaluation of high-throughput exposure model predictions.

METHODS

Problem description

Biomonitoring of concentrations of chemicals within the body represents the downstream integration of exposure to the body from all pathways and routes. The goal of this work is to infer upstream exposure from these downstream data sources. The major challenge of the exposure inference problem is the appropriate handling of multiple sources of uncertainty [10, 33, 34]. The first contributor to uncertainty is that biomonitoring data often reports metabolite (‘transformation product’) concentrations from which we can only infer parent chemical exposures [35]. The stoichiometry relating a parent to multiple metabolites is complex [33, 34, 36]. When a parent molecule can be metabolized to one of several product molecules, the proportions φ that quantify the probabilities of each path from parent to product are often unknown [36]. Furthermore, multiple parents may be metabolized to the same product molecules. A second major contributor to uncertainty comes from limitations in our ability to measure chemicals within biological media [10, 34]. Analytical technologies can only detect chemicals if they occur at a high enough concentration, which is referred to as the limit of detection (LOD) [35]. Measurements below this LOD in an individual’s biological sample indicate a concentration smaller than the LOD or absence of the chemical. Note that, for the biomonitoring study used, it is assumed that the chemicals being measured are detectable in urine. In addition to uncertainty, there is also variability in that each metabolite is measured in a population of individuals, meaning the observed chemical concentration is represented by a distribution rather than a single value [33, 34, 36]. Being able to incorporate this variance and uncertainty into the model will provide better estimates of exposure.

Model description

Here we describe a general statistical model with a Bayesian framework for estimating human intake rates from biomonitoring measurements, based on urine metabolite concentrations and known parent-metabolite (transformation product) relationships (Fig. 1). The general approach described is a revision to one that was reviewed by a Federal Insecticide, Fungicide, and Rodenticide Act (FIFRA) Scientific Advisory Panel in 2014 [37] including, wherever possible, improvements suggested by that panel. Bayesian formalism is a rigorous statistical methodology for incorporating uncertainty into mathematical models using probability distributions of plausible values for each parameter. For example, a typical model parameter that is normally distributed would be characterized by a mean and standard deviation; the more accurately we know the behavior of a parameter in our model, the less uncertainty we must afford it in the model (that is, the smaller the standard deviation). Through Bayesian methods, prior assumptions about the value of parameters are informed by the addition of new data to produce posterior distributions for the parameters that reflect both the prior assumptions and the data. The result of a Bayesian analysis is a posterior probability distribution for each parameter, often summarized by quantiles such as the median (50th percentile) and 95% “credible interval” (lower 2.5th to upper 97.5th percentile range).

Fig. 1. Depiction of the Bayesian inference methodology employed to estimate human exposure to parent chemicals of metabolites measured in urine biomonitoring data.

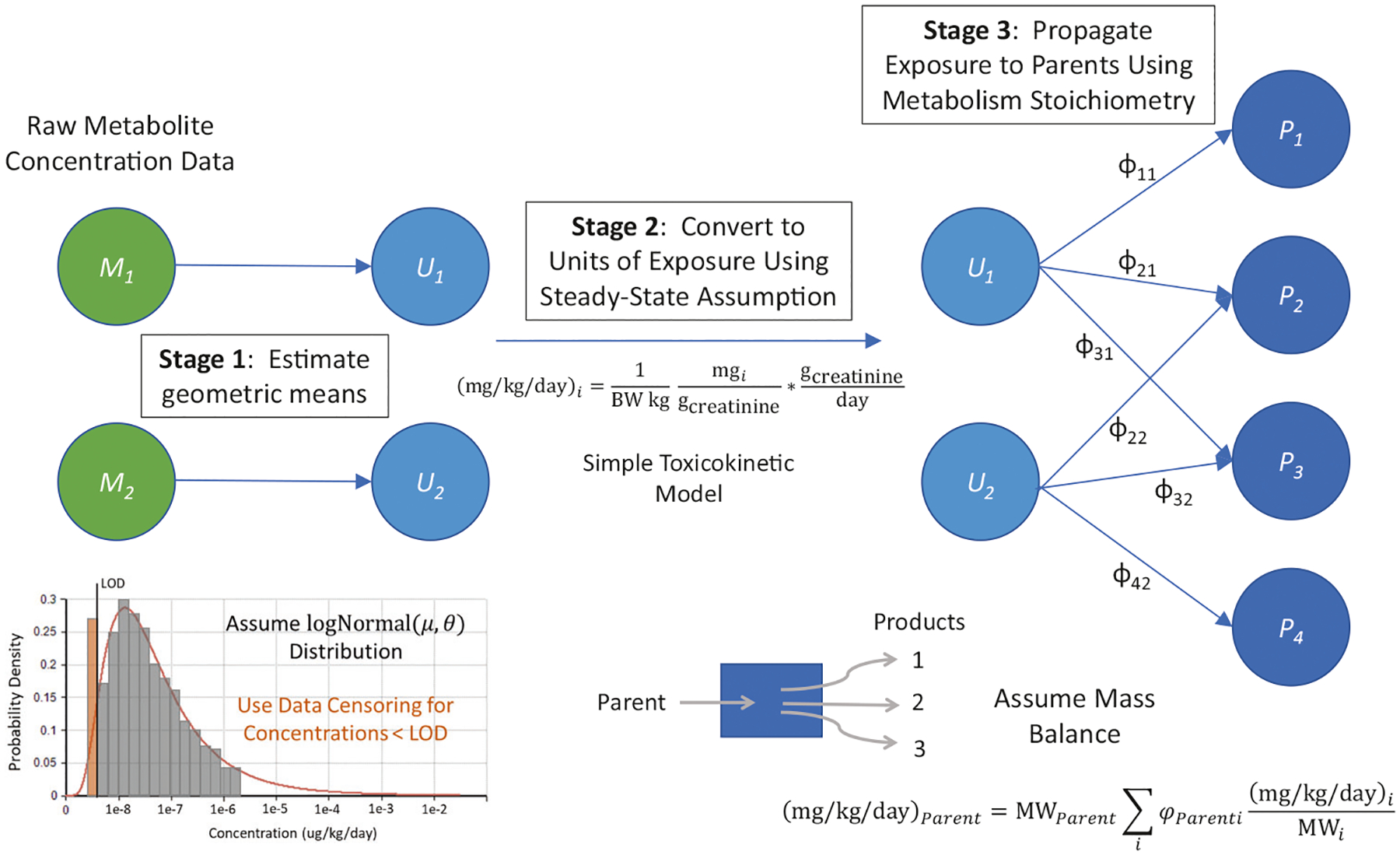
The approach consists of three stages. Stage 1 involves estimating the geometric mean concentration of each metabolite. The concentration distribution for a population is assumed to be lognormal, and concentrations below the limit of detection (LOD) are handled by left-censoring the data. Stage 2 uses a simple toxicokinetic model (steady-state is assumed) to convert concentration measurements into a dose value (mg/kg/day). Stage 3 makes use of prior knowledge, in the form of known chemical metabolism (linking parents to their products), along with conservation of mass balance to propagate or translate metabolite exposures to parent intake rates.

The toxicokinetic model linking urine concentrations to parent chemical exposures assumes steady-state equilibrium with mass balance to minimize the parameters needed (such as chemical-specific biological half-lives, magnitude, and timing of exposures) [9, 20, 21, 36]. Assumptions similar to those of Lakind and Naiman [27] were made – chiefly that the individuals were at steady-state due to a constant rate of exposure and therefore the urine concentrations were the result of this constant exposure [38]. Wambaugh et al. (2015) assessed 349 chemicals based on multiple data sources and appropriateness of toxicokinetic models, which showed that humans can reach a steady-state with respect to environmental exposures (majority of chemicals reach steady-state within 3 weeks), that steady-state concentration is a reasonable surrogate when exposure is more episodic, and that 100% absorption is reasonable [39]. There are of course cases where a steady-state model may have limitations (see Discussion), but for the high-throughput approach presented in this work, we believe it is sufficient in most cases. Because we are inferring a dose (intake) rate consistent with an eliminated concentration in urine, we refer to this simple toxicokinetic model as steady-state “reverse dosimetry” or “reverse toxicokinetics” [32, 36].

The Bayesian inference statistical model that is the focus of this work has three stages: (1) Calculate statistics (mean, standard deviation, etc.) for the population urine concentration measurements, (2) Convert to units of exposure via a simple toxicokinetic model, and (3) Propagate exposures from metabolites to parent chemicals. In stage 1, the log of geometric means is calculated from estimates of population quantiles generated from the individual urine concentration measurements using the statistical survey weights provided by NHANES. We assume that the true population distribution is log-normal, and parameters of the log-normal distribution are used to estimate observations that are below the limit of detection [40]. The data input for this model are the estimates of the 50%, 75%, 90%, and 95%-iles (obtained using the survey weights of the biomonitoring data) from the biomonitoring study being analyzed and estimates of their standard errors. Assuming the natural log-transformed estimates are approximately normally distributed, we estimate a standard error by dividing the difference (on the log scale) between the upper and lower 95% confidence limit by 2*1.96. The lower limit is missing in the biomonitoring data if the lower confidence limit would fall below the nominal limit of detection for the chemical. In that case, the standard error is estimated by dividing the difference between the log-transformed upper confidence limit and the log-transformed central estimate. The standard error for the estimates of the quantiles for chemical j (se_j) is the square root of the mean of the squared standard errors for the quantiles of that chemical. So, the expected value of the log-transformed $Q_i^{th}$ quantile (Q_i = 0.5, 0.75, 0.9, 0.95 for i = 1–4, respectively) for chemical j given mean lU_j and population standard deviation s is F⁻¹(Q_j, lU_j, s_j), where F⁻¹() is the inverse of the normal cumulative distribution function. We simplify the estimation by assuming the standard errors for the quantile estimates are estimated without error.

Then, for stage 2, if ly_ij is the observed value of the $Q_i^{th}$ quantile of the j^th chemical, which has been converted via reverse dosimetry from an observed concentration in urine to a parent chemical exposure,

$$l{y}_{ij}\underset{\_}{\underset{\_}{\text{def}}}N\left(F^{-1}\left(Q_i,I{U}_j,s_j\right),s{e}_j\right),I{y}_{ij}>LO{D}_j$$

$$I{y}_{ij}\underset{\_}{\underset{\_}{\text{def}}}\mathit{\text{Pr}}\left\{N\left(F^{-1}\left(Q_i,I{U}_j,s_j\right),s{e}_j\right)<LO{D}_j\right\},I{y}_{ij}<LO{D}_j$$

$$I{U}_j=\text{ln}\left(U_j\right)$$

Thus, ly_ij is left-censored for measurements below the LOD in this stage based on the observed LOD and other characteristics of the distribution. We use a lognormal prior for s_j to help regularize estimation:

$$s_j~\mathit{\text{IN}}(\mathit{\text{Isd}},\mathit{\text{Isd}}.\mathit{\text{sd}})$$

$$\mathit{\text{Isd}}~N(0,1000)$$

$$\mathit{\text{Isd}}.\mathit{\text{sd}}=\left|\mathit{\text{Isd}}.z\right|~t\left(0,\frac{1}{625},1df\right)$$

That is, lsd.sd is a half-Cauchy distribution, as recommended in Gelman [41] (where N() and IN() indicate the normal and log-normal distributions respectively).

Finally, in stage 3 the median concentration of metabolite U_j is the sum of contributions from exposures to each parent k that can be metabolized to product j. That is, if P_k is the median exposure to parent k, then

$$U_j={\sum }_k{P}_k{\phi }_{kj}.$$

Here ${\sum }_j{\phi }_{kj}=1$ or 2. The sum is 2 for parent chemicals that are cleaved in half, with each half possibly being further metabolized. For most chemicals with multiple potential metabolites, each parent molecule results in only a single product molecule, and the sum will be 1. In these data, when the sum is 2, one of the φ_kj values is 1. Finally, the φ_kj values that are not set to be 0 (meaning parent k cannot produce product j), or 1 (meaning a molecule of parent k always produces a molecule of product j) need to be estimated, given the constraints that for each k, ${\sum }_{j:{\phi }_{kj}\notin \left\{0,1\right\}}{\phi }_{kj}=1$. This is done by assigning an element δ_l to each non-zero φ_kj so that, if L_k is the set of indices for δ that corresponds to the φ_kj that need to be estimated, and l is the index of δ that corresponds to j of φ, set ${\phi }_{kj}=d_l/{\sum }_{z\in L_k}{d}_z$ with prior d_l ~ U(0,1). Therefore, when φ_kj is not 0 or 1, it means parent k is broken down into multiple products with some non-zero proportion, which we model based on the observe metabolite concentrations and parent-metabolite relationships. Corresponding Just Another Gibbs Sampler (JAGS) [42] code is included in the supplemental material.

Model inputs

There are two main inputs to the model used to obtain exposure estimates based on the NHANES survey data: (1) the metabolite concentrations, which are represented by a distribution of values over the individuals; and (2) a numeric matrix indicating metabolism stoichiometry (see previous section regarding φ) where rows represent the parent chemicals and columns represent the metabolites.

Reverse dosimetry is straightforward for a metabolite that is related to only one parent compound, but many metabolites can have multiple parent compounds and many parent compounds can have multiple metabolites. A mapping of parents to metabolites, shown in Fig. 2, was originally derived [13, 14] from the NHANES reports to identify relationships and potential non-identifiability of parent compounds from a given metabolite [24, 25]. Further linkages were obtained by text mining PubMed abstracts for co-occurrences of the NHANES metabolites (along with all of their known synonyms listed in the EPA’s CompTox Chemical’s Dashboard [43]) with keywords related to metabolism (for example, “metabolite of” and “its metabolite”) where evidence in humans was required, followed by manual curation of the full-text of the corresponding publications for confirmation of the relationships. A 1:1 stoichiometry of parent to metabolite molecule was assumed (in other words, φ = 1) unless known otherwise (and confirmed by manual inspection wherever SMILES descriptors were available for parent and metabolites). The proportion of different product molecules was generally unknown and treated as such in the estimation process while preserving mass balance.

Fig. 2. Network representation of the parent-metabolite mapping for all NHANES metabolites.

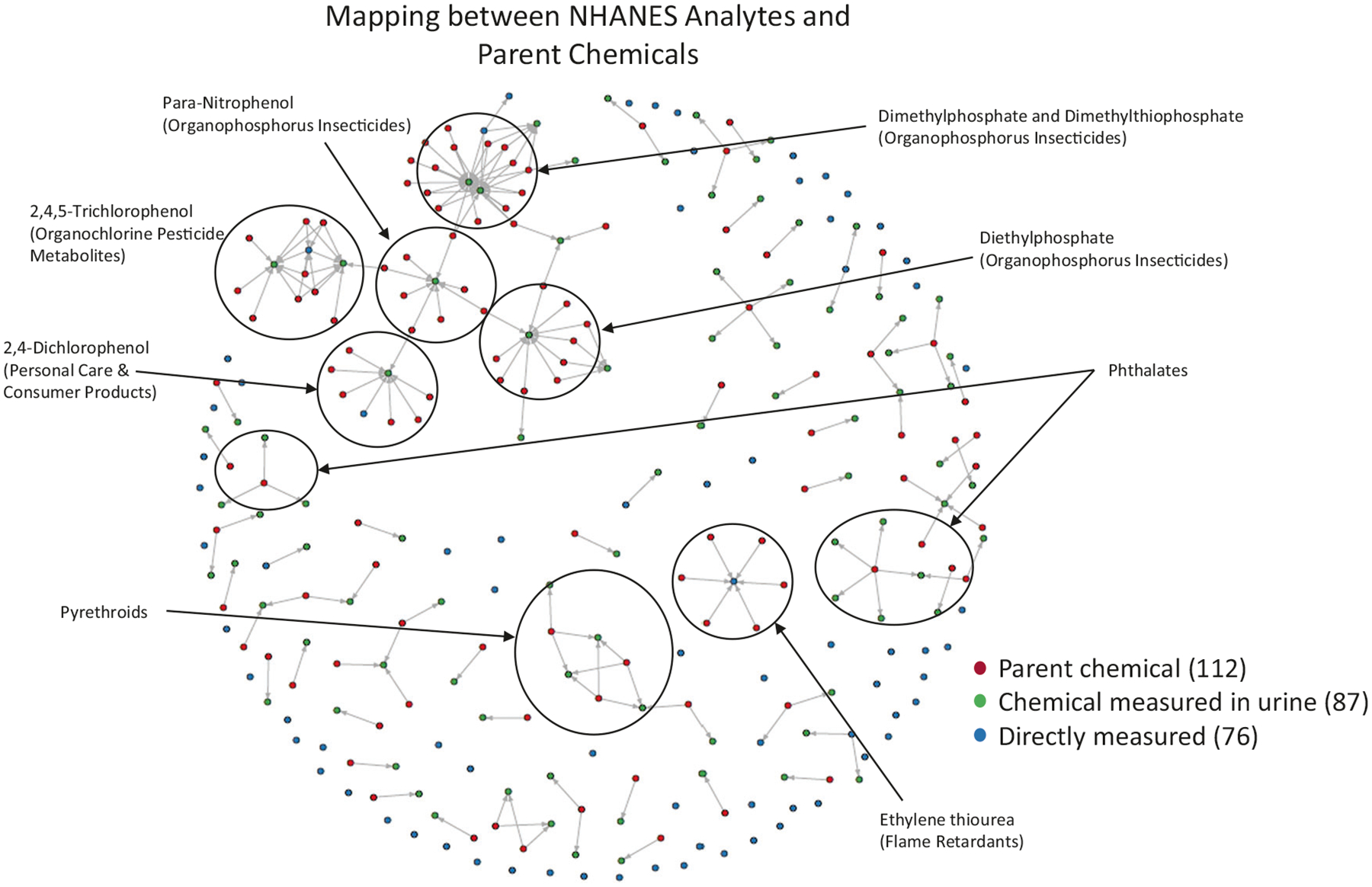
Parent chemicals were identified using the NHANES reports and text mining of PubMed abstracts based on metabolite synonyms and keywords such as “metabolism” or “metabolite”. Nodes are either exclusively a parent chemical (red), exclusively a metabolite (green), or a chemical that was directly measured in urine (blue). For chemicals in this latter set, they are chemicals for which we wished to report an exposure inference and could be a “metabolite” according to NHANES but also have known metabolites (for example, about a dozen of these are metals). Links (edges) are directed in the direction of metabolism (in other words, parent -> metabolite). Denser areas of the graph are annotated by chemical class, which was also obtained from the NHANES reports.

The distribution of each metabolite concentration was characterized by a geometric mean, standard deviation, and standard error. For each metabolite, the geometric mean concentration was calculated across 11 population groups (the total population, males, females, age 3–5 years, age 6–11, age 12–19, age 20–65, age 66 and older, BMI ≤ 30, BMI > 30, and females of reproductive age) using urine concentration, a scaling factor based on glomerular filtration (estimated from creatinine concentration), and each individual’s bodyweight. It is important to note that for the group labeled 1–5 years of age by NHANES, urine concentration measurements were not obtained for children under the age of 3. Thus, we refer to this group as age 3–5 throughout the manuscript to more appropriately represent the data that was analyzed. Metabolites were restricted to those measured in urine, as opposed to those in serum, to meet mass balance assumptions. Daily creatinine excretion was estimated using a predictive model that incorporates the individual’s gender, ethnicity, age, and kilogram body weight (see next section). Using the Bayesian framework together with the relative molecular weights of the parents and metabolites (Table S3), urine concentrations were converted to exposure rates. Measurements below the LOD were estimated by drawing samples from the derived log-normal distribution for each chemical.

Modeling creatinine excretion rates

In stage 2 of the model described above, the metabolite concentrations are converted to exposure rates by using a simple toxicokinetic model and assuming steady-state exposure (Fig. 1). This requires estimating the rate at which chemicals are filtered into urine by the kidneys, which is known as the glomerular filtration rate (GFR). It is common practice to use urinary creatinine excretion rates (CER) from timed urine collections as an estimate of GFR [44]. At steady state, creatinine generation is a function of muscle mass [45] and is influenced by sex, race, age, and body weight [46–49]. To accurately scale metabolite concentrations using estimated CER, we extrapolated CER from urinary creatinine concentration and the volume and time of last void for the urine samples provided by the 2009–2010 NHANES cohort (first cohort with this data available; using this NHANES cohort to build a general model for CER). The analysis was carried out with the R statistical programming environment [50] accounting for sampling design using the package “survey” [51]. The model for log₁₀(CER) was defined by

$${\mathit{\text{log}}}_{10}\left(\text{CER}\right)=M_{\mathit{\text{Gender}}}+D_{\mathit{\text{Ethnicity}}}+ns\left(\mathit{\text{Age}},\mathit{\text{knots}}=c\left(20,60\right)\right)+ns(\mathit{\text{Bwt}},\mathit{\text{\hspace{0.17em}knots}}=c(50,100))+s\times E$$

where E ~ t(df = 3.5), ns is natural cubic spline (with knots being the cut points of the piece-wise cubic polynomial), t is the Student’s t distribution with df degrees of freedom (to handle “outliers”). Model parameters were taken directly from SAS xport files for the 2009–2010 cohort from the variables RIAGENDR, RIDRETH, BMXWT, and RIDAGEYR, and this model was used for all NHANES cohorts.

Obtaining exposure estimates

Markov Chain Monte Carlo (MCMC) methods were used to sample from the posterior distribution [52]. MCMC was performed using JAGS v. 4.3.0 via rjags v. 4–10 in R v. 3.6.1 using 18 cores on a cluster of hexa core CPUs. Parallelization was accomplished using the parallel and foreach packages [53, 54]. The model was run for all chemicals and for each population group. Parameters known imperfectly were assigned probability distributions that characterize the degree of uncertainty. Using Bayes’ rule, we defined a joint probability distribution for model parameters (for both statistical and more deterministic parts of the model). This is the posterior distribution, and summarizes all the information in the data, the prior information, and the model posited for the data. Priors assumed that the exposure values were log-normally distributed around a mean (normally distributed with mean 0 and variance 1000) with standard deviation sd, and the proportions of the metabolites from a parent compound are Dirichlet-distributed with α_i set to 1.

The process concluded by testing the samples for convergence with the coda package (v. 0.19–4), which summarizes the output from the Markov Chain Monte Carlo (MCMC) simulations. Convergence was tested using two diagnostics, namely Heidelberger and Welch’s convergence [55] and Gelman and Rubin’s convergence [56] with r-hat set to 1.05. Acceptable convergence of the samples imply that earlier and later samples have similar enough distributions and that different chains converge to the same distribution (that is, the estimate of the posterior is stable/stationary).

Bioactivity:exposure ratio calculation

The inferred exposure estimates can be extrapolated to a measure of overall expected risk using toxicological data and toxicokinetic modeling. One measure of relative risk is the bioactivity:exposure ratio (BER). BER is the ratio of chemical hazard (the expected human dose to induce a toxic effect; obtained from toxicity data) to the exposure estimate (expressed as a dose metric). These two values were calculated using the httk R package [57]. Doses exhibiting toxicity in rats, specifically the median lethal dose (LD50), have been predicted for thousands of chemicals via EPA’s Collaborative Acute Toxicity Modeling Suite (CATMoS) [58]. LD50 values were obtained through the OPEn Structure-activity/property Relationship App (OPERA; UI version 2.7) [59] and transformed to translate them from a measure of acute toxicity in rats to a chronic toxicity endpoint for humans, namely a no-observed-adverse-effect level (or NOAEL). This was achieved by multiplying the LD50 values by an acute-to-chronic application factor of 0.0001 based on work by Venman and Flaga [60]. These transformed LD50s were then used as input to the httk package’s calc_tkstats function to generate human equivalent doses (HEDs). Our median exposure estimates were used as input to the calc_mc_css function to obtain a steady-state plasma concentration with dose units (ug/L). BERs for each chemical and population group were calculated from these two values and ranked from lowest to highest BER to aid in chemical prioritization. Uncertainty was propagated from the estimated intake rates to obtain a 95% confidence interval on the BER values for the total population by repeatedly MCMC sampling from the inferred exposure distribution for each chemical. One chemical, di-n-octyl phthalate, was predicted to reach steady-state after 139 years, a clear outlier (next longest time to steady-state was 34 days), and therefore was excluded from BER calculation only.

Comparison with SEEM

SEEM, the Systematic Empirical Evaluation of Models, is a consensus modeling approach that predicts exposure to thousands of chemicals [22]. SEEM calibrates its predictors using a small set of inferred exposure intake rates, which were the result of the precursor study to this work (in other words, the same underlying model as described so far was used to estimate exposure values for the chemicals used to calibrate SEEM) [14]. A total of 106 chemicals with inferences from NHANES prior to the 2011–2012 cohort were used to calibrate SEEM. Here, incorporation of the latest NHANES cohorts and additional curation of parent-chemical metabolites produced inferred exposure intake rates for 62 additional chemicals not in the calibration set. Of these 62 chemicals, 39 had SEEM exposure predictions. Exposure inferences for these 39 chemicals were obtained for each NHANES cohort between 2009–2010 and 2015–2016, where data was available, and compared to the SEEM predictions for the total population with 95% confidence intervals obtained from the quantiles function of the stats R package. A simple linear model was used to investigate correlation between SEEM and bayesmarker predictions. Samples were drawn from the MCMC exposure distribution and used as the variable for the linear model with the weights being the inverse square of the standard deviation of the drawn exposure samples. This was performed 1000 times to generate a distribution of R^2 values, from which a median and 95% CIs were obtained.

Bayesmarker package

The method described above (excluding BER calculation and SEEM comparison) has been organized into an R [50] package called bayesmarker. It is currently designed to work on the NHANES survey but will be made more generalizable to operate on any urine biomonitoring study. Figure S1 depicts the basic structure of the package and how the previously discussed steps and elements are organized. The input is a single Excel file that contains three sheets of data tables (Tables S1–S3). These tables were created manually based on which metabolites and NHANES cohorts were of interest and the relationships between different elements of the data. The first two tables are based on the biomonitoring data (NHANES data structure) designating required data files and relevant columns (for example, the BMI column name from the bodyweight file from a specific cohort). The third table of the input file is the parent-metabolite mapping (that is, a table matching parent compounds to metabolites). In addition to adding more links to this mapping, we made multiple refinements to the original method published by Wambaugh et al., 2013 [14]. First, the analysis pipeline is organized using more concise code such that five main functions are called consecutively, starting with obtaining the data files to finalizing exposure estimate units and observing model convergence. Various checks in the form of print statements and options for parallel execution as well as locally saving logs and plots are available throughout the pipeline. Lastly, the package allows for choosing subsets of chemicals, population groups, and NHANES cohorts as well as the ability to combine data from multiple cohorts. A more detailed description along with vignettes to reproduce the analysis herein can be found on the bayesmarker GitHub page (https://github.com/USEPA/CompTox-HumanExposure-bayesmarker).

RESULTS

Estimating chemical exposure

Using the most recent NHANES cohort in which each metabolite was measured (see Table S1; up to the 2015–2016 cohort), our method was applied to obtain up-to-date parent chemical exposure estimates (Table S4). The parent-metabolite relationship may be thought of as a directed graph in which chemical entities are represented by nodes and transformations from one chemical to another are described by edges [61]. A total of 270 edges in the metabolite mapping linked 151 metabolites to 179 parent chemicals (Fig. 2). Estimates were generated for each chemical per population group using the method depicted in Fig. 1.

To identify population group specific patterns and their potential vulnerabilities, the log2 fold differences in the mean exposure estimates for each population group compared to total population was calculated (Fig. 3; data in Table S5). Population groups were clustered by similarity across all chemicals, grouped by chemical class. Chemicals not measured in the 3–5 age group are indicated in gray. Red color indicates higher estimated exposure of a chemical in a group compared to the total population and blue represents lower exposure. A value of 1 (or 2) in the log2(fold change) scale indicates a doubling (or quadrupling) of exposure whereas a value of −1 (or −2) indicates a halving (or quartering) of exposure. There were 75 chemical-population group pairs that exhibited significant differences in estimated exposure compared to all individuals (significance defined by no overlap of the 95% confidence intervals; Table S6).

Fig. 3. Difference in inferred chemical exposure between each population group and the total population.

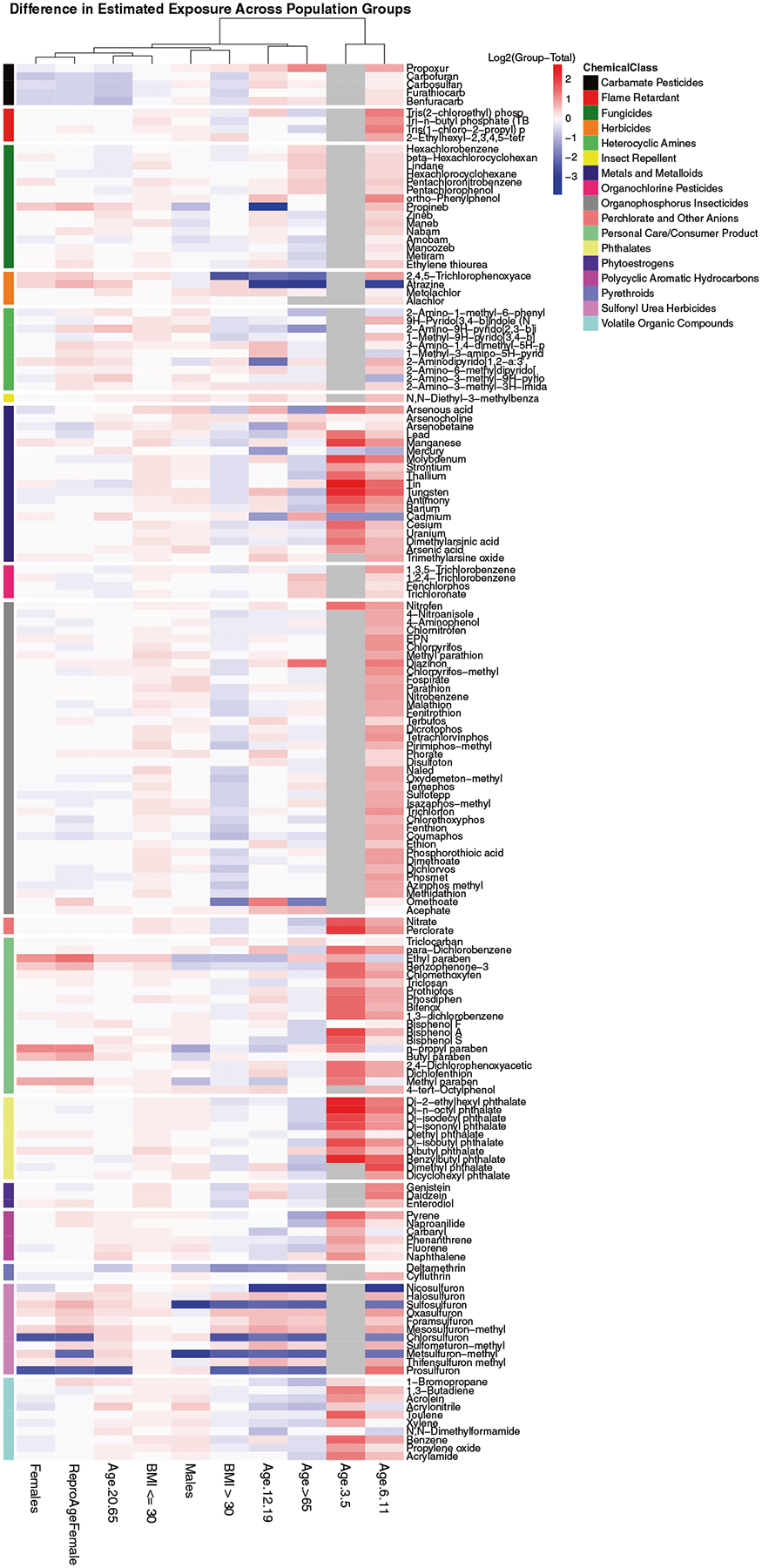
Chemicals are arranged by class (indicated on the top of the heatmap) and population groups are clustered by similarity. Estimates were calculated using the most recent NHANES cohort for each metabolite. The log2 difference in median intake rate estimates from a population group and all individuals is shown. Red indicates relatively higher exposure, blue lower exposure, and gray missing data. Chemicals with an insufficient number of observations above the limit of detection (LOD) were removed.

When considering all chemicals, the relative median exposure estimates were generally lower for individuals with a BMI > 30 and higher for children, especially younger children. Examining chemicals by group allows identification of many patterns across and within individual population groups and chemical classes. We observed, for example, that five personal care and consumer product chemicals (color-coded light green) exhibited relatively higher exposure in females (including those of reproductive age). These chemicals include 4 parabens (particularly ethyl paraben and n-propyl paraben) and benzophenone-3, which are commonly used in cosmetic products. Other population groups (specifically age 6–11, age 12–19, and age 65 and older) had lower exposure for a few herbicides (coded orange; atrazine and 2,4,5-Trichlorophenoxyacetic acid) and a few sulfonyl urea herbicides (coded dull pink). For the latter case, all other sulfonyl urea herbicide chemicals had high exposure for those same population groups, except in males, which showed similar exposure to the total population. Four carbamate pesticides exhibited lower exposure to females and 20- to 65-year-olds (coded black), in addition to a few sulfonyl urea herbicides. As for individuals over the age of 65, 3 organochlorine pesticides (middle, coded in pink; trichloronate, fenchlorphos, and 1,2,4-trichlorobenzene) exhibited higher estimated exposure compared to all individuals, while half of the fungicides (coded dark green) also showed this higher exposure and the other half showed lower exposure. At the individual chemical level, one organophosphorous insecticide (coded gray; diazinon) showed much higher exposure to individuals over the age of 65, and one fungicide (coded dark green; propineb) exhibited much lower exposure for 12–19-year-olds.

Translating exposure to risk

While exposure estimates are useful in many cases or applications, we ideally want to perform chemical prioritization based on overall chemical risk, which incorporates exposure and hazard [62–65]. By coupling our inferred exposure intake rates (median exposure value across all NHANES survey participants) with predicted toxic doses and high throughput toxicokinetics, we can identify public health priority chemicals via risk-based bioactivity:exposure ratios (BER). The smaller a chemical’s bioactivity exposure ratio, the more of a priority it is for further study because the average, population-level exposure is closer to the toxic effect dose. We estimated a range of roughly 8 orders of magnitude in the BER values for parent chemicals of NHANES metabolites (Fig. 4; data in Table S7). The chemical with the lowest BER was styrene with a BER value of 169.5. The 4 smallest BERs were seen for two volatile organic compounds and two phytoestrogens. Most of the organophosphorus insecticides had a BER value that fell within the middle of the range and sulfonyl urea herbicides had the highest BER values. The BER value for most chemicals is smallest for child population groups (3 to 5-year-olds and 6 to 11-year-olds).

Fig. 4. Inferred bioactivity:exposure ratios (BERs) for parent chemicals of NHANES metabolites.

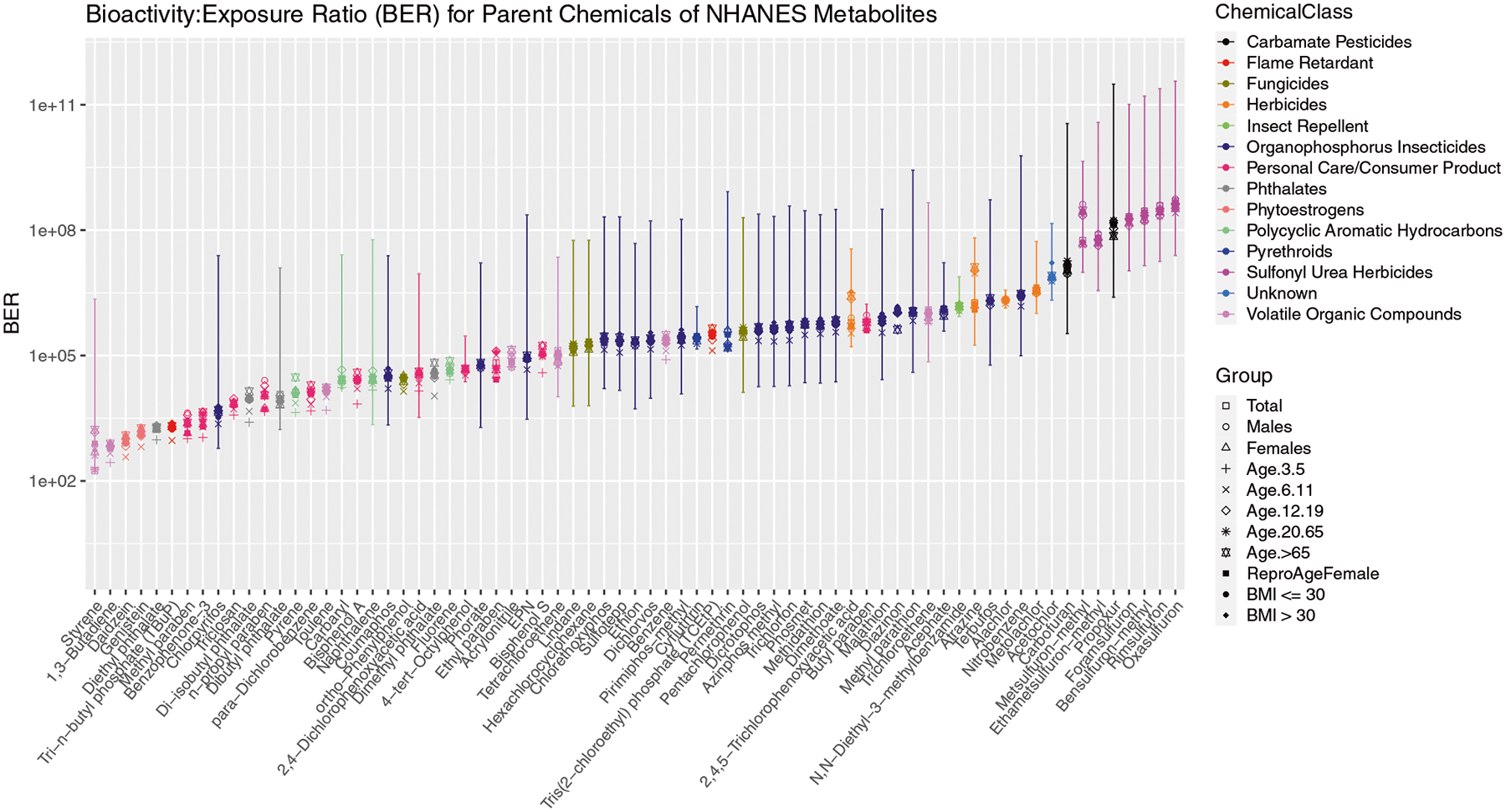
BER = human equivalent dose (HED)/exposure. HED is the human dose of a chemical that is expected to induce the same magnitude of toxic effect as the experimental animal dose, calculated here using the httk R package and rat oral LD50 values (LD50 is the concentration that causes the death of 50% of a group of test animals). LD50 values were scaled using a traditional acute-to-chronic transformation factor of 0.0001 to represent a surrogate human chronic No-Observed-Adverse-Effect-Level (NOEAL). The exposure value was obtained by scaling our median (point estimate) intake rate estimates by each chemical’s predicted steady state concentration. Error bars represent the 95% CI on the estimated BER for the total population. Chemicals with smaller BERs are of more interest as the inferred exposure is closer to the concentration at which bioactivity occurs. Points indicate population group by shape and chemical class by color.

Exposure case study: children aged 3–5

Wambaugh et al. [13] showed that children aged 6–11 typically had higher exposure to most chemicals when compared to other population groups. At that point, ages 6–11 was the youngest cohort with chemical exposure data in NHANES, but, starting with the 2015–2016 cohort, some data on children aged 3–5 was included. This newly reported demographic group generally had higher estimated exposure for most chemicals compared to other population groups (Fig. 3). For chemicals without data for the age 3–5 group, the population group with the highest estimated intake rate was usually children aged 6–11. We looked more closely at these two groups to determine patterns and potential vulnerabilities, which may be of particular interest as it relates to topics in environmental justice and the importance of developing tools to address exposure differences.

Estimated intake rates for children aged 3 to 5 and 6 to 11 were each compared to intake rate estimates to the total population (Fig. 5; data in Table S8). Of the 69 parent chemicals with metabolite data from the 2015–2016 cohort, all but 8 chemicals exhibited a higher estimated exposure in 3 to 5-year-olds compared to all individuals (gold bars). This was true for all but 13 chemicals for 6 to 11-year-olds as well (gray bars). Our estimates indicate that most children experience higher exposure to chemicals than adults, and the difference ranges up to almost 7-foldhigher for 3 to 5-year-olds and threefold higher for 6 to 11-year-olds. Furthermore, exposure to most chemicals is higher for 3 to 5-year-olds compared to 6 to 11-year-olds (gold bars higher than gray bars), with chemicals like tin, cyanide, and multiple phthalates exhibiting exposure increases by twofold or more. On the other hand, some chemicals (for example, parabens) showed lower exposure in 6 to 11-year-olds when compared to the total population but much higher exposure in 3 to 5-year-olds versus the total population. In other words, increased exposure was only seen for children under 6. This may be the result of various behavioral traits, exposure routes specific to young children, or physiological differences (for example, child inhalation rates have been shown to result in a higher volume inhaled per kilogram bodyweight). Comparing population groups in this manner helps in the identification of patterns and chemicals of interest in terms of population-specific vulnerabilities.

Fig. 5. Comparison of estimated intake rates of the new population group, 3–5-year-olds, introduced in the 2015–2016 NHANES cohort with 6–11-year-olds and all participants (labeled “Total”).

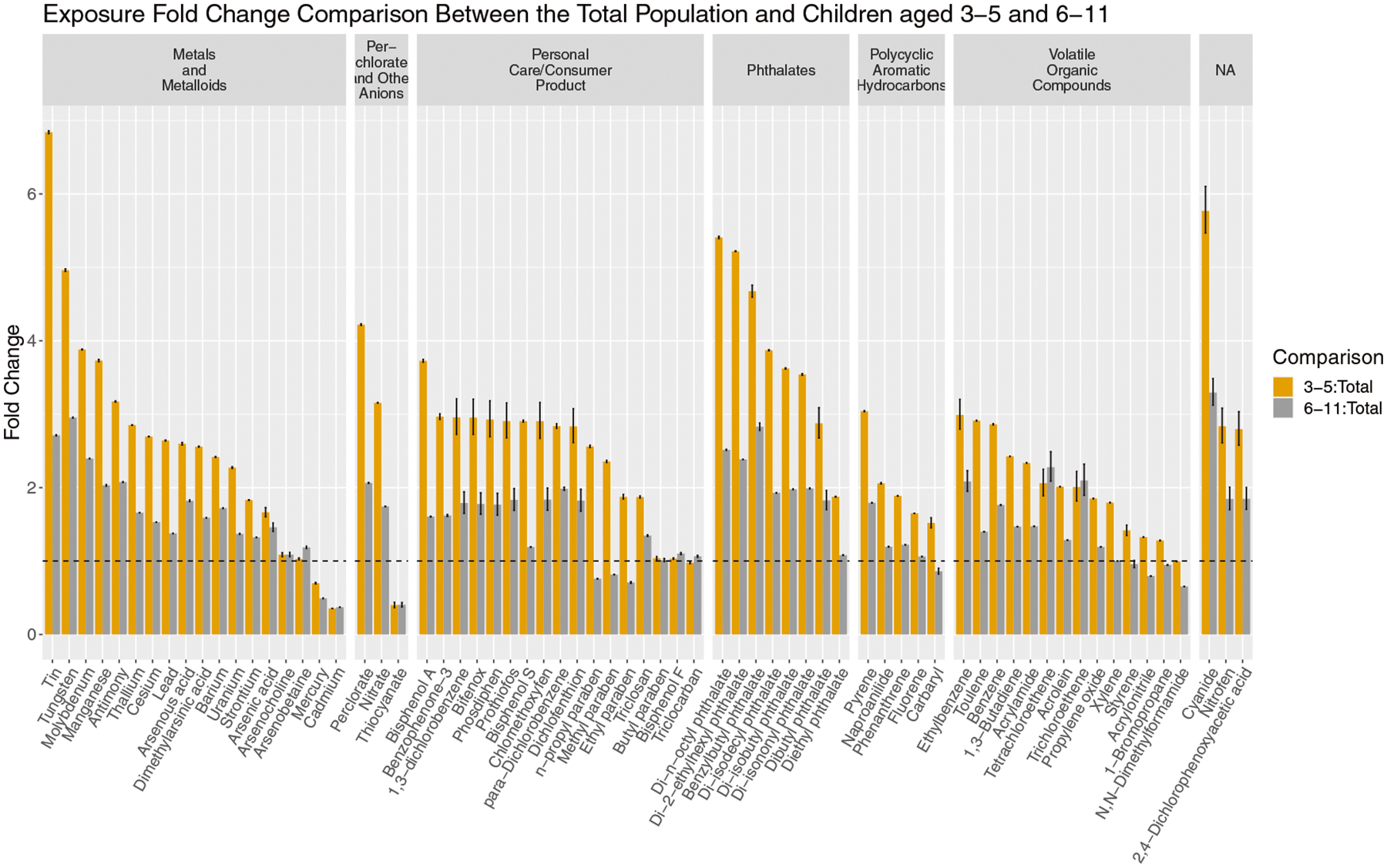
Bars represent the median exposure fold change between 3–5-year-olds and all NHANES participants (in gold) and between 6–11-year-olds and the total population (in gray). The error bars represent the 95% CI on the fold change between median exposure estimates. The dotted line indicates a fold change of 1 (in other words, no change in exposure) and chemicals are grouped by their chemical class as reported by NHANES.

Consistency with SEEM predictions

To evaluate the SEEM consensus model [22], which uses intake rates inferred for a subset of the chemicals analyzed here as training data, we examined the model predictions for the chemicals not included in the training data. Comparison across the 2009–2010, 2011–2012, 2013–2014, and 2015–2016 cohorts was performed using all individuals with 95% confidence intervals included (Fig. 6; data in Table S9). Observing the results by cohort, no strong correlations were identified between bayesmarker and SEEM predictions (all cohort R² < 0.1; all R² values in Table S10). When looking at agreement within individual chemical classes, some correlation was seen for VOCs in 3 cohorts (average R² ~ 0.225; Fig. 6B–D). A slightly higher correlation was observed for heterocyclic amines in the 2013–2014 cohort comparison (R² = 0.36 ± 0.018), and the greatest agreement between predictions within chemical class and cohort was for personal care and consumer product chemicals in the 2013–2014 cohort (R² = 0.49 ± 0.024). No correlation was observed for phytoestrogens in 2009–2010 or flame retardants in 2011–2012 and 2013–2014. Importantly, only one of the chemical classes in this evaluated set of chemicals was represented in the training data (personal care and consumer product chemicals). Therefore, this observed less-than-expected correlation between SEEM and bayesmarker predictions may be explained by the fact that these new chemicals are potentially out of the domain of applicability of the current iteration of SEEM. In other words, the training data lacked chemicals of these various types that we are evaluating it on, leading to lower performance in some cases. There were 16 personal care and consumer product chemicals in the SEEM training data (106 total chemicals) and 2013–2014 for these chemicals achieved the highest R². There were also 3 chemicals of this class in 2015–2016, but they exhibited higher uncertainty in their exposure estimates than those in the 2013–2014 cohort, resulting in a lower R². By retraining SEEM with this evaluation set added, which represents 6 new chemical classes (ranging from 1 to 13 new chemicals for each class), we can likely expand the applicability and accuracy of SEEM in the area of high-throughput exposure prediction.

Fig. 6. Comparison of bayesmarker estimated intake rates with SEEM predictions for chemicals not in the SEEM calibration set.

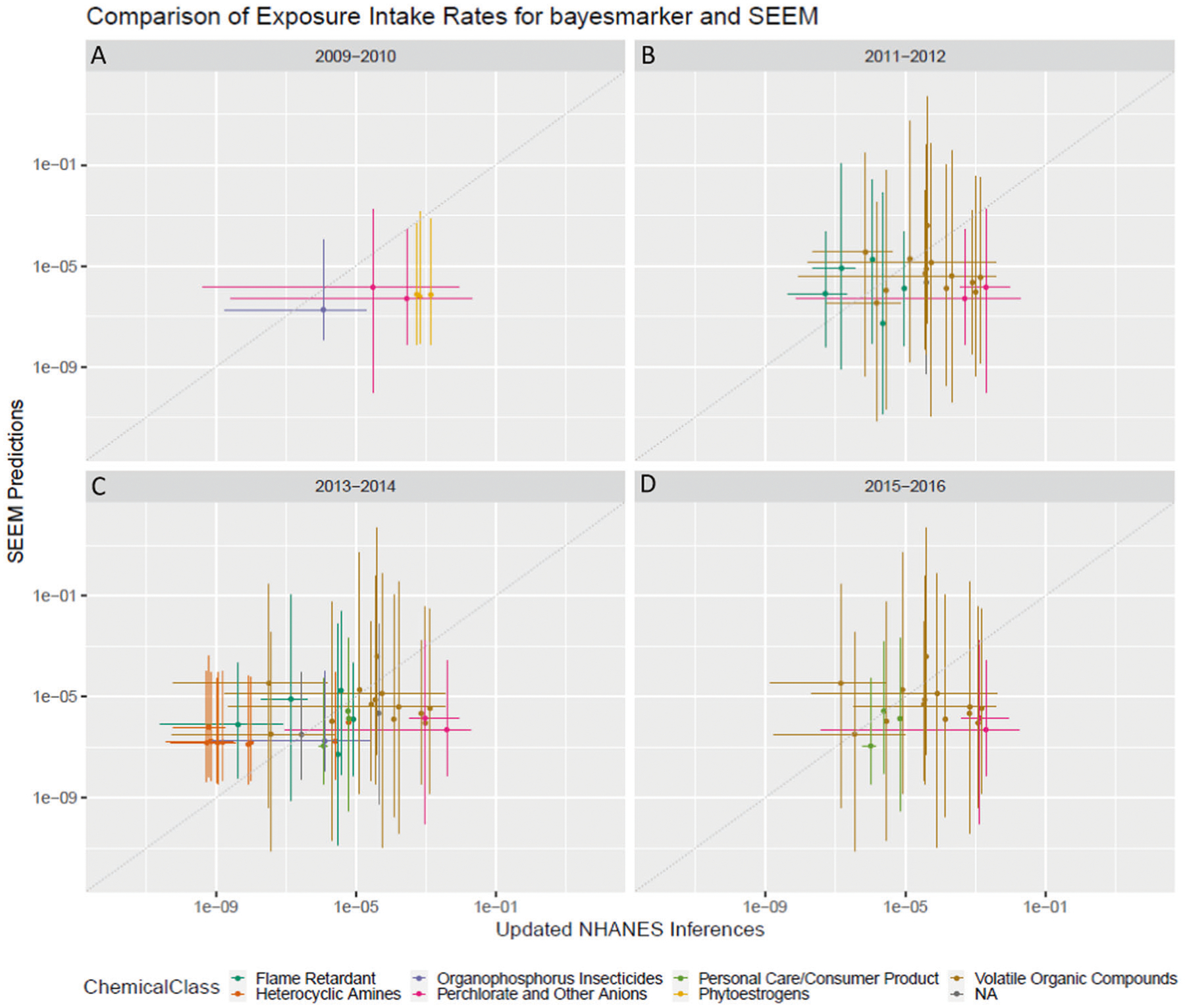
SEEM predictions were originally calibrated using the 106 chemical exposure inferences from Wambaugh et al 2013. Using bayesmarker with the latest NHANES cohorts resulted in parent chemical exposures for 39 new parents that had original SEEM predictions. The bayesmarker inferences were compared with SEEM predictions using all individuals (total population) for each new cohort: A 2009–2010, B. 2011–2012, C 2013–2014, and D 2015–2016. Each point is a parent chemical with color indicating chemical class and error bars (x for bayesmarker, y for SEEM) indicating 95% confidence intervals. The dotted gray line indicates exact correlation.

Understanding uncertainty

As mentioned previously, an important aspect of this work is dealing with uncertainty. In Figs. 4–6, uncertainty is depicted using 95% credible intervals, which are calculated from the Markov Chains representing a population distribution from the Bayesian model calculation of parent chemical exposures. As can be seen from Figs. 4–6, the range of these 95% CIs can be quite large across all chemicals. We attempted to explain the observed uncertainty based on the expected contributors, which have been discussed throughout this work: measurements below the LOD and the number of parent chemicals of a given metabolite. Figure 7 shows how these factors contribute to the observed uncertainty in exposure estimates for personal care and consumer product chemicals. A number of conclusions can be drawn from this result: (1) For a simple one-to-one parent-metabolite relationship, uncertainty is driven by the fraction of measurements below the LOD (more measurements below the LOD result in higher uncertainty), (2) For a parent sharing a metabolite with other parents, uncertainty is driven by the number of shared parents (more shared parents results in higher uncertainty), and (3) Between 1 and 2, 2 results in much greater uncertainty (in other words, the uncertainty from a large number of shared parents is order of magnitudes greater than having many measurements below the LOD). Regarding this last point, if all measurements are below the LOD, there is still the knowledge that the exposure value is low. However, if a single metabolite has multiple parent chemicals, which is common in NHANES as they want to represent the most parent chemicals via the least number of metabolites, all of the observed exposure could be from one parent (meaning this one parent chemical has relatively higher exposure than the other parents) or each parent could contribute equally (meaning small exposure was seen for all parents to lead to the aggregate exposure that is the observed metabolite concentration). These two scenarios result in uncertainty spanning multiple orders of magnitude. Additionally, a chemical directly measured in urine by NHANES but also sharing multiple parents of a metabolite results in less uncertainty. Lastly, the cohort in which a metabolite was measured also seems to have a small effect, with the general trend being the older the cohort, the higher the uncertainty. For a similar examination for all chemicals, see Fig. S1. Understanding uncertainty of our exposure estimates and how different data characteristics contribute is important for interpreting our results and moving forward in terms of chemical prioritization and subsequent analyses.

Fig. 7. Visualization of the influence of various potential contributors to uncertainty on inferred intake rates from urine biomonitoring data for personal care and consumer product chemicals.

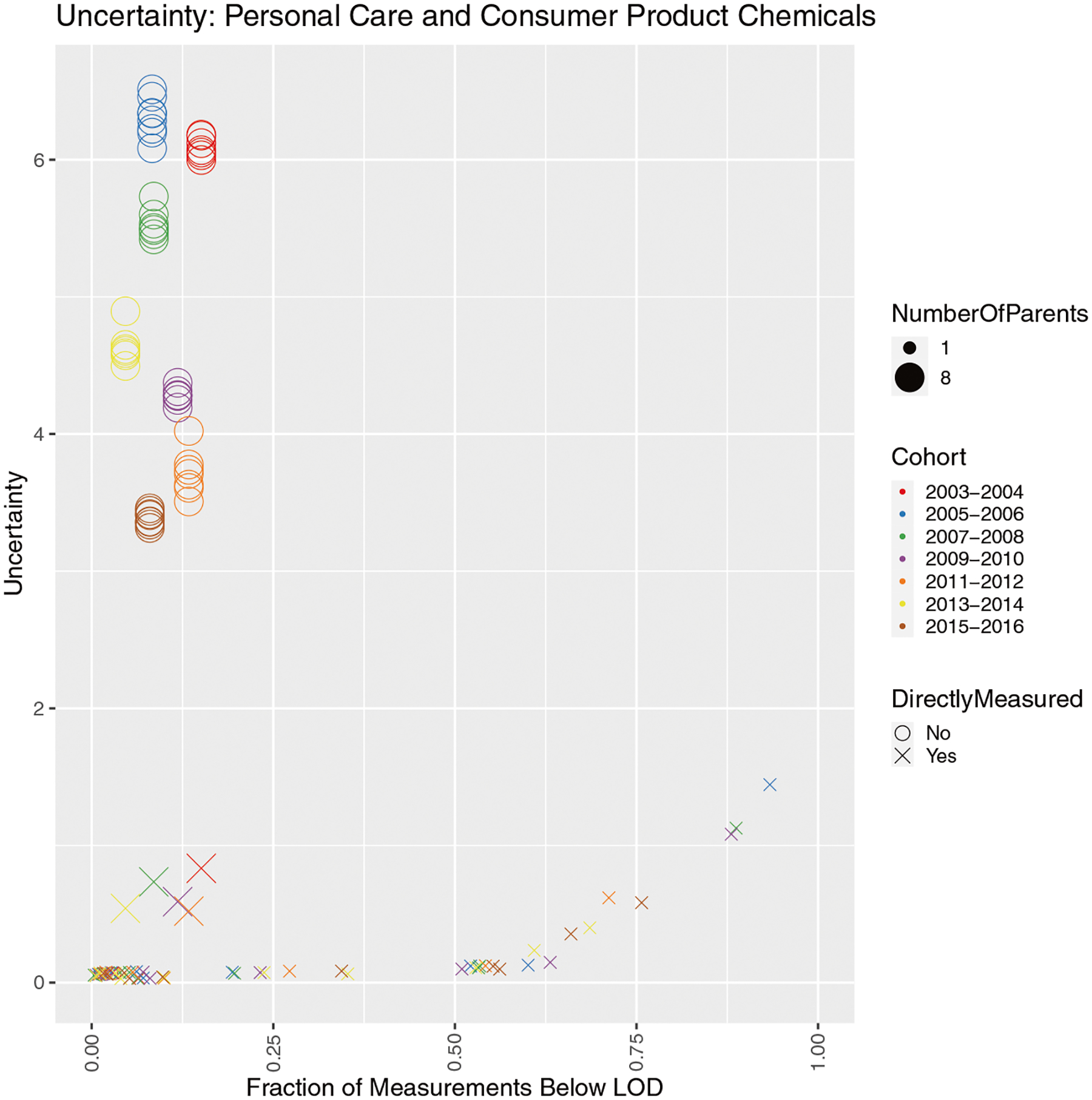
Each data point represents a parent chemical in a single NHANES cohort for each of its metabolites measured in that cohort (so all unique parent-cohort-metabolite triplets). Uncertainty (on the y-axis) is the order of magnitude spanned by the 95% credible interval around the median estimated intake rate (in other words, log₁₀(upper 95% CI/lower 95% CI) = uncertainty), and the fraction below the LOD (on the x-axis) represents the number of measurements below the LOD divided by the total number of measurements for the relevant metabolite. Chemicals are stratified by chemical class, points are colored by NHANES cohort, point size represents the number of parent chemicals shared by the relevant metabolite, and the point shape indicates whether or not a chemical was directly measured in NHANES (in other words, a urine concentration was obtained by NHANES for that parent chemical).

DISCUSSION

In this work, we describe a Bayesian inference approach to estimate chemical intake rates from urine biomonitoring data across multiple population groups. This methodology appropriately handles and incorporates various sources of uncertainty to provide a distribution of exposure for each chemical rather than a point estimate. We demonstrated the utility of this method using the CDC NHANES data to obtain estimates of exposure and a measure of risk for 179 chemicals. Children aged 3 to 5, included in the 2015–2016 NHANES cohort, were investigated more closely to identify exposure patterns and potential vulnerabilities. This method provides a means to not only prioritize chemicals based on exposure and risk, but also data to which many other exposure models can, where appropriate, be compared or even calibrated (for example, SEEM3).

Chemical prioritization

The bioactivity exposure ratios (BERs) shown in Fig. 4 represent a metric of risk for each chemical, and therefore can serve to prioritize chemicals for further study. This may include additional toxicity studies or data gathering (for example, monitoring chemicals in various environmental media) such that further comparisons to exposure models can be performed. While certain concentrations of metabolites may themselves indicate potential risk, we are choosing to focus on parent chemicals as they are typically the focus of toxicity testing. Additionally, rather than being treated as an exact risk estimate, the BER values are to be used more as a way to relatively rank the potential risk across a number of chemicals. Regarding the parent chemicals of NHANES metabolites that had available toxicity data, the chemical with the highest risk/priority was styrene. Styrene is regarded as a known carcinogen. Approximately 25 million metric tons of styrene were produced in 2010 [66] and this increased to around 35 million metric tons by 2018, which could have resulted in higher exposure and therefore a lower BER value. During the SEEM comparison, the median estimated exposure for styrene did exhibit about a 3-fold increase from the 2011–2012 cohort to the 2015–2016 cohort, which would lead to a lower BER. It will be important to continue to track production and exposure to styrene over time (via studies like biomonitoring). The chemical with the second lowest BER is also a volatile organic compound and known carcinogen, 1,3-butadiene. The next two lowest values are phytoestrogens, daidzein and genistein, however, 2009–2010 was the last NHANES cohort to measure these chemicals. Chemicals previously prioritized for further assessment by other initiatives, like certain phthalates, parabens, benzophenone-3, chlorpyrifos, triclosan, and bisphenol A all had lower BERs than most chemicals in Fig. 4. Tracking of chemical exposure through biomonitoring studies is important, but it is just as important to translate this to risk as certain exposure changes may be more important for some chemicals than others based on their known toxicity.

Exposure to young children

Children exhibited the highest exposure estimates out of all population groups, based on this method, for most chemicals, and this translated to higher bioactivity:exposure ratios (BERs), meaning higher potential risk. Increased exposure rates of certain chemicals to young children may be attributed to a number of reasons related to their physiology or behavioral habits (for example, crawling on the ground, oral exploratory behaviors, and food preferences) as well as parental actions (“take-home” exposures, adult hobbies, or use of ethnic home health remedies or religious practices that incorporate certain powders, cosmetics, or metal implements) [67] or use of products (for example, diaper creams and baby hygiene products).

In Fig. 5, tin exhibited the highest difference between children aged 3–5 and all individuals as well as the greatest fold change differential when comparing both child groups to all individuals. As discussed in Lehmler et al (2018), there are several factors that may contribute to the elevated levels of tin observed in children, including the higher food intake of children, ingestion of household dust, or more (dermal) contact with products containing tin [68]. Other metals also showed higher estimated exposure in children. In addition to the routes of exposure mentioned for tin, there is a potential role for soil ingestion or soil-pica behavior that could lead to higher metal intakes, particularly in playgrounds and parks [69, 70]. Cyanide showed the second largest fold change in 3–5-year-olds compared to all individuals. This chemical occurs in various foods, suggesting that dietary differences (for example, higher consumption of fruit juices) may be important [71]. Two phthalates, di-n-octyl phthalate (DNOP) and di-2-ethylhexyl phthalate (DEHP), also exhibited some of the largest fold change differences in Fig. 6. Phthalates are used in plastics and may exhibit higher exposure in 3 to 5-year-olds due to more hand-to-mouth activity with plastic toys in young children [72]. Phthalates are also present in dust and children tend to have increased dust ingestion. Over the past two decades, the Consumer Product Safety Commission (CPSC) has instituted bans on certain phthalates from children’s toys and childcare articles at concentrations above 0.1 percent (permanent ban on DEHP and interim ban on DNOP in 2008 [73]), which may have led to the use of other phthalates or similar chemicals as substitute ingredients. This likely led to a changing exposure profile for young children over time as new ingredients are incorporated. The latest proposed rule [74], effective October 2017, lifts the interim ban on DNOP being present in concentrations greater than 0.1 percent in any children’s toy that can be placed in a child’s mouth or child care article. For this reason, continuation of the NHANES survey as well as the evaluation of the data will be needed to assess exposure changes in children based on ever evolving ingredient choices for the products they encounter.

One last consideration regarding child exposures is the steady-state assumption both in the model and for the BER calculation. A previous study showed that clearance of drugs in children over the age of 2 could be appropriately modeled using simple dosage formulas and allometric scaling [75]. Considering urine collection for biomonitoring in the NHANES survey of children falling in the 1–5-year-old age group was only completed for individuals aged 3 years and older (hence our labeling of 3–5-year-olds throughout this manuscript), a steady-state assumption is appropriate for this population group.

Data and model limitations

Much of the data used in this work will continue to grow in terms of the information available for each chemical as well as the quality of that information. For this reason, it will be important to identify useful data updates and incorporate them into the input files of bayesmaker. The first example of such data updates stems from the fact that exposures are constantly changing, which is why NHANES continues to collect biomonitoring data. Thus, new exposure inferences will need to be calculated regularly. Second, the mapping between parents and metabolites was populated using the NHANES reports and text mining of PubMed abstracts. There may be other sources or databases that have more information on metabolism of various chemicals. Additionally, more experimental research in chemical metabolism work will increase the existing literature pool, which will eventually allow for an increase in the number of chemicals for which exposure estimates can be calculated.

In NHANES a small number of chemicals had very few, and sometimes zero, measurements above the LOD. While exposure inferences for the parents of these metabolites can still be obtained based on data censoring limits (that is, intake rates must be low enough that metabolites are less than LOD), the resulting estimates often have large uncertainties. This is an important caveat and was partially addressed by incorporating a check on sample size and measurements below the LOD such that metabolites with very large uncertainties were identified and excluded from subsequent analyses. One potential explanation for why a metabolite may have many measurements below the LOD is half-life. While the reverse dosimetry approach used in this work has been used successfully in the past [76] with several VOCs, a group of compounds with complex exposure pathways and rapid clearance by metabolism and exhalation, there is still a chance that chemicals with very short half-lives may be absorbed and eliminated faster than the time between exposure events or urine collection. NHANES monitors blood, plasma, and urine and tends to look for shorter half-life chemicals in urine because it is more informative and concentrations are likely to be higher for these chemicals than the other two media (conversely, NHANES measures persistent chemicals in blood or plasma). Measurement timeframes for chemicals with short half-lives can be an issue when extrapolating daily exposure from spot urine measurements, which NHANES performs. Doing so can lead to greater uncertainty and a potential underestimation of exposure. This is one of the limiting factors imposed by NHANES, due to the vast amount of time and resources needed to perform 24-h urine sampling on a large scale. Comparisons to studies estimating exposure using continuous urine sampling would help provide a benchmark for chemicals with varying elimination half-lives. Additionally, biomonitoring data can be diluted by “non-users” (individuals that don’t encounter exposure to certain chemicals; can result in more measurements below the LOD), which results in population averages covering both users and non-user but can sometimes lead to lower estimated intake rates for certain chemicals. If exposure is underestimated, either due to rapidly cleared chemicals or inclusion of non-users, then we in turn may underestimate risk posed by those chemicals.

Here we assume that the measured concentration in a spot sample (a single urinary aliquot at a point in time) is a reasonable surrogate for 24-h average urinary concentration (either on a volume or creatinine-corrected basis). Multiple exposure scenarios (different sequences, timings, magnitudes, and routes) might all be consistent with the same spot sample concentration [21]. Setzer et al. [77] used a hierarchical Monte Carlo simulation study to show that for various distributions of complex exposures to chemicals with varied half-lives that population average spot samples can only be used to estimate the central tendency (which is the median for a log-normal distribution). This is what we report here; the median intake rate for a population with an uncertainty (95% credible interval) around that median estimate. Aylward et al. [78] used longitudinal biomonitoring data and pharmacokinetic simulations of concentrations in spot samples and found that intra-individual variability in repeated spot samples for the analytes they examined exceeded inter-individual variability for compounds with relatively short elimination half-lives. Together, these two studies indicate that the methods used here are suitable for capturing the median exposure for a population but not the tails of the exposure distribution (for example, highly exposed individuals at the 95% percentile).

Comparing our estimated intake rates with estimates from other reverse-dosimetry methods using the NHANES data to focus on specific chemicals and classes allows the evaluation of the confidence in our model. Looking at 3 [27, 29, 30] studies spanning 10 unique chemicals (6 phthalates, BPA, and 3 pesticides), our estimated intake rates were within one order of magnitude for 8 out of the 10 chemicals, suggesting fair agreement. A major goal of ours in modeling chemical exposure is to generate estimates for as many chemicals as possible, usually achieved by high-throughput data and computational modeling. However, the use of biomonitoring data in this form (reverse modeling via inference) has clear limitations. To be able to estimate exposure of a chemical, at least one of its transformation products must be in the metabolite panel that NHANES chooses to measure. We chose to use urine data as it typically has a greater number of measured metabolite concentrations than other media (for example, blood or serum). It should be noted that urine is sometimes considered less suitable as a biological matrix for certain chemicals (for example, the most accurate matrix for metals is expected to be blood). Future efforts should compare estimated intake rates from multiple matrices to assess the extent of agreement. Furthermore, a metabolite needs to be a good biomarker (specific and sensitive enough) such that it reflects parent chemical exposure. This needs to be addressed on a chemical-specific basis, especially when interpreting exposure and risk-related prioritization. Current biomonitoring studies use a targeted approach (for example, chemicals are preselected by the study team). The emergence of non-targeted analysis (NTA) can potentially measure all metabolites present in the human body (excluding those below the LOD), which could provide analysis opportunities for a greater number of parent chemicals.

Another limitation comes from the fact that urine measurements represent the totality of exposure from all routes, but we rarely know which routes are relevant for a given chemical. Additionally, it is not just an issue of how we encounter chemicals but also how they enter the body (for example, exposure to some chemicals through skin absorption does not occur because they cannot permeate the dermis). We would need to know much more of the toxicokinetic information at a chemical-specific level to correctly model all the different exposure routes. It could be possible to implement this by using a Bayesian approach that considers all exposure scenarios and attributes some fraction of exposure to various routes based on prior chemical knowledge (properties, occurrence in media, and potential product use). In the current iteration of bayesmarker, we lack information to attribute exposure to all routes and so typically interpret it as an oral route (in other words, equivalent oral intake dose assuming 100% absorption in mg/kg bodyweight/day) for subsequent analyses such as bioactivity exposure ratios.

As for converting urine concentrations into exposure, one important step involves adjustments based on glomerular filtration rate (GFR), which is estimated using creatinine concentrations and urine metrics. In this work, as was done in previous works [13, 14, 22], we estimated GFR using a model based on age, sex, ethnicity, and bodyweight trained on data from the 2009–2010 cohort of NHANES. While this approach has served well in previous studies, more data has since become available to allow for estimations of GFR at the individual basis for NHANES participants (urine flow data since 2009). This will be implemented in future versions of bayesmarker, however, the model used in this work can still be useful for other biomonitoring studies that lack the appropriate urine flow data. Another important aspect of urine biomonitoring data regards metabolism rates and clearance routes. The literature may indicate that a parent chemical metabolizes into a biomarker, but we often do not know what fraction of the parent is metabolized or other pharmacokinetic properties of that chemical (half-life, absorption, distribution, metabolism, and excretion). For this reason, we chose to apply a simple toxicokinetic model for all metabolites. In future iterations of bayesmarker, we can incorporate more sophisticated approaches to handle these various cases when that data becomes available for more chemicals.

This work can immediately enhance the area of high-throughput exposure prediction by providing additional exposure intake rates against which forward modeling approaches can be calibrated. The SEEM consensus modeling approach extrapolated from 106 chemicals to forecast chemical intake rates for thousands of chemicals with little to no exposure data [22]. In this work we showed that the inferred intake rates from new parent chemicals (obtained using the updated NHANES data) indicated that there was room for improvement in the performance of the SEEM consensus exposure model for chemicals belonging to certain classes (heterocyclic amines, perchlorates, phytoestrogens, VOCs, and flame retardants) not previously included in the SEEM calibration set. Considering our results for some chemicals that did have representation in the calibration set (personal care and consumer product chemicals for example) showed that SEEM predictions were moderately correlated (R² = 0.49), we expect better performance across the entire chemical space with these additions of previously unrepresented chemical classes to the calibration set of chemicals. Iterative comparisons of this nature where the data and methods are continually updated is important to achieve steady improvement in our ability to prioritize chemicals through estimation of exposure and risk.

Future work

The method presented in this work has been incorporated into an R package called bayesmarker. This package will be maintained and updated in the future as new data becomes available and additional analyses are performed. With access to biomonitoring data from individuals spanning almost two decades, one of the further analyses that can be addressed is to look at changes in concentrations of metabolites in urine and their inferred parent compound exposures over time. Along the same lines, data from different NHANES cohorts can be combined for greater statistical power or to perform more encompassing comparisons across time periods. While we provide inferred exposures as a distribution, usually summarized by mean and 95% CI, providing other percentiles (mainly most at-risk population via the 95^th percentile of exposure) is highly desired in the exposure community due to its importance in regulatory decision making and protecting the most vulnerable individuals. Due to the nature of exposure variability and urine biomonitoring data, obtaining estimates for percentiles other than the 50^th is a difficult statistical problem but one we plan to work on. Lastly, the bayesmarker package is expected to have wide applicability, as it can handle biomonitoring studies or data from sources other than NHANES. Working with other datasets will help ensure a more general form of this analysis or a specific set of instructions for study leaders to organize their data in the correct form. These updates to the bayesmarker package will allow for the number of chemicals with exposure estimates to quickly increase and provide an overall better understanding of exposure, as well as risk prioritization, for hundreds of chemicals across multiple population groups.

DATA AVAILABILITY

All biomonitoring data from NHANES is hosted online by the CDC (https://wwwn.cdc.gov/nchs/nhanes). The bayesmarker input data (metabolite table, weights table, and metabolite map) along with data used to generate each figure is included in the supplemental data file. The supplemental data also includes the exposure estimates (median and 95% CIs) using the most recent NHAHES cohort data for each metabolite.