Abstract
In this work ground
and excited electronic states of
Heisenberg
cluster models, in the form of configuration interaction many-body
wave functions, are characterized within the spin-adapted Graphical
Unitary Group Approach framework, and relying on a novel combined
unitary and symmetric group approach. Finite-size cluster models of
well-defined point-group symmetry and of general local-spin 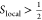 are presented,
including J1–J2 triangular and
tetrahedral clusters, which are often used to describe magnetic interactions
in biological and biomimetic polynuclear transition metal clusters
with unique catalytic activity, such as nitrogen fixation and photosynthesis.
We show that a unique block-diagonal structure of the underlying Hamiltonian
matrix in the spin-adapted basis emerges when an optimal lattice site
ordering is chosen that reflects the internal symmetries of the model
investigated. The block-diagonal structure is bound to the commutation
relations between cumulative spin operators and the Hamiltonian operator,
that in turn depend on the geometry of the cluster investigated. The
many-body basis transformation, in the form of the orbital/site reordering,
exposes such commutation relations. These commutation relations represent
a rigorous and formal demonstration of the block-diagonal structure
in Hamiltonian matrices and the compression of the corresponding spin-adapted
many-body wave functions. As a direct consequence of the block-diagonal
structure of the Hamiltonian matrix, it is possible to selectively
optimize electronic excited states without the overhead of calculating
the lower-energy states by simply relying on the initial ansatz for the targeted wave function. Additionally, more compact many-body
wave functions are obtained. In extreme cases, electronic states are
precisely described by a single configuration state function, despite
the curse of dimensionality of the corresponding Hilbert space. These
findings are crucial in the electronic structure theory framework,
for they offer a conceptual route toward wave functions of reduced
multireference character, that can be optimized more easily by approximated
eigensolvers and are of more facile physical interpretation. They
open the way to study larger ab initio and model Hamiltonians of increasingly larger number of correlated
electrons, while keeping the computational costs at their lowest.
In particular, these elements will expand the potential of electronic
structure methods in understanding magnetic interactions in exchange-coupled
polynuclear transition metal clusters.
are presented,
including J1–J2 triangular and
tetrahedral clusters, which are often used to describe magnetic interactions
in biological and biomimetic polynuclear transition metal clusters
with unique catalytic activity, such as nitrogen fixation and photosynthesis.
We show that a unique block-diagonal structure of the underlying Hamiltonian
matrix in the spin-adapted basis emerges when an optimal lattice site
ordering is chosen that reflects the internal symmetries of the model
investigated. The block-diagonal structure is bound to the commutation
relations between cumulative spin operators and the Hamiltonian operator,
that in turn depend on the geometry of the cluster investigated. The
many-body basis transformation, in the form of the orbital/site reordering,
exposes such commutation relations. These commutation relations represent
a rigorous and formal demonstration of the block-diagonal structure
in Hamiltonian matrices and the compression of the corresponding spin-adapted
many-body wave functions. As a direct consequence of the block-diagonal
structure of the Hamiltonian matrix, it is possible to selectively
optimize electronic excited states without the overhead of calculating
the lower-energy states by simply relying on the initial ansatz for the targeted wave function. Additionally, more compact many-body
wave functions are obtained. In extreme cases, electronic states are
precisely described by a single configuration state function, despite
the curse of dimensionality of the corresponding Hilbert space. These
findings are crucial in the electronic structure theory framework,
for they offer a conceptual route toward wave functions of reduced
multireference character, that can be optimized more easily by approximated
eigensolvers and are of more facile physical interpretation. They
open the way to study larger ab initio and model Hamiltonians of increasingly larger number of correlated
electrons, while keeping the computational costs at their lowest.
In particular, these elements will expand the potential of electronic
structure methods in understanding magnetic interactions in exchange-coupled
polynuclear transition metal clusters.
1. Introduction
Symmetry represents a core concept in physics and chemistry, as it helps to dramatically reduce interpretational and computational costs. Translational symmetry in lattices defines its long-range periodic order. Point-group symmetry in crystals and molecules defines the local (point) symmetry, which includes reflections, rotations, and the inversion. The Pauli exclusion principle for Fermionic systems offers another crucial example of the importance of symmetry in electronic structure theory (exchange symmetry). It requires any many-body wave function of a Fermionic system to be antisymmetric with respect to exchange of two particles. This feature has prompted the electronic structure theory community to adopt the Slater determinants as basis to describe the many-body wave functions of multifermionic systems. Resolving the antisymmetry during the optimization of the many-body wave function on an unsymmetrized basis, such as the Hartree products, would represent a major challenge for approximated eigensolvers, both for the much larger optimization space and for the optimization coefficients must perfectly couple across the space to guarantee antisymmetry. Generally, it is not possible to rigorously meet the latter condition via approximated eigensolvers.
Turning our attention toward
spin symmetries, it is worth mentioning
the spin-projection 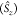 preserving symmetry,
and the total spin
preserving symmetry,
and the total spin 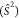 preserving symmetry,
embedded in Slater
determinants and configuration state functions (CSFs) bases, respectively.
In analogy to Slater determinant bases, which enforce antisymmetry
and the spin-projection quantum number by construction, spin-adapted
bases enforce total spin symmetry, while reducing the size of the
corresponding Hilbert space, limited to the components of the desired
total spin. There are multiple ways to create a basis of spin-adapted
CSFs.1−3 In this work, we use the unitary group approach to
spin adaptation in its graphical form (GUGA), pioneered by Paldus4−7,10,12 and Shavitt,8,9,11 which
relies on the generators
preserving symmetry,
embedded in Slater
determinants and configuration state functions (CSFs) bases, respectively.
In analogy to Slater determinant bases, which enforce antisymmetry
and the spin-projection quantum number by construction, spin-adapted
bases enforce total spin symmetry, while reducing the size of the
corresponding Hilbert space, limited to the components of the desired
total spin. There are multiple ways to create a basis of spin-adapted
CSFs.1−3 In this work, we use the unitary group approach to
spin adaptation in its graphical form (GUGA), pioneered by Paldus4−7,10,12 and Shavitt,8,9,11 which
relies on the generators 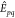 and
and 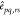 of the special unitary group of order 2,
SU(2), and on the spin-free formulation of the Hamiltonian operators.
For example, the spin-free ab initio nonrelativistic
molecular electronic Hamiltonian within the Born–Oppenheimer
approximation reads as
of the special unitary group of order 2,
SU(2), and on the spin-free formulation of the Hamiltonian operators.
For example, the spin-free ab initio nonrelativistic
molecular electronic Hamiltonian within the Born–Oppenheimer
approximation reads as
| 1 |
where 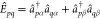 and
and 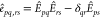 are the spin-free
excitation operators,
and hpq and gpqrs the molecular one- and two-body
electron integrals.13 The GUGA approach
is widely utilized within the chemistry community, and it is at the
core of many electronic structure methodologies,14 including complete/restricted/generalized active space
self-consistent field (CASSCF,15−18 RASSCF,19 GASSCF),20 and more recently, GUGA full configuration-interaction
quantum Monte Carlo, (GUGA-FCIQMC)21,22 and Stochastic-CASSCF.23
are the spin-free
excitation operators,
and hpq and gpqrs the molecular one- and two-body
electron integrals.13 The GUGA approach
is widely utilized within the chemistry community, and it is at the
core of many electronic structure methodologies,14 including complete/restricted/generalized active space
self-consistent field (CASSCF,15−18 RASSCF,19 GASSCF),20 and more recently, GUGA full configuration-interaction
quantum Monte Carlo, (GUGA-FCIQMC)21,22 and Stochastic-CASSCF.23
Discrete symmetry transformations, given
by an operator  that
commutes with a given Hamiltonian
operator,
that
commutes with a given Hamiltonian
operator, 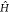 , are pivotal in electronic structure
calculations.
Commuting operators admit common eigensolutions. Thus, the operator
, are pivotal in electronic structure
calculations.
Commuting operators admit common eigensolutions. Thus, the operator  can be used to filter eigenstates
of
can be used to filter eigenstates
of 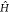 with specific eigenvalues of
with specific eigenvalues of  . For example, we may take advantage
of
the fact that
. For example, we may take advantage
of
the fact that 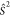 and
and 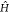 commute,
construct the modified
commute,
construct the modified 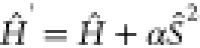 Hamiltonian, and, by tuning the
parameter
α, control the spectral ordering of the
Hamiltonian, and, by tuning the
parameter
α, control the spectral ordering of the 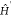 eigenstates.
This strategy has been recently
used to gain control over the spin in the Slater-determinant (SD)
based full configuration-interaction quantum Monte Carlo (SD-FCIQMC)
method to approximate eigenstates of full configuration-interaction
(full-CI) quality in large active space calculations, while being
able to selectively target states of specific spin.24 In virtue of the vanishing commutator the modified Hamiltonian,
eigenstates.
This strategy has been recently
used to gain control over the spin in the Slater-determinant (SD)
based full configuration-interaction quantum Monte Carlo (SD-FCIQMC)
method to approximate eigenstates of full configuration-interaction
(full-CI) quality in large active space calculations, while being
able to selectively target states of specific spin.24 In virtue of the vanishing commutator the modified Hamiltonian, 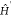 , shifts the
eigenvalues proportionally
to αS(S + 1) while keeping
the eigenstates unchanged compared to those of the original Hamiltonian
operator,
, shifts the
eigenvalues proportionally
to αS(S + 1) while keeping
the eigenstates unchanged compared to those of the original Hamiltonian
operator,  .
.
Other transformations exist
that
lead to a modified Hamiltonian 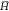 with a unique block-diagonal
structure
in the transformed basis, and to more compact eigenstates, while keeping
the electronic spectrum unchanged compared to the original
with a unique block-diagonal
structure
in the transformed basis, and to more compact eigenstates, while keeping
the electronic spectrum unchanged compared to the original 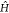 operator. These transformations
can be
described as a similarity transformation of the original
Hamiltonian,
operator. These transformations
can be
described as a similarity transformation of the original
Hamiltonian,
| 2 |
where 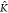 is for example an orthogonal orbital
permutation
matrix.
is for example an orthogonal orbital
permutation
matrix.
We have recently studied the effect of exchanging orbitals or lattice sites on spin-free ab initio and model Hamiltonian matrices and on their eigenstates
expressed
in a spin-adapted basis.23,25−28 Orbital permutations can be described as a 90° rotation between
pairs, from which the 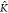 matrix
is promptly recognized. We found
that specific chemically and physically motivated site permutations
bring the Hamiltonian matrices into a unique (quasi-)block-diagonal structure, and many-body wave functions into embarrassingly
compact forms, indicated by larger leading CI coefficients, small L1-norm and large L4-norms of L2-normalized eigenvectors.25,28 As a direct consequence of the block-diagonal structure of the Hamiltonian
matrices, it is possible to selectively optimize electronic excited
states without the overhead of calculating the lower-energy states,
by simply relying on the initial ansatz for the targeted
wave function. This strategy has been numerically shown for the singlet
low-energy excited states of two Fe4S4 cubane
clusters.26 The block-diagonal structure
of the Hamiltonian matrix, the compression of its eigenstates, that
emerge in the GUGA Hamiltonian matrix, and the possibility to selectively
target specific excited electronic states, represent three additional
theoretical advantages (to the best of our knowledge reported by us
for the very first time) in employing spin-adapted bases in electronic
structure calculations, in addition to the already known advantages
of preserving spin symmetry.
matrix
is promptly recognized. We found
that specific chemically and physically motivated site permutations
bring the Hamiltonian matrices into a unique (quasi-)block-diagonal structure, and many-body wave functions into embarrassingly
compact forms, indicated by larger leading CI coefficients, small L1-norm and large L4-norms of L2-normalized eigenvectors.25,28 As a direct consequence of the block-diagonal structure of the Hamiltonian
matrices, it is possible to selectively optimize electronic excited
states without the overhead of calculating the lower-energy states,
by simply relying on the initial ansatz for the targeted
wave function. This strategy has been numerically shown for the singlet
low-energy excited states of two Fe4S4 cubane
clusters.26 The block-diagonal structure
of the Hamiltonian matrix, the compression of its eigenstates, that
emerge in the GUGA Hamiltonian matrix, and the possibility to selectively
target specific excited electronic states, represent three additional
theoretical advantages (to the best of our knowledge reported by us
for the very first time) in employing spin-adapted bases in electronic
structure calculations, in addition to the already known advantages
of preserving spin symmetry.
Why are such block-diagonal structure and the corresponding wave function compression desirable in quantum chemical simulations of ground and excited electronic states of strongly correlated systems? In quantum chemistry, multiconfigurational approaches are used to generate qualitatively correct wave functions for electronic states of molecules that are not adequately described by single-reference approaches, exemplified by Hartree–Fock, single-reference coupled-cluster and density functional theory methodologies. Exchange-coupled polynuclear transition metal (PNTM) clusters represent a broad class of chemical compounds that are far from being well characterized by single-reference techniques. In multiconfigurational methods, electronic state wave functions are described as linear combinations of electronic configurations, in the form of Slater determinants or spin-adapted functions. Typically multiconfigurational wave functions of PNTM clusters feature multiple dominant coefficients. We refer to those as multireference wave functions. The number of electronic configurations defines the configuration interaction (CI) space. The CI space that includes all symmetry allowed configurations within the chosen one-electron basis is referred to as the full-CI space. If a subset of the one-electron basis is chosen (the active space) the many-body expansion is referred to as the complete active space (CAS) wave function. The size of full-CI (or CAS) expansion grows exponentially with the number of correlated electrons and one-electron basis functions.13,14,29 For Hamiltonian matrices of small dimensions (up to a few thousand configurations), the optimization of the CI expansion coefficients is generally done by exact diagonalization procedures, such as the Jacobi eigensolver for real symmetric matrices. For larger CI problems (approaching a billion many-body functions), Davidson or Lanczos techniques are utilized to compute few smallest (or largest) eigenvalues (and eigenvectors).13,14,30 For even larger problems, approximate techniques are employed. Density-matrix renormalization group, DMRG,31−33 and FCIQMC21,34,35 are two examples. While DMRG requires a low entanglement entropy of the ground state to yield accurate results, FCIQMC benefits from sparsity of the ground-state vector. In the latter case, transformations that lead to Hamiltonian matrices with a block-diagonal structure have the obvious advantage of reducing the optimization space to the block of interest.
This paper focuses on how to identify such transformations in Heisenberg Hamiltonian matrices for multisite clusters within the GUGA spin-adapted framework. Ab initio Hamiltonian matrices of exchange-coupled PNTM systems, which can be mapped to equivalent Heisenberg models, behave similarly up to the leading terms (quasi-block-diagonal structure), as we have numerically shown in earlier works.26
The unprecedented wave function compression
and block-diagonal
structure of the nonrelativistic ab initio Hamiltonian
matrix in the similarity-transformed spin adapted basis has been discussed
in great detail in a number of earlier works of ours, via numerical
examples offered by exchange-coupled PNTM clusters, exemplified by
iron–sulfur clusters (dimers and cubanes),23,25,26 and manganese–oxygen trinuclear molecular
systems.27 We have also applied this strategy
to the one-dimensional s-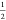 isotropic Heisenberg model with
nearest-neighbor
(NN) interactions (single J magnetic coupling constant),
and to ab initio Hamiltonians in the form of chains
of equally spaced hydrogen atoms.28 For
all the cases above we discussed the rationale behind the spin-adapted
ground state wave function compression as a function of the permutational
symmetry.
isotropic Heisenberg model with
nearest-neighbor
(NN) interactions (single J magnetic coupling constant),
and to ab initio Hamiltonians in the form of chains
of equally spaced hydrogen atoms.28 For
all the cases above we discussed the rationale behind the spin-adapted
ground state wave function compression as a function of the permutational
symmetry.
While the one-dimensional Heisenberg model with NN interactions is exactly solvable via the Bethe ansatz,37−39 Heisenberg Hamiltonians with higher dimensions and/or with long-range interactions (already from second NN interactions) and more complex Hamiltonians, such as the ab initio nonrelativistic Hamiltonian, remain elusive.40 Methods based on the matrix product state paradigm,41−44 such as DMRG,31−33 are very successful for 1D systems, even with periodic boundary conditions45,46 and long-range interactions. For lattice models of higher dimensions, tensor network state approaches have been applied with some success.47−51 Also, quantum Monte Carlo procedures have been able to provide accurate numerical solutions as the Heisenberg model can be solved without a sign problem on a bipartite lattice.52−76
In the present work, we expand our understanding of the block-diagonal
structure of the spin-free many-body Hamiltonian matrices and the
related compression of spin-adapted eigensolutions as a function of
site permutations. We generalize the compression to ground- and excited-states
wave functions of finite-size Heisenberg Hamiltonians, for sites with 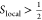 , and consider
more than one magnetic coupling
constant. Such models are often used to describe magnetic interactions
in biological and biomimetic PNTM clusters with unique catalytic activity,
such as the nitrogen fixation and the photosynthesis. The Heisenberg
models discussed here exhibit a more complex electronic spectrum as
compared to the single-J one-dimensional Heisenberg
model (chain).
, and consider
more than one magnetic coupling
constant. Such models are often used to describe magnetic interactions
in biological and biomimetic PNTM clusters with unique catalytic activity,
such as the nitrogen fixation and the photosynthesis. The Heisenberg
models discussed here exhibit a more complex electronic spectrum as
compared to the single-J one-dimensional Heisenberg
model (chain).
In our previous works a more phenomenological approach
has been undertaken to explore the compression of the electronic wave
functions as a function of the orbital/site reordering. For molecular ab initio Hamiltonians of PNTM clusters, including high-valent 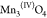 trinuclear clusters and iron–sulfur
dimers
trinuclear clusters and iron–sulfur
dimers 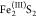 and cubanes
and cubanes 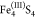 , chemically motivated reorderings were
suggested.23,26,27 Similarly, for the one-dimensional Heisenberg chain conclusions
were obtained following a thorough exploration of the permutational
space, also adopting a simulated annealing strategy.28 In the present work we undertake a more rigorous and fundamental
strategy to the block-diagonal structure of the electronic Hamiltonian
within a spin-adapted formulation, based on commutation relations
between partial cumulative spin operators and the Hamiltonian operator.
These commutation relations represent a new tool to predict orbital/site
permutations that lead to wave function compression without necessarily
explore numerically the permutational space. The strength of this
strategy is its generality and transferability to other model systems
and Hamiltonians. The proposed approach greatly enlarges the applicability
of wave function-based strategies, allowing for computationally inexpensive
and reliable characterizations (and predictions) of the electronic
structures and magnetic interactions in the ground and/or excited
states of exchange-coupled PNTM clusters.
, chemically motivated reorderings were
suggested.23,26,27 Similarly, for the one-dimensional Heisenberg chain conclusions
were obtained following a thorough exploration of the permutational
space, also adopting a simulated annealing strategy.28 In the present work we undertake a more rigorous and fundamental
strategy to the block-diagonal structure of the electronic Hamiltonian
within a spin-adapted formulation, based on commutation relations
between partial cumulative spin operators and the Hamiltonian operator.
These commutation relations represent a new tool to predict orbital/site
permutations that lead to wave function compression without necessarily
explore numerically the permutational space. The strength of this
strategy is its generality and transferability to other model systems
and Hamiltonians. The proposed approach greatly enlarges the applicability
of wave function-based strategies, allowing for computationally inexpensive
and reliable characterizations (and predictions) of the electronic
structures and magnetic interactions in the ground and/or excited
states of exchange-coupled PNTM clusters.
In Sec. 2 we define
the Heisenberg model both in terms of the usual spin operators and
in terms of the 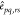 spin-free operators. In Sec. 3 we show the effect
of the site/orbital
reordering on the spin-adapted Hamiltonian matrices and their eigenstates
for a few selected systems, including the 2- and 3-sites s-
spin-free operators. In Sec. 3 we show the effect
of the site/orbital
reordering on the spin-adapted Hamiltonian matrices and their eigenstates
for a few selected systems, including the 2- and 3-sites s- clusters. In Sec. 4 a connection between the block-diagonal
structure of the Hamiltonian matrix and commutation relations between
partial cumulative spin operators and the Hamiltonian operator is
made, that allows us to estimate whether block-diagonal structure
is possible and what site ordering is to be chosen in order to reveal
this feature. We also derive a generalization of the model Hamiltonians
and the corresponding optimal site reordering, that induce the block-diagonal
structure of the Hamiltonian matrix for clusters with multiple magnetic
centers. Our conclusions are offered in Sec. 5.
clusters. In Sec. 4 a connection between the block-diagonal
structure of the Hamiltonian matrix and commutation relations between
partial cumulative spin operators and the Hamiltonian operator is
made, that allows us to estimate whether block-diagonal structure
is possible and what site ordering is to be chosen in order to reveal
this feature. We also derive a generalization of the model Hamiltonians
and the corresponding optimal site reordering, that induce the block-diagonal
structure of the Hamiltonian matrix for clusters with multiple magnetic
centers. Our conclusions are offered in Sec. 5.
2. The Heisenberg Model
The quantum Heisenberg model77−81 is a long-studied model Hamiltonian, widely used to describe magnetism in solids82−93 and molecules.94,95 In its general form it reads as
| 3 |
where the indices i and j run over all N lattice sites, 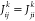 (with k = x, y, z) are the anisotropic magnetic
coupling constants and
(with k = x, y, z) are the anisotropic magnetic
coupling constants and 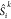 are the components of the local (per site)
spin operators. In the NN Heisenberg model, the sum is only performed
over neighboring sites ⟨ij⟩. The main
focus of this work is the isotropic Heisenberg model, for which the
Hamiltonian reads as
are the components of the local (per site)
spin operators. In the NN Heisenberg model, the sum is only performed
over neighboring sites ⟨ij⟩. The main
focus of this work is the isotropic Heisenberg model, for which the
Hamiltonian reads as
| 4 |
where
the 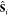 are the local (per site)
spin operators
corresponding to the local quantum number
are the local (per site)
spin operators
corresponding to the local quantum number 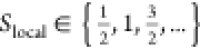 . In the previous work,28 we focused on
the single-J s-
. In the previous work,28 we focused on
the single-J s-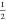 Heisenberg model with isotropic antiferromagnetic NN interactions, Jij = J < 0
Heisenberg model with isotropic antiferromagnetic NN interactions, Jij = J < 0
| 5 |
For spin-1/2 particles the second-quantized
spin-free representation
of the scalar product 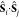 reads
reads
| 6 |
For the more general case of Sloc > 1/2, eq 6 becomes
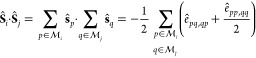 |
7 |
where Sloc is
the coupled spin at each site, obtained as sum of spin-1/2 vectors 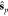 located at lattice site i and
located at lattice site i and 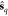 at site j, respectively.
at site j, respectively. 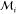 is the set of all electron indices
at site i. The condition that
is the set of all electron indices
at site i. The condition that  for i ≠ j is implied. Inserting eq 7 (or similarly eq 6) into eq 4 allows
us to express the Heisenberg Hamiltonian in terms of the spin-free
excitation operators:13,96−98
for i ≠ j is implied. Inserting eq 7 (or similarly eq 6) into eq 4 allows
us to express the Heisenberg Hamiltonian in terms of the spin-free
excitation operators:13,96−98
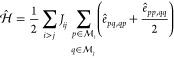 |
8 |
Notably, the operator 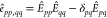 in eq 8 provides nonvanishing contributions only
to the diagonal
elements of the Heisenberg Hamiltonian, for (1) δpq = 0 (because
in eq 8 provides nonvanishing contributions only
to the diagonal
elements of the Heisenberg Hamiltonian, for (1) δpq = 0 (because  ), and (2) considering that the Heisenberg
model consists of singly occupied sites, only one term in
), and (2) considering that the Heisenberg
model consists of singly occupied sites, only one term in 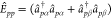 can contribute for each
function the operator
acts on. Consequently,
can contribute for each
function the operator
acts on. Consequently, 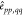 equals 1 for each interacting (p, q) pair, and it represents
a constant shift in the spin-free formulation of the Heisenberg Hamiltonian,
which consequently only couples CSFs by pure exchange interactions
via the
equals 1 for each interacting (p, q) pair, and it represents
a constant shift in the spin-free formulation of the Heisenberg Hamiltonian,
which consequently only couples CSFs by pure exchange interactions
via the  operator. Equation 7 represents the link between the Heisenberg
Hamiltonians and the ab initio molecular Hamiltonian used in quantum
chemistry. For systems with more than one electron per site, states
with variable Sloc populate the Hamiltonian
matrix. However, for chemical complexes featuring weak ligand-field
effects, non-Hund states characterize the higher portion of the electronic
spectrum, while for the low-energy electronic states electrons at
each site couple to maximize the local spin (Hund states). In model
Heisenberg Hamiltonians, non-Hund states can be pushed at the higher
end of the energy spectrum by adding an effective ferromagnetic interaction JHund > 0 between electrons residing on the
same
site. This term is to be added to eq 8. It is relevant to stress that within the Heisenberg
model only singly occupied orbitals have been considered (unpaired
electrons); thus, there are no configurations coupled via
operator. Equation 7 represents the link between the Heisenberg
Hamiltonians and the ab initio molecular Hamiltonian used in quantum
chemistry. For systems with more than one electron per site, states
with variable Sloc populate the Hamiltonian
matrix. However, for chemical complexes featuring weak ligand-field
effects, non-Hund states characterize the higher portion of the electronic
spectrum, while for the low-energy electronic states electrons at
each site couple to maximize the local spin (Hund states). In model
Heisenberg Hamiltonians, non-Hund states can be pushed at the higher
end of the energy spectrum by adding an effective ferromagnetic interaction JHund > 0 between electrons residing on the
same
site. This term is to be added to eq 8. It is relevant to stress that within the Heisenberg
model only singly occupied orbitals have been considered (unpaired
electrons); thus, there are no configurations coupled via 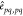 excitations (a geminal excitation).
excitations (a geminal excitation).
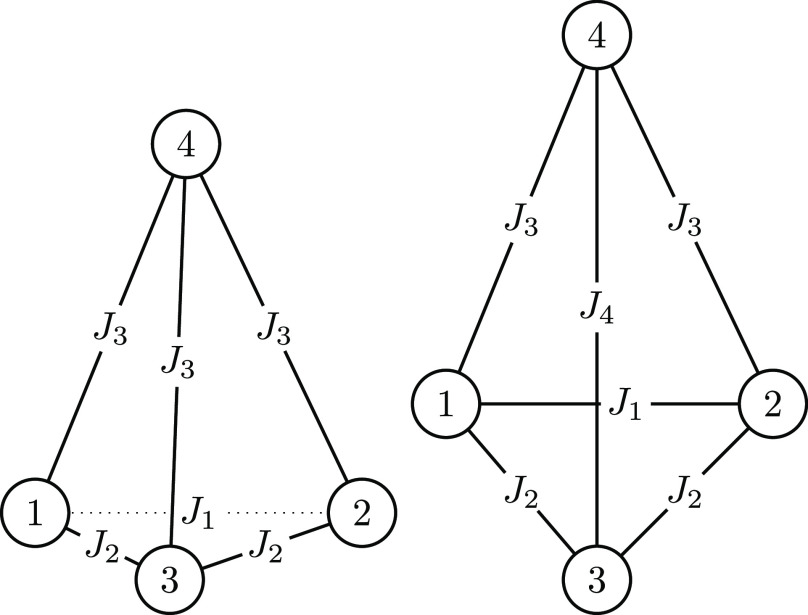
In the following, we will investigate in greater detail the block-diagonal structure of Heisenberg Hamiltonian matrices and the compactness of its eigenstates for triangular clusters of isosceles (C2v point group symmetry), equilateral (D3h) and scalene (Cs point group) symmetry, and 4-site clusters of various point group symmetries. The isotropic Heisenberg Hamiltonian for the isosceles triangle is written as
| 9 |
where the JBC = JAC equality applies. This model Hamiltonian has been used to describe magnetic interactions in Mn3O4 clusters.27 For a scalene triangle JAB ≠ JBC ≠ JAC and the Hamiltonian reads as
| 10 |
while for an equilateral triangle JAB = JBC = JAC. The one-dimensional 3-site chain with periodic boundaries is identical to the equilateral triangle, and the one with open boundaries is topologically identical to the isosceles triangle Heisenberg Hamiltonian with J12 = J23 and J13 = 0. For a square lattice (D4h point group symmetry) two nonequivalent magnetic coupling constants exist: a 4-fold Js (short) corresponding to the edges of the square (AB, BC, CD, and DA) and a 2-fold Jl (long) corresponding to the diagonal interactions (AC and BD). In this case the Heisenberg Hamiltonian is given by the following expression
| 11 |
This Hamiltonian has been used to describe magnetic interactions in Fe4S4 cubane clusters.26
3. Permutation Effects on Spin Adapted Basis
In earlier works we have shown the compression
effects on ground
state wave functions for ab initio Hamiltonians25 and for the s-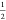 one-dimensional Heisenberg model.28 In the case of the Fe4S4 cubane model we have also numerically shown the unique block-diagonal
structure of the ab initio Hamiltonian matrix that
emerges from specific sites/orbitals reordering, and the possibility
to selectively target excited states within the same total spin sector
and differing in the intermediate spin coupling.26 In this section, the effect of the orbital/site reordering
and the subsequent wave function compression of ground and excited
eigenstates is explored for two Heisenberg cluster models, namely,
(a) a two-site cluster with local s-
one-dimensional Heisenberg model.28 In the case of the Fe4S4 cubane model we have also numerically shown the unique block-diagonal
structure of the ab initio Hamiltonian matrix that
emerges from specific sites/orbitals reordering, and the possibility
to selectively target excited states within the same total spin sector
and differing in the intermediate spin coupling.26 In this section, the effect of the orbital/site reordering
and the subsequent wave function compression of ground and excited
eigenstates is explored for two Heisenberg cluster models, namely,
(a) a two-site cluster with local s-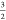 spins, and (b) a 3-site s-
spins, and (b) a 3-site s-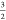 cluster, in isosceles triangle geometry.
Generalizations to different sizes (multisite clusters) and different
topologies (isosceles, equilateral, scalene triangles) are discussed
in the next section.
cluster, in isosceles triangle geometry.
Generalizations to different sizes (multisite clusters) and different
topologies (isosceles, equilateral, scalene triangles) are discussed
in the next section.
The full Hilbert space size for an electronic system in a spin adapted basis is provided by the Weyl-Paldus dimension formula4
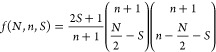 |
12 |
where N, n, and S refer to the number of correlated electrons, orbitals, and the targeted total spin quantum number (S = 0 for singlet, S = 1 for triplet, and so on), respectively. However, in the Heisenberg model electrons are not permitted to pair in the same orbital, and charge-transfer states obtained via hopping are not considered. Thus, the configurational space consists solely of configurations commonly known as spin flips. The size of the Heisenberg configurational space is provided by the van Vleck–Sherman formula99
| 13 |
where n0 refer to the number of singly occupied (open) sites.
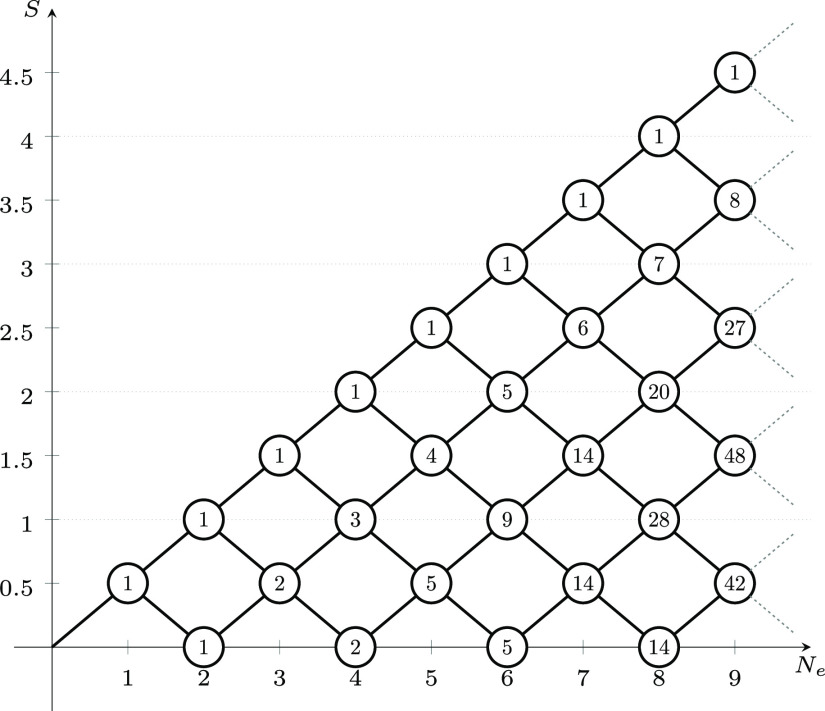
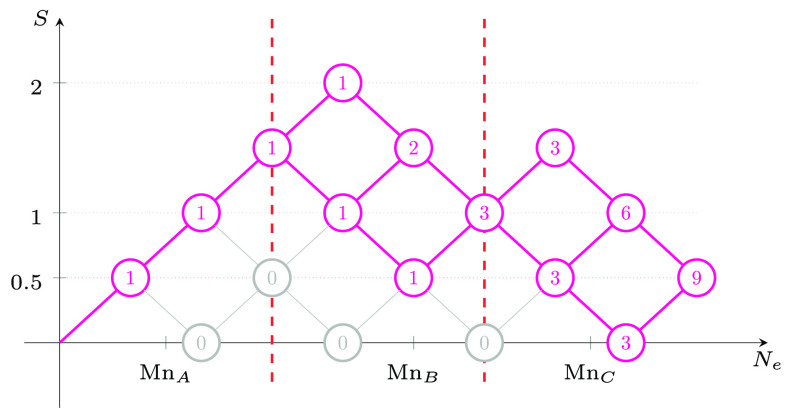
The spin-adapted basis for any Heisenberg systems can be graphically represented as paths branching through the genealogical branching diagrams (see Figure 1).1,13,14,100
Figure 1.
Generic genealogical branching diagram for up to 9 electrons (Ne). The node weights represent the number of paths starting from the root node, (Ne, Stot) = (0, 0) to reach the targeted node. This number is given by the van Vleck–Sherman formula, eq 13.
In these diagrams starting from the root
node (origin
of the graph), electrons are cumulatively spin-coupled,
contributing positively (up-spin, u, 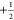 ) or negatively (down-spin, d,
) or negatively (down-spin, d, 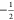 ) to the spin. Thus, for a six-electron
system a possible spin-adapted electronic configuration is written
as |uududd⟩, where the first 2 electrons are
positively spin-coupled contributing to the partial cumulative spin s = 1; the next electron lowers the partial cumulative spin
to
) to the spin. Thus, for a six-electron
system a possible spin-adapted electronic configuration is written
as |uududd⟩, where the first 2 electrons are
positively spin-coupled contributing to the partial cumulative spin s = 1; the next electron lowers the partial cumulative spin
to 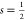 ; the next three electrons
further spin
couple leading to the final S = 0. In the hypothetical
two-site system with local s-
; the next three electrons
further spin
couple leading to the final S = 0. In the hypothetical
two-site system with local s-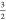 spins, considering that the first
3 and
last 3 singly occupied orbitals reside on site A and B, respectively, the |uud, udd⟩ CSF is interpreted as follows: the first three unpaired
electrons on the magnetic center A are coupled to
a doublet (violating Hund’s rule), and the other 3 electrons
on site B are antiferromagnetically aligned to the
spin on A, thus leading to the total spin S = 0. The CSF strings are not to be confused with ms conserving basis, such as
the SDs; in fact, each CSF can be expanded into a linear combination
of SDs spanning the same orbital/site space, for example as discussed
by Grabenstetter.101
spins, considering that the first
3 and
last 3 singly occupied orbitals reside on site A and B, respectively, the |uud, udd⟩ CSF is interpreted as follows: the first three unpaired
electrons on the magnetic center A are coupled to
a doublet (violating Hund’s rule), and the other 3 electrons
on site B are antiferromagnetically aligned to the
spin on A, thus leading to the total spin S = 0. The CSF strings are not to be confused with ms conserving basis, such as
the SDs; in fact, each CSF can be expanded into a linear combination
of SDs spanning the same orbital/site space, for example as discussed
by Grabenstetter.101
3.1. Two-Site
s-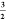 Model
Model
We first consider the ground
and excited states of singlet spin symmetry, for a two-site s-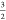 Heisenberg model. The system consists of
six electrons. On each site parallel spin alignment is favored (large
on-site JHund > 0), while keeping an
antiferromagnetic
interaction JAB < 0 across the sites.
For the singlet spin symmetry sector the basis of spin-adapted functions
consists of 5 CSFs, namely, |uuuddd⟩, |ududud⟩, |uuddud⟩, |uduudd⟩, and |uududd⟩. These
CSFs can be identified as branches in Figure 1. Two orbital orderings are considered, one,
where electrons from the two sites are nonsite-separated (1A – 2B – 3B – 2A – 3A –
1B), and the site-separated ordering (1A – 2A – 3A –
1B – 2B – 3B). The Hamiltonian matrices
in the two orderings are represented in Figure 2.
Heisenberg model. The system consists of
six electrons. On each site parallel spin alignment is favored (large
on-site JHund > 0), while keeping an
antiferromagnetic
interaction JAB < 0 across the sites.
For the singlet spin symmetry sector the basis of spin-adapted functions
consists of 5 CSFs, namely, |uuuddd⟩, |ududud⟩, |uuddud⟩, |uduudd⟩, and |uududd⟩. These
CSFs can be identified as branches in Figure 1. Two orbital orderings are considered, one,
where electrons from the two sites are nonsite-separated (1A – 2B – 3B – 2A – 3A –
1B), and the site-separated ordering (1A – 2A – 3A –
1B – 2B – 3B). The Hamiltonian matrices
in the two orderings are represented in Figure 2.
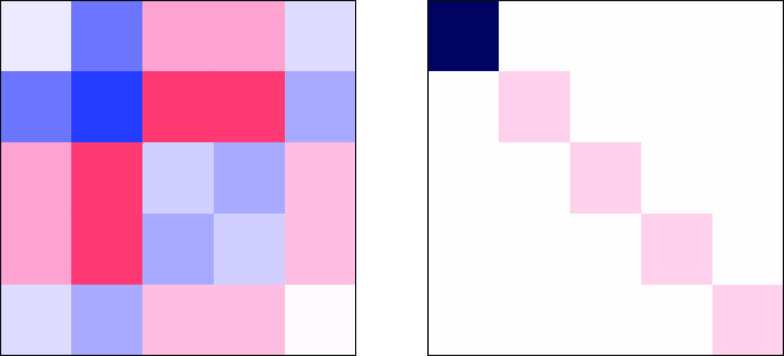
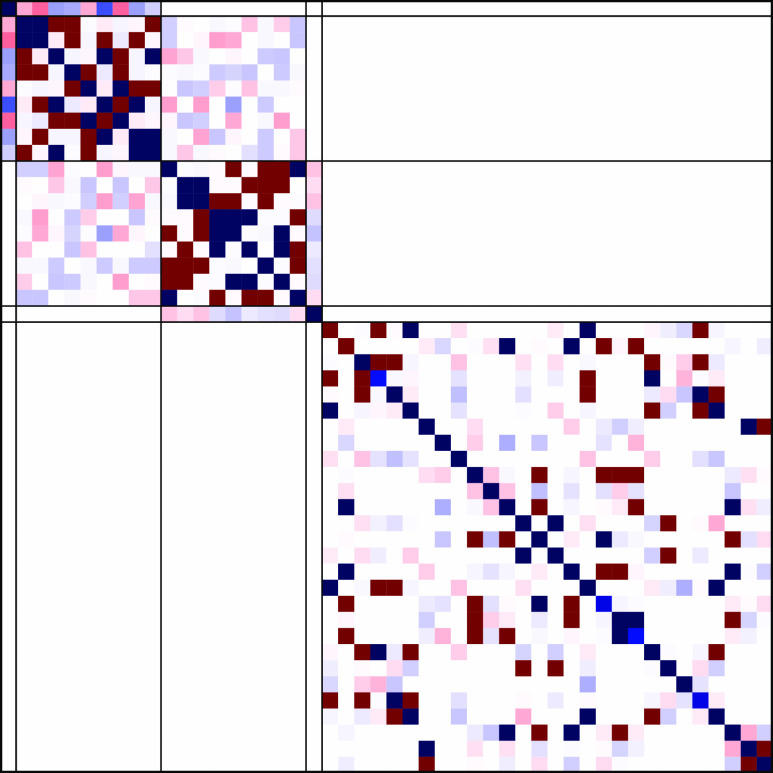
Figure 2.
Heisenberg Hamiltonian matrices (S = 0) for a
2-site s-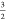 system in the GUGA spin-adapted basis and
using an arbitrary ordering (1A –
2B – 3B – 2A – 3A – 1B) (left) and the site-separated ordering (1A –
2A – 3A – 1B – 2B – 3B) (right). Red and
blue colors refer to elements of opposite sign.
system in the GUGA spin-adapted basis and
using an arbitrary ordering (1A –
2B – 3B – 2A – 3A – 1B) (left) and the site-separated ordering (1A –
2A – 3A – 1B – 2B – 3B) (right). Red and
blue colors refer to elements of opposite sign.
Strikingly, in the site-separated ordering the
Hamiltonian matrix is already in diagonal form. A similar feature
was already observed for the N2 and the Cr2 molecules
at stretched geometry and using a nonrelativistic ab initio Hamiltonian.25 The ground state as well
as all excited states are inherently single-reference, with only one
CSF completely characterizing the many-body wave function. In particular
the ground state is fully characterized by the |uuuddd⟩ CSF, that is promptly interpreted as two s-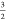 local spins coupled antiferromagnetically.
In the nonsite-separated ordering the matrix is dense indicating the
multireference character of the eigenstates when this particular ordering
is chosen. Thus, through a simple process of site/orbital reordering,
a diagonal Hamiltonian is obtained, graphically shown in Figure 2, which corresponds
to highly compressed eigenvector, to the limit of single-reference
wave functions.
local spins coupled antiferromagnetically.
In the nonsite-separated ordering the matrix is dense indicating the
multireference character of the eigenstates when this particular ordering
is chosen. Thus, through a simple process of site/orbital reordering,
a diagonal Hamiltonian is obtained, graphically shown in Figure 2, which corresponds
to highly compressed eigenvector, to the limit of single-reference
wave functions.
3.2. 3-Site s-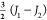 Model
Model
In this section we consider
the s-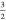 Heisenberg model of a 3-site cluster in
the isosceles triangle topology, with JBC = JAC ≠ JAB.
Heisenberg model of a 3-site cluster in
the isosceles triangle topology, with JBC = JAC ≠ JAB.
Combining two spin angular momenta with local spin Slocal = 3/2 results in four intermediate spin states, Sinterm = Γ(3/2) ⊗ Γ(3/2) = Γ(3) ⊕ Γ(2) ⊕ Γ(1) ⊕ Γ(0). The
resulting intermediate spins, Sinterm,
further couple to the third local spin, Slocal = 3/2, leading to 12 spin states (see eq 14).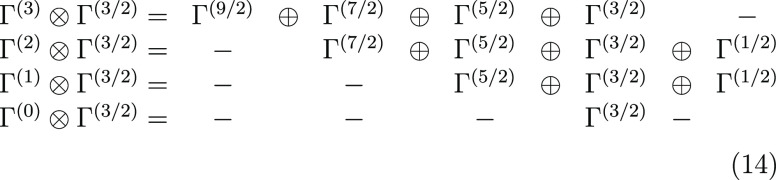
These states range from Stotal = 9/2 to Stotal = 1/2. For Sinterm = 3, the spins on the first two centers are collinear parallel and the third center can further couple in a collinear manner, leading to Stotal = 9/2, with all spins parallel aligned, and Stotal = 3/2, with the spin on the third center antiparallel with respect to AB. Similarly, for Sinterm = 0 the first two centers show collinear antiparallel spins, while the third center is left uncoupled. The remaining 9 spin states are characterized by noncolinear spin couplings.
The size of the Heisenberg spin-adapted basis for each of the possible total spin states is given by eq 13 and graphically reported in Figure 1. For a total of 9 unpaired electrons 42, 48, 27, 8, and 1 CSFs form the bases for Stotal = 1/2, 3/2, 5/2, 7/2, and 9/2, respectively. In Figure 3 the Hamiltonian matrices in the GUGA spin-adapted basis are reported for the three largest spin symmetries, namely, Stotal = 1/2, 3/2, and 5/2.
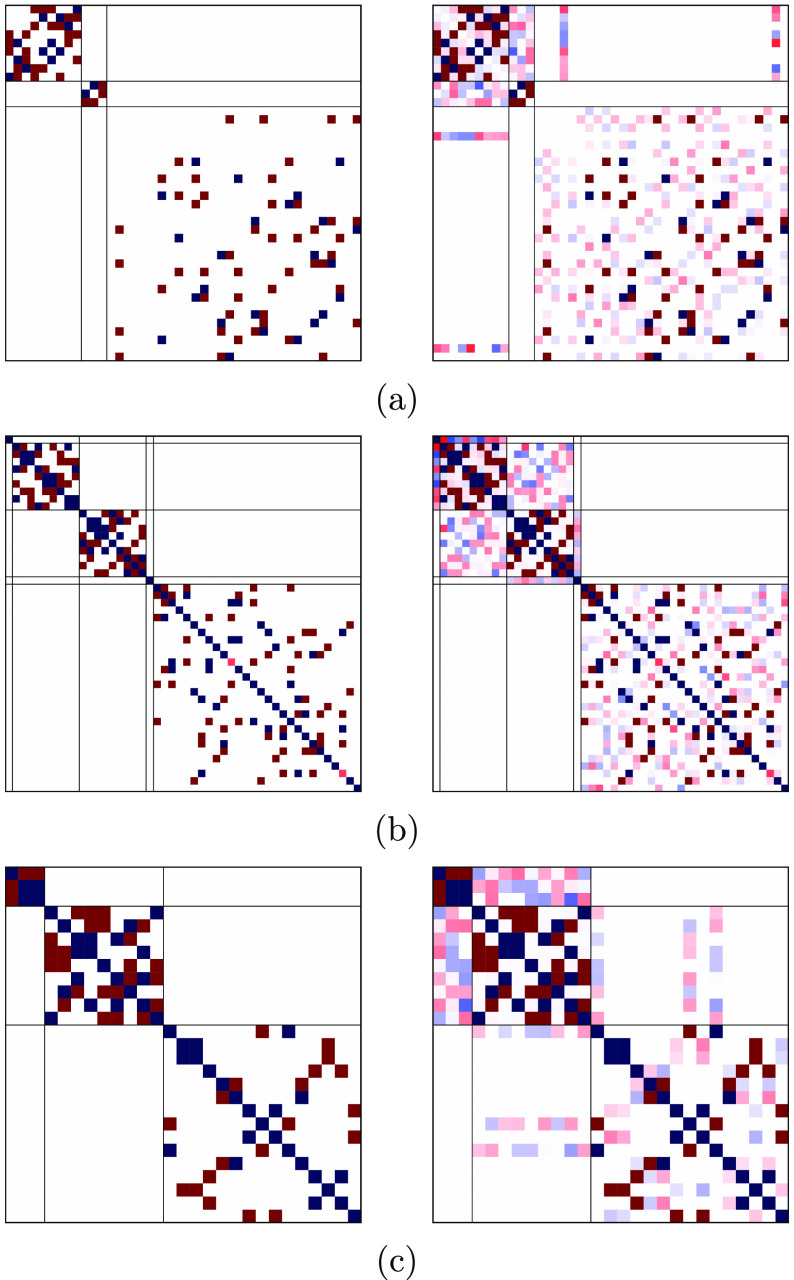
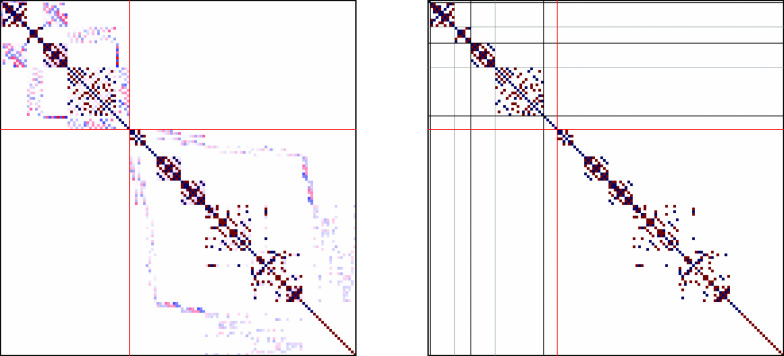
Figure 3.
Heisenberg Hamiltonian matrices for a 3-site s-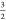 system in the GUGA spin-adapted basis for
(a) Stotal = 1/2, (b) Stotal = 3/2, and (c) Stotal = 5/2 total spin symmetries. The ABC (left) and ACB (right) orderings have
been considered. Red and blue colors refer to elements of opposite
sign.
system in the GUGA spin-adapted basis for
(a) Stotal = 1/2, (b) Stotal = 3/2, and (c) Stotal = 5/2 total spin symmetries. The ABC (left) and ACB (right) orderings have
been considered. Red and blue colors refer to elements of opposite
sign.
In Sec. 3.1 we have shown that site-separated orbital orderings lead to maximal compression of the GUGA wave function. For the 3-site case we adopt the same strategy. However, for the 3-site problem the site-permutation degree of freedom are also to be addressed. Of the 3! = 6 possible site permutations (ABC, ACB, BAC, BCA, CAB, CBA) only permutations that are nonequivalent by symmetry are retained, namely, ABC and ACB. Notably, ACB and CAB orderings are equivalent because the interactions between the first two sites, AC or CA, and the last site, B, are identical by symmetry.
In Figure 3 we see
an important difference between the ABC (left) and
the ACB (right) orderings. A clear block-diagonal
structure emerges for the ABC site ordering that
is largely lost for the ACB ordering. In the following
we will analyze in greater details the Hamiltonian matrices of the
quartet spin state, Figure 3b. Moving from the upper-left part of the Hamiltonian matrix
in ABC ordering 4 blocks can clearly be distinct
from the rest of the matrix. All four blocks share a common feature,
that is the local spin expectation value 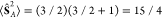 .
Next, CSFs with common well-defined cumulative
.
Next, CSFs with common well-defined cumulative 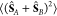 value characterize the 4 distinct
blocks.
The first block only contains the |uuu, ddd, uuu⟩ CSF with
value characterize the 4 distinct
blocks.
The first block only contains the |uuu, ddd, uuu⟩ CSF with 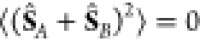 . The
second block contains CSFs with
. The
second block contains CSFs with 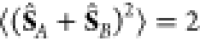 , such as |uuu, ddu, duu⟩ and |uuu, dud, duu⟩. The third block
contains CSFs with
, such as |uuu, ddu, duu⟩ and |uuu, dud, duu⟩. The third block
contains CSFs with 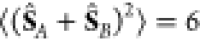 , such as |uuu, duu, udd⟩, and the fourth block
contains solely the |uuu, uuu, ddd⟩ CSF with intermediate
, such as |uuu, duu, udd⟩, and the fourth block
contains solely the |uuu, uuu, ddd⟩ CSF with intermediate 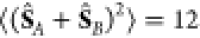 .
The remaining CSFs that populate the fifth
block are CSFs that violate the local Hund’s rule already on
the first site, Thus,
.
The remaining CSFs that populate the fifth
block are CSFs that violate the local Hund’s rule already on
the first site, Thus, 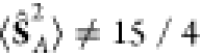 ,
which is obtained for all those CSFs starting
with |uud...⟩ or |udu...⟩.
Sparsity is also observed in the non-Hund block.
,
which is obtained for all those CSFs starting
with |uud...⟩ or |udu...⟩.
Sparsity is also observed in the non-Hund block.
On the right-hand side of Figure 3, for which the ACB ordering is utilized, nonvanishing matrix elements populate the off-diagonal blocks. However, the block-separation between Hund-states and non-Hund states holds even in the less-optimal ACB ordering. This feature is a direct consequence of retaining the site-separated orbital list in the ACB site ordering.
A similar block-diagonal structure has already been reported for nonrelativistic ab initio Hamiltonians applied to trinuclear Mn3O4 clusters.27
The block-diagonal structure in the ABC site-ordering
leads to an extraordinary compression of the ground- and excited-state
many-body wave functions. Additionally, it allows to selectively target
excited states, exclusively relying on the initial wave function ansatz. In the example above, choosing the |uuu, ddu, duu⟩ CSF as trial
wave function unequivocally leads to the lowest electronic state of
the second block, a state with 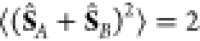 . This strategy has already been employed
for ab initio Hamiltonians of Fe4S4 cubane systems, featuring local spin
. This strategy has already been employed
for ab initio Hamiltonians of Fe4S4 cubane systems, featuring local spin 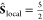 .23,26 In the case of the
less-optimal ACB ordering it is not possible to separate
states with different intermediate spin coupling
.23,26 In the case of the
less-optimal ACB ordering it is not possible to separate
states with different intermediate spin coupling 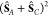 , due to the presence of the off-diagonal
blocks, thus in general any choice of trial wave function inevitably
leads to the ground state wave function, preventing any selective
optimization of excited states.
, due to the presence of the off-diagonal
blocks, thus in general any choice of trial wave function inevitably
leads to the ground state wave function, preventing any selective
optimization of excited states.
Interestingly, the size of the
blocks obtained in the ABC ordering can be anticipated
by means of the genealogical branching
diagrams. In Figure 4 the branching diagram of 9 electrons coupled to a doublet spin state
is reported, under the constraint  . There
are precisely three paths that lead
to
. There
are precisely three paths that lead
to  while
preserving the local spin on site
A (SA = 3/2 in this example).
Three more paths exist for the coupling with the C site. Thus, a total of nine paths and equivalent CSFs are the only
possible for this spin-state. Similar arguments can be utilized to
identify the basis contributing to the different blocks of the Hamiltonian
matrix. Figure 4 represents
a concrete measure of the minimal multireference character of electronic
states in an optimal site ordering and within the GUGA spin-adapted
basis.
while
preserving the local spin on site
A (SA = 3/2 in this example).
Three more paths exist for the coupling with the C site. Thus, a total of nine paths and equivalent CSFs are the only
possible for this spin-state. Similar arguments can be utilized to
identify the basis contributing to the different blocks of the Hamiltonian
matrix. Figure 4 represents
a concrete measure of the minimal multireference character of electronic
states in an optimal site ordering and within the GUGA spin-adapted
basis.
Figure 4.
Genealogical branching diagram for 9 electrons distributed over
3 magnetic sites (MnA, MnB, and MnC). The paths
compatible with SA =
3/2 (local Hund state on the MnA site)
and  are
highlighted in magenta. These paths
correspond to the 9 CSFs of the Stot =
1/2 state with a
are
highlighted in magenta. These paths
correspond to the 9 CSFs of the Stot =
1/2 state with a 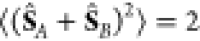 intermediate spin coupling.
intermediate spin coupling.
4. Block-Diagonal Hamiltonians and Commutators
While in Sec. 3 we collected examples of model Hamiltonians exhibiting a block-diagonal structure, and analyzed in detail the structure of those matrices and their eigensolutions, in this section we provide a more rigorous rationale for the emerging of such unique and computationally advantageous matrix structures, which complement the chemically/physically motivated site reorderings and the simulated annealing strategy to identify the optimal site permutations.28
For this, we turn our attention to commutator relations between
cumulative spins and the Heisenberg Hamiltonians. Commuting operators,  , admit common eigensolutions.
Thus, in
a basis of eigenfunctions of
, admit common eigensolutions.
Thus, in
a basis of eigenfunctions of  ,
the matrix
,
the matrix  has a block-diagonal structure
according
to the degenerate eigenvalues of
has a block-diagonal structure
according
to the degenerate eigenvalues of  .
.
For a two-site system,
the Heisenberg
Hamiltonian is proportional
to the 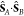 operator. Because of
the commutation relation
operator. Because of
the commutation relation
| 15 |
(see Appendix A.1 for a proof), on the basis of eigenfunctions
of 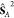 ,
, 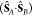 and therefore the corresponding
Heisenberg
Hamiltonian are blocked according to different values SA(SA + 1). In the site-separated orbital ordering,
each CSF represents an eigenfunction of the cumulative partial spin
operators
and therefore the corresponding
Heisenberg
Hamiltonian are blocked according to different values SA(SA + 1). In the site-separated orbital ordering,
each CSF represents an eigenfunction of the cumulative partial spin
operators 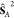 ,
, 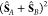 ,
, 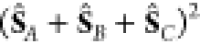 , and so on, and they can certainly be separated
according to the
, and so on, and they can certainly be separated
according to the 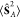 value. In the non-site-separated orbital ordering
each individual GUGA CSF is not an eigenfunction
of
value. In the non-site-separated orbital ordering
each individual GUGA CSF is not an eigenfunction
of 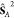 . From this, the dense
structure of the
Hamiltonian matrix and of the resulting eigensolutions follow.
. From this, the dense
structure of the
Hamiltonian matrix and of the resulting eigensolutions follow.
| 16 |
and
| 17 |
(see Appendix A.2 for an alternative proof). Therefore,
as already shown for the two-site case, any eigensolution of the isosceles
triangle Heisenberg Hamiltonian, is also an eigensolution of the partial
cumulative spin 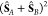 (or, in the case of degeneracies,
can be
cast in this form). In the ABC ordering, CSFs with
a common
(or, in the case of degeneracies,
can be
cast in this form). In the ABC ordering, CSFs with
a common 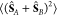 expectation value, will form blocks
in
the Hamiltonian matrix, orthogonal to the other blocks. When the ACB ordering is chosen, CSFs only form an eigenbasis of
the cumulative
expectation value, will form blocks
in
the Hamiltonian matrix, orthogonal to the other blocks. When the ACB ordering is chosen, CSFs only form an eigenbasis of
the cumulative 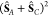 , which does not commute with the
Hamiltonian.
Thus, operating on an intermediate eigenbasis of
, which does not commute with the
Hamiltonian.
Thus, operating on an intermediate eigenbasis of 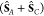 does not bring any advantageous
blocking
structure, as opposed to the ABC case.
does not bring any advantageous
blocking
structure, as opposed to the ABC case.
The relation between commuting operators and block-diagonal structure for the isosceles triangle can trivially be extended to the 3-site chain with open boundaries (a special case with JAB = 0) and the equilateral triangle (another edge case with JAB = JBC = JAC).
We stress here that 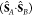 commutes with the sum
of
commutes with the sum
of 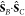 and
and 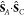 but not with individual
terms. Precisely
for this reason, no commutation relations exist for a scalene triangle
(JAB ≠ JBC ≠ JAC), except the commutator of local spin
but not with individual
terms. Precisely
for this reason, no commutation relations exist for a scalene triangle
(JAB ≠ JBC ≠ JAC), except the commutator of local spin 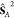 with the Hamiltonian.
Thus, the block-diagonal
structure that separates states with different partial cumulative
spin
with the Hamiltonian.
Thus, the block-diagonal
structure that separates states with different partial cumulative
spin 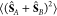 is not present for the scalene
triangle,
but the block-diagonal structure over
is not present for the scalene
triangle,
but the block-diagonal structure over 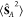 (Hund and non-Hund states) remains. This
finding is also shown graphically in Figure 5. This matrix should be compared to the one
reported in Figure 3b (left). The value of the off-diagonal matrix elements for the scalene
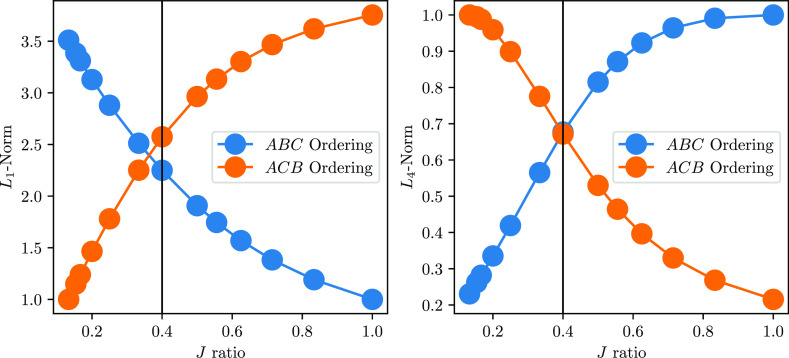
triangle is proportional to the (JBC – JAC)
difference. The closer JBC and JAC, the more the
off-diagonal elements become vanishingly small. In these cases the
quasi-block-diagonal structure, albeit not exact,
allows partial compression (in the numerical sense of increasing the L1-norm), which is beneficial for methods that
approximate the full-CI wave functions, such as FCIQMC,21,34,35 as it enhances the numerical
stability of the eigensolver. Also, as we have observed for the isotropic
one-dimensional Heisenberg model,28 the
leading CSFs already carry the most important forms of (long-range)
electron correlation, even though they are numerically not converged
to the exact solution. The dependency of the compression with respect
to the deviation from the isosceles triangle topology is illustrated
in Figure 6 for two
different reorderings.
(Hund and non-Hund states) remains. This
finding is also shown graphically in Figure 5. This matrix should be compared to the one
reported in Figure 3b (left). The value of the off-diagonal matrix elements for the scalene
triangle is proportional to the (JBC – JAC)
difference. The closer JBC and JAC, the more the
off-diagonal elements become vanishingly small. In these cases the
quasi-block-diagonal structure, albeit not exact,
allows partial compression (in the numerical sense of increasing the L1-norm), which is beneficial for methods that
approximate the full-CI wave functions, such as FCIQMC,21,34,35 as it enhances the numerical
stability of the eigensolver. Also, as we have observed for the isotropic
one-dimensional Heisenberg model,28 the
leading CSFs already carry the most important forms of (long-range)
electron correlation, even though they are numerically not converged
to the exact solution. The dependency of the compression with respect
to the deviation from the isosceles triangle topology is illustrated
in Figure 6 for two
different reorderings.
Figure 5.
Hamiltonian matrix for a 3-site s-3/2 Heisenberg system with three nonequivalent magnetic coupling constants (JAB ≠ JBC ≠ JAC). Red and blue colors refer to elements of opposite sign.
Figure 6.
L1-norm (left) and L4-norm (right) of the lowest quartet spin state for the 3-site s-3/2 Heisenberg Hamiltonian with fixed Jab = −150 and Jac = −20 values and variable Jbc, spanning the [−20, −150] range (arbitrary units). The Jac/Jbc ratio is used for the x-axis. Lower values of the L1-norm and higher values of the L4-norm are associated with a more compressed wave function. The vertical black line at Jac/Jbc = 0.4 (corresponding to Jbc = −50) marks the compression flipping point. For Jac/Jbc < 0.4 the ACB ordering and for Jac/Jbc > 0.4 the ABC ordering are to be preferred, respectively.
With the commutation relations
discussed above
it is possible to
make predictions on more complex model systems containing a larger
number of magnetically coupled sites. In the following we consider
the Heisenberg Hamiltonian for a 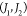 4-site
square cluster, eq 11. Using the commutation relation
4-site
square cluster, eq 11. Using the commutation relation
| 18 |
it is easy to demonstrate that 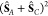 commutes with the Heisenberg Hamiltonian
in eq 11. Equation 18 suggests that in the ACBD ordering CSFs with common partial spins
commutes with the Heisenberg Hamiltonian
in eq 11. Equation 18 suggests that in the ACBD ordering CSFs with common partial spins 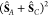 eigenvalues group together forming a block-diagonal
structure of the full Hamiltonian matrix. This result is numerically
confirmed in Figure 7.
eigenvalues group together forming a block-diagonal
structure of the full Hamiltonian matrix. This result is numerically
confirmed in Figure 7.
Figure 7.
Heisenberg Hamiltonian matrix for a 4-site s-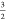 square cluster, with two J magnetic coupling
parameters, JAB = JBC = JCD = JDA = Jshort and JAC = JBD = Jlong, in the GUGA spin adapted
basis, for a singlet spin state (Stot =
0). The ABCD (left) and ACBD (right)
site orderings have been considered. The ACBD ordering
ensures a bock-diagonal structure of the matrix with eigenbasis of
the cumulative
square cluster, with two J magnetic coupling
parameters, JAB = JBC = JCD = JDA = Jshort and JAC = JBD = Jlong, in the GUGA spin adapted
basis, for a singlet spin state (Stot =
0). The ABCD (left) and ACBD (right)
site orderings have been considered. The ACBD ordering
ensures a bock-diagonal structure of the matrix with eigenbasis of
the cumulative 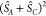 with common eigenvalues grouped together.
In the ABCD ordering such block-diagonal structure
is partially lifted. Red and blue colors refer to elements of opposite
sign.
with common eigenvalues grouped together.
In the ABCD ordering such block-diagonal structure
is partially lifted. Red and blue colors refer to elements of opposite
sign.
This finding explains on a rigorous ground, what we have numerically shown for the iron–sulfur cubanes in an earlier work.26 The same argument justifies the block-diagonal structure and corresponding wave function compression in the 4-site chain with periodic boundaries (extreme case of a 2J Heisenberg model with Jl = 0). When open boundaries are considered the commutation relation of eq 18 does not hold, and eigensolutions of the Hamiltonian are no longer eigensolutions of partial spin operators, and a denser Hamiltonian is to be expected.
The commutation relations found above can also be proven using the language of second quantization. To that end we write the local spin operator (per site) as
| 19 |
and utilize eq 7 for the spin–spin
correlation operator 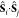 .
.
4.1. Cumulative-Spin-Blocked Heisenberg Hamiltonian
A general
expression of a n-site Heisenberg Hamiltonian
can be derived, which in the spin-adapted GUGA framework features
a block diagonal matrix structure for all cumulative
spins, 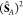 ,
, 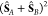 ,
, 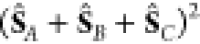 , and so on. The cumulative spin of the
first m sites can be expressed as
, and so on. The cumulative spin of the
first m sites can be expressed as
| 20 |
Using eq 17 it can be easily shown that a product of the cumulative spin with the spin of another site commutes with any other product of any cumulative spin with another site,
| 21 |
Finally, we introduce the following n-site Heisenberg Hamiltonian,
| 22 |
which commutes with all cumulative spins calculated in the same order, as can be demonstrated by utilizing eqs 20 and 21.
Examples for this type of system are the isosceles triangle, vide supra, and a 4-sites structure as depicted in Figure 8 (left)
| 23 |
Figure 8.
4-site Heisenberg model with the optimal cumulative-spin blocking (left), and with the blocking only according to the cumulative spin of the first two sites (right).
Instead of enforcing commutation of the model Hamiltonian with all cumulative spins (eq 22), another Hamiltonian can be introduced that commutes only with the first m cumulative spins (a less strict requirement),
| 24 |
The 4-site square model Hamiltonian is a special case of eq 24, for which only blocking according to the cumulative spin of the first two sites is assured. A more general example of a 4-site cluster that features blocking only up to a certain level of cumulative spin is depicted in Figure 8 (right).
5. Conclusions
In this work we have described in great detail a novel combined symmetric and unitary group approach that yields a unique block-diagonal structure of the many-body Hamiltonian matrix for general Heisenberg cluster models. As a consequence of the block-diagonal structure, more compact ground- and excited-state wave functions are obtained. This compression arises from well-defined ordering of the molecular orbitals and sites, combined with the GUGA cumulative spin coupling. We demonstrate that molecular orbital (and site) ordering is bound to specific commutation relations between cumulative spin operators and the Hamiltonian operator.
In the compressed many-body
wave functions a greatly reduced number
of spin-adapted electronic configurations (CSFs) is necessary to characterize
the electronic structure of the targeted state, to the limit of single
reference wave functions (one CSF). The wave function compression
greatly facilitates the convergence of methods that approximate the
full-CI solutions, such as the spin-adapted GUGA-FCIQMC21,22 approach, as their accuracy strongly depends on the sparsity of
the Hamiltonian and its eigensolutions. Moreover, the block-diagonal
structure of the Hamiltonian allows direct state-specific wave function optimizations of ground and excited states, while
removing the undesired overhead of computing all states energetically
more stable than the targeted one. This framework is of general applicability.
While in this work we have used Heisenberg cluster models, and explained
in greater detail the role of commutation relations, we have observed
equivalent compressions in ground- and excited-state wave functions
of exchange-coupled PNTM clusters, such as the 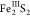 ,
, 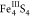 , and
, and 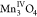 clusters.23,25−27 The strategy has successfully been applied also to
other model Hamiltonians
(one-dimensional s-1/2 Heisenberg model) and their ab initio equivalent (chain of equally spaced hydrogen atoms).
clusters.23,25−27 The strategy has successfully been applied also to
other model Hamiltonians
(one-dimensional s-1/2 Heisenberg model) and their ab initio equivalent (chain of equally spaced hydrogen atoms).
While
the previous works were based on general chemical/physical
considerations and partially automated techniques (simulated annealing)28 to identify the optimal ordering, in the present
work we show that a sufficient condition exists to
predict at the most fundamental level the optimal site ordering: Block-diagonal Hamiltonian matrices and highly compressed eigenvectors
are obtained for site orderings that make the cumulative spin and
the Hamiltonian operators commute. For example, eq 15 suggests that it is
possible to find solutions to the 2-site Heisenberg model that are
also solutions of the local 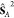 operator. And
considering that in site-separated
orbital ordering, CSFs are already eigensolutions of the cumulative
local spin operators, CSFs with different local spin eigenvalues do
not mix, nor they will mix via the Heisenberg Hamiltonian (due to eq 15), from which the block
diagonal structure arises. Similar commutation relations have been
discussed for tri- and tetra-nuclear cluster models, showing also
the differences that emerge from different topologies (isosceles,
equilateral, scalene triangles). For each case, the commutation relations
between partial cumulative spin operator and Hamiltonian suggest the
optimal site-ordering. A generalization of these commutation rules
has been derived. PNTM clusters with topologies matching the one suggested
by our general commutation rules are to be expected in nature. For
those clusters our strategy offers the best possible ordering for
the most compact wave function representation for ground and excited
states. The commutation relations represent a sufficient condition, thus it is possible to observe compressions and block-diagonal
structures also in cases where the above commutation relations are
not fulfilled. Finally, it is important to realize, as shown in Figure 6, that if deviations
from the ideal topology exist for the cluster model investigated,
one may still experience wave function compression and a quasi-block diagonal structure of the Hamiltonian. This situation in still
highly advantageous for methods that approximate the exact full-CI
solutions, as the most important correlation effects are already contained
in the few leading electronic configurations. The main practical target
of our strategy is the computational study and fundamental understanding
of magnetic interactions in exchange-coupled PNTM clusters occurring
in nature or the corresponding biomimetic counterparts, such as the
manganese cluster in photosystem II, the active sites of the nitrogenases,
or the synthetic
operator. And
considering that in site-separated
orbital ordering, CSFs are already eigensolutions of the cumulative
local spin operators, CSFs with different local spin eigenvalues do
not mix, nor they will mix via the Heisenberg Hamiltonian (due to eq 15), from which the block
diagonal structure arises. Similar commutation relations have been
discussed for tri- and tetra-nuclear cluster models, showing also
the differences that emerge from different topologies (isosceles,
equilateral, scalene triangles). For each case, the commutation relations
between partial cumulative spin operator and Hamiltonian suggest the
optimal site-ordering. A generalization of these commutation rules
has been derived. PNTM clusters with topologies matching the one suggested
by our general commutation rules are to be expected in nature. For
those clusters our strategy offers the best possible ordering for
the most compact wave function representation for ground and excited
states. The commutation relations represent a sufficient condition, thus it is possible to observe compressions and block-diagonal
structures also in cases where the above commutation relations are
not fulfilled. Finally, it is important to realize, as shown in Figure 6, that if deviations
from the ideal topology exist for the cluster model investigated,
one may still experience wave function compression and a quasi-block diagonal structure of the Hamiltonian. This situation in still
highly advantageous for methods that approximate the exact full-CI
solutions, as the most important correlation effects are already contained
in the few leading electronic configurations. The main practical target
of our strategy is the computational study and fundamental understanding
of magnetic interactions in exchange-coupled PNTM clusters occurring
in nature or the corresponding biomimetic counterparts, such as the
manganese cluster in photosystem II, the active sites of the nitrogenases,
or the synthetic 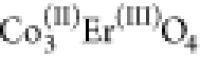 complex. The extension of this
strategy
to other classes of chemical systems is currently under investigation
and we do not exclude its application to transition metal complexes
featuring strong interactions with noninnocent ligands.
complex. The extension of this
strategy
to other classes of chemical systems is currently under investigation
and we do not exclude its application to transition metal complexes
featuring strong interactions with noninnocent ligands.
Acknowledgments
The authors gratefully acknowledge the support of the Max Planck Society. The authors dedicate this manuscript to the memory of the late Prof. Josef Paldus and his invaluable contributions to GUGA, which provides the foundation for the work presented here.
Appendix: Proof of Commutation Relations
A.1. Two-site case
We want to show that
| 25 |
We start by writing the scalar products explicitly as
| 26 |
All summations in this section run over the Cartesian coordinates (i, j, k ∈ {x, y, z}). Using the commutation relation
| 27 |
we can rewrite this as
| 28 |
The other two terms vanish because they only contain commutators of operators that solely act on different sites, which are zero. We then input the usual commutation relation for angular momentum operators
| 29 |
where ϵijk is the Levi-Civita symbol. This leads to
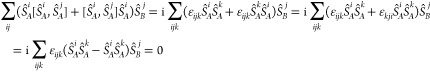 |
30 |
In the last three lines the indices in the second term were first renamed and then reordered to restore the ordering ijk in the Levi-Civita symbol which leads to sign change.
A.2. Three-Site Isosceles Triangle
With a similar argument, we can prove that
| 31 |
For this, we split up cAB,AC+BC into cAB,BC and cAB,AC and again utilize eq 27. This time, three of the four terms vanish for each of the commutators. This leads to
| 32 |
Again, by renaming and reordering i and k in the second commutator, we can write the sum as
Open access funded by Max Planck Society.
The authors declare no competing financial interest.
References
- Pauncz R.Spin Eigenfunctions: Construction and Use; Springer, 1979. [Google Scholar]
- Pauncz R.The Symmetric Group in Quantum Chemistry; CRC Press, 2018. [Google Scholar]
- Flocke N.; Karwowski J.. Theoretical and Computational Chemistry; Elsevier, 2002; pp 603–634. [Google Scholar]
- Paldus J. Group theoretical approach to the configuration interaction and perturbation theory calculations for atomic and molecular systems. J. Chem. Phys. 1974, 61, 5321. 10.1063/1.1681883. [DOI] [Google Scholar]
- Paldus J. Unitary-group approach to the many-electron correlation problem: Relation of Gelfand and Weyl tableau formulations. Phys. Rev. A 1976, 14, 1620. 10.1103/PhysRevA.14.1620. [DOI] [Google Scholar]
- Paldus J. In Theoretical Chemistry Advances and Perspectives, Eyring H., Ed.; Elsevier Science, 2012. [Google Scholar]
- Paldus J. Matrix elements of unitary group generators in many-fermion correlation problem. II. Graphical methods of spin algebras. J. Math. Chem. 2021, 59, 37–71. 10.1007/s10910-020-01173-8. [DOI] [Google Scholar]
- Shavitt I. Graph theoretical concepts for the unitary group approach to the many-electron correlation problem. Int. J. Quantum Chem. 1977, 12, 131. 10.1002/qua.560120819. [DOI] [Google Scholar]
- Shavitt I. Matrix Element Evaluation in the Unitary Group Approach to the Electron Correlation Problem. Int. J. Quantum Chem. 1978, 14, 5–32. 10.1002/qua.560140803. [DOI] [Google Scholar]
- Paldus J.; Boyle M. J. Unitary Group Approach to the Many-Electron Correlation Problem via Graphical Methods of Spin Algebras. Phys. Scr. 1980, 21, 295. 10.1088/0031-8949/21/3-4/012. [DOI] [Google Scholar]
- Shavitt I. In The Unitary Group for the Evaluation of Electronic Energy Matrix Elements, Hinze J., Ed.; Springer Berlin Heidelberg: Berlin, Heidelberg, 1981; pp 51–99. [Google Scholar]
- Paldus J. In Unitary Group Approach to Many-Electron Correlation Problem, Hinze J., Ed.; Springer Berlin Heidelberg: Berlin, Heidelberg, 1981; pp 1–50. [Google Scholar]
- Helgaker T.; Jørgensen P.; Olsen J.. Molecular Electronic Structure Theory; John Wiley & Sons, Ltd: Chichester, England, 2000. [Google Scholar]
- Li Manni G.; Guther K.; Ma D.; Dobrautz W.. Quantum Chemistry and Dynamics of Excited States; John Wiley & Sons, Ltd, 2020; Chapter (6), , pp 133–203. [Google Scholar]
- Roos B. O.; Taylor P. R.; Sigbahn P. E. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. 10.1016/0301-0104(80)80045-0. [DOI] [Google Scholar]
- Roos B. O.; Taylor P. R.; Siegbahn P. E. M. A Complete Active Space SCF Method (CASSCF) Using a Density Matrix Formulated Super-CI Approach. Chem. Phys. 1980, 48, 157–173. 10.1016/0301-0104(80)80045-0. [DOI] [Google Scholar]
- Siegbahn P. E. M.; Almlöf J.; Heiberg A.; Roos B. O. The Complete Active Space SCF (CASSCF) Method in a Newton–Raphson Formulation with Application to the HNO Molecule. J. Chem. Phys. 1981, 74, 2384–2396. 10.1063/1.441359. [DOI] [Google Scholar]
- Roos B. O. The Complete Active Space SCF Method in a Fock-Matrix-Based Super-CI Formulation. Int. J. Quantum Chem. 1980, 18, 175–189. 10.1002/qua.560180822. [DOI] [Google Scholar]
- Malmqvist P.-Å.; Rendell A.; Roos B. O. The Restricted Active Space Self-Consistent-Field Method, Implemented with a Split Graph Unitary-Group Approach. J. Phys. Chem. 1990, 94, 5477–5482. 10.1021/j100377a011. [DOI] [Google Scholar]
- Ma D.; Li Manni G.; Gagliardi L. The generalized active space concept in multiconfigurational self-consistent field methods. J. Chem. Phys. 2011, 135, 044128. 10.1063/1.3611401. [DOI] [PubMed] [Google Scholar]
- Guther K.; Anderson R. J.; Blunt N. S.; Bogdanov N. A.; Cleland D.; Dattani N.; Dobrautz W.; Ghanem K.; Jeszenszki P.; Liebermann N.; Li Manni G.; Lozovoi A. Y.; Luo H.; Ma D.; Merz F.; Overy C.; Rampp M.; Samanta P. K.; Schwarz L. R.; Shepherd J. J.; Smart S. D.; Vitale E.; Weser O.; Booth G. H.; Alavi A. NECI: N-Electron Configuration Interaction with an emphasis on state-of-the-art stochastic methods. J. Chem. Phys. 2020, 153, 034107. 10.1063/5.0005754. [DOI] [PubMed] [Google Scholar]
- Dobrautz W.; Smart S. D.; Alavi A. Efficient formulation of full configuration interaction quantum Monte Carlo in a spin eigenbasis via the graphical unitary group approach. J. Chem. Phys. 2019, 151, 094104. 10.1063/1.5108908. [DOI] [PubMed] [Google Scholar]
- Dobrautz W.; Weser O.; Bogdanov N. A.; Alavi A.; Li Manni G. Spin-Pure Stochastic-CASSCF via GUGA-FCIQMC Applied to Iron–Sulfur Clusters. J. Chem. Theory Comput. 2021, 17, 5684–5703. 10.1021/acs.jctc.1c00589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weser O.; Liebermann N.; Kats D.; Alavi A.; Li Manni G. Spin Purification in Full-CI Quantum Monte Carlo via a First-Order Penalty Approach. J. Phys. Chem. A 2022, 126, 2050–2060. 10.1021/acs.jpca.2c01338. [DOI] [PMC free article] [PubMed] [Google Scholar]; PMID: 35298155.
- Li Manni G.; Dobrautz W.; Alavi A. Compression of Spin-Adapted Multiconfigurational Wave Functions in Exchange-Coupled Polynuclear Spin Systems. J. Chem. Theory Comput. 2020, 16, 2202–2215. 10.1021/acs.jctc.9b01013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Manni G.; Dobrautz W.; Bogdanov N. A.; Guther K.; Alavi A. Resolution of Low-Energy States in Spin-Exchange Transition-Metal Clusters: Case Study of Singlet States in [Fe(III)4S4] Cubanes. J. Phys. Chem. A 2021, 125, 4727–4740. 10.1021/acs.jpca.1c00397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Manni G. Modeling magnetic interactions in high-valent trinuclear [Mn3(IV)O4]4+ complexes through highly compressed multi-configurational wave functions. Phys. Chem. Chem. Phys. 2021, 23, 19766–19780. 10.1039/D1CP03259C. [DOI] [PubMed] [Google Scholar]
- Dobrautz W.; Katukuri V. M.; Bogdanov N. A.; Kats D.; Li Manni G.; Alavi A. Combined unitary and symmetric group approach applied to low-dimensional Heisenberg spin systems. Phys. Rev. B 2022, 105, 195123. 10.1103/PhysRevB.105.195123. [DOI] [Google Scholar]
- Aquilante F.; Autschbach J.; Carlson R. K.; Chibotaru L. F.; Delcey M. G.; De Vico L.; Fdez Galván I.; Ferré N.; Frutos L. M.; Gagliardi L.; Garavelli M.; Giussani A.; Hoyer C. E.; Li Manni G.; Lischka H.; Ma D.; Malmqvist P.-Å.; Müller T.; Nenov A.; Olivucci M.; Pedersen T. B.; Peng D.; Plasser F.; Pritchard B.; Reiher M.; Rivalta I.; Schapiro I.; Segarra-Martí J.; Stenrup M.; Truhlar D. G.; Ungur L.; Valentini A.; Vancoillie S.; Veryazov V.; Vysotskiy V. P.; Weingart O.; Zapata F.; Lindh R. Molcas 8: New Capabilities for Multiconfigurational Quantum Chemical Calculations Across the Periodic Table. J. Comput. Chem. 2016, 37, 506–541. 10.1002/jcc.24221. [DOI] [PubMed] [Google Scholar]
- Olsen J.; Jørgensen P.; Simons J. Passing the one-billion limit in full configuration-interaction (FCI) calculations. Chem. Phys. Lett. 1990, 169, 463–472. 10.1016/0009-2614(90)85633-N. [DOI] [Google Scholar]
- White S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. 10.1103/PhysRevLett.69.2863. [DOI] [PubMed] [Google Scholar]
- White S. R. Density-matrix algorithms for quantum renormalization groups. Phys. Rev. B 1993, 48, 10345–10356. 10.1103/PhysRevB.48.10345. [DOI] [PubMed] [Google Scholar]
- Schollwöck U. The density-matrix renormalization group. Rev. Mod. Phys. 2005, 77, 259–315. 10.1103/RevModPhys.77.259. [DOI] [Google Scholar]
- Booth G. H.; Thom A. J. W.; Alavi A. Fermion Monte Carlo Without Fixed Nodes: A Game of Life, Death and Annihilation in Slater Determinant Space. J. Chem. Phys. 2009, 131, 054106. 10.1063/1.3193710. [DOI] [PubMed] [Google Scholar]
- Cleland D.; Booth G. H.; Alavi A. Communications: Survival of the fittest: Accelerating convergence in full configuration-interaction quantum Monte Carlo. J. Chem. Phys. 2010, 132, 041103. 10.1063/1.3302277. [DOI] [PubMed] [Google Scholar]
- Bethe H. Zur Theorie der Metalle. Z. Phys. 1931, 71, 205–226. 10.1007/BF01341708. [DOI] [Google Scholar]
- Karabach M.; Müller G.; Gould H.; Tobochnik J. Introduction to the Bethe Ansatz I. Comput. Phys. 1997, 11, 36–43. 10.1063/1.4822511. [DOI] [Google Scholar]
- Hulthén L.Über das Austauschproblem eines Kristalles. Ph.D. thesis, Stockholm College, 1938. [Google Scholar]
- Sandvik A. W.; Avella A.; Mancini F.. Computational Studies of Quantum Spin Systems, 2010.
- Schollwöck U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011, 326, 96–192. 10.1016/j.aop.2010.09.012. [DOI] [Google Scholar]; January 2011 Special Issue.
- Perez-Garcia D.; Verstraete F.; Wolf M. M.; Cirac J. I. Matrix Product State Representations. Quantum Info. Comput. 2007, 7, 401–430. 10.26421/QIC7.5-6-1. [DOI] [Google Scholar]
- Verstraete F.; Murg V.; Cirac J. Matrix product states, projected entangled pair states, and variational renormalization group methods for quantum spin systems. Adv. Phys. 2008, 57, 143–224. 10.1080/14789940801912366. [DOI] [Google Scholar]
- Östlund S.; Rommer S. Thermodynamic Limit of Density Matrix Renormalization. Phys. Rev. Lett. 1995, 75, 3537–3540. 10.1103/PhysRevLett.75.3537. [DOI] [PubMed] [Google Scholar]
- Pippan P.; White S. R.; Evertz H. G. Efficient matrix-product state method for periodic boundary conditions. Phys. Rev. B 2010, 81, 081103. 10.1103/PhysRevB.81.081103. [DOI] [Google Scholar]
- Dey D.; Maiti D.; Kumar M. An efficient density matrix renormalization group algorithm for chains with periodic boundary condition. Papers in Physics 2016, 8, 080006. 10.4279/pip.080006. [DOI] [Google Scholar]
- Vidal G. Entanglement Renormalization. Phys. Rev. Lett. 2007, 99, 220405. 10.1103/PhysRevLett.99.220405. [DOI] [PubMed] [Google Scholar]
- Murg V.; Verstraete F.; Cirac J. I. Exploring frustrated spin systems using projected entangled pair states. Phys. Rev. B 2009, 79, 195119. 10.1103/PhysRevB.79.195119. [DOI] [Google Scholar]
- Orús R. A practical introduction to tensor networks: Matrix product states and projected entangled pair states. Ann. Phys. 2014, 349, 117–158. 10.1016/j.aop.2014.06.013. [DOI] [Google Scholar]
- Wang L.; Gu Z.-C.; Verstraete F.; Wen X.-G. Tensor-product state approach to spin-1/2 square J1 – J2 antiferromagnetic Heisenberg model: Evidence for deconfined quantum criticality. Phys. Rev. B 2016, 94, 1. [Google Scholar]
- Li S.-H.; Shi Q.-Q.; Su Y.-H.; Liu J.-H.; Dai Y.-W.; Zhou H.-Q. Tensor network states and ground-state fidelity for quantum spin ladders. Phys. Rev. B 2012, 86, 1. 10.1103/PhysRevB.86.064401. [DOI] [Google Scholar]
- Suzuki M. Generalized Trotters formula and systematic approximants of exponential operators and inner derivations with applications to many-body problems. Commun. Math. Phys. 1976, 51, 183–190. 10.1007/BF01609348. [DOI] [Google Scholar]
- Suzuki M. Relationship between d-Dimensional Quantal Spin Systems and (d+1)-Dimensional Ising Systems: Equivalence, Critical Exponents and Systematic Approximants of the Partition Function and Spin Correlations. Prog. Theor. Phys. 1976, 56, 1454–1469. 10.1143/PTP.56.1454. [DOI] [Google Scholar]
- Trotter H. F. On the product of semi-groups of operators. Proc. Am. Math. Soc. 1959, 10, 545–545. 10.1090/S0002-9939-1959-0108732-6. [DOI] [Google Scholar]
- Nyfeler M.; Jiang F.-J.; Kämpfer F.; Wiese U.-J. Nested Cluster Algorithm for Frustrated Quantum Antiferromagnets. Phys. Rev. Lett. 2008, 100, 247206. 10.1103/PhysRevLett.100.247206. [DOI] [PubMed] [Google Scholar]
- Sandvik A. W.Springer Proceedings in Physics; Springer Berlin Heidelberg, 2002; pp 182–187. [Google Scholar]
- Sandvik A. W.; Kurkijärvi J. Quantum Monte Carlo simulation method for spin systems. Phys. Rev. B 1991, 43, 5950–5961. 10.1103/PhysRevB.43.5950. [DOI] [PubMed] [Google Scholar]
- Syljuåsen O. F.; Sandvik A. W. Quantum Monte Carlo with directed loops. Phys. Rev. E 2002, 66, 046701. 10.1103/PhysRevE.66.046701. [DOI] [PubMed] [Google Scholar]
- Sandvik A. W. Stochastic series expansion method with operator-loop update. Phys. Rev. B 1999, 59, R14157–R14160. 10.1103/PhysRevB.59.R14157. [DOI] [Google Scholar]
- Gubernatis J.; Kawashima N.; Werner P.. Quantum Monte Carlo Methods; Cambridge University Press, 2016. [Google Scholar]
- Prokof’ev N. V.; Svistunov B. V.; Tupitsyn I. S. Exact, complete, and universal continuous-time worldline Monte Carlo approach to the statistics of discrete quantum systems. J. Exp. Theor. Phys. 1998, 87, 310–321. 10.1134/1.558661. [DOI] [Google Scholar]
- Blankenbecler R.; Scalapino D. J.; Sugar R. L. Monte Carlo calculations of coupled boson-fermion systems. I. Phys. Rev. D 1981, 24, 2278–2286. 10.1103/PhysRevD.24.2278. [DOI] [Google Scholar]
- Hirsch J. E. Two-dimensional Hubbard model: Numerical simulation study. Phys. Rev. B 1985, 31, 4403–4419. 10.1103/PhysRevB.31.4403. [DOI] [PubMed] [Google Scholar]
- Evertz H. G.; Lana G.; Marcu M. Cluster algorithm for vertex models. Phys. Rev. Lett. 1993, 70, 875–879. 10.1103/PhysRevLett.70.875. [DOI] [PubMed] [Google Scholar]
- Evertz H. G. The loop algorithm. Adv. Phys. 2003, 52, 1–66. 10.1080/0001873021000049195. [DOI] [Google Scholar]
- Kalos M. H.; Levesque D.; Verlet L. Helium at zero temperature with hard-sphere and other forces. Phys. Rev. A 1974, 9, 2178–2195. 10.1103/PhysRevA.9.2178. [DOI] [Google Scholar]
- Ceperley D. M. Path integrals in the theory of condensed helium. Rev. Mod. Phys. 1995, 67, 279–355. 10.1103/RevModPhys.67.279. [DOI] [Google Scholar]
- Zhang S.; Krakauer H. Quantum Monte Carlo Method using Phase-Free Random Walks with Slater Determinants. Phys. Rev. Lett. 2003, 90, 136401. 10.1103/PhysRevLett.90.136401. [DOI] [PubMed] [Google Scholar]
- Ghanem K.; Liebermann N.; Alavi A. Population control bias and importance sampling in full configuration interaction quantum Monte Carlo. Phys. Rev. B 2021, 103, 155135. 10.1103/PhysRevB.103.155135. [DOI] [Google Scholar]
- Sorella S.; Baroni S.; Car R.; Parrinello M. A Novel Technique for the Simulation of Interacting Fermion Systems. EPL 1989, 8, 663–668. 10.1209/0295-5075/8/7/014. [DOI] [Google Scholar]
- Hirsch J. E.; Fye R. M. Monte Carlo Method for Magnetic Impurities in Metals. Phys. Rev. Lett. 1986, 56, 2521–2524. 10.1103/PhysRevLett.56.2521. [DOI] [PubMed] [Google Scholar]
- Assaad F.; Evertz H.. Computational Many-Particle Physics; Springer Berlin Heidelberg, 2008; pp 277–356. [Google Scholar]
- Troyer M.; Imada M.; Ueda K. Critical Exponents of the Quantum Phase Transition in a Planar Antiferromagnet. J. Phys. Soc. Jpn. 1997, 66, 2957–2960. 10.1143/JPSJ.66.2957. [DOI] [Google Scholar]
- Beard B. B.; Wiese U.-J. Simulations of Discrete Quantum Systems in Continuous Euclidean Time. Phys. Rev. Lett. 1996, 77, 5130–5133. 10.1103/PhysRevLett.77.5130. [DOI] [PubMed] [Google Scholar]
- Foulkes W. M. C.; Mitas L.; Needs R. J.; Rajagopal G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 2001, 73, 33–83. 10.1103/RevModPhys.73.33. [DOI] [Google Scholar]
- Tahara D.; Imada M. Variational Monte Carlo Method Combined with Quantum-Number Projection and Multi-Variable Optimization. J. Phys. Soc. Jpn. 2008, 77, 114701. 10.1143/JPSJ.77.114701. [DOI] [Google Scholar]
- Heisenberg W. Zur Theorie des Ferromagnetismus. Z. Phys. 1928, 49, 619–636. 10.1007/BF01328601. [DOI] [Google Scholar]
- Dirac P. A. M. On the theory of quantum mechanics. Proc. R. Soc. A 1926, 112, 661–677. [Google Scholar]
- Dirac P. A. M. Quantum mechanics of many-electron systems. Proc. R. Soc. A 1929, 123, 714–733. [Google Scholar]
- Heisenberg W. Mehrkörperproblem und Resonanz in der Quantenmechanik. Z. Phys. 1926, 38, 411–426. 10.1007/BF01397160. [DOI] [Google Scholar]
- Van Vleck J. H. The Dirac Vector Model in Complex Spectra. Phys. Rev. 1934, 45, 405–419. 10.1103/PhysRev.45.405. [DOI] [Google Scholar]
- Mohn P.Magnetism in the Solid State. Solid-State Sciences; Springer-Verlag, 2006; Vol. 134; pp 63–74. [Google Scholar]
- Kittel C.Quantum theory of solids; Wiley: New York, 1963. [Google Scholar]
- Nolting W.; Ramakanth A.. Quantum Theory of Magnetism; Springer Berlin Heidelberg, 2009. [Google Scholar]
- White R. M.Quantum Theory of Magnetism; Springer Berlin Heidelberg, 2007. [Google Scholar]
- Auerbach A.Interacting Electrons and Quantum Magnetism; Springer: New York, 1994. [Google Scholar]
- Fazekas P.Lecture Notes on Electron Correlation and Magnetism; Series in Modern Condensed Mat; World Scientific, 1999. [Google Scholar]
- Mattis D. C.The Theory of Magnetism I; Springer Berlin Heidelberg, 1981. [Google Scholar]
- Anderson P. W. The Resonating Valence Bond State in La2CuO4 and Superconductivity. Science 1987, 235, 1196–1198. 10.1126/science.235.4793.1196. [DOI] [PubMed] [Google Scholar]
- Chakravarty S.; Halperin B. I.; Nelson D. R. Two-dimensional quantum Heisenberg antiferromagnet at low temperatures. Phys. Rev. B 1989, 39, 2344–2371. 10.1103/PhysRevB.39.2344. [DOI] [PubMed] [Google Scholar]
- Manousakis E. The spin-1/2 Heisenberg antiferromagnet on a square lattice and its application to the cuprous oxides. Rev. Mod. Phys. 1991, 63, 1–62. 10.1103/RevModPhys.63.1. [DOI] [Google Scholar]
- Dagotto E.; Rice T. M. Surprises on the Way from One- to Two-Dimensional Quantum Magnets: The Ladder Materials. Science 1996, 271, 618–623. 10.1126/science.271.5249.618. [DOI] [Google Scholar]
- Eggert S.; Affleck I.; Takahashi M. Susceptibility of the spin 1/2 Heisenberg antiferromagnetic chain. Phys. Rev. Lett. 1994, 73, 332–335. 10.1103/PhysRevLett.73.332. [DOI] [PubMed] [Google Scholar]
- Boča R., Ed. Theoretical Foundations of Molecular Magnetism, Vol. 1; Elsevier, 1999; Vol. 1. [Google Scholar]
- de Graaf C.; Broer R.. Magnetic Interactions in Molecules and Solids; Theoretical Chemistry and Computational Modelling; Springer International Publishing: Cham, 2016. [Google Scholar]
- Matsen F.Advances in Quantum Chemistry Vol. 11; Elsevier, 1978; pp 223–250. [Google Scholar]
- Duch W.; Karwowski J. Symmetric group approach to configuration interaction methods. Comput. Phys. Rep. 1985, 2, 93–170. 10.1016/0167-7977(85)90001-2. [DOI] [Google Scholar]
- Paldus J.Electrons in Finite and Infinite Structures; Springer US, 1977; pp 411–429. [Google Scholar]
- Sherman A.; van Vleck J. H. The Quantum Theory of Valence. Rev. Mod. Phys. 1935, 7, 167–228. 10.1103/RevModPhys.7.167. [DOI] [Google Scholar]
- Salmon W. I.Advances in Quantum Chemistry Vol. 8; Elsevier, 1974; pp 37–94. [Google Scholar]
- Grabenstetter J. E.; Tseng T. J.; Grein F. Generation of genealogical spin eigenfunctions. Int. J. Quantum Chem. 1976, 10, 143–149. 10.1002/qua.560100112. [DOI] [Google Scholar]