Optical ptychography for biomedical imaging: recent progress and future directions [Invited]

Abstract

Ptychography is an enabling microscopy technique for both fundamental and applied sciences. In the past decade, it has become an indispensable imaging tool in most X-ray synchrotrons and national laboratories worldwide. However, ptychography’s limited resolution and throughput in the visible light regime have prevented its wide adoption in biomedical research. Recent developments in this technique have resolved these issues and offer turnkey solutions for high-throughput optical imaging with minimum hardware modifications. The demonstrated imaging throughput is now greater than that of a high-end whole slide scanner. In this review, we discuss the basic principle of ptychography and summarize the main milestones of its development. Different ptychographic implementations are categorized into four groups based on their lensless/lens-based configurations and coded-illumination/coded-detection operations. We also highlight the related biomedical applications, including digital pathology, drug screening, urinalysis, blood analysis, cytometric analysis, rare cell screening, cell culture monitoring, cell and tissue imaging in 2D and 3D, polarimetric analysis, among others. Ptychography for high-throughput optical imaging, currently in its early stages, will continue to improve in performance and expand in its applications. We conclude this review article by pointing out several directions for its future development.

1. Introduction

Conventional light detectors can only measure intensity variations of the incoming light wave. Phase information that characterizes the optical delay is lost during the data acquisition process. The loss of phase information is termed ‘the phase problem’. It was first noted in the field of crystallography: the real-space crystal structure can be determined if the phase of the diffraction pattern can be recovered in reciprocal space [1]. To regain the phase information of a complex field, it typically involves interferometric measurements with a known reference wave, in the process of holography.

In 1969, Hoppe proposed the original concept of ptychography in a three-part paper series, aiming to solve the phase problem encountered in electron crystallography [2]. The name ‘ptychography’ is pronounced tie-KOH-gra-fee, where ‘p’ is silent. The word is derived from the Greek ‘ptycho’, meaning convolution in German. By translating a confined coherent probe beam on a crystalline object, Hoppe aspired to extract the phase of the Bragg peaks in reciprocal space. If successful, the crystal structure in real space can be determined through Fourier synthesis. In the original concept, the object-probe multiplication in real space is modeled by a convolution between the Bragg peaks and the probe’s Fourier spectrum in reciprocal space. Therefore, convolution is a key aspect of this technique, justifying its name.

In 2004, Faulkner and Rodenburg adopted the iterative phase retrieval framework [3] for ptychographic reconstruction, thereby bringing the technique to its modern form [4]. Although the original concept was developed to solve the phase problem in crystallography, the modern form of this technique is equally applicable to non-crystalline structures. The experimental procedure is similar to Hoppe’s original idea: The object is laterally translated across a confined probe beam in real space, and the corresponding diffraction patterns are acquired in reciprocal space without using any lens. However, different from the original concept, the reconstruction process iteratively imposes two different sets of constraints. In real space, the confined probe beam limits the physical extent of the object for each measurement, serving as the compact support constraint. In reciprocal space, the diffraction measurements are enforced for the estimated solution, serving as the Fourier magnitude constraints. The iterative reconstruction process effectively looks for an object estimate that satisfies both constraints, in a way similar to the Gerchberg-Saxton algorithm where the phase is recovered from intensity measurements at different planes [5].

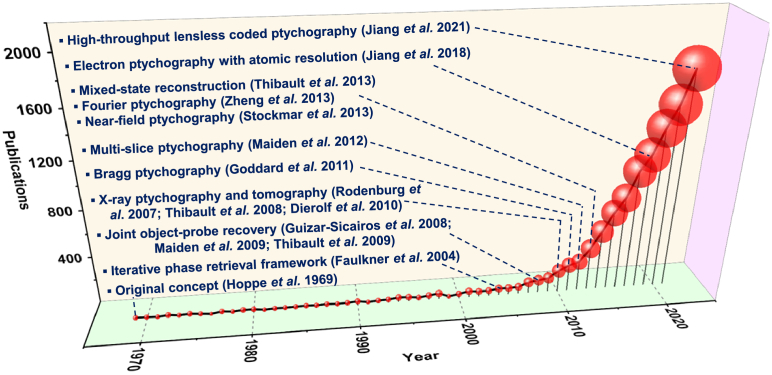
With the help of the iterative phase retrieval framework, ptychography has since proliferated and evolved into an enabling microscopy technique with imaging applications in different fields. Figure 1 shows the number of related publications since its conception in 1969. We also highlight several milestones of its development in this figure.

Fig. 1.

Development of the ptychography technique. The number of ptychography-related publications grows exponentially since the adoption of the iterative phase retrieval framework for reconstruction. Several milestones are highlighted for its development.

The key advantages of the technique can be summarized as follows: First, it does not need a stable reference beam as required in holography. A low-coherence light source can be used for sample illumination. This advantage is an important consideration for coherent X-ray imaging, where the coherence property of the light source is often poor compared to that of laser. Second, the requirement of isolated objects in conventional coherent diffraction imaging (CDI) is no longer required for ptychography. The spatially confined probe beam naturally imposes the compact support constraint for the phase retrieval process. Ptychography can routinely image contiguously connected samples over an extended area via object translation. Third, the lensless operation of this technique makes it appealing for high-resolution imaging in the X-ray and extreme ultraviolet (EUV) regimes, where lenses are costly and challenging to manufacture [6–8]. The recovered phase further allows high-contrast visualization of the object and provides quantitative morphological measurements. Fourth, the richness of the ptychographic dataset contains information on both the object and different system components in the setup. For example, the captured dataset can be used to jointly recover the object and the probe beam [9–11]. Similarly, the dataset can characterize and computationally compensate for the pupil aberration of a lens [12,13]. Multi-slice modeling of the object allows it to recover 3D volumetric information [14–17]. State mixture modeling [18] allows it to remove the effect of partial coherence in a light source [18,19] and perform multiplexed imaging at different spectral channels [20–22]. The diffraction data beyond the detector size limit can also be recovered for super-resolution imaging [23]. Lastly, ptychography has been recognized as a dose-efficient imaging technique for both X-ray [24] and electron microscopy [25,26].

Ptychography’s unique advantages have rapidly attracted attention from different research communities. In the past decade, it has become an indispensable imaging tool at most X-ray synchrotrons and national laboratories worldwide [27]. For electron microscopy, recent developments have also pushed the imaging resolution to the record-breaking deep sub-angstrom limit [28]. In the visible light regime, however, ptychography needs to compete with the well-optimized optical imaging systems. Conventional lensless ptychography has a limited resolution and throughput compared to that of regular light microscopy, thus preventing its widespread adoption in biomedical research. Recent developments of Fourier ptychography [29] and coded ptychography [30,31] can address these issues in the visible light regime. They can overcome the intrinsic tradeoff between imaging resolution and field of view, allowing researchers to have the best of both worlds. The imaging throughput can now be greater than that of high-end whole slide scanners [30,32,33], offering unique solutions for various biomedical applications.

In this review article, we will orient our discussions around optical ptychography and its biomedical imaging applications. In Section 2, we will first review and discuss the imaging models and operations of four representative ptychographic implementations. In Section 3, we will survey and discuss different ptychographic implementations based on their lensless / lens-based configurations and coded-illumination / coded-detection operations. In Section 4, we will discuss different software implementations, including the conventional phase retrieval algorithms, system corrections and extensions, and neural network-based implementations. In Section 5, we will highlight the related biomedical imaging applications, including digital pathology, drug screening, urinalysis, blood analysis, cytometric analysis, rare cell screening, cell culture monitoring, cell and tissue imaging in 2D and 3D, polarimetric analysis, among others. In Section 6, we will conclude this review article by pointing out several promising directions for future development.

We note that the field of ptychography has rapidly progressed in recent years. This review article only covers a small fraction of its developments. We encourage interested readers to visit the following relevant resources for more information: A recent comprehensive book chapter by Rodenburg and Maiden [34], an excellent introduction article by Guizar-Sicairos and Thibault [35], recent review papers on X-ray ptychography [27], Fourier ptychography [36–38], and EUV ptychography [39], surveys on ptychography-related phase retrieval algorithms [40–43], and an open-source MATLAB application [44].

2. Concepts and operations of representative ptychographic schemes

In this section, we will discuss the imaging models and operations of four representative ptychographic schemes, namely conventional ptychography [4], lensless coded ptychography [30,31], Fourier ptychography [29], and lens-based ptychographic structured modulation [45]. We choose these four implementations based on their lensless / lens-based configurations and coded-illumination / coded-detection operations. In the following, we will use the coordinates $(x,y)$ to denote the real space and $(k_x,k_y)$ to denote the reciprocal space (i.e., the Fourier space) of an imaging system. A Fourier transform can convert the complex-valued light field from the real space $(x,y)$ to the reciprocal (Fourier) space $(k_x,k_y)$ .

2.1. Conventional ptychography: lensless configuration with coded illumination

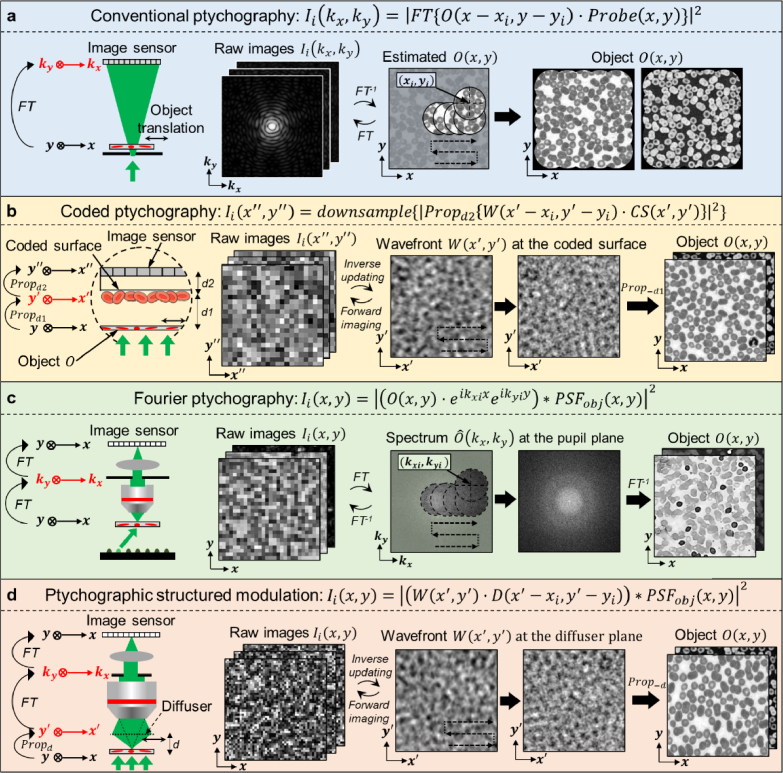
Figure 2(a) shows the imaging model and operation of conventional ptychography [4]. In this scheme, a spatially confined aperture limits the extent of the illumination probe beam $P(x,y)$ , and the image sensor is placed at the far field for data acquisition. In its operation, the complex-valued object $O(x,y)$ is mechanically translated to different position ( $x_i$ , $y_i$ ) in real space. The resulting product between the object and the probe beam propagates to the far-field via a Fourier transform. As such, the diffraction measurement can be obtained in reciprocal space with the coordinates of $(k_x,k_y)$ . The resulting dataset $I_i(k_x,k_y)(i=1,2,3\dots )$ , termed ptychogram, is a collection of diffraction measurements for all translated positions of the object.

Fig. 2.

Imaging models and operations of four ptychographic schemes chosen based on their lensless / lens-based configuration and coded-illumination / coded-detection operations. (a) Conventional ptychography: lensless configuration with coded illumination. $O(x,y)$ denotes the complex object, ( $x_i$ , $y_i$ ) denotes the translational shift of the object in real space, $Probe(x,y)$ denotes the spatially confined probe beam, ‘FT’ denotes Fourier transform, and ‘·’ denotes point-wise multiplication. (b) Coded ptychography: lensless configuration with coded detection. $W(x^{\mathrm{\prime }},y^{\mathrm{\prime }})$ denotes the object exit wavefront at the coded surface plane, $CS(x^{\mathrm{\prime }},y^{\mathrm{\prime }})$ denotes the transmission profile of the coded surface, and ‘Prop_d’ denotes free-space propagation for a distance d. (c) Fourier ptychography: lens-based configuration with coded illumination. $(k_{xi},k_{yi})$ denotes the incident wavevector of the i^th LED element, ‘*’ denotes the convolution operation, ‘PSF_obj’ denotes the point spread function of the objective lens. (d) Ptychographic structured modulation: lens-based configuration with coded detection. $D(x^{\mathrm{\prime }},y^{\mathrm{\prime }})$ denotes the transmission profile of the diffuser placed between the object and the objective lens.

The reconstruction process of conventional ptychography is shown in Fig. 2(a). It is performed by iteratively imposing two different sets of constraints: The first constraint is the support constraint for each measurement in real space. It is imposed by setting the signals outside the probe beam area to zeros while keeping the signals inside unchanged [46]. The second constraint is the Fourier magnitude constraint in reciprocal space. It is implemented by replacing the modulus of the estimated pattern with the measurement while keeping the phase unchanged. The iterative process will converge to an object recovery with both intensity and phase properties as shown in the right panel of Fig. 2(a).

One key consideration for conventional ptychography is the overlapped area of illumination during the object translation process (the overlapped circular region in the middle panel of Fig. 2(a)). The overlapped area allows the object to be visited multiple times in the acquisition process. The resulting additional information can resolve the ambiguities of the phase retrieval process. If no overlap is imposed, the recovery process will be carried out independently for each acquisition, leading to the usual ambiguities inherent to the phase problem [47].

In summary, conventional ptychography does not use any lens, and the operation is based on coded illumination of the spatially confined probe beam. There are many variants of this scheme, including the near-field implementation by placing the object closer to the detector [48], the tomographic implementation by rotating the object for 3D volumetric imaging [49–52], the reflective Bragg ptychography [53–58], and more. We will discuss them in Section 3.1.

2.2. Coded ptychography: lensless configuration with coded detection

Figure 2(b) shows the imaging model and operation of coded ptychography [30,31]. The system configuration is shown in the left panel of Fig. 2(b): The specimen is placed at the object plane $(x,y)$ , the coded surface is placed at the modulation plane $(x\mathrm{\prime },y\mathrm{\prime })$ , and the detector is placed at the image plane $(x\mathrm{\prime }\mathrm{\prime },y\mathrm{\prime }\mathrm{\prime })$ . In the image formation process, the light waves propagate for a distance $d_1$ from the object plane $(x,y)$ to the modulation plane $(x\mathrm{\prime },y\mathrm{\prime })$ , and a distance $d_2$ from the modulation plane $(x\mathrm{\prime },y\mathrm{\prime })$ to the image plane $(x\mathrm{\prime }\mathrm{\prime },y\mathrm{\prime }\mathrm{\prime })$ . The coded surface placed at the modulation plane can redirect large-angle diffracted light waves into smaller angles that can be detected by the underlying pixel array. Consequently, previously inaccessible high-resolution object details can now be acquired with the sensor pixel array. The operation of this coded surface is similar to that of structured illumination microscopy [59], where the high-frequency object information is down-modulated into the low-frequency passband of the system for detection.

To prepare the coded surface, one can etch micron-sized phase scatterers on the image sensor’s coverglass followed by printing sub-wavelength absorbers on the etched surface [30]. The left panel of Fig. 2(b) shows an alternative approach where a drop of blood is directly smeared on the image sensor’s coverglass and fixated with alcohol [60,61]. The rich spatial feature of the coded surface makes it an effective high-resolution lens with a theoretically unlimited field of view (the coded layer can be made of any size). It can unlock an optical space with spatial extent $(x,y)$ and spatial frequency content $(k_x,k_y)$ that is inaccessible using conventional lens-based optics [30].

In a typical implementation of coded ptychography, a fiber-coupled laser beam is used to illuminate the entire object over an extended area. By translating the object (or the integrated coded sensor) to different lateral positions, the system records a set of intensity images $I_i(x\mathrm{\prime }\mathrm{\prime },y\mathrm{\prime }\mathrm{\prime })$ ( $i=1,2,\dots$ ) for reconstruction. In the forward imaging model of Fig. 2(b), we use ‘downsample’ to denote the down-sampling process of the pixel array. To achieve high-resolution reconstruction, spatial and angular responses of individual pixels need to be considered in the imaging model [30]. The spatial response characterizes the pixel sensitivity at different regions of the sensing area (pixel sensitivity is often higher at the central region than the edge). The angular response characterizes the pixel readout with respect to different incident angles. Following the iterative phase retrieval process, one can recover the complex object exit wavefront $W(x\mathrm{\prime },y\mathrm{\prime })$ at the coded surface plane. This recovered wavefront can then be digitally propagated back to the object plane to obtain the high-resolution object profile $O(x,y)$ .

In coded ptychography, the coded surface on the image sensor serves as an effective ptychographic probe beam (the coded surface multiplies the object wavefront in the imaging model of Fig. 2(b)). We assume the transmission profile remains unchanged for diffracted waves with different incident angles. The transmission matrix [62] of the coded layer can be approximated as a diagonal matrix. This assumption is valid when the coded surface is a thin layer on the sensor. For a thick coded surface, one may need to measure the full transmission matrix to characterize its modulation property.

The coded ptychography scheme has several unique advantages among different ptychographic implementations: First, the modulation effect of the coded surface enables high-resolution imaging without using any optical lens. The current setup can resolve the 308-nm linewidth on the resolution target. The best-demonstrated resolution corresponds to a numeral aperture (NA) of ∼0.8, among the highest in lensless imaging demonstrations. The resolution can be further improved by integrating angle-varied illumination for aperture synthesizing [29].

Second, the illumination beam covers the entire object over a large field of view. The scanning step size is on the micron level between adjacent acquisitions. As a result, one can continuously acquire images at the full camera frame rate during the scanning process, enabling whole slide imaging of various bio-specimens at high speed. It has been shown that gigapixel high-resolution images with a 240 mm² effective field of view can be acquired in 15 seconds [30]. The corresponding imaging throughput is comparable to or higher than that of the fastest whole slide scanner [63].

Third, the spatially confined (structured) probe beam in conventional ptychography may vary between different experiments. For example, it is challenging to place different specimens in the same exact position of the probe beam. The probe beam profile may also vary between different experiments. In the phase retrieval process, it is often required to jointly recover both the object and the probe beam simultaneously. However, in some cases, the object and the probe beam can never be completely and unambiguously separated from one another, especially when both contain slow-varying phase features with many 2π wraps [30]. In coded ptychography, the coded layer serves as the effective probe beam for the imaging process. This effective probe beam is hardcoded into the imaging system and stays unchanged between different experiments. It can quantitatively recover the slow-varying phase profiles (with many 2π wraps) of different samples, including optical prisms and lenses [30], bacterial colonies [64], urine crystals [61], unstained thyroid smears obtained from fine needle aspiration [60].

Fourth, the small distance between the object and the coded sensor allows the direct recovery of the object’s positional shift based on the raw diffraction measurements. As a result, coded ptychography allows open-loop optical acquisition without requiring any positional feedback from the mechanical stage. A coded ptychography platform can be built with low-cost stepper motors or even a Blu-ray drive [61]. In contrast, precise positional feedback is often an important consideration for conventional ptychography.

Fifth, rapid autofocusing is a challenge for conventional lens-based whole slide imaging systems. Common whole slide scanners often generate a focus map prior to the image acquisition process [63]. With coded ptychography, the recovered wavefront can be propagated back to any axial plane post-measurement. Focusing is no longer required in the image acquisition process. Post-acquisition autofocusing can be performed by maximizing the phase contrast of the recovered images [60].

Lastly, the recovered object wavefront in coded ptychography depends solely on how the complex wavefront exits the sample and not on how it enters. Therefore, the sample thickness becomes irrelevant in modeling the image formation process and this scheme can image objects with arbitrary thicknesses. In contrast, coded-illumination approaches (including conventional ptychography and Fourier ptychography) have requirements for object thickness [6,37]. Multi-slice or diffraction tomography approaches may be needed for modeling and imaging thick specimens [14,65].

In summary, coded ptychography does not use any lens, and the operation is based on coded detection of the structured surface on the image sensor. There are many variants of this scheme, including the rotational implementation by placing the object on a spinning disk [61], an on-chip optofluidic implementation by translating the object through a microfluidic channel [66], and synthetic aperture implementation by translating the coded sensor at the far field [67], among others. We will discuss them in Section 3.2.

2.3. Fourier ptychography: lens-based configuration with coded illumination

Figure 2(c) shows the imaging model and operation of Fourier ptychographic microscopy (FPM) [29]. Unlike the two lensless schemes discussed above, FPM is a lens-based implementation built using a regular microscope platform. The left panel of Fig. 2(c) shows a typical FPM setup: A programmable LED array is used for angle-varied illumination, and a low-NA objective lens is used for image acquisition. In this setup, the specimen is placed at the object plane $(x,y)$ , the pupil aperture is located at the Fourier plane $(k_x,k_y)$ , and the detector is placed at the image plane $(x,y)$ . In the image formation process, the microscope objective lens performs a Fourier transform to convert the light waves from the object plane $(x,y)$ to the aperture plane $(k_x,k_y)$ . The tube lens then performs a second Fourier transform to convert the light waves from the aperture plane $(k_x,k_y)$ to the image plane $(x,y)$ [37].

In the operation of FPM, the programmable LED array sequentially illuminates the object from different incident angles and the FPM system records the corresponding low-resolution intensity images $I_i(x,y)$ ( $i=1,2,\dots$ ). If the object is a 2D thin section, changing the illumination wavevector $(k_{xi},k_{yi})$ in real space effectively translates the object spectrum in reciprocal (Fourier) space:

$$FT\{O(x,y)\cdot e^{i{k}_{xi}x}{e}^{i{k}_{yi}y}\}=\hat{O}(k_x-k_{xi},k_y-k_{yi}),$$ (1)

where $FT$ denotes the Fourier transform operation and $\hat{O}(k_x,k_y)$ denotes the object spectrum. Therefore, the imaging model in Fig. 2(c) can be re-written as

$$I_i(x,y)=|F{T}^{-1}\{\hat{O}(k_x-k_{xi},k_y-k_{yi})\cdot Pupil(k_x,k_y)\}{|}^2$$ (2)

In this model, we can see that the pupil aperture of the microscope system serves as the effective ptychographic probe beam for object spectrum. The translational shift of the object spectrum is determined by the $i^{th}$ LED element’s illumination wave vector ( $k_{xi},k_{yi}$ ). As such, each captured raw image corresponds to a circular aperture region centered at position ( $k_{xi},k_{yi}$ ) in the Fourier space, as shown in the middle panel of Fig. 2(c).

While conventional ptychography stitches measurements in real space to expand the imaging field of view, the reconstruction process of FPM stitches measurements in reciprocal (Fourier) space to expand the spatial-frequency passband. Therefore, the synthesized object spectrum $\hat{O}(k_x,k_y)$ in FPM can generate a bandwidth that far exceeds the original NA of the microscope platform, as shown in the right panel of Fig. 2(c). Once the object spectrum is recovered from the phase retrieval process, the high-resolution object image $O(x,y)$ can be obtained by performing an inverse Fourier transform. The resolution of the recovered object image is no longer limited by the NA of the employed objective lens. Instead, it is determined by the synthesized bandwidth of the object spectrum: The larger the incident angle, the higher the resolution. Meanwhile, the recovered object image retains the low-NA objective’s large field of view, thus having a high resolution and a large field of view simultaneously.

Compared with conventional ptychography, FPM swaps real space and reciprocal space using a microscopy system [29,68]. With conventional ptychography, the confined probe beam serves as the finite support constraint in real space. With FPM, the confined pupil aperture serves as the finite support constraint in Fourier space. Both techniques share the same imaging model and require aperture overlap in-between adjacent acquisitions to resolve phase ambiguity of the recovery process. Similarly, both techniques are based on coded-illumination operations and have requirements on the object thickness. However, the aperture synthesizing process in FPM provides a straightforward solution for resolution improvement. By utilizing a high-resolution objective lens with a NA of 0.95, FPM can synthesize a NA of 1.9, which is close to the maximum possible synthetic NA of 2 in free space [69]. The lens elements in FPM can also compensate for the chromatic dispersion of light at different wavelengths, thereby leading to less stringent requirements on the temporal coherence of the light source. Board-band LED sources can be used in FPM for sample illumination. With conventional ptychography and other lensless ptychographic implementations, signals at different wavelengths will be dispersed to different axial planes. Thus, laser sources are often preferred in these setups. Other differences between FPM and conventional ptychography include the dynamic range of the detector, real-space sampling versus Fourier-space sampling, and the initialization strategies [37].

Compared to coded ptychography, FPM replaces the coded layer with the pupil aperture at the Fourier space. The two free-space propagation processes in coded ptychography are also replaced by two Fourier transforms in FPM. Both techniques can perform large-field-of-view and high-resolution microscopy imaging. With coded ptychography, the phase retrieval process recovers the object wavefront at the coded surface plane. The wavefront is then propagated back to the object plane to obtain the final object recovery. With FPM, the process first recovers the object spectrum in the Fourier space, and the object image can then be obtained via an inverse Fourier transform. One key distinction between coded ptychography and FPM is the sample thickness requirement. As a coded-illumination technique, the imaging model of FPM depends on how the incident beam enters the sample. Thick objects must be modeled as multiple layers or 3D scattering potential. In contrast, the imaging model of coded ptychography depends solely on how the complex wavefront exits the sample. Therefore, coded ptychography can image 3D objects with arbitrary thickness. Another distinction between coded ptychography and FPM is the angularly- and spatially-varying properties of the effective ptychographic probe beams. With coded ptychography, the thin coded surface on the image sensor serves as the effective ptychographic probe beam. The transmission profile of this coded surface is assumed to be angle invariant. With FPM, the pupil aperture serves as the effective ptychographic probe beam, and it varies for different spatial locations of the imaging field of view. For best results, the spatially varying property of the pupil needs to be modeled in FPM or recovered in a calibration experiment [12,13,70].

In summary, FPM is a lens-based implementation, and its operation is based on coded illumination with a programmable LED array. There are also many variants of this scheme, including Fourier ptychographic diffraction tomography [65,71], reflective implementations [72–76], single-shot implementations [77–79], annular illumination [78,80,81], and beam steering implementations [82–84]. We will discuss them in Section 3.3.

2.4. Ptychographic modulation: lens-based configuration with coded detection

Figure 2(d) shows the imaging model and operation of the ptychographic structured modulation scheme [45]. In this scheme, a thin diffuser is placed in between the object and the objective lens. The left panel of Fig. 2(d) shows the system configuration: The sample is placed at the object plane $(x,y)$ , the diffusing layer is placed at the modulation plane $(x\mathrm{\prime },y\mathrm{\prime })$ , and the microscope system relays the image plane to the object plane $(x,y)$ .

In a typical structured ptychographic modulation implementation, a plane wave is used to illuminate the entire object over an extended area. By translating the diffuser (or the object) to different lateral positions, the system records a set of intensity images $I_i(x,y)$ ( $i=1,2,\dots$ ) using the microscope system. Following the iterative phase retrieval process, the complex object exit wavefront $W(x\mathrm{\prime },y\mathrm{\prime })$ will be recovered at the diffuser plane. This recovered wavefront can then be digitally propagated back to the object plane to obtain the high-resolution object profile $O(x,y)$ . Like coded ptychography, the diffuser in this scheme serves as a computational lens for modulating the object’s diffracted waves. With the diffuser, the otherwise inaccessible high-resolution object information can now be encoded into the system. Thus, it can be viewed as a lens-based implementation of coded ptychography.

Compared to FPM, this scheme performs coded detection for super-resolution imaging. The multiplication process between the object and the tilted planewave in FPM becomes a multiplication process between the object exit wavefront $W(x\mathrm{\prime },y\mathrm{\prime })$ and the diffuser profile $D(x\mathrm{\prime },y\mathrm{\prime })$ in ptychographic structured modulation. As a result, this scheme converts the thin object requirement in FPM to a thin diffuser requirement. Once the object wavefront is recovered, it can be digitally propagated to any plane along the optical axis for post-measurement refocusing. Similar to FPM, this scheme can also bypass the resolution limit set by the NA of the objective lens. To this end, Song et al. demonstrated a 4.5-fold resolution gain using a low-NA objective lens [45]. A low-cost microscope add-on module can also be made by attaching the diffuser to a vibration holder. By applying voltages to two vibrational motors, users can introduce random positional shifts to the diffuser and these shifts can be recovered via a correlation analysis process [85].

In summary, ptychographic structured modulation is lens-based implementation, and its operation is based on coded detection of the diffusing layer. It can be viewed as a lens-based version of coded ptychography or a coded-detection version of FPM. There are several variants of this scheme, including configurations by translating the diffuser at the image plane [86] and the aperture plane [87] of the microscope platform, an aperture-scanning Fourier ptychography scheme [88], among others. We will further discuss these variants in Section 3.4.

3. Survey on different ptychographic implementations

With the four representative schemes discussed in the previous section, we further categorize different ptychographic implementations into four groups based on their lensless / lens-based configuration and coded-illumination / coded detection operations in Table 1. Figure 3 shows some of the representative schematics of these four groups, whose operations will be discussed in Sections 3.1–3.4. The key considerations for different hardware implementations will be summarized in Section 3.5.

Table 1. Different hardware implementations of ptychography.

Lensless implementations via coded illumination ▪Conventional ptychography: The first demonstration of modern ptychography [4], implementations with coherent X-ray [6,8], single-pixel implementation [92]. ▪Ptychographic tomography: X-ray ptychographic tomography [49–52], multi-slice modeling [93]. ▪Reflective ptychography: Visible light implementation [89], Bragg ptychography [53–58], EUV reflective ptychography [7,90,91]. ▪Near-field ptychography: The first demonstration for X-ray imaging with speckle illumination [48], translated speckle illumination with pixel super-resolution for on-chip microscopy [94], multi-slice modeling [95], pinhole and divergent beam illumination [96], mask-modulated implementation with multi-angle illumination [97–102].

Lensless implementations via coded detection ▪Aperture-plane modulation: Phase plate translation [103], object translation with random diffuser modulation [104], 1-D diffuser scanning [105], spatial light modulator modulation [106]. ▪Coded ptychography: Near-field diffuser translation for on-chip imaging [31], multi-spectral microscopy via wavelength multiplexing [21], disorder-engineered surface for high-throughput on-chip imaging [30], temporal correlation constraint for live-cell monitoring with high-spatiotemporal resolution [64], rotational ptychography using a modified Blu-ray drive [61], blood-coated sensor for ptychographic whole slide imaging [60,61], height-varying modulation [107]. ▪Optofluidic ptychography: Translation of objects via a coded microfluidic channel [66]. ▪Synthetic aperture ptychography: Coded sensor translation for synthetic aperture imaging [67].

Lens-based implementations via coded illumination ▪Single-shot ptychography: Multi-beam illumination [108–110], pinhole array [111–116]. ▪Conventional Fourier ptychography: The first demonstration of FPM [29], LED multiplexing [117–119], optimized sampling strategy [119–121], high-speed implementation with better initialization [122], high-resolution implementations with large incident angles [69,123–129], annular illumination [78,80,81], laser beam scanning [82–84], liquid crystal display for beam steering [130], multi-slice and tomography [16,17,65,71], portable implementations [131–134], parallel implementations [32,135], multiple objective lenses in a Scheimpflug arrangement [33]. ▪Reflective Fourier ptychography: LED ring implementation [72], aperture scanning [73–75], mirror-based implementations [76], laser beam scanning [136]. ▪Single-shot Fourier ptychography: Lens-array implementation [77], color-multiplexed implementation [78], deep learning-based illumination pattern designing [79]. ▪Translated speckle illumination for super-resolution imaging: Coherent imaging [137,138], far-field speckle scanning [137,139], extensions for incoherent fluorescence imaging [138,140,141]. ▪Ptychographic optical coherence tomography: Swept-source laser for volumetric imaging [142].

Lens-based implementations via coded detection ▪Selected area ptychography: Electron microscopy [143] and optical implementation [144]. ▪Camera-scanning Fourier ptychography: Camera translation for synthetic aperture imaging [88,145,146], X-ray Fourier ptychography [147], camera array for snapshot operation [148]. ▪Aperture-scanning Fourier ptychography: Mechanical scanning of a confined aperture [88,149,150] or a diffuser [87], digital scanning via a spatial light modulator [151–153], dual-wavelength implementation [149], correcting the spatially-varying pupil aberrations [154]. ▪Single-shot Fourier ptychography: Diffraction grating placed at the detection path [155,156]. ▪Diffuser modulation: Diffuser placed between the object and the objective lens [45,85], diffuser placed at the imaging plane [86,157].

Fig. 3.

Different ptychographic implementations are categorized into four groups based on their lensless / lens-based configuration and coded-illumination / coded-detection operations.

3.1. Lensless implementations via coded illumination

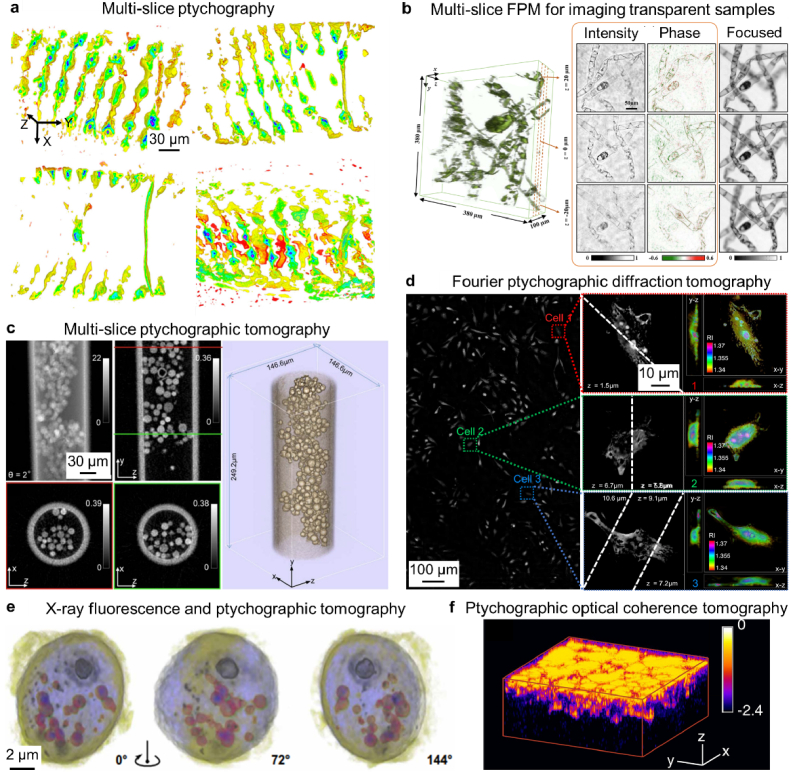
The scheme of conventional ptychography is reproduced in Fig. 3(a1). Its first demonstration attracted significant attention from the X-ray imaging community, as nanometer-scale resolution can be achieved using coherent X-ray sources [6,8]. By integrating the concept of conventional ptychography with computed tomography (CT), it is also possible to perform 3D imaging of thick samples using coherent X-ray sources [49–52]. As shown in Fig. 3(a2), a thick 3D object is rotated to different angles in the experiment. For each angle, a lateral x-y scan of the object produces one ptychographic reconstruction. With different orientation angles, one can obtain multiple ptychographic reconstructions and they can be used to recover the 3D volumetric information in a way similar to that of a CT scan. This ptycho-tomography scheme has demonstrated great success in imaging different specimens, from bone to silicon chips, with impressive 3D resolution at the nanometer-scale.

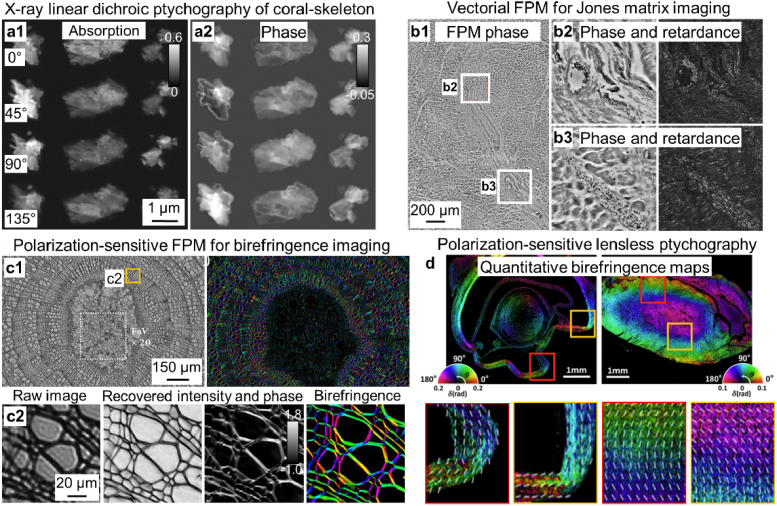
Conventional ptychography can also be implemented in a reflection configuration. In the visible light regime, the phase of the reflected light can be used to recover the surface topology of an object, and the sensitivity is comparable to that of white light interferometry [89]. In the X-ray regime, one prominent example is Bragg ptychography (Fig. 3(a3)) [54]. In this scheme, an X-ray beam is focused on a crystalline sample and the reflected light is acquired using a detector placed in the far field. This configuration can be used to image the strain of an epitaxial layer on a silicon-on-insulator device and map the 3D strain of semiconductors [55,56]. Likewise, the reflection configuration can also be implemented in the EUV regime, where the object surface structure can be recovered with high resolution [7,90,91].

Another notable development in this group is near-field ptychography demonstrated by Stockmar et al. in 2013 [48] (also referred to as Fresnel ptychography [34]). As shown in Fig. 3(a4), this scheme places the object closer to the detector. An extended structured beam also replaces the original spatially confined beam for object illumination. As a result, this scheme generally produces a larger field of view and requires fewer measurements for the phase retrieval process [48]. Additionally, since the entire image sensor is evenly illuminated, this scheme does not require conventional high dynamic range detection as in conventional ptychography. In the visible light regime, Zhang et al. demonstrated a field-portable near-field ptychography platform for high-resolution on-chip imaging [94]. As shown in Fig. 3(a5), this platform places a diffuser next to a laser diode to generate an extended structured illumination beam on the object. A low-cost galvo scanner then steers the structured beam to slightly tilted incident angles. These tilted incident angles result in lateral translations of the structured probe beam at the object plane. Thus, the object translation process in conventional ptychography can now be implemented by an efficient angle steering process in this platform. Additionally, this platform’s pixel super resolution model bypasses the resolution limit set by the detector pixel size [94].

Lastly, the implementation of conventional ptychography is not limited to using 2D image sensors. For example, Li et al. demonstrated the use of a single-pixel detector for data acquisition [92]. In this single-pixel implementation, a sequence of binary modulation patterns was projected on a 2D object and the DC component of the diffracted wavefront was acquired using a single-pixel detector. The recorded signals were then used to recover the object’s intensity and phase information. The use of a single-pixel detector enables ptychographic imaging at the THz frequency range and other regimes where 2D detector arrays would otherwise be expensive or unavailable.

3.2. Lensless implementations via coded detection

Instead of using an aperture to generate a spatially confined probe beam for object illumination, one can place the same confined aperture at the detection path to modulate the object’s diffracted wavefront, as shown in Fig. 3(b1). By translating the aperture [103] (or the object [104]) to different lateral positions for image acquisition, the object wavefront can be recovered at the aperture plane and then propagated back to the object plane. Other implementations of this aperture modulation scheme include 1D scanning of a diffuser at the aperture plane [105] and programmable aperture control using a spatial light modulator [106].

The left panel of Fig. 3(b2) reproduces the coded ptychography setup where a spatially extended coded surface is attached to the image sensor for wavefront modulation. In addition to the coded ptychography scheme discussed in Section 2.2, the coded surface layer can be scanned to different lateral positions, and the corresponding images can be acquired for ptychographic reconstruction. To this end, Jiang et al. demonstrated a near-field blind ptychographic modulation scheme to image different types of bio-specimens, including transparent and stained tissue sections, a thick biological sample, and in vitro cell cultures [31].

Instead of performing lateral translation in coded ptychography, one can also place the object on a spinning disc of a Blu-ray drive for image acquisition, as shown in the left panel of Fig. 3(b2). The laser beam can be obtained by coupling the light from the Blu-ray drive’s laser diode to an optical fiber. In this respect, Jiang et al. modified a Blu-ray drive for large-scale, high-resolution ptychographic imaging and demonstrated the device’s capacity for different biomedical applications, including live bacterial culture monitoring, high-throughput urinalysis, and blood-cell analysis [61]. By integrating the temporal correlation constraint for phase retrieval, a compact cell culture platform has also been developed for antimicrobial drug screening and quantitatively tracking bacterial growth from single cells to micro-colonies [64].

The coded ptychography approach can be combined with a wavelength multiplexing strategy for spectral imaging [18,20]. For example, Song et al. reported an angle-titled, wavelength-multiplexed coded ptychography setup for multispectral lensless on-chip imaging [21]. As shown in the right panel of Fig. 3(b2), the platform places a prism at the illumination path to disperse light waves at different wavelengths to different incident angles. As such, the coded surface profiles become uncorrelated at different wavelengths, breaking the ambiguities in state-mixed ptychographic reconstruction. More recently, a handheld ptychographic whole slide scanner has also been developed to perform high-throughput color imaging of tissue sections [60]. This platform can acquire gigapixel images with a 14 mm by 11 mm area in ∼70 seconds. The recovered phase can then be used to visualize the 3D height map of unstained bio-specimen such as thyroid smears obtained via fine needle aspiration.

Figure 3(b3) shows another notable development of the coded ptychography scheme, termed ‘optofluidic ptychography’ [66]. In this approach, a microfluidic channel is attached to the top surface of a coverslip, and a layer of microbeads coats the bottom surface of the same coverslip. The device utilizes microfluidic flow to deliver specimens across the channel, and the microbead layer modulates the object diffractive waves reaching the coverslip. By automatically tracking the object’s motion in the microfluidic channel, one can recover the high-resolution object images from the diffraction measurements. This ptychographic implementation complements the miniaturization provided by microfluidics and allows the integration of ptychography into various lab-on-a-chip devices [66].

Another important development in this group is the synthetic aperture ptychography approach shown in Fig. 3(b4) [67]. In this scheme, an object is illuminated with an extended planewave, and a coded image sensor is translated at the far field for data acquisition. The coded sensor translation process can effectively synthesize the object wavefront over a large area at the aperture plane. By propagating this wavefront back to the object plane, one can simultaneously widen the field of view in real space and expand the Fourier bandwidth in reciprocal space. Both the transmission and reflection configurations have been demonstrated for this approach [67]. A 20-mm aperture was synthesized using a 5-mm coded sensor, achieving a 4-fold gain in resolution and a 16-fold gain in the field of view. If the image sensor does not have the coded layer on top of it, the sensor translation process will simply produce one diffraction measurement with a large field of view. The loss of phase information in this single-intensity measurement prevents the recovery of the object information.

3.3. Lens-based implementations via coded illumination

Ptychographic imaging can be implemented with a lens-based microscope setup. The first example of this group of configurations is the single-shot ptychography scheme reported by Sidorenko and Cohen [111]. As shown in Fig. 3(c1), a pinhole array is used to illuminate the object from different incident angles and the object is placed close to the Fourier plane of the lens. As such, different incident angles from the pinhole array generate separated diffraction patterns at the detector plane in Fig. 3(c1). In addition to this pinhole-based scheme, one can also use multiple tilted beams for single-shot ptychography [108–110]. These different single-shot implementations essentially compromise the imaging field of view to achieve single-shot capabilities [37].

The second example of this group is the Fourier ptychography approach discussed in Section 2.3. The left panel of Fig. 3(c2) reproduces the original FPM scheme with a programmable LED matrix [29]. Different strategies can be applied to reduce the number of acquisitions, including LED multiplexing [117–119], phase initialization via differential phase contrast recovery [122], non-uniform or content-based sampling in the Fourier domain [120,121], rapid laser beam scanning [82–84], annular illumination [78,80,81], among others. By modeling the sample as multiple slices or with diffraction tomography, it is possible to recover the 3D volumetric information of the object [16,17,65,71]. To this end, Zuo et al. utilized both bright-field and darkfield images to recover high-resolution 3D objects in a Fourier ptychographic diffraction tomography platform [71].

Fourier ptychography can also be implemented in a reflection configuration. The right panel of Fig. 3(c2) shows a typical reflective FPM setup where an LED ring is mounted outside the objective lens for sample illumination with large incident angles [72,76]. It is also possible to perform aperture scanning to steer the illuminating beam on a reflective target [73–75]. Recently, Park et al. demonstrated a reflective Fourier ptychography platform using the 193-nm deep ultraviolet light.

Figure 3(c3) shows another notable implementation of Fourier ptychography, where the angle-varied plane waves are replaced by translated speckle patterns [137,138]. The speckle pattern can be viewed as an amalgamation of localized phase gradients, each approximating a plane wave with a different angle [37]. Therefore, translating the speckle on the object is equivalent to sequentially illuminating the object with different plane waves.

We note that Fourier ptychography has evolved from a simple microscopy tool to a general technique for different communities [37]. Table 1 covers only a small fraction of its implementations, and we direct interested readers to the recent review articles [36–38].

The concept of ptychography can also be integrated with optical coherence tomography for depth-resolving volumetric imaging. Figure 3(c4) shows the recent implementation of ptychographic optical coherent tomography by Du et al. [142]. This scheme uses a swept-source laser to project a spatially confined probe beam onto the object. For each wavelength of the light source, the system records a ptychographic dataset by translating the object to different positions. In this way, one can obtain many ptychographic reconstructions at different wavelengths. A Fourier transform along the wavelength axis then recovers the depth information of the object. This novel scheme provides a simple yet robust solution for 3D imaging and can be applied in various biomedical applications.

3.4. Lens-based implementations via coded detection

Coded illumination in FPM generally requires modeling of how the illumination beam interacts with the object. A thin sample assumption is often required to facilitate the point-wise multiplication between the structured beam and the object. To address this issue, one can perform coded detection in lens-based ptychographic implementations.

The first example of this group is the selected area ptychography approach shown in Fig. 3(d1). In this scheme, a microscope is used to relay the object to a magnified image at the image plane. A spatially confined aperture is placed at the image plane for performing coded detection, serving as an effective confined probe beam for the virtual object. Another lens is adopted to transform the virtual object image to reciprocal space for diffraction data acquisition. By translating the object to different lateral positions, the corresponding diffraction measurements can then be used to recover the virtual object at the image plane. This scheme was first demonstrated in an electron microscope [143]. The visible light implementation generated high-contrast quantitative phase images of cell cultures [144]. We also note that a commercial product of this scheme has been developed by Phasefocus (phasefocus.com).

The second example of this group is camera-scanning Fourier ptychography shown in Fig. 3(d2) [88,145]. In this scheme, the object is placed far away from the camera. As such, light propagation from the object to the camera aperture corresponds to the operation of a Fourier transform. By translating the entire camera to different lateral positions, one can acquire the corresponding images for synthetic aperture ptychographic reconstruction. The aperture size of the camera lens does not limit the final resolution. Instead, the resolution is determined by how far one can translate the camera. This scheme has been demonstrated in both visible light [88,145] and X-ray regimes [147]. More recently, Wang et al. reported an imaging platform built with a 16-camera array [148]. High-resolution synthetic aperture images can be recovered with a single snapshot acquisition.

The third example of this group is aperture-scanning Fourier ptychography shown in Fig. 3(d3). In this approach, the object is illuminated by a fixed extended beam, and an aperture is placed at the Fourier plane of the optical system. By translating the aperture to different lateral positions, it records a set of corresponding low-resolution object images that are synthesized in the Fourier domain for reconstruction. This approach can be implemented by performing mechanical scanning of a confined aperture [88,149,150] or a diffuser [87]. A spatial light modulator can also be used to perform rapid digital scanning of the aperture [151–153]. One limitation of this approach is that the NA of the first objective lens limits the resolution.

The fourth example of this group is the diffuser modulation scheme for lens-based ptychographic imaging. In the left panel of Fig. 3(d4), a diffuser is placed at the image plane for light modulation, and the detector is placed at a defocused position for diffraction pattern acquisition [86]. By translating the object (or the diffuser) to different positions, one can acquire multiple images for ptychographic reconstruction. Based on this scheme, Zhang et al. demonstrated a microscope add-on that can be attached to the camera port of a microscope for ptychographic imaging [157]. Instead of placing the diffuser at the image plane, one can also place it between the object and the objective lens. As shown in the right panel of Fig. 3(d4), the diffuser in this configuration serves as a thin scattering lens for light wave modulation. The otherwise inaccessible high-resolution object information can thus be modulated by this scattering lens and enters the optical system for detection. The detailed imaging model and related discussions of this scheme can be found in Section 2.4.

3.5. Key considerations for different hardware implementations

In Fig. 4, we show several hardware platforms from the current literature in ptychography. In Fig. 4(a), a commercially available system of selected area ptychography is built using a regular microscope. The operation of this platform relies on a high-resolution objective lens to generate a virtual object image at the image plane. This product also integrates fluorescence imaging capabilities for different biological applications.

Fig. 4.

Hardware platforms for different ptychographic implementations. (a) A commercial product based on selected area ptychography (by PhaseFocus). (b) A prototype platform of Fourier ptychography built with a programmable LED matrix [37]. (c) A Fourier ptychographic diffraction tomography platform [71]. (d) A microscope add-on for near-field ptychography [157]. Fourier ptychography setups built using a smartphone [134] (e), a Raspberry Pi system [131] (f), a cell phone lens [132] (g). (h) Lensless on-chip ptychography via rapid galvo mirror scanning [94]. (i) Parallel coded ptychography using an array of coded image sensors [30]. (j) Color-multiplexed ptychographic whole slide scanner [60]. (k) Optofluidic ptychography with a microfluidic chip for sample delivery [66]. (l) Rotational coded ptychography implemented using a blood-coated sensor and a Blu-ray player [61].

Figure 4(b) shows a prototype platform of FPM built with a programmable LED matrix [37]. The LED array is custom-made with a small 2.5 mm pitch. Figure 4(c) shows a Fourier ptychographic diffraction tomography platform, where the captured images are used to update the 3D Ewald sphere in the Fourier space [71]. Figure 4(d) shows a microscope add-on termed ‘ptycho-cam’ for lens-based near-field ptychography [157]. Figures 4(e)–4(g) show three compact FPM platforms built using a smartphone [134], a Raspberry-Pi system [131], and a cell phone lens [132].

Figures 4(h)–4(l) show the hardware platforms for lensless ptychographic implementations. In Fig. 4(h), a low-cost galvo scanner is used to project the translated speckle patterns on the object to implement lensless near-field ptychography [94]. Figure 4(i) shows the parallel coded ptychography platform for high-throughput optical imaging [30]. Using a disorder-engineered surface for coded detection (inset of Fig. 4(i)), this setup can resolve the 308 nm linewidth on the resolution target and achieve a NA of ∼0.8, which is the highest NA among different lensless ptychographic implementations. Figure 4(j) shows a prototype of a color-multiplexed ptychographic whole slide scanner for digital pathology applications [60]. This platform utilizes one coded image sensor for ptychographic acquisition and one bare image sensor to track the positions of the slide holder. Figure 4(k) shows a prototype platform of optofluidic ptychography, where a microfluidic chip is used for sample delivery [66]. Figure 4(l) shows an implementation of rotational coded ptychography using a modified Blu-ray drive [61]. The laser diode of the Blu-ray drive was used for sample illumination in this platform. The coded surface on the image sensor was made by smearing a drop of blood on the sensor’s coverglass (inset of Fig. 4(l)). The entire device can be placed within an incubator to monitor cell culture growth in a longitudinal study.

In the following, we summarize several key considerations for different hardware implementations in the visible light regime:

• 1)Resolution. The resolution r of a ptychography system is determined by both the illumination and detection NA: $r=\lambda /(N{A}_{detection}+N{A}_{illumination})$ , where λ denote the illumination wavelength.

  For lens-based FPM, resolution improvement can be achieved by using an objective lens and an LED array with large incident angles. Currently, the best resolution was achieved using a 40×, 0.95 NA objective lens with an illumination NA of ∼0.85. The corresponding synthetic NA is ∼1.9 [69], which is the best among all ptychographic implementations. For camera-scanning Fourier ptychography, the illumination NA is 0. The spanning angle of the lens aperture does not limit the detection NA. Instead, the detection NA is determined by the aperture size synthesized by the camera translation process.

  For lens-based selected area ptychography, the illumination NA is 0, and the NA of the employed objective lens determines the resolution. Similarly, lens-based ptychographic structured modulation has an illumination NA of 0. Its detection NA is determined by the summation of the scattering diffuser’s NA and the objective’s NA. As a result, placing the diffuser between the object and the objective lens increases the effective detection NA of the system.

  For conventional ptychography, the illumination NA is often very small. Therefore, the spanning angle of the detector (i.e., the detection NA) determines the achievable resolution, as shown in Fig. 2(a). It is also possible to use a focused beam or a structured illumination beam to increase the illumination NA [19,23,48].

  For lensless coded ptychography, the illumination NA is 0, and the resolution is determined by the detection NA of the coded image sensor. Currently, the demonstrated detection NA is ∼0.8, which is the highest among different lensless ptychographic implementations. It is also possible to further improve the resolution by increasing the illumination NA for aperture synthesizing, as seen in FPM.

  For lensless synthetic aperture ptychography, the illumination is 0. The spanning angle of the lens aperture does not limit the detection NA. Instead, the detection NA is determined by the aperture synthesized by the coded sensor translation process.

• 2)Field of view and imaging throughput. For lens-based implementations, the employed objective lens determines the maximum imaging field of view. For FPM, a typical 2×, 0.1 NA objective lens has a field of view of ∼1 cm in diameter. To synthesize a NA of 0.5, the acquisition time is on the order of 1 min, which corresponds to an imaging throughput comparable to or lower than that of a whole slide scanner [63]. However, the low-NA objective lens often contains severe aberrations at the edge of the field of view [12,13,70]. The aberrations of these regions need to be properly calibrated or measured prior to the imaging process. The reconstruction qualities in these regions are generally not as good as those captured using a regular high-NA objective lens.

  For selected area ptychography and high-resolution FPM implementation, a 40× objective lens can be used for image acquisition, and the field of view is ∼0.5 mm in diameter. To widen the field of view, one needs to move the sample stage to different spatial positions, stop the stage and then acquire the corresponding datasets. The image acquisition process cannot be operated at the full camera framerate and the overall imaging throughput is lower than that of a whole slide scanner.

  For conventional ptychography, the field of view is limited by the confined probe beam for each measurement. In the visible light regime, the size of the confined probe beam typically ranges from several hundred microns to a few millimeters in diameter. The object translation process can widen the field of view to cover arbitrarily large specimens. However, the scanning step size between adjacent acquisitions is often > 100 microns. As a result, one needs to stop the motion of the mechanical stage for data acquisition, and the camera cannot be operated at its full framerate. The resulting imaging throughput is much lower than that of a whole slide scanner.

  For lensless coded ptychography, the field of view is limited by the image sensor size for each measurement, which is ∼40 mm² in current demonstrations [30,60]. The translation operation of the coded sensor can naturally widen the field of view and image large-scale bio-specimens such as the entire 35-mm Petri dish [61,64]. The scanning step size is on the micron level, allowing continuous image acquisition without needing to stop the motion of the mechanical stage. For example, whole slide images of pathology sections (∼15 mm by 15 mm) can be acquired by stitching together 6 detector’s fields of view. The corresponding acquisition time is 1-2 mins with the camera operating at its full framerate [60], and the imaging throughput is comparable to or higher than that of a whole slide scanner. By using an array of coded sensors, the imaging throughput can even surpass the fastest whole slide scanner at a small fraction of the cost [30]. Compared to FPM, coded ptychography has no spatially varying aberration at different regions of the field of view. The quality of reconstruction is generally comparable to that obtained with a high-NA objective lens [30].

  For lensless synthetic aperture ptychography, the translation process of the coded sensor can widen the imaging field of view. The scanning step size between adjacent acquisitions is on the millimeter scale. The resulting imaging throughput is much lower than that of a whole slide scanner. However, compared to other lensless ptychographic implementations, the coded sensor translation process can also expand the Fourier bandpass to improve the resolution.

• 3)Light source. Ptychography is a coherent imaging modality that requires using coherent or partially coherent light sources for object illumination. We typically have two options for implementations in the visible light regime: LED and laser. If the detector is placed at the image plane of a lens-based system, the wavelength dispersion can be partially compensated by the lens system. Therefore, LED light sources can be used for object illumination. FPM is one example that uses a programmable LED array for angle-varied illumination. The key advantages of LED sources include less coherent artifacts and ease of operation for various applications. However, the major challenge of LED sources is the low optical flux that leads to long exposure time for image acquisition. Thus, the throughput of a typical FPM platform is currently limited by the relatively long exposure time required for darkfield image acquisition.

  If the detector is placed at the defocused plane or the far-field diffraction plane for image acquisition, a laser source is preferred for its monochromatic nature. Another key advantage of a laser source is its high optical flux. For example, a 10-mW fiber-coupled laser can be used for object illumination in coded ptychography. The exposure time is on the sub-millisecond level. This short exposure time can effectively freeze the object motion during the image acquisition process, allowing for continuous image acquisition at the full camera framerate. The demonstrated throughput of coded ptychography is only limited by the data transfer speed of USB cables. On the other hand, the major challenge of a laser source is the coherent artifacts caused by the multiple reflections from different surfaces. The captured images often contain interference patterns that are difficult to model and remove in the reconstruction process. To address this issue, one can reduce the spatial coherence of the laser by using a multi-mode fiber coupled to a mode scrambler.

• 4)Detector. For lens-based implementations, detectors with a high pixel count are often preferred. One cost-effective option is the Sony IMX 183, a 20-megapixel monochromatic camera with a 2.4-µm pixel size. Other options include the Sony IMX 455 (a 60-megapixel monochromatic camera with a 3.76-µm pixel size) and the Sony IMX 571 (a 26-megapixel monochromatic camera with a 3.76-µm pixel size).

  For lensless implementations, detectors with a small pixel size are often preferred. In coded ptychography setups, current choices include the Sony IMX 226 (a 12-megapixel monochromatic camera with a 1.85-µm pixel size) and the ON Semiconductor MT9J003 (a 10-megapixel monochromatic camera with a 1.67-µm pixel size). Cell phone image sensors with smaller pixel sizes can also be used for this lensless implementation.

• 5)Sample thickness. Coded-illumination schemes have certain requirements for the sample thickness [6]. For example, a typical FPM setup assumes the sample to be a thin 2D section. For a thick 3D object, changing the illumination angle would modify the object’s spectrum rather than just shifting it in the Fourier space [37]. Multi-slice and diffraction tomography can partially address this problem. In contrast, coded detection schemes have no requirement on the object thickness. The recovered object exit wavefront can be digitally propagated to any plane along the axial direction.
• 6)Sample focusing. Sample focusing is often needed to achieve the best performance in coded-illumination schemes. For example, samples need to be placed at the proper position of the probe beam in conventional ptychography. In FPM, a defocused pupil can be introduced in the reconstruction process for post-measurement refocusing (termed ‘digital refocusing’ in the original demonstration [29]). However, this solution requires knowledge of the focal position. Searching for the focal positions would be computationally expensive if, for example, the sample is tilted with respect to the objective lens. Furthermore, a recent paper has shown that the refocusing process in FPM cannot be disentangled from the iterative phase retrieval process [158].

  For coded-detection schemes, the sample-focusing process can be disentangled from the iterative phase retrieval process. With the recovered object exit wavefront, one can propagate it back to different axial positions and use a focus metric to locate the best focal position. Intensity-based focus metrics can be used for stained samples while phase-based focus metrics can be used for unstained samples [60].

4. Reconstruction approaches and algorithms

Table 2 summarizes different reconstruction approaches and algorithms for ptychographic imaging. We categorize them into three groups for discussion: Reconstruction algorithms (Section 4.1), approaches for system corrections and extensions (Section 4.2), and neural network-based approaches (Section 4.3).

Table 2. Reconstruction approaches and algorithms.

Phase retrieval algorithms ▪Ptychographic reconstructions: Wigner distribution deconvolution [25,159–165], non-linear optimization [9], ptychographic iterative engine [4,11,18,166,167], maximum-likelihood optimization [18,42,168], difference map [18,169], relaxed averaged alternating reflections [170], Douglas-Rachford algorithm [117,171], alternating direction methods of multipliers [172–176], stochastic proximal gradient descent [174,177,178], Gauss-Newton method with amplitude-based cost function [41], adaptive step size for gradient descent [179], Wirtinger gradient [99,180–185], convex relaxation [186], regularization via sparsity [146,187,188], noise modeling and denoising [181,185,189–191], low-rank recovery [192].

System corrections and other extensions ▪Correction for conventional ptychographic systems: Joint object-probe retrieval [9–11,31,193], state mixture decomposition [18,194–196], positional error correction [197–200], partial coherence correction [18,19,201,202], fly scan ptychography [203–207], optimization of probe overlapping area [208], angle calibration for the reflection configuration [209]. ▪Correction for Fourier ptychographic systems: LED intensity correction [210,211], joint sample-pupil recovery [12,13,81,150,152] LED alignment calibration and incident angle correction [37,41,117,211–218], correcting under- and over-exposed pixels [219], sample motion correction [220,221], stray light detection [222], vignetting effect [223], an open-source MATLAB application for correcting different system parameters [44], Miscalibration-tolerant multi-look FPM [224–226], pose correction for camera-scanning Fourier ptychography [227]. ▪Other extensions: Multiplexing algorithm [20,117,228], Multi-slice modeling [14–17,229–232], 3D diffraction tomography [49–52,65,71,93,233–236], super-resolution ptychography [23,96], autofocusing [60,237], parallel computation [238–240], GPU-based solver [239,241], correlation analysis for imaging through diffusing media [242–244], refraction index reconstruction to avoid phase wrapping [245], sub-pixel modeling [30,246], temporal correlation constraint for time-lapse experiment [64], high-dynamic range acquisition using a color camera [247], vectorial extensions for polarization-sensitive imaging [102,248–251].

Neural network and related approaches ▪Automatic differentiation (neural networks for modeling the forward imaging process): Recovering object and other system parameters for FPM [252–257] and for conventional ptychography [258–261]. ▪Optimizing the illumination strategy and other system parameters: Incorporating physical model for designing the coded illumination pattern [79,119,262–266], parameter refinement [267,268]. ▪Deep learning-based reconstruction: Image recovery from raw measurements via data-driven deep neural networks [114,148,225,269–275], physics-guided network [270,276]. ▪Post-reconstruction processing and analysis: Virtual staining and image translation [30,277–281], post-reconstruction cytometric analysis [60,264,265,282].

4.1. Reconstruction algorithms

The Wigner distribution deconvolution was first proposed to solve the ptychographic phase problem with densely sampled data [159]. As a non-iterative approach, it is remarkable that this approach can solve a nonlinear phase problem with linear computations (Fourier transforms). However, a key step in this approach involves filtering out the phase differences between different areas of the diffraction patterns. Therefore, it requires that the object be translated over positions separated by the desired resolution of the reconstruction, leading to a prohibitively large amount of data for any practical imaging application.

In 2004, an iterative phase retrieval algorithm, termed ‘ptychographic iterative engine (PIE)’, was adopted for ptychographic reconstruction. It can recover the complex-valued object from a significantly smaller dataset by iteratively imposing the support constraint and the Fourier magnitude constraint [4]. In 2009, Maiden et al. reported an extension of the original PIE algorithm, termed ‘extended PIE (ePIE)’, to remove the requirement for an accurate model of the illumination function [11]. Due to its simplicity and effectiveness, ePIE became a widely adopted algorithm for ptychographic reconstruction. The PIE algorithm was recently further extended to deliver a speed increase and handle difficult data sets where the original version would have failed [167].

In parallel with the development of the PIE family, Guizar-Sicairos and Fienup derived the analytical expressions for the gradient of a squared-error metric with respect to the object, illumination probe beam, and translations [9]. A nonlinear optimization process was then developed to jointly update the object and system parameters. Similarly, Thibault et al. used the difference map approach [283] to jointly recover the object and the illumination probe beam [10]. This group of authors also introduced the maximum-likelihood principle to formulate the optimization problem for ptychography [168]. More recently, Odstrcil et al. demonstrated a ptychographic reconstruction scheme using a least-squares maximum-likelihood approach that is based on an optimal decomposition of the exit wave update into several directions [42]. The optimal updating step size was also derived from the optimization model. For FPM, Bian et al. proposed an iterative optimization framework based on the Wirtinger flow algorithm with noise relaxation. This framework can be used for FPM reconstruction without requiring high signal-to-noise (SNR) measurements captured with a long exposure time [180].

To compare the performance of different algorithms, Wen et al. performed a wide-ranging survey that covered the alternating direction method, conjugate gradient, Newton-type optimization, set projection approaches, and the relaxed average alternating reflections method [172]. The convergence performances of common ptychographic algorithms are provided in the book chapter by Rodenburg and Maiden [34]. For FPM, Yeh et al. performed a comprehensive review of first- and second-order optimization approaches [41]. It was shown that the second-order Gauss-Newton method with amplitude-based cost function gave the best results in general.

For biomedical applications, the dataset’s quality is critical for a successful ptychographic reconstruction. If the dataset is free from artifacts and has adequate redundancy, the phase retrieval process is typically well-conditioned. Any iterative algorithm may be used – from alternating projection to other advanced nonlinear algorithms [37].

4.2. System corrections and extensions

The limitation of requiring exact knowledge of the probe function can be partially resolved by the joint object-probe recovery scheme [9–11,193]. In FPM, pupil aberration can be characterized using a calibration target [70]. It can also be jointly recovered in the ptychographic reconstruction process like that in conventional ptychography [12]. However, unlike conventional ptychography, the spatially varying property of pupil aberration needs to be considered in FPM. To this end, Song et al. reported a full-field recovery scheme that models the spatially varying pupil with only a dozen parameters [13]. In coded ptychography, the transmission profile of the coded layer can be jointly recovered with the object from a calibration experiment [31]. However, it has been shown that the joint object-probe recovery scheme (i.e., blind ptychography) would fail if the object contains slow-varying phase features [30]. This is due to the intrinsic ambiguity introduced by the slow-varying phase gradient that cannot be effectively encoded in the intensity measurements (the phase transfer function is close to 0 [284]). To properly recover the coded layer, a blood smear can be utilized as a suitable calibration object due to its rich spatial feature and the absence of slow-varying phase features.

To address the issues caused by limited light source coherence and system stability, Thibault et al. demonstrated a general approach to model diffractive imaging systems with low-rank mixed states [18]. Mode decomposition of the probe beam and object can then be performed to address the limited coherence of the light source and the system stability issue. By modeling the object profiles at different wavelengths as different coherent states, Batey et al. demonstrated the reconstruction of a color object under color multiplexed illumination [20]. Similarly, the color multiplexing scheme can be implemented in FPM [118] and coded ptychography [60] for high-throughput digital pathology applications. To model the time-varying illumination probe beam during the data acquisition process, Odstrcil et al. reported the strategy of orthogonal probe relaxation in the reconstruction process [195]. Other notable developments in this direction include the fly-scan scheme by introducing multiple mutually incoherent modes into the illumination probe [205].

To correct the positional errors of conventional ptychography, the positional shifts of the object can be jointly updated with the object and/or the probe beam in the iterative phase retrieval process [9,42,197–200]. To improve the reconstruction quality, Dierolf et al. introduced a non-rectangular scanning route to avoid difficulties with the raster grid ambiguity inherent in ptychographic reconstruction [285]. In FPM, if an LED matrix is used for sample illumination, its sampling positions in the Fourier domain can be precisely calibrated based on the brightfield-to-darkfield transition zone of the captured raw images [37]. If the LED array does not have a well-defined pitch, the illumination angles can be iteratively refined in the reconstruction process [41,211–215], similar to the positional correction process in conventional ptychography. Recently, Bianco et al. demonstrated a multi-look approach for miscalibration-tolerant Fourier ptychographic imaging [224–226]. This approach generates and combines multiple reconstructions of the same set of observables where phase artifacts are largely uncorrelated and, thus, automatically suppress each other.

Ptychographic implementations with coded illumination assume the sample to be a 2D thin section. However, extending the imaging model to handle 3D objects is possible. One notable development is the multi-slice modeling for conventional ptychography [14]. In this approach, the 3D object is represented by a series of thin slices separated by a certain distance. With this strategy, Godden et al. demonstrated the recovery of 34 sections of semi-transparent bio-specimens [15]. Li et al. further combined this multi-slice modeling with sample rotation to image thick specimens with an isotropic 3D resolution [93]. The multi-slice modeling can also be adopted in FPM for imaging 3D specimens. To this end, Tian et al. [16] and Li et al. [17] have demonstrated the imaging of multiple slides of transparent objects using a conventional microscope with an LED array.

Another notable extension of ptychography is the integration of diffraction tomography with FPM for 3D imaging [65]. This approach models the object as 3D scattering potentials in the Fourier domain. Each captured FPM image is used to update a spherical cap region of the scattering potential. As such, one can obtain the real-space 3D image from the recovered 3D scattering potential in the Fourier domain. To this end, Zuo et al. demonstrated impressive 3D high-resolution recovery of different bio-specimens [71].

4.3. Neural networks and the related approaches

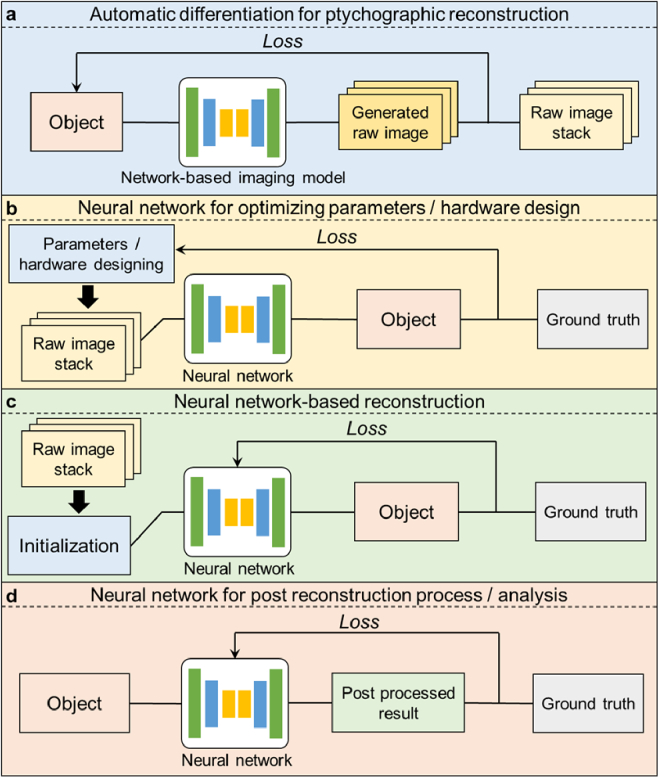
The developments of neural networks and related approaches can be categorized into four groups shown in Fig. 5. The first group of developments in Fig. 5(a) is to model the ptychographic forward imaging process using a neural network. This strategy is also termed ‘automatic differentiation’ [252–255,258–261]. In this approach, the derivatives can be efficiently evaluated and the optimization process can be performed via the network training process [286]. Unlike data-driven approaches, this process requires no training data for the recovery process. For FPM, Jiang et al. utilized this framework to model the complex object as the learnable weights of a convolutional layer and minimize the loss function using different built-in optimizers of a machine learning library, TensorFlow [252]. Additional parameters like pupil function and LED positions can also be included in this framework for joint refinement [253–255]. Likewise, Nashed et al. reported the automatic differentiation scheme for conventional ptychography [258]. Kandel et al. reported the automatic differentiation scheme for near-field ptychography and multi-angle Bragg ptychography [260].

Fig. 5.

Neural networks and related approaches for ptychographic reconstruction. (a) A neural network is used to model the imaging formation process of ptychography (also termed automatic differentiation). The training process recovers the object and other system parameters. (b) The physical model is incorporated into the design of the network. (c) The network takes the raw measurements and outputs reconstructions. (d) The network takes the ptychographic reconstructions and outputs virtual-stained images or images with other improvements.

The second group focuses on incorporating the physical model into the design of the network [79,119,262–264]. The training of the network can jointly optimize the physical parameters used in the imaging model, such as the illumination pattern of the LED array in FPM. To this end, Horstmeyer et al. demonstrated the use of a neural network to jointly optimize the LED array illumination to highlight important sample features for the classification task [262]. Kellman et al. demonstrated a framework to create interpretable context-specific illumination patterns for optimized FPM reconstructions [119].

The third group focuses on inferring the high-resolution intensity and/or the phase images from low-resolution FPM measurements [269–274]. For example, Nguyen et al. and Zhang et al. demonstrated the use of deep neural networks to produce high-resolution images from FPM raw measurements [269,274]. More recently, Xue et al. demonstrated the use of a Bayesian network to output both the high-resolution phase images and the uncertainty maps that quantifies the uncertainty of the predictions [272].

Lastly, the recovered images from ptychographic imaging setups can be further improved by neural networks. For example, virtual brightfield and fluorescence staining can be performed on FPM-recovered images without paired training data [277]. Coherent artifacts of FPM reconstructions can also be reduced in this unsupervised image-to-image translation process. Similarly, the recovered images from conventional ptychography and coded ptychography can also be virtually stained using data-driven deep neural networks [30,278].

5. Biomedical applications

5.1. Large field of view, high-resolution microscopy for digital pathology

The utilization of light microscopy in pathology and histology remains the gold standard for diagnosing a large number of diseases, including almost all types of cancers. The development of whole slide imaging systems can replace conventional light microscopes for quantitative and accelerated histopathological analyses. A key milestone was accomplished in 2017 when the Philips’ whole slide scanner was approved for primary diagnostic use in the United States [287]. The rapid development of artificial intelligence (AI) in medical diagnostics promises further growth of this field in the coming decades [288].

Compared to conventional whole slide imaging systems, ptychographic imaging setups have several advantages for digital pathology. For example, FPM and coded ptychography can acquire high-resolution, large-field-of-view images of histology sections rapidly. They also allow post-acquisition autofocusing and thus avoid the focusing issue that plagues conventional whole slide scanners. Another key advantage of ptychographic implementations is the recovery of the phase images that reveal the quantitative morphology features of the tissue sections [30,144,289]. For example, one can plot the height map of cytology smears to virtualize the 3D topographic profiles. The phase imaging capability also provides a label-free strategy to inspect unstained specimens. This is useful for rapid on-site evaluation of samples obtained from fine needle aspiration, where real-time pathology guidance is highly desired.

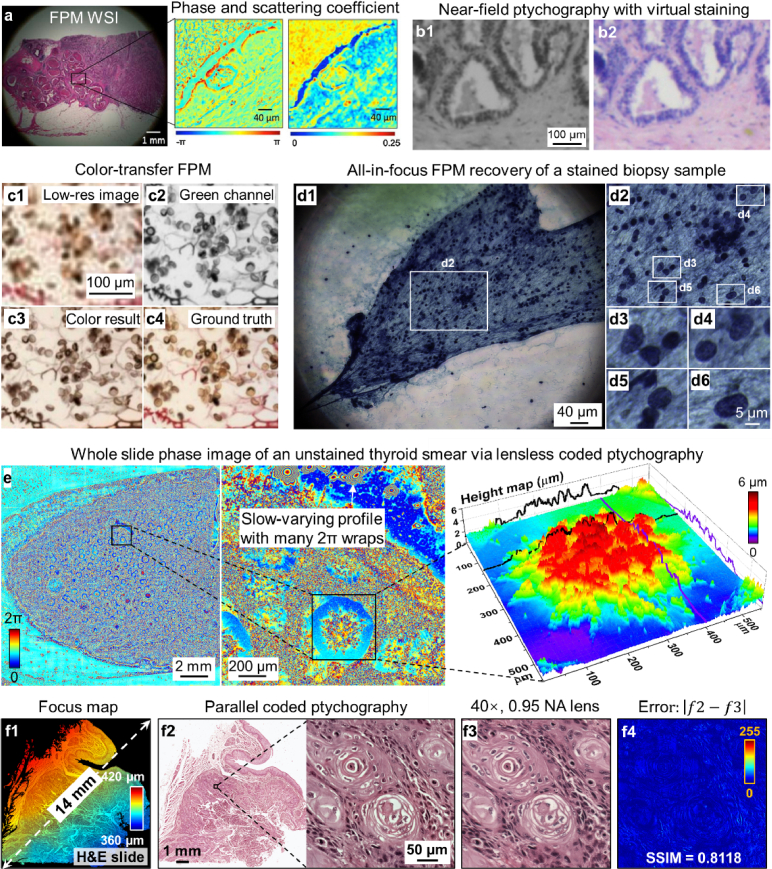
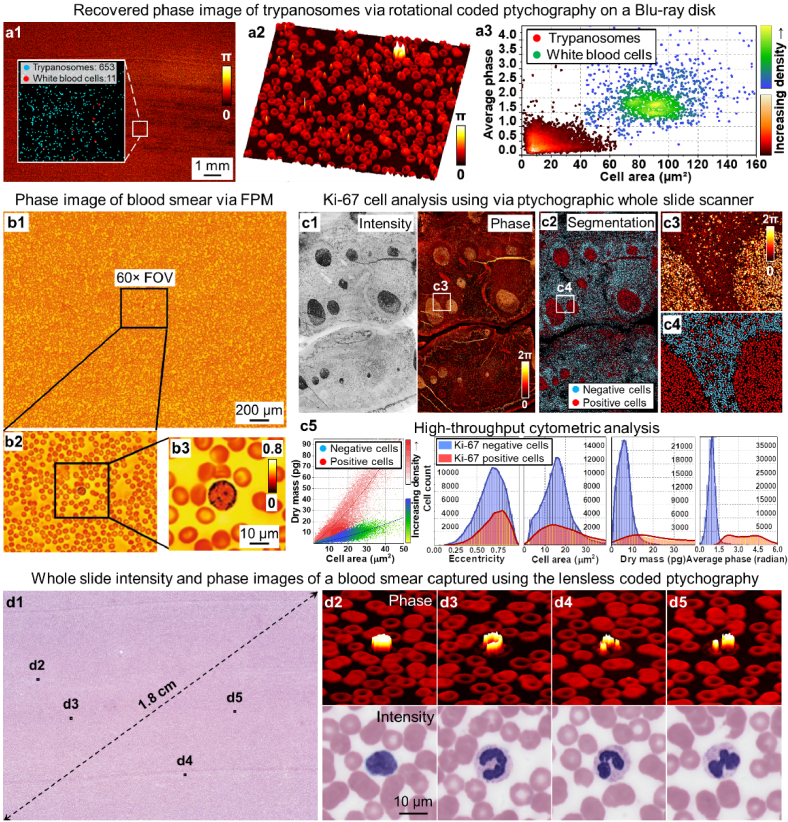
Figure 6(a) shows a recovered FPM image of a histology slide [290]. The field of view is the same as that of a 2× objective lens while the synthetic NA is similar to that of a 20× objective lens. The recovered phase can be used to obtain the local scattering and reduced scattering coefficients of the specimen, as shown in the zoomed-in views of Fig. 6(a).

Fig. 6.

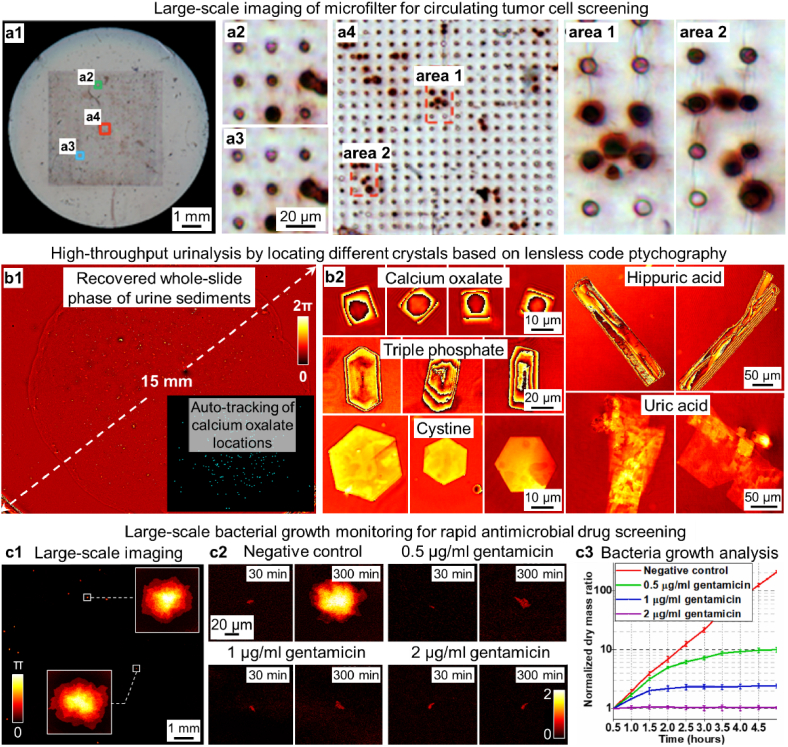
Digital pathology applications via different ptychographic implementations. (a) The recovered whole slide image by FPM [290]. (b) The recovered monochromatic image via near-field ptychography and the virtually stained image [278]. (c) Virtual staining of a recovered FPM image based on the color transfer strategy [279]. (d) All-in-focus recovered image of a biopsy sample based on the digital refocusing capability of FPM [292]. (e) Whole slide phase image recovered by the lensless ptychographic whole slide scanner [60]. (f) Rapid whole slide imaging using the parallel coded ptychography platform [30]. (f1) The focus map generated by maximizing a focus metric post-measurement. (f2) The recovered whole slide image by coded ptychography. (f3) The ground truth image captured using a regular light microscope. (f4) The difference between (f2) and (f3).

An important aspect of digital pathology is to acquire color information of the stained histology sections. One can sequentially illuminate the slides with red, green, and blue light to obtain the color information as in Fig. 6(a). It is also possible to apply image-to-image translation to convert the recovered monochromatic FPM image to the style of regular incoherent microscopy. To this end, Wang et al. adopted a cycle generative adversarial network (cycleGAN) [291] to perform unsupervised virtual staining of FPM images [277]. The coherent artifacts of FPM recovery can also be reduced in this image-to-image translation process [281]. Similarly, one can also perform virtual staining to the recovered images obtained from other ptychographic implementations, such as coded ptychography [30] and near-field ptychography [278]. Figure 6(b1) shows the recovered monochromatic image using a near-field ptychography platform. Figure 6(b2) shows the virtual stained image using the cycleGAN [278]. Figure 6(c) demonstrates another strategy of virtual staining. Instead of using a neural network for image translation, Gao et al. reported a color transfer strategy to virtually stain an FPM image [279]. In this approach, the color texture information was extracted from a captured color image using the low-NA lens in an FPM platform. The texture information was then applied to the high-resolution FPM monochromatic recovery for virtual staining.

An important advantage of FPM is its capability of performing post-acquisition refocusing. Figure 6(d) shows a recovered image of a thick thyroid biopsy smear based on the digital refocusing capability of FPM. The digitally refocused patches of the sample were synthesized into one all-in-focus image in this demonstration [292].

Figures 6(e) and 6(f) demonstrate the applications of coded ptychography for high-throughput digital pathology. Figure 6(e) shows the recovered phase image of an unstained thyroid smear sample [60]. The zoomed-in height map reveals the 3D topographic structure of this thick cytology smear sample. Figure 6(f) shows the recovered whole slide image of a stained histology slide. The focus map in Fig. 6(f1) was generated by maximizing a focus metric post-measurement. Figure 6(f2) shows the recovered gigapixel whole slide image and the zoomed-in view of the slide. Figure 6(f3) shows the ground truth captured using a regular light microscope [30]. The difference between the coded ptychography and the ground truth is shown in Fig. 6(f4).

5.2. High-throughput cytometric analysis and screening

With the recovered gigapixel images of the bio-specimens, ptychography can also find applications in cytometric analysis and screening, where different parameters of the cells can be precisely measured and analyzed. Figure 7(a) shows a recovered gigapixel phase image of a blood smear sample using the rotational coded ptychography platform [61]. The recovered image was used to automatically segment the white blood cells and Trypanosoma brucei parasites. The inset of Fig. 7(a1) shows the locations of white blood cells and parasites, marked with red and blue dots, respectively. Figure 7(a2) shows a zoomed-in view of the gigapixel whole slide image. Figure 7(a3) shows a scatter plot of the cell area versus the average phase for the white blood cells and the parasites. The two different clusters in this figure indicate the two types of cells. Similarly, Fig. 7(b1) shows the recovered phase image of a blood smear using a high-NA FPM system [128]. The recovered phase image can be used to identify the white blood cells as shown in the zoomed-in views of Fig. 7(b2) and 7(b3).

Fig. 7.

High-throughput cytometric analysis via different ptychographic implementations. (a) The recovered whole slide phase image of trypanosomes in a blood smear. The image was acquired using rotational coded ptychography with the specimen mounted on the spinning disk of a Blu-ray drive [61]. (b) The high-resolution recovered phase image of a blood smear using FPM [128]. (c) Ki-67 cell analysis based on the recovered images using the lensless ptychographic whole slide scanner [60]. (d) Whole slide intensity and phase images of a blood smear captured using coded ptychography [30]. The zoomed-in views highlight the phase and intensity images of the white blood cells, which can be used for performing high-throughput differential white blood cell counting.

In Fig. 7(c), Jiang et al. performed a cytometric analysis of Ki-67 cells using the lensless ptychographic whole slide scanner [60]. The Ki-67 biomarker is a proliferation-associated nuclear protein for labeling dividing cells. The fraction of Ki-67 positive tumor cells is often correlated with the clinical course of cancer. Figure 7(c1) shows the recovered whole slide intensity and phase images of a tissue section labeled with the Ki-67 biomarkers. Figure 7(c2) shows the segmentation results using a deep neural network. Figures 7(c3) and 7(c4) show the zoomed-in views of Fig. 7(c1) and 7(c2). Figure 7(c5) shows the measurement of dry mass and cell area of the segmented Ki-67 positive and negative cells. The histogram analysis of the cell eccentricity, cell area, dry mass, and average phase for both the positive and negative cells are also provided in this figure. Figure 7(d) shows the application of the high-throughput parallel coded ptychography platform for white blood cell counting [30]. Figure 7(d1) shows the recovered whole slide image of a blood smear. Figures 7(d2)-7(d5) show the zoomed-in views of the white blood cells.

Ptychographic imaging platforms can also be used for high-throughput screening of biological cells, drugs, and other objects. Figure 8(a1) shows the full field-of-view image of the entire microfilter obtained by an FPM platform [293]. The zoomed-in views of Fig. 8(a2)-8(a4) show the circulating tumor cells captured by the microfilter array. Circulating tumor cells are recognized as a candidate biomarker with strong prognostic and predictive potentials in metastatic disease. High-throughput screening of these cells allows for early cancer detection and treatment effectiveness monitoring.

Fig. 8.

High-throughput screening via different ptychographic implementations. (a) Large-scale color imaging of the entire microfilter for circulating tumor cell screening [293]. (b) High-throughput urinalysis based on the rotational coded ptychography platform built with a Blu-ray drive [61]. (c) Large-scale bacterial growth monitoring for rapid antimicrobial drug screening [64]. By imposing the temporal correlation constraint in coded ptychography, the imaging platform can achieve a centimeter-scale field of view, a half-pitch resolution of 488 nm, and a temporal resolution of 15-second intervals [64].

Figure 8(b) shows the application of the rotational coded ptychography platform for high-throughput urine sediment examination [61]. Inspection of urine sediments is currently performed using a regular light microscope, offering a direct indication of the state of the renal and genitourinary systems. However, the process is labor-intensive and time-consuming, and the imaging area is only limited to a small field of view of the urine sediment slide. As a result, the result is imprecise with wide variability. Lensless coded ptychography can address these issues by imaging the entire urine sediment slide at high speeds. Figure 8(b1) shows the recovered phase image of the entire sediment slide. The inset of Fig. 8(b1) shows the locations of calcium oxalate crystals tracked by an automated screening algorithm (crystal locations are labeled by the blue dots). A large number of calcium oxalate crystals often implies kidney diseases. Figure 8(b2) shows the recovered phase images of different crystals on the urine sediment slide. The slow-varying phase profiles of these crystals are challenging to obtain using other common lensless techniques, such as lensless in-line holography [294,295], transport-of-intensity equation approach [284], and blind ptychography [173].

Figure 8(c) shows the application of an integrated coded ptychographic sensor for microbial monitoring and detection [64]. Performing rapid microbial detection can shorten the time required by antimicrobial susceptibility tests. These susceptibility arrays determine whether an antibiotic drug is effective in stopping the growth of a specific bacterial strain. If an effective drug can be found in the early stages of the clinical course, proper administration and adherence can avert the development of antibiotic resistance. Current optical detection methods often rely on the overall optical property of microbial cultures. They cannot resolve individual growth events at the single-cell level. As a result, one may need to wait until the bacteria grow to confluence before the results can be interpreted. Coded ptychography can perform lensless cytometric analysis of microbial cultures over a large scale and with high spatiotemporal resolution. In a time-lapse experiment, the microbial cultures often change little in-between adjacent acquisitions. Therefore, the recovered image from the last time point can be used as the initial guess for the object estimate in the current time point. By imposing this temporal correlation constraint in coded ptychography, Jiang et al. demonstrated an integrated imaging platform for achieving a centimeter-scale field of view, a half-pitch resolution of 488 nm, and a temporal resolution of 15-second intervals [64]. Figure 8(c1) shows the recovered large-scale phase image of bacterial cultures on an agar plate. Figure 8(c2) shows the growth of bacterial colonies under different treatment conditions. Figure 8(c3) shows bacterial cells’ average dry mass measurements over time. The minimum inhibitory concentration value was determined to be ∼1 µg/mL from the growth curves. The combination of high phase sensitivity, high spatiotemporal resolution, and large field of view of this platform can facilitate various cell screening and cytometric analysis applications.

5.3. Quantitative cell and tissue imaging in 2D and 3D

Ptychography’s capability of generating quantitative phase contrast can find applications when imaging various biological samples. Figure 9(a) shows the recovered phase images of live cell cultures using a high-speed FPM platform, where initial phase estimates were obtained from the differential phase contrast approach [122]. Similarly, Fig. 9(b) shows the recovered phase images of HeLa cell culture captured using an annular illumination FPM platform [80]. At each time point, four images were captured under four annular illumination angles in this platform. These measurements were then used to recover the phase images of the cell culture. Cell mitotic and apoptotic events can be acquired at a frame rate of 25 Hz [80]. Figure 9(c) shows the recovered phase of live A549 cells using a lens-based selected-area ptychography system [144]. The high-contrast, artifact-free, and focus-free images distinguish the dividing cells from non-dividing cells. In contrast with the images obtained from lens-based implementations, Fig. 9(d) shows the recovered phase image of U87MG cell culture using coded ptychography [31]. This lensless imaging approach offers a centimeter-scale large field of view and sub-cellular resolution for cell culture monitoring.

Fig. 9.

2D live-cell imaging via different ptychographic implementations. (a) The recovered phase images of U2OS cell culture using the in-vitro FPM system [122], where the phase is initialized using the differential-phase-contrast approach. (b) Video-rate phase imaging of HeLa cells using annular-illumination FPM [80], where the slow-varying phase information is effectively converted into intensity variations in the captured images. (c) Phase imaging and cell state identification of A549 cells using a lens-based selected-area ptychography system [144]. The white arrows show a proportion of brighter dividing cells, and the intense lines within the cells mark chromosome alignment prior to cytokinesis. (d) The recovered large-scale phase image of U87MG cell culture obtained by a lensless coded ptychography platform [31].

Ptychography can also find applications in 3D imaging of different biological samples. Figure 10(a) shows the recovered 3D volume of a Spirogyra sample using multi-slice ptychography [15]. This approach models the sample as multiple slices separated by a certain distance in the forward imaging process. The difference between the estimated signal and the actual measurement is back-propagated to different object layers to update the corresponding slices. Thus, this approach does not require rotation of the specimen with respect to the illumination source. The same multi-slice modeling can also be implemented in FPM. Figure 10(b) shows the recovered intensity and phase images of a 3D Spirogyra algae sample using multi-slice FPM [16].

Fig. 10.

Ptychography for 3D microscopy. (a) The recovered 3D volume of a Spirogyra sample via multi-slice ptychography [15]. (b) The recovered intensity and phase images of a 3D Spirogyra algae sample based on multi-slice FPM [16]. (c) Phase projection and 3D rendering of a 3D sample using multi-slice ptychographic tomography [93]. (d) Wide-field-of-view and high-resolution 3D imaging of a large population of HeLa cells via Fourier ptychographic diffraction tomography [71], where 3D refractive index of the cell culture is recovered from the FPM intensity measurements. (e) Different projected views of X-ray fluorescence and ptychographic tomography reconstructions [52], where pyrenoid locates near the top region and acidocalcisomes near the bottom region. (f) 3D rendering of a reconstructed mouse brain using ptychographic optical coherence tomography [142]. The colorscale represents the logarithm of the normalized reflectivity.

In Fig. 10(c), Li et al. demonstrated a ptychographic tomography approach by combining multi-slice modeling with rotation-based tomographic reconstruction [93]. The recovered images in Fig. 10(c) show a glass tube filled with glass beads. This platform can achieve isotropic 3D resolution with a small number of rotational measurements. Multi-slice modeling in this approach improves reconstructions by accounting for propagation effects inside the 3D sample. In Fig. 10(d), Zuo et al. demonstrated the use of Fourier ptychographic diffraction tomography for 3D imaging. In this approach, each captured image is used to update a spherical cap of the Ewald sphere in the 3D Fourier space [65]. Figure 10(d) shows the recovered high-resolution 3D refractive index distribution of live HeLa cell culture [71]. In Fig. 10(e), Deng et al. performed correlative 3D imaging through a combination of simultaneous cryogenic X-ray ptychographic tomography and X-ray fluorescence microscopy [52]. High-quality 3D maps of the unlabeled cellular structure and elemental distributions within the cell can be clearly visualized from the recovered projections in Fig. 10(e). Lastly, Fig. 10(f) shows the recovered 3D volume of a mouse brain captured with ptychographic optical coherent tomography [142]. The color scale in this figure represents the logarithm of the normalized reflectivity of the brain tissue sample.

5.4. Polarization-sensitive imaging

Polarization techniques can be combined with ptychography to measure the vectorial properties of light or the vectorial transformations imposed on light by bio-specimens. Biomedical polarimetry can provide extra vectorial information through methods compatible with existing optical systems, such as microscopes and endoscopes. In particular, it provides an additional intrinsic contrast mechanism for imaging anisotropic bio-specimen in a label-free manner. In the past decade, it has become a rapidly developing field for biomedical imaging [297].

In Fig. 11(a), Lo et al. performed polarization-sensitive detection using an X-ray ptychography platform [296]. The ptychographic datasets were collected at four different linear polarization states in Fig. 11(a). The corresponding ptychographic reconstructions were then used to generate the polarization-dependent imaging contrast of anisotropic crystalline materials.

Fig. 11.

Polarization-sensitive imaging using different ptychographic implementations. (a) The recovered absorption and phase images of coral-skeleton particles via X-ray linear dichroic ptychography [296]. (b) The large-area phase and retardance reconstruction of a thin cardiac tissue section using vectorial FPM [250]. (c) The recovered intensity, phase, and birefringence map of a Tilia stem using polarization-sensitive FPM [251]. (d) Recovered birefringence maps of mouse eye and heart tissue using polarization-sensitive lensless ptychography [102].

In the visible light regime, Ferrand et al. reported the formalism of vectorial ptychography for polarization-sensitive imaging [248]. To retrieve the full anisotropic properties of the sample, the authors proposed a measurement scheme using linearly polarized probes and polarization analyzers. With this vectorial ptychography framework, Ferrand et al. reported the first experimental demonstration of recovering the Jones matrix of an anisotropic specimen [249]. The same vectorial imaging concept can also be adapted for FPM. Figure 11(b) shows the phase and retardance reconstructions of a thin cardiac tissue section using vectorial FPM [250]. In this approach, a generator polarizer is placed between the object and the LED array, and an analyzer polarizer is placed at the detection path. With four generator-analyzer configurations, the authors then recovered the Jones matrix of the object. Similarly, it is possible to use a polarization-sensitive camera (the polarizer array is directly placed on top of the pixels) to acquire four different polarization states simultaneously [251]. With this strategy, Fig. 11(c) shows large-scale, high-resolution intensity, phase, and birefringence maps of a Tilia stem. The same strategy has also been implemented in a lensless ptychography platform [102] built based on a mask-modulated configuration with angle-varied illumination [97,100]. Figure 11(d) shows the recovered birefringence maps of mouse eye (the left panel) and heart tissue (the right panel) using this platform. The overlaid short white line indicates the mean orientation of the optical axis evaluated over a small region.

6. Summary and outlook

This review provides an overview of the ptychography technique, with a focus on its optical implementations. In particular, we categorize different implementations into four groups based on their lensless / lens-based configurations and coded-illumination / coded-detection operations. We anticipate that high-throughput optical ptychography, currently in its early stage, will continue to grow and expand in its applications. We identified the following directions for further potential developments.

• 1)Metasurface for coded ptychography. The optimal choice of the coded pattern in coded ptychography remains an exciting research topic. Current implementations using disorder-engineered surfaces [21,30,31,64,66] and blood-coated surfaces [60,61] have achieved some degree of success. However, we envision that better metasurface designs can further improve the resolution [298]. For example, one can tailor the angular scattering profile with subwavelength scatters to achieve the best resolution performance. Spectral responses can also be integrated with the metasurface design for ptychographic spectroscopy.
• 2)Synthetic aperture coded ptychography. Currently, the best detection NA of coded ptychography was achieved without performing aperture synthesizing. It is possible to implement angle-varied illumination for coded ptychography to further improve the resolution in a similar way to FPM. We note that angle-varied illumination has been demonstrated in lensless near-field ptychographic setups [97–100]. However, the achieved resolution is relatively low due to the limited temporal coherence of the light sources. To push the resolution limit in coded ptychography, we can steer an extended laser beam for angle-varied illumination in high speed [83].
• 3)Lensless coded ptychographic tomography. The concept of diffraction tomography can be integrated into coded ptychography for 3D high-resolution imaging in a similar way to Fourier ptychographic diffraction tomography [65,71]. By illuminating the object from different incident angles, one can acquire a sequence of diffraction measurements. Each measurement corresponds to a spherical cap of the Ewald sphere in the Fourier space. Stitching all spherical caps can recover the 3D scattering potential of the object. Efforts in this direction are ongoing.
• 4)Synthetic aperture ptychography for EUV and X-ray imaging. In a typical X-ray or EUV ptychography setup, the object is translated to different lateral positions for image acquisition. The resolution is largely limited by the spanning angle of the detector. Synthetic aperture ptychography can bypass this limit by translating a coded sensor at the far field (Fig. 3(b4)). The resolution is no longer limited by the spanning angle of the detector. Instead, it is determined by how far one translates the coded sensor. As a coded detection scheme, it also waives the thin sample requirement in conventional ptychography. For EUV imaging, the penetration depth is often limited to the surface layer. Therefore, we envision the implementation of synthetic aperture ptychography in a reflection modality. On the other hand, X-ray imaging has a long penetration depth, and we envision a transmission-mode implementation.
• 5)A better light source to improve the imaging throughput. The captured raw images of lensless and lens-based implementations often suffer from coherent artifacts of laser sources, such as the interference patterns caused by light reflection from multiple surfaces. LED sources can partially address this problem. However, the limited temporal coherence of LED often leads to a degraded resolution in lensless implementations. In addition, the low optical flux of LED further limits the achievable imaging throughput, especially when darkfield images need to be acquired. An ideal source for optical ptychography can be a laser with high temporal coherence but relatively low spatial coherence. This source can be achieved using a multiple-mode fiber coupled to a mode scrambler. With an optimal coherent light source, we envision a significant reduction in the number of acquisitions in a lensless implementation.
• 6)Chemical imaging in the near-infrared and infrared regimes. Near-infrared and infrared wavelengths contain vibration modes of many molecular bonds. Implementing lens-based or lensless ptychography in these regimes can lead to important applications in label-free chemical imaging. One challenge would be the relatively large pixel size for imaging in this regime. Sub-pixel modeling [30,246] may be an important consideration in recovering high-resolution images.
• 7)Imaging model and phase retrieval algorithm. Ptychographic imaging setups can be a testbed for different phase retrieval algorithms. The large amount of data acquired for biomedical applications also necessitates the development of memory-efficient optimization algorithms. Recovery guarantee is another important research topic for applied mathematicians. The design of the coded pattern in coded ptychography may provide extra degrees of freedom to tailor the measurement matrix with recovery guarantee [299,300]. For lensless implementations, the pixel down-sampling process needs to be properly modeled in the image formation process. For example, we may need to consider the spatial and angular response of the pixels for high-resolution imaging [30]. The crosstalk between different pixels may also need to be modeled in the image formation process, especially for image sensors with sub-micron pixel sizes.
• 8)Education. An FPM experiment can provide hands-on microcontroller programming, image acquisition, and processing experiences. It also serves as an exemplary demonstration of several important concepts in Fourier optics, including the optical transfer function, NA, Ewald sphere, pupil aberration, and free-space propagation, among others. On the other hand, the DIY nature of the coded ptychography platform allows it to be implemented with minimum resources. As we have demonstrated, one can modify a Blu-ray drive to develop a rotational coded ptychography platform [61]. A high-throughput ptychographic whole slide scanner can be built by modifying a low-cost 3-axis manual stage (XYZ 3-Axis Manual Linear Stage, Amazon, ∼ $\mathrm{\$}$ 120) [60]. Configuring these setups can serve as excellent projects for lab courses that teach circuits and electronics, optics, biomedical instrumentation, and robotics. It can also be part of a capstone project for secondary, post-secondary, and graduate students.

Funding

UConn10.13039/100007710 Spark grant; National Science Foundation10.13039/100000001 (2012140).

Disclosures

The authors declare no competing financial interests.

Data availability

No data were generated or analyzed in the presented research.