Abstract
Diffuse correlation spectroscopy (DCS) is a promising noninvasive technique for monitoring cerebral blood flow and measuring cortex functional activation tasks. Taking multiple parallel measurements has been shown to increase sensitivity, but is not easily scalable with discrete optical detectors. Here we show that with a large 500 × 500 SPAD array and an advanced FPGA design, we achieve an SNR gain of almost 500 over single-pixel mDCS performance. The system can also be reconfigured to sacrifice SNR to decrease correlation bin width, with 400 ns resolution being demonstrated over 8000 pixels.
1. Introduction
The ability to measure deep-tissue biological events in a noninvasive and precise manner is critical for many clinical applications. Various technologies such as diffuse optical spectroscopy [1], diffuse optical tomography [2], and near-infrared spectroscopy [3–5] have been used to quantify the optical properties of deep tissue; however, the produced images primarily reflect the sample’s static, or slowly evolving, properties. For the measurement of faster dynamic events (i.e., changes in blood flow), speckle-based modalities are among the most widely used [6].
When laser light illuminates a scattering medium (i.e., tissue), it will produce a random interference effect, or speckle. Movement in the object can result in a measurable speckle decorrelation [7]. Quantifying and analyzing these effects provides information about the movement. Techniques such as laser speckle contrast imaging [8] and speckle visibility spectroscopy [9,10] generally consider the dynamics of the speckle ensemble as a whole; sampling for much longer than the average speckle decorrelation time. In comparison, temporal sampling methods such as diffuse correlation spectroscopy (DCS) can reconstruct the temporal dynamics of the speckle field at time scales determined by the speckle decorrelation time. DCS has become a popular technique for deep tissue measurement, aiding successful analysis of the brain [11,12], breast [13,14], and skin [15].
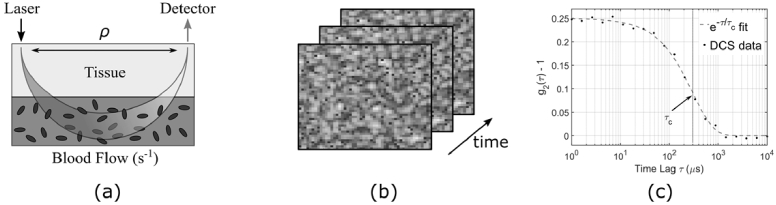
As shown in Fig. 1, the concept behind DCS is relatively simple. Highly coherent light is coupled into a scattering medium, and the speckle pattern coupling out is collected using a photon-counting detector. Photon statistics are integrated over a desired time interval, and used to calculate a temporal autocorrelation curve. The average speckle decorrelation time τc is then estimated by fitting the measured data to a model reflecting the expected behavior of the scatterers, e.g., Brownian motion (diffusive) or random flow motion (ballistic). Variations to τc can then be directly attributed to changes in tissue dynamics (e.g., blood flow).
Fig. 1.
Conceptual illustration of mDCS measurement. Coherent light is coupled into a scattering medium (a), and collected by one or more single-photon detectors. The photon statistics of the speckle pattern (b) are stored for the duration of an integration time, and analyzed to produce a temporal correlation curve (c). After fitting the data to an expected behavioral model, the average correlation time τc is estimated. Changes to τc can be directly attributed to, for example, a change in blood flow. Note that (b) represents a speckle pattern from a multipixel array, whereas DCS systems have conventionally utilized one detector.
After entering the medium the scattered light is most likely to follow a banana-shaped distribution [16], with the average penetration depth falling between one-third and one-half of the source-detector separation ρ. Increasing ρ allows for deeper tissue illumination; however, absorption, scattering, and radial spread causes fewer diffuse photons to reach the detector. Consequently, deep-tissue DCS measurements utilizing a single detector suffer from a very low signal-to-noise ratio (SNR) at longer ρ. The clear need for increased sensitivity in DCS measurements has resulted in a variety of approaches including interferometric approaches [17–19], acousto-optic modulation [20], time-domain methods [21–23], speckle contrast integral methods [24,25], and infrared region DCS [26,27].
The light diffusing out of a sample can easily contain millions of individual speckles (modes), each almost completely uncorrelated. Assuming that shot noise dominates, measuring multiple speckles with one detector is not advantageous. However, simultaneously measuring light from N independent speckles results in a proportional increase to signal, a increase to the noise, and a increase to the SNR. Thus, one immediate solution is to sample multiple speckles in parallel, with multiple detectors [7].
Initially, multichannel DCS (mDCS) systems were limited in size and utilized multiple discrete detectors. As each detector is fiber-coupled to the sample this quickly limits the upper bound for convenient experimental setups. Examples of early mDCS systems include those with four channels [21,28,29], eight channels [30], twenty five channels [31], and twenty eight channels [32]. With the fairly recent introduction of CMOS SPAD arrays, however, a new paradigm has become available. In 2021 two experiments demonstrated a factor of ∼32 increase to SNR, versus a single detector system, with a commercially available 1024 pixel SPAD array [33,34]. With such a high number of independent measurements at a fast sampling rate (∼333 kfps), the advantage of CMOS SPAD arrays in mDCS is apparent.
In this work we extend this approach to our large-format 250,000 pixel SPAD camera, SwissSPAD3 (SS3) [35]. Coupled with an advanced FPGA-based acquisition design we are able to demonstrate a factor of ∼470 increase in SNR versus a single-detector DCS system, and over an order of magnitude increase over state-of-the-art mDCS systems. Such a high number of parallel channels allows for more sensitive measurements over shorter time scales, and opens up new possibilities for resolving faster physiological dynamics in deep tissue applications.
2. Implementation
Our experimental setup for DCS is shown in Fig. 2. A long coherence length 785 nm CW laser (Thorlabs DBR785P) is coupled into single-mode fiber (SMF) and onto a scattering medium; a commonly used liquid phantom comprised of water and 3.5% fat whole milk. At this wavelength, the photon detection probability of the sensor is approximately 15% [35]. The diffuse light is captured by a large core (Thorlabs FP1500U RT, 1500 µm, NA = 0.50) multi-mode fiber (MMF). One tip of the fiber is immersed in the liquid phantom, the other is placed a distance z away from the surface of the SS3 sensor, and the resulting speckle pattern is imaged onto the SS3 camera. The total optical power incident on the detector is approximately 1 nW. During the measurement, the SS3 captures a series of exposures, and binary photon detection information is streamed to one of two OpalKelly 7360 FPGAs. Each FPGA processes half of the array (250 pixels × 500 pixels); accumulating detection history and calculating g2 correlations.
Fig. 2.
Setup for multi-pixel DCS experiment. A continuous wave 785 nm laser is fiber coupled into a water / milk liquid phantom. Scattered photons are collected by a multimode, large core (1500 µm, NA = 0.5) fiber placed a separation distance ρ away, and imaged onto SwissSPAD3. Binary detection data for each half of the array is sent to one of two XEM7360 FPGAs where intermediate data analysis is performed, with results continuously streamed to a PC over two USB 3.0 interfaces. Final calculations and curve plotting is done with MATLAB on a PC.
To perform a DCS measurement, the speckle field characteristics are evaluated by calculating a temporal autocorrelation curve, given by the following equation:
| (1) |
Here is the number of detected photons during each exposure, is the exposure time lag, and the angled brackets denote the averaging operator, which is applied over one integration period. This formula is calculated on a per-pixel basis; to achieve an increased SNR gain, M discrete pixels are averaged together:
| (2) |
where i is the pixel index, which for the full sensor has a maximum value of 250,000.
When configured with the DCS FPGA firmware, SwissSPAD3’s maximum full-sensor frame rate is approximately 92.2 kfps, or a minimum exposure time (TEX) of 10.81 µs. Data is collected and calculated over the duration of an integration time (TINT), which has an upper limit of 216 exposures; however, multiple integration times can be concatenated in post processing to extend this limit. Due to resource constraints, correlations for 16 bins (including τ = 0) can be calculated by an FPGA during each TINT. Bins can be assigned by the user to either be successive, or spaced by an equal amount of τLAG exposures. If τLAG ≠ 0, single ‘valid’ exposures are spaced between τLAG ‘dummy’ exposures, which are not considered in the g2 calculation. Additionally, each FPGA can be configured to have a varying range of τLAG values. This flexibility allows for the ability to simultaneously evaluate a wide range of time constants, which may evolve over different time scales. After the duration of an integration time the FPGA passes the unaveraged numerator and denominator of Eq. (1) to the PC for every pixel. The final division operation, averaging of various ensemble sizes, and curve plotting is performed in MATLAB.
Performing the correlation analysis on the FPGA greatly reduces the required data bandwidth to the PC. For example, if a full sensor’s binary data were to be directly transferred at a 100 kfps frame rate, the required data rate is approximately 3 GB/s. Although this approaches SS3’s capabilities when a PCI express interface is used, the subsequent data processing to calculate a g2 DCS curve is substantial, taking several minutes on a typical PC. In comparison, performing the g2 calculation on FPGA and during acquisition greatly compresses the data transfer requirement to 140 MB/s at an integration time of 50 ms. This is well within the capabilities of USB 3.0, and allows for a continuously updating DCS curve that can be viewed and analyzed with MATLAB in a semi real-time fashion. For example, at a 50 ms integration time an intensity image, DCS curve, speckle width estimation, and DCS decorrelation fit can be calculated and refreshed at approximately 17 Hz.
3. Experimental results
3.1. Calibration of speckle size
To achieve the optimal SNR-to-pixel advantage, it is necessary that each individual pixel of the SwissSPAD3 measure an independent speckle process. Due to the large sensor format, it is not feasible to align only one speckle to each pixel. Thus, we ensure that the average speckle’s area is small enough such that it is not sampled by multiple pixels, and that the probability of one pixel measuring multiple speckles (possibly out of phase) is significantly reduced. For SS3, the pixels are arranged in a square grid with 16.38 µm pitch (267 µm2 area), and each pixel’s active area is roughly circular with an area of 28.27 µm2 (10.6% fill factor) and a diameter of dp = 6 µm. The average diameter of the speckles output from the MMF fiber can be approximated [36] by the equation
where d is the average speckle diameter, the wavelength of the light (785 nm), z the distance from the fiber end to the SPAD camera (see Fig. 2), and D the fiber core diameter (1500 µm).
To validate this estimation, the 2D spatial autocorrelation function (ACF) of the speckle field’s intensity was measured using the setup of Fig. 2, with the liquid phantom replaced by a diffusive phantom (INO Biomimic optical phantom, µa = 0.1 cm-1, µs’ = 13.4 cm-1) in a transmission geometry, and the MMF was placed at various z distances away from the camera’s surface. The ACF was fit to a Gaussian distribution, and the 1/e width used to estimate the average speckle diameter. Because the fill factor, or ratio of optically active to inactive area of each pixel is low (∼10%), it is possible to have speckles that are larger than one pixel’s active area in diameter, but do not overlap with the adjacent pixel’s active area. Thus, only z distances corresponding to speckle diameters significantly larger than the pixel pitch (16.38 µm) were used in this evaluation, to determine the optimal z where the average speckle diameter is comparable to the active area. As shown in Fig. 3, a z distance of 94 ± 1 mm results in a speckle field with average speckle diameter of three times the pixel pitch, or 49.0 ± 4.9 µm. This analysis was performed for speckle diameters between 3.0 ≤ d ≤ 8.0 pixels, and the measured ACF was in agreement with the expected linear relationship. Thus, to avoid oversampling the speckle field, these calibrated distances were used to set d approximately equal to the diameter of each pixel’s active area (dp = 6 µm), corresponding to z = 11.5 mm.
Fig. 3.
Example speckle field (left) and measured autocorrelation function (right) of 100 pixels × 100 pixels when the distance between the optical fiber and the SPAD camera is set to z = 94 ± 1 mm. The left figure illustrates the recorded photon detections when integrated for approximately one second at a frame rate of approximately 92.2 kfps. A slice of the 2D ACF (blue dots) was compared to a Gaussian fit (red line) to estimate the average speckle diameter of 3.0 ± 0.1 pixels. “Hot pixels” have been removed in post processing.
3.2. Maximum SNR gain with 250,000 pixels
Under the assumption of speckle ergodicity, multi-speckle DCS with M pixels has been shown to provide an M1/2 increase to the signal-to-noise ratio (SNR). Demonstrated for up to 1024 pixels [33,34], we now extend this to 250,000 pixels with SwissSPAD3. A DCS measurement was performed using the liquid phantom setup of Fig. 2. The milk-to-water ratio was 1:5 (µa = 0.033 cm-1, µs’ = 4.1 cm-1), the fiber separation distance was ρ = 11 mm, and the fiber to sensor distance z = 11.5 mm. The optical properties were measuring using a time-domain (TD) setup, and derived by fitting the TD curves. The SS3 was temperature controlled with a Peltier element to 27 °C, the exposure time TEX = 10.81 µs, the integration time TINT = 50 ms, and average detections per exposure <n > = 0.1 ± 0.01. To cover the majority of the DCS curve the SS3 was configured for two τLAG values, τLAG = 0 exposures and τLAG = 5 exposures. Hot pixels were excluded from the DCS measurements in post-processing, and identified as those with a dark count rate exceeding 20 cps.
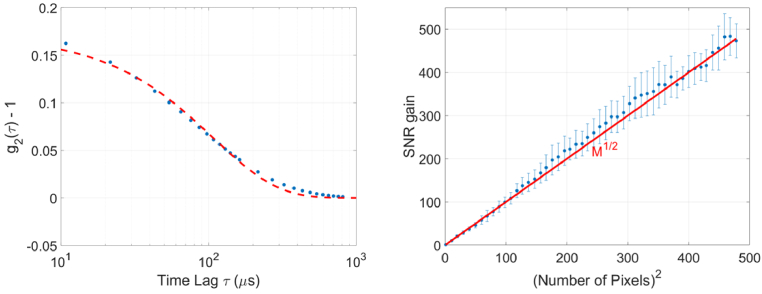
The g2(τ) function was calculated over 160 integration periods; both for each pixel individually, and for ensemble averages ḡ2(τ)|M of various pixel areas. Shown in Fig. 4 (left) is the ensemble average ḡ2(τ)|M = 2.5e5 for all 500 pixels × 500 pixels, excluding the hot pixels. The source detector distance was ρ = 11 mm, short compared to typical DCS measurements, to capture the majority of the DCS curve. The measured data (blue dots) is shown alongside a g2(τ) ≈ 1 + βe(-τ/τc) model (dashed red line, τc = 107.7 µs), where β is the coherence factor [37]. The single-exponential fit is a simplified functional form of an otherwise multi-parameter function, however, in our liquid phantom (with Brownian motion scattering and at small time lags), it has been shown to be a valid simplification [33,37–39]. For the single-pixel case the standard deviation of the measured g2 for the first correlation bin, or STD(g2(τ = 10.81 µs)) = 0.123, the amplitude of which is in agreement with the expected noise model of [38,40]. When the entire sensor is averaged, STD(ḡ2(τ = 10.81 µs)|M = 2.5e5) = 2.6 × 10−4.
Fig. 4.
DCS ensemble average of the entire 500 pixel × 500 pixel area of the SwissSPAD3 (left). The water-to-milk ratio of the liquid phantom was 1:5. The measured ḡ2(τ)|M = 2.5e5 (blue dots) has been fit (red dashed line) to the expected diffusive scattering model of e(-τ/τc), with τc = 107.7 µs. The SNR increases with pixel area (right), and averaging over the entire 500 pixels × 500 pixels (excluding hot pixels and edge effects) allows for unprecedented accuracy, with STD(ḡ2(τ)|M = 2.5e5) = 2.6 × 10−4, and an SNR gain of 473.0 over a single pixel.
Shown in Fig. 4 (right) is the measured SNR gain versus ensemble average size. We calculated the mean and standard deviation of g2 for the first bin at increasing averaging sizes. The SNR for each ensemble average size was calculated by the equation SNR(ḡ2(τ)) = mean(ḡ2(τ)-1) / std(ḡ2(τ)). The SNR gain is then calculated by comparing the averaged SNR to that of the single-pixel case. For or each point, a square beginning in the lower left-hand corner of the array is considered. The dashed red line denotes the expected M1/2 increase with pixel size, and blue dots indicate the SNR. Error bars indicate one standard deviation of error when a random selection of start pixels are chosen as the single-pixel comparison. Deviation from the expected SNR gain of M1/2 is primarily due to variation in the intensity profile across the array; areas with slightly less photons will have a larger standard deviation. After approximately 20,000 pixels are removed in post processing due to edge effects or hot pixels, the average SNR gain is a factor of 473.0 over a single pixel.
3.3. Trading SNR gain for measurement flexibility
Although using all 250,000 pixels greatly increases the SNR, the full-sensor speed of SS3 prohibits the accurate measurement of processes with shorter characteristic decorrelation times. For example, the deep tissue DCS experiment [32] performed on the adult human head (ρ ≈ 27 mm) measured processes with decorrelation timescales of 1 µs ≤ τc ≤ 10 µs. Because the full-sensor minimum exposure time of SS3 is TEX = 10.81µs, much of the relevant information would be lost for these types of measurements.
SwissSPAD3 has been designed to give the user a large amount of flexibility when choosing their desired mode of operation. The full sensor minimum exposure time (TEX = 10.81 µs) is almost entirely due to the time required to transfer 250,000 pixel’s information to the two FPGAs through 250 output pins. It is possible, however, to reduce the number of pixel rows read out per exposure. Because each pixel is reset upon readout, this option allows for the measurement of smaller τ bins, and the characterization of faster decorrelation times. When operated in this fashion, however, fewer speckles are measured simultaneously, and the maximum SNR gain is lowered accordingly. Shown in Table 1 are examples of tested exposure time settings for SS3.
Table 1. Tested configuration settings for SwissSPAD3. By reducing the number of rows read out from the sensor the minimum TEX (and thus τ bin size) can also be reduced. Such modes result in a reduction in the expected maximum SNR gain, but allow for the characterization of processes with shorter decorrelation times. The SNR gain factor is measured relative to the SNR of a single pixel.
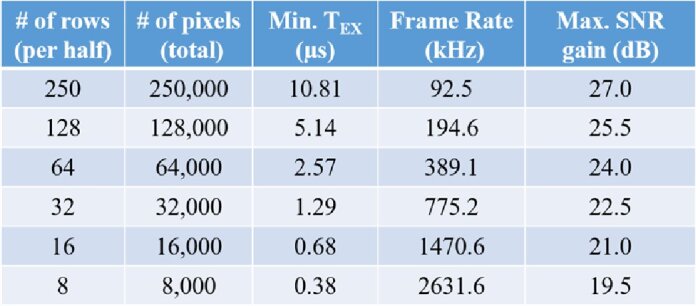
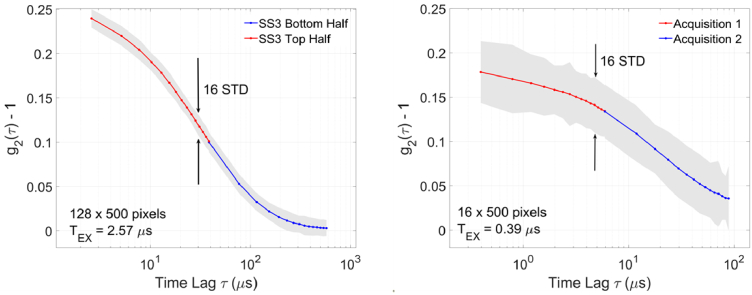
Shown in Fig. 5 are two DCS curves taken with the liquid phantom setup of Fig. 2, when smaller sections of SS3 are considered. In the left plot, 1/4th of the sensor (128 rows) are sampled at TEX = 2.57 µs. In the right plot, 1/32nd of the sensor (16 rows) is sampled at TEX = 0.395 µs. The source-to-fiber distance ρ was increased from 11.0 mm to 33.0 mm (left) and 22.0 mm (right) and the milk concentration 1:4 (left, µa = 0.033 cm-1, µs’ = 6.3 cm-1) and 1:3 (right, µa = 0.033 cm-1, µs’ = 8.1 cm-1). Increasing ρ and the milk concentration shortens the expected decorrelation time τc. The average number of detections per exposure is <n > ≈ 0.01 for both plots, an order of magnitude less than in the previous section.
Fig. 5.
DCS measurements using reduced areas of SwissSPAD3. By lowering the number of measured pixels, the exposure time (and shortest measurable time lag τ) can be reduced. This allows for the measurement of processes with faster decorrelation times, at the cost of a reduced SNR. In the left plot (1:4 milk-to-water, µa = 0.033 cm-1, µs’ = 6.3 cm-1, ρ = 33.0 mm), the two SS3 halves were configured to measure different temporal correlation ranges simultaneously (red = top, blue = bottom). This allowed for a wider range of measurement per acquisition, but lowers the number of effective pixels (and maximum SNR gain). In the right plot (1:3 milk-to-water, µa = 0.033 cm-1, µs’ = 8.1 cm-1, ρ = 22.0 mm), all measured pixels were used to capture two distinct temporal ranges, = 0 (red) and = 14 (blue) bins. Each acquisition was separated by approximately 1 ms. The solid line corresponds to the mean value of g2(τ) over 160 integration periods, and the shade corresponds to 16 standard deviations.
In the left plot each SS3 half was configured independently; each measuring a different set of correlation delays. Although the base time bin size for both halves is 2.57 µs, the bottom half measures 16 temporally consecutive bins (τLAG = 0), while the bottom half measured 16 bins separated by 35.98 µs (τLAG = 14). This increases the temporal range of a single acquisition, covering more of the DCS curve. Note that although 64,000 pixels are used, the two halves are configured to measure different correlation delays simultaneously. Thus, the effective ensemble average size is 32000 pixels, and the maximum SNR gain ∼178 over the single pixel case.
In the right plot two separate data acquisitions were performed, each separated by approximately 1 ms. As before, two τLAG values (0 and 14) were chosen to encompass more of the DCS curve, and the base exposure time is 390 ns. Because all 16 rows are sampling the same speckle field the number of effective pixels is 8000, and maximum expected SNR gain is ∼90. Both plots represent 160 acquisitions of TINT = 50 ms.
For the 128 pixels × 500 pixels measurement, the single-pixel error was STD[g2(τ)] = 0.23, and for the ensemble average STD(ḡ2(τ)|M = 3.2e4) = 1.4 × 10−3. The SNR gain is a factor of 169.3 over the single-pixel case; in agreement with the expected gain of approximately 179. The measured data fits an e(-τ/τc) model with a decorrelation lifetime of τc = 44.28 µs ± 2.3 µs.
For the 16 pixels × 500 pixels measurement, the single-pixel error was STD[g2(τ)] = 0.39, and for the ensemble average STD(ḡ2(τ)|M = 8e3) = 4.4 × 10−3. The SNR gain of 87.2 is in agreement with the expected gain of approximately 90. The measured data fits an e(-τ/τc) model with a decorrelation lifetime of τc = 19.34 µs ± 1.8 µs.
In theory, the shortest possible exposure time is TEX ≈ 45 ns; in which only one row of pixels per half-sensor is read out. Averaging 1000 pixels would be nearly equivalent to the 32 pixel × 32 pixel sensor used in [33,34], however, the shorter exposure time would facilitate the measurement of τc in the hundreds of nanoseconds. In this regime, however, the performance of the SPADs needs to be considered. Often persisting hundreds of nanoseconds after an initial detection, afterpulsing could contribute significantly to the g2 calculation, especially in photon-starved deep-tissue measurements. Thus, we have chosen to limit the DCS measurements in this work to TEX ≥ 390 ns, or 8 rows per half of the sensor. Nevertheless, the ability to average 8,000 pixels at a time-bin resolution of 390 ns opens up an entirely new range of measurement over previously reported systems.
3.4. Fast characterization of evolving media
In single detector DCS systems, it can be necessary to integrate for a long period of time to achieve an acceptable signal-to-noise ratio. This can eliminate the possibility of precisely characterizing processes which persist only for short times. SS3 can overcome this limitation owing to the extremely high number of independent parallel measurements. For example, a single detector with a 100 ns dead time requires 25 ms to perform 250,000 measurements. The 1024 pixel systems at TEX = 3 µs require 0.732 ms, and SwissSPAD3 requires a single 10.81 µs exposure.
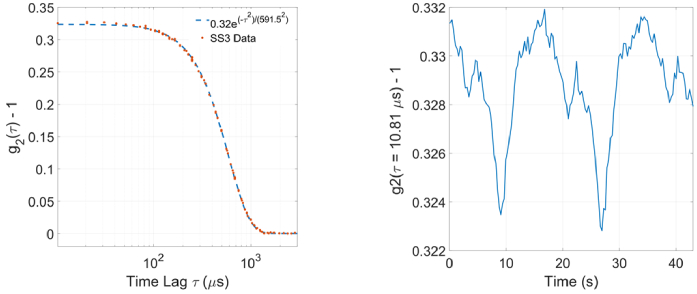
A rotating diffuser is a convenient method to reduce temporal correlations, and has been used in previous multi-pixel DCS experiments. We replaced the liquid phantom of Fig. 2 with a calibrated diffuser (INO Biomimic optical phantom, µa = 0.1 cm-1, µs’ = 13.4 cm-1), rotating at a velocity of 20 °/s in a transmission geometry. The two fibers were placed off-axis from the diffuser’s center to reduce the velocity gradient across the surface of the fiber. The SS3 was set to integrate for TINT = 50 ms and the τLAG spacing was varied several times. As shown in Fig. 6 (left), the resulting DCS curve follows a ballistic scattering model ( ), instead of the diffusive model ( ) of the liquid phantom.
Fig. 6.
Measured DCS curve (left) of a calibrated diffuser (INO Biomimic optical phantom, µa = 0.1 cm-1, µs’ = 13.4 cm-1), when rotating at 20 °/s in a transmission geometry. Beta variation (∼3%) due to slight optical nonuniformity across the surface of the diffuser is resolved in a single 50 ms integration time.
Shown in Fig. 6 (right) is (g2(τ = 10.81 µs) – 1) as the diffuser is rotated, or the value of the first bin in Fig. 6 (left). The period of the pattern is consistent with the rotation speed of 20 °/s. Although the variation in β across the diffuser is very small, it can be resolved within a single 50 ms integration time. These results highlight the speed at which SwissSPAD3 can make a sensitive DCS measurement.
4. Future work and conclusions
In this work we have presented a massively parallel multi-pixel DCS implementation with SwissSPAD3, a photon-counting camera. Whereas smaller systems may be unable to make rapid and accurate DCS measurements in photon-starved deep tissue situations, SS3 has more than two orders of magnitude more pixels than previously reported SPAD arrays [33,34]. Additionally, the flexibility to easily configure a desired pixel count to balance SNR gain versus correlation bin width makes this system attractive for many clinical measurements over a large range of time scales.
The custom hardware and firmware was designed to make the camera entirely reconfigurable, whereas one can trade readout speed for spatial resolution. It is also possible to transfer correlation data from each half-sensor’s FPGA to the other and to designate simple regions of interest within each sensor half. This allows the user to calculate a multiple simultaneous DCS curves, or even cross correlations (instead of the current auto correlation) between pixels in various areas, measuring and comparing the dynamics of different processes simultaneously. Such capabilities, along with the unprecedentedly large format of 500 500 pixels, represent a considerable improvement over existing photon-counting cameras, which can result in immediate uses in quantum photon correlation measurements and quantum imaging.
Additionally, this work was performed entirely without the use of the SS3’s temporal gate channel. It has been shown that by gating DCS events to sub-nanosecond resolution, layer-specific information within a sample can be separated and distinguished [22,23]. With a minimum gate width of 1 ns and temporal resolution of 18 ps, such time-domain diffuse correlation spectroscopy (TD-DCS) experiments could be performed using our SPAD camera to validate experimental works towards facilitating targeted and precise deep tissue measurements [41].
Finally, the work presented in this manuscript was primarily intended as an introduction to the possibilities of our large format SPAD sensors in DCS experiments. Although the measurements here were performed on a liquid phantom mimicking human tissue, active collaborations have produced promising results in biological in-vivo measurements. Preliminary experiments have measured changes in blood flow within both the arm and brain at source-detector separations (SDS) of up to 4 cm. These initial experiments were performed with only half an array (125,000 pixels). With the addition of the other half, greater SDS are expected to be possible, allowing for faster and more precise deep tissue measurements.
Acknowledgements
This research was supported by funding from Meta Platforms Inc. M.W., P.M., A.U. and A.A. acknowledge partial support by the Swiss National Science Foundation (grants 20QT21_187716 Qu3D “Quantum 3D Imaging at high speed and high resolution” and 200021_166289).
Funding
Meta Platforms Inc.; Swiss National Science Foundation10.13039/501100001711 (200021_166289, grants 20QT21_187716 Qu3D).
Disclosures
MAW: Meta Platforms Inc. (F), EJS: Meta Platforms Inc. (E), PM: Meta Platforms Inc. (F), FM: Meta Platforms Inc. (E), EC: Fasttree3D SA (I,S) and PI Imaging Technology SA (I, S), CB: PI Imaging Technology SA (I, S).
Data Availability
Data underlying the results presented in this paper may be obtained from the authors upon reasonable request.
References
- 1.Cerussi A., Hsiang D., Shah N., Mehta R., Durkin A., Butler J., Tromberg B. J., “Predicting response to breast cancer neoadjuvant chemotherapy using diffuse optical spectroscopy,” Proc. Natl. Acad. Sci. U. S. A. 104(10), 4014–4019 (2007). 10.1073/pnas.0611058104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Boas D. A., Brooks D. H., Miller E. L., DiMarzio C. A., Kilmer M., Gaudette R. J., Zhang Q., “Imaging the body with diffuse optical tomography,” IEEE Signal Process. Mag. 18(6), 57–75 (2001). 10.1109/79.962278 [DOI] [Google Scholar]
- 3.Ferrari M., Quaresima V., “A brief review on the history of human functional near-infrared spectroscopy (fNIRS) development and fields of application,” NeuroImage 63(2), 921–935 (2012). 10.1016/j.neuroimage.2012.03.049 [DOI] [PubMed] [Google Scholar]
- 4.Borycki D., Kholiqov O., Chong S. P., Srinivasan V. J., “Interferometric Near-Infrared Spectroscopy (iNIRS) for determination of optical and dynamical properties of turbid media,” Opt. Express 24(1), 329 (2016). 10.1364/OE.24.000329 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Samaei S., Nowacka K., Gerega A., Pastuszak Ż., Borycki D., “Continuous-wave parallel interferometric near-infrared spectroscopy (CW πNIRS) with a fast two-dimensional camera,” Biomed. Opt. Express 13(11), 5753 (2022). 10.1364/BOE.472643 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.O’Doherty J., McNamara N. T., Clancy J. G., Enfield M. J., Leahy, “Comparison of instruments for investigation of microcirculatory blood flow and red blood cell concentration.,” J. Biomed. Opt. 14(3), 034025 (2009). 10.1117/1.3149863 [DOI] [PubMed] [Google Scholar]
- 7.Xu J., Jahromi A. K., Yang C., “Diffusing wave spectroscopy: A unified treatment on temporal sampling and speckle ensemble methods.,” APL Photonics 6(1), 016105 (2021). 10.1063/5.0034576 [DOI] [Google Scholar]
- 8.Briers D., Duncan D. D., Hirst E. R., Kirkpatrick S. J., Larsson M., Steenbergen W., Stromberg T., Thompson O. B., “Laser speckle contrast imaging: theoretical and practical limitations,” J. Biomed. Opt. 18(6), 066018 (2013). 10.1117/1.JBO.18.6.066018 [DOI] [PubMed] [Google Scholar]
- 9.Bandyopadhyay R., Gittings A. S., Suh S. S., Dixon K., Durian D. J., “Speckle-visibility spectroscopy: a tool to study time-varying dyamics,” Rev. Sci. Instrum. 76(9), 093110 (2005). 10.1063/1.2037987 [DOI] [Google Scholar]
- 10.Inoue I., Shinohara Y., Watanbe A., Amemiya Y., “Effect of shot noise on X-ray speckle visibility spectroscopy,” Opt. Express 20(24), 26878 (2012). 10.1364/OE.20.026878 [DOI] [PubMed] [Google Scholar]
- 11.Buckley E. M., Miller B. F., Golinski J. M., Sadeghian H., McAllister L. M., Vangel M., Ayata C., Meehan W. P., Franceschini M. A., Whalen M. J., “Decreased microvascular cerebral blood flow assessed by diffuse correlation spectroscopy after repetitive concussions in mice.,” J. Cereb. Blood Flow Metab. 35(12), 1995–2000 (2015). 10.1038/jcbfm.2015.161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rajaram A., Bale G., Kewin M., Morrison L. B., Tachtsidis I., St. Lawrence K., Diop M., “Simultaneous monitoring of cerebral perfusion and cytochrome c oxidase by combining broadband near-infrared spectroscopy and diffuse correlation spectroscopy,” Biomed. Opt. Express 9(6), 2588–2603 (2018). 10.1364/BOE.9.002588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.He L., Lin Y., Huang C., Irwin D., Szabunio M. M., Yu G., “Noncontact diffuse correlation tomography of human breast tumor,” J. Biomed. Opt. 20(8), 086003 (2015). 10.1117/1.JBO.20.8.086003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yazdi H. S., O’Sullivan T. D., Leproux A., Hill B., Durkin A., Telep S., Lam J., Yazdi S. S., Police A. M., Carroll R. M., Combs F. J., Strömberg T., Yodh A. G., Tromberg B. J., “Mapping breast cancer blood flow index, composition, and metabolism in a human subject using combined diffuse optical spectroscopic imaging and diffuse correlation spectroscopy,” J. Biomed. Opt. 22(4), 045003 (2017). 10.1117/1.JBO.22.4.045003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Agochukwu N. B., Huang C., Zhao M., Bahrani A. A., Chen L.), McGrath G., Yu L., Wong, “A novel noncontact diffuse correlation spectroscopy device for assessing blood flow in mastectomy skin flaps: a prospective study in patients undergoing prosthesis-based reconstruction,” Plast. Reconstr. Surg. 140(1), 26–31 (2017). 10.1097/PRS.0000000000003415 [DOI] [PubMed] [Google Scholar]
- 16.Durduran T., Yodh A. G., “Diffuse correlation spectroscopy for non-invasive, micro-vascular cerebral blood flow measurement,” NeuroImage 85, 51–63 (2014). 10.1016/j.neuroimage.2013.06.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhou W., Kholiqov O., Zhu J., Zhao M., Zimmermann L. L., Martin R. M., Lyeth B. G., Srinivasan V. J., “Functional interferometric diffusing wave spectroscopy of the human brain,” Sci. Adv. 7(20), eabe0150 (2021). 10.1126/sciadv.abe0150 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhou W., Zhao M., Kholiqov O., Srinivasan V. J., “Multi-exposure interferometric diffusing wave spectroscopy,” Opt. Lett. 46(18), 4498 (2021). 10.1364/OL.427746 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.James E., Powell S., Munro P., “Performance optimisation of a holographic Fourier domain diffuse correlation spectroscopy instrument,” Biomed. Opt. Express 13(7), 3836 (2022). 10.1364/BOE.454346 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Robinson M. B., Carp S. A., Peruch A., Boas D. A., Franceschini M. A., Sakadžić S., “Characterization of continuous wave ultrasound for acousto-optic modulated diffuse correlation spectroscopy (AOM-DCS),” Biomed. Opt. Express 11(6), 3071 (2020). 10.1364/BOE.390322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tamborini D., Stephens K. A., Wu M. M.), Farzam A. M., Siegel O., Shatrovoy M., Blackwell D. A., Boas S. A., Carp M. A., Franceschini, “Portable system for time-domain diffuse correlation spectroscopy,” IEEE Trans. Biomed. Eng. 66(11), 3014–3025 (2019). 10.1109/TBME.2019.2899762 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sutin J., Zimmerman B., Tyulmankov D., Tamborini D., Wu K. C., Selb J., Gulinatti A., Rech I., Tosi A., Boas D. A., Franceschini M. A., “Time-domain diffuse correlation spectroscopy,” Optica 3(9), 1006 (2016). 10.1364/OPTICA.3.001006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Samaei S., Sawosz M., Kacprzak Ż., Pastuszak D., Borycki A., Liebert, “Time-domain diffuse correlation spectroscopy (TD-DCS) for noninvasive, depth-dependent blood flow quantification in human tissue in vivo,” Sci. Rep. 11(1), 1817 (2021). 10.1038/s41598-021-81448-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Murali K., Varma H. M., “Multi-speckle diffuse correlation spectroscopy to measure cerebral blood flow,” Biomed. Opt. Express 11(11), 6699 (2020). 10.1364/BOE.401702 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Murali K., Nandakumaran A. K., Durduran T., Varma H. M., “Recovery of the diffuse correlation spectroscopy data-type from speckle contrast measurements: towards low-cost, deep-tissue blood flow measurements,” Biomed. Opt. Express 10(10), 5395 (2019). 10.1364/BOE.10.005395 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ozana N., Zavriyev A. I., Mazumder D., Robinson M., Kaya K., Blackwell M., Carp S. A., Franceschini M. A., “Superconducting nanowire single-photon sensing of cerebral blood flow,” Neurophoton. 8(03), 1 (2021). 10.1117/1.NPh.8.3.035006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Carp S. A., Tamborini D., Mazumder D., Wu K.-C., Robinson M. R., Stephens K. A., Shatrovoy O., Lue N., Ozana N., Blackwell M. H., Franceschini M. A., “Diffuse correlation spectroscopy measurements of blood flow using 1064 nm light,” J. Biomed. Opt. 25(09), 1 (2020). 10.1117/1.JBO.25.9.097003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Irwin D., Dong L., Shang Y., Cheng R., Kudrimoti M., Stevens S. D., Yu G., “Influences of tissue absorption and scattering on diffuse correlation spectroscopy blood flow measurements,” Biomed. Opt. Express 2(7), 1969 (2011). 10.1364/BOE.2.001969 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Han S., Hoffman M. D., Proctor A. R., Vella J. B., Mannoh E. A., Barber N. E., Kim H. J., Jung K. W., Benoit D. S. W., Choe R., “Non-invasive monitoring of temporal and spatial blood flow during bone graft healing using diffuse correlation spectroscopy,” PLoS One 10(12), e0143891 (2015). 10.1371/journal.pone.0143891 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Stapels C. J., Kolodziejski N. J., McAdams D., Podolsky M. J., Fernandez D. E., Farkas D., Christian J. F., “A scalable correlator for multichannel diffuse correlation spectroscopy,” San Francisco, California, United States 969816 (2016). [DOI] [PMC free article] [PubMed]
- 31.Johansson J. D., Portaluppi D., Buttafava M., Villa F., “A multipixel diffuse correlation spectroscopy system based on a single photon avalanche diode array,” J. Biophotonics 12(11), 1 (2019). 10.1002/jbio.201900091 [DOI] [PubMed] [Google Scholar]
- 32.Dietsche G., Ninck M., Ortolf C., Li J., Jaillon F., Gisler T., “Fiber-based multispeckle detection for time-resolved diffusing-wave spectroscopy: characterization and application to blood flow detection in deep tissue,” Appl. Opt. 46(35), 8506 (2007). 10.1364/AO.46.008506 [DOI] [PubMed] [Google Scholar]
- 33.Sie E., Chen H., Saung E.-F., Catoen R., Tiecke T., Chevillet M., Marsili F., “High-sensitivity multispeckle diffuse correlation spectroscopy,” Neurophoton. 7(03), 035010 (2020). 10.1117/1.NPh.7.3.035010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Liu W., Qian R., Xu S.), Chandra Konda J., Jönsson M., Harfouche D., Borycki C., Cooke E., Berrocal Q., Dai H., Wang R., Horstmeyer, “Fast and sensitive diffuse correlation spectroscopy with highly parallelized single photon detection,” APL Photonics 6(2), 026106 (2021). 10.1063/5.0031225 [DOI] [Google Scholar]
- 35.Wayne M., Ulku A., Ardelean A.), Mos C., Bruschini E., Charbon, “A 500 × 500 dual-gate SPAD imager with 100% temporal aperture and 1 ns minimum gate length for FLIM and phasor imaging applications,” IEEE Trans. Electron Devices 69(6), 2865–2872 (2022). 10.1109/TED.2022.3168249 [DOI] [Google Scholar]
- 36.Goodman J. W., Speckle Phenomena in Optics: Theory and Applications , 2nd Edition (SPIE, 2020). [Google Scholar]
- 37.Boas D. A., Yodh A. G., “Spatially varying dynamical properties of turbid media probed with diffusing temporal light correlation,” J. Opt. Soc. Am. A 14(1), 192 (1997). 10.1364/JOSAA.14.000192 [DOI] [Google Scholar]
- 38.Zhou C., Yu G., Furuya D., Greenberg J. H., Yodh A. G., Durduran T., “Diffuse optical correlation tomography of cerebral blood flow during cortical spreading depression in rat brain,” Opt. Express 14(3), 1125–1144 (2006). 10.1364/OE.14.001125 [DOI] [PubMed] [Google Scholar]
- 39.Boas D. A., Sakadžic S., Selb J.), Farzam M. A., Franceschini S. A., Carp, “Establishing the diffuse correlation spectroscopy signal relationship with blood flow,” Neurophotonics 3(3), 031412 (2016). 10.1117/1.NPh.3.3.031412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Koppel D. E., “Statistical accuracy in fluorescence correlation spectroscopy,” Phys. Rev. A 10(6), 1938–1945 (1974). 10.1103/PhysRevA.10.1938 [DOI] [Google Scholar]
- 41.Cheng X., Chen H., Sie E. J., Marsili F., Boas D. A., “Development of a Monte Carlo-wave model to simulate time domain diffuse correlation spectroscopy measurements from first principles,” J. Biomed. Opt. 27(08), 1 (2022). 10.1117/1.JBO.27.8.083009 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper may be obtained from the authors upon reasonable request.