Abstract
Perception of dynamic scenes in our environment results from the evaluation of visual features such as the fundamental spatial and temporal frequency components of a moving object. The ratio between these two components represents the object's speed of motion. The human middle temporal cortex hMT+ has a crucial biological role in the direct encoding of object speed. However, the link between hMT+ speed encoding and the spatiotemporal frequency components of a moving object is still under explored. Here, we recorded high resolution 7T blood oxygen level‐dependent BOLD responses to different visual motion stimuli as a function of their fundamental spatial and temporal frequency components. We fitted each hMT+ BOLD response with a 2D Gaussian model allowing for two different speed encoding mechanisms: (1) distinct and independent selectivity for the spatial and temporal frequencies of the visual motion stimuli; (2) pure tuning for the speed of motion. We show that both mechanisms occur but in different neuronal groups within hMT+, with the largest subregion of the complex showing separable tuning for the spatial and temporal frequency of the visual stimuli. Both mechanisms were highly reproducible within participants, reconciling single cell recordings from MT in animals that have showed both encoding mechanisms. Our findings confirm that a more complex process is involved in the perception of speed than initially thought and suggest that hMT+ plays a primary role in the evaluation of the spatial features of the moving visual input.
Keywords: 7T fMRI, gaussian modelling, hMT +, spatial frequency, speed encoding, visual motion
The human middle temporal cortex hMT+ has a crucial biological role in the direct encoding of object speed. Here, we recorded high resolution 7T blood oxygen level‐dependent BOLD responses to different visual motion stimuli as a function of their fundamental spatial and temporal frequency components. Overall the complex encodes speed according to the combination of the spatial and temporal frequencies presented. A small subregion within the complex encodes speed directly. Our findings suggest that hMT+ plays a primary role in the evaluation of the spatial features of the moving visual input.

1. INTRODUCTION
Encoding of visual features from dynamic visual images is essential in humans and nonhuman primates to reconstruct the visual scene and rapidly respond to the ever changing environment. Among visual areas, the human homologue of the macaque middle temporal cortex (hMT+ also known as V5) has been shown to play a functional role in the encoding of features such as the spatial and temporal frequency components of visual motion stimuli (Lui et al., 2007; Priebe, 2006; Priebe et al., 2003; 2006). Using electrocorticography, we recently showed that hMT+ neuronal populations separated visual motion into its spatial and temporal components, with speed preferences changing in accordance with the fundamental spatial frequency of the visual stimuli, rather than being tuned for a particular speed of the attended moving stimuli (Gaglianese et al., 2017). These findings, paired with single cell recording studies in animals, describe hMT+ neurons as spatiotemporal frequency sensors for motion extraction (Lui et al., 2007; Priebe et al., 2003; 2006). However, debate continues about the speed encoding mechanisms of MT since pure speed tuning encoding has been reported in different MT cells in primates (Liu & Newsome, 2003; 2005; Perrone & Krauzlis, 2008; Perrone & Thiele, 2001). Therefore, there are two different mechanisms of speed tuning characterizing area MT in primates and the homologous hMT complex in humans rather than separating motion into its spatial and temporal components (Holub & Morton‐Gibson, 1981; Perrone & Thiele, 2001; Tolhurst & Movshon, 1975). The second proposes that MT neurons have an active role in encoding the low features of the visual stimuli acting as spatial filter such that their representation of speed encodes the stimulus properties rather than speed per se (Lui et al., 2007; Movshon, 1975; Simoncelli & Heeger, 1997). One major issue of animal single‐cell recordings and human electrocorticography measurements is the reduced coverage of MT+ due to the closely‐spaced recording sites. Therefore, it remains elusive whether there is a functional organization within the complex for the different mechanisms of speed encoding, that is separable tuning for spatial and temporal frequencies vs pure speed tuning. The rapid development of ultra‐high field (7 Tesla, 7T) functional Magnetic Resonance Imaging (fMRI) allows us to reveal the fine‐scale functional organization of the human cortex in vivo (Dumoulin, Fracasso, et al., 2017; Yang et al., 2021). Many 7T fMRI studies have been carried out in primary visual cortex V1, although studies have been recently extended to reveal the fine‐scale functional organization of the human extrastriate cortex and association areas (Dumoulin, Harvey, et al., 2017; Fracasso et al., 2018; 2021; Harvey et al., 1979; 2020; Harvey & Dumoulin, 2016; Huber et al., 2020; Tootell & Nasr, 2017; Yu et al., 2022). A recent high spatial resolution 7T fMRI study in hMT+ in particular, has demonstrated a functional organization into columnar clusters with preferences for horizontal or vertical motion, similar to the columnar organization in monkeys (Schneider et al., 2019). However, human research to date has tended to focus on the spatial organisation of responses to the location and direction of motion in hMT+ (d'Avossa et al., 2007; Emmerling et al., 2016; Rezk et al., 2020; Schneider et al., 2019; van Kemenade et al., 2014; Zimmermann et al., 2011), rather than the mechanisms involved in the encoding of speed of motion.
Here, we use 7T fMRI to distinguish between the different speed mechanisms of neural response properties to different combinations of fundamental spatial and temporal frequency components of visual motion stimuli in response to speed in the human brain. We take advantage to the high spatial resolution possible with 7T fMRI and custom surface coils to simultaneously record from many small, spatially separable neural populations in the individual participants. This allows us to ask how response properties differ within hMT+ rather than assuming homogenous response profiles throughout hMT+. We modelled BOLD responses with a 2D Gaussian model that allows for either speed tuning encoding or separable tuning of the spatial and temporal frequencies components. We were able to characterize the mechanisms involved in the encoding of speed of motion and to demonstrate that both encoding mechanisms occur in hMT+, with the majority of the complex exhibiting temporal and spatial frequency selectivity.
2. METHODS
Five healthy volunteers (all male, mean age + SD = 36.2 ± 3 years) participated in the study after giving written informed consent. The study was approved by the Ethics Committee of the University Medical Center of Utrecht in accordance with the Declaration of Helsinki (2013) and the Dutch Medical Research Involving Human Subjects Act.
As in previous similar studies using visual paradigm such as population receptive field pRF and visual motion discrimination of fMRI data (Dumoulin & Wandell, 2008; Gaglianese et al., 2015; Harvey et al., 1979, 2020; Harvey & Dumoulin, 2017; Klein et al., 2014; Schneider et al., 2019), we aim for a detailed assessment of functional neural response properties in each participant (Gordon et al., 2017) and therefore focus on internal replication using a large amount of data from each participant rather than large numbers of participants (Baker et al., 2021).
2.1. hMT+ localizer stimulus
Area hMT+ was functionally identified based on responses to moving compared to stationary visual stimuli, as conventionally used in literature (Huk et al., 2002; Tootell et al., 1995). We used a full field high‐contrast square‐wave black‐and‐white dartboard patterns instead of standard random dots to match the contrast of the visual stimulus used in the visual motion stimulation experiment. During the motion condition, the dartboard pattern expanded from the fixation point for 10 s with a temporal frequency of 5 Hz, interleaved with a stationary period of 10 s during which the same dartboard was presented static. The stimuli subtended a visual angle of 30.7 × 16.1°.
2.2. Visual motion stimulation
The visual motion stimulation consisted of five runs of high‐contrast square‐wave black and white dartboard patterns presented with three different fundamental spatial and temporal frequency combinations (0.33 cycle/°;1 Hz, 0.33 cycle/°; 3 Hz, 0.33 cycle/°; 5 Hz, 0.2 cycle/°; 3 Hz, 1 cycle/°; 3 Hz). The range of spatial frequencies was based on our previous EcOG study and fMRI recordings in humans showing peak responses in hMT+/V5 around 0.33 cycle/° and reaching the minimum response amplitude for a spatial frequency of 1.24 cycle/° (Aghajari et al., 2020; Gaglianese et al., n.d.; Henriksson et al., 2008; Singh et al., 2000; Yu et al., 2010). Given that the speed of motion of each square‐wave dartboard presented is defined by the ratio of temporal to spatial frequencies, speeds of 3, 9, and 15 °/s were presented respectively. Each run is either classified as a fast (15 °/s), intermediate (9 °/s) or slow (3 °/s) moving stimuli, depending on the fundamental spatial and temporal frequency that gives origin to the stimuli speed. The fast and the slow speed respectively were presented twice by using two different spatiotemporal frequency combinations of the moving dartboards (see Figure 1). In each run, we presented only one spatiotemporal frequency combination for a total of 26 trials. Each run lasted 366 s. The dartboard pattern expanded from the fixation point for 1 s alternating with a baseline period during which the dartboard was static to enhance the effect of motion. Baseline periods were of variable length ranging from 6 to 15 s, presented in a pseudo‐randomized order. Three additional baseline periods of 24 s were randomly added to allow the BOLD response to return to baseline. To maintain fixation and consistent level of arousal, participants were instructed to press a button when the central fixation dot changed color from red to green and vice versa (Figure 1). Participant performance was recorded via Matlab software, and detection rate was consistently above chance for each run and participant.
FIGURE 1.
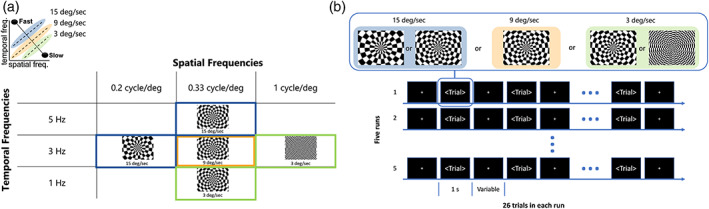
Graphical summary of the five combinations of spatial and temporal frequencies used to characterize the five visual motion stimuli (high‐contrast black‐and‐white dartboard) presented during the five runs of the study following the localizer run. Each run is either classified as a fast (represented by blue colour), intermediate (represented by orange colour) or slow (represented by green colour) moving stimuli, depending on the spatial and temporal frequency that gives origin to the stimulus speed. Graphic on the upper left provides a simplified depiction of the stimulus space. (b) Each single spatiotemporal combination was presented in a single run in an event related design. The high‐contrast black‐and‐white dartboard was moving for a second in each single trial and staying still in the rest period of variable length (6–12 s)
3. fMRI METHODS
3.1. fMRI data acquisition
Functional MRI data were acquired using a Philips 7T scanner equipped with a volume transmit (Nova Medical, USA) and two high‐density 16‐channel surface coils (Petridou et al., 2013). The surface coils covered the left and right lateral occipital pole of the participant to maximize the signal‐to‐noise (SNR) and BOLD sensitivity in the left and right hMT+. A gradient echo echo‐planar‐imaging (EPI) sequence was used for both the localizer and the visual motion stimulation experiments. Functional images for the localizer were acquired every 1.8 s, with an echo time (TE) of 27 ms, an isotropic voxel of 1.5 mm and 27 coronal slices covering hMT+ bilaterally. For the visual motion stimulation experiment we acquired 15 coronal slices at a fast temporal resolution TR of 0.849 ms, TE = 27 ms, and an isotropic voxel resolution of 1.4 mm. For both functional acquisitions, EPIs were acquired with a SENSE factor of 2 in the right–left direction. High‐resolution T1‐weighted anatomical MRI images were acquired with a 32‐channel head coil (Nova Medical, MA, USA) in a different session at a resolution of 0.8 × 0.8 × 0.8 mm. Repetition time (TR) was 7 ms, TE was 2.84 ms, and flip angle was 8°. Visual stimuli were projected onto a 27 × 9.5 cm screen placed inside the magnet bore behind the participant's head, using a projector (Benq W6000, 1600 × 538 pixels display resolution). Participants viewed the projected visual stimulus via a mirror and prism glasses, at an effective distance of 41 cm.
3.2. Data pre‐processing
All the pre‐processing steps were performed using AFNI (Analysis of Functional NeuroImages, https://afni.nimh.nih.gov/). First, the functional data of the localizer and visual motion stimulation runs were corrected for motion and aligned to the first image of the first run of each session respectively using the function 3dVolreg. Subsequently, low frequency signal intensity drifts were removed with quadratic detrending using the 3dDetrend function. No spatial smoothing was employed. The visual motion stimulation runs were non linearly co‐registered to the localizer using the 3WarpDrive function. To avoid time series interpolation of the visual stimulation runs, we extracted the Regions of Interest (ROIs) in the localizer space (see Localization of hMT+) and co‐registered them to the visual motion stimulation runs using the inverse of the obtained transformation matrix.
The T1‐w anatomical images were segmented automatically using the MIPAV software package implemented in CBStool (https://www.nitrc.org/projects/cbs-tools/). White matter and pial surfaces were generated and then imported in SUMA (afni.nimh.nih.gov). For each participant, maps obtained from the functional runs (see below) were co‐registered on the pial surface using first the function 3dAllineate with mutual information as cost function, and then non‐linearly using the 3dWarpdrive function.
3.3. Localization of hMT+
For each participant, left and right hMT+ areas were functionally defined from the localizer runs by contrasting responses for the moving and stationary high contrast black and white dartboard stimuli. All statistical computations were performed at a single participant level using a general linear model (GLM) with a standard gamma variate hemodynamic response function approach, using the 3dDeconvolve function in AFNI. For each run, outliers due to residual motion were detected via 3dTOutCount function and included in the GLM analysis as regressors of no interest. Voxels that exhibited significant responses for moving vs stationary dartboards (p < .001, Bonferroni corrected) and located within the EPI space regions spanning 1 cm in the intersection of the junction between the ascending limb of the inferior temporal sulcus and the sulcus itself as described by Dumoulin et al. (2000) were selected to define hMT+ ROIs.
3.4. Quantification of BOLD responses for the visual motion stimulation
The BOLD responses to each combination of spatial and temporal frequencies presented during the visual motion stimulation runs were estimated for all voxels using a finite impulse response deconvolution approach (Costagli et al., 2014; Dale, 1999; Gardner et al., 2005) implemented in mrTools (available for free download at http://gru.stanford.edu/doku.php/mrTools/overview), a software package running in MATLAB. Following Costagli and colleagues' approach, for each voxel and spatiotemporal combination (e.g. run), the following matricial model was assumed:
where B is the voxel's time course (dimensions: V volumes per run × 1), S is the stimulus convolution matrix (dimensions: V × TP, where T is the number of conditions per run [i.e., 1] and P is the number of time points in the hemodynamic response), H is the hemodynamic response (dimensions: TP × 1) and N is the residual zero‐mean Gaussian‐distributed noise (dimensions: V × 1). Here, P is the only parameter (set to 25 s) defined a priori to estimate the HRF of each single voxel. No assumption of the shape or amplitude of the expected HRF (i.e., H) is imposed in the model. As such, the HRF for each voxel and run is computed as:
H = (S T S)−1 S T B. Estimated HRF for each voxel were then smoothed with a moving average filter with a heuristically defined span. Then the response to a given stimulus type was quantified for each voxel by computing the maximum of the estimated HRF response. Only amplitude values of voxels that exhibited significant responses to the visual motion localizer and confined within each hMT+ ROI were selected for further analysis. Finally, voxels likely located on larger veins with maximum values higher than 6 were discarded.
We computed the significance of the effect of the spatial and temporal frequency components of the visual motion stimulation on the hMT+ BOLD response amplitudes by a one‐way repeated measures ANOVA within participants. Furthermore, we computed a three‐way analysis of variance (ANOVA) considering each of the three speeds as a factor. We found a significant effect of speed on the BOLD responses of each bilateral ROIs (F = 6.97 and p = .0001). Finally, to investigate if the BOLD response amplitude changes according to the spatiotemporal frequency combination of the stimuli rather than the speed per se, we performed a two‐sample t‐test between the 0.33 cycle/° 1 Hz and 1 cycle/° 3 Hz spatiotemporal frequency combination (both representing 3 °/s speed of motion of the visual stimuli) and 0.33 cycle/° 5 Hz and 0.2 cycle/° 3 Hz (both representing 15 °/s speed of motion).
3.5. Tuning model of hMT+ BOLD responses
We ask whether the BOLD responses in hMT+ are consistent with tuning for the fundamental spatiotemporal frequency combination of the presented moving visual stimuli or whether they are consistent with pure speed tuning. To answer this, we compared the measured BOLD response amplitudes with the predicted BOLD response amplitudes obtained by both a spatiotemporal frequency tuning model and a speed tuning model (Gaglianese et al., 2017; Lui et al., 2007; Miura et al., 2014; Priebe et al., 2006). The first model retains separate and independent responses for the spatial and temporal frequency components of the visual stimuli. The second model describes direct encoding of the speed of motion, resulting in a preference for the same speed at different spatial frequencies, with temporal frequency tuning varying in accordance with the spatial frequency. Both models are represented by a two‐dimensional Gaussian function with the addition of an extra parameter Q that allows to characterize the two different types of tuning. A value of Q equal to zero (Q = 0) describes separable responses for each spatial and temporal frequency combination of the stimuli. A value of Q equal to 1 (Q = 1) describes tuning for particular speeds, that is, predicts the same optimal speed at different spatial frequencies. Both models are described by the equation below:
| (1) |
where is defined as:
| (2) |
The term A is the peak of the BOLD response amplitude, sfopt and tfopt are the optimal spatial and temporal frequency, and σsf and σtf are the bandwidths of the spatial and temporal frequencies tuning curves. We fitted the BOLD response amplitudes of each voxel in each hMT+ ROI to both the spatiotemporal frequency and the speed tuned models (setting Q = 0 or Q = 1 respectively). Model fits was performed testing all the possible combination of the five free parameters reported on equations 1 and 2. Based on literature (Gaglianese et al., 2017; Lui et al., 2007) we constrained each parameter to these values: tfopt = 0.25–10 Hz; σtf = 0.2–10; sfopt = 0.1–1.2 cycle/°; σsf = 0.2–2. For each parameter we tested 10 linearly equally spaced points between the lower and the upper points reported above. Then we used linear square optimization to estimate the goodness of the fit and we select the combination of the parameters giving the highest variance explained. Therefore, for each voxel and model, five parameters were obtained: (a) optimal fundamental spatial frequency sfopt, (b) optimal fundamental temporal frequency tfopt, (c) bandwidth of the Gaussian along the spatial dimension σsf, and (d) bandwidth of the Gaussian along the temporal dimension σtf, (e) A, accounting for the size of the peak response. Both σsf and σtf were kept as a free parameter since they allow the bandwidth of the Gaussian along the spatial and temporal frequency dimensions to vary and to provide a better estimation of the two speed tuning profiles under examination. For further analysis, only the estimated fundamental optimal spatial and temporal frequency and the variance explained were used. In addition, we computed the preferred speed for each voxel as:
3.6. Cross validation
We cross‐validated each model's goodness of fit in predicting the BOLD response amplitude for each voxel by fitting the BOLD response amplitudes of one half of the measured data and testing how well the resultant parameters predict the BOLD response amplitudes in the complementary half, assessed by the variance explained (Mante et al., 2005). For this purpose, two independent halves of the data are needed. Since in our visual motion stimulation paradigm we presented each spatiotemporal condition in a unique run we split each run in two halves according to the incidence of the second 24 s baseline period. This time point was chosen to minimize the possibility that the BOLD response following the last trial in the first split half would affect the measurement of the first trial in the second split half. We applied this approach for both the speed tuning model (parameter Q = 1) and the spatiotemporal frequency tuning model (Q = 0). Voxels with variance explained below 0.1 were discarded from the subsequent analysis for each model separately. On average 39.2 ± 4.27 percent of voxels were discarded from each bilateral hMT+ ROI. A two‐sided paired t‐test between the average variance explained of each model within each bilateral hMT ROI+ was computed to define the model that best represented the measured BOLD responses. To test the reproducibility of the model fitting, the same analysis was performed by fitting the BOLD responses on the second half of the data and testing on the complementary first half of the data for both Q = 0 and Q = 1 model. We define the repeatability of the best model fits for each ROI using a permutation test (n = 1000 shuffle repetitions) on each bilateral hMT+ ROIs variance explained obtained from the two split halves for the two models. Here we determined how many voxels were fit better by the Q = 1 model in both halves of the data. We then performed a permutation analysis where we shuffled the voxels to determine how many voxels would be better fit by the Q = 1 model in both halves by chance, if there were no relationship between the winning models in the two halves of the data. The proportion of these random permutations that showed a greater proportion of repeatable Q = 1 voxels than the data itself gave the probability of observing this repeatability by chance.
3.7. Separable tuning of hMT+ BOLD responses for temporal and spatial frequencies
For each half split and each ROI we obtained a spatial map of optimal spatial and temporal frequencies. We quantified the reproducibility of these maps by computing a Spearman correlation coefficient between the two‐half split spatial distribution of the sfopt and tfopt parameters. Based on our previous ECoG study in humans using the same paradigm (Gaglianese et al., 2017) and neurophysiological findings in animals (Henriksson et al., 2008; Issa et al., 2000; Singh et al., 2000), we expected hMT+ to be more tuned toward low spatial frequency rather than high spatial frequency. To quantify this effect, we classified the distribution of the optimal fundamental spatial frequencies obtained from the Q = 0 model in k clusters. To guide the choice of the number k of clusters to be used to classify the spatial frequencies we computed the within sum of squares accounting for the number of clusters, by using the Bayesian information criterion BIC. We then classified independently the spatial frequency parameters using k‐means. Mean and standard deviation of the center of clusters and cluster size for each hMT+ ROI were computed across participants.
4. RESULTS
4.1. hMT+ BOLD responses showed differential responses for each combination of spatial and temporal frequency of the visual motion stimuli
Regions of interest (ROIs) for hMT+ were defined for each hemisphere based on the functional localizer. The mean grey matter area for the right and left ROIs were 451 ± 90.5 mm (Priebe et al., 2003) and 251 ± 18.4 mm (Priebe et al., 2003) respectively.
Figure 2a depicts the ROI extent in the anatomical space. Each voxel within each ROI was assigned a spatiotemporal frequency combination preference in accordance with the maximum BOLD response amplitude across combinations. Mean estimated HRFs for each spatiotemporal frequency combination of each participant were shown on Figure 2b.
FIGURE 2.
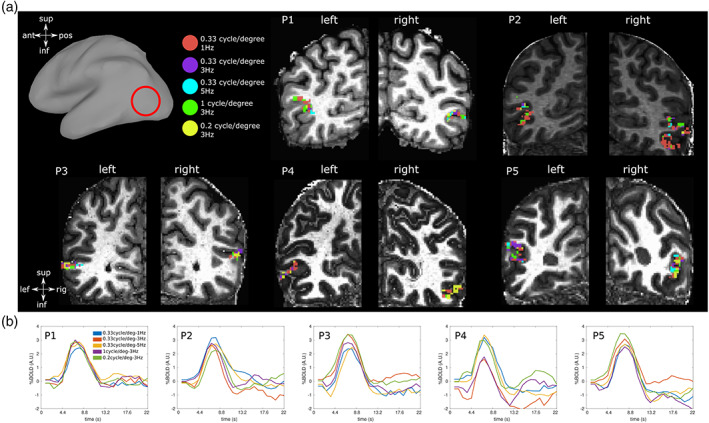
(a) Spatiotemporal frequency preference within hMT+ ROI of each participant plotted on each anatomical space. The amplitude with the highest value across all spatiotemporal frequency conditions determined the preferred spatiotemporal frequency combination of each voxel. (b) Mean HRF across each bilateral ROI in response to each spatiotemporal combination of the visual stimuli for each participant. Mean r 2 across conditions were significant at p = .05 and equal to 0.12, 0.12 0.14, 0.10 and 0.14 for each participant respectively
The effect of each fundamental spatiotemporal frequency combination on the bilateral hMT+.
ROIs was significant across participants (one‐way ANOVA, F = 4.45, p = .0005). The amplitude of BOLD responses was significantly different for each measured spatial and temporal combination. Four out of five participants exhibited significantly different BOLD response amplitudes (p < .05) for the two pairs of spatiotemporal frequency combinations leading to the same speed of motion of the presented dartboard (0.33 cycle/° 1–1 Hz 0.33 cycle/° and 0.33 cycle/° 5 Hz–0.2 cycle/° 3 Hz, respectively).
4.2. hMT+ BOLD response amplitudes were mainly characterized by independent tuning for spatial and temporal frequency
The two‐dimensional Gaussian models allowing independent tuning for spatial and temporal frequency (Q = 0) or tuning dependent on speed (Q = 1), were able to characterize the hMT+ BOLD amplitude responses (Figure 3a). For each model, we fitted each voxel's BOLD response amplitude for each combination of the fundamental spatial and temporal frequency on one split half of the data and computed the variance explained by the resulting model in the second complementary half. Overall, for each participant's bilateral hMT+ ROIs, in cross validation, the Q = 0 model explained significantly more variance than the speed encoding model Q = 1 (two‐sided t‐test, p < .001 for each participant, see Figure 3a). Each bilateral hMT+ ROIs also included a number of voxels exhibiting higher variance explained for the Q = 1 model compared to the Q = 0 model. The percentage of grey matter area within each bilateral hMT+ ROI of each participant that is better explained by the Q = 0 or Q = 1 model respectively is shown in Figure 3b. These two groups of voxels exhibiting different speed tuning profile are repeatable across the split run validation (Figure 3c,d). The group of Q = 1 voxels is highly repeatable (p < .001) across subjects, although it does not reach significance in every participant.
FIGURE 3.
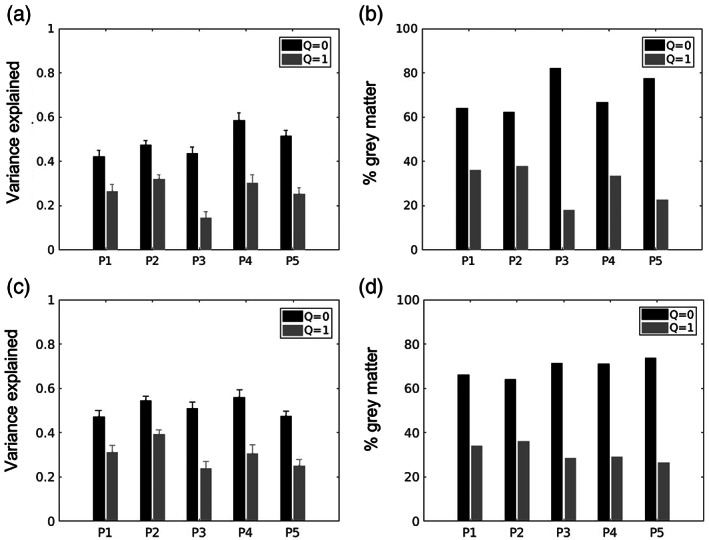
(a) Single participant variance explained in split‐run cross validation (fitted on first half of the run and validated on second half) by Gaussian tuning models with independent spatial and temporal frequency tuning (Q = 0) and tuning for speed (Q = 1). Each bar represents the mean variance explained and standard error for bilateral hMT+ ROI voxels of each participant (P1–P5, x‐axis). (b) Single participant percentage of voxels within hMT+ ROIs exhibiting separable spatiotemporal frequency tuning (Q = 0, black bars) or speed tuning, that is same temporal frequency preference for the different spatial frequency of the moving dartboard (Q = 1, grey bars), (c,d) same as a and b tested in split‐run cross validation on second half and validated on first half
Figure 4 shows the histograms of the optimal fundamental spatial and temporal frequencies, variance explained, and speed preferences within bilateral hMT+ ROI voxels of each participant for the fitting with the spatiotemporal frequency tuning model Q = 0 (Figure 4a) and the speed tuning model Q = 1 (Figure 4b). Median optimal fundamental spatial and temporal frequency values for each model fitting were consistent across participants (Table 1).
FIGURE 4.
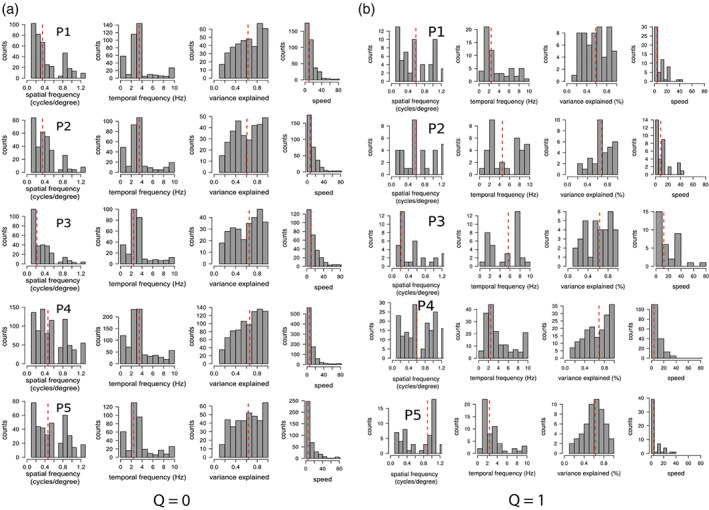
Histograms of estimated optimal temporal frequencies, spatial frequencies, variance explained, and speeds obtained in cross validation for each participant's bilateral hMT+ ROI for the model Q = 0 (a) and for the speed tuning model Q = 1 (b). Red dashed line shows the median values across voxels. Red dashed line shows the median values across voxels. Voxels with variance explained below 0.1 were discarded for each model separately
TABLE 1.
Median optimal values for spatial and temporal frequency, variance explained and speed for both the Q = 0 and the Q = 1 model
| sfopt | tfopt | var exp | Speed | |
|---|---|---|---|---|
| Q = 0 | 0.34 | 3.5 | 0.63 | 10.16 |
| 0.34 | 3.5 | 0.61 | 7.5 | |
| 0.22 | 2.42 | 0.65 | 10.16 | |
| 0.47 | 3.5 | 0.66 | 5.94 | |
| 0.47 | 2.42 | 0.63 | 5.5 | |
| Q = 1 | 0.59 | 2.42 | 0.58 | 4.1 |
| 0.59 | 4.58 | 0.68 | 8.33 | |
| 0.22 | 5.67 | 0.63 | 12.54 | |
| 0.59 | 2.42 | 0.69 | 4.1 | |
| 0.89 | 2.42 | 0.62 | 3.87 |
We further tested the reproducibility of the cortical organisation of the optimal spatial and temporal frequency preferences across the two half splits of the data using Spearman's correlation. Only maps of the spatial frequency preferences exhibited a significant correlation in all the participants' bilateral hMT+ ROIs (r 2 = 0.64, 0.59, 0.79, 0.65, 0.61 respectively, p < .0001). Optimal fundamental spatial frequency values for each participant and each half split were then classified in two clusters respectively using kmeans. K = 2 was based on the optimum value displayed by the BIC score (Figure 5a). Optimal spatial frequency clusters for the complete run and each half split for a representative participant are shown in Figure 6a–c. A parallel‐coordinates plot for spatial frequencies is shown in Figure 6d,e in which the starting point of each line on the left side of each plot indicates the spatial location of the voxel and the cluster classification, and the ending point the correspondent classification in the second half. Mean centroids across participants (Figure 5b) were consistent and centered on 0.20 ± 0.013 cycle/° (low spatial frequencies cluster) and 0.79 ± 0.035 (high spatial frequencies cluster). The percentage of voxels normalized by the size of each cluster is shown in Figure 5c.
FIGURE 5.
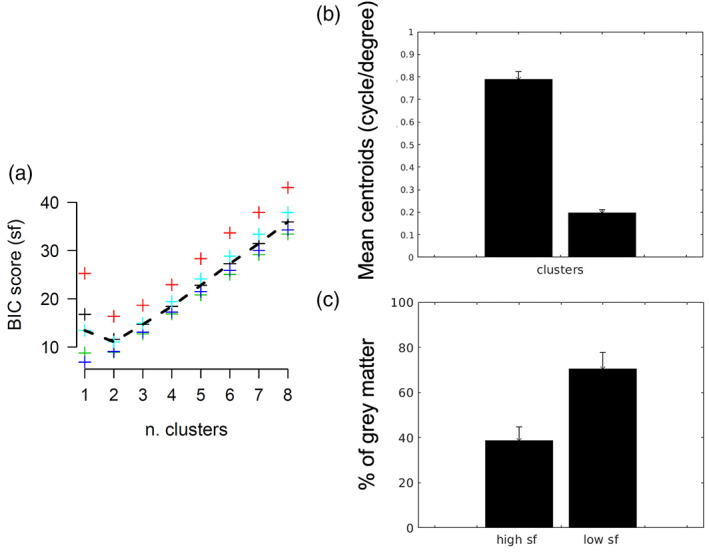
(a) Bayesian information criterion score as a function of the number k of clusters for the optimal spatial frequency values. Each color represents a single participant. Dashed line represents the mean score across participants. K = 2 was selected for the optimal number of clusters (b) mean centroids value and standard deviation across participants hMT+ ROIs for each spatial frequency cluster (c) mean percentage of grey matter and standard deviation across participants hMT+ ROIs for each spatial frequency cluster
FIGURE 6.
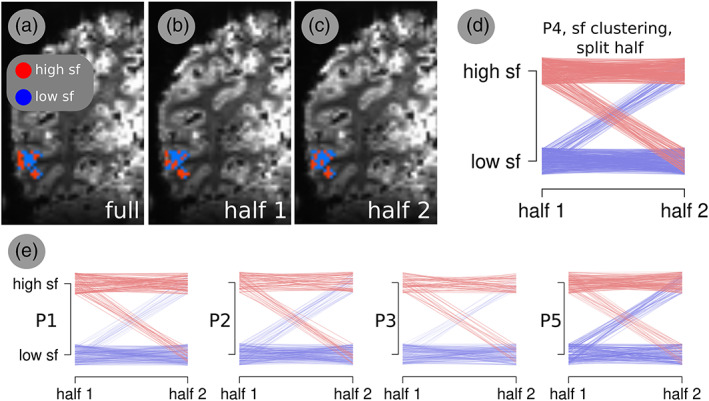
Optimal spatial frequency clusters and their reproducibility for a representative participant. (a–c) Spatial frequency clusters represented on the cortex for the entire run, half 1 and half 2, respectively. (d) Parallel‐coordinates plot. It represents optimal spatial frequency of each voxel in the first (left side) and second half (right side) run respectively. Y axis maps voxel coordinates in space. (e) Same as d for each measured participant
5. DISCUSSION
In the current study we investigated the speed encoding mechanisms of hMT+ BOLD responses in response to different combinations of the fundamental spatial and temporal frequency components of visual motion stimuli. Overall, our results support the coexistence of two sub‐populations within the complex exhibiting two different mechanisms of speed encoding. The bigger cluster exhibited separable tuning for the spatial and temporal frequency components of the visual motion stimuli, where the neuronal population speed preference changes in accordance with the spatial frequency. The smaller cluster exhibited direct speed tuning, where the same speed preference was maintained for different spatial frequency components of the stimuli.
These two different mechanisms have been previously reported in the literature. The first and more conventional one foresees direct speed tuning, where the same speed preference is maintained for different spatial frequency components of the stimuli. The second proposes independent tuning for the spatial and temporal frequency components of the visual stimuli, where the neuronal population speed preference changes in accordance with the spatial frequency. Animal studies using intracellular recordings (Lui et al., 2007; Miura et al., 2014; Priebe et al., 2003; Priebe et al., 2006) have shown in MT/V5 the presence of both mechanisms and in particular: (1) the existence of a percentage of MT cells responding to the speed of motion of the presented visual stimuli (Liu & Newsome, 2003; Perrone & Thiele, 2001), (2) separable neuronal response within MT/V5 neuronal population (Lui et al., 2007; Priebe, 2006) and (3) a continuum of both mechanisms (Duijnhouwer et al., 2013). In humans we have recently shown using electrocorticography ECoG that sampled neuronal population within the complex exhibited distinct and independent selectivity for spatial and temporal frequencies of the visual stimuli (Gaglianese et al., 2017). Our results were limited to the coverage of the ECoG electrodes, possibly hiding smaller neuronal populations tuned for speed. We were now able to investigate the speed encoding mechanisms of the entire hMT+ complex with higher detail, bridging the gap between single cell recordings in animal studies and electrophysiological recordings of single neuronal populations in the human brain and reconciling the different results reported in the literature.
Moreover, for the regions of the complex exhibiting separable responses we further tested the spatial selectivity for spatial and temporal frequency by estimating the optimal fundamental spatial and temporal frequency values for each voxel of each participant's hMT+ ROI. Optimal spatial frequency maps were highly reproducible within participants, in line with the hypothesis that visual areas with specific visual field maps such as MT/V5 exhibit specific responses for the spatial frequency component of the perceived stimuli. Indeed, tuning for spatial frequencies in the occipital cortex has been shown using optical imaging in cat and fMRI in humans (Henriksson et al., 2008; Issa et al., 2000; Singh et al., 2000), by showing a decrease in optimal spatial frequency tuning moving from V1 to V3 and to extrastriate cortex such as MT+. It has been shown (Singh et al., 2000), using fMRI in humans, low pass tuning responses for spatial frequency in V5/MT, exhibiting a significant drop in responses for spatial frequencies above 0.4 cycle/°. This in line with a recent fMRI study reporting preferences for lower spatial frequencies in regions located up in the dorsal stream with larger receptive field, when presented with visual stimuli at different spatial frequencies but same temporal frequency (Mikellidou et al., 2018). In our dataset we measured the same effect: the optimal spatial frequencies were distributed along two clusters, peaking respectively on low spatial frequencies (0.20 cycle/°) and on high spatial frequencies (0.79 cycle/°), where the largest number of voxels in the entire hMT+ complex was tuned for the low spatial frequency cluster. Although the limited spatial frequency sampling of our experiment does not allow us to draw a firm conclusion, we suggest that this effect may reflect the change in eccentricity across the visual field maps, or different responses in the MT and MST (or TO1 and TO2) subdivisions of the complex. A single neuron recording study in the homologue V5 area in monkeys showed different spatial frequency preferences within the area (higher for MT and lower for MST) in accordance with the increase in eccentricity in MST compared to MT (Huk et al., 2002). In humans, the visual field map TO2 has larger pRFs than TO1 (Amano et al., 2009; Kolster et al., 2010). Also, within both of these visual field maps, pRF sizes increase with eccentricity. Spatial frequency preferences typically decrease where pRF sizes increase, at higher eccentricities and in visual field maps with larger pRF sizes (Aghajari et al., 2020).
Finally, although the estimated optimal temporal frequency across participants were highly reproducible in cross‐validation, the stability of the temporal frequency spatial map within each bilateral ROI was not reproducible within participants. This can be due to the range of the temporal frequencies used in our experiment (from 1 Hz up to 5 Hz). It has been shown that the optimal contrast sensitivity of the primate visual system is found at approximately 8 Hz (Hawken et al., 1996; Himmelberg & Wade, 2019; Kastner et al., 2004). A recent fMRI study in humans shows a peak at around 10 Hz across visual areas independent of pRF size (Himmelberg & Wade, 2019). Further studies exploring a wider range of spatial and temporal frequencies may help elucidating the spatial organization of the complex with higher detail.
Overall, our findings suggest that the majority of hMT+ responses to speed change in accordance with the spatial frequency component of the visual motion stimuli. We speculate that speed tuning properties may emerge from non‐linear integration of patches within the MT complex preferring the same speed but different spatial frequency.
Then, at a later stage, this information is computed in other subregions within the complex as suggested by the presence of small patches showing speed tuning properties rather than separable responses. Moreover, the fact that hMT+ exhibited the same properties as the primary visual cortex V1 in encoding basic features of a visual stimuli, such as the spatial and temporal frequency components, is consistent with previous studies in both humans and primates showing that area MT receives, and is able to process, fundamental properties of the visual input directly from the thalamus, bypassing the V1 (Ffytche et al., 1995; Gaglianese et al., 2012; Sincich et al., 2004) and could explain the absence of deficit in biological motion perception in patients affected by congenital visual deprivation (Bottari et al., 2015). This fundamental low level mechanism of the hMT complex in processing visual motion features could explain the multisensory role of this area in encoding motion via other sensory modalities such touch and hearing (Avanzini et al., 2016; Gaglianese et al., 2020; Poirier et al., 2005; van Kemenade et al., 2014). Indeed, asensory specific areas rely on the process of task information (e.g. motion) responses based on specific low‐level properties of the input regardless the sensory modalities in which they are delivered (Amedi et al., 2017; Murray & Wallace, 2002).
6. CONCLUSION
We provided evidence of the coexistence within hMT+ of a functional selectivity for spatial frequency, with speed preference changing in accordance with the fundamental spatial component of the presented visual motion stimuli and of a mechanism of pure tuning for the speed of the motion. These findings suggest that speed encoding in hMT+ is more complex than initially thought and underline the role of this area in computing feature properties of visual stimuli in a similar manner as primary visual cortex.
ACKNOWLEDGMENTS
This work was supported by the Netherlands Organization for Scientific Research (NWO), Vidi Grant number 13339 (Natalia Petridou) and by the National Institute Of Mental Health of the National Institutes of Health under Award Number R01MH111417. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Alessio Fracasso is supported by a grant from the Biotechnology and Biology research council (BBSRC, grant number: BB/S006605/1) and the Fundação Bial, Fundação Bial Grants Programme 2020/21, A‐29315, number 203/2020, grant edition: G‐15516. Ben Harvey is supported by the Netherlands Organization for Scientific Research (NWO), Vidi Grant number 452.17.012 to Ben Harvey. This work was also supported by Marie Curie program grant funded to Anna Gaglianese, grant number DLV‐894612.
Gaglianese, A. , Fracasso, A. , Fernandes, F. G. , Harvey, B. , Dumoulin, S. O. , & Petridou, N. (2023). Mechanisms of speed encoding in the human middle temporal cortex measured by 7T fMRI . Human Brain Mapping, 44(5), 2050–2061. 10.1002/hbm.26193
Funding information Bial foundation, Grant/Award Numbers: A‐29315, 203/2020, G‐15516; Biotechnology and Biology research council BBSRC, Grant/Award Number: BB/S006605/1; H2020 Marie Skłodowska‐Curie Actions, Grant/Award Number: 894612; National Institute of Mental Health, Grant/Award Number: R01MH111417; Netherlands Organization for Scientific Research (NWO), Vidi Grant, Grant/Award Number: 452.17.012; Netherlands Organization for scientific research NWO VIDI grant, Grant/Award Number: 13339
Contributor Information
Anna Gaglianese, Email: anna.gaglianese@chuv.ch, Email: anna.gaglianese@gmail.com.
Natalia Petridou, Email: n.petridou@umcutrecht.nl.
DATA AVAILABILITY STATEMENT
All the analysis code can be obtained by emailing a request to the first author. Code used for the speed modelling results is available on a github repository: https://github.com/befrancislikeme/Encoding-spatiotemporal-frequencies-hMT. Sharing of data at this stage is not possible because we do not have consent from the participants to share their data. The authors will investigate if possible to get permission from the Ethics Review Board of the University Medical Center Utrecht to make anonymized processed data available upon request.
REFERENCES
- Aghajari, S. , Vinke, L. N. , & Ling, S. (2020). Population spatial frequency tuning in human early visual cortex. Journal of Neurophysiology, 123, 773–785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amano, K. , Wandell, B. A. , & Dumoulin, S. O. (2009). Visual field maps, population receptive field sizes, and visual field coverage in the human MT+ complex. Journal of Neurophysiology, 102, 2704–2718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amedi, A. , Hofstetter, S. , Maidenbaum, S. , & Heimler, B. (2017). Task selectivity as a comprehensive principle for brain organization. Trends in Cognitive Sciences, 21, 307–310. [DOI] [PubMed] [Google Scholar]
- Avanzini, P. , Abdollahi, R. O. , Sartori, I. , Caruana, F. , Pelliccia, V. , Casaceli, G. , Mai, R. , Lo Russo, G. , Rizzolatti, G. , & Orban, G. A. (2016). Four‐dimensional maps of the human somatosensory system. Proceedings of the National Academy of Sciences, 113, E1936–E1943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker, D. H. , Vilidaite, G. , Lygo, F. A. , Smith, A. K. , Flack, T. R. , Gouws, A. D. , & Andrews, T. J. (2021). Power contours: Optimising sample size and precision in experimental psychology and human neuroscience. Psychological Methods, 26, 295–314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bottari, D. , Troje, N. F. , Ley, P. , Hense, M. , Kekunnaya, R. , & Röder, B. (2015). The neural development of the biological motion processing system does not rely on early visual input. Cortex, 71, 359–367. [DOI] [PubMed] [Google Scholar]
- Costagli, M. , Ueno, K. , Sun, P. , Gardner, J. L. , Wan, X. , Ricciardi, E. , Pietrini, P. , Tanaka, K. , & Cheng, K. (2014). Functional signalers of changes in visual stimuli: Cortical responses to increments and decrements in motion coherence. Cerebral Cortex, 24, 110–118. [DOI] [PubMed] [Google Scholar]
- d'Avossa, G. , et al. (2007). Spatiotopic selectivity of BOLD responses to visual motion in human area MT. Nature Neuroscience, 10, 249–255. [DOI] [PubMed] [Google Scholar]
- Dale, A. M. (1999). Optimal experimental design for event‐related fMRI. Human Brain Mapping, 8, 109–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duijnhouwer, J. , Noest, A. J. , Lankheet, M. J. M. , van den Berg, A. V. , & van Wezel, R. J. A. (2013). Speed and direction response profiles of neurons in macaque MT and MST show modest constraint line tuning. Frontiers in Behavioral Neuroscience, 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumoulin, S. O. , & Wandell, B. A. (2008). Population receptive field estimates in human visual cortex. NeuroImage, 39, 647–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumoulin, S. O. , Bittar, R. G. , Kabani, N. J. , Baker Jr, C. L. , le Goualher, G. , Bruce Pike, G. , & Evans, A. C. (2000). A new anatomical landmark for reliable identification of human area V5/MT: A quantitative analysis of sulcal patterning. Cerebral Cortex, 10, 454–463. [DOI] [PubMed] [Google Scholar]
- Dumoulin, S. O. , Fracasso, A. , van der Zwaag, W. , Siero, J. C. W. , & Petridou, N. (2017). Ultra‐high field MRI: Advancing systems neuroscience towards mesoscopic human brain function. NeuroImage, 168, 345–357. 10.1016/j.neuroimage.2017.01.028 [DOI] [PubMed] [Google Scholar]
- Dumoulin, S. O. , Harvey, B. M. , Fracasso, A. , Zuiderbaan, W. , Luijten, P. R. , Wandell, B. A. , & Petridou, N. (2017). In vivo evidence of functional and anatomical stripe‐based subdivisions in human V2 and V3. Scientific Reports, 7, 733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emmerling, T. C. , Zimmermann, J. , Sorger, B. , Frost, M. A. , & Goebel, R. (2016). Decoding the direction of imagined visual motion using 7T ultra‐high field fMRI. NeuroImage, 125, 61–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ffytche, D. H. , Guy, C. N. , & Zeki, S. (1995). The parallel visual motion inputs into areas V1 and V5 of human cerebral cortex. Brain, 118, 1375–1394. [DOI] [PubMed] [Google Scholar]
- Fracasso, A. , Dumoulin, S. O. , & Petridou, N. (2021). Point‐spread function of the BOLD response across columns and cortical depth in human extra‐striate cortex. Progress in Neurobiology, 102, 34. 10.1016/j.pneurobio.2021.102034 [DOI] [PubMed] [Google Scholar]
- Fracasso, A. , Luijten, P. R. , Dumoulin, S. O. , & Petridou, N. (2018). Laminar imaging of positive and negative BOLD in human visual cortex at 7T. NeuroImage, 164, 100–111. [DOI] [PubMed] [Google Scholar]
- Gaglianese, A. , Branco, M. P. , Groen, I. I. A. , Benson, N. C. , Vansteensel, M. J. , Murray, M. M. , Petridou, N. , & Ramsey, N. F. (2020). Electrocorticography evidence of tactile responses in visual cortices. Brain Topography, 33, 559–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaglianese, A. , Costagli, M. , Bernardi, G. , Ricciardi, E. , & Pietrini, P. (2012). Evidence of a direct influence between the thalamus and hMT+ independent of V1 in the human brain as measured by fMRI. NeuroImage, 60, 1440–1447. [DOI] [PubMed] [Google Scholar]
- Gaglianese, A. , Costagli, M. , Ueno, K. , Ricciardi, E. , Bernardi, G. , Pietrini, P. , & Cheng, K. (2015). The direct, not V1‐mediated, functional influence between the thalamus and middle temporal complex in the human brain is modulated by the speed of visual motion. Neuroscience, 284, 833–844. [DOI] [PubMed] [Google Scholar]
- Gaglianese, A. , Fernandes, G. F. , Fracasso, A. , & Petridou, N. Spatial and temporal frequency selectivity in the human Middle Temporal cortex measured by 7T fMRI. in International conference for cognitive neuroscience (2017).
- Gaglianese, A. , Harvey, B. M. , Vansteensel, M. J. , Dumoulin, S. O. , Ramsey, N. F. , & Petridou, N. (2017). Separate spatial and temporal frequency tuning to visual motion in human MT+ measured with ECoG. Human Brain Mapping, 38, 293–307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner, J. L. , Sun, P. , Waggoner, R. A. , Ueno, K. , Tanaka, K. , & Cheng, K. (2005). Contrast adaptation and representation in human early visual cortex. Neuron, 47, 607–620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon, E. M. , Laumann, T. O. , Gilmore, A. W. , Newbold, D. J. , Greene, D. J. , Berg, J. J. , Ortega, M. , Hoyt‐Drazen, C. , Gratton, C. , Sun, H. , Hampton, J. M. , Coalson, R. S. , Nguyen, A. L. , McDermott, K. B. , Shimony, J. S. , Snyder, A. Z. , Schlaggar, B. L. , Petersen, S. E. , Nelson, S. M. , & Dosenbach, N. U. F. (2017). Precision functional mapping of individual human brains. Neuron, 95, 791–807.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey, B. M. , & Dumoulin, S. O. (2016). Visual motion transforms visual space representations similarly throughout the human visual hierarchy. NeuroImage, 127, 173–185. [DOI] [PubMed] [Google Scholar]
- Harvey, B. M. , & Dumoulin, S. O. (2017). A network of topographic numerosity maps in human association cortex. Nature Human Behaviour, 1, 36. [Google Scholar]
- Harvey, B. M. , Dumoulin, S. O. , Fracasso, A. , & Paul, J. M. (2020). A network of topographic maps in human association cortex hierarchically transforms visual timing‐selective responses. Current Biology, 30, 1424–1434.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey, B. M. , Klein, B. P. , Petridou, N. , & Dumoulin, S. O. (1979). Topographic representation of Numerosity in the human parietal cortex. Science, 341, 1123–1126 2013. [DOI] [PubMed] [Google Scholar]
- Hawken, M. J. , Shapley, R. M. , & Grosof, D. H. (1996). Temporal‐frequency selectivity in monkey visual cortex. Vision Research, 13, 477–492. [DOI] [PubMed] [Google Scholar]
- Henriksson, L. , Nurminen, L. , Hyvarinen, A. , & Vanni, S. (2008). Spatial frequency tuning in human retinotopic visual areas. Journal of Vision, 8, 5–513. [DOI] [PubMed] [Google Scholar]
- Himmelberg, M. M. , & Wade, A. R. (2019). Eccentricity‐dependent temporal contrast tuning in human visual cortex measured with fMRI. NeuroImage, 184, 462–474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holub, R. A. , & Morton‐Gibson, M. (1981). Response of visual cortical neurons of the cat to moving sinusoidal gratings: Response‐contrast functions and spatiotemporal interactions. Journal of Neurophysiology, 46, 1244–1259. [DOI] [PubMed] [Google Scholar]
- Huber, L. , Finn, E. S. , Handwerker, D. A. , Bönstrup, M. , Glen, D. R. , Kashyap, S. , Ivanov, D. , Petridou, N. , Marrett, S. , Goense, J. , Poser, B. A. , & Bandettini, P. A. (2020). Sub‐millimeter fMRI reveals multiple topographical digit representations that form action maps in human motor cortex. NeuroImage, 208, 116463. [DOI] [PubMed] [Google Scholar]
- Huk, A. C. , Dougherty, R. F. , & Heeger, D. J. (2002). Retinotopy and functional subdivision of human areas MT and MST. The Journal of Neuroscience, 22, 7195–7205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Issa, N. P. , Trepel, C. , & Stryker, M. P. (2000). Spatial frequency maps in cat visual cortex. Journal of Neuroscience, 20, 8504–8514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kastner, S. , O'Connor, D. H. , Fukui, M. M. , Fehd, H. M. , Herwig, U. , & Pinsk, M. A. (2004). Functional imaging of the human lateral geniculate nucleus and Pulvinar. Journal of Neurophysiology, 91, 438–448. [DOI] [PubMed] [Google Scholar]
- Klein, B. P. , Harvey, B. M. , & Dumoulin, S. O. (2014). Attraction of position preference by spatial attention throughout human visual cortex. Neuron, 84, 227–237. [DOI] [PubMed] [Google Scholar]
- Kolster, H. , Peeters, R. , & Orban, G. A. (2010). The retinotopic organization of the human middle temporal area MT/V5 and its cortical neighbors. The Journal of Neuroscience, 30, 9801–9820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, J. , & Newsome, W. T. (2003). Functional organization of speed tuned neurons in visual area MT. Journal of Neurophysiology, 89, 246–256. [DOI] [PubMed] [Google Scholar]
- Liu, J. , & Newsome, W. T. (2005). Correlation between speed perception and neural activity in the middle temporal visual area. The Journal of Neuroscience, 25, 711–722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lui, L. L. , Bourne, J. A. , & Rosa, M. G. P. (2007). Spatial and temporal frequency selectivity of neurons in the middle temporal visual area of new world monkeys (Callithrix jacchus). European Journal of Neuroscience, 25, 1780–1792. [DOI] [PubMed] [Google Scholar]
- Mante, V. , Frazor, R. A. , Bonin, V. , Geisler, W. S. , & Carandini, M. (2005). Independence of luminance and contrast in natural scenes and in the early visual system. Nature Neuroscience, 8, 1690–1697. [DOI] [PubMed] [Google Scholar]
- Mikellidou, K. , Frijia, F. , Montanaro, D. , Greco, V. , Burr, D. C. , & Morrone, M. C. (2018). Cortical BOLD responses to moderate‐ and high‐speed motion in the human visual cortex. Scientific Reports, 8, 8357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miura, K. , Inaba, N. , Aoki, Y. , & Kawano, K. (2014). Difference in visual motion representation between cortical areas MT and MST during ocular following responses. The Journal of Neuroscience, 34, 2160–2168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Movshon, J. A. (1975). The velocity tuning of single units in cat striate cortex. The Journal of Physiology, 249, 445–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray, M. M. & Wallace, M. T. (2002). The neural bases of multisensory processes. Boca Raton: CRC Press/Taylor & Francis. [PubMed] [Google Scholar]
- Perrone, J. A. , & Krauzlis, R. J. (2008). Spatial integration by MT pattern neurons: A closer look at pattern‐to‐component effects and the role of speed tuning, 8, 1–14. [DOI] [PubMed] [Google Scholar]
- Perrone, J. A. , & Thiele, A. (2001). Speed skills: Measuring the visual speed analyzing properties of primate MT neurons. Nature Neuroscience, 4, 526–532. [DOI] [PubMed] [Google Scholar]
- Petridou, N. , Italiaander, M. , van de Bank, B. L. , & Siero, J. C. W. (2013). Pushing the limits of high‐resolution functional MRI using a simple high‐density multi‐element coil design, 26, 65–73. 10.1002/nbm.2820 [DOI] [PubMed] [Google Scholar]
- Poirier, C. , Collignon, O. , DeVolder, A. G. , Renier, L. , Vanlierde, A. , Tranduy, D. , & Scheiber, C. (2005). Specific activation of the V5 brain area by auditory motion processing: An fMRI study. Cognitive Brain Research, 25, 650–658. [DOI] [PubMed] [Google Scholar]
- Priebe, N. J. (2006). Tuning for spatiotemporal frequency and speed in directionally selective neurons of macaque striate cortex. Journal of Neuroscience, 26, 2941–2950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe, N. J. , Cassanello, C. R. , & Lisberger, S. G. (2003). The neural representation of speed in macaque area MT/V5. The Journal of Neuroscience, 23, 5650–5661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe, N. J. , Lisberger, S. G. , & Movshon, J. A. (2006). Tuning for spatiotemporal frequency and speed in directionally selective neurons of macaque striate cortex. The Journal of Neuroscience, 26, 2941–2950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rezk, M. , Cattoir, S. , Battal, C. , Occelli, V. , Mattioni, S. , & Collignon, O. (2020). Shared representation of visual and auditory motion directions in the human middle‐temporal cortex. Current Biology, 30, 2289–2299.e8. [DOI] [PubMed] [Google Scholar]
- Schneider, M. , Kemper, V. G. , Emmerling, T. C. , de Martino, F. , & Goebel, R. (2019). Columnar clusters in the human motion complex reflect consciously perceived motion axis. Proceedings of the National Academy of Sciences, 116, 5096–5101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simoncelli, E. P. , & Heeger, D. J. (1997). A model of neuronal responses in visual area MT. Vision Research, 38, 743–761. [DOI] [PubMed] [Google Scholar]
- Sincich, L. C. , Park, K. F. , Wohlgemuth, M. J. , & Horton, J. C. (2004). Bypassing V1: A direct geniculate input to area MT. Nature Neuroscience, 7, 1123–1128. [DOI] [PubMed] [Google Scholar]
- Singh, K. D. , Smith, A. T. , & Greenlee, M. W. (2000). Spatiotemporal frequency and direction sensitivities of human visual areas measured using fMRI. NeuroImage, 564, 550–564. [DOI] [PubMed] [Google Scholar]
- Tolhurst, D. J. , & Movshon, J. A. (1975). Spatial and temporal contrast sensitivity of neurones. Nature, 257, 674–675. [DOI] [PubMed] [Google Scholar]
- Tootell, R. B. H. , & Nasr, X. S. (2017). Columnar segregation of magnocellular and parvocellular streams in human extrastriate cortex. The Journal of Neuroscience, 37, 8014–8032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tootell, R. B. H. , et al. (1995). Functional analysis of human MT and related visual cortical areas using magnetic resonance imaging. Journal of Neuroscience, 15, 3215–3230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Kemenade, B. M. , Seymour, K. , Wacker, E. , Spitzer, B. , Blankenburg, F. , & Sterzer, P. (2014). Tactile and visual motion direction processing in hMT+/V5. NeuroImage, 84, 420–427. [DOI] [PubMed] [Google Scholar]
- Yang, J. , Huber, L. , Yu, Y. , & Bandettini, P. A. (2021). Linking cortical circuit models to human cognition with laminar fMRI. Neuroscience and Biobehavioral Reviews, 128, 467–478. [DOI] [PubMed] [Google Scholar]
- Yu, H.‐H. , Verma, R. , Yang, Y. , Tibballs, H. A. , Lui, L. L. , Reser, D. H. , & Rosa, M. G. P. (2010). Spatial and temporal frequency tuning in striate cortex: Functional uniformity and specializations related to receptive field eccentricity. The European Journal of Neuroscience, 31, 1043–1062. [DOI] [PubMed] [Google Scholar]
- Yu, Y. , Huber, L. , Yang, J. , Fukunaga, M. , Chai, Y. , Jangraw, D. C. , Chen, G. , Handwerker, D. A. , Molfese, P. J. , Ejima, Y. , Sadato, N. , Wu, J. , & Bandettini, P. A. (2022). Layer‐specific activation in human primary somatosensory cortex during tactile temporal prediction error processing. NeuroImage, 248, 118,867. [DOI] [PubMed] [Google Scholar]
- Zimmermann, J. , Goebel, R. , de Martino, F. , van de Moortele, P. F. , Feinberg, D. , Adriany, G. , Chaimow, D. , Shmuel, A. , Uğurbil, K. , & Yacoub, E. (2011). Mapping the organization of axis of motion selective features in human area MT using high‐field fMRI. PLoS One, 6, e28716. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All the analysis code can be obtained by emailing a request to the first author. Code used for the speed modelling results is available on a github repository: https://github.com/befrancislikeme/Encoding-spatiotemporal-frequencies-hMT. Sharing of data at this stage is not possible because we do not have consent from the participants to share their data. The authors will investigate if possible to get permission from the Ethics Review Board of the University Medical Center Utrecht to make anonymized processed data available upon request.


