Geophysical and numerical stability analysis of landslide incident

Abstract

Landslide is known for its precarious impact on environment, resources and human life. Recently, landslide has occurred in Lalisa village, Jimma Zone, Ethiopia which harshly caused damage to life and property. The incident resulted in perilous damage of about 27 ha of accessible land. This study hence particularly aimed at investigating the root cause of the incident and analyzing safety of the sliding slope so that the applicable remedial actions can be proposed. Geophysical analysis without soil structure disturbance was adopted to investigate the vertical soil profile, morphological stratification, location and alignment of discontinuity planes. Stability analysis by using Limit Equilibrium method was carried out for both normal and worst conditions to rate safety of the failing slope. Lithology of the site is characterized by highly weathered and fractured rock units exhibiting a significant variability over a little horizontal distance and depth. The stratigraphy also constitutes loose soil near the surface and saturated layer ranging from depth of 10 m to 25 m. The slope failure occurred at the site is of deep by its type that origin of its slip plane extends up to a depth of 12 m from the surface. Furthermore, factor of safety of the slope along the failed zone fell below 1.5 with the maximum value of 1.303 for the normal condition. The conducted investigation also indicated that the detachment and propagation of the sliding mass develops much faster with rise in soil moisture content whereas it categorically remains mild during dry seasons. Hence, the driving agent for the occurrence and propagation of the landslide incident was rainfall infiltration and the existence of weak saturated zone at the stated depth.

1. Introduction

Landslides represent the directly gravity-driven component of soil or rock mass, ranging in size from individual rocks falling to whole mountainsides collapsing [1]. Landslides commonly happen in areas characterized with rugged topography where ground displacement is of random and fast which makes the condition so tough to fully control and prevent. But mitigation measures to lessen the resulting impact can possibly be taken [2]. According to M.T. Daniel et al. [2], the influencing aspects of land slide include slope gradient, ground saturation and land cover in addition to some geological features (degree and depth of weathering, soil type, type and structure of rock).

As studied by A. Nemcok, J. Pasek and J. Rybar [3], the main agents of landslide occurrence in vulnerable areas are geomorphological, geological and hydrological features of the areas. However, A. O. Oliva-Gonzalez et al. [1] pointed out that in sloppy landscapes the landslide incident does not necessarily emanate only from the critical combination of geomorphological, geological and hydrological conditions, but also induced by heavy rainfall and rearrangement because of geodynamic processes in a soil mass situated along the sliding zone. According to S. Dapporto et al. [4], the commonly known major external stimulus considered as direct triggering factors of land slide are intense rainfall, earthquake shaking, water level change, deforestation, storm waves, or rapid stream erosion. Furthermore, M. Jakob and H. Weatherly [5] reported that heavy rainfall is the most frequently encountering challenge inducing landslides in tropical and temperate climatic zones [6,7].

There are two commonly applied methods for stability analysis of slopes in geotechnics. The first conventionally used approach is limit equilibrium method (LEM) and the other one is finite element method (FEM). From accuracy and effectiveness perspective, the latter is more powerful than the former [8]. Application of finite element method for stability of slopes can be executed either with the principle of limit analysis or displacement based FEM [9,10]. The limit analysis FEM combines both numerical analysis and classic limit analysis method [11]. Unlike the finite element method, limit equilibrium analysis method does not require information on stress-strain behavior of soil hence provides no information regarding magnitude of movements of slope [[12], [13], [14], [15], [16]]. Besides, V. Janták [8] in his study in which he analyzed stability of landslide on expressway by using both finite element and limit equilibrium methods, pointed out that more convincing results are obtained when numerical analysis approach is adopted in which the ambiguous and conservative assumptions made in limit equilibrium method are partially or fully avoided and hence certainty of the analysis can be improved. Finding of the study also revealed that the factor of safety values obtained through analytical method appeared to be so exaggerated figures than that of the finite element analysis. According to W.U. Weigao [9], limit analysis is more rigorous than limit equilibrium method even though it is less attractive due to its dependency on mesh density and computational capacity available.

Factors of safety play paramount role in stability analysis of slopes as well as in slope engineering design [17]. However, it is impossible to fully pinpoint the exact origin and propagation axis of the detached soil mass along inclined surfaces by using only stability analysis of sliding slopes through numerical or analytical approaches [12,[18], [19], [20], [21], [22], [23], [24]].

In relation to this, M.S. Akram et al. [14] posits that any investigation and analysis made on land slide requires careful and comprehensive model so as to generate more detailed and acceptable findings especially with regard to alignment and depth of slip planes. Because, the conventional slope stability analysis methods hardly speak about intensity and severity of collapsing slope. Similarly, M.T. Daniel et al., J. J. Clague and O. Korup [1,2] stated that investigation of the causes, unique characteristics and the nature of landslides have to be supported with purposive integration of various exploration methods like geological and geophysical analyses.

The type and applicability, effectiveness of the mitigation measures to be taken to manage the precarious impacts of land slide depends on various factors like slope gradient, size of affected area and population density [25]. According to E. N. Bromhead [26], removal of all or part of the sliding mass to modify slope geometry is one of the effective mitigation mechanisms typically applied in shallow landslides and in areas where volume of the sliding mass is not massive. As indicated by L.K. Sharma et al. [15], drainage is also another widely accepted and viable safety factor improvement approach used for slope stabilization. Surface and subsurface drainage systems should have a capacity to decrease development of pore water pressure at the failure surface. J. N. Hutchinson [27], also indicated that drainage is the principal measure used in the repair of landslides. In addition to this, vegetation cover also has an imperative role in stabilizing landslides by reducing pore water pressure through evapotranspiration and controlling infiltration. Most importantly, the binding action of plant root system is critical in keeping blocks of collapsing mass together specially in shallow landslides. Apart from these conventionally practiced measures, Z. Zakaria et al. [17] proposed a mitigation method named Starlet Model. It is slope stabilization and soil movement mitigation method designed with critical combination of engineering and social aspects through environmental management and monitoring which comparatively makes it versatile and inclusive.

In the existing literatures, effectiveness of the combined application of numerical and geophysical methods for stability analysis of failed slopes has not been documented. In the current study hence stability analysis of the failing slope is carried out by using both geophysical and numerical approaches. Geotechnical and geophysical investigations were conducted in order to characterize lithological set up of the site and identify causes of the incident. Likewise, stability analysis of the slope was undertaken through numerical modeling with the principle of limit equilibrium.

2. Material and methods

2.1. Overview of the study area

Lalisa village (study area) is geographically located in Jimma Zone, South Western part of Ethiopia at about 320 km away from Addis Ababa, metropolis of the country (Fig. 1(a), (b), (c), (d)). It is geographically bounded between 07° 59′ 126.0″ N 037° 18′ 289″ E and 07° 54′ 59″ N 037° 18′ 59″ E with elevation ranging from 2106 m to 2176 m above sea level. Its climatic condition was warm humid with an average temperature varying between 11 °C and 30 °C and inter-annual rainfall variability of 1900 ± 800 mm.

Fig. 1.

Location map of the study area: (a) Location of the site in Ethiopia, (b) Location of the site in the state Oromia, (c) Location of the site in Jimma Zone, (d) Specific location of the site in Lalisa Village.

The area is of densely populated where farmers whose livelihood is fully dependent on traditional agricultural practices have been living. The incident came out in the area where farm land is highly significant resource to support life of the resident community. Due to the landslide, a total of about 27 ha of farm and grazing land was left out of use. Accessing the affected zone for anything is unthinkable due to the erratic ground displacement and development of wide open cracks from time to time. Consequently, hundreds of residents were forced to be displaced which seriously exposed them to inconvenience and disturbance to their livelihood. Hence, the limited accessibility of the area made it very sensitive threat to livestock and human life as well. The area is almost bare land which was deforested for agricultural purpose except a few sparsely observed trees over a large area of land.

2.2. Reconnaissance of the site

A careful reconnaissance survey was made and dwellers of the area were also contacted so as to collect the required preliminary data. Accordingly, the presence of small spring at the toe of the slope, development of scars, large surface cracks, ground subsidence, destruction of natural features, damages and tilting of plants, affected farm and grazing land, landscape disturbance, and alteration of topography were among the witnessed occurrences during the site reconnaissance (Fig. 2(a), (b), (c), (d)). Additional information obtained during the site visit was that propagation of the detached soil mass develops fast during rainy seasons and remains relatively inactive during dry seasons. The cracks formed because of downward and outward movement of sliding mass begin opening wide immediately as rainy season enters.

Fig. 2.

Photo captures of the site indicating down ward and outward movement of soil mass.

The area is predominantly covered by red clay soil probably originated from highly weathered and fractured rock mass. The top exposed portion of the soil mass is of very loose, compressible and residual by its nature. Small seasonal stream flows at toe of the collapsing slope and movement of the sliding mass is transversely to the direction of stream flow. Starting point of the detachment is at about 500 m away from the slope toe. Landscape of the study area (landslide site) is characterized by its sloppy topographical feature with the natural gradient varying between 30° and 52°.

2.3. Geophysical investigation

In addition to the painstakingly conducted site reconnaissance, geophysical methods were also used for investigating ground formation of the site. Geophysical surveys were under taken to indirectly determine the extent and nature of the geologic materials beneath the surface. The geophysical survey adopted in this study was Electrical resistivity method. The method was used to verify variation of resistivity with depth with the most commonly employed technique, namely vertical electrical soundings (VES). It provides detailed information on the vertical succession of various conducting zones, their individual thicknesses and true resistivity. In other words, the method can be used to obtain quickly and economically details about the location, depth and resistivity of subsurface formations. Schlumberger array electrode arrangement was used so as to keep the effect of shallow resistivity variation constant and to save time and labor because most of the time only two electrodes need to move in the system. The basis for making VES is that a deeper vertical penetration or probing will be achieved by expanding electrode spacing between readings. Accordingly, VES was conducted by a maximum distance of current electrodes of 1000 m (AB/2 = 500 m), and maximum potential electrode distance of 90 m (MN/2 = 45 m). A total of two vertical electrical soundings were carried out along both outlet and inlet of the slope with electrodes configured parallel to the detachment axis which is parallel to direction of the small stream flow. Besides, one vertical electrical profiling was conducted at a midpoint between the slope inlet and outlet.

2.4. Geotechnical investigations

In order to conduct laboratory tests, disturbed and undisturbed representative soil samples were collected from test pits indicated in Fig. 3 and the boreholes were dug up to 16 m depth. The required soil samples were taken from two different points (slope inlet and slope outlet) along the sliding mass. Hence, the geotechnical investigation was conducted for the two points. Both test pits (Test Pit 1 and Test Pit 2) are situated along the failed slope. The first test pit (Test Pit 1) and the second test pit (Test Pit 2) are situated at slope inlet and outlet respectively. Even though two test pits were considered for geotechnical characterization of the subsurface material, average values of the soil parameters obtained from the two test pits were used for the numerical slope stability analysis. As indicated in Table 1, no noticeable variation in properties of the soil material is observed between the slope inlet and outlet. Soil samples were taken from depths of 0.5 m, 8 m and 16 m in order to determine some engineering properties of the ground materials. Accordingly, soil laboratory tests like Unit weight determination; Atterberg Limits (Liquid limit, Plastic limit and Plastic index), Specific gravity, Permeability and Triaxial Compression (Cohesion and friction angle) were carried out (Table 1).

Fig. 3.

The specific location of test pits; Test pit 1 (07°58′08.48″N, 37°23′14.93″ E) and Test pit 2 (07°58′09.44″N, 37°23′13.25″E).

Table 1.

Some physical and mechanical properties of the soil found in the study area.

Soil Properties	At slope inlet			At slope outlet
		Depth (m)			Depth (m)
	0.5 m	8 m	16 m	0.5 m	8 m	16 m
Unit Weight (kN/m3)	16.73	17.82	18.64	17.00	17.88	18.76
Water content (%)	37.25	40.41	43.83	38.49	44.23	45.02
Liquid Limit (%)	65.79	62.00	61.25	66.15	63.00	66.00
Plastic Index (%)	34.04	30.92	30.23	33.62	33.52	31.56
Initial Void Ratio (eo)	0.70	0.71	0.71	0.72	0.70	0.72
Specific Gravity (Gs)	2.66	2.68	2.68	2.67	2.69	2.70
At rest lateral earth coefficient (Ko)	0.44	0.45	0.45	0.41	0.42	0.45
Poisson's Ratio	0.35	0.34	0.34	0.35	0.35	0.33
Eur (kPa)	13,020	13,810	15,658	13,116	14,701	16,014
E50 (kPa)	1860	1902	2014	1885	2117	2619
Eoed (kPa)	5560	5926	6258	5801	6004	6607
Cohesion (kPa)	34	33	33	36	35	33
Friction Angle (o)	17	19	19	17	18	19
Permeability, k (cm/s)	0.006152	0.00428	0.005614	0.00584	0.00561	0.00467
Field density (g/cc)	1.605	1.716	1.8	1.633	1.722	1.812

2.5. Numerical analysis

The slope stability analysis was carried out by using Limit Equilibrium based Slope W 2D package. Various limit equilibrium methods have been developed to analyze stability of natural or engineered slopes. These methods differ from one another in two aspects: i) the assumptions made to make up the balance between the number of equations of equilibrium and the number of unknowns and ii) assumptions regarding location and orientation of the internal forces. Stability analysis of the slope was carried out with the principles and applicable assumptions of Morgenstern-Price method. Among all developed methods, Morgenstern-Price analysis method is considered to be the least conservative limit equilibrium method used [28].

The soil layers considered for numerical slope stability analysis anonymous to lithological set up and stratigraphy identified through the conducted electrical resistivity survey. Accordingly, the model geometry considered for the analysis has a depth of 32 m and width of 38 m (Fig. 7, Fig. 8, Fig. 9, Fig. 10). The dimensions (depth and width) of the model used for the numerical simulation corresponds to depth of the weak zone identified via the geophysical method which is approximately between 10 m and 25 m. To intentionally incorporate the weak zone in the entire geometry of the numerical model hence depth of 32 m was considered and it is believed to be sufficient. Depth of the model was fixed based on result of the geophysical investigation. Since entire length of the sliding slope is 500 m long, it is difficult to numerically model entire stretch of the slope using a single model. Due to extension of the failing slope over large area, only certain segment of the slope was considered for the stability analysis. Accordingly, two segments having width of 38 m and depth of 32 m each were modelled for two different gradients. The first segment is situated around inlet of the slope whereas the second segment is part of the slope outlet. The first considered gradient is the real existing gradient of the failing slope whereas the second gradient is less in magnitude than actual gradient of the slope. The second gradient was considered as if inclination of the slope was modified by 10% (assumed). This was purposely done to investigate the effect of gradient on factor of safety values. Accordingly, condition 1 and 2 have the same gradient with the natural slope whereas condition 3 and 4 represents the modified slope gradient. In relation to this, the first segment of the slope (passing through C1 and T1) was modelled in condition 1 and 3 and the second segment (passing through C2 and T2) was modelled in condition 2 and 4.

Fig. 7.

Critical slip surface and FOS for natural slope of T1 and C1: a) Wet condition, b) Dry condition.

Fig. 8.

Critical slip surface and factor of safety for natural slope at T2 and C2: a) Wet condition, b) Dry condition.

Fig. 9.

Critical slip surface and FOS of the modified slope gradient at T1 and C1: a) Wet condition, b) Dry condition.

Fig. 10.

Critical slip surface and FOS for the modified slope gradient at T2 and C2: a) Wet condition, b) Dry condition.

Crest of the first segment (C1) and toe of the second segment (T2) are the actual point on the ground where the slope surface starts getting inclined and its gradient begin becoming zero respectively. However, toe of the first slope segment (T1) and crest of the second slope segment (C2) are author defined points along the sliding slope anonymously detected by Slope W as end point of the first segment and beginning of the second one respectively. Length of the backslope in each condition was intentionally varied in order to incorporate the effect of variation in backslope length on magnitude of slope safety factor. The critical failure surfaces were not manually predefined in the model. They are rather part of outputs of the numerical simulation. Even though dimensions of the backslope is different from model to model, the soil properties and other input parameters remain unchanged. Besides, gradient of the slope surface is the same for the comparable conditions.

The simulation incorporated the model geometry made of four different soil layers with their own typical properties. The top most (upper layer) is purely red clay relatively with expansive characteristics and the second layer (middle layer) is dark clay with some fractions of silt. Similarly, the third (lower layer) and the fourth layers are sandy clay and highly weathered rocks of granular nature respectively. In order to investigate the critical effect of moisture fluctuation on safety factor of the slope, simulation was done both for normal case (dry condition) and worst case (wet condition). The input parameters (soil properties) used for the numerical analysis were summarized in Table 2. Location of the weak zone or detachment depth was detected by the geophysical investigation. In detecting the probable depth of weak zone, geophysical methods are more preferred than numerical approaches. The LEM stability analysis however speaks more about safety of the failing slopes based on the magnitude of calculated safety factors. The LEM based numerical analysis hardly speaks about the exact depth and location of weak zone except the arbitrarily defined inclined slip planes. In order to overcome this challenge hence the LEM was executed in combination with geophysical analysis.

Table 2.

Properties (input parameters) of the layers used for numerical model.

Soil Properties	Top layer	Middle layer	Bottom layer	Fractured rock
Unit Weight (kN/m3)	16.08	17.32	17.15	18.40
Water content (%)	38.00	39.64	42.14	40.38
Initial Void Ratio (eo)	0.71	0.72	0.72	0.71
Specific Gravity	2.67	2.68	2.68	2.70
At rest lateral earth coefficient (Ko)	0.44	0.44	0.45	0.40
Poisson's Ratio	0.35	0.35	0.35	0.25
Eur (kPa)	13,621	13,774	14,907	15,106
E50 (kPa)	1775	1954	1983	2082
Eoed (kPa)	5112	5871	6008	6349
Cohesion (kPa)	33	33	32	21
Friction Angle (o)	16	15	15	20
Compression Index, Cc	1.31	1.3	1.3	–
Recompression Index, Cr	12.62	12.18	11.67	–

3. Results and discussions

3.1. Vertical electrical profiling survey

The results of electrical profiling based geophysical survey are function of apparent resistivity and current electrode separation. Different layers of electrical resistivity were derived from the generated profiling image at midpoint between inlet and outlet of the slope. Fig. 4(a) depicts site electrical profiling specifically at the maximum investigated depth (the center point is in focus) and Fig. 4(b) shows the vertical electrical profiling for offsets with uniform depth. The profiling identified potential ground water depth and the contoured lithological arrangement of the specific area. Resistivity of the profile over the depth of 114 m ranges from 10.8 Ωm to 532 Ωm. Variation in resistivity values of the stratigraphy along the profile lines indicates variation in soil matrix, grain size distribution and saturation within the specified depth. Even though electrical resistivity of soils is critically a function of factors like temperature, moisture, chemical content, cation exchange capacity, nature and arrangement of solid grains, hydraulic conductivity and salinity [29], M. Long et al. [30] categorized soils into three major groups based on their resistivity values. Soils with high conductivity but lower resistivity (1–10 Ωm) are literary considered as non-leached clay deposit whereas leached clay deposit, silt and fine grained till have resistivity values ranging from 10 to 100 Ωm. Besides, bedrocks have higher resistivity sometimes over 100 Ωm [30].

Fig. 4.

The two-dimensional site electrical profiling: (a) the center point is in focus, (b) uniform depth for all offsets.

Accordingly, the soil strata extending from 10 m to 25 m below the ground surface experiences low resistivity but high conductivity values in the study area which signify presence of saturated, highly fractured and weathered material. These layers of soil are the regions where soil mass detachment began due to development of weak zone which led to further propagation of movement along the slanted surface. In contrast, highly fractured and weathered rock with high resistivity (greater than 500 Ωm) was detected at shallow depths. The electrical profiling survey result also revealed that ground water is situated at depth of less than 15 m at some points along the affected area.

3.2. Vertical electrical sounding (VES)

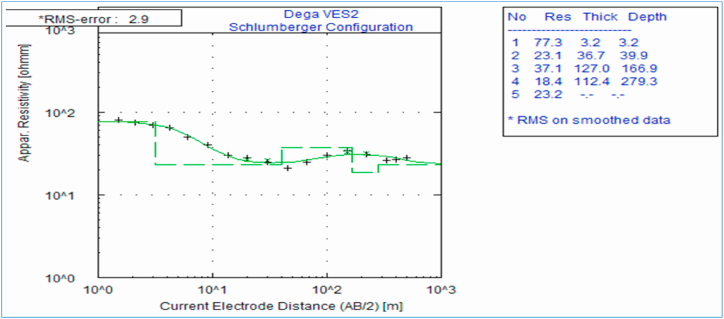
The resistivity inversion model VES along electrical resistivity tomography of the site both at inlet and outlet of the slope was given in Fig. 5, Fig. 6 respectively. Accordingly, five geo electrical layers with distinct properties and varying thicknesses were known to appear within the 225 m investigation depth at the slope inlet (Table 3). The result of the first VES survey gave a five layer model of resistivity ρ1 > ρ2 < ρ3 > ρ4 < ρ5. The first three top layers (0–58.5 m) belong to the same rock family in their formation even though a little disparity is observed in their degree of weathering which irregularly varies with depth. The top 3 m thick layer is of red clay type with expansive and shrinking typical characteristics upon variation of soil moisture. The massive fourth layer having a thickness of 166.5 m experienced the lowest resistivity. This massive layer was bedded between layers of relatively high resistivity and was originated from pyroclastic rocks (Table 3).

Fig. 5.

Resistivity inversion model at slope inlet.

Fig. 6.

Resistivity inversion model at slope outlet.

Table 3.

Summary of the Lithological set up at slope inlet.

Layer	Resistivity (ohm m	Thickness (m)	Depth (m)	Inferred Lithology
1	42.2	3.0	3.0	Highly weathered and loose soil
2	25.7	16.2	19.3	Moderately fractured and weathered ignimbrite deposit
3	141.2	39.2	58.5	Highly fractured and weathered ignimbrite massive ignimbrite
4	10.6	166.5	225.0	Moderately weathered pyroclastic rock
5	42.9	–	–	Highly weathered pyroclastic deposit

Similarly, five layers were identified within the investigation depth of 279.3 m at slope outlet. The result for the second VES gave five layer model of resistivity ρ1 > ρ2 < ρ3 > ρ4 < ρ5. Resistivity values of the layers revealed no regular decrement or increment with respect to variation in depth that it is erratic record. This indicates that the degree of weathering of the soil stratigraphy is not necessarily a function of depth of the layers from ground surface. Lithology of the layers at the two points (inlet and outlet) is almost similar and no significant alteration were observed. For the surveying conducted at slope outlet, the soil layer with the least resistivity value (18.4 Ωm) was located at bottom end of investigated depth whereas the first top layer has the largest resistivity (Table 4). The electrical sounding survey result also revealed that only the first layer is clay by its nature whereas the other layers are weathered ignimbrite and pyroclastic rocks.

Table 4.

Summary of the Lithological set up at slope outlet.

Layer	Resistivity (ohm m)	Thickness (m)	Depth (m)	Inferred Lithology
1	77.3	3.2	3.2	Highly weathered and erodible deposit
2	23.1	36.6	39.9	Slightly fractured pyroclastic rocks
3	37.1	127.0	166.9	Fractured and weathered ignimbrite rocks massive ignimbrite
4	18.4	112.4	279.3	Slightly weathered pyroclastic rock
5 5	25.2	–	–	Weathered pyroclastic rocks

3.3. Stability analysis of the slope

3.3.1. The critical slip surface

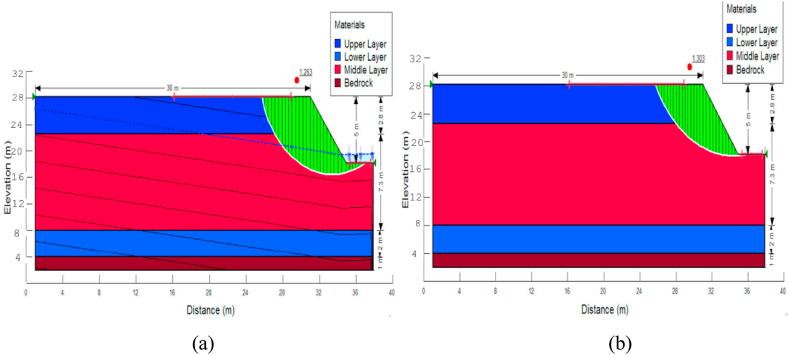
The critical slip surfaces (CSS) and factor of safety (FOS) of the slope for four different conditions of wet and dry slope are presented in Fig. 7 through 10. Condition 1 and 2 represents the existing natural state of the collapsing slope without applying any mitigation measure so as to improve its stability for the slip plane passing through Toe 1 (T1) and Crest 1 (C1). Likewise, condition 3 and 4 represents the modified slope as if inclination of the slope is reduced for the slip plane passing through Toe 2 (T2) and Crest 2 (C2). Fig. 7, Fig. 8, Fig. 9, Fig. 10 represent the wet conditions. The conducted numerical analysis revealed that the critical failure surface in normal condition passes below toe of the slope whereas it directly coincides with slope toe in dry condition. The failure plane extends up to bottom side of the slope toe in wet condition which increases depth of the slip from ground surface. It also leads to significant augmentation in volume of the sliding mass which is an evident for the fact that propagation and displacement of falling slope at higher rate literally is witnessed during rainy seasons due to acute rise in ground water level. Likewise, the massive slip surface passing below the toe of the slope in wet condition was due to ground water effect. Fig. 7, Fig. 8, Fig. 9, Fig. 10 represent simulation of CSS and FOS for dry conditions.

Condition 1

CSS and FOS at T1 and C1

Condition 2

CSS and FOS at T2 and C2

Condition 3

CSS and FOS for modified slope gradient at T1 and C1

Condition 4

CSS and FOS determination of the modified slope gradient at T2 and C2

An increase in ground moisture content during winter season resulted in gradual development of destabilizing stress along the inclined soil mass which in turn adversely perpetuates displacement rate of the sliding mass. Accordingly, rise in ground water table up to the level of slope toe lessened the apparent factor of safety by an average of 6.75%. The numerical analysis result also revealed that the negative impact of moisture content and ground water table rise is more sensitive in steep slopes than gentle slopes. Besides, the critical angle (the maximum safest inclination) of the slope in normal condition was found to be 44.2° whereas the slope no more remains safe above 36.4° inclination in the worst case scenario. The significant difference observed between critical angles of the two cases is obviously due to moisture and ground water effect. Furthermore, as indicated in Fig. 8, Fig. 9 reducing the slope gradient by 34.62% improves safety factor of the slope by 24.1% and 6.5% for wet and dry conditions respectively. This implies that reshaping and modifying topographic configuration of the area is critical in mitigating stability of slopes through decreasing driving (destabilizing) forces.

3.3.2. Free body diagram and force polygon

The Morgenstern Price analysis method satisfies the static equilibrium conditions (force and moment equilibriums). Hence, factor of safety of slopes is computed both for force and moment equilibrium and interslice forces are calculated by iteration procedure until the stabilizing stress equals the destabilizing stresses. In this method, the interslice force inclination varies with an arbitrary function f(x) as illustrated in Equation (1). As indicated in Fig. 11, the force polygon closure is very good since both shear and normal inter slice forces are included.

$$T=f(x)\lambda E$$ (1)

Fig. 11.

Free body diagram and force polygons of Morgenstern-Price method for the conditions.

Where f(x) is interslice force function that varies continuously along the slip surface, λ is scale factor of the assumed function and (T,E) is combination of interslice shear and normal forces. Fig. 11(a), (b), (d) and (f) depicts force polygon for wet condition 1, 2, 3 and 4 respectively. Similarly, Fig. 11(c), (e) and (g) depicts force polygon for dry condition 2, 3 and 4 respectively.

3.3.3. Factor of safety determination and slide mass

Table 5 shows the characteristics of sliding mass in terms of weight, volume, moment and body force. As indicated in the table, the maximum and the lowest safety factor was obtained in the fourth condition (Modified slope angle at T2 and C2) and the first condition (at T1 and C1) respectively. The factor of safety values derived from the conducted numerical analysis ranges from 0.993 to 1.263 for the wet condition of the natural slope whereas it falls in the range of 1.064–1.303 for the normal case (dry condition). Similarly, under application of inclination modification, factor of safety varies between 1.261 and 1.401 for wet condition and between 1.401 and 1.514 for the normal condition. Hence, factor of safety of the dry slope is by far greater than that of wet slope due to the driving effect of pore water pressure. It can be inferred that safety factor of the collapsing slope falls below 1.5 which is conventionally the lowest margin of safety considered in many practices of slope stability analysis.

Table 5.

Summary of slide mass and factor of safety of different conditions.

Conditions		TV	TW	TRM	TAM	TRF	TAF	FOS	Remark
1	Wet	15.97	316.98	1022.60	1028.90	123.53	124.4	0.993	unsafe
	Dry	15.97	317.01	1115.40	1048.10	133.22	125.25	1.064	AF
2	Wet	33.03	657.35	2405.70	1905.20	241.91	191.52	1.263	AF
	Dry	24.36	487.77	2616.50	2007	220.29	169.05	1.303	AF
3	Wet	31.8	636.68	2202.60	1746.50	222.87	176.79	1.261	AF
	Dry	22.28	444.23	2517.30	1797.70	208.77	149.01	1.401	AF
4	Wet	58.28	1150.20	4365.90	3115.90	355.59	253.79	1.401	AF
	Dry	26.47	524.08	2233.80	1475.60	230.46	152.28	1.514	stable

According to Bowles J E [31], slope conditions can be summarized under three categories based on the value of safety factor. The conditions where factor of safety remain less than 1.07 (labile), are characterized by usual occurrence of collapse. Similarly, slope collapses that ever occurred usually have factor of safety in a range of 1.07–1.25 (critical) and rarely collapsing slopes are known for their larger safety factor literally exceeding 1.25 (stable). Almost at all points along the collapsing slope, the numerically obtained safety factors fell in the range of 1.07–1.25 for the dry case which is critical by its consequences. In contrast, the magnitude of safety factors in the worst case entirely remained below 1.07 which is a good indicator for the incident's labile condition.Where, TV is total volume, TW is total weight, TRM is total resisting moment, TAM is total activating moment, TRF is total resisting force, TAF is total activating force, FOS is factor of safety and AF represents approaching to failure.

3.3.4. Safety map of the slope

Safety map is an effective way of graphically viewing a summary of the trial slip surfaces. All the valid trial slip surfaces are grouped into bands with the same factor of safety. Starting from the highest factor of safety band to the lowest factor of safety band, these bands are painted with a different color. The result is a rainbow of colors arranged in a systematic sequential order. Colors representing region with the lowest factor of safety band is painted on top of the rest of the color bands. Accordingly, the green colored portion of soil mass situated on the top is the region experiencing lowest safety factor.

Fig. 12 illustrates safety map of the slope for Morgenstern-Price analysis method. This kind of presentation clearly shows location of the critical slip surface with respect to all trial slip surfaces. The arch shaped white band indicates the probable location of critical slip surface. Thickness of the white band is very small in Morgenstern‐Price analysis method comparatively with other methods of stability analysis.

Fig. 12.

Safety map of the slope.

3.3.5. Classification of the landslide

The landslide is classified as rotational type because of the developed curved failure surface. The resulting displacement was outward and downward along the circular plane. The slip plane assumed curved shape and bulging out of soil mass at slope toe was observed. From depth point of view, the weak plane originates from a depth of greater than 10 m and hence the landslide (slope failure) is considered as deep landslide. According to J. Dou et al. [32], shallow landslides are landslides having depth between 1.5 m and 10 m from the existing ground surface. Likewise, landslides originating from depths greater than 10 m are generally considered as deep landslides.

Depth of the discontinuous zone was confirmed by the standard penetration test. Penetration resistance of the ground up to a depth of 36 m was tested. As indicated in Fig. 13 the strata situated between 10 m and 25 m experiences low values of resistance to penetration. This implies that the stated zone is of less dense and highly weathered comparatively with the top and bottom bounding layers. It is water bearing strata as well.

Fig. 13.

The SPT result at intermediate point between crest and toe of the slope.

3.4. Probable causes of the slope failure

Erosion, earthquakes, rainfall, external loading and tension cracks are some of the commonly known triggering factors of slope failure [4]. However, none of these factors are attributed to the existing reality of the area except erosion and rainfall which is typical characteristics of the site. The area has not experienced any earthquake and is not subjected to any externally applied load as well. Contrarily, it receives high precipitation especially during rainy season and it is also topographically exposed to erosion due to its high gradient and sparse vegetation cover.

According to the data collected from local residents and the careful reconnaissance survey conducted on the site, advance of the incident becomes more severe during rainy seasons whereas it completely remains mild during the dry times. The metrological data obtained from zonal agricultural office also indicated that the most pronounced precipitations are recorded during wet season especially from June to August.

S. Dapporto et al. [4] stated that shallow landslides usually less than 2 m depth are primarily caused by intense rainfall encountered during the rainy season. This type of land slide is commonly triggered by infiltration of rainfall. In contrast, M. Jakob and H. Weatherly [5] posits that the adverse effect of rainfall infiltration is not basically limited to shallow slides that it can precariously extend to greater depths giving rise to a massive downward and outward displacement of soil mass along falling slopes.

In relation this, the nature of landslide encountered in the study area is of deep in its type. Point of origin of the incident is hence the highly weathered and saturated zone situated between depths extending from 10 to 25 m. As observed from the conducted field investigation, ground water was detected within the stated range of depth. Slip plane was also developed in the stated layer due to the driving effect of rain water in perpetuating rate of the slide. Hence, the root cause of the incident is rainfall in filtration, which results in an increase in water content and reduction in matric suction in the soil.

3.5. Remedial measures to be taken

According to E. N. Bromhead, V. Ranjan et al. [26,33], there are three categories of commonly used slope stabilization techniques (Geometric, Hydrological, and Chemical and mechanical) in geotechnics. The existing reality of the affected area however calls for some mechanical and hydrological techniques whereas application of the geometric techniques is not found to be feasible.

Accordingly, one of the hydrological techniques recommended to be applied is diversion of flow direction of the existing small stream. The geophysical investigation results indicated that the water bearing strata found between depths of 10 m and 25 m is hydraulically connected with the stream and hence it is the zone which probably recharges the flowing stream. Existence of the water bearing layer highly increases the driving force (destabilizing force) of the falling slope which perpetuates displacement rate of the sliding mass. Hence, systematically diverting flow route of the stream outside the unstable zone can significantly improve safety of the slope in lessening soil mass sliding due to drainage. However, the diversion work should be preceded by painstakingly conducted environmental and social impact assessment not to introduce additional problem [34].

Due to its high gradient, topography of the site supports rapid flow of runoff water which increased its vulnerability to gully erosion. Hence, extensive plantation of light weight Rooty trees can reduce the adverse effect of erosion on stability of the slope through binding action of the deep extending roots. Tree roots play both mechanical and hydrological roles in stabilizing slopes. Tree root is the major contributor to slope stability since it mechanically support soil mass through its tensile strength, frictional and adhesive properties [35].

According to E. N. Bromhead [26], modification of slope geometry like flattening of slopes to reduce gradient is one of the effective remedial measures taken especially in shallow landslides. In slopes having shallow depth and covering small area, making slopes gentle such that decreasing driving forces is widely acceptable approach of improving factor of safety [36]. However, this technique is not feasible approach to be adopted in the study area. Since the affected area covers large hectares of land, the volume of soil to be removed in order to modify the landscape is massive and incurs extremely huge operational cost.

4. Conclusions

Lithological set up of the site is predominantly made up of pyroclastic and ignimbrite rock families situated in irregular arrangement and random distribution of rock materials with varying degree of weathering. Ground formation of the site is typically characterized by scattered distribution of rocks having similar properties. Likewise, the conducted electrical resistivity survey revealed that the resistivity potential of the layers inconsistently varies irrespective of variation in depth which is an indicator for existence of significant heterogeneity in degree of weathering and moisture content. The sensitivity of slope gradient to moisture content fluctuation is more visible in steep slopes than the gentle slopes. Besides, critical angle of the slope in the dry case by far exceeds that of the wet condition.

The main triggering factor causing the land slide is infiltration of heavy rainfall into the loose and severely weathered water bearing strata extending from 10 m to 25 m depth. Hence, the saturated layer situated at the stated depth is the key contributor of development of discontinuity plane. Erosion is also another factor exacerbating the case as the area is topographically known for its high gradient which creates suitable condition for running gully erosion. The critical effect of rain infiltration in triggering slope failure is not confined to shallow landslides that it can also significantly gives rise to failure of slopes whose slip plane originates from larger depths. The numerically obtained safety factor of the slope for the normal condition is by far greater than the wet condition. However, the obtained factor of safety value of the slope is insignificant which confirmed that the slope is unsafe. To this end, the appropriately viable slope treatment techniques preferred to be applied are the hydrological and mechanical techniques whereas application of the geometric technique is not feasible to be used.

Author contribution statement

Narobika Tesema Hatehu: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper. Fekadu Fufa; Damtew Tsige: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data. Adamu Beyene Negesa: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data will be made available on request.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.