GCNSA: DNA storage encoding with a graph convolutional network and self-attention

Summary

DNA Encoding, as a key step in DNA storage, plays an important role in reading and writing accuracy and the storage error rate. However, currently, the encoding efficiency is not high enough and the encoding speed is not fast enough, which limits the performance of DNA storage systems. In this work, a DNA storage encoding system with a graph convolutional network and self-attention (GCNSA) is proposed. The experimental results show that DNA storage code constructed by GCNSA increases by 14.4% on average under the basic constraints, and by 5%-40% under other constraints. The increase of DNA storage codes effectively improves the storage density of 0.7-2.2% in the DNA storage system. The GCNSA predicted more DNA storage codes in less time while ensuring the quality of codes, which lays a foundation for higher read and write efficiency in DNA storage.

Graphical abstract

Highlights

• •A learning-based artificial intelligence approach is applied to DNA storage coding
• •GCNSA predicts more DNA stored codes under the same combinatorial constraints
• •Reduced time cost and improved storage density of DNA storage systems
• •Overcomes the coding barrier caused by increasing coding length

Computational chemistry; Biological sciences; Biochemistry

Introduction

The information age is generating massive amounts of data. International Data Corporation (IDC) has predicted that by 2025,¹ the volume of data will reach 163 ZB (i.e., 1.63 × 10¹¹ TB). Massive data (such as metagenomic sequencing data,² video surveillance data, and so forth) poses challenges to traditional data storage methods and storage media. DNA is a storage medium with high density, high durability, and widespread existence in nature. Compared to traditional storage media, DNA storage has virtually zero maintenance energy requirement, and it can be preserved at room temperature and in dry conditions for thousands of years. The use of DNA to store abiotic information dates back to 1940, when Davis cloned DNA into plasmids for data preservation.³ However, at that time, the prevailing synthesis and sequencing technologies limited the development of DNA storage. In recent years, synthesis and sequencing technologies have continued to advance, and DNA storage has once again become a hotspot of global research.^4,5,6,7 In 2012, Church et al. used a binary model for DNA storage.⁸ Subsequently, Yazdi et al. proposed a DNA storage system with error correction.⁹ Fountain code is a high-density coding scheme with error tolerance mechanism. It was used by Erlich et al.¹⁰ to improve the coding rate in DNA storage. In 2019, Ceze et al.¹¹ completed a systemically integrated DNA storage system for digital microfluidics. In order to better predict the hybridization reaction process in DNA storage, Buterez¹² proposed a deep learn-based hybridization prediction method, which reduced the prediction time by two orders of magnitude in the case of high fidelity. In order to expand the storage density,^13,14 synthetic bases are also used in DNA storage.¹⁵ In terms of DNA storage miniaturization, some researchers have also proposed DNA storage systems based on nanopore sequencing¹⁶ and nanoscale electrodes.¹⁷ To reduce the rate of DNA degradation and its resistance to harsh conditions, the researchers combined the information stored in DNA with non-biological materials, such as nano-silicon balls,¹⁸ 3D-printed rabbits,⁵ and magnetic nanoparticles,¹⁹ to further improve the durability of DNA storage.

The first step of DNA storage is DNA encoding, which is an important step in the overall storage system. Huffman encoding is an encoding method widely used for data file compression. Goldman et al.²⁰ proposed a scheme using Huffman encoding to improve the coding potential of DNA storage to 1.58 bits/nt. In 2015, Grass et al.¹⁸ used GF (Galois Field) and RS (Reed-Solomon) codes to correct storage-related errors. The fountain code scheme proposed by Erlich et al.¹⁰ prevents homopolymers and extreme GC content. Jeong²¹ and Anavy⁷ made improvements by using fountain code, which respectively reduced the reading cost and increased the storage density, but they were still distant from the theoretical optima. In addition to fountain code, other error-correcting codes applied to DNA storage include WMU (weakly mutually uncorrelated) code,²² RS code,¹⁸ HEDGES,²³ and the error-correcting storage system proposed by Lenz et al.²⁴ In 2020, Liu’s team²⁵ proposed a DNA storage system based on Base64 encoding and inserted circular plasmids for long-term storage. Subsequently, they proposed a storage system based on RaptorQ,²⁶ which realized DNA error correction and reduced homomers. A coding efficiency of 1.50 bits/nt was achieved for natural bases. Limbachiya et al.²⁷ proposed a constraint family DNA storage coding, but only the distance constraint and GC content were considered. Subsequently, Cao et al. proposed storage coding based on the DMVO (Damping Multiulti-Verse Optimizer),²⁸ which satisfied more constraints, and proposed a coding scheme based on thermodynamic MFE (minimum free energy) constraints, which was closer to the nature of biochemical reactions. Rasool et al.²⁹ proposed a DNA storage constraint coding based on LSTM, but unfortunately not based on learning features, LSTM is only used to screen sequences that meet constraints. Zhang’s research group successively proposed the DBWO (Double-strategy Black Widow Optimization)³⁰ and CLGBO (Cauchy and Levy mutation strategy)³¹ algorithms and new combinative constraints for DNA storage coding and constructed coding sets with stronger stability, but the time complexity of the coding process was too high. Although researchers have proposed a variety of DNA storage coding schemes and preliminarily verified the coding potential of DNA storage and the possibility of replacing silicon-based storage,³² the recently proposed DNA storage systems still have the problems of low coding density and slow coding speed.³³

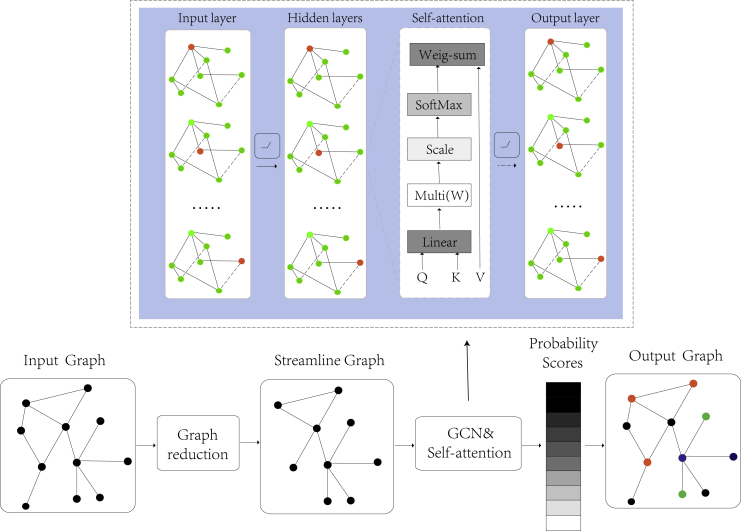
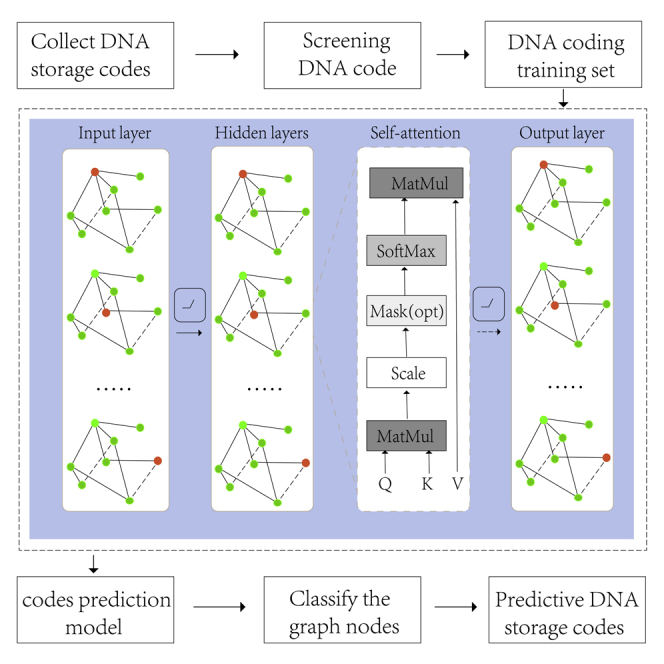
Although theoretical derivation³⁴ and heuristic algorithms³⁵ have led to some achievements in DNA storage coding, and the disadvantage of theoretical derivation is that it does not get an exact value. The search speed of heuristic algorithms is not fast enough, and the optimal solution still has a distance from the Pareto boundary of the DNA coding problem.³⁶ Moreover, DNA storage code words have higher requirements in DNA storage systems³⁷ with a random access.^14,38,39,40 Inspired by convolutional neural networks, cyclic neural networks, complex systems, the concept of graph neural networks was first proposed by Gori et al.⁴¹ Graph neural networks can capture the interdependence between data in more non-Euclidean spaces. Moreover, the GCN proposed by Li et al.⁴² is focused on dealing with combinatorial optimization problems, which promotes the application of graph neural networks in practical problems. In recent years, graph neural networks have been widely applied in systems biology and bioinformatics,⁴³ especially in the fields of drug prediction^44,45 and gene interaction.^46,47 In this article, a DNA storage encoding with a graph convolutional network⁴⁸ and self-attention⁴³ is proposed. More features are extracted by the graph convolutional network, and the contributions of different coding vectors are learned by an attention mechanism. To solve the problem of low efficiency of DNA storage encoding, a dataset was established by screening the DNA storage codes that met the constraints, and the GCNSA was used for prediction after training (Figure 1). In the GCNSA, the original code graph is reduced to an equivalent smaller graph to reduce the time complexity of the encoding process. Second, the GCN was used to extract features and the self-attention mechanism was used to capture the relationship between local DNA code words. Weighted aggregation of corresponding vectors of DNA code words was carried out to improve the efficiency of DNA storage and coding. Finally, the performance of GCNSA is verified by comparing it with baseline methods on DNA stored coding datasets. To further evaluate the GCNSA, DNA storage codes were predicted under a variety of combinatorial constraints. Experimental results show that the GCNSA is superior to other advanced algorithms. It significantly increased the number of DNA storage codes by 5%-40%, encoding speed by up to 15 times, and storage density by 0.7%-1.0% in a DNA random access storage system. In addition, lexicographic encoding using the coding set generated by GCNSA can also improve the coding density by 2.2% under the same constraints.

Figure 1.

Schematic diagram of the GCNSA model

The equivalent smaller streamline graph is obtained by the reduction of the input DNA coding graph, which is input into the graph neural network to predict the DNA storage codes that satisfying the constraints.

Results

In this article, i7-9900K and RTX3090 were used to carry out all experiments on the same platform. Due to the nature of graph data (Figure 6) and the particularity of DNA storage code constraints, it is difficult to evaluate the model by using the method of 5-fold cross-validation. Therefore, this article uses a model evaluation method that divides the data into a fixed training set and test set. The dataset of each type was divided into 8:1:1 (Table 11), corresponding to the training set, test set, and prediction set. In order to better illustrate the performance of the GCNSA model, the trained model was used to predict DNA storage codes under fixed constraints, and the number of codes and encoding time was compared with several representative construction codes. In the DNA random access storage system, the influence of the DNA storage code predicted by the GCNSA on storage density was compared and analyzed.

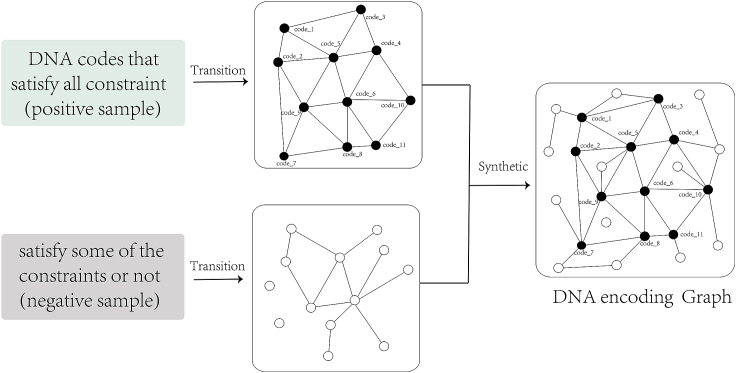
Figure 6.

The process of converting DNA storage codes into graph data, the forward transformation can be used in the training process, and the reverse transformation can obtain the DNA storage codes that satisfy the constraints

Where the black dots (positive samples) represent DNA storage codes that satisfy the constraints, and the white dots (negative samples) represent those that do not. Edges are connected between points that meet the constraints, and some edges that may be crossed are omitted for clarity, and only positive samples are labeled.

Table 11.

Details of five different datasets

Name	Negative	Positive	Constraints
GNH_db	4820	97,603	GC content, no-runlength, Hamming distance
GNHN_db	3068	99,355	GC content, no-runlength, non-adjacent subsequence, Hamming distance
GNHE_db	2450	99,973	GC content, no-runlength, Hamming distance, end constraint
GNHS_db	3034	99,389	GC content, no-runlength, Hamming distance, Self-complementary
GNE_db	3012	99,411	GC content, no-runlength, storage edit distance

Ablation experiments

In order to verify the influence of different network structure models on the performance of the GCNSA, we performed ablation experiments (Figure 2, Table 1) on the GCNSA model and fine-tuned the model parameters, and the corresponding hyperparameters are given in the Table S1. The abbreviations of the relevant constraints are shown in Table 2. Two different network structures were first designed, namely GCNSA with self-attention and GCN without attention. The convolution layer was set to five layers. The DNA storage codes results are shown in Table 1. The GCNSA with self-attention is superior to the GCN. After determining the use of the self-attention mechanism, the influence of the depth of the convolutional layers on optimization performance and time complexity was explored. The convolutional layers were set as 5, 10, 20, and the GNH_db dataset was used to evaluate the model results. The results show that the GCNSA with 20-layer convolution has better performance. GCNSA-20 was selected as the final framework, which is abbreviated as GCNSA in this article.

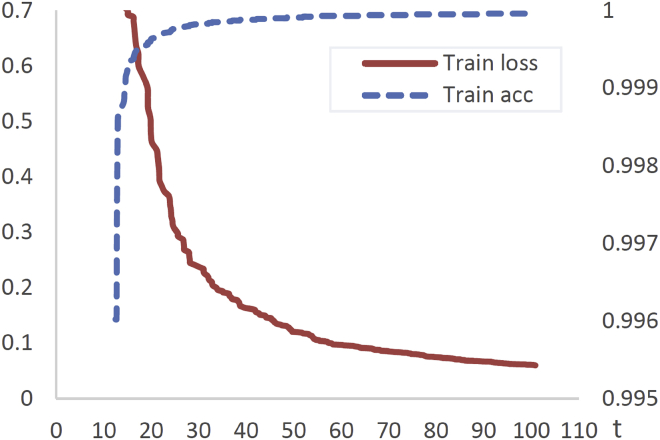
Figure 2.

Acc and loss of GCNSA training

In the curve of Loss and ACC in the training process, the red line represents the training Loss corresponding to the primary coordinate axis, while the blue dashed line represents the training ACC corresponding to the secondary coordinate axis.

Table 1.

Ablation experiments on GNH_db

	Solved	Code	Time (s)
GCN-5	90.7%	353	43
GCNSA-5	91.7%	357	50
GCN-10	95.8%	373	54
GCNSA-10	96.4%	375	59
GCN-20	95.1%	370	60
GCNSA-20	99.7%	388	64

Table 2.

The abbreviation of DNA storage encoding constraints and meanings

Abbreviation	Meaning
d	Hamming distance threshold49
d1	Store edit distance threshold28
GC	GC content constraint28
NL	No-runlength constraint28
NS	Non-adjacent subsequence constraint31
ED	End constraint30
SC	Self-complementary constraint50

Performance of the graph convolutional network and self-attention

To illustrate the performance of the proposed model, the GCNSA is compared with the following benchmarks. Both KMVO⁴⁹ and BMVO²⁸ are improved algorithms based on the MVO algorithm by K-means clustering and Brownian motion, which reduces the possibility of the algorithm falling into local optimal in the optimization process. However, there is still a defect in that the coding results have certain randomness. BC²⁹ was the first to use neural networks to encode DNA storage, but it only used LSTM as an encoder without the training process. NHO⁵¹ and EP³⁰ are recently proposed DNA storage coding methods, which further improve the performance of coding results under new constraints, but the iteration speed is slow and the time cost is high. In DNA storage, more DNA codes can not only ensure storage density but also reduce the synthesis and sequencing costs under the condition of quality assurance. Therefore, in this section, the DNA storage encoding of the GCNSA method is compared with other benchmark methods on GNH_db. In training, GNH_db was divided into 10 parts, eight of which were used as training sets, and the remaining two were used as test sets and prediction sets, respectively. Acc and Loss in the training process are shown in Figure 2. It can be seen from the figure that the GCNSA model has an ideal convergence process in the training.

GNH_db is composed of DNA storage codes that satisfy the GC content, no-runlength, and Hamming distance constraints. In Table 3, n represents the length of the current DNA storage code, and d represents the threshold that meets the Hamming distance constraint. Because the number of DNA storage codes is small and unrepresentative when n and d are too small or d is too close to N, only the situation of 5 < n < 9, 2 < d < n−1 in GNH_db is compared.

Table 3.

GCNSA compares the number of encodings dataset that satisfy the GC content, no-runlength, and Hamming distance constraints with different baseline methods

	n = 6, d = 3	n = 6, d = 4	n = 7, d = 3	n = 7, d = 4	n = 7, d = 5	n = 8, d = 3	n = 8, d = 4	n = 8, d = 5	n = 8, d = 6
BC29	95.16%	67.86%	100.0%	100.0%	100.0%	78.09%	89.84%	80.00%	50.00%
EP30	96.77%	100.0%	88.81%	88.46%	84.21%	84.02%	85.94%	82.22%	70.00%
NHO51	88.71%	82.14%	84.62%	80.77%	73.68%	87.37%	84.38%	77.78%	65.00%
KMVO49	90.32%	82.14%	88.81%	86.54%	89.47%	82.22%	73.44%	71.11%	65.00%
BMVO52	93.55%	85.71%	87.41%	84.62%	89.47%	83.51%	82.81%	77.78%	70.00%
GCN	93.55%	85.71%	93.01%	90.38%	94.74%	95.36%	91.41%	86.67%	95.00%
GCNSA	100.0%	100.0%	96.50%	94.23%	100.0%	99.74%	100.0%	100.0%	100.0%

The percentage in the table is the ratio of the current method to the optimal number. and the bold represents the optimal value under the current coding length (n) and Hamming distance value (d).

As seen in Table 3, the GCNSA achieved the best results in most cases. The first column shows different DNA storage coding methods. The percentage represents the ratio between the number of codewords generated by this coding method and the number of existing optimal coding sets, and the bold represents the optimal value under the current coding length (n) and Hamming distance value (d). In the optimal case of n = 8, d = 6, the GCNSA increased the number of DNA stored codes by 30% and had good predictive performance for GNH_db. When n = 6, 7, and 8, respectively, the average prediction results were 100%, 96.91%, and 99.96%, which improved the EP³⁰ by 1.65% compared with the suboptimal result when n = 6 and BMVO²⁸ by 21.47% compared with the suboptimal result when n = 8. However, when n = 7, the GCNSA model was weaker than BC,²⁹ which may be related to the calculation method of the GC content when it is odd. However, from a global perspective, the GCNSA model achieved an average improvement of 14.42% in each case compared with BC, achieving an ideal result. The GCNSA was also significantly better than the spectral GCN, with an average improvement of 7.18% in each case.

DNA storage encoding results

The strong performance of the GCNSA was verified by multiple comparisons on GNH_db. However, the GNH considers fewer constraints and has insufficient performance in reducing the error rate in DNA storage. Therefore, in recent years, researchers have proposed some advanced constraints based on thermodynamic properties, distance, and DNA structure. In order to better explain the actual performance of the GCNSA model in DNA storage, in this section, the GCNSA model is used to predict DNA storage coding under more advanced constraints, and it is compared with the current optimal work. A description of superscripts and meanings is given in Table 4.

Table 4.

Different baseline of Abbreviations and meanings of superscripts

Superscript	Meaning
o	DBWO algorithm30
q	QRSS-MPA50
c	CLGBO algorithm31
m	DMVO algorithm28
a	GCNSA

Satisfying GC content, no-runlength, non-adjacent subsequence, Hamming distance（GNHN） combination constraints

${\mathrm{A}}_4^{GC,NL,NS}\left(n,d,w\right)$ is defined as a set of DNA storage codes satisfying GC content constraint, no-runlength constraint, non-adjacent subsequence constraint, and hamming distance constraint. Non-adjacent subsequence can better reduce the cross-talk in synthesis and sequencing relative to the no-runlength constraint. In this section, the GCNSA model is used to predict the combined constraint DNA storage coding set containing non-adjacent subsequence. The variables n, d, and w represent the coding length, hamming distance and GC content weight respectively, and the results in the table are the coding numbers of GCNSA and CLGBO. As can be seen from Table 5, compared with the coding results of CLGBO, GCNSA has significantly improved in quantity. When n = 7 and d = 3, the number of codes increased by 13%, and when n = 8 and d = 5, it increased by 14%. With the same code length, more available high-quality codes can be predicted and more valid data can be indexed. In addition, Table 6 shows the coding time of some representative CLGBO and GCNSA. When n = 7 and d = 4, the coding time is reduced by 88.8%. When n = 8 and d = 5, the reduction is more than an order of magnitude, and overall the coding time is significantly reduced in each case. In this article, the values for the optimal results in the table are bolded, which is helpful for readers to quickly evaluate the performance of different methods.

Table 5.

Comparison of the number of coding set ${\mathrm{A}}_4^{GC,NL,NS}\left(n,d,w\right)$ of GCNSA and CLGBO methods under GC content weight (w = 50%), hamming distance, no-runlength and non-adjacent subsequence constraint constraints

n\d	3	4	5	6	7
6	51c	22c	8c
	55a	23a	8a
7	113c	42c	15c	6c
	122a	47a	15a	6a
8	319c	105c	35c	15c
	334a	114a	40a	16a
9	635c	206c	66c	25c	10c
	650a	213a	67a	25a	10a
10	1634c	518c	157c	56c	21c
	1659a	533a	166a	56a	21a

Table 6.

Comparison of ${\mathrm{A}}_4^{GC,NL,NS}\left(n,d,w\right)$ encoding results between the CLGBO and GCNSA, where the Number and time in the second column represent the number and time of coding under the current coding length (n) and distance constraint threshold (d), respectively

		n = 7, d = 3	n = 7, d = 4	n = 8, d = 3	n = 8, d = 4	n = 8, d = 5
CLGBO31	Number	113	42	319	105	35
	time (min)	10	9	11	12	11.5
GCNSA	Number	122	47	334	114	40
	time (min)	1.5	1.0	2.0	1.9	0.9

Satisfying GC content, no-runlength, storage edit distance（GNE） combination constraints

Compared with Hamming distance, edit distance can better reduce the error rate in DNA storage because the calculation method of insert, delete, and replace of storage edit distance is quite consistent with the common insert, delete, and replace errors in DNA sequencing. ${\mathrm{A}}_4^{GC,NL}\left(n,d_1,w\right)$ is defined as the DNA storage code set that meets the GC content constraint, no-runlength constraint, and storage edit distance constraint.²⁸ When the DMVO algorithm is used to encode under combinatorial constraints including storage edit distance, it often adds a large time cost. The GCNSA proposed in this article overcomes this shortcoming and can obtain a better solution in a shorter time.

In Table 7, n and d₁ represent encoding length and edit distance threshold, respectively, and the results in the table are the results of DNA storage encoding under the current constraints. When n and d are too small and d is too close to n, the number of DNA storage codes is small and unrepresentative; so, we compared 6 < n < 10. As can be seen in Table 7, the GCNSA predicted more DNA storage codes in the combinatorial constraints containing the storage edit distance. In particular, the number of encoded DNA stores increased by 22% at n = 8 and d = 4, by 40% at n = 7 and d = 4, and significantly increased in other conditions. Overall, the number of DNA stored codes increased by 4.5% under the GNE constraints. In addition, because the GNE contains storage editing distance, the complexity of the traditional calculation method of editing distance is exponential, whereas the DNA storage encoding predicted by the GCNSA in this article has the advantage of fast speed. It is clear from Table 8 that the time cost plummets. For example, when n = 7 and d = 4, the encoding time decreases by 15 times, and more DNA storage encoding is predicted. Thus, the GCNSA’s prediction of effective codes satisfying the constraints promotes the development of random DNA storage systems and improves the applicability of random DNA storage systems. In order to better illustrate the performance of GCNSA in constraint coding, we also compare various other combined constraints (Tables 9 and 10, File S1) with the current optimal scheme.^30,50

Table 7.

Comparison of the number of coding set ${\mathrm{A}}_4^{GC,NL}\left(n,d_1,w\right)$ of GCNSA and DMVO methods under GC content weight (w = 50%), Store edit distance, and no-runlength constraint

n\d1	3	4	5	6	7
6	32m	12m	8m
	40a	12a	8a
7	71m	19m	5m
	82a	25a	7a
8	178m	45m	14m
	188a	55a	15a
9	350m	84m	19m	7m
	359a	92a	19a	7a
10	893m	190m	42m	16m	12m
	912a	194a	45a	16a	12a

Table 8.

Comparison of ${\mathrm{A}}_4^{GC,NL}\left(n,d_1,w\right)$ encoding results between the GCNSA and DMVO, where the Number and time in the second column represent the number and time of coding under the current coding length (n) and distance constraint threshold (d₁), respectively

		n = 7, d1 = 3	n = 7, d1 = 4	n = 8, d1 = 3	n = 8, d1 = 4	n = 8, d1 = 5
DMVO28	Number	71	19	150	45	14
	time (min)	12	18	22	20	24
GCNSA	Number	82	25	188	55	14
	time (min)	1.9	1.1	2.5	2.3	1.2

Table 9.

Comparison of the number of coding set ${\mathrm{A}}_4^{GC,NL,ED}\left(n,d,w\right)$ of GCNSA and DBWO methods under GC content weight (w = 50%), hamming distance, no-runLength, and End constraint

n\d	3	4	5	6	7
6	32o	13o	5o
	38a	17a	5a
7	106o	40o	16o	6o
	72a	33a	12a	6a
8	178o	71o	24o	10o
	196a	68a	30a	14a
9	527o	189o	48o	23o	10o
	497a	172a	46a	23a	10a
10	1187o	376o	108o	41o	12o
	1212a	382a	111a	43a	12a

Table 10.

Comparison of the number of coding set ${\mathrm{A}}_4^{GC,NL,SC}\left(n,d,w\right)$ of GCNSA and QRSS-MPA methods under GC content weight (w = 50%), hamming distance, no-runlength, and self-complementary constraint

n\d	3	4	5	6	7
6	43q	21q	7q
	46a	25a	8a
7	95q	37q	14q	6q
	101a	37a	15a	6a
8	225q	81q	30q	12q
	299a	94a	35a	16a
9	520q	174q	60q	22q	10q
	550a	190a	69a	23a	10a
10	1155q	321q	111q	50q	15q
	1173a	327a	118a	53a	15a

Storage density analysis

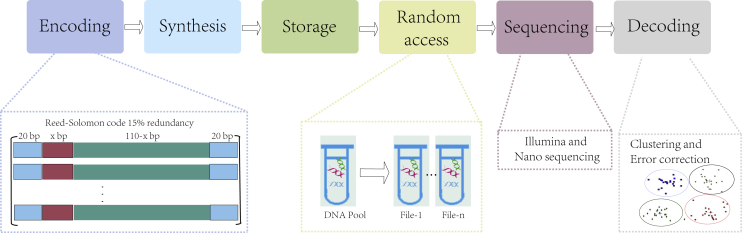
The DNA storage encoding predicted in this article is mainly used for non-data bits in the DNA storage system; so, this section takes the large-scale random DNA storage system proposed by Lee et al.³⁹ as an example to compare the storage density. Figure 3 shows the whole process of DNA storage, including encoding, synthesis, storage, sequencing, and decoding. In the storage system that supports random access, only the target information is extracted for sequencing, so it is necessary to consider the implementation of random access module in the design process of the DNA storage system. In the process of encoding, not only data bit encoding should be considered, but also non-data (address) bit design should be carried out. In Figure 3, green represents data bits, blue represents primers, and red represents address bits designed through GCNSA. The x in xbp depends on the number of DNA sequences that need to be addressed, and GCNSA can construct a larger set of address bits for the same x, that is, more valid information can be addressed. In the process of random access, address bit primers need to be designed for access information. After a series of separation and purification operations, the target DNA sequence was extracted by adding address primers into the DNA pool. The fastq files were obtained by Illumina or nanopore sequencing, and the target information was obtained by clustering, error correction, and decoding operations. Unlike their use of tandem coding in data bit coding, fountain codes are used in this section, but the distribution of different functional locations on each DNA sequence is the same as Lee’s, as shown in Figure 3. We encoded the 498 kB file as 22,200 Oligo using LT and RS encoding and generated 24,900 Oligo using LT encoding with 1.12 redundancy. Then, the data bits were assembled with the DNA storage codes (address bits) predicted above through the assembly technique, and the coding densities of DNA storage systems constructed with different address bit lengths were compared (Figure 4).

Figure 3.

Standard DNA random access storage system encoding and decoding process

Among them, the red part of the coding graph on the left is the application position of generating short codes in this article, that is, address bits. Under a fixed length, more address bits can index more effective information and improve the capacity of the DNA random access storage system.

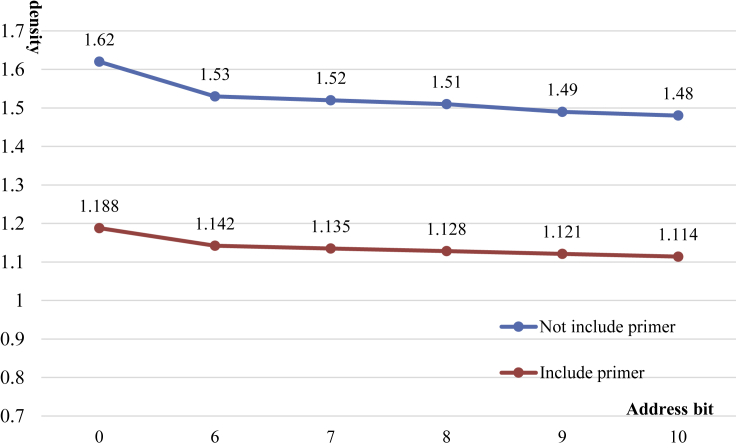
Figure 4.

Comparison of coding densities of conventional DNA random storage systems with different address bit lengths

The horizontal coordinate represents the length of the address bit. When the length of the address bit is 0, random storage is generally not supported. When the length of the address bit is longer, the addressable DNA sequence will increase, that is, the capacity of the DNA random storage system will be larger.

The benchmark test indexes of the DNA storage algorithm include storage density, storage capacity, error rate, and length of DNA sequence. Storage density directly affects the performance of the DNA storage system and can measure the amount of digital information that can be stored per unit base. In Figure 4, the vertical axis represents the encoding density and the horizontal axis represents the length of the address bits; 0 represents a DNA storage system with no address bits and no random access; and 6-10 represent the length of the address bit, which is also the purpose of the DNA storage code mentioned above. Taking address bit coding that meets the GC content constraint, no-runlength constraint, and storage editing distance constraint as an example, when 180 address blocks need to be randomly accessed, if the encoding method is DMVO, the address bits with length 9 can only be selected because there are not enough address blocks with length 8. If the GCNSA predictive codes proposed in this article are used, 180 address blocks can be randomly accessed when the address bit length is 8. The GCNSA can predict 188 different DNA storage codes under current combinatorial constraints. As an example, the storage density of 498 kB files in the preceding paragraph can be increased by 0.7% and 1% when primers are included and no primers are included, respectively. Although 1% coding density is not very obvious, 24,900 bases can be synthesized less for 498 kB data. If these bases are used for data bit storage, 4.52 kB more data can be stored, accounting for 0.9% of the total data amount. So, even 1% storage density makes sense for DNA storage of huge amounts of data.

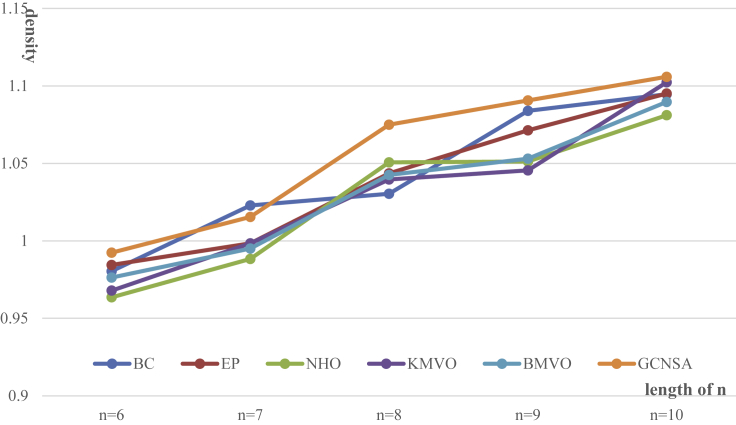
The DNA codes constructed by GCNSA can also be used in DNA storage systems with lexicographic encoding.³² Codebooks composed of short sequences contain codewords that can be freely concatenated and still satisfy constraints after binding. When the Hamming distance constraint (d = 3), GC content constraint, and no-runlength constraint were satisfied, GCNSA was compared with other five representative methods in the DNA storage systems with lexicographic encoding for coding density. It can be clearly seen from Figure 5 that in most cases, the storage density of GCNSA is higher than that of other baseline methods, especially when n = 8, and the coding density result of GCNSA can improve the coding density by 2.2% compared with the previous optimal.⁵² The coding density of the code words generated by GCNSA for lexicography is still far from the theoretical value of DNA storage. This is because the coding set constructed by GCNSA has better quality and meets more constraints. Appropriate constraint coding can effectively reduce the error rate in DNA storage, which has been proved in the work of Zhang et al.⁵² In conclusion, GCNSA generates a higher quality DNA storage coding set and can be used in different types of DNA storage systems, with certain scalability.

Figure 5.

Comparison of GCNSA with other methods in terms of density

When the Hamming distance constraint (d = 3), GC content constraint, and no-runlength constraint were satisfied, GCNSA was compared with other five representative methods in DNA storage systems with lexicographic encoding for coding density.

In most cases, the storage density of GCNSA is higher than that of other methods, especially when n = 8, the coding density result of GCNSA is significant. The storage density in the figure is calculated in the same way as F. L öchel³² et al.

Discussion

In this article, we proposed a DNA storage encoding with the GCN and self-attention, namely the GCNSA. By screening the existing DNA storage code sets that meet the constraints, the training sets (Table 11) that meet the GC content,⁴⁹ no-runlength,⁵² non-adjacent subsequence,³¹ end constraint,³⁰ and self-complementary⁵⁰ constraint were established. We trained the DNA storage encoding prediction model and compared it with previous representative work and obtained superior results. GCNSA can influence downstream tasks of DNA storage in two aspects. On the one hand, DNA storage has a high delay, which is not only reflected in the DNA sequence synthesis and data reading stage but also leads to the delay in the process of encoding data into DNA sequence. Compared with previous coding algorithms, GCNSA can be one order of magnitude faster under the same coding conditions. The higher encoding efficiency of non-data bits in DNA storage can ensure the smooth process of the whole encoding phase. On the other hand, GCNSA can construct a larger set of non-data bits under the same DNA sequence length and coding conditions, and can address more DNA sequences with fewer bases, thus improving the density of DNA storage. To sum up, GCNSA is mainly used for non-data bit encoding in DNA storage. Based on good encoding results, the delay in DNA storage is reduced and the storage density of DNA storage is improved.

In order to further verify the applicability of the GCNSA prediction model, we predicted DNA storage codes with more constraints in practical problems. We predicted and evaluated DNA storage code sets with four different combinations of constraints and predicted more DNA storage codes within the effective time in most cases. Not only is the number of codes 5%-40% higher but the simple training of the GCNSA also saves time compared to traditional methods. In particular, the GCNSA not only predicted more encodings satisfying the constraints but also ran an order of magnitude faster in the combined constraint with the storage edit distance constraint case. This indicates that the GCNSA reduced the computation overhead of editing distance and completed the DNA storage and coding work desirably. Finally, in terms of practicability, it was verified that the DNA random access storage system encoded by the GCNSA can increase the storage density by 0.7%-1.0%, or store 0.9% more data. In addition, lexicographic encoding using the coding set generated by GCNSA can also improve the coding density by 2.2% under the same constraints. The rapid prediction of more effective DNA storage codes that meet the constraints promotes the development of DNA storage systems and improves the applicability of DNA storage systems.

Limitations of the study

Although the graph model’s natural topology can capture more information, as the length of the DNA code increases, the number of nodes in the graph increases exponentially, which poses a huge challenge to computation and memory. Therefore, more consideration should be given to the graph reduction process in future work. How to obtain equivalent smaller maps more efficiently according to the characteristics of DNA in the DNA storage encoding model is another future research direction that will entail using a graph model to predict DNA codes.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
Python	Python	https://www.python.org/downloads/release/python-362/ Version:3.6.2
MATLAB	Mathworks	https://ww2.mathworks.cn/products/matlab.html/ Version:9.9.1524771(R2020b)
Numpy	Github	https://github.com/numpy/numpy/releases/tag/v1.18.5
Tensorflow	Github	https://github.com/tensorflow/docs/tree/r1.13/site/en/api_docs
Simulation codes	This paper	https://github.com/caobencs/DEGCA-DNAstroagecoding

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Qiang Zhang (zhangq@dlut.edu.cn).

Materials availability

This study did not generate new unique reagents.

Method details

Collection and processing of datasets

A DNA storage code set can be defined as follows. For $\sum =\left\{A,C,G,T\right\}$, if $\partial \in {\sum }^n$, the corresponding i position in the sequence $\partial$ is ${\partial }_i$, and $\partial ={\partial }_1{\partial }_2{\partial }_3...{\partial }_n\in {\sum }^n$. Similarly, another sequence, $\sigma ={\sigma }_1{\sigma }_2{\sigma }_3...{\sigma }_n\in {\sum }^n$, can be generated this way. DNA stored coding datasets usually satisfy basic constraints,^30,31,40,50 such as Hamming distance constraints.⁴⁹ If $\partial$ and $\sigma$ satisfy the Hamming distance constraint, define $d_H\left(\partial ,\sigma \right)$, which satisfies the following formula:

$$d_H\left(\phi ,\sigma \right)=\left|\left\{1\le i\le n,\phi \ne \sigma \right\}\right|\text{,}$$ (Equation 1)

In addition to the distance constraint, $\phi ,\sigma \in {\sum }^n$ may also need to satisfy the constraints of GC content,⁴⁹ no-runlength,⁵² non-adjacent subsequence,³¹ end constraint,³⁰ and self-complementary⁵⁰ constraint. The detailed description and mathematical model expression of these constraints are as follows.

Hamming distance constraint

For any two sequences (u and v) of length n. The Hamming distance (H (v, u)) is expressed as the number of different elements at the same position between two sequences v and u. The Hamming distance constraint is expressed as H(v, u)≥d, where d is an autonomously defined threshold, and the formula for calculating the Hamming distance of two sequences is as follows:

$$\begin{array}{cc}\mathrm{H}\left(v,u\right)=\sum _{i=1}^{n}h\left(v_i,u_i\right)\text{,}& h\left(v_i,u_i\right)=\{\begin{array}{cc}0\text{,}& v_i=u_i\\ 1& v_i\ne u_i\end{array}\end{array}\text{,}$$ (Equation 2)

Storage edit distance constraint

In DNA storage, storage edit distance²⁸ is used to reduce the error rate in DNA synthesis and nano sequencing. The storage edit distance is defined as follows. For the DNA code words a and b of length n, d_E(a, b) is defined as the storage edit distance between a and b. SE(a_i) defines the minimum d_E(a_i, b_j) in all DNA coding sets, which should not be greater than the element d. The specific expression is Equation (2):

$$\mathrm{SE}\left(a_i\right)=\underset{1\le j\le n,j\ne i}{\min }\left\{d\_E\left(a_i,b_j\right)\right\}\ge d\text{,}$$ (Equation 3)

GC content constraint

Among them, GC content refers to the proportion of the sum of bases G and C in the total number of bases in the oligonucleotide sequence. Sequences with large deviation in GC content are difficult to synthesize, and it is difficult to obtain high-quality sequencing data during sequencing. Generally, GC-content constraint²⁸ of about 50% in a DNA sequence is defined as stable. As shown in the formula, the GC-content of a DNA sequence of length l is defined as GC(l) in Equation (3), and | G + C | represents the sum number of G and C. In this study, | G + C | was assigned the value $\lfloor l/2\rfloor$:

$$GC\left(l\right)=\left|G+C\right|/\left|l\right|\text{,}$$ (Equation 4)

No-runlength constraint refers to the prohibition of continuous repeated bases in oligonucleotide. This is because in the process of DNA synthesis and sequencing, continuous bases may be misinterpreted as a single signal, which eventually leads to incorrect data reading. Therefore, the no-runlength constraint²⁸ is proposed, and its mathematical modeling is as follows:

$$\begin{array}{cc}{S}_i\ne S_{i+1}& ,i\in \left[1,n-1\right]\end{array}\text{,}$$ (Equation 5)

Non-adjacent subsequence constraint

Similarly, DNA sequences containing consecutive repeated subsequences are more likely to be misaligned during sequencing, resulting in errors in the read data. In addition, in the DNA synthesis stage, the sequence containing repeated subsequences will lead to polymerase slip, which increases the error rate at this stage. The non-adjacent subsequence constraint,³¹ refers to any sequence S (S = s₁, s₂ … s_n) meet the following requirements:

$$\begin{array}{ccc}when& K=2& \\ & & s_i{s}_{i+1}\ne s_{i+2}{s}_{i+3},0<i\le n-\left(2k-1\right)\\ when& K=3& \\ & & s_i{s}_{I+1}{s}_{I+2}\ne s_{i+3}{s}_{I+4}{s}_{i+5},0<i\le n-\left(2k-1\right)\end{array}\text{,}$$ (Equation 6)

End constraint

When the sequence is stored as a double strand, it is difficult to solve the mismatch of GC at the 3 'end. The occurrence of multiple GC bases in the last five bases has a great influence on the thermodynamic and physical properties of the whole sequence. Therefore, the GC content of the last five bases of the 3′ end is limited by terminal constraint. The terminal constraint refers to the sequence S(s₁,s₂,s₃, …,s_n), the last five bases cannot have three or more GC. The end constraint³⁰ formula is expressed as follows:

$$\left|G_{S_{Last5}}\right|+\left|C_{S_{Last5}}\right|<3\text{,}$$ (Equation 7)

Where $\left|G_{S_{Last5}}\right|$ and $\left|C_{S_{Last5}}\right|$ represent the number of G and C in the last five bases of sequence S, respectively.

Self-complementary constraint

For each designed sequence, if there are consecutive and complementary paired bases, the sequences will involuntarily undergo non-specific hybridization to form a secondary hairpin structure. If this problem occurs when the constructed sequence is used as a primer library, it will lead to serious consequences such as sequencing failure and data loss. To address this issue, self-complementary constraint⁵⁰ strictly prohibits Watson-Crick pairings from using three or more consecutive bases in each sequence.

In the past, due to the lack of fair datasets, DNA storage coding algorithms could not be compared on benchmark datasets as in other fields, so this paper conducted extensive collection and summary of DNA storage coding data.^{28,29,30,31,49,51,52} The generation of a DNA storage code dataset is mainly divided into three steps. First, the DNA storage code results under different constraints were obtained from previous works,^{28,29,30,31,51,52} and the code datasets under five different combination constraints were counted, with 16,384 negative samples and 49,731 positive samples. Second, the data were classified and screened, and DNA codes with lengths less than 5 were screened out. As the sequences with lengths less than 5 have only 4⁴ = 256 permutations under the condition of quaternion code (ATGC), the candidate solution set is too small, and the conventional algorithm can encode quickly. The coded datasets of the five different combination constraints were named GNH_db, GNHN_db, GNHE_db, GNHS_db, and GNE_db. Finally, the dataset was preprocessed to convert the relationship between the DNA storage codes and encoding information into the form of graphs. The detailed information is shown in Table 11. The dataset was divided according to the ratio of 8:1:1.

The encoding of data sequence data into graph data is a key step in graph neural network, so this process is described in Figure 6. As mentioned above, by collecting the set of DNA codes satisfying the constraints in existing research results,^{28,30,40,50,52} codes in the set of codes satisfying the constraints are taken as positive sample nodes of the graph, and all nodes satisfying the constraints (DNA codes) should have edges between them. Then, on this basis, equal amount and equal length of DNA codes that do not satisfying the coding constraints are added as negative sample nodes. However, it is worth noting that some nodes in the negative sample nodes and individual nodes of the positive sample may also meet the constraints, so there are also edges between them. In particular, the construction process of the above graph only takes place within the set of codes of the same length. Codes of different lengths will not appear in the same graph even if they meet the same constraints.

Construction of networks

In the early stages of development, neighbor information was transmitted in an iterative manner by circulating the neural structure in order to learn the representation of target nodes. Computation in the learning process is very expensive; so, a model based on a graph convolutional network and self-attention is used in this paper to the learn adjacent features of DNA codes. The representation of node v_i is generated by a learning function f, and its own features and neighbor features X_j are gathered by self-attention, where j∈N (v_i). Because the spectral method provides a well-defined localization operator on the graph, we defined the convolution filter through the spectral method and overcame O (nˆ2) expensive multiplication with a Fourier basis through the special choice of filter parameterization.⁵³ According to the convolution theorem, convolution in the spatial domain is equal to direct multiplication in the frequency domain:

$$f{\ast }_{G}g=F^{-1}\left(F\left(f\right)·F\left(g\right)\right)\text{,}$$ (Equation 8)

where F⁻¹ and F are Fourier transforms and inverse Fourier transforms, respectively. A basis for Fourier transform is required. The graph is transferred from spatial expression to the frequency domain space of this basis,⁵⁴ and a basis for the Fourier transform is found by constructing the Laplacian matrix. So, we construct the degree matrix D and adjacency matrix A:

$$D\left(i,j\right)=\{\begin{array}{cc}{d}_i& ifi=j\\ 0& otherwise\end{array}\text{,}$$ (Equation 9)

$$A\left(i,j\right)=\{\begin{array}{cc}1& ifi\in N_{\delta }\left[j\right]\\ 0& otherwise\end{array}\text{,}$$ (Equation 10)

The Laplace matrix L can be written as:

$$L=D-A\text{,}$$ (Equation 11)

As the graph in this paper is an undirected graph, L is a symmetric matrix. So, L can be decomposed according to the following formula:⁴²

$$L=U\mathrm{\Lambda }{U}^T\text{,}$$ (Equation 12)

$$U=\left[u_1,u_2,\dots ,u_n\right]\text{,}$$ (Equation 13)

$$\mathrm{\Lambda }=\left|\begin{array}{ccc}{\lambda }_1& \dots & 0\\ \dots & \dots & \dots \\ 0& \dots & {\lambda }_n\end{array}\right|\text{,}$$ (Equation 14)

U is the basis for the Fourier transform, and the eigenvalue A is the weight of the eigenvector.⁴² we can convert the input x_i from the spatial domain to the frequency domain:

$$F\left(x_i\right)=U^T{x}_i\text{,}$$ (Equation 15)

Therefore, the convolution formula⁵⁴ of the graph can be expressed as

$$x_i{\ast }_G{F}_{i,j}=U\left(U^T{x}_i·U^T{F}_{i,j}\right)=U\left(U^T{F}_{i,j}·U^T{x}_i\right)\text{,}$$ (Equation 16)

$U^T{F}_{i,j}$ is regarded as a convolution kernel that can be learned, denoted as $F_{i,j}^{\theta }$, and the final convolution formula⁴² can be expressed as

$$x_i{\ast }_G{F}_{i,j}=U{F}_{i,j}^{\theta }{U}^T{x}_i\text{,}$$ (Equation 17)

After adding the channel and the excitation function, the convolution of the K-th layer can be written as

$$o_{k,j}=h\left(\sum _{i=1}^{f_{k-1}}U{F}_{k,i,j}^{\theta }{U}^T{x}_{k,i}\right)=h\left(U\sum _{i=1}^{f_{k-1}}{F}_{k,i,j}^{\theta }{U}^T{x}_{k,i}\right)\text{,}$$ (Equation 18)

Self-attention is a kind of attention mechanism.⁵⁵ It is also an important part of the transformer. Self-attention focuses on some details according to the target instead of analyzing the whole situation. Therefore, the core of self-attention is to determine the parts that need attention based on the target. By calculating its own weight and considering the connections between different vectors, it can reduce the dependence on external information. Besides, self-attention is better at capturing the internal correlation of data, especially the long-distance dependence in similar graph structures. The input vector L = [l₁, l₂, l₃ … l_n] contains n inputs; li represents the eigenvector of the ith input; and the output vector L∗ is obtained by considering all the input vectors. For the single-head attention module, the L∗ is the weighted sum of all the input feature vectors,⁴³ which can be calculated by Equation 12:

$$h_i=\sum _{j=1}^N\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\frac{{\mathbf{q}}_i{\mathbf{k}}_j^T}{\sqrt{d_k}}\right){\mathbf{v}}_j\text{,}$$ (Equation 19)

where square root of d_k represents the scaling factor to control the magnitude of the dot product; and q_i, k_i, and v_i represent the query, key, and value of the i-th vector, respectively.

DNA storage encoding model

Based on the excellent performance of graph convolutional networks⁵⁶ and self-attention mechanisms,⁵⁷ this paper proposes a GCNSA for DNA storage encoding. The DNA storage codes that meet the constraints can be predicted not only by post-calculation screening but also by extracting and summarizing the features of the existing DNA storage code sets. Unlike natural language processing or the time series approach, every code word in a DNA storage code set is directly related to every other code word. If LSTM or GRU and other recurrent neural networks are used for prediction, the network memory capacity is limited. Therefore, this paper processes the code data into the form of a graph and transforms the encoding problem into the node classification problem of graph theory.⁵⁸ Moreover, a graph convolutional network has the natural feature extraction ability for non-Euclidean data along with the characteristics of local parameter sharing, which are suitable for feature extraction and prediction of graph data. However, insufficient attention is paid to local features in the GCN.⁵³ Therefore, in the feature extraction layer, this paper dynamically focuses on key points in the graph⁵⁴ through the self-attention mechanism, adjusts the weights, and captures the features of a single point to avoid the problem of unequal importance of adjacent nodes in the graph network. In addition, self-attention has a strong ability to extract internal features, and it is widely used to capture long-range dependencies between tokens in sequential data. The potential relationships between the points and edges in the graph are used to obtain more accurate information.

The DNA encoding problem can be mapped to a graph G and transformed into the node classification problem of graph theory. By extracting and summarizing the features of existing DNA storage code sets, more complex DNA storage codes can be predicted. Consider $G=\left(V,\phi ,R\right)$, where $V={\left\{v_i\right\}}_{i=1}^M$ is the set of M vertices; $G,\phi$ is the set of E edges; and $R\in {\left\{\mathrm{0,1}\right\}}^{M\mathrm{x}M}$ is the corresponding symmetric adjacency matrix. The vertices in the graph correspond to DNA code words, and a binary label needs to be generated for each vertex, with label 1 indicating that the current point is in the DNA storage code set and label 0 indicating that it is not in the set. The relationships between the code words in DNA storage encoding correspond to the edges in the graph, and this can be used to complete the construction of the coding model in the graph. The goal of the GCNSA model is to build more high-quality DNA storage codes within an effective time. The input of GCNSA is a set of encoded DNA stores preprocessed for the graph, and then enters the graph reduction module. The main principle of graph reduction module is pruning the nodes and edges that can quickly judge the attributes in the encoded graph. For example, in the DNA storage code construction map satisfying continuity, GC content and Hamming distance, the continuity within the code is easier to calculate than the Hamming distance between the codes. Therefore, the number of nodes and edges in the graph can be reduced by reducing the number of points (DNA coding) that do not satisfy the no-runlength. Self-attention strengthens the feature extraction of GCN, better captures the interdependence between codewords, completes the prediction of vertex scores, and outputs the DNA storage encoding sets that satisfying the constraints. The overall architecture of the model and the detailed construction of the network are shown in Figure 1.

Published: February 19, 2023

Data and code availability

The source data and code is available at: https://github.com/caobencs/DEGCA-DNAstroagecoding. Supplementary data to this article can be found at iScience online, any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.