Fuzzy Portfolio Selection Using Stochastic Correlation

Abstract

Here we have proposed fuzzy portfolio selection model using stochastic correlation (FPSMSC) to overcome limitations both in fuzzy and stochastic world. The newly proposed model not only gets harmonious efficient frontier, but also considers the future movement of stock prices based on fuzzy expertise knowledge. The investment weights of the model have been optimized based on the monthly return data of 18 stocks listed in S&P500 from October 2011 to September 2015. The proposed model has provided higher returns in the whole regime of risk for the period from October 2014 to September 2015, whose monthly return data are used as training data than other available portfolio selection models, i.e., fuzzy portfolio selection models with credibility and possibility and statistic model. Also, the present model has shown the better smoothness of the variations of returns with respect to risk aversion parameter, λ, from the monthly data from October 2015 to September 2016, which is not included to training database. Especially, our model is superior to other models in the regime of 0–0.3 for the risk aversion level. It is demonstrating that the FPSMSC is efficient for the investors who tend to seek the high return in portfolio management.

Supplementary Information

The online version contains supplementary material available at 10.1007/s10614-023-10371-w.

Introduction

Portfolio selection deals with how to diversify one’s capital over the large number of securities so that investment can take most profitable return. Since mean–variance models based on stochastic theory in Markowitz (1952, 1959) had been developed, stochastic variance has been typically recognized as a risk measure. Many researchers (Deng et al., 2005; Hirschberger et al., 2007; Leung et al., 2001; Liu et al., 2003) developed a variety of models regarded a stochastic variance as a risk measure. However, it has limitations because analysis based on stochastic variance does not consider undesirable outliers that will contribute to the extreme of variance (Grootveld & Hallerbach, 1999; Markowitz, 1959). Also, security returns are not symmetric and asymmetric returns make variance a poor measure of investment risk because portfolio based on stochastic variance is likely to have a potential danger to sacrifice too much expected return in eliminating outliers.

Many empirical evidences (Arditti, 1971; Chunhachinda et al., 1997; Fama, 1965; Simkowitz & Beedles, 1978) presented that in reality most security returns are not symmetrically distributed. Many researchers are trying to find risk measure against asymmetric return distributions. Some scholars hired skewness to assess the asymmetry degree of return distributions (Chunhachinda et al., 1997; Konno & Suzuki, 1994; Lai, 1991; Leung et al., 2001; Liu et al., 2003), others attempted to use downside risk measure that is focused only on negative deviations against certain return level. There are many forms of downside risk measure introduced in Roy (1952), Chow and Denning(1994), Fishburn (1977), Harlow and Rao(1989), Homaifar and Graddy (1990), Lee and Rao (1988), Nawrocki(1991), Rom and Ferguson(1994) and Bawa(1975). Semivariance is one of the well-known downside risk measures. Because it is direct, clear and comparatively simple in reflecting investors’ intuition about risk, it receives much attention. Many scholars such as Mao (1970), Choobineh and Branting (1986), Markowitz (1993), Kaplan and Alldredge (1997), Grootveld and Hallerbach (1999), and Huang (2007a; b) studied the properties and computation problem of semivariance. Their studies show that semivariance has merits in measuring risk. Bavarsad Salehpoor and Molla-Alizadeh-Zavardehi (2018) developed five different meta-heuristics namely the Electronmagnetism-like algorithm (EM), genetic algorithm (GA) genetic network programming (GNP), particle swarm optimization (PSO) and simulated annealing (SA) to find optimal solution for portfolio selection by using three different risk measures; mean absolute deviation (MAD), semi variance (SV) and variance with skewness (VWS). However, all statistical methods have limitations, which portfolio cannot be optimized because probability theory does not hold in the case of insufficient information. Recently, the fuzzy theory in portfolio selection has been given a priority because it is based on expertise knowledge of financial market affected by human’s psychological impact. In some situations, which it is hard to use probability theory researchers formulated new portfolio selection models by using fuzzy set which can reflect the ambiguity and vagueness of security returns (2007a; b; Bawa, 1975; Huang, 2006). Many scholars have made a lot of accomplishments in extending Markowitz’s stochastic mean–variance idea to fuzzy environment in different ways. For example, mean and variance of a portfolio were computed based on fuzzy probability and possibility distributions by Tanaka and Guo (1999) and Tanaka et al. (2000). Zhang and Nie (2004) supposed tolerable errors on the expected return and risk of the asset as adopting Tanaka et al.’s (2000) definition of possibility grade. Heilpern (1992) defined expected intervals on fuzzy set and Arenas-Parra et al. (2001) suggested a fuzzy goal programming model according to Heilpern’s definition. Carlsson and Fullér (2001) introduced their own definitions of mean and variance of fuzzy numbers and found the optimal portfolio by maximizing utility. Bilbao-Terol et al. (2006) formulated a fuzzy compromise programming problem. In particular, Huang (2006) computed portfolio return and risk by the expected value and variance based on credibility measure, and proposed two new fuzzy mean–variance models for portfolio selection with fuzzy returns. In addition, Huang (2006) presented two types of fuzzy chance-constrained models to find optimal portfolio. Jalota et al. (2017) proposed a credibilistic decision Support system for generating a suitable portfolio for an investor in an uncertain multi-criteria framework. They mentioned the credibility measure had an advantage of being self-dual as compared to usual possibility measure. Zhai and Bai (2017) discussed an uncertain portfolio selection problem in which background risk is considered and the security returns and background assets return are given by experienced experts’ evaluations instead of historical data.

The above studies consider the single-period fuzzy portfolio optimization problem. Many researchers have studied on multi-period fuzzy portfolio selection problems for investors who want to manage their assets not for short term, but for long term. In particular, Liagkouras and Metaxiotis (2018) proposed the multi-period portfolio optimization problem with transaction costs. Li et al. (2017) discussed a multi-period portfolio selection problem under uncertain environment, which maximizes the final wealth and minimizes the risk of investment. Wang et al. (2017) concerned with human risk attitude and presented two multi-period portfolio selection models in light of the different risk attitudes by applying dynamic risk tolerance and expected return level. Tofighian et al. (2018) released a multi-period projection portfolio selection problem in which the available budget is invested on the best portfolio of projects in each period such that the net profit is maximized.

However, so far, there is no research on fuzzy portfolio selection combining fuzzy variable with stochastic theory. The stochastic correlation of portfolio assets plays an important role in modern portfolio theory. Fuzzy logics can estimate the future movement of stock price with expertise intelligent system in the case of insufficient information and make rational portfolio that investors want. In fuzzy portfolio selection, one of the risk measure of portfolio is a credibility variance that does not consider the correlation of portfolio assets. In reality, financial market does not follow historical pattern, but their correlation may be inherited from historical data.

Our paper introduces hybrid risk measure of portfolio that combines fuzzy credibility variance with stochastic correlation and provides the fuzzy portfolio selection model using stochastic correlation. The aim of the present work is multiple. Firstly, we suggest the hybrid risk measure method to overcome the limitations both in fuzzy and stochastic portfolio models. Secondly, we formulate the fuzzy portfolio selection model using hybrid risk measure and optimize the model. The proposed model which includes advantages for each theory reflects the reality based on the expertise knowledge and provides harmonious efficient frontier. Thirdly, we examine the efficiency of the present model using the stock price data not included to training database in comparison with other portfolio models.

The paper is organized as follows. For the better understanding of the paper, we review some preliminary knowledge about fuzzy variable in Sect. 2 and suggest a hybrid portfolio risk measure in Sect. 3. Then, we propose a Fuzzy Portfolio Selection Model using Stochastic Correlation (FPSMSC) in Sect. 4 and find optimal portfolio with triangular fuzzy variable fuzzified using 18 stock price data in S&P500 and verify the performance of the proposed model comparing to those of other models in Sect. 5. Finally, we conclude the paper in Sect. 6.

Preliminaries

In fuzzy set the possibility and credibility variance was generally accepted as the risk measure of portfolio (Huang, 2007a, 2007b; Liu, 2004; Tanaka et al., 2000).

For better understanding, let’s briefly review the necessary knowledge on fuzzy set.

Let’s $\xi ,\eta$ be fuzzy variables. The possibility that fuzzy variable $\xi$ is smaller than fuzzy variable $\eta$ is defined by Zadeh (1978).

$$pos\left[\xi \le \eta \right]=\underset{x\le y}{sup}min\left\{\xi (x),\eta (y)\right\}$$ 1

From possibility of two fuzzy variables we can easily know the fact as follows.

$$\xi \le \eta \iff {\int }_0^1\gamma \left({\xi }_1(\gamma )+{\xi }_2(\gamma )\right)d\gamma \le {\int }_0^1\gamma \left({\eta }_1(\gamma )+{\eta }_2(\gamma )\right)d\gamma$$ 2

where $\gamma \in [0,1],{\xi }_1,{\xi }_2,{\eta }_1,{\eta }_1$ are the maximum and minimum value of fuzzy set in $\gamma$ level.

From the formula (1) and (2) the expected value and variance of fuzzy variable $\xi$ in terms of possibility are defined as follows:

$$E_p(\xi )={\int }_0^1\gamma ({\xi }_1(\gamma )+{\xi }_2(\gamma ))d\gamma ,$$ 3

$$\begin{array}{cc}\hfill V_p(\xi )=& {\int }_0^1{\sigma }_{U_{\gamma }}^{2}2\gamma d\gamma =\frac{1}{12}{\int }_0^1{({\xi }_1(\gamma )-{\xi }_2(\gamma ))}^{2}2\gamma d\gamma \hfill \\ \hfill =& \frac{1}{6}{\int }_0^1{({\xi }_1(\gamma )-{\xi }_2(\gamma ))}^2\gamma d\gamma ,\hfill \\ \hfill \end{array}$$ 4

where $U_{\gamma }$ the uniform distribution of fuzzy variable $\xi$ in the level $\gamma$, ${\sigma }_{U_{\gamma }}^2$ the variance of this distribution.

In possibility theory the covariance of two fuzzy variables can be defined as

$$Co{v}_p(\xi ,\eta )=\frac{1}{6}\underset{0}{\overset{1}{\int }}\left(({\xi }_1(\gamma )-{\xi }_2(\gamma )\right)\left(({\eta }_1(\gamma )-{\eta }_2(\gamma )\right)\gamma d\gamma$$ 5

Liu and Liu (2002) proposed credibility measure in fuzzy to overcome the disadvantage of possibility measure, which is that it has no self-dual property. The credibility theory has been widely accepted in fuzzy portfolio selection problems because of a self-dual property that is very important both in practice and theory.

Let’s $\xi$ be a fuzzy variable with a membership function $\mu$. The credibility of fuzzy event, characterized by $\xi \le r$, is defined by Liu (2004).

$$Cr\{\xi \le r\}=\frac{1}{2}\left(\underset{u\le r}{sup}\mu (u)+1-\underset{u>r}{sup}\mu (u)\right)$$ 6

The value of credibility takes values in [0,1] (Liu & Liu, 2002). It has self-dual property that can be easily verified as $Cr\left\{\xi \le r\right\}+Cr\left\{\xi >r\right\}=1$.

The expected value of a fuzzy variable $\xi$ is defined in Liu (2004).

$$E\left[\xi \right]=\underset{0}{\overset{\infty }{\int }}Cr\left\{\xi \ge r\right\}dr-\underset{-\infty }{\overset{0}{\int }}Cr\left\{\xi \le r\right\}dr$$ 7

Provided that at least one of the two integrals is finite.

Let’s $\xi$ be a fuzzy variable with finite expected value $e$. The variance of $\xi$ is defined by Liu (2004).

$$V\left[\xi \right]=E\left[{(\xi -e)}^2\right]$$ 8

They proposed the following two theorems according to the expected value of fuzzy variable.

Theorem 1

Let $\xi$ be a fuzzy variable with finite expected value. Then, for any real numbers ${\lambda }_1$ and ${\lambda }_2$, it holds that

$$E[{\lambda }_1\xi +{\lambda }_2]={\lambda }_{1}E[\xi ]+{\lambda }_2$$

Theorem 2

Let $\xi$ and $\eta$ be two independent fuzzy variables with finite expected values. Then, for any real numbers ${\lambda }_1$ and ${\lambda }_2$, it holds that

$$E[{\lambda }_1\xi +{\lambda }_2\eta ]={\lambda }_{1}E[\xi ]+{\lambda }_{2}E[\eta ]$$

Example 1

Let $\xi$ be a triangular fuzzy number denoted as $\xi =(a,\alpha ,\beta )$. It has the following membership function.

$$\mu (x)=\left\{\begin{array}{cc}1-\frac{a-x}{\alpha },\hfill & \text{if}a-\alpha \le x\le a\\ 1-\frac{x-a}{\beta },\hfill & \text{if}a\le x\le a+\beta \\ 0,\hfill & \text{otherwise}\end{array}\right)$$

Using Eqs. (3) and (4) the possibilistic expected value and variance of fuzzy variable $\xi =(a,\alpha ,\beta )$ are

$$E_p\left(\xi \right)=a+\frac{\beta -\alpha }{6},V_p\left(\xi \right)=\frac{{(\alpha +\beta )}^2}{72}$$

and the possibilistic covariance of two fuzzy variable ${\xi }_1,{\xi }_2$ is

$$Co{v}_p\left({\xi }_1,{\xi }_2\right)=\frac{({\alpha }_1+{\beta }_1)({\alpha }_2+{\beta }_2)}{72}.$$

Example 2

Using Eq. (6), the credibility of a triangular fuzzy variable $\xi =(a,\alpha ,\beta )$ is.

$$Cr\left\{\xi \le x\right\}=\left\{\begin{array}{cc}0,\hfill & \text{if}x\le a-\alpha \\ \frac{1}{2}+\frac{x-a}{2\alpha },\hfill & \text{if}a-\alpha \le x\le a\\ \frac{1}{2}+\frac{x-a}{2\beta },\hfill & \text{if}a\le x\le a+\beta \\ 1,\hfill & \text{if}x\ge a+\beta \end{array}\right)Cr\left\{\xi \ge x\right\}=\left\{\begin{array}{cc}1,\hfill & \text{if}x\le a-\alpha \\ \frac{1}{2}+\frac{a-x}{2\alpha },\hfill & \text{if}a-\alpha \le x\le a\\ \frac{1}{2}+\frac{a-x}{2\beta },\hfill & \text{if}a\le x\le a+\beta \\ 0,\hfill & \text{if}x\ge a+\beta \end{array}\right).$$

From Eqs. (7) and (8) the credibilistic expected value and variance of a triangular fuzzy variable $\xi =(a,\alpha ,\beta )$ are

$$E_c(\xi )=a+\frac{\beta -a}{4},\text{and}{V}_c\left[\xi \right]=\left\{\begin{array}{cc}\frac{33{\alpha }^3+11\alpha {\beta }^2+21{\alpha }^2\beta -{\beta }^3}{384\alpha },\hfill & \text{if}\alpha >\beta \\ \frac{{\alpha }^2}{24},\hfill & \text{if}\alpha =\beta \\ \frac{33{\beta }^3+21\alpha {\beta }^2+11{\alpha }^2\beta -{\alpha }^3}{384\beta },\hfill & \text{if}\alpha <\beta \end{array}\right)$$

Example 3

Let ${\xi }_i$ be a triangular fuzzy number of $i$th security return denoted as ${\xi }_i=(a_i,{\alpha }_i,{\beta }_i)$. The fuzzy variable $\xi =(a,\alpha ,\beta )$ for the return of whole portfolio is

$$\xi =(a,\alpha ,\beta )={\xi }^{+}-{\xi }^{-}=(a^{+}-a^{-},{\alpha }^{+}+{\beta }^{-},{\beta }^{+}+{\alpha }^{-})$$

$\begin{array}{c}{\xi }^{+}=(a^{+},{\alpha }^{+},{\beta }^{+})=(\sum {}_{{\omega }_i\ge 0}{\omega }_i·a_i,\sum {}_{{\omega }_i\ge 0}{\omega }_i·{\alpha }_i,\sum {}_{{\omega }_i\ge 0}{\omega }_i·{\beta }_i\\ {\xi }^{-}=(a^{-},{\alpha }^{-},{\beta }^{-})=(\sum {}_{{\omega }_i<0}\left|{\omega }_i\right|·a_i,\sum {}_{{\omega }_i<0}\left|{\omega }_i\right|·{\alpha }_i,\sum {}_{{\omega }_i<0}\left|{\omega }_i\right|·{\beta }_i\\ \end{array}$ where ${\omega }_i$ is proportional weight of the ith security of the portfolio using Theorem 2.

Problem Definition

Portfolio selection is one of the most attractive fields for investors. Stochastic portfolio selection model has been considered as the best appropriate one, if the future movement of stock prices follows the historical sample distribution. However, the characteristic of sample distribution oriented from insufficient or inaccurate information cannot provide the reasonable prediction of the future movement of stock prices. Newly listed stock in stock exchange has no enough information and also, extraordinary events such as COVID-19 pandemic make the future movement of stock price to get rid of past pattern. To overcome this weak point of the stochastic portfolio model, the fuzzy portfolio selection model has been suggested. Fuzzy portfolio theory gives portfolio managers a possibility that they can estimate the future movement of stock prices based on expertise knowledge. In fuzzy theory, the risk of portfolio is defined in terms of credibility and possibility for fuzzy variable. Many studies paid attention to credibility measure because of its self-dual property, but it cannot reflect the correlation of fuzzy variables. The correlation of stock prices plays an important role to minimize the portfolio risk and gets harmonious efficient frontier of portfolio. Portfolio managers need an alternative portfolio method that gives a solution to the problems of fuzzy and stochastic variables.

We assume that the correlation of fuzzy variables in credibility theory is very similar to the stochastic correlation that shows the degree how much the stochastic variables move together.

Portfolio Selection Models

Statistical Portfolio Selection Model

Many scholars (Deng et al., 2005; Hirschberger et al., 2007; Leung et al., 2001; Liu et al., 2003; Markowitz, 1959) introduced statistical portfolio selection models (SPSM).

In SPSM it is assumed that stock returns follow the normal distribution and the portfolio return and risk are evaluated through statistical expected return and variance.

The standard statistical portfolio selection model is

$$\begin{array}{cc}& \text{minimize}\lambda \left[\sum _i\sum _j{\omega }_i{\omega }_j{\sigma }_{\mathit{ij}}\right]+(1-\lambda )\left[-\sum _i{\omega }_i{\mu }_i\right]\hfill \\ \hfill & \text{subject to}\sum _i{\omega }_i=1,\hfill \\ \hfill \end{array}$$ 9

where $\lambda \in \left[0,1\right]$ is the risk aversion parameter, ${\omega }_i$ investment proportion of ith portfolio asset, ${\mu }_i$ statistical expected return of ith portfolio asset, ${\sigma }_{\mathit{ij}}$ covariance of ith, jth portfolio assets.

If $\lambda =0$, it stands for maximizing the portfolio return and the only asset with greatest return will be optimal solution that means the investor does not concern about portfolio risk. Conversely if $\lambda =1$, it stands for minimizing portfolio variance regardless of portfolio return.

Fuzzy Portfolio Selection Model

In previous studies (Huang, 2006, ; Tanaka et al. 2000), many fuzzy portfolio selection models with possibility and credibility variance was presented. The fuzzy possibility theory is similar to stochastic probability, but it has no self-dual property that is very important.

The Fuzzy portfolio selection model (FPSM) by using possibility theory in fuzzy set is as follow.

$$\begin{array}{c}\text{minimize}\lambda \left[\sum _i\sum _j{\omega }_i{\omega }_{j}Co{v}_p({\xi }_i,{\xi }_j)\right]+(1-\lambda )\left[-\sum _i{\omega }_i{\mu }_p({\xi }_i)\right]\hfill \\ \text{subject to}\sum _i{\omega }_i=1\hfill \end{array},$$ 10

where $Co{v}_p({\xi }_i,{\xi }_j)$ the possibility covariance of fuzzy variables, ${\mu }_p({\xi }_i)$ the possibility expected return of fuzzy variable. When $i=j$, possibility covariance of fuzzy variables $Co{v}_p({\xi }_i,{\xi }_j)$ becomes possibility variance $V_p({\xi }_i)$.

Other scholars introduce credibility theory that shows how much we believe fuzzy variable is true. According to credibility theory they defined the expected return and variance of fuzzy variable and made portfolio selection model as follow.

$$\begin{array}{c}\text{minimize}\lambda \left[E_c\left({(\xi -E_c(\xi ))}^2\right)\right]+(1-\lambda )\left[-\sum _i{\omega }_i{E}_c({\xi }_i)\right]\hfill \\ \text{subject to}\sum _i{\omega }_i=1\hfill \end{array},$$ 11

In order to find the credibility of portfolio we should get fuzzy variable of whole portfolio by using fuzzy variable of individual portfolio asset like Example 3.

Proposed Fuzzy Portfolio Selection Model

The credibility variance of fuzzy set shows ambiguity and vagueness of fuzzy variable, but it does not consider the correlation of stock prices that plays an important role in portfolio optimization. Stochastic correlation ${\rho }_{\mathit{ij}}$ varies within $-1\sim 1$. ${\rho }_{\mathit{ij}}=-1$ means that the movement directions of ith and jth stock prices are completely opposite each other. Conversely, ${\rho }_{\mathit{ij}}=1$ means that both of stocks completely move together. When the movement of two stocks has no any relationship, the stochastic correlation will be zero.

The stochastic correlation is calculated as follows:

$${\rho }_{\mathit{ij}}=\frac{{\sigma }_{\mathit{ij}}}{{\sigma }_i·{\sigma }_j}$$ 12

where ${\sigma }_i$ and ${\sigma }_j$ are the stadard diviation of the ith and jth stocks, respectively. ${\sigma }_{\mathit{ij}}$ is covariace of the ith and jth stocks. The stochastic correlation is the main attribute for portfolio selection to have harmonious efficient frontier that makes the investors find the slope of the return with respect to risk. The relationship of the fuzzy numbers based on expertise knowledge may also follow the stochastic correlation because the stochastic correlation which reflects concrete economic relationship between two stocks is not almost affected by exogenous variables.

We suggest hybrid portfolio risk measure by combining fuzzy credibilistic variance with stochastic correlation.

The credibilistic variance of portfolio with stochastic correlation can be defined as follows.

$$\begin{array}{cc}& V^c(\xi )=\sum _i\sum _j{\omega }_i{\omega }_j{V}_{{}_{{\xi }_{\mathit{ij}}}}^c\hfill \\ \hfill & V_{{}_{{\xi }_{\mathit{ij}}}}^c={\rho }_{\mathit{ij}}·{\sigma }_{{}_{{\xi }_i}}^c·{\sigma }_{{}_{{\xi }_j}}^c\hfill \\ \hfill \end{array}$$ 13

${\rho }_{\mathit{ij}}$: Stochastic correlation of portfolio asset $i,j$, ${\sigma }_{{}_{{\xi }_i}}^c$:credibility standard deviation of fuzzy variable ${\xi }_i$ as portfolio asset $i$, ${\omega }_i$:the investment weights of $i^{\mathit{th}}$ portfolio asset.

The hybrid risk measure suggested here shows not only the ambiguity and vagueness of fuzzy variable, but also the stochastic correlation of portfolio assets.

Fuzzy portfolio selection might be improved by using credibility, but the credibility variance of portfolio does not reflect the correlation of portfolio assets. Therefore, the fuzzy portfolio model with credibility variance does not provide the harmonious efficient frontier of portfolio. To overcome this limitation, we develop the fuzzy portfolio selection model using the fuzzy credibility variance with stochastic correlation. The fuzzy portfolio selection model with stochastic correlation (FPSMSC) is

$$\begin{array}{c}\text{minimize}\lambda \left[\sum _i\sum _j{\omega }_i{\omega }_j{V}_{{}_{{\xi }_{\mathit{ij}}}}^c\right]+(1+\lambda )\left[-\sum _i{\omega }_i{E}_c({\xi }_i)\right]\hfill \\ \text{subject to}\sum _i{\omega }_i=1\hfill \end{array}.$$ 14

where $V_{{\xi }_{\mathit{ij}}}^c$ the credibility covariance with stochastic correlation of ith and jth portfolio assets, ${\omega }_i$ investment proportion of ith portfolio asset. When $i=j$, $V_{{\xi }_{\mathit{ij}}}^c$ is the credibility variance with stochastic correlation of the ith stock.

Computational Experiment and Comparison

In order to find optimal portfolio, we use monthly return data of 18 stocks listed in S&P500 from October 2011 to September 2015 as training data. For comparison with other portfolios the monthly return data from November 2015 to September 2016 is used as testing data. The company tickers of 18 stocks listed in S&P500 are GD, ORCL, JCI, BBY, BBBY, BAC, ADI, APPL, VLO, VF, QCOM, PBI, ESRX, DUK, CVX, CLX, CAH and BLL.

The triangular fuzzy variables $\xi (a,\alpha ,\beta )$ are fuzzified according to maximum and minimum value of individual stock price from monthly return data for 4 years. Table 1 shows the expected return and variance of triangular fuzzy variables in terms of possibility and credibility theory in fuzzy set. The credibility covariance matrix using stochastic correlation is obtained by using formula (13).

Table 1.

The triangular fuzzy variables a, α and β, the credibilistic expected returns and variances E_c and V_c and the possibilistic expected returns and variances E_p and V_p of 18 stocks (%)

Ticker of stock	a	α	β	Ec	Vc	Ep	Vp
GD	1.93	7.96	11.64	2.85	0.18	2.55	0.05
ORCL	0.54	7.91	7.89	0.53	0.10	0.53	0.04
JCI	1.19	7.05	6.03	0.94	0.08	1.02	0.02
BBY	1.42	25.09	26.65	1.81	1.14	1.68	0.37
BBBY	0.18	11.00	8.44	− 0.46	0.17	− 0.25	0.05
BAC	2.18	17.16	20.83	3.09	0.65	2.79	0.20
ADI	1.25	9.68	9.09	1.10	0.15	1.15	0.05
APPL	1.68	12.86	14.52	2.10	0.33	1.96	0.10
VLO	2.94	12.73	20.46	4.88	0.55	4.23	0.15
VF	1.78	6.91	8.54	2.19	0.11	2.05	0.03
QCOM	0.26	10.38	9.02	− 0.08	0.17	0.03	0.05
PBI	0.30	15.71	19.17	1.16	0.55	0.87	0.17
ESRX	1.76	16.86	9.57	− 0.06	0.36	0.55	0.10
DUK	0.35	7.74	5.47	− 0.21	0.08	− 0.03	0.02
CVX	− 0.31	12.58	7.46	− 1.59	0.20	− 1.16	0.06
CLX	1.13	5.39	6.67	1.45	0.07	1.34	0.02
CAH	1.43	7.40	14.19	3.13	0.25	2.56	0.07
BLL	1.59	7.63	7.79	1.63	0.10	1.61	0.03

The efficient frontiers of optimal portfolio by using SPSM, FPSM and FPSMSC are given in Fig. 1. In order to find optimal portfolio in FPSM with credibility measure, we used the Genetic Algorithm (GA) with population size of 20, generation of 4000, crossover rate of 0.8 and mutation rate of 0.08. The investment proportion of all portfolio assets is limited within [0, 1] to restrict short sell. Except for FPSM with credibility measure, other portfolio models used portfolio class in Matlab2015 library to find optimal portfolio. As shown in Fig. 1, the efficient frontiers of FPSMs with possibility and credibility measure have almost linearity between return and risk and the efficient frontier of FPSMSC and SPSM are quadratic so that small changes of portfolio risk could cause significant changes of portfolio return. Thus, the FPSMSC and SPSM have the feasible portfolio with maximum Sharpe ratio.

Fig. 1.

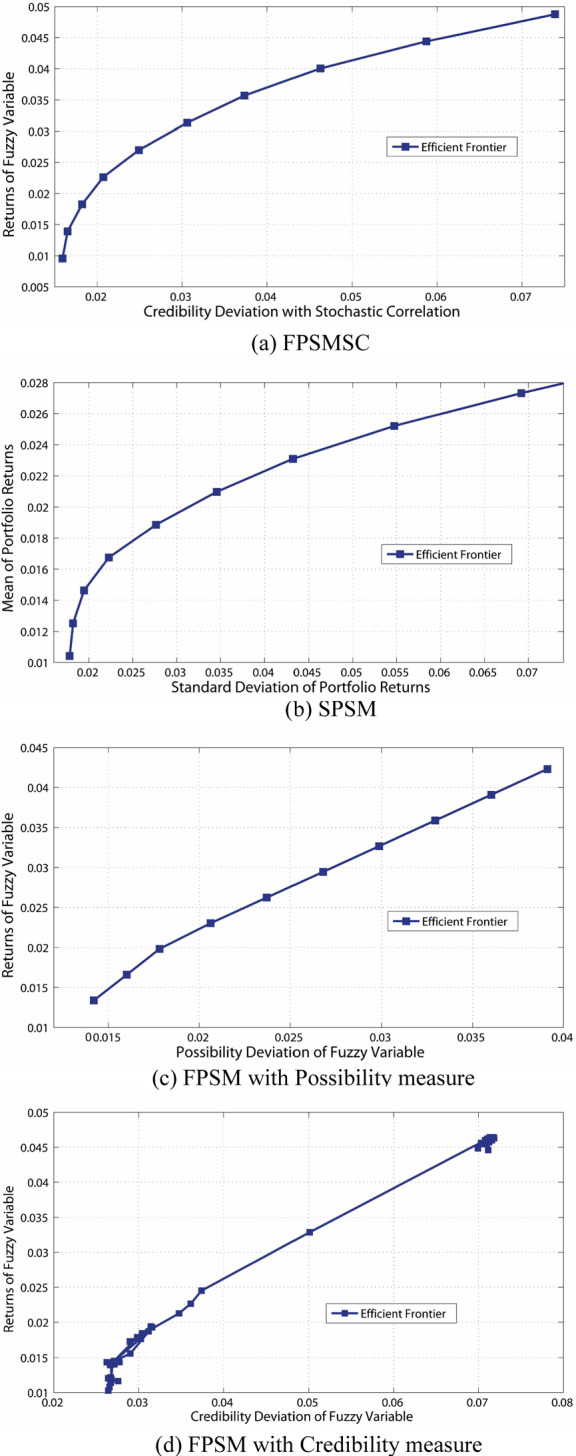
Efficient frontiers of several portfolio selection models

For the detailed comparison of the present model with SPSM, we obtained the investment proportion of the FPSMSC and SPSM provided that maximum Sharpe ratio in Table 2. It shows that the dispersion of two portfolios are almost the same. But something interesting in investment weights of two models is that the differences between those of two models for VLO, VF and BLL are significantly large. The reason is because the FPSMSC fuzzified the returns of them as triangular fuzzy variable by using expertise knowledge under the assumption that distributions of these assets does not follow the same distribution of historical data after 2015.

Table 2.

The investment proportion of FPSMSC and SPSM

Ticker of stock	FPSMSC	SPSM
GD	0.261336736	0.255385
ORCL	0	0
JCI	0	0
BBY	0	0
BBBY	0	0
BAC	0	0
ADI	0	0
APPL	0	0.017983
VLO	0.039953246	0.114529
VF	0.066777311	0.004119
QCOM	0	0
PBI	0	0
ESRX	0.019349375	0
DUK	0	0
CVX	0	0
CLX	0.363958205	0.413965
CAH	0.071561862	0.113562
BLL	0.177063265	0.080457

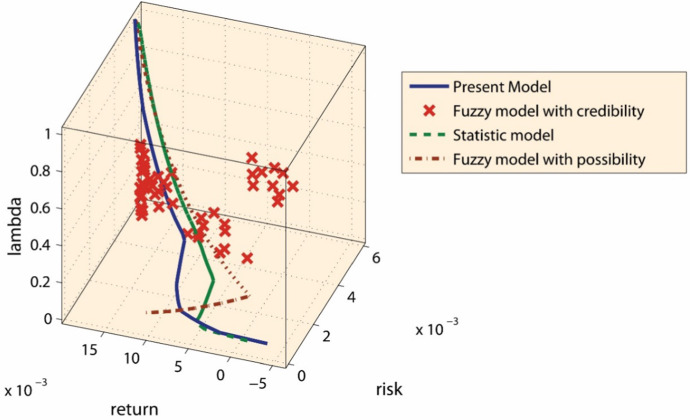
We validate the proposed model by using 10 months return data of stock selected from training database. Figure 2 shows that the proposed model is superior to other portfolio models in the whole regime of risk aversion parameter $\lambda$.

Fig. 2.

The result of validation test for the present model from October 2014 to September 2015 which is included in training database

Fuzzy model with credibility can be excluded from comparison because it has no continuity and a certain tendency with respect to risk aversion parameter $\lambda$. The present model gives the highest value of return at every risk aversion level among the models mentioned here. Furthermore, the present curve has more smooth tendency than other curves, showing that the present model is suitable for all investors in the whole regime of risk aversion level.

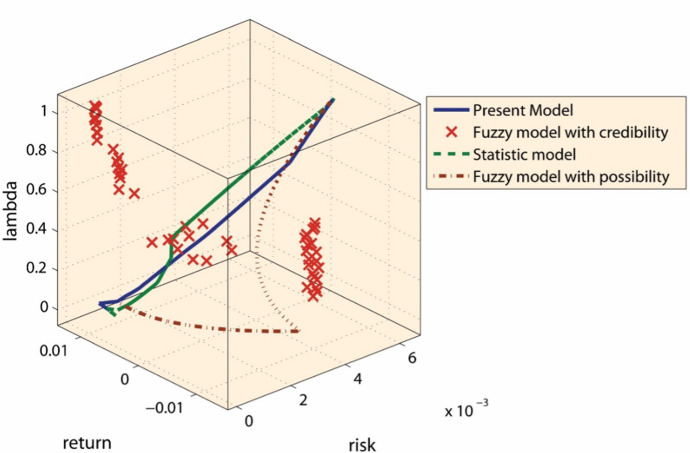
We use the monthly return data from November 2015 to September 2016 as testing data which is not included in training database to verify the efficiency of the proposed model. We are sure that the propose model is advantageous in terms of continuity and tendency according to Fig. 3. Especially, when the risk aversion parameter $\lambda \in [0,0.3]$, the proposed model recorded the highest returns. The fact that the speculative investors pay more attention to the return in portfolio management encourages them to use the present model.

Fig. 3.

The result of testing by using new data from November 2015 to September 2016 which is not included in training database

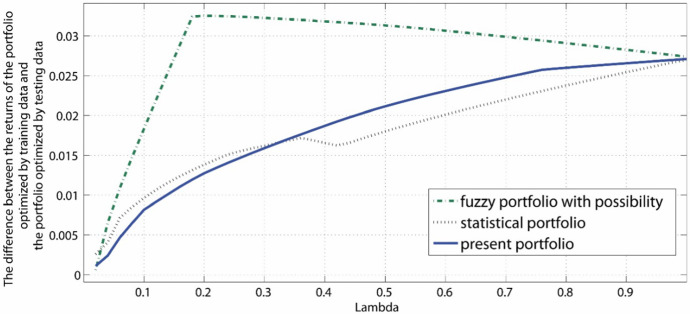
We calculated the difference from the statistic portfolio model optimized using the monthly return data from November 2015 to September 2016. As shown in Fig. 4, the present portfolio with the lowest difference within 0–0.3 of the risk aversion level might be preferred by the investors who tend to seek the high return in portfolio management. While, when the risk aversion level is bigger than 0.3, the present curve overestimates the statistic curve. However, the present model keeps the smoothness in the whole regime of risk, which shows the safety of the model. It is seen that the present model is also better than statistical model for the testing period through comparing with the statistical portfolio optimized using testing period data. From this characteristics, many portfolio managers are willing to use it for portfolio optimization.

Fig. 4.

The difference from portfolio optimized using the monthly return data from November 2015 to September 2016

We conduct hypothesis test to determine which model is the best. For hypothesis test on FPSM with Possibility measure, FPSMSC and SPSM, we select 30 feasible portfolios of each model as statistical sample according to random risk aversion parameter. ANOVA table of the returns of the 30 feasible portfolios of each model for testing year shows that there exists significant difference in terms of return because the P value is 0.003804 in Table 3.

Table 3.

Statistical summary and ANOVA of the return of 3 models

Groups	Count	Sum	Average	Variance
SUMMARY
FPSM with possibility	30	0.277821	0.009261	8.43E−07
Proposed model	30	0.288178	0.009606	1.29E−06
SPSM	30	0.263517	0.008784	4.49E−07

Source of variation	SS	Df	MS	F	P value	F crit
ANOVA
Between groups	1.02E−05	2	5.11E−06	5.944381	0.003804	3.101296
Within groups	7.48E−05	87	8.6E−07
Total	8.5E−05	89

The result of Wilcoxon’s signed rank test confirms which model is best in terms of return is presented in Table 4. It can be seen that the fuzzy portfolio model outperforms stochastic model due to low P values less than 0.05 as significant level and the hypothesis that FPSM with possibility measure is better than FPSMSC will be rejected, because it is insignificant as P value of 0.1915. Overall, we can conclude that the proposed model outperforms other portfolio models.

Table 4.

The result of Wilcoxon’s signed rank test for return

Hypothesis	FPSMSC > SPSM	FPSM with possibility > SPSM	FPSM with possibility > FPSMSC
P value	0.0243	0.0041	0.1915

Conclusion

In this paper we have proposed fuzzy portfolio model using stochastic correlation that overcomes limitations both in fuzzy and stochastic environment. Fuzzy portfolio theory has been attractive for investors because it uses expertise knowledge to estimate future movement of stock price. However, the fuzzy portfolio model cannot obtain the harmonious efficient frontier derived from stochastic correlation, which gives a solution to minimize risk and maximize return. We have suggested a hybrid risk measure to combine fuzzy credibility variance with stochastic correlation and verified the performance of the fuzzy portfolio selection model using stochastic correlation. Numerical experiment with 18 stocks’ price data listed in S&P500 has been performed to demonstrate the efficiency of the proposed model. The results have shown that our model has the advantages of fuzzy and stochastic portfolio theories. The proposed model has provided the harmonious efficient frontier and fitted well to the future movement of stock prices. The proposed model has shown the smoothness of the change of portfolio return and the highest returns in the whole regime of risk for the period of validation. Especially, the proposed model has been superior to other original models in terms of return within risk aversion level $[0,0.3]$, when we applied our model to new data which is not included to training data.

Supplementary Information

Below is the link to the electronic supplementary material.

Funding

The authors have not disclosed any funding.

Declaration

Competing Interests

The authors have not disclosed any competing interests.