Abstract
Bovine pericardium (BP) has been used as leaflets of prosthetic heart valves. The leaflets are sutured on metallic stents and can survive 400 million flaps (~10-year life span), unaffected by the suture holes. This flaw-insensitive fatigue resistance is unmatched by synthetic leaflets. We show that the endurance strength of BP under cyclic stretch is insensitive to cuts as long as 1 centimeter, about two orders of magnitude longer than that of a thermoplastic polyurethane (TPU). The flaw-insensitive fatigue resistance of BP results from the high strength of collagen fibers and soft matrix between them. When BP is stretched, the soft matrix enables a collagen fiber to transmit tension over a long length. The energy in the long length dissipates when the fiber breaks. We demonstrate that a BP leaflet greatly outperforms a TPU leaflet. It is hoped that these findings will aid the development of soft materials for flaw-insensitive fatigue resistance.
Collagenous soft tissues derive their extraordinary fatigue resistance from the synergy of strong collagen fiber and soft matrix.
INTRODUCTION
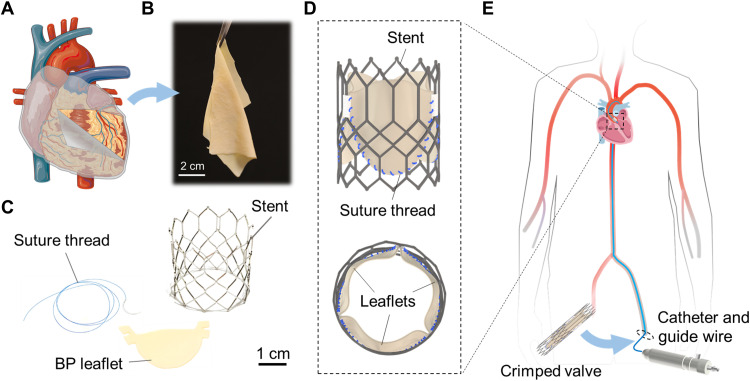
Soft tissues, such as vocal cord, tendons, ligaments, and heart valves, function by repeated stretches. These soft tissues show extraordinary fatigue resistance. When damaged by diseases, they may be replaced with prosthetics. For example, a damaged heart valve can be replaced with a transcatheter heart valve through minimally invasive surgery (Fig. 1) (1). The leaflets of such a prosthetic heart valve are commonly made of the bovine pericardium (BP), a collagenous membrane harvested from a bovine heart (Fig. 1, A and B) (2). The leaflets are sutured onto a metallic stent (Fig. 1, C and D) and delivered from a leg to the heart using a guide wire through an artery (Fig. 1E). When the leaflets flap cyclically, the suture holes would cause many synthetic materials to grow cracks. However, the BP leaflets can survive 400 million flaps (~10-year life span) (3). This extraordinary flaw-insensitive fatigue resistance is unmatched by synthetic leaflets.
Fig. 1. Transcatheter heart valves.
(A) BP is a collagenous membrane covering the bovine heart. (The figure was partly generated using Servier Medical Art, licensed under a Creative Commons Attribution 3.0 unported license.) (B) A photo of BP, thickness ~ 200 μm, harvested from the heart. (C) Photographs of a suture thread of a diameter of ~150 μm, BP leaflet, and metallic stent. (D) A schematic of BP leaflets sutured on a metallic stent to assemble into a transcatheter heart valve. (E) The transcatheter heart valve is compressed in a catheter and is pushed from a leg to the heart through an artery using a guide wire. Upon reaching the site of the aortic valve, the material expands into the shape of the heart valve, and then, the catheter is removed.
The BP leaflets usually do not fail by growing cracks but by calcification (4, 5). This fact, along with the high cost of BP, has long motivated the development of synthetic materials (6–8). Advances have been made to develop synthetic leaflets that resist calcification (9–12), but their fatigue resistance remains far inferior to BP (13, 14). What makes BP so fatigue resistant in the presence of suture holes?
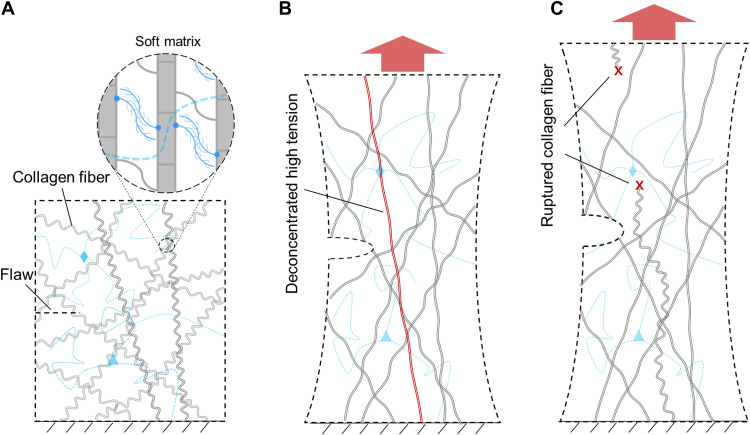
This paper studies how BP resists crack growth under cyclic stretch. In particular, the BP is chemically fixed by glutaraldehyde following the common practice in bioprosthetic heart valves. We show that BP is insensitive to flaws of size ~1 cm. By contrast, a synthetic material, thermoplastic polyurethane (TPU), is insensitive to flaws of size ~100 μm. Digital image correlation (DIC) shows that a crack tip does not concentrate strain in BP but does concentrate strain in TPU. Optical microscopy shows that rupture of BP pulls out long lengths of collagen fibers. These experiments interpret the extraordinary flaw-insensitive fatigue resistance of BP. A BP membrane consists of a network of strong collagen fibers embedded in a soft matrix (Fig. 2A). When the membrane is stretched, the soft matrix enables the tension in an individual collagen fiber to transmit over a long length (Fig. 2B). The long-length transmission of tension alleviates the stress concentration at the tip of flaws, which is called stress deconcentration. The elastic energy stored in the long length of the fiber dissipates when the fiber breaks (Fig. 2C). Consequently, BP derives its flaw-insensitive fatigue resistance from both the strong collagen fibers that bear high tension and the soft matrix that deconcentrates the high tension over long length. We further demonstrate that a BP heart valve remains intact after 2 × 108 cycles of pulsation, but a TPU heart valve grows many cracks after 2.7 × 106 cycles. It is hoped that these findings will aid in the development of synthetic soft materials for high fatigue resistance.
Fig. 2. In BP, strong collagen fibers bear high tension, and soft matrix deconcentrates the high tension over long length.
(A) In an undeformed BP membrane, a network of strong collagen fibers is embedded in a soft matrix. (B) When the membrane is stretched, the soft matrix deconcentrates high tension in an individual collagen fiber over a long length. (C) When the collagen fiber ruptures, the elastic energy stored in the long length of the fiber dissipates.
The hierarchical structures of BP have been extensively studied (Fig. 3A). Three peptide chains bind into a helix, called a tropocollagen, by hydrogen bonds. Numerous tropocollagens assemble into a collagen fibril by noncovalent interactions and covalent bonds (15–17). The staggered assembly of tropocollagen results in d-bands in collagen fibrils (18). The lengths of collagen fibrils range from 0.5 mm to over 10 mm (19). The strength of an individual collagen fibril is as high as ~200 MPa (20). At the microscale (~1 μm), thousands of collagen fibrils align in parallel to assemble into a bundle through proteoglycans (PGs) and other fibrils, called a collagen fiber (21). The collagen fibers are crimped and form a network embedded in a matrix of low modulus and high elasticity (22). The matrix consists of PGs, elastin, and small-diameter fibrils (23). PG keeps the tissue hydrated and promotes interfibrillar sliding (24) due to the high negative fixed charge density. Elastin enables high elasticity of the collagen network (25). Small-diameter collagen fibrils fuse with different neighboring collagen fibers to transfer shear loads (23).
Fig. 3. Structure of the BP.
(A) Schematics of the structure at several length scales. A BP membrane is observed in transmission and scanning electron microscopes (TEM/SEM) with various resolutions. (B) A TEM image shows individual collagen fibrils with a diameter of 100 nm and d-bands with a spacing of ~65 nm. SEM images: (C) A bundle of collagen fibrils constitute a collagen fiber, which is surrounded by elastin fibers. (D) Collagen fibers are wavy, and multiple collagen fibers are aligned. (E) Collagen fibers are embedded in a soft matrix.
For the BP membrane used in our work, we observe the structure in transmission and scanning electron microscopes. The diameter of a collagen fibril is ~100 nm, and the d-bands with the spacing of ~65 nm on a collagen fibril can be observed (Fig. 3B). A bundle of collagen fibrils constitutes a collagen fiber of diameter ~30 μm (Fig. 3C). Collagen fibers are crimped (Fig. 3D) and form a network embedded in a soft matrix (Fig. 3E). Also visible is one component of the matrix, elastin fibers.
That some soft tissues resist crack growth must be known when ancients prepared leathers (26). The quantification of resistance to crack growth began only in the last century, after fracture mechanics was developed. Fracture toughness is measured by stretching a sample with a precut. This approach has been applied to many soft tissues (table S1) (27–42). Fracture toughness ranges from 1000 J/m2 for porcine aorta to 80,000 J/m2 for rhinoceros dermal. These values may be compared with ~10,000 J/m2 for natural rubber (43). It is known that the strength of a tough soft tissue is flaw insensitive, nearly unchanged even for a sample containing a precut of millimeters to centimeters (30, 39, 41, 42, 44).
The microstructural changes of soft tissues under cyclic stretches have been extensively studied for tendons, ligaments, cartilages, and valvular tissues (45–55). For example, cyclic stretches cause kink, rupture, and slip of collagen fibrils in tendons (47, 56, 57) and reduce crimps of collagen fibers in valvular tissues (53, 55). However, far less is known about crack growth resistance of soft tissues under cyclic stretches.
RESULTS
This paper characterizes flaw-insensitive fatigue resistance and relates it to microstructural changes under cyclic stretches. We mark a BP membrane with rectangular grids of dimensions 20 mm by 20 mm and detect the preferred orientation of collagen fibers in each region using the small-angle light scattering (SALS; fig. S1). The BP membrane is cut into samples. The stress-stretch curves vary greatly between samples of different degrees of collagen alignment, but vary much less among samples of a similar degree of collagen alignment (fig. S2). In the following sections, we test samples of a high degree of collagen alignment. The stretch is applied perpendicular to the preferred orientation of collagen fibers, and precuts are introduced parallel to that direction.
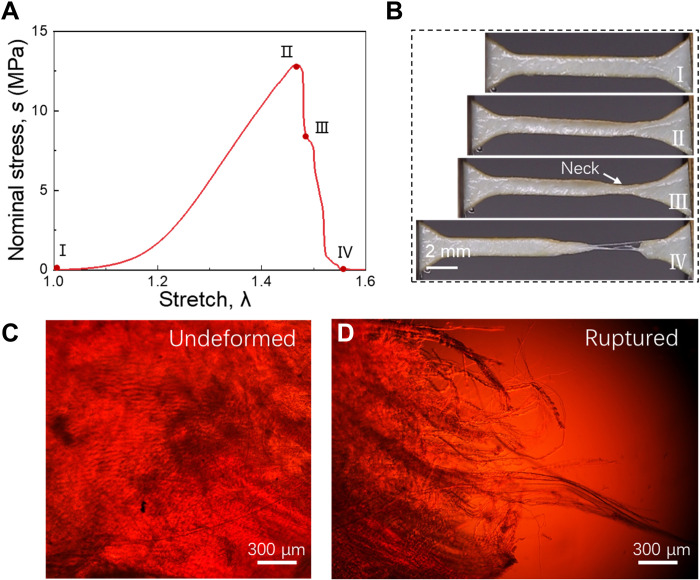
We cut a dog bone-shaped sample from a membrane, monotonically stretch the sample to rupture, and record the stress-stretch curve (Fig. 4A). The sample ruptures at a stretch of 1.45 and a stress of 12 MPa. The area under the stress-stretch curve is the work of fracture, Wc ~ 1.3 × 106 J/m3. We mark four states of deformation on the stress-stretch curve and take snapshots of the sample in these states (Fig. 4B). Starting in the undeformed state (I), the stress-stretch curve rises gently in the beginning and then steeply to a peak (II). Before the peak, the sample deforms homogeneously. After the peak, the stress drops sharply, and the sample forms a localized neck (III). When the sample breaks at the neck, collagen fibers are pulled out (IV). We observe samples using a polarized light microscope. In the undeformed sample, a network of crimped collagen fibers is observed because of birefringence (Fig. 4C). At the rupture surface, bundles of collagen fibers are observed to pull out with a length of ~3 mm (Fig. 4D).
Fig. 4. Tension and pullout of collagen fibers.
(A) Stress-stretch curve. (B) Snapshots of four states of deformation. Polarized light micrographs of (C) an undeformed sample and (D) the rupture surface of the sample. In the uniaxial tensile test, the number of samples, n = 6. Thickness of samples, t = 0.28 ± 0.03 mm (means ± SD).
The matrix and the fibers have very different moduli, which can be approximately determined by the stress-stretch curve (Fig. 4A). At a small stretch, from 1.0 to 1.05, the collagen fibers are crimped, and the slope of the stress-stretch curve is small, ~ 0.2 MPa, taken to be the modulus of the matrix. At a large stretch, from 1.2 to 1.4, the collagen fibers are decrimped, and the slope of the stress-stretch curve is large, ~100 MPa, taken to be the modulus of the collagen fibers. Because the matrix is much softer than the fibers, when the sample is stretched, the matrix shears substantially, and high tension transmits over a long length of an individual collagen fiber (Fig. 2B). The rupture of the fiber dissipates the energy in a long segment of the fiber.
We also conduct a tensile test on samples with 1-mm edged precuts. The strength and extensibility of the sample are not affected by the precut (fig. S3A). The precracked sample fails similarly to that of intact samples, forming necking and rupturing gracefully. The pullout length of collagen fibers at the rupture surface of the precracked sample is longer than ~3 mm (fig. S3B). The long pullout length of the collagen fibers demonstrates deconcentration of high tension because long and dispersed pullout length indicates that the failure of individual collagen fiber is dominated by statistically distributed fiber strength or length rather than concentrated high stress adjacent to the crack tip.
We further demonstrate the importance of the soft matrix in deconcentrating tension in collagen fibers. We dehydrate a BP membrane in air for 5 hours and then stretch the sample to rupture (fig. S3C). The stress rises steeply to a peak and drops suddenly to zero. The stress-stretch curve has a constant and high slope, ~720 MPa, which indicates that dehydration stiffens the matrix. The sample ruptures without forming a neck but by propagating a crack (fig. S3C). The polarized light micrograph of the crack surfaces shows that the pullout length of collagen fibers is ~50 μm, two orders of magnitude shorter than that in the hydrated sample (fig. S3D). The dehydration stiffens the matrix, which limits the transmission of tension in collagen fibers within a short length. This interpretation is consistent with the observed short pullout length.
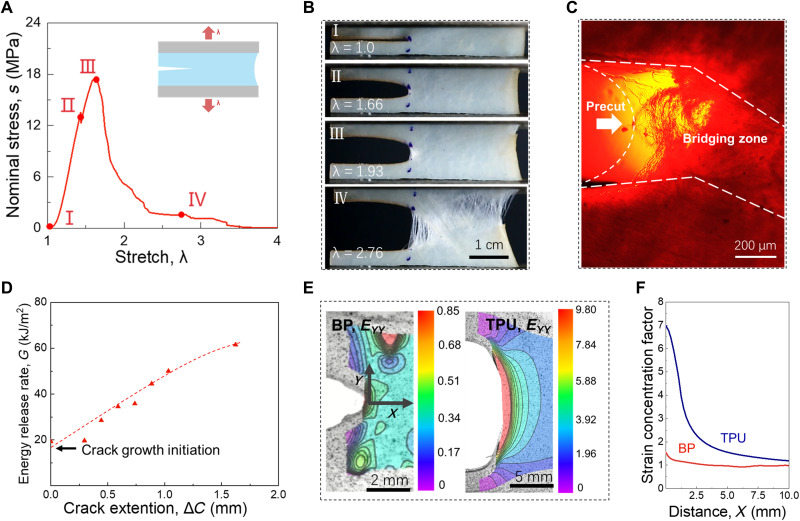
We study the fracture of the membrane using a sample with a precut. The stress-stretch curve and a sequence of snapshots for the fracture process are recorded (Fig. 5, A and B). Starting in the undeformed state (I), the crack opens when the sample is stretched. At the onset of crack growth, a small white zone appears at the crack tip (II). At state II, the stress does not drop immediately because the collagen fibers in the white zone can still sustain forces. As the stress increases to the peak (III), the crack propagates; meanwhile, the white zone enlarges, resulting in the further increase of the stress. At a stretch of 2.76, collagen fibers rupture and pull out in multiple regions, and the stress drops close to zero (IV). This stretch is close to the rupture stretch of samples without precuts. We further use a polarized light microscope to observe the morphology of the crack tip in state III (Fig. 5C). Two separated crack surfaces are marked with dashed lines. Between the separated crack surfaces, bundles of collagen fibers rupture and pull out from the matrix, forming a bridging zone, which is white to the naked eye. The crack is bridged by the collagen fibers in this zone and propagates by breaking and pulling out the fibers in this zone. The crack often grows in a direction somewhat different from the direction normal to the applied stretch. In preparing the sample, the collagen fibers have a preferred orientation normal to the applied stretch. The observed deviation in the direction of the crack growth is likely due to the imperfect alignment of the preferred fiber orientation in the undeformed sample.
Fig. 5. Fracture and deconcentration of strain.
(A) The stress-stretch curve. (B) Snapshots of a membrane with a precut in four states of deformation. (C) A polarized light micrograph of the crack tip. (D) The resistance curve. (E) Contours of strain EYY observed using DIC. Both BP and TPU are imaged for comparison. (F) The concentration factor of strain EYY at distance X from the crack tip measured in the undeformed state. In the fracture test, the number of samples, n = 3. Thickness of samples, t = 0.31 ± 0.04 mm (means ± SD).
The energy release rate increases with the extension of the crack (Fig. 5D). We observe the crack extension by DIC, which gives a resolution of crack extension of ~200 μm. The crack initiates at an energy release rate of 15 kJ/m2. After the crack propagates for 1.5 mm, the energy release rate increases to 60 kJ/m2. Then, the whole sample grows multiple cracks. We designate fracture toughness by the energy release rate at the onset of crack growth Gc = 15 kJ/m2.
At the onset of the crack growth, we visualize the distribution of strain EYY around the crack tip by DIC (Fig. 5E). For comparison, both BP and TPU are imaged. The local strain divided by the applied strain defines the strain concentration factor, which is plotted as a function of distance X from the crack tip (Fig. 5F). The strain is nearly uniform in BP but is highly concentrated in TPU.
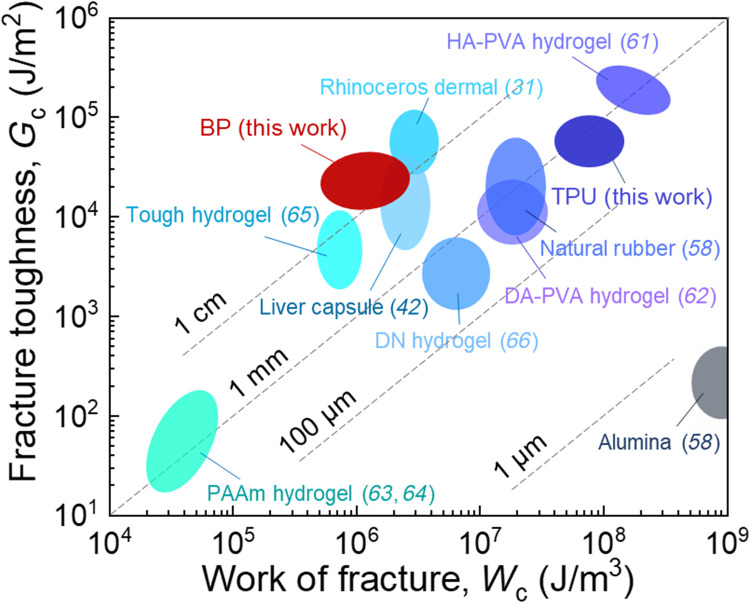
We have measured the work of fracture Wc using samples without precut and measured the fracture toughness Gc using samples with precut. The ratio of the two material properties, Gc/Wc, has a dimension of length, called the fractocohesive length (58, 59). When the crack propagates in a sample, a region around the crack tip dissipates energy, which resists crack growth. The approximate size of this dissipative zone is given by the fractocohesive length Gc/Wc (59, 60). The fractocohesive length also measures the flaw sensitivity of a material. The strength of a material decreases in the presence of flaws if they are larger than the fractocohesive length and is insensitive to flaws if they are smaller than the fractocohesive length.
We plot various materials on the plane of Gc and Wc (Fig. 6). Soft tissues, such as BP, rhinoceros dermal (31), and liver capsule (42), have a long fractocohesive length of ~1 cm. This length is larger than the fractocohesive lengths of most synthetic materials, including hierarchical Poly(vinyl alcohol) (PVA) hydrogel (61), dry-annealed PVA hydrogel (62), polyacrylamide hydrogel (63, 64), tough hydrogel (65), double-network hydrogel (66), natural rubber (58), and TPU. For example, TPU has a fractocohesive length of ~100 μm. The work of fracture Wc of TPU is two orders of magnitude higher than that of BP (fig. S4), but the fracture toughness Gc of BP and TPU is similar (fig. S5). Thus, the fractocohesive length of TPU is two orders of magnitude lower than that of BP.
Fig. 6. Flaw sensitivity of materials under monotonic stretch.
Various materials are plotted on the plane of fracture toughness Gc and work of fracture Wc. The ratio Gc/Wc defines the fractocohesive length, several values of which are marked. HA-PVA, hierarchical PVA; DA-PVA, dry-annealed PVA; PAAm, polyacrylamide; DN, double network.
The flaw insensitivity of BP can be qualitatively interpreted by a discrete model, where the BP membrane is simplified into a unidirectional fiber-reinforced composite (fig. S6). Collagen fibers aligned perpendicular to the loading direction are viewed as a part of the matrix, transmitting loads from broken fibers to intact fibers. By normalizing the governing equations, a characteristic length scale can be derived, i.e., the load transfer length lT. lT is related to the diameter of fiber and the moduli contrast of fiber and matrix (67, 68), which measures the length of an overload region on intact fiber at the crack tip, equivalent to the fractocohesive length in fiber-reinforced composite. Upon the crack propagation, the overloaded region in the fiber will undergo inelastic deformation and dissipates energy. Given the crack size a and the sample size L, we show how the strain concentration in intact fibers ahead the crack tip is affected by the flaw insensitivity of materials. For materials with large lT and flaw insensitivity, the strain does not concentrate at the crack tip [blue lines in fig. S6, (C and D)]. This phenomenon is similar to the observation in BP membrane (Fig. 5, E and F). In contrast, the strain concentrates markedly at the crack tip for materials with small lT and flaw insensitivity [red lines in fig. S6 (C and D)]. This is the case for the fracture of TPU (Fig. 5, E and F) because a homogenous material can be idealized by a composite with small moduli contrast of fiber and matrix.
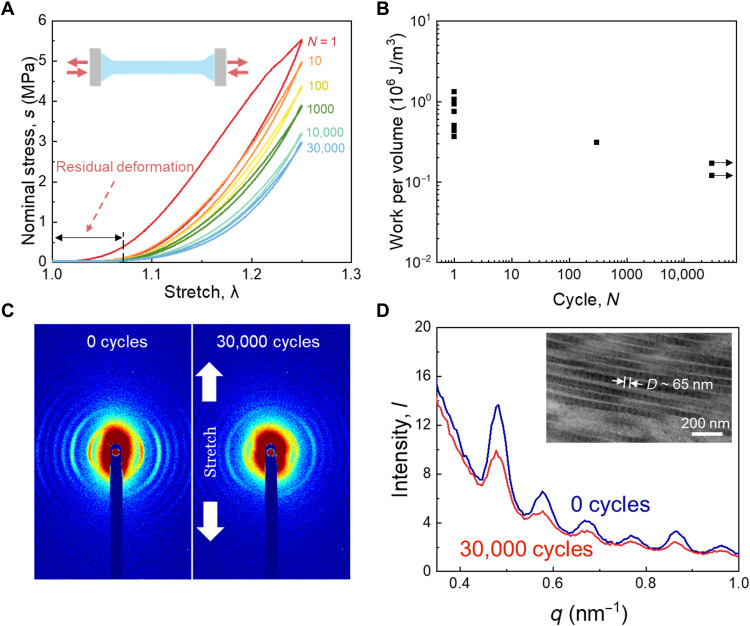
We then characterize the fatigue behavior of samples without precut. Dog bone-shaped samples are stretched cyclically under a prescribed amplitude of stretch. We take necking as a failure symptom of BP samples. A camera with 100-μm resolution is used to take photographs of samples during cyclic stretching every 15 min. When necking is observed and the peak stress drops markedly, e.g., decreasing by over 50% within 200 cycles (fig. S7), we take the cycle of the last recording period as the number of cycles to rupture. When the amplitude is low, the sample sustains 30,000 cycles without necking (Fig. 7A). The stress-stretch curve shows a large hysteresis loop in the first few cycles. As the cycle progresses, the hysteresis becomes smaller and the maximum stress shakes down to a steady value after ~10,000 cycles. Residual deformation of samples is observed after 30,000 cycles. The hysteresis, shakedown of stress, and residual deformation correspond to the irreversible damage of the material. When the amplitude of stretch is close to the rupture stretch under monotonic loading, the sample ruptures in the first cycle. The strength has a large statistical variation from sample to sample. For a moderate amplitude of stretch, we observe that the sample ruptures after 300 cycles.
Fig. 7. Cyclic stretch of membranes without precut.
(A) Stress-stretch curves under cyclic stretch. (B) The number of cycles to rupture is a function of the amplitude of work per volume. (C) Patterns of small-angle x-ray scattering (SAXS) before and after cyclic stretch. (D) Intensity-q spectra lines before and after 30,000 cyclic stretches. Inset: Periodic d-band structure of collagen fibrils. In the fatigue test of samples without precut, the number of samples for each stretch amplitude, n = 1. Thickness of samples in the whole fatigue test group, t = 0.27 ± 0.04 mm (means ± SD).
We convert the amplitude of stretch to the amplitude of work per volume W by integrating the stress-stretch curve of the last loading cycle. We plot the experimental data on the plane of the amplitude of work per volume, W, and the number to rupture, N (Fig. 7B). Each ruptured sample is plotted as a point, and each surviving sample is plotted as an arrow. The amplitude of work per volume is between two limits: the work of fracture Wc, at which the sample ruptures under monotonic stretch, and the work of endurance We, at which the sample survives a prescribed number of cycles of stretch. The work of endurance is We ~ 1.7 × 105 J/m3, below which the sample does not rupture after 30,000 cycles. Between Wc and We, the sample ruptures after a smaller number of cycles of stretch.
We conduct the small-angle x-ray scattering (SAXS) test to reveal the microstructural evolution corresponding to the fatigue damage during the cyclic stretch. The unstretched sample (0 cycles) displays sharp diffraction arcs (Fig. 7C), indicating a narrow angular distribution of collagen fiber alignment. The arcs are dominated by Bragg reflections because of the interaction of x-rays with d-band structure on collagen fibrils (69, 70). After 30,000 cycles of stretch, the diffraction arcs transform into tarnished circles, suggesting that collagen fibers are oriented more randomly. We can extract the spacing of the periodic d-band structure on the collagen fibrils from the Bragg peaks on the diffraction patterns to detect the deformation at the collagen fibril level. The intensity decreases after 30,000 cycles of stretch because of reorientation of collagen fibers, while the peak positions remain the same (Fig. 7D). Thus, the spacing of the d-bands on collagen fibrils before and after 30,000 cyclic stretches is identical, ~65 nm. This value is consistent with the value reported before (71). Our observations indicate that the spacing of the d-bands remains constant after cyclic stretch, although the collagen fibers are decrimped and reoriented. Thus, the residual deformation of the sample is not caused by the stretch of individual collagen fibril but the sliding of collagen fibers in the network.
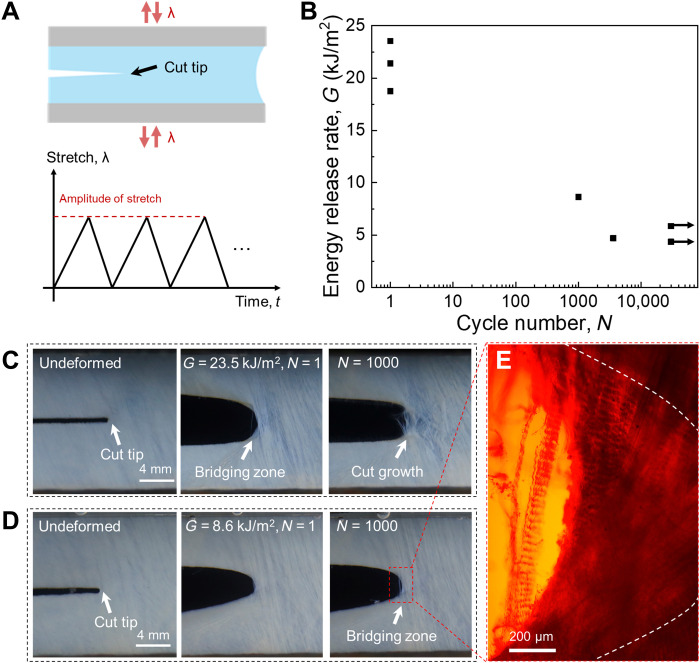
We introduce a precut in a membrane and apply cyclic stretch (Fig. 8A). We use a digital camera with a resolution of 100 μm to take a photograph of the precut tip every 15 min. When a white zone is observed, we take the cycle as the onset of crack growth. On the plane of the energy release rate, G, and the number of cycles to the onset of crack growth, N, we plot each observation of onset of crack as a point and plot each sample that survives 30,000 cycles without the onset of crack as an arrow (Fig. 8B). The latter indicates the fatigue threshold, which is as high as 4.3 kJ/m2. The fatigue behavior of BP under different energy release rates is compared. Under a high energy release rate, G = 23.5 kJ/m2, the crack grows on the first cycle, with bundles of collagen fibers bridging the crack (Fig. 8C). As the sample is further cycled, the collagen fibers at the tail of the bridging zone start to break and pull out from the crack surfaces. Under an intermediate energy release rate, G = 8.6 kJ/m2, the crack growth initiates at ~1000 cycles (Fig. 8D). The separated crack surfaces and bridging collagen bundles can be observed by polarized light micrograph (Fig. 8E). Under a low-energy release rate, G = 4.3 kJ/m2, the crack does not grow after 30,000 cycles by the end of the test (fig. S8). No break of collagen fibers is observed.
Fig. 8. Cyclic stretch of membranes with precut.
(A) Schematic of a membrane with precut subjects to cyclic stretch, with a prescribed amplitude of stretch. (B) The plane of the energy release rate and the number of cycles to the onset of crack growth. A point represents a failed sample, and an arrow represents a sample surviving 30,000 cycles without crack growth. (C) A membrane with precut is subject to cyclic stretch of amplitude λ = 1.45 and the energy release rate being G = 23.5 kJ/m2. (D) A membrane with precut is subject to cyclic stretch of amplitude λ = 1.35 and G = 8.6 kJ/m2. (E) Polarized light micrograph of the crack tip. In the fatigue fracture test, the number of samples for each stretch amplitude, n = 1. Thickness of samples in the whole fatigue test group, t = 0.30 ± 0.03 mm (means ± SD).
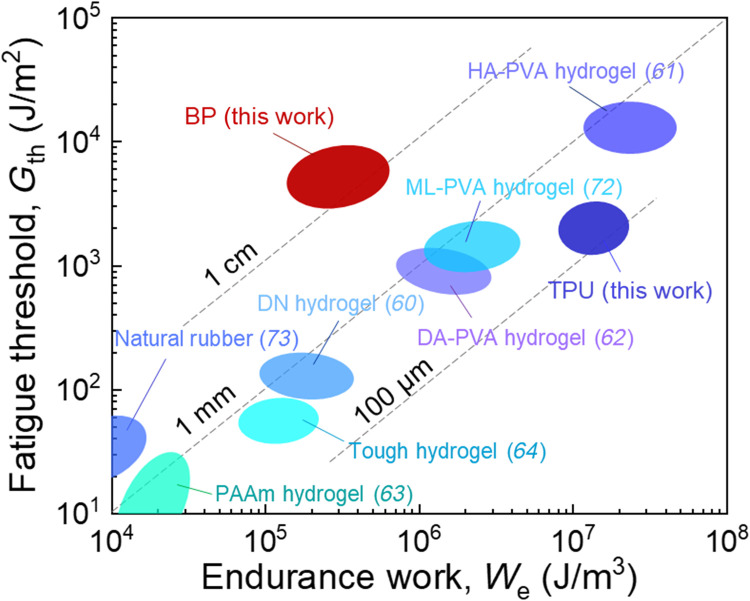
We can also define a characteristic length by the ratio of Gth/We, which represents the flaw sensitivity of the material under cyclic stretch. The length is called endurance fractocohesive length (60). When the precut is shorter than that length, the fatigue strength is insensitive to the precut. When the precut is long, the fatigue strength is smaller than the values of a sample without precut. The transition takes place at the length comparable to the endurance fractocohesive length.
On the plane of Gth and We, we plot various materials to compare their flaw sensitivity under cyclic stretch (Fig. 9). Unlike fracture under monotonic stretch (Fig. 6), fatigue under cyclic stretch has seldom been characterized for soft biological tissues. The only data available to us are from our own measurements of BP, which we compare with available data for synthetic soft materials (60, 62–64, 72, 73). Most synthetic soft materials have an endurance fractocohesive length in the range 100 μm to 1 mm, which is one or two orders of magnitude lower than that of BP (~1 cm).
Fig. 9. Flaw sensitivity of materials under cyclic stretch.
Various materials are plotted on the plane of fatigue threshold Gth and work of endurance We. The ratio Gth/We defines the endurance fractocohesive length, several values of which are marked. ML-PVA, muscle-like PVA.
The endurance fractocohesive length of a material measures its flaw sensitivity under cyclic stretch. Here, we highlight the significance of the endurance fractocohesive length in prosthetic heart valves. Each year, 40.5 million people suffer from heart valve disease, and many of them need heart valves replaced with prosthetics (6). As noted before, prosthetic leaflets are sutured on an expandable metallic stent. After implantation, the leaflets are required to flap at least 200 million times according to the ISO 5840 standard (8). So far, only biological tissues such as BP are used for the leaflets. Because biological soft tissues are costly and prone to calcification, synthetic materials have been widely investigated (6). Among the synthetic materials, TPU has been a leading candidate (14, 74).
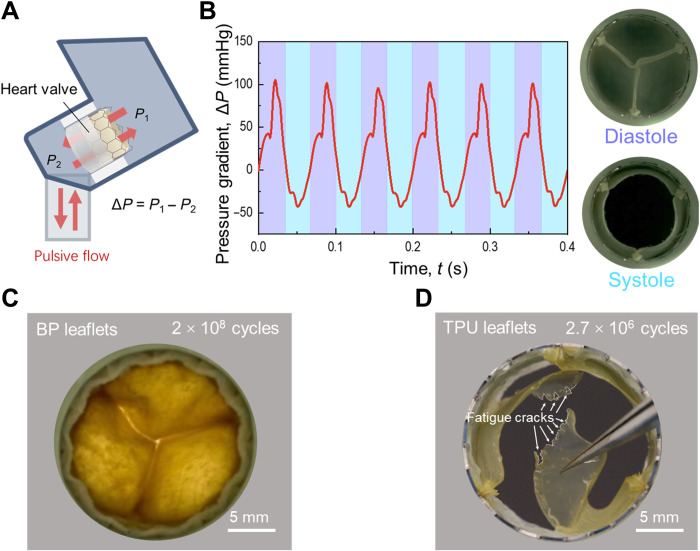
We fabricate transcatheter heart valves using BP and TPU and subject them to an in vitro-accelerated test of cyclic pulsive flow (Fig. 10, A and B). BP leaflets remain intact after 2 × 108 cycles, but TPU leaflets grow many cracks after 2.7 × 106 cycles (Fig. 10, C and D). We interpret this great difference in durability on the basis of endurance fractocohesive length. The leaflets always have large flaws: suture holes of a diameter of ~150 μm. The size of the suture holes is comparable to the endurance fractocohesive length of TPU (~100 μm). From the suture holes, the TPU leaflets grow cracks under cyclic pulsation. The size of the suture holes, however, is smaller than the endurance fractocohesive length of BP (~1 cm) so that the BP leaflets remain intact under cyclic pulsation.
Fig. 10. Accelerated fatigue test of transcatheter heart valves.
(A) Schematic of accelerated fatigue test. A transcatheter heart valve is mounted in an accelerated wearing test machine to endure cyclic pulsive flow. (B) During the test, the transvalvular pressure gradient of the pulsive flow is controlled at an amplitude of 100 mmHg and a frequency of 15 Hz. (C) A BP valve remains intact after 2 × 108 cycles of pulsive flow. (D) A TPU valve grows cracks after 2.7 × 106 cycles of pulsive flow.
DISCUSSION
Soft polymeric valve leaflets often suffer from fatigue crack growth. While biological tissues address this problem with their extraordinary flaw-insensitive fatigue resistance endowed by the strong collagen fiber and soft matrix. The synthetic materials should mimic the heterogeneous structures of biological tissues. In recent years, synthetic soft materials have been developed to exhibit high fatigue resistance. Examples include poly(vinyl alcohol) hydrogels (61, 62, 72), soft composite materials (75–80), TPUs (81), and highly entangled hydrogels and elastomers (82). In the coming years, it is likely that synthetic materials will be developed for applications in which flaw-insensitive fatigue resistance is critical, along with biochemical requirements, such as resistance to calcification and thrombosis.
In this work, we mainly investigate BP membranes fixed by glutaraldehyde aqueous solution. The glutaraldehyde has long been used to treat fresh BP membranes to improve their durability and prevent immune response (3). We have also demonstrated that the fresh BP membranes are insensitive to a long precut of ~1 cm under both monotonic and cyclic stretch (figs. S9 and S10). The duration of fatigue tests is 30,000 cycles here, which is short compared to the lifetime of heart valves. Thus, we have also demonstrated that the BP membrane is flaw insensitive to a precut in a longer duration of 1 million cycles (fig. S14). The assumption that data obtained in these experiments can be used to predict the durability of valve leaflets is, of course, open to criticism. Whereas, even in short fatigue tests, the BP membrane displays a higher flaw insensitivity compared to elastomeric leaflets.
In summary, we have stretched BP membranes with or without precuts. Under both monotonic and cyclic stretches, the BP membranes are insensitive to large flaws (~1 cm). By contrast, a synthetic material, TPU, is insensitive to flaws of size ~800 μm under monotonic stretch and insensitive to flaws of size ~100 μm under cyclic stretch. Transcatheter heart valves contain large flaws: the suture holes of a diameter ~150 μm. Consequently, a BP heart valve remains intact after 2 × 108 cycles of pulsation, but a TPU heart valve grows many cracks after 2.7 × 106 cycles. We further demonstrate that the endurance of the BP membranes results from the transmission of tension in the collagen fibers over a long length. Dehydrated membranes without such mechanism are even sensitive to the precut with ~1 mm in length (fig. S11). It is hoped that these findings will aid in the future development of synthetic soft materials for high fatigue resistance.
MATERIALS AND METHODS
Materials
Commercial-grade BP membranes were supplied by courtesy from Shanghai NewMed Medical Co. Ltd. (China), which were purchased from Maverick Biosciences Corporation (New South Wales, Australia). Following a common practice, the BP membranes were treated with glutaraldehyde aqueous solution (volume fraction, 0.625%). The glutaraldehyde acts as a cross-linker of collagen, forming interfiber bonding, which stiffens the membranes and reduces the stress relaxation (83–85).
TPU particles (Estane 58201) were purchased from Lubrizol Corporation (OH, USA). The particles were first dried in an oven at 104°C for 2 hours. A thermocompressor (Gongjiang Y002, Zhengzhou) was used to shape TPU particles into membranes with thin steel spacers. The TPU particles were first melted at the temperature of 200°C for 10 min, compressed at the pressure of 0.2 MPa for 30 min, and cooled by a water-cooling system. TPU membranes with the prescribed thickness were obtained.
Scanning electron microscopy
Strips of BP membranes were cut using a laser cutter. The strips were first immersed in 2.5% glutaraldehyde for 5 hours to fix the structure. The strips were then immersed in water-ethanol solutions of ascending fractions of ethanol (30, 50, 70, 90, 95, and 100 volume % twice) to replace water in the strips with ethanol. The ethanol-soaked strips were dried in a freeze-dryer (Autosamdri-815A, Tousimis). The dried samples were coated with platinum using a sputter coater (Hitachi MC1000) and observed in a scanning electron microscope (Hitachi SU3500).
Small-angle light scattering
We used a SALS method to nondestructively detect the preferred orientation of collagen fibers (fig. S1). The custom-designed SALS device consists of a He-Ne laser source (wavelength, 640 nm), a sample positioner, a projecting screen, and a digital camera (fig. S1A). During the test, a BP membrane was sandwiched between two glass plates. After the He-Ne laser beam perpendicularly passed the BP membrane and the glass plates, a scattering pattern was projected on the projecting screen. The scattering pattern revealed the preferred orientation of collagen fibers. A circular scattering pattern indicates a random orientation of collagen fibers, and an elliptical scattering pattern indicates a preferred orientation (fig. S1B). The elliptical scattering pattern with a larger eccentricity suggests that a larger part of collagen fibers align to the preferred orientation.
An intact BP membrane has a square shape with dimensions of ~12 cm by 12 cm. The alignment of collagen fibers in the membrane may vary from region to region, so the membrane was divided into smaller square areas (2 cm by 2 cm) by grid lines. Each square area was detected using the laser, and the scattering patterns on the projecting screen were recorded using a digital camera. The eccentricity and the direction of the short axis of the scattering patterns were extracted using MATLAB. The preferred direction of collagen fibers coincides with the short axis of the elliptical scattering pattern. According to the eccentricity of scattering patterns, different parts of the membrane were sorted into two groups. The parts with eccentricity over 0.7 were sorted into groups where collagen fibers align in a preferred direction. The parts with eccentricity below 0.5 were sorted into groups where collagen fibers align randomly. Samples of collagen fibers with preferred orientation were used here.
Uniaxial tensile tests
The dog bone-shaped samples (2 mm by 12 mm) were cut perpendicular to the preferred orientation of collagen fibers. The thickness of samples was measured through an electrical spiral micrometer with a resolution of 10 μm. Samples were immersed in deionized water for 24 hours and then tested immediately to retain the hydration state. Samples were clamped tightly and stretched by a tensile machine (Shimadzu AGS-X) with a load cell of 100 N and a stretch rate of 0.03 s−1. The stress-stretch curves were recorded. The nominal stress was calculated by dividing the force by the section area of the undeformed sample. The stretch was defined by dividing the current length of the sample by its undeformed length. To accurately measure the stretch, we adopted the DIC method to calibrate the relation between the stretch and the global displacement of clampers (fig. S12).
Fracture tests
The fracture tests were conducted with a method introduced by Thomas (86). We prepared a rectangular BP membrane (width, 37.5 mm; height, 22.5 mm) and introduced a 15-mm-long precut in the middle plane. The precut was parallel to the preferred orientation of collagen fibers. Samples were immersed in deionized water for 24 hours and then tested immediately to retain the hydration state. Before the test, the samples were glued and sutured on four acrylic plates with cyanoacrylate and surgery threads to enhance the clamping force. Samples were then clamped tightly, and the initial height of the sample between two clampers was 10 mm. The samples were stretched by a tensile machine (Shimadzu AGS-X) with a load cell of 500 N at a stretch rate of 0.03 s−1.
The energy release rate is calculated by G = W(λ)H, where W denotes the energy per volume stored in the uncracked samples and H denotes the height of samples in the undeformed state, which is 10 mm in our tests. Considering the large statistical variation from sample to sample, we did not use uncut samples to calculate the strain energy density, W. Instead, we directly used the area under the stress-stretch curve of samples with precuts to determine W. Here, the nominal stress was calculated by dividing the force by the uncut section area of the undeformed samples because the strain is almost homogeneous ahead of the crack tip (Fig. 3F).
DIC method
We sprayed black paint on the surface of the membrane to obtain random speckles. As the sample was stretched, a charge-coupled device digital camera was used to take images of speckles with 10 frames per second. The series of images were then analyzed by a commercial software VIC-2D to extract the strain field.
In data analysis, the sample surface with speckle texture is separated into many elements. Each element is ~200 μm in length and width in the undeformed state. Upon crack growth, the elements penetrated by separated crack surfaces will be deleted (fig. S13A). The deletion is implemented when the correlation coefficient of speckle textures in the element is lower than a specific threshold. By checking the deletion of elements, we can detect the crack growth onset. By counting the number of deleted elements, we measure the crack extension in the undeformed state (fig. S13B).
Fatigue tests
In fatigue tests, the samples were cyclically stretched at prescribed amplitudes of stretch on a tensile machine (Shimadzu AGS-X) with a strain rate of 0.3 s−1. During fatigue tests, samples were submerged in a homemade water chamber with deionized water to maintain the hydration state (fig. S12A). We evaluated the influence of the aqueous environment on the mechanical response of fixed BP membranes. The swelling ratio shows that the fixed membrane has only 5% change in mass after immersing 24 hours in saline solution (fig. S15A). The stress-stretch curves indicate that the aqueous environment influences the mechanical response of fixed BP membranes slightly (fig. S15B). During cyclic stretching, a digital camera (Canon EOS 5DS) with 100-μm resolution was used to take a photograph every 15 min. For the uncut samples, we used the same dimensions and orientations of collagen fibers as those in uniaxial tensile tests. Necking was taken as failure of the uncut samples, and the corresponding number of cycles was recorded. For the precut samples, we used the same dimensions and orientations of collagen fibers as those in fracture tests. The crack tip was photographed using the digital camera. When a white damage zone around the crack tip was observed, the number of cycles was recorded.
The stress-stretch curves were recorded at the 1st, 10th, 100th, 1000th, 5000th, 10,000th, 20,000th, and 30,000th cycles. For the precut samples, we calculated the energy release rate by G = W(λ)H. Because the stress-stretch curves reached steady state after ~10,000 cycles, we determined the energy density, W, by the area of the stress-stretch curves at the 10,000th cycle.
Small-angle x-ray scattering
BP strips with dimensions of 20 mm by 4 mm by 0.3 mm were cut from the membrane using a laser cutter. The strips were tested using a SAXS machine (SAXSpoint 2.0). The obtained diffraction patterns were analyzed by the software Fit2D. The diffraction maxima occurring at angles 2θ to the x-ray beam (Bragg reflections) are given by the equation: 2sin(θ) = Λn/d, where n is the order of the reflection, Λ is the wavelength of x-ray, and d is the spacing between the d-bands on collagen fibrils.
In vitro accelerated fatigue test
The BP membranes and TPU membranes were cut into the shape of valve leaflets with a laser cutter. The leaflets were then sutured on polyethylene terephthalate fabric-covered expandable metallic stents to assemble into transcatheter heart valves.
The transcatheter heart valves were mounted on an accelerated wearing tester (TA Instruments, USA) to endure cyclically pulsive flow. The transvalvular pressure gradient in diastole duration was controlled to be 100 mmHg to simulate the in vivo conditions. The frequency of the pulsive flow was ~15 Hz to accelerate the experiment.
Acknowledgments
We thank Y. Zhou and H. Guo for help in performing fatigue experiment. We acknowledge Y. Xu and H. Zhan for help in conducting in vitro accelerated fatigue test.
Funding: This research was supported by the National Natural Science Foundation of China (grant nos. 12172272 and 11820101001). J.T. acknowledges the support of K. C. Wong Education Foundation. Z.S. acknowledges the support from the Harvard University Materials Research Science and Engineering Center (DMR-2011754).
Author contributions: Conceptualization: Z.S., J.Y., and J.T. Methodology: L.Z., F.L., Z.S., and J.T. Investigation: L.Z., F.L., C.J., and Q.Y. Visualization: L.Z. and F.L. Supervision: Z.S., J.Y., and J.T. Writing (review and editing): L.Z., F.L., Z.S., and J.T.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Table S1
Figs. S1 to S15
REFERENCES AND NOTES
- 1.A. Cribier, Development of transcatheter aortic valve implantation (TAVI): A 20-year odyssey. Arch. Cardiovasc. Dis. 105, 146–152 (2012). [DOI] [PubMed] [Google Scholar]
- 2.T. Ishihara, V. J. Ferrans, M. Jones, S. W. Boyce, W. C. Roberts, Structure of bovine parietal pericardium and of unimplanted Ionescu-Shiley pericardial valvular bioprostheses. J. Thorac. Cardiovasc. Surg. 81, 747–757 (1981). [PubMed] [Google Scholar]
- 3.J. Sathananthan, S. Lauck, J. Polderman, M. Yu, A. Stephenson, G. Sathananthan, R. Moss, A. Cheung, J. Ye, P. Blanke, J. Leipsic, D. A. Wood, J. G. Webb, Ten year follow-up of high-risk patients treated during the early experience with transcatheter aortic valve replacement. Catheter. Cardiovasc. Interv. 97, E431–E437 (2021). [DOI] [PubMed] [Google Scholar]
- 4.F. J. Schoen, C. E. Hobson, Anatomic analysis of removed prosthetic heart valves: Causes of failure of 33 mechanical valves and 58 bioprostheses, 1980 to 1983. Hum. Pathol. 16, 549–559 (1985). [DOI] [PubMed] [Google Scholar]
- 5.F. J. Schoen, R. J. Levy, Calcification of tissue heart valve substitutes: Progress toward understanding and prevention. Ann. Thorac. Surg. 79, 1072–1080 (2005). [DOI] [PubMed] [Google Scholar]
- 6.D. Bezuidenhout, D. F. Williams, P. Zilla, Polymeric heart valves for surgical implantation, catheter-based technologies and heart assist devices. Biomaterials 36, 6–25 (2015). [DOI] [PubMed] [Google Scholar]
- 7.F. Oveissi, S. Naficy, A. Lee, D. Winlaw, F. Dehghani, Materials and manufacturing perspectives in engineering heart valves: A review. Materials Today Bio 5, 100038 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.H. T. Bui, N. Khair, B. Yeats, S. Gooden, S. P. James, L. P. Dasi, Transcatheter heart valves: A biomaterials perspective. Adv. Healthc. Mater. 10, e2100115 (2021). [DOI] [PubMed] [Google Scholar]
- 9.B. Rahmani, G. Burriesci, M. Mullen, A. Seifalian, S. Tzamtzis, J. Yap, TCT-109 A new generation transcatheter heart valve with a novel nanocomposite material and fully retrievable design. J. Am. Coll. Cardiol. 60, B34 (2012). [Google Scholar]
- 10.B. Zhang, X. Chen, T. Y. Xu, Z. G. Zhang, X. Li, L. Han, Z. Y. Xu, Transcatheter pulmonary valve replacement by hybrid approach using a novel polymeric prosthetic heart valve: Proof of concept in sheep. PLOS ONE 9, e100065 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.J. Scherman, D. Bezuidenhout, C. Ofoegbu, D. F. Williams, P. Zilla, TAVI for low to middle income countries. Eur. Heart J. 38, 1182–1184 (2017). [Google Scholar]
- 12.O. M. Rotman, B. Kovarovic, M. Bianchi, M. J. Slepian, D. Bluestein, In vitro durability and stability testing of a novel polymeric transcatheter aortic valve. ASAIO J. 66, 190–198 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.C. Jenney, P. Millson, D. W. Grainger, R. Grubbs, P. Gunatillake, S. J. McCarthy, J. Runt, J. Beith, Assessment of a siloxane poly (urethane-urea) elastomer designed for implantable heart valve leaflets. Adv. NanoBiomed Res. 1, 2000032 (2021). [Google Scholar]
- 14.M. Kütting, J. Roggenkamp, U. Urban, T. Schmitz-Rode, U. Steinseifer, Polyurethane heart valves: Past, present and future. Expert Rev. Med. Devices 8, 227–233 (2011). [DOI] [PubMed] [Google Scholar]
- 15.H. Hofmann, P. Fietzek, K. Kühn, Comparative analysis of the sequences of the three collagen chains α1(I), α2 and α1(III): Functional and genetic aspects. J. Mol. Biol. 141, 293–314 (1980). [DOI] [PubMed] [Google Scholar]
- 16.T. Itoh, M. Kobayashi, M. Hashimoto, The role of intermolecular electrostatic interaction on appearance of the periodic band structure in type I collagen fibril. Jpn. J. Appl. Phys. 37, L190 (1998). [Google Scholar]
- 17.A. J. Hodge, J. Petruska, Recent studies with the electron microscope on ordered aggregates of the tropocollagen macromolecule, in Aspects of Protein Structure (Academic Press, 1963), p. 289–300. [Google Scholar]
- 18.M. J. Buehler, Nature designs tough collagen: Explaining the nanostructure of collagen fibrils. Proc. Natl. Acad. Sci. U.S.A. 103, 12285–12290 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.A. S. Craig, M. J. Birtles, J. F. Conway, D. A. Parry, An estimate of the mean length of collagen fibrils in rat tail-tendon as a function of age. Connect. Tissue Res. 19, 51–62 (1989). [DOI] [PubMed] [Google Scholar]
- 20.Z. L. Shen, M. R. Dodge, H. Kahn, R. Ballarini, S. J. Eppell, Stress-strain experiments on individual collagen fibrils. Biophys. J. 95, 3956–3963 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.M. A. Meyers, P.-Y. Chen, A. Y.-M. Lin, Y. Seki, Biological materials: Structure and mechanical properties. Prog. Mater. Sci. 53, 1–206 (2008). [DOI] [PubMed] [Google Scholar]
- 22.I. Vesely, The role of elastin in aortic valve mechanics. J. Biomech. 31, 115–123 (1997). [DOI] [PubMed] [Google Scholar]
- 23.S. E. Szczesny, K. L. Fetchko, G. R. Dodge, D. M. Elliott, Evidence that interfibrillar load transfer in tendon is supported by small diameter fibrils and not extrafibrillar tissue components. J. Orthop. Res. 35, 2127–2134 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.S. Rigozzi, R. Müller, A. Stemmer, J. G. Snedeker, Tendon glycosaminoglycan proteoglycan sidechains promote collagen fibril sliding—AFM observations at the nanoscale. J. Biomech. 46, 813–818 (2013). [DOI] [PubMed] [Google Scholar]
- 25.H. Oxlund, J. Manschot, A. Viidik, The role of elastin in the mechanical properties of skin. J. Biomech. 21, 213–218 (1988). [DOI] [PubMed] [Google Scholar]
- 26.F. O’Flaherty, W. T. Roddy, R. M. Lollar, The Chemistry and Technology of Leather. Vol. IV. Evaluation of Leather (R.E. Krieger Publishing Company, 1965). [Google Scholar]
- 27.P. Purslow, Measurement of the fracture toughness of extensible connective tissues. J. Mater. Sci. 18, 3591–3598 (1983). [Google Scholar]
- 28.P. P. Purslow, Positional variations in fracture toughness, stiffness and strength of descending thoracic pig aorta. J. Biomech. 16, 947–953 (1983). [DOI] [PubMed] [Google Scholar]
- 29.Z. Hu, B. Zhang, W. Sun, Cutting characteristics of biological soft tissues. CIRP Annals 61, 135–138 (2012). [Google Scholar]
- 30.P. P. Purslow, The physical basis of meat texture: Observations on the fracture behaviour of cooked bovine M. Semitendinosus. Meat Sci. 12, 39–60 (1985). [DOI] [PubMed] [Google Scholar]
- 31.R. E. Shadwick, A. P. Russell, R. F. Lauff, The structure and mechanical design of rhinoceros dermal armour. Philos. Trans. R. Soc. Lond. B Biol. Sci. 337, 419–428 (1992). [DOI] [PubMed] [Google Scholar]
- 32.M. V. Chin-Purecell, J. Lewis, Fracture of articular cartilage. 118, 545–556 (1996). [DOI] [PubMed] [Google Scholar]
- 33.N. Simha, C. Carlson, J. Lewis, Evaluation of fracture toughness of cartilage by micropenetration. J. Mater. Sci. Mater. Med. 15, 631–639 (2004). [DOI] [PubMed] [Google Scholar]
- 34.N. Broom, Further insights into the structural principles governing the function of articular cartilage. J. Anat. 139, 275–294 (1984). [PMC free article] [PubMed] [Google Scholar]
- 35.B. P. Pereira, P. W. Lucas, T. Swee-Hin, Ranking the fracture toughness of thin mammalian soft tissues using the scissors cutting test. J. Biomech. 30, 91–94 (1997). [DOI] [PubMed] [Google Scholar]
- 36.T. Chanthasopeephan, J. P. Desai, A. C. W. Lau, Determining fracture characteristics in scalpel cutting of soft tissue, in Proceedings of the First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics, Pisa, Italy, 20 to 22 February 2006, p. 971. [Google Scholar]
- 37.C. Gokgol, C. Basdogan, D. Canadinc, Estimation of fracture toughness of liver tissue: Experiments and validation. Med. Eng. Phys. 34, 882–891 (2012). [DOI] [PubMed] [Google Scholar]
- 38.K. Comley, N. A. Fleck, The toughness of adipose tissue: Measurements and physical basis. J. Biomech. 43, 1823–1826 (2010). [DOI] [PubMed] [Google Scholar]
- 39.D. Taylor, N. O’Mara, E. Ryan, M. Takaza, C. Simms, The fracture toughness of soft tissues. J. Mech. Behav. Biomed. Mater. 6, 139–147 (2012). [DOI] [PubMed] [Google Scholar]
- 40.A. Tobaruela, M. Elices, J. Y. Bourges, F. J. Rojo, J. M. Atienza, G. Guinea, Tear and decohesion of bovine pericardial tissue. J. Mech. Behav. Biomed. Mater. 63, 1–9 (2016). [DOI] [PubMed] [Google Scholar]
- 41.E. A. Trowbridge, C. E. Crofts, The tearing strength of glutaraldehyde fixed bovine pericardium. Biomater. Artif. Cells Artif. Organs 17, 315–328 (1989). [DOI] [PubMed] [Google Scholar]
- 42.K. Bircher, M. Zundel, M. Pensalfini, A. E. Ehret, E. Mazza, Tear resistance of soft collagenous tissues. Nat. Commun. 10, 792 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.W. Yang, V. R. Sherman, B. Gludovatz, E. Schaible, P. Stewart, R. O. Ritchie, M. A. Meyers, On the tear resistance of skin. Nat. Commun. 6, 6649 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.G. A. Von Forell, P. S. Hyoung, A. E. Bowden, Failure modes and fracture toughness in partially torn ligaments and tendons. J. Mech. Behav. Biomed. Mater. 35, 77–84 (2014). [DOI] [PubMed] [Google Scholar]
- 45.X. T. Wang, R. F. Ker, R. M. Alexander, Fatigue rupture of wallaby tail tendons. J. Exp. Biol. 198, 847–852 (1995). [DOI] [PubMed] [Google Scholar]
- 46.H. Schechtman, D. Bader, Fatigue damage of human tendons. J. Biomech. 35, 347–353 (2002). [DOI] [PubMed] [Google Scholar]
- 47.D. T. Fung, V. M. Wang, D. M. Laudier, J. H. Shine, J. Basta-Pljakic, K. J. Jepsen, M. B. Schaffler, E. L. Flatow, Subrupture tendon fatigue damage. J. Orthop. Res. 27, 264–273 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.G. M. Thornton, T. D. Schwab, T. R. Oxland, Fatigue is more damaging than creep in ligament revealed by modulus reduction and residual strength. Ann. Biomed. Eng. 35, 1713–1721 (2007). [DOI] [PubMed] [Google Scholar]
- 49.B. Weightman, Tensile fatigue of human articular cartilage. J. Biomech. 9, 193–200 (1976). [DOI] [PubMed] [Google Scholar]
- 50.N. D. Broom, The stress/strain and fatigue behaviour of glutaraldehyde preserved heart-valve tissue. J. Biomech. 10, 707–724 (1977). [DOI] [PubMed] [Google Scholar]
- 51.N. D. Broom, Simultaneous morphological and stress-strain studies of the fibrous components in wet heart valve leaflet tissue. Connect. Tissue Res. 6, 37–50 (1978). [DOI] [PubMed] [Google Scholar]
- 52.M. S. Sacks, D. B. Smith, Effects of accelerated testing on porcine bioprosthetic heart valve fiber architecture. Biomaterials 19, 1027–1036 (1998). [DOI] [PubMed] [Google Scholar]
- 53.W. Sun, M. Sacks, G. Fulchiero, J. Lovekamp, N. Vyavahare, M. Scott, Response of heterograft heart valve biomaterials to moderate cyclic loading. J. Biomed. Mater. Res. A 69, 658–669 (2004). [DOI] [PubMed] [Google Scholar]
- 54.M. S. Sacks, F. J. Schoen, Collagen fiber disruption occurs independent of calcification in clinically explanted bioprosthetic heart valves. J. Biomed. Mater. Res. 62, 359–371 (2002). [DOI] [PubMed] [Google Scholar]
- 55.N. D. Broom, An ‘in vitro’ study of mechanical fatigue in glutaraldehyde-treated porcine aortic valve tissue. Biomaterials 1, 3–8 (1980). [DOI] [PubMed] [Google Scholar]
- 56.T. W. Herod, N. C. Chambers, S. P. Veres, Collagen fibrils in functionally distinct tendons have differing structural responses to tendon rupture and fatigue loading. Acta Biomater. 42, 296–307 (2016). [DOI] [PubMed] [Google Scholar]
- 57.A. H. Lee, S. E. Szczesny, M. H. Santare, D. M. Elliott, Investigating mechanisms of tendon damage by measuring multi-scale recovery following tensile loading. Acta Biomater. 57, 363–372 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.C. Chen, Z. Wang, Z. Suo, Flaw sensitivity of highly stretchable materials. Extreme Mech. Lett. 10, 50–57 (2017). [Google Scholar]
- 59.J. Liu, C. Yang, T. Yin, Z. Wang, S. Qu, Z. Suo, Polyacrylamide hydrogels. II. Elastic dissipater. J. Mech. Phys. Solids 133, 103737 (2019). [Google Scholar]
- 60.Y. Zhou, J. Hu, P. Zhao, W. Zhang, Z. Suo, T. Lu, Flaw-sensitivity of a tough hydrogel under monotonic and cyclic loads. J. Mech. Phys. Solids 153, 104483 (2021). [Google Scholar]
- 61.M. Hua, S. Wu, Y. Ma, Y. Zhao, Z. Chen, I. Frenkel, J. Strzalka, H. Zhou, X. Zhu, X. He, Strong tough hydrogels via the synergy of freeze-casting and salting out. Nature 590, 594–599 (2021). [DOI] [PubMed] [Google Scholar]
- 62.S. Lin, X. Liu, J. Liu, H. Yuk, H.-C. Loh, G. A. Parada, C. Settens, J. Song, A. Masic, G. H. McKinley, X. Zhao, Anti-fatigue-fracture hydrogels. Sci. Adv. 5, eaau8528 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.J. Tang, J. Li, J. J. Vlassak, Z. Suo, Fatigue fracture of hydrogels. Extreme Mech. Lett. 10, 24–31 (2017). [Google Scholar]
- 64.R. Bai, Q. Yang, J. Tang, X. P. Morelle, J. Vlassak, Z. Suo, Fatigue fracture of tough hydrogels. Extreme Mech. Lett. 15, 91–96 (2017). [Google Scholar]
- 65.J.-Y. Sun, X. Zhao, W. R. K. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak, Z. Suo, Highly stretchable and tough hydrogels. Nature 489, 133–136 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.J. P. Gong, Y. Katsuyama, T. Kurokawa, Y. Osada, Double-network hydrogels with extremely high mechanical strength. Adv. Mater. 15, 1155–1158 (2003). [Google Scholar]
- 67.J. M. Hedgepeth, Stress Concentrations in Filamentary Structures (National Aeronautics and Space Administration, 1961). [Google Scholar]
- 68.C.-Y. Hui, Z. Liu, S. L. Phoenix, Size effect on elastic stress concentrations in unidirectional fiber reinforced soft composites. Extreme Mech. Lett. 33, 100573 (2019). [Google Scholar]
- 69.P. P. Purslow, T. J. Wess, D. W. Hukins, Collagen orientation and molecular spacing during creep and stress-relaxation in soft connective tissues. J. Exp. Biol. 201, 135–142 (1998). [DOI] [PubMed] [Google Scholar]
- 70.J. Liao, L. Yang, J. Grashow, M. S. Sacks, Molecular orientation of collagen in intact planar connective tissues under biaxial stretch. Acta Biomater. 1, 45–54 (2005). [DOI] [PubMed] [Google Scholar]
- 71.V. R. Sherman, W. Yang, M. A. Meyers, The materials science of collagen. J. Mech. Behav. Biomed. Mater. 52, 22–50 (2015). [DOI] [PubMed] [Google Scholar]
- 72.S. Lin, J. Liu, X. Liu, X. Zhao, Muscle-like fatigue-resistant hydrogels by mechanical training. Proc. Natl. Acad. Sci. U.S.A. 116, 10244–10249 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.N. A. Fleck, K. J. Kang, M. F. Ashby, Overview no. 112: The cyclic properties of engineering materials. Acta Metall. Mater. 42, 365–381 (1994). [Google Scholar]
- 74.T. Mackay, D. Wheatley, G. Bernacca, A. Fisher, C. Hindle, New polyurethane heart valve prosthesis: Design, manufacture and evaluation. Biomaterials 17, 1857–1863 (1996). [DOI] [PubMed] [Google Scholar]
- 75.Z. Wang, C. Xiang, X. Yao, P. le Floch, J. Mendez, Z. Suo, Stretchable materials of high toughness and low hysteresis. Proc. Natl. Acad. Sci. U.S.A. 116, 5967–5972 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.C. Xiang, Z. Wang, C. Yang, X. Yao, Y. Wang, Z. Suo, Stretchable and fatigue-resistant materials. Mater. Today 34, 7–16 (2020). [Google Scholar]
- 77.H. Yang, C. Li, M. Yang, Y. Pan, Q. Yin, J. Tang, H. J. Qi, Z. Suo, Printing hydrogels and elastomers in arbitrary sequence with strong adhesion. Adv. Funct. Mater. 29, 1901721 (2019). [Google Scholar]
- 78.C. Li, H. Yang, Z. Suo, J. Tang, Fatigue-resistant elastomers. J. Mech. Phys. Solids 134, 103751 (2020). [Google Scholar]
- 79.X. Liu, J. Wu, K. Qiao, G. Liu, Z. Wang, T. Lu, Z. Suo, J. Hu, Topoarchitected polymer networks expand the space of material properties. Nat. Commun. 13, 1622 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.C. Mo, H. Long, J. R. Raney, Tough, aorta-inspired soft composites. Proc. Natl. Acad. Sci. 119, e2123497119 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.G. Scetta, E. Euchler, J. Ju, N. Selles, P. Heuillet, M. Ciccotti, C. Creton, Self-organization at the crack tip of fatigue-resistant thermoplastic polyurethane elastomers. Macromolecules 54, 8726–8737 (2021). [Google Scholar]
- 82.J. Kim, G. Zhang, M. Shi, Z. Suo, Fracture, fatigue, and friction of polymers in which entanglements greatly outnumber cross-links. Science 374, 212–216 (2021). [DOI] [PubMed] [Google Scholar]
- 83.J. M. Lee, S. A. Haberer, D. R. Boughner, The bovine pericardial xenograft: I. Effect of fixation in aldehydes without constraint on the tensile viscoelastic properties of bovine pericardium. J. Biomed. Mater. Res. 23, 457–475 (1989). [DOI] [PubMed] [Google Scholar]
- 84.A. C. Duncan, D. Boughner, Effect of dynamic glutaraldehyde fixation on the viscoelastic properties of bovine pericardial tissue. Biomaterials 19, 777–783 (1998). [DOI] [PubMed] [Google Scholar]
- 85.M. S. Sacks, C. J. Chuong, Orthotropic mechanical properties of chemically treated bovine pericardium. Ann. Biomed. Eng. 26, 892–902 (1998). [DOI] [PubMed] [Google Scholar]
- 86.A. Thomas, Rupture of rubber. VI. Further experiments on the tear criterion. J. Appl. Polym. Sci. 3, 168–174 (1960). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1
Figs. S1 to S15