Abstract
This article summarizes technical advances contained in the fifth major release of the Q-Chem quantum chemistry program package, covering developments since 2015. A comprehensive library of exchange–correlation functionals, along with a suite of correlated many-body methods, continues to be a hallmark of the Q-Chem software. The many-body methods include novel variants of both coupled-cluster and configuration-interaction approaches along with methods based on the algebraic diagrammatic construction and variational reduced density-matrix methods. Methods highlighted in Q-Chem 5 include a suite of tools for modeling core-level spectroscopy, methods for describing metastable resonances, methods for computing vibronic spectra, the nuclear–electronic orbital method, and several different energy decomposition analysis techniques. High-performance capabilities including multithreaded parallelism and support for calculations on graphics processing units are described. Q-Chem boasts a community of well over 100 active academic developers, and the continuing evolution of the software is supported by an “open teamware” model and an increasingly modular design.
I. INTRODUCTION
The era of electronic computing began with the “ENIAC” machine,1 developed at the University of Pennsylvania beginning in 1943, and the first commercial machines began to be produced around 1950. Although originally developed for military applications, molecular physics was not far behind.2 The existence of these machines in universities led to the first development of quantum chemistry software starting in the mid-1950s.3 Prognosticating on the future of electronic structure theory in his 1966 Nobel Lecture, Mulliken stated that4
… the era of computing chemists, when hundreds if not thousands of chemists will go to the computing machine instead of the laboratory for increasingly many facets of chemical information, is already at hand.
However, he did caution that
… at the present time the rapid progress which could be made even with existing machine programs is not being made, simply because available funds to pay for machine time are far too limited.
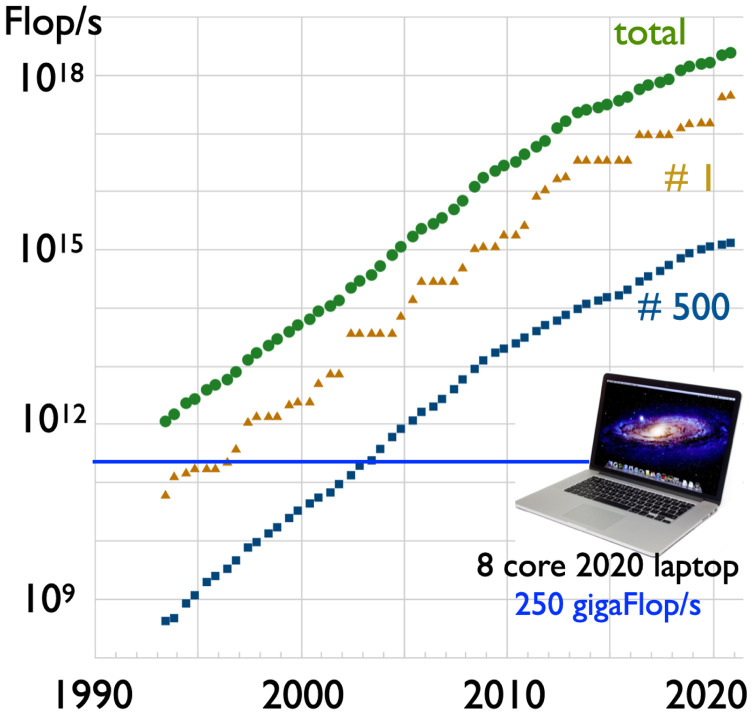
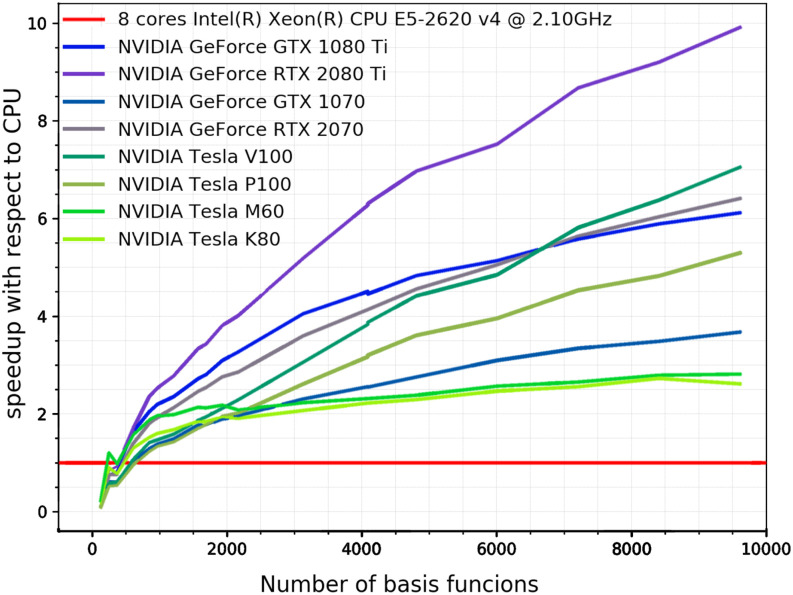
In the ensuing half-century, the problem of inadequate funds was resolved by the revolution in inexpensive computer hardware that traces its origin to the invention of the integrated circuit in the late 1950s and the microprocessor in the mid-1970s. Perhaps ironically, a desire for realistic simulation in computer games has led to such a massive market for high-performance hardware that today’s laptop computers have the power of the world’s most powerful supercomputer from the mid-1990s, as shown in Fig. 1. It is also worth noting that the roughly 100 W power consumption of today’s eight-core laptop is an impressive 5000× smaller than the corresponding supercomputer (e.g., the Fujitsu Numerical Wind Tunnel Computer, which was No. 1 in 1996, consumes 500 kW). At the other extreme, computing resources well into the terascale are routinely available on computer clusters, and leadership supercomputing is in the midst of a transition from petascale toward exascale computing.
FIG. 1.
Development of leading edge computer capabilities, as documented through the performance of the world’s top 500 supercomputers, as measured on dense linear algebra in units of double precision floating-point operations per second (Flops/s). The data are adapted from Top500.org and compared against the performance of an eight-core laptop, which evidently has performance comparable to the world’s fastest supercomputer of the mid-1990s to late-1990s.
This revolution in computer hardware is only meaningful to practicing chemists if corresponding software is available to enable straightforward and realistic simulation of molecules, molecular properties, and chemical reaction pathways. The first electronic structure codes were already working at the time of Mulliken’s Nobel address, and indeed, Charles Coulson had warned in 1959 of a growing split between theoretical chemists who were numerical simulators (primarily early code developers) and those who developed chemical concepts.5 Today one would rather say that quantum chemistry calculations are simulations whose results represent numerical experiments. Just like real experiments, results from these in silico experiments (even if reliable) must still be understood in conceptual terms, to the extent possible. The aspirations of early electronic structure codes are reflected in program names such as Polyatom,6 and such efforts rarely achieved useful accuracy or else did so via fortuitous cancellation of errors.7 However, today there are many useful program packages including ≈20 that are actively developed and supported.8
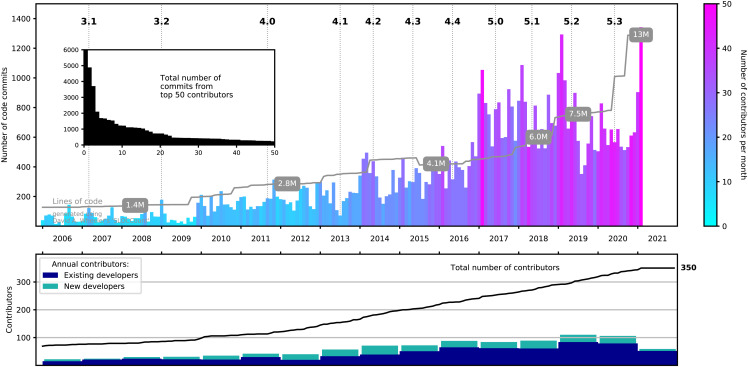
One of those is the Q-Chem project, which began in the late 1992.9 Since its inception, Q-Chem has operated as a large collaboration that defines its genre as open teamware scientific software.9,10 The Q-Chem source code is open to a large group of developers that currently includes more than 100 individuals in at least 9 countries. Developers can submit their contributions for inclusion in the official releases as long as the changes do not violate the integrity of the overall package and are scientifically sound. In addition, several Q-Chem modules are distributed as open source software.11–17 Figure 2 illustrates some statistics regarding developer activity derived from the Q-Chem source code repository logs. These data provide clear evidence of the sustained growth of the developer community and the code itself over the past decade.
FIG. 2.
Statistics showing Q-Chem developer activity since 2006. Top: total number of code commits, organized chronologically by month. The color of each monthly entry indicates the number of individual developers who made commits. (Light blue is single-digit numbers, and the January 2021 peak represents about 50 developers committing code that month.) Bottom: growth of the developer base broken down into existing developers vs those who committed code for the first time. The inset depicts the total number of commits by the 50 most prolific developers.
The Q-Chem collaboration has delivered useful and reliable quantum chemistry software over the course of five major releases (as documented in earlier review articles)18–20 and ≈15 minor releases. The present paper addresses progress made since 2015 by the relatively large team of academic developers and the relatively small team of professional programmers who contribute to the package. The authors of this paper710 represent contributors to Q-Chem v. 4 and v. 5, while contributors to earlier versions are recognized in overview articles describing v. 2,18 v. 3,19 and v. 4.20
The remainder of this paper is organized as follows: Sec. II provides an overview of density functional theory (DFT) capabilities in Q-Chem, including a survey of the 200+ exchange–correlation (XC) functionals that are presently available (Sec. II A).21 A variety of excited-state DFT capabilities are described in Sec. II C, including time-dependent (TD-)DFT in both its linear-response and its explicitly time-dependent (“real-time”) versions. Next, Sec. III describes single-reference correlated wave function methods and other many-body capabilities, while Sec. IV describes multireference methods. Section V highlights some specialty features, including methods for computing core-level (x-ray) excitation spectra, methods for describing metastable resonance states, methods for computing vibronic lineshapes, and finally the nuclear–electronic orbital (NEO) method for describing proton quantum effects. Section VI surveys methods for describing a molecule’s extended environment [e.g., quantum mechanics/molecular mechanics (QM/MM), dielectric continuum, and embedding methods]. Energy decomposition analysis methods are described in Sec. VII. Section VIII describes the Q-Chem software development environment, and Sec. IX provides an overview of high-performance capabilities, including multithreaded parallelism and algorithms that exploit graphics processing units (GPUs). Section X describes graphical user interfaces (GUIs). Finally, Sec. XI provides a wrap-up and a glimpse toward the future.
II. DENSITY FUNCTIONAL THEORY
Standard quantum mechanics, including wave function-based quantum chemistry, employs an approximate N-electron wave function |Ψ⟩ to evaluate the energy, . By contrast, DFT is based on the Hohenberg–Kohn theorems,22–25 which assert that the ground state energy E can be expressed as a functional of the electron density, E = E[ρ(r)]. While the exact functional is unknown and is almost certainly unknowable in explicit form, tremendous progress has been made toward achieving useful approximations. After some minimal background, this section summarizes recent aspects of that progress that are available in Q-Chem.
A. Exchange–correlation functionals
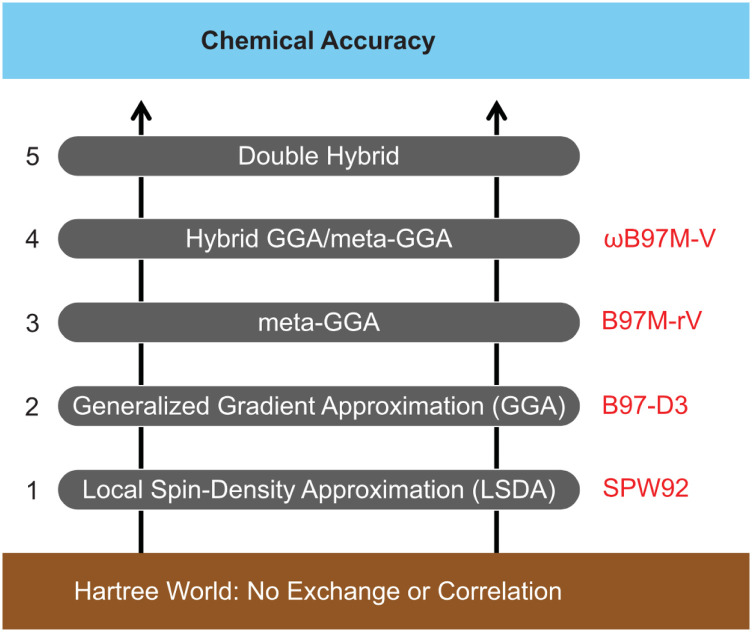
Nearly all modern density functionals are of the Kohn–Sham type,23–26 in which the density is constructed from an auxiliary Slater determinant |Φs⟩ composed of Kohn–Sham molecular orbitals (MOs), {ϕk}. The determinant |Φs⟩ describes a system of noninteracting electrons (or partially interacting electrons,27 for rungs 4 and 5 on the hierarchy in Fig. 3), which has the same density as the physical system of interest. This ensures so-called N-representability24,25 and is also used to exactly evaluate the noninteracting kinetic energy, . The Kohn–Sham DFT energy is expressed as
| (1) |
where the electron–nuclear attraction term (or “external potential,” Vext) and the classical Coulomb mean-field energy (EJ) are known functionals of ρ(r). This leaves only the non-classical exchange–correlation (XC) energy (EXC) as unknown, and density functional approximations (DFAs) represent models for EXC.
FIG. 3.
Illustration of the ladder-based classification of density functionals. Also shown at each rung are the top-performing functionals (out of 200 DFAs from rungs 1–4), as assessed using the MGCD84 database containing nearly 5000 data points.21 Adapted with permission from N. Mardirossian and M. Head-Gordon, Mol. Phys. 115, 2315 (2017). Copyright 2017 Taylor and Francis.
Given a DFA, the energy is obtained by minimizing the energy of Eq. (1) with respect to the density . This minimization is equivalent to solving the Kohn–Sham eigenvalue equation
| (2) |
This is a one-electron analog of the time-independent Schrödinger equation. By analogy to the single-determinant Hartree–Fock approach in wave function theory (WFT),28 the effective one-electron Hamiltonian is known as the Fock operator, and it depends on its own eigenfunctions (as in Hartree–Fock theory). The power of Kohn–Sham DFT is that that the solution of the self-consistent field (SCF) problem in Eq. (2) would be equivalent to solving the full N-electron Schrödinger equation, if the exact functional EXC were available.
While that is sadly not the case, the lack of an exact XC functional happily keeps electronic structure theorists gainfully employed, and there are many useful DFAs that far exceed the accuracy of the cost-equivalent Hartree–Fock method. The manner in which different DFAs depend on various descriptors of the density ρ(r) leads to five broadly recognized categories of density functionals that are commonly visualized as rungs of the metaphorical “Jacob’s ladder.”29,30 The rungs are illustrated in Fig. 3. From lowest to highest, the rungs correspond to the following:
-
1.
Local Spin Density Approximation (LSDA). The LSDA functional EXC[ρ(r)] depends strictly on the density and solves the model problem of a uniform electron gas. Common fits to the uniform electron gas data are known as VWN31 and PW92,32 which are quite similar.33 Most higher rungs of Jacob’s ladder introduce corrections based on LSDA as a starting point.
-
2.
Generalized Gradient Approximations (GGAs). GGAs add a dependence on to EXC, making the ansatz potentially exact for slowly varying electron densities, not just uniform ones. Many useful GGAs have been developed, including PBE,34 BLYP,35,36 and B97-D.37 Q-Chem 5 also includes the nonseparable gradient approximation, GAM.38 It is nowadays standard to add empirical dispersion corrections (of the D, D3, or D4 form, for example) to these functionals,39 in order to improve their performance for non-bonded interactions.
-
3.
Meta-GGAs. These functionals incorporate an additional dependence on the kinetic energy density, τ(r). Functionals on this rung are still under active development and noteworthy recent meta-GGAs include SCAN,40 B97M-V,41 and revM06-L.42 The “-V” suffix in B97M-V indicates that the functional also includes a nonlocal correlation functional (VV10),43 which can (at least in principle) account for dispersion interactions for the right physical reasons,44 whereas “semilocal” functionals that depend only on ρ(r), , and/or τ(r) lack the nonlocality to describe correlated density fluctuations between nonoverlapping densities.
-
4.
Hybrid functionals. Hybrid DFAs include some portion of the “exact” (or Hartree–Fock) exchange energy associated with the Kohn–Sham determinant. The traditional approach has used a fixed fraction of exact exchange, and such functionals are known as “global” hybrid functionals. Popular examples include B3LYP,35,36 PBE0,45 and M06-2X,46 while some more recent and noteworthy examples of global hybrids include SCAN0,47 MN15,48 and revM06.49 A popular alternative to global hybrids uses a variable fraction of exact exchange that typically increases with the inter-electron distance, r12. These are known as range-separated hybrid (RSH) functionals, and notable older examples include ωB97X50 and ωB97X-D,51 while newer examples include ωB97X-V52 and ωB97M-V.53 More specialized RSH functionals are also widely used for time-dependent DFT calculations of excited states; see Sec. II C.
-
5.
Double-Hybrid (DH) functionals. Hybrid DFAs depend only on the occupied Kohn–Sham orbitals, but DH-DFAs add an additional dependence on the virtual (unoccupied) Kohn–Sham MOs, which facilitates description of nonlocal electron correlation, as in second-order Møller–Plesset perturbation theory (MP2). DH-DFAs have undergone rapid recent development,54,55 and established models such as B2PLYP-D3,56 XYG3,57 and ωB97X-258 have been joined by promising new DH-DFAs, including ωB97M(2),59 and a slew of functionals that involve empirical scaling of the MP2 spin components.60–62 Relative to the lower rungs of the ladder, the prospect of higher accuracy from DH-DFAs also comes with the cost of significantly higher computational demands, and significantly slower convergence of the results toward the complete basis set limit.
With respect to DFT, the most important feature of Q-Chem is that an exceptionally rich set of density functionals is supported: well over 200 functionals are available for a user to choose between.21 A closely related feature is that Q-Chem contains a very complete set of methods for accurate treatment of dispersion interactions. These include Grimme’s D,37 D3,63,64 and D4 corrections,65 as well as a variety of nonlocal correlation and van der Waals functionals,43,66–68 the exchange dipole model (XDM),69,70 the Tkatchenko–Scheffler (TS) model,71 and the many-body dispersion (MBD) model.72–74 In addition, for calculations on large molecules using the small def2-SVPD basis set,75,76 a built-in geometric counterpoise correction method (the so-called DFT-C approach77) is available. Q-Chem also has analytic nuclear gradients and Hessians for most of this long list of functionals through rung 4. Some modern DFAs are more challenging to integrate than older ones, and a set of modern quadrature grids is available,78 with sensible defaults.
This broad selection of available functionals is a perhaps unfortunate necessity due to the fact that the “best” functional often depends on the problem at hand. According to Pople’s concept of a theoretical model chemistry,79,80 one should validate candidate approximations using known results that are related (as closely as possible) to the desired area of chemical application and then proceed to make predictions for related but unknown systems. The best functional(s) for modeling hydrogen storage in a host material,81 for example, may differ significantly from the best functional(s) to describe elementary steps in a CO2 reduction catalyst,82 or the best functional may even differ from one catalyst to another,83 as dictated by the need to get reduction potentials in reasonable agreement with experiment. (Excited-state calculations bring in a host of other considerations,84–89 as discussed in Sec. II C.) Problem-specific validation of the choice of DFA for a given application is therefore a good idea, particularly if there are good available data to benchmark several candidate DFAs.
To bring some order to this situation, it is important to recognize that there are general classes of energy differences that are common to most applications in chemistry. Such classes include non-covalent interactions, thermochemical energy differences, isomerization energies, and reaction barrier heights. The large main-group chemistry database (MGCDB84) developed by Mardirossian and Head-Gordon is categorized along these lines and contains 84 distinct subsets and almost 5000 data points.21 The top-ranked functional at each rung of Jacob’s ladder, according to this dataset, is shown in Fig. 3.
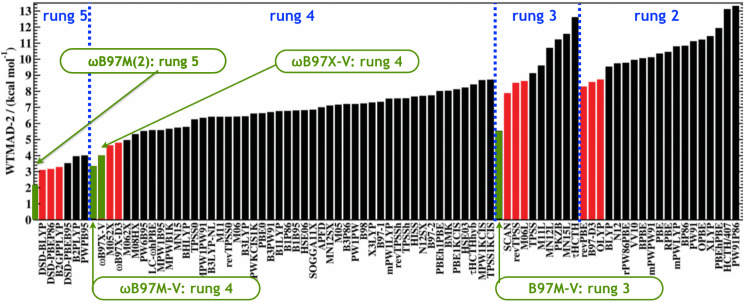
The GMTKN55 dataset is another large diverse set of benchmarks for main-group chemistry,90 and Fig. 4 summarizes the performance of a large range of functionals for this dataset. Consistent with the Jacob’s ladder taxonomy, the performance of the best functional improves at each rung of the ladder, showing that the inclusion of additional physical content does indeed improve accuracy. While it is often (correctly) stated that DFT results on a given molecule are not systematically improvable by switching from one functional to another, these results illustrate that in a statistical sense, DFT does systematically improve when represented by the best functional at each rung of the ladder. The same need not be true if one considers worse-performing functionals at each level, as the additional flexibility associated with higher rungs on Jacob’s ladder makes it quite possible to overfit complicated functional forms using limited data, especially where meta-GGA functionals are concerned.
FIG. 4.
Weighted errors (in kcal/mol) for a range of functionals, assessed using the GMTKN55 dataset and arranged according to the rungs of Jacob’s ladder in Fig. 3. The figure is adapted from Ref. 90 but includes additional data from Refs. 91 and 62. Adapted with permission from Goerigk et al., Phys. Chem. Chem. Phys. 19, 32184 (2017). Copyright 2017 Published by the PCCP Owner Societies.
Diving a bit deeper into the data shown in Fig. 4 reveals a variety of other interesting observations.
-
•
LSDA (rung 1) is essentially useless for chemical applications. A good GGA such as B97-D3 is the simplest and lowest-cost DFT method that is useful for chemistry.
-
•
A good meta-GGA, as exemplified by B97M-V, offers striking improvements over the best GGA across all categories. It is clear that meta-GGAs can deliver significantly higher accuracy than GGAs.
-
•
Significant further improvement is delivered by the best hybrid functionals, exemplified by ωB97X-V as a RSH-GGA and ωB97M-V as a corresponding RSH-meta-GGA. This improvement arises primarily from better accuracy for barrier heights, thermochemistry, and isomerization energies. There is good reason for hybrids to be a default choice for chemical modeling.
-
•
The best DH-DFAs offer further improvements in the same categories where hybrids improve over meta-GGAs: barrier heights, thermochemistry, and isomerization energies. However, the significantly higher cost of DH-DFAs means that they are often used only for single-point energy calculations at stationary points optimized at lower levels of theory. Q-Chem includes the efficient occ-RI-K algorithm92 to significantly reduce the additional compute cost of DH-DFAs. Some parallel timings are given in Sec. IX.
-
•
The gap in accuracy between DFT and the best wave function theories remains quite substantial. For both bonded and non-bonded interactions, errors associated with coupled-cluster (CC) methods that include triple excitations [CCSD(T) or better] are on the order of 5× smaller than those for the best rung-5 density functionals.59 Therefore, despite the much higher computational costs, there remains strong incentive to perform CC calculations when possible. Some of Q-Chem’s CC capabilities are described in Sec. III.
Further details regarding the combinatorial design strategy used to obtain the best functionals at rungs 3, 4, and 5 can be found in the work of Mardirossian and Head-Gordon.41,52,53,59 It should be noted that statistical assessments of DFAs are only as transferable as the data they are built upon. The transferability of the conclusions discussed above to similar systems is supported by the fact that broadly similar conclusions can be drawn from other large-scale data assessments, e.g., comparing MGCDB84 vs GMTKN55 for main-group compounds. It is a separate issue to investigate the performance of density functionals for very different classes of molecules, such as transition metal compounds. (These have been the target of several other recent benchmark studies.93,94) Similarly, interest in the quality of densities derived from DFT must be separately assessed, either directly95 or via properties such as electrical moments.96–99 Similar considerations apply to other molecular properties, such as polarizabilities100 and nuclear magnetic resonance (NMR) chemical shifts.101
B. Thermally assisted-occupation DFT
Systems with strong static correlation remain very challenging for conventional Kohn–Sham DFT. Q-Chem 5 contains thermally assisted-occupation (TAO-)DFT,102–104 an efficient means to explore ground-state properties of large electronic systems with strong static correlation. Unlike Fermi smearing105 (also supported by Q-Chem), which is a convergence aid for small-gap systems, TAO-DFT aims to access densities beyond those obtainable from a single Kohn–Sham determinant. TAO-DFT is similar to Kohn–Sham DFT in computational complexity but represents the ground-state electron density in terms of orbitals with fractional occupation numbers governed by a Fermi–Dirac distribution at a fictitious temperature that is related to the strength of static correlation. In TAO-DFT, static correlation can be approximately described by the entropy contribution,102 even when semilocal102,103 or hybrid104 density functionals are employed. A self-consistent scheme defining the fictitious temperature has been recently developed for diverse applications.106 By combining computational efficiency with reasonable accuracy, TAO-DFT is well positioned to investigate the ground-state properties of electronic systems at the nanoscale, especially those possessing strong static correlation effects.107–111 TAO-DFT has recently been combined with ab initio molecular dynamics.112
C. Excited-state DFT methods
The TDDFT approach113,114 extends ground-state DFT to electronically excited states via the linear response (LR) formalism,115,116 incorporating electron correlation at a computational cost equivalent to its uncorrelated Hartree–Fock analog, the configuration-interaction singles (CIS) method.114 This relatively low cost makes LR-TDDFT (Sec. II C 1) the most widely used method for computing vertical excitation spectra and for exploring excited-state potential energy surfaces (computational photochemistry, Sec. II C 2). An alternative to the LR formalism is “real-time” TDDFT,117,118 also known as time-dependent Kohn–Sham (TDKS) theory,119–121 which is discussed in Sec. II C 3 and which can be used to compute broadband excitation spectra. Finally, an altogether different category of DFT-based excited-state methods is the ΔSCF formalism, which is a state-specific approach that fully accounts for orbital relaxation in the excited state and can be used to describe challenging problems such as excited-state charge separation and states with double-excitation character, thereby sidestepping known systemic problems with LR-TDDFT while retaining SCF cost. The ΔSCF approach is discussed in Sec. II C 4.
1. LR-TDDFT
Despite its popularity, LR-TDDFT does have systemic problems for certain classes of excited states, the most infamous of which is its dramatic underestimation of excitation energies having charge-transfer (CT) character.85–87,122–127 Nevertheless, this method often achieves an impressive statistical accuracy of 0.2–0.3 eV for low-lying valence excitation energies,128 giving it a wide domain of applicability despite recognized shortcomings.
The CT problem, in particular, can be largely ameliorated through the use of long-range corrected (LRC) functionals,84–89 which are RSH functionals in which the fraction of Hartree–Fock exchange is required to go to unity as r12 → ∞. The most popular such functional is LRC-ωPBE,87,129 along with its short-range hybrid cousin, LRC-ωPBEh,126 although other variants are available, including LRC-μBLYP and LRC-μBOP.86,88,130 In addition to these LRC-GGAs, Q-Chem 5 also includes the relatively new revM11 functional,131 a LRC-meta-GGA functional specifically optimized for long-range CT excitations.
For best results, the range-separation parameter (ω or μ) is often “tuned” in order to set the frontier energies based on the molecule’s own (ΔSCF) ionization energy (IE),89,132–134
| (3) |
In Q-Chem 5, an alternative “global density-dependent” (GDD) tuning procedure is available.135–137 Following a standard SCF calculation with a functional such as LRC-ωPBE, the GDD procedure automatically determines a new tuned value (ωGDD) based on the size of the exchange hole. This approach appears to avoid system-size-dependent problems with the value of ω tuned according to Eq. (3).137
2. Exploring excited-state potential surfaces
Q-Chem 5 contains new tools that enable the exploration of excited-state potential energy surfaces with LR-TDDFT, including algorithms for locating minimum-energy crossing points (MECPs) along conical seams. For a molecule with nvib = 3natoms − 6 vibrational degrees of freedom, the conical seam (or “conical intersection”) is a (nvib − 2)-dimensional subspace within which two electronic states are exactly degenerate. Conical intersections serve as photochemical funnels for nonadiabatic dynamics,138,139 so locating the MECP (i.e., the lowest-energy point within the degenerate subspace) can help to rationalize excited-state dynamics by providing a single chemical structure to represent the whole seam space.140
Orthogonal to the conical seam is the two-dimensional branching space, within which any infinitesimal displacement lifts the degeneracy between electronic states |ΨJ⟩ and |ΨK⟩.138,141 The branching space is spanned by two (nonorthogonal) vectors,
| (4) |
and
| (5) |
where R indicates the nuclear coordinates. Operationally, the gradient difference (“g-vector”) is easily computed using any excited-state method for which analytic gradients are available, but the nonadiabatic coupling (“h-vector”) is less routinely available. Analytic h-vectors are available in Q-Chem 5 for both CIS and LR-TDDFT,141–145 which greatly facilitates efficient optimization of MECPs by means of a projected-gradient algorithm that optimizes directly in the seam space.146 Alternatively, for excited-state methods where analytic gradients (and therefore gJK) are available but analytic derivative couplings (hJK) are not, Q-Chem provides a branching-plane updating algorithm to optimize MECPs.140,147 This is significantly more efficient140 than alternative penalty-function methods,148 which can also be used in the absence of hJK. The projected-gradient algorithm is the most efficient approach of all, however, converging in fewer steps while the computation of hJK adds a modest 10%–20% overhead to the cost of computing the gradients for states J and K.142,149,150 For molecules with intersystem crossing, analytic gradients and derivative couplings at the CIS and LR-TDDFT levels are available within both the spin-diabatic and spin-adiabatic representations.151,152
Nonadiabatic trajectory simulations at the LR-TDDFT level are available in Q-Chem and take advantage of these analytic derivative couplings. These simulations can be performed using the Tully’s “fewest switches” surface hopping (FSSH) algorithm153,154 or using an “augmented” FSSH algorithm that includes decoherence effects on the electronic amplitudes.155,156 These corrections are necessary in order to maintain detailed balance and to describe both short- and long-time relaxation dynamics, including Marcus theory.157–159 A Python framework for performing FSSH simulations using Q-Chem is also available.160
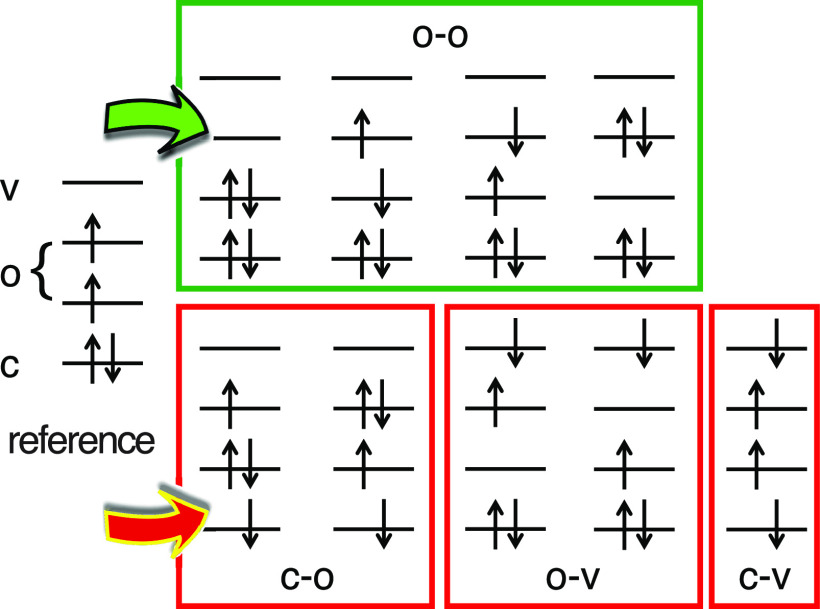
A systematic shortcoming of LR-TDDFT that is relevant here is an incorrect description of the topology around any conical intersection that involves the ground state; in such cases, the branching space predicted by LR-TDDFT is one-dimensional rather than two-dimensional.141,161 This problem has its roots in the fact that any excited-state method based on response theory treats the “reference state” (usually the ground state) in a fundamentally different manner as compared to the “response” (excited) states. This can cause difficulties when the reference state becomes quasi-degenerate with the lowest excited state, and in the context of nonadiabatic trajectory simulations, this imbalance can manifest as SCF convergence failure in the vicinity of a conical intersection.162 The “spin–flip” approach to LR-TDDFT163–165 resolves this problem141,142 by using a reference state with a different spin multiplicity as compared to the target states of interest. An example is shown in Fig. 5, which depicts the excitation space for a case where a high-spin triplet reference state is used to generate determinants for singlet states, including the closed-shell S0 ground state. The spin–flip single-excitation manifold contains a subset of the possible determinants that are doubly excited with respect to S0, including the one (in the “o–o” subspace in Fig. 5) that is necessary to provide proper topology at the S0/S1 conical intersection.142,161 In Q-Chem 5, nonadiabatic coupling vectors hJK are available for both conventional and spin–flip variants of LR-TDDFT.142
FIG. 5.
Illustration of the spin–flip TDDFT excitation space for a (4e, 4o) model, starting from a high-spin triplet reference. Proper spin eigenfunctions can be formed from the four determinants in the o–o subspace, but the remaining determinants are missing one or more complementary spin functions. Adapted from X. Zhang and J. M. Herbert, J. Chem. Phys. 143, 234107 (2015) with the permission of AIP Publishing.
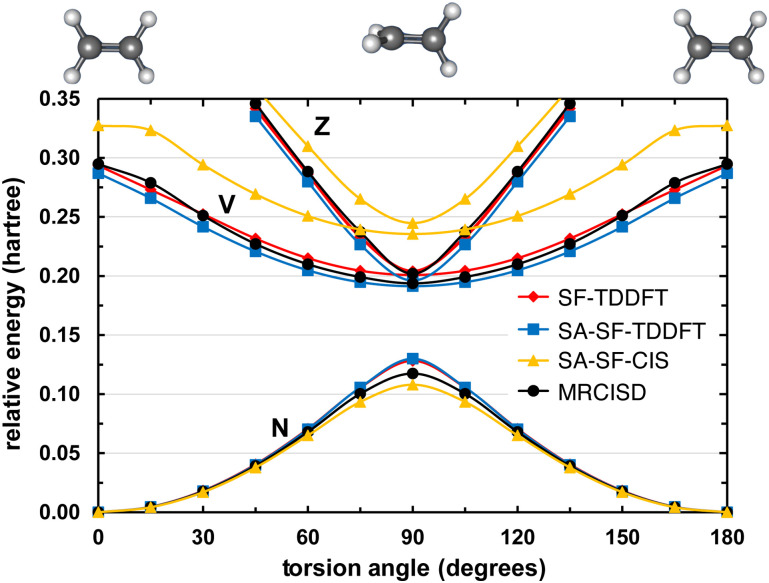
While the spin–flip approach rigorously cures the topology problem at conical intersections,141,142 it unfortunately exacerbates problems with spin contamination. This is especially true as one moves away from the Franck–Condon region and starts to break bonds, for which singlet and triplet states often become comparable in energy, and may necessitate the use of state-tracking algorithms to ensure that a geometry optimization or dynamics trajectory remains on a potential surface of consistent spin multiplicity.166–169 At the heart of this problem is the fact that each of the determinants in the c-o, o-v, and c-v subspaces in Fig. 5 is missing one or more of the complementary determinants170–172 needed to form an eigenstate. The missing determinants are absent because they cannot be generated from the reference state via a single excitation combined with a single α → β spin flip. However, these determinants can be generated, in an automated manner that does not increase the formal computational scaling of LR-TDDFT, by means of a tensor equation-of-motion (EOM) formalism.169,173–175 This formalism has been used to develop a “spin-adapted spin–flip” (SA-SF) TDDFT method,169 which preserves proper topology at conical intersections but also restores spin multiplicity as a good quantum number. Figure 6 shows that SA-SF--TDDFT results are close to multireference benchmarks for the challenging problem of twisting ethylene by 90° about its C–C axis. Analytic gradients for SA-SF-TDDFT are not yet available, but this method can be used to check the veracity of any heavily spin-contaminated results that are obtained with other flavors of LR-TDDFT.
FIG. 6.
Potential energy curves for the singlet N [], V [], and Z [] states of C2H4, twisting along the C–C axis, computed using various spin–flip methods in comparison to multireference benchmarks. Both SA-SF-TDDFT and SA-SF-CIS correctly describe the topology around a conical interaction, but the latter lacks dynamical correlation and therefore excitation energies are not accurate. Adapted from X. Zhang and J. M. Herbert, J. Chem. Phys. 143, 234107 (2015) with the permission of AIP Publishing.
SF-TDDFT methods are also suitable for treating other types of electronic structure that are not accessible by the standard Kohn–Sham DFT, such as polyradicals and single-molecule magnets.163,164,176,177
3. “Real-time” TDDFT
The term “TDDFT” is used almost universally to refer specifically to LR-TDDFT, which despite its name is a strictly frequency-domain theory with no explicit time dependence, at least not within the ubiquitous adiabatic approximation that is used in all practical implementations.114,115 However, just as the ground-state Kohn–Sham problem is based on a one-electron analog of the time-independent Schrödinger equation [Eq. (2)], at the foundation of TDDFT is a one-electron analog of the time-dependent Schrödinger equation, which governs the time evolution of |Φs⟩ and thus the Kohn–Sham MOs. The latter evolve in time according to
| (6) |
Using this TDKS equation, the MOs can be propagated in time following a perturbation of the ground state density at t = 0 that generates a (non-stationary) superposition of excited states. Information about electronic excitation energies is encoded into the time evolution of this superposition state, and an entire broadband excitation spectrum can be obtained via Fourier transform of the time-dependent dipole moment function, with a spectral resolution that improves upon further time propagation.117,178 This approach has been given the unwieldy moniker of “real-time” TDDFT,117,118 although calling it TDKS theory avoids confusion with the more widespread LR-TDDFT approach.119–121
In the limit of a weak perturbation at t = 0, propagated to t → ∞ to obtain narrow spectral lines, TDKS spectra are equivalent to those obtained using LR-TDDFT,178 but the TDKS approach need not be limited to the weak-field LR regime and can be used to explore strong-field dynamics,179 strong-field ionization,180–183 and high-harmonic spectra,120,184–187 for example. [Ionization requires the use of complex absorbing potentials (CAPs), which are discussed in Sec. V B. These are available for use in TDKS simulations,120,121 along the lines of the atom-centered potentials described in Refs. 180–183.] In this way, TDKS simulations can describe time-dependent electron dynamics beyond the Born–Oppenheimer approximation, where the electrons are out of equilibrium with the nuclei. At present, Q-Chem’s implementation of the TDKS method120,121 is limited to clamped-nuclei simulations, meaning electron dynamics only.
Time propagation according to Eq. (6) is complicated by the fact that depends on the MOs and thus the effective Hamiltonian is time-dependent. The most widely used propagation algorithm is the modified-midpoint method,188 for which the cost of one time step is the same as the cost of one SCF cycle of a ground-state calculation. (It should be noted that for electron dynamics, the fundamental timescale is attoseconds, and therefore, time steps Δt ∼ 0.04 a.u. = 10−18 s are typical.119) Q-Chem’s implementation of the TDKS approach also contains several predictor/corrector algorithms as alternatives to the modified-midpoint approach.119 These are stable over longer time steps Δt and furthermore facilitate on-the-fly detection of instabilities that can lead to spurious peak-shifting but are not always evident simply by monitoring energy conservation, which is a necessary but not a sufficient condition for accurate integration of Eq. (6).119
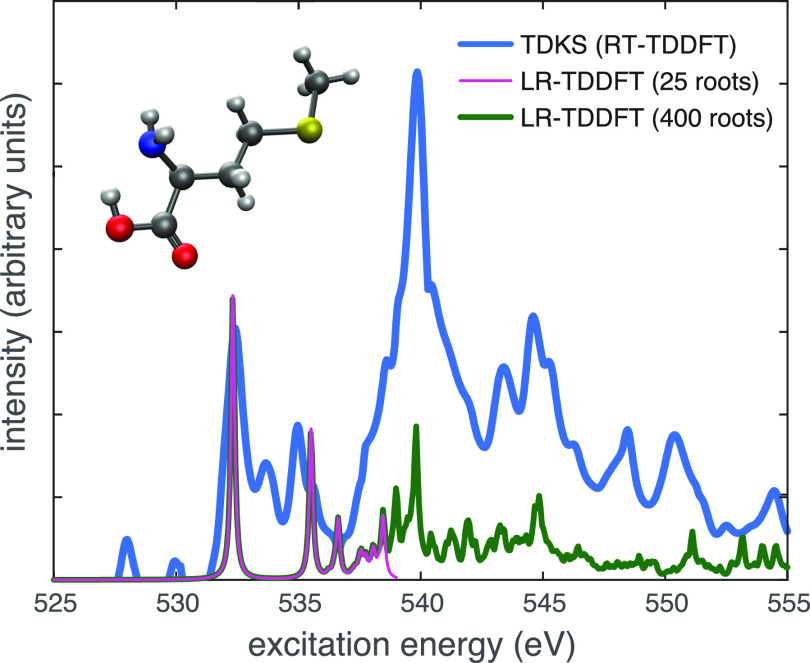
Figure 7 illustrates a TDKS calculation of a broadband excitation spectrum, corresponding to x-ray absorption (XAS) at the oxygen K-edge above 530 eV.120,121 This spectrum was obtained from 7.3 fs of time propagation with Δt = 0.02 a.u. (meaning 15 140 time steps) using Padé approximants to accelerate convergence of the Fourier transform.120,121,190 Also shown are two LR-TDDFT excitation spectra computed using the same functional and basis set, which reproduce the same basic features; however, hundreds of excited states are required in order to get beyond the near-edge peak, corresponding to the O(1s) → LUMO transition. In the TDKS approach, the carbon or nitrogen K-edge spectra (at lower excitation energies) are obtained from the same calculation, although the sulfur K-edge appears at significantly higher energy (above 2400 eV) and requires a smaller time step. In contrast, LR-TDDFT excitation spectra must be computed in terms of individual eigenstates; frozen occupied orbitals are required in order to make core-level excitations emerge as the lowest-energy states, and even so, hundreds of eigenstates are required to converge the features of the spectrum. For the LR-TDDFT calculations in Fig. 7, only the two O(1s) orbitals of the methionine molecule were active from the occupied space. Despite this restriction, several hundred states are required in order to access excitation energies above the first near-edge features, and this quickly becomes prohibitive for large molecules, especially in terms of memory. These requirements for the LR-TDDFT calculation can be reduced by judicious use of frozen orbitals,191,192 and much larger examples (e.g., C70) have been reported using Q-Chem’s LR-TDDFT code.191 However, the memory requirement for TDKS (without approximation) is a mere 2× the memory for a ground-state SCF calculation, which is quite minimal. That said, whereas LR-TDDFT naturally provides CIS-like excitation amplitudes that characterize each excited state, from TDKS calculations it is more difficult to extract information regarding the specific MOs that contribute to various spectral features, although some ideas to this end have been put forward.190,193
FIG. 7.
Absorption spectra of methionine at the oxygen K-edge computed at the level of SRC1-R1189/def2-TZVPD.75,76 A broadband TDKS calculation is shown along with two LR-TDDFT spectra using different numbers of roots. The former is obtained from 7.3 fs of time propagation with Δt = 0.02 a.u. The LR-TDDFT calculations use an active space consisting of all virtual MOs but only the O(1s) orbitals from the occupied space. Features below 531 eV in the TDKS spectrum correspond to N(1s) → continuum transitions that are excluded by this active-space approximation. Data are taken from Ref. 121.
Some of these same considerations apply when many-body methods are used to compute x-ray spectra, as described in Sec. V A. The LR-TDDFT approach to core-level spectroscopy is discussed alongside these approaches in that section.
4. SCF and ROKS methods
LR-TDDFT tends to fail systematically for excited states that involve a significant change in the density, including the aforementioned CT excitations, but also states with double-excitation character,194 which are often either missing entirely from the LR-TDDFT excitation spectrum or else are badly in error. Both types of states are characterized by significant orbital relaxation. Indeed, it has recently been argued that much of what passes for double-excitation character (e.g., in the well-known case of the 21Ag state of butadiene) is simply orbital relaxation and that double excitations are required within a single-reference CI formalism simply because the optimal excited-state MOs are very different from those optimized for the ground state.195 In such cases, it may make sense to optimize the MOs for the excited state directly. This is the basis for the “ΔSCF” approach to excitation energies, in which one uses an orbital-relaxed, non-aufbau Slater determinant as an approximation for the excited-state wave function. In general, these non-aufbau solutions are saddle points (rather than local minima) in the space of MO coefficients, and orbital optimization runs the risk of variational collapse to the ground-state solution.
A popular means to overcome this limitation is the maximum overlap method (MOM) of Gill and co-workers,196–198 which has been improved in Q-Chem 5 by the addition of an “initial MOM” (IMOM) variant.198 Starting from a user-specified non-aufbau electron configuration (using MOs determined from a previous calculation), the MOM and IMOM algorithms attempt to preserve the character of this state at each step of the SCF orbital optimization procedure. While the IMOM algorithm tends to be more robust as compared to the original MOM, neither one is guaranteed to avoid variational collapse. Q-Chem 5 offers two new algorithms that are much more reliable in this capacity: squared-gradient minimization (SGM)199 and state-targeted energy projection (STEP).200
The SGM algorithm converts the unstable saddle-point search associated with excited-state orbital optimization into a simpler minimization problem by considering the squared-gradient of an excited-state Lagrangian , where θ is a vector of orbital-rotation variables. SGM is far more robust than either MOM or IMOM, although it is a few times more expensive (per iteration) as compared to the ground-state SCF technology that underlies MOM,199 and furthermore, not every local minimum of corresponds to a physically meaningful state.200 An alternative is the STEP algorithm, which has the same cost as MOM but tends to be more robust.200 This approach uses a level-shift in order to optimize a determinant containing a “hole” in the occupied space, using nothing more than the ground-state machinery of iterative Fock-matrix diagonalizations.
Both the SGM and STEP algorithms succeed in a variety of cases where MOM and IMOM suffer variational collapse.199,200 For a challenging database of doubly excited states,201 ΔSCF excitation energies computed with the B97M-V functional are only 0.15 eV away from theoretical best estimates, with a maximum error <0.5 eV.199,200 (Errors for the same dataset at the CC3 level are ∼1 eV,201 despite the inclusion of triple excitations.) The ΔSCF approach can also be used for ionization energies, to access the full valence photoelectron spectrum by systematically removing an electron from orbitals below the HOMO.200 Because the ΔSCF approach is based on ground-state machinery, analytic nuclear gradients and even analytic Hessians are available for many different density functionals. Geometry optimization can be performed in the presence of a valence hole in order to compute the adiabatic ionization energy for ionization below the HOMO.200
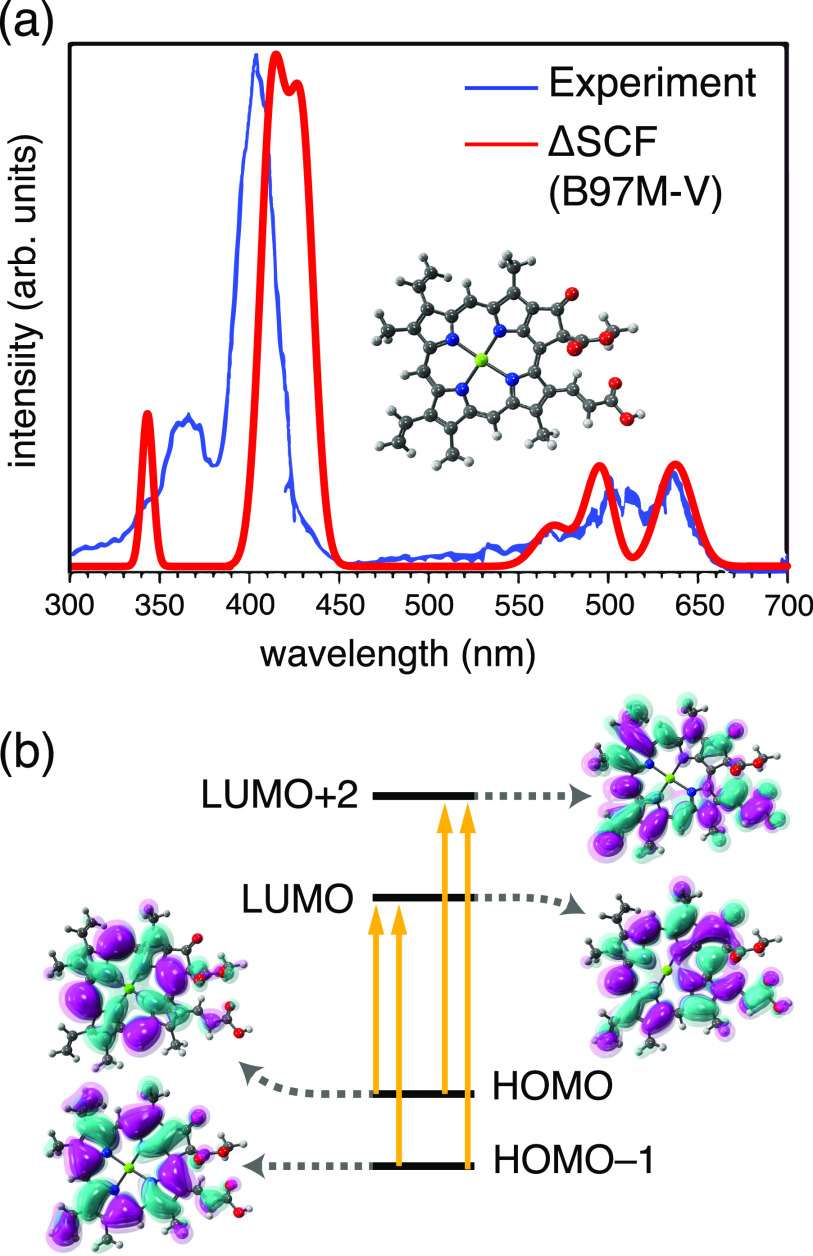
As a showcase of the ΔSCF approach, Fig. 8(a) presents a computed absorption spectrum for the chlorin moiety of chlorophyll a.200 In accordance with Gouterman’s four-orbital model,203 the ΔSCF calculation includes the four excitations that are shown in Fig. 8(b), and the result is in semiquantitative agreement with a recent gas-phase experimental spectrum.202 It is worth noting that the ΔSCF approach uses a single Slater determinant to describe the excited-state wave function, but for an open-shell singlet, a minimum of two determinants is required in order to obtain a spin eigenstate. It is therefore not unusual for the ΔSCF wave functions to exhibit (in units of ℏ2), indicating approximately equal mixture of singlet and triplet. A simple spin-purification procedure,204,205
| (7) |
can be used as an a posteriori correction that requires only the triplet energy (Etriplet) in addition to the spin-contaminated energy Emixed.
FIG. 8.
(a) Absorption spectra of the Mg-chlorin chromophore of Chl a (structure shown), comparing a gas-phase experimental spectrum202 to a ΔSCF calculation at the B97M-V/def2-TZVPD level, which is then spin-purified using Eq. (7).200 (b) Four-orbital model demonstrating the states that were targeted using the STEP algorithm and included in the excitation spectrum shown in (a). Adapted with permission from K. Carter-Fenk and J. M. Herbert, J. Chem. Theory Comput. 16, 5067 (2020). Copyright 2020 American Chemical Society.
A more elaborate method is to optimize the orbitals directly using Eq. (7) as the total energy expression, which forms the basis of the restricted open-shell Kohn–Sham (ROKS) formalism.206,207 ROKS has been found to be effective in predicting energies of excited states of small molecules,207 as well as charge-separated excited states of organic light emitting diode materials,208 to an accuracy of ∼0.2–0.3 eV. In conjunction with the SGM algorithm, the ROKS approach can be used to predict core-level excitation energies to an accuracy of 0.2–0.3 eV,209 as described in Sec. V A. Nuclear gradients for ROKS are available in Q-Chem,207 permitting geometry optimizations and (finite-difference) frequency calculations in the excited state. Finally, note that Eq. (7) is only appropriate in the case of two unpaired electrons, and more elaborate treatments are necessary in more complicated cases.210–212
III. MANY-BODY METHODS
Whereas Jacob’s ladder of DFT provides a hierarchy of methods that are improvable only in a statistical sense, meaning that the best functionals on a given rung are usually (but not always) better than the ones on the rung below, many-body approaches to the electron correlation problem provide a systematic and rigorous way to approach the exact solution for any given molecule.213 Particularly powerful are the hierarchical approximations built upon the Møller–Plesset (MP) perturbation theory and coupled-cluster (CC) frameworks,214 which do not involve system-specific parameterization. Q-Chem offers fast and efficient implementations of the standard many-body approaches, including MP2, MP3, CCSD, and CCSD(T). These codes exploit shared-memory parallelism (OpenMP) as well as numerous cost-reduction and resource-reduction techniques. Among these are resolution-of-identity approximations (also known as density fitting),215 Cholesky decomposition of the electron repulsion integrals (ERIs),215,216 frozen natural orbitals,217,218 and efficient tensor libraries.12,13 Mixed-precision CC and EOM-CC calculations are also available for energies, properties, and gradients.219 Q-Chem 5 also features mixed precision (T) calculation. A combination of these techniques enabled calculations of magnetic properties of single-molecule magnets and even infinite spin-chains at the CC/EOM-CC level of theory.177,220–223 A new object-oriented implementation of the MP2 energy and gradient and of MP3 energies (including orbital-optimized variants) requires no storage of amplitudes or four-index electron repulsion integrals and is optimized for OpenMP parallelism.
Single-reference wave function methods can be extended to tackle many problems traditionally described as “multi-reference.” For example, many types of open-shell and electronically excited species can be handled by equation-of-motion (EOM)-CC methods224–226 as well as by methods based on the algebraic diagrammatic construction (ADC).227 At the same time, Q-Chem also contains methods based on the CI formalism, including active-space methods for the treatment of strong correlation. Those methods are described in Sec. IV, whereas the present section highlights some examples of new development in MPn and CC methods.
A. Extensions of MPn theory
MPn theory is traditionally applied to the Hartree–Fock determinant, on the assumption that it is the best single-determinant approximation to the correlated wave function, an assumption that may not be valid for open-shell systems or cases where static correlation is important. Deficiencies of Hartree–Fock orbitals include excessive spin polarization (i.e., artificial symmetry breaking)228 and charge distributions that are slightly too diffuse and too polar.229 These deficiencies can be addressed using orbital-optimized (OO) approaches in which the orbitals are determined by minimizing a correlated energy expression. In the context of MP2, this can be done using either the opposite-spin correlation energy230 or the total MP2 correlation energy.231,232 However, OOMP2 exaggerates correlation effects and this can lead to artifacts, especially when orbital energy gaps become small.233 This issue is addressed by an improved version of OOMP2, termed κ-OOMP2,234 which applies a novel energy-dependent regularization to the electron repulsion integrals,
| (8) |
This removes divergences associated with small denominators in the κ-OOMP2 energy expression
| (9) |
With the recommended choice of κ = 1.45 a.u., κ-OOMP2 significantly improves upon standard MP2 for thermochemical properties, non-covalent interactions, and reaction barrier heights.
The use of κ-OOMP2 orbitals also sidesteps artificial symmetry breaking, and in this capacity the method can be useful for diagnosing the presence of strong correlation. By design, κ-OOMP2 includes a simple treatment of dynamical (or weak) correlation but zero contribution in the strongly correlated limit.235 In molecules without strong correlation, spin symmetry-breaking (SSB) exhibited by Hartree–Fock orbitals is dramatically reduced by κ-OOMP2, signifying that the SSB in question was “artificial,” caused by the absence of dynamic correlation. In molecules with strong correlation, Hartree–Fock SSB is preserved in the κ-OOMP2 orbitals, signifying the presence of essential SSB associated with multireference character.
This approach helped to resolve a controversy236,237 regarding the character of electron correlations in fullerenes. Hartree–Fock theory shows dramatic SSB in C60, with the global-minimum solution exhibiting complex and general symmetry breaking, which has been interpreted as a signature of strong correlation and polyradical character. However, the κ-OOMP2 global-minimum orbitals remove this artificial SSB and are spin-pure, thus establishing that C60 is not a strongly correlated system, which is consistent with other observables.235 By contrast, more reactive fullerenes, such as C30, do exhibit essential SSB in κ-OOMP2. In conjunction with other observables, this confirms the presence of strong correlations in their ground states. By using κ-OOMP2 with either spin projection or complex orbitals, one can treat large diradicaloid systems, on the size scale of the reactive fullerenes.238
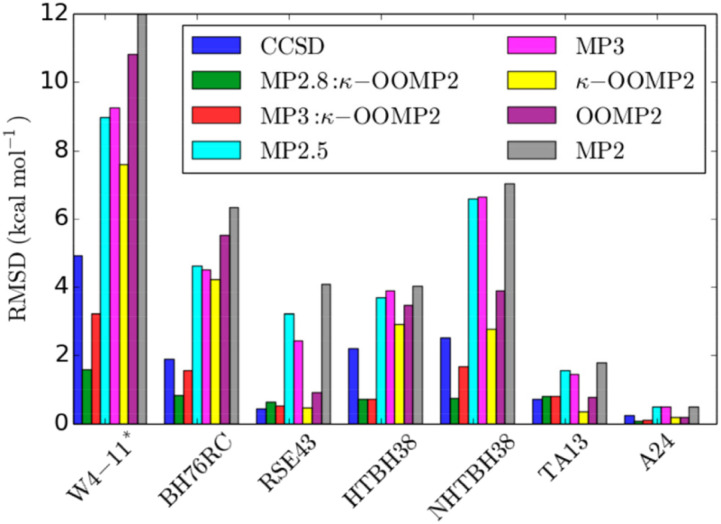
The κ-OOMP2 energy and gradient are implemented in Q-Chem 5 within a modern MPn suite that includes MP3. The long-neglected MP3 ansatz, when used with orbitals from either κ-OOMP2 or a good DFA, can deliver accuracy comparable to that of CCSD but is 20–30× faster.239,240 Figure 9 illustrates the improvement of κ-OOMP2 relative to MP2, as well as the dramatic improvement in MP3 when using κ-OOMP2 orbitals instead of Hartree–Fock orbitals.
FIG. 9.
RMS errors (in kcal/mol) relative to benchmark CCSD(T) values for seven different datasets assessed using MP2, MP3, and CCSD methods. Reprinted with permission from Bertels et al., J. Phys. Chem. Lett. 10, 4170 (2019). Copyright 2019 American Chemical Society.
B. CC/EOM-CC and ADC methods for open-shell and electronically excited species
Q-Chem contains an ever-growing suite of many-body methods for describing open-shell molecules and excited states.172 The EOM-CC224–226 and ADC227,241 formalisms are two powerful approaches for describing multiconfigurational wave functions within a black-box single-reference formalism. Target states |Ψex⟩ are described as excitations from a reference state |Ψ0⟩,
| (10) |
where is an excitation operator parameterized via amplitudes that are determined by solving an eigenvalue problem. In EOM-CC, these amplitudes are eigenvectors of the effective Hamiltonian
| (11) |
in which is either the CC or the MP2 operator for the reference state. Currently, EOM-CCSD and EOM-MP2 models are available. In ADC, an effective shifted Hamiltonian is constructed using perturbation theory and the intermediate state representation (ISR) formalism,227,241 similar to Eq. (10), to afford
| (12) |
where E0 is the energy of the MPn reference state. Diagonalization of the Hermitian matrix M yields excitation energies, and the ADC eigenvectors give access to the excited-state wave function. Second-order standard ADC(2), extended ADC(2)-x, and ADC(3) are available.241 For the second-order ADC schemes, spin-opposite-scaled (SOS) variants are also implemented.242
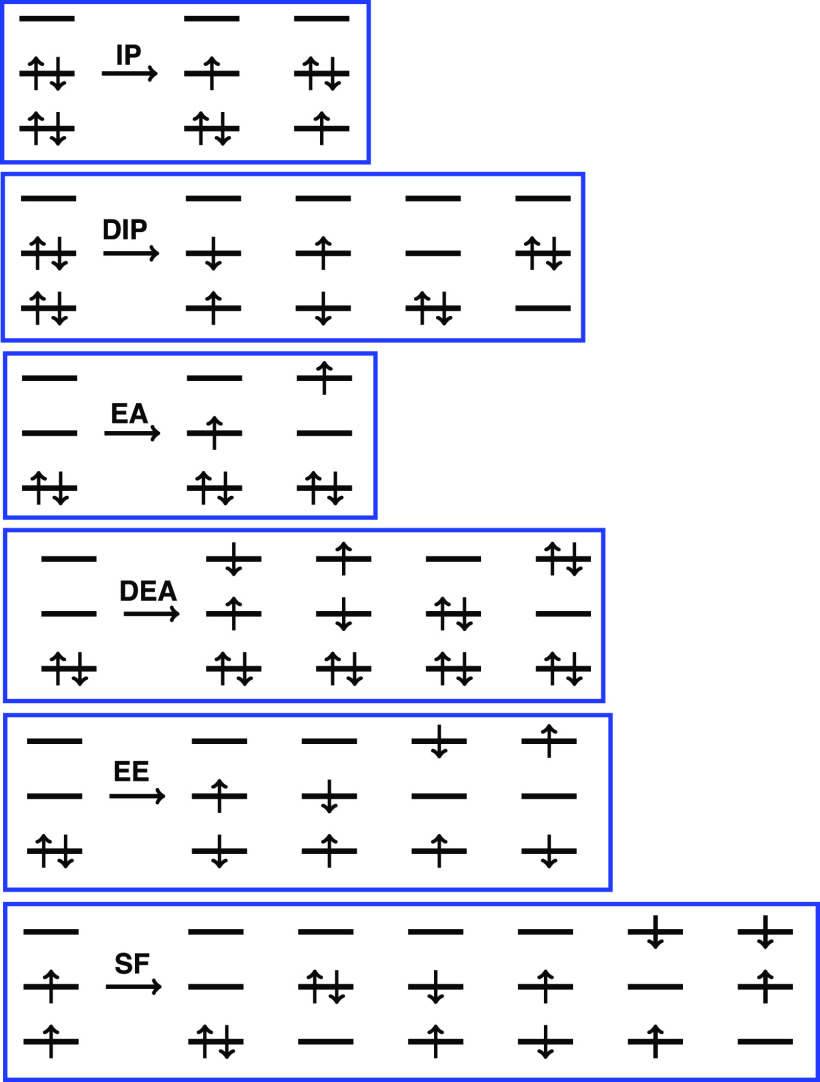
Various EOM-CC and ADC models are defined by the choice of reference state |Ψ0⟩ and excitation operator , as illustrated in Fig. 10. The following models are available:224,227,241 EE (excitation energies), IP (ionization potentials), EA (electron affinities), SF (spin–flip, for triplet and quartet references), 2SF (double SF, for quintet references); DIP (double IP), and DEA (double EA). At present, the 2SF, DIP, and DEA variants are only available in combination with an EOM treatment.243
FIG. 10.
Schematic representation of the manifolds of target states that are accessed within various EOM-CC and ADC formalisms by combining particular choices of reference state and excitation operator in Eq. (10). For example, in the EE models for electronically excited states, the reference |Ψ0⟩ is the closed-shell ground-state wave function and the operator conserves the number of α and β electrons in generating a target manifold of correlated excited-state basis functions. Non-particle-conserving operators (IP, EA, DIP, and DEA) and spin-flipping (SF) operators open a route to the multi-configurational wave functions encountered in radicals, diradicals, triradicals, and bond-breaking processes. Reprinted with permission from D. Casanova and A. I. Krylov, Phys. Chem. Chem. Phys. 22, 4326 (2020). Copyright 2020 Published by the PCCP Owner Societies.
Analytic gradients244,245 and properties246–248 are available for most of these models, including transition properties between different target states (e.g., transition dipoles, angular momentum, and electronic circular dichroism rotatory strengths),249 nonadiabatic couplings,250 spin–orbit couplings,220,251,252 and nonlinear optical properties, including two-photon transition moments and (hyper)polarizabilities for both ground and excited states.253–256 Extensions of these theories to metastable states257 (resonances) and to core-level excitations258–260 are also available and are highlighted in Sec. V.
The IP and EA variants of these models afford spin-pure descriptions of ground and excited doublet states and are useful for modeling charge-transfer processes. EOM-SF and SF-ADC methods are suitable for treating diradicals, triradicals, and conical intersections. The DEA and DIP ansätze further expand the scope of applicability.243 Spin–flip methods can be used to treat strongly correlated systems within an effective Hamiltonian formalism,221,261,262 with applications to single-molecule magnets and even infinite spin chains.222
For visualization purposes, both Dyson orbitals264 and natural transition orbitals265 (NTOs) are available,15,88,220,266–269 including NTOs of the response density matrices for analyzing two-photon absorption270 and resonant inelastic x-ray scattering.271 Figure 11 highlights the application of these tools to model magnetic properties and spin-forbidden chemistry. Exciton analyses,267,268,272–274 bridging the gap between the quasiparticle and MO pictures of excited states, enable the calculation and visualization of electron–hole correlation.89,267,268,272,273
FIG. 11.
Spinless NTOs for selected transitions between two quintet d6 states in a tris(pyrrolylmethyl)amine Fe(II) single-molecule magnet,263 which are responsible for its large (158 cm−1) spin-reversal barrier. Q-Chem’s efficient EOM-CC implementation using the spin–orbit mean-field approximation and the Wigner–Eckart theorem enables calculations for medium-size molecules such as the one shown here. The computed spin-reversal barrier is within 1 cm−1 of the experimental value.252 The key object, the spinless triplet transition density matrix, provides valuable information about the nature of spin–orbit coupling and the related properties. Spinless NTOs (shown here) allow one to quantify and validate El-Sayed’s rules.252 Reprinted with permission from Pokhilko et al., J. Phys. Chem. Lett. 10, 4857 (2019). Copyright 2019 American Chemical Society.
IV. ACTIVE-SPACE METHODS FOR STRONG CORRELATION
The applicability of single-reference methods rests on an assumption that the wave function is dominated by a single Slater determinant. While justified for ground states of well-behaved closed-shell molecules, this assumption is inappropriate for systems exhibiting strong (or static) correlation, where many Slater determinants may make comparable contributions. Examples of multiconfigurational systems include organic polyradicals and transition metals.275,276 While certain classes of multiconfigurational wave functions can be effectively described by single-reference methods, such as EOM-CC and ADC (Sec. III B), more general treatments are sometimes desirable.
The exact solution to the finite-basis Born–Oppenheimer electronic structure problem is the full configuration interaction (FCI) wave function, but factorial scaling generally limits its applicability to very small systems. It is thus more effective to solve the FCI problem within an active space of chemically relevant orbitals that contains the strong correlations, leaving the other orbitals to be described via mean-field theory. Although the introduction of an active space imparts an arbitrariness, which is undesirable for a theoretical model chemistry,79 the necessity of active-space methods cannot be denied, despite the need to carefully validate the active-space selection for each particular system and process.
This complete active-space (CAS-)CI ansatz can be used on its own277 but is more commonly combined with orbital optimization, which defines the popular CASSCF method,278,279 also known as the fully optimized reaction space (FORS).280 Both CASCI and CASSCF are available in Q-Chem 5, including analytic nuclear gradients.
The CASCI problem still exhibits factorial scaling with respect to the size of the active space. The total number of Slater determinants in an active space with M spatial orbitals is
| (13) |
where Nα and Nβ are the number of α- and β-spin electrons. This equates to Ndet ∼ 5 × 1011 for M = 22 and Nα = Nβ = 11, which is close to the practical upper limit and is only feasible within a massively parallel framework.281 With more typical resources, the limit is M ≤ 18. On the other hand, the overwhelming majority of these determinants make only a miniscule contribution to the energy.282,283 This enables the development of approximate active-space methods that attempt to identify the most important determinants in an automated way, without solving the full CASCI problem, and are thus extensible to much larger active spaces than conventional CASCI or CASSCF methods. The ability to deploy large active spaces helps to reduce the dependence on the active-space choice and affords more robust performance, including a more balanced treatment of dynamic and non-dynamic correlation. Two such methods, adaptive CI and incremental FCI, are described in this section.
The CASCI method can be extended by adding electronic excitations beyond the active space, as in the restricted active space CI (RAS-CI) approach, with single excitations into (hole) and out of (particle) the active space.284 This method has been implemented in Q-Chem using an integral-driven algorithm with exact integrals285 and also using the RI approximation.286 Similar to EOM-CC and ADC methods, target RAS-CI wave functions can be constructed with a general excitation-type operator (EE, nIP, nEA or nSF; see Fig. 10). The intrinsic lack of dynamic correlation within the RAS-CI family can be addressed by means of multi-reference perturbation theory [RAS-CI(2)]287 or by the use of short-range density functional correlation energy (RAS–CI–srDFT).288,289 Q-Chem's RAS-CI implementation can compute state and transition properties, including transition dipole moments and spin–orbit couplings.290
A. CI with adaptive selection
“Selected” CI (SCI) methods aim to exploit the sparsity of the Hilbert space by identifying important determinants and diagonalizing the Hamiltonian only within the space of important configurations. Although formulated long ago,291–296 these methods have re-emerged recently due to breakthroughs in efficient search of the determinantal space.297–304 Q-Chem 5 contains an implementation of the adaptive sampling configuration interaction (ASCI) method,304–306 which efficiently selects important configurations to yield compact CI wavefunctions that account for most of the correlation energy. Based on the computer resources available, the user selects a maximum number of determinants t to keep in the variational CI wave function and a cutoff of the top c determinants in this list to generate new determinants that are iteratively considered to replace the least significant members of the t-list. While still exponential-scaling, the ASCI algorithm permits dramatically larger FCI calculations than the standard approach. To correct for missing configurations, ASCI can be complemented with a second-order perturbation theory correction for the missing configurations to approach chemical accuracy of ∼1 kcal/mol.
While the “soft exponential” scaling of ASCI is a tremendous improvement over conventional FCI, it is still critically important to minimize the size of the FCI problem if the ASCI algorithm is to obtain chemical accuracy. ASCI can be used as an approximate CASCI solver for CASSCF calculations, with the resulting ASCI-SCF method extends the applicability of CASSCF to problems as large as CAS(50, 50) so that periacenes or iron porphyrin can be handled in this way.307 The difference between this and the conventional “hard exponential” limit of around CAS(18, 18) illustrates the utility of the ASCI-SCF method for extending the scale of feasible chemical applications. ASCI-SCF nuclear gradients for geometry optimizations are also available in Q-Chem 5.
B. Incremental full CI
The method of increments308–310 provides an alternative means to approach the FCI solution without the associated exponential scaling via an incremental expansion of correlation energy,311
| (14) |
Q-Chem 5 contains an incremental FCI (iFCI) method based on this idea,312–317 using occupied MOs for the indices p, q, r, …. Successive n-body contributions to Eq. (14) can be computed in a manner that is highly parallelizable, and iFCI recovers both static and dynamic correlation with polynomial scaling. Both the cost and the fraction of Ec that is recovered depend upon the level of truncation in Eq. (14); tests have shown that a three-body expansion (through ɛijk) recovers most of the correlation energy, but a four-body expansion is needed to reproduce full CI to within ∼10−3 Eh. Equally important to systematic convergence is the use of a localized orbital basis, which greatly speeds up the recovery of dynamic correlation. The generalized valence bond perfect-pairing (GVB-PP) method in Q-Chem318 suits this purpose well, providing localized bonding/antibonding pairs of orbitals for iFCI.314 When applied to butadiene and benzene, which are two standard test cases for FCI-level approaches,319 the four-body iFCI method provides total energies that are within 10−3 Eh of other benchmarks.314,317
The iFCI method has also provided solutions equivalent to the largest CI problems to date, including a recent study of transition metal complexes.317 For example, the vanadium maltolato dimer, [(μOCH3)VO(ma)]2, was examined to quantify its singlet–triplet gap (Fig. 12). The unpaired electrons of the vanadium atoms are coupled through a μ-oxo bridge, making for a complicated correlation problem involving both static and dynamic correlation. A three-body iFCI approach, correlating all 142 electrons in the 444 orbital space, affords a singlet–triplet gap within a few tens of cm−1 of experiment. To achieve this result, a systematic truncation scheme was used to eliminate over 90% of the three-body contributions, based on selecting incremental terms that do not significantly affect the gap.317
FIG. 12.
A challenging case of strong and weak correlation: the [(μOCH3)VO(ma)]2 dimer complex and its two singly occupied MOs. The three-body iFCI yields a singlet–triplet gap within 30 cm−1 of experiment.317
C. Other methods
Q-Chem contains several novel active-space methods that blend together aspects of CC and valence bond (VB) theories.320–325 These CCVB methods separate n electron pairs into arbitrary radical fragments such that the dissociation energy matches CASSCF but the computational cost is only polynomial. However, these methods are difficult to use in practice due to a nonlinear wave function ansatz and a lack of orbital invariance, which leads to a challenging multiple-minimum problem in the orbital optimization. The CCVB-SD method326 restores invariance with respect to orbital mixing within the core, active-occupied, active-virtual, and inactive-virtual subspaces while retaining the desirable formal features of the CCVB expansion. Q-Chem 5 contains a production-level implementation of the CCVB-SD energy and gradient327 using the same tensor tools used in Q-Chem’s efficient implementation of other CC methods.12 As such, the cost of CCVB-SD is nearly identical to CCSD, but the former can tackle strongly correlated systems. It is natural to use CCVB-SD with an active space because it can describe both strong and weak correlations but not simultaneously. See Ref. 327 for recent applications of CCVB-SD.
Direct variational determination of the two-electron reduced density matrix (2RDM) provides an efficient description of many-electron systems that naturally captures strong correlation effects. The variational 2RDM (v2RDM) approach can be used as a driver for approximate CASSCF calculations with polynomial scaling.328,329 Q-Chem 5 supports v2RDM-driven CASSCF calculations in which the active-space 2RDM is constrained to satisfy two-particle (“PQG”) positivity conditions,330 partial three-particle conditions,331 or else full three-particle N-representability conditions.332 Using PQG conditions only, v2RDM-driven CASSCF can be applied to systems with active spaces as large as (64, 64).333 Analytic energy gradients are available for v2RDM-CASSCF calculations with all three choices of N-representability conditions.334
V. SPECIALIZED METHODS
This section highlights some specialized features of contemporary interest. Quantum chemistry is witnessing a surge of interest in x-ray spectroscopy,192,335–339 fueled by advanced light sources and free-electron lasers, and by the recent availability of tabletop laser sources with femtosecond time resolution.340–344 For that reason, we highlight Q-Chem’s capabilities for core-level spectroscopy in Sec. V A. Q-Chem also features a suite of methods for describing metastable resonances, which are more often handled with specialized scattering codes, and Q-Chem’s functionality here is unique among widely used electronic structure packages. Unlike bound states, resonance wave functions are not square-integrable, and their description requires specialized methods based on non-Hermitian quantum mechanics,345 which are summarized in Sec. V B. Methods for vibronic lineshapes are described in Sec. V C, and Sec. V D describes the nuclear–electronic orbital method for the description of proton quantum effects.
A. Modeling core-level spectroscopy
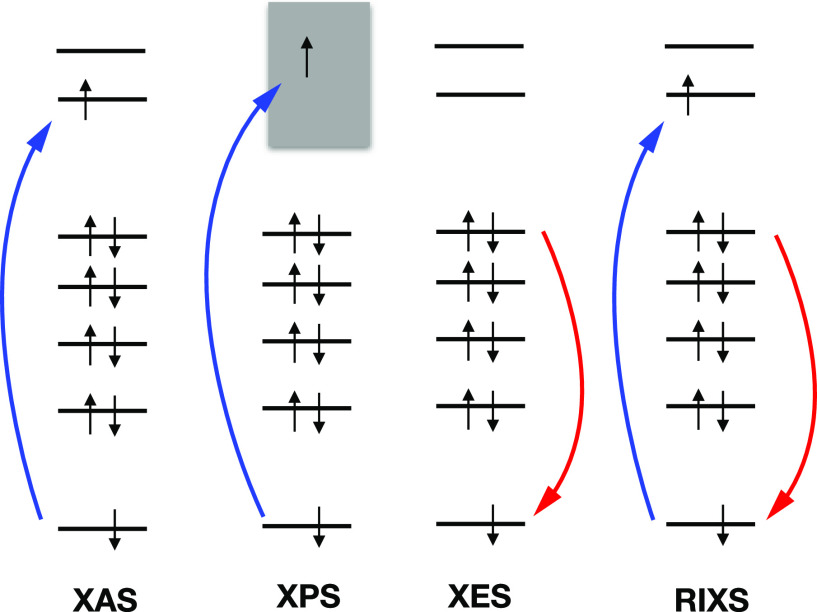
Various core-level (x-ray) processes are illustrated schematically in Fig. 13. These include x-ray absorption (XAS), x-ray emission (XES), resonant inelastic x-ray scattering (RIXS), and x-ray photoelectron spectroscopy (XPS). The relaxation of the core-level states can also result in secondary ionization, giving rise to Auger spectroscopy. These techniques correspond to photon energies above 200 eV such that core-to-valence excitations are embedded in an ionization continuum. Standard quantum chemistry approaches require modification in order to deal with these highly energetic excitations,192,335 especially in models with double (and higher) excitations that allow core-level states to decay. Because core-level states are Feshbach resonances that decay via two-electron processes, attempts to solve unmodified EOM-CCSD or ADC equations for core-level states lead to the same physically correct but practically disastrous behavior as attempts to describe transient anions (e.g., , ) by standard bound-state methods.257,346 In both cases, the solutions depend strongly on basis set (which affects how the continuum is discretized),346 and in the limit of a complete basis set, these states dissolve into the continuum.257,346,347
FIG. 13.
Schematic illustrations of core-level phenomena. The XAS and XPS processes involve excitation into a virtual bound molecular orbital or into the continuum, respectively, whereas the XES signal is produced by radiative relaxation of a valence electron into a core hole. The nonlinear RIXS phenomenon can be described as a coherent combination of XAS and XES transitions.
The ionization continuum can be projected out using the core/valence separation (CVS) scheme,348 which entails pruning the target Fock space by removing the configurations that do not engage the core electrons. By doing so, CVS effectively blocks the ionization channels, artificially making core-excited states bound with respect to electron loss. In addition, CVS removes the large manifold of valence excited states so that core-level excitations appear at the bottom of the excited-state manifold, within easy reach of standard iterative eigensolvers. Uncontracted or otherwise specialized basis sets are sometimes required,192,197,349–354 because standard Gaussian basis sets are designed for valence chemistry and may not describe the strong orbital relaxation induced by the creation of the core holes. (TDDFT is considerably less sensitive in this regard, however.121,351) In addition, relativistic effects and spin–orbit coupling become important for L- and M-edge excitations.338
Q-Chem offers a variety of methods for computing transitions involving core orbitals and the corresponding spectroscopic properties. These can be classified as follows:
-
•
Calculations based on orbital eigenvalue differences, often using fractional orbital occupations.355–359
-
•
State-specific ΔSCF methods197,200,337 (or ΔMP2, etc.) and spin-recoupled ROKS methods209,211 based on a non-aufbau determinant containing an orbital-relaxed core hole.
-
•
Non-orthogonal CIS (NOCIS), which employs relaxed core holes and returns a spectrum of core excitation energies.360–362
-
•
LR-TDDFT calculations using a restricted excitation window.189,191,337,363 In conjunction with a non-aufbau reference determinant, this approach can also be used to simulate XES.364
-
•
Real-time TDDFT calculations of an entire broadband excitation spectrum (Sec. II C 3).
-
•
Correlated methods within the CVS scheme, such as CVS-ADC258,259 and CVS-EOM-CC,260,365–367 for XAS, XPS, XES, x-ray electronic circular dichroism (or simply XCD), RIXS, and Auger spectroscopy. These may also be used with a non-aufbau reference determinant to simulate excited-state XAS and XPS, as needed in the context of time-resolved experiments.364,368–370
With the exception of real-time TDDFT, each of these methods invokes some sort of decoupling from the valence continuum. Neglecting the valence continuum is an approximation, which can affect the position of the core-level resonances. Apart from fully time-dependent treatment, the effect of the continuum can also be incorporated via the Feshbach–Fano formalism by combining the CVS treatment with the continuum orbitals371 or with other non-Hermitian methods described in Sec. V B.
Methods based on SCF eigenvalue differences ϵa − ϵi have their origins in Slater’s transition method,372,373 which is based on a proof that ϵa − ϵi is the leading-order approximation to a true excitation energy if the SCF calculation is performed with fractional occupation numbers ni = 1/2 = na. Due to the impracticality of computing an entire spectrum state-by-state, it is often assumed that the potential generated by placing 1/2 electron in the LUMO will approximately mimic that obtained by placing 1/2 electron into a higher-lying virtual orbital so that only a single fractional-electron SCF calculation is required. This approach is usually known as the transition potential method.355–357 Other occupancy schemes have sometimes been considered,359,374,375 with names such as “half core-hole,” “full core-hole,” and “excited core-hole.”375
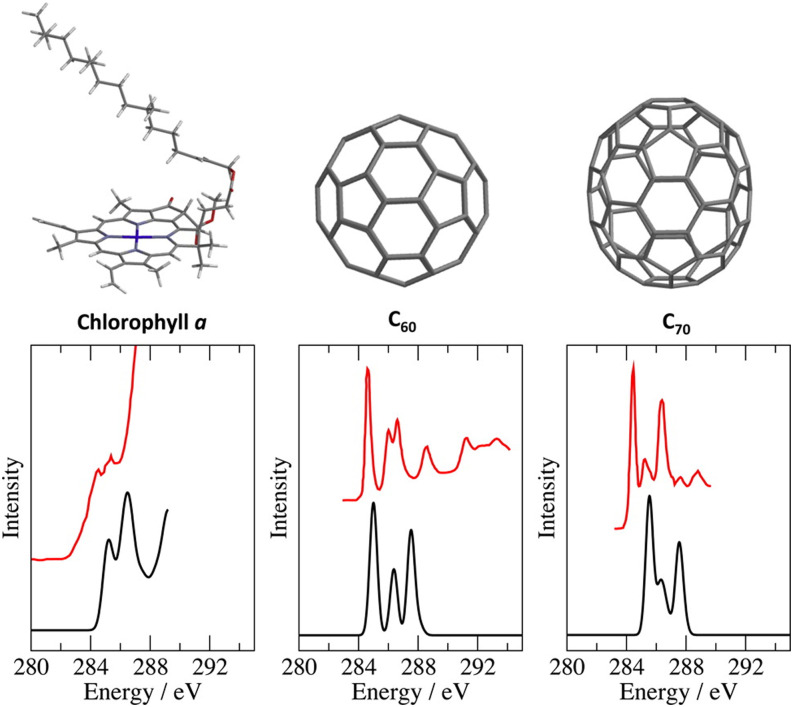
The state-specific ΔSCF approach was described in Sec. II C 4. Here, the requisite non-aufbau determinant (containing a core hole) can be optimized using one of several algorithms that are available in Q-Chem, including MOM,197 IMOM,198 SGM,199 or STEP.200 This approach accounts for orbital relaxation and works very well for core-level ionization (XPS), but in the context of XAS it suffers from the same impracticality that limits Slater’s transition method. State-specific calculations are most commonly performed at DFT levels of theory (hence ΔSCF), but in principle a non-aufbau Hartree–Fock determinant could be used as a reference state for a subsequent wave function treatment of correlation, e.g., ΔMP2 or ΔCCSD.197,200 It should be kept in mind that non-aufbau determinants do suffer from spin-contamination (see Sec. II C 4) and sometimes from artificial symmetry breaking. The convergence of CC methods can sometimes be problematic when using a highly excited reference state.376
Regarding LR-TDDFT, it is worth noting that workhorse functionals for the ground-state SCF problem, which might be accurate to 0.2–0.3 eV for valence excitation energies,128 afford much larger errors where core-level excitation energies are concerned, e.g., shifts >10 eV are typically required using B3LYP.377 (That said, a recent benchmark study suggests that these large shifts do not dramatically affect the precision of LR-TDDFT excitation energies,378 such that the features of a shifted spectrum might be acceptable.) To improve the absolute accuracy, early studies suggested increasing the fraction of Hartree–Fock exchange in B3LYP to 50%–70%189,364,379–381 in order to balance core and valence self-interaction, but such severe modification makes these functionals inappropriate for application to valence chemistry.
An alternative is to use range separation to dial in a large fraction of exact exchange on very short length scale (<1 Å), preserving the balance of semilocal vs Hartree–Fock exchange at larger distances. This is the basis of short-range corrected (SRC) functionals developed specifically for x-ray spectroscopy,189,388 which afford an absolute accuracy of ∼0.3 eV for core-level excitations of second-row elements when used with LR-TDDFT.
Q-Chem has the capability to perform LR-TDDFT calculations that are optimized for XAS, reducing both the computational time and memory requirements.191,192 Examples of what is feasible with this approach, using a restricted excitation window approximation (analogous to the CVS approximation) at the carbon K-edge, are shown in Fig. 14. These spectra were computed at the TD-SRC2189/6-31G*382,383 level of theory and are compared directly to experiment,384–387 without empirical shifts.
FIG. 14.
Carbon K-edge spectra for several large molecules computed with LR-TDDFT (SRC2 functional189 and 6-31G* basis set,382,383 in black) in comparison to experimental near-edge x-ray absorption fine structure (NEXAFS, in red). The experimental data are from Refs. 384–387. Reprinted with permission from N. A. Besley, J. Chem. Theory Comput. 12, 5018 (2016). Copyright 2016 American Chemical Society.
Whereas ΔSCF calculations are a single-determinant approximation for the excited state, ROKS calculations provide a spin-pure treatment of open-shell singlet excited states, as discussed in Sec. II C 4, while also providing full core-hole relaxation. ROKS with Hartree–Fock orbitals attains a root-mean-square error (RMSE) of 0.6 eV for K-edge excitations of second-row elements,212 without any correlation, highlighting the importance of orbital relaxation in describing core-level states. Inclusion of dynamic correlation via DFT can lead to better results, with the modern SCAN meta-GGA40 affording a RMSE of ∼0.2 eV for K-edge excitations of C, N, O, and F.209 Similarly, small errors are obtained at the L-edges of third-row elements.209 The relatively low computational scaling of the semilocal SCAN functional (as compared to hybrid DFAs) makes this approach particularly appealing for larger systems. While it might appear tedious to optimize each possible excitation individually with ROKS, the suite of excited state orbital optimization methods in Q-Chem permits explicit computation of a full spectrum without too much difficulty. This is demonstrated in Fig. 15, which depicts the carbon K-edge spectrum of adenine computed via ROKS using the SCAN functional and the SGM algorithm.
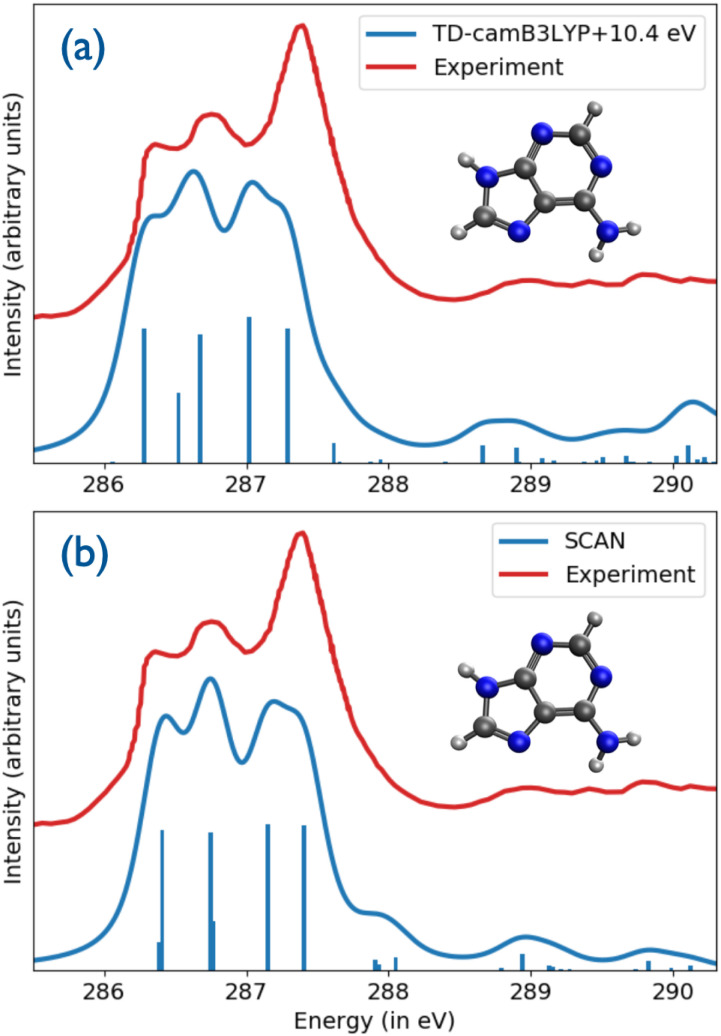
FIG. 15.
Carbon K-edge spectra of adenine obtained using (a) LR-TDDFT with the CAM-B3LYP functional389 vs (b) state-specific ROKS calculations using the SCAN functional. All calculations used a mixed basis set consisting of aug-cc-pCVTZ390 on the core-excited atom and aug-cc-pVDZ391,392 on all other atoms. The LR-TDDFT calculations require a 10.4 eV shift to align the low-energy edge of the calculated spectrum with experiment,393 whereas the ROKS spectrum is unshifted.
It is also possible to compute multiple excited states simultaneously while accounting for core–hole relaxation. The non-orthogonal CIS (NOCIS) approach achieves this by performing CIS with relaxed orbitals for the core-ionized state.360,362 Specifically, NOCIS computes optimal core-ionized orbitals for each possible atomic core-excitation site, builds all singly excited configurations that preserve the desired core hole, and then diagonalizes the Hamiltonian within the subspace spanned by these (non-orthogonal) determinants. Some additional considerations involving ΔSCF states are necessary to extend NOCIS to open-shell systems,361,362 and the lack of dynamic correlation leads to small (0.5–1.0 eV) overestimation of excitation energies. However, these drawbacks should be balanced against the ability to compute multiple excited states simultaneously, which is not possible with the more accurate ROKS approach. Much efficiency is gained and almost no accuracy is lost by restricting the CI space to individual atoms.362
Finally, many-body methods, such as ADC227 and EOM-CC,224 provide the means to compute core-excited transitions with systematically improvable accuracy. These methods include both orbital relaxation and electron correlation in a single computational step, within a multi-state formalism that naturally affords transition properties. These methods are naturally spin-adapted when used with a closed-shell reference determinant. Q-Chem 5 facilitates calculation of XPS, XAS, and XES using the CVS-EOM-IP-CCSD approach260,366 and XAS using either CVS-EOM-EE-CCSD260,366 or CVS-EE-ADC.259,394,395
CVS-EOM methods combined with spin–orbit coupling have been used to compute L-edge XPS,369 as in Fig. 16(a). Time-resolved variants of XPS or XAS can be modeled by using a non-aufbau reference determinant366,368,370 or directly as transitions between target ADC/EOM states,260,368 as illustrated in Fig. 16(b). Nonlinear spectra, including RIXS, can also be computed with correlated methods,367,399 as in Fig. 16(c). Features such as Dyson orbitals,264,366 attachment/detachment densities,400 and NTOs15,88,266,267,401 facilitate analysis and interpretation of the computed spectra. A unique feature of Q-Chem is the ability to compute Auger decay rates and Auger spectra using the Feshbach–Fano formalism combined with CVS-EOM-CC and an explicit description of the free electron,371 as illustrated in Fig. 16(d).
FIG. 16.
Exemplary applications of CVS-EOM-CCSD methods to x-ray spectroscopy. (a) Sulfur L-edge XPS spectra of thiophene with and without spin–orbit coupling computed at the fc-CVS-EOM-CCSD/u6-311+G(3df) level. The notation u6-311+G(3df) indicates an uncontracted version197,353 of 6-311+G(3df).396–398 (b) Oxygen K-edge XAS spectra of uracil in its S0, S1, and S2 states computed at the fc-CVS-EOMEE-CCSD/6-311++G** level. Intensity of the excited state bands has been reduced assuming 15% population. NTOs of the 1s → SOMO transition in S1 are also shown. (c) RIXS/REXS two-dimensional energy-loss spectrum of benzene vs pumping frequency ωex computed at the fc-CVS-EOM-CCSD/u6-311(2+,+)G** level. Intensities are on a logarithmic scale. (d) Illustrations of various Auger effects: (1) regular Auger decay, (2) resonant (participator) decay, and (3) resonant (spectator) decay. Regular Auger decay is relevant for XPS, whereas resonant Auger processes occur in XAS. These processes can be modeled within the Feshbach–Fano framework using CVS-EOM-CC to describe the initial core-excited or core-ionized state and EOM-IP-CC or DIP-CC to describe the final state. Panel (a) is adapted with permission from Vidal et al., J. Phys. Chem. Lett. 11, 8314 (2020). Copyright 2020 American Chemical Society. Panel (b) is adapted from Vidal et al., J. Chem. Theory Comput. 15, 3117 (2019). Copyright 2019 American Chemical Society. Panel (c) is reproduced with permission from Nanda et al. Phys. Chem. Chem. Phys. 22, 2629 (2020). Published by the PCCP Owner Societies. Panel (d) is reproduced from W. Skomorowski and A. I. Krylov, J. Chem. Phys. 154, 084124 (2021) with the permission of AIP Publishing.
B. Methods for metastable resonances
Electronic resonances, meaning states that are unstable with respect to electron loss, are ubiquitous in energetic environments such as plasmas, in combustion, and in the presence of ionizing radiation.257,345 Resonances are also relevant to condensed-phase processes under milder conditions, e.g., plasmonic catalysis,402 and may play a role in radiation-induced damage to living tissue.403 Because resonances lie in the continuum, their wave functions are not square-integrable and cannot be described using standard quantum-chemical methods designed for isolated bound states. Naïve application of bound-state quantum chemistry to metastable states does not capture genuine resonances but rather “orthogonalized discretized continuum states,”346 where the metastable state behaves like a poor approximation to a plane wave, trapped by a finite Gaussian basis set, with properties that are artificial and prone to change erratically as the basis set is changed, especially if additional diffuse functions are introduced.
This computational predicament is elegantly circumvented within non-Hermitian quantum mechanics based on complex-variable techniques,345 which generalizes and extends concepts from bound-state quantum chemistry to the case of electronic resonances.257,345,346 Within this modified formulation, electronic resonances can be described as square-integrable quasi-stationary states albeit with complex-valued energies, E = ER − iΓ/2, where ER is the resonance position and Γ is the resonance width, the latter of which arises from lifetime broadening.
Q-Chem offers three different complex variable techniques: complex coordinate scaling (CS),346,404–409 complex basis functions (CBFs),410–413 and complex absorbing potentials (CAPs).414–417 The CS approach regularizes the resonance wave function by rotating all coordinates in the Hamiltonian into the complex plane, x → xeiθ. This approach has a rigorous mathematical foundation but is not compatible with the Born–Oppenheimer approximation, limiting its applicability to atoms, whereas CBFs and CAPs are applicable to molecules. (The latter approaches can be considered as approximations to “exterior” CS.418,419) CBF methods utilize mixed basis sets in which the exponents of the most diffuse functions are complex-scaled, whereas the CAPs simply add an imaginary potential to the molecular Hamiltonian ,
| (15) |
The CAP serves to absorb the non-normalizable tail of the resonance wave function, and several functional forms for (x) are available in Q-Chem. Although there is some arbitrariness associated with the details of the CAP, these methods are generally easier to use as compared to alternative “stabilization” methods,346,420,421 in which Gaussian exponents or atomic numbers are modified in order to stabilize the resonance (making it amenable to standard bound-state methods), with the results then extrapolated back to the physical system of interest. If applied carefully, both the stabilization and CAP methods afford useful results;422 however, the CAP approach is more rigorous and more straightforward to extend to other molecular properties.
The CS, CBF, and CAP techniques can each be combined with the full EOM-CCSD suite of methods implemented in Q-Chem. The CAP technique is also available for all ADC methods,248 implemented via a subspace projection approach.423 The EOM-EA or EA-ADC variants are appropriate for treating metastable radical anions of closed-shell molecules, whereas super-excited states of neutral molecules and metastable excited states of closed-shell anions are best described using EOM-EE or EE-ADC.
Q-Chem offers several functionalities for the characterization of electronic resonances beyond their positions and widths, including
-
•
first-order one-electron state properties and transition moments for all complex-variable EOM-CC methods,415,424
-
•
Dyson orbitals for all complex-variable EOM-CC methods,424–426
-
•
NTOs for CAP-EOM-CC methods,427 and
-
•
analytic gradients for CAP-EOM-CC methods.428
These tools are useful for investigating the spectroscopy and chemical reactivity of electronic resonances. Dyson orbitals and NTOs, for example, provide compact representations of changes in the wave function upon electron attachment or electronic excitation. Since complex-valued Hamiltonians are not Hermitian but rather complex-symmetric, these quantities conform to a modified metric in which the real part of the complex electron density integrates to the number of electrons, while its imaginary part integrates to zero.406 Related results hold for density matrices, transition density matrices, orbitals, and wave functions, all of which also feature a real and an imaginary part. Analogous to the case of bound states, a singular value decomposition of the one-electron transition density matrix affords pairs of NTOs, which facilitate the interpretation of an electronic excitation in terms of MO theory.269
Further analysis of NTOs and exciton wave functions can be accomplished based on the Feshbach formalism,429 wherein a resonance is described as a bound state coupled to a continuum of scattering states. This analysis demonstrates that the real part of the excitonic wave function describes changes in the electron density corresponding to the bound part of the resonance, while the imaginary component of the wave function can be interpreted as virtual states that facilitate one-electron decay into the continuum.427 Singular values associated with particular NTOs can be related to the partial widths of the respective decay channels. As an example, Fig. 17 illustrates NTOs for the 1Σ+ resonance in C7N−, a chain-like cyanopolyyne anion relevant to astrochemistry.430
FIG. 17.
Real and imaginary NTOs for the 1Σ+ resonance in C7N−. This state has mixed π → π* and σ → σ* character, as apparent from the participation ratio PRNTO(γRe) ≈ 3. Based on the singular values , the total width of 0.13 eV can be separated into two contributions, ΓΣ = 0.10 eV and ΓΠ = 0.03 eV, corresponding to the two decay channels in which the C7N radical is either formed in the 2Σ+ or the 2Π state. Reprinted with permission from W. Skomorowski and A. I. Krylov, J. Phys. Chem. Lett. 9, 4101 (2018). Copyright 2018 American Chemical Society.
Analytic gradients enable the search for special points on the complex-valued potential surfaces of polyatomic resonances. Algorithms are available for equilibrium structures,428,431 for crossings between resonances and their parent states,432 and for crossings between two resonances,433 the latter of which are known as exceptional points. These critical points govern the nuclear dynamics following the formation of a resonance state and, if that resonance is long-lived enough, can be connected to features in electron transmission and energy-loss spectra. In particular, exceptional points may be considered the non-Hermitian analogs of conical intersections and play a similar role for electron-induced chemistry as conical intersections do for photochemistry.433 An example involving a dissociative electron attachment process434–436 is considered in Fig. 18, in which a resonance anion state is accessible at the equilibrium structure of the neutral parent molecule, chloroethylene.433 The dissociative state has character but is too high in energy to be accessed directly, and the reaction proceeds via nonadiabatic transition between the two resonances, along a seam of exceptional points. The complex-valued potential surfaces for the and resonances around the minimum-energy exceptional point are shown in Fig. 18, computed using CAP-EOM-EA-CCSD.
FIG. 18.
(a) Schematic representation of dissociative electron attachment to chloroethylene. The exceptional point is marked by a blue circle. (b) Real and imaginary part of the potential surfaces in the vicinity of the minimum-energy exceptional point between the π* and the σ* states of the chloroethylene anion, plotted above the plane spanned by the real gradient difference vector (xRe) and the imaginary gradient difference vector orthogonalized to xRe (). Reprinted with permission from Z. Benda and T.-C. Jagau, J. Phys. Chem. Lett. 9, 6978 (2018). Copyright 2018 American Chemical Society.
C. Calculation of vibronic lineshapes
The vibrational structure of electronic transitions encodes rich information about molecular structure, in both linear spectroscopies (UV–Vis, XAS, XPS, etc.) and nonlinear ones (2PA, RIXS, resonance Raman, etc.). Quantitative modeling of these spectra combines calculations of electronic structure and nuclear wave functions via either a static (time-independent) or a dynamic (time-dependent) formalism.437–443 Q-Chem 5 provides several capabilities to calculate the vibrationally resolved spectra and certain types of electronic cross sections.
Within the dipole approximation, the probability of transition between an initial state (i) and a final state (f) is proportional to the square of the transition dipole matrix element,
| (16) |
when the photon is resonant with the energy gap. Here, is the electronic dipole moment operator, and coordinates R and r represent nuclei and electrons, respectively. Within the Born–Oppenheimer approximation,444,445 the wave functions Ψ(r, R) can be factored into a nuclear wave function χ(R) and an electronic wave function ψ(r; R) so that
| (17) |
Indices i′ and f″ denote the vibrational states of the two electronic states. Within the Born–Oppenheimer approximation, the vibrational wave functions are determined solely from the nuclear Schrödinger equation with a potential defined by the electronic Schrödinger equation. Integration over the electronic coordinates in Eq. (17) affords the electronic transition dipole moment for the i → f transition,
| (18) |
The transition probability can therefore be written as
| (19) |
Equation (19) is the basis for modeling the spectrum. It contains an electronic transition moment μif(R) in addition to vibrational wave functions for the initial and final states.
Within the Condon approximation,446 it is assumed that μif(R) depends weakly on the nuclear coordinates so can be evaluated at a fixed nuclear geometry, e.g., at the equilibrium geometry Re of the initial state. Then,
| (20) |
The overlap integral between the two nuclear wave functions is called a Franck–Condon factor (FCF),441,446–448 which is directly related to the intensities of vibrational progressions via Eq. (20).
FCFs for various spectroscopic transitions (photoelectron, UV–Vis, etc.) can be computed in a post-processing step using the ezFCF module of the stand-alone software ezSpectra,449 which implements FCFs within the double-harmonic approximation, either with or without consideration of Duschinsky rotation,441,450 i.e., changes in the normal modes between the ground and excited electronic states. These calculations require optimized structures and normal mode analysis for both electronic states but are completely agnostic regarding the level of electronic structure theory at which these calculations are performed. ezSpectra also contains a module ezDyson, which can be used to compute total and angular-resolved photoelectron spectra. This requires Dyson orbitals that can be computed using Q-Chem.
To go beyond the Condon approximation, one can invoke the Herzberg–Teller (HT) normal mode expansion of μif(R) around the equilibrium nuclear geometry,440,441,451 in order to account for geometry-dependent changes in the transition dipole moment. Although the Condon approximation is generally accurate for strongly allowed transitions for weak or forbidden transitions, the Franck–Condon term [Eq. (20)] is nearly or exactly zero, and therefore higher-order terms may become important. These give rise to the HT effect.440,441
Raman scattering is a two-photon process (see Fig. 19), and resonance Raman scattering (RRS) is a particular type of vibrational Raman spectroscopy in which the incident laser frequency lies close to an electronic transition.452,453 In RRS, an incident photon with frequency ωL (the laser frequency) is absorbed and another with frequency ωS is emitted, with the difference corresponding to a vibrational level spacing. The differential photon scattering cross section is given by442,454–456
| (21) |
where
| (22) |
and the transition operator
| (23) |
involves a sum over virtual vibronic states k. In the RRS process, the initial (i) and final (f) electronic states both correspond to the ground state, so ℏωfi represents a difference between ground-state vibrational energy levels, as depicted in Fig. 19. When the energy gap ωk − ωi between the k state and the i state is close to the laser frequency ωL, the intermediate state k (a vibrational level of an excited electronic state) dominates the scattering cross section and non-resonant contributions can be neglected.
FIG. 19.
Schematic diagram for one-photon absorption and one-photon emission (left) and for resonance Raman scattering (RRS, at right).
The formalism described above is inconvenient because even in the resonant case where only a single excited electronic state is important, Eq. (23) still requires a sum over vibrational levels on that state. An alternative strategy is based on a time-dependent formalism,457,458 which circumvents the evaluation of the multidimensional integrals that appear when FCFs are computed beyond the parallel-mode approximation, i.e., when Duschinsky rotation is included. In this approach, matrix elements of (which generates the polarizability tensor) are avoided and the scattering cross section is expressed in terms of the Fourier transform of a time correlation function representing the overlap between the final state |ψf⟩ and the time-evolving wave function |Ψ(t)⟩ following excitation to the upper electronic state,
| (24) |
(Here, “NRT” denotes the non-resonant terms that can be neglected in RRS, and Γ is a damping factor.) A detailed theoretical background is given in Ref. 442.
Q-Chem 5 includes a built-in implementation of the time-dependent correlation function approach at the LR-TDDFT level, which enables calculation of vibrationally resolved one-photon and two-photon absorption and emission spectra462,463 and RRS spectra440 within the double-harmonic approximation, including both Duschinsky rotation and HT effects in the time domain. To illustrate the capabilities of the theory, Fig. 20 compares calculated FC and FC-HT spectra for the benzyl radical to experiment. The absorption and fluorescence spectra arise from the D0 → D3 and D1 → D0 transitions, respectively. In particular, for the stimulated emission and the RRS spectra, agreement with experiment improves upon inclusion of the HT terms.
FIG. 20.
(a) Absorption spectra, (b) emission spectra, and (c) RRS spectra of benzyl radical, comparing experimental results to calculations within the FC approximation (in blue) vs the FC-HT approximation (in red). A damping factor of Γ = 300 cm−1 and temperature T = 298 K were used for the absorption spectrum vs Γ = 20 cm−1 and T = 0 K for the emission spectrum. For the RRS spectrum, a damping factor of 100 cm−1, Lorentzian broadening of Γ = 20 cm−1, and T = 298 K are used. All electronic structure calculations are performed at the (TD-)B3LYP/6-311G** level. To make the simulated spectra consistent with experiment,459–461 the adiabatic energy gap is shifted by 0.04 eV for absorption, −0.34 eV for emission, and −0.11 eV for RRS. The wavelength of incident light for the RRS simulation is 315 nm, as in the experiment.460
For semiquantitative calculations, a short-time approximation to Eq. (24) can be used, which turns out to be equivalent to the “independent mode, displaced harmonic oscillator” model,438,456,464 in which it is assumed that equilibrium displacements of the vibrational normal modes change upon electronic excitation but not the modes themselves or their frequencies. Under those assumptions, the dimensionless displacement for normal mode Qk can be related to the excited-state gradient, i.e., the derivative ∂Ω/∂Qk of the electronic excitation energy, Ω:465,466
| (25) |
The relative resonant enhancement in the intensity of mode Qj vs mode Qk is466
| (26) |
Within this approximation, the resonant enhancement in RRS (as compared to normal Raman scattering) consists of the excited-state gradient projected onto ground-state normal modes {Qk}, so this approach has also been called the excited-state gradient approximation.465,467 It has been implemented in Q-Chem 5 for CIS and LR-TDDFT excitation energies and used to compute the resonance Raman spectra of complex systems, such as e−(aq).466 This approach has also been combined with ab initio molecular dynamics to simulate transient (excited-state) RRS,468 which is measurable via the emerging technique of femtosecond stimulated Raman spectroscopy.469,470
D. Nuclear–electronic orbital methods
Nuclear quantum effects are essential in many chemical and biological processes, such as proton transfer and proton-coupled electron transfer reactions. The nuclear–electronic orbital (NEO) method provides a framework for the accurate and computationally efficient incorporation of the significant nuclear quantum effects within an electronic structure calculation.471,472 In this approach, specified nuclei are treated quantum mechanically alongside the MO description of the electrons, thereby avoiding the Born–Oppenheimer separation between the electrons and the quantum nuclei. Treating at least two nuclei classically prevents complications with translations and rotations. Typically, the quantum nuclei are chosen to be protons or deuterons, although the NEO method has also been applied to positrons.473,474 For simplicity, the formalism presented below assumes quantum protons. A significant advantage of the NEO method is that anharmonicity, proton delocalization, and zero-point energy are included directly in energies, geometry optimizations, reaction paths, and molecular dynamics. Both wave function and DFT methods have been developed within the NEO framework for the accurate description of nuclear quantum effects in the ground and excited states of molecular systems.474–490
The NEO Hamiltonian operator is471
| (27) |
where , , and are the conventional electronic operators corresponding to kinetic energy, electron–nuclear attraction (for the classical nuclei only), and electron–electron repulsion, respectively. Operators , , and represent the analogous quantities for the quantum protons. Finally, is the operator corresponding to the electron–proton Coulomb interaction. Simultaneous mean-field descriptions of both the electrons and the quantum protons results in the NEO-Hartree–Fock ansatz,471 but unfortunately the omission of electron–proton correlation effects makes this model inadequate for predictions of reliable energies or geometries.472 The rest of this section describes DFT-based alternatives.
1. NEO-DFT
The NEO-DFT method is a multicomponent extension of the conventional electronic DFT formalism, in which different types of particles (e.g., electrons and protons) are treated quantum mechanically.491–493 Similar to NEO-HF, the NEO-DFT Kohn–Sham wave function is the product of electronic and protonic Slater determinants composed of the Kohn–Sham spin orbitals. The NEO-DFT energy is
| (28) |
Here, Eext[ρe, ρp] is the interaction of the electronic and protonic densities, ρe and ρp, with the external potential created by the classical nuclei. The term Eref[ρe, ρp] contains the electron–electron, proton–proton, and electron–proton classical Coulomb energies, as well as the noninteracting kinetic energies of both electrons and quantum protons. The final three terms are electron–electron XC, proton–proton XC, and electron–proton correlation functionals. Variational minimization of the NEO-DFT energy with respect to the densities leads to two sets of coupled Kohn–Sham equations for electrons and protons, which are strongly coupled and must be solved together self-consistently.
Implementation of the NEO-DFT method requires the functionals in Eq. (28). Within this framework, any conventional electron–electron XC functional can be employed.477 Due to the local nature of the quantum protons in molecular systems, the proton–proton XC energies are negligible,472 but the Hartree–Fock proton–proton exchange is included. The electron–proton correlation (epc) functional is essential for accurate calculations of proton densities and energies. The epc17 (LDA form)475,476 and epc19 (GGA form)478 functionals were formulated as extensions of the Colle–Salvetti formalism for electron–electron correlation494,495 to the case of electron–proton correlation. These functionals are designed to accurately describe proton densities and energies of molecular systems.
The importance of electron–proton correlation for the prediction of accurate proton densities is shown in Fig. 21 for the FHF− molecular ion, where results from NEO-DFT with several different electron–proton correlation treatments are compared to a near-exact result computed using the Fourier grid method.496–498 In the absence of electron–proton correlation (NEO-DFT/no-epc in Fig. 21), the proton density is much too localized, similar to NEO-HF results. Inclusion of electron–proton correlation using either the epc17-2 functional475,476 or the epc19 functional478 significantly improves the proton densities.
FIG. 21.
(a) On-axis and (b) off-axis proton density for FHF− computing using NEO-DFT with no electron–proton correlation and two different electron–proton correlation functionals, in comparison to a grid-based reference calculation. All calculations use the B3LYP electronic functional, def2-QZVP electronic basis set,75 and an even-tempered 8s8p8d protonic basis set. Adapted with permission from Pavošević et al., Chem. Rev. 120, 4222 (2020). Copyright 2020 American Chemical Society.
In addition to accurate proton densities, these two epc functionals were shown to predict accurate proton affinities for a diverse set of molecules composed of amines, carboxylates, aromatics, and inorganic species.476,478 Because the NEO-DFT method inherently includes the zero-point energy contributions from the quantum protons, the proton affinity of molecule A is simply
| (29) |
where EA is the energy of A computed with conventional DFT and is the energy of the protonated species calculated using NEO-DFT. This procedure does not require the calculation of computationally expensive Hessians because the zero-point energy contributions from the other nuclei have been shown to be negligible due to cancellation.480 Moreover, the NEO-DFT method includes the anharmonic effects associated with the quantized proton.
Analytic geometry gradients for the NEO-DFT method with the epc17-2 and epc19 functionals allow geometry optimizations that include the effects of proton delocalization, anharmonicity, and zero-point energy. Figure 22 shows that the NEO-DFT/epc17-2 method accurately predicts the increased F–F bond length in the FHF− ion, which is shifted by ≈0.02 Å due to proton quantization.476 The NEO-DFT/epc17-2 method has been used to optimize the geometries of protonated water tetramers with all nine protons treated quantum-mechanically and correctly predicts the energetic ordering of the four isomers.490
FIG. 22.
Energy as a function of F–F distance for FHF−, comparing conventional DFT and NEO-DFT results to a grid-based reference. Quantization of the proton increases the equilibrium F–F distance. These calculations were performed using the B3LYP electronic functional, the def2-QZVP electronic basis set, and an even tempered 8s8p8d protonic basis set. Data are from Ref. 476.
The NEO-HF, NEO-DFT/no-epc, NEO-DFT/epc17-2, and NEO-DFT/epc19 methods are available in Q-Chem 5 in both restricted and unrestricted formalisms. The quantum protons are always assumed to be high-spin. Analytic gradients are available for each of these methods, enabling geometry optimizations. The user must specify the quantum protons, the electronic and protonic basis sets,475,483,499 and the electron and electron–proton correlation functionals.
2. NEO-TDDFT
NEO-TDDFT is a multicomponent extension of conventional electronic LR-TDDFT that allows for the simultaneous calculation of electronic and protonic (vibrational) excitation energies,479 as depicted in Fig. 23. The formalism follows from the linear response of the NEO Kohn–Sham equations to an external perturbation, and NEO-TDDFT excitation energies Ω are obtained by solving the following multicomponent equation:479
| (30) |
The matrices Ae, Be, Xe, and Ye are analogous to the orbital Hessians (A and B) and response amplitudes (X and Y) that appear in conventional LR-TDDFT,114,115 albeit with an additional term associated with electron–proton correlation in Ae and Be. The quantities Ap, Bp, Xp, and Yp are their protonic counterparts. The quantity C is a coupling matrix that includes terms associated with electron–proton Coulomb interactions and electron–proton correlation.
FIG. 23.
(a) Schematic depiction of the electronic and proton vibrational excitations obtained from a single NEO-TDDFT calculation. (b) Transition densities for the bend and stretch modes of FHF−. Panel (a) is reproduced with permission from Yang et al., J. Phys. Chem. Lett. 9, 1765 (2018). Copyright 2018 American Chemical Society. Panel (b) is reproduced from Culpitt et al., J. Chem. Phys. 150, 201101 (2019) with the permission of AIP Publishing.
NEO-TDDFT predicts proton vibrational excitation energies that are in a good agreement with grid-based reference values for the fundamental vibrational modes.483,484 The electronic excitation energies for the lower electronic states are similar to those obtained with conventional electronic LR-TDDFT,479 but vibronic mixing is found to impact the electronic excitation energies for some of the higher electronic states.486 The Tamm–Dancoff approximation114 can be applied to Eq. (30), eliminating the Ye and Yp amplitudes, though the resulting NEO-TDA method tends to significantly overestimate proton vibrational frequencies.479
The NEO-TDDFT, NEO-TDHF, NEO-TDA, and NEO-CIS methods are available in Q-Chem 5 in both restricted and unrestricted versions. The quantum protons are always assumed to be high-spin. These methods provide electronic, proton vibrational, and electron–proton (vibronic) excitation energies.
VI. MODELING THE ENVIRONMENT
Most chemistry occurs in the condensed phase, and 21st-century quantum chemistry is characterized by a variety of increasingly sophisticated theoretical models to describe the extended environment around a smaller part of the system that is modeled in detail using electronic structure theory. The simplest approach to modeling a solution-phase molecule is to replace vacuum boundary conditions with dielectric continuum boundary conditions.500,501 Section VI A highlights some continuum methods that are new in Q-Chem 5, including capabilities for describing solvent effects on spectroscopy (vertical excitation and ionization energies) and for using a continuum model to describe an anisotropic solvation environment, such as an air/water or aqueous/organic interface.
Hybrid quantum mechanics/molecular mechanics (QM/MM) methods represent a higher degree of sophistication that allows the environment to have atomistic structure, although this necessitates sampling over those atomistic degrees of freedom, at increased cost. Available QM/MM functionality, including interfaces with various MM software packages, is described in Sec. VI B. Taking this one step further, one can imagine “QM/QM” methods that describe the environment at a lower but still quantum level of theory. Historically, this was often accomplished via “subtractive” approaches,502,503 as pioneered by Morokuma and co-workers in the “ONIOM” scheme,504 but more recently there is growing interest in QM/QM embedding schemes that stitch together two levels of theory in a potentially more natural way. For this purpose, Q-Chem contains a version of projection-based embedding505,506 that is described in Sec. VI C. Finally, for a homogeneous QM description of a system that is too large to be tackled in a straightforward way, one can turn to fragmentation methods,507 a few of which are described in Sec. VI E.
A. Continuum solvation models
Dielectric continuum models represent a form of implicit solvation that sidesteps configurational averaging over solvent degrees of freedom, as that averaging is contained (implicitly) within the value of the solvent’s static or zero-frequency dielectric constant, ɛ0. Within quantum chemistry, the oldest of these models are the polarizable continuum models (PCMs),508 but historically the best black-box solvation models are the “SMx” models developed by Cramer and Truhlar.509 See Refs. 501 and 510 for a discussion of the similarities, differences, and nuances of these various models. Q-Chem 5 contains a range of these models,511 built upon a smooth discretization procedure for the cavity that defines the interface between the atomistic solute and the structureless continuum.511–515 This procedure eliminates numerical artifacts such as discontinuities in the potential energy surface, which can appear in some implementations.511–513
1. Models for solvation energies
Q-Chem includes the SM8,516 SM12,517 and SMD518 variants of SMx, where the “D” in SMD stands for “density”. Of these, SMD is perhaps the most interesting because it uses density-based electrostatic interactions based on a PCM, and is available (with analytic gradient) in arbitrary basis sets. In addition to these models, Q-Chem 5 also includes the “composite model for implicit representation of solvent” (CMIRS) approach, originally developed by Pomogaeva and Chipman,519–522 and later modified by You and Herbert.523 CMIRS is designed as a less-empirical continuum solvation model and uses dramatically fewer parameters as compared to the SMx models, although the trade-off is that it is presently parameterized for only a few solvents. For the important case of aqueous solvation, error statistics (versus experiment) for small-molecule hydration energies ΔhydG° are provided in Table I, and these statistics demonstrate that CMIRS outperforms the SMx models for ions in aqueous solution. The dataset is the Minnesota solvation database,518,524,525 for which the error bars on the single-ion hydration energies are estimated to be ±3 kcal/mol.525 This means that the CMIRS model has reached the limit of the accuracy of the experimental data against which all of the models in Table I were parameterized.
TABLE I.
Mean unsigned errors (MUEs) for hydration energies ΔhydG° using continuum solvation models.a
| MUE (kcal/mol) | ||||
|---|---|---|---|---|
| Datasetb | N data | SM12 | SMD | CMIRS |
| Neutrals | 274 | 1.3 | 0.8 | 0.8 |
| Cations | 52 | 3.5 | 3.4 | 1.8 |
| Anions | 60 | 3.8 | 6.3 | 2.8 |
| All ions | 112 | 3.7 | 4.7 | 2.4 |
Computed at the B3LYP/6-31G* level, from Ref. 501.
Minnesota solvation database.518,524,525
CMIRS uses an isocontour of the solute’s electron density ρ(r) to define the cavity surface,526 which is therefore defined in terms of a single empirical parameter and is pleasantly free of other parameters such as atomic van der Waals radii. The disadvantage is that the isodensity construction lacks analytic energy gradients, which are available in Q-Chem 5 for SMD. In Q-Chem, the self-consistent reaction field problem defined by the continuum model can be iterated to self-consistency with any SCF level of theory. For post-Hartree–Fock methods, the use of solvent-polarized MOs in the subsequent electron correlation calculation affords a “zeroth-order” correction for solvation effects that is probably accurate to within the limitations of the continuum approach itself.501
There is significant confusion in the literature regarding terminology for continuum solvation models.501,510 PCMs themselves are electrostatics-only models,501 which must be augmented with nonelectrostatic contributions (Pauli repulsion, dispersion, cavitation, etc.) in order to model solvation energies. Models for these nonelectrostatic contributions to ΔsolvG° are included as part of the SMx and CMIRS solvation models but are not included in PCMs. Even relatively sophisticated electrostatics treatments, such as the “integral equation formulation” (IEF-PCM)508 and the closely related “surface and simulation of volume polarization for electrostatics” [SS(V)PE] model,527,528 are electrostatics-only descriptions of solvation, as is the much simpler “conductor-like screening model” (COSMO),529,530 which often affords results quite similar to IEF-PCM and SS(V)PE.531 All of these models are available in Q-Chem; see Ref. 501 for a detailed comparison of them. While not appropriate for computing ΔsolvG°, a PCM alone can still be useful for spectroscopic applications, where the frontier orbital energy levels are modified by the dielectric continuum and this is reflected in the computed excitation energies. Application of PCMs to solvatochromic shifts is discussed next.
2. Nonequilibrium models for vertical excitation and ionization
What is the appropriate manner to describe a sudden change in the solute’s electron density, which occurs upon electronic excitation or ionization, within a continuum representation of the solvent? A simple approach is to partition the solvent polarization into “fast” (electronic) and “slow” (nuclear) components and assume that the former responds instantaneously but that the latter is frozen and remains polarized with respect to the initial state.532–535 The slow polarization is therefore out of equilibrium with the solute’s electrons, and such approaches are known as nonequilibrium solvation models.501 Within this approach, the solvent’s frequency-dependent permittivity ɛ(ω) is modeled using only its ω = 0 limit (the static dielectric constant, ɛ0) and its ω → ∞ limit (the “optical” dielectric constant, ɛ∞). The latter is equal to the square of the solvent’s index of refraction (), with values in the range ɛ∞ = 1.8–2.5 for common solvents.501
For an electronic transition from initial state |Ψ0⟩ to final state |Ψk⟩, the Schrödinger equation that one would like to solve is
| (31) |
where is the vacuum Hamiltonian and is the reaction-field operator, partitioned into a “slow” initial-state component , representing polarization using wave function |Ψ0⟩ and dielectric constant ɛ0, and a “fast” final-state component , representing polarization using wave function |Ψk⟩ and dielectric constant ɛ∞.501 The state-specific nature of the Hamiltonian in Eq. (31) is problematic, however.536 A simple solution is to treat using first-order perturbation theory in a basis of mutually orthogonal eigenstates of . This has been called the perturbation theory state-specific (ptSS) approach to nonequilibrium solvation.537–539 When applied to the CIS-like eigenvalue problem that defines LR-TDDFT, the ptSS approach is closely related to the “corrected LR” approach of Caricato et al.;540 see Ref. 501 for details.
The ptSS model for solvatochromic shifts is available in Q-Chem 5 for LR-TDDFT537,538 and ADC methods.538,539 Figure 24 shows some results for a set of nitrobenzene derivatives, with excitation energies computed at the ADC(2) level. The ptSS-PCM solvatochromic shifts compare very well with experiment, and the details of how electron correlation contributions are included in the excited-state density (iteratively alongside the PCM correction or not) matter very little.539 In conjunction with LR-TDDFT, the ptSS-PCM approach can also be applied to emission and photoelectron spectroscopies.537 In the latter case, nonequilibrium effects of 0.5–1.0 eV on vertical ionization energies (VIEs) have been documented.541–543 The nonequilibrium corrections are not yet available for other kinds of excited-state methods (such as EOM-CC), but in those cases, one can still include zeroth-order solvation effects simply by using solvent-polarized Hartree–Fock orbitals in the correlated calculation.
FIG. 24.
Solvatochromic shifts in the lowest 1ππ* state for derivatives of nitrobenzene (PhNO2) in different solvents, comparing experimental values to those computed at the ADC(2) level using the ptSS-PCM approach.538 The PTE, PTD, and PTD* variants represent slightly different ways of treating the correlated excited-state density.501,539 Adapted with permission from Mewes et al., J. Phys. Chem. A 119, 5446 (2015). Copyright 2015 American Chemical Society.
3. Poisson–Boltzmann approach for arbitrary dielectric environments
The solvation models discussed above are designed for the isotropic environment of a bulk solvent, in which case the solvent is characterized by a scalar dielectric constant and Poisson’s equation (which defines the continuum electrostatics problem) can be replaced by a more efficient PCM formalism.501 However, if the environment is anisotropic (at an interface, for example), then the continuum electrostatics problem is defined instead by the generalized Poisson equation
| (32) |
in which ɛ(r) is an inhomogeneous permittivity function and ρsol(r) is the charge density (nuclei + electrons) of the atomistic solute that is described using quantum chemistry. The solution of Eq. (32) is more expensive than a PCM calculation because it requires discretization of three-dimensional space, but an advantage of the three-dimensional approach is that it provides an exact solution (within the model problem defined by a continuum environment) for the “volume polarization” that arises when the tail of the solute’s charge density penetrates beyond the cavity.501,544,545 Equation (32) can also be modified to include the effects of ionic strength (Poisson–Boltzmann equation).501,546
Q-Chem 5 includes a generalized Poisson equation solver (PEqS) for Eq. (32) and the analogous Poisson–Boltzmann equation.542,546 For isotropic solvation, ɛ(r) can be designed to interpolate smoothly across the atomic van der Waals radii, between a “vacuum” value ɛ = 1 in the atomistic (quantum chemistry) region and a bulk solvent value outside of that region. A similar construction can be used to obtain a continuum model for the air/water interface,541–543 as shown schematically in Fig. 25. Other permittivity models ɛ(r) have been constructed to describe host/guest systems, where the inside of a molecular capsule screens a guest molecule from the high-dielectric solvent outside, with consequences for the spectroscopy of the guest.547
FIG. 25.
Illustration of an anisotropic permittivity function ɛ(r) for the air/water interface. The atomistic solute is Cl(H2O)30, which amounts to two solvation shells around the ion. Adapted with permission from J. M. Herbert, Wiley Interdiscip. Rev.: Comput. Mol. Sci. 11, e1519 (2021). Copyright 2021 John Wiley and Sons.
The nonequilibrium ptSS formalism for ionization537 (Sec. VI A 2) has also been formulated for use with generalized Poisson boundary conditions,541,542 and this ptSS-PEqS approach has been used to compute solution-phase VIEs, including those for ions at the air/water interface.541–543 These applications require the use of some explicit water molecules in the atomistic QM region, as shown in Fig. 25. However, whereas aqueous VIEs are notoriously slow to converge, often requiring >500 explicit water molecules,548–555 the use of continuum boundary conditions leads to converged results using only about two solvation shells of explicit water.541,543 Importantly, only the nonequilibrium version of continuum solvation affords VIEs in agreement with experiment.501,543 The equilibrium PCM approach may be adequate for adiabatic ionization energies but lacks the correct physics to describe vertical excitation or ionization.501
B. QM/MM methods
By itself, Q-Chem contains some limited functionality for QM/MM simulations using standard non-polarizable force fields. This functionality does include periodic boundary conditions for solution-phase QM/MM calculations,556,557 and these features have been used to simulate the electronic spectroscopy of aqueous chromophores,558 including solvated electrons and other aqueous radicals.466,557,559–562 A QM/MM model for physisorption, inspired by dispersion-corrected DFT, is new in Q-Chem 5.563
For QM/MM calculations with polarizable force fields, Q-Chem can perform calculations using the effective fragment potential (EFP) method,564 a QM-derived polarizable force field.564–566 QM/EFP calculations can be performed through an interface between Q-Chem and the open-source libefp library.11,565 As in previous versions of Q-Chem, QM/EFP calculations are supported at QM levels of theory, including EOM-CC, CIS(D), and LR-TDDFT for excited-state calculations;567 in Q-Chem 5, support has been added for ADC/EFP568 and for two-photon absorption calculations using EOM-CC/EFP.569
Even more flexibility with respect to polarizable force fields is provided by the polarizable embedding (PE) framework,570 calculations with which are enabled via an interface between Q-Chem and the open-source cppe library.14 PE/SCF calculations are currently enabled for all ground-state SCF methods, and excited-state calculations can be performed at the PE/ADC level.14 The latter method has been used to tackle excited states of large biomolecular systems.571
For many biomolecular QM/MM applications, it is crucial to have sophisticated tools for visualization and manipulation of coordinates and trajectory data, as well as access to advanced methods for sampling potential energy surfaces. For these purposes, Q-Chem includes interfaces to several popular MM software packages, which serve as front-end drivers to Q-Chem’s computational quantum chemistry engine. An interface to the CHARMM program572 has long been a part of Q-Chem,573 which can also be accessed via the “CHARMMing” web portal.574,575 New in Q-Chem 5 are interfaces to the GROMACS576 and NAMD577 classical molecular dynamics programs. The GROMACS interface, in particular, supports nonadiabatic trajectory surface-hopping simulations at the CIS and LR-TDDFT levels of theory, including SF-TDDFT (see Sec. II C 2), with GROMACS as the driver for the dynamics. Some tools for “QM-cluster” modeling578 of enzyme active sites are also available in Q-Chem itself.579
C. Embedding methods
Taking one step further than QM/MM, one can employ a cost-effective QM theory to describe the environment. The projection-based QM embedding theory505,506 provides a robust and formally exact approach to partition a chemical system into two subsystems (A and B) that are treated at two different levels of QM theory. Typically a small, chemically important part of the system (A) is described by a correlated wave function theory (WFT, e.g., MPn or CC), while its environment (subsystem B) is described using DFT. This scheme goes beyond the electrostatic embedding formalism that is common in ONIOM-style treatments,504 as the interaction between the two subsystems is described at the DFT level and is therefore fully quantum-mechanical. Q-Chem 5’s implementation of projection-based embedding supports the use of a myriad of WFT/DFT combinations, thanks to its broad coverage of these two families of electronic structure methods.
A WFT(A)-in-DFT(B) calculation comprises the following steps:
-
•
Converge the SCF calculation for the full system at the DFT level of theory.
-
•
Partition the occupied orbitals by localizing the canonical MOs and assigning the localized MOs to subsystems A and B.
-
•
Perform the WFT calculation for the embedded subsystem A, which means performing a Hartree–Fock calculation followed by a correlated wave function calculation using the MOs for A.
In the final step of this procedure, the MOs assigned to subsystem B remain frozen and are employed to construct a projection operator that enforces orthogonality between the MOs of A and B when the former’s MOs are being re-optimized. Meanwhile, the “environment” subsystem (B) affects the QM calculation of A by contributing an embedding potential to the one-electron Hamiltonian of A, which comprises the Coulomb and XC interactions between two subsystems.
Compared to the original formulation of the projection-based embedding theory,505 the implementation in Q-Chem 5 has (i) replaced the use of a somewhat arbitrary level-shift parameter with a strict projection scheme; (ii) implemented the subsystem-projected atomic orbital decomposition (SPADE) partition of the occupied space,580 which is more robust than the original scheme based on the Pipek-Mezey localization procedure;581 and (iii) includes a “concentric localization” scheme to truncate the virtual space with systematically improvable accuracy.582 Truncation of the virtual space is essential to reducing the cost of a WFT-in-DFT calculation (relatively to a full WFT treatment), especially for CC methods whose cost increases steeply with the number of virtual orbitals.
Besides the projection-based embedding theory, other notable QM/QM embedding schemes that are available in Q-Chem 5 include frozen-density embedding,583–587 embedded mean-field theory,588 and the related polarized many-body expansion (MBE) scheme.589
D. Molecules under pressure
Q-Chem includes methods to incorporate the effects of hydrostatic pressure or mechanical forces on molecular structures in geometry optimizations and ab initio molecular dynamics simulations. The application of mechanical forces to molecules is modeled by the “external force is explicitly included” approach.590 Application of pressure can be modeled either by the hydrostatic compression force field approach,591 in which forces point toward the molecular centroid, or via a more refined algorithm, in which mechanical forces are applied perpendicular to the molecular van der Waals surface.592 These methods can be deployed in combination with any electronic structure method for which nuclear gradients are available, with no additional computational overhead. Benchmarks show that physically sound geometries are retained even at high pressure.592 A more sophisticated approach for applying pressure to chemical systems is the Gaussians on surface tesserae simulate hydrostatic pressure (GOSTSHYP) algorithm.593 This approach uses Gaussian potentials that are distributed evenly on the discretized molecular van der Waals surface to compress the electron density and affords accurate results for energies, structural parameters, dipole moments, and chemical reactions under pressure.593 GOSTSHYP energies and gradients are currently implemented only at the SCF level, enabling Hartree–Fock and DFT calculations of compressed atoms and molecules.
E. Fragment-based methods
Fragmentation methods507 seek to sidestep the steep nonlinear scaling of traditional quantum chemistry by sub-dividing a large system into small pieces that can be tackled more tractably by means of distributed computing. Although a plethora of approaches have been discussed in the literature,507,594 they are most often implemented at the level of external scripts or driver programs and only a few of them are tightly integrated with Q-Chem itself. A few of these are discussed in the present section, including a general-purpose n-body expansion for ground-state energies, an ab initio exciton model for representing delocalized excited states in a basis of fragment-localized excitations, and finally a scheme for computing energy-transfer couplings. The energy decomposition methods that are described in Sec. VII can also be considered as examples of fragment-based methods but are discussed separately.
1. Many-body expansion
A simple and straightforward method is the many-body expansion (MBE),595–601
| (33) |
which accounts incrementally for two-body interactions (ΔEIJ = EIJ − EI − EJ), three-body interactions (ΔEIJK), etc. Both the MBE and its analytic gradient are available in Q-Chem 5 for ground-state energies of fragments that are not covalently bonded to one another. MBE calculations can be parallelized using either OpenMP (across a node) or MPI, though not both.
Careful analysis of the n-body expansion suggests that ostensibly slow convergence is sometimes an artifact of basis-set superposition error (BSSE).598–600,602–604 To avoid this, many-body counterpoise corrections are available,598,599 which are consistent order-by-order with Eq. (33).
2. Ab initio exciton model
The Frenkel exciton model605 is an old idea to represent collective, delocalized excitations in multi-chromophore systems using direct-product basis states in which a single monomer is excited,
| (34) |
The advantage of this “site-basis” is that ground- and excited-state monomer wave functions (|ΨX⟩ and , respectively) can be computed independently of one another, and applications to very large aggregates are feasible by means of distributed computing.141 The model is completed by computing matrix elements between the direct-product basis states, e.g., , and also the corresponding overlap integrals because basis functions computed on different monomers are not orthogonal. Addition of higher-lying excited states adds variational flexibility to the ansatz in Eq. (34), and one solves a generalized eigenvalue problem whose dimension is a few times the number of sites, depending on how many excitations are included per monomer.
Historically, it is common to invoke a dipole-coupling approximation to evaluate matrix elements of , and this approximation continues to be made even in modern implementations.606–608 The dipole approximation may be satisfactory to describe energy transfer between well-separated chromophores but is questionable under crystal-packing conditions, as in organic photovoltaic materials. The dipole-coupling approximation is not required, and in the ab initio Frenkel exciton model developed by Morrison and Herbert,141,609–611 these matrix elements are evaluated exactly, within a single-excitation ansatz for the monomer excited states,
| (35) |
Here, represents a singly excited Slater determinant composed of MOs on monomer X. This is consistent with either a CIS or a LR-TDDFT calculation for each monomer, incorporating as many individual states as desired. In this way, the ab initio exciton model can be viewed as a specialized form of nonorthogonal configuration interaction in a customizable diabatic basis.
Using this flexibility, the ab initio exciton model has been used to study the singlet fission process in organic photovoltaics,89,611,612 meaning the spin-allowed formation of a pair of triplet charge carriers (T + T) via one-photon excitation,
| (36) |
The intermediate “multi-exciton” state 1(TT), involving triplet states on two different chromophores that are spin-coupled to a singlet, is challenging to describe using standard quantum chemistry because it involves a true double excitation,613,614 and such states are absent from conventional LR-TDDFT.194 Within the ansatz in Eq. (34), however, the 1(TT) state simply involves a pair of single excitations with appropriate Clebsch–Gordan coefficients to couple them.89,612 The importance of charge-transfer excitons can be interrogated as well, simply by including basis states involving ionized monomers.612 In this way, the ab initio exciton model allows one to construct a tailored diabatic basis, letting Schrödinger’s equation decide which basis states are important. Calculations on cluster models of crystalline pentacene have helped to resolve a long-standing debate about the presence of charge-separated states in the low-energy optical spectrum of this material.89
Analytic derivative couplings ⟨ΞI|(∂/∂x)|ΞJ⟩ between excitonic states are also available.611 The key ingredient in these couplings are derivatives of the matrix elements of in the exciton site-basis, e.g.,
| (37) |
Following a transformation from nuclear Cartesian coordinates to normal modes (x → Q), the quantities are essentially the linear exciton–phonon coupling parameters gABθ that appear in the phenomenological Holstein–Peierls Hamiltonian.615 The diagonal coupling parameters gAAθ are the “Holstein couplings” that describe how the site energies are modulated by phonons θ, whereas the off-diagonal couplings gABθ are the “Peierls couplings” that quantify how the energy-transfer integrals HAB are coupled to the phonons.611 Often these are treated as phenomenological parameters, but the ab initio exciton model affords a means to compute them from first principles. This can be used for a priori identification and characterization of the vibrational modes that couple strongly to excitation energy transfer (EET). An example is shown in Fig. 26 for crystalline tetracene, a singlet fission material, where the ab initio exciton model identifies several localized vibrational modes on the tetracene monomers that strongly modulate the energy-transfer dynamics.611,612
FIG. 26.
Holstein coupling parameters for crystalline tetracene, obtained from an ab initio exciton calculation of for the unit cell projected onto phonon modes from a periodic DFT calculation. The couplings are plotted as relaxation energies , where ωθ is the phonon frequency, and indicate several modes that strongly modulate the site energies. Peierls couplings for this system are several orders of magnitude smaller; see Ref. 611. Adapted from A. F. Morrison and J. M. Herbert, J. Chem. Phys. 146, 224110 (2017) with the permission of AIP Publishing.
3. Excitation energy transfer couplings
The ab initio exciton model described above represents one means to compute EET couplings, but alternative methods exist.616 One of these is the fragment excitation difference (FED) scheme, an extension of the fragment charge difference (FCD) method.617 In the FED approach, the charge density difference in FCD is replaced by an excitation difference density operator (i.e., the sum of electron and hole densities created upon excitation). Within a single excitation theory such as CIS, one can easily obtain analytic expressions for the matrix elements of the excitation density. However, for multi-excitation wavefunctions, no simple expressions exist for the off-diagonal elements. To circumvent this problem, a new scheme was developed known as θ-FED.618,619 In this approach, the diabatic states are assumed to be functions of a mixing angle θ; thus, the difference density Δx depends on θ as well. In order to obtain “ideal” diabatic states, the angle θ is scanned from −π/4 to π/4 in order to maximize the difference of the excitation,
| (38) |
with i and f indicating the initial and final diabatic states. The corresponding θ-dependent coupling can then be written as
| (39) |
where Em and En are the excitation energies for the two adiabatic states in question.
For wave functions consisting only of single excitations, it has been demonstrated that this generalized θ-FED scheme provides results identical to the original FED,618 but the former can be extended beyond CIS. In Q-Chem 5, the θ-FED scheme is implemented for both CIS and XCIS,620 as well as RAS-CI.285
VII. ANALYSIS
Q-Chem offers numerous tools to aid interpretation of ab initio calculations and to provide conceptual insights. Some of the more popular ones include natural bond orbital (NBO) analysis,621 along with wave function (orbital and density matrix) analysis,88,269,622 provided by the libwfa module.15 Some recent applications of these tools have been highlighted in Sec. III B, so the present section will focus specifically on a different topic, namely, methods for energy decomposition analysis (EDA).
Successful quantum chemistry calculations are akin to numerical experiments, whose physical or chemical interpretation remains a separate problem. To address this problem in the context of intermolecular interactions, EDA methods seek to partition the intermolecular interaction energy between a collection of molecules (or “fragments,” as in Sec. VI E) into physically meaningful components. Two separate approaches for intermolecular EDA are available in Q-Chem 5, one based on variational minimization with constraints, via absolutely localized MOs (the ALMO-EDA scheme,623 Sec. VII A), and another based on symmetry-adapted perturbation theory (SAPT),624 as described in Sec. VII B.
A. ALMO-EDA method
The ALMO-EDA scheme identifies contributions to the intermolecular interaction energy by performing variational minimization of the supramolecular DFT energy in the presence of constraints that first prevent polarization and charge transfer (CT), then prevent only CT, and finally with all constraints released. The total DFT interaction energy for a collection of fragments F,
| (40) |
is partitioned according to
| (41) |
The geometric distortion energy (ΔEGD ≥ 0) is the penalty to distort the fragments from their isolated structures to the geometry of the intermolecular complex. The frozen energy change (ΔEFRZ) is the net effect of permanent electrostatics, Pauli repulsion, and dispersion. ΔEPOL is the energy lowering due to electrical polarization (constrained to prevent charge delocalization). Finally, ΔECT is the stabilization due to electron delocalization from one fragment to another,625 which is automatically corrected for BSSE in Q-Chem. Key advantages of the variational supramolecular approach include (i) immunity from any convergence questions of perturbation theory and (ii) the ability to select the best density functional for the problem at hand (the theory is applicable, in principle, to the exact density functional, though sadly, it remains unavailable).
Q-Chem 5 contains the latest (second-generation) version of the ALMO-EDA,626,627 which includes several significant improvements over the original version.628,629 A detailed discussion of the theory can be found elsewhere,623 but the following two major improvements warrant specific mention:
-
1.
The polarization energy is defined in a new way that is largely independent of details of the atomic orbital basis set and has a useful complete-basis limit. Intra-fragment relaxation of the frozen orbitals is accomplished by allowing them to mix with fragment-specific electric response functions (FERFs).630 These are the virtual orbitals that exactly describe the linear response of the frozen orbitals to uniform electric fields (which requires three dipolar FERFs per occupied orbital) and the spatial gradients of those fields (which requires an additional five quadrupolar FERFs per occupied orbital). The mixing between frozen orbitals and FERFs on each fragment minimize the energy of the complex subject to the constraint of no charge flow between fragments, using the SCF for the molecular interactions (SCF-MI) procedure.631
-
2.
The frozen energy change can be decomposed into contributions from its three underlying components: permanent electrostatics, Pauli repulsion, and dispersion.632 The dispersion contribution is separated with the aid of a “dispersion-free” density functional, e.g., Hartree–Fock theory in the case that an RSH functional such as ωB97X-V or ωB97M-V is used to compute EFULL. Electrostatics can be separated using the traditional quasi-classical definition of the electrostatic interaction between isolated fragments, and what remains is identified as Pauli repulsion.633 This traditional approach may be appropriate for force field assessments because fragment densities do not change as the complex is rearranged, but a quantum-mechanically correct alternative definition is also available, wherein the fragment densities deform so as to sum to the total frozen density.632
The well-behaved separation of an interaction energy into physically interpretable contributions has permitted use of the ALMO-EDA to assess polarizable force fields633,634 and, recently, to develop a highly accurate polarizable force field for water.635
An important new capability is that ALMO-EDA is properly integrated with Q-Chem’s polarizable continuum models (PCMs) of solvent,511–513 specifically C-PCM and IEF-PCM, which are electrostatics-only, and also SMD518 (see Sec. VI A 1). This ALMO-EDA(solv) model636 is a significant new capability because the solvent can exert both qualitative and quantitative effects on the binding of a complex. For example, electrostatic interactions may be screened by high-dielectric solvents such as water, whose polarity may also permit larger polarization and/or CT interactions by stabilizing the resulting deformed densities. An example of the application of ALMO-EDA(solv) to a CO2 reduction catalyst (in acetonitrile solution) is presented in Fig. 27, illustrating the effects of different substituent groups toward stabilizing binding of an activated CO2 substrate.636
FIG. 27.
ALMO-EDA(solv) results for the additional binding of CO2 when two positively charged substituents (tetramethylammonium, TMA, and an imidazolium-carrying group denoted as “imid”) are introduced at the ortho position of the meso-phenyl group in FeTPP, a promising molecular catalyst for CO2 reduction. Compared to unsubstituted FeTPP, the o-TMA groups stabilize CO2 mainly by alleviating the Pauli repulsion between CO2 and the FeTPP core, while the o-imid groups stabilize CO2 primarily through attractive Coulomb interactions. The solvent is acetonitrile (modeled using C-PCM with ɛ = 35.88), and the calculations were performed at the ωB97X-V/def2-TZVPP level of theory.636
In addition, many useful visualization tools are available in conjunction with ALMO-EDA calculations, including the automatic generation of significant complementary occupied-virtual pairs (COVPs)629,637 for characterizing charge transfer between fragments, electron density difference (EDD) plots between different intermediate stages of ALMO-EDA, and its further partition into natural orbitals for chemical valence (NOCV) pairs.638 Beyond SCF methods, ALMO-EDA is also available at the MP2 level for both closed- and open-shell reference determinants.639–641 Beyond ground states, ALMO-EDA can be used to analyze excited states of intermolecular complexes (excimers and exciplexes) at the level of either CIS or LR-TDDFT.642,643
One of the traditional criticisms of EDA techniques is that the energy components themselves are not observables,644,645 so there is some arbitrariness in their definitions. A substantive step to address this issue has been taken with the introduction of an adiabatic EDA (aEDA),646 where observable quantities such as structure and vibrational frequencies are computed on the potential energy surface belonging to each constrained energy. These include the frozen energy (EFRZ), the polarized energy (EPOL), and the individual fragment energies, {EF}, as well as the final unconstrained supramolecular energy EFULL. This enables calculation of negative semidefinite aEDA energy components,
| (42) |
The components in Eq. (42) are given as the energy difference between the optimal structures in each consecutive pair of states. For example, if the optimized structures on the FRZ and POL surfaces are denoted as RFRZ and RPOL, then
| (43) |
Shifts in structures, vibrational frequencies, etc., can be associated with each of the EDA components so that, for example, the difference RPOL −RFRZ demonstrates the effect of polarization on geometry. The example in Fig. 28 illustrates that the redshift of the hydrogen-bonded O–H stretch in the water dimer is primarily associated with CT.
FIG. 28.
Adiabatic EDA (aEDA) for the water dimer. (a) Comparison of aEDA components vs the conventional (vertical) EDA components. (b) Illustration of the water dimer showing two of the key geometric parameters, whose values at each level of the aEDA are reported in (c). It is striking that linearity of the hydrogen bond is already present at the frozen energy optimization (i.e., it is not critically dependent on polarization or CT) and also striking that the redshift in the proton donor O–H stretch can be directly associated with CT.
Closely related to the aEDA is the possibility of separately assessing the energetic and observable effects of forward and backward CT, which can be accomplished via a variational forward–backward (VFB) scheme.641 The VFB approach uses a generalized SCF-MI method that can disable either forward- or back-donation effects in DFT calculations, thus enabling one to assess the individual role of each, on both the interaction energy but also structure and vibrational frequencies (by performing optimization on the constrained surfaces, as in the aEDA).646 This VFB approach is a powerful tool that has been applied to assess the character of a variety of interesting bi-directional metal–ligand interactions, including the novel ligand BF (iso-electronic to CO and N2) and also BeO and BeCO3 interactions with CO.641
Finally, the ALMO-EDA can be employed for analysis of single chemical bonds,647,648 yielding a fingerprint picture of the chemical bond in terms of energy components. Development of the bonded ALMO-EDA required generalization of the frozen orbital interaction to include the energy lowering associated with spin-coupling of two unpaired electrons, generalization of the geometric distortion term (to become a “preparation energy” that includes the electronic energy cost of hybridizing the orbitals), and finally generalization of the polarization term to include the energy lowering associated with orbital contraction. The latter requires the use of monopolar FERFs.649 One interesting use of the bonded ALMO-EDA is to clarify how the fingerprints of exotic chemical bonds compare to those of more familiar bonds, as illustrated in Fig. 29. As one example, the Zn(I)–Zn(I) bond in dizincocene (Cp − Zn − Zn − Cp) emerges as a conventional covalent chemical bond, analogous to H2. By contrast, the Mn(0)–Mn(0) bond in (CO)5Mn–Mn(CO)5 behaves as a charge-shift bond650 that is more similar to F2 than to H2. An interesting recent application of the bonded ALMO-EDA was to investigate the role of kinetic energy lowering in chemical bond formation.651 The results are controversial because in contrast to the decrease in kinetic energy upon spin coupling in H2 (as a result of greater electron delocalization), the bonded EDA shows that kinetic energy rises upon spin-coupling to make covalent single bonds such as H3C–CH3 due to Pauli repulsion with core electrons.
FIG. 29.
Bond fingerprint in terms of energy components (PREP, FRZ + SC, POL, CT) for several single bonds, showing the contrast between a conventional covalent bond (H3C–CH3), a polar covalent bond (HCl), the strongest single bond (F3Si–F), a charge-shift bond (F2), and an ionic bond (LiF). PREP is the generalization of the geometric distortion (GD) energy of Eq. (41) to include electronic hybridization, while the energy lowering due to spin-coupling (SC) between the two radical electrons upon bond-formation is grouped with the frozen (FRZ) energy of Eq. (41).647
B. Symmetry-adapted perturbation theory
Symmetry-adapted perturbation theory (SAPT) offers an alternative kind of EDA for intermolecular interactions, which is at the same time designed for accurate calculation of interaction energies.624,652,653 Unlike supramolecular calculations, the interaction energy Eint is not computed by the energy difference [as in Eq. (40)] and SAPT is therefore free of BSSE. Instead, Eint is computed directly from perturbation theory, using isolated-monomer wave functions as an unperturbed basis, in a manner that naturally partitions into physically meaningful components, including electrostatics, Pauli repulsion (“exchange”), induction, and dispersion. Through second order in the perturbation, which includes both intermolecular Coulomb operators and the antisymmetrizer that brings in Pauli repulsion, this affords
| (44) |
Here, δEHF is an optional correction to account for higher-order induction based on a counterpoise-corrected dimer Hartree–Fock calculation.652 If Hartree–Fock wave functions are used to describe the monomers, then this second-order approach is known as “SAPT0”653 because it is zeroth-order in the Møller–Plesset fluctuation potentials, i.e., it neglects monomer electron correlation effects. These can be incorporated using perturbation theory, albeit at rather high cost.652,653 A low-cost alternative is to use Eq. (44) in conjunction with Kohn–Sham wave functions for the monomers in a method known as SAPT0(KS), although care must be taken to use functionals with correct asymptotic behavior, else the anomalously small Kohn–Sham gaps wreak havoc with second-order dispersion.654,655 As such, SAPT0(KS) should only be used in conjunction with tuned LRC functionals.655 In Q-Chem 5, this tuning can be performed in an automated way during the SCF calculation via a global density-dependent (GDD) tuning procedure.135–137
Missing from Eq. (44) is a CT term because CT is contained within the induction energy in the traditional formulation of SAPT.656,657 The two can be separated, in a manner that is well-defined and stable, by using constrained DFT (cDFT) to define CT-free reference states for the monomers.658–661 The SAPT0 induction energy,
| (45) |
can thereby be separated into a part that represents “pure” or CT-free polarization, along with a CT energy that is defined as the energy lowering upon lifting the cDFT charge constraint.
Figure 30 presents an example in which the combined SAPT/cDFT-EDA is used to understand halide–water hydrogen bonding.661 Whereas the textbook picture of anion–water interactions imagines a C2v-symmetric structure for X−(H2O),663 with X− at the positive end of the H2O dipole moment, gas-phase vibrational spectroscopy convincingly demonstrates the incorrectness of this picture.662 According to SAPT/cDFT-EDA analysis,661 the existence of quasi-linear hydrogen bonds is driven primarily by CT, which turns on sharply in the vicinity of linear X−⋯H–O angles but is negligible at the C2v “dipolar” geometry.
FIG. 30.
Total interaction potential (Eint) for F−(H2O) along a relaxed radial scan of the XOH angle, θ. Also shown is a SAPT/cDFT-EDA decomposition of Eint into a CT component (ECT) and a CT-free interaction energy, Eint − ECT. As the ion circumscribes the water molecule, ECT turns on sharply in the vicinity of quasi-linear hydrogen bonds. Removal of CT stabilization results in a C2v-symmetric structure, in disagreement with experiment,662 although the “dipolar” C2v structure can still be found in many undergraduate textbooks, e.g., Ref. 663. Adapted with permission from J. M. Herbert and K. Carter-Fenk, J. Phys. Chem. A 125, 1243 (2021). Copyright 2021 American Chemical Society.
The SAPT interaction formula in Eq. (44) is traditionally understood to apply to dimers but has been extended to clusters of molecules through a combination with the “XPol” self-consistent charge embedding scheme,654,664–667 which is used to capture many-body polarization effects. The combined method, “XSAPT,”136,624,654,666–672 is a many-body extension of SAPT that is currently available exclusively in Q-Chem for both closed- and open-shell systems.
Although useful for qualitative and perhaps semiquantitative purposes, second-order SAPT0 is not a benchmark-quality method,653,669 primarily due to the limitations of second-order dispersion,
| (46) |
SAPT0 calculations are often performed using a limited basis set such as jun-cc-pVDZ673 in order to affect some error cancellation.653 An alternative is to seek replacements for , and two such methods are available in Q-Chem:
-
•
XSAPT + aiD,136,624,668,669 which adds an ab initio dispersion potential in place of . Although similar in form to “+D” corrections in DFT + D,674 the +aiD correction is fitted to pure dispersion data from DFT-SAPT, SAPT2+(3), and SAPT2+3(CCD) calculations, each of which provides CCSD(T)-quality interaction energies but remains separable into components.652,653 Taking advantage of the separability of the SAPT interaction energy, XSAPT + aiD avoids the double-counting that is inherent in DFT + D.674 (As a result, the +D corrections in DFT + D should never be interpreted as genuine dispersion.37,659) The third-generation + aiD3 correction is the latest and most accurate.624
-
•
XSAPT + MBD,667,672 which incorporates a modified form672 of the many-body dispersion (MBD) model.72–74 As compared to XSAPT + aiD, this is much closer to a first-principles model and also more accurate.
Although designed as intermolecular EDAs, XSAPT methods are also among the most accurate quantum chemistry methods for predicting intermolecular interaction energies, as demonstrated by error statistics for the L7 dataset675 [Fig. 31(a)]. MP2-based methods dramatically overestimate these dispersion-dominated interaction energies, with the exception of the “attenuated” att-MP2 method,676 which is also available in Q-Chem. The selection of DFT methods in Fig. 31(a) is chosen carefully to focus on those that do well for non-covalent interactions. Hence, it is impressive that XSAPT + MBD approaches the MAE of the best density functional tested, B97M-V, and has lower maximum error. The combination of benchmark-quality energies with a physically meaningful decomposition is one reason that SAPT-based methods are used to parameterize physically motivated force fields.677 These desirable properties have also been used to make fundamental inquiries regarding the nature of π–π interactions.678,679 The latter studies demonstrate, for example, that the textbook680 Hunter–Sanders (quadrupolar electrostatic) model of π-stacking is simply wrong.678 The frequently asked question,681 “is π-stacking a unique form of dispersion?”, can be answered in the affirmative using XSAPT + MBD calculations, although a detailed analysis suggests that stacking is driven by molecular shape rather than by aromaticity per se, in what has been called the “pizza-π” model of stacking interactions.679
FIG. 31.
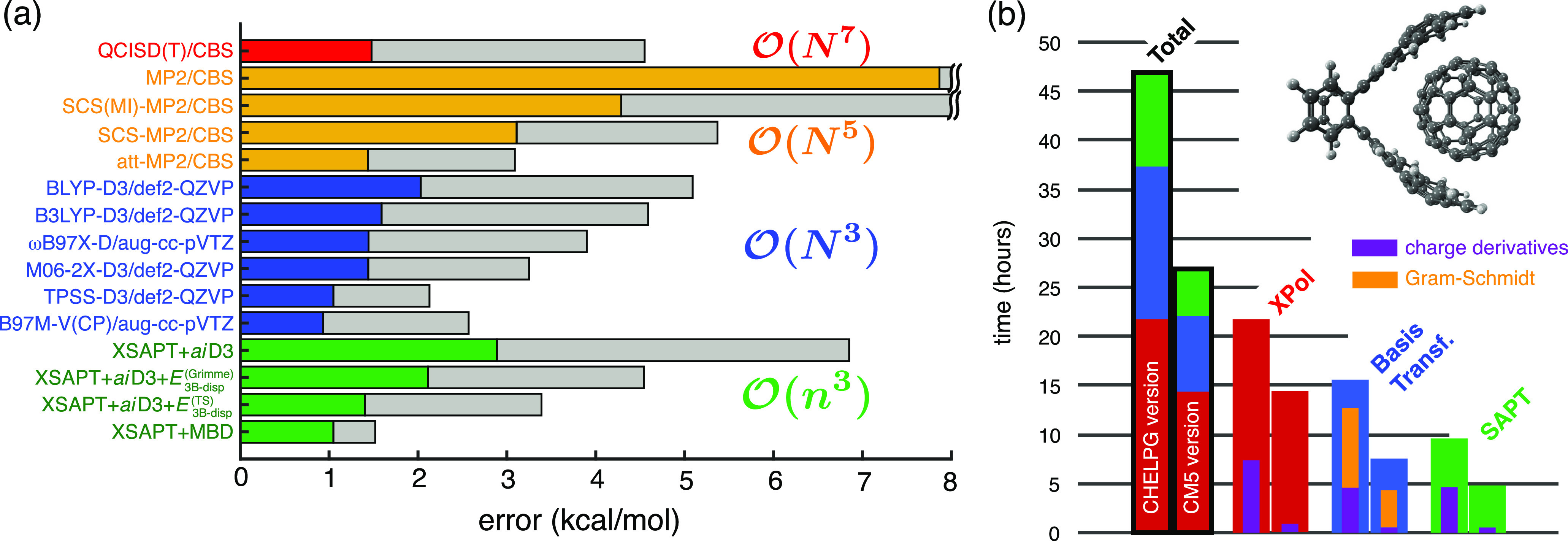
(a) Errors in interaction energies for the L7 set of large dispersion-bound dimers,675 as predicted by a variety of quantum-chemical methods in comparison to complete-basis set (CBS) CCSD(T) benchmarks. Gray bars indicate maximum errors whereas colored bars indicate mean absolute errors. The latter are color-coded according to computational cost, with indicating pth-order scaling with respect to the size N of the supramolecular complex, whereas means cubic scaling with respect to the size n of the largest monomer. These comparisons were originally reported in Ref. 672, but the XSAPT + MBD statistics have been updated to reflect modifications reported in Ref. 667. (b) Timing breakdown for an XSAPT + aiD calculation of the C60 @ C60H28 “buckycatcher” complex (4592 basis functions) on a single 28-core node. The left bar in each pair uses the original XPol embedding based on ChElPG charges,654 and the right bar is a new implementation based on CM5 charges. 667. Panel (a) is adapted with permission from K. Carter-Fenk, K. U. Lao, K.-Y. Liu, and J. M. Herbert, J. Phys. Chem. Lett. 10, 2706 (2019). Copyright 2019 American Chemical Society. Panel (b) is reproduced from Liu et al., J. Chem. Phys. 151, 031102 (2019) with the permission of AIP Publishing.
Notably, XSAPT calculations are considerably less expensive than supramolecular DFT due to the monomer-based nature of XSAPT. For XSAPT + aiD and XSAPT + MBD, the rate-limiting step is with respect to the monomer size (n), rather than the supersystem size. The method can be implemented efficiently in the atomic orbital basis,136 and a new XPol embedding scheme based on CM5 charges,682 available in Q-Chem 5, offers almost 2× speedup over earlier versions;667 see Fig. 31(b). Cost savings relative to supramolecular DFT are most pronounced in systems that can be divided into more than two fragments, such as the DNA intercalation complex that is shown in Fig. 32(a). For this system, a counterpoise-corrected interaction energy calculation at the level of ωB97M-V/def2-TZVPPD (4561 basis functions) requires 3 × 13 h on a 40-core compute node, i.e., 13 h for each of the three supramolecular calculations that are needed to compute Eint = EAB − EA − EB. In contrast, an XSAPT + MBD calculation using the same basis set requires 7 × 6 h running on the same hardware.672 Like the fragment methods discussed in Sec. VI E (of which XSAPT can be considered an example), these seven constituent calculations can be run independently on different compute nodes.
FIG. 32.
Model systems for drug binding: (a) DNA/ellipticine intercalation complex (157 atoms) and (b) the protease inhibitor molecule indinavir, situated in a model of HIV-2 protease (323 atoms). The table shows XSAPT + MBD energy components from Ref. 667.
Figure 32 shows two pharmacologically relevant examples of ligand–macromolecule binding, along with the XSAPT + MBD energy decomposition for each.667 One of these is a DNA intercalation complex [Fig. 32(a)], emblematic of π-stacking interactions, but the other does not exhibit any obvious dominant binding motif yet has a dispersion energy that is almost twice as large as that of the DNA intercalation complex. In the HIV + indinavir system, which is considerably larger, dispersion arises from a large number of small contributions that must be treated carefully. Notably, for the DNA/ellipticine complex, the XSAPT + MBD interaction energy (reported as −40.7 or −41.7 kcal/mol, depending on the details of the charge embedding667) is in better agreement with the complete-basis CCSD(T) benchmark (−38.6 ± 2.2 kcal/mol683) than an earlier quantum Monte Carlo estimate (−33.6 ± 0.9 kcal/mol684).
VIII. SOFTWARE ENGINEERING
This article focuses primarily on the diverse scientific advances made by the research groups that comprise the Q-Chem developer community. Figure 2 is a convincing demonstration of sustained energetic growth of the software and the developer community over the past 10+ years. Despite its age, the Q-Chem software shows no signs of aging.
As a software development platform, Q-Chem comes with many challenges for developers and maintainers. Many features are contributed by novice coders without much prior training for whom Q-Chem is their first software development project. This is coupled with an enormous body of computer code that no single person can fully grasp. Software developed by scientists is often notorious for its poor quality assurance and software engineering practices,685–688 but Q-Chem developers benefit from the network effect and the stability that the Q-Chem platform provides. The Q-Chem core team and experienced developers provide training and assistance to new community members. Events such as regular developer workshops and webinars, visits to the Q-Chem office in California, and a “Summer at Q-Chem” program facilitate networking, encourage cross-pollination, and help to integrate new developers.
Below, we describe some of the software engineering practices that help to maintain productivity with such a large group of developers.
A. Software development environment
The Q-Chem code began in the early 1990s as a set of individual components that communicated through temporary files. These components were soon linked together for better performance (by avoiding file-based communication involving large amounts of data), becoming a monolithic code, but while this new structure delivered performance gains, it became difficult to read and maintain over time. The problem is easy to recognize, but the optimal solution is far from obvious. Should we give up, abandon the legacy code, and rewrite the software from scratch? Or should we continue to develop around the old infrastructure and simply adjust to its idiosyncrasies? Following a discussion among the developers, around 2003, a decision was made to pursue slow modernization: continuous code refactoring, gradual rewriting, and quick adoption of newly created component replacements. This strategy has proven to be effective, and Q-Chem’s code has undergone significant improvement while continuing to serve the computational chemistry community. One by one, legacy modules are rewritten and replaced by modern versions with improved performance and enhanced capabilities. Importantly, this process simultaneously preserves the rich functionality of the software, which is essential for applications, while providing a platform for developing new features.
Many Q-Chem developers now choose to begin working on new capabilities within development packages, i.e., small code-development environments with a minimal set of components required to enable a new feature. (The concept is very similar to package management in the context of software development in other languages.) Development packages are very quick to compile and link, which cannot be said of Q-Chem as a whole with its > 106 lines of compilable code. New features are first verified via unit testing and then, following their integration into the Q-Chem package, as end-to-end Q-Chem jobs.
B. Infrastructure
A small team of software maintainers at Q-Chem provides a number of systems for code and documentation version control, issue tracking, merge requests, continuous integration, and quality control. Q-Chem contributors follow the standard workflow of developing and testing new features, enhancements, and bugfixes on a branch, followed by submission of a merge request. The automated code merge procedure incorporates the changes into the main line of development and executes a suite of pre-commit tests. If any of the tests fails, the merge is rejected and the developer is requested to resolve any issues with assistance from the core Q-Chem team when necessary.
This automated approach provides Q-Chem’s large developer community with assurance that their features will be rolled into release versions in a predictable way. Indeed, Q-Chem software is released on a time-based schedule, with one major release and two minor releases per year. Beyond automation, the Q-Chem developer community is encouraged to interact via an online forum, and typically there is an in-person developer meeting once a year. These mechanisms help to minimize issues that can arise in a sizable developer community over overlapping or even duplicative contributions.
The back-end infrastructure is a complex system that is largely hidden from the developers. It utilizes a combination of open source, proprietary, and in-house software running on premises as well as in the cloud. Continuous integration and deployment is powered by Jenkins equipped with automated pipelines for software builds, testing, benchmarking, and other routine tasks. Version control is provided by Subversion. Software testing and performance benchmarking is automated using CTest, and the results can be visualized with specialized tools. Trac is used as a wiki-based programmer’s reference, issue tracker, and release planning tool.
C. Third-party components
Q-Chem makes use of several software libraries developed outside of our own developer community. For example, the Armadillo C++ library689 provides convenient template-based C++ application programming interfaces for linear algebra. If requested by the user, libecpint (a C++ library for the evaluation of effective core potentials,690 based on the Gauss–Chebyshev quadrature) can be used instead of Q-Chem’s internal algorithms.691
IX. HIGH PERFORMANCE COMPUTING
A. Platforms
Computational quantum chemistry spans a diverse range of myriad calculation types, ranging from exploratory qualitative analysis to high-accuracy calculations based on many-body theory, and furthermore spans a range from large-scale calculations on hundreds of atoms to high-throughput calculations on thousands of small molecules. Different researchers may therefore use Q-Chem in very different modes of operation, and our vision is to provide all of them with a versatile and flexible software engine that can meet these needs. Q-Chem runs effectively on a variety of architectures, from laptops and desktops to leadership-class supercomputers, and is also now available for cloud computing, for which we provide a ready-to-deploy machine image for use on Amazon Web Services. Users can interact with the Cloud via a Linux shell or by using either IQmol or WebMO.
To enable this versatility, we rely on a variety of techniques for reducing the memory footprint of the software using flexible rebalancing tools for disk vs in-core storage and effective shared-memory (OpenMP) parallelization of key software elements, such as integrals and tensors. That said, Q-Chem to date has focused most performance optimization effort on enabling efficient use of mid-scale computing resources for a single job. Leadership computing or supercomputing resources can then be effectively leveraged via workflows (i.e., job-level parallelism). With this in mind, Q-Chem has placed emphasis on OpenMP (shared memory parallel) capabilities and the use of GPU resources associated with a single node. Below, we discuss some recent advances in these capabilities and present example timings.
B. Improved OpenMP parallel capabilities
OpenMP is a standard paradigm for shared memory parallel computing. Efficient OpenMP parallelism is thus the key to enabling significantly reduced time-to-solution for single jobs using mid-range computing, where the single job can take as much as an entire single node of a computer cluster or the entire resources of a workstation. Typical modern compute nodes consist of 16–64 cores, but nodes with as many as 128 cores are already available. OpenMP parallel capabilities for DFT calculations were already quite good at the time of the review article describing Q-Chem 4,20 but progress since that time has been continuous and significant. Below, some representative snapshots of current OpenMP parallel capabilities for DFT and MP2 are reported. Q-Chem also has excellent OpenMP parallel computing capabilities at the CC/EOM-CC and ADC levels, which have been documented elsewhere.12,13,215,219
OpenMP parallel speedups for DFT calculations are summarized in Fig. 33. For single-point energy evaluation on naphthalene in a large basis (M06-2X/def2-QZVPPD level of theory), it is evident that Q-Chem’s parallel efficiency is very high indeed, with speedups of 16× on 16 cores and 27× on 32 cores. The parallel efficiency is also very good, although noticeably lower, for the two energy + gradient examples in the medium-sized def2-TZVP basis set, performed on the anthracene dimer (C28H20, 988 basis functions). Using the B97M-V functional, a parallel speedup of 22× is obtained on 32 cores vs 12.7× using 16 cores; the 32-core calculation requires only 516 s of wall time. Energy and gradient evaluation at the ωB97M-V/def2-TZVP level of theory exhibits similar scaling. The overhead associated with RSH functionals is not excessive for this calculation: the 32-core job requires 787 s, which is only 50% more than the corresponding pure (semilocal) functional.
FIG. 33.
Illustration of OpenMP parallel scaling for DFT calculations. The first example is a single-point energy evaluation in a large basis set (M06-2X/def2-QZVPPD, blue diamonds), as might be performed after structure optimization in a smaller basis set. The other two examples are for the evaluation of the DFT energy and gradient in a triple-ζ basis, as often used for geometry optimization. One case is with a semilocal functional (B97M-V/def2-TZVP, orange circles), and the other uses a hybrid functional (ωB97M-V/def2-TZVP, gray squares). All calculations were performed on a 32 core dual-socket Intel Xeon CPU E5-2697A server.
Q-Chem’s new fully object-oriented code for MP2 energies and gradients (as well as the other advanced methods discussed in Sec. III A) requires no storage of amplitudes or four-center electron repulsion integrals and is optimized for OpenMP parallelism. To illustrate the performance of the code, Fig. 34 shows the parallel scaling of the MP2 gradient for three different molecules ranging from 5 to 64 heavy atoms. For all three cases, the results indicate good OpenMP performance all the way out to 32 cores, with speedups of ≈22× (69% parallel efficiency) on 32 cores and somewhat higher efficiency (79%) on 24 cores.
FIG. 34.
Illustration of OpenMP parallel scaling for evaluation of the MP2 energy and gradient for three molecules: dichloromethyl ethene (C3H4Cl2) with aug-cc-pVQZ,391,392 a hydrogen-bonded complex between adenine and guanine (C10N10H10O) in the aug-cc-pVTZ basis,391,392 and a circumcoronene complex with adenine (C59N5H23) in the VDZ basis.692 The calculations were performed using SCF with exact integrals and MP2 with standard auxiliary (resolution-of-identity or density fitting) basis sets,693 with a frozen core approximation. All timings were obtained on a 32 core dual socket Intel Xeon CPU E5-2697A server.
C. GPU capabilities
A new capability in Q-Chem 5 is the ability to build and diagonalize the Fock matrix using graphics processing units (GPUs). This is achieved through a partnership with StreamNovation Ltd., producers of the BrianQC module,694 which functions as an add-on to Q-Chem for the calculation of electron repulsion integrals (ERIs).
ERI computation in Q-Chem exploits a variety of algorithms depending on the properties of the Gaussian basis set, such as the angular momentum classes and the degree of contraction, with an optimal strategy selected based upon the “PRISM” meta-algorithm.695 The BrianQC module implements several standard ERI algorithms as well, including McMurchie–Davidson,696 Head-Gordon–Pople,697 Obara–Saika,698,699 and Rys quadrature,700,701 and these are controlled by a “BRUSH” meta-algorithm that is optimized for use with GPUs.702
In contrast to PRISM and other approaches that were optimized for central processing units (CPUs), the computational power of GPUs is often quite different for single-precision vs double-precision operations, and quantum chemistry integral calculations often require the latter. For that reason, precision and speed requirements are balanced carefully in BrianQC and integrals are evaluated in single or double precision based on a pre-computed strict Cauchy upper bound on their magnitude.703 The BRUSH algorithm automatically determines the best possible approach to compute each type of ERI, selecting from among various algorithms and (in the GPU case) between mixed-precision implementations.702,703 Each route to ERIs has been implemented and optimized for each supported type of GPU using computer algebra to automatically generate the GPU kernels. (Automatic code generation of this kind is increasingly popular in GPU-based quantum-chemistry code development.704) The BrianQC system has its own internal representation for the scalar and tensor expressions that naturally arise in quantum chemistry calculations.
The BrianQC GPU-based ERI engine includes the following features:
-
•
optimization for large molecules;
-
•
support for s, p, d, f, and g basis functions;
-
•
support for all NVIDIA GPU architectures (Kepler, Maxwell, Pascal, Volta, and Turing);
-
•
support for 64-bit Linux and Windows operating systems;
-
•
mixed-precision implementation with double-precision accuracy; and
-
•
multi-GPU and supercomputer support.
The BrianQC module speeds up every Q-Chem calculation that uses Coulomb and/or exchange integrals and their first derivatives, including Hartree–Fock and DFT energies and geometry optimizations for most functionals. Figure 35 shows speedups vs a CPU-only implementation for B3LYP/cc-pVDZ calculations on a test set of alkanes, and Fig. 36 presents speedups for M06-2X/def2-QZVP calculations on a set of organometallic complexes.
FIG. 35.
Speedup obtained for single-point B3LYP/cc-pVDZ calculations with BrianQC for randomly generated branched alkanes. Hardware: Intel(R) Xeon(R) CPU E5-2620 v4 2.10 GHz (2 × 8 core); NVIDIA GeForce GTX 1080 Ti, 1070, 980 Ti, RTX 2080 Ti, 2070; Micron 9ASF1G72PZ-2G3B1 DDR4 2400 MHz 8 × 8 GB; ASUS Z10PG-D16 Series Motherboard. For the K80 and M60 GPUs, Amazon Web Service p2.xlarge and g3.4×large instances were used; in the case of P100 and V100 GPUs, Google Cloud instances were used with similar parameters. All CPU timings were obtained with Q-Chem 5.2.2. All GPU timings were obtained using BrianQC 1.0 + Q-Chem 5.2.2.
FIG. 36.
Wall times for DFT (M06-2X/def2-QZVP) energy calculations using Q-Chem with BrianQC. Hardware details can be found in the caption of Fig. 35.
X. GRAPHICAL USER INTERFACES
Q-Chem jobs can be set up and deployed by WebMO,705 a popular web-based interface to quantum chemistry programs, and Q-Chem results can also be visualized using a variety of third-party software, including MolDen, Jmol, and Gabedit. In this section, we focus on two especially fully featured graphical front ends, IQmol17 and Spartan.
A. IQmol visualizer
IQmol is an open-source molecular visualization package17 that has been developed within the Q-Chem community and is designed to facilitate the Q-Chem workflow: building molecular structures, generating Q-Chem input files, submitting calculations, and visualizing the results.
Molecular structures can be built from the included molecular library by entering the SMILES ID for simple molecules or by using the free-form builder. Tools are included that enable structures to be quickly optimized using molecular mechanics and to symmetrize geometries to ensure they have the desired point-group symmetry.
Setting up Q-Chem jobs is made easier by an input generator that is aware of the many Q-Chem options and settings and presents these in a hierarchical fashion to avoid overwhelming the new user. Once generated, these inputs can be submitted to either the local machine, a compute server running scheduling software such as PBS or SLURM, or to a freely accessible demonstration server. The latter is a service provided by Q-Chem, Inc. and allows access to Q-Chem’s full functionality, with only a time restriction. This service has been used to great effect in undergraduate and graduate teaching programs in universities around the world.
Results from the Q-Chem output file and associated formatted checkpoint file can be analyzed and visualized in a range of ways depending on the type of calculation. IQmol recognizes and can plot a range of molecular surfaces such as densities and orbitals, including localized orbitals, NTOs, NBOs, and Dyson orbitals. Animations can be generated for vibrational frequencies and pathways, including optimization, intrinsic reaction coordinates, and ab initio molecular dynamics trajectories. Visual representations of spectroscopic data are also available, including model spectra for IR, UV, and NMR.
IQmol uses OpenGL shaders to provide a range of appealing and configurable visual effects out of the box, as shown in Fig. 37. In addition, IQmol supports the export of cube file data346 and POV-Ray formatted files for import into third-party software for complete control over the appearance of molecular structures and surfaces.
FIG. 37.
IQmol a provides a convenient front-end and visualization tool for Q-Chem users.
B. Integration into Spartan
The Spartan program was first introduced in 1991 and since 2000 has provided easy-to-use access to the majority of functionality available in Q-Chem. This includes Hartree–Fock as well as a full range of DFT and wave function-based correlated models, coupled with a wide selection of basis sets. Molecular mechanics models (MMFF and Sybyl) and a selection of semi-empirical models are implemented in Spartan as well.
Multiple molecules (or sets of molecules) may be open in Spartan, and multiple molecules may be submitted to Q-Chem from Spartan. Interface operations and compute tasks are independent. Once a job is “submitted,” either locally or to a remote server, it is marked as “read only,” and the interface is free to deal with other molecules. Upon completion, the job is “unlocked.” Queuing logic allows full control of local and remote resources.
Spartan provides 2D sketching and 3D building tools for organic, organometallic, and inorganic molecules as well as specialized 3D builders for polypeptides and polynucleotides. It also accesses a wide selection of 2D and 3D molecular formats. Guesses for transition states may be obtained with the aid of an internal database by adding “curly arrows” to reactant or product structures. Tools are available for generating regio- and stereoisomers, tautomers, and conformers of flexible cyclic and non-cyclic molecules and for aligning molecules. Job selection (task, method, basis set, and requests for spectra or other properties) is accomplished via simple but open-ended dialogs. Composite tasks (for example), required for the G3 and G4 thermochemical recipes706,707 or for the calculation of a Boltzmann-averaged NMR spectrum, are available.
Output for Spartan includes not only text from the Q-Chem output file but also an easy-to-read summary of “important” calculated quantities, e.g., atomic charges and NMR chemical shifts and J-couplings. IR, Raman, UV/visible, and NMR spectra (both 1- and 2D) may be plotted and visually compared to experimental spectra. NMR chemical shifts from selected density-functional models may be empirically corrected.
Spartan seamlessly accesses a variety of experimental databases, including the Cambridge Structural Database (CSD) of over a million x-ray crystal structures, the NIST thermochemical database, and the NMR shift database. CSD is under license, while the latter two are freely available. In addition, Spartan accesses the Spartan Structure and Properties database (SSPD), a collection of 300 000 organic and organometallic molecules with ωB97X-V/6-311+G(2df,2p) energies obtained at ωB97X-D/6-31G* equilibrium geometries and EDF2708/6-31G* vibrational frequencies that facilitate calculation of thermochemical quantities (ΔH, ΔS and ΔG). Proton and 13C NMR spectra computed at the ωB97X-D/6-31G* level are included in SSPD as well. A databases of calculated natural product structures that includes experimental chemical shifts is also provided.
Spartan is released on a two-year schedule with a version number corresponding to the calendar year. The latest version is Spartan’20. Further details about Spartan are available from Wavefunction, Inc.709
XI. CONCLUSIONS AND OUTLOOK
This article has surveyed the broad range of new capabilities developed in Q-Chem over the past six years. Both the author list and the length of this paper itself attest to the strength of the community that has coalesced around contributions to the code. It is this community of developers that has enabled the large majority of the new features and most of the new innovations in methodology reported here. At the same time, support for this community is delivered by a small core group of Q-Chem scientists who have themselves created and tuned critical features, including the substantial modernization of the software development infrastructure to adopt modern best practices of object-oriented programming. This synergy has been critical to the ongoing development of the code: academic developers of Q-Chem have the advantage of using a well-supported infrastructure upon which to build new features, while Q-Chem scientists can focus on commercially critical developments and optimizations. While open source is a powerful movement whose value is unquestioned, the idea that the large community of end users should contribute to the sustainability of the code through a modest purchase price is central to Q-Chem’s approach. However, there is no boundary between the two classes of Q-Chem customers—developers and end-users. It is worth reiterating that anyone or any group that purchases Q-Chem is eligible to join the developer community and help contribute to future advances. We hope that the recent accomplishments reviewed here will inspire future contributions to the code, as well as inspiring myriad chemical applications of this full-featured electronic structure program package.
DEDICATION
We dedicate this paper to Dr. Michael Wormit and Prof. Nick Besley, whose lives were cut short by tragic accidents in March 2015 and June 2021, respectively. Michael and Nick were dedicated and inspiring members of the Q-Chem family and we remember them as enthusiastic researchers, inspiring teachers, and good friends. We celebrate their important contributions to our community with annual awards: the existing Michael Wormit Award for an outstanding young Q-Chem developer and the newly established Nick Besley Award for contributions to computational spectroscopy in the Q-Chem community.
ACKNOWLEDGMENTS
Electronic structure software development at Q-Chem has been supported during the period reviewed in this paper by SBIR grants from the National Institutes of Health (Grants Nos. R43GM096678, R43GM121126, R43GM126804, R43GM128480, R43GM133270, R44GM076847, R44GM081928, R44GM084555, R44GM121126, and R44GM128480), the Department of Energy (Grant Nos. DE-SC0011297 and DE-SC0021568), and the Department of Defense (Grant Nos. W911NF-14-P-0032, W911NF-16-C0124, and W911NF-19-C0048). In addition, the academic research groups that have contributed to Q-Chem have been supported within the U.S. by grants from the Department of Energy, the National Science Foundation, the Army Research Office, and other Federal agencies as well as by the corresponding national agencies in other countries, as acknowledged in the respective original publications.
E.E., A.T.B.G., P.M.W.G., S.F., M.H.-G., J.M.H., A.I.K., and Y.S. are part-owners of Q-Chem, Inc.
Contributor Information
Martin Head-Gordon, Email: mailto:mhg@cchem.berkeley.edu.
John M. Herbert, Email: mailto:herbert@chemistry.ohio-state.edu.
Anna I. Krylov, Email: mailto:krylov@usc.edu.
DATA AVAILABILITY
The data that support the findings of this study are available within the article.
REFERENCES
- 1.Goldstine H. H., The Computer: From Pascal to von Neumann (Princeton University Press, Princeton, NJ, 1972). [Google Scholar]
- 2.Metropolis N., Rosenbluth A. W., Rosenbluth M. N., Teller A. H., and Teller E., “Equation of state calculations by fast computing machines,” J. Chem. Phys. 21, 1087–1092 (1953). 10.1063/1.1699114 [DOI] [Google Scholar]
- 3.Boys S. F., Cook G. B., Reeves C. M., and Shavitt I., “Automatic fundamental calculations of molecular structure,” Nature 178, 1207–1209 (1956). 10.1038/1781207a0 [DOI] [Google Scholar]
- 4.Mulliken R. S., “Spectroscopy, molecular orbitals, and chemical bonding,” in Nobel Lectures, Chemistry 1963–1970 (Elsevier, Amsterdam, 1972), pp. 131–160. [Google Scholar]
- 5.Neese F., Atanasov M., Bistoni G., Maganas D., and Ye S., “Chemistry and quantum mechanics in 2019: Give us insight and numbers,” J. Am. Chem. Soc. 141, 2814–2824 (2019). 10.1021/jacs.8b13313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Moskowitz J. W. and Snyder L. C., “POLYATOM: A general computer program for ab initio calculations,” in Methods of Electronic Structure Theory, Modern Theoretical Chemistry Vol. 3, edited by Schaefer H. F. III (Springer Science + Business Media, New York, 1977), Chap. 10, pp. 387–412. [Google Scholar]
- 7.Pitzer R. M. and Lipscomb W. N., “Calculation of the barrier to internal rotation in ethane,” J. Chem. Phys. 39, 1995–2004 (1963). 10.1063/1.1734572 [DOI] [Google Scholar]
- 8.Sherrill C. D., Manolopoulos D. E., Martínez T. J., and Michaelides A., “Electronic structure software,” J. Chem. Phys. 153, 070401 (2020). 10.1063/5.0023185 [DOI] [PubMed] [Google Scholar]
- 9.Krylov A. I. and Gill P. M. W., “Q-Chem: An engine for innovation,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 3, 317–326 (2013). 10.1002/wcms.1122 [DOI] [Google Scholar]
- 10.Krylov A. I., Herbert J. M., Furche F., Head-Gordon M., Knowles P. J., Lindh R., Manby F. R., Pulay P., Skylaris C.-K., and Werner H.-J., “What is the price of open-source software?,” J. Phys. Chem. Lett. 6, 2751–2754 (2015). 10.1021/acs.jpclett.5b01258 [DOI] [PubMed] [Google Scholar]
- 11.Kaliman I. A. and Slipchenko L. V., “LIBEFP: A new parallel implementation of the effective fragment potential method as a portable software library,” J. Comput. Chem. 34, 2284–2292 (2013). 10.1002/jcc.23375 [DOI] [PubMed] [Google Scholar]
- 12.Epifanovsky E., Wormit M., Kuś T., Landau A., Zuev D., Khistyaev K., Manohar P., Kaliman I., Dreuw A., and Krylov A. I., “New implementation of high-level correlated methods using a general block tensor library for high-performance electronic structure calculations,” J. Comput. Chem. 34, 2293–2309 (2013). 10.1002/jcc.23377 [DOI] [PubMed] [Google Scholar]
- 13.Kaliman I. A. and Krylov A. I., “New algorithm for tensor contractions on multi-core CPUs, GPUs, and accelerators enables CCSD and EOM-CCSD calculations with over 1000 basis functions on a single compute node,” J. Comput. Chem. 38, 842–853 (2017). 10.1002/jcc.24713 [DOI] [PubMed] [Google Scholar]
- 14.Scheurer M., Reinholdt P., Kjellgren E. R., Haugaard Olsen J. M., Dreuw A., and Kongsted J., “CPPE: An open-source C++ and Python library for polarizable embedding,” J. Chem. Theory Comput. 15, 6154–6163 (2019). 10.1021/acs.jctc.9b00758 [DOI] [PubMed] [Google Scholar]
- 15.Plasser F., Wormit M., and Dreuw A., “New tools for the systematic analysis and visualization of electronic excitations. I. Formalism,” J. Chem. Phys. 141, 024106 (2014). 10.1063/1.4885819 [DOI] [PubMed] [Google Scholar]
- 16.Herbst M. F. (2019). “ctx: Key-value C++ datastructures for organised hierarchical storage,” Zenodo. 10.5281/zenodo.2590706. [DOI]
- 17.Gilbert A. T. B., IQmol molecular viewer, http://iqmol.org; accessed April 2021.
- 18.Kong J., White C. A., Krylov A. I., Sherrill D., Adamson R. D., Furlani T. R., Lee M. S., Lee A. M., Gwaltney S. R., Adams T. R., Ochsenfeld C., Gilbert A. T. B., Kedziora G. S., Rassolov V. A., Maurice D. R., Nair N., Shao Y., Besley N. A., Maslen P. E., Dombroski J. P., Daschel H., Zhang W., Korambath P. P., Baker J., Byrd E. F. C., Van Voorhis T., Oumi M., Hirata S., Hsu C.-P., Ishikawa N., Florian J., Warshel A., Johnson B. G., Gill P. M. W., Head-Gordon M., and Pople J. A., “Q-Chem 2.0: A high-performance ab initio electronic structure program package,” J. Comput. Chem. 21, 1532–1548 (2000). [DOI] [Google Scholar]
- 19.Shao Y., Molnar L. F., Jung Y., Kussmann J., Ochsenfeld C., Brown S. T., Gilbert A. T. B., Slipchenko L. V., Levchenko S. V., O’Neill D. P., R. A. DiStasio, Jr., Lochan R. C., Wang T., Beran G. J. O., Besley N. A., Herbert J. M., Yeh Lin C., Van Voorhis T., Chien S. H., Sodt A., Steele R. P., Rassolov V. A., Maslen P. E., Korambath P. P., Adamson R. D., Austin B., Baker J., Byrd E. F. C., Dachsel H., Doerksen R. J., Dreuw A., Dunietz B. D., Dutoi A. D., Furlani T. R., Gwaltney S. R., Heyden A., Hirata S., Hsu C.-P., Kedziora G., Khalliulin R. Z., Klunzinger P., Lee A. M., Lee M. S., Liang W., Lotan I., Nair N., Peters B., Proynov E. I., Pieniazek P. A., Rhee Y. M., Ritchie J., Rosta E., Sherrill C. D., Simmonett A. C., Subotnik J. E., Woodcock H. L. III, Zhang W., Bell A. T., Chakraborty A. K., Chipman D. M., Keil F. J., Warshel A., Hehre W. J., Schaefer H. F. III, Kong J., Krylov A. I., Gill P. M. W., and Head-Gordon M., “Advances in methods and algorithms in a modern quantum chemistry program package,” Phys. Chem. Chem. Phys. 8, 3172–3191 (2006). 10.1039/b517914a [DOI] [PubMed] [Google Scholar]
- 20.Shao Y., Gan Z., Epifanovsky E., Gilbert A. T. B., Wormit M., Kussmann J., Lange A. W., Behn A., Deng J., Feng X., Ghosh D., Goldey M., Horn P. R., Jacobson L. D., Kaliman I., Khaliullin R. Z., Kuś T., Landau A., Liu J., Proynov E. I., Rhee Y. M., Richard R. M., Rohrdanz M. A., Steele R. P., Sundstrom E. J., Woodcock H. L. III, Zimmerman P. M., Zuev D., Albrecht B., Alguire E., Austin B., Beran G. J. O., Bernard Y. A., Berquist E., Brandhorst K., Bravaya K. B., Brown S. T., Casanova D., Chang C.-M., Chen Y., Chien S. H., Closser K. D., Crittenden D. L., Diedenhofen M., R. A. DiStasio, Jr., Do H., Dutoi A. D., Edgar R. G., Fatehi S., Fusti-Molnar L., Ghysels A., Golubeva-Zadorozhnaya A., Gomes J., Hanson-Heine M. W. D., Harbach P. H. P., Hauser A. W., Hohenstein E. G., Holden Z. C., Jagau T.-C., Ji H., Kaduk B., Khistyaev K., Kim J., Kim J., King R. A., Klunzinger P., Kosenkov D., Kowalczyk T., Krauter C. M., Lao K. U., Laurent A. D., Lawler K. V., Levchenko S. V., Lin C. Y., Liu F., Livshits E., Lochan R. C., Luenser A., Manohar P., Manzer S. F., Mao S.-P., Mardirossian N., Marenich A. V., Maurer S. A., Mayhall N. J., Neuscamman E., Oana C. M., Olivares-Amaya R., O’Neill D. P., Parkhill J. A., Perrine T. M., Peverati R., Prociuk A., Rehn D. R., Rosta E., Russ N. J., Sharada S. M., Sharma S., Small D. W., Sodt A., Stein T., Stück D., Su Y.-C., Thom A. J. W., Tsuchimochi T., Vanovschi V., Vogt L., Vydrov O., Wang T., Watson M. A., Wenzel J., White A., Williams C. F., Yang J., Yeganeh S., Yost S. R., You Z.-Q., Zhang I. Y., Zhang X., Zhao Y., Brooks B. R., Chan G. K. L., Chipman D. M., Cramer C. J., Goddard W. A. III, Gordon M. S., Hehre W. J., Klamt A., Schaefer H. F. III, Schmidt M. W., Sherrill C. D., Truhlar D. G., Warshel A., Xu X., Aspuru-Guzik A., Baer R., Bell A. T., Besley N. A., Chai J.-D., Dreuw A., Dunietz B. D., Furlani T. R., Gwaltney S. R., Hsu C.-P., Jung Y., Kong J., Lambrecht D. S., Liang W., Ochsenfeld C., Rassolov V. A., Slipchenko L. V., Subotnik J. E., Van Voorhis T., Herbert J. M., Krylov A. I., Gill P. M. W., and Head-Gordon M., “Advances in molecular quantum chemistry contained in the Q-Chem 4 program package,” Mol. Phys. 113, 184–215 (2015). 10.1080/00268976.2014.952696 [DOI] [Google Scholar]
- 21.Mardirossian N. and Head-Gordon M., “Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals,” Mol. Phys. 115, 2315–2372 (2017). 10.1080/00268976.2017.1333644 [DOI] [Google Scholar]
- 22.Hohenberg P. and Kohn W., “Inhomogeneous electron gas,” Phys. Rev. B 136, B864–B871 (1964). 10.1103/physrev.136.b864 [DOI] [Google Scholar]
- 23.Koch W. and Holthausen M. C., A Chemist’s Guide to Density Functional Theory, 2nd ed. (Wiley-VCH, New York, 2001). [Google Scholar]
- 24.von Barth U., “Basic density functional theory—An overview,” Phys. Scr. 2004(T109), 9–39. 10.1238/physica.topical.109a00009 [DOI] [Google Scholar]
- 25.Capelle K., “A bird’s-eye view of density-functional theory,” Braz. J. Phys. 36, 1318–1343 (2006). 10.1590/s0103-97332006000700035 [DOI] [Google Scholar]
- 26.Kohn W. and Sham L. J., “Self-consistent equations including exchange and correlation effects,” Phys. Rev. 140, A1133–A1138 (1965). 10.1103/physrev.140.a1133 [DOI] [Google Scholar]
- 27.Görling A. and Levy M., “Hybrid schemes combining the Hartree–Fock method and density-functional theory: Underlying formalism and properties of correlation functionals,” J. Chem. Phys. 106, 2675–2680 (1997). 10.1063/1.473369 [DOI] [Google Scholar]
- 28.Szabo A. and Ostlund N. S., Modern Quantum Chemistry (Dover, 1996). [Google Scholar]
- 29.Perdew J. P. and Schmidt K., “Jacob’s ladder of density functional approximations for the exchange-correlation energy,” AIP Conf. Proc. 577, 1–20 (2001). 10.1063/1.1390175 [DOI] [Google Scholar]
- 30.Perdew J. P., Ruzsinszky A., Constantin L. A., Sun J., and Csonka G. I., “Some fundamental issues in ground-state density functional theory: A guide for the perplexed,” J. Chem. Theory Comput. 5, 902–908 (2009). 10.1021/ct800531s [DOI] [PubMed] [Google Scholar]
- 31.Vosko S. H., Wilk L., and Nusair M., “Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis,” Can. J. Phys. 58, 1200–1211 (1980). 10.1139/p80-159 [DOI] [Google Scholar]
- 32.Perdew J. P. and Wang Y., “Accurate and simple analytic representation of the electron-gas correlation energy,” Phys. Rev. B 45, 13244 (1992); 10.1103/physrevb.45.13244 [DOI] [PubMed] [Google Scholar]; Erratum, Phys. Rev. B 98, 079904(E) (2018). 10.1103/PhysRevB.98.079904 [DOI] [Google Scholar]
- 33.Bhattarai P., Patra A., Shahi C., and Perdew J. P., “How accurate are the parameterized correlation energies of the uniform electron gas?,” Phys. Rev. B 97, 195128 (2018). 10.1103/physrevb.97.195128 [DOI] [Google Scholar]
- 34.Perdew J. P., Burke K., and Ernzerhof M., “Generalized gradient approximations made simple,” Phys. Rev. Lett. 77, 3865–3868 (1996); 10.1103/physrevlett.77.3865 [DOI] [PubMed] [Google Scholar]; Erratum, Phys. Rev. Lett. 78, 1396 (1997). 10.1103/PhysRevLett.78.1396 [DOI] [Google Scholar]
- 35.Becke A. D., “Density-functional exchange-energy approximation with correct asymptotic behavior,” Phys. Rev. A 38, 3098–3100 (1988). 10.1103/physreva.38.3098 [DOI] [PubMed] [Google Scholar]
- 36.Lee C., Yang W., and Parr R. G., “Development of the Colle–Salvetti correlation-energy formula into a functional of the electron density,” Phys. Rev. B 37, 785–789 (1988). 10.1103/physrevb.37.785 [DOI] [PubMed] [Google Scholar]
- 37.Grimme S., “Semiempirical GGA-type density functional constructed with a long-range dispersion correction,” J. Comput. Chem. 27, 1787–1789 (2006). 10.1002/jcc.20495 [DOI] [PubMed] [Google Scholar]
- 38.Yu H. S., Zhang W., Verma P., He X., and Truhlar D. G., “Nonseparable exchange–correlation functional for molecules, including homogeneous catalysis involving transition metals,” Phys. Chem. Chem. Phys. 17, 12146–12160 (2015). 10.1039/c5cp01425e [DOI] [PubMed] [Google Scholar]
- 39.Grimme S., Hansen A., Brandenburg J. G., and Bannwarth C., “Dispersion-corrected mean-field electronic structure methods,” Chem. Rev. 116, 5105–5154 (2016). 10.1021/acs.chemrev.5b00533 [DOI] [PubMed] [Google Scholar]
- 40.Sun J., Ruzsinszky A., and Perdew J. P., “Strongly constrained and appropriately normed semilocal density functional,” Phys. Rev. Lett. 115, 036402 (2015). 10.1103/PhysRevLett.115.036402 [DOI] [PubMed] [Google Scholar]
- 41.Mardirossian N. and Head-Gordon M., “Mapping the genome of meta-generalized gradient approximation density functionals: The search for B97M-V,” J. Chem. Phys. 142, 074111 (2015). 10.1063/1.4907719 [DOI] [PubMed] [Google Scholar]
- 42.Wang Y., Jin X., Yu H. S., Truhlar D. G., and He X., “Revised M06-L functional for improved accuracy on chemical reaction barrier heights, noncovalent interactions, and solid-state physics,” Proc. Natl. Acad. Sci. U. S. A. 114, 8487–8492 (2017). 10.1073/pnas.1705670114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Vydrov O. A. and Van Voorhis T., “Nonlocal van der Waals density functional: The simpler the better,” J. Chem. Phys. 133, 244103 (2010). 10.1063/1.3521275 [DOI] [PubMed] [Google Scholar]
- 44.Calbo J., Ortí E., Sancho-García J. C., and Aragó J., “The nonlocal correlation density function VV10: A successful attempt to accurately capture noncovalent interactions,” Annu. Rep. Comput. Chem. 11, 37–102 (2015). 10.1016/bs.arcc.2015.09.002 [DOI] [Google Scholar]
- 45.Adamo C. and Barone V., “Toward reliable density functional methods without adjustable parameters: The PBE0 model,” J. Chem. Phys. 110, 6158–6170 (1999). 10.1063/1.478522 [DOI] [Google Scholar]
- 46.Zhao Y. and Truhlar D. G., “The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals,” Theor. Chem. Acc. 120, 215–241 (2008); 10.1007/s00214-007-0310-x [DOI] [Google Scholar]; Erratum, Theor. Chem. Acc. 119, 525 (2008). 10.1007/s00214-007-0401-8 [DOI] [Google Scholar]
- 47.Hui K. and Chai J.-D., “SCAN-based hybrid and double-hybrid density functionals from models without fitted parameters,” J. Chem. Phys. 144, 044114 (2016). 10.1063/1.4940734 [DOI] [PubMed] [Google Scholar]
- 48.Yu H. S., He X., Li S. L., and Truhlar D. G., “MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions,” Chem. Sci. 7, 5032–5051 (2016). 10.1039/c6sc00705h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wang Y., Verma P., Jin X., Truhlar D. G., and He X., “Revised M06 density functional for main-group and transition-metal chemistry,” Proc. Natl. Acad. Sci. U. S. A. 115, 10257–10262 (2018). 10.1073/pnas.1810421115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Chai J.-D. and Head-Gordon M., “Systematic optimization of long-range corrected hybrid density functionals,” J. Chem. Phys. 128, 084106 (2008). 10.1063/1.2834918 [DOI] [PubMed] [Google Scholar]
- 51.Chai J.-D. and Head-Gordon M., “Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections,” Phys. Chem. Chem. Phys. 10, 6615–6620 (2008). 10.1039/b810189b [DOI] [PubMed] [Google Scholar]
- 52.Mardirossian N. and Head-Gordon M., “ωB97X-V: A 10-parameter, range-separated hybrid, generalized gradient approximation density functional with nonlocal correlation, designed by a survival-of-the-fittest strategy,” Phys. Chem. Chem. Phys. 16, 9904–9924 (2014). 10.1039/c3cp54374a [DOI] [PubMed] [Google Scholar]
- 53.Mardirossian N. and Head-Gordon M., “ωB97M-V: A combinatorially optimized, range-separated hybrid, meta-GGA density functional with VV10 nonlocal correlation,” J. Chem. Phys. 144, 214110 (2016). 10.1063/1.4952647 [DOI] [PubMed] [Google Scholar]
- 54.Goerigk L. and Grimme S., “Double-hybrid density functionals,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 4, 576–600 (2014). 10.1002/wcms.1193 [DOI] [Google Scholar]
- 55.Martin J. M. L. and Santra G., “Empirical double-hybrid density functional theory: A ‘third way’ in between WFT and DFT,” Isr. J. Chem. 60, 787–804 (2020). 10.1002/ijch.201900114 [DOI] [Google Scholar]
- 56.Grimme S., “Semiempirical hybrid density functional with perturbative second-order correction,” J. Chem. Phys. 124, 034108 (2006). 10.1063/1.2148954 [DOI] [PubMed] [Google Scholar]
- 57.Zhang Y., Xu X., and Goddard W. A. III, “Doubly hybrid density functional for accurate descriptions of nonbond interactions, thermochemistry, and thermochemical kinetics,” Proc. Natl. Acad. Sci. U. S. A. 106, 4963–4968 (2009). 10.1073/pnas.0901093106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Chai J.-D. and Head-Gordon M., “Long-range corrected double-hybrid density functionals,” J. Chem. Phys. 131, 174105 (2009). 10.1063/1.3244209 [DOI] [PubMed] [Google Scholar]
- 59.Mardirossian N. and Head-Gordon M., “Survival of the most transferable at the top of Jacob’s ladder: Defining and testing the ωB97M(2) double hybrid density functional,” J. Chem. Phys. 148, 241736 (2018). 10.1063/1.5025226 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kozuch S. and Martin J. M. L., “DSD-PBEP86: In search of the best double-hybrid DFT with spin-component scaled MP2 and dispersion corrections,” Phys. Chem. Chem. Phys. 13, 20104–20107 (2011). 10.1039/c1cp22592h [DOI] [PubMed] [Google Scholar]
- 61.Kozuch S. and Martin J. M. L., “Spin-component-scaled double hybrids: An extensive search for the best fifth-rung functionals blending DFT and perturbation theory,” J. Comput. Chem. 34, 2327–2344 (2013). 10.1002/jcc.23391 [DOI] [PubMed] [Google Scholar]
- 62.Santra G., Sylvetsky N., and Martin J. M. L., “Minimally empirical double-hybrid functionals trained against the GMTKN55 database: revDSD-PBEP86-D4, revDOD-PBE-D4, and DOD-SCAN-D4,” J. Phys. Chem. A 123, 5129–5143 (2019). 10.1021/acs.jpca.9b03157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Grimme S., Antony J., Ehrlich S., and Krieg H., “A consistent and accurate ab initio parameterization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu,” J. Chem. Phys. 132, 154104 (2010). 10.1063/1.3382344 [DOI] [PubMed] [Google Scholar]
- 64.Witte J., Mardirossian N., Neaton J. B., and Head-Gordon M., “Assessing DFT-D3 damping functions across widely used density functionals: Can we do better?,” J. Chem. Theory Comput. 13, 2043–2052 (2017). 10.1021/acs.jctc.7b00176 [DOI] [PubMed] [Google Scholar]
- 65.Caldeweyher E., Ehlert S., Hansen A., Neugebauer H., Spicher S., Bannwarth C., and Grimme S., “A generally applicable atomic-charge dependent London dispersion correction,” J. Chem. Phys. 150, 154122 (2019). 10.1063/1.5090222 [DOI] [PubMed] [Google Scholar]
- 66.Vydrov O. A., Wu Q., and Van Voorhis T., “Self-consistent implementation of a nonlocal van der Waals density functional with a Gaussian basis set,” J. Chem. Phys. 129, 014106 (2008). 10.1063/1.2948400 [DOI] [PubMed] [Google Scholar]
- 67.Vydrov O. A. and Van Voorhis T., “Nonlocal van der Waals density functional made simple,” Phys. Rev. Lett. 103, 063004 (2009). 10.1103/PhysRevLett.103.063004 [DOI] [PubMed] [Google Scholar]
- 68.Vydrov O. A. and Van Voorhis T., “Implementation and assessment of a simple nonlocal van der Waals density functional,” J. Chem. Phys. 132, 164113 (2010). 10.1063/1.3398840 [DOI] [PubMed] [Google Scholar]
- 69.Becke A. D. and Johnson E. R., “Exchange-hole dipole moment and the dispersion interaction,” J. Chem. Phys. 122, 154104 (2005). 10.1063/1.1884601 [DOI] [PubMed] [Google Scholar]
- 70.Kong J., Gan Z., Proynov E., Freindorf M., and Furlani T., “Efficient computation of the dispersion interaction with density-functional theory,” Phys. Rev. A 79, 042510 (2009). 10.1103/physreva.79.042510 [DOI] [Google Scholar]
- 71.Tkatchenko A. and Scheffler M., “Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data,” Phys. Rev. Lett. 102, 073005 (2009). 10.1103/PhysRevLett.102.073005 [DOI] [PubMed] [Google Scholar]
- 72.Tkatchenko A., R. A. DiStasio, Jr., Car R., and Scheffler M., “Accurate and efficient method for many-body van der Waals interactions,” Phys. Rev. Lett. 108, 236402 (2012). 10.1103/physrevlett.108.236402 [DOI] [PubMed] [Google Scholar]
- 73.Ambrosetti A., Reilly A. M., R. A. DiStasio, Jr., and Tkatchenko A., “Long-range correlation energy calculated from coupled atomic response functions,” J. Chem. Phys. 140, 18A508 (2014). 10.1063/1.4865104 [DOI] [PubMed] [Google Scholar]
- 74.Hermann J., R. A. DiStasio, Jr., and Tkatchenko A., “First-principles models for van der Waals interactions in molecules and materials: Concepts, theory, and applications,” Chem. Rev. 117, 4714–4758 (2017). 10.1021/acs.chemrev.6b00446 [DOI] [PubMed] [Google Scholar]
- 75.Weigend F. and Ahlrichs R., “Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy,” Phys. Chem. Chem. Phys. 7, 3297–3305 (2005). 10.1039/b508541a [DOI] [PubMed] [Google Scholar]
- 76.Rappoport D. and Furche F., “Property-optimized Gaussian basis sets for molecular response calculations,” J. Chem. Phys. 133, 134105 (2010). 10.1063/1.3484283 [DOI] [PubMed] [Google Scholar]
- 77.Witte J., Neaton J. B., and Head-Gordon M., “Effective empirical corrections for basis set superposition error in the def2-SVPD basis: gCP and DFT-C,” J. Chem. Phys. 146, 234105 (2017). 10.1063/1.4986962 [DOI] [PubMed] [Google Scholar]
- 78.Dasgupta S. and Herbert J. M., “Standard grids for high-precision integration of modern density functionals: SG-2 and SG-3,” J. Comput. Chem. 38, 869–882 (2017). 10.1002/jcc.24761 [DOI] [PubMed] [Google Scholar]
- 79.Pople J. A., “Theoretical models for chemistry,” in Energy, Structure, and Reactivity: Proceedings of the 1972 Boulder Summer Research Conference on Theoretical Chemistry, edited by Smith D. W. and McRae W. B. (John Wiley & Sons, New York, 1973), pp. 51–61. [Google Scholar]
- 80.Hehre W. J., Radom L., Schleyer P. V. R., and Pople J. A., Ab Initio Molecular Orbital Theory (Wiley, New York, 1986). [Google Scholar]
- 81.Veccham S. P. and Head-Gordon M., “Density functionals for hydrogen storage: Defining the H2Bind275 test set with ab initio benchmarks and assessment of 55 functionals,” J. Chem. Theory Comput. 16, 4963–4982 (2020). 10.1021/acs.jctc.0c00292 [DOI] [PubMed] [Google Scholar]
- 82.Loipersberger M., Zee D. Z., Panetier J. A., Chang C. J., Long J. R., and Head-Gordon M., “Computational study of an iron(II) polypyridine electrocatalyst for CO2 reduction: Key roles for intramolecular interactions in CO2 binding and proton transfer,” Inorg. Chem. 59, 8146–8160 (2020). 10.1021/acs.inorgchem.0c00454 [DOI] [PubMed] [Google Scholar]
- 83.Loipersberger M., Cabral D. G. A., Chu D. B. K., and Head-Gordon M., “Mechanistic insights into Co and Fe quaterpyridine-based CO2 reduction catalysts: Metal–ligand orbital interaction as the key driving force for distinct pathways,” J. Am. Chem. Soc. 143, 744–763 (2021). 10.1021/jacs.0c09380 [DOI] [PubMed] [Google Scholar]
- 84.Tawada Y., Tsuneda T., Yanagisawa S., Yanai T., and Hirao K., “A long-range corrected time-dependent density functional theory,” J. Chem. Phys. 120, 8425–8433 (2004). 10.1063/1.1688752 [DOI] [PubMed] [Google Scholar]
- 85.Lange A. W., Rohrdanz M. A., and Herbert J. M., “Charge-transfer excited states in a π-stacked adenine dimer, as predicted using long-range-corrected time-dependent density functional theory,” J. Phys. Chem. B, 112, 6304–6308 (2008); 10.1021/jp802058k [DOI] [PubMed] [Google Scholar]; Erratum, J. Phys. Chem. B 112, 7345 (2008). 10.1021/jp803803j [DOI] [Google Scholar]
- 86.Rohrdanz M. A. and Herbert J. M., “Simultaneous benchmarking of ground- and excited-state properties with long-range-corrected density functional theory,” J. Chem. Phys. 129, 034107 (2008). 10.1063/1.2954017 [DOI] [PubMed] [Google Scholar]
- 87.Rohrdanz M. A., Martins K. M., and Herbert J. M., “A long-range-corrected density functional that performs well for both ground-state properties and time-dependent density functional theory excitation energies, including charge-transfer excited states,” J. Chem. Phys. 130, 054112 (2009). 10.1063/1.3073302 [DOI] [PubMed] [Google Scholar]
- 88.Richard R. M. and Herbert J. M., “Time-dependent density-functional description of the 1La state in polycyclic aromatic hydrocarbons: Charge-transfer character in disguise?,” J. Chem. Theory Comput. 7, 1296–1306 (2011). 10.1021/ct100607w [DOI] [PubMed] [Google Scholar]
- 89.Alam B., Morrison A. F., and Herbert J. M., “Charge separation and charge transfer in the low-lying excited states of pentacene,” J. Phys. Chem. C 124, 24653–24666 (2020). 10.1021/acs.jpcc.0c07932 [DOI] [Google Scholar]
- 90.Goerigk L., Hansen A., Bauer C., Ehrlich S., Najibi A., and Grimme S., “A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions,” Phys. Chem. Chem. Phys. 19, 32184–32215 (2017). 10.1039/c7cp04913g [DOI] [PubMed] [Google Scholar]
- 91.Najibi A. and Goerigk L., “The nonlocal kernel in van der Waals density functionals as an additive correction: An extensive analysis with special emphasis on the B97M-V and ωB97M-V approches,” J. Chem. Theory Comput. 14, 5725–5738 (2018). 10.1021/acs.jctc.8b00842 [DOI] [PubMed] [Google Scholar]
- 92.Manzer S., Horn P. R., Mardirossian N., and Head-Gordon M., “Fast, accurate evaluation of exact exchange: The occ-RI-K algorithm,” J. Chem. Phys. 143, 024113 (2015). 10.1063/1.4923369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Dohm S., Hansen A., Steinmetz M., Grimme S., and Checinski M. P., “Comprehensive thermochemical benchmark set of realistic closed-shell metal organic reactions,” J. Chem. Theory Comput. 14, 2596–2608 (2018). 10.1021/acs.jctc.7b01183 [DOI] [PubMed] [Google Scholar]
- 94.Chan B., Gill P. M. W., and Kimura M., “Assessment of DFT methods for transition metals with the TMC151 compilation of data sets and comparison with accuracies for main-group chemistry,” J. Chem. Theory Comput. 15, 3610–3622 (2019). 10.1021/acs.jctc.9b00239 [DOI] [PubMed] [Google Scholar]
- 95.Medvedev M. G., Bushmarinov I. S., Sun J., Perdew J. P., and Lyssenko K. A., “Density functional theory is straying from the path toward the exact functional,” Science 355, 49–52 (2017). 10.1126/science.aah5975 [DOI] [PubMed] [Google Scholar]
- 96.Verma P. and Truhlar D. G., “Can Kohn–Sham density functional theory predict accurate charge distributions for both single-reference and multi-reference molecules?,” Phys. Chem. Chem. Phys. 19, 12898–12912 (2017). 10.1039/c7cp01576c [DOI] [PubMed] [Google Scholar]
- 97.Hait D. and Head-Gordon M., “How accurate is density functional theory at predicting dipole moments? An assessment using a new database of 200 benchmark values,” J. Chem. Theory Comput. 14, 1969–1981 (2018). 10.1021/acs.jctc.7b01252 [DOI] [PubMed] [Google Scholar]
- 98.Hait D. and Head-Gordon M., “Communication: xDH double hybrid functionals can be qualitatively incorrect for non-equilibrium geometries: Dipole moment inversion and barriers to radical-radical association using XYG3 and XYGJ-OS,” J. Chem. Phys. 148, 171102 (2018). 10.1063/1.5031027 [DOI] [PubMed] [Google Scholar]
- 99.Hait D., Liang Y. H., and Head-Gordon M., “Too big, too small, or just right? A benchmark assessment of density functional theory for predicting the spatial extent of the electron density of small chemical systems,” J. Chem. Phys. 154, 074109 (2021). 10.1063/5.0038694 [DOI] [PubMed] [Google Scholar]
- 100.Hait D. and Head-Gordon M., “How accurate are static polarizability predictions from density functional theory? An assessment of over 132 species at equilibrium geometry,” Phys. Chem. Chem. Phys. 20, 19800–19810 (2018). 10.1039/c8cp03569e [DOI] [PubMed] [Google Scholar]
- 101.Flaig D., Maurer M., Hanni M., Braunger K., Kick L., Thubauville M., and Ochsenfeld C., “Benchmarking hydrogen and carbon NMR chemical shifts at HF, DFT, and MP2 levels,” J. Chem. Theory Comput. 10, 572–578 (2014). 10.1021/ct400780f [DOI] [PubMed] [Google Scholar]
- 102.Chai J.-D., “Density functional theory with fractional orbital occupations,” J. Chem. Phys. 136, 154104 (2012). 10.1063/1.3703894 [DOI] [PubMed] [Google Scholar]
- 103.Chai J.-D., “Thermally-assisted-occupation density functional theory with generalized-gradient approximations,” J. Chem. Phys. 140, 18A521 (2014). 10.1063/1.4867532 [DOI] [PubMed] [Google Scholar]
- 104.Chai J.-D., “Role of exact exchange in thermally-assisted-occupation density functional theory: A proposal of new hybrid schemes,” J. Chem. Phys. 146, 044102 (2017). 10.1063/1.4974163 [DOI] [PubMed] [Google Scholar]
- 105.Rabuck A. D. and Scuseria G. E., “Improving self-consistent field convergence by varying occupation numbers,” J. Chem. Phys. 110, 695 (1999). 10.1063/1.478177 [DOI] [Google Scholar]
- 106.Lin C.-Y., Hui K., Chung J.-H., and Chai J.-D., “Self-consistent determination of the fictitious temperature in thermally-assisted-occupation density functional theory,” RSC Adv. 7, 50496–50507 (2017). 10.1039/c7ra10241k [DOI] [Google Scholar]
- 107.Wu C.-S. and Chai J.-D., “Electronic properties of zigzag graphene nanoribbons studied by TAO-DFT,” J. Chem. Theory Comput. 11, 2003–2011 (2015). 10.1021/ct500999m [DOI] [PubMed] [Google Scholar]
- 108.Wu C.-S., Lee P.-Y., and Chai J.-D., “Electronic properties of cyclacenes from TAO-DFT,” Sci. Rep. 6, 37249 (2016). 10.1038/srep37249 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Yeh C.-N. and Chai J.-D., “Role of Kekulé and non-Kekulé structures in the radical character of alternant polycyclic aromatic hydrocarbons: A TAO-DFT study,” Sci. Rep. 6, 30562 (2016). 10.1038/srep30562 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Seenithurai S. and Chai J.-D., “Effect of Li adsorption on the electronic and hydrogen storage properties of acenes: A dispersion-corrected TAO-DFT study,” Sci. Rep. 6, 33081 (2016). 10.1038/srep33081 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Seenithurai S. and Chai J.-D., “TAO-DFT investigation of electronic properties of linear and cyclic carbon chains,” Sci. Rep. 10, 13133 (2020). 10.1038/s41598-020-70023-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Li S. and Chai J.-D., “TAO-DFT-based ab initio molecular dynamics,” Front. Chem. 8, 589432 (2020). 10.3389/fchem.2020.589432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Elliott P., Furche F., and Burke K., “Excited states from time-dependent density functional theory,” in Reviews in Computational Chemistry (Wiley-VCH, 2009), Vol. 26, Chap. 3, pp. 91–165. [Google Scholar]
- 114.Dreuw A. and Head-Gordon M., “Single-reference ab initio methods for the calculation of excited states of large molecules,” Chem. Rev. 105, 4009–4037 (2005). 10.1021/cr0505627 [DOI] [PubMed] [Google Scholar]
- 115.Furche F., “On the density matrix based approach to time-dependent density functional response theory,” J. Chem. Phys. 114, 5982–5992 (2001). 10.1063/1.1353585 [DOI] [Google Scholar]
- 116.Furche F. and Ahlrichs R., “Adiabatic time-dependent density functional methods for excited state properties,” J. Chem. Phys., 117, 7433–7447 (2002); 10.1063/1.1508368 [DOI] [Google Scholar]; Erratum, J. Chem. Phys. 121, 12772–12 773 (2004). 10.1063/1.1824903 [DOI] [Google Scholar]
- 117.Provorse M. R. and Isborn C. M., “Electron dynamics with real-time time-dependent density functional theory,” Int. J. Quantum Chem. 116, 739–749 (2016). 10.1002/qua.25096 [DOI] [Google Scholar]
- 118.Li X., Govind N., Isborn C., DePrince A. E. III, and Lopata K., “Real-time time-dependent electronic structure theory,” Chem. Rev. 120, 9951–9993 (2020). 10.1021/acs.chemrev.0c00223 [DOI] [PubMed] [Google Scholar]
- 119.Zhu Y. and Herbert J. M., “Self-consistent predictor/corrector algorithms for stable and efficient integration of the time-dependent Kohn-Sham equation,” J. Chem. Phys. 148, 044117 (2018). 10.1063/1.5004675 [DOI] [PubMed] [Google Scholar]
- 120.Zhu Y., “Implementation of real-time time-dependent density functional theory and applications from the weak field to the strong field regime,” Ph.D. thesis, The Ohio State University, Columbus, OH, 2020. [Google Scholar]
- 121.Zhu Y., Alam B., and Herbert J. M., “Broadband x-ray absorption spectra from time-dependent Kohn-Sham calculations,” 10.26434/chemrxiv.14766960.v1 (2021). [DOI]
- 122.Dreuw A., Weisman J. L., and Head-Gordon M., “Long-range charge-transfer excited states in time-dependent density functional theory require non-local exchange,” J. Chem. Phys. 119, 2943–2946 (2003). 10.1063/1.1590951 [DOI] [Google Scholar]
- 123.Dreuw A. and Head-Gordon M., “Failure of time-dependent density functional theory for long-range charge-transfer excited-states: The zincbacteriochlorin–bacteriochlorin and bacteriochlorophyll–spheroidene complexes,” J. Am. Chem. Soc. 126, 4007–4016 (2004). 10.1021/ja039556n [DOI] [PubMed] [Google Scholar]
- 124.Magyar R. J. and Tretiak S., “Dependence of spurious charge-transfer excited states on orbital exchange in TDDFT: Large molecules and clusters,” J. Chem. Theory Comput. 3, 976–987 (2007). 10.1021/ct600282k [DOI] [PubMed] [Google Scholar]
- 125.Lange A. and Herbert J. M., “Simple methods to reduce charge-transfer contamination in time-dependent density-functional calculations of clusters and liquids,” J. Chem. Theory Comput. 3, 1680–1690 (2007). 10.1021/ct700125v [DOI] [PubMed] [Google Scholar]
- 126.Lange A. W. and Herbert J. M., “Both intra- and interstrand charge-transfer excited states in B-DNA are present at energies comparable to, or just above, the 1ππ* excitonic bright states,” J. Am. Chem. Soc. 131, 3913–3922 (2009). 10.1021/ja808998q [DOI] [PubMed] [Google Scholar]
- 127.Carter-Fenk K., Mundy C. J., and Herbert J. M., “Natural charge-transfer analysis: Eliminating spurious charge-transfer states in time-dependent density functional theory via diabatization, with application to projection-based embedding,” J. Chem. Theory Comput. 17, 4195–4210 (2021). 10.1021/acs.jctc.1c00412 [DOI] [PubMed] [Google Scholar]
- 128.Laurent A. D. and Jacquemin D., “TD-DFT benchmarks: A review,” Int. J. Quantum Chem. 113, 2019–2039 (2013). 10.1002/qua.24438 [DOI] [Google Scholar]
- 129.Henderson T. M., Janesko B. G., and Scuseria G. E., “Generalized gradient approximation model exchange holes for range-separated hybrids,” J. Chem. Phys. 128, 194105 (2008). 10.1063/1.2921797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Iikura H., Tsuneda T., Yanai T., and Hirao K., “A long-range correction scheme for generalized-gradient-approximation exchange functionals,” J. Chem. Phys. 115, 3540–3544 (2001). 10.1063/1.1383587 [DOI] [Google Scholar]
- 131.Verma P., Wang Y., Ghosh S., He X., and Truhlar D. G., “Revised M11 exchange-correlation functional for electronic excitation energies and ground-state properties,” J. Phys. Chem. A 123, 2966–2990 (2019). 10.1021/acs.jpca.8b11499 [DOI] [PubMed] [Google Scholar]
- 132.Baer R., Livshits E., and Salzner U., “Tuned range-separated hybrids in density functional theory,” Annu. Rev. Phys. Chem. 61, 85–109 (2010). 10.1146/annurev.physchem.012809.103321 [DOI] [PubMed] [Google Scholar]
- 133.Refaely-Abramson S., Baer R., and Kronik L., “Fundamental and excitation gaps in molecules of relevance for organic photovoltaics from an optimally tuned range-separated hybrid functional,” Phys. Rev. B 84, 075144 (2011). 10.1103/physrevb.84.075144 [DOI] [Google Scholar]
- 134.Kümmel S., “Charge-transfer excitations: A challenge for time-dependent density functional theory that has been met,” Adv. Energy Mater. 7, 1700440 (2017). 10.1002/aenm.201700440 [DOI] [Google Scholar]
- 135.Modrzejewski M., Rajchel Ł., Chalasinski G., and Szczesniak M. M., “Density-dependent onset of the long-range exchange: A key to donor–acceptor properties,” J. Phys. Chem. A 117, 11580–11586 (2013). 10.1021/jp4088404 [DOI] [PubMed] [Google Scholar]
- 136.Lao K. U. and Herbert J. M., “Atomic orbital implementation of extended symmetry-adapted perturbation theory (XSAPT) and benchmark calculations for large supramolecular complexes,” J. Chem. Theory Comput. 14, 2955–2978 (2018). 10.1021/acs.jctc.8b00058 [DOI] [PubMed] [Google Scholar]
- 137.Gray M. and Herbert J. M., “Simplified tuning of long-range corrected density functionals for use in symmetry-adapted perturbation theory,” J. Chem. Phys. 155, 034103 (2021). 10.1063/5.0059364 [DOI] [PubMed] [Google Scholar]
- 138.Yarkony D. R., “Conical intersections: The new conventional wisdom,” J. Phys. Chem. A 105, 6277–6293 (2001). 10.1021/jp003731u [DOI] [Google Scholar]
- 139.Matsika S. and Krause P., “Nonadiabatic events and conical intersections,” Annu. Rev. Phys. Chem. 62, 621–643 (2011). 10.1146/annurev-physchem-032210-103450 [DOI] [PubMed] [Google Scholar]
- 140.Zhang X. and Herbert J. M., “Excited-state deactivation pathways in uracil versus hydrated uracil: Solvatochromatic shift in the 1nπ* state is the key,” J. Phys. Chem. B 118, 7806–7817 (2014). 10.1021/jp412092f [DOI] [PubMed] [Google Scholar]
- 141.Herbert J. M., Zhang X., Morrison A. F., and Liu J., “Beyond time-dependent density functional theory using only single excitations: Methods for computational studies of excited states in complex systems,” Acc. Chem. Res. 49, 931–941 (2016). 10.1021/acs.accounts.6b00047 [DOI] [PubMed] [Google Scholar]
- 142.Zhang X. and Herbert J. M., “Analytic derivative couplings for spin-flip configuration interaction singles and spin-flip time-dependent density functional theory,” J. Chem. Phys. 141, 064104 (2014). 10.1063/1.4891984 [DOI] [PubMed] [Google Scholar]
- 143.Ou Q., Fatehi S., Alguire E., Shao Y., and Subotnik J. E., “Derivative couplings between TD-DFT excited states obtained by direct differentiation in the Tamm-Dancoff approximation,” J. Chem. Phys. 141, 024114 (2014). 10.1063/1.4887256 [DOI] [PubMed] [Google Scholar]
- 144.Alguire E. C., Ou Q., and Subotnik J. E., “Calculating derivative couplings between time-dependent Hartree–Fock excited states with pseudo-wavefunctions,” J. Phys. Chem. B 119, 7140–7149 (2015). 10.1021/jp505767b [DOI] [PubMed] [Google Scholar]
- 145.Ou Q., Alguire E. C., and Subotnik J. E., “Derivative couplings between time-dependent density functional theory excited states in the random-phase approximation based on pseudo-wavefunctions: Behavior around conical intersections,” J. Phys. Chem. B 119, 7150–7161 (2015). 10.1021/jp5057682 [DOI] [PubMed] [Google Scholar]
- 146.Bearpark M. J., Robb M. A., and Schlegel H. B., “A direct method for the location of the lowest energy point on a potential surface crossing,” Chem. Phys. Lett. 223, 269–274 (1994). 10.1016/0009-2614(94)00433-1 [DOI] [Google Scholar]
- 147.Maeda S., Ohno K., and Morokuma K., “Updated branching plane for finding conical intersections without coupling derivative vectors,” J. Chem. Theory Comput. 6, 1538–1545 (2010). 10.1021/ct1000268 [DOI] [PubMed] [Google Scholar]
- 148.Levine B. G., Coe J. D., and Martínez T. J., “Optimizing conical intersections without derivative coupling vectors: Application to multistate multireference second-order perturbation theory (MS-CASPT2),” J. Phys. Chem. B 112, 405–413 (2008). 10.1021/jp0761618 [DOI] [PubMed] [Google Scholar]
- 149.Send R. and Furche F., “First-order nonadiabatic couplings from time-dependent hybrid density functional response theory: Consistent formalism, implementation, and performance,” J. Chem. Phys. 132, 044107 (2010). 10.1063/1.3292571 [DOI] [PubMed] [Google Scholar]
- 150.Parker S. M., Roy S., and Furche F., “Multistate hybrid time-dependent density functional theory with surface hopping accurately captures ultrafast thymine photodeactivation,” Phys. Chem. Chem. Phys. 21, 18999–19010 (2019). 10.1039/c9cp03127h [DOI] [PubMed] [Google Scholar]
- 151.Bellonzi N., Medders G. R., Epifanovsky E., and Subotnik J. E., “Configuration interaction singles with spin-orbit coupling: Constructing spin-adiabatic states and their analytical nuclear gradients,” J. Chem. Phys. 150, 014106 (2019). 10.1063/1.5045484 [DOI] [PubMed] [Google Scholar]
- 152.Bellonzi N., Alguire E., Fatehi S., Shao Y., and Subotnik J. E., “TD-DFT spin-adiabats with analytic nonadiabatic derivative couplings,” J. Chem. Phys. 152, 044112 (2020). 10.1063/1.5126440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Tully J. C., “Molecular dynamics with electronic transitions,” J. Chem. Phys. 93, 1061–1071 (1990). 10.1063/1.459170 [DOI] [Google Scholar]
- 154.Hammes-Schiffer S. and Tully J. C., “Proton transfer in solution: Molecular dynamics with quantum transitions,” J. Chem. Phys. 101, 4657–4667 (1994). 10.1063/1.467455 [DOI] [Google Scholar]
- 155.Jain A., Alguire E., and Subotnik J. E., “An efficient, augmented surface hopping algorithm that includes decoherence for use in large-scale simulations,” J. Chem. Theory Comput. 12, 5256–5258 (2016). 10.1021/acs.jctc.6b00673 [DOI] [PubMed] [Google Scholar]
- 156.Subotnik J. E., Jain A., Landry B., Petit A., Ouyang W., and Bellonzi N., “Understanding the surface hopping view of electronic transitions and decoherence,” Annu. Rev. Phys. Chem. 67, 387–417 (2016). 10.1146/annurev-physchem-040215-112245 [DOI] [PubMed] [Google Scholar]
- 157.Landry B. R. and Subotnik J. E., “How to recover Marcus theory with fewest switches surface hopping: Add just a touch of decoherence,” J. Chem. Phys. 137, 22A513 (2012). 10.1063/1.4733675 [DOI] [PubMed] [Google Scholar]
- 158.Jain A., Herman M. F., Ouyang W., and Subotnik J. E., “Surface hopping, transition state theory and decoherence. I. Scattering theory and time-reversibility,” J. Chem. Phys. 143, 134106 (2015). 10.1063/1.4930548 [DOI] [PubMed] [Google Scholar]
- 159.Jain A. and Subotnik J. E., “Surface hopping, transition state theory and decoherence. II. Thermal rate constants and detailed balance,” J. Chem. Phys. 143, 134107 (2015). 10.1063/1.4930549 [DOI] [PubMed] [Google Scholar]
- 160.Menger M. F. S. J., Ehrmaier J., and Faraji S., “PySurf: A framework for database accelerated direct dynamics,” J. Chem. Theory Comput. 16, 7681–7689 (2020). 10.1021/acs.jctc.0c00825 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Levine B. G., Ko C., Quenneville J., and Martínez T. J., “Conical intersections and double excitations in time-dependent density functional theory,” Mol. Phys. 104, 1039–1051 (2006). 10.1080/00268970500417762 [DOI] [Google Scholar]
- 162.Yue L., Liu Y., and Zhu C., “Performance of TDDFT with and without spin-flip in trajectory surface hopping dynamics: cis–trans azobenzene photoisomerization,” Phys. Chem. Chem. Phys. 20, 24123–24139 (2018). 10.1039/c8cp03851a [DOI] [PubMed] [Google Scholar]
- 163.Shao Y., Head-Gordon M., and Krylov A. I., “The spin-flip approach within time-dependent density functional theory: Theory and applications to diradicals,” J. Chem. Phys. 118, 4807–4818 (2003). 10.1063/1.1545679 [DOI] [Google Scholar]
- 164.Bernard Y. A., Shao Y., and Krylov A. I., “General formulation of spin-flip time-dependent density functional theory using non-collinear kernels: Theory, implementation, and benchmarks,” J. Chem. Phys. 136, 204103 (2012). 10.1063/1.4714499 [DOI] [PubMed] [Google Scholar]
- 165.Casanova D. and Krylov A. I., “Spin-flip methods in quantum chemistry,” Phys. Chem. Chem. Phys. 22, 4326–4342 (2020). 10.1039/c9cp06507e [DOI] [PubMed] [Google Scholar]
- 166.Harabuchi Y., Keipert K., Zahariev F., Taketsugu T., and Gordon M. S., “Dynamics simulations with spin-flip time-dependent density functional theory: Photoisomerization and photocyclization mechanisms of cis-stilbene in ππ* states,” J. Phys. Chem. A 118, 11987–11998 (2014). 10.1021/jp5072428 [DOI] [PubMed] [Google Scholar]
- 167.Maeda S., Harabuchi Y., Taketsugu T., and Morokuma K., “Systematic exploration of minimum energy conical intersection structures near the Franck–Condon region,” J. Phys. Chem. A 118, 12050–12058 (2014). 10.1021/jp507698m [DOI] [PubMed] [Google Scholar]
- 168.Minezawa N. and Nakajima T., “Trajectory surface hopping molecular dynamics simulation by spin-flip time-dependent density functional theory,” J. Chem. Phys. 150, 204120 (2019). 10.1063/1.5096217 [DOI] [PubMed] [Google Scholar]
- 169.Zhang X. and Herbert J. M., “Spin-flip, tensor equation-of-motion configuration interaction with a density-functional correction: A spin-complete method for exploring excited-state potential energy surfaces,” J. Chem. Phys. 143, 234107 (2015). 10.1063/1.4937571 [DOI] [PubMed] [Google Scholar]
- 170.Sears J. S., Sherrill C. D., and Krylov A. I., “A spin-complete version of the spin-flip approach to bond breaking: What is the impact of obtaining spin eigenfunctions?,” J. Chem. Phys. 118, 9084–9094 (2003). 10.1063/1.1568735 [DOI] [Google Scholar]
- 171.Krylov A. I., “The spin-flip equation-of-motion coupled-cluster electronic structure method for a description of excited states, bond-breaking, diradicals, and triradicals,” Acc. Chem. Res. 39, 83 (2006). 10.1021/ar0402006 [DOI] [PubMed] [Google Scholar]
- 172.Krylov A. I., “The quantum chemistry of open-shell species,” in Reviews in Computational Chemistry, edited by Parrill A. L. and Lipkowitz K. B. (John Wiley & Sons, Inc., 2017), Vol. 30, Chap. 4, pp. 151–224. [Google Scholar]
- 173.Li Z. and Liu W., “Spin-adapted open-shell random phase approximation and time-dependent density functional theory. I. Theory,” J. Chem. Phys. 133, 064106 (2010). 10.1063/1.3463799 [DOI] [PubMed] [Google Scholar]
- 174.Li Z., Liu W., Zhang Y., and Suo B., “Spin-adapted open-shell time-dependent density functional theory. II. Theory and pilot application,” J. Chem. Phys. 134, 134101 (2011). 10.1063/1.3573374 [DOI] [PubMed] [Google Scholar]
- 175.Li Z. and Liu W., “Spin-adapted open-shell time-dependent density functional theory. III. An even better and simpler formulation,” J. Chem. Phys. 135, 194106 (2011). 10.1063/1.3660688 [DOI] [PubMed] [Google Scholar]
- 176.Krylov A. I., “Triradicals,” J. Phys. Chem. A 109, 10638–10645 (2005). 10.1021/jp0528212 [DOI] [PubMed] [Google Scholar]
- 177.Orms N. and Krylov A. I., “Singlet–triplet energy gaps and the degree of diradical character in binuclear copper molecular magnets characterized by spin-flip density functional theory,” Phys. Chem. Chem. Phys. 20, 13127–13144 (2018). 10.1039/c7cp07356a [DOI] [PubMed] [Google Scholar]
- 178.Tussupbayev S., Govind N., Lopata K., and Cramer C. J., “Comparison of real-time and linear-response time-dependent density functional theories for molecular chromophores ranging from sparse to high densities of states,” J. Chem. Theory Comput. 11, 1102–1109 (2015). 10.1021/ct500763y [DOI] [PubMed] [Google Scholar]
- 179.Ullrich C. A. and Bandrauk A. D., “Atoms and molecules in strong laser fields,” in Fundamentionals of Time-Dependent Density Functional Theory, Lecture Notes in Physics Vol. 837, edited by Marques M. A. L., Maitra N. T., Nogueira F. M. S., Gross E. K. U., and Rubio A. (Springer-Verlag, Berlin, 2012), Chap. 18, pp. 351–371. [Google Scholar]
- 180.Krause P. and Schlegel H. B., “Strong field ionization rates of linear polyenes simulated with time-dependent configuration interaction and an absorbing potential,” J. Chem. Phys. 141, 174104 (2014). 10.1063/1.4900576 [DOI] [PubMed] [Google Scholar]
- 181.Krause P., Sonk J. A., and Schlegel H. B., “Strong field ionization rates simulated with time-dependent configuration interaction and an absorbing potential,” J. Chem. Phys. 140, 174113 (2014). 10.1063/1.4874156 [DOI] [PubMed] [Google Scholar]
- 182.Krause P. and Schlegel H. B., “Angle-dependent ionization of small molecules by time-dependent configuration interaction and an absorbing potential,” J. Phys. Chem. Lett. 6, 2140–2146 (2015). 10.1021/acs.jpclett.5b00929 [DOI] [PubMed] [Google Scholar]
- 183.Hoerner P. and Schlegel H. B., “Angular dependence of strong field ionization of CH3X (X = F, Cl, Br, or I) using time-dependent configuration interaction with an absorbing potential,” J. Phys. Chem. A 121, 5940–5946 (2017). 10.1021/acs.jpca.7b06108 [DOI] [PubMed] [Google Scholar]
- 184.Luppi E. and Head-Gordon M., “Computation of high-harmonic generation spectra of H2 and N2 in intense laser pulses using quantum chemistry methods and time-dependent density functional theory,” Mol. Phys. 110, 909–923 (2012). 10.1080/00268976.2012.675448 [DOI] [Google Scholar]
- 185.Luppi E. and Head-Gordon M., “The role of Rydberg and continuum levels in computing high harmonic generation spectra of the hydrogen atom using time-dependent configuration interaction,” J. Chem. Phys. 139, 164121 (2013). 10.1063/1.4824482 [DOI] [PubMed] [Google Scholar]
- 186.Luppi E. and Coccia E., “Probing the molecular frame of uracil and thymine with high-harmonic generation spectroscopy,” Phys. Chem. Chem. Phys. 23, 3729–3738 (2021). 10.1039/d0cp05559j [DOI] [PubMed] [Google Scholar]
- 187.Pauletti C. F., Coccia E., and Luppi E., “Role of exchange and correlation in high-harmonic generation spectra of H2, N2, and CO2: Real-time time-dependent electronic structure approaches,” J. Chem. Phys. 154, 014101 (2021). 10.1063/5.0033072 [DOI] [PubMed] [Google Scholar]
- 188.Li X., Smith S. M., Markevitch A. N., Romanov D. A., Levis R. J., and Schlegel H. B., “A time-dependent Hartree–Fock approach for studying the electronic optical response of molecules in intense fields,” Phys. Chem. Chem. Phys. 7, 233–239 (2005). 10.1039/b415849k [DOI] [PubMed] [Google Scholar]
- 189.Besley N. A., Peach M. J. G., and Tozer D. J., “Time-dependent density functional theory calculations of near-edge x-ray absorption fine structure with short-range corrected functionals,” Phys. Chem. Chem. Phys. 11, 10350–10358 (2009). 10.1039/b912718f [DOI] [PubMed] [Google Scholar]
- 190.Bruner A., LaMaster D., and Lopata K., “Accelerated broadband spectra using transition dipole decomposition and Padé approximants,” J. Chem. Theory Comput. 12, 3741–3750 (2016). 10.1021/acs.jctc.6b00511 [DOI] [PubMed] [Google Scholar]
- 191.Besley N. A., “Fast time-dependent density functional theory calculations of the x-ray absorption spectroscopy of large systems,” J. Chem. Theory Comput. 12, 5018–5025 (2016). 10.1021/acs.jctc.6b00656 [DOI] [PubMed] [Google Scholar]
- 192.Besley N. A., “Modeling of the spectroscopy of core electrons with density functional theory,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. (published online) (2021). 10.1002/wcms.1527 [DOI] [Google Scholar]
- 193.Kasper J. M., Lestrange P. J., Stetina T. F., and Li X., “Modeling L2,3-edge x-ray absorption spectroscopy with real-time exact two-component relativistic time-dependent density functional theory,” J. Chem. Theory Comput. 14, 1998–2006 (2018). 10.1021/acs.jctc.7b01279 [DOI] [PubMed] [Google Scholar]
- 194.Elliott P., Goldson S., Canahui C., and Maitra N. T., “Perspective on double-excitations in TDDFT,” Chem. Phys. 391, 110–119 (2011). 10.1016/j.chemphys.2011.03.020 [DOI] [Google Scholar]
- 195.Barca G. M. J., Gilbert A. T. B., and Gill P. M. W., “Excitation number: Characterizing multiply excited states,” J. Chem. Theory Comput. 14, 9–13 (2018). 10.1021/acs.jctc.7b00963 [DOI] [PubMed] [Google Scholar]
- 196.Gilbert A. T. B., Besley N. A., and Gill P. M. W., “Self-consistent field calculations of excited states using the maximum overlap method (MOM),” J. Phys. Chem. A 112, 13164–13171 (2008). 10.1021/jp801738f [DOI] [PubMed] [Google Scholar]
- 197.Besley N. A., Gilbert A. T. B., and Gill P. M. W., “Self-consistent-field calculations of core excited states,” J. Chem. Phys. 130, 124308 (2009). 10.1063/1.3092928 [DOI] [PubMed] [Google Scholar]
- 198.Barca G. M. J., Gilbert A. T. B., and Gill P. M. W., “Simple models for difficult electronic excitations,” J. Chem. Theory Comput. 14, 1501–1509 (2018). 10.1021/acs.jctc.7b00994 [DOI] [PubMed] [Google Scholar]
- 199.Hait D. and Head-Gordon M., “Excited state orbital optimization via minimizing the square of the gradient: General approach and application to singly and doubly excited states via density functional theory,” J. Chem. Theory Comput. 16, 1699–1710 (2020). 10.1021/acs.jctc.9b01127 [DOI] [PubMed] [Google Scholar]
- 200.Carter-Fenk K. and Herbert J. M., “State-targeted energy projection: A simple and robust approach to orbital relaxation of non-aufbau self-consistent field solutions,” J. Chem. Theory Comput. 16, 5067–5082 (2020). 10.1021/acs.jctc.0c00502 [DOI] [PubMed] [Google Scholar]
- 201.Loos P.-F., Boggio-Pasqua M., Scemama A., Caffarel M., and Jacquemin D., “Reference energies for double excitations,” J. Chem. Theory Comput. 15, 1939–1956 (2019). 10.1021/acs.jctc.8b01205 [DOI] [PubMed] [Google Scholar]
- 202.Stockett M. H., Musbat L., Kjær C., Houmøller J., Toker Y., Rubio A., Milne B. F., and Nielsen S. B., “The Soret absorption band of isolated chlorophyll a and b tagged with quaternary ammonium ions,” Phys. Chem. Chem. Phys. 17, 25793–25798 (2015). 10.1039/c5cp01513h [DOI] [PubMed] [Google Scholar]
- 203.Gouterman M., Wagnière G. H., and Snyder L. C., “Spectra of porphyrins: Part II. Four orbital model,” J. Mol. Spectrosc. 11, 108–127 (1963). 10.1016/0022-2852(63)90011-0 [DOI] [Google Scholar]
- 204.Ziegler T., Rauk A., and Baerends E. J., “On the calculation of multiplet energies by the Hartree-Fock-Slater method,” Theor. Chim. Acta 43, 261–271 (1977). 10.1007/bf00551551 [DOI] [Google Scholar]
- 205.Daul C., “Density functional theory applied to the excited states of coordination compounds,” Int. J. Quantum Chem. 52, 867–877 (1994). 10.1002/qua.560520414 [DOI] [Google Scholar]
- 206.Filatov M. and Shaik S., “Spin-restricted density functional approach to the open-shell problem,” Chem. Phys. Lett. 288, 689–697 (1998). 10.1016/s0009-2614(98)00364-9 [DOI] [Google Scholar]
- 207.Kowalczyk T., Tsuchimochi T., Chen P.-T., Top L., and Van Voorhis T., “Excitation energies and Stokes shifts from a restricted open-shell Kohn-Sham approach,” J. Chem. Phys. 138, 164101 (2013). 10.1063/1.4801790 [DOI] [PubMed] [Google Scholar]
- 208.Hait D., Zhu T., McMahon D. P., and Van Voorhis T., “Prediction of excited-state energies and singlet–triplet gaps of charge-transfer states using a restricted open-shell Kohn–Sham approach,” J. Chem. Theory Comput. 12, 3353–3359 (2016). 10.1021/acs.jctc.6b00426 [DOI] [PubMed] [Google Scholar]
- 209.Hait D. and Head-Gordon M., “Highly accurate prediction of core spectra of molecules at density functional theory cost: Attaining sub-electronvolt error from a restricted open-shell Kohn–Sham approach,” J. Phys. Chem. Lett. 11, 775–786 (2020). 10.1021/acs.jpclett.9b03661 [DOI] [PubMed] [Google Scholar]
- 210.Kowalczyk T., Yost S. R., and Van Voorhis T., “Assessment of the ΔSCF density functional theory approach for electronic excitations in organic dyes,” J. Chem. Phys. 134, 054128 (2011). 10.1063/1.3530801 [DOI] [PubMed] [Google Scholar]
- 211.Hait D., Haugen E. A., Yang Z., Oosterbaan K. J., Leone S. R., and Head-Gordon M., “Accurate prediction of core-level spectra of radicals at density functional theory cost via square gradient minimization and recoupling of mixed configurations,” J. Chem. Phys. 153, 134108 (2020). 10.1063/5.0018833 [DOI] [PubMed] [Google Scholar]
- 212.Hait D. and Head-Gordon M., “Orbital optimized density functional theory for electronic excited states,” J. Phys. Chem. Lett. 12, 4517–4529 (2021). 10.1021/acs.jpclett.1c00744 [DOI] [PubMed] [Google Scholar]
- 213.Helgaker T., Jørgensen P., and Olsen J., Molecular Electronic-Structure Theory (John Wiley & Sons, 2000). [Google Scholar]
- 214.Bartlett R. J., “How and why coupled-cluster theory became the preeminent method in ab initio quantum chemistry,” in Theory and Applications of Computational Chemistry: The First 40 Years, edited by Dykstra C., Frenking G., and Scuseria G. (Elsevier, 2005), Chap. 42, pp. 1191–1221. [Google Scholar]
- 215.Epifanovsky E., Zuev D., Feng X., Khistyaev K., Shao Y., and Krylov A. I., “General implementation of resolution-of-the-identity and Cholesky representations of electron-repulsion integrals within coupled-cluster and equation-of-motion methods: Theory and benchmarks,” J. Chem. Phys. 139, 134105 (2013). 10.1063/1.4820484 [DOI] [PubMed] [Google Scholar]
- 216.Feng X., Epifanovsky E., Gauss J., and Krylov A. I., “Implementation of analytic gradients for CCSD and EOM-CCSD using Cholesky decomposition of the electron-repulsion integrals and their derivatives: Theory and benchmarks,” J. Chem. Phys. 151, 014110 (2019). 10.1063/1.5100022 [DOI] [PubMed] [Google Scholar]
- 217.Landau A., Khistyaev K., Dolgikh S., and Krylov A. I., “Frozen natural orbitals for ionized states within equation-of-motion coupled-cluster formalism,” J. Chem. Phys. 132, 014109 (2010). 10.1063/1.3276630 [DOI] [PubMed] [Google Scholar]
- 218.Pokhilko P., Izmodenov D., and Krylov A. I., “Extension of frozen natural orbital approximation to open-shell references: Theory, implementation, and application to single-molecule magnets,” J. Chem. Phys. 152, 034105 (2019). 10.1063/1.5138643 [DOI] [PubMed] [Google Scholar]
- 219.Pokhilko P., Epifanovsky E., and Krylov A. I., “Double precision is not needed for many-body calculations: Emergent conventional wisdom,” J. Chem. Theory Comput. 14, 4088–4096 (2018). 10.1021/acs.jctc.8b00321 [DOI] [PubMed] [Google Scholar]
- 220.Pokhilko P. and Krylov A. I., “Quantitative El-Sayed rules for many-body wave functions from spinless transition density matrices,” J. Phys. Chem. Lett. 10, 4857–4862 (2019). 10.1021/acs.jpclett.9b02120 [DOI] [PubMed] [Google Scholar]
- 221.Pokhilko P. and Krylov A. I., “Effective Hamiltonians derived from equation-of-motion coupled-cluster wave functions: Theory and application to the Hubbard and Heisenberg Hamiltonians,” J. Chem. Phys. 152, 094108 (2020). 10.1063/1.5143318 [DOI] [PubMed] [Google Scholar]
- 222.Pokhilko P., Bezrukov D. S., and Krylov A. I., “Is solid copper oxalate a spin chain or a mixture of entangled spin pairs?,” J. Phys. Chem. C 125, 7502–7510 (2021). 10.1021/acs.jpcc.1c01548 [DOI] [Google Scholar]
- 223.Alessio M. and Krylov A. I., “Equation-of-motion coupled-cluster protocol for calculating magnetic properties: Theory and applications to single-molecule magnets,” J. Chem. Theory Comput. 17, 4225–4241 (2021). 10.1021/acs.jctc.1c00430 [DOI] [PubMed] [Google Scholar]
- 224.Krylov A. I., “Equation-of-motion coupled-cluster methods for open-shell and electronically excited species: The hitchhiker’s guide to Fock space,” Annu. Rev. Phys. Chem. 59, 433–462 (2008). 10.1146/annurev.physchem.59.032607.093602 [DOI] [PubMed] [Google Scholar]
- 225.Sneskov K. and Christiansen O., “Excited state coupled cluster methods,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2, 566–584 (2012). 10.1002/wcms.99 [DOI] [Google Scholar]
- 226.Bartlett R. J., “Coupled-cluster theory and its equation-of-motion extensions,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2, 126–138 (2012). 10.1002/wcms.76 [DOI] [Google Scholar]
- 227.Dreuw A. and Wormit M., “The algebraic diagrammatic construction scheme for the polarization propagator for the calculation of excited states,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 5, 82–95 (2015). 10.1002/wcms.1206 [DOI] [Google Scholar]
- 228.Menon A. S. and Radom L., “Consequences of spin contamination in unrestricted calculations on open-shell species: Effect of Hartree–Fock and Møller–Plesset contributions in hybrid and double-hybrid density functional theory approaches,” J. Phys. Chem. A 112, 13225–13230 (2008). 10.1021/jp803064k [DOI] [PubMed] [Google Scholar]
- 229.Thirman J. and Head-Gordon M., “Electrostatic domination of the effect of electron correlation in intermolecular interactions,” J. Phys. Chem. Lett. 5, 1380–1385 (2014). 10.1021/jz500165u [DOI] [PubMed] [Google Scholar]
- 230.Lochan R. C. and Head-Gordon M., “Orbital-optimized opposite-spin scaled second-order correlation: An economical method to improve the description of open-shell molecules,” J. Chem. Phys. 126, 164101 (2007). 10.1063/1.2718952 [DOI] [PubMed] [Google Scholar]
- 231.Neese F., Schwabe T., Kossmann S., Schirmer B., and Grimme S., “Assessment of orbital-optimized, spin-component scaled second-order many-body perturbation theory for thermochemistry and kinetics,” J. Chem. Theory Comput. 5, 3060–3073 (2009). 10.1021/ct9003299 [DOI] [PubMed] [Google Scholar]
- 232.Bozkaya U., “Orbital-optimized second-order perturbation theory with density-fitting and Cholesky decomposition approximations: An efficient implementation,” J. Chem. Theory Comput. 10, 2371–2378 (2014). 10.1021/ct500231c [DOI] [PubMed] [Google Scholar]
- 233.Stück D. and Head-Gordon M., “Regularized orbital-optimized second-order perturbation theory,” J. Chem. Phys. 139, 244109 (2013). 10.1063/1.4851816 [DOI] [PubMed] [Google Scholar]
- 234.Lee J. and Head-Gordon M., “Regularized orbital-optimized second-order Møller–Plesset perturbation theory: A reliable fifth-order-scaling electron correlation model with orbital energy dependent regularizers,” J. Chem. Theory Comput. 14, 5203–5219 (2018). 10.1021/acs.jctc.8b00731 [DOI] [PubMed] [Google Scholar]
- 235.Lee J. and Head-Gordon M., “Distinguishing artificial and essential symmetry breaking in a single determinant: Approach and application to the C60, C36, and C20 fullerenes,” Phys. Chem. Chem. Phys. 21, 4763–4768 (2019). 10.1039/c8cp07613h [DOI] [PubMed] [Google Scholar]
- 236.Stück D., Baker T. A., Zimmerman P., Kurlancheek W., and Head-Gordon M., “On the nature of electron correlation in C60,” J. Chem. Phys. 135, 194306 (2011). 10.1063/1.3661158 [DOI] [PubMed] [Google Scholar]
- 237.Jiménez-Hoyos C. A., Rodríguez-Guzmán R., and Scuseria G. E., “Polyradical character and spin frustration in fullerene molecules: An ab initio non-collinear Hartree–Fock study,” J. Phys. Chem. A 118, 9925–9940 (2014). 10.1021/jp508383z [DOI] [PubMed] [Google Scholar]
- 238.Lee J. and Head-Gordon M., “Two single-reference approaches to singlet biradicaloid problems: Complex, restricted orbitals and approximate spin-projection combined with regularized orbital-optimized Møller–Plesset perturbation theory,” J. Chem. Phys. 150, 244106 (2019). 10.1063/1.5097613 [DOI] [PubMed] [Google Scholar]
- 239.Bertels L. W., Lee J., and Head-Gordon M., “Third-order Møller–Plesset perturbation theory made useful? Choice of orbitals and scaling greatly improves accuracy for thermochemistry, kinetics, and intermolecular interactions,” J. Phys. Chem. Lett. 10, 4170–4176 (2019). 10.1021/acs.jpclett.9b01641 [DOI] [PubMed] [Google Scholar]
- 240.Rettig A., Hait D., Bertels L. W., and Head-Gordon M., “Third-order Møller–Plesset theory made more useful? The role of density functional theory orbitals,” J. Chem. Theory Comput. 16, 7473–7489 (2020). 10.1021/acs.jctc.0c00986 [DOI] [PubMed] [Google Scholar]
- 241.Dreuw A., “The algebraic-diagrammatic construction scheme for the polarization propagator,” in Quantum Chemistry and Dynamics of Excited States: Methods and Applications, edited by González L. and Lindh R. (Wiley, 2020), pp. 109–131. [Google Scholar]
- 242.Krauter C. M., Pernpointner M., and Dreuw A., “Application of the scaled-opposite-spin approximation to algebraic diagrammatic construction schemes of second order,” J. Chem. Phys. 138, 044107 (2013). 10.1063/1.4776675 [DOI] [PubMed] [Google Scholar]
- 243.Gulania S., Kjønstad E. F., Stanton J. F., Koch H., and Krylov A. I., “Equation-of-motion coupled-cluster method with double electron-attaching operators: Theory, implementation, and benchmarks,” J. Chem. Phys. 154, 114115 (2021). 10.1063/5.0041822 [DOI] [PubMed] [Google Scholar]
- 244.Rehn D. R. and Dreuw A., “Analytic nuclear gradients of the algebraic-diagrammatic construction scheme for the polarization propagator up to third order of perturbation theory,” J. Chem. Phys. 150, 174110 (2019). 10.1063/1.5085117 [DOI] [PubMed] [Google Scholar]
- 245.Levchenko S. V., Wang T., and Krylov A. I., “Analytic gradients for the spin-conserving and spin-flipping equation-of-motion coupled-cluster models with single and double substitutions,” J. Chem. Phys. 122, 224106 (2005). 10.1063/1.1877072 [DOI] [PubMed] [Google Scholar]
- 246.Dempwolff A. L., Paul A. C., Belogolova A. M., Trofimov A. B., and Dreuw A., “Intermediate state representation approach to physical properties of molecular electron-detached states. I. Theory and implementation,” J. Chem. Phys. 152, 024113 (2020). 10.1063/1.5137792 [DOI] [PubMed] [Google Scholar]
- 247.Dempwolff A. L., Paul A. C., Belogolova A. M., Trofimov A. B., and Dreuw A., “Intermediate state representation approach to physical properties of molecular electron-detached states. II. Benchmarking,” J. Chem. Phys. 152, 024125 (2020). 10.1063/1.5137794 [DOI] [PubMed] [Google Scholar]
- 248.Dempwolff A. L., Belogolova A. M., Trofimov A. B., and Dreuw A., “Intermediate state representation approach to physical properties of molecular electron-attached states: Theory, implementation, and benchmarking,” J. Chem. Phys. 154, 104117 (2021). 10.1063/5.0043337 [DOI] [PubMed] [Google Scholar]
- 249.Scott M., Rehn D. R., Coriani S., Norman P., and Dreuw A., “Electronic circular dichroism spectra using the algebraic diagrammatic construction schemes of the polarization propagator up to third order,” J. Chem. Phys. 154, 064107 (2021). 10.1063/5.0038315 [DOI] [PubMed] [Google Scholar]
- 250.Faraji S., Matsika S., and Krylov A. I., “Calculations of non-adiabatic couplings within equation-of-motion coupled-cluster framework: Theory, implementation, and validation against multi-reference methods,” J. Chem. Phys. 148, 044103 (2018). 10.1063/1.5009433 [DOI] [PubMed] [Google Scholar]
- 251.Epifanovsky E., Klein K., Stopkowicz S., Gauss J., and Krylov A. I., “Spin-orbit couplings within the equation-of-motion coupled-cluster framework: Theory, implementation, and benchmark calculations,” J. Chem. Phys. 143, 064102 (2015). 10.1063/1.4927785 [DOI] [PubMed] [Google Scholar]
- 252.Pokhilko P., Epifanovsky E., and Krylov A. I., “General framework for calculating spin–orbit couplings using spinless one-particle density matrices: Theory and application to the equation-of-motion coupled-cluster wave functions,” J. Chem. Phys. 151, 034106 (2019). 10.1063/1.5108762 [DOI] [PubMed] [Google Scholar]
- 253.Knippenberg S., Rehn D. R., Wormit M., Starcke J. H., Rusakova I. L., Trofimov A. B., and Dreuw A., “Calculations of nonlinear response properties using the intermediate state representation and the algebraic-diagrammatic construction polarization propagator approach: Two-photon absorption spectra,” J. Chem. Phys. 136, 064107 (2012). 10.1063/1.3682324 [DOI] [PubMed] [Google Scholar]
- 254.Nanda K. D. and Krylov A. I., “Two-photon absorption cross sections within equation-of-motion coupled-cluster formalism using resolution-of-the-identity and Cholesky decomposition representations: Theory, implementation, and benchmarks,” J. Chem. Phys. 142, 064118 (2015). 10.1063/1.4907715 [DOI] [PubMed] [Google Scholar]
- 255.Nanda K. D. and Krylov A. I., “Static polarizabilities for excited states within the spin-conserving and spin-flipping equation-of-motion coupled-cluster singles and doubles formalism: Theory, implementation, and benchmarks,” J. Chem. Phys. 145, 204116 (2016). 10.1063/1.4967860 [DOI] [PubMed] [Google Scholar]
- 256.Nanda K. D., Krylov A. I., and Gauss J., “Communication: The pole structure of the dynamical polarizability tensor in equation-of-motion coupled-cluster theory,” J. Chem. Phys. 149, 141101 (2018). 10.1063/1.5053727 [DOI] [PubMed] [Google Scholar]
- 257.Jagau T.-C., Bravaya K. B., and Krylov A. I., “Extending quantum chemistry of bound states to electronic resonances,” Annu. Rev. Phys. Chem. 68, 525–553 (2017). 10.1146/annurev-physchem-052516-050622 [DOI] [PubMed] [Google Scholar]
- 258.Wenzel J., Holzer A., Wormit M., and Dreuw A., “Analysis and comparison of CVS-ADC approaches up to third order for the calculation of core-excited states,” J. Chem. Phys. 142, 214104 (2015). 10.1063/1.4921841 [DOI] [PubMed] [Google Scholar]
- 259.Wenzel J., Wormit M., and Dreuw A., “Calculating core-level excitations and x-ray absorption spectra of medium-sized closed-shell molecules with the algebraic-diagrammatic construction scheme for the polarization propagator,” J. Comput. Chem. 35, 1900–1915 (2015). 10.1002/jcc.23703 [DOI] [PubMed] [Google Scholar]
- 260.Vidal M. L., Feng X., Epifanovsky E., Krylov A. I., and Coriani S., “New and efficient equation-of-motion coupled-cluster framework for core-excited and core-ionized states,” J. Chem. Theory Comput. 15, 3117–3133 (2019). 10.1021/acs.jctc.9b00039 [DOI] [PubMed] [Google Scholar]
- 261.Mayhall N. J. and Head-Gordon M., “Computational quantum chemistry for single Heisenberg spin couplings made simple: Just one spin flip required,” J. Chem. Phys. 141, 134111 (2014). 10.1063/1.4896659 [DOI] [PubMed] [Google Scholar]
- 262.Mayhall N. J. and Head-Gordon M., “Computational quantum chemistry for multiple-site Heisenberg spin couplings made simple: Still only one spin–flip required,” J. Phys. Chem. Lett. 6, 1982–1988 (2015). 10.1021/acs.jpclett.5b00733 [DOI] [PubMed] [Google Scholar]
- 263.Freedman D. E., Harman W. H., Harris T. D., Long G. J., Chang C. J., and Long J. R., “Slow magnetic relaxation in a high-spin iron(II) complex,” J. Am. Chem. Soc. 132, 1224–1225 (2010). 10.1021/ja909560d [DOI] [PubMed] [Google Scholar]
- 264.Oana C. M. and Krylov A. I., “Dyson orbitals for ionization from the ground and electronically excited states within equation-of-motion coupled-cluster formalism: Theory, implementation, and examples,” J. Chem. Phys. 127, 234106 (2007). 10.1063/1.2805393 [DOI] [PubMed] [Google Scholar]
- 265.Martin R. L., “Natural transition orbitals,” J. Chem. Phys. 118, 4775–4777 (2003). 10.1063/1.1558471 [DOI] [Google Scholar]
- 266.Plasser F., Bäppler S. A., Wormit M., and Dreuw A., “New tools for the systematic analysis and visualization of electronic excitations. I. Applications,” J. Chem. Phys. 141, 024107 (2014). 10.1063/1.4885820 [DOI] [PubMed] [Google Scholar]
- 267.Mewes S. A., Plasser F., Krylov A., and Dreuw A., “Benchmarking excited-state calculations using exciton properties,” J. Chem. Theory Comput. 14, 710–725 (2018). 10.1021/acs.jctc.7b01145 [DOI] [PubMed] [Google Scholar]
- 268.Mewes S. A. and Dreuw A., “Density-based descriptors and exciton analyses for visualizing and understanding the electronic structure of excited states,” Phys. Chem. Chem. Phys. 21, 2843–2856 (2019). 10.1039/c8cp07191h [DOI] [PubMed] [Google Scholar]
- 269.Krylov A. I., “From orbitals to observables and back,” J. Chem. Phys. 153, 080901 (2020). 10.1063/5.0018597 [DOI] [PubMed] [Google Scholar]
- 270.Nanda K. D. and Krylov A. I., “Visualizing the contributions of virtual states to two-photon absorption cross-sections by natural transition orbitals of response transition density matrices,” J. Phys. Chem. Lett. 8, 3256–3265 (2017). 10.1021/acs.jpclett.7b01422 [DOI] [PubMed] [Google Scholar]
- 271.Nanda K. D. and Krylov A. I., “A simple molecular orbital picture of RIXS distilled from many-body damped response theory,” J. Chem. Phys. 152, 244118 (2020). 10.1063/5.0010295 [DOI] [PubMed] [Google Scholar]
- 272.Bäppler S. A., Plasser F., Wormit M., and Dreuw A., “Exciton analysis of many-body wave functions: Bridging the gap between the quasiparticle and molecular orbital pictures,” Phys. Rev. A 90, 052521 (2014). 10.1103/physreva.90.052521 [DOI] [Google Scholar]
- 273.Plasser F., Thomitzni B., Bäppler S. A., Wenzel J., Rehn D. R., Wormit M., and Dreuw A., “Statistical analysis of electronic excitation processes: Spatial location, compactness, charge transfer, and electron-hole correlation,” J. Comput. Chem. 36, 1609–1620 (2015). 10.1002/jcc.23975 [DOI] [PubMed] [Google Scholar]
- 274.Plasser F., “TheoDORE: A toolbox for a detailed and automated analysis of electronic excited state computations,” J. Chem. Phys. 152, 084108 (2020). 10.1063/1.5143076 [DOI] [PubMed] [Google Scholar]
- 275.Olivares-Amaya R., Hu W., Nakatani N., Sharma S., Yang J., and Chan G. K.-L., “The ab-initio density matrix renormalization group in practice,” J. Chem. Phys. 142, 034102 (2015). 10.1063/1.4905329 [DOI] [PubMed] [Google Scholar]
- 276.Hait D., Tubman N. M., Levine D. S., Whaley K. B., and Head-Gordon M., “What levels of coupled cluster theory are appropriate for transition metal systems? A study using near-exact quantum chemical values for 3d transition metal binary compounds,” J. Chem. Theory Comput. 15, 5370–5385 (2019). 10.1021/acs.jctc.9b00674 [DOI] [PubMed] [Google Scholar]
- 277.Levine B. G., Durden A. S., Esch M. P., Liang F., and Shu Y., “CAS without SCF—Why to use CASCI and where to get the orbitals,” J. Chem. Phys. 154, 090902 (2021). 10.1063/5.0042147 [DOI] [PubMed] [Google Scholar]
- 278.Roos B. O., Taylor P. R., and Sigbahn P. E. M., “A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach,” Chem. Phys. 48, 157–173 (1980). 10.1016/0301-0104(80)80045-0 [DOI] [Google Scholar]
- 279.Siegbahn P. E. M., Almlöf J., Heiberg A., and Roos B. O., “The complete active space SCF (CASSCF) method in a Newton–Raphson formulation with application to the HNO molecule,” J. Chem. Phys. 74, 2384–2396 (1981). 10.1063/1.441359 [DOI] [Google Scholar]
- 280.Ruedenberg K., Schmidt M. W., Gilbert M. M., and Elbert S. T., “Are atoms intrinsic to molecular electronic wavefunctions? I. The FORS model,” Chem. Phys. 71, 41–49 (1982). 10.1016/0301-0104(82)87004-3 [DOI] [Google Scholar]
- 281.Vogiatzis K. D., Ma D., Olsen J., Gagliardi L., and de Jong W. A., “Pushing configuration-interaction to the limit: Towards massively parallel MCSCF calculations,” J. Chem. Phys. 147, 184111 (2017). 10.1063/1.4989858 [DOI] [PubMed] [Google Scholar]
- 282.Ivanic J. and Ruedenberg K., “Identification of deadwood in configuration spaces through general direct configuration interaction,” Theor. Chem. Acc. 106, 339–351 (2001). 10.1007/s002140100285 [DOI] [Google Scholar]
- 283.Bytautas L. and Ruedenberg K., “A priori identification of configurational deadwood,” Chem. Phys. 356, 64–75 (2009). 10.1016/j.chemphys.2008.11.021 [DOI] [Google Scholar]
- 284.Casanova D. and Head-Gordon M., “Restricted active space spin-flip configuration interaction approach: Theory, implementation and examples,” Phys. Chem. Chem. Phys. 11, 9779–9790 (2009). 10.1039/b911513g [DOI] [PubMed] [Google Scholar]
- 285.Casanova D., “Efficient implementation of restricted active space configuration interaction with the hole and particle approximation,” J. Comput. Chem. 34, 720–730 (2013). 10.1002/jcc.23188 [DOI] [PubMed] [Google Scholar]
- 286.Zimmerman P. M., Bell F., Goldey M., Bell A. T., and Head-Gordon M., “Restricted active space spin-flip configuration interaction: Theory and examples for multiple spin flips with odd numbers of electrons,” J. Chem. Phys. 137, 164110 (2012). 10.1063/1.4759076 [DOI] [PubMed] [Google Scholar]
- 287.Casanova D., “Second-order perturbative corrections to the restricted active space configuration interaction with the hole and particle approach,” J. Chem. Phys. 140, 144111 (2014). 10.1063/1.4870638 [DOI] [PubMed] [Google Scholar]
- 288.Casanova D., “Short-range density functional correlation within the restricted active space CI method,” J. Chem. Phys. 148, 124118 (2018). 10.1063/1.5018895 [DOI] [PubMed] [Google Scholar]
- 289.Rodríguez-Jiménez J. A., Carreras A., and Casanova D., “Short-range DFT energy correction to multiconfigurational wave functions for open-shell systems,” J. Chem. Phys. 154, 124116 (2021). 10.1063/5.0046404 [DOI] [PubMed] [Google Scholar]
- 290.Carreras A., Jiang H., Pokhilko P., Krylov A. I., Zimmerman P. M., and Casanova D., “Calculation of spin–orbit couplings using RASCI spinless one-particle density matrices: Theory and applications,” J. Chem. Phys. 153, 214107 (2020). 10.1063/5.0029146 [DOI] [PubMed] [Google Scholar]
- 291.Bender C. F. and Davidson E. R., “Studies in configuration interaction: The first-row diatomic hydrides,” Phys. Rev. 183, 23–30 (1969). 10.1103/physrev.183.23 [DOI] [Google Scholar]
- 292.Huron B., Malrieu J. P., and Rancurel P., “Iterative perturbation calculations of ground and excited state energies from multiconfigurational zeroth order wavefunctions,” J. Chem. Phys. 58, 5745–5759 (1973). 10.1063/1.1679199 [DOI] [Google Scholar]
- 293.Buenker R. J. and Peyerimhoff S. D., “Individualized configuration selection in CI calculations with subsequent energy extrapolation,” Theor. Chem. Acc. 35, 33–58 (1974). 10.1007/bf02394557 [DOI] [Google Scholar]
- 294.Evangelisti S., Daudey J.-P., and Malrieu J.-P., “Convergence of an improved CIPSI algorithm,” Chem. Phys. 75, 91–102 (1983). 10.1016/0301-0104(83)85011-3 [DOI] [Google Scholar]
- 295.Illas F., Rubio J., Ricart J. M., and Bagus P. S., “Selected versus complete configuration interaction expansions,” J. Chem. Phys. 95, 1877–1883 (1991). 10.1063/1.461037 [DOI] [Google Scholar]
- 296.Povill A., Rubio J., and Illas F., “Treating large intermediate spaces in the CIPSI method through a direct selected CI algorithm,” Theor. Chem. Acc. 82, 229–238 (1992). 10.1007/bf01113255 [DOI] [Google Scholar]
- 297.Evangelista F. A., “Adaptive multiconfigurational wave functions,” J. Chem. Phys. 140, 124114 (2014). 10.1063/1.4869192 [DOI] [PubMed] [Google Scholar]
- 298.Holmes A. A., Tubman N. M., and Umrigar C. J., “Heat-bath configuration interaction: An efficient selected configuration interaction algorithm inspired by heat-bath sampling,” J. Chem. Theory Comput. 12, 3674–3680 (2016). 10.1021/acs.jctc.6b00407 [DOI] [PubMed] [Google Scholar]
- 299.Holmes A. A., Umrigar C. J., and Sharma S., “Excited states using semistochastic heat-bath configuration interaction,” J. Chem. Phys. 147, 164111 (2017). 10.1063/1.4998614 [DOI] [PubMed] [Google Scholar]
- 300.Smith J. E. T., Mussard B., Holmes A. A., and Sharma S., “Cheap and near exact CASSCF with large active spaces,” J. Chem. Theory Comput. 13, 5468–5478 (2017). 10.1021/acs.jctc.7b00900 [DOI] [PubMed] [Google Scholar]
- 301.Schriber J. B. and Evangelista F. A., “Communication: An adaptive configuration interaction approach for strongly correlated electrons with tunable accuracy,” J. Chem. Phys. 144, 161106 (2016). 10.1063/1.4948308 [DOI] [PubMed] [Google Scholar]
- 302.Schriber J. B. and Evangelista F. A., “Adaptive configuration interaction for computing challenging electronic excited states with tunable accuracy,” J. Chem. Phys. 13, 005354–5366 (2017). 10.1021/acs.jctc.7b00725 [DOI] [PubMed] [Google Scholar]
- 303.Garniron Y., Scemama A., Giner E., Caffarel M., and Loos P.-F., “Selected configuration interaction dressed by perturbation,” J. Chem. Phys. 149, 064103 (2018). 10.1063/1.5044503 [DOI] [PubMed] [Google Scholar]
- 304.Tubman N. M., Lee J., Takeshita T. Y., Head-Gordon M., and Whaley K. B., “A deterministic alternative to the full configuration interaction quantum Monte Carlo method,” J. Chem. Phys. 145, 044112 (2016). 10.1063/1.4955109 [DOI] [PubMed] [Google Scholar]
- 305.Tubman N. M., Freeman C. D., Levine D. S., Hait D., Head-Gordon M., and Whaley K. B., “Modern approaches to exact diagonalization and selected configuration interaction with the adaptive sampling CI method,” J. Chem. Theory Comput. 16, 2139–2159 (2020). 10.1021/acs.jctc.8b00536 [DOI] [PubMed] [Google Scholar]
- 306.Tubman N. M., Levine D. S., Hait D., Head-Gordon M., and Whaley K. B., “An efficient deterministic perturbation theory for selected configuration interaction methods,” arXiv:1808.02049 (2018).
- 307.Levine D. S., Hait D., Tubman N. M., Lehtola S., Whaley K. B., and Head-Gordon M., “CASSCF with extremely large active spaces using the adaptive sampling configuration interaction method,” J. Chem. Theory Comput. 16, 2340–2354 (2020). 10.1021/acs.jctc.9b01255 [DOI] [PubMed] [Google Scholar]
- 308.Stoll H., “Correlation energy of diamond,” Phys. Rev. B 46, 6700–6704 (1992). 10.1103/physrevb.46.6700 [DOI] [PubMed] [Google Scholar]
- 309.Stoll H., “The correlation energy of crystalline silicon,” Chem. Phys. Lett. 191, 548–552 (1992). 10.1016/0009-2614(92)85587-z [DOI] [Google Scholar]
- 310.Stoll H., “On the correlation energy of graphite,” J. Chem. Phys. 97, 8449–8454 (1992). 10.1063/1.463415 [DOI] [Google Scholar]
- 311.Eriksen J. J. and Gauss J., “Incremental treatments of the full configuration interaction problem,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 11, e1525 (2021). 10.1002/wcms.1525 [DOI] [Google Scholar]
- 312.Zimmerman P. M., “Incremental full configuration interaction,” J. Chem. Phys. 146, 104102 (2017). 10.1063/1.4977727 [DOI] [PubMed] [Google Scholar]
- 313.Zimmerman P. M., “Singlet–triplet gaps through incremental full configuration interaction,” J. Phys. Chem. A 121, 4712–4720 (2017). 10.1021/acs.jpca.7b03998 [DOI] [PubMed] [Google Scholar]
- 314.Zimmerman P. M., “Strong correlation in incremental full configuration interaction,” J. Chem. Phys. 146, 224104 (2017). 10.1063/1.4985566 [DOI] [PubMed] [Google Scholar]
- 315.Zimmerman P. M. and Rask A. E., “Evaluation of full valence correlation energies and gradients,” J. Chem. Phys. 150, 244117 (2019). 10.1063/1.5100934 [DOI] [PubMed] [Google Scholar]
- 316.Dang D.-K. and Zimmerman P. M., “Fully variational incremental CASSCF,” J. Chem. Phys. 154, 014105 (2021). 10.1063/5.0031208 [DOI] [PubMed] [Google Scholar]
- 317.Rask A. E. and Zimmerman P. M., “Toward full configuration interaction for transition-metal complexes,” J. Phys. Chem. A 125, 1598–1609 (2021). 10.1021/acs.jpca.0c07624 [DOI] [PubMed] [Google Scholar]
- 318.Beran G. J. O., Austin B., Sodt A., and Head-Gordon M., “Unrestricted perfect pairing: The simplest wave-function-based model chemistry beyond mean field,” J. Phys. Chem. A 109, 9183–9192 (2005). 10.1021/jp053780c [DOI] [PubMed] [Google Scholar]
- 319.Eriksen J. J., Anderson T. A., Deustua J. E., Ghanem K., Hait D., Hoffmann M. R., Lee S., Levine D. S., Magoulas I., Shen J., Tubman N. M., Whaley K. B., Xu E., Yao Y., Zhang N., Alavi A., Chan G. K.-L., Head-Gordon M., Liu W., Piecuch P., Sharma S., Ten-no S. L., Umrigar C. J., and Gauss J., “The ground state electronic energy of benzene,” J. Phys. Chem. Lett. 11, 8922–8929 (2020). 10.1021/acs.jpclett.0c02621 [DOI] [PubMed] [Google Scholar]
- 320.Small D. W. and Head-Gordon M., “Tractable spin-pure methods for bond breaking: Local many-electron spin-vector sets and an approximate valence bond model,” J. Chem. Phys. 130, 084103 (2009). 10.1063/1.3069296 [DOI] [PubMed] [Google Scholar]
- 321.Small D. W. and Head-Gordon M., “Post-modern valence bond theory for strongly correlated electron spins,” Phys. Chem. Chem. Phys. 13, 19285–19297 (2011). 10.1039/c1cp21832h [DOI] [PubMed] [Google Scholar]
- 322.Small D. W., Lawler K. V., and Head-Gordon M., “Coupled cluster valence bond method: Efficient computer implementation and application to multiple bond dissociations and strong correlations in the acenes,” J. Chem. Theory Comput. 10, 2027–2040 (2014). 10.1021/ct500112y [DOI] [PubMed] [Google Scholar]
- 323.Small D. W. and Head-Gordon M., “Coupled cluster valence bond theory for open-shell systems with application to very long range strong correlation in a polycarbene dimer,” J. Chem. Phys. 147, 024107 (2017). 10.1063/1.4991797 [DOI] [PubMed] [Google Scholar]
- 324.Small D. W. and Head-Gordon M., “Independent amplitude approximations in coupled cluster valence bond theory: Incorporation of 3-electron-pair correlation and application to spin frustration in the low-lying excited states of a ferredoxin-type tetrametallic iron-sulfur cluster,” J. Chem. Phys. 149, 144103 (2018). 10.1063/1.5046318 [DOI] [PubMed] [Google Scholar]
- 325.Lee J., Small D. W., and Head-Gordon M., “Open-shell coupled-cluster valence-bond theory augmented with an independent amplitude approximation for three-pair correlations: Application to a model oxygen-evolving complex and single molecular magnet,” J. Chem. Phys. 149, 244121 (2018). 10.1063/1.5052667 [DOI] [PubMed] [Google Scholar]
- 326.Small D. W. and Head-Gordon M., “A fusion of the closed-shell coupled cluster singles and doubles method and valence-bond theory for bond breaking,” J. Chem. Phys. 137, 114103 (2012). 10.1063/1.4751485 [DOI] [PubMed] [Google Scholar]
- 327.Lee J., Small D. W., Epifanovsky E., and Head-Gordon M., “Coupled-cluster valence-bond singles and doubles for strongly correlated systems: Block-tensor based implementation and application to oligoacenes,” J. Chem. Theory Comput. 13, 602–615 (2017). 10.1021/acs.jctc.6b01092 [DOI] [PubMed] [Google Scholar]
- 328.Gidofalvi G. and Mazziotti D. A., “Active-space two-electron reduced-density-matrix method: Complete active-space calculations without diagonalization of the N-electron Hamiltonian,” J. Chem. Phys. 129, 134108 (2008). 10.1063/1.2983652 [DOI] [PubMed] [Google Scholar]
- 329.Fosso-Tande J., Nguyen T.-S., Gidofalvi G., and DePrince A. E. III, “Large-scale variational two-electron reduced-density-matrix-driven complete active space self-consistent field methods,” J. Chem. Theory Comput. 12, 2260 (2016). 10.1021/acs.jctc.6b00190 [DOI] [PubMed] [Google Scholar]
- 330.Garrod C. and Percus J. K., “Reduction of the N-particle variational problem,” J. Math. Phys. 5, 1756–1776 (1964). 10.1063/1.1704098 [DOI] [Google Scholar]
- 331.Zhao Z., Braams B. J., Fukuda M., Overton M. L., and Percus J. K., “The reduced density matrix method for electronic structure calculations and the role of three-index representability conditions,” J. Chem. Phys. 120, 2095 (2004). 10.1063/1.1636721 [DOI] [PubMed] [Google Scholar]
- 332.Mazziotti D. A., “Variational reduced-density-matrix method using three-particle N-representability conditions with application to many-electron molecules,” Phys. Rev. A 74, 032501 (2006). 10.1103/physreva.74.032501 [DOI] [Google Scholar]
- 333.Mullinax J. W., Maradzike E., Koulias L. N., Mostafanejad M., Epifanovsky E., Gidofalvi G., and DePrince A. E. III, “Heterogeneous CPU + GPU algorithm for variational two-electron reduced-density matrix-driven complete active-space self-consistent field theory,” J. Chem. Theory Comput. 15, 6164–6178 (2019). 10.1021/acs.jctc.9b00768 [DOI] [PubMed] [Google Scholar]
- 334.Mullinax J. W., Epifanovsky E., Gidofalvi G., and DePrince A. E. III, “Analytic energy gradients for variational two-electron reduced-density matrix methods within the density fitting approximation,” J. Chem. Theory Comput. 15, 276–289 (2019). 10.1021/acs.jctc.8b00973 [DOI] [PubMed] [Google Scholar]
- 335.Norman P. and Dreuw A., “Simulating x-ray spectroscopies and calculating core-excited states of molecules,” Chem. Rev. 118, 7208–7248 (2018). 10.1021/acs.chemrev.8b00156 [DOI] [PubMed] [Google Scholar]
- 336.Bokarev S. I. and Kühn O., “Theoretical X-ray spectroscopy of transition metal compounds,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 10, e1433 (2020). 10.1002/wcms.1433 [DOI] [Google Scholar]
- 337.Besley N. A., “Density functional theory based methods for the calculation of x-ray spectroscopy,” Acc. Chem. Res. 53, 1306–1315 (2020). 10.1021/acs.accounts.0c00171 [DOI] [PubMed] [Google Scholar]
- 338.Kasper J. M., Stetina T. F., Jenkins A. J., and Li X., “Ab initio methods for L-edge x-ray absorption spectroscopy,” Chem. Phys. Rev. 1, 011304 (2020). 10.1063/5.0029725 [DOI] [Google Scholar]
- 339.Rankine C. D. and Penfold T. J., “Progress in the theory of x-ray spectroscopy: From quantum chemistry to machine learning and ultrafast dynamics,” J. Phys. Chem. A 125, 4276–4293 (2021). 10.1021/acs.jpca.0c11267 [DOI] [PubMed] [Google Scholar]
- 340.Depresseux A., Oliva E., Gautier J., Tissandier F., Nejdl J., Kozlova M., Maynard G., Goddet J. P., Tafzi A., Lifschitz A., Kim H. T., Jacquemot S., Malka V., Ta Phuoc K., Thaury C., Rousseau P., Iaquaniello G., Lefrou T., Flacco A., Vodungbo B., Lambert G., Rousse A., Zeitoun P., and Sebban S., “Table-top femtosecond X-ray laser by collisional ionization gating,” Nat. Photonics 9, 817–822 (2015). 10.1038/nphoton.2015.225 [DOI] [Google Scholar]
- 341.Kleine C., Ekimova M., Goldsztejn G., Raabe S., Strüber C., Ludwig J., Yarlagadda S., Eisebitt S., Vrakking M. J. J., Elsaesser T., Nibbering E. T. J., and Rouzée A., “Soft x-ray absorption spectroscopy of aqueous solutions using a table-top femtosecond soft x-ray source,” J. Phys. Chem. Lett. 10, 52–58 (2019). 10.1021/acs.jpclett.8b03420 [DOI] [PubMed] [Google Scholar]
- 342.Schoenlein R., Elsaesser T., Holldack K., Huang Z., Kapteyn H., Murnane M., and Woerner M., “Recent advances in ultrafast X-ray sources,” Philos. Trans. R. Soc., A 377, 20180384 (2019). 10.1098/rsta.2018.0384 [DOI] [PubMed] [Google Scholar]
- 343.Geneaux R., Marroux H. J. B., Guggenmos A., Neumark D. M., and Leone S. R., “Transient absorption spectroscopy using high harmonic generation: A review of ultrafast X-ray dynamics in molecules and solids,” Philos. Trans. R. Soc., A 377, 20170463 (2019). 10.1098/rsta.2017.0463 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 344.Smith A. D., Balčiūnas T., Chang Y.-P., Schmidt C., Zinchenko K., Nunes F. B., Rossi E., Svoboda V., Yin Z., Wolf J.-P., and Wörner H. J., “Femtosecond soft-X-ray absorption spectroscopy of liquids with a water-window high-harmonic source,” J. Phys. Chem. Lett. 11, 1981–1988 (2020). 10.1021/acs.jpclett.9b03559 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 345.Moiseyev N., Non-Hermitian Quantum Mechanics (Cambridge University Press, 2011). [Google Scholar]
- 346.Herbert J. M., “The quantum chemistry of loosely-bound electrons,” in Reviews in Computational Chemistry, edited by Parill A. L. and Lipkowitz K. (Wiley, 2015), Vol. 28, pp. 391–517. [Google Scholar]
- 347.Sadybekov A. and Krylov A. I., “Coupled-cluster based approach for core-level states in condensed phase: Theory and application to different protonated forms of aqueous glycine,” J. Chem. Phys. 147, 014107 (2017). 10.1063/1.4990564 [DOI] [PubMed] [Google Scholar]
- 348.Cederbaum L. S., Domcke W., and Schirmer J., “Many-body theory of core holes,” Phys. Rev. A 22, 206–222 (1980). 10.1103/physreva.22.206 [DOI] [Google Scholar]
- 349.Tolbatov I. and Chipman D. M., “Comparative study of Gaussian basis sets for calculation of core electron binding energies in first-row hydrides and glycine,” Theor. Chem. Acc. 133, 1560 (2014). 10.1007/s00214-014-1560-z [DOI] [Google Scholar]
- 350.Tolbatov I. and Chipman D. M., “Benchmarking density functionals and Gaussian basis sets for calculation of core-electron binding energies in amino acids,” Theor. Chem. Acc. 136, 82 (2017). 10.1007/s00214-017-2115-x [DOI] [Google Scholar]
- 351.Fouda A. E. A. and Besley N. A., “Assessment of basis sets for density functional theory-based calculations of core-electron spectroscopies,” Theor. Chem. Acc. 137, 6 (2018). 10.1007/s00214-017-2181-0 [DOI] [Google Scholar]
- 352.Hanson-Heine M. W. D., George M. W., and Besley N. A., “Basis sets for the calculation of core-electron binding energies,” Chem. Phys. Lett. 699, 279–285 (2018). 10.1016/j.cplett.2018.03.066 [DOI] [Google Scholar]
- 353.Sarangi R., Vidal M. L., Coriani S., and Krylov A. I., “On the basis set selection for calculations of core-level states: Different strategies to balance cost and accuracy,” Mol. Phys. 118, e1769872 (2020). 10.1080/00268976.2020.1769872 [DOI] [Google Scholar]
- 354.Ambroise M. A., Dreuw A., and Jensen F., “Probing basis set requirements for calculating core ionization and core excitation spectra using correlated wave function methods,” J. Chem. Theory Comput. 17, 2832–2842 (2021). 10.1021/acs.jctc.1c00042 [DOI] [PubMed] [Google Scholar]
- 355.Stener M., Lisini A., and Decleva P., “Density functional calculations of excitation energies and oscillator strengths for C1s → π* and O1s → π* excitations and ionization potentials in carbonyl containing molecules,” Chem. Phys. 191, 141–154 (1995). 10.1016/0301-0104(94)00347-d [DOI] [Google Scholar]
- 356.Triguero L., Pettersson L. G. M., and Ågren H., “Calculations of near-edge x-ray-absorption spectra of gas-phase and chemisorbed molecules by means of density-functional and transition-potential theory,” Phys. Rev. B 58, 8097–8110 (1998). 10.1103/physrevb.58.8097 [DOI] [Google Scholar]
- 357.Triguero L., Pettersson L. G. M., and Ågren H., “Calculations of X-ray emission spectra of molecules and surface adsorbates by means of density functional theory,” J. Phys. Chem. A 102, 10599–10607 (1998). 10.1021/jp980824r [DOI] [Google Scholar]
- 358.Hanson-Heine M. W. D., George M. W., and Besley N. A., “Kohn-Sham density functional theory calculations of non-resonant and resonant x-ray emission spectroscopy,” J. Chem. Phys. 146, 094106 (2017). 10.1063/1.4977178 [DOI] [Google Scholar]
- 359.Michelitsch G. S. and Reuter K., “Efficient simulation of near-edge x-ray absorption fine structure (NEXAFS) in density-functional theory: Comparison of core-level constraining approaches,” J. Chem. Phys. 150, 074104 (2019). 10.1063/1.5083618 [DOI] [PubMed] [Google Scholar]
- 360.Oosterbaan K. J., White A. F., and Head-Gordon M., “Non-orthogonal configuration interaction with single substitutions for the calculation of core-excited states,” J. Chem. Phys. 149, 044116 (2018). 10.1063/1.5023051 [DOI] [PubMed] [Google Scholar]
- 361.Oosterbaan K. J., White A. F., and Head-Gordon M., “Non-orthogonal configuration interaction with single substitutions for core-excited States: An extension to doublet radicals,” J. Chem. Theory Comput. 15, 2966–2973 (2019). 10.1021/acs.jctc.8b01259 [DOI] [PubMed] [Google Scholar]
- 362.Oosterbaan K. J., White A. F., Hait D., and Head-Gordon M., “Generalized single excitation configuration interaction: An investigation into the impact of the inclusion of non-orthogonality on the calculation of core-excited states,” Phys. Chem. Chem. Phys. 22, 8182–8192 (2020). 10.1039/c9cp06592j [DOI] [PubMed] [Google Scholar]
- 363.Stener M., Fronzoni G., and de Simone M., “Time dependent density functional theory of core electrons excitations,” Chem. Phys. Lett. 373, 115–123 (2003). 10.1016/s0009-2614(03)00543-8 [DOI] [Google Scholar]
- 364.Wadey J. D. and Besley N. A., “Quantum chemical calculations of X-ray emission spectroscopy,” J. Chem. Theory Comput. 10, 4557–4564 (2014). 10.1021/ct500566k [DOI] [PubMed] [Google Scholar]
- 365.Coriani S. and Koch H., “Communication: X-ray absorption spectra and core-ionization potentials within a core-valence separated coupled cluster framework,” J. Chem. Phys. 143, 181103 (2015). 10.1063/1.4935712 [DOI] [PubMed] [Google Scholar]
- 366.Vidal M. L., Krylov A. I., and Coriani S., “Dyson orbitals within the fc-CVS-EOM-CCSD framework: Theory and application to X-ray photoelectron spectroscopy of ground and excited states,” Phys. Chem. Chem. Phys. 22, 2693–2703 (2020). 10.1039/c9cp03695d [DOI] [PubMed] [Google Scholar]
- 367.Nanda K. D., Vidal M. L., Faber R., Coriani S., and Krylov A. I., “How to stay out of trouble in RIXS calculations within equation-of-motion coupled-cluster damped response theory? Safe hitchhiking in the excitation manifold by means of core–valence separation,” Phys. Chem. Chem. Phys. 22, 2629–2641 (2020). 10.1039/c9cp03688a [DOI] [PubMed] [Google Scholar]
- 368.Tsuru S., Vidal M. L., Pápai M., Krylov A. I., Møller K. B., and Coriani S., “Time-resolved near-edge X-ray absorption fine structure of pyrazine from electronic structure and nuclear wave packet dynamics simulations,” J. Chem. Phys. 151, 124114 (2019). 10.1063/1.5115154 [DOI] [PubMed] [Google Scholar]
- 369.Vidal M. L., Pokhilko P., Krylov A. I., and Coriani S., “Equation-of-motion coupled-cluster theory to model L-edge x-ray absorption and photoelectron spectra,” J. Phys. Chem. Lett. 11, 8314–8321 (2021). 10.1021/acs.jpclett.0c02027 [DOI] [PubMed] [Google Scholar]
- 370.Tsuru S., Vidal M. L., Pápai M., Krylov A. I., Møller K. B., and Coriani S., “An assessment of different electronic structure approaches for modeling time-resolved x-ray absorption spectroscopy,” Struct. Dyn. 8, 024101 (2021). 10.1063/4.0000070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 371.Skomorowski W. and Krylov A. I., “Feshbach-Fano approach for calculation of Auger decay rates using equation-of-motion coupled-cluster wave functions: I. Theory and implementation,” J. Chem. Phys. 154, 084124 (2021). 10.1063/5.0036976 [DOI] [PubMed] [Google Scholar]
- 372.Slater J. C. and Wood J. H., “Statistical exchange and the total energy of a crystal,” Int. J. Quantum Chem. 5, 3–34 (1971). 10.1002/qua.560050703 [DOI] [Google Scholar]
- 373.Slater J. C., “Statistical exchange-correlation in the self-consistent field,” Adv. Quantum Chem. 6, 1–92 (1972). 10.1016/s0065-3276(08)60541-9 [DOI] [Google Scholar]
- 374.Leetmaa M., Ljungberg M. P., Lyubartsev A., Nilsson A., and Pettersson L. G. M., “Theoretical approximations to X-ray absorption spectroscopy of liquid water and ice,” J. Electron Spectrosc. Relat. Phenom. 177, 135–157 (2010). 10.1016/j.elspec.2010.02.004 [DOI] [Google Scholar]
- 375.Zhang Y., Hua W., Bennett K., and Mukamel S., “Nonlinear spectroscopy of core and valence excitations using short x-ray pulses: Simulation challenges,” in Density-Functional Methods for Excited States, Topics in Current Chemistry Vol. 368, edited by Ferré N., Filatov M., and Huix-Rotllant M. (Springer International Publishing, Cham, Switzerland, 2016), pp. 273–346. [DOI] [PubMed] [Google Scholar]
- 376.Zheng X. and Cheng L., “Performance of delta-coupled-cluster methods for calculations of core-ionization energies of first-row elements,” J. Chem. Theory Comput. 15, 4945–4955 (2019). 10.1021/acs.jctc.9b00568 [DOI] [PubMed] [Google Scholar]
- 377.Roemelt M., Beckwith M. A., Duboc C., Collomb M.-N., Neese F., and DeBeer S., “Manganese K-edge X-ray absorption spectroscopy as a probe of metal–ligand interactions in coordination compounds,” Inorg. Chem. 51, 680–687 (2012). 10.1021/ic202229b [DOI] [PubMed] [Google Scholar]
- 378.Fransson T., Brumboiu I. E., Vidal M. L., Norman P., Coriani S., and Dreuw A., “XABOOM: An x-ray absorption benchmark of organic molecules based on carbon, nitrogen, and oxygen 1s → π* transitions,” J. Chem. Theory Comput. 17, 1618–1637 (2021). 10.1021/acs.jctc.0c01082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 379.Nakata A., Imamura Y., and Nakai H., “Hybrid exchange-correlation functional for core, valence, and Rydberg excitations: Core-valence-Rydberg B3LYP,” J. Chem. Phys. 125, 064109 (2006). 10.1063/1.2227379 [DOI] [PubMed] [Google Scholar]
- 380.Nakata A., Imamura Y., and Nakai H., “Extension of the core-valence-Rydberg B3LYP functional to core-excited-state calculations of third-row atoms,” J. Chem. Theory Comput. 3, 1295–1305 (2007). 10.1021/ct600368f [DOI] [PubMed] [Google Scholar]
- 381.Besley N. A. and Noble A., “Time-dependent density functional theory study of the x-ray absorption spectroscopy of acetylene, ethylene, and benzene on Si(100),” J. Phys. Chem. C 111, 3333–3340 (2007). 10.1021/jp065160x [DOI] [Google Scholar]
- 382.Hehre W. J., Ditchfield R., and Pople J. A., “Self-consistent molecular orbital methods. XII. Further extensions of Gaussian-type basis sets for use in molecular orbital studies of organic molecules,” J. Chem. Phys. 56, 2257–2261 (1972). 10.1063/1.1677527 [DOI] [Google Scholar]
- 383.Hariharan P. C. and Pople J. A., “Influence of polarization functions on molecular orbital hydrogenation energies,” Theor. Chem. Acc. 28, 213–222 (1973). 10.1007/bf00533485 [DOI] [Google Scholar]
- 384.Luo Y., Ågren H., Gel’mukhanov F., Guo J., Skytt P., Wassdahl N., and Nordgren J., “Symmetry-selective resonant inelastic x-ray scattering of C60,” Phys. Rev. B 52, 14479–14496 (1995). 10.1103/physrevb.52.14479 [DOI] [PubMed] [Google Scholar]
- 385.Guo J., Skytt P., Wassdahl N., Nordgren J., Luo Y., Vahtras O., and Ågren H., “Resonant and non-resonant X-ray scattering from C70,” Chem. Phys. Lett. 235, 152–159 (1995). 10.1016/0009-2614(95)00083-g [DOI] [Google Scholar]
- 386.Nyberg M., Luo Y., Triguero L., Pettersson L. G. M., and Ågren H., “Core-hole effects in x-ray-absorption spectra of fullerenes,” Phys. Rev. B 60, 7956–7960 (1999). 10.1103/physrevb.60.7956 [DOI] [Google Scholar]
- 387.Legall H., Stiel H., Beck M., Leupold D., Gruszecki W. I., and Lokstein H., “Near edge X-ray absorption fine structure spectroscopy (NEXAFS) of pigment-protein complexes: Peridinin–chlorophyll a protein (PCP) of Amphidinium carterae,” J. Biochem. Biophys. Methods 70, 369–376 (2007). 10.1016/j.jbbm.2006.08.005 [DOI] [PubMed] [Google Scholar]
- 388.Besley N. A. and Asmuruf F. A., “Time-dependent density functional theory calculations of the spectroscopy of core electrons,” Phys. Chem. Chem. Phys. 12, 12024–12039 (2010). 10.1039/c002207a [DOI] [PubMed] [Google Scholar]
- 389.Yanai T., Tew D. P., and Handy N. C., “A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP),” Chem. Phys. Lett. 393, 51–57 (2004). 10.1016/j.cplett.2004.06.011 [DOI] [Google Scholar]
- 390.Woon D. E. and T. H. Dunning, Jr., “Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon,” J. Chem. Phys. 103, 4572–4585 (1995). 10.1063/1.470645 [DOI] [Google Scholar]
- 391.T. H. Dunning, Jr., “Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen,” J. Chem. Phys. 90, 1007–1023 (1989). 10.1063/1.456153 [DOI] [Google Scholar]
- 392.Kendall R. A., T. H. Dunning, Jr., and Harrison R. J., “Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions,” J. Chem. Phys. 96, 6796–6806 (1992). 10.1063/1.462569 [DOI] [Google Scholar]
- 393.Plekan O., Feyer V., Richter R., Coreno M., de Simone M., Prince K. C., Trofimov A. B., Gromov E. V., Zaytseva I. L., and Schirmer J., “A theoretical and experimental study of the near edge X-ray absorption fine structure (NEXAFS) and X-ray photoelectron spectra (XPS) of nucleobases: Thymine and adenine,” Chem. Phys. 347, 360–375 (2008). 10.1016/j.chemphys.2007.09.021 [DOI] [Google Scholar]
- 394.Fransson T. and Dreuw A., “Simulating X-ray emission spectroscopy with algebraic diagrammatic construction schemes for the polarization propagator,” J. Chem. Theory Comput. 15, 546–556 (2019). 10.1021/acs.jctc.8b01046 [DOI] [PubMed] [Google Scholar]
- 395.Wenzel J., Wormit M., and Dreuw A., “Calculating x-ray absorption spectra of open-shell molecules with the unrestricted algebraic-diagrammatic construction scheme for the polarization propagator,” J. Chem. Theory Comput. 10, 4583–4598 (2014). 10.1021/ct5006888 [DOI] [PubMed] [Google Scholar]
- 396.Krishnan R., Binkley J. S., Seeger R., and Pople J. A., “Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions,” J. Chem. Phys. 72, 650–654 (1980). 10.1063/1.438955 [DOI] [Google Scholar]
- 397.Clark T., Chandrasekhar J., Spitznagel G. W., and Schleyer P. v. R., “Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li–F,” J. Comput. Chem. 4, 294–301 (1983). 10.1002/jcc.540040303 [DOI] [Google Scholar]
- 398.Frisch M. J., Pople J. A., and Binkley J. S., “Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets,” J. Chem. Phys. 80, 3265–3269 (1984). 10.1063/1.447079 [DOI] [Google Scholar]
- 399.Rehn D. R., Dreuw A., and Norman P., “Resonant inelastic x-ray scattering amplitudes and cross sections in the algebraic diagrammatic construction/intermediate state representation (ADC/ISR) approach,” J. Chem. Theory Comput. 13, 5552–5559 (2017). 10.1021/acs.jctc.7b00636 [DOI] [PubMed] [Google Scholar]
- 400.Head-Gordon M., Graña A. M., Maurice D., and White C. A., “Analysis of electronic transitions as the difference of electron attachment and detachment densities,” J. Phys. Chem. 99, 14261–14270 (1995). 10.1021/j100039a012 [DOI] [Google Scholar]
- 401.Wenzel J. and Dreuw A., “Physical properties, exciton analysis and visualization of core-excited states: An intermediate state representation approach,” J. Chem. Theory Comput. 12, 1314–1330 (2016). 10.1021/acs.jctc.5b01161 [DOI] [PubMed] [Google Scholar]
- 402.Aslam U., Rao V. G., Chavez S., and Linic S., “Catalytic conversion of solar to chemical energy on plasmonic metal nanostructures,” Nat. Catal. 1, 656–665 (2018). 10.1038/s41929-018-0138-x [DOI] [Google Scholar]
- 403.Alizadeh E., Orlando T. M., and Sanche L., “Biomolecular damage induced by ionizing radiation: The direct and indirect effects of low-energy electrons on DNA,” Annu. Rev. Phys. Chem. 66, 379–398 (2015). 10.1146/annurev-physchem-040513-103605 [DOI] [PubMed] [Google Scholar]
- 404.Aguilar J. and Combes J. M., “A class of analytic perturbations for one-body Schrödinger Hamiltonians,” Commun. Math. Phys. 22, 269–279 (1971). 10.1007/bf01877510 [DOI] [Google Scholar]
- 405.Balslev E. and Combes J. M., “Spectral properties of many-body Schrödinger operators with dilatation-analytic interactions,” Commun. Math. Phys. 22, 280–294 (1971). 10.1007/bf01877511 [DOI] [Google Scholar]
- 406.Moiseyev N., Certain P. R., and Weinhold F., “Resonance properties of complex-rotated Hamiltonians,” Mol. Phys. 36, 1613–1630 (1978). 10.1080/00268977800102631 [DOI] [Google Scholar]
- 407.Reinhardt W. P., “Complex coordinates in the theory of atomic and molecular structure and dynamics,” Annu. Rev. Phys. Chem. 33, 223–255 (1982). 10.1146/annurev.pc.33.100182.001255 [DOI] [Google Scholar]
- 408.Moiseyev N., “Quantum theory of resonances: Calculating energies, widths and cross-sections by complex scaling,” Phys. Rep. 302, 212–293 (1998). 10.1016/s0370-1573(98)00002-7 [DOI] [Google Scholar]
- 409.Bravaya K. B., Zuev D., Epifanovsky E., and Krylov A. I., “Complex-scaled equation-of-motion coupled-cluster method with single and double substitutions for autoionizing excited states: Theory, implementation, and examples,” J. Chem. Phys. 138, 124106 (2013). 10.1063/1.4795750 [DOI] [PubMed] [Google Scholar]
- 410.McCurdy C. W. and Rescigno T. N., “Extension of the method of complex basis functions to molecular resonances,” Phys. Rev. Lett. 41, 1364–1368 (1978). 10.1103/physrevlett.41.1364 [DOI] [Google Scholar]
- 411.White A. F., Head-Gordon M., and McCurdy C. W., “Complex basis functions revisited: Implementation with applications to carbon tetrafluoride and aromatic N-containing heterocycles within the static-exchange approximation,” J. Chem. Phys. 142, 054103 (2015). 10.1063/1.4906940 [DOI] [PubMed] [Google Scholar]
- 412.White A. F., McCurdy C. W., and Head-Gordon M., “Restricted and unrestricted non-Hermitian Hartree-Fock: Theory, practical considerations, and applications to metastable molecular anions,” J. Chem. Phys. 143, 074103 (2015). 10.1063/1.4928529 [DOI] [PubMed] [Google Scholar]
- 413.White A. F., Epifanovsky E., McCurdy C. W., and Head-Gordon M., “Second order Møller-Plesset and coupled cluster singles and doubles methods with complex basis functions for resonances in electron-molecule scattering,” J. Chem. Phys. 146, 234107 (2017). 10.1063/1.4986950 [DOI] [PubMed] [Google Scholar]
- 414.Riss U. V. and Meyer H.-D., “Calculation of resonance energies and widths using the complex absorbing potential method,” J. Phys. B: At., Mol. Opt. Phys. 26, 4503–4536 (1993). 10.1088/0953-4075/26/23/021 [DOI] [Google Scholar]
- 415.Jagau T.-C., Zuev D., Bravaya K. B., Epifanovsky E., and Krylov A. I., “A fresh look at resonances and complex absorbing potentials: Density matrix based approach,” J. Phys. Chem. Lett. 5, 310–315 (2014). 10.1021/jz402482a [DOI] [PubMed] [Google Scholar]
- 416.Zuev D., Jagau T.-C., Bravaya K. B., Epifanovsky E., Shao Y., Sundstrom E., Head-Gordon M., and Krylov A. I., “Complex absorbing potentials within EOM-CC family of methods: Theory, implementation, and benchmarks,” J. Chem. Phys. 141, 024102 (2014). 10.1063/1.4885056 [DOI] [PubMed] [Google Scholar]
- 417.Sommerfeld T. and Ehara M., “Complex absorbing potentials with Voronoi isosurfaces wrapping perfectly around molecules,” J. Chem. Theory Comput. 11, 4627–4633 (2015). 10.1021/acs.jctc.5b00465 [DOI] [PubMed] [Google Scholar]
- 418.Simon B., “The definition of molecular resonance curves by the method of exterior complex scaling,” Phys. Lett. A 71, 211–214 (1978). 10.1016/0375-9601(79)90165-8 [DOI] [Google Scholar]
- 419.Rom N., Engdahl E., and Moiseyev N., “Tunneling rates in bound systems using smooth exterior complex scaling within the framework of the finite basis set approximation,” J. Chem. Phys. 93, 3413–3419 (1990). 10.1063/1.458821 [DOI] [Google Scholar]
- 420.Hazi A. U. and Taylor H. S., “Stabilization method of calculating resonance energies: Model problem,” Phys. Rev. A 1, 1109–1120 (1970). 10.1103/physreva.1.1109 [DOI] [Google Scholar]
- 421.Feuerbacher S., Sommerfeld T., and Cederbaum L. S., “Extrapolating bound state data of anions into the metastable domain,” J. Chem. Phys. 121, 6628–6633 (2004). 10.1063/1.1792031 [DOI] [PubMed] [Google Scholar]
- 422.Thodika M., Fennimore M., Karsili T. N. V., and Matsika S., “Comparative study of methodologies for calculating metastable states of small to medium-sized molecules,” J. Chem. Phys. 151, 244104 (2019). 10.1063/1.5134700 [DOI] [PubMed] [Google Scholar]
- 423.Sommerfeld T. and Santra R., “Efficient method to perform CAP/CI calculations for temporary anions,” Int. J. Quantum Chem. 82, 218–226 (2001). 10.1002/qua.1042 [DOI] [Google Scholar]
- 424.Jagau T.-C. and Krylov A. I., “Characterizing metastable states beyond energies and lifetimes: Dyson orbitals and transition dipole moments,” J. Chem. Phys. 144, 054113 (2016). 10.1063/1.4940797 [DOI] [PubMed] [Google Scholar]
- 425.Jagau T.-C., “Investigating tunnel and above-barrier ionization using complex-scaled coupled-cluster theory,” J. Chem. Phys. 145, 204115 (2016). 10.1063/1.4967961 [DOI] [PubMed] [Google Scholar]
- 426.Jagau T.-C., “Coupled-cluster treatment of molecular strong-field ionization,” J. Chem. Phys. 148, 204102 (2018). 10.1063/1.5028179 [DOI] [PubMed] [Google Scholar]
- 427.Skomorowski W. and Krylov A. I., “Real and imaginary excitons: Making sense of resonance wavefunctions by using reduced state and transition density matrices,” J. Phys. Chem. Lett. 9, 4101–4108 (2018). 10.1021/acs.jpclett.8b01794 [DOI] [PubMed] [Google Scholar]
- 428.Benda Z. and Jagau T.-C., “Communication: Analytic gradients for the complex absorbing potential equation-of-motion coupled-cluster method,” J. Chem. Phys. 146, 031101 (2017). 10.1063/1.4974094 [DOI] [PubMed] [Google Scholar]
- 429.Feshbach H., “A unified theory of nuclear reactions. II,” Ann. Phys. 19, 287–313 (1962). 10.1016/0003-4916(62)90221-x [DOI] [Google Scholar]
- 430.Skomorowski W., Gulania S., and Krylov A. I., “Bound and continuum-embedded states of cyanopolyyne anions,” Phys. Chem. Chem. Phys. 20, 4805–4817 (2018). 10.1039/c7cp08227d [DOI] [PubMed] [Google Scholar]
- 431.Benda Z., Rickmeyer K., and Jagau T.-C., “Structure optimization of temporary anions,” J. Chem. Theory Comput. 14, 3468–3478 (2018). 10.1021/acs.jctc.8b00128 [DOI] [PubMed] [Google Scholar]
- 432.Benda Z. and Jagau T.-C., “Understanding processes following resonant electron attachment: Minimum-energy crossing points between anionic and neutral potential energy surfaces,” J. Chem. Theory Comput. 14, 4216–4223 (2018). 10.1021/acs.jctc.8b00444 [DOI] [PubMed] [Google Scholar]
- 433.Benda Z. and Jagau T.-C., “Locating exceptional points on multidimensional complex-valued potential energy surfaces,” J. Phys. Chem. Lett. 9, 6978–6984 (2018). 10.1021/acs.jpclett.8b03228 [DOI] [PubMed] [Google Scholar]
- 434.Balog R., Langer J., Gohlke S., Stano M., Abdoul-Carime H., and Illenberger E., “Low energy electron driven reactions in free and bound molecules: From unimolecular processes in the gas phase to complex reactions in a condensed environment,” Int. J. Mass Spectrom. 233, 267–291 (2004). 10.1016/j.ijms.2003.12.030 [DOI] [Google Scholar]
- 435.Arumainayagam C. R., Lee H.-L., Nelson R. B., Haines D. R., and Gunawardane R. P., “Low-energy electron-induced reactions in condensed matter,” Surf. Sci. Rep. 65, 1–44 (2010). 10.1016/j.surfrep.2009.09.001 [DOI] [Google Scholar]
- 436.Fabrikant I. I., Eden S., Mason N. J., and Fedor J., “Recent progress in dissociative electron attachment: From diatomics to biomolecules,” Adv. At., Mol., Opt. Phys. 66, 545–657 (2017). 10.1016/bs.aamop.2017.02.002 [DOI] [Google Scholar]
- 437.Cappelli C. and Biczysko M., “Time-independent approach to vibrational spectroscopies,” in Computational Strategies for Spectroscopy: From Small Molecules to Nano Systems, 1st ed., edited by Barone V. (Wiley, Hoboken, 2011), Chap. 7, pp. 309–360. [Google Scholar]
- 438.Biczysko M., Bloino J., Santoro F., and Barone V., “Time independent approaches to simulate electronic spectra lineshapes: From small molecules to macrosystems,” in Computational Strategies for Spectroscopy: From Small Molecules to Nano Systems, 1st ed., edited by Barone V. (Wiley, Chichester, 2011), pp. 361–443. [Google Scholar]
- 439.Lami A. and Santoro F., “Time-dependent approaches to calculation of steady-state vibronic spectra: From fully quantum to classical approaches,” in Computational Strategies for Spectroscopy: From Small Molecules to Nano Systems, 1st ed., edited by Barone V. (Wiley, Chichester, 2011), pp. 475–516. [Google Scholar]
- 440.Ma H., Liu J., and Liang W., “Time-dependent approach to resonance Raman spectra including Duschinsky rotation and Herzberg–Teller effects: Formalism and its realistic applications,” J. Chem. Theory Comput. 8, 4474–4482 (2012). 10.1021/ct300640c [DOI] [PubMed] [Google Scholar]
- 441.Baiardi A., Bloino J., and Barone V., “General time-dependent approach to vibronic spectroscopy including Franck–Condon, Herzberg–Teller, and Duschinsky effects,” J. Chem. Theory Comput. 9, 4097–4115 (2013). 10.1021/ct400450k [DOI] [PMC free article] [PubMed] [Google Scholar]
- 442.Liang W., Ma H., Zang H., and Ye C., “Generalized time-dependent approaches to vibrationally resolved electronic and Raman spectra: Theory and applications,” Int. J. Quantum Chem. 115, 550–563 (2015). 10.1002/qua.24824 [DOI] [Google Scholar]
- 443.Bloino J., Baiardi A., and Biczysko M., “Aiming at an accurate prediction of vibrational and electronic spectra for medium-to-large molecules: An overview,” Int. J. Quantum Chem. 116, 1543–1574 (2016). 10.1002/qua.25188 [DOI] [Google Scholar]
- 444.Born M. and Oppenheimer R., “Zur Quantentheorie der Molekeln,” Ann. Phys. 389, 457–484 (1927). 10.1002/andp.19273892002 [DOI] [Google Scholar]
- 445.Born M. and Huang K., Dynamical Theory of Crystal Lattices (Oxford University Press, New York, 1954). [Google Scholar]
- 446.Condon E., “A theory of intensity distribution in band systems,” Phys. Rev. 28, 1182–1201 (1926). 10.1103/physrev.28.1182 [DOI] [Google Scholar]
- 447.Franck J. and Dymond E. G., “Elementary processes of photochemical reactions,” Trans. Faraday Soc. 21, 536–542 (1926). 10.1039/tf9262100536 [DOI] [Google Scholar]
- 448.Coon J. B., DeWames R. E., and Loyd C. M., “The Franck-Condon principle and the structure of excited electronic states of molecules,” J. Mol. Spectrosc. 8, 285–299 (1962). 10.1016/0022-2852(62)90029-2 [DOI] [Google Scholar]
- 449.Gozem S. and Krylov A. I., “The ezSpectra suite: An easy-to-use toolkit for spectroscopy modeling,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. (published online) (2021). 10.1002/wcms.1546 [DOI] [Google Scholar]
- 450.Duschinsky F., “The importance of the electron spectrum in multi atomic molecules. Concerning the Franck-Condon principle,” Acta Physicochim. URSS 7, 551–566 (1937). [Google Scholar]
- 451.Herzberg G., Molecular Spectroscopy and Molecular Structure: Electronic Spectra and Electronic Structure of Polyatomic Molecules (van Nostrand Reinhold, New York, 1966). [Google Scholar]
- 452.Myers A. B. and Mathies R. A., “Resonance Raman intensities: A probe of excited-state structure and dynamics,” in Biological Applications of Raman Spectroscopy, edited by Spiro T. G. (Wiley, New York, 1987), Vol. 2, pp. 1–58. [Google Scholar]
- 453.Myers Kelley A., “Resonance Raman and resonance hyper-Raman intensities: Structure and dynamics of molecular excited states in solution,” J. Phys. Chem. A 112, 11975–11991 (2008). 10.1021/jp805530y [DOI] [PubMed] [Google Scholar]
- 454.Albrecht A. C., “On the theory of Raman intensities,” J. Chem. Phys. 34, 1476–1484 (1961). 10.1063/1.1701032 [DOI] [Google Scholar]
- 455.Long D. A., The Raman Effect: A Unified Treatment of the Theory of Raman Scattering by Molecules (John Wiley & Sons, Chichester, 2002). [Google Scholar]
- 456.Guthmuller J., “Calculation of vibrational resonance Raman spectra of molecules using quantum chemistry methods,” in Molecular Spectroscopy: A Quantum Chemistry Approach, edited by Ozaki Y., Wójcik M. J., and Popp J. (Wiley-VCH, Weinheim, Germany, 2019), Vol. 1, Chap. 17, pp. 497–536. [Google Scholar]
- 457.Heller E. J., “The semiclassical way to molecular spectroscopy,” Acc. Chem. Res. 14, 368–375 (1981). 10.1021/ar00072a002 [DOI] [Google Scholar]
- 458.Heller E. J., Sundberg R. L., and Tannor D., “Simple aspects of Raman scattering,” J. Phys. Chem. 86, 1822–1833 (1982). 10.1021/j100207a018 [DOI] [Google Scholar]
- 459.McAskill N. A. and Sangster D. F., “Ultraviolet absorption spectra of the benzyl radical formed during pulse radiolysis,” Aust. J. Chem. 30, 2107–2113 (1977). 10.1071/ch9772107 [DOI] [Google Scholar]
- 460.Langkilde F. W., Bajdor K., Wilbrandt R., Negri F., Zerbetto F., and Orlandi G., “Resonance Raman spectra and quantum chemical vibrational analysis of the C7H7· and C7D7· benzyl radicals,” J. Chem. Phys. 100, 3503–3513 (1994). 10.1063/1.466392 [DOI] [Google Scholar]
- 461.Uejob K., “Fluorescence spectrum of the benzyl radical in methylcyclohexane at 4.2 K,” Spectrochim. Acta, Part A 60, 595–602 (2004). 10.1016/s1386-1425(03)00267-1 [DOI] [PubMed] [Google Scholar]
- 462.Liang W., Zhao Y., Sun J., Song J., Hu S., and Yang J., “Electronic excitation of polyfluorenes: A theoretical study,” J. Phys. Chem. B 110, 9908–9915 (2006). 10.1021/jp0572481 [DOI] [PubMed] [Google Scholar]
- 463.Ma H., Zhao Y., and Liang W., “Assessment of mode-mixing and Herzberg-Teller effects on two-photon absorption and resonance hyper-Raman spectra from a time-dependent approach,” J. Chem. Phys. 140, 094107 (2014). 10.1063/1.4867273 [DOI] [PubMed] [Google Scholar]
- 464.Kane K. A. and Jensen L., “Calculation of absolute resonance Raman intensities: Vibronic theory vs short-time approximation,” J. Phys. Chem. C 114, 5540–5546 (2010). 10.1021/jp906152q [DOI] [Google Scholar]
- 465.Silverstein D. W., Govind N., van Dam H. J. J., and Jensen L., “Simulating one-photon absorption and resonance Raman scattering spectra using analytical excited state energy gradients within time-dependent density functional theory,” J. Chem. Theory Comput. 9, 5490–5503 (2013). 10.1021/ct4007772 [DOI] [PubMed] [Google Scholar]
- 466.Dasgupta S., Rana B., and Herbert J. M., “Ab initio investigation of the resonance Raman spectrum of the hydrated electron,” J. Phys. Chem. B 123, 8074–8084 (2019). 10.1021/acs.jpcb.9b04895 [DOI] [PubMed] [Google Scholar]
- 467.Jarzȩcki A. A., “Quantum-mechanical calculations of resonance Raman intensities: The weighted-gradient approximation,” J. Phys. Chem. A 113, 2926–2934 (2009). 10.1021/jp8095715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 468.Dasgupta S. and Herbert J. M., “Ab initio approach to femtosecond stimulated Raman spectroscopy: Investigating vibrational modes probed in excited-state relaxation of quaterthiophenes,” J. Phys. Chem. A 124, 6356–6362 (2020). 10.1021/acs.jpca.0c06307 [DOI] [PubMed] [Google Scholar]
- 469.Kukura P., McCamant D. W., and Mathies R. A., “Femtosecond stimulated Raman spectroscopy,” Annu. Rev. Phys. Chem. 58, 461–488 (2007). 10.1146/annurev.physchem.58.032806.104456 [DOI] [PubMed] [Google Scholar]
- 470.Dietze D. R. and Mathies R. A., “Femtosecond stimulated Raman spectroscopy,” ChemPhysChem 17, 1224–1251 (2016). 10.1002/cphc.201600104 [DOI] [PubMed] [Google Scholar]
- 471.Webb S. P., Iordanov T., and Hammes-Schiffer S., “Multiconfigurational nuclear-electronic orbital approach: Incorporation of nuclear quantum effects in electronic structure calculations,” J. Chem. Phys. 117, 4106–4118 (2002). 10.1063/1.1494980 [DOI] [Google Scholar]
- 472.Pavošević F., Culpitt T., and Hammes-Schiffer S., “Multicomponent quantum chemistry: Integrating electronic and nuclear quantum effects via the nuclear–electronic orbital method,” Chem. Rev. 120, 4222–4253 (2020). 10.1021/acs.chemrev.9b00798 [DOI] [PubMed] [Google Scholar]
- 473.Brorsen K. R., Pak M. V., and Hammes-Schiffer S., “Calculation of positron binding energies and electron–positron annihilation rates for atomic systems with the reduced explicitly correlated Hartree–Fock method in the nuclear–electronic orbital framework,” J. Phys. Chem. A 121, 515–522 (2017). 10.1021/acs.jpca.6b10124 [DOI] [PubMed] [Google Scholar]
- 474.Pavošević F. and Hammes-Schiffer S., “Multicomponent equation-of-motion coupled cluster singles and doubles: Theory and calculation of excitation energies for positronium hydride,” J. Chem. Phys. 150, 161102 (2019). 10.1063/1.5094035 [DOI] [PubMed] [Google Scholar]
- 475.Yang Y., Brorsen K. R., Culpitt T., Pak M. V., and Hammes-Schiffer S., “Development of a practical multicomponent density functional for electron-proton correlation to produce accurate proton densities,” J. Chem. Phys. 147, 114113 (2017). 10.1063/1.4996038 [DOI] [PubMed] [Google Scholar]
- 476.Brorsen K. R., Yang Y., and Hammes-Schiffer S., “Multicomponent density functional theory: Impact of nuclear quantum effects on proton affinities and geometries,” J. Phys. Chem. Lett. 8, 3488–3493 (2017). 10.1021/acs.jpclett.7b01442 [DOI] [PubMed] [Google Scholar]
- 477.Brorsen K. R., Schneider P. E., and Hammes-Schiffer S., “Alternative forms and transferability of electron-proton correlation functionals in nuclear-electronic orbital density functional theory,” J. Chem. Phys. 149, 044110 (2018). 10.1063/1.5037945 [DOI] [PubMed] [Google Scholar]
- 478.Tao Z., Yang Y., and Hammes-Schiffer S., “Multicomponent density functional theory: Including the density gradient in the electron-proton correlation functional for hydrogen and deuterium,” J. Chem. Phys. 151, 124102 (2019). 10.1063/1.5119124 [DOI] [PubMed] [Google Scholar]
- 479.Yang Y., Culpitt T., and Hammes-Schiffer S., “Multicomponent time-dependent density functional theory: Proton and electron excitation energies,” J. Phys. Chem. Lett. 9, 1765–1770 (2018). 10.1021/acs.jpclett.8b00547 [DOI] [PubMed] [Google Scholar]
- 480.Pavošević F., Culpitt T., and Hammes-Schiffer S., “Multicomponent coupled cluster singles and doubles theory within the nuclear-electronic orbital framework,” J. Chem. Theory Comput. 15, 338–347 (2018). 10.1021/acs.jctc.8b01120 [DOI] [PubMed] [Google Scholar]
- 481.Yang Y., Schneider P. E., Culpitt T., Pavošević F., and Hammes-Schiffer S., “Molecular vibrational frequencies within the nuclear–electronic orbital framework,” J. Phys. Chem. Lett. 10, 1167–1172 (2019). 10.1021/acs.jpclett.9b00299 [DOI] [PubMed] [Google Scholar]
- 482.Pavošević F. and Hammes-Schiffer S., “Multicomponent coupled cluster singles and doubles and Brueckner doubles methods: Proton densities and energies,” J. Chem. Phys. 151, 074014 (2019). 10.1063/1.5116113 [DOI] [PubMed] [Google Scholar]
- 483.Culpitt T., Yang Y., Pavošević F., Tao Z., and Hammes-Schiffer S., “Enhancing the applicability of multicomponent time-dependent density functional theory,” J. Chem. Phys. 150, 201101 (2019). 10.1063/1.5099093 [DOI] [PubMed] [Google Scholar]
- 484.Culpitt T., Yang Y., Schneider P. E., Pavošević F., and Hammes-Schiffer S., “Molecular vibrational frequencies with multiple quantum protons within the nuclear-electronic orbital framework,” J. Chem. Theory Comput. 15, 6840–6849 (2019). 10.1021/acs.jctc.9b00665 [DOI] [PubMed] [Google Scholar]
- 485.Pavošević F., Rousseau B. J. G., and Hammes-Schiffer S., “Multicomponent orbital-optimized perturbation theory methods: Approaching coupled cluster accuracy at lower cost,” J. Phys. Chem. Lett. 11, 1578–1583 (2020). 10.1021/acs.jpclett.0c00090 [DOI] [PubMed] [Google Scholar]
- 486.Zhao L., Tao Z., Pavošević F., Wildman A., Hammes-Schiffer S., and Li X., “Real-time time-dependent nuclear–electronic orbital approach: Dynamics beyond the Born–Oppenheimer approximation,” J. Phys. Chem. Lett. 11, 4052–4058 (2020). 10.1021/acs.jpclett.0c00701 [DOI] [PubMed] [Google Scholar]
- 487.Pavošević F., Tao Z., Culpitt T., Zhao L., Li X., and Hammes-Schiffer S., “Frequency and time domain nuclear–electronic orbital equation-of-motion coupled cluster methods: Combination bands and electronic–protonic double excitations,” J. Phys. Chem. Lett. 11, 6435–6442 (2020). 10.1021/acs.jpclett.0c01891 [DOI] [PubMed] [Google Scholar]
- 488.Yu Q. and Hammes-Schiffer S., “Nuclear-electronic orbital multistate density functional theory,” J. Phys. Chem. Lett. 11, 10106–10113 (2020). 10.1021/acs.jpclett.0c02923 [DOI] [PubMed] [Google Scholar]
- 489.Schneider P. E., Tao Z., Pavošević F., Epifanovsky E., Feng X., and Hammes-Schiffer S., “Transition states, reaction paths, and thermochemistry using the nuclear–electronic orbital analytic Hessian,” J. Chem. Phys. 154, 054108 (2021). 10.1063/5.0033540 [DOI] [PubMed] [Google Scholar]
- 490.Pavošević F., Tao Z., and Hammes-Schiffer S., “Multicomponent coupled cluster singles and doubles with density fitting: Protonated water tetramers with quantized protons,” J. Phys. Chem. Lett. 12, 1631–1637 (2021). 10.1021/acs.jpclett.0c03771 [DOI] [PubMed] [Google Scholar]
- 491.Pak M. V., Chakraborty A., and Hammes-Schiffer S., “Density functional theory treatment of electron correlation in the nuclear–electronic orbital approach,” J. Phys. Chem. A 111, 4522–4526 (2007). 10.1021/jp0704463 [DOI] [PubMed] [Google Scholar]
- 492.Chakraborty A., Pak M. V., and Hammes-Schiffer S., “Development of electron-proton density functionals for multicomponent density functional theory,” Phys. Rev. Lett. 101, 153001 (2008). 10.1103/physrevlett.101.153001 [DOI] [PubMed] [Google Scholar]
- 493.Chakraborty A., Pak M. V., and Hammes-Schiffer S., “Properties of the exact universal functional in multicomponent density functional theory,” J. Chem. Phys. 131, 124115 (2009). 10.1063/1.3236844 [DOI] [PubMed] [Google Scholar]
- 494.Colle R. and Salvetti O., “Approximate calculation of the correlation energy for the closed shells,” Theor. Chem. Acc. 37, 329–334 (1975). 10.1007/bf01028401 [DOI] [Google Scholar]
- 495.Colle R. and Salvetti O., “Approximate calculation of the correlation energy for the closed and open shells,” Theor. Chem. Acc. 53, 55–63 (1979). 10.1007/bf00547606 [DOI] [Google Scholar]
- 496.Kosloff R., “Time-dependent quantum-mechanical methods for molecular dynamics,” J. Phys. Chem. 92, 2087–2100 (1988). 10.1021/j100319a003 [DOI] [Google Scholar]
- 497.Marston C. C. and Balint‐Kurti G. G., “The Fourier grid Hamiltonian method for bound state eigenvalues and eigenfunctions,” J. Chem. Phys. 91, 3571–3576 (1989). 10.1063/1.456888 [DOI] [Google Scholar]
- 498.Webb S. P. and Hammes-Schiffer S., “Fourier grid Hamiltonian multiconfigurational self-consistent-field: A method to calculate multidimensional hydrogen vibrational wavefunctions,” J. Chem. Phys. 113, 5214–5227 (2000). 10.1063/1.1289528 [DOI] [Google Scholar]
- 499.Yu Q., Pavošević F., and Hammes-Schiffer S., “Development of nuclear basis sets for multicomponent quantum chemistry methods,” J. Chem. Phys. 152, 244123 (2020). 10.1063/5.0009233 [DOI] [PubMed] [Google Scholar]
- 500.Cramer C. J. and Truhlar D. G., “Implicit solvation models: Equilibria, structure, spectra, and dynamics,” Chem. Rev. 99, 2161–2200 (1999). 10.1021/cr960149m [DOI] [PubMed] [Google Scholar]
- 501.Herbert J. M., “Dielectric continuum methods for quantum chemistry,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 11, e1519 (2021). 10.1002/wcms.1519 [DOI] [Google Scholar]
- 502.Senn H. M. and Thiel W., “QM/MM methods for biological systems,” in Atomistic Approaches in Modern Biology, Topics in Current Chemistry Vol. 268, edited by Reiher M. (Springer-Verlag: Berlin, 2007), pp. 173–290. [Google Scholar]
- 503.Cao L. and Ryde U., “On the difference between additive and subtractive QM/MM calculations,” Front. Chem. 6, 89 (2018). 10.3389/fchem.2018.00089 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 504.Chung L. W., Sameera W. M. C., Ramozzi R., Page A. J., Hatanaka M., Petrova G. P., Harris T. V., Li X., Ke Z., Liu F., Li H.-B., Ding L., and Morokuma K., “The ONIOM method and its applications,” Chem. Rev. 115, 5678–5796 (2015). 10.1021/cr5004419 [DOI] [PubMed] [Google Scholar]
- 505.Manby F. R., Stella M., Goodpaster J. D., and Miller T. F. III, “A simple, exact density-functional-theory embedding scheme,” J. Chem. Theory Comput. 8, 2564–2568 (2012). 10.1021/ct300544e [DOI] [PMC free article] [PubMed] [Google Scholar]
- 506.Lee S. J. R., Welborn M., Manby F. R., and Miller T. F. III, “Projection-based wavefunction-in-DFT embedding,” Acc. Chem. Res. 52, 1359–1368 (2019). 10.1021/acs.accounts.8b00672 [DOI] [PubMed] [Google Scholar]
- 507.Herbert J. M., “Fantasy versus reality in fragment-based quantum chemistry,” J. Chem. Phys. 151, 170901 (2019). 10.1063/1.5126216 [DOI] [PubMed] [Google Scholar]
- 508.Tomasi J., Mennucci B., and Cancès E., “The IEF version of the PCM solvation method: An overview of a new method addressed to study molecular solutes at the QM ab initio level,” J. Mol. Struct.: THEOCHEM 464, 211–226 (1999). 10.1016/s0166-1280(98)00553-3 [DOI] [Google Scholar]
- 509.Cramer C. J. and Truhlar D. G., “A universal approach to solvation modeling,” Acc. Chem. Res. 41, 760–768 (2008). 10.1021/ar800019z [DOI] [PubMed] [Google Scholar]
- 510.Cramer C. J. and Truhlar D. G., “Reply to comment on ‘A universal approach to solvation modeling’,” Acc. Chem. Res. 42, 493–497 (2009). 10.1021/ar900004j [DOI] [PubMed] [Google Scholar]
- 511.Lange A. W. and Herbert J. M., “Symmetric versus asymmetric discretization of the integral equations in polarizable continuum solvation models,” Chem. Phys. Lett. 509, 77–87 (2011). 10.1016/j.cplett.2011.04.092 [DOI] [Google Scholar]
- 512.Lange A. W. and Herbert J. M., “Polarizable continuum reaction-field solvation models affording smooth potential energy surfaces,” J. Phys. Chem. Lett. 1, 556–561 (2010). 10.1021/jz900282c [DOI] [Google Scholar]
- 513.Lange A. W. and Herbert J. M., “A smooth, nonsingular, and faithful discretization scheme for polarizable continuum models: The switching/Gaussian approach,” J. Chem. Phys. 133, 244111 (2010). 10.1063/1.3511297 [DOI] [PubMed] [Google Scholar]
- 514.Herbert J. M. and Lange A. W., “The polarizable continuum model for (bio)molecular electrostatics: Basic theory and recent advances for macromolecules and simulations,” in Many-Body Effects and Electrostatics in Multi-Scale Computations of Biomolecules, edited by Cui Q., Ren P., and Meuwly M. (Pan Stanford, 2016), Chap. 11, pp. 363–416. [Google Scholar]
- 515.Lange A. W., Herbert J. M., Albrecht B. J., and You Z.-Q., “Intrinsically smooth discretisation of Connolly’s solvent-excluded molecular surface,” Mol. Phys. 118, e1644384 (2020). 10.1080/00268976.2019.1644384 [DOI] [Google Scholar]
- 516.Marenich A. V., Olson R. M., Kelly C. P., Cramer C. J., and Truhlar D. G., “Self-consistent reaction field model for aqueous and nonaqueous solutions based on accurate polarized partial charges,” J. Chem. Theory Comput. 3, 2011–2033 (2007). 10.1021/ct7001418 [DOI] [PubMed] [Google Scholar]
- 517.Marenich A. V., Cramer C. J., and Truhlar D. G., “Generalized Born solvation model SM12,” J. Chem. Theory Comput. 9, 609–620 (2013). 10.1021/ct300900e [DOI] [PubMed] [Google Scholar]
- 518.Marenich A. V., Cramer C. J., and Truhlar D. G., “Universal solvation model based on solute electron density and a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions,” J. Phys. Chem. B 113, 6378–6396 (2009). 10.1021/jp810292n [DOI] [PubMed] [Google Scholar]
- 519.Pomogaeva A. and Chipman D. M., “Field-extremum model for short-range contributions to hydration free energy,” J. Chem. Theory Comput. 7, 3952–3960 (2011). 10.1021/ct200575c [DOI] [PubMed] [Google Scholar]
- 520.Pomogaeva A. and Chipman D. M., “New implicit solvation models for dispersion and exchange energies,” J. Phys. Chem. A 117, 5812–5820 (2013). 10.1021/jp404624x [DOI] [PubMed] [Google Scholar]
- 521.Pomogaeva A. and Chipman D. M., “Hydration energy from a composite method for implicit representation of the solvent,” J. Chem. Theory Comput. 10, 211–219 (2014). 10.1021/ct400894j [DOI] [PubMed] [Google Scholar]
- 522.Pomogaeva A. and Chipman D. M., “Composite method for implicit representation of solvent in dimethyl sulfoxide and acetonitrile,” J. Phys. Chem. A 119, 5173–5180 (2015). 10.1021/jp5098519 [DOI] [PubMed] [Google Scholar]
- 523.You Z.-Q. and Herbert J. M., “Reparameterization of an accurate, few-parameter implicit solvation model for quantum chemistry: Composite method for implicit representation of solvent, CMIRS v. 1.1,” J. Chem. Theory Comput. 12, 4338–4346 (2016). 10.1021/acs.jctc.6b00644 [DOI] [PubMed] [Google Scholar]
- 524.Thompson J. D., Cramer C. J., and Truhlar D. G., “New universal solvation model and comparison of the accuracy of the SM5.42R, SM5.43R, C-PCM, D-PCM, and IEF-PCM continuum solvation models for aqueous and organic solvation free energies and for vapor pressures,” J. Phys. Chem. A 108, 6532–6542 (2004). 10.1021/jp0496295 [DOI] [Google Scholar]
- 525.Kelly C. P., Cramer C. J., and Truhlar D. G., “SM6: A density functional theory continuum solvation model for calculating aqueous solvation free energies of neutrals, ions, and solute–water cluster,” J. Chem. Theory Comput. 1, 1133–1152 (2005). 10.1021/ct050164b [DOI] [PubMed] [Google Scholar]
- 526.Chipman D. M. and Dupuis M., “Implementation of solvent reaction fields for electronic structure,” Theor. Chem. Acc. 107, 90 (2002). 10.1007/s00214-001-0303-0 [DOI] [Google Scholar]
- 527.Chipman D. M., “Reaction field treatment of charge penetration,” J. Chem. Phys. 112, 5558 (2000). 10.1063/1.481133 [DOI] [Google Scholar]
- 528.Chipman D. M., “Comparison of solvent reaction field representations,” Theor. Chem. Acc. 107, 80 (2002). 10.1007/s00214-001-0302-1 [DOI] [Google Scholar]
- 529.Klamt A. and Schüürmann G., “COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient,” J. Chem. Soc., Perkin Trans. 2 1993, 799–805. 10.1039/p29930000799 [DOI] [Google Scholar]
- 530.Klamt A., “The COSMO and COSMO-RS solvation models,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 8, e1338 (2018). 10.1002/wcms.1338 [DOI] [Google Scholar]
- 531.Klamt A., Moya C., and Palomar J., “A comprehensive comparison of the IEFPCM and SS(V)PE continuum solvation methods with the COSMO approach,” J. Chem. Theory Comput. 11, 4220–4225 (2015). 10.1021/acs.jctc.5b00601 [DOI] [PubMed] [Google Scholar]
- 532.Aguilar M. A., Olivares del Valle F. J., and Tomasi J., “Nonequilibrium solvation: An ab initio quantum-mechanical method in the continuum cavity model approximation,” J. Chem. Phys. 98, 7375–7384 (1993). 10.1063/1.464728 [DOI] [Google Scholar]
- 533.Klamt A., “Calculation of UV/Vis spectra in solution,” J. Phys. Chem. 100, 3349–3353 (1996). 10.1021/jp950607f [DOI] [Google Scholar]
- 534.Cossi M. and Barone V., “Solvent effect on vertical electronic transitions by the polarizable continuum model,” J. Chem. Phys. 112, 2427–2435 (2000). 10.1063/1.480808 [DOI] [Google Scholar]
- 535.Li J., Cramer C. J., and Truhlar D. G., “Two-response-time model based on CM2/INDO/S2 electrostatic potentials for the dielectric polarization component of solvatochromic shifts on vertical excitation energies,” Int. J. Quantum Chem. 77, 264–280 (2000). [DOI] [Google Scholar]
- 536.Jacobson L. D. and Herbert J. M., “A simple algorithm for determining orthogonal, self-consistent excited-state wave functions for a state-specific Hamiltonian: Application to the optical spectrum of the aqueous electron,” J. Chem. Theory Comput. 7, 2085–2093 (2011). 10.1021/ct200265t [DOI] [PubMed] [Google Scholar]
- 537.You Z.-Q., Mewes J.-M., Dreuw A., and Herbert J. M., “Comparison of the Marcus and Pekar partitions in the context of non-equilibrium, polarizable-continuum reaction-field solvation models,” J. Chem. Phys. 143, 204104 (2015). 10.1063/1.4936357 [DOI] [PubMed] [Google Scholar]
- 538.Mewes J.-M., You Z.-Q., Wormit M., Kriesche T., Herbert J. M., and Dreuw A., “Experimental benchmark data and systematic evaluation of two a posteriori, polarizable-continuum corrections for vertical excitation energies in solution,” J. Phys. Chem. A 119, 5446–5464 (2015). 10.1021/jp511163y [DOI] [PubMed] [Google Scholar]
- 539.Mewes J.-M., Herbert J. M., and Dreuw A., “On the accuracy of the general, state-specific polarizable-continuum model for the description of correlated ground- and excited states in solution,” Phys. Chem. Chem. Phys. 19, 1644–1654 (2017). 10.1039/c6cp05986d [DOI] [PubMed] [Google Scholar]
- 540.Caricato M., Mennucci B., Tomasi J., Ingrosso F., Cammi R., Corni S., and Scalmani G., “Formation and relaxation of excited states in solution: A new time dependent polarizable continuum model based on time dependent density functional theory,” J. Chem. Phys. 124, 124520 (2006). 10.1063/1.2183309 [DOI] [PubMed] [Google Scholar]
- 541.Coons M. P., You Z.-Q., and Herbert J. M., “The hydrated electron at the surface of neat liquid water appears to be indistinguishable from the bulk species,” J. Am. Chem. Soc. 138, 10879–10886 (2016). 10.1021/jacs.6b06715 [DOI] [PubMed] [Google Scholar]
- 542.Coons M. P. and Herbert J. M., “Quantum chemistry in arbitrary dielectric environments: Theory and implementation of nonequilibrium Poisson boundary conditions and application to compute vertical ionization energies at the air/water interface,” J. Chem. Phys. 148, 222834 (2018); 10.1063/1.5023916 [DOI] [PubMed] [Google Scholar]; Erratum, J. Chem. Phys. 151, 189901 (2019). 10.1063/1.5132808 [DOI] [PubMed] [Google Scholar]
- 543.Paul S. K. and Herbert J. M., “Probing interfacial effects on ionization energies: The surprising banality of anion–water hydrogen bonding at the air/water interface,” J. Am. Chem. Soc. 143, 10189–10202 (2021). 10.1021/jacs.1c03131 [DOI] [PubMed] [Google Scholar]
- 544.Chipman D. M., “Charge penetration in dielectric models of solvation,” J. Chem. Phys. 106, 10194 (1997). 10.1063/1.474048 [DOI] [Google Scholar]
- 545.Zhan C.-G., Bentley J., and Chipman D. M., “Volume polarization in reaction field theory,” J. Chem. Phys. 108, 177–192 (1998). 10.1063/1.475371 [DOI] [Google Scholar]
- 546.Stein C. J., Herbert J. M., and Head-Gordon M., “The Poisson–Boltzmann model for implicit solvation of electrolyte solutions: Quantum chemical implementation and assessment via Sechenov coefficients,” J. Chem. Phys. 151, 224111 (2019). 10.1063/1.5131020 [DOI] [PubMed] [Google Scholar]
- 547.Aksu H., Paul S. K., Herbert J. M., and Dunietz B. D., “How well does a solvated octa-acid capsule shield the embedded chromophore? A computational analysis based on an anisotropic dielectric continuum model,” J. Phys. Chem. B 124, 6998–7004 (2020). 10.1021/acs.jpcb.0c04032 [DOI] [PubMed] [Google Scholar]
- 548.Jacobson L. D. and Herbert J. M., “A one-electron model for the aqueous electron that includes many-body electron-water polarization: Bulk equilibrium structure, vertical electron binding energy, and optical absorption spectrum,” J. Chem. Phys. 133, 154506 (2010). 10.1063/1.3490479 [DOI] [PubMed] [Google Scholar]
- 549.Ghosh D., Isayev O., Slipchenko L. V., and Krylov A. I., “Effect of solvation on the vertical ionization energy of thymine: From microhydration to bulk,” J. Phys. Chem. A 115, 6028–6038 (2011). 10.1021/jp110438c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 550.Ghosh D., Roy A., Seidel R., Winter B., Bradforth S., and Krylov A. I., “First-principle protocol for calculating ionization energies and redox potentials of solvated molecules and ions: Theory and application to aqueous phenol and phenolate,” J. Phys. Chem. B 116, 7269–7280 (2012). 10.1021/jp301925k [DOI] [PMC free article] [PubMed] [Google Scholar]
- 551.Bose S., Chakrabarty S., and Ghosh D., “Effect of solvation on electron detachment and excitation energies of a green fluorescent protein chromophore variant,” J. Phys. Chem. B 120, 4410–4420 (2016). 10.1021/acs.jpcb.6b03723 [DOI] [PubMed] [Google Scholar]
- 552.Bose S. and Ghosh D., “An interaction energy driven biased sampling technique: A faster route to ionization spectra in condensed phase,” J. Comput. Chem. 38, 2248 (2017). 10.1002/jcc.24875 [DOI] [PubMed] [Google Scholar]
- 553.Tóth Z., Kubečka J., Muchová E., and Slavíček P., “Ionization energies in solution with the QM:QM approach,” Phys. Chem. Chem. Phys. 22, 10550–10560 (2020). 10.1039/c9cp06154a [DOI] [PubMed] [Google Scholar]
- 554.Mukherjee M., Tripathi D., Brehm M., Riplinger C., and Dutta A. K., “Efficient EOM-CC-based protocol for the calculation of electron affinity of solvated nucleobases: Uracil as a case study,” J. Chem. Theory Comput. 17, 105–116 (2021). 10.1021/acs.jctc.0c00655 [DOI] [PubMed] [Google Scholar]
- 555.D’Annibale V., Nardi A. N., Amadei A., and D’Abramo M., “Theoretical characterization of the reduction potentials of nucleic acids in solution,” J. Chem. Theory Comput. 17, 1301–1307 (2021). 10.1021/acs.jctc.0c00728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 556.Holden Z. C., Richard R. M., and Herbert J. M., “Periodic boundary conditions for QM/MM calculations: Ewald summation for extended Gaussian basis sets,” J. Chem. Phys. 139, 244108 (2013); 10.1063/1.4850655 [DOI] [PubMed] [Google Scholar]; Erratum, J. Chem. Phys. 142, 059901 (2015). 10.1063/1.4907623 [DOI] [PubMed] [Google Scholar]
- 557.Holden Z. C., Rana B., and Herbert J. M., “Analytic gradient for the QM/MM-Ewald method using charges derived from the electrostatic potential: Theory, implementation, and application to ab initio molecular dynamics simulation of the aqueous electron,” J. Chem. Phys. 150, 144115 (2019). 10.1063/1.5089673 [DOI] [PubMed] [Google Scholar]
- 558.Nguyen T. S., Koh J. H., Lefelhocz S., and Parkhill J., “Black-box, real-time simulations of transient absorption spectroscopy,” J. Phys. Chem. Lett. 7, 1590–1595 (2016). 10.1021/acs.jpclett.6b00421 [DOI] [PubMed] [Google Scholar]
- 559.Herbert J. M., “Structure of the aqueous electron,” Phys. Chem. Chem. Phys. 21, 20538–20565 (2019). 10.1039/c9cp04222a [DOI] [PubMed] [Google Scholar]
- 560.Loh Z.-H., Doumy G., Arnold C., Kjellsson L., Southworth S. H., Al Haddad A., Kumagai Y., Tu M.-F., Ho P. J., March A. M., Schaller R. D., Bin Mohd Yusof M. S., Debnath T., Simon M., Welsch R., Inhester L., Khalili K., Nanda K., Krylov A. I., Moeller S., Coslovich G., Koralek J., Minitti M. P., Schlotter W. F., Rubensson J.-E., Santra R., and Young L., “Observation of the fastest chemical processes in the radiolysis of water,” Science 367, 179–182 (2020). 10.1126/science.aaz4740 [DOI] [PubMed] [Google Scholar]
- 561.Kjellsson L., Nanda K. D., Rubensson J.-E., Doumy G., Southworth S. H., Ho P. J., March A. M., Al Haddad A., Kumagai Y., Tu M.-F., Schaller R. D., Debnath T., Bin Mohd Yusof M. S., Arnold C., Schlotter W. F., Moeller S., Coslovich G., Koralek J. D., Minitti M. P., Vidal M. L., Simon M., Santra R., Loh Z.-H., Coriani S., Krylov A. I., and Young L., “Resonant inelastic x-ray scattering reveals hidden local transitions of the aqueous OH radical,” Phys. Rev. Lett. 124, 236001 (2020). 10.1103/physrevlett.124.236001 [DOI] [PubMed] [Google Scholar]
- 562.Rana B. and Herbert J. M., “Role of hemibonding in the structure and ultraviolet spectroscopy of the aqueous hydroxyl radical,” Phys. Chem. Chem. Phys. 22, 27829–27844 (2020). 10.1039/d0cp05216g [DOI] [PubMed] [Google Scholar]
- 563.Mason S. E., Beton P. H., and Besley N. A., “AIRBED: A simplified density functional theory model for physisorption on surfaces,” J. Chem. Theory Comput. 15, 5628–5634 (2019). 10.1021/acs.jctc.9b00576 [DOI] [PubMed] [Google Scholar]
- 564.Ghosh D., Kosenkov D., Vanovschi V., Williams C. F., Herbert J. M., Gordon M. S., Schmidt M. W., Slipchenko L. V., and Krylov A. I., “Noncovalent interactions in extended systems described by the effective fragment potential method: Theory and application to nucleobase oligomers,” J. Phys. Chem. A 114, 12739–12754 (2010). 10.1021/jp107557p [DOI] [PMC free article] [PubMed] [Google Scholar]
- 565.Ghosh D., Kosenkov D., Vanovschi V., Flick J., Kaliman I., Shao Y., Gilbert A. T. B., Krylov A. I., and Slipchenko L. V., “Effective fragment potential method in Q-Chem: A guide for users and developers,” J. Comput. Chem. 34, 1060–1070 (2013). 10.1002/jcc.23223 [DOI] [PubMed] [Google Scholar]
- 566.Slipchenko L. V. and Gurunathan P. K., “Effective fragment potential method: Past, present, and future,” in Fragmentation: Toward Accurate Calculations on Complex Molecular Systems, edited by Gordon M. S. (Wiley, Hoboken, 2017), Chap. 6, pp. 183–208. [Google Scholar]
- 567.Slipchenko L. V., “Solvation of excited states of chromophores in polarizable environment: Orbital relaxation versus polarization,” J. Phys. Chem. A 114, 8824–8830 (2010). 10.1021/jp101797a [DOI] [PubMed] [Google Scholar]
- 568.Sen R., Dreuw A., and Faraji S., “Algebraic diagrammatic construction for the polarisation propagator in combination with effective fragment potentials,” Phys. Chem. Chem. Phys. 21, 3683–3694 (2019). 10.1039/c8cp06527f [DOI] [PubMed] [Google Scholar]
- 569.Nanda K. D. and Krylov A. I., “The effect of polarizable environment on two-photon absorption cross sections characterized by the equation-of-motion coupled-cluster singles and doubles method combined with the effective fragment potential approach,” J. Chem. Phys. 149, 164109 (2018). 10.1063/1.5048627 [DOI] [PubMed] [Google Scholar]
- 570.Olsen J. M., Aidas K., and Kongsted J., “Excited states in solution through polarizable embedding,” J. Chem. Theory Comput. 6, 3721–3734 (2010). 10.1021/ct1003803 [DOI] [Google Scholar]
- 571.Scheurer M., Herbst M. F., Reinholdt P., Olsen J. M. H., Dreuw A., and Kongsted J., “Polarizable embedding combined with the algebraic diagrammatic construction: Tackling excited states in biomolecular systems,” J. Chem. Theory Comput. 14, 4870–4883 (2018). 10.1021/acs.jctc.8b00576 [DOI] [PubMed] [Google Scholar]
- 572.Brooks B. R., Brooks C. L. III, A. D. Mackerell, Jr., Nilsson L., Petrella R. J., Roux B., Won Y., Archontis G., Bartels C., Boresch S., Caflisch A., Caves L., Cui Q., Dinner A. R., Feig M., Fischer S., Gao J., Hodoscek M., Im W., Kuczera K., Lazaridis T., Ma J., Ovchinnikov V., Paci E., Pastor R. W., Post C. B., Pu J. Z., Schaefer M., Tidor B., Venable R. M., Woodcock H. L., Wu X., Yang W., York D. M., and Karplus M., “CHARMM: The biomolecular simulation program,” J. Comput. Chem. 30, 1545–1614 (2009). 10.1002/jcc.21287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 573.Woodcock H. L. III, Hodošček M., Gilbert A. T. B., Gill P. M. W., Schaefer H. F. III, and Brooks B. R., “Interfacing Q-Chem and CHARMM to perform QM/MM reaction path calculations,” J. Comput. Chem. 28, 1485–1502 (2007). 10.1002/jcc.20587 [DOI] [PubMed] [Google Scholar]
- 574.Miller B. T., Singh R. P., Klauda J. B., Hodošček M., Brooks B. R., and Woodcock H. L. III, “CHARMMing: A new, flexible web portal for CHARMM,” J. Chem. Inf. Model. 48, 1920–1929 (2008). 10.1021/ci800133b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 575.Miller B. T., Singh R. P., Schalk V., Pevzner Y., Sun J., Miller C. S., Boresch S., Ichiye T., Brooks B. R., and Woodcock H. L. III, “Web-based computational chemistry education with CHARMMing I: Lessons and tutorial,” PLoS Comput. Biol. 10, e1003719 (2014). 10.1371/journal.pcbi.1003719 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 576.Páll S., Zhmurov A., Bauer P., Abraham M., Lundborg M., Gray A., Hess B., and Lindahl E., “Heterogeneous parallelization and acceleration of molecular dynamics simulations in GROMACS,” J. Chem. Phys. 153, 134110 (2020). 10.1063/5.0018516 [DOI] [PubMed] [Google Scholar]
- 577.Phillips J. C., Hardy D. J., Maia J. D. C., Stone J. E., Ribeiro J. V., Bernardi R. C., Buch R., Fiorin G., Hénin J., Jiang W., McGreevy R., Melo M. C. R., Radak B. K., Skeel R. D., Singharoy A., Wang Y., Roux B., Aksimentiev A., Luthey-Schulten Z., Kalé L. V., Schulten K., Chipot C., and Tajkhorshid E., “Scalable molecular dynamics on CPU and GPU architectures with NAMD,” J. Chem. Phys. 153, 044130 (2020). 10.1063/5.0014475 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 578.Himo F., “Recent trends in quantum chemical modeling of enzymatic reactions,” J. Am. Chem. Soc. 139, 6780–6786 (2017). 10.1021/jacs.7b02671 [DOI] [PubMed] [Google Scholar]
- 579.Dasgupta S. and Herbert J. M., “Using atomic confining potentials for geometry optimization and vibrational frequency calculations in quantum-chemical models of enzyme active sites,” J. Phys. Chem. B 124, 1137–1147 (2020). 10.1021/acs.jpcb.9b11060 [DOI] [PubMed] [Google Scholar]
- 580.Claudino D. and Mayhall N. J., “Automatic partition of orbital spaces based on singular value decomposition in the context of embedding theories,” J. Chem. Theory Comput. 15, 1053–1064 (2019). 10.1021/acs.jctc.8b01112 [DOI] [PubMed] [Google Scholar]
- 581.Pipek J. and Mezey P. G., “A fast intrinsic localization procedure applicable for ab initio and semiempirical linear combination of atomic orbital wave functions,” J. Chem. Phys. 90, 4916–4926 (1989). 10.1063/1.456588 [DOI] [Google Scholar]
- 582.Claudino D. and Mayhall N. J., “Simple and efficient truncation of virtual spaces in embedded wave functions via concentric localization,” J. Chem. Theory Comput. 15, 6085–6096 (2019). 10.1021/acs.jctc.9b00682 [DOI] [PubMed] [Google Scholar]
- 583.Wesołowski T. A., “Embedding a multideterminantal wave function in an orbital-free environment,” Phys. Rev. A 77, 012504 (2008). 10.1103/PhysRevA.77.012504 [DOI] [Google Scholar]
- 584.Gomes A. S. P. and Jacob C. R., “Quantum-chemical embedding methods for treating local electronic excitations in complex chemical systems,” Annu. Rep. Prog. Chem., Sect. C: Phys. Chem. 108, 222–277 (2012). 10.1039/c2pc90007f [DOI] [Google Scholar]
- 585.Wesolowski T. A., Shedge S., and Zhou X., “Frozen-density embedding strategy for multilevel simulations of electronic structure,” Chem. Rev. 115, 5891–5928 (2015). 10.1021/cr500502v [DOI] [PubMed] [Google Scholar]
- 586.Prager S., Zech A., Aquilante F., Dreuw A., and Wesolowski T. A., “First time combination of frozen density embedding theory with the algebraic diagrammatic construction scheme for the polarization propagator of second order,” J. Chem. Phys. 144, 204103 (2016). 10.1063/1.4948741 [DOI] [PubMed] [Google Scholar]
- 587.Prager S., Zech A., Wesolowski T. A., and Dreuw A., “Implementation and application of the frozen density embedding theory with the algebraic diagrammatic construction scheme for the polarization propagator up to third order,” J. Chem. Theory Comput. 13, 4711–4725 (2017). 10.1021/acs.jctc.7b00461 [DOI] [PubMed] [Google Scholar]
- 588.Fornace M. E., Lee J., Miyamoto K., Manby F. R., and Miller T. F. III, “Embedded mean-field theory,” J. Chem. Theory Comput. 11, 568–580 (2015); 10.1021/ct5011032 [DOI] [PubMed] [Google Scholar]; Erratum, J. Chem. Theory Comput. 11, 3968 (2015). 10.1021/acs.jctc.5b00630 [DOI] [PubMed] [Google Scholar]
- 589.Veccham S. P., Lee J., and Head-Gordon M., “Making many-body interactions nearly pairwise additive: The polarized many-body expansion approach,” J. Chem. Phys. 151, 194101 (2019). 10.1063/1.5125802 [DOI] [PubMed] [Google Scholar]
- 590.Ribas-Arino J., Shiga M., and Marx D., “Understanding covalent mechanochemistry,” Angew. Chem., Int. Ed. 48, 4190–4193 (2009). 10.1002/anie.200900673 [DOI] [PubMed] [Google Scholar]
- 591.Stauch T., Chakraborty R., and Head‐Gordon M., “Quantum chemical modeling of pressure-induced spin crossover in octahedral metal-ligand complexes,” ChemPhysChem 20, 2742–2747 (2019). 10.1002/cphc.201900853 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 592.Stauch T., “A mechanochemical model for the simulation of molecules and molecular crystals under hydrostatic pressure,” J. Chem. Phys. 153, 134503 (2020). 10.1063/5.0024671 [DOI] [PubMed] [Google Scholar]
- 593.Scheurer M., Dreuw A., Epifanovsky E., Head-Gordon M., and Stauch T., “Modeling molecules under pressure with Gaussian potentials,” J. Chem. Theory Comput. 17, 583–597 (2021). 10.1021/acs.jctc.0c01212 [DOI] [PubMed] [Google Scholar]
- 594.Richard R. M. and Herbert J. M., “A generalized many-body expansion and a unified view of fragment-based methods in electronic structure theory,” J. Chem. Phys. 137, 064113 (2012). 10.1063/1.4742816 [DOI] [PubMed] [Google Scholar]
- 595.Richard R. M., Lao K. U., and Herbert J. M., “Aiming for benchmark accuracy with the many-body expansion,” Acc. Chem. Res. 47, 2828–2836 (2014). 10.1021/ar500119q [DOI] [PubMed] [Google Scholar]
- 596.Richard R. M., Lao K. U., and Herbert J. M., “Understanding the many-body expansion for large systems. I. Precision considerations,” J. Chem. Phys. 141, 014108 (2014). 10.1063/1.4885846 [DOI] [PubMed] [Google Scholar]
- 597.Lao K. U., Liu K.-Y., Richard R. M., and Herbert J. M., “Understanding the many-body expansion for large systems. II. Accuracy considerations,” J. Chem. Phys. 144, 164105 (2016). 10.1063/1.4947087 [DOI] [PubMed] [Google Scholar]
- 598.Liu K.-Y. and Herbert J. M., “Understanding the many-body expansion for large systems. III. Critical role of four-body terms, counterpoise corrections, and cutoffs,” J. Chem. Phys. 147, 161729 (2017). 10.1063/1.4986110 [DOI] [PubMed] [Google Scholar]
- 599.Richard R. M., Lao K. U., and Herbert J. M., “Achieving the CCSD(T) basis-set limit in sizable molecular clusters: Counterpoise corrections for the many-body expansion,” J. Phys. Chem. Lett. 4, 2674–2680 (2013). 10.1021/jz401368u [DOI] [PubMed] [Google Scholar]
- 600.Richard R. M., Lao K. U., and Herbert J. M., “Approaching the complete-basis limit with a truncated many-body expansion,” J. Chem. Phys. 139, 224102 (2013). 10.1063/1.4836637 [DOI] [PubMed] [Google Scholar]
- 601.Liu K.-Y. and Herbert J. M., “Energy-screened many-body expansion: A practical yet accurate fragmentation method for quantum chemistry,” J. Chem. Theory Comput. 16, 475–487 (2020). 10.1021/acs.jctc.9b01095 [DOI] [PubMed] [Google Scholar]
- 602.Ouyang J. F., Cvitkovic M. W., and Bettens R. P. A., “Trouble with the many-body expansion,” J. Chem. Theory Comput. 10, 3699–3707 (2014). 10.1021/ct500396b [DOI] [PubMed] [Google Scholar]
- 603.Ouyang J. F. and Bettens R. P. A., “Many-body basis set superposition effect,” J. Chem. Theory Comput. 11, 5132–5143 (2015). 10.1021/acs.jctc.5b00343 [DOI] [PubMed] [Google Scholar]
- 604.Heindel J. P. and Xantheas S. S., “The many-body expansion for aqueous systems revisited: I. Water–water interactions,” J. Chem. Theory Comput. 16, 6843–6855 (2020). 10.1021/acs.jctc.9b00749 [DOI] [PubMed] [Google Scholar]
- 605.Bardeen C. J., “The structure and dynamics of molecular excitons,” Annu. Rev. Phys. Chem. 65, 127–148 (2014). 10.1146/annurev-physchem-040513-103654 [DOI] [PubMed] [Google Scholar]
- 606.Sisto A., Glowacki D. R., and Martinez T. J., “Ab initio nonadiabatic dynamics of multichromophore complexes: A scalable graphical-processing-unit-accelerated exciton framework,” Acc. Chem. Res. 47, 2857–2866 (2014); 10.1021/ar500229p [DOI] [PubMed] [Google Scholar]; Erratum, Acc. Chem. Res. 49, 1331 (2016). 10.1021/acs.accounts.6b00217 [DOI] [PubMed] [Google Scholar]
- 607.Sisto A., Stross C., van der Kamp M. W., O’Connor M., McIntosh-Smith S., Johnson G. T., Hohenstein E. G., Manby F. R., Glowacki D. R., and Martinez T. J., “Atomistic non-adiabatic dynamics of the LH2 complex with a GPU-accelerated ab initio exciton model,” Phys. Chem. Chem. Phys. 19, 14924–14936 (2017). 10.1039/c7cp00492c [DOI] [PubMed] [Google Scholar]
- 608.Li X., Parrish R. M., Liu F., Kokkila Schumacher S. I. L., and Martínez T. J., “An ab initio exciton model including charge-transfer excited states,” J. Chem. Theory Comput. 13, 3493–3504 (2017). 10.1021/acs.jctc.7b00171 [DOI] [PubMed] [Google Scholar]
- 609.Morrison A. F., You Z.-Q., and Herbert J. M., “Ab initio implementation of the Frenkel–Davydov exciton model: A naturally parallelizable approach to computing collective excitations in crystals and aggregates,” J. Chem. Theory Comput. 10, 5366–5376 (2014). 10.1021/ct500765m [DOI] [PubMed] [Google Scholar]
- 610.Morrison A. F. and Herbert J. M., “Low-scaling quantum chemistry approach to excited-state properties via an ab initio exciton model: Application to excitation energy transfer in a self-assembled nanotube,” J. Phys. Chem. Lett. 6, 4390–4396 (2015). 10.1021/acs.jpclett.5b02109 [DOI] [PubMed] [Google Scholar]
- 611.Morrison A. F. and Herbert J. M., “Analytic derivative couplings and first-principles exciton/phonon coupling constants for an ab initio Frenkel–Davydov exciton model: Theory, implementation, and application to compute triplet exciton mobility parameters for crystalline tetracene,” J. Chem. Phys. 146, 224110 (2017). 10.1063/1.4985607 [DOI] [PubMed] [Google Scholar]
- 612.Morrison A. F. and Herbert J. M., “Evidence for singlet fission driven by vibronic coherence in crystalline tetracene,” J. Phys. Chem. Lett. 8, 1442–1448 (2017). 10.1021/acs.jpclett.7b00230 [DOI] [PubMed] [Google Scholar]
- 613.Zimmerman P. M., Musgrave C. B., and Head-Gordon M., “A correlated electron view of singlet fission,” Acc. Chem. Res. 46, 1339–1347 (2013). 10.1021/ar3001734 [DOI] [PubMed] [Google Scholar]
- 614.Kim H. and Zimmerman P. M., “Coupled double triplet state in singlet fission,” Phys. Chem. Chem. Phys. 20, 30083–30094 (2018). 10.1039/c8cp06256k [DOI] [PubMed] [Google Scholar]
- 615.Zhugayevych A. and Tretiak S., “Theoretical description of structural and electronic properties of organic photovoltaic materials,” Annu. Rev. Phys. Chem. 66, 305–330 (2015). 10.1146/annurev-physchem-040214-121440 [DOI] [PubMed] [Google Scholar]
- 616.Hsu C.-P., You Z.-Q., and Chen H.-C., “Characterization of the short-range couplings in excitation energy transfer,” J. Phys. Chem. C 112, 1204–1212 (2008). 10.1021/jp076512i [DOI] [Google Scholar]
- 617.Voityuk A. A. and Rösch N., “Fragment charge difference method for estimating donor-acceptor electronic coupling: Application to DNA π-stacks,” J. Chem. Phys. 117, 5607–5616 (2002). 10.1063/1.1502255 [DOI] [Google Scholar]
- 618.Kue K. Y., Claudio G. C., and Hsu C.-P., “Hamiltonian-independent generalization of the fragment excitation difference scheme,” J. Chem. Theory Comput. 14, 1304–1310 (2018). 10.1021/acs.jctc.7b01103 [DOI] [PubMed] [Google Scholar]
- 619.Lin H.-H., Kue K. Y., Claudio G. C., and Hsu C.-P., “First principle prediction of intramolecular singlet fission and triplet triplet annihilation rates,” J. Chem. Theory Comput. 15, 2246–2253 (2019). 10.1021/acs.jctc.8b01185 [DOI] [PubMed] [Google Scholar]
- 620.Maurice D. and Head-Gordon M., “On the nature of electronic transitions in radicals: An extended single excitation configuration interaction method,” J. Phys. Chem. 100, 6131–6137 (1996). 10.1021/jp952754j [DOI] [Google Scholar]
- 621.Weinhold F., Landis C. R., and Glendening E. D., “What is NBO analysis and how is it useful?,” Int. Rev. Phys. Chem. 35, 399–440 (2016). 10.1080/0144235x.2016.1192262 [DOI] [Google Scholar]
- 622.Kimber P. and Plasser F., “Toward an understanding of electronic excitation energies beyond the molecular orbital picture,” Phys. Chem. Chem. Phys. 22, 6058–6080 (2020). 10.1039/d0cp00369g [DOI] [PubMed] [Google Scholar]
- 623.Mao Y., Loipersberger M., Horn P. R., Das A., Demerdash O., Levine D. S., Prasad Veccham S., Head-Gordon T., and Head-Gordon M., “From intermolecular interaction energies and observable shifts to component contributions and back again: A tale of variational energy decomposition analysis,” Annu. Rev. Phys. Chem. 72, 641–666 (2021). 10.1146/annurev-physchem-090419-115149 [DOI] [PubMed] [Google Scholar]
- 624.Lao K. U. and Herbert J. M., “Accurate and efficient quantum chemistry calculations of noncovalent interactions in many-body systems: The XSAPT family of methods,” J. Phys. Chem. A 119, 235–252 (2015). 10.1021/jp5098603 [DOI] [PubMed] [Google Scholar]
- 625.Mao Y., Ge Q., Horn P. R., and Head-Gordon M., “On the computational characterization of charge-transfer effects in noncovalently bound molecular complexes,” J. Chem. Theory Comput. 14, 2401–2417 (2018). 10.1021/acs.jctc.7b01256 [DOI] [PubMed] [Google Scholar]
- 626.Horn P. R., Mao Y., and Head-Gordon M., “Probing non-covalent interactions with a second generation energy decomposition analysis using absolutely localized molecular orbitals,” Phys. Chem. Chem. Phys. 18, 23067–23079 (2016). 10.1039/c6cp03784d [DOI] [PubMed] [Google Scholar]
- 627.Mao Y., Levine D. S., Loipersberger M., Horn P. R., and Head-Gordon M., “Probing radical–molecule interactions with a second generation energy decomposition analysis of DFT calculations using absolutely localized molecular orbitals,” Phys. Chem. Chem. Phys. 22, 12867–12885 (2020). 10.1039/d0cp01933j [DOI] [PubMed] [Google Scholar]
- 628.Khaliullin R. Z., Cobar E. A., Lochan R. C., Bell A. T., and Head-Gordon M., “Unravelling the origin of intermolecular interactions using absolutely localized molecular orbitals,” J. Phys. Chem. A 111, 8753–8765 (2007). 10.1021/jp073685z [DOI] [PubMed] [Google Scholar]
- 629.Khaliullin R. Z., Bell A. T., and Head-Gordon M., “Analysis of charge transfer effects in molecular complexes based on absolutely localized molecular orbitals,” J. Chem. Phys. 128, 184112 (2008). 10.1063/1.2912041 [DOI] [PubMed] [Google Scholar]
- 630.Horn P. R. and Head-Gordon M., “Polarization contributions to intermolecular interactions revisited with fragment electric-field response functions,” J. Chem. Phys. 143, 114111 (2015). 10.1063/1.4930534 [DOI] [PubMed] [Google Scholar]
- 631.Khaliullin R. Z., Head-Gordon M., and Bell A. T., “An efficient self-consistent field method for large systems of weakly interacting components,” J. Chem. Phys. 124, 204105 (2006). 10.1063/1.2191500 [DOI] [PubMed] [Google Scholar]
- 632.Horn P. R., Mao Y., and Head-Gordon M., “Defining the contributions of permanent electrostatics, Pauli repulsion, and dispersion in density functional theory calculations of intermolecular interaction energies,” J. Chem. Phys. 144, 114107 (2016). 10.1063/1.4942921 [DOI] [PubMed] [Google Scholar]
- 633.Mao Y., Demerdash O., Head-Gordon M., and Head-Gordon T., “Assessing ion–water interactions in the AMOEBA force field using energy decomposition analysis of electronic structure calculations,” J. Chem. Theory Comput. 12, 5422–5437 (2016). 10.1021/acs.jctc.6b00764 [DOI] [PubMed] [Google Scholar]
- 634.Demerdash O., Mao Y., Liu T., Head-Gordon M., and Head-Gordon T., “Assessing many-body contributions to intermolecular interactions of the AMOEBA force field using energy decomposition analysis of electronic structure calculations,” J. Chem. Phys. 147, 161721 (2017). 10.1063/1.4999905 [DOI] [PubMed] [Google Scholar]
- 635.Das A. K., Urban L., Leven I., Loipersberger M., Aldossary A., Head-Gordon M., and Head-Gordon T., “Development of an advanced force field for water using variational energy decomposition analysis,” J. Chem. Theory Comput. 15, 5001–5013 (2019). 10.1021/acs.jctc.9b00478 [DOI] [PubMed] [Google Scholar]
- 636.Mao Y., Loipersberger M., Kron K. J., Derrick J. S., Chang C. J., Sharada S. M., and Head-Gordon M., “Consistent inclusion of continuum solvation in energy decomposition analysis: Theory and application to molecular CO2 reduction catalysts,” Chem. Sci. 12, 1398–1414 (2021). 10.1039/d0sc05327a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 637.Veccham S. P., Lee J., Mao Y., Horn P. R., and Head-Gordon M., “A non-perturbative pairwise-additive analysis of charge transfer contributions to intermolecular interaction energies,” Phys. Chem. Chem. Phys. 23, 928–943 (2021). 10.1039/d0cp05852a [DOI] [PubMed] [Google Scholar]
- 638.Michalak A., Mitoraj M., and Ziegler T., “Bond orbitals from chemical valence theory,” J. Phys. Chem. A 112, 1933–1939 (2008). 10.1021/jp075460u [DOI] [PubMed] [Google Scholar]
- 639.Thirman J. and Head-Gordon M., “An energy decomposition analysis for second-order Møller–Plesset perturbation theory based on absolutely localized molecular orbitals,” J. Chem. Phys. 143, 084124 (2015). 10.1063/1.4929479 [DOI] [PubMed] [Google Scholar]
- 640.Thirman J. and Head-Gordon M., “Efficient implementation of energy decomposition analysis for second-order Møller–Plesset perturbation theory and application to anion–π interactions,” J. Phys. Chem. A 121, 717–728 (2017). 10.1021/acs.jpca.6b11516 [DOI] [PubMed] [Google Scholar]
- 641.Loipersberger M., Mao Y., and Head-Gordon M., “Variational forward–backward charge transfer analysis based on absolutely localized molecular orbitals: Energetics and molecular properties,” J. Chem. Theory Comput. 16, 1073–1089 (2020). 10.1021/acs.jctc.9b01168 [DOI] [PubMed] [Google Scholar]
- 642.Ge Q., Mao Y., and Head-Gordon M., “Energy decomposition analysis for exciplexes using absolutely localized molecular orbitals,” J. Chem. Phys. 148, 064105 (2018). 10.1063/1.5017510 [DOI] [PubMed] [Google Scholar]
- 643.Ge Q. and Head-Gordon M., “Energy decomposition analysis for excimers using absolutely localized molecular orbitals within time-dependent density functional theory and configuration interaction with single excitations,” J. Chem. Theory Comput. 14, 5156 (2018). 10.1021/acs.jctc.8b00537 [DOI] [PubMed] [Google Scholar]
- 644.Andrés J., Ayers P. W., Boto R. A., Carbó‐Dorca R., Chermette H., Cioslowski J., Contreras‐García J., Cooper D. L., Frenking G., Gatti C., Heidar‐Zadeh F., Joubert L., Martín Pendás Á., Matito E., Mayer I., Misquitta A. J., Mo Y., Pilmé J., Popelier P. L. A., Rahm M., Ramos‐Cordoba E., Salvador P., Schwarz W. H. E., Shahbazian S., Silvi B., Solà M., Szalewicz K., Tognetti V., Weinhold F., and Zins É. L., “Nine questions on energy decomposition analysis,” J. Comput. Chem. 40, 2248–2283 (2019). 10.1002/jcc.26003 [DOI] [PubMed] [Google Scholar]
- 645.Andrada D. M. and Foroutan-Nejad C., “Energy components in energy decomposition analysis (EDA) are path functions; why does it matter?,” Phys. Chem. Chem. Phys. 22, 22459–22464 (2020). 10.1039/d0cp04016a [DOI] [PubMed] [Google Scholar]
- 646.Mao Y., Horn P. R., and Head-Gordon M., “Energy decomposition analysis in an adiabatic picture,” Phys. Chem. Chem. Phys. 19, 5944–5958 (2017). 10.1039/c6cp08039a [DOI] [PubMed] [Google Scholar]
- 647.Levine D. S. and Head-Gordon M., “Energy decomposition analysis of single bonds within Kohn–Sham density functional theory,” Proc. Natl. Acad. Sci. U. S. A. 114, 12649 (2017). 10.1073/pnas.1715763114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 648.Levine D. S., Horn P. R., Mao Y., and Head-Gordon M., “Variational energy decomposition analysis of chemical bonding. 1. Spin-pure analysis of single bonds,” J. Chem. Theory Comput. 12, 4812 (2016). 10.1021/acs.jctc.6b00571 [DOI] [PubMed] [Google Scholar]
- 649.Levine D. S. and Head-Gordon M., “Quantifying the role of orbital contraction in chemical bonding,” J. Phys. Chem. Lett. 8, 1967 (2017). 10.1021/acs.jpclett.7b00766 [DOI] [PubMed] [Google Scholar]
- 650.Shaik S., Danovich D., Wu W., and Hiberty P. C., “Charge-shift bonding and its manifestations in chemistry,” Nat. Chem. 1, 443–449 (2009). 10.1038/nchem.327 [DOI] [PubMed] [Google Scholar]
- 651.Levine D. S. and Head-Gordon M., “Clarifying the quantum mechanical origin of the covalent chemical bond,” Nat. Commun. 11, 4893 (2020). 10.1038/s41467-020-18670-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 652.Hohenstein E. G. and Sherrill C. D., “Wavefunction methods for noncovalent interactions,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2, 304–326 (2012). 10.1002/wcms.84 [DOI] [Google Scholar]
- 653.Parker T. M., Burns L. A., Parrish R. M., Ryno A. G., and Sherrill C. D., “Levels of symmetry adapted perturbation theory (SAPT). I. Efficiency and performance for interaction energies,” J. Chem. Phys. 140, 094106 (2014). 10.1063/1.4867135 [DOI] [PubMed] [Google Scholar]
- 654.Herbert J. M., Jacobson L. D., Lao K. U., and Rohrdanz M. A., “Rapid computation of intermolecular interactions in molecular and ionic clusters: Self-consistent polarization plus symmetry-adapted perturbation theory,” Phys. Chem. Chem. Phys. 14, 7679–7699 (2012). 10.1039/c2cp24060b [DOI] [PubMed] [Google Scholar]
- 655.Lao K. U. and Herbert J. M., “Symmetry-adapted perturbation theory with Kohn-Sham orbitals using non-empirically tuned, long-range-corrected density functionals,” J. Chem. Phys. 140, 044108 (2014). 10.1063/1.4862644 [DOI] [PubMed] [Google Scholar]
- 656.Stone A. J., “Computation of charge-transfer energies by perturbation theory,” Chem. Phys. Lett. 211, 101–109 (1993). 10.1016/0009-2614(93)80058-w [DOI] [Google Scholar]
- 657.Stone A. J. and Misquitta A. J., “Charge-transfer in symmetry-adapted perturbation theory,” Chem. Phys. Lett. 473, 201–205 (2009). 10.1016/j.cplett.2009.03.073 [DOI] [Google Scholar]
- 658.Řezáč J. and de la Lande A., “Robust, basis-set independent method for the evaluation of charge-transfer energy in noncovalent complexes,” J. Chem. Theory Comput. 11, 528–537 (2015). 10.1021/ct501115m [DOI] [PubMed] [Google Scholar]
- 659.Lao K. U. and Herbert J. M., “Energy decomposition analysis with a stable charge-transfer term for interpreting intermolecular interactions,” J. Chem. Theory Comput. 12, 2569 (2016). 10.1021/acs.jctc.6b00155 [DOI] [PubMed] [Google Scholar]
- 660.Řezáč J. and de la Lande A., “On the role of charge transfer in halogen bonding,” Phys. Chem. Chem. Phys. 19, 791 (2017). 10.1039/C6CP07475H [DOI] [PubMed] [Google Scholar]
- 661.Herbert J. M. and Carter-Fenk K., “Electrostatics, charge transfer, and the nature of the halide–water hydrogen bond,” J. Phys. Chem. A 125, 1243–1256 (2021). 10.1021/acs.jpca.0c11356 [DOI] [PubMed] [Google Scholar]
- 662.Robertson W. H. and Johnson M. A., “Molecular aspects of halide ion hydration: The cluster approach,” Annu. Rev. Phys. Chem. 54, 173–213 (2003). 10.1146/annurev.physchem.54.011002.103801 [DOI] [PubMed] [Google Scholar]
- 663.T. L. Brown, Jr., LeMay H. E., Bursten B. E., Murphy C. J., and Woodward P. M., Chemistry: The Central Science, 12th ed. (Pearson, 2012). [Google Scholar]
- 664.Xie W., Song L., Truhlar D. G., and Gao J., “The variational explicit polarization potential and analytical first derivative of energy: Towards a next generation force field,” J. Chem. Phys. 128, 234108 (2008). 10.1063/1.2936122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 665.Gao J., Truhlar D. G., Wang Y., Mazack M. J. M., Löffler P., Provorse M. R., and Rehak P., “Explicit polarization: A quantum mechanical framework for developing next generation force fields,” Acc. Chem. Res. 47, 2837–2845 (2014). 10.1021/ar5002186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 666.Jacobson L. D. and Herbert J. M., “An efficient, fragment-based electronic structure method for molecular systems: Self-consistent polarization with perturbative two-body exchange and dispersion,” J. Chem. Phys. 134, 094118 (2011). 10.1063/1.3560026 [DOI] [PubMed] [Google Scholar]
- 667.Liu K.-Y., Carter-Fenk K., and Herbert J. M., “Self-consistent charge embedding at very low cost, with application to symmetry-adapted perturbation theory,” J. Chem. Phys. 151, 031102 (2019). 10.1063/1.5111869 [DOI] [PubMed] [Google Scholar]
- 668.Lao K. U. and Herbert J. M., “Accurate intermolecular interactions at dramatically reduced cost: XPol + SAPT with empirical dispersion,” J. Phys. Chem. Lett. 3, 3241–3248 (2012). 10.1021/jz301015p [DOI] [Google Scholar]
- 669.Lao K. U. and Herbert J. M., “An improved treatment of empirical dispersion and a many-body energy decomposition scheme for the explicit polarization plus symmetry-adapted perturbation theory (XSAPT) method,” J. Chem. Phys. 139, 034107 (2013); 10.1063/1.4813523 [DOI] [PubMed] [Google Scholar]; Erratum, J. Chem. Phys. 140, 119901 (2014). 10.1063/1.4869543 [DOI] [Google Scholar]
- 670.Jacobson L. D., Richard R. M., Lao K. U., and Herbert J. M., “Efficient monomer-based quantum chemistry methods for molecular and ionic clusters,” Annu. Rep. Comput. Chem. 9, 25–58 (2013). 10.1016/b978-0-444-62672-1.00002-9 [DOI] [Google Scholar]
- 671.Lao K. U. and Herbert J. M., “A simple correction for nonadditive dispersion within extended symmetry-adapted perturbation theory (XSAPT),” J. Chem. Theory Comput. 14, 5128–5142 (2018). 10.1021/acs.jctc.8b00527 [DOI] [PubMed] [Google Scholar]
- 672.Carter-Fenk K., Lao K. U., Liu K.-Y., and Herbert J. M., “Accurate and efficient ab initio calculations for supramolecular complexes: Symmetry-adapted perturbation theory with many-body dispersion,” J. Phys. Chem. Lett. 10, 2706–2714 (2019). 10.1021/acs.jpclett.9b01156 [DOI] [PubMed] [Google Scholar]
- 673.Papajak E., Zheng J., Xu X., Leverentz H. R., and Truhlar D. G., “Perspectives on basis sets beautiful: Seasonal plantings of diffuse basis functions,” J. Chem. Theory Comput. 7, 3027–3034 (2011). 10.1021/ct200106a [DOI] [PubMed] [Google Scholar]
- 674.Grimme S., “Density functional theory with London dispersion corrections,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 1, 211–228 (2011). 10.1002/wcms.30 [DOI] [Google Scholar]
- 675.Sedlak R., Janowski T., Pitoňák M., Řezáč J., Pulay P., and Hobza P., “Accuracy of quantum chemical methods for large noncovalent complexes,” J. Chem. Theory Comput. 9, 3364–3374 (2013). 10.1021/ct400036b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 676.Goldey M. and Head-Gordon M., “Attenuating away the errors in inter- and intramolecular interactions from second-order Møller–Plesset calculations in the small aug-cc-pVDZ basis set,” J. Phys. Chem. Lett. 3, 3592–3598 (2012). 10.1021/jz301694b [DOI] [PubMed] [Google Scholar]
- 677.McDaniel J. G. and Schmidt J. R., “Next-generation force fields from symmetry-adapted perturbation theory,” Annu. Rev. Phys. Chem. 67, 467–488 (2016). 10.1146/annurev-physchem-040215-112047 [DOI] [PubMed] [Google Scholar]
- 678.Carter-Fenk K. and Herbert J. M., “Electrostatics does not dictate the slip-stacked arrangement of aromatic π–π interactions,” Chem. Sci. 11, 6758–6765 (2020). 10.1039/d0sc02667k [DOI] [PMC free article] [PubMed] [Google Scholar]
- 679.Carter-Fenk K. and Herbert J. M., “Reinterpreting π-stacking,” Phys. Chem. Chem. Phys. 22, 24870–24886 (2020). 10.1039/d0cp05039c [DOI] [PubMed] [Google Scholar]
- 680.Fagnani D. E., Sotuyo A., and Castellano R. K., “π–π interactions,” in Comprehensive Supramolecular Chemistry II (Elsevier, Oxford, 2017), Vol. 1, pp. 121–148. [Google Scholar]
- 681.Grimme S., “Do special noncovalent π–π stacking interactions really exist?,” Angew. Chem., Int. Ed. 47, 3430–3434 (2008). 10.1002/anie.200705157 [DOI] [PubMed] [Google Scholar]
- 682.Marenich A. V., Jerome S. V., Cramer C. J., and Truhlar D. G., “Charge model 5: An extension of Hirshfeld population analysis for the accurate description of molecular interactions in gaseous and condensed phases,” J. Chem. Theory Comput. 8, 527–541 (2012). 10.1021/ct200866d [DOI] [PubMed] [Google Scholar]
- 683.Ballesteros F., Dunivan S., and Lao K. U., “Coupled cluster benchmarks of large noncovalent complexes: The L7 dataset as well as DNA–ellipticine and buckycatcher–fullerene,” J. Chem. Phys. 154, 154104 (2021). 10.1063/5.0042906 [DOI] [PubMed] [Google Scholar]
- 684.Benali A., Shulenburger L., Romero N. A., Kim J., and von Lilienfeld O. A., “Application of diffusion Monte Carlo to materials dominated by van der Waals interactions,” J. Chem. Theory Comput. 10, 3417–3422 (2014). 10.1021/ct5003225 [DOI] [PubMed] [Google Scholar]
- 685.Merali Z., “Computational science: …Error,” Nature 467, 775–777 (2010). 10.1038/467775a [DOI] [PubMed] [Google Scholar]
- 686.Kanewala U. and Bieman J. M., “Testing scientific software: A systematic literature review,” Inf. Software Technol. 56, 1219–1232 (2014). 10.1016/j.infsof.2014.05.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 687.Kelly D., Wassyng A., and Orton C. G., “The most suitable person to establish quality assurance guidelines for the generation and use of noncommercial clinical software is a medical physicist,” Med. Phys. 41, 090601 (2014). 10.1118/1.4883877 [DOI] [PubMed] [Google Scholar]
- 688.Wiese I., Polato I., and Pinto G., “Naming the pain in developing scientific software,” IEEE Software 37, 75–82 (2020). 10.1109/ms.2019.2899838 [DOI] [Google Scholar]
- 689.Sanderson C. and Curtin R., “Armadillo: A template-based C++ library for linear algebra,” J. Open Source Software 1, 26 (2016). 10.21105/joss.00026 [DOI] [Google Scholar]
- 690.Shaw R. A. and Hill J. G., “Prescreening and efficiency in the evaluation of integrals over ab initio effective core potentials,” J. Chem. Phys. 147 074108 (2017). 10.1063/1.4986887 [DOI] [PubMed] [Google Scholar]
- 691.McKenzie S. C., Epifanovsky E., Barca G. M. J., Gilbert A. T. B., and Gill P. M. W., “Efficient method for calculating effective core potential integrals,” J. Phys. Chem. A 122, 3066–3075 (2018). 10.1021/acs.jpca.7b12679 [DOI] [PubMed] [Google Scholar]
- 692.Schäfer A., Horn H., and Ahlrichs R., “Fully optimized contracted Gaussian basis sets for atoms Li to Kr,” J. Chem. Phys. 97, 2571–2577 (1992). 10.1063/1.463096 [DOI] [Google Scholar]
- 693.Weigend F., Köhn A., and Hättig C., “Efficient use of the correlation consistent basis sets in resolution of the identity MP2 calculations,” J. Chem. Phys. 116, 3175–3183 (2002). 10.1063/1.1445115 [DOI] [Google Scholar]
- 694.See https://www.BrianQC.com for a description of the BrianQC module for GPU-accelerated Q-Chem calculations; accessed July 26, 2021.
- 695.Gill P. M. W., “Molecular integrals over Gaussian basis functions,” Adv. Quantum Chem. 25, 141 (1994). 10.1016/s0065-3276(08)60019-2 [DOI] [Google Scholar]
- 696.McMurchie L. E. and Davidson E. R., “One- and two-electron integrals over Cartesian Gaussian functions,” J. Comput. Phys. 26, 218–231 (1978). 10.1016/0021-9991(78)90092-x [DOI] [Google Scholar]
- 697.Head-Gordon M. and Pople J. A., “A method for two-electron Gaussian integral and integral derivative evaluation using recurrence relations,” J. Chem. Phys. 89, 5777–5786 (1988). 10.1063/1.455553 [DOI] [Google Scholar]
- 698.Obara S. and Saika A., “Efficient recursive computation of molecular integrals over Cartesian Gaussian functions,” J. Chem. Phys. 84, 3963–3974 (1986). 10.1063/1.450106 [DOI] [Google Scholar]
- 699.Obara S. and Saika A., “General recurrence formulas for molecular integrals over Cartesian Gaussian functions,” J. Chem. Phys. 89, 1540–1559 (1988). 10.1063/1.455717 [DOI] [Google Scholar]
- 700.Dupuis M., Rys J., and King H. F., “Evaluation of molecular integrals over Gaussian basis functions,” J. Chem. Phys. 65, 111–116 (1976). 10.1063/1.432807 [DOI] [Google Scholar]
- 701.Rys J., Dupuis M., and King H. F., “Computation of electron repulsion integrals using the Rys quadrature method,” J. Comput. Chem. 4, 154–157 (1983). 10.1002/jcc.540040206 [DOI] [Google Scholar]
- 702.Rák Á. and Cserey G., “The BRUSH algorithm for two-electron integrals on GPU,” Chem. Phys. Lett. 622, 92–98 (2015). 10.1016/j.cplett.2015.01.023 [DOI] [Google Scholar]
- 703.Tornai G. J., Ladjánszki I., Rák Á., Kis G., and Cserey G., “Calculation of quantum chemical two-electron integrals by applying compiler technology on GPU,” J. Chem. Theory Comput. 15, 5319–5331 (2019). 10.1021/acs.jctc.9b00560 [DOI] [PubMed] [Google Scholar]
- 704.Morrison A. F., Epifanovsky E., and Herbert J. M., “Double-buffered, heterogeneous CPU + GPU integral digestion algorithm for single-excitation calculations involving a large number of excited states,” J. Comput. Chem. 39, 2173–2182 (2018). 10.1002/jcc.25531 [DOI] [PubMed] [Google Scholar]
- 705.Polik W. F. and Schmidt J. R., “WebMO: Web-based computational chemistry calculations in education and research,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. (published online) (2021).
- 706.Curtiss L. A., Raghavachari K., Redfern P. C., Rassolov V., and Pople J. A., “Gaussian-3 (G3) theory for molecules containing first and second-row atoms,” J. Chem. Phys. 109, 7764 (1998). 10.1063/1.477422 [DOI] [Google Scholar]
- 707.Curtiss L. A., Redfern P. C., and Raghavachari K., “Gaussian-4 theory,” J. Chem. Phys. 126, 084108 (2007). 10.1063/1.2436888 [DOI] [PubMed] [Google Scholar]
- 708.Lin C. Y., George M. W., and Gill P. M. W., “EDF2: A density functional for predicting molecular vibrational frequencies,” Aust. J. Chem. 57, 365 (2004). 10.1071/ch03263 [DOI] [Google Scholar]
- 709.See https://www.wavefun.com for details about the Spartan program; accessed July 26, 2021..
- 710.The author list is organized in five categories: major contributors (Epifanovsky–White), middle contributors (Coons–Zhu, ordered alphabetically), minor contributors (Alam–Zuev, ordered alphabetically), senior supervising contributors (Aspuru-Guzik–Zimmerman, ordered alphabetically), and board members (Faraji–Krylov).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available within the article.