Abstract
The interior reconstruction of completely truncated projection data is a frontier research hotspot in cone-beam computed tomography (CBCT) application. It is difficult to find a method with acceptable accuracy and high efficiency to solve it. Based on the simplified algebraic reconstruction technique (S-ART) algorithm and the filtered back projection (FBP) algorithm with the new filter, an efficient and feasible interior reconstruction algorithm is proposed in this paper. The algorithm uses the S-ART algorithm to quickly recover the complete projection data and then uses the new ramp filter which can suppress the high-frequency noise in the projection data to filter the recovered complete projection data. Finally, the interior reconstructed images are obtained by back projection. The computational complexity of the proposed algorithm is close to that of the FBP algorithm for the reconstruction of the whole object, and the reconstructed image quality is acceptable, which provides an effective method for interior reconstruction in CBCT. Simulation results show the effectiveness of the method.
Keywords: CT, Interior reconstruction, Truncated projection data, FBP algorithm, Data recovery
Introduction
As a new generation of computed tomography (CT) technology, cone-beam CT (CBCT) uses cone beam and region array detector to obtain all the projection data required for image reconstruction through one rotation scanning [1]. It has the advantages of fast scanning speed, high ray utilization and high resolution of reconstructed image. CBCT has become one of the most important imaging techniques in the fields of medicine, industrial detection, biology, aerospace, and public safety, among others. With CBCT, the size of the detector is limited due to the limitation of technology and cost. When the size of the detected object is too large or needs high spatial resolution imaging, the scanning field of view (FOV) cannot completely cover the object [2]. Moreover, in order to reduce the radiation dose, only the region of interest (ROI) is scanned by controlling the scanning FOV. All of these will lead to interior reconstruction problems. Interior reconstruction provides a solution for the realization of low-dose medical CT by irradiating only the focus of interest, which is particularly important [3].
The classic imaging geometry for CBCT is through collection of un-truncated projection data and reconstruction of a local image, with the Fourier transform as the theoretical foundation that is intrinsically non-local [4]. However, interior reconstruction is the reconstruction problem with incomplete projection data. FOV only covers the interior region of the object, and the projection data is completely truncated at any angle. If the interior image is reconstructed directly with the analytical reconstruction algorithm commonly used in CBCT and the truncated projection data, the value of the reconstructed image is bigger than the true value, especially at the edge of the image. It is mainly due to the lack of the side-lobe data in the filtering process, resulting in large filtering results. Therefore, directly using the existing reconstruction algorithms for global projection data to reconstruct completely truncated projection data has no good reconstruction quality [5].
In the recent 20 years, interior reconstruction algorithms for completely truncated projection data have been investigated and developed. In 1992, Faridani proposed an interior reconstruction algorithm based on lambda tomography, which used the truncated projection data to reconstruct a function with the same singularity as ROI density function [6]. Subsequently, Katsevich proposed an interior reconstruction algorithm based on pseudolocal tomography, which replaces the original function by reconstructing a part of the Hilbert transform of the density function [7]. However, these functions cannot replace the CT images of the reconstructed object and are difficult to meet the needs of practical engineering applications. In 1996, the wavelet analysis was applied to interior reconstruction, and a feasible wavelet interior reconstruction algorithm was proposed [8–10]. The reconstruction formula based on wavelet can realize interior reconstruction, but this reconstruction algorithm had a great dependence on the selection of wavelet function. The wavelet function must have good time–frequency domain analysis properties in the interior region. In 2007, Ye made a breakthrough in interior reconstruction [11]. By adding a known region as a “priori knowledge”, it has been proved that there is a unique and stable solution for interior reconstruction. Subsequently, Kudo et al. [12] and Gompel et al. [13] also proved similar results. However, in routine clinical application of CBCT imaging, it is difficult to obtain the prior information inside the reconstructed object in advance. Therefore, this proposed method has certain limitations in practical application. In 2009, considering that it is difficult to obtain prior knowledge, Li et al. [14] proposed another method to solve interior reconstruction based on the work of Ye et al. [11]. He selected the region outside the object support as the known region, that is, without any prior knowledge, obtained the projection of the interior region and the known region through two separate scans and reconstructed the interior image using the projection data of the two scans. In 2014, Wang et al. conducted further research on the implementation of the algorithm based on the rotation translation scanning model [2]. However, acquiring two scans has a negative impact on the speed and accuracy of CT imaging, as well as increasing the patient radiation dose, which means that this method cannot be used for the interior reconstruction of clinical low-dose CBCT. In 2016, Hu et al. focused on taking into account the statistical nature of local projection data and recovering fine structures which were lost in the conventional total variation (TV) minimization reconstruction [15]. The proposed method falls within the compressed sensing framework of TV minimization. Although the method did not need any additional prior knowledge, but it assumed that the interior region was piecewise constant or polynomial, which determined it was lack of universality [16]. This proposed methodology is a kind of iteration algorithm, and thus, its computational complexity is high. Moreover, it is difficult to determine the parameters of controlling the iterative operation in the image reconstruction of real data.
For the interior reconstruction of completely truncated projection data in CBCT, an efficient and feasible interior reconstruction algorithm is proposed by using the respective advantages of iterative algorithm and analytical algorithm. The completely truncated projection data contains not only the attenuation coefficient information of the interior region, but also the attenuation coefficient information of the external region. The attenuation coefficient of the whole object can be recovered by using the iterative algorithm, and then the projection data of the external region can be obtained. For the iterative reconstruction algorithm, interior reconstruction can be seen as the lack of partial reconstruction equations. The proportion of the interior region to the whole object is higher, the number of reconstruction equations is more, and the accuracy of the recovered projection data is higher. It is certain that the accuracy of the projection data of external region with this method is much higher than that of the method of directly using the edge data of the interior region. In the FBP algorithm, the energy of the filter function is concentrated in the main lobe, so the filter itself has an inhibitory effect on the external projection data. The filtered value of the interior region mainly depends on the nearby projection data. The farther the external projection data is from the interior projection data, the smaller the impact of the projection data on the filtering results of the interior projection data. The projection data of the interior region is relatively accurate. In addition to the approximate external projection data obtained above, if the filter with the better effect of suppressing the external projection data is selected, the FBP algorithm can be used to reconstruct the interior images with good accuracy.
The remainder of this paper is organized as follows. The “Interior reconstruction” section describes the interior reconstruction. In the “External projection data recovery” section, the recovery method of the external projection data is proposed based on the S-ART algorithm. In the “FBP algorithm using the new filter” section, the FBP algorithm using the new filter is proposed to reconstruct the interior images. In the “Simulation experiments” section, the numerical experiments are carried out to verify the proposed method. Finally, we summarize the paper in the “Conclusion” section.
Interior Reconstruction
When the ROI is located inside the reconstructed object, the reconstruction of the attenuation coefficient information of the ROI is called interior reconstruction [17, 18]. An example for this include the following: reconstructing the heart of the human body or a specific part inside industrial devices. Figure 1 shows a schematic diagram of the interior region and its projection data. The ray is emitted from the source and projected onto the detector after passing through the interior region of the object through the control device of the scanning FOV. The projection information between AB is the projection data of the interior region, and the projection information between AC and BD is the projection data of the external region. Different from the traditional global CBCT, interior reconstruction only uses the projection data of AB, which greatly reduces the size of the exposure region. Therefore, it can effectively reduce the hardware cost of CBCT system, reduce the amount of data, improve the image reconstruction speed, and reduce the X-ray radiation dose. Interior reconstruction has great potential in the engineering application of CBCT.
Fig. 1.
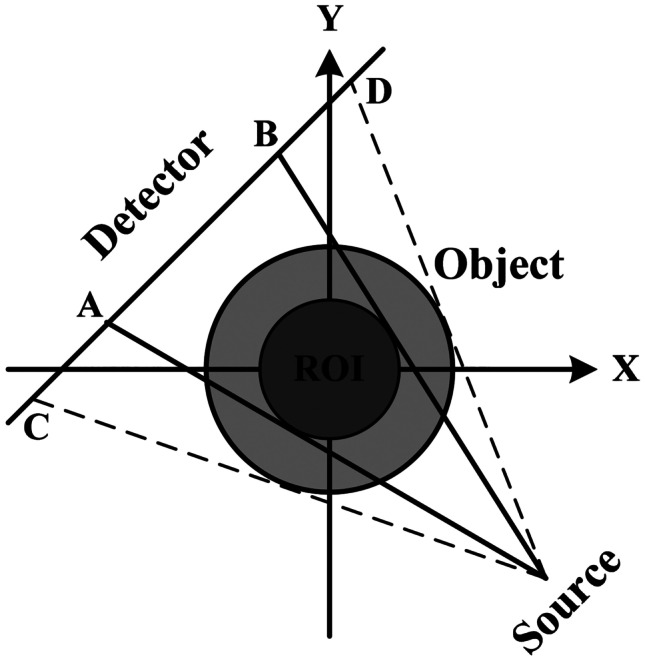
Diagram of interior region and its projection data
From Fig. 1, the projection data between AB includes the projection of the interior region and the external region. The projection of the external region is the region we are not interested. The result reconstructed directly with FBP-type analytical algorithm contains serious noise. If the projection information of the external region contained in the interior projection data is used well, the approximate attenuation coefficient of the external region can be obtained by using the iterative algorithm, and then the projection data other than the interior projection data can be obtained by forward projection.
External Projection Data Recovery
Iterative reconstruction algorithm transforms the image reconstruction problem into a system of linear equations to solve the relationship between the voxel’s attenuation coefficient and the projection data. The lost projection data can be regarded as the missing equations. So the impact of the truncation of projection data on image reconstruction can be reduced. A simplified ART (S-ART) algorithm is designed to reconstruct the whole object, and then the complete projection data is obtained.
Reconstruction Model and Algorithm
The reconstruction model is established as follows. The whole reconstructed object is discretized into K voxels, and the attenuation coefficient of each voxel is supposed as a constant, which is denoted as . The rays are considered to have no width, and the projection value of the jth ray is denoted as . The reconstruction model is expressed as
| 1 |
Here, N is the number of projection data collected by the detector, and is denoted as the weighting factor, which represents the contribution of the attenuation coefficient of the ith voxel to the jth projection value.
Through the reconstruction model, it can be seen that CT image reconstruction becomes the solution of high-dimensional linear equations. Due to the error of weighting factor and the noise in the actual projection data, the reconstruction equations are often incompatible. Therefore, it is incapable to solve them by the use of the analytical algorithm.
The ART iterative method was originally proposed by Kaczmarz, when solving compatible linear equations. It has been widely used for CT image reconstruction, and it can still reconstruct high-precision images by combining some prior knowledge, when there are few projection data in different data acquisition models [19]. The iterative structure of the ART algorithm is concise and is given in the following [20].
| 2 |
where is the relaxation factor used to control the speed of iterative convergence, and m is the marking of iterations. The iterative process of ART algorithm can be divided into the forward projection and the back projection. The forward projection is used to calculate the sum of the attenuation coefficient of all voxels passed by a ray. The back projection uses the error between the result of forward projection and the projection value to update the attenuation coefficient of all voxels passed by the ray. After the ART algorithm traverses all projection data, the reconstruction result needs to be iterated again as the initial value until the reconstruction result converges.
Simplified ART Algorithm
The commonly used method to calculate the weighting factor is to obtain the index and intersection length of the voxels traversed by the ray by use of the grid traversal method [21]. Based on the method, Siddon and Gao proposed the forward projection method and the improved fast forward projection matrix calculation method, respectively [22, 23]. However, the computational complexity of this kind of calculation method is still very high, and a large amount of memory space is required to store the data of the intersections of ray and grid.
In order to improve the calculation speed of weighting factor, a simplified calculation method of weighting factor is proposed. Firstly, it is assumed that the attenuation value of the voxel is concentrated in the center of the voxel. Secondly, suppose that each projection ray is regarded as a pyramid, as shown in Fig. 2. If the center of a voxel is located in a projection ray, the projection contribution of the voxel to the ray is 1; otherwise, it is 0.
Fig. 2.

Schematic diagram of four pyramidal structures of a ray
The specific implementation process of the weighting factor calculation method is as follows. Under a certain scanning angle, calculate the projection position of each voxel on the detector, which determines which ray the voxel is contained in, and then obtain the weighting factor of the voxel. Adding all voxels contained in the same ray to equal the projection value of the ray, a reconstruction equation is obtained. The reconstruction equations under all scanning angles are combined to obtain the reconstruction model. It can be seen from the calculation process of the weighting factor that its calculation process is the same as that of the back projection in the FBP algorithm. If the scanning angle, the voxel index, and its corresponding projection position are stored in the calculation process of the weighting factor, the back projection operation in the FBP algorithm can be avoided. Here, a method similar to the three element group table is used to store the scanning angle, the projection position and the index of the voxels contained in the ray, that is , where is the scanning angle, is the index of the projection value , and is the index of the voxels contained in the projection ray. For the ART algorithm, just represents all the information of a ray or a reconstruction equation.
In order to reduce the computation of the ART algorithm, let . The iterative formula of the S-ART is
| 3 |
It can be seen from Eq. (3) that the S-ART algorithm only uses the storage information when calculating the weighting factor. The simplified weighting factor calculation and storage method greatly improve the amount of calculation and required storage space of the new iterative process compared with the original ART algorithm. The amount of computation of the S-ART algorithm in one iteration is equivalent to that of the FBP algorithm for the whole object. If there is the storage space required to store the three element group table, the amount of computation of multiple iterations of the S-ART algorithm is slightly larger than that of the FBP algorithm for the whole object. Of course, the accuracy of the weighting factor has been lost in exchange for its fast calculation.
Recovery of External Projection Data
The truncated projection data contains the attenuation coefficient information of the parts outside the interior region of the reconstructed object. Here, the S-ART algorithm proposed above is used to quickly reconstruct the attenuation coefficient of the whole reconstructed object. Through the forward projection operation, the global projection data at all scanning angles can be obtained, in which the projection data of the interior region is accurate. The accuracy of the projection data of the external region is affected by the number of iterations and the number of reconstruction equations, which are mainly determined by the size of the interior region.
FBP Algorithm Using the New Filter
The FBP algorithm is an image reconstruction algorithm widely used in CBCT [24–26]. Firstly, the projection data in the different directions are filtered and preprocessed, and then the reconstructed images are obtained through back projection. Its mathematical expression is
| 4 |
| 5 |
where R is the radius of the circular orbit, represents the coordinate vector of the reconstruction point, represents the unit vector from the source to the rotation center, is the projection data of the intersection point between the reconstruction point and the detector in the viewing angle , and is the spatial domain slope filter.
The key of the FBP algorithm for image reconstruction is the selection of filter, and the performance of filter directly affects the quality of the reconstructed images. The slope filter in the FBP algorithm is an ideal filter with infinite bandwidth in frequency domain, which cannot be realized physically. However, in the actual imaging process, as long as the sampling interval of the detector is small enough, the difference between adjacent data in the collected projection data is relatively small, that is, the high-frequency energy in the projection data spectrum is very small. Therefore, the ideal filter is usually truncated by the window function in the frequency domain.
The common filtering functions in the FBP algorithm are the Ram-Lak (R-L) filter and the Shepp-Logan (S-L) filter [27]. The window function of the R-L filter is rectangular window. The main lobe of the inverse Fourier transform is high and narrow, which improves the spatial resolution of the reconstructed image, while the side lobe is prominent, which cannot suppress the image noise well, and the density resolution is low. Supposing the size of the detector pixel is d, the sampling sequence of the corresponding impulse response of the R-L filter is
| 6 |
The window function of the S-L filter is the sinc function. The side lobe of the inverse Fourier transform decays rapidly, while the main lobe decreases. The noise of the reconstructed image is well suppressed, but the spatial resolution is low. The sampling sequence of the corresponding impulse response of the S-L filter is
| 7 |
Different from the windowing method in frequency domain, the unit impulse response formula of a new ideal slope filter in real space is derived as follows [28]. If sgn is the sign function, then
| 8 |
where denotes Fourier transform, and f is the frequency. According to the symmetry of Fourier transform, there are
| 9 |
sgn is an odd function, so
| 10 |
By the differential properties of Fourier transform, there are
| 11 |
Simplify the above formula and get
| 12 |
Finally, the unit impulse response of the ideal slope filter is
| 13 |
If the signal h(t) is sampled using the sampling interval d, the discrete form of ideal ramp filter is
| 14 |
For , the discrete form of ideal ramp filter is not a practical filter. To design practical filter, should be evaluated using some approximate method. Using and , the new practical digital filter according to the ideal ramp filter is given as follows.
| 15 |
The two main indexes to evaluate image quality are spatial resolution and density resolution, but they are contradictory when the projection data is certain. In order to obtain a high spatial resolution of the reconstructed image, the function of the filter in the spatial domain should have a high and narrow main lobe, but its prominent side lobe can produce artifacts, so as to reduce the density resolution. Reducing the side lobe can suppress the noise and improve the density resolution, but at the same time, it reduces the main lobe and loses the spatial resolution.
Figure 3 shows the spatial distribution of the R-L filter, S-L filter, and new filter. It can be seen that the new filter can suppress the high-frequency noise in the projection data and greatly reduce the Gibbs phenomenon without significant reduction in spatial resolution. And its side lobe attenuates more rapidly than the S-L filter, which is suitable for interior reconstruction with noise in the external projection data. In the practical application, if more projection data is collected in the adjacent region of ROI, the reconstruction effect will be better.
Fig. 3.
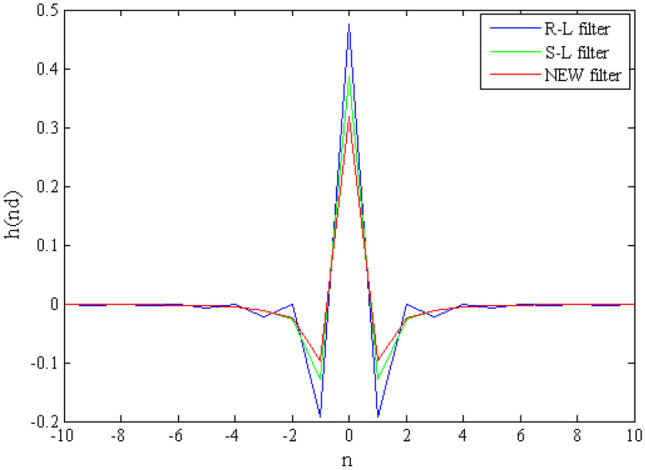
Spatial distribution of the R-L filter, S-L filter, and new filter
So far, the method of using the iterative algorithm and analytical algorithm to solve the interior reconstruction problem has been proposed. The S-ART algorithm is used to recover the projection data of the external region, and then the FBP algorithm with the new filter is used to reconstruct the image of the interior region. The whole algorithm is simple and clear, and the computational complexity of the proposed method is slightly larger than that of using the FBP algorithm to reconstruct the whole object.
Simulation Experiments
In this section, we perform some numerical experiments with simulated data to validate the proposed method. For simplicity, the numerical experiments are restricted to fan-beam CT, and thus, generalization to CBCT is straightforward. We evaluated the results with a 512 × 512 standard 2D Shepp-Logan phantom [29]. In the circular fan-beam configuration, the trajectory has a radius of 980 mm and a source-detector distance of 1250 mm. The fan-beam projection data was generated with the 360 projection views uniformly distributed over the 2π circular trajectory. The initial value of iteration is 0.
In order to analyze the influence of the number of iterations on the accuracy of the projection data, the following simulation experiments were carried out. The interior region is 128 × 128 in the center of the phantom. Figure 4 shows the projection data recovered from the reconstruction results of 1, 10, and 100 iterations. Between the dotted lines are the projection data of the interior region. Since the projection data of the interior region is known, that is, the number of the equations about the voxels of the interior region is relatively large, after iterative correction, the projection accuracy of the interior region of the corresponding restored projection data is acceptable.
Fig. 4.

Recovered projection data from the reconstruction images using S-ART
Figure 5 is the reconstruction results of 1, 10, and 100 iterations, respectively. It can be seen that the reconstructed images of the interior region have good quality.
Fig. 5.
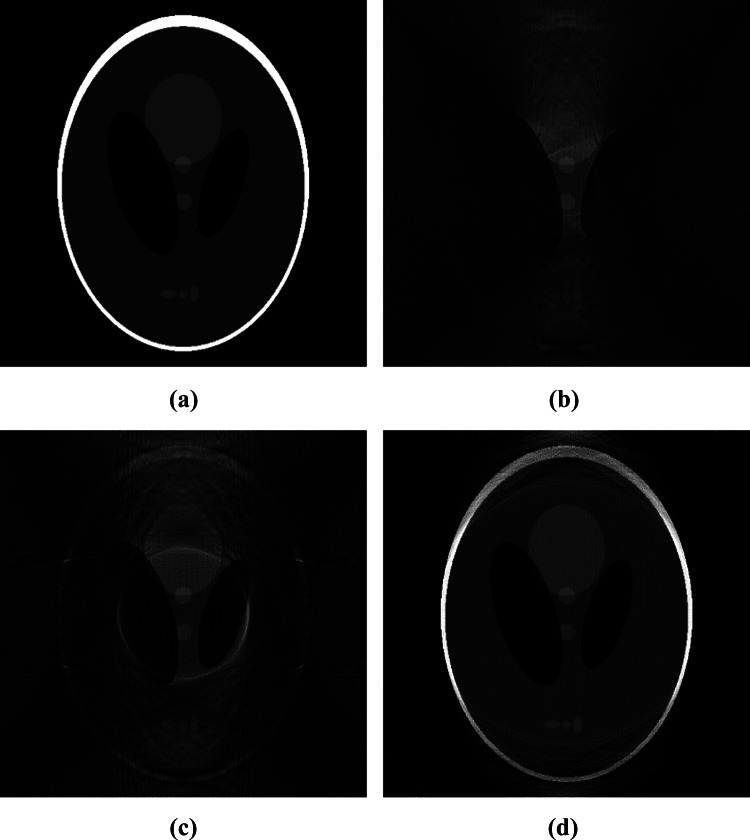
Reconstruction results of interior region: a phantom; b reconstructed image of iteration number 1; c reconstruction image of iteration number 10; d reconstruction image of iteration number 100
In order to verify the influence of the size of the interior region on the restoration of the projection data, the method proposed in this paper is used to restore the projection data of the interior reconstruction with 64 × 64, 128 × 128, and 256 × 256. Figure 6 is the result of the recovered projection data, in which the S-ART algorithm is iterated 100 times. From the reconstruction results, the proportion of the interior region to the whole object is higher, the number of reconstruction equations is more, and the accuracy of the recovered projection data is higher. On the contrary, the proportion of the interior region in the whole object is smaller, the number of reconstruction equations is fewer, and the accuracy of the recovered projection data is lower. Figure 7 shows the interior reconstruction results. It can be seen that as the interior reconstruction region becomes larger, the accuracy of the reconstructed images is higher. It is certain that the accuracy of the projection data of this method is much higher than that of the method of directly using the edge data of the interior region.
Fig. 6.
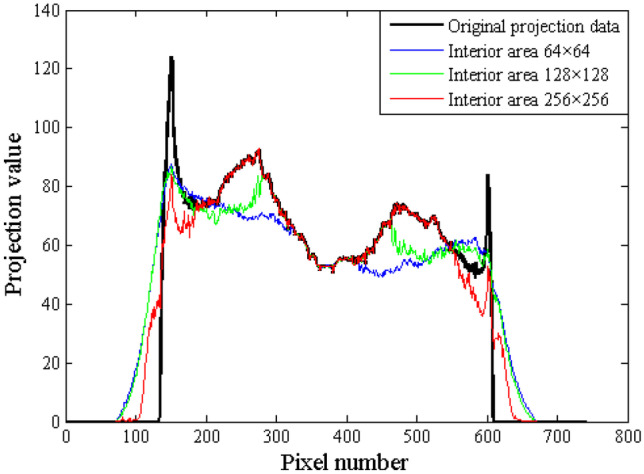
Recovered projection data using different interior region
Fig. 7.
Reconstruction results of interior regions with different sizes: a phantom; b reconstructed image of interior region 64 × 64; c reconstruction image of interior region 128 × 128; d reconstruction image of interior region 256 × 256
When the interior region is small, we need to reduce the angle interval of collecting projection data and improve the amount of information about the interior region. In addition, the iteration number of the S-ART algorithm needs to be increased, which can improve the accuracy of the recovered projection data.
Conclusion
Interior reconstruction provides a solution to large-object imaging with high spatial resolution and low-dose imaging. Aiming at the interior reconstruction problem of the completely truncated projection data in CBCT, the completely truncated projection data includes not only the attenuation coefficient information of the interior region, but also the attenuation coefficient information of the external region. The attenuation coefficient of the whole object can be recovered by iterative algorithm, and then the projection data of the external region can be obtained. Of course, the higher the proportion of the interior region to the whole object, the more the number of reconstruction equations, and the higher the accuracy of the recovered projection data. The projection of the interior region is relatively accurate. Combined with the approximate external projection data obtained in front, the complete projection data is obtained. Finally, the FBP algorithm with the new filter is selected to reconstruct the interior region. In the end, an efficient and approximate interior reconstruction algorithm is proposed by combining the advantages of the iterative algorithm and the analytical algorithm.
In the process of proposing the S-ART algorithm, this paper proposes a method to calculate the weighting factor and uses the three element group table to store the projection angle, the index of the projection value, and the index of the voxel contained in the ray. This not only simplifies the ART algorithm but also avoids the back projection calculation in the subsequent FBP algorithm. This method better combines the iterative ART algorithm with the analytical FBP algorithm. The amount of computation of the method is close to that of the FBP reconstruction of the whole object, which means that the proposed method is concise and efficient. In addition, its implementation does not include the control parameters that change according to the change of the density distribution characteristics of the reconstructed object, which makes the method proposed in this paper more universal. It gives an approximate solution to the interior reconstruction problem that is difficult to solve.
Funding
This work was supported by the Scientific Research Startup Fund of Nanchang Institute of Science and Technology (Grant No. 20201072), the Nanchang Key Laboratory of Internet of Things Information Visualization Technology (Grant No. 2020-NCZDSY-017), and the Science and Technology Research Project of Jiangxi Province (Grant No. GJJ212503).
Declarations
Competing Interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Tang SJ, Li BL, Qiao ZW, et al. An imperceptible incorrectness in deriving data consistency condition from John's equation for cone-beam CT imaging. Optik. 2020;202(3):163603. doi: 10.1016/j.ijleo.2019.163603. [DOI] [Google Scholar]
- 2.Wang XC, Tang ZY, Yan B, et al. Interior reconstruction method based on rotation-translation scanning model. Journal of X-ray Science and Technology. 2014;22(1):37–45. doi: 10.3233/XST-130407. [DOI] [PubMed] [Google Scholar]
- 3.Wang XC, Hu GE, Bin Y, et al. Fast low-dose reconstruction from truncated data in dental CT. IEEE Transactions on Nuclear Science. 2013;60(1):174–181. doi: 10.1109/TNS.2012.2236653. [DOI] [Google Scholar]
- 4.Smith BD. Image reconstruction from cone-beam projections: necessary and sufficient condition and reconstruction method. IEEE Transactions on Medical Imaging. 1985;4(1):14–28. doi: 10.1109/TMI.1985.4307689. [DOI] [PubMed] [Google Scholar]
- 5.Wang G, Yu HY. The meaning of interior tomography. Physics in Medicine and Biology. 2013;58(16):161–186. doi: 10.1088/0031-9155/58/16/R161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Faridani A, Ritman EL, Smith KT. Local tomography. SIAM Journal on Applied Mathematics. 1992;52(2):459–484. doi: 10.1137/0152026. [DOI] [Google Scholar]
- 7.Katsevich AJ, Ramm AG. Pseudolocal tomography. SIAM Journal on Applied Mathematics. 1996;56(1):167–191. doi: 10.1137/S0036139994266116. [DOI] [Google Scholar]
- 8.Bhatia M, Karl WC, Willsky AS. A wavelet-based method for multiscale tomographic reconstruction. IEEE Transactions On Medical Imaging. 1996;15(1):92–101. doi: 10.1109/42.481444. [DOI] [PubMed] [Google Scholar]
- 9.Farrokhi FR, Liu KJR, Berenstein CA, et al. Wavelet-based multiresolution local tomography. IEEE Transaction on Image Processing. 1997;10(6):1412–1429. doi: 10.1109/83.624961. [DOI] [PubMed] [Google Scholar]
- 10.Zhao SY, Wang G. Feldkamp-type cone beam tomography in the wavelet framework. IEEE Transactions on Medical Imaging. 2000;19(9):922–929. doi: 10.1109/42.887839. [DOI] [PubMed] [Google Scholar]
- 11.Ye YB, Yu HY, Wei YC, et al. A general local reconstruction approach based on a truncated Hilbert transform. International Journal of Biomedical Imaging. 2007;1(1):1–8. doi: 10.1155/2007/63634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kudo H, Courdurier M, Noo F, et al. Tiny a priori knowledge solves the interior problem in computed tomography. Physics in Medicine and Biology. 2008;53(9):2207–2231. doi: 10.1088/0031-9155/53/9/001. [DOI] [PubMed] [Google Scholar]
- 13.Gompel GV, Defrise M, Batenburg KJ. Reconstruction of a uniform star object from interior x-ray data: uniqueness, stability and algorithm. Inverse Problem. 2009;25(6):1–19. [Google Scholar]
- 14.Li L, Kang KJ, Chen ZQ, et al. A general region-of-interest image reconstruction approach with truncated Hilbert transform. Journal of X-ray Science and Technology. 2009;17(2):135–152. doi: 10.3233/XST-2009-0218. [DOI] [PubMed] [Google Scholar]
- 15.Hu ZL, Zhang YW, Liu JB, et al. A feature refinement approach for statistical interior CT reconstruction. Physics in Medicine and Biology. 2016;61(14):5311–5334. doi: 10.1088/0031-9155/61/14/5311. [DOI] [PubMed] [Google Scholar]
- 16.Qu ZY, Yan XM, Pan JX, et al. Sparse view CT image reconstruction based on total variation and wavelet frame regularization. IEEE Access. 2020;8:57400–57413. doi: 10.1109/ACCESS.2020.2982229. [DOI] [Google Scholar]
- 17.Cai AL, Li L, Wang LY, et al. Optimization-based region-of-interest reconstruction for X-ray computed tomography based on total variation and data derivative. Physica Medica. 2018;48:91–102. doi: 10.1016/j.ejmp.2018.01.003. [DOI] [PubMed] [Google Scholar]
- 18.Yu HY, Wang G, Hsieh J, et al. Compressive sensing-based interior tomography. Journal of Computer Assisted Tomography. 2011;35(6):762–764. doi: 10.1097/RCT.0b013e318231c578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gordon R, Bender R, Herman GT. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and x-ray photography. Journal of Theoretical Biology. 1970;29(3):471–481. doi: 10.1016/0022-5193(70)90109-8. [DOI] [PubMed] [Google Scholar]
- 20.Zhao YS, Zhao X, Zhang P. An extended algebraic reconstruction technique (E-ART) for dual spectral CT. IEEE Transactions on Medical Imaging. 2015;34(3):761–768. doi: 10.1109/TMI.2014.2373396. [DOI] [PubMed] [Google Scholar]
- 21.Wang XC, Li SY, Jiang CS. Fast system matrix calculation based on voxel projection in cone-beam CT. Optik. 2021;231(2):166422. doi: 10.1016/j.ijleo.2021.166422. [DOI] [Google Scholar]
- 22.Siddon RL. Fast calculation of the exact radiological path for a three-dimensional CT array. Medical Physics. 1985;12(2):252–255. doi: 10.1118/1.595715. [DOI] [PubMed] [Google Scholar]
- 23.Gao H. Fast parallel algorithm for the x-ray transform and its adjoint. Medical Physics. 2012;39(11):7110–7120. doi: 10.1118/1.4761867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang XC, Li L, Yu CQ, et al. Fast reconstruction of flat region in a super-short scan based on MD-FBP algorithm. Journal of X-Ray Science and Technology. 2012;20(1):69–77. doi: 10.3233/XST-2012-0319. [DOI] [PubMed] [Google Scholar]
- 25.L. A. Feldkamp, L. C. Davis, J. W. Kress, Practical cone-beam algorithm, Journal of the Optical Society America 1(A) (1984) 612–619.
- 26.Tao X, Zhang H, Wang YB, et al. VVBP-tensor in the FBP algorithm: its properties and application in low-dose CT reconstruction. IEEE Transactions on Medical Imaging. 2019;39(3):764–776. doi: 10.1109/TMI.2019.2935187. [DOI] [PubMed] [Google Scholar]
- 27.Shepp LA, Logan BF. The Fourier reconstruction of a head section. IEEE Transactions on Nuclear Science. 1974;21(3):21–43. doi: 10.1109/TNS.1974.6499235. [DOI] [Google Scholar]
- 28.Wei YC, Wang G. An intuitive discussion on the ideal ramp filter in computed tomography. Computers and Mathematics with Applications. 2005;49(5):731–740. doi: 10.1016/j.camwa.2004.10.034. [DOI] [Google Scholar]
- 29.Wang XC, Tang ZY, Zhu ZB, et al. Cone-beam reconstruction of flat specimens in a super-short scan. Insight. 2015;57(10):571–575. doi: 10.1784/insi.2015.57.10.571. [DOI] [Google Scholar]