An Explainable Convolutional Neural Network for the Early Diagnosis of Alzheimer’s Disease from 18F-FDG PET

Abstract

Convolutional Neural Networks (CNN) which support the diagnosis of Alzheimer’s Disease using 18F-FDG PET images are obtaining promising results; however, one of the main challenges in this domain is the fact that these models work as black-box systems. We developed a CNN that performs a multiclass classification task of volumetric 18F-FDG PET images, and we experimented two different post hoc explanation techniques developed in the field of Explainable Artificial Intelligence: Saliency Map (SM) and Layerwise Relevance Propagation (LRP). Finally, we quantitatively analyze the explanations returned and inspect their relationship with the PET signal. We collected 2552 scans from the Alzheimer’s Disease Neuroimaging Initiative labeled as Cognitively Normal (CN), Mild Cognitive Impairment (MCI), and Alzheimer’s Disease (AD) and we developed and tested a 3D CNN that classifies the 3D PET scans into its final clinical diagnosis. The model developed achieves, to the best of our knowledge, performances comparable with the relevant literature on the test set, with an average Area Under the Curve (AUC) for prediction of CN, MCI, and AD 0.81, 0.63, and 0.77 respectively. We registered the heatmaps with the Talairach Atlas to perform a regional quantitative analysis of the relationship between heatmaps and PET signals. With the quantitative analysis of the post hoc explanation techniques, we observed that LRP maps were more effective in mapping the importance metrics in the anatomic atlas. No clear relationship was found between the heatmap and the PET signal.

Supplementary Information

The online version contains supplementary material available at 10.1007/s10278-022-00719-3.

Introduction

Alzheimer’s Disease (AD) is the most common form of dementia, and its main symptoms include memory loss and cognitive decline, interfering significantly with the daily living of subjects affected. It is generally accepted that AD begins to develop many years before the dementia stage without any symptoms of cognitive impairment, a condition known as “pre-clinical stage” [1–3].

At present, the standard reference for the diagnosis of AD is the brain histopathological analysis, which verifies the presence of intraneuronal deposits of phosphorylated $\tau$ protein (neurofibrillary tangles) and extracellular $\beta$-amyloid (senile plaques) [1, 4]. Brain biopsy is not applicable in clinical routine practice, so in-vivo diagnosis is performed via a clinical evaluation of the patient and neuropsychological testing. Clinically based tests are useful, but they do not usually enable the clinician to make a definitive diagnosis, and the detection of the disease in its early stage is particularly challenging. In addition, the absence of a known definite treatment makes the early diagnosis a fundamental step to mitigate the cognitive decline of the patient, because emerging therapeutic regimens vary depending on the cause of the dementia [1].

We can observe a progressive development of criteria for the detection of AD over the years. Guidelines are gradual including the usage of quantitative biomarkers to support the clinical evaluation of the patient, which have the advantage of being objective measures suitable to detect and monitor disease’s progression. In 2018 the National Institute on Aging and Alzheimer’s Association (NIA-AA) developed a research framework to group AD’s biomarkers in the ATN classification, where A group includes biomarkers for $\beta$-amyloid plaques deposition, T group for pathological fibrillar $\tau$ deposits and N group for the neurodegenerative process. Among these measurements we can find anatomical and functional Neuroimaging examinations, like structural MRI, Amyloid PET and Fluorodeoxyglucose (FDG) PET [5, 6].

FDG is an artificial analog of glucose and mimics its action in brain cells’ metabolism until the phosphorylation step. The rate of FDG trapping is proportional to glucose metabolism and is an index of the synaptic activity, so the presence of hypometabolic patterns is interpreted as a sign of neurodegeneration [2]. Areas of glucose hypometabolism are commonly observed in patients with early AD in the parietotemporal association cortices, posterior cingulate cortex, and the precuneus. With disease progression affected regions involved are the frontal cortices, while areas in the striatum, thalamus primary sensorimotor cortices, visual cortices, and cerebellum are relatively preserved [2, 7].

A key factor, but also one of the main issues, is to determine how FDG-PET images should be evaluated. To date, PET scans are still analyzed qualitatively by nuclear medicine physicians, but this approach may have the limit of the potentially high intra- and inter-user variability. The usage of automatic or semi-automatic tools which perform a voxel-wise statistical analysis compared to a healthy population can reduce this variability, but the existing guidelines report that this kind of output still needs to be evaluated by an expert, especially if statistical maps highlight sparse hypometabolic clusters. How 18F-FDG PET scans should be analyzed is still under discussion and standardized approaches are lacking [8].

Alternative methods include the use of Deep Learning algorithms, which have been showing remarkable performance in a large variety of medical imaging applications. We can find several publications which employed different 2D or 3D Convolution Neural Network (CNN) architectures to support the prediction of Alzheimer’s disease obtaining interesting results. For instance, based on Inception V3 net, Xception net, or other custom architectures [9–16]. However, one of the main challenges in this application is that these models work as black-box system [17–22].

The field of Explainable Artificial Intelligence (XAI) was born to overcome this issue, building new types of interpretable models, or generating explanations for the predictions returned by the black-box system. A commonly exploited approach in the imaging domain is to produce an individual heatmap for every input image which indicates how important each pixel is for the final classification decision; this kind of method can be a powerful tool that could be easily integrated into a potential Computer-Aided Diagnosis software, to produce a human-intuitive explanation of what drives the classifier to a certain classification decision [23].

Although we can find different heatmaps’ generation techniques, it’s not clear if and why one explanation strategy should be preferred to another. In addition, although we can observe an increasing number of works that apply these techniques to explain the CNN’s output in AD application [12, 13, 15], only a few works propose a quantitative evaluation of them [23, 24]. The most limited their analysis to a visual qualitative evaluation of the averaged heatmaps of subjects to verify that the network had based its prediction focusing on the anatomical regions known to be the most affected in Alzheimer. XAI has further objectives than earning the trust of the model’s user: giving insight between the input-output relationship can also be useful for the model’s developer to improve the algorithm itself and to discover new facts and information from the specific application domain [20]. However, analyzing every single heatmap produced by post hoc explanation techniques in order to detect any potential bias or misoperation of the black-box model is a long-lasting and potentially non-trivial task. Performing a quantitative evaluation of these explanations could produce synthetic measures which may help the software’s developer in understanding the behavior of the model without the need to visually inspect thousands of maps.

This study aims to give insight about the prediction returned by the model using two different XAI techniques, Saliency Map and Layerwise Relevance Propagation, and to perform a group-wise analysis of the explanation returned to inspect their characteristics and the relationship between them and the PET signal.

Material and Methods

Data Collection

Data used in the preparation of this article was obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD).

The training and testing of the model were implemented using dynamic 3D 18F-FDG PET images preprocessed by the ADNI team. Currently, there are four types of processed PET image data available in the ADNI database; we selected images with the highest level of preprocessing (Co-reg, Avg, Std Img and Vox Siz, Uniform Resolution). The preprocessing steps include the co-registration of the frames of every dynamic acquisition; the averaging of the frames to produce a single PET image; a reorientation into a standard 160 × 160 × 96 voxel image grid with 1.5 mm isotropic voxels; an intensity normalization using a subject-specific mask to obtain an average of the signal within the mask equal to one and finally, the application of a smoothing filter to approximate the lowest scanner’s resolution used in ADNI. Complete details about acquisition protocols and preprocessing steps can be found on the ADNI website (http://www.adni-info.org/).

We downloaded an amount of 2552 images of 836 different subjects in DICOM format from the LONI platform acquired using different scanners. Acquisitions belong to three different classes and are labeled according to the clinical evaluation performed by ADNI centers: Cognitively Normal, CN (918 scans), Mild Cognitive Impairment, MCI (1148 scans), and Alzheimer’s Disease, AD (486 scans). Each scan is composed by 96 slices ($160\times 160$) with voxel size $1.5\times 1.5\times 1.5$ mm.

Convolutional Neural Network Architecture

To implement the classification task, we developed and trained a 3D CNN. We designed the network using the following path:

$$\begin{array}{cc}\hfill [[Conv3D\to ReLU]& \times N\to MaxPool\to BatchNorm]\hfill \\ \hfill & \times M\to [FullyCon\to ReLU]\times L\to Softmax\hfill \end{array}$$ 1

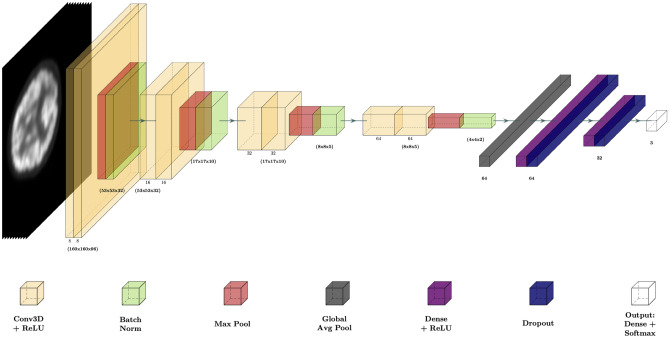
The first decoder path of the CNN, which extract the features from the images, is composed of 4 blocks: each block is made up of 2 layers of 3D convolutional filters with the same number of filters, a $(3\times 3\times 3)$ kernel and ReLU activation function, followed by a Max Pooling layer with a $(3\times 3\times 3)$ kernel in the first 2 blocks and a $(2\times 2\times 2)$ in the 2 last and finally a Batch Normalization layer. The number of filters in each block is respectively 8, 16, 32, 64. To further prevent overfitting, we add an L2 regularization strategy to the weights of Conv3D and Fully Connected layers. To give as input the features extracted by the Conv3D filters to the first Fully Connected layer we use a Global Average Pooling operation, which returns as output the average of every feature map as it has been demonstrated that have a regularization effect in preventing overfitting [12]. The last layers of the network perform the classification tasks and they consist of two Fully Connected layers with a ReLU activation function. Each layer is followed by a Dropout operation, to limit the overfitting of the network during the training process, and an Output layer with a Softmax activation. The complete architecture is reported in Fig. 1. A complete description of the network is reported in Supplementary Materials 1.

Fig. 1.

Convolutional Neural Network representation

The CNN takes as input the single channel 160 × 160 × 96 × 1 PET images preprocessed as described in the Data Collection section and returns the score of the output classes: CN, MCI, and AD.

Training Specification

We first split the dataset at the subject’s level to avoid data leakage problems, ensuring that, for each fold, no exams from the same subjects are present both in the training, validation and test sets [25]. We selected 20% of images as a test set and we further divided the residual 80% into 80–20%, respectively as training and validation sets. Random splitting has been performed preserving the original class distribution. The distribution of exams among training, validation, and test set is reported as Supplementary Material 2.

After the creation of dataset we applied data augmentation on the training set in order to increase its dimension; we used an augmentation factor of 13 applying random rotation (range $[-{10}^{\circ }÷{10}^{\circ }]$), translation (range $[-5÷5]$ px) and zoom (range $[-1.1÷1.3]$ factor).

We trained the CNN using the Adam optimizer of the categorical cross-entropy loss with a mini-batch strategy. We weighted the loss function for the inverse of the frequency of every class sample to handle the under-represented class and we used a batch size $=32$. We set an initial learning rate of $5\ast {10}^{-6}$ which was decreased during the training process with decay rate $=0.96$ and decay steps $=100000$. All the other optimizer’s parameters were left at the default value. We set a maximum number of epochs $=100$ and we implemented early stopping monitoring the validation accuracy with patience $=15$. We set a regularization penalty $=0.01$. K-fold cross-validation was performed with K = 5.

Post Hoc Explanation

We used two different XAI techniques to produce post hoc explanation of the class predicted: Saliency Map (SM) and Layerwise Relevance Propagation (LRP). We generated an individual heatmap for each patient in the input image domain which indicates the importance of each voxel for the final classification decision. SM measures the susceptibility of the output to changes in the input while LRP decomposes the network’s output score into the individual contributions of the input neurons while keeping the total amount of relevance constant across layers, a property known as the conservation principle.

SM [26] calculates the gradient of the output class score function $S_c$ with respect to the pixel of input image I for the specific instance to explain $I_0$ using a single pass of the back-propagation algorithm:

$$\begin{array}{c}\hfill w={\left(\frac{\partial S_c}{\partial I}\right|}_{I_0}\end{array}$$ 2

This attention map highlights how output value changes with respect to a small change in input image pixels. Voxels of the resulting map with the highest magnitude indicate which pixels need to be changed the least to affect the class score the most.

LRP technique [27] highlights positive contributions to Neural Network classification in the input space tracing back the score of the final output node layer by layer.

Firstly, we gave as input to the network the image for which we want to explain the prediction returned, to collect the network’s activation at each layer. Secondly, the score obtained as output f(x) is backpropagated into lower layers until the input using a propagation rule. The prediction f(x) is decomposed into a sum of V terms $R_d$ called Relevance, where V is the input dimension:

$$\begin{array}{c}\hfill f(x)\approx \sum _{d=1}^V{R}_d\end{array}$$ 3

With a relevance score $R_d^{(l+1)}$ for each dimension of the vector z at layer $(l+1)$, $z_d^{(l+1)}$ we need to find a a relevance score $R_d^{(l)}$ for each dimension of the vector z at the previous layer (l), $z_d^{(l)}$. Relevance needs to satisfy the following conservation law:

$$\begin{array}{c}\hfill f(x)=...=\sum _{d\in l+1}{R}_d^{(l+1)}=\sum _{d\in l}{R}_d^{(l)}=...=\sum _{d\in 1}{R}_d^{(1)}\end{array}$$ 4

The relevance of the $i-th$ neuron in the $l-th$ layer can be defined as:

$$\begin{array}{c}\hfill R_i^{(l)}=\sum _k{R}_{i\leftarrow k}^{(l,l+1)}\end{array}$$ 5

Where i is the input for neuron k direction during classification time. By joining conservation law with the previous definition, we obtain:

$$\begin{array}{c}\hfill R_i^{(l+1)}=\sum _i{R}_{i\leftarrow k}^{(l,l+1)}\end{array}$$ 6

The relevance $R_j$ can be obtained using a specific propagation rule which implements the conservation property of LRP. Several propagation rules are proposed in the literature, in our work we used the $ϵ-$rule:

$$\begin{array}{c}\hfill R_j=\sum _k\frac{a_j{w}_{\mathit{jk}}^{+}}{ϵ+{\sum }_j{a}_j{w}_{\mathit{jk}}^{+}}{R}_k\end{array}$$ 7

Where $a_j$ is neuron activation, $w_{\mathit{ij}}$ are parameters of the model, and $ϵ$ is a parameter chosen to obtain explanations sparser in terms of input features and less noisy. By changing $ϵ$ we modulate the resulting explanation, in our work we left $ϵ$ to its default value ${10}^{-6}$.

Quantitative Atlas-Based Heatmaps Evaluation

To quantitatively evaluate and perform a group-wise analysis of the heatmaps generated, we registered all the images and the corresponding maps with the Talairach Atlas [28]. We determined all the registration transformations using the atlas as a fixed image and every PET image as a floating image. Heatmaps were aligned with the atlas using the same transformation of the image associated with each of them.

We used an initial alignment to align the geometrical centers of the two volumes setting the center of rotation to the center of the fixed image. Next, we optimize a similarity 3D global transformation (rototranslation + isotropic scaling) using mutual information as a similarity metric, a linear interpolator, and the gradient descent method as optimizer with maximum iteration $=100$, convergence window size $=10$ and a threshold of similarity metric ${10}^{-6}$. Registration was performed using a multi-resolution framework with a three-tier pyramid.

For every SM and LRP, we evaluated, as an atlas-based importance metric, the average of the heatmap’s voxel intensity inside each brain region defined by the anatomic atlas. For every class of heatmaps, we sorted the brain region in descendent order of the average among the subjects of the importance metrics: in this way, we can see for every subject’s class what are (on average) the regions where the score of the class predicted has the highest susceptibility to input changes (according to the SM) and which has given the higher contribution to the score predicted (according to the LRP). We analyzed the metrics obtained with statistical tests.

We computed the average of every registered PET image in each atlas region, and we used statistical tests to detect where the average of registered PET signal significantly differs between subjects belonging to different classes.

Statistical Methods

We reconstructed the distribution of the atlas-based importance metrics of subjects belonging to different classes using Violin Plot. To evaluate if the distribution in each region significantly differs between classes, we performed a statistical test of the three different groups of data.

Firstly, we tested if all three groups belonged to a Gaussian distribution, and we performed Bartlett’s test to verify if all input samples came from populations with equal variances. If all samples belonged to a homoscedastic Gaussian population, we used one-way ANOVA to identify if we have at least one distribution that differs from the others; otherwise, we applied the non-parametric Kruskal Wallis test. If ANOVA/Kruskal Wallis identified that at least one group of samples differs from the others, we performed a post hoc comparison using respectively pairwise t-test and Dunn test.

Finally, we evaluated if the importance assigned to a given atlas’ region for a certain class correlates with the ability to observe in that region a relevant difference between the PET signal of different classes. We considered the detection of a difference inside a brain region of images belonging to a certain class compared to images of the other two classes as a boolean vector. Every item of the vector represents a region and takes True as a value when post hoc comparison had highlighted a difference between the class under analysis and at least in one of the other groups. We evaluated the correlation between the average of the importance metric distribution and the detection of a difference in images of different classes using the Point-biserial Correlation Coefficient (PbCC), since the latter is a binary variable. PbCC returns a coefficient in a range [-1:1]; where 1, -1, and 0 indicate respectively a maximum degree of correlation, maximum inverse correlation, and no correlation.

All Statistical Test has been executed using a significance $\alpha =0.05$.

Hardware and Software Specification

The proposed Deep Learning model was implemented using Python utilities (version 3.9), with Keras framework on Tensorflow backend (version 2.6.0). The training was performed on an Intel Core i7 5.1 MHz PC, 32 Gb RAM, equipped with an NVIDIA RTX3090 GPU with 24 Gb of embedded RAM. To handle a dataset of large dimensions during the training, each set had been stored in a tfrecord file and passed during fitting in TFRecordDataset format. To produce the post hoc explanation we exploited the keras-vis package (version 0.8.1) [29] for SM while for the LRP Maps we converted the Keras CNN architecture in PyTorch and we used the PyTorch implementation of the LRP algorithm implemented by Bohle et al. [23]. Image registration was performed using SimpleITK interface [30] while Statistical Inference was implemented using Python library SciPy [31]. Developed code is available at https://github.com/Alzheimer-PET-XAI/3DCNN-SM-LRP.

Results

Classification Result

During the training we reached a validation accuracy of $0.54\pm 0.01$, each training process requires on average 6 h. In Table 1 we reported the values of different classification metrics evaluated in the test sets over the 5 trials using a one-vs-all approach. We computed accuracy, sensitivity, specificity, Area Under the Curve (AUC), precision, F1 score, and Matthews Correlation Coefficient (MCC).

Table 1.

Mean ± St Dev classification metrics over 5 trials evaluated in the test set

Classification Task	Accuracy	Sensitivity	Specifity	AUC	Precision	F1 score	MCC
CN vs. all	0.74 ± 0.05	0.69 ± 0.07	0.77 ± 0.09	0.81 ± 0.04	0.63 ± 0.08	0.66 ± 0.05	0.46 ± 0.09
MCI vs. all	0.59 ± 0.03	0.47 ± 0.12	0.70 ± 0.80	0.63 ± 0.04	0.56 ± 0.04	0.50 ± 0.08	0.17 ± 0.07
AD vs. all	0.78 ± 0.02	0.52 ± 0.12	0.84 ± 0.02	0.77 ± 0.04	0.43 ± 0.04	0.47 ± 0.07	0.33 ± 0.09

In Table 2 we summarized the results of the most recent works which had performed a binary or multiclass classification using the same image modality of our research (18F-FDG PET), to identify a gold standard reference.

Table 2.

Classification results obtained on the test set in other works in literature. All the selected works had employed the ADNI dataset, except Etminani et al. (2021) [15] which integrated the ADNI dataset with data of the European-Dementia of Lewy Body (DLB) Consortium (E-DLB)

Author	Classification Task	Data Collection	Test Set	Accuracy	Sensitivity	Specifity	AUC	Precision	F1 score	MCC
Cheng and Lui [9]	AD vs. CN	339 subjects from ADNI	10% (10-fold validation)	0.91	0.91	0.91	0.95
	MCI vs. CN			0.79	0.78	0.80	0.84
Lu et al. [10]	AD vs. CN	1051 subjects from ADNI	10% (10-fold validation)	0.94	0.92	0.92
Zheng et al. [11]	AD vs. CN	962 images from ADNI	20% (5-fold validation)	0.91	0.86	0.95
Yee et al. [12]	AD vs. CN	596 subjects from ADNI	20% (5-fold validation)	0.93	0.92	0.94	0.98
Ding et al. [13]	AD vs. all	2109 images from 1002 subjects	10% (10-fold validation)		0.81	0.94		0.76	0.78
	MCI vs. all				0.54	0.68		0.55	0.55
	CN vs. all				0.59	0.75		0.60	0.59
Tufail et al. [14]	AD vs. all	90 images (Training + Validation)	23 images (12 CN, 7 MCI, 4 AD)	0.80	0.71	0.84	0.78	0.68	0.70	0.55
	MCI vs. all			0.60	0.35	0.72	0.53	0.38	0.36	0.68
	CN vs. all			0.74	0.65	0.79	0.72	0.62	0.63	0.43
Etminani et al. [15]	AD vs all	556 subjects from ADNI, 201 subjects from E-DLB	10% (73 cases)		0.91	0.92		0.83	0.87
	MCI vs. all				0.17	0.94		0.20	0.18
	DLB vs. all				0.86	1.00		1.00	0.92
	CN vs. all				0.88	0.90		0.81	0.84
Yiăit et al. [16]	AD vs CN	985 images from ADNI	20% (six-fold validation)	0.72
	MCI vs. CN			0.92

Averaged Heatmaps

We applied XAI techniques in the test set which produced the best results over the 5 trials (k-fold #5). We generated the SM and the LRP of the class predicted by the CNN for every scan correctly classified, obtaining an amount of 114 images for CN, 114 for MCI, and 54 for AD.

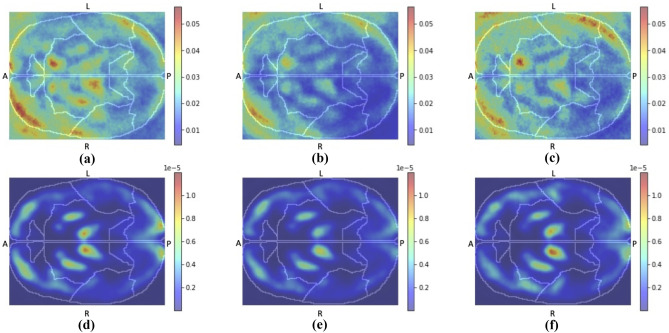
For each class in Figs. 2 and 3, we reported the average of the heatmaps of all patients for the three different classes: SM/LRP of subject CN classified as CN, SM/LRP of subject MCI classified as MCI and SM/LRP of subject AD classified as AD. Slice #50 of all the averaged maps is reported in Fig. 4.

Fig. 2.

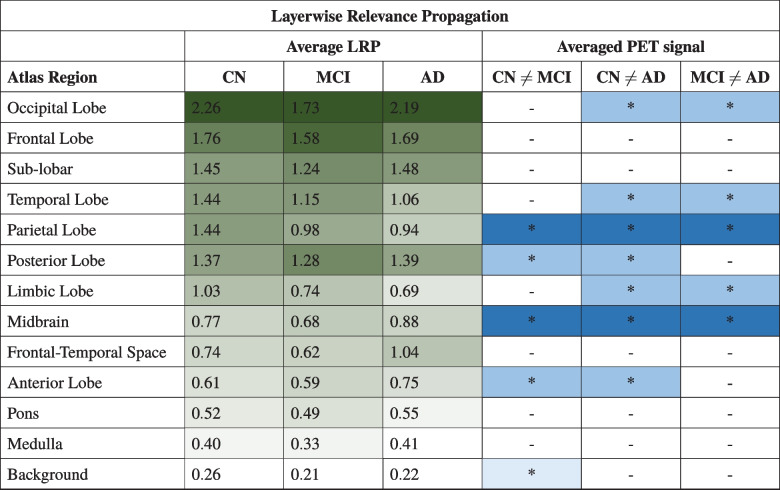
Average of SM registered with Talairach of subjects CN classified as CN (a), MCI classified as MCI (b) and AD classified as AD (c)

Fig. 3.

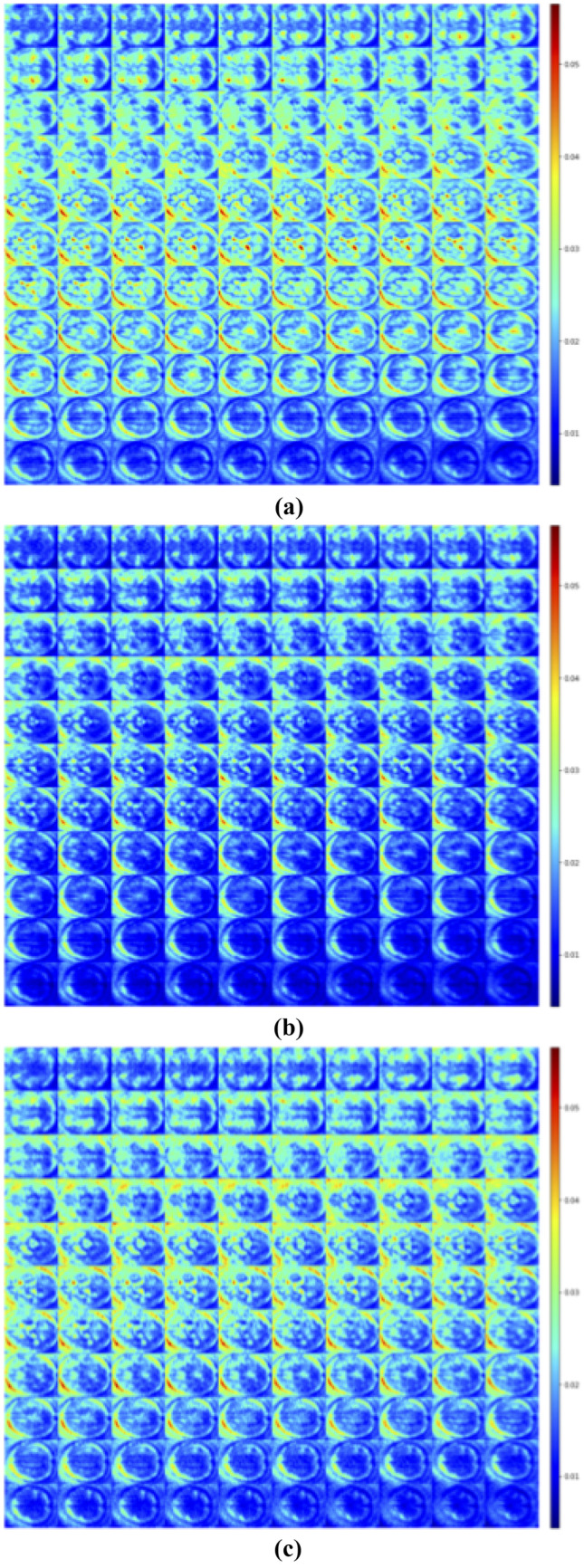
Average of LRP registered with Talairach of subjects CN classified as CN (a), MCI classified as MCI (b) and AD classified as AD (c)

Fig. 4.

Slice n = 50 of all the averaged post hoc explanation heatmaps: SM of CN (a), MCI (b) and AD (c) subjects and LRP of CN (d), MCI (e) and AD (f) subjects; “L”, “R”, “A”, “P” indicate respectively Left, Right, Anterior, Posterior

Heatmaps Quantitative Evaluation

To limit the number of anatomical regions inspected by the atlas we selected the labels at Lobe’s hierarchy level. In this way, we can identify some of the cerebral regions which are commonly reported to be affected by Alzheimer’s Disease, such as the temporal, parietal, and frontal lobes [1, 2].

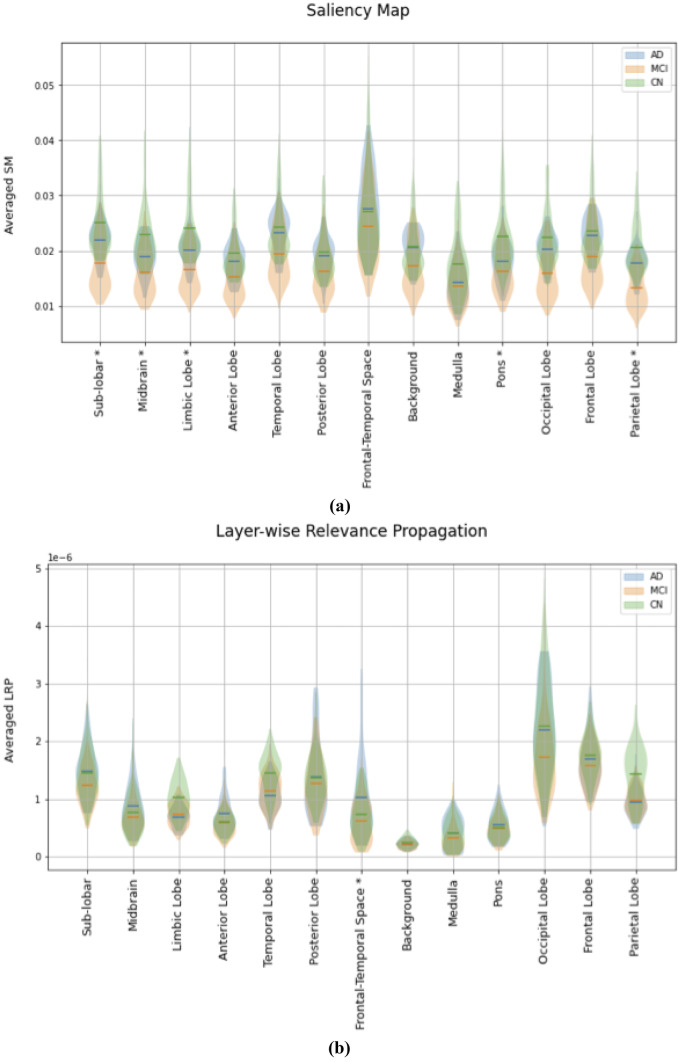
In Fig. 5 we reported the subjects’ distribution of the average of SM/LRP in each brain region, in a violin plot. We performed statistical inference to quantitatively evaluate if we can observe a relevant difference in the distribution of the average of SM/LRP between different classes in every atlas region.

Fig. 5.

Violin Plots for the evaluation of the average in each brain atlas’ region of the SM (a) and LRP (b) for correctly classified subject. Horizontal lines show the average value for all AD (blue), MCI (orange) and CN subjects (green) in the test set correctly classified; shaded areas (blue, orange and green shaded area for AD MCI and CN respectively) show the distribution of these values. ‘*’ denotes where the statistical inference highlighted a significant difference between the distribution in all the three classes

In Table 3 we reported the brain regions followed the descendent order of the average of importance metrics.

Table 3.

Atlas’ Anatomical Regions sorted by descending average between subject of SM/LRP

Saliency Map
CN	MCI	AD
Frontal-Temporal Space	Frontal-Temporal Space	Frontal-Temporal Space
Sub-lobar	Temporal Lobe	Temporal Lobe
Temporal Lobe	Frontal Lobe	Frontal Lobe
Limbic Lobe	Sub-lobar	Sub-lobar
Frontal Lobe	Background	Background
Midbrain	Limbic Lobe	Occipital Lobe
Pons	Pons	Limbic Lobe
Occipital Lobe	Posterior Lobe	Posterior Lobe
Background	Midbrain	Midbrain
Parietal Lobe	Occipital Lobe	Pons
Posterior Lobe	Anterior Lobe	Anterior Lobe
Anterior Lobe	Medulla	Parietal Lobe
Medulla	Parietal Lobe	Medulla

Layerwise Relevance Propagation
CN	MCI	AD
Occipital Lobe	Occipital Lobe	Occipital Lobe
Frontal Lobe	Frontal Lobe	Frontal Lobe
Sub-lobar	Posterior Lobe	Sub-lobar
Temporal Lobe	Sub-lobar	Posterior Lobe
Parietal Lobe	Temporal Lobe	Temporal Lobe
Posterior Lobe	Parietal Lobe	Frontal-Temporal Space
Limbic Lobe	Limbic Lobe	Parietal Lobe
Midbrain	Midbrain	Midbrain
Frontal-Temporal Space	Frontal-Temporal Space	Anterior Lobe
Anterior Lobe	Anterior Lobe	Limbic Lobe
Pons	Pons	Pons
Medulla	Medulla	Medulla
Background	Background	Background

Explanation and PET Signal Analysis

We performed the inference test to highlight in what anatomical regions the average of the registered PET images significantly differ between subjects belonging to different classes.

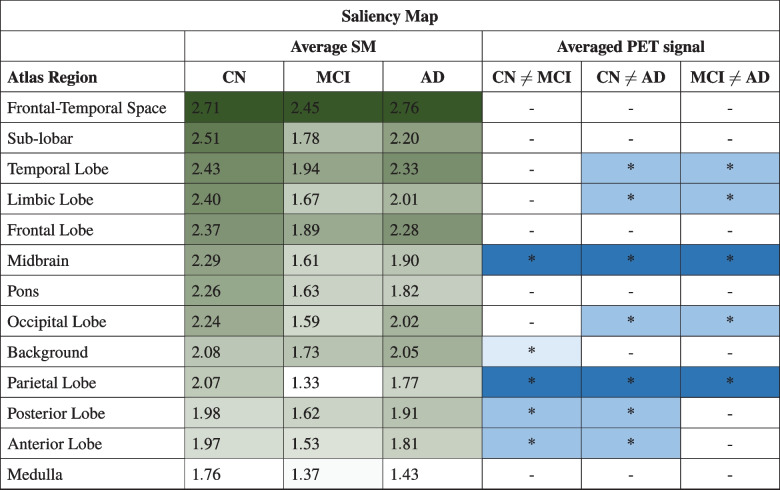
In Tables 4 and 5 we sorted all the regions according to SM/LRP by the descending average of importance metrics of CN subjects. We reported the average of the importance metrics in all regions for all classes and we highlighted them using a gradient colormap where the darkest color corresponds to a higher value of the mean importance metrics, which implies a more important region according to heatmap’s criteria for that prediction. We reported results of post hoc comparison of registered PET scans in all the different class combinations and we noted with “*” the regions where statistical tests had identified a relevant difference. The pattern of color distribution further emphasizes the higher inter-class variability of the average importance in the atlas region in SM compared to LRP.

Table 4.

Atlas’ Anatomical Regions sorted by descending average between CN subject of SM, every Average SM must be multiplied by a $\ast {10}^{-2}$ factor

Table 5.

Atlas’ Anatomical Regions sorted by descending average between CN subject of LRP, every Average LRP must be multiplied by a $\ast {10}^{-6}$ factor

The correlation coefficients of the average regions’ importance and the detection of differences in registered images between classes inside every brain region were respectively -0.28, -0.35, and -0.20 for SM in CN, MCI, and AD classes, and 0.15, 0.07, and 0.22 for LRP. Results showed that at this level of detail we are not able to observe a relevant correlation between the two measurements.

Discussion

In our study, we built a 3D CNN to classify FDG PET images into CN, MCI, and AD and we propose a framework to quantitatively evaluate (1) the explanation of the class predicted with two different XAI techniques and (2) their relationship with the PET signal.

As far as we know, from Tables 1 and 2 we observed that our Deep Neural Network has achieved performances comparable with the relevant literature. Some of studies reported in Table 2 describe a binary classifier [9–12, 16]; however, his kind of data is not directly comparable with ours. Similar classification performances were obtained by comparing our results with Tufail et al. [14], which exploited a smaller version of the ADNI database. With respect to the study of Ding et al. [13] our approach achieved slightly worse performances on the ADNI test. However, it should be noted that the authors performed data splitting at the exams level, so different exams of the same subject can be presented in the training and test data with possible data leakage. The four-class study of Etminani et al. [15] is not directly comparable with ours.

SM and LRP were generated for every sample of the test set, and we registered them on the Talairach Atlas. We reported the averaged heatmaps for all the three classes in Figs. 2 and 3 and the slice #50 of all the averaged maps in Fig. 4. From a visual qualitative inspection, we observed that independently from the patient’s group heatmaps highlighted mostly the Rich Frontal Region, the Left Temporo-occipital Region, the Left Caudatus and Thalamus. We can also observe that SM produces maps with higher noise compared to LRP.

Some of the aforementioned authors had also exploited post hoc explanation techniques to produce explanations of the prediction returned by their networks. From their results, it seems that there is no agreement on which XAI’s algorithm provides the best prediction explanation; moreover, the techniques employed vary from one study to another. It should also be noted that if on one side we observed a high variability on the post hoc explanation technique employed, on the other hand, all the previous works inspected had included a registration step of the heatmaps generated and their average for every group of subjects. Yee et al. [12] developed a 3D CNN that returns a Dementia of the Alzheimer’s type (DAT) probability score and employed the Guided Backpropagation (GB) [32] for DAT class and Gradient-weighted class activation mapping (GradCAM) [33] for DAT and CN class respectively. GB and GradCAM maps were registered into a common space, averaged, and visually interpreted: the averaged maps highlighted different regions consistent with literature like the posterior cingulate cortex, precuneus, angular gyrus, and hippocampus in GB DAT and the posterior cingulate cortex DAT GradCAM, while the CN GradCAM surprisingly features the cerebellum that instead shouldn’t be a region affected in AD. Ding et al. [13] trained a 2D CNN, an Inception-V3 architecture and, to obtain further information on how the network makes its decisions, they showed the average Saliency Map of the test dataset evaluating the gradient of the AD class score. In this case, the visual evaluation of SM suggests the deep learning algorithm uses the whole brain to predict the clinical classes and did not reveal a distinctly human interpretable imaging biomarker influential for AD prediction. Etminani et al. [15] developed a 3D CNN and to visualize the attention of the network they generated the average for all four classes using Occlusion Sensitivity heatmaps [34]. From visual inspection, the most discriminating regions highlighted are the posterior and anterior cingulate cortex, the temporal lobes in AD; similar regions in MCI with more emphasis on the posterior cingulate cortex, the middle temporal gyrus, gyrus rectus/orbital gyri, and also the parieto-occipital cortex, the occipital cortex, the cerebellum and slightly postcentral gyrus and striatum in CN and finally the posterior cingulate cortex and the occipital cortex in DLB.

We decided to quantitatively assess the importance of atlas brain regions for the prediction, by computing the average of every heatmap within the regions. In Fig. 5 we reported the distribution of the importance metrics evaluated in every atlas’ region of all the three different classes for the two different explanation techniques employed. Performing statistical inference, we observed that the distributions of the atlas-based average SM significantly differ between all three classes in more brain regions, including the background, compared to the distribution of ROI averaged LRP.

We sorted the brain regions according to the average of these distributions in Table 3. Table 3 highlights that the order of importance returned is significantly different according to the heatmaps’ generation techniques considered. This is because the two techniques use different definitions of “importance”. Another observation from Table 3 is that while LRP approximately assigned the same importance order to the brain region in all the three different classes, suggesting that the CNN bases its prediction looking into the same areas, SM has higher inter-class variability in assigning the importance for the final prediction, as previously observed in Fig. 5. These results seem to suggest that SM and LRP capture different aspects of the CNN learning process. In particular, SM considered the frontal-temporal space as the most important region for the prediction of all three classes, while in LRP the occipital lobe resulted as the most relevant region. This finding obtained thanks to a quantitative evaluation confirmed the strong dependence of the post hoc explanation on the used approach [35].

Jyoti and Zhang [24] developed a 3D CNN which classifies 18F-FDG PET images and showed the averaged heatmaps for class AD using five different visualization techniques including SM and LRP. They observed that all the visualization techniques focus mostly on similar brain regions and underlined that gradient-based methods had generated more distributed heatmaps; this finding was not fully confirmed by our result (Table 3 and Fig. 4c, f). They evaluated as a quantitative measurement the sum of heatmaps’ values in the same brain region. Our findings are not directly comparable as we used a different atlas our result confirmed the presence of the temporal lobe as an important side of activation in both SM and LRP. A final noteworthy work that deals with the application of post hoc explanation techniques in the AD domain is that of Böhle et al. [23]. They trained a CNN to classify T1-weighted MRI data into AD and healthy patients and focused their attention on the quantitative evaluation of the generated heatmaps.

In our work we sorted anatomical brain regions according to an importance criterion based on SM and LRP Maps, so we were interested in inspecting if the regions resulted as the most relevant for the prediction returned, we were able to identify any relevant differences in the average voxels’ intensity inside ROI of subject belonging to different classes. For example, according to LRP, the occipital lobe seems a relevant area to determine class output, so we would expect to find a relevant difference in voxels’ intensity in this area in subjects belonging to a certain class compared to the distribution between subjects of a different class. On the other hand, the background area has the lowest average relevance, so we would expect to not find a relevant difference in this area in voxels’ intensity between a subject belonging to a different class.

The main novelty of the present study is the investigation of the relationship between activation maps and PET signals. Tables 4 and 5 report the averages importance metrics values and the existence of a statistical difference in PET signal between classes in the brain regions, for SM and LRP respectively. Brain regions are sorted by importance order of class CN defined in Table 3. From statistical inference we observed a relevant difference in PET signal in parietal lobes in all three different classes and in the temporal lobe in AD with respect to CN and MCI as expected from relevant literature [1, 2]. We also observed a relevant difference in all three classes also in the midbrain.

PbCC showed that we are not able to observe a clear relationship between the average value of the importance metrics assigned by the two heatmaps generation techniques and the fact that the average of the image in these regions significantly differs between the classes. For example, according to both metrics, sub-lobar should be a relevant region for the detection of all three classes, but in fact, we are not able to identify a relevant difference in the average of the image in these regions between subjects belonging to different classes. On the other hand, the parietal lobe shouldn’t be so relevant according to SM but in fact, in the input data, we detected a relevant difference in all three classes.

One possible reason for this, which is also one of the main limitations of our study, is that we mapped an importance metrics on an anatomic atlas to provide a human-intuitive reference. However, the CNN could consider a different combination of patterns to return its prediction that may not have any relationship with the atlas employed. Should also be noted that in our study we used a normalized dataset, so the link with the raw PET signal was missed.

Another possible interpretation can be that, although post hoc visual explanations are the most exploited technique to explain Deep Learning models in medical imaging applications [35], they present some limitations. As stated in the perspective of Rudin [36], post hoc explanations still do not provide information about how the black-box classifier uses the important part of the image to return their predictions, so they provide an incomplete and potentially misleading explanation. This may also suggest trying other approaches in the XAI field, for example exploiting interpretable models instead explanations of black boxes.

Other different limitations could be recognized in the present study. As concerns classification performances, we didn’t test our network on an independent test set different from the ADNI dataset as done in other research [13]. In addition, we performed a group-wise study to statistically assess the significance of the results and with this approach, we could lose subject-specific information.

Conclusion

In our research, we built a 3D CNN architecture that performed multiclass classification of 18F-FDG PET images for the diagnosis of the clinical stage of Alzheimer’s disease. We have also proposed a framework to quantitatively evaluate the heatmaps produced by two different post hoc explanation techniques, Saliency Map and Layerwise Relevance Propagation and their relationship with PET scans. While LRP assigned on average a similar importance order to all brain regions for the class prediction, in SM we observed that this order changes with the class, suggesting that LRP maps seem more effective in mapping the importance metrics in the anatomic atlas. However, a clear relationship between the importance assigned and characteristics of differences in PET signal is still missing and future research on this subject is needed.

Supplementary Information

Below is the link to the electronic supplementary material.

Author Contribution

All authors contributed to the study conception and design. All authors read and approved the final manuscript.

Data Availability

Data used in preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). As such, the investigators within the ADNI contributed to the design and implementation of ADNI and/or provided data but did not participate in analysis or writing of this report. A complete listing of ADNI investigators can be found at: http://adni.loni.usc.edu/wp-content/uploads/how_to_apply/ADNI_Acknowledgement_List.pdf.

Code Availability

Developed code is available at https://github.com/Alzheimer-PET-XAI/3DCNN-SM-LRP

Declarations

Ethics Approval

Since a public dataset was used, there is no need of Ethical Approval.

Conflict of Interest

The authors declare no competing interests.