Selection of healthcare waste management treatment using fuzzy rough numbers and Aczel–Alsina Function

Abstract

The COVID-19 pandemic led to an increase in healthcare waste (HCW). HCW management treatment needs to be re-taken into focus to deal with this challenge. In practice, there are several treatments of HCW with their advantages and disadvantages. This study is conducted to select the appropriate treatment for HCW in the Brčko District of Bosnia and Herzegovina. Six HCW management treatments are analyzed and observed through twelve criteria. Ten-level linguistic values were used to bring this evaluation closer to human thinking. A fuzzy rough approach is used to solve the problem of inaccuracy in determining these values. The OPA method from the Bonferroni operator is used to determine the weights of the criteria. The results of the application of this method showed that the criterion Environmental Impact ($C_4$) received the highest weight, while the criterion Automation Level ($C_8$) received the lowest value. The ranking of HCW management treatments was performed using MARCOS methods based on the Aczel–Alsina function. The results of this analysis showed that the best-ranked HCW management treatment is microwave (A6) while landfill treatment (A5) is ranked worst. This study has provided a new approach based on fuzzy rough numbers where the Bonferroni function is used to determine the lower and upper limits, while the application of the Aczel–Alsina function reduced the influence of decision-makers on the final decision because this function stabilizes the decision-making process.

1. Introduction

Healthcare Waste (HCW) is generated from operations of healthcare institutions and is defined as waste generated in the diagnosis, treatment, or immunization of humans or animals, which includes blood, body parts, chemicals, drugs, medical devices, radioactive materials (Pamučar et al., 2021) and others waste generated from operations of health care institutions. HCW management is a very important issue especially nowadays when there is a pandemic caused by the COVID-19 virus (Manupati et al., 2021). Due to the pandemic, there is more volume of HCW that needs to be disposed of adequately. The problem of efficient HCW has become a crucial issue. The main motivation in HCW management is to focus on proper collection to reduce the impact of this type of waste on human and animal health and the environment. Improper disposal of HCW leads to environmental pollution (Ju et al., 2020).

As a developing country, Bosnia and Herzegovina have faced problems with the HCW. Namely, HCW is often mixed with ordinary municipal waste, which can be a major problem (Pamučar et al., 2021). Even a small volume of HCW can pose major risks to human and animal health and the environment if not managed properly (Hasan and Rahman, 2018). Therefore, it is necessary to pay attention to the proper handling and disposal of HCW (Mythili et al., 2021). It is important that healthcare professionals properly separate HCW at the site of origin and dispose of it properly and carefully in appropriate packaging (Badi et al., 2019).

In Bosnia and Herzegovina, as in other underdeveloped and developing countries, it is necessary to determine appropriate technologies for the safe collection, treatment, and disposal of HCWs. This is of great importance for human and animal health as well as for the preservation of the environment (Xiao, 2018). There are different ways of HCW treatment such as incineration, autoclave, chemical disinfection, disposal in the ground, deep burial, etc. (Geetha et al., 2019). Each of these treatments has its advantages and disadvantages. The selection of HCW management treatment is of great importance, especially when a large volume of HCW is present. Proper treatment and removal of HCW are of great importance especially during and after the pandemic (Manupati et al., 2021). HCWs need to be treated appropriately to reduce risks and protect human and animal life and the environment.

The problem of HCW management in Bosnia and Herzegovina is a serious concern and needs to be addressed in the best possible way. This study analyzed the current HCW management system in the Brčko District. This study aims to investigate which of the HCW management treatments most effectively solves the HCW problem in Brčko District using expert decision-making. When applying expert decision-making, there is a problem of inaccuracy in the assessment of alternatives. To solve this problem, the application of the fuzzy rough methodology will be offered in the research. The contribution of this methodology is in the application of the fuzzy approach, which is based on linguistic values adapted to human thinking. The use of rough numbers solves the problem of inaccuracy in the assessment of HCW management treatment. The methodology based on the application of the fuzzy rough approach represents an innovation in the selection of HCW treatment.

Linguistic values based on fuzzy rough numbers are used to adapt decision-making to human thinking because there is a problem of inaccuracy in human thinking (Pamučar et al., 2019). When evaluating HCW management treatments, it is not possible to pinpoint each treatment, although linguistic values are used, so this approach was applied. That is why this innovative approach is applied in this study.

When selecting a treatment, four main criteria are used as follows: technical, economic, environmental, and social criteria. Each of these criteria is divided into several sub-criteria in a way that the total number of sub-criteria s equal to twelve. The application of this approach is generally accepted in the selection of HCW management treatment (Dursun et al., 2011, Lu et al., 2016, Shi et al., 2017, Xiao, 2018, Hinduja and Pandey, 2019, Mishra et al., 2020, Manupati et al., 2021, Makan and Fadili, 2021, Puška et al., 2022).

Dursun et al. (2011) evaluated the treatment in HCW management and showed that Steam sterilization is the best treatment for HCW management. Özkan (2013) in his research showed that the best treatment is off-site steam sterilization in the example of Istanbul. Voudrias (2016) evaluated five different treatments in his paper and proved that Steam disinfection treatment is the best treatment offered. Lu et al. (2016) selected HCW management treatments in the example of Shanghai. They obtained results showing that the application of steam sterilization gives the best results. Zimmermann (2017) compared microwave and autoclave treatments and proved that microwave treatments consume less energy than autoclaves and have more advantages. Shi et al. (2017) showed from the observed treatments in Shanghai that Steam sterilization treatment gave the best results. Xiao (2018) used the example of Shanghai to select a treatment for HCW management and found that steam sterilization treatment showed the best results in HCW management. Hasan and Rahman (2018) evaluated various treatments in the example of Khulna city and found that incineration is the best option for HCW management. Hinduja and Pandey (2019) selected HCW management treatments in the example of Chhattisgarh, India. Their results showed that steam sterilization is the best treatment for HCW management. Manupati et al. (2021) selected HCW management treatments and showed that incinerator applications were the best HCW management solution during the COVID-19 virus pandemic. As can be seen from these studies, there is no specific treatment that has proven to be the best, the results are different, and it all depends on which type of HCW predominates.

To achieve the aim of the research and choose the treatment that would be the best for Brčko District, the fuzzy rough approach was used. So far, different methods have been used to manage HCW: model fuzzy and uncertain information, including fuzzy sets, intuitionistic fuzzy sets, interval-valued intuitionistic fuzzy sets, linguistic arguments, hesitant fuzzy sets, neutrosophic sets, and rough sets, etc. (Narayanamoorthy et al., 2020). As can be seen, the application of the fuzzy rough approach is a new approach when choosing a treatment for the management of HCW. In the management of HCW, it is necessary to mention the work of Yazdani et al. (2020). They used the rough set theory when selecting the HCW disposal site. They used interval rough numbers together with Dombi-Bonferroni means in the example of a private clinic in Madrid. However, the application of rough theory is also present in other waste management problems. Pramanik et al. (2018) applied rough theory to the selection of models for the selection of waste management facilities. Li & Jin (2019) applied rough-interval type-2 fuzzy stochastic linear programming to solve the problem of municipal waste management. Tomasz et al. (2017) applied rough theory to investigate the rate of waste accumulation in households in rural areas. Using fuzzy rough solves the inaccuracy that occurs in expert decision-making (Zhan et al., 2020). This is because experts have to evaluate criteria and alternatives. Sometimes it is difficult to judge how important some of the criteria or alternatives are and what rating they should receive. That is why experts often cannot give a precise assessment (Sun et al., 2018). Developing different models based on the fuzzy rough approach is significant for making more complete decisions (Jiang and Hu, 2021). Lessons learned in this way will respect human thinking and decision-making imprecision (Tiwari et al., 2018).

Due to the existence of several criteria, multi-criteria decision-making (MCDM) methods were applied. The selection of HCW management treatment is classics a problem in decision-making (Adar and Delice, 2019).

Group expert decision-making is used to determine the value of HCW treatment. Experts who participated in this study were appointed in cooperation with the Government of the Brčko District. Selected experts selected criteria and alternatives for the selection of HCW management treatment. Criteria and alternatives were assessed by experts using a linguistic value that ranges from absolutely low to perfect. This value scale is based on will have 10 degrees. The OPA (Ordinal Priority Approach) method, which is based on fuzzy rough numbers, is used to determine the weight of the criteria, and the alternatives are evaluated using the MARCOS (Measurement of Alternatives and Ranking according to COmpromise Solution) method, which was based on fuzzy rough Aczel–Alsina​ methodology.

In addition to the main aim of the study, auxiliary goals were set. The first ancillary objective relates to the improvement and enrichment of the methodology for solving the uncertainty problem in the application of group decision-making using the fuzzy rough approach. The second aim is to bridge the research gap, i.e., to investigate which treatment would give the best results in HCW management. The third aim is to improve HCW management by taking advantage of the fuzzy and rough approach to ranking alternatives. Applying this approach can determine not only the best treatment method but also their order based on expert judgment. This improves the management of HCW. To improve the management of HCW, it is necessary to apply several different treatments for different types of HCW. Only in this way, HCW can be managed efficiently. The fourth aim is to popularize the application of the hybrid fuzzy rough approach in group decision-making.

During the operation of healthcare institutions, different types of waste occur, infectious waste, pathological waste, sharps, pharmaceutical waste, genotoxic waste, chemical waste, wastes with high content of heavy metals, pressurized containers, and radioactive waste (Pamučar et al., 2021). In previous research, they were used several different HCW management treatments are mostly observed using criteria, namely: economic, environmental, technical, and social criteria. Using these criteria, different results were obtained as to which treatment is best for HCW.

2. Preliminaries

In this section, some key concepts are presented that are important for defining the multi-criteria framework presented in this study.

2.1. Fuzzy rough numbers

Rough sets (Pawlak, 1982) and fuzzy sets (Zadeh, 1965) belong to the group of key tools for dealing with uncertainty and vagueness in human reasoning (Agarwal et al., 2020). This is the reason why rough and fuzzy sets have taken a significant place in the field of soft switching and modeling decision-making systems. Numerous scholars have shown that rough and fuzzy numbers are an adequate tool for processing inaccuracies in information. This is done through the modeling of complex systems for objective and rational decision-making (Bozanic et al., 2020, Pamučar and Janković, 2020, Kazemitash et al., 2021; Ali et al. 2021; Ayub et al., 2022).

Even though certain efforts have been made in manipulating uncertainty and subjectivity in the decision-making process, this problem remains a challenging task. Most traditional techniques in multi-criteria optimization, based on the application of fuzzy and rough numbers, can exploit only part of such incomplete and indeterminate information. One of the limitations of fuzzy sets is subjectivism in defining the boundaries of fuzzy sets, which can affect the performance of the proposed solution (Durmic et al., 2020). On the other hand, rough sets (Pawlak, 1982) are an adequate tool for processing inaccuracies in information without the influence of subjectivism (Pamucar et al., 2022). However, rough sets cannot define the degree of membership (membership). Therefore, a new methodological framework based on hybrid fuzzy rough numbers is proposed in this study. This framework combines the advantages of fuzzy and rough sets.

Using fuzzy and rough sets together provides more accurate and objective results (Chen et al., 2020). The advantages of fuzzy sets and rough sets are combined in such a way that the problem of uncertainty in decision-making can be solved. The application of the fuzzy rough set allows defining the degree of membership for each element in the rough boundary interval (Pamucar et al., 2022)

In this study, a novel methodology for defining fuzzy rough numbers is proposed. This methodology is based on a new concept for defining lower and upper limits for rough numbers. The new concept eliminates the shortcomings of classical arithmetic averaging used to define lower and upper limits in traditional rough numbers. In this study, the introduction of Bonferroni functions for defining the lower and upper limits of fuzzy rough sequences is proposed. The new methodology makes it possible to consider the interrelationships between a set of objects in a fuzzy rough interval. Furthermore, the new approach allows flexible representation of the rough boundary interval and defines the degree of risk depending on the dynamic environmental conditions. In the following, a new methodology for defining the lower and upper limits of fuzzy rough numbers is presented.

Assuming it is a universe containing a set of triangular fuzzy objects ${\tilde{\psi }}_i=\left({\psi }_i^{\left(l\right)},{\psi }_i^{\left(m\right)},{\psi }_i^{\left(u\right)}\right)$ with the mode, left endpoint, and right endpoint. Suppose that fuzzy objects are divided into h classes that satisfy the condition that ${\tilde{\psi }}_1\le {\tilde{\psi }}_2\le ,\dots ,{\tilde{\psi }}_i,\dots ,\le {\tilde{\psi }}_b$. Assuming it is a $\mathbb{R}$ collection of $\left({\tilde{\psi }}_1,{\tilde{\psi }}_2,\dots ,{\tilde{\psi }}_b\right)$, then for each $\forall \xi \in \Im$, $\forall {\tilde{\psi }}_i\in \mathbb{R}$, $1\le i\le h$, we can define lower and upper approximation class ${\tilde{\psi }}_i$:

(a) lower approximation:

$$\begin{array}{c}{\underset{\_}{\psi }}_i^{\left(l\right)}=\bigcup _{1\le i\le h}\left\{\xi \in \Im /\mathbb{R}\left(\xi \right)\le {\psi }_i^{\left(l\right)}\right\}\hfill \\ {\underset{\_}{\psi }}_i^{\left(m\right)}=\bigcup _{1\le i\le h}\left\{\xi \in \Im /\mathbb{R}\left(\xi \right)\le {\psi }_i^{\left(m\right)}\right\}\hfill \\ {\underset{\_}{\psi }}_i^{\left(u\right)}=\bigcup _{1\le i\le h}\left\{\xi \in \Im /\mathbb{R}\left(\xi \right)\le {\psi }_i^{\left(u\right)}\right\}\hfill \end{array}$$ (1)

where ${\psi }_i^{\left(l\right)},{\psi }_i^{\left(m\right)}$ and ${\psi }_i^{\left(u\right)}$ present the left endpoint, mode, and right endpoint of triangular fuzzy objects ${\tilde{\psi }}_i$, $\xi \in \Im$, $1\le i\le h$ and h represents the total number of classes in the considered set.

(b) upper approximation:

$$\begin{array}{c}{\overline{\psi }}_i^{\left(l\right)}=\bigcup _{1\le i\le h}\left\{\xi \in \Im /\mathbb{R}\left(\xi \right)\ge {\psi }_i^{\left(l\right)}\right\}\hfill \\ {\overline{\psi }}_i^{\left(m\right)}=\bigcup _{1\le i\le h}\left\{\xi \in \Im /\mathbb{R}\left(\xi \right)\ge {\psi }_i^{\left(m\right)}\right\}\hfill \\ {\overline{\psi }}_i^{\left(u\right)}=\bigcup _{1\le i\le h}\left\{\xi \in \Im /\mathbb{R}\left(\xi \right)\ge {\psi }_i^{\left(u\right)}\right\}\hfill \end{array}$$ (2)

where ${\psi }_i^{\left(l\right)},{\psi }_i^{\left(m\right)}$ and ${\psi }_i^{\left(u\right)}$ present the left endpoint, mode, and right endpoint of triangular fuzzy objects ${\tilde{\psi }}_i$, $\xi \in \Im$, $1\le i\le h$ and h represents the total number of classes in the considered set.

Based on Eqs. (1), (2), we can define lower and upper limits as follows:

(a) lower limit:

$$\begin{array}{cc}\hfill & \underset{\_}{Lim}\left({\psi }_i^{\left(l\right)}\right)={\left(\frac{1}{{ƛ}_{Ll}}\sum _{i,j=1}^{{ƛ}_{Ll}}{\psi }_i^{\left(l\right)d_1}{\left(\prod _{j=1}^{{ƛ}_{Ll}}{\psi }_j^{\left(l\right)d_2}\right)}^{\frac{1}{{ƛ}_{Ll}-1}}\right)}^{\frac{1}{d_1+d_2}}\left|{\psi }_i^{\left(l\right)d_1},{\psi }_j^{\left(l\right)d_2}\right)\in {\underset{\_}{\psi }}_i^{\left(l\right)}\hfill \\ \hfill & \underset{\_}{Lim}\left({\psi }_i^{\left(m\right)}\right)={\left(\frac{1}{{ƛ}_{Lm}}\sum _{i,j=1}^{{ƛ}_{Lm}}{\psi }_i^{\left(m\right)d_1}{\left(\prod _{j=1}^{{ƛ}_{Lm}}{\psi }_j^{\left(m\right)d_2}\right)}^{\frac{1}{{ƛ}_{Lm}-1}}\right)}^{\frac{1}{d_1+d_2}}\left|{\psi }_i^{\left(m\right)d_1},{\psi }_j^{\left(m\right)d_2}\right)\in {\underset{\_}{\psi }}_i^{\left(m\right)}\hfill \\ \hfill & \underset{\_}{Lim}\left({\psi }_i^{\left(u\right)}\right)={\left(\frac{1}{{ƛ}_{Lu}}\sum _{i,j=1}^{{ƛ}_{Lu}}{\psi }_i^{\left(u\right)d_1}{\left(\prod _{j=1}^{{ƛ}_{Lu}}{\psi }_j^{\left(u\right)d_2}\right)}^{\frac{1}{{ƛ}_{Lu}-1}}\right)}^{\frac{1}{d_1+d_2}}\left|{\psi }_i^{\left(u\right)d_1},{\psi }_j^{\left(u\right)d_2}\right)\in {\underset{\_}{\psi }}_i^{\left(u\right)}\hfill \end{array}$$ (3)

where ${ƛ}_{Ll}$, ${ƛ}_{Lm}$ and ${ƛ}_{Lu}$ represent the number of elements in the lower approximations (1), and $d_1,d_2\ge 0$.

(b) upper limit:

$$\begin{array}{cc}\hfill & \overline{Lim}\left({\psi }_i^{\left(l\right)}\right)\hfill \\ \hfill & ={\left(\frac{1}{{ƛ}_{Ul}}\sum _{i,j=1}^{{ƛ}_{Ul}}{\psi }_i^{\left(l\right)d_1}{\left(\prod _{j=1}^{{ƛ}_{Ul}}{\psi }_j^{\left(l\right)d_2}\right)}^{\frac{1}{{ƛ}_{Ul}-1}}\right)}^{\frac{1}{d_1+d_2}}\left|{\psi }_i^{\left(l\right)d_1},{\psi }_j^{\left(l\right)d_2}\right)\in {\overline{\psi }}_i^{\left(l\right)}\hfill \\ \hfill & \overline{Lim}\left({\psi }_i^{\left(m\right)}\right)\hfill \\ \hfill & ={\left(\frac{1}{{ƛ}_{Um}}\sum _{i,j=1}^{{ƛ}_{Um}}{\psi }_i^{\left(m\right)d_1}{\left(\prod _{j=1}^{{ƛ}_{Um}}{\psi }_j^{\left(m\right)d_2}\right)}^{\frac{1}{{ƛ}_{Um}-1}}\right)}^{\frac{1}{d_1+d_2}}\left|{\psi }_i^{\left(m\right)d_1},{\psi }_j^{\left(m\right)d_2}\right)\in {\overline{\psi }}_i^{\left(m\right)}\hfill \\ \hfill & \overline{Lim}\left({\psi }_i^{\left(u\right)}\right)\hfill \\ \hfill & ={\left(\frac{1}{{ƛ}_{Uu}}\sum _{i,j=1}^{{ƛ}_{Uu}}{\psi }_i^{\left(u\right)d_1}{\left(\prod _{j=1}^{{ƛ}_{Uu}}{\psi }_j^{\left(u\right)d_2}\right)}^{\frac{1}{{ƛ}_{Uu}-1}}\right)}^{\frac{1}{d_1+d_2}}\left|{\psi }_i^{\left(u\right)d_1},{\psi }_j^{\left(u\right)d_2}\right)\in {\overline{\psi }}_i^{\left(u\right)}\hfill \end{array}$$ (4)

where ${ƛ}_{Ul}$, ${ƛ}_{Um}$ and ${ƛ}_{Uu}$ represent the number of elements in the upper approximations (2), and $d_1,d_2\ge 0$.

Based on Eqs. (1)–(4) we can define the fuzzy rough number

${\overline{\psi }}_i=\left(\left[\underset{\_}{Lim}\left({\psi }_i^{\left(l\right)}\right),\overline{Lim}\left({\psi }_i^{\left(l\right)}\right)\right],\right)\left(\left[\underset{\_}{Lim}\left({\psi }_i^{\left(m\right)}\right),\overline{Lim}\left({\psi }_i^{\left(m\right)}\right)\right],\left[\underset{\_}{Lim}\left({\psi }_i^{\left(u\right)}\right),\overline{Lim}\left({\psi }_i^{\left(u\right)}\right)\right]\right)$, that is

${\overline{\psi }}_i=\left(\left[{\psi }_i^{\left(l\right)-},{\psi }_i^{\left(l\right)+}\right],\left[{\psi }_i^{\left(m\right)-},{\psi }_i^{\left(m\right)+}\right],\left[{\psi }_i^{\left(u\right)-},{\psi }_i^{\left(u\right)+}\right]\right)$.

where ${\psi }_i^{\left(l\right)-}$ and ${\psi }_i^{\left(l\right)+}$ presents left endpoints of fuzzy rough numbers, ${\psi }_i^{\left(m\right)-}$ and ${\psi }_i^{\left(m\right)+}$ presents modal values of fuzzy rough number, while ${\psi }_i^{\left(u\right)-}$ and ${\psi }_i^{\left(u\right)+}$ presents right endpoints of fuzzy rough numbers.

2.2. Aczel–Alsina T-norm and T-conorm

Definition 1 Aczel and Alsina, 1982 —

Suppose that ${\zeta }_1$ and ${\zeta }_2$ are two real numbers. Then Aczel–Alsina T-norm and T-conorm between ${\zeta }_1$ and ${\zeta }_2$ we can define it as follows:

(a) Aczel–Alsina T-norm $t_{\left({\zeta }_1,{\zeta }_2\right)}^{\varphi }$:

$$t_{\left({\zeta }_1,{\zeta }_2\right)}^{\varphi }=\left\{\begin{array}{c}t\left({\zeta }_1,{\zeta }_2\right)if\varphi =0,\hfill \\ min\left({\zeta }_1,{\zeta }_2\right)if\varphi =\infty ,\hfill \\ e^{-{\left({\left(-ln\left({\zeta }_1\right)\right)}^{\varphi }+{\left(-ln\left({\zeta }_2\right)\right)}^{\varphi }\right)}^{1/\varphi }}\text{ otherwise}.\hfill \end{array}\right)$$ (5)

where $({\zeta }_1,{\zeta }_2)\in \left[0,1\right]$ and $\varphi \in \left[0,\infty \right]$.

(b) Aczel–Alsina T-norm $t_{\left({\zeta }_1,{\zeta }_2\right)}^{\varphi }$, where $\varphi \in \left[0,\infty \right]$:

$$t{c}_{\left({\zeta }_1,{\zeta }_2\right)}^{\varphi }=\left\{\begin{array}{c}tc\left({\zeta }_1,{\zeta }_2\right)if\varphi =0,\hfill \\ max\left({\zeta }_1,{\zeta }_2\right)if\varphi =\infty ,\hfill \\ 1-e^{-{\left({\left(-ln\left(1-{\zeta }_1\right)\right)}^{\varphi }+{\left(-ln\left(1-{\zeta }_2\right)\right)}^{\varphi }\right)}^{1/\varphi }}\text{ otherwise}.\hfill \end{array}\right)$$ (6)

where $({\zeta }_1,{\zeta }_2)\in \left[0,1\right]$ and $\varphi \in \left[0,\infty \right]$.

The Aczel–Alsina t -norms and Aczel–Alsina t -conorms families are strictly increasing and decreasing, respectively, as shown in the susceptibility analysis presented in this study.

Based on Definition 1 and the operational laws of rough numbers, we can define arithmetic operations with rough numbers based on Aczel–Alsina t -norms and conorms.

Definition 2

Suppose that ${\overline{\eta }}_1=\left(\left[{\eta }_1^{\left(l\right)-},{\eta }_1^{\left(l\right)+}\right],\left[{\eta }_1^{\left(m\right)-},{\eta }_1^{\left(m\right)+}\right],\left[{\eta }_1^{\left(u\right)-},{\eta }_1^{\left(u\right)+}\right]\right)$ and ${\overline{\eta }}_2=\left(\left[{\eta }_2^{\left(l\right)-},{\eta }_2^{\left(l\right)+}\right],\left[{\eta }_2^{\left(m\right)-},{\eta }_2^{\left(m\right)+}\right],\left[{\eta }_2^{\left(u\right)-},{\eta }_2^{\left(u\right)+}\right]\right)$ are two fuzzy rough numbers, $\tau ,\varphi >0$ and let it be $f\left({\overline{\eta }}_i\right)={\overline{\eta }}_i/{\sum }_{i=1}^n{\overline{\eta }}_i$ fuzzy rough function, then based on Eqs. (5), (6) we can define arithmetic rules with fuzzy rough numbers based on the application of Aczel–Alsina t -norms and conorms:

(1) Addition “$\oplus$”

$${\overline{\eta }}_1\oplus {\overline{\eta }}_2=\left(\begin{array}{c}\left[\right)1-e^{-{\left({\left(-ln\left(1-{\eta }_1^{\left(l\right)-}\right)\right)}^{\varphi }+{\left(-ln\left(1-{\eta }_2^{\left(l\right)-}\right)\right)}^{\varphi }\right)}^{1/\varphi }},\hfill \\ 1-e^{-{\left({\left(-ln\left(1-{\eta }_1^{\left(l\right)+}\right)\right)}^{\varphi }+{\left(-ln\left(1-{\eta }_2^{\left(l\right)+}\right)\right)}^{\varphi }\right)}^{1/\varphi }}\left(\right],\hfill \\ \left[\right)1-e^{-{\left({\left(-ln\left(1-{\eta }_1^{\left(m\right)-}\right)\right)}^{\varphi }+{\left(-ln\left(1-{\eta }_2^{\left(m\right)-}\right)\right)}^{\varphi }\right)}^{1/\varphi }},\hfill \\ 1-e^{-{\left({\left(-ln\left(1-{\eta }_1^{\left(m\right)+}\right)\right)}^{\varphi }+{\left(-ln\left(1-{\eta }_2^{\left(m\right)+}\right)\right)}^{\varphi }\right)}^{1/\varphi }}\left(\right]\hfill \\ \left[\right)1-e^{-{\left({\left(-ln\left(1-{\eta }_1^{\left(u\right)-}\right)\right)}^{\varphi }+{\left(-ln\left(1-{\eta }_2^{\left(u\right)-}\right)\right)}^{\varphi }\right)}^{1/\varphi }},\hfill \\ 1-e^{-{\left({\left(-ln\left(1-{\eta }_1^{\left(u\right)+}\right)\right)}^{\varphi }+{\left(-ln\left(1-{\eta }_2^{\left(u\right)+}\right)\right)}^{\varphi }\right)}^{1/\varphi }}\left(\right]\hfill \end{array}\right)$$ (7)

(2) Multiplication “$\otimes$”

$${\overline{\eta }}_1\otimes {\overline{\eta }}_2=\left(\begin{array}{c}\left[\right)e^{-{\left({\left(-ln\left({\eta }_1^{\left(l\right)-}\right)\right)}^{\varphi }+{\left(-ln\left({\eta }_2^{\left(l\right)-}\right)\right)}^{\varphi }\right)}^{1/\varphi }},\hfill \\ e^{-{\left({\left(-ln\left({\eta }_1^{\left(l\right)+}\right)\right)}^{\varphi }+{\left(-ln\left({\eta }_2^{\left(l\right)+}\right)\right)}^{\varphi }\right)}^{1/\varphi }}\left(\right],\hfill \\ \left[\right)e^{-{\left({\left(-ln\left({\eta }_1^{\left(m\right)-}\right)\right)}^{\varphi }+{\left(-ln\left({\eta }_2^{\left(m\right)-}\right)\right)}^{\varphi }\right)}^{1/\varphi }},\hfill \\ e^{-{\left({\left(-ln\left({\eta }_1^{\left(m\right)+}\right)\right)}^{\varphi }+{\left(-ln\left({\eta }_2^{\left(m\right)+}\right)\right)}^{\varphi }\right)}^{1/\varphi }}\left(\right],\hfill \\ \left[\right)e^{-{\left({\left(-ln\left({\eta }_1^{\left(u\right)-}\right)\right)}^{\varphi }+{\left(-ln\left({\eta }_2^{\left(u\right)-}\right)\right)}^{\varphi }\right)}^{1/\varphi }},\hfill \\ e^{-{\left({\left(-ln\left({\eta }_1^{\left(u\right)+}\right)\right)}^{\varphi }+{\left(-ln\left({\eta }_2^{\left(u\right)+}\right)\right)}^{\varphi }\right)}^{1/\varphi }}\left(\right]\hfill \end{array}\right)$$ (8)

(3) Scalar multiplication, where $\tau >0$.

$$\tau {\overline{\eta }}_1=\left(\begin{array}{c}\left[1-e^{-{\left(\tau {\left(-ln\left(1-{\eta }_1^{\left(l\right)-}\right)\right)}^{\varphi }\right)}^{1/\varphi }},1-e^{-{\left(\tau {\left(-ln\left(1-{\eta }_1^{\left(l\right)+}\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right],\hfill \\ \left[1-e^{-{\left(\tau {\left(-ln\left(1-{\eta }_1^{\left(m\right)-}\right)\right)}^{\varphi }\right)}^{1/\varphi }},1-e^{-{\left(\tau {\left(-ln\left(1-{\eta }_1^{\left(m\right)+}\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right]\hfill \\ \left[1-e^{-{\left(\tau {\left(-ln\left(1-{\eta }_1^{\left(u\right)-}\right)\right)}^{\varphi \varphi }\right)}^{1/\varphi }},1-e^{-{\left(\tau {\left(-ln\left(1-{\eta }_1^{\left(u\right)+}\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right]\hfill \end{array}\right)$$ (9)

(4) Power, where $\tau >0$

$${\overline{\eta }}_1^{\tau }=\left(\begin{array}{c}\left[e^{-{\left(\tau {\left(-ln\left({\eta }_1^{\left(l\right)-}\right)\right)}^{\varphi }\right)}^{1/\varphi }},e^{-{\left(\tau {\left(-ln\left({\eta }_1^{\left(l\right)+}\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right],\hfill \\ \left[e^{-{\left(\tau {\left(-ln\left({\eta }_1^{\left(m\right)-}\right)\right)}^{\varphi }\right)}^{1/\varphi }},e^{-{\left(\tau {\left(-ln\left({\eta }_1^{\left(m\right)+}\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right]\hfill \\ \left[e^{-{\left(\tau {\left(-ln\left({\eta }_1^{\left(u\right)-}\right)\right)}^{\varphi }\right)}^{1/\varphi }},e^{-{\left(\tau {\left(-ln\left({\eta }_1^{\left(u\right)+}\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right]\hfill \end{array}\right)$$ (10)

where $\varphi >0$ presents the real number, and e presents Euler’s number.

Based on Definition 2 we can report the following relations between any two rough numbers ${\overline{\eta }}_1=\left(\left[{\eta }_1^{\left(l\right)-},{\eta }_1^{\left(l\right)+}\right],\left[{\eta }_1^{\left(m\right)-},{\eta }_1^{\left(m\right)+}\right],\left[{\eta }_1^{\left(u\right)-},{\eta }_1^{\left(u\right)+}\right]\right)$ and ${\overline{\eta }}_2=\left(\left[{\eta }_2^{\left(l\right)-},{\eta }_2^{\left(l\right)+}\right],\left[{\eta }_2^{\left(m\right)-},{\eta }_2^{\left(m\right)+}\right],\left[{\eta }_2^{\left(u\right)-},{\eta }_2^{\left(u\right)+}\right]\right)$:

(1) ${\overline{\eta }}_1\oplus {\overline{\eta }}_2={\overline{\eta }}_2\oplus {\overline{\eta }}_1$;

(2) ${\overline{\eta }}_1\otimes {\overline{\eta }}_2={\overline{\eta }}_2\otimes {\overline{\eta }}_1$;

(3) $\tau \left({\overline{\eta }}_1\oplus {\overline{\eta }}_2\right)=\tau {\overline{\eta }}_1\oplus \tau {\overline{\eta }}_2$;

(4) $\left({\tau }_1+{\tau }_2\right){\overline{\eta }}_1={\tau }_1{\overline{\eta }}_1\oplus {\tau }_2{\overline{\eta }}_1$;

(5) ${\left({\overline{\eta }}_1\otimes {\overline{\eta }}_2\right)}^{\tau }={\overline{\eta }}_1^{\tau }\otimes {\overline{\eta }}_2^{\tau }$;

(6) ${\overline{\eta }}_1^{{\tau }_1}\otimes {\overline{\eta }}_1^{{\tau }_2}={\overline{\eta }}_1^{\left({\tau }_1+{\tau }_2\right)}$. where $\tau ,{\tau }_1,{\tau }_2>0$.

3. A hybrid MCDM model based on interval Fuzzy rough numbers

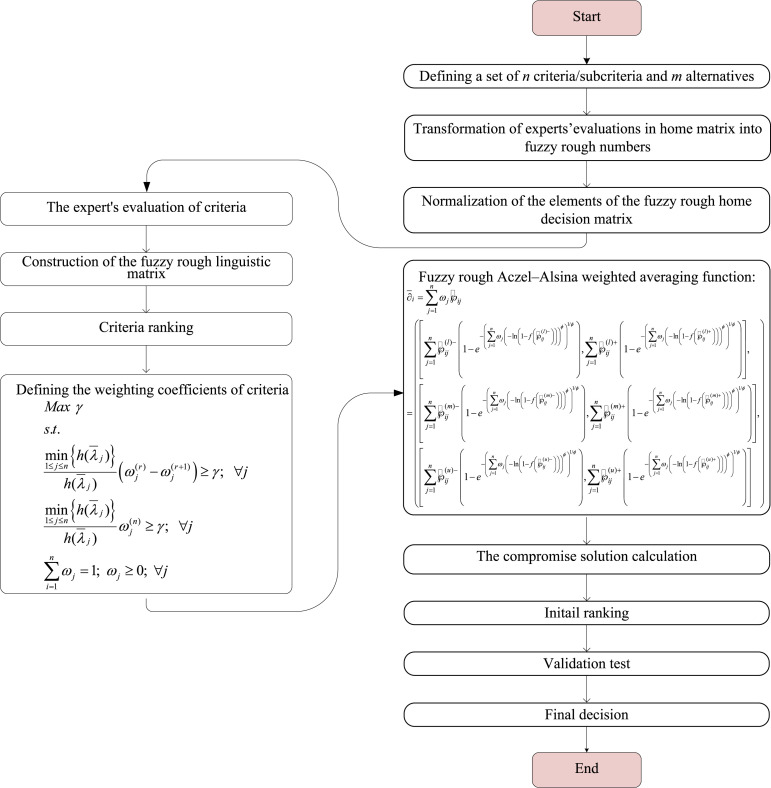
The following section presents a multi-criteria framework (see Fig. 1) based on information processing using fuzzy rough numbers. The Ordinal Priority Approach (OPA) Ataei et al., (2020) method, based on fuzzy rough numbers, was used to define the criterion weight coefficients. Measurement of Alternatives and Ranking according to the COmpromise Solution (MARCOS) method (Stevic et al., 2020) in a fuzzy rough environment was used to evaluate alternatives. The traditional MARCOS method has been improved by using fuzzy rough numbers and Aczel–Alsina norms. Aczel–Alsina norms were used to determine the weighted segments in the MARCOS method, while fuzzy rough numbers were used to process incomplete and inaccurate information in the home matrix. The application of the fuzzy rough Aczel–Alsina function in the MARCOS method enables nonlinear processing of subjectivity. Also, Aczel–Alsina functions improve the flexibility of the MARCOS method, which enables the adaptation of the methodological framework to the dynamic environment.

Fig. 1.

Fuzzy rough Aczel–Alsina OPA-MARCOS methodology.

In the following section, the fuzzy rough OPA methodology for defining criterion weight coefficients and the fuzzy rough Aczel–Alsina MARCOS model for evaluating alternatives are presented.

3.1. Fuzzy rough ordinal priority approach method

The Fuzzy rough OPA algorithm is implemented through the steps presented in the following section:

Step 1: Defining and ranking criteria. Suppose that p experts participate in the research which is marked with a set $E_e$ $\left(e=1,2,\dots ,p\right)$. Also, suppose that the experts defined the final set of n criteria $C_j$ $\left(j=1,2,\dots ,n\right)$. After defining the final set of criteria/ sub-criteria, it is defined fuzzy linguistic matrix ${\Omega }^{\alpha }={\left[{\lambda }_j^{\alpha }\right]}_{n\times 1}$ ($1\le \alpha \le p$) in which the experts represent the relative importance of the criteria/ sub-criteria:

$${\Omega }^{\alpha }=\begin{array}{c}{C}_1\hfill \\ C_2\hfill \\ C_3\hfill \\ \dots \hfill \\ C_n\hfill \end{array}\left[\begin{array}{c}{\lambda }_1^{\alpha }\hfill \\ {\lambda }_2^{\alpha }\hfill \\ {\lambda }_3^{\alpha }\hfill \\ \dots \hfill \\ {\lambda }_n^{\alpha }\hfill \end{array}\right]$$ (11)

where ${\lambda }_j^{\alpha }=\left({\lambda }_j^{\left(l\right)\alpha },{\lambda }_j^{\left(m\right)\alpha },{\lambda }_j^{\left(u\right)\alpha }\right)$ represents the relative importance of criterion j which is defined by the expert $\alpha$ ($1\le \alpha \le p$) and ${\Omega }^{\alpha }$ presents a fuzzy linguistic matrix.

Relative importance is determined using a predefined fuzzy linguistic scale. By applying Eqs. (1)–(4) the expert estimates from the matrix (11) are transformed into fuzzy rough values. Thus, we obtain p expert fuzzy rough linguistic matrices ${\overline{\Omega }}^{\alpha }={\left[{\overline{\lambda }}_j^{\alpha }\right]}_{n\times 1}$ ($1\le \alpha \le p$). Using the Bonferroni operator (12), a fuzzy rough estimation fusion was performed, and an aggregated fuzzy rough linguistic matrix was generated. $\overline{\Omega }={\left[{\overline{\lambda }}_j\right]}_{n\times 1}$.

$${\overline{\lambda }}_{ij}={\left(\frac{1}{p(p-1)}\sum _{\begin{array}{c}{y}_1,y_2=1\hfill \\ y_1\ne y_2\hfill \end{array}}^p{\overline{\lambda }}_{j\left(y_1\right)}^{k_1}\otimes {\overline{\lambda }}_{j\left(y_2\right)}^{k_2}\right)}^{\frac{1}{k_1+k_2}}$$ (12)

where p represents the total number of experts participating in the research, $y_1,y_2>0$ and $1\le \alpha \le p$.

Step 2: Ranking the criteria within the defined set of criteria/ sub-criteria. In this step, the rank of the criteria is defined $C_j$ $\left(j=1,2,\dots ,n\right)$. Based on values from the fuzzy rough linguistic matrix $\overline{\Omega }={\left[{\overline{\lambda }}_j\right]}_{n\times 1}$ score functions are defined $h\left({\overline{\lambda }}_j\right)=\left({\lambda }_2^{\left(l\right)-}+{\lambda }_2^{\left(l\right)+}+2{\lambda }_2^{\left(m\right)-}+2{\lambda }_2^{\left(m\right)+}+\right)\left({\lambda }_2^{\left(u\right)-}+{\lambda }_2^{\left(u\right)+}\right)/8$ provided that it is ${\overline{\lambda }}_j>{\overline{\lambda }}_{j+1}$ if $h\left({\overline{\lambda }}_j\right)>h\left({\overline{\lambda }}_{j+1}\right)$. Based on the value of the score function criterion ($h\left({\overline{\lambda }}_j\right)$) the criteria are ranked according to their significance.

The weighting coefficients of successive criteria by rank should satisfy the condition from Eq. (13).

$$\begin{array}{c}{\omega }_j^{\left(1\right)}-{\omega }_j^{\left(2\right)}\ge 0;\hfill \\ {\omega }_j^{\left(2\right)}-{\omega }_j^{\left(3\right)}\ge 0;\hfill \\ \dots \hfill \\ {\omega }_j^{\left(r\right)}-{\omega }_j^{(r+1)}\ge 0;\hfill \\ \dots \hfill \\ {\omega }_j^{(n-1)}-{\omega }_j^{\left(n\right)}\ge 0.\hfill \end{array}$$ (13)

where ${\omega }_j^{\left(r\right)}$ represents the significance of the $j$th attribute at the r-$\mathrm{th}$ rank. that is, Eq. (13) can be abbreviated as follows:

$$h\left({\overline{\lambda }}_j\right)\left({\omega }_j^{\left(r\right)}-{\omega }_j^{(r+1)}\right)\ge 0;\forall j$$ (14)

where ${\omega }_j^{\left(r\right)}$ represents the significance of the $j$th attribute at the r-$\mathrm{th}$ rank.

Step 3: Create a model for calculating the weighting factors. The weighting coefficients of the criteria are defined by applying a linear mathematical model as follows:

$$\begin{array}{c}Max\gamma \hfill \\ s.t.\hfill \\ \frac{\underset{1\le j\le n}{min}\left\{h\left({\overline{\lambda }}_j\right)\right\}}{h\left({\overline{\lambda }}_j\right)}\left({\omega }_j^{\left(r\right)}-{\omega }_j^{(r+1)}\right)\ge \gamma ;\forall j\hfill \\ \frac{\underset{1\le j\le n}{min}\left\{h\left({\overline{\lambda }}_j\right)\right\}}{h\left({\overline{\lambda }}_j\right)}{\omega }_j^{\left(n\right)}\ge \gamma ;\forall j\hfill \\ \sum _{i=1}^n{\omega }_j=1;{\omega }_j\ge 0;\forall j\hfill \end{array}$$ (15)

where ${\omega }_j$ represents the weighting factor of the $j$th attribute while $h\left({\overline{\lambda }}_j\right)$ represents the score function of the j criteria.

3.2. Fuzzy rough Aczel–Alsina MARCOS methodology

The following section presents the fuzz rough Aczel–Alsina MARCOS methodology.

Step 1: Suppose it is necessary to evaluate m alternatives against n criteria. Then we can present the information within the multicriteria model using the initial home matrix ${\Psi }^{\alpha }={\left[{\tilde{\wp }}_{ij}^{\alpha }\right]}_{m\times n}$,($1\le \alpha \le p$), where p represents the total number of experts. Elements of the initial home matrix ${\tilde{\wp }}_{ij}^{\alpha }=\left({\wp }_{ij}^{\left(l\right)\alpha },{\wp }_{ij}^{\left(m\right)\alpha },{\wp }_{ij}^{\left(u\right)\alpha }\right)$ are defined based on a predefined fuzzy linguistic scale. By applying Eqs. (1)–(4), matrix elements ${\Psi }^{\alpha }={\left[{\tilde{\wp }}_{ij}^{\alpha }\right]}_{m\times n}$ ($1\le \alpha \le p$) are transformed into fuzzy rough sequences ${\overline{\wp }}_{ij}^{\alpha }=\left(\left[{\wp }_{ij}^{\alpha \left(l\right)-},{\wp }_{ij}^{\alpha \left(l\right)+}\right],\left[{\wp }_{ij}^{\alpha \left(m\right)-},{\wp }_{ij}^{\alpha \left(m\right)+}\right],\left[{\wp }_{ij}^{\alpha \left(u\right)-},{\wp }_{ij}^{\alpha \left(u\right)+}\right]\right)$. The fuzzy rough matrices are further aggregated into the final fuzzy rough home matrix $\overline{\Psi }={\left[{\overline{\wp }}_{ij}\right]}_{m\times n}$.

Step 2: Using Eq. (16), it is defined the ideal alternative (${\mathbb{N}}^{+}$) and anti-ideal alternative (${\mathbb{N}}^{-}$) in the final fuzzy rough home matrix $\overline{\Psi }={\left[{\overline{\wp }}_{ij}\right]}_{m\times n}$.

$$\begin{array}{c}{\mathbb{N}}^{+}=\underset{1\le i\le m}{max}\left({\overline{\wp }}_{ij}\right)ifj\in Band\underset{1\le i\le m}{min}\left({\overline{\wp }}_{ij}\right)ifj\in C\hfill \\ {\mathbb{N}}^{-}=\underset{1\le i\le m}{min}\left({\overline{\wp }}_{ij}\right)ifj\in Band\underset{1\le i\le m}{max}\left({\overline{\wp }}_{ij}\right)ifj\in C\hfill \end{array}$$ (16)

where ${\overline{\wp }}_{ij}$ presents elements of the fuzzy rough home matrix $\overline{\Psi }$, $j=1$,2,…, n presents a number of criteria, while B and C represent a benefit and cost group of criteria, respectively.

Step 3: By applying Eq. (17) elements, the standardization of matrix elements was performed $\overline{\Psi }={\left[{\overline{\wp }}_{ij}\right]}_{m\times n}$.

$${\hat{\wp }}_{ij}=\left\{\begin{array}{c}{\hat{\wp }}_{ij}=\left(\left[\frac{{\wp }_{ij}^{\left(l\right)-}}{{\wp }^{+}},\frac{{\wp }_{ij}^{\left(l\right)+}}{{\wp }^{+}}\right],\left[\frac{{\wp }_{ij}^{\left(m\right)-}}{{\wp }^{+}},\frac{{\wp }_{ij}^{\left(m\right)+}}{{\wp }^{+}}\right],\left[\frac{{\wp }_{ij}^{\left(u\right)-}}{{\wp }^{+}},\frac{{\wp }_{ij}^{\left(u\right)+}}{{\wp }^{+}}\right]\right);ifj\in \mathrm{B}\hfill \\ {\hat{\wp }}_{ij}=\left(\begin{array}{c}\left[\begin{array}{c}-\frac{{\wp }_{ij}^{\left(l\right)-}}{{\wp }^{+}}+\underset{1\le i\le m}{max}\left\{\frac{{\wp }_{ij}^{\left(l\right)-}}{{\wp }^{+}}\right\}+\underset{1\le i\le m}{min}\left\{\frac{{\wp }_{ij}^{\left(l\right)-}}{{\wp }^{+}}\right\},\hfill \\ -\frac{{\wp }_{ij}^{\left(l\right)+}}{{\wp }^{+}}+\underset{1\le i\le m}{max}\left\{\frac{{\wp }_{ij}^{\left(l\right)+}}{{\wp }^{+}}\right\}+\underset{1\le i\le m}{min}\left\{\frac{{\wp }_{ij}^{\left(l\right)+}}{{\wp }^{+}}\right\}\hfill \end{array}\right],\hfill \\ \left[\begin{array}{c}-\frac{{\wp }_{ij}^{\left(m\right)-}}{{\wp }^{+}}+\underset{1\le i\le m}{max}\left\{\frac{{\wp }_{ij}^{\left(m\right)-}}{{\wp }^{+}}\right\}+\underset{1\le i\le m}{min}\left\{\frac{{\wp }_{ij}^{\left(m\right)-}}{{\wp }^{+}}\right\},\hfill \\ -\frac{{\wp }_{ij}^{\left(m\right)+}}{{\wp }^{+}}+\underset{1\le i\le m}{max}\left\{\frac{{\wp }_{ij}^{\left(m\right)+}}{{\wp }^{+}}\right\}+\underset{1\le i\le m}{min}\left\{\frac{{\wp }_{ij}^{\left(m\right)+}}{{\wp }^{+}}\right\}\hfill \end{array}\right],\hfill \\ \left[\begin{array}{c}-\frac{{\wp }_{ij}^{\left(u\right)-}}{{\wp }^{+}}+\underset{1\le i\le m}{max}\left\{\frac{{\wp }_{ij}^{\left(u\right)-}}{{\wp }^{+}}\right\}+\underset{1\le i\le m}{min}\left\{\frac{{\wp }_{ij}^{\left(u\right)-}}{{\wp }^{+}}\right\},\hfill \\ -\frac{{\wp }_{ij}^{\left(u\right)+}}{{\wp }^{+}}+\underset{1\le i\le m}{max}\left\{\frac{{\wp }_{ij}^{\left(u\right)+}}{{\wp }^{+}}\right\}+\underset{1\le i\le m}{min}\left\{\frac{{\wp }_{ij}^{\left(u\right)+}}{{\wp }^{+}}\right\}\hfill \end{array}\right]\hfill \end{array}\right);ifj\in \mathrm{C}\hfill \end{array}\right)$$ (17)

where ${\wp }_j^{+}={max}_{1\le i\le m}\left({\overline{\wp }}_{ij}\right)$ and ${\wp }_j^{-}={min}_{1\le i\le m}\left({\overline{\wp }}_{ij}\right)$, $i=1$,2,…, m presents the number of alternatives, and B and C represent a benefit and cost set of criteria, respectively.

Step 4: Calculate the degree of usefulness of alternatives in relation to ${\mathbb{N}}^{+}$ and ${\mathbb{N}}^{-}$. Degrees of utility are defined by applying Eqs. (18), (19):

$${{\aleph }_i}^{-}=\frac{{\overline{\partial }}_i}{{\overline{\partial }}_i^{-}}$$ (18)

$${{\aleph }_i}^{+}=\frac{{\overline{\partial }}_i}{{\overline{\partial }}_i^{+}}$$ (19)

where ${\overline{\partial }}_i$, ${\overline{\partial }}_i^{-}$ and ${\overline{\partial }}_i^{+}$ ($i=1$,2,.., m) represents the weighted sequence defined using the Aczel–Alsina function (20).

Theorem 1

Let it be $\left({\hat{\wp }}_{i1},{\hat{\wp }}_{i2},\dots ,{\hat{\wp }}_{in}\right)$ a set of elements of a normalized home matrix, also, let it be $\varphi >0$ and let it be ${\omega }_j={\left({\omega }_1,{\omega }_2,\dots ,{\omega }_n\right)}^T$ vector of weighting coefficients. Then fuzzy rough weighted Aczel–Alsina function ( ${\overline{\partial }}_i$ ) can be presented as follows:

$${\overline{\partial }}_i=\left(\begin{array}{c}\left[\right)\sum _{j=1}^n{\hat{\wp }}_{ij}^{\left(l\right)-}\left(1-e^{-{\left(\sum _{j=1}^n{\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(l\right)-}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right),\hfill \\ \sum _{j=1}^n{\hat{\wp }}_{ij}^{\left(l\right)+}\left(1-e^{-{\left(\sum _{j=1}^n{\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(l\right)+}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right)\left(\right],\hfill \\ \left[\right)\sum _{j=1}^n{\hat{\wp }}_{ij}^{\left(m\right)-}\left(1-e^{-{\left(\sum _{j=1}^n{\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(m\right)-}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right),\hfill \\ \sum _{j=1}^n{\hat{\wp }}_{ij}^{\widehat{\left(m\right)+}}\left(1-e^{-{\left(\sum _{j=1}^n{\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\widehat{\left(m\right)+}}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right)\left(\right],\hfill \\ \left[\right)\sum _{j=1}^n{\hat{\wp }}_{ij}^{\widehat{\left(u\right)-}}\left(1-e^{-{\left(\sum _{j=1}^n{\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\widehat{\left(u\right)-}}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right),\hfill \\ \sum _{j=1}^n{\hat{\wp }}_{ij}^{\widehat{\left(u\right)+}}\left(1-e^{-{\left(\sum _{j=1}^n{\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\widehat{\left(u\right)+}}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right)\left(\right]\hfill \end{array}\right)$$ (20)

where $\varphi >0$ represents the stabilization parameter of the Aczel–Alsina function, ${\omega }_j$ represents the significance of the $j$ th attribute, while $f\left({\hat{\wp }}_j\right)={\hat{\wp }}_j/{\sum }_{j=1}^n{\hat{\wp }}_j$ . The proof for Theorem 1 is presented in Appendix .

Step 5: The compromise solution is defined by applying the fuzzy rough utility function $f\left({\Lambda }_i\right)$, Eq. (21)

$$f\left({\Lambda }_i\right)=\frac{{{\aleph }_i}^{+}+{{\aleph }_i}^{-}}{1+\frac{1-f\left({\aleph }_i^{+}\right)}{f\left({\aleph }_i^{+}\right)}+\frac{1-f\left({\aleph }_i^{-}\right)}{f\left({\aleph }_i^{-}\right)}};$$ (21)

where $f\left({\aleph }_i^{-}\right)={\aleph }_i^{+}/\left({\aleph }_i^{+}+{\aleph }_i^{-}\right)$ represents a fuzzy rough utility function compared to ${\mathbb{N}}^{-}$, $f\left({\aleph }_i^{+}\right)={\aleph }_i^{-}/\left({\aleph }_i^{+}+{\aleph }_i^{-}\right)$ represents a function of utility in relation to ${\mathbb{N}}^{+}$, while ${{\aleph }_i}^{+}$ and ${{\aleph }_i}^{-}$ are defined using Eqs. (18), (19).

The ranking of alternatives is done based on values $f\left({\Lambda }_i\right)$, whereby the alternative should have as much value as possible $f\left({\Lambda }_i\right)$.

4. Case study

The Brčko District is a separate administrative unit in Bosnia and Herzegovina. Two entities in Bosnia and Herzegovina have no jurisdiction in the Brčko District. In the administrative-legal sense, it is common ownership (condominium) of both entities with direct jurisdiction of state authorities of Bosnia and Herzegovina. The Brčko District has one medical center, six polyclinics, 5 laboratories, and over 50 pharmacies and private medical clinics. During the COVID-19 pandemic, the amount of HCW greatly increased (Ilyas et al., 2020). This has been the case also for the Brčko District. The question that arises is whether these medical facilities have prescribed procedures for HCW management and where this waste is disposed of? Often we can see that HCW is not adequately managed. It is a regular practice that this waste is mixed with municipal waste which leads to environmental pollution that increases the risk to humans and animals. To solve this problem, it is necessary to evaluate the treatment methods for HCW management. This study was conducted together with the Government of the Brčko District.

The expert group was formed in cooperation with the Government of the Brčko District and their Public Health Institute. Members of the expert group were appointed from different Departments of the Brčko District Government of their experience in HCW management. A total of five experts were appointed: two experts from the Department of Health, two experts from the Public Health Institute, and one expert from the Department of Public Safety. These experts determined the criteria and sub-criteria to be used for the evaluation of alternatives as well as the determination of alternatives. They refused six different HCW management treatments (see Table 3) that would achieve the best results in the Brčko District.

Table 3.

Fuzzy linguistic evaluation scale.

Linguistic terms	Membership function
Absolutely low (AL)	(1,1,1)
Very low (VL)	(1,2,3)
Low (L)	(2,3,4)
Medium–low (ML)	(3,4,5)
Equal (E)	(4,5,6)
Medium–high (MH)	(5,6,7)
High (H)	(6,7,8)
Extremely high (EH)	(7,8,9)
Absolutely high (AH)	(8,9,10)
Perfect (P)	(9,10,10)

To select the alternative that would best solve the problem of HCW management in the Brčko District, the criteria for the evaluation of these alternatives were formed (see Table 4). All of these criteria are divided into four main criteria, and each of these criteria is divided into sub-criteria. The main criteria are Economic, Ecological, Technical, and Social. These criteria were formed based on a review of previous studies in the field of HCW (see Table 1). The main criteria are extended sustainability criteria with a technical criterion. In this way, the selection of HCW management treatment was made considering the strict requirements imposed on HCW management. Each of the main criteria was divided into three sub-criteria to give all these criteria the same importance.

Table 4.

Expert assessment of the significance of the criteria/ sub-criteria.

Crit.	Expert 1	Expert 2	Expert 3	Expert 4	Expert 5
MC1	E	MH	H	MH	MH
C${}_1$	MH	H	H	MH	E
C${}_2$	H	MH	H	MH	MH
C${}_3$	E	MH	H	MH	MH
MC2	H	H	H	H	MH
C${}_4$	H	H	H	H	H
C${}_5$	MH	MH	E	MH	E
C${}_6$	H	H	H	H	MH
MC3	MH	MH	E	H	E
C${}_7$	H	H	H	H	MH
C${}_8$	E	MH	E	E	ML
C${}_9$	E	H	E	E	E
MC4	MH	MH	MH	MH	E
C${}_{10}$	E	H	MH	H	MH
C${}_{11}$	H	H	H	MH	MH
C${}_{12}$	H	H	H	H	H

Table 1.

HCW Treatments.

Id	Alternative	Definition
A1	Chemical disinfection	Treatment with chemical disinfection is performed by deactivating degradable chemicals caused by the work of medical institutions. Chemical treatment is also performed in this treatment.
A2	Deep burial	Method of HCW treatment by burying waste. Deep burial reduces water contamination, as well as air pollution
A3	Incineration	Controlled incineration at high temperatures (above 1000 °C) is a technology that can dispose of all types of HCW with a significant reduction in the volume and weight of incoming waste.
A4	Autoclave	The autoclave combines the action of high temperature, elevated pressure, and humidity to deactivate microorganisms. This is usually done by heating the water to temperatures around 135 °C
A5	Landfill disposal	Disposal of HCW in landfills is done as if it were a municipal waste. Waste is placed in appropriate bags and disposed of i.e. municipal waste.
A6	Microwave	The process of disposal in a microwave oven is similar to the autoclave treatment, in which microorganisms are decontaminated with heat. Microwaves are used here for heating, instead of water and water vapor. The temperature in this treatment is between 95 and 110 °C.

After the alternatives and criteria for evaluating these alternatives were formed, the experts evaluated these criteria. During the assessment of the Benefit criteria, the experts evaluated the benefits of these alternatives for the criterion. In assessing the Cost criterion, the experts assessed the damage that a particular alternative to that criterion has. If the criterion has more benefits and less damage, it will receive a lower score in the cost criterion. For benefit criteria, the greater the benefit and less damage to a particular alternative to a given criterion, the higher the value of that alternative. The rating given by the experts ranged from Very low (VL) to Very High (VH). In addition, the experts assessed the weight of the criteria themselves, because it is necessary to know the importance of this criterion to rank the alternatives.

This study attempted to answer the questions of which treatment gives the best results for the management of HCW in the example of the Brčko District of Bosnia and Herzegovina. That answer will assist the Government of the Brčko District of Bosnia and Herzegovina to decide which equipment to purchase for which treatment. The acquisition of this equipment will reduce the impact of HCW on the environment and human health, as the waste will be treated adequately.

5. Research findings

5.1. Determining criteria weights: Fuzzy rough OPA method

The following section presents the application of the fuzzy rough OPA methodology for determining the weighting coefficients of the criteria:

Step 1: Five experts, who evaluated the criteria/sub-criteria, participated in the research (see Table 2). The experts evaluated the criteria and sub-criteria using the fuzzy scale given in Table 3. The same fuzzy linguistic scale (Table 3) was used to evaluate the criterion and alternative, which has 10 levels and ranges from Absolutely low (AL) to Perfect (P). When evaluating criteria and alternatives, the experts chose one of these values that, in their opinion, best evaluates that criterion or alternatives.

Table 2.

Definition of sub-criteria.

Id	Criteria	Definition	Type
C1	The price of the treatment	It represents the monetary value of carrying out a particular treatment	Cost
C2	Operating and maintenance costs	It represents the value of the costs of implementing and maintaining an individual treatment	Cost
C3	Waste disposal costs	It represents the value of costs related to the disposal of waste treated with a particular treatment	Cost
C4	Environmental impact	It implies how a particular treatment affects the environment and how waste treated with that treatment affects the environment	Cost
C5	Energy consumption	It represents the amount of energy expended in carrying out the treatment and disposing of the waste with that treatment	Cost
C6	Environmental acceptability	It implies how much of which treatment is accepted for the environment during the treatment and when disposing of the treated waste	Benefit
C7	Efficacy of treatment	It represents the extent to which a particular treatment is good for HCW management	Benefit
C8	Level of automation	It represents the level to which a particular treatment is automated	Benefit
C9	Treatment capacities	It represents the capacity of individual treatments	Benefit
C10	Public acceptance	It implies how the public accepts certain treatments and waste treated with that treatment	Benefit
C11	Safety of treatment	It represents the level of safety of individual treatments and disposal of treated waste	Benefit
C12	Health and safety risks	It implies the impact on the health of the workers who manage the tools and the risk of disposing of the treated waste	Cost

Expert assess ments of the significance of the criteria are presented in the fuzzy linguistic matrix given in Table 4.

Using Eqs. (1)–(4), the expert estimates from Table 6 were transformed into fuzzy rough values. For example, based on expert assessments of the significance of criterion $C_2$ (see Table 1), fuzzy values were obtained: ${\lambda }_2^1={\lambda }_2^3=\left(6,7,8\right)$ and ${\lambda }_2^2={\lambda }_2^4={\lambda }_2^5=\left(5,6,7\right)$. Based on the displayed fuzzy values, we can form three sequences ${\lambda }_2^{\left(l\right)}=\left\{6,5,6,5,5\right\}$, ${\lambda }_2^{\left(m\right)}=\left\{7,6,7,6,6\right\}$ and ${\lambda }_2^{\left(u\right)}=\left\{8,7,8,7,7\right\}$. By applying Eqs. (1)–(4) and provided that it is ${\mathit{d}}_1$ = d ₂ =1, we can define the lower and upper limits of defined sequences according to the following:

Table 6.

Expert assessments of alternatives.

Criteria	A${}_1$	A${}_2$	A${}_3$
C${}_1$	L, VL, VL, L, ML	VL, VL, VL, VL, ML	ML, L, ML, ML, E
C${}_2$	VL, VL, AL, VL, VL	L, VL, L, L, VL	L, ML, L, ML, E
C${}_3$	VL, L, L, ML, ML	VL, L, L, L, L	VL, VL, VL, VL, ML
C${}_4$	E, ML, MH, ML, ML	ML, ML, MH, E, ML	VL, AL, VL, VL, VL
C${}_5$	ML, L, L, ML, E	VL, AL, VL, VL, VL	L, L, VL, ML, ML
C${}_6$	E, ML, L, ML, ML	ML, ML, VL, ML, VL	MH, H, H, MH, E
C${}_7$	E, H, H, H, MH	ML, L, L, L, ML	MH, H, H, H, E
C${}_8$	E, MH, MH, MH, E	ML, E, L, E, E	MH, MH, H, MH, MH
C${}_9$	E, H, H, E, E	E, E, H, E, MH	ML, MH, ML, E, E
C${}_{10}$	E, E, ML, L, ML	ML, VL, L, VL, VL	MH, MH, H, MH, MH
C${}_{11}$	E, MH, H, E, E	ML, MH, ML, ML, MH	MH, MH, H, MH, MH
C${}_{12}$	ML, E, MH, ML, ML	ML, MH, ML, ML, E	ML, ML, L, L, VL
Criteria	A${}_4$	A${}_5$	A${}_6$
C${}_1$	ML, L, E, ML, E	E, H, E, E, E	AL, VL, VL, VL, VL
C${}_2$	VL, VL, VL, L, ML	ML, E, E, ML, MH	VL, VL, VL, VL, AL
C${}_3$	VL, VL, VL, VL, ML	VL, ML, L, L, ML	VL, L, L, VL, VL
C${}_4$	AL, VL, VL, VL, VL	L, ML, VL, L, L	MH, H, H, H, E
C${}_5$	ML, L, VL, L, L	L, L, VL, ML, ML	AL, AL, AL, AL, AL
C${}_6$	H, H, H, MH, E	MH, E, ML, ML, ML	L, VL, L, VL, VL
C${}_7$	H, H, H, E, E	MH, E, H, E, MH	L, L, ML, VL, L
C${}_8$	H, MH, H, MH, E	MH, E, H, MH, E	E, ML, E, ML, MH
C${}_9$	ML, MH, ML, E, ML	ML, L, E, E, ML	MH, H, MH, MH, H
C${}_{10}$	MH, MH, H, MH, MH	MH, MH, E, E, ML	VL, VL, VL, VL, AL
C${}_{11}$	H, MH, H, E, MH	MH, E, H, E, E	VL, AL, VL, VL, VL
C${}_{12}$	ML, E, ML, L, L	ML, ML, VL, L, ML	H, H, H, MH, H

(a) Lower limits:

$$\underset{\_}{Lim}\left({\lambda }_2^{\left(l\right)2}\right)=\underset{\_}{Lim}\left({\lambda }_2^{\left(l\right)4}\right)=\underset{\_}{Lim}\left({\lambda }_2^{\left(l\right)5}\right)=5.0;$$

$$\underset{\_}{Lim}\left({\lambda }_2^{\left(l\right)1}\right)=\underset{\_}{Lim}\left({\lambda }_2^{\left(l\right)3}\right)=\left(\right)\frac{1}{5}\left\{\right)6\cdot {\left(5\cdot 6\cdot 5\cdot 5\right)}^{1/4}+5\cdot {\left(6\cdot 6\cdot 5\cdot 5\right)}^{1/4}+\cdots +5\cdot {\left(6\cdot 5\cdot 6\cdot 5\right)}^{1/4}\left(\right\}{\left(\right)}^{\frac{1}{1+1}}=5.41;$$

;

$$\underset{\_}{Lim}\left({\lambda }_2^{\left(m\right)2}\right)=\underset{\_}{Lim}\left({\lambda }_2^{\left(m\right)4}\right)=\underset{\_}{Lim}\left({\lambda }_2^{\left(m\right)5}\right)=6.0;$$

$$\underset{\_}{Lim}\left({\lambda }_2^{\left(m\right)1}\right)=\underset{\_}{Lim}\left({\lambda }_2^{\left(m\right)3}\right)=\left(\right)\frac{1}{5}\left\{\right)7\cdot {\left(6\cdot 7\cdot 6\cdot 6\right)}^{1/4}+6\cdot {\left(7\cdot 7\cdot 6\cdot 6\right)}^{1/4}+\cdots +6\cdot {\left(7\cdot 6\cdot 7\cdot 6\right)}^{1/4}\left(\right\}{\left(\right)}^{\frac{1}{1+1}}=6.41;$$

$$\underset{\_}{Lim}\left({\lambda }_2^{\left(u\right)2}\right)=\underset{\_}{Lim}\left({\lambda }_2^{\left(u\right)4}\right)=\underset{\_}{Lim}\left({\lambda }_2^{\left(u\right)5}\right)=7.0;$$

$$\underset{\_}{Lim}\left({\lambda }_2^{\left(u\right)1}\right)=\underset{\_}{Lim}\left({\lambda }_2^{\left(u\right)3}\right)=\left(\right)\frac{1}{5}\left\{\right)8{\left(7\cdot 8\cdot 7\cdot 7\right)}^{1/4}+7\cdot {\left(8\cdot 8\cdot 7\cdot 7\right)}^{1/4}+\cdots +7\cdot {\left(8\cdot 7\cdot 8\cdot 7\right)}^{1/4}\left(\right\}{\left(\right)}^{\frac{1}{1+1}}=7.41$$

(b) Upper limits:

$$\overline{Lim}\left({\lambda }_2^{\left(l\right)2}\right)=\overline{Lim}\left({\lambda }_2^{\left(l\right)4}\right)=\overline{Lim}\left({\lambda }_2^{\left(l\right)5}\right)=\left(\right)\frac{1}{5}\left\{\right)6\cdot {\left(5\cdot 6\cdot 5\cdot 5\right)}^{1/4}+5\cdot {\left(6\cdot 6\cdot 5\cdot 5\right)}^{1/4}+\cdots +5\cdot {\left(6\cdot 5\cdot 6\cdot 5\right)}^{1/4}\left(\right\}{\left(\right)}^{\frac{1}{1+1}}=5.41$$

$$\overline{Lim}\left({\lambda }_2^{\left(l\right)1}\right)=\overline{Lim}\left({\lambda }_2^{\left(l\right)3}\right)=6.0;$$

$$\overline{Lim}\left({\lambda }_2^{\left(m\right)2}\right)=\overline{Lim}\left({\lambda }_2^{\left(m\right)4}\right)=\overline{Lim}\left({\lambda }_2^{\left(m\right)5}\right)=\left(\right)\frac{1}{5}\left\{\right)7\cdot {\left(6\cdot 7\cdot 6\cdot 6\right)}^{1/4}+6\cdot {\left(7\cdot 7\cdot 6\cdot 6\right)}^{1/4}+\cdots +6\cdot {\left(7\cdot 6\cdot 7\cdot 6\right)}^{1/4}\left(\right\}{\left(\right)}^{\frac{1}{1+1}}=6.41$$

$$\overline{Lim}\left({\lambda }_2^{\left(m\right)1}\right)=\overline{Lim}\left({\lambda }_2^{\left(m\right)3}\right)=7.0;$$

$$\overline{Lim}\left({\lambda }_2^{\left(u\right)2}\right)=\overline{Lim}\left({\lambda }_2^{\left(u\right)4}\right)=\overline{Lim}\left({\lambda }_2^{\left(u\right)5}\right)=\left(\right)\frac{1}{5}\left\{\right)8{\left(7\cdot 8\cdot 7\cdot 7\right)}^{1/4}+7\cdot {\left(8\cdot 8\cdot 7\cdot 7\right)}^{1/4}+\cdots +7\cdot {\left(8\cdot 7\cdot 8\cdot 7\right)}^{1/4}\left(\right\}{\left(\right)}^{\frac{1}{1+1}}=7.41$$

$$\overline{Lim}\left({\lambda }_2^{\left(u\right)1}\right)=\overline{Lim}\left({\lambda }_2^{\left(u\right)3}\right)=8.0$$

Based on the defined limit values, we can define fuzzy rough numbers ${\overline{\lambda }}_2^1={\overline{\lambda }}_2^3=\left(\left[5.41,6.00\right],\left[6.41,7.0\right],\left[7.41,8.0\right]\right)$ and ${\overline{\lambda }}_2^2={\overline{\lambda }}_2^4={\overline{\lambda }}_2^5=\left(\left[5.0,5.41\right],\left[6.0,6.41\right],\left[7.0,7.41\right]\right)$. Using Eq. (12), the obtained fuzzy rough values were merged into a single fuzzy rough value ${\overline{\lambda }}_2=\left(\left[5.16,5.65\right],\left[6.16,6.65\right],\left[7.17,7.65\right]\right)$. The residual values in the aggregated fuzzy rough matrix (see Table 5) were obtained similarly.

Table 5.

Aggregate fuzzy rough matrix of experts’ opinions.

Crit.	Aggregated values		Score function	Rank
	Local	Global
MC1	([4.63,5.33],[5.63,6.34],[6.64,7.34])	–	–	–
C1	([4.73,5.63],[5.73,6.63],[6.74,7.63])	([21.89,30.02],[32.3,42.01],[44.71,56.01])	37.66	8
C2	([5.16,5.65],[6.16,6.65],[7.17,7.65])	([23.91,30.11],[34.74,42.11],[47.56,56.12])	38.92	5
C3	([4.63,5.33],[5.63,6.34],[6.64,7.34])	([21.45,28.45],[31.75,40.15],[44.05,53.85])	36.45	9
MC2	([5.63,5.96],[6.63,6.96],[7.63,7.96])	–	–	–
C4	([6.00,6.00],[7.00,7.00],[8.00,8.00])	([33.78,35.75],[46.42,48.71],[61.06,63.67])	48.06	1
C5	([4.35,4.83],[5.35,5.83],[6.35,6.83])	([24.47,28.78],[35.47,40.59],[48.47,54.39])	38.53	7
C6	([5.63,5.96],[6.63,6.96],[7.63,7.96])	([31.69,35.49],[43.97,48.41],[58.25,63.34])	46.69	2
MC2	([4.34,5.22],[5.34,6.23],[6.35,7.23])	–	–	–
C7	([5.63,5.96],[6.63,6.96],[7.63,7.96])	([24.43,31.13],[35.44,43.35],[48.44,57.56])	39.89	4
C8	([3.63,4.33],[4.63,5.33],[5.63,6.34])	([15.74,22.62],[24.75,33.23],[35.76,45.83])	29.49	12
C9	([4.07,4.67],[5.07,5.68],[6.07,6.69])	([17.67,24.41],[27.1,35.39],[38.54,48.36])	31.75	11
MC3	([4.63,4.96],[5.63,5.96],[6.63,6.96])	–	–	–
C10	([4.73,5.63],[5.73,6.63],[6.74,7.63])	([21.87,27.9],[32.27,39.5],[44.67,53.11])	36.39	10
C11	([5.35,5.83],[6.35,6.83],[7.35,7.83])	([24.75,28.91],[35.75,40.71],[48.75,54.51])	38.73	6
C12	([6.00,6.00],[7.00,7.00],[8.00,8.00])	([27.76,29.74],[39.4,41.7],[53.05,55.66])	41.05	3

Global values of fuzzy rough expert estimates were obtained by multiplying the local values of the criteria with the values of the sub-criteria from the corresponding group of criteria.

Step 2: Global values of expert assessments (see Table 7) were used for defining the score functions. This was a basis for the ranking of criteria. Score functions and rank criteria are presented in Table 7.

Table 7.

Degrees in utility alternatives.

Alt.	${{\aleph }_i}^{-}$	${{\aleph }_i}^{+}$
A${}_1$	([1.05,1.53],[1.84,2.53],[3.72,4.71])	([0.42,0.54],[0.62,0.8],[0.89,1.19])
A${}_2$	([0.89,1.42],[1.67,2.43],[3.51,4.62])	([0.35,0.5],[0.56,0.77],[0.84,1.17])
A${}_3$	([1.34,1.89],[2.24,3.02],[4.42,5.52])	([0.53,0.66],[0.75,0.96],[1.05,1.4])
A${}_4$	([1.37,1.97],[2.29,3.13],[4.51,5.68])	([0.54,0.70],[0.77,1.00],[1.07,1.44])
A${}_5$	([1.01,1.44],[1.79,2.49],[3.64,4.72])	([0.40,0.51],[0.6,0.79],[0.87,1.20])
A${}_6$	([0.57,0.91],[1.23,1.85],[2.80,3.84])	([0.23,0.32],[0.41,0.59],[0.67,0.97])

Step 3: Based on the rank criteria and score functions, a linear model is defined. This was a basis for defining the weight coefficients of the criteria. The linear mathematical model is presented in the following section:

$$\begin{array}{c}Max\gamma \hfill \\ s.t.\hfill \\ \begin{array}{cc}\begin{array}{c}0.614\left({\omega }_4-{\omega }_6\right)\ge \gamma ;\hfill \\ 0.632\left({\omega }_6-{\omega }_{12}\right)\ge \gamma ;\hfill \\ 0.718\left({\omega }_{12}-{\omega }_7\right)\ge \gamma ;\hfill \\ 0.739\left({\omega }_7-{\omega }_2\right)\ge \gamma ;\hfill \\ 0.758\left({\omega }_2-{\omega }_{11}\right)\ge \gamma ;\hfill \\ 0.761\left({\omega }_{11}-{\omega }_5\right)\ge \gamma ;\hfill \\ 0.765\left({\omega }_5-{\omega }_1\right)\ge \gamma ;\hfill \end{array}\hfill & \begin{array}{c}0.783\left({\omega }_1-{\omega }_3\right)\ge \gamma ;\hfill \\ 0.809\left({\omega }_3-{\omega }_{10}\right)\ge \gamma ;\hfill \\ 0.810\left({\omega }_{10}-{\omega }_9\right)\ge \gamma ;\hfill \\ 0.929\left({\omega }_9-{\omega }_8\right)\ge \gamma ;\hfill \\ 1.00\left({\omega }_8\right)\ge \gamma ;\hfill \\ \sum _{i=1}^{12}{\omega }_j=1;{\omega }_j\ge 0;\forall j\hfill \end{array}\hfill \end{array}\hfill \end{array}$$

Lingo 17.0 software was used to solve the linear model. By solving the linear model, the vector of weight coefficients was obtained as follows:

$${\omega }_j=\left(\right)0.0610,0.1022,0.0476,0.1645,0.0746,0.1475,0.1164,0.0105,0.0217,0.0347,0.0884,0.1309{\left(\right)}^T$$

5.2. Evaluation of alternatives: Rough Hamacher MARCOS methodology

The following section presents the implementation of the fuzzy rough Aczel–Alsina​ MARCOS methodology for the evaluation of alternative solutions.

Step 1: Five experts participated in the research and evaluated six alternatives. The fuzzy scale presented in Table 3 was used to evaluate the alternatives. Expert estimates of the alternatives are reported in Table 6.

Using Eqs. (1)–(4) of the expert assessment (Table 8), fuzzy rough values were transformed. After obtaining a fuzzy rough estimate, using the Bonferroni function, their aggregation was performed. Then, the final fuzzy rough home matrix was defined. $\overline{\Psi }={\left[{\overline{\wp }}_{ij}\right]}_{6\times 12}$ which is given in Table A.1 (see Appendix).

Table 8.

The comparisons of MARCOS methods.

Characteristics of the MCDM method	FRN Aczel-Alsina MARCOS	Fuzzy MARCOS	Rough MARCOS	D-MARCOS	Gray MARCOS
Flexible fuzzy intervals	Yes	No	No	No	No
Flexible membership degree	Yes	No	No	No	No
Flexible boundary intervals	Yes	No	Yes	No	No
Flexible decision-making due to decision-makers’ risk attitude	Yes	No	No	Partially	No
Flexibility in real-world applications	Yes	No	Partially	Partially	No

Table A.1.

Final fuzzy rough home matrix.

Crit.	A${}_1$	A${}_2$	A${}_3$
C${}_1$	([1.30,2.18],[2.33,3.21],[3.34,4.22])	([1.06,1.59],[2.06,2.64],[3.07,3.66])	([2.62,3.32],[3.63,4.33],[4.63,5.33])
C${}_2$	([1.00,1.00],[1.60,1.95],[2.15,2.89])	([1.32,1.81],[2.33,2.82],[3.34,3.83])	([2.33,3.21],[3.34,4.22],[4.34,5.22])
C${}_3$	([1.67,2.60],[2.71,3.62],[3.72,4.62])	([1.60,1.95],[2.62,2.95],[3.62,3.96])	([1.06,1.59],[2.06,2.64],[3.07,3.66])
C${}_4$	([3.16,4.03],[4.16,5.04],[5.16,6.04])	([3.16,4.03],[4.16,5.04],[5.16,6.04])	([1.00,1.00],[1.60,1.95],[2.15,2.89])
C${}_5$	([2.33,3.21],[3.34,4.22],[4.34,5.22])	([1.00,1.00],[1.60,1.95],[2.15,2.89])	([1.67,2.60],[2.71,3.62],[3.72,4.62])
C${}_6$	([2.62,3.32],[3.63,4.33],[4.63,5.33])	([1.59,2.59],[2.63,3.62],[3.66,4.64])	([4.73,5.63],[5.73,6.63],[6.74,7.63])
C${}_7$	([4.90,5.82],[5.91,6.82],[6.91,7.82])	([2.16,2.63],[3.16,3.64],[4.16,4.64])	([4.90,5.82],[5.91,6.82],[6.91,7.82])
C${}_8$	([4.35,4.83],[5.35,5.83],[6.35,6.83])	([2.87,3.81],[3.89,4.81],[4.90,5.82])	([5.04,5.35],[6.04,6.35],[7.04,7.35])
C${}_9$	([4.31,5.27],[5.32,6.27],[6.32,7.28])	([4.16,5.04],[5.16,6.04],[6.17,7.05])	([3.34,4.22],[4.34,5.22],[5.34,6.23])
C${}_{10}$	([2.71,3.62],[3.72,4.62],[4.73,5.63])	([1.14,1.98],[2.15,3.01],[3.16,4.03])	([5.04,5.35],[6.04,6.35],[7.04,7.35])
C${}_{11}$	([4.16,5.04],[5.16,6.04],[6.17,7.05])	([3.30,4.25],[4.31,5.27],[5.32,6.27])	([5.04,5.35],[6.04,6.35],[7.04,7.35])
C${}_{12}$	([3.16,4.03],[4.16,5.04],[5.16,6.04])	([3.16,4.03],[4.16,5.04],[5.16,6.04])	([1.67,2.60],[2.71,3.62],[3.72,4.62])
Crit.	A${}_4$	A${}_5$	A${}_6$
C${}_1$	([2.71,3.62],[3.72,4.62],[4.73,5.63])	([4.07,4.67],[5.07,5.68],[6.07,6.69])	([1.00,1.00],[1.60,1.95],[2.15,2.89])
C${}_2$	([1.14,1.98],[2.15,3.01],[3.16,4.03])	([3.34,4.22],[4.34,5.22],[5.34,6.23])	([1.00,1.00],[1.60,1.95],[2.15,2.89])
C${}_3$	([1.06,1.59],[2.06,2.64],[3.07,3.66])	([1.67,2.60],[2.71,3.62],[3.72,4.62])	([1.15,1.62],[2.16,2.63],[3.16,3.64])
C${}_4$	([1.00,1.00],[1.60,1.95],[2.15,2.89])	([1.59,2.31],[2.62,3.32],[3.63,4.33])	([4.90,5.82],[5.91,6.82],[6.91,7.82])
C${}_5$	([1.59,2.31],[2.62,3.32],[3.63,4.33])	([1.67,2.60],[2.71,3.62],[3.72,4.62])	([1.00,1.00],[1.00,1.00],[1.00,1.00])
C${}_6$	([4.90,5.82],[5.91,6.82],[6.91,7.82])	([3.16,4.03],[4.16,5.04],[5.16,6.04])	([1.15,1.62],[2.16,2.63],[3.16,3.64])
C${}_7$	([4.67,5.65],[5.68,6.65],[6.68,7.66])	([4.34,5.22],[5.34,6.23],[6.35,7.23])	([1.59,2.31],[2.62,3.32],[3.63,4.33])
C${}_8$	([4.73,5.63],[5.73,6.63],[6.74,7.63])	([4.34,5.22],[5.34,6.23],[6.35,7.23])	([3.34,4.22],[4.34,5.22],[5.34,6.23])
C${}_9$	([3.16,4.03],[4.16,5.04],[5.16,6.04])	([2.71,3.62],[3.72,4.62],[4.73,5.63])	([5.16,5.65],[6.16,6.65],[7.17,7.65])
C${}_{10}$	([5.04,5.35],[6.04,6.35],[7.04,7.35])	([3.72,4.62],[4.73,5.63],[5.73,6.63])	([1.00,1.00],[1.60,1.95],[2.15,2.89])
C${}_{11}$	([4.73,5.63],[5.73,6.63],[6.74,7.63])	([4.16,5.04],[5.16,6.04],[6.17,7.05])	([1.00,1.00],[1.60,1.95],[2.15,2.89])
C${}_{12}$	([2.33,3.21],[3.34,4.22],[4.34,5.22])	([1.83,2.79],[2.87,3.81],[3.89,4.81])	([5.63,5.96],[6.63,6.96],[7.63,7.96])

Steps 2 and 3: Using Eq. (16), ideal and anti-ideal solutions were defined in the final fuzzy rough home matrix. Furthermore, the normalization of the fuzzy rough matrix was performed using Eq. (17). The normalized fuzzy rough matrix is presented in Table A.2, Appendix.

Step 4: The degrees of the usefulness of alternatives to ideal and anti-ideal solutions are defined by applying Eqs. (18), (19). The utility rates of the alternatives are given in Table 7.

The following section presents the procedure for defining the degree of usefulness of alternative $A_1$:

(1) By applying Eq. (20) we obtain the sum of the weighted elements of the normalized matrix (see Table A.2):

$$\begin{array}{c}\hfill {{\overline{\partial }}_1}^{\varphi =1}=\left(\left[0.443,0.513\right],\left[0.560,0.640\right],\left[0.675,0.766\right]\right);\hfill \\ \hfill {{\overline{\partial }}_2}^{\varphi =1}=\left(\left[0.380,0.463\right],\left[0.496,0.590\right],\left[0.610,0.716\right]\right);\hfill \\ \hfill {{\overline{\partial }}_3}^{\varphi =1}=\left(\left[0.554,0.626\right],\left[0.672,0.752\right],\left[0.789,0.879\right]\right);\hfill \\ \hfill {{\overline{\partial }}_4}^{\varphi =1}=\left(\left[0.558,0.641\right],\left[0.676,0.767\right],\left[0.793,0.893\right]\right);\hfill \\ \hfill {{\overline{\partial }}_5}^{\varphi =1}=\left(\left[0.447,0.509\right],\left[0.555,0.634\right],\left[0.662,0.759\right]\right);\hfill \\ \hfill {{\overline{\partial }}_6}^{\varphi =1}=\left(\left[0.275,0.356\right],\left[0.403,0.497\right],\left[0.529,0.637\right]\right).\hfill \end{array}$$

The sum of the aggravated elements of the rough normalized matrix for alternative $A_1$ was obtained by applying the Aczel–Alsina function, as follows (see Box I):

Box I.

$$\begin{array}{c}{{\overline{\partial }}_1}^{\varphi =1}=\left\{\begin{array}{c}{{\partial }_1}^{\left(l\right)-}=5.40\cdot \left(1-e^{-{\left(0.061\cdot {\left(-ln(1-0.1)\right)}^1+0.102\cdot {\left(-ln(1-0.1)\right)}^1+0.048\cdot {\left(-ln(1-0.04)\right)}^1+\cdots +0.131\cdot {\left(-ln(1-0.1)\right)}^1\right)}^{1/1}}\right)=0.443\hfill \\ {{\partial }_1}^{\left(l\right)+}=6.30\cdot \left(1-e^{-{\left(0.061\cdot {\left(-ln(1-0.08)\right)}^1+0.102\cdot {\left(-ln(1-0.11)\right)}^1+0.048\cdot {\left(-ln(1-0.05)\right)}^1+\cdots +0.131\cdot {\left(-ln(1-0.09)\right)}^1\right)}^{1/1}}\right)=0.513\hfill \\ \dots \hfill \\ {{\partial }_1}^{\left(u\right)+}=9.42\cdot \left(1-e^{-{\left(0.061\cdot {\left(-ln(1-0.09)\right)}^1+0.102\cdot {\left(-ln(1-0.11)\right)}^1+0.048\cdot {\left(-ln(1-0.08)\right)}^1+\cdots +0.131\cdot {\left(-ln(1-0.09)\right)}^1\right)}^{1/1}}\right)=0.766\hfill \end{array}\right)\hfill \\ =\left(\left[0.443,0.513\right],\left[0.56,0.64\right],\left[0.675,0.766\right]\right)\hfill \end{array}$$

(2) Then, by applying Eqs. (18), (19), we define ${{\aleph }_i}^{-}$ and ${{\aleph }_i}^{+}$ for alternative $A_1$:

$${{\aleph }_1}^{-}=\frac{\left(\left[0.443,0.513\right],\left[0.560,0.640\right],\left[0.675,0.766\right]\right)}{\left(\left[0.156,0.184\right],\left[0.246,0.303\right],\left[0.333,0.422\right]\right)}=\left(\left[1.05,1.54\right],\left[1.84,2.60\right],\left[3.67,4.93\right]\right)$$

$${{\aleph }_1}^{+}=\frac{\left(\left[0.443,0.513\right],\left[0.560,0.640\right],\left[0.675,0.766\right]\right)}{\left(\left[0.607,0.715\right],\left[0.750,0.858\right],\left[0.892,1.00\right]\right)}=\left(\left[0.44,0.58\right],\left[0.65,0.85\right],\left[0.94,1.26\right]\right)$$

Step 5: The compromise solution was defined by applying the fuzzy rough utility function, Eq. (21). Utility Functions Alternatives were used to define score functions $h\left({\Lambda }_i\right)$. These were used to define the final rank of the alternatives.

$$\begin{array}{c}h\left({\Lambda }_i\right)Rank\hfill \\ \begin{array}{cc}\begin{array}{c}A1\hfill \\ A2\hfill \\ A3\hfill \\ A4\hfill \\ A5\hfill \\ A6\hfill \end{array}\hfill & \left[\begin{array}{c}0.984\hfill \\ 0.982\hfill \\ 1.085\hfill \\ 1.106\hfill \\ 0.960\hfill \\ 1.516\hfill \end{array}\right]\left[\begin{array}{c}4\hfill \\ 5\hfill \\ 3\hfill \\ 2\hfill \\ 6\hfill \\ 1\hfill \end{array}\right]\hfill \end{array}\hfill \end{array}$$

Based on the value of the score function, alternatives $A_6$ and $A_4$ are singled out as dominant from the considered set of alternatives. Dominant alternatives are those alternatives that have the highest values of score functions.

6. Sensitivity analysis

In this section, the influence of the parameters of the Bonferroni function and the Aczel–Alsina​ function on the stability of the initiated solution is analyzed. Three stabilization parameters have been identified in the multicriteria framework:

(1) Parameters ${\mathit{d}}_1$ and ${\mathit{d}}_2$ which are used in the Bonferroni function to define the lower and upper limits of fuzzy rough numbers; and

(2) Parameter $\varphi$ used in the Aczel-Alsina function for the weighted arithmetic averaging of a normalized fuzzy rough home matrix.

In the sensitivity analysis, the change of the stated parameters within the limit intervals was simulated and the changes in the initial solution were monitored.

6.1. Influence of parameters d1 and d2 on the initial results of the model

During the calculation of the initial solution, the values d1 $=$ d2 $=$ 1 were adopted, which simulated the minimum level of risk when making a decision. Since the parameters d1 and d2 cause a mathematical transformation of the Bonferroni function, it is necessary to analyze the influence of other values of these parameters on the results of the model. In the following section, the dependence of the fuzzy rough utility function of the alternatives on the change in the values of the parameters ${\mathit{d}}_1$ and ${\mathit{d}}_2$ was analyzed. During the simulation, the parameters in the interval were changed 1$\le$ ${\mathit{d}}_1$ ,d ₂ $\le$80. The limit values of the parameters were defined based on the conditions that the parameters should be ${\mathit{d}}_1$ and ${\mathit{d}}_2$ satisfy, that is ${\mathit{d}}_1$, ${\mathit{d}}_2$ $\ge$0. The upper limit of the interval was defined based on a large number of simulations. It was determined that for the values ${\mathit{d}}_1$ ,d ₂>80 there are no significant changes in criterion functions. Fig. 2 shows the changes in the fuzzy rough utility functions of alternative $A_3$ and alternative $A_4$ that occurred as a result of the change in value 1$\le$ ${\mathit{d}}_1$ ,d ₂ $\le$80. Similar changes occur with the remaining alternatives.

Fig. 2.

Dependence of the fuzzy rough utility function of alternatives $A_3$ and $A_4$ on the change of parameters d1 and d2.

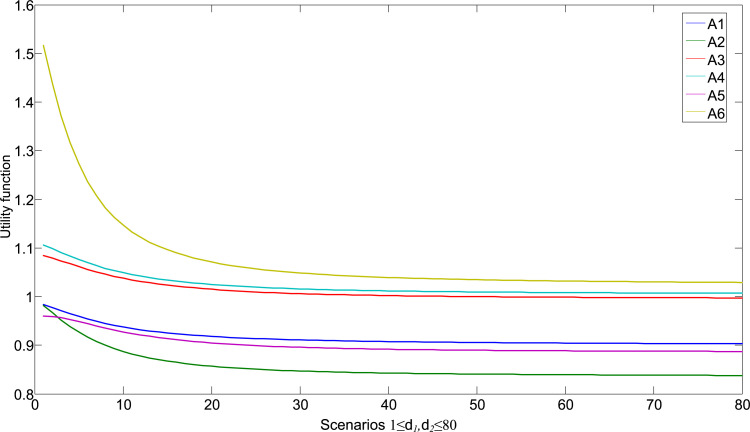
The results from Fig. 2 confirm the dependence of the value of the utility function alternatives by changing the parameters d1 and d2. The following section (see Fig. 3) provides a comparative overview of the change in utility functions of all considered alternatives. As the number of scenarios increases, the impact on the utility function changes. By increasing the number of scenarios, the impact of the alternative on the utility function was reduced.

Fig. 3.

Comparative presentation of the impact of changing utility functions of all considered alternatives.

In the experiment conducted in this section, 80 scenarios were formed. In the first scenario, a value of one was added for both parameters. In each subsequent scenario, the value of both parameters was increased by one. In this way, by increasing the value of the parameters, the increase in risk when making a decision is simulated. The results from Fig. 4 indicate the sensitivity of the model to changes in the values of d1 and d2, which allows the simulation of different levels of risk in the information through the change of these parameters.

Fig. 4.

Comparative presentation of the impact of parameter changes 1 $\le$$\varphi$$\le$ 80 to change utility function alternative.

Also, the results in Fig. 2 indicate that the initial solution is stable. Through 80 scenarios, the dominant alternatives ($A_6$ and $A_4$) retained their positions. Minor changes in the rankings occurred with the worst alternatives from the considered set ($A_5$ and $A_2$). However, these changes are not statistically significant, which is confirmed by Spearman’s correlation coefficient. The average value of Spearman’s coefficient through scenarios is 0.944. This indicates a significant correlation through scenarios. Based on the presented analysis, we can conclude that the initial solution is stable and that alternatives $A_6$ and $A_4$ are the dominant solutions.

6.2. Influence of parameter $\varphi$ on the results of the model

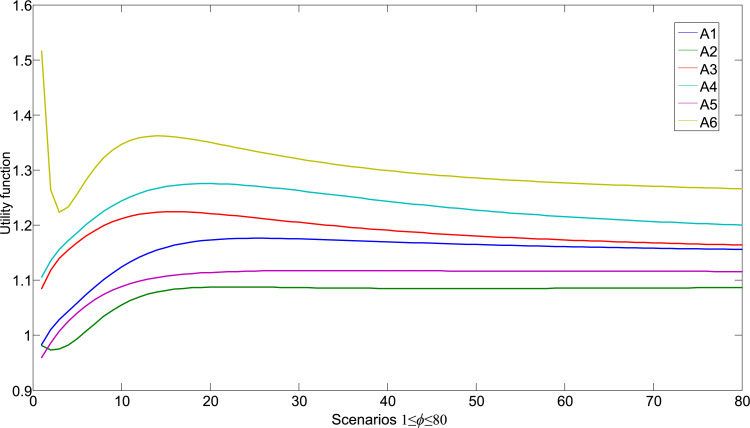
During the calculation of the initial solution, the value was adopted $\varphi =1$. By analyzing expression (20), we can see the dependence of the Aczel–Alsina function on the parameter values $\varphi$. In the following section, the impact of changing this parameter on the initial results was analyzed. Similar to the previous section, in the next experiment, the change of the parameter in the interval was simulated at 1 $\le$ $\varphi$ $\le$ 80. Similar to the previous case experiment, the limit value of the parameter $\varphi$ is defined based on $\varphi$ $\ge$0. A value was adopted for the upper limit of the interval $\varphi =80$, since it was found that for values $\varphi$>80 lead to negligible changes in criterion functions. Fig. 5 gives a comparative view of the change in utility functions of alternatives across 80 scenarios.

Fig. 5.

Comparison of alternative ranking.

From Fig. 4 it is observable that despite significant changes in the value of the utility function of alternatives, there are no changes in the ranks of dominant alternatives. Similar to the previous experiment, changes occur only in the worst alternatives ($A_2$ and $A_5$). Since the dominant alternatives do not change in rankings, we can conclude that the initial solution is credible and stable. The alternative $A_6$ dominates as the best solution from the considered set.

6.3. Comparison with different MCMD approaches

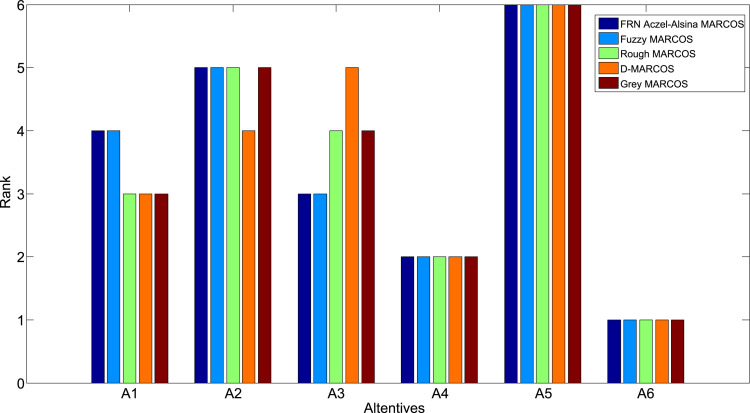
In the next part, the FRN Aczel-Alsina MARCOS model was compared with the results of four extensions of the MARCOS methodology. This was done using different uncertainty theories: fuzzy MARCOS (Bakır and Atalık, 2021), rough MARCOS (Deveci et al., 2021), D-MARCOS (Chakraborty et al., 2020) and gray MARCOS (Torkayesh et al., 2021) methods. Fig. 5 shows a comparative view of the results after the application of the mentioned multi-criteria techniques.

The results showed that applying different extensions of the MARCOS method gives a similar ranking. A complete correlation of ranks was obtained by applying FRN Aczel-Alsina MARCOS and fuzzy MARCOS methods, while minor deviations occurred with rough MARCOS and gray MARCOS models. The results of the fuzzy MARCOS model confirmed the initial results. However, the criteria functions in the fuzzy MARCOS model do not have adaptive interval values, which leads to a linear transformation of data and neglect of inaccuracies in expert assessments. The biggest deviations appeared with the D-MARCOS model. This is expected since D numbers require statistical processing of expert preferences and defining their agreement by applying an algorithm for combining D numbers. On the other hand, deviations in the rough MARCOS and gray MARCOS models appeared due to the neglect of the degree of membership in the considered data sets.

However, the dominance of the first-ranked alternative (A6) and the second-ranked alternative (A4) was confirmed for all methodologies. This indicates the fact that alternatives A6 and A4 represent the best solutions from the considered set. Also, all methodologies confirmed that A2 and A5 represent the worst alternatives in the considered set. Differences in ranks appeared for the third-ranked (A3) and fourth-ranked (A1) alternatives. In the following part, the applied methodologies were compared in terms of their advantages and disadvantages, Table 8.

One of the advantages of FRN MARCOS methodology compared to fuzzy, rough, D and gray MARCOS methods are that it uses flexible nonlinear Aczel–Alsina aggregation functions. On the other hand, fuzzy, rough, D and gray MARCOS methods use linear functions, which in certain situations can lead to a violation of the stability and quality of the obtained solution. Aczel–Alsina​ functions enable flexible decision-making due to decision makers’ risk attitude, so the FRN Aczel–Alsina MARCOS methodology is more general and more flexible. Also, by creating adaptive rough boundary intervals of triangular fuzzy numbers, the objectivity of decision-making increases, since the uncertainties that exist in expert preferences are retained. The fuzzy rough-based Aczel–Alsina MARCOS framework belongs to the group of hybrid models that overcome the limitations of traditional fuzzy and rough numbers. Fuzzy sets type-1 and type-2 are characterized by subjectivism when defining the boundaries of the set and the footprint of uncertainty. To eliminate the above-mentioned subjectivities, the authors in this paper propose a novel approach that represents the modification of fuzzy sets using the rough approach. Fuzzy-rough numbers take advantage of both theories, fuzzy sets, and rough numbers. At the same time, using the advantages of both approaches (fuzzy and rough), FRNs eliminate the limitations of fuzzy sets type-1 and type-2, which are related to subjectivism when defining the boundaries of the set and the footprint of uncertainty. In the FRN approach, the fuzzy theory is used to represent uncertainty in information, while the rough theory is used to create flexible boundary intervals of fuzzy numbers. By applying hybrid fuzzy rough numbers, the limitation of classic fuzzy type 2 numbers, which have a predefined uncertainty footprint, is eliminated. With fuzzy rough numbers, the uncertainty footprint is defined based on the internal uncertainties and inaccuracies that exist in the original data set. If there are greater uncertainties and inaccuracies in the information, the rough boundary interval increases. This affects the increase in the footprint of uncertainty. Also, in the case of minor uncertainties and inaccuracies, the rough boundary interval is reduced, which affects the reduction of the uncertainty footprint. On the other hand, in the absence of uncertainty, the fuzzy rough number is transformed into a classic fuzzy number, since in that case, the rough boundary interval is equal to zero.

On the other hand, the fuzzy MARCOS methodology (Bakır and Atalık, 2021) changes fuzzy numbers with predefined boundaries of fuzzy sets. That is why with the fuzzy MARCOS methodology, it is necessary to apply additional operators for the fusion of expert uncertainties in case of greater uncertainties in expert preferences. This eliminates part of the uncertainty and generalizes the data. The situation is similar to the rough MARCOS (Deveci et al., 2021) and gray MARCOS (Badi and Pamucar, 2020, Torkayesh et al., 2021) methods. Also, the flexibility of the FRN Aczel-Alsina MARCOS methodology can be seen through the transformation of fuzzy rough numbers into traditional fuzzy numbers. If there are greater imprecisions in expert assessments, the rough boundary interval of fuzzy rough numbers increases. However, if there is complete agreement in expert assessments, fuzzy rough numbers are transformed into classic fuzzy numbers. This adaptability of the FRN Aczel-Alsina MARCOS methodology enables flexibility in real-world applications and objective decision-making.

When applying the FRN Aczel-Alsina MARCOS methodology, the values of stabilization parameters Bonferroni and Aczel-Alsina were adopted ${\mathit{d}}_1$ =d ₂ =$\phi$=1. By varying the mentioned parameters, a different risk attitude is simulated by the decision maker. This feature represents a significant advantage compared to crisp, fuzzy, rough, and D numbers approaches. Thus, we can conclude that the proposed multi-criteria framework is more adequate for solving real problems in a dynamic environment.

6.4. Advantages of using fuzzy rough numbers

The advantages of treating uncertainty using the fuzzy rough approach are explained by the example of evaluating alternative A1 (Chemical disinfection) about an arbitrarily chosen criterion. The evaluation of alternatives was performed by five experts using triangular fuzzy numbers. Evaluations by experts are shown in Table 9.

Table 9.

Fuzzy valuations of alternative A${}_1$.

Expert	Alternative A${}_1$
E1	(2,3,4)
E2	(4,5,6)
E3	(3,4,5)
E4	(2,3,4)
E5	(4,5,6)

Based on the expert valuations presented in Table 9, it can be concluded that there is no consensus among experts regarding the impact of the evaluation criteria on the choice of alternative A1. To compare the fuzzy approach with the fuzzy rough concept, expert preferences from Table 9 were transformed into fuzzy rough numbers, Table 10.

Table 10.

Fuzzy rough expert valuations of alternative A${}_1$.

Expert	Alternative A${}_1$
E1	([2.00,2.93],[3.00,3.95],[4.00,4.97])
E2	([2.93,3.95],[4.00,4.97],[5.00,6.00])
E3	([2.29,3.31],[3.64,4.31],[4.64,5.65])
E4	([2.00,2.93],[3.00,3.95],[4.00,4.97])
E5	([2.93,3.95],[4.00,4.97],[5.00,6.00])

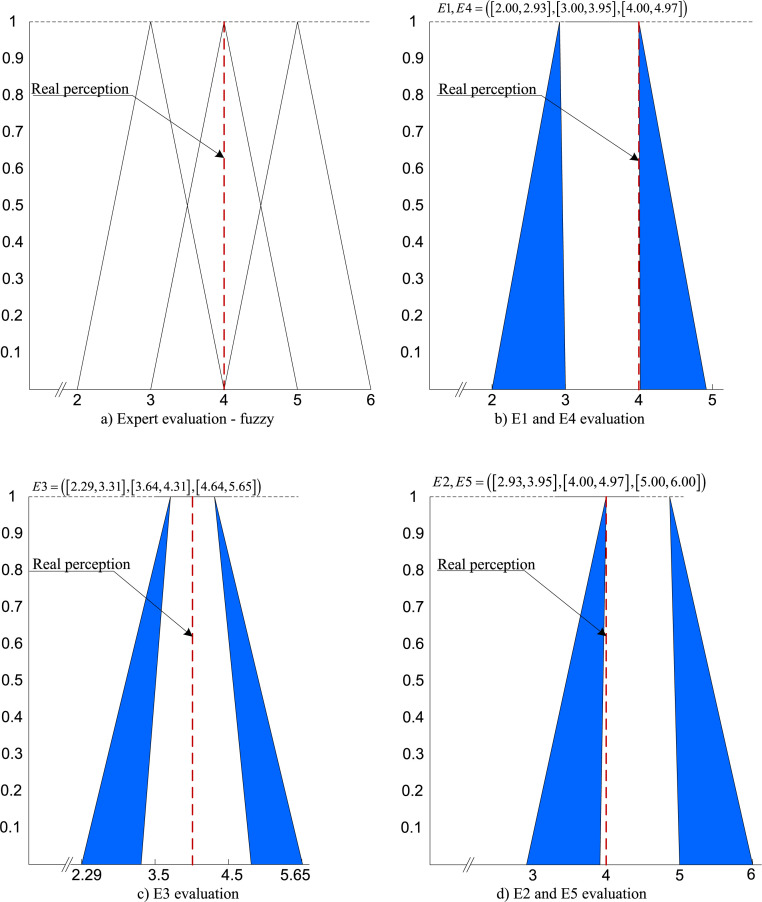
Valuations performed with triangular fuzzy numbers use pre-defined intervals to represent uncertainty, where the boundaries of the fuzzy number intervals are determined based on subjective expert assessments. The lower limit of the fuzzy number is defined as the crisp value that is reduced by the value of $\mu$, while the upper limit is defined as the crisp value that is increased by the value of $\mu$. The value $\mu$ is obtained based on experts’ assessments and is unique for the entire fuzzy scale. In our example, the value $\mu$=1 was used. The limitation of this approach is that all elements of the fuzzy scale have the same fuzzy boundary intervals, which are fixed at the value $\mu$=1. This limitation can be eliminated by using other values of $\mu$, which would lead to the introduction of partial adaptivity of the interval of fuzzy numbers. However, even with such an approach, the limit values of the interval of fuzzy numbers are defined based on subjective expert assessments. Similar limitations exist with interval-valued fuzzy (Karnik and Mendel, 2001).

The fuzzy rough approach presented in this study eliminates the mentioned limitations since unique adaptive interval limits are formed for each rating by a decision maker. The limits of the interval in FRN do not depend on subjective assessments but are defined based on existing uncertainties in the original data set. If there are uncertainties in expert assessments, the footprint of uncertainty increases, which has the effect of transforming the original fuzzy numbers into FRN. Larger differences in expert assessments influence the increase of the uncertainty footprint and FRN limit intervals. Also, the increase in agreement in expert assessments leads to minimal changes in FRN limits. However, in the case of full expert consensus, the boundaries of the fuzzy number do not change, since in such cases there is an absence of uncertainty. Then the expert assessments are described with linguistic expressions from the initial fuzzy scale.

Representation of expert preferences from Table 9 in traditional MCDM approaches implies aggregation of expert assessments. By applying the arithmetic averaging of the crisp expert valuations from Table 9, the “real perception” was obtained, so we can conclude that the “real perception” that fuzzy and FRN approaches should strive for should include the value 4. The position of “real perception” in the fuzzy and FRN approaches is shown in Fig. 6.

Fig. 6.

Expert evaluation using crisp, fuzzy, and fuzzy rough numbers.

From Fig. 6, it can be seen that the “real perception” is in the composition of the maximum values of all three FRN functions (Fig. 6b, c, and d). On the other hand, with fuzzy numbers (Fig. 6a), “real perception” belongs to only one of the three fuzzy numbers, the remaining two fuzzy numbers (2,3,4) and (4,5,6) do not include “real perception” by their functions. Based on the presented analysis, we can conclude that compared to fuzzy numbers, FRNs more faithfully describe the perceptions of decision-makers since they are much closer to “real perceptions”.

7. Discussion

The pandemic caused by the COVID-19 virus has shown that medical facilities must put focus on HCW management. This pandemic affected all spheres of life (Đukić et al., 2021). Different measures have been taken to prevent the spread of the COVID-19 virus. However, this increased the amount of HCW that needs to be disposed of in the prescribed manner (Manupati et al., 2021). In addition, HCW management is not so widespread in Bosnia and Herzegovina facing major problems with the disposal of this waste. The selection of the appropriate treatment for HCW management was analyzed in this study. For this purpose, extended sustainability criteria were used, and technical criteria were added to the sustainability criteria (economic, social, and economic). An extension of technical criteria is necessary because certain technological processes are applied in the management of HCW (Makan and Fadili, 2021). Each of the main criteria was divided into three auxiliary criteria. The reason for this is to assess each alternative with an equal number of criteria.

There are several treatments available to manage HCW. In this study, six alternatives were used \: incineration, deep burial, autoclave, microwave, chemical disinfection, and landfill. Each of these treatments has its advantages and disadvantages (Geetha et al., 2019). To select the appropriate treatment for HCW management, the expert opinion of five experts was used in this study. The experts are subject matter experts in hazardous and HCW management. They used a 10-level linguistic scale in the questionnaire to select a linguistic value ranging from absolutely low to perfect. The specificity of this study is that the classical transformation of linguistic values into fuzzy values was not used. Instead, the fuzzy rough approach was used. This represents a new approach to HCW management. The application of the fuzzy rough approach in HCW management was done through on-site selection for HCW disposal (Yazdani et al., 2020). Unlike this approach, the Bonferroni operator and Aczel–Alsina functions were not used.

The Fuzzy rough OPA method was used to determine the weights of the sub-criteria. The results obtained by this method showed that the best-ranked sub-criterion is Environmental Impact ($C_4$), while the worst-ranked criteria are Automation Level ($C_8$) and Treatment Capacities ($C_9$). In this way, more attention was paid to the impact on the environment because both the second and third-ranked criteria were Environmental Acceptability ($C_6$) and Health and Safety Risks ($C_{12}$). Less attention was paid to the technical characteristics of the treatment. The specificity of the calculation of the criteria is that the Bonferroni operator was used in the fusion of the fuzzy rough estimate and the generated aggregate fuzzy rough linguistic matrix. In this way, the problem of multiple comparisons of criteria was suppressed, while the application of the fuzzy rough approach solved the problem of uncertainty in assessing an expert opinion.

After the weights of the criteria were determined, the ranking of alternatives was implemented and the fuzzy rough Aczel-Alsina MARCOS methodology for evaluating alternatives was used. The Aczel-Alsina function was used for the sum of the aggravated elements of the normalized rough matrix. The results obtained with this approach have shown that the best treatment is the application of a microwave oven ($A_6$). These results confirm that hazardous HCWs must first be neutralized to be disposed of in a landfill (Pamučar et al., 2021). In this case, it is best to first treat HCW with a microwave oven and autoclave because these alternatives have shown the best results. After that, the waste can be disposed of by deep burial or landfill with the worst results. In this way, the impact on the environment will be reduced. HCW waste that does not pose a major danger to the environment can be disposed of at a landfill (Shi et al., 2017).

Validation of these results was performed using sensitivity analysis. It was carried out by analyzing the influence of the parameters of the Bonferroni function and the Aczel–Alsina function on the stability of the initiated solution. For that purpose, 80 scenarios were formed to observe the lower and upper limits of fuzzy rough numbers. Through these scenarios, it was confirmed that the dominant alternatives are microwave ovens ($A_6$) and autoclaves ($A_4$), while the worst alternatives are landfill treatment ($A_5$) and deep burial ($A_2$). Choosing these HCW management treatments would reduce the environmental impact of HCW and contribute to nature conservation. However, to get the full effect, it is necessary to apply at least two HCW management treatments.

Based on the conducted study using the fuzzy rough approach, the advantages and disadvantages of this approach can be identified. In scholarly practice, other methods based on the fuzzy rough approach have also been developed. One of the examples is the fuzzy multi neighborhood rough set model (Wan et al., 2021a), which effectively improves the performance of the classification of subsets while at the same time reducing the performance of spatial features. In addition, Wan et al. (2021b) have developed another approach based on the fuzzy rough set, which is the dynamic interactions method. In future research, different fuzzy rough approaches should be used to find out the advantages and disadvantages of these approaches. This is the reason why it is necessary to develop new innovative approaches based on the fuzzy rough set for subsequent research.

8. Conclusion

Due to the COVID-19 pandemic, there has been a major change in HCW management. The amount of waste produced by medical institutions and individuals has increased. All countries in the world, especially developing countries, must take great efforts to solve the problem of HCW management. Bosnia and Herzegovina is a developing country that has poorly regulated management of HCW, causing this waste not to be disposed of adequately. This study was conducted on the example of the Brčko District to select HCW management treatment enabling efficient management. The Brčko District as a special administrative unit in Bosnia and Herzegovina has its legal framework and state laws in the field of HCW management are directly applied.

Many factors influence the selection of HCW management treatment. For the evaluation of the HCW treatment, decision-making is applied using several criteria for evaluation among different alternatives. This decision problem can successfully be solved by applying MCDM methods. This approach uses expert decision-making and the study itself is adapted to human thinking, while linguistic values were used to evaluate criteria and alternatives. To solve the problem of inaccuracy in determining the linguistic values of the expert, a fuzzy rough approach to the evaluation of alternatives was used. The fuzzy rough approach is a new approach to solving the selection problem for HCW treatment. In addition, an integrated methodology was used to combine the application of two methods: OPA and MARCOS methods. In the OPA method, a fuzzy rough approach was fused using the Bonferroni operator and the weights of the sub-criteria were calculated. Based on these results, the highest value of weight was given to the sub-criterion Environmental Impact ($C_4$), while the lowest value was given to the sub-criterion Level of Automation ($C_8$). Furthermore, the MARCOS method based on the Aczel-Alsina function was applied to rank alternatives in HCW management treatments. The results showed that the most efficient and economical approach is the microwave oven ($A_6$) treatment, while the landfill treatment ($A_5$) treatment was rated as the worst. These results were confirmed by sensitivity analysis.

In addition to the fact that HCW is sterilized by microwave rays or steam, it must be disposed of in waste, because every HCW cannot be disposed of immediately in a landfill. Therefore, sterilization of waste must be performed using appropriate treatments such as a microwave or autoclave, which showed the best results in this study. Thus, it is necessary at least to apply two treatments with HCW in the Brčko District, first disinfect this waste using a microwave oven and then dispose of it in a landfill to reduce the impact on the environment. Therefore, a combination of HCW management treatments should be considered in future studies, as one treatment may not cover every HCW, especially when it comes to infectious or chemical waste. In future research, it is necessary to make a selection of treatments for a particular type of waste. In addition, more criteria need to be included in this selection to adequately manage HCW. This study provided a new approach based on fuzzy rough numbers to define the lower and upper limits of rough numbers based on the Bonferroni function. It helps to define risks depending on dynamic conditions because it combines fuzzy and rough sets and thus uses the advantages of these approaches in decision-making. In addition, the use of the Aczel-Alsina function in the MARCOS method reduced the influence of decision-makers on the final decision as decision stabilization was performed.

CRediT authorship contribution statement

Dragan Pamučar: Conceptualization, Methodology, Software, Validation, Formal analysis, Data curation, Writing, Visualization. Adis Puška: Conceptualization, Methodology, Investigation, Resources, Data curation, Writing, Visualization. Vladimir Simić: Software, Validation,Formal analysis, Writing. Ilija Stojanović: Supervision, Project administration. Muhammet Deveci: Software, Project administration.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix.

Proof for Theorem 1

An expression for arithmetic weighted averaging ${\overline{\partial }}_i={\sum }_{j=1}^n{\omega }_j{\hat{\wp }}_{ij}$ it is divided into segments in order to gradually perform the Eq. (20). From the Eqs. (5), (9) it is computed:

$${\omega }_j\cdot {\hat{\wp }}_{ij}=\left(\begin{array}{c}\left[1-e^{-{\left({\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(l\right)-}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }},1-e^{-{\left({\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(l\right)+}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right],\hfill \\ \left[1-e^{-{\left({\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(m\right)-}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }},1-e^{-{\left({\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(m\right)+}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right],\hfill \\ \left[1-e^{-{\left({\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(u\right)-}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }},1-e^{-{\left({\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(u\right)+}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right]\hfill \end{array}\right)$$ (A.1)

By applying the Eq. (7), fuzzy Aczel–Alsina weighted averaging function is developed (20)

$$\begin{array}{c}{\overline{\partial }}_i=\sum _{j=1}^n{\omega }_j{\hat{\wp }}_{ij}\hfill \\ =\left(\begin{array}{c}\left[\right)\sum _{j=1}^n{\hat{\wp }}_{ij}^{\left(l\right)-}\left(1-e^{-{\left(\sum _{j=1}^n{\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(l\right)-}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right),\hfill \\ \sum _{j=1}^n{\hat{\wp }}_{ij}^{\left(l\right)+}\left(1-e^{-{\left(\sum _{j=1}^n{\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(l\right)+}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right)\left(\right],\hfill \\ \left[\right)\sum _{j=1}^n{\hat{\wp }}_{ij}^{\left(m\right)-}\left(1-e^{-{\left(\sum _{j=1}^n{\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(m\right)-}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right),\hfill \\ \sum _{j=1}^n{\hat{\wp }}_{ij}^{\left(m\right)+}\left(1-e^{-{\left(\sum _{j=1}^n{\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(m\right)+}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right)\left(\right],\hfill \\ \left[\right)\sum _{j=1}^n{\hat{\wp }}_{ij}^{\left(u\right)-}\left(1-e^{-{\left(\sum _{j=1}^n{\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(u\right)-}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right),\hfill \\ \sum _{j=1}^n{\hat{\wp }}_{ij}^{\left(u\right)+}\left(1-e^{-{\left(\sum _{j=1}^n{\omega }_j{\left(-ln\left(1-f\left({\hat{\wp }}_{ij}^{\left(u\right)+}\right)\right)\right)}^{\varphi }\right)}^{1/\varphi }}\right)\left(\right]\hfill \end{array}\right)\hfill \end{array}$$ (A.2)

where ${\omega }_j$ vector of weight coefficients of the criterion, while $f\left({\hat{\wp }}_j\right)={\hat{\wp }}_j/{\sum }_{j=1}^n{\hat{\wp }}_j$.

Table A.2.

The normalized rough initial matrix.

Crit.	A${}_1$	A${}_2$	A${}_3$
C${}_1$	([0.19,0.33],[0.35,0.48],[0.50,0.63])	([0.16,0.24],[0.31,0.39],[0.46,0.55])	([0.39,0.50],[0.54,0.65],[0.69,0.80])
C${}_2$	([0.16,0.16],[0.26,0.31],[0.35,0.46])	([0.21,0.29],[0.37,0.45],[0.54,0.61])	([0.37,0.51],[0.54,0.68],[0.70,0.84])
C${}_3$	([0.36,0.56],[0.59,0.78],[0.80,1.00])	([0.35,0.42],[0.57,0.64],[0.78,0.86])	([0.23,0.34],[0.45,0.57],[0.66,0.79])
C${}_4$	([0.40,0.52],[0.53,0.64],[0.66,0.77])	([0.40,0.52],[0.53,0.64],[0.66,0.77])	([0.13,0.13],[0.20,0.25],[0.28,0.37])
C${}_5$	([0.45,0.61],[0.64,0.81],[0.83,1.00])	([0.19,0.19],[0.31,0.37],[0.41,0.55])	([0.32,0.50],[0.52,0.69],[0.71,0.88])
C${}_6$	([0.33,0.42],[0.46,0.55],[0.59,0.68])	([0.20,0.33],[0.34,0.46],[0.47,0.59])	([0.60,0.72],[0.73,0.85],[0.86,0.98])
C${}_7$	([0.63,0.74],[0.76,0.87],[0.88,1.00])	([0.28,0.34],[0.40,0.47],[0.53,0.59])	([0.63,0.74],[0.76,0.87],[0.88,1.00])
C${}_8$	([0.57,0.63],[0.70,0.76],[0.83,0.90])	([0.38,0.50],[0.51,0.63],[0.64,0.76])	([0.66,0.70],[0.79,0.83],[0.92,0.96])
C${}_9$	([0.56,0.69],[0.70,0.82],[0.83,0.95])	([0.54,0.66],[0.68,0.79],[0.81,0.92])	([0.44,0.55],[0.57,0.68],[0.70,0.81])
C${}_{10}$	([0.37,0.49],[0.51,0.63],[0.64,0.77])	([0.16,0.27],[0.29,0.41],[0.43,0.55])	([0.69,0.73],[0.82,0.86],[0.96,1.00])
C${}_{11}$	([0.55,0.66],[0.68,0.79],[0.81,0.92])	([0.43,0.56],[0.56,0.69],[0.70,0.82])	([0.66,0.70],[0.79,0.83],[0.92,0.96])
C${}_{12}$	([0.40,0.51],[0.52,0.63],[0.65,0.76])	([0.40,0.51],[0.52,0.63],[0.65,0.76])	([0.21,0.33],[0.34,0.45],[0.47,0.58])
Crit.	A${}_4$	A${}_5$	A${}_6$
C${}_1$	([0.40,0.54],[0.56,0.69],[0.71,0.84])	([0.61,0.7],[0.76,0.85],[0.91,1.00])	([0.15,0.15],[0.24,0.29],[0.32,0.43])
C${}_2$	([0.18,0.32],[0.35,0.48],[0.51,0.65])	([0.54,0.68],[0.7,0.84],[0.86,1.00])	([0.16,0.16],[0.26,0.31],[0.35,0.46])
C${}_3$	([0.23,0.34],[0.45,0.57],[0.66,0.79])	([0.36,0.56],[0.59,0.78],[0.8,1.00])	([0.25,0.35],[0.47,0.57],[0.68,0.79])
C${}_4$	([0.13,0.13],[0.20,0.25],[0.28,0.37])	([0.20,0.30],[0.33,0.42],[0.46,0.55])	([0.63,0.74],[0.76,0.87],[0.88,1.00])
C${}_5$	([0.31,0.44],[0.50,0.64],[0.69,0.83])	([0.32,0.50],[0.52,0.69],[0.71,0.88])	([0.19,0.19],[0.19,0.19],[0.19,0.19])
C${}_6$	([0.63,0.74],[0.76,0.87],[0.88,1.00])	([0.40,0.52],[0.53,0.64],[0.66,0.77])	([0.15,0.21],[0.28,0.34],[0.40,0.47])
C${}_7$	([0.60,0.72],[0.73,0.85],[0.85,0.98])	([0.56,0.67],[0.68,0.80],[0.81,0.92])	([0.20,0.30],[0.33,0.42],[0.46,0.55])
C${}_8$	([0.62,0.74],[0.75,0.87],[0.88,1.00])	([0.57,0.68],[0.70,0.82],[0.83,0.95])	([0.44,0.55],[0.57,0.68],[0.70,0.82])
C${}_9$	([0.41,0.53],[0.54,0.66],[0.68,0.79])	([0.35,0.47],[0.49,0.60],[0.62,0.74])	([0.68,0.74],[0.81,0.87],[0.94,1.00])
C${}_{10}$	([0.69,0.73],[0.82,0.86],[0.96,1.00])	([0.51,0.63],[0.64,0.77],[0.78,0.90])	([0.14,0.14],[0.22,0.27],[0.29,0.39])
C${}_{11}$	([0.62,0.74],[0.75,0.87],[0.88,1.00])	([0.55,0.66],[0.68,0.79],[0.81,0.92])	([0.13,0.13],[0.21,0.26],[0.28,0.38])
C${}_{12}$	([0.29,0.40],[0.42,0.53],[0.55,0.66])	([0.23,0.35],[0.36,0.48],[0.49,0.60])	([0.71,0.75],[0.83,0.87],[0.96,1.00])

Data availability

No data was used for the research described in the article.