Determining the internal orientation, degree of ordering, and volume of elongated nanocavities by NMR: Application to studies of plant stem

Abstract

This study investigates the fibril nanostructure of fresh celery samples by modeling the anisotropic behavior of the transverse relaxation time (T₂) in nuclear magnetic resonance (NMR). Experimental results are interpreted within the framework of a previously developed theory, which was successfully used to model the nanostructures of several biological tissues as a set of water filled nanocavities, hence explaining the anisotropy the T₂ relaxation time in vivo. An important feature of this theory is to determine the degree of orientational ordering of the nanocavities, their characteristic volume, and their average direction with respect to the macroscopic sample. Results exhibit good agreement between theory and experimental data, which are, moreover, supported by optical microscopic resolution. The quantitative NMR approach presented herein can be potentially used to determine the internal ordering of biological tissues noninvasively.

1. Introduction

Deep understanding of the function of biological tissues requires mapping their internal structure. Nuclear magnetic resonance (NMR) spectroscopy is one of the efficient tools for mapping the structure in biological samples at the morphological, molecular, and atomic levels [1]. NMR has two main applications in biology and medicine: NMR spectroscopy for the determination of the chemical composition of macromolecules, and magnetic resonance imaging (MRI) for mapping anatomy, physiology, and metabolism functions [1-3]. These applications require development of specialized magnets, radio frequency (RF) pulses, and signal processing techniques.

It has long been known that the second moment of the NMR signal [4] and the transverse relaxation time (T₂) [5] of liquids exhibit anisotropic properties when contained in fibril tissues. Namely, the values of these properties depend on the orientation of the tissue relative to the external magnetic field. The anisotropy of the T₂ relaxation time was previously explored, via its dependency on the orientation of bound water molecules along hydrophilic tissue fibrils [4-9].

The phenomenon of relaxation anisotropy in collagenous tissues is usually attributed to non-averaged dipolar couplings of water bound to the collagen [4-13]. Alternative models for this phenomenon include the formation of strong water bridges [11] and bound water molecules along hydrophilic tissue fibrils [4-9,13]. These theories, however, did not consider the residual inter-molecular dipole–dipole interactions in water entrapped in the cavity itself.

Recently, a method based on modeling fibril’s internal structure as composed of water filled nanocavities has been successfully used to explain the anisotropy of the transverse and longitudinal relaxation times observed in biological tissues [14-18]. The developed model [14-18] is based on consideration of the averaged Hamiltonian for water entrapped in nanocavities and the bivariate normal distribution of the polar and azimuthal angles, which determine the fibril direction. As such, this model links the water relaxation time’ anisotropy, and the degree of orientational ordering of fibrils.

For an adequate description of a spin system bounded by a cavity, the Hamiltonian of the dipole–dipole interaction must be averaged over the coordinate space. Let us estimate the characteristic size l of a nanocavity that contain water. The Hamiltonian of spins in this water pool can be represented by its non-zero average shape due to the limited molecular motion in the nanocavity. The characteristic size l_ch of a cavity in which the dipolar Hamiltonian (3) does not average to zero is estimated from the condition: $l_{ch}<\sqrt{8D{t}_{mag}}$, where D ≈ 3 · 10⁶ nm²/ms is the diffusion coefficient of water [19] and t_mag ≈ 2.74 · 10⁻² ms is the typical NMR time scale for protons which characterizes the flip-flop transition due to the dipole–dipole interaction [20]. Estimation gives that the characteristic size should be less than 810 nm.

The relaxation time anisotropy can thus be used as an indirect and sensitive probe of the three-dimensional (3D) tissue morphology at the microscopic and nanoscopic length-scales. Herein we further establish the correlation between the anisotropy of the transverse relaxation time (T₂) and the orientation and degree of ordering of fibrils in plant samples. The manuscript is organized as follows: in Section 2, for convenience of the readers, we briefly show that the angular dependency of the transverse relaxation time results from residual dipole–dipole interaction in liquid entrapped in nanocavities. We then consider the transverse relaxation time for various sets of nanocavities with different average directions relative to the external magnetic field, and different angle distributions. In Section 3, we describe the tested samples and experimental procedures. In Section 4, the theoretical predictions and the experimental data are compared, and in the last section, we conclude that the transverse relaxation time is strongly correlated with the internal degree of nanofibril ordering in biological tissues.

2. Theory

In this section we recapitulate, for the convenience of the readers, the mechanisms of the transverse relaxation in a single nanocavity containing liquid (e.g., water), and then consider the influence of internal orientational ordering of the nanocavities on the transverse relaxation times.

2.1. Anisotropy of transverse relaxation time

In liquids entrapped in nanocavities transverse relaxation may be the result of several types of interactions with different relative weights. The main contribution, however, originates from dipole-dipole (DD) interaction of the nuclear spins [3-5,10,21-27]. Due to restricted motion of water molecules in nanocavities the inter-molecular DD interactions are not averaged completely to zero and the averaged Hamiltonian of the DD interaction takes the following form [28]:

$${\overline{H}}_d=G_d\sum _{j<k}^{\mathrm{N}}\left(3I_{zj}{I}_{zk}-\overrightarrow{I}{}_j\overrightarrow{I}{}_k\right),$$ (1)

Here, $\overrightarrow{I}{}_j$ is the angular momentum operators of the j-th nuclear spin, I_zj is the projection of the spin operator $\overrightarrow{I}{}_j$ onto the z-axis where j = 1,2,…,N. G_d in Eq. (1) is the space-averaged coupling constant for a pair of the nuclear spins, given by.

$$G_d=-\frac{{\gamma }_{{}_2}\mathrm{h}}{V}{P}_2(\cos {\theta }_n)F$$ (2)

where γ is the gyromagnetic ratio of nucleus, V is the volume of nanocavity, P₂ is the second Legendre polynomial, i.e., the angle θ_n between the main axis Z_n of the n-th nanocavity and the external magnetic field (see Fig. 1), and F is the form-factor [14-18,28].

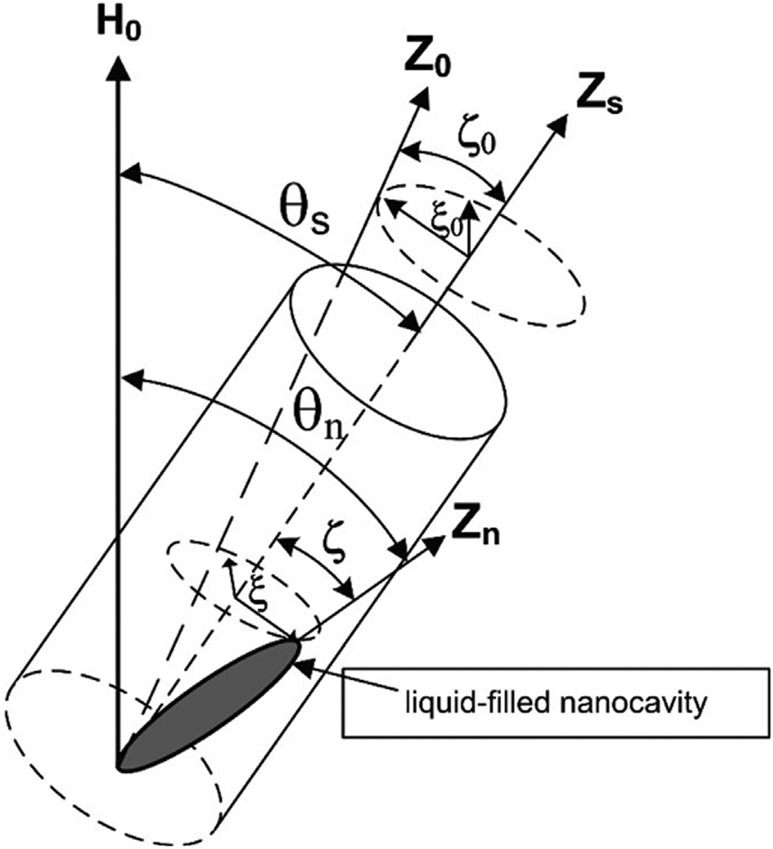
Fig. 1.

Model of a sample containing liquid entrapped in nanocavities. θ_s is the angle between the external magnetic field and the sample main axis (Z_s). θ_n denotes the angle between the external magnetic field H₀ and the axis of a n-th nanocavity (Z_n). Z₀ axis represents the averaged orientation of the ensemble of all nanocavities. The polar ζ and azimuthal ξ angles reflect the deviation of the main axis of a specific nanocavity (Z_n) from the main Z_s axis. Lastly, ζ₀ and ξ₀ are the polar and azimuthal angles which determine the deviation of the Z₀-axis from the Z_s-axis.

Using Eqs. (1) and (2) the transverse relaxation rate R₂ = 1/T₂ can be expressed by [18].

$$R_2({\theta }_n)=\frac{{\gamma }_{{}_2}\mathrm{h}\sqrt{\rho }}{\sqrt{V}}\mid P_2(\cos {\theta }_n)F\mid ,$$ (3)

where ρ is the proton density in the tissue. According to Eq. (3), R₂ is proportional to the square root of the concentration of the liquid contained in the nanocavity and is inversely proportional to the square root of the volume of the nanocavity. Importantly, it also depends on the orientation of the main axis of the nanocavity (Z_n) relative to the external magnetic field, causing R₂ to vanish at an angle equal to the magic angle where no relaxation occurs and T₂ → ∞.

2.2. Orientational distribution of nanocavities

Eq. (3) describes the orientation dependency of R₂ for a single nanocavity. If all nanocavities are oriented along the sample Z_s axis, then Eq. (3) describes the angular anisotropy of R₂ for the entire sample. In actual biological samples, however, a deviation from this ideal ordering is usually observed. Moreover, the volume and form factors may also vary across different nanocavities, and the main axis of each nanocavity can then be thought of as distributed around a single averaged orientation.

To expand Eq. (3) to account for a range of orientations (rather than a single one) it is necessary to average R₂ over an ensemble of nanocavities, each having a different orientation (ζ, ξ) relative to the main sample axis Z_s (see Fig. 1). The measured signal is usually modeled by a decaying exponential function, which, for an ensemble of nanocavities can be expressed by:

$$Signal=\sum _n{A}_n\text{exp}\left(-\frac{t}{T_{2n}}\right)$$ (5)

where n is an index running over all nanocavities. Assuming t ⪡ T₂, the averaged relaxation rate can be expressed as.

$$\begin{gathered} \langle R_2({\theta }_s)\rangle =\frac{1}{T_2}=\sum _n{A}_n\frac{1}{T_{2n}}=\frac{1}{A}\sum _n{A}_n{R}_2({\theta }_n) \\ ={\gamma }_{{}_2}\mathrm{h}\sqrt{\rho }\sum _n{A}_n\frac{\mid F_n\mid }{\sqrt{V_n}}\mid P_2(\cos {\theta }_n)\mid \end{gathered}$$ (6)

where A_n is the relative fraction of each nanocavity.

The form factor of elongated axis-symmetrical nanocavities, a >> b = c is practically independent of the cavity size [12]. In biological and plant fibril tissues this condition is met, allowing to replace V_n and F_n with average volume V and form factor F, which characterize the tissue’s nanostructure,

$$\langle R_2({\theta }_s)\rangle \approx \eta \sum _n{A}_n\mid P_2(\cos {\theta }_n)\mid$$ (7)

where

$$\eta ={\gamma }^2\mathrm{h}\mid F\mid \sqrt{\frac{\rho }{V}}$$ (8)

To average all orientations, we define the deviation of each nanocavity from the main axis of the sample (Z_s) by the polar ζ and azimuthal ξ angles (Fig. 1). Several previous studies have shown that a Gaussian distribution is good approximation for the angular distribution of nanocavities [14-18], showing good agreement between theory and experimentally measured spin–lattice and transverse relaxation rates R₁ and R₂. Similarly, we assume here that the distribution of nanocavities over both polar ζ and azimuthal ξ angles is given by a bivariate normal distribution function, with mean orientation denoted by Z₀. The sum in Eq. (7) can be now expressed as integration over all possible values of ζ = 0, …, π and ξ = 0, …, 2π, yielding,

$$\langle R_2({\theta }_S)\rangle =\eta \frac{{\int }_0^{2\pi }d\xi {\int }_0^{\pi }d\zeta \sin \zeta \Phi (\zeta ,\xi )\mid P_2(\cos {\theta }_S\cos \zeta -\sin {\theta }_S\sin \zeta \cos \xi )\mid }{{\int }_0^{2\pi }d\xi {\int }_0^{\pi }d\zeta \sin \zeta \Phi (\zeta ,\xi )}$$ (9)

Φ(ζ, ξ) is the probability density function given by.

$$\Phi (\zeta ,\xi )=\frac{1}{2\pi {\sigma }_{\zeta }{\sigma }_{\xi }}\text{exp}\left\{-\frac{(\zeta -{\zeta }_0{)}^2}{2{\sigma }_{\zeta }^2}-\frac{(\xi -{\xi }_0{)}^2}{2{\sigma }_{\xi }^2}\right\},$$ (10)

with σ_ζ and σ_ξ denoting the standard deviations (SD) around the average orientation Z₀, defined using ζ₀ and ξ₀ relative to the Z_s axis (Fig. 1). Since we do not know a priori the values of Vand F, it is useful to define a normalized relaxation rate which does not include these parameters according to:

$$\langle {\overline{R}}_2({\theta }_S)\rangle =\frac{\langle R_2({\theta }_S)\rangle }{{\max }_{{\theta }_S}[\langle R_2({\theta }_S)\rangle ]},$$ (11)

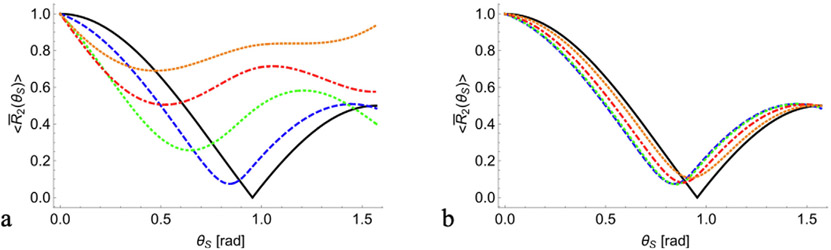
Examining Eq. (11) we note that this operation eliminates the dependency of the normalized transverse relaxation rate on the volume and form factor, thereby isolating the dependency on the orientation of sample’s main axis θ_s. Fig. 2 presents computer simulations of the angular dependency of $\langle {\overline{R}}_2({\theta }_S)\rangle$ for several choices for the SD of ζ and ξ around Z₀. As can be seen R₂ vanishes at the magic angle only when all nanocavities are perfectly aligned oriented along the sample Z_s axis (solid black curves), while for non-zero SD R₂ minimum moves away from zero. The difference between the maximum and minimum of the function decreases as SD values increase, making the effect of anisotropy less noticeable. Accordingly, an increase of σ_ζ causes the minimum of the function to monotonically shifts towards θ_s = 0 (Fig. 2a). An increase of σ_ζ, on the other hand, does not exhibit monotonic trend monotonic and the function’s minimum moves towards θ_s = 0 and then away from zero angle. Comparison of Fig. 2a and Fig. 2b shows that variations in the SD of the polar angle σ_ζ causes significantly stronger changes in the angular dependence of R₂ than variations in the SD of the azimuthal angle σ_ξ.

Fig. 2.

Angular dependency of the normalized transverse relaxation rate $\langle {\overline{R}}_2({\theta }_S)\rangle$ on the SD of the polar and azimuthal angles ζ and ξ around the averaged orientation ζ₀ = 0 and ξ₀ = 0. The solid black curves are calculated according to Eq. (3) for an ensemble of nanocavities, which are all perfectly oriented along the sample axis Z_s (i.e., zero SD). (a) $\langle {\overline{R}}_2({\theta }_S)\rangle$ for fixed SD σ_ξ = 0.1 of the azimuthal angle, and varying SD of the polar angle σ_ζ = 0.1, 0.3, 0.5, 0.7 (blue dashed, green dotted, red dash-dotted, and light brown dotted lines respectively). (b) $\langle {\overline{R}}_2({\theta }_S)\rangle$ for fixed SD σ_ζ = 0.1 of the polar angle, and varying SD of the azimuthal angle σ_ξ = 0.1, 0.4, 1.0, 1.7 (blue dashed, green dotted, red dash-dotted, and light brown dotted lines respectively). Note that the dashed blue line in (a) and in (b) was calculated using the same parameter values. All curves were calculated using Eq. (11).

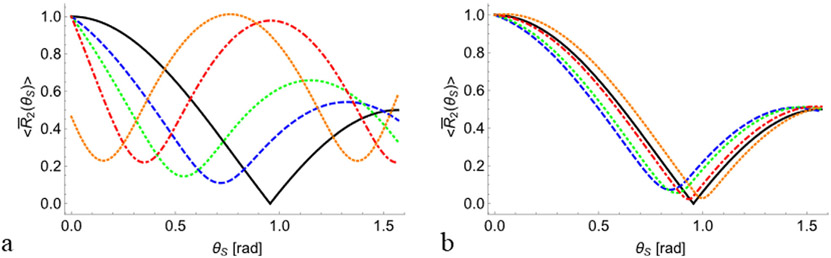
The angular dependency of R₂ is determined not only by the degree of internal ordering of nanocavities (i.e., σ_ζ and σ_ξ), but also by the averaged direction of all nanoparticles Z₀, determined by the polar ζ₀ and azimuthal ξ₀ angles (Fig. 1). Fig. 3 shows this dependency of R₂ on the deviation of Z₀ from the sample main axis Z_s. As can be seen, even small changes in the polar angle ζ₀ lead to significant changes in R₂ anisotropy, while changes in the azimuthal angle ξ₀ have a much smaller effect on the relaxation rate. The analysis above shows how the transverse relaxation rate depends on the nanoscale ordering of a set of nanocavities, and specifically the average orientation and the standard deviation around this orientation (Figs. 2 and 3). To consider the effect of the orientational distributions on the relaxation time T₂, we use Eq. (9) to calculate the dimensionless value ηT₂ according to,

$$\eta T_2({\theta }_S)=\frac{\eta }{\langle R_2({\theta }_s)\rangle },$$ (12)

Fig. 3.

Angular dependency of the normalized transverse relaxation rate $\langle {\overline{R}}_2({\theta }_S)\rangle$ on the deviation of the averaged orientation Z₀ from the main sample axis Z_s, for fixed distribution pattern given by σ_ξ = 0.1 and σ_ζ = 0.1. The solid black lines are calculated according to Eq. (3) for an ensemble of nanocavities, which are perfectly oriented along the sample axis Z_s (i.e., zero SD, ξ₀ = 0, and ζ₀ = 0). (a) $\langle {\overline{R}}_2({\theta }_S)\rangle$ for fixed ξ₀ = 0, and varying ζ₀ equal to 0.2, 0.4, 0.6, and 0.8 (blue dashed, green dotted, red dash-dotted, and light brown dotted lines respectively). (b) $\langle {\overline{R}}_2({\theta }_S)\rangle$ for fixed ζ₀ = 0, and varying ξ₀ set to 0.2, 0.8, 1.4, 2.0, and 0.8 (blue dashed, green dotted, red dash-dotted, and light brown dotted lines respectively). All curves were calculated using Eq. (11).

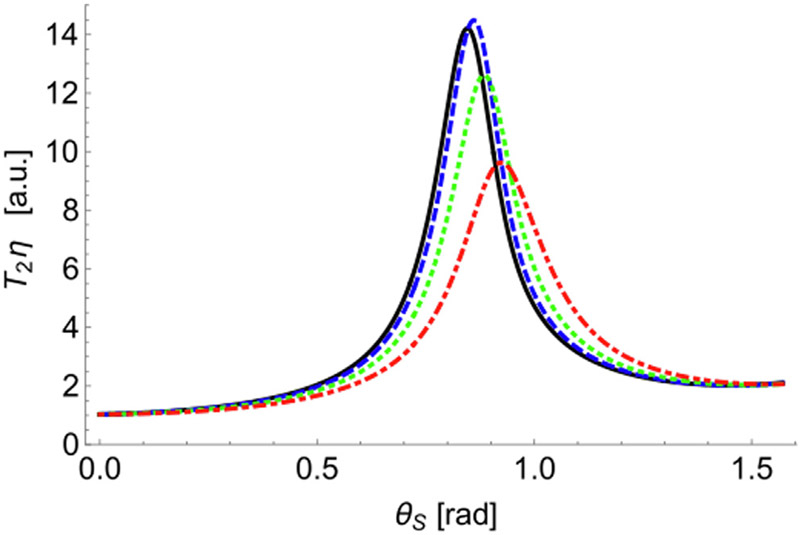
Fig. 4 shows the dependency of ηT₂ on the standard deviations σ_ζ and σ_ξ. The maximum of the relaxation time shifts to higher values of θ_s, and decreases by a factor of ~1.5 as the standard deviation of the azimuthal angle σ_ξ increases.

Fig. 4.

Relaxation time T₂ multiplied by the factor η as a function of the SD of the azimuthal angle and fixed SD of the polar angle σ_ζ = 0.1. Curves correspond to σ_ξ = 0.3, 0.6, 1.0, and 1.7 (black solid, blue dashed, green dotted, and red dot-dashed curves). All curves were calculated using Eq. (12).

3. Methods

3.1. Preparation of celery samples

Fig. 5a presents a schematic view of an axial slice of a fresh celery stem, marked with two regions of interest (ROIs). Fig. 5b and 5c contain light microscopy images of a transverse section of a fresh celery stem, showing the structural variations of celery at 2 μm² pixel resolution. Each image in Fig. 5b and 5c covers a tissue region of 2.8 × 2.0 mm².

Fig. 5.

Transverse vibratome-cut section of a stem celery (a). The areas from which samples were cut out. Sample #1, outer (lateral) part of the stem celery (red inset); sample #2, core part of the stem celery (blue inset). (b-c) Microscopic images of sample ROIs #1 & #2 respectively [x, xylems; ph, phloems; c, collenchyma; c, parenchyma; e, epidermis].

Four types of tissue structure can be identified inside of a celery stem: the vascular bundles that include water-transporting xylems (marked by ‘x’ in Fig. 5b); nutrient-transporting phloems (marked by ‘ph’ in Fig. 5b); collenchyma that provides support for rigidity of the plant (marked by ‘c’ in Fig. 5b); and parenchyma that is isodiametric ground tissue (marked by ‘p’ in Fig. 5b and 5c). The outmost layer of a celery stem is the epidermis (skin, marked by ‘e’ in Fig. 5b and 5c). The vessels of the xylem and phloem are formed by overlapping cells that form hollow cavities connected into one long micrometer-diameter tube. Collenchyma consists of elongated living cells filled with water and is located along the outer edges of the stem and tissue of the vascular bundle, being in a longitudinal orientation. Collenchyma cells do not divide as much as the surrounding parenchyma cells. Importantly, the cell walls have a fibril structure and consist of nanofibers with a diameter in the range of 6–25 nm [28-31]. The parenchyma consists of non-oriented living cells filled with water and cell fluid, which are larger in diameter and often shorter than that of collenchyma [29]. Water is also part of the fibril structure and is located between microfibrils, presumably serving to stabilize them due to hydrogen bonds. Since a fresh celery is very hydrated and contains up to 95% water, the NMR signal comes mainly from water molecules.

Two test samples were used in this study, both cut from fresh celery purchased from local supermarkets.

3.1.1. Celery sample #1

Sample #1 was cut out from the outer (lateral) part of the celery stem in the form of a small piece of about 1 cm long and 2 × 2 mm² cross-section [33]. The sample consisted mainly of collenchyma, xylem, and phloem (Fig. 5b), with minimal parenchyma. Thus, Sample #1 contains mainly the oriented fibril tissues without the epidermis (i.e., without the skin, marked by ‘e’ in Fig. 5b). The sample was placed in an empty glass tube before scanning.

3.1.2. Celery sample #2

Sample #2 was cut out from the inner (core) part of the celery stem. Its dimensions were about 2.5 cm long and 0.9 × 0.9 mm² cross-section and consisted of mainly parenchyma without the epidermis (i.e., without the skin, marked by e in Fig. 5c). These parenchyma cells consist of cellulose microfibrils, which are characterized by uniform orientation, and has the potential to show a magic angle effect [29-31]. The celery sample was placed in an Eppendorf tube filled with Fluorinert, which does not produce any MR signal. This helped in keeping the external magnetic field as homogeneous as possible, while ensuring that the only signal arrives from water molecules inside the celery.

3.2. NMR scans

3.2.1. Sample #1 scans

¹H NMR scans were carried out at ambient temperature (293 ± 0.5 K) using a Tecmag pulse solid state NMR spectrometer, a home-built NMR probe and an Oxford superconducting magnet of 8.0 T . The spin–spin, transverse, relaxation times T₂ were measured using the Carr-Purcell-Meiboom-Gill (CPMG) pulse sequence [32]. Remaining experimental details are presented in [33].

3.2.2. Sample #2 scans

MRI experiments on Sample #2 were performed on the Bruker Biospec 7 T MRI magnet, running a Paravision 6.0 software. Scans consisted of a high-resolution morphologic scan (RARE), eleven multi echo spin echo (MESE) scans to measure T₂ at different angles, and a diffusion tensor imaging (DTI) scan used to correct diffusion related bias of T₂ measurements [34,35].

A 360° rotating bed was used to rotate the sample while inside the MRI scanner. The bed is shown in Fig. 6 and consists of a circular steering wheel located outside the scanner, which is connected through a cogwheel rack to a rotating test tube base located inside the scanner. This allowed to scan the sample at different angles, without the need to extract and re-insert the sample between scans, thereby largely reducing inter-scan variability which might result from repeating the matching, tuning, and shimming calibration steps. The sample was centered within a test Eppendorf tube in order to maintain the field of view (FOV) as small as possible.

Fig. 6.

The 3D printed rotating bed device used in this study, allowing rotation of the sample while inside the MRI scanner. The ability to image at different angles without the need to extract and reinsert the sample reduces spurious variability due to the need to repeat the processes of matching, tuning, and shimming between scans.

MESE scans parameters were: N_Echoes = 32, TE = 18 ms, N_slices = 9, slice-thickness = 0.8 mm, in-plane resolution = 0.375 × 0.375 mm², FOV = 36 × 36 mm², and a total scan time of 4:48 min. Sample main axis orientation with respect to B₀ was set to 0°, 9°, 18°, 27°, 36°, 45°, 54°, 63°, 72°, 81°, 90° degrees. DTI scan parameters included TE = 18 ms, TR = 3000 ms, N_averages = 3, N_slices = 5, slice-thickness = 0.5 mm, in-plane resolution = 0.5 × 0.5 mm², and FOV = 32 × 32 mm². Diffusion encoding used four b values = 0, 200, 500, 1000 sec/mm² along 3 orthogonal directions and a total scan time was 11:42 min.

4. Results and discussion

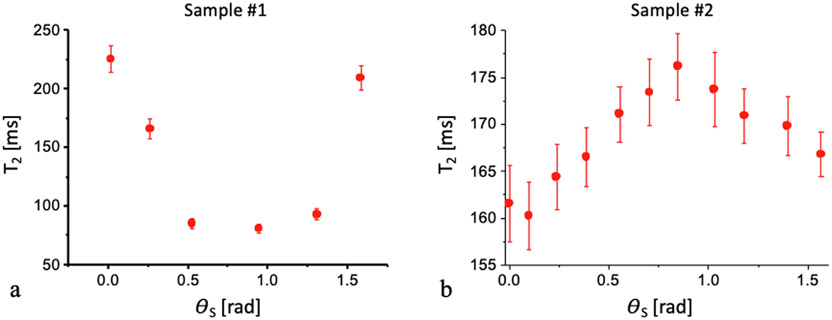
Fig. 7 shows the dependence of the relaxation time T₂ on the angle between the main sample axis and H₀ for the two assayed samples. A clear dependency was observed with extremum values at different values of the angle θ_s.

Fig. 7.

Transverse relaxation time T₂ (ms) as a function of the rotation angle (rad) for sample #1 (a) and sample #2 (b) (panel (a) is reproduced with permission from [33]

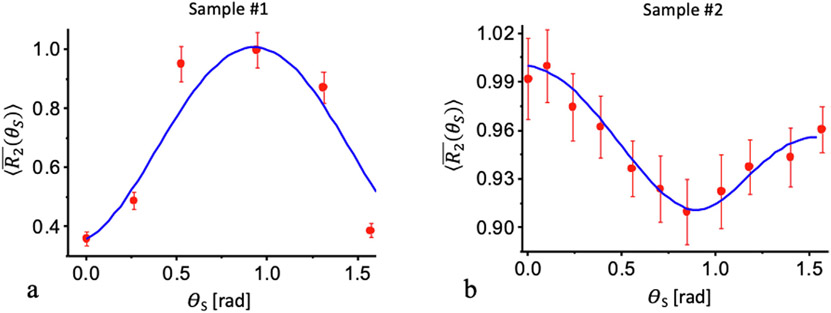
The model resented herein allows to search for the angular distribution and average direction of nanocavities which best fits the experimental measurements of the relaxation rates. Fitting to the model yielded SD and average directions of σ_ζ = 0.33; σ_ξ = 0.1; ζ₀ = 2.3; ξ₀ = 0.1 for sample #1 and σ_ζ = 1.18; σ_ξ = 0.8; ζ₀ = 0.36; ξ₀ = 1.5 for sample #2 (both ζ₀ and ξ₀ are in unit of radians). Fig. 8 presents the averaged transverse relaxation rates calculated according to Eq. (11) overlaid on the experimentally measured data.

Fig. 8.

Angular dependence of the transverse relaxation rate in the celery. Red circles mark the experimentally measured relaxation rate value, while the blue solid line represent the theoretically fitted model. (a) Normalized relaxation rate$\langle {\overline{R}}_2({\theta }_S)\rangle$, measured using a CPMG pulse sequence for sample #1 (data reproduced with permission from [33]). (b) $\langle {\overline{R}}_2({\theta }_S)\rangle$ values for sample #2, measured using an imaging MESE protocol and fitted using the echo modulation curve (EMC) algorithm. The solid blue curves are calculated according to Eq. (8) with the parameters of σ_ζ = 0.33; σ_ξ = 0.1; ζ₀ = 2.3; ξ₀ = 0.1 for sample #1 and σ_ζ = 1.18; σ_ξ = 0.8; ζ₀ = 0.36; ξ₀ = 1.5 for sample #2.

Good agreement is achieved for both assayed samples, which exhibit different orientational dependency. To interpret these results, we consider the microscopic and morphological structures of the celery. According to Fig. 1, the polar and azimuthal angles (ζ₀ and ξ₀) determine the deviation of the average orientation of all nanocavities Z₀ from the main sample axis Z_S. For the polar angles, the model fits the experimental data best when ζ₀ = 2.3 and σ_ζ = 0.33 for sample #1, and ζ₀ = 0.36 and σ_ζ = 1.18 for sample #2. The value of ζ₀ for Sample #1 (2.3 rad, 131.8°) means that the average orientation of the nanocavities is almost perpendicular to Z_S. Sample #2 on the other hand produced ζ₀ = 0.36 rad, or 20.6° meaning that the average axis of nanocavities is almost in parallel to Z_S. This illustrates the different in the nanoscopic morphology of the two specimens, which is congruent with the microstructural differences between the two samples as shown in Fig. 5b-c. In addition, a much smaller variability was observed in the polar angle of sample #1 (σ_ζ = 0.33) compared to sample #2 (σ_ζ = 1.18), meaning that the first sample exhibited higher degree of internal ordering.

With regard to the azimuthal angle ξ₀, the model fits best when ξ₀ = 0.1 and σ _ξ = 0.1 for sample #1, and ξ₀ = 1.5 and σ_ξ = 0.8 for sample #2. These values also reflect the morphological differences between the two samples: sample #1 contains mostly the organized nanocavities with small baseline and variability of the azimuthal angle, while sample #2 contains mostly isodiametric ground tissue (parenchyma), characterized by large azimuthal angle and large standard deviations around the mean.

To summarize, good agreement is achieved between the theoretical and experimental values, indicating that the nanoscale ordering in sample #1 is higher than that in sample #2. The best agreement of calculations is achieved with the following values: in the sample #1 the average polar and azimuthal angles equal to ζ₀ = 2.3 and ξ₀ = 0.1, while for the sample #2 these angles came out to be ζ₀ = 0.3 and ξ₀ = 1.5, respectively. These angles determine the average directions of the nanocavities relative to the probe axes. On one hand various orientations of the samples inside the probes can explain different angular positions of the maxima and minima of the relaxation rates (Fig. 8). On the other hand, the average direction Z₀ relative to the sample axis Z_S can be considered as one of the structural ordering parameters of the fibril tissue.

As can be seen in Fig. 5, the physical dimensions of the anatomic structures in celery are in tens of microns (from 60 to 80 μm in parenchyma, to 8–10 μm in collenchyma). Hence the water molecules inside each biological structure (e.g., parenchyma) should have an isotropic motion. However, the walls of parenchyma, which consist of layers of cellulose microfibrils with uniform orientation, are much smaller in dimension and highly anisotropic, which can be used to explain the marked differences in the polar and azimuthal angles in samples #1 and #2.

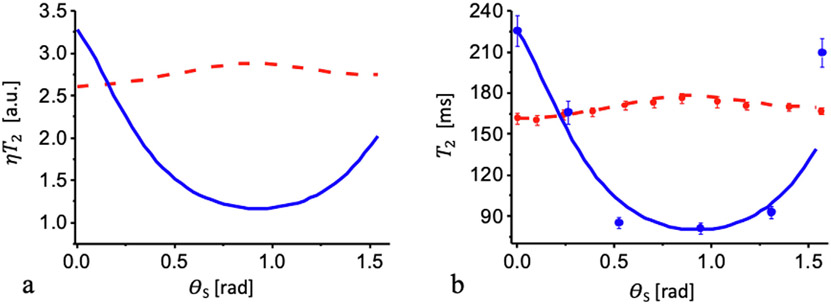
Significant differences in the experimentally obtained angular dependence of relaxation times from different parts of the sample (Fig. 8) can be explained based on the examples shown previously in Figs. 2 and 3. Fig. 9 presents the results of calculation multiplied by factor η according to Eq. (12) with the parameters obtained for fitting the experimental results for the relaxation rates above: σ_ζ = 0.33; σ_ξ = 0.1; ζ₀ = 2.3; ξ₀ = 0.1 for sample #1 and σ_ζ = 1.18; σ_ξ = 0.8; ζ₀ = 0.3; ξ₀ = 1.5 for sample #2. The factor can be found comparing the theoretical (Fig. 9a) and experimental (Fig. 7) relaxation times T₂: η = (1/67.8) = 1.46 × 10⁻² for sample #1 (Fig. 9b), and η = (1/61.8) = 1.62 × 10⁻² for sample #2 (Fig. 9b). These values can now be used to estimate the characteristic volume for a nanocavity according to Eq. (8). Assuming nanocavities having elongated ellipsoidal shape where a⪢b the form factor is equal to F ≈ 2π/3 [36], the spin density for water is ρ = 66 spin/nm³, and the term γ²h is equal to 2π × 0.120 nm³/ms. The resulting volumes are 7.7 × 10⁵ nm³ for sample #1 and 6.0 × 10⁵ nm³ for sample #2. For b ≈ 10 nm [29], the length of the nanocavity for the first and second samples will be about 1430 nm and 1840 nm, respectively. A precise verification of these modeling results awaits further experiments.

Fig. 9.

Angular dependency of the transverse relaxation time T₂. (a) T₂ multiplied by the factor η. (b) The transverse relaxation time T₂: blue dot – experimental data for sample #1; red dot – for sample #2. Solid blue and dashed red curves are calculated according to Eq. (12) for sample #1 and sample #2, respectively. Values of the factors are given in the text.

5. Conclusions

In this study we performed experimental and theoretical investigation of the angular dependence of water transverse relaxation time in a celery plant stem. Experimental results were interpreted within the framework of the previously developed theory [14-18], in which the fibril structure of biological tissues is represented as a set of aqueous nanocavities containing water, while the transverse relaxation time is determined by the dipole–dipole spin interaction which are affected by the restricted tumbling and rotational motion of water molecule inside the nanocavities.

This model is successfully applied to explain the anisotropy of R₂ relaxation rate in fibril tissues. Good agreement was achieved between the calculations and experimental data with the use of few fitting parameters: the standard deviations of the bivariate Gaussian distribution of the nanocavities, and the polar and azimuth angles of their averaged direction. The approach allows the use of NMR data for quantitative determination of the nanostructural ordering of biological tissues non-invasively and non-destructively. We have shown that dependence of the relaxation time on the angle between the magnetic field and the main axis of the sample makes it possible to identify the nanoscale properties of fibrillar tissues [37].

An important feature of this study is that we were able to determine the degree of orientational ordering of nanocavities in the celery and the average direction of nanocavities with respect to the orientation of the sample. The obtained values of standard deviations (σ_ζ = 0.33 and σ_ξ = 0.1 for sample #1 and σ_ζ = 1.18 and σ_ξ = 0.8 for sample #2) indicate a noticeable ordering of the cavities in the first sample and less ordering in the second sample, which agree with the microscopic images of celery stem.

Our approach showed that NMR can be used to study the microscopic vascular structure of plants. Variations in these structures can be associated with the economic characteristics of plants, for example, high / low yields of food crops or long / short growth times of vegetables [38,39]. Since NMR and MRI methods are completely non-invasive and non-destructive, they can be used to study the fine vascular structures of living organisms both in situ and in vivo, as well as to diagnose human pathology that involves changes to the tissues’ nanostructure, e.g., around collagen rich tissues like tendons and cartilage [40].