Abstract
Autonomously firing GABAergic neurons in the external globus pallidus (GPe) form a local synaptic network. In slices, most GPe neurons receive a continuous inhibitory synaptic barrage from 1 or 2 presynaptic GPe neurons. We measured the barrage’s effect on the firing rate and regularity of GPe neurons in male and female mice using perforated patch recordings. Silencing the firing of parvalbumin-positive (PV+) GPe neurons by activating genetically expressed Archaerhodopsin current increased the firing rate and regularity of PV– neurons. In contrast, silencing Npas1+ GPe neurons with Archaerhodopsin had insignificant effects on Npas1– neuron firing. Blocking spontaneous GABAergic synaptic input with gabazine reproduced the effects of silencing PV+ neuron firing on the firing rate and regularity of Npas1+ neurons and had similar effects on PV+ neuron firing. To simulate the barrage, we constructed conductance waveforms for dynamic clamp based on experimentally measured inhibitory postsynaptic conductance trains from 1 or 2 unitary local connections. The resulting inhibition replicated the effect on firing seen in the intact active network in the slice. We then increased the number of unitary inputs to match estimates of local network connectivity in vivo. As few as 5 unitary inputs produced large increases in firing irregularity. The firing rate was also reduced initially, but PV+ neurons exhibited a slow spike-frequency adaptation that partially restored the rate despite sustained inhibition. We conclude that the irregular firing pattern of GPe neurons in vivo is largely due to the ongoing local inhibitory synaptic barrage produced by the spontaneous firing of other GPe neurons.
SIGNIFICANCE STATEMENT Functional roles of local axon collaterals in the external globus pallidus (GPe) have remained elusive because of difficulty in isolating local inhibition from other GABAergic inputs in vivo, and in preserving the autonomous firing of GPe neurons and detecting their spontaneous local inputs in slices. We used perforated patch recordings to detect spontaneous local inputs during rhythmic firing. We found that the autonomous firing of single presynaptic GPe neurons produces inhibitory synaptic barrages that significantly alter the firing regularity of other GPe neurons. Our findings suggest that, although GPe neurons receive input from only a few other GPe neurons, each local connection has a large impact on their firing.
Keywords: autonomous firing, basal ganglia, collateral network, globus pallidus, oscillations, recurrent inhibition
Introduction
Neurons in the external globus pallidus (GPe) are thought to encode information about volition and movement in the changes of their firing rates and patterns and transmit this information to neurons in all other basal ganglia nuclei (Mink, 1996; Bergman et al., 1998; Bevan et al., 2002; Kita, 2007; Wilson, 2013, 2017; Gittis et al., 2014; Hegeman et al., 2016; Courtney et al., 2021). In vivo, GPe neurons exhibit highly irregular firing and a wide range of firing rates (DeLong, 1971; Wichmann and Soares, 2006; Elias et al., 2007; Mallet et al., 2012; Ketzef and Silberberg, 2021). These high entropy spike trains could in principle be information rich (Cruz et al., 2009), but this depends on the origin of irregular firing, which has never been identified. Firing rate heterogeneity in the GPe arises partly from intrinsic membrane properties (Mercer et al., 2007; Deister et al., 2013; Abdi et al., 2015), while the fine temporal structure of each neuron’s spike train is due to synaptic input, especially GABAergic synaptic input. When glutamatergic synaptic input is blocked locally, GPe neurons spike less rapidly and slightly more rhythmically. When GABAergic input is subsequently blocked, GPe neurons spike autonomously at a rate near their original rate and become highly rhythmic (Kita et al., 2004).
Most synapses in the GPe are GABAergic. They arise primarily from striatal projection neurons but also from local axon collaterals of other GPe neurons (Shink and Smith, 1995). Although the local collaterals account for only a small proportion of the GABAergic synapses, each forms multiple large synapses, which constellate in basket-like connections on cell bodies and proximal dendrites (Kita and Kitai, 1994; Sadek et al., 2007). These connections can produce powerful inhibitory currents (Sims et al., 2008; Bugaysen et al., 2013), which occur spontaneously at intervals matching the rate and regularity of the presynaptic neuron’s autonomous firing (Higgs et al., 2021). The spontaneous activity and synaptic organization of GPe neurons make them a good candidate for the origin of firing irregularity in the GPe.
A large fraction of GPe neurons (∼50%) are GABAergic, express parvalbumin (PV) (Hernández et al., 2015), and project to classic indirect pathway targets, the subthalamic nucleus (STN), the SNr, and the internal globus pallidus (Sato et al., 2000). Some of these neurons also send collaterals to the striatum (Bevan et al., 1998). Another set of GPe neurons (∼30%) are also GABAergic, express Npas1 instead of PV (Hernández et al., 2015), and do not participate in the indirect pathway but project either exclusively to the striatum (Sato et al., 2000) or to the cortex and/or thalamus (Abecassis et al., 2020) but not to the STN. PV+ neurons have higher intrinsic firing rates with more regular intervals (Hernández et al., 2015) and form more local synapses (Mallet et al., 2012; Fujiyama et al., 2016) compared with Npas1+ neurons.
Local collaterals of GABAergic GPe neurons form a sparsely connected synaptic network (Bar-Gad et al., 2003; Bugaysen et al., 2013). A network model of PV+ GPe neurons based on their physiological and anatomic properties predicts that, while GPe neurons receive input from few other GPe neurons, each unitary local connection has a large effect on the firing of the postsynaptic neuron (Olivares et al., 2022). In slices, GPe neurons receive unitary currents from 1 or 2 active, presynaptic PV+ GPe neurons (Higgs et al., 2021). In this study, we revealed the effects of the unitary local currents on the firing rate and regularity of PV+ and Npas1+ GPe neurons. First, we suppressed the local currents and measured the effects on firing. We then simulated the conductance produced by unitary inputs, scaled the number of unitary inputs to in vivo levels, and determined its effects on firing. Finally, we modeled GPe neurons based on their intrinsic rate, phase-resetting curves (PRCs), and spike-frequency adaptation to identify the factors that determine the effects of local inhibition on firing.
Materials and Methods
All experimental procedures followed National Institutes of Health guidelines, and all animal experiments were approved by the Institutional Animal Care and Use Committee of the University of Texas at San Antonio.
Animals
Experiments were performed on brain slices from male and female transgenic mice (Table 1) at least 4 weeks of age.
Table 1.
Transgenic mice used for experiments
| Applications | Mouse strain | Breeders | No. of mice |
|---|---|---|---|
| Transduce PV+ neurons | PV-Crea | — | 10 |
| Identify and transduce PV+ neurons | PV-Cre-tdTomato | PV-Cre,a Ai14b | 17 |
| Identify and silence PV+ neurons | PV-Arch-GFP | PV-Cre,a Ai40Dc | 10 |
| Identify and transduce Npas1+ neurons | Npas1-Cre-tdTomatod | — | 36 |
aB6.129P2-Pvalbtm1(cre)Arbr/J.
bB6.Cg-Gt(ROSA)26Sortm14(CAG-tdTomato)hze/J.
cB6.Cg-Gt(ROSA)26Sortm40.1(CAG-aop3/EGFP)Hze/J.
dC57BL/6-Tg(Npas1-icre,-tdTomato)1Cschn/J.
Viral construct injection
For silencing GPe neurons of identified cell types using the inhibitory opsin Archaerhodopsin (Arch), AAV9-Flex-Arch-GFP (AAV9.Flex.CBA.Arch-GFP.WPRE.SV.40, University of Pennsylvania Vector Core) was injected into the GPe of PV-Cre, PV-Cre-tdTomato, or Npas1-Cre-tdTomato mice (Table 1, The Jackson Laboratory). We injected viral constructs 0 mm anterior, 2.5 mm lateral, and 3.0 mm ventral to bregma. Electrophysiological or histologic experiments were performed on brain slices from injected mice 4-8 weeks after injection.
Histology
After the postinjection period, PV-Cre and Npas1-Cre-tdTomato mice were deeply anesthetized with 5% isoflurane and perfused with 10 ml PBS followed by 20 ml 4% formaldehyde solution. Brains were extracted and stored in 4% formaldehyde overnight, and then stored in 30% sucrose solution at 4°C the following night; 50 μm sagittal sections were prepared using a frozen microtome. Slices containing the GPe were mounted on glass slides, covered, and allowed to dry for 2 nights in the dark at 4°C. Slides were imaged with 5×, 20×, and 40× objectives and a 16-bit depth with Zen Black software using a Zeiss LSM-710 confocal microscope (Carl Zeiss).
Brain slice preparation for recording
Mice were deeply anesthetized with isoflurane and killed by decapitation; 300 μm coronal brain slices containing the GPe were prepared using a Leica Vibratome in ice-cold cutting solution containing the following (in mm): 110 choline chloride, 2.5 KCl, 1.25 NaH2PO4, 0.5 CaCl2, 7 MgSO4, 25 glucose, 11.6 Na ascorbate, 3.1 Na pyruvate, and 26 NaHCO3, bubbled with 95% oxygen, 5% carbon dioxide. Slices were collected in ACSF containing the following (in mm): 126 NaCl, 2.5 KCl, 1.25 NaH2PO4, 2 CaCl2, 1 MgSO4, and 10 glucose, bubbled with 95% oxygen, 5% carbon dioxide. The slice storage ACSF (but not the recording ACSF) also contained the following (in mm): 0.005 glutathione, 1 Na ascorbate, and 1 Na pyruvate. Slices were heated to 34°C for 30 min and then allowed to cool to room temperature until use.
Recording
Slices were superfused continuously with oxygenated ACSF heated to 33°C-35°C. In all experiments, glutamatergic transmission was blocked by bath-applying NBQX (5 μm) and CPP (2 μm). In some experiments, GABA-A receptors were blocked by bath-applying SR-95531 hydrochloride (gabazine, 10 μm), or GABA-B receptors were blocked by bath-applying CGP 55845 hydrochloride (1 μm). Neurons were visualized with an Olympus BX51WI microscope with a 40× water-immersion objective and Dodt gradient contrast optics. Fluorescent-labeled neurons were identified by epifluorescence.
A total of 156 of 184 neurons were recorded using the perforated patch-clamp technique. Filamented borosilicate glass capillary recording pipettes (G150F-4; Warner Instruments) were pulled to resistances of 4-7 mΩ using a Flaming-Brown pipette puller (model P-97; Sutter Instruments). The pipette tip was filled with the following (in mm): 140 KMeSO4, 10 HEPES, 7.5 NaCl, and 0.1 phosphocreatine, and the pipette was then back-filled with the same solution containing 1 μm Gramicidin-D (MP Biomedicals). After forming a gigaseal, 10-30 min were allowed for gramicidin to perforate the membrane to establish sufficient electrical access (20-70 mΩ); 27 of 184 neurons were recorded using the cell-attached technique. For cell-attached recordings, 4-7 mΩ pipettes were filled with the same pipette solution that was used for perforated patch recordings, but without the addition of Gramicidin-D. The data in Figure 5A were recorded using whole-cell voltage clamp. For whole-cell recordings, glass pipettes (World Precision Instruments) were pulled to resistances of 3-5 mΩ, and the pipette solution contained the following (in mm): 140.5 KCl, 7.5 NaCl, 10 HEPES, 0.2 EGTA, 2 Mg-ATP, and 0.21 Na-GTP.
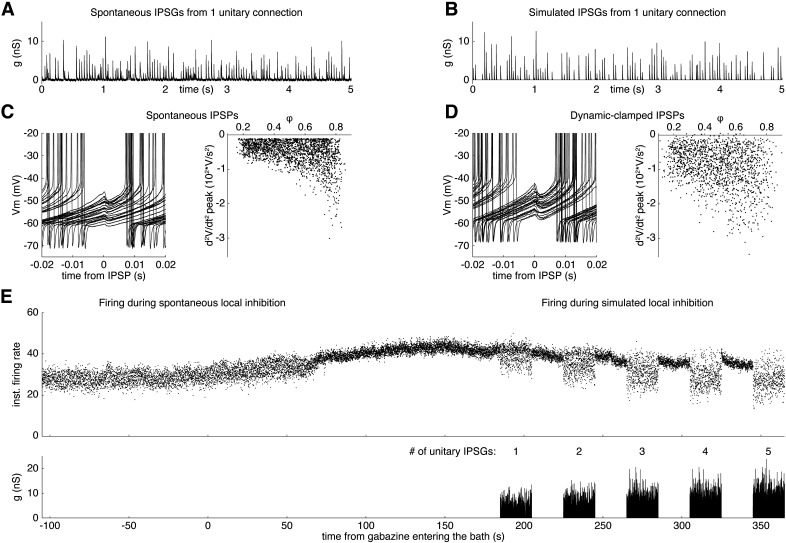
Figure 5.
Simulating spontaneous GABAergic synaptic inhibition from unitary local connections using dynamic clamp. A, Whole-cell voltage-clamp recording of spontaneous IPSG trains produced by a unitary synaptic connection. B, Conductance waveform simulating a single unitary input. C, Left, Overlay of spontaneous IPSPs. Right, Dependence of IPSP amplitude on the phase of oscillatory spiking. D, Left, Overlay of IPSPs simulated by injecting the waveform in B using dynamic clamp. Right, Dependence of IPSP amplitude on phase. E, Top, Instantaneous firing rate as a function for time of the neuron in C, D before and during gabazine wash-on. Bottom, Waveform of the simulated inhibitory conductance.
All recordings were obtained using a MultiClamp 700B amplifier (Molecular Devices) connected to an ITC-18 A/D converter (HEKA Instruments) and a Macintosh computer running custom software written in Igor Pro (WaveMetrics). A second computer running RTXI (Real-Time eXperiment Interface; www.rtxi.org) and using a National Instruments PCIe-6251 analog-to-digital board was used to apply simulated inhibitory postsynaptic conductance (IPSG) trains. Conductance waveforms were prepared offline, and dynamic current, calculated from the conductance waveform and the membrane potential, was injected into the cell using RTXI. Data were low pass filtered at 10 kHz and sampled at 20 or 40 kHz.
Arch activation
Arch current was activated using light produced by an LED (Mightex) and directed at the GPe through the microscope objective via a green excitation (550 nm) filter cube. We selected the minimum light level that silenced firing for the full 10 s stimulation period but did not prevent recovery of baseline firing at light offset; ∼1 mW light (measured over the entire illuminating cone of the objective) was sufficient to silence firing in transduced mice, and ∼4 mW light was necessary to silence firing in PV-Arch-GFP mice.
Detecting synaptic current and potential
Current and voltage data were analyzed in Mathematica (Wolfram). Traces were differentiated twice and smoothed by convolution with a Gaussian filter (0.8 ms SD). IPSCs and IPSPs produced negative deflections in the second derivative of the traces. To detect IPSCs, the threshold was set to −3.5 times the SD of the second derivative of each current trace. IPSC times were taken at the minimum value of each negative deflection crossing the threshold, which corresponded in time to the onset of each IPSC.
Negative peaks in the second derivative of the membrane voltage trace occur at the time of IPSP onset and correlate in size with IPSP amplitude. Action potentials also produce negative deflections in the second derivative. To prevent contamination of the IPSP data by action potentials, we did not analyze the second derivative within 5 ms of each action potential. To determine the optimal threshold for detecting IPSPs, we analyzed the second derivative of the membrane potential before and after bath application of gabazine (10 μm). For control and gabazine traces, excluding the spikes, we detected all negative peaks in the second derivative and calculated the relationship between set detection thresholds and the rate of detected events. Events detected in the gabazine trace were considered false events. The lowest detection threshold that yielded a false event rate <1/s in the gabazine trace was applied to the control trace to detect IPSPs. This method was used to detect IPSPs for Figures 3A–C, 4, and 5. Because we did not apply gabazine for Figure 3D–G experiments, we used the average threshold determined in gabazine experiments to detect IPSPs in these experiments.
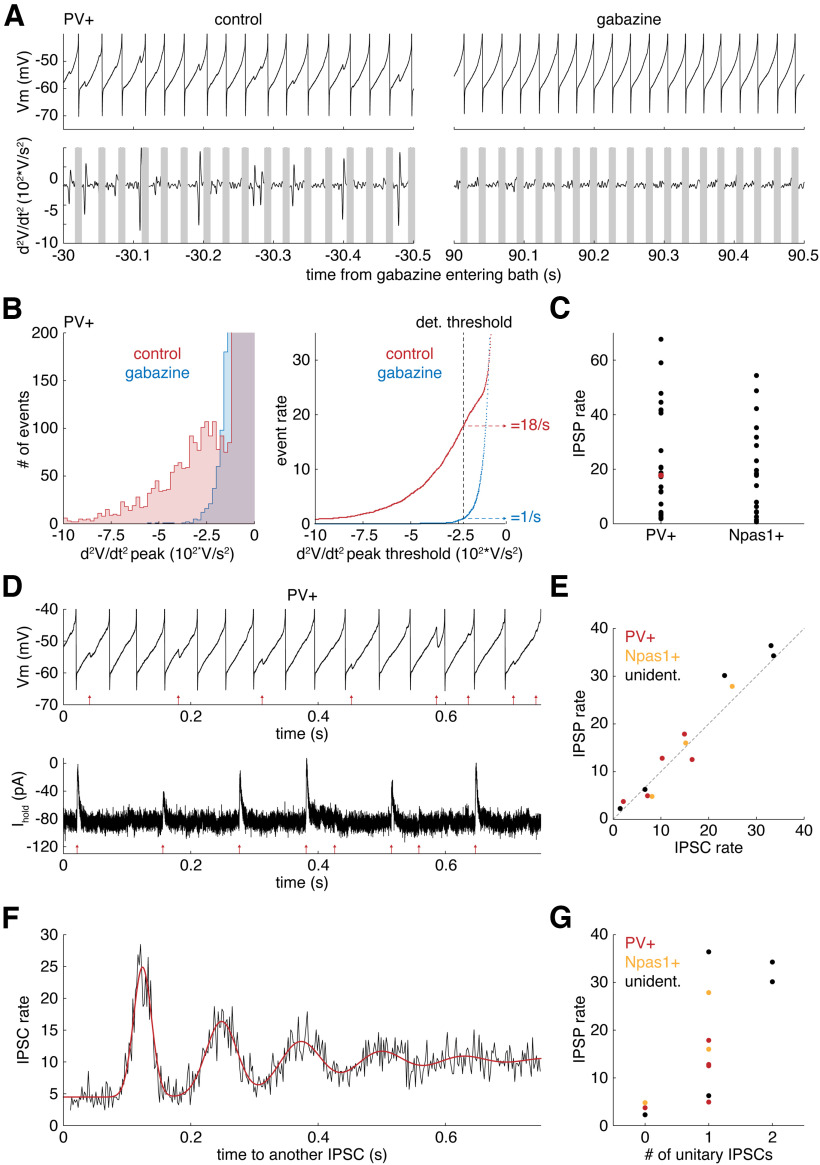
Figure 3.
Spontaneous GABAergic synaptic potentials from unitary local connections can be detected accurately during firing. A, Top, Vm and (bottom) the second derivative of Vm for a PV+ neuron (left) in control solution and (right) during gabazine bath application. B, Left, Histogram of negative peaks in the second derivative of the Vm. Right, Event rate plotted as a function of second derivative threshold. The data shown are from a single PV+ neuron. Red represents control solution. Blue represents gabazine solution. C, IPSP rates of PV+ neurons and Npas1+ neurons. Red dot is data from the neuron in B. D, Top, Membrane potential and (bottom) current recorded in a PV+ neuron. Red arrows indicate detected IPSP/IPSC times. E, IPSP rates versus IPSC rates recorded successively from GPe neurons. F, Autocorrelation of the IPSC times from the neuron in D with a sum-of-Gaussians model fit (red). G, The relationship between IPSP rate and the number of unitary IPSCs determined from the IPSC time autocorrelation.
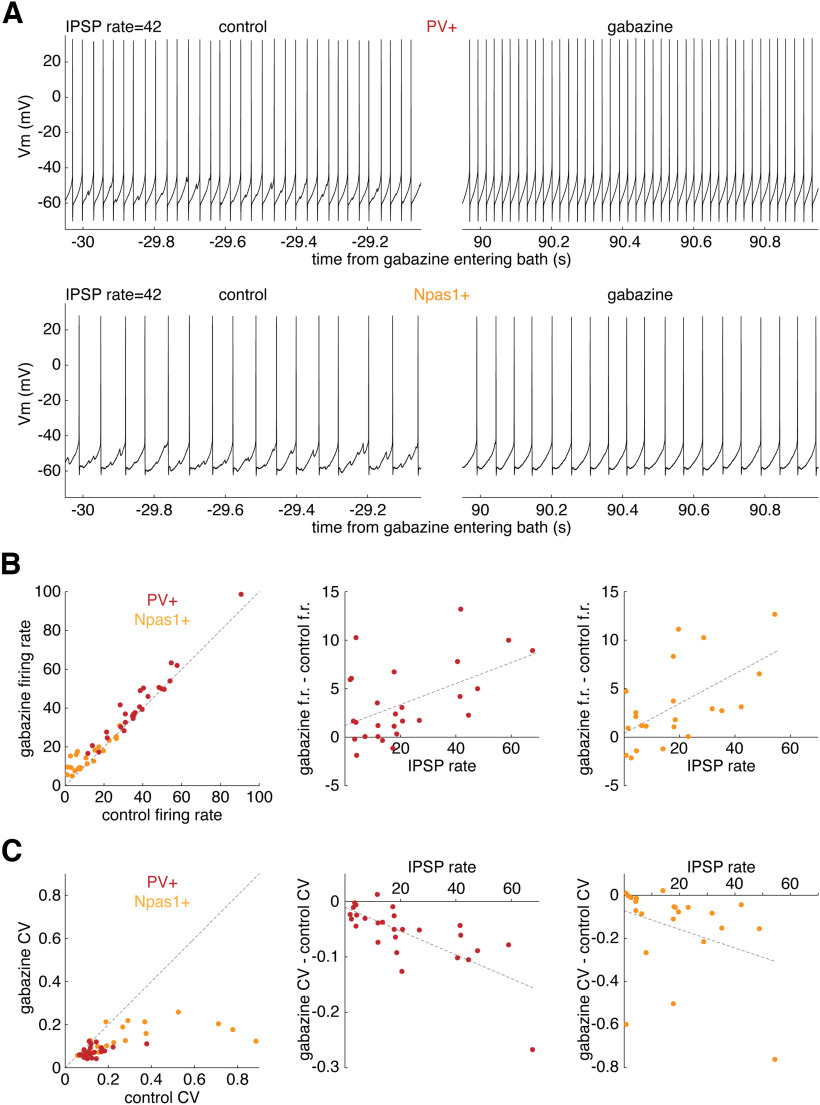
Figure 4.
Higher spontaneous IPSP rates produce larger reductions in the firing rate and regularity of PV+ neurons and Npas1+ neurons. A, Membrane potential of (top) a PV+ neuron and (bottom) an Npas1+ neuron (left) in control solution and (right) following gabazine bath application. B, Left, Relationship between the firing rates of PV+ neurons (red) and Npas1+ neurons (yellow) in gabazine and control solutions. Middle, Relationship between changes in rate because of gabazine and IPSP rates in PV+ neurons. Right, Same as middle but in Npas1+ neurons. C, Left, CVs of PV+ neurons and Npas1+ neurons in control and gabazine solutions. Middle, Relationship between changes in CV because of gabazine and IPSP rates in PV+ neurons. Right, Same as middle but in Npas1+ neurons.
Measuring IPSP amplitudes in repetitively firing neurons is complicated by the ongoing cyclic changes in membrane potential (Vm) on which the IPSPs are superimposed. Interspike Vm trajectories vary in shape among GPe neurons. Most IPSPs peaked 1-3 ms after onset, but the natural trajectory of the neuron may cause a substantial Vm change in this time, particularly in faster GPe neurons. Thus, the maximal negative deflection in voltage may not be an accurate measure of the IPSP amplitude, relative to the natural trajectory. In contrast, the second derivative of the interspike Vm is small across the natural trajectory except during the action potentials and IPSPs. For this reason, the peak negative deflection in the second derivative was used as a proxy of IPSP amplitude, rather than attempting to measure IPSP amplitude directly.
Analysis of the synaptic current time series
IPSCs from a unitary local connection recorded in voltage-clamp measurements were identified by the presence of a periodic component in the autocorrelation of IPSC times (Higgs and Wilson, 2016). The autocorrelation was obtained for IPSC time differences of 0.01-1.0 s with a bin width of 2 ms and was expressed as the expected value of the IPSC rate following a reference IPSC time. Time differences of 0-0.01 s between IPSCs were not analyzed because IPSCs may shadow the detection of other IPSCs during their falling phase. Autocorrelations with a periodic component were fit with the model described in detail in our previous studies (Higgs and Wilson, 2016; Higgs et al., 2021). Autocorrelations with a single periodic component were interpreted as a single unitary IPSC plus aperiodic, action potential-independent IPSCs, while those with two periodic components were interpreted as two unitary IPSCs plus aperiodic IPSCs. In essence, the Higgs and Wilson (2016) model is a sum of autocorrelations for each unitary IPSC train plus a constant term arising from aperiodic IPSCs and the cross-correlations of different unitary IPSC trains that are assumed to be uncorrelated with one another. The model estimates parameter values of each unitary input to produce a waveform that best fits the height, width, and damping of peaks in the autocorrelation. These values include the mean firing rate of the presynaptic neuron, the SD of the presynaptic interspike intervals (ISIs), and the success rate of the unitary synaptic connection. The model also estimates the rate of aperiodic IPSCs, which are assumed to represent miniature IPSCs.
Applying artificial unitary synaptic conductance trains by dynamic clamp
We used the statistics of unitary synaptic currents in GPe neurons reported in our previous study (Higgs et al., 2021) to construct conductance waveforms recapitulating the mean rate, amplitude, kinetics, and synaptic reliability of IPSG trains from unitary local connections. IPSG trains were produced by convolving an IPSG waveform with a pulse waveform having a single-point pulse at each IPSG onset time. The IPSG waveform was the sum of two exponential curves. The time constant of the rising portion was 0.28 ms, and the time constant of the falling portion was 2.36 ms when the IPSGs were applied to PV+ neurons and 4.49 ms for Npas1+ neurons, as this was the only statistical difference in the properties of the IPSGs recorded in these two cell types (Higgs et al., 2021). IPSG times were calculated from a simulated presynaptic neuron with a firing rate of 26.6 spikes/s, a CV of the ISI of 0.12 and a synaptic reliability of 0.7, producing an average IPSG rate of 18.6/s. IPSG amplitudes were drawn from a Gaussian distribution with a mean of 3.79 ± 3.79 nS, but the distribution was limited to amplitudes of 0.75-15.15 nS. Conductance waveforms were composed of 1-5 simulated unitary IPSGs. Dynamic current was calculated and injected by RTXI based on the conductance waveform, G(t), a GABAergic reversal potential (Erev) of −74 mV, and the Vm recorded in real time, as follows:
Spike-frequency adaptation
To measure spike-frequency adaptation in GPe neurons, we injected 20 s current pulses ranging from −100 to 90 pA in 10 pA steps, each followed by 20 s of no current injection, and measured the spike frequency responses of GPe neurons to current onset and offset. We fit the full 20 s of instantaneous firing rates (i.e., the inverse of each ISI) during current application, fcurrent(t), with exponential decay curves, as follows:
We set ω to the baseline firing rate (before current onset) and estimated the values of parameters Δωsteady, b, and τa that produced the best exponential curve fits. We fit the full 20 s of instantaneous firing rates after the current step, fno current(t), with exponential decay curves, as follows:
We estimated the values of b and τa that produced the best fit.
PRCs
The PRC quantifies the sensitivity of a rhythmically firing neuron’s ISI to external current input, as a function of the phase of the ISI at which the input arrives. We measured the infinitesimal PRCs (i.e., the PRC for small-amplitude input, scaled to the input amplitude) of GPe neurons using the method described by Wilson et al. (2014). We measured spike-time responses to a contiguous sequence of brief (0.25 ms) current pulses with amplitudes drawn from a Gaussian distribution centered at 0 pA with a SD of 40 pA. We divided ISIs into 40 time bins and calculated the charge, Q, delivered during each time bin for each ISI. Each time bin represents a phase of the spiking oscillation. We determined PRC values for each phase using a multiple linear regression. The independent variables were the charge delivered in each bin of each ISI, the dependent variables were the ISI lengths, and the regression coefficients provided the PRC values for each phase. All PRCs were fit with the 7-parameter ad hoc function used by Olivares et al. (2022) to yield PRC values as a smooth function of phase, Z(φ).
Phase model of GPe neurons
Using the experimentally measured infinitesimal PRC, Z(φ), a simple model can be constructed to estimate the change in spike time of a neuron produced by any arbitrary current, I(t) arriving during the ISI. In the absence of current input an oscillating neuron advances in phase, φ, at its intrinsic spike rate, ω, and current input changes the rate of phase advance with a sensitivity given by the PRC, as follows:
We built phase models of GPe neurons to predict their spike-time responses to conductance waveforms simulating input from 1 to 5 unitary synaptic connections. In this application of the model, the current input is not prespecified but is determined dynamically by a membrane potential variable that can be approximated as a function of phase, so I(t) becomes I(t, φ). We calculated the driving force of this current as the difference between the reversal potential (Erev), −74 mV, and the membrane potential at each φ during the natural unperturbed trajectory, or V(φ). To determine V(φ), the baseline interspike Vm trajectories of each neuron were sampled and averaged to obtain Vm as a function of spike oscillation phase (Simmons et al., 2018). I(t, φ) also included a zero-mean Gaussian white noise current, IN(0, σ), used to recreate the experimentally measured coefficient of variation (CV) of the ISI, as follows:
The SD, σ, of I(0, σ) was calculated based on the formula first introduced by Ermentrout et al. (2011) as follows:
Z(φ) accounts for the effects of I(t, φ) on the cycle during which it arrives. But current inputs can produce spike-frequency adaptation on a much slower timescale than one cycle (Benda and Herz, 2003). We added a spike-frequency adaptation variable, ωa, to account for this, as follows:
ωa opposed the effect of current input on the evolution of φ with the strength, a, and time course, τa, observed in real neurons, as follows:
In response to sustained negative current pulses, PV+ GPe neurons recovered to a steady-state spike frequency that was on average 56% (a = 0.56) of their baseline spike frequency. This spike-frequency adaptation occurred with an average decay time constant, τa, of 5.4 s. Because Npas1+ GPe neurons did not spike enough to fit exponential decay curves to their spike frequency responses to negative current, we used the average values of a and τa determined for PV+ neurons when incorporating spike-frequency adaptation into phase models of both PV+ and Npas1+ GPe neurons. The evolution of φ was estimated numerically using the Euler method with a time step of 0.05 ms to integrate the differential equations for dφ/dt and dωa/dt. When φ reached 1, indicating a spike, it was reset to 0.
Statistical comparisons
The data reported are mean ± SD, except as indicated otherwise. Paired comparisons were made using a Wilcoxon Signed-Rank Test. Comparisons of two group means were made using a Mann–Whitney U test. Comparisons of three or more related measures were made using a one-way repeated-measures ANOVA. Correlations were evaluated using a linear regression.
Results
The effect of spontaneous GABAergic synaptic input from local connections on the firing rate and regularity of identified PV+ and Npas1+ GPe neurons was measured in slice preparations. Striato-pallidal projections, the only other known source of GABA in the GPe, are severed in coronal slice preparations of the GPe. Action potential-independent GABA release from severed striato-pallidal axons can produce postsynaptic currents in GPe neurons, but these are aperiodic and occur at very low rates (Higgs et al., 2021). Importantly, a proportion of unitary local connections remain intact in coronal slices. GPe neurons can receive high rates of action potential-dependent synaptic currents from up to 2 active, intact presynaptic GPe neurons firing periodically (Higgs et al., 2021). This allowed us to isolate the effect of local inhibition from striato-pallidal inhibition. To isolate the effects of local GABA from any effects of spontaneously released glutamate, the AMPAR blocker NBQX (5 μm) and the NMDAR blocker CPP (2 μm) were bath-applied during all recordings. To maintain the natural internal chloride concentration of neurons and prevent changes in firing activity because of intracellular dialysis, all recordings of membrane potential were obtained using the perforated patch technique (see Materials and Methods).
PV+ neurons continuously reduce the firing rate and regularity of PV– neurons
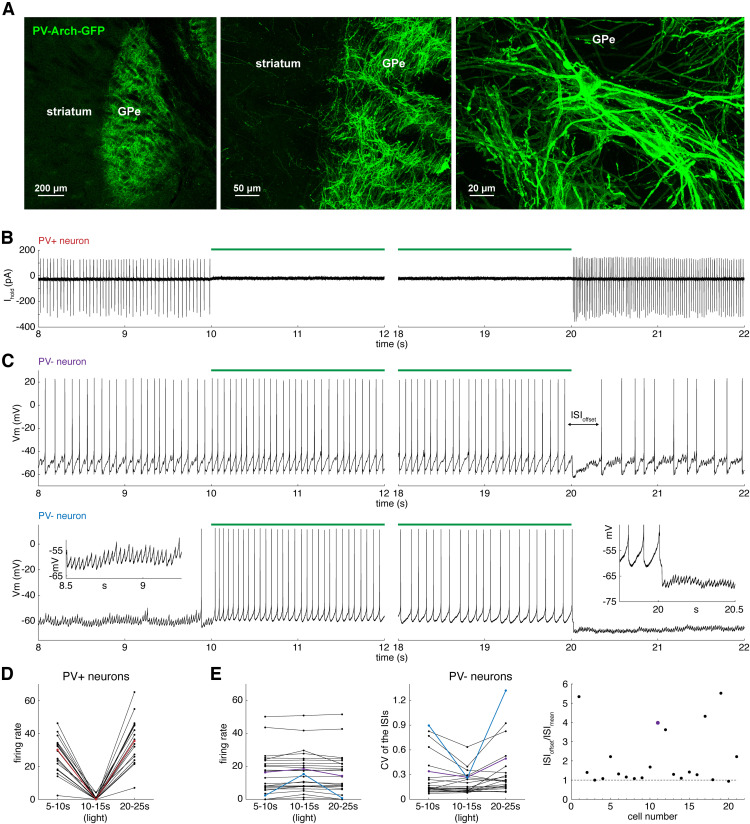
Spontaneous GABAergic currents in slice preparations of the GPe originate mostly from the spontaneous firing of PV+ GPe neurons (Higgs et al., 2021). In this study, we measured the effect of silencing the firing of PV+ neurons on the firing of the PV– neurons using brain slices from mice with Archaerhodopsin (Arch) expressed selectively in PV+ neurons. To induce Arch expression, we performed stereotaxic injection of AAV9-Flex-Arch-GFP into the GPe of PV-Cre mice or used PV-Arch-GFP mice (see Materials and Methods). AAV-encoded GFP expression in PV+ neurons is shown in Figure 1A. On 19 PV+ neurons from 7 mice, we performed cell-attached recordings of the firing responses to 10 s of green light, which activates Arch. We recorded for 10 s before, during, and after light for five trials. Firing rates during the first 5 s before, during, and after light were averaged across trials for each neuron. Green light reduced and usually abolished the firing of PV+ neurons (Fig. 1B). At light offset, PV+ neurons exhibited rebound increases in firing rate (Fig. 1B, right), which adapted back to baseline firing rates before the beginning of the next trial. We observed GPe neurons slowly adapt their firing frequency to a variety of stimuli in all experiments, and this phenomenon will be described in detail later in this study. The mean firing rate of PV+ neurons was 27.1 ± 10.7 spikes/s before, 0.6 ± 1.3 during, and 35.8 ± 13.3 after light (Fig. 1D).
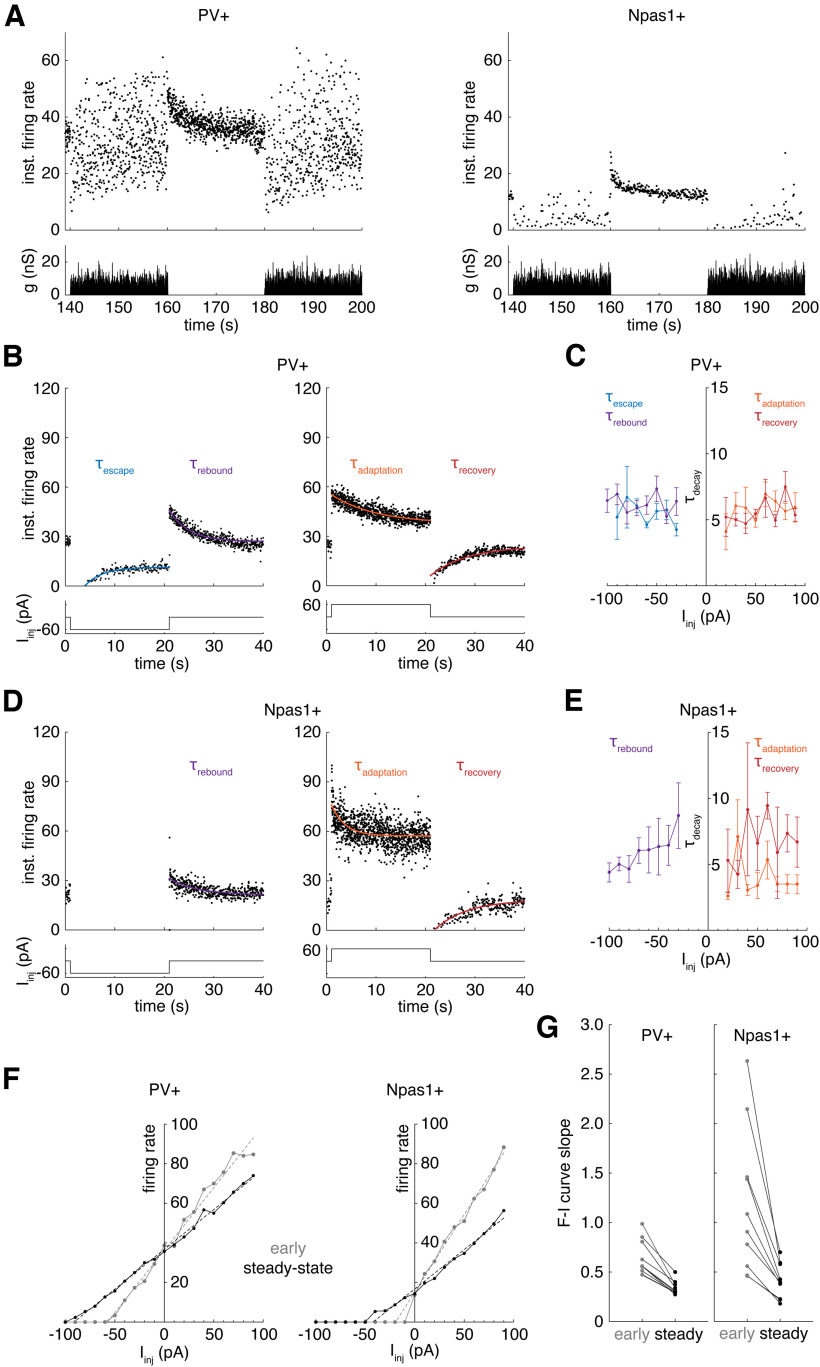
The spontaneous firing of PV+ neurons reduces the firing rate and regularity of PV– neurons. A, A sagittal section from a PV-Cre mouse injected with AAV9-Flex-Arch-GFP in the GPe. PV-Arch-GFP was imaged along the striato-pallidal border with (left) 5× and (middle) 20× objectives and (right) in the GPe with a 40× objective. B, Cell-attached recording of a PV+ neuron. Left, Onset and (right) offset of 10 s green light. C, Perforated patch recordings of two PV– neurons. D, Firing rate of PV+ neurons before, during, and after light. Red line indicates data from the neuron in B. E, Left, Firing rate of PV– neurons before, during, and after light. Middle, CV of the ISI of PV– neurons before, during, and after light. Right, ISI of PV– neurons at light offset normalized by the mean ISI (ISIoffset/ISImean). Data correspond in color with example neurons in C.
Next, we performed perforated patch current-clamp recordings of 27 PV– neurons from 17 mice while applying the same light protocol. We identified PV– neurons by the absence of GFP fluorescence and the lack of a sustained hyperpolarizing response to green light. Of the 27 PV– neurons, 21 fired repetitively before and after the light. In 9 of 21 of these neurons, there was a visible reduction in the rate of IPSPs during illumination and an increase in IPSP rate at light offset (e.g., Fig. 1C, top). The other 6 of 27 PV– neurons exhibited long periods of at least 10 s without firing. Of these 6 neurons, 2 did not fire before, during, or after light. In 4 of 6 of these neurons, Arch activation caused a reduction in IPSP rate that depolarized the average membrane potential by 2-4 mV, and Arch caused 2 of these 4 neurons to fire (e.g., Fig. 1C, bottom).
To quantify the effect of silencing PV+ neurons on the firing of PV– neurons, we measured the firing rate and CV of ISIs occurring 0-5 s before, during, and after the light. PV– neurons had a wide range of baseline firing rates and CVs, but within-cell measurements revealed that they slightly but significantly increased their firing rate (F = 5.58, df = 2,52, p = 0.0064, one-way repeated-measures ANOVA) and reduced their CV (F = 5.48, df = 2,42, p = 0.0077, one-way repeated-measures ANOVA) during light-induced suppression of the spontaneous firing of PV+ neurons. The mean firing rate of PV– neurons was 14.0 ± 13.0 spikes/s before, 15.3 ± 12.6 during, and 13.8 ± 12.9 after light (Fig. 1E, left). The mean CV of active PV– neurons was 0.278 ± 0.260 before, 0.206 ± 0.135 during, and 0.341 ± 0.313 after light (Fig. 1E, middle). Some PV– neurons exhibited a long pause in firing in response to light offset (Fig. 1C, top). To quantify the pause, we normalized the ISI at light offset (ISIoffset) by the mean ISI (ISImean) 0-1 s before light onset. Of the 27 PV– neurons, 8 exhibited ISIs at offset that were >50% longer than their mean ISI (Fig. 1E, right), indicating that rebound PV+ firing can produce transient effects on firing that are more pronounced than the sustained effect of spontaneous PV+ firing.
When the spontaneous firing of Npas1+ neurons was silenced with Arch, this rarely produced a change in the rate of IPSCs in GPe neurons, and change was only observed as an increase in IPSC rate at light offset (Higgs et al., 2021). In this study, we measured the effect of silencing the spontaneous firing of Npas1+ neurons on the firing of the Npas1– neurons using brain slices from mice with Arch expressed selectively in Npas1+ GPe neurons. To induce Arch expression, we performed stereotaxic injection of AAV9-Flex-Arch-GFP into the GPe of Npas1-Cre mice (see Materials and Methods). AAV-encoded GFP expression in Npas1+ neurons is shown in Figure 2A. On 7 Npas1+ neurons from 4 mice, we performed cell-attached recordings of the firing responses to Arch current activation with the same light protocol described for the PV-Arch experiment. Green light silenced the firing of Npas1+ neurons (Fig. 2B). At light offset, Npas1+ neurons also exhibited rebound firing, which adapted back to baseline firing rates before the beginning of the next trial (Fig. 2B, right). Of the 7 Npas1+ neurons, 2 did not fire before, during, or after the light. To confirm that the absence of firing was not an artifact of the cell-attached recording method, we repeated the experiment while recording the membrane potential in perforated patch recordings of 4 Npas1+ neurons from 2 mice. One of these Npas1+ neurons did not fire during our recording session. Because we observed neurons that did not fire in both recording modes, we included all 11 Npas1+ neurons in our sample. Firing rates during the first 5 s before, during, and after light were averaged across five trials for each neuron. The mean firing rate of Npas1+ neurons was 13.6 ± 9.5 before, 0.0 ± 0.0 spikes/s during, and 18.0 ± 12.5 spikes/s after light (Fig. 2D).
Figure 2.
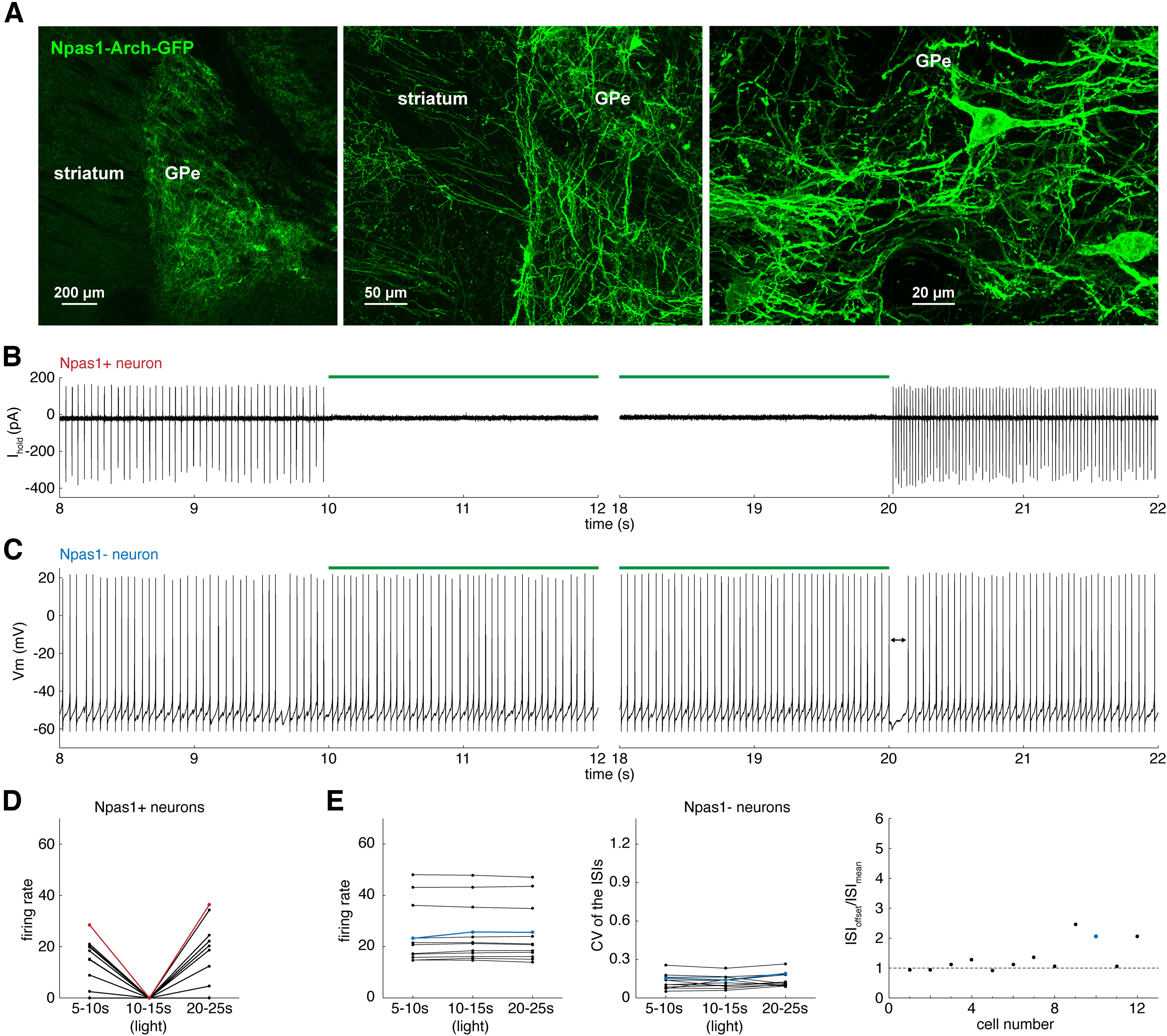
The spontaneous firing of Npas1+ neurons does not reduce the firing rate or regularity of Npas1– neurons. A, A sagittal section from an Npas1-Cre mouse injected with AAV9-Flex-Arch-GFP in the GPe. Npas1-Arch-GFP was imaged along the striato-pallidal border with (left) 5× and (middle) 20× objectives and (right) in the GPe with a 40× objective. B, Cell-attached recording of an Npas1+ neuron. Left, Onset and (right) offset of 10 s green light. C, Perforated patch recording of an Npas1– neuron. D, Firing rate of Npas1+ neurons before, during, and after light. Red line indicates data from the neuron in B. E, Left, Firing rate of Npas1– neurons before, during, and after light. Middle, CV of the ISI of Npas1– neurons before, during, and after light. Right, ISI of Npas1– neurons at light offset normalized by the mean ISI (ISIoffset/ISImean). Blue data represent the neuron in C.
We obtained perforated patch current-clamp recordings of 12 Npas1– neurons from 6 mice while applying the same light stimulus to silence the spontaneous firing of Npas1+ neurons (Fig. 2C). All Npas1– neurons fired reliably before and after the light. Silencing Npas1+ neurons had no significant effect on the mean firing rate (F = 1.76, df = 2,22, p = 0.20, one-way repeated-measures ANOVA) or CV (F = 1.13, df = 2,22, p = 0.34, one-way repeated-measures ANOVA) of Npas1– neurons. The mean firing rate of Npas1– neurons was 24.7 ± 11.4 spikes/s before, 25.1 ± 11.1 spikes/s during, and 24.9 ± 11.1 spikes/s after light (Fig. 2E, left). The mean CV of Npas1– neurons was 0.128 ± 0.056 before, 0.127 ± 0.048 during, and 0.139 ± 0.054 after light (Fig. 2E, middle). Of the 12 Npas1– neurons, 3 exhibited a moderate hyperpolarization at light offset (Fig. 2C, right), suggesting that rebound firing of Npas1+ neurons at light offset might have produced a transient increase in IPSC rate and/or amplitude that was visible in the postsynaptic neuron, although suppressing the baseline synaptic activity had no apparent effect. In addition, the ISIs of these neurons at light offset were >50% longer than their mean ISIs (Fig. 2E, right), indicating that, while the spontaneous firing of Npas1+ neurons has no sustained effect, their rebound firing can produce a transient effect on the firing of Npas1– neurons.
Spontaneously active unitary local connections can be detected accurately during spontaneous firing
If spontaneous synaptic inhibition from local connections can alter the firing of GPe neurons, blocking it should affect the firing of a particular GPe neuron only when that cell receives an intact local connection. To determine the relationship between unitary local inputs and the firing of GPe neurons, it was necessary to detect IPSPs during ongoing firing. In voltage-clamp recordings, unitary inputs from connected, rhythmically firing neurons can be identified and characterized by a periodic component in the autocorrelation of the spontaneous IPSC time series (Higgs and Wilson, 2016). In current-clamp recordings from a GPe neuron, some periodic IPSPs are obscured by action potentials, posing a challenge for accurate detection of periodic input. However, IPSPs occurring a sufficient time before or after an action potential can be detected, and a high IPSP rate measured this way may indicate the presence of an active local connection.
To detect IPSPs in GPe neurons, we first optimized our detection method, with the premise that the false detection rate should be held to an acceptable level when IPSPs are blocked. We developed a simple algorithm to measure gabazine-sensitive IPSP rates from the membrane potential of periodically firing neurons. We recorded the membrane potential of 30 Npas1+ neurons from 17 mice and 27 PV+ neurons from 17 mice for >100 s in control extracellular solution and >300 s during bath application of the GABA-A receptor antagonist gabazine (10 μm). Of the 30 Npas1− neurons, 8 fired only while gabazine was bath-applied and exhibited stable resting membrane potentials in control solution. These neurons were excluded from the analysis of IPSPs because they rested significantly closer to the GABA reversal potential than regularly firing GPe neurons; thus, there was a greater possibility that their IPSPs were too small to be accurately detected. IPSPs in neurons that fired repetitively in control and gabazine solution were detected using a filtered second derivative of the membrane potential trace (see Materials and Methods). The second derivative of the control membrane potential exhibited transient peaks that corresponded in time to each IPSP onset and correlated in size with IPSP amplitude (Fig. 3A, left). Gabazine blocked the IPSPs, as observed in the membrane potential and in the second derivative trace (Fig. 3A, right). Membrane potential noise produced small, transient peaks in both control and gabazine traces, whereas IPSPs produced large, transient peaks only in control traces (Fig. 3B, left). We analyzed the gabazine second derivative traces to determine the optimal IPSP detection threshold in each neuron for a false detection rate of ≤ 1 event/s (Fig. 3B, right, see Materials and Methods). The mean IPSP rate was 21.5 ± 18.3/s in PV+ neurons and 18.5 ± 16.1 in Npas1+ neurons (Fig. 3C) (p = 0.69, Mann–Whitney U test). The distributions of IPSP rates in PV+ and Npas1+ neurons were similar to those of IPSC rates measured by Higgs et al. (2021), indicating that we detected GABAergic synaptic events sensitively, even in current-clamp recordings during spontaneous firing.
As a relative measure of IPSP amplitude that is robust to the changes in membrane potential associated with the postsynaptic neuron’s spiking oscillation, we determined the negative peak of the second derivative associated with each IPSP onset (see Materials and Methods). Based on this measure, IPSPs detected in GPe neurons never reversed to become depolarizing at any time during the normal interspike membrane potential trajectories. The IPSP amplitudes of PV+ neurons and Npas1+ neurons were not significantly different (p = 0.67, Mann–Whitney U test).
To determine whether IPSP rates measured in this way can predict the number of periodic synaptic currents, we measured IPSP rates from the membrane potential traces of GPe neurons in perforated patch current clamp (Fig. 3D, top), and then measured IPSCs in perforated patch voltage clamp, in which spikes do not interfere with detection of synaptic events (Fig. 3D, bottom). We selected recordings with a series resistance <50 mΩ, (mean = 37 ± 11 mΩ). The voltage error introduced by the high access resistance in perforated patch recording was considered tolerable, as these recordings were only used to measure the timing of IPSCs. These data were obtained from 5 PV+, 3 Npas1+, and 5 unidentified neurons from 12 mice. IPSP rate was highly predictive of IPSC rate (Fig. 3E) (R2 = 0.95, p = 1.553–8, linear regression). For each neuron, we analyzed the autocorrelation of the IPSC time series, quantifying periodic inputs using a sum-of-Gaussians model fit introduced by Higgs and Wilson (2016) (see Materials and Methods). Figure 3F shows an autocorrelation of the IPSC time series in Figure 3D with the sum-of-Gaussians fit (red). In this case, based on the fit, we estimate that the neuron received a single unitary IPSC train. In the sample of 13 neurons, 3 neurons had no periodic IPSC trains, 8 had one, and 2 had two; these results were consistent with our previous study of GPe neurons using whole-cell voltage clamp (Higgs et al., 2021). IPSP rate alone was not sufficient to predict the exact number of periodic unitary inputs (as expected because of variation in presynaptic neuron firing rate) but was significantly correlated with the number of connections (R2 = 0.55, p = 0.0037, linear regression). An IPSP rate >10 was usually associated with the presence of at least one periodic input from an active unitary local connection (Fig. 3G).
Spontaneously active unitary local connections alter the spontaneous firing of PV+ and Npas1+ neurons
If intact local synaptic connections substantially affect GPe neurons’ firing rates and regularities, we predict that blocking synaptic inhibition will have substantial effects on firing in neurons that receive high rates of spontaneous IPSPs from one or more active unitary local connections. To examine this, we bath-applied gabazine to 30 Npas1+ neurons and 27 PV+ neurons and measured the relationship between IPSP rate and the changes in firing rate and CV caused by gabazine. While our Arch experiment confirmed that PV+ neurons provide the majority of unitary local inputs, we were not able to confirm the identities of postsynaptic neurons receiving the local input. In this gabazine experiment, we were able to determine the relationship between unitary local inputs and the firing output of identified PV+ and Npas1+ neurons. Examples are shown in Figure 4A for a PV+ neuron (top) and an Npas1+ neuron (bottom). For each neuron, mean firing rates and CVs were calculated from ISIs recorded 0-30 s before gabazine entered the bath and 150-180 s after gabazine entry. Consistent with previous reports (Hernández et al., 2015; Abrahao and Lovinger, 2018; Abecassis et al., 2020; Higgs et al., 2021), PV+ neurons fired with significantly higher rates (p = 4.83e-8, Mann–Whitney U test) and lower CVs than Npas1+ neurons (p = 0.0023, Mann–Whitney U test). We observed a wide range of baseline firing rates and CVs both before and after gabazine, but within-cell measurements revealed that gabazine significantly increased the rates and lowered the CVs of PV+ neurons and Npas1+ neurons. The mean firing rate of PV+ neurons was 37.7 ± 16.1 spikes/s in control solution and 41.2 ± 16.8 spikes/s in the presence of gabazine (Fig. 4B, left) (p = 0.00010, Signed-Rank Test). The mean CV of PV+ neurons was 0.132 ± 0.075 before and 0.075 ± 0.023 during gabazine application (Fig. 4C, left) (p = 0.000010, Signed-Rank Test). Eight Npas1+ neurons did not fire for >100 s in control solution, and the effect of gabazine on these neurons varied. Of these 8 neurons, 7 began firing in gabazine solution, but all at different latencies. Npas1+ neurons that did not fire at least 1 spike/s before and after gabazine application were excluded from analysis of firing rate and CV. The mean firing rate of active Npas1+ neurons was 11.4 ± 8.6 spikes/s in control solution and 14.6 ± 7.0 spikes/s in the presence of gabazine (Fig. 4B, left) (p = 0.0023, Signed-Rank Test). The mean CV of active Npas1+ neurons was 0.280 ± 0.129 before and 0.239 ± 0.064 during gabazine application (Fig. 4C, left) (p = 0.00011, Signed-Rank Test). The changes in firing rate caused by gabazine were significantly correlated with IPSP rates in PV+ neurons (Fig. 4B, middle) (R2 = 0.26, p = 0.00061, linear regression) and Npas1+ neurons (Fig. 4B, right) (R2 = 0.35, p = 0.0039, linear regression). The changes in CV caused by gabazine were significantly correlated with IPSP rates in PV+ neurons (Fig. 4C, middle) (R2 = 0.53, p = 0.000016, linear regression) but not in Npas1+ neurons (Fig. 4C, right) (R2 = 0.11, p = 0.13, linear regression).
It is possible that some effect of local inhibition on CV might be secondary to the effect on mean firing rate. It was shown previously that the SD of ISIs has a hyperbolic relationship with the mean firing rate in GPe neurons (Deister et al., 2013). In terms of CV, the SD/mean ISI, this relationship predicts that the CV will decrease as the mean rate increases. In later experiments (see Fig. 6), we dissociate the effects of unitary local inhibition on firing rate and SD.
Figure 6.
Simulated local network inhibition primarily deregularizes the firing of most GPe neurons but silences some Npas1+ GPe neurons. A, Membrane potential responses of a PV+ neuron to simulated inhibition from 1-5 unitary local connections. B, The effect of 0 (brown) to 5 (blue) simulated unitary local inputs on (left) the steady state firing rate and (right) SD of the ISI of PV+ neurons. C, The SD of PV+ neurons as a function of their firing rate in response to 0 (brown) and 5 (blue) unitary inputs D–F, Same as in A–C, but for Npas1+ neurons.
We also investigated the effects of GABA-B receptors on the firing of GPe neurons. GABA-B receptors are expressed on both presynaptic and postsynaptic specializations in the GPe (Chen et al., 2004). Kaneda and Kita (2005) reported that local electrical stimulation produced a pause in the spontaneous firing of GPe neurons in slices that was eradicated by the GABA-B receptor antagonist CGP55845. They also found that the GABA-B agonist baclofen reduced the frequency of IPSCs, indicative of a presynaptic effect. To determine whether spontaneously released GABA from local connections produced GABA-B receptor-dependent effects on firing or synaptic release, we obtained perforated patch current-clamp recordings of 7 Npas1+ neurons from 4 mice and 5 PV+ neurons from 2 mice for >100 s in control extracellular solution and >300 s during bath application of CGP55845 (1 μm). The membrane potential and firing patterns of GPe neurons were analyzed 0-30 s before and 150-180 s after CGP entered the recording bath. One Npas1+ neuron did not fire at least 1 spike/s and was excluded from this analysis. Signed-Rank Tests were used for statistical comparisons before and during CGP bath application. In PV+ neurons, CGP had no significant effect on the firing rate (p = 1.00), CV of the ISI (p = 1.00), IPSP rate (p = 0.59), or IPSP amplitude (p = 0.79). Similarly, in Npas1+ neurons, CGP had no significant effect on the firing rate (p = 0.53), CV of the ISI (p = 0.83), IPSP rate (p = 0.41), or IPSP amplitude (p = 0.21). These results indicate that, in slice preparations of the GPe, spontaneous GABA release from local synapses does not activate GABA-B receptors on local connections enough to have a substantial effect on the detected IPSPs or the firing of the postsynaptic neuron. Possibly, GABA-B receptor modulation requires a greater number of intact connections or correlated release from multiple presynaptic neurons to affect firing.
Application of simulated local network inhibition using dynamic clamp
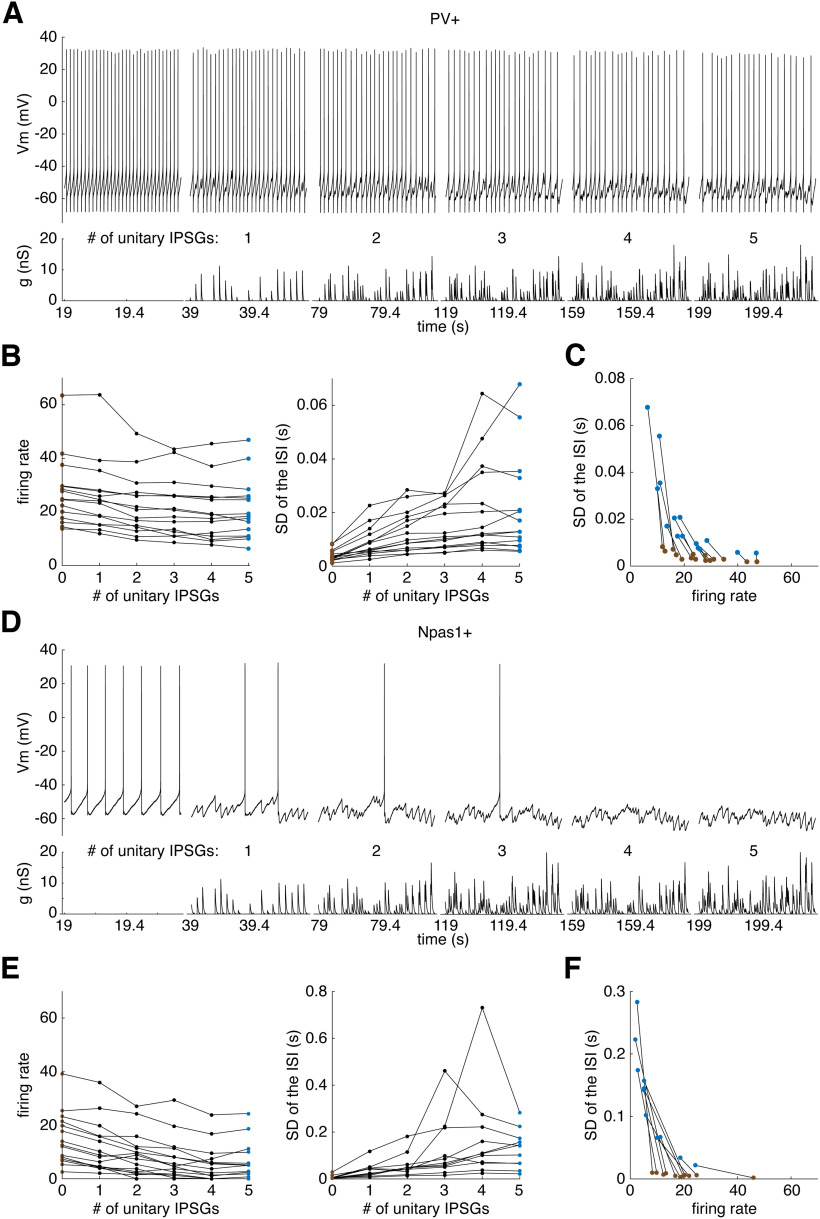
In vivo, we expect GPe neurons to receive >2 unitary local connections. Individual GPe neurons form up to 650 local boutons (Sadek et al., 2007; Mallet et al., 2012; Fujiyama et al., 2016). Sadek et al. (2007) reported one case in which a single GPe axon formed 14 boutons making synapses on a single GPe soma, but quantitative anatomic data on the number of unitary connections received by each GPe neuron are not available. Based on comparison of minimal and maximal amplitudes of IPSCs evoked by optogenetic stimulation of local PV+ inputs, we (Higgs et al., 2021) estimated that each GPe neuron receives synaptic inhibition from ∼10 local PV+ neurons. This same study also characterized the synaptic currents from unitary connections. Figure 5A shows a whole-cell voltage-clamp recording from a GPe neuron receiving a single periodic IPSC train, which was converted to units of conductance by dividing by the calculated driving force for chloride. We used the statistics measured and reported by Higgs et al. (2021) to construct conductance waveforms recapitulating the mean rate, mean amplitude, intraneuron amplitude variability, mean kinetics, and mean synaptic reliability of IPSG trains from unitary local connections (Fig. 5B; see Materials and Methods). We bath-applied gabazine to block spontaneous inhibition and recorded the responses of GPe neurons to dynamic-clamp injections of conductance waveforms simulating input from up to 5 unitary local connections, a conservative estimate of the number of connections present in vivo.
As described earlier, we recorded the spontaneous firing of GPe neurons before and during gabazine bath application, and a subset of these neurons exhibited an IPSP rate suggestive of 1 or 2 active unitary local connections. Figure 5C (left) shows an overlay of spontaneous IPSPs recorded from a PV+ neuron with an IPSP rate of 41.4/s. The interspike voltage trajectories of GPe neurons exhibited a depolarizing ramp across most of the ISI. IPSPs that occurred early in the ISI were smaller in amplitude than those that more closely preceded a spike, as expected from the change in synaptic driving force. To visualize this, we plotted the amplitudes of detected IPSPs as a function of spike oscillation phase (φ), which was defined as IPSP onset time relative to the previous spike divided by the ISI length (Fig. 5C, right). Once gabazine took effect and blocked the spontaneous IPSPs, we injected the conductance waveform in Figure 5B using dynamic clamp with a GABAergic reversal potential set to −74 mV. Dynamic-clamped IPSGs produced IPSPs with a similar shape as spontaneous IPSPs (Fig. 5C,D, left) and a similar amplitude distribution (Fig. 5C,D, right). On average, spontaneous IPSPs were marginally smaller than dynamic-clamp IPSPs, which was expected because some spontaneous IPSPs are produced by action potential-independent IPSCs, which are usually smaller than unitary local IPSCs (Higgs et al., 2021).
To determine the impact of increasing the number of unitary local inputs, we constructed a conductance waveform consisting of 20 s periods of IPSGs representing 1-5 unitary inputs, separated by 20 s recovery periods (Fig. 5E, bottom). Waveforms representing >1 unitary IPSG were composites of unitary IPSG waveforms that differed only in their timing (and thus were uncorrelated) because of their CV (see Materials and Methods). Dynamic-clamped IPSGs simulating input from 1 or 2 unitary local connections had effects on the firing rate and CV that were like those of spontaneous local inhibition. As few as 3-5 unitary local connections produced large effects on the regularity and rate of firing. To visualize these data, we plotted the inverse of each ISI (instantaneous rate) as a function of time (Fig. 5E, top).
We performed the dynamic clamp experiment illustrated in Figure 5 in 15 PV+ neurons from 8 mice and 16 Npas1+ neurons from 10 mice. Approximately 25% of the Npas1+ neurons we recorded fired <1 spike/s, which was too slow to perform the dynamic clamp experiment. Synaptic barrage currents perturbed the membrane potential and firing pattern of PV+ neurons (Fig. 6A) and Npas1+ neurons (Fig. 6D). All PV+ neurons maintained firing throughout the inhibitory barrages but showed moderate decreases in firing rate. Of the 16 Npas1+ neurons, 5 were so inhibited by the simulated synaptic input that they did not fire at all during at least one period of barrage application. We included data from these 5 Npas1+ neurons in the rate analysis but not in the analysis of the SD of the ISI, as it could not be calculated for some periods. The instantaneous firing rates of PV+ and Npas1+ neurons adapted over the course of our stimulation periods. To measure the steady-state firing responses, we analyzed the firing rate and SD of the ISI during the final 5 s of stimulation. Increasing the number of unitary IPSGs reduced the firing rates in PV+ neurons (Fig. 6B, left) (F = 22.79, df = 5,70, p = 1.7 × 10−13, one-way repeated-measures ANOVA) and in Npas1+ neurons (Fig. 6E, left) (F = 36.67, df = 5, 70, p = 0.0, one-way repeated-measures ANOVA) independent of the rate, and dramatically increased the irregularity of firing as indicated by the SD of the ISI in PV+ neurons (Fig. 6B, right) (F = 13.37, df = 5,70, p = 3.8 × 10−9, one-way repeated-measures ANOVA) and in Npas1+ neurons (Fig. 6E, right) (F = 5.80, df = 5,50, p = 0.00027, one-way repeated-measures ANOVA).
As expected (Deister et al., 2013), the intrinsic SD of the ISI in GPe neurons had a hyperbolic relationship with spike rate, suggesting the possibility that the increase in SD might be secondary to the reduction in rate. A barrage by 5 unitary inputs only moderately reduced the rate of PV+ neurons and active Npas1+ neurons, but dramatically increased their SD well above the level expected from their change in rate alone (Fig. 6C,F). This occurred in part because all repetitively firing PV+ neurons and Npas1+ neurons slowly adapted their instantaneous firing rate over the course of our stimulation periods. This adaptation to the inhibitory barrage was most evident in PV+ neurons. In brief respites from dynamic current during the stimulation period, we observed ISIs shorter in length than the shortest baseline ISI in the absence of stimulation (Fig. 7A), further suggesting the neurons had adapted their firing rates during the inhibitory current. Spike-frequency adaptation not only sped up the cells during inhibition, opposing the initial slowing, but also slowed the cells after rebound firing rate increases after the current.
Figure 7.
GPe neurons exhibit slow spike-frequency adaptation. A, Top, Instantaneous firing rate responses of (left) a PV+ neuron and (right) an Npas1+ neuron to simulated inhibition from 5 unitary local connections. B, Left, Instantaneous firing rate response of a PV+ neuron to a 20 s, −60 pA current pulse. Right, Response to a 60 pA pulse. Exponential curve fits measure the escape from negative current (blue), the rebound after negative current (purple), the adaptation to positive current (orange), and the recovery from positive current (red). C, Decay time constants of exponential fits for each of the four types of adaptation at each level of current injected. D, Same as in B, but for an Npas1+ neuron. E, Same as in C, but for Npas1+ neurons. F, Left, Early (gray) and steady-state (black) F-I curves with linear regression fits (dotted lines) for a PV+ neuron. Right, Same for an Npas1+ neuron. G, Left, Early and steady F-I curve slopes for PV+ neurons. Right, Same for Npas1+ neurons.
GPe neurons exhibit four types of slow spike-frequency adaptation
To understand the slow changes in responses to sustained inhibitory barrages, we measured the time course of spike-frequency adaptation in GPe neurons using simpler current stimuli. It is well established that GPe neurons exhibit spike-frequency adaptation to brief (250 ms to 2 s) positive current pulses (Kita and Kitai, 1991; Cooper and Stanford, 2000; Bugaysen et al., 2010; Abdi et al., 2015), but the time course of this adaptation and its dependence on the strength and sign of current are not known. We injected long-duration (20 s) current pulses from −100 to 90 pA (by increments of 10 pA) into 10 PV+ neurons from 6 mice and 10 Npas1+ neurons from 8 mice. To estimate the time course of adaptation, we fit exponential decays to their instantaneous rate versus time plots. GPe neurons exhibited four types of spike-frequency adaptation: (1) escape from negative current, in which they depolarize and resume firing during the current step (Fig. 7B,D, blue fit); (2) rebound after negative current, in which their firing rate is increased but gradually decays back to baseline (purple fit); (3) classical adaptation, a gradual decrease in firing rate after an initial increase during a positive current step (orange fit); and (4) recovery, a gradual return to baseline firing after an initial decrease that follows the offset of positive current (red fit). This experiment revealed an intrinsic difference between Npas1+ and PV+ neurons; 9 of 10 Npas1+ neurons showed very limited escape from hyperpolarizing current, remaining silent during the full course of the −60 pA, 20 s current injection, whereas 10 of 10 PV+ neurons exhibited profound recovery and resumed firing before the current was terminated. The two cell types could be positively identified by this simple test. Because of the limited escape of Npas1+ neurons, we were not able to fit exponential curves to their instantaneous firing rates during hyperpolarizing current steps, so we excluded that analysis from measures of their adaptation.
The time constants of the four varieties of spike-frequency adaptation were independent of the strength of applied current in PV+ neurons (Fig. 7C) (escape: R2 = 0.046, p = 0.19; rebound: R2 = 0.0040, p = 0.63; adaptation: R2 = 0.017, p = 0.36; recovery: R2 = 0.022, p = 0.25, linear regression) and Npas1+ neurons (Fig. 7E) (rebound: R2 = 0.070, p = 0.050; adaptation: R2 = 0.0077, p = 0.57; recovery: R2 = 0.024, p = 0.40, linear regression). Because of this, we averaged decay time constants from all current levels for each of the four adaptation types. The mean decay time constants (in seconds) were statistically different between response types in Npas1+ neurons, with adaptation occurring faster than either rebound or recovery (Fig. 7E) (rebound: 5.89 ± 4.01 s, adaptation: 3.92 ± 2.59 s, recovery: 6.64 ± 4.12 s, F = 6.15, df = 2, 129, p = 0.0028, one-way ANOVA). There was no difference between response types in PV+ neurons (Fig. 7C) (escape: 5.50 ± 2.51 s, rebound: 6.22 ± 2.20 s, adaptation: 5.81 ± 2.37 s, recovery: 5.65 ± 2.51 s, F = 0.92, df = 3, 209, p = 0.43, one-way ANOVA).
To examine the strength of adaptation, we measured the firing rate responses during the first 0.1 s after current onset or offset (early and before adaptation) and the final 10 s with or without the current (adapted steady state). We measured the relationship between current injected and firing rate (F-I curve) for both early and steady-state responses. There was no significant difference between the early F-I curve slopes of Npas1+ neurons and PV+ neurons (Fig. 7F,G) (p = 0.10, Mann–Whitney U test). There was also no significant difference between the steady-state F-I curve slopes of Npas1+ neurons and PV+ neurons (p = 0.31, Mann–Whitney U test). The early F-I curve was significantly steeper than the steady-state F-I curve in PV+ neurons (Fig. 7G, left) (p = 0.0059, Signed-Rank Test) and in Npas1+ neurons (Fig. 7G, right) (p = 0.0059, Signed-Rank Test), confirming that PV+ neurons and Npas1+ neurons adapt their firing rate to sustained changes in their mean input.
Predicting the effect of local inhibition on neuronal firing rate and regularity
PV+ and Npas1+ neurons varied widely in their firing rate and regularity during real and simulated local synaptic inhibition because of differences in their intrinsic firing rate, firing regularity, sensitivity to current, and spike-frequency adaptation to sustained current. To test our understanding of the experimental results, we simulated GPe neurons using phase models based on intrinsic firing rates, infinitesimal PRCs, and spike-frequency adaptation (see Materials and Methods).
Most Npas1+ neurons and all PV+ neurons exhibited rhythmic repetitive firing and so can be treated as oscillators. The dynamic variables of pacemaking currents that govern spiking oscillate concurrently with spiking and remain near a limit cycle defined by a fixed set of values at any given phase (φ), or time-fraction of the natural spiking oscillation. Thus, to a first approximation, the multidimensional state of the oscillating neuron can be represented by a single variable, φ. The spike-time response of an oscillating neuron to a transient input depends on the state of the dynamical system, φ, when the input arrives and is summarized by the neuron’s infinitesimal PRC (Wilson et al., 2014). We experimentally measured the PRCs of 12 PV+ neurons and 15 Npas1+ neurons using a current noise stimulation and multiple linear regression analysis (Wilson et al., 2014) (see Materials and Methods). Example PRCs from a PV+ neuron and an Npas1+ neuron are shown in Figure 8A. Npas1+ neurons had significantly larger PRC means than PV+ neurons (Fig. 8B, left) (PV+: 0.57 ± 0.18 cycles/pA-s, Npas1+: 0.92 ± 0.44 cycles/pA-s, p = 0.010, Mann–Whitney U test). The PRCs of PV+ and Npas1+ neurons were heterogeneous in shape but were right-weighted (i.e., higher at late vs early phases) on average. There was no significant difference in PRC center of mass (center φ) between PV+ and Npas1+ neurons (Fig. 8B, right) (PV+: 0.62 ± 0.06, Npas1+: 0.61 ± 0.08, p = 0.68, Mann–Whitney U test).
Figure 8.
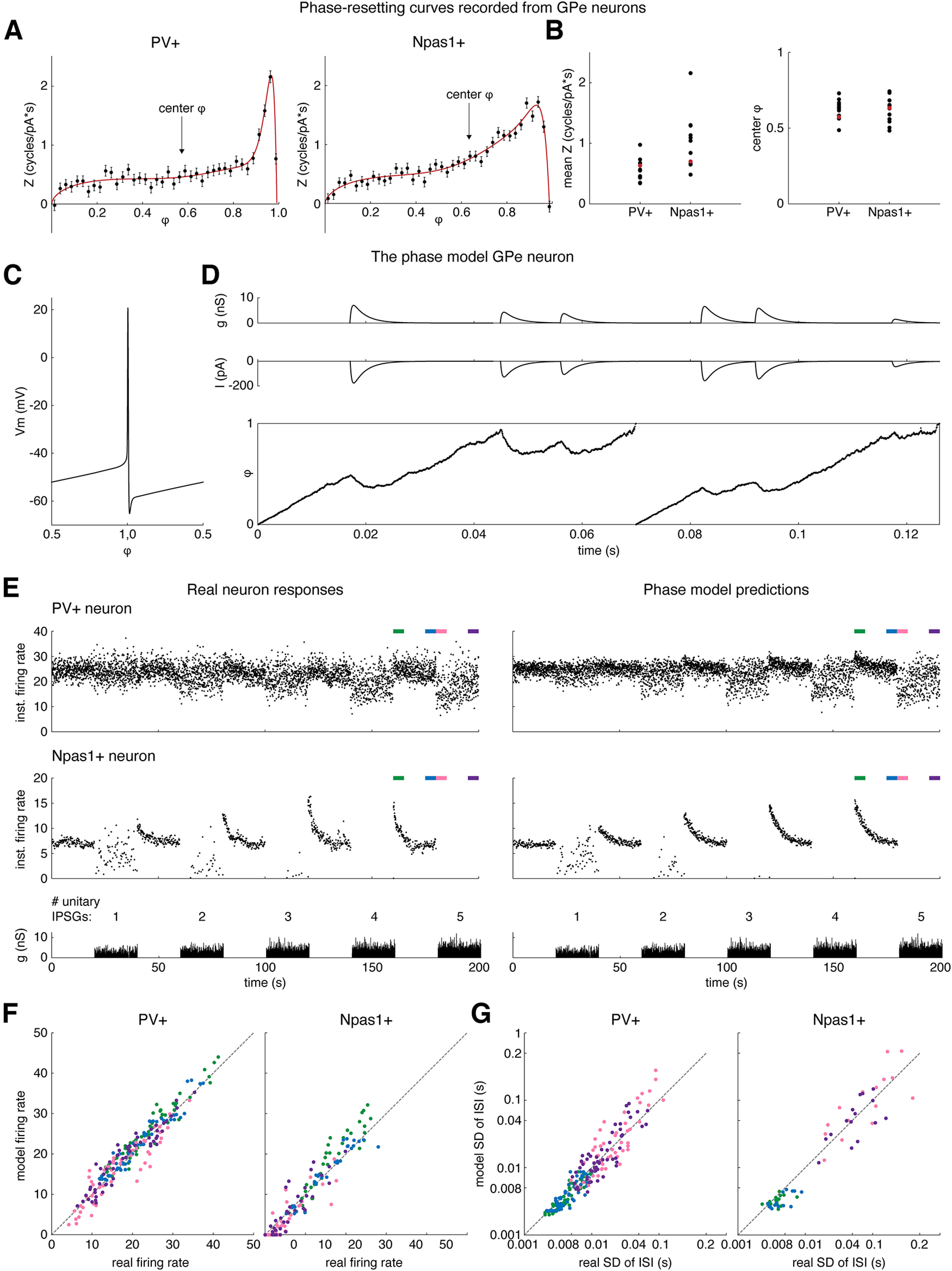
The intrinsic firing rates, PRCs, and slow spike-frequency adaptation of GPe neurons together determine their firing responses to local inhibition. A, PRCs of (left) a PV+ neuron and (right) an Npas1+ neuron fit with ad hoc functions (red, Z[φ]). Error bars indicate SE of the estimate. B, The mean PRC (left) and the mean PRC center of mass (center φ) of PV+ and Npas1+ neurons. C, The membrane voltage of a PV+ neuron as a function of its oscillation φ (V[φ]). D, Top, Simulated conductance waveform from 1 unitary local connection. Middle, Inhibitory current waveform produced by the conductance waveform and received by the model. Bottom, Phase evolution of a model PV+ neuron receiving the inhibitory current. E, Left, Instantaneous firing rate responses of real GPe neurons to unitary local inhibition: Top, PV+. Middle, Npas1+. Bottom, Waveform of the simulated inhibitory conductance. Right, Same for the phase models simulating each neuron. F, Model firing rate compared with real neuron rate (left) in PV+ neurons and (right) in Npas1+ neurons. G, Model SD compared with real neuron SD (left) in PV+ neurons and (right) in Npas1+ neurons.
Phase models of oscillating neurons based on their experimentally measured PRC are highly predictive of their spike-time responses to Gaussian noise, sinusoidal current, and transient conductance inputs (Wilson et al., 2014; Wilson, 2017; Simmons et al., 2018, 2020; Morales et al., 2020). In 11 PV+ neurons from 6 mice and 7 Npas1+ neurons from 6 mice, we measured both the PRC and the responses to dynamic currents simulating 1-5 unitary inputs, allowing us to construct a phase model of each neuron and test its ability to predict the responses to the inhibitory inputs. Because the inputs to the model were conductance waveforms with a reversal potential (Erev), it was necessary to define the driving force to convert the conductance to current, which alters the neuron’s rate of phase advance according to the PRC. By the argument above, a phase model has only one state variable, φ; thus, in the model, the voltage V must be defined as a function of φ. To construct a function V[φ] from the experimental data, we sampled the interspike voltage trajectories of GPe neurons, normalized the time across each trajectory to a range of values from 0 to 1, and averaged the sampled trajectories to obtain V[φ] (Fig. 8C) (Simmons et al., 2018) (see Materials and Methods). We then calculated the driving force for current generated by the conductance waveforms as Erev – V[φ]. The GABAergic Erev was set to −74 mV, the value used in our dynamic clamp experiments. In the absence of external input, φ evolved at each neuron’s intrinsic firing rate, ω, jittering along this trajectory based on the neuron’s CV; neurons with higher intrinsic CVs exhibited noisier phase trajectories. The rate of phase evolution, dφ/dt, was altered by the synaptic current with a neuron-specific sensitivity given by the neuron’s PRC, Z[φ] (see Materials and Methods). When φ reached 1, a spike time was recorded and φ was reset to 0.
Phase models using only the ω and Z[φ] of GPe neurons did not include their spike-frequency adaptation, so could not possibly predict the spike-frequency adaptation that occurred during unitary local inhibition (Fig. 7A). J. Cui et al. (2009) found that phase model predictions of firing responses in adapting neurons are greatly improved by measuring PRCs using fully adapted spike-time responses to single, fixed-amplitude current pulses applied at fixed latencies for prolonged periods to ensure that adaptation is complete when measuring the PRC. We could not incorporate their method to account for adaptation because we applied a contiguous sequence of varying-amplitude current pulses to measure PRCs. As an alternative, we accounted for adaptation by adding a spike-frequency adaptation variable that depended on the amount and sign of current applied and slowly opposed the response of dφ/dt to the current, adapting dφ/dt with the same time course observed in our experiments (Fig. 8D; see Materials and Methods).
Our phase models with adaptation accurately predicted the changes in firing rate and regularity of GPe neurons receiving realistic trains of unitary local IPSGs. The spike-frequency adaptation variable in the phase model produced a similar time course of adaptation compared with that observed in the real neurons (Fig. 8E, compare left and right panels). Comparing the neurons in Figure 8E (top left vs bottom left panels), the top neuron had weaker initial responses to local network barrages and less pronounced spike-frequency adaptation, characteristics that were all captured by the model. For real neurons and their phase model counterparts, we measured the rate and SD of the ISI for the first 5 s following current offset (Fig. 8E, green bar), the 5 s preceding current (blue bar), the 5 s following current onset (pink bar), and the final 5 s of current (purple bar). Four of seven Npas1+ neurons and their phase model counterparts did not fire during at least one 20 s period of IPSGs and were excluded from analysis of the SD of the ISI. The firing rates of the real neurons were significantly correlated with the rates of corresponding phase model neurons for PV+ neurons (Fig. 8F, left) (F = 2302.26, df = 1,218, p = 7.69e-118, R2 = 0.91, linear regression) and for Npas1+ GPe neurons (Fig. 8F, right) (F = 1325.01, df = 1,138, p = 1.26e-72, R2 = 0.91, linear regression). The ISI SD data also showed significant correlations between the real neurons and the corresponding phase models for PV+ neurons (Fig. 8G, left) (F = 1651.41, df = 1,218, p = 1.08e-103, R2 = 0.88, linear regression) and for active Npas1+ neurons (Fig. 8G, right) (F = 1224.08, df = 1,58, p = 3.86e-64, R2 = 0.91, linear regression). These results indicate that the intrinsic rates, PRCs, and spike-frequency adaptation of GPe neurons provide an adequate explanation for the irregular firing generated by the local inhibitory network.
Discussion
In this study, we measured the impact of spontaneous local input on spiking output in the GPe. Because firing is autonomous, unitary synaptic currents are large and brief, and GPe neurons are highly sensitive to their input, the activity in the local network strongly perturbs the intrinsic oscillations of GPe neurons, deregularizing their firing. We found that the spontaneous firing of even a single presynaptic PV+ neuron can produce a large GABAergic synaptic barrage that alters the firing rate and regularity of postsynaptic GPe neurons. Our experimental results were accurately predicted by phase-oscillator models of each GPe neuron, confirming that phase-reset is the mechanism underlying deregularization. The intrinsic rate, phase-resetting properties, and spike-frequency adaptation of PV+ and Npas1+ neurons determine their firing responses to the synaptic barrages produced by local connections. In response to network levels of local inhibition, PV+ GPe neurons restore their firing rate but maintain high spike-time irregularity.
A GABAergic synaptic network, active in slices
GPe neurons alter the spontaneous firing of one another through local GABAergic synapses. We found that, when spontaneous IPSPs were present, blocking GABA-A receptors both blocked the IPSPs and increased the firing rates and regularities of individual GPe neurons. The effect of gabazine on firing scaled with the rate of IPSPs, which originated primarily from active unitary local connections intact in our slices. We think that the large heterogeneity in firing rate masked these effects of GABA-A antagonists in previous studies using across-cells comparisons (Chan et al., 2004; Deister et al., 2013).
Local inhibition may not involve GABA-B receptors. Anatomical data indicate that GABA-B receptors are expressed on local synapses (Charara et al., 2005), but blocking them in our experiments produced no measurable effect on the local IPSP rate, IPSP amplitude, firing rate, or regularity of GPe neurons, suggesting that GABA-B receptors do not affect local inhibition during spontaneous firing. In contrast, GABA-B receptors clearly modulate striato-pallidal inhibition (Sitzia et al., 2023). Moreover, pallido-nigral inhibition is exclusively GABA-A receptor-dependent, while striato-nigral inhibition depends on both GABA-A and GABA-B receptors (Evans et al., 2020). This could be a general difference between inhibition from the striatum and the GPe.
Npas1+ neurons rarely affect firing in the GPe
The spontaneous firing of Npas1+ GPe neurons, which do not contribute to the classic indirect pathway, did not produce effective local inhibition in our slices. When we silenced presynaptic Npas1+ neurons with Arch, there was no effect on the IPSP rate or firing activity of other GPe neurons. Some Npas1+ neurons may not provide local collaterals (Mallet et al., 2012), and those that do may fire too slowly or undergo too much synaptic depression to participate in the local network. Most Npas1+ neurons in our sample had low firing rates, and some did not fire for long periods. Possibly, they participate in the local network when their firing is elevated. We were able to recruit local inhibition from a subset of Npas1+ neurons by inducing rebound firing at the offset of Arch silencing, but in each case, Npas1+ inhibition perturbed only a single ISI, presumably because Npas1+ neuron synapses depress rapidly (Q. Cui et al., 2021). The firing rate of Npas1+ neurons could be elevated by excitatory synaptic currents from cortical pyramidal neurons (Karube et al., 2019) or STN neurons (Pamukcu et al., 2020). Alternatively, disinhibition could elevate the firing of Npas1+ neurons and recruit their local inhibition.
PV+ neurons can silence Npas1+ neurons
The spontaneous firing of PV+ GPe neurons, which contribute to the indirect pathway, produced powerful local inhibition in our slices. We found that a single PV+ neuron can silence an otherwise active Npas1+ neuron. When we blocked spontaneous PV+ inputs, some Npas1+ neurons began to fire repetitively, whereas active Npas1+ neurons continued firing, but at higher rates and regularities. Realistic local inhibition, simulating input from five presynaptic PV+ neurons, dramatically inhibited most Npas1+ neurons, and prevented a large subset from firing during the inhibition. These results suggest that many Npas1+ neurons fire at elevated rates in vivo only during disinhibition from the PV+ network.
PV+ neurons deregularize one another
The PV+ network’s most prominent effect is on the regularity, not the rate, of PV+ neuron firing. Because unitary IPSGs are large and fast, the spontaneous firing of even a single PV+ neuron can substantially alter the spike times of another PV+ neuron, even if that input produces little effect on the average rate. Five local connections to each PV+ neuron produced only moderate changes in rate, never silencing the postsynaptic cell, but increased irregularity to levels approaching those seen in vivo. The difference between PV+ and Npas1+ neurons in this regard is determined by their intrinsic rate, sensitivity to current, the kinetics of their local inhibition, but primarily by their spike-frequency adaptation. PV+ neurons apparently express depolarizing currents that restore their firing rates at or near their resting rate when inhibition is sustained for several seconds. This was seen in all experiments in which PV+ neurons were subjected to inhibition, whether it was a constant hyperpolarizing current or a barrage of synaptic inhibition. In contrast, Npas1+ neurons showed a very limited ability to escape inhibition, although their adaptation in response to depolarization was comparable to that of the PV+ neurons. The difference in adaptive escape from inhibition between PV+ and Npas1+ neurons was large and consistent enough to allow their identification on the basis of this one property. Firing rate adaptation may be an important feature of the indirect pathway neurons that maintains tonic activity despite the intense barrage generated within the local network.
The advantage of irregularity
Irregular spike trains possess greater entropy than regular ones, and so could convey much information (Cruz et al., 2009), if the variations in ISI were meaningful, and not simply random. The origin of the irregularity may provide an important clue to its meaning. If irregularity is generated by afferent inputs, for example, from the striatum, it may contain meaningful signals to be communicated by the indirect pathway. The component of irregularity that is generated locally in the GPe when disconnected from its inputs, as studied here, is not meaningful; it is random. This does not rule out the imposition of meaningful temporal signals on the indirect pathway by the striatum or the STN, but it does mean that they are superimposed on spike trains that are already randomized by the internal network. What could be the benefit for the network in generating this deregularizing inhibitory barrage?
By randomizing the baseline spike timing, the local PV+ network may increase the capacity of GPe neurons to encode meaningful afferent signals over a wide range of frequencies. Oscillatory neurons like those of the indirect pathway in the GPe are most efficient at propagating input patterns with frequency components approximating their own firing rates (Wilson, 2017; Morales et al., 2020). On each ISI, synaptic currents produce changes in spike timing relative to the baseline interval set by the cell’s background rate. Frequency components in the synaptic input current resonate with harmonics of the baseline firing frequency, with an efficiency determined by the frequency components of the PRC (Morales et al., 2020). That interaction determines the effectiveness of the synaptic current in influencing spike timing. Synaptic currents from striatal projection neurons are not expected to contribute to the continuous randomization of neuronal firing in the GPe because they exhibit sparse episodes of firing (Berke et al., 2004). Striatal projection neurons may instead provide signals which entrain neuronal firing in the GPe. Embedded in the striato-pallidal signal will be low frequencies representing interepisode intervals, moderate frequencies representing ISIs within episodes of firing, and high frequencies representing the onset of firing episodes, each of which may be meaningful signals. The local inhibitory network may impose variance on the baseline ISI to allow GPe neurons to encode striato-pallidal signals with different frequency composition on alternate ISIs, increasing the effective bandwidth of communication in the indirect pathway.
The output of the PV+ network
The PV+ GPe network may be a major source of deregularization for target nuclei in the indirect pathway of the basal ganglia. Like neurons in the GPe, neurons in the STN, SNr, and internal globus pallidus, which participate in the indirect pathway, are highly irregular in vivo, yet very rhythmic in slices (Wilson, 2013). However, internal globus pallidus neurons have no reported local collaterals, STN collaterals have no reported effect on firing, and SNr collaterals deregularize firing, but not as strongly as those in the GPe, suggesting that firing irregularity in these nuclei is not locally generated. But neurons in these regions are innervated by PV+ GPe neurons (Mallet et al., 2012), which may be a primary source of their irregularity. For example, when unitary GPe inputs are preserved in slices, they strongly deregularize neuronal firing in the STN (Hallworth and Bevan, 2005). The irregular firing of autonomously active neurons at multiple stages of the indirect pathway may be due largely to the PV+ GPe network.
Footnotes
This work was supported by National Institute of Neurological Disorders and Stroke Grant R35 NS097185 to C.J.W. and F31 NS127499 to J.A.J. We thank Sharmon Lebby for excellent technical assistance; Dr. Hitoshi Kita for great discussions and insightful comments on this study; and Dr. Savio Chan for providing the Npas1-Cre-tdTomato mice.
The authors declare no competing financial interests.
References
- Abdi A, Mallet N, Mohamed FY, Sharott A, Dodson PD, Nakamura KC, Suri S, Avery SV, Larvin JT, Garas FN, Garas SN, Vinciati F, Morin S, Bezard E, Baufreton J, Magill PJ (2015) Prototypic and arkypallidal neurons in the dopamine-intact external globus pallidus. J Neurosci 35:6667–6688. 10.1523/JNEUROSCI.4662-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abecassis ZA, Berceau BL, Win PH, García D, Xenias HS, Cui Q, Pamukcu A, Cherian S, Hernández VM, Chon U, Lim BK, Kim Y, Justice NJ, Awatramani R, Hooks BM, Gerfen CR, Boca SM, Chan CS (2020) Npas1+-Nkx2.1+ neurons are an integral part of the cortico-pallido-cortical loop. J Neurosci 40:743–768. 10.1523/JNEUROSCI.1199-19.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abrahao KP, Lovinger DM (2018) Classification of GABAergic neuron subtypes from the globus pallidus using wild-type and transgenic mice. J Physiol 596:4219–4235. 10.1113/JP276079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bar-Gad I, Heimer G, Ritov Y, Bergman H (2003) Functional correlations between neighboring neurons in the primate globus pallidus are weak or nonexistent. J Neurosci 23:4012–4016. 10.1523/JNEUROSCI.23-10-04012.2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benda J, Herz AV (2003) A universal model for spike-frequency adaptation. Neural Comput 15:2523–2564. 10.1162/089976603322385063 [DOI] [PubMed] [Google Scholar]
- Bergman H, Feingold A, Nini A, Raz A, Slovin H, Abeles M, Vaadia E (1998) Physiological aspects of information processing in the basal ganglia of normal and parkinsonian primates. Trends Neurosci 21:32–38. 10.1016/s0166-2236(97)01151-x [DOI] [PubMed] [Google Scholar]
- Berke JD, Okatan M, Skurski J, Eichenbaum HB (2004) Oscillatory entrainment of striatal neurons in freely moving rats. Neuron 43:883–896. 10.1016/j.neuron.2004.08.035 [DOI] [PubMed] [Google Scholar]
- Bevan MD, Booth PA, Eaton SA, Bolam JP (1998) Selective innervation of neostriatal interneurons by a subclass of neuron in the globus pallidus of the rat. J Neurosci 18:9438–9452. 10.1523/JNEUROSCI.18-22-09438.1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bevan MD, Magill PJ, Terman D, Bolam JP, Wilson CJ (2002) Move to the rhythm: oscillations in the subthalamic nucleus-external globus pallidus network. Trends Neurosci 25:525–531. 10.1016/S0166-2236(02)02235-X [DOI] [PubMed] [Google Scholar]
- Bugaysen J, Bronfeld M, Tischler H, Bar-Gad I, Korngreen A (2010) Electrophysiological characteristics of globus pallidus neurons. PLoS One 5:e12001. 10.1371/journal.pone.0012001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bugaysen J, Bar-Gad I, Korngreen A (2013) Continuous modulation of action potential firing by a unitary GABAergic connection in the globus pallidus in vitro. J Neurosci 33:12805–12809. 10.1523/JNEUROSCI.1970-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan CS, Shigemoto R, Mercer JN, Surmeier DJ (2004) HCN2 and HCN1 channels govern the regularity of autonomous pacemaking and synaptic resetting in globus pallidus neurons. J Neurosci 24:9921–9932. 10.1523/JNEUROSCI.2162-04.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charara A, Pare JF, Levey AI, Smith Y (2005) Synaptic and extrasynaptic GABA-A and GABA-B receptors in the globus pallidus: an electron microscopic immunogold analysis in monkeys. Neuroscience 131:917–933. 10.1016/j.neuroscience.2004.12.004 [DOI] [PubMed] [Google Scholar]
- Chen L, Boyes J, Yung WH, Bolam JP (2004) Subcellular localization of GABAB receptor subunits in rat globus pallidus. J Comp Neurol 474:340–352. 10.1002/cne.20143 [DOI] [PubMed] [Google Scholar]
- Cooper AJ, Stanford IM (2000) Electrophysiological and morphological characteristics of three subtypes of rat globus pallidus neurone in vitro. J Physiol 527:291–304. 10.1111/j.1469-7793.2000.t01-1-00291.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courtney CD, Pamukcu A, Chan CS (2021) The external pallidum: think locally. Act globally. arXiv:2104.10795. 10.48550/arXiv.2104.10795. [DOI] [Google Scholar]
- Cruz AV, Mallet N, Magill PJ, Brown P, Averbeck BB (2009) Effects of dopamine depletion on network entropy in the external globus pallidus. J Neurophysiol 102:1092–1102. 10.1152/jn.00344.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui J, Canavier CC, Butera RJ (2009) Functional phase response curves: a method for understanding synchronization of adapting neurons. J Neurophysiol 102:387–398. 10.1152/jn.00037.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui Q, Pamukcu A, Cherian S, Chang IY, Berceau BL, Xenias HS, Higgs MH, Rajamanickam S, Chen Y, Du X, Zhang Y, McMorrow H, Abecassis ZA, Boca SM, Justice NJ, Wilson CJ, Chan CS (2021) Dissociable roles of pallidal neuron subtypes in regulating motor patterns. J Neurosci 41:4036–4059. 10.1523/JNEUROSCI.2210-20.2021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deister CA, Dodla R, Barraza D, Kita H, Wilson CJ (2013) Firing rate and pattern heterogeneity in the globus pallidus arise from a single neuronal population. J Neurophysiol 109:497–506. 10.1152/jn.00677.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeLong MR (1971) Activity of pallidal neurons during movement. J Neurophysiol 34:414–427. 10.1152/jn.1971.34.3.414 [DOI] [PubMed] [Google Scholar]
- Elias S, Joshua M, Goldberg JA, Heimer G, Arkadir D, Morris G, Bergman H (2007) Statistical properties of pauses of the high-frequency discharge neurons in the external segment of the globus pallidus. J Neurosci 27:2525–2538. 10.1523/JNEUROSCI.4156-06.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout GB, Beverlin B 2nd, Troyer T, Netoff TI (2011) The variance of phase-resetting curves. J Comput Neurosci 31:185–197. 10.1007/s10827-010-0305-9 [DOI] [PubMed] [Google Scholar]
- Evans RC, Twedell EL, Zhu M, Ascencio J, Zhang R, Khaliq ZM (2020) Functional dissection of basal ganglia inhibitory inputs onto substantia nigra dopaminergic neurons. Cell Rep 32:108156. 10.1016/j.celrep.2020.108156 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujiyama F, Nakano T, Matsuda W, Furuta T, Udagawa J, Kaneko T (2016) A single-neuron tracing study of arkypallidal and prototypic neurons in healthy rats. Brain Struct Funct 221:4733–4740. [DOI] [PubMed] [Google Scholar]
- Gittis AH, Berke JD, Bevan MD, Chan CS, Mallet N, Morrow MM, Schmidt R (2014) New roles for the external globus pallidus in basal ganglia circuits and behavior. J Neurosci 34:15178–15183. 10.1523/JNEUROSCI.3252-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallworth NE, Bevan MD (2005) Globus pallidus neurons dynamically regulate the activity pattern of subthalamic nucleus neurons through the frequency-dependent activation of postsynaptic GABAA and GABAB receptors. J Neurosci 25:6304–6315. 10.1523/JNEUROSCI.0450-05.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hegeman DJ, Hong ES, Hernández VM, Chan CS (2016) The external globus pallidus: progress and perspectives. Eur J Neurosci 43:1239–1265. 10.1111/ejn.13196 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernández VM, Hegeman DJ, Cui Q, Kelver DA, Fiske MP, Glajch KE, Pitt JE, Huang TY, Justice NJ, Chan CS (2015) Parvalbumin+ neurons and Npas1+ neurons are distinct neuron classes in the mouse external globus pallidus. J Neurosci 35:11830–11847. 10.1523/JNEUROSCI.4672-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Higgs MH, Wilson CJ (2016) Unitary synaptic connections among substantia nigra pars reticulata neurons. J Neurophysiol 115:2814–2829. 10.1152/jn.00094.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Higgs MH, Jones JA, Chan CS, Wilson CJ (2021) Periodic unitary synaptic currents in the mouse globus pallidus during spontaneous firing in slices. J Neurophysiol 125:1482–1500. 10.1152/jn.00071.2021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaneda K, Kita H (2005) Synaptically released GABA activates both pre- and postsynaptic GABA(B) receptors in the rat globus pallidus. J Neurophysiol 94:1104–1114. 10.1152/jn.00255.2005 [DOI] [PubMed] [Google Scholar]
- Karube F, Takahashi S, Kobayashi K, Fujiyama F (2019) Motor cortex can directly drive the globus pallidus neurons in a projection neuron type-dependent manner in the rat. Elife 8:e49511. 10.7554/eLife.49511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ketzef M, Silberberg G (2021) Differential synaptic input to external globus pallidus neuronal subpopulations in vivo. Neuron 109:516–529.e5. 10.1016/j.neuron.2020.11.006 [DOI] [PubMed] [Google Scholar]
- Kita H (2007) Globus pallidus external segment. Prog Brain Res 160:111–133. 10.1016/S0079-6123(06)60007-1 [DOI] [PubMed] [Google Scholar]
- Kita H, Kitai ST (1991) Intracellular study of rat globus pallidus neurons: membrane properties and responses to neostriatal, subthalamic and nigral stimulation. Brain Res 564:296–305. 10.1016/0006-8993(91)91466-e [DOI] [PubMed] [Google Scholar]
- Kita H, Kitai ST (1994) The morphology of globus pallidus projection neurons in the rat: an intracellular staining study. Brain Res 636:308–319. 10.1016/0006-8993(94)91030-8 [DOI] [PubMed] [Google Scholar]
- Kita H, Nambu A, Kaneda K, Tachibana Y, Takada M (2004) Role of ionotropic glutamatergic and GABAergic inputs on the firing activity of neurons in the external pallidum in awake monkeys. J Neurophysiol 92:3069–3084. 10.1152/jn.00346.2004 [DOI] [PubMed] [Google Scholar]
- Mallet N, Micklem BR, Henny P, Brown MT, Williams C, Bolam JP, Nakamura KC, Magill PJ (2012) Dichotomous organization of the external globus pallidus. Neuron 74:1075–1086. 10.1016/j.neuron.2012.04.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mercer JN, Chan CS, Tkatch T, Held J, Surmeier DJ (2007) Nav1.6 sodium channels are critical to pacemaking and fast spiking in globus pallidus neurons. J Neurosci 27:13552–13566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mink JW (1996) The basal ganglia: focused selection and inhibition of competing motor programs. Prog Neurobiol 50:381–425. 10.1016/s0301-0082(96)00042-1 [DOI] [PubMed] [Google Scholar]
- Morales JC, Higgs MH, Song SC, Wilson CJ (2020) Broadband entrainment of striatal low-threshold spike interneurons. Front Neural Circuits 14:36. 10.3389/fncir.2020.00036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olivares E, Higgs MH, Wilson CJ (2022) Local inhibition in a model of the indirect pathway globus pallidus network slows and deregularizes background firing, but sharpens and synchronizes responses to striatal input. J Comput Neurosci 50:251–272. 10.1007/s10827-022-00814-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pamukcu A, Cui Q, Xenias HS, Berceau BL, Augustine EC, Fan I, Chalasani S, Hantman AW, Lerner TN, Boca SM, Chan CS (2020) Parvalbumin+ and Npas1+ pallidal neurons have distinct circuit topology and function. J Neurosci 40:7855–7876. 10.1523/JNEUROSCI.0361-20.2020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadek AR, Magill PJ, Bolam JP (2007) A single-cell analysis of intrinsic connectivity in the rat globus pallidus. J Neurosci 27:6352–6362. 10.1523/JNEUROSCI.0953-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato F, Lavallée P, Lévesque M, Parent A (2000) Single-axon tracing study of neurons of the external segment of the globus pallidus in primate. J Comp Neurol 417:17–31. [DOI] [PubMed] [Google Scholar]
- Shink E, Smith Y (1995) Differential synaptic innervation of neurons in the internal and external segments of the globus pallidus by the GABA and glutamate-containing terminals in the squirrel monkey. J Comp Neurol 358:119–141. 10.1002/cne.903580108 [DOI] [PubMed] [Google Scholar]
- Simmons DV, Higgs MH, Lebby S, Wilson CJ (2020) Indirect pathway control of firing rate and pattern in the substantia nigra pars reticulata. J Neurophysiol 123:800–814. 10.1152/jn.00678.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmons DV, Higgs MH, Lebby S, Wilson CJ (2018) Predicting responses to inhibitory synaptic input in substantia nigra pars reticulata neurons. J Neurophysiol 120:2679–2693. 10.1152/jn.00535.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sims RE, Woodhall GL, Wilson CL, Stanford IM (2008) Functional characterization of GABAergic pallidopallidal and striatopallidal synapses in the rat globus pallidus in vitro. Eur J Neurosci 28:2401–2408. 10.1111/j.1460-9568.2008.06546.x [DOI] [PubMed] [Google Scholar]
- Sitzia G, Abrahao KP, Liput D, Calandra GM, Lovinger DM (2023) Distinct mechanisms of CB1 and GABAB receptor presynaptic modulation of striatal indirect pathway projections to mouse globus pallidus. J Physiol 601:195–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wichmann T, Soares J (2006) Neuronal firing before and after burst discharges in the monkey basal ganglia is predictably patterned in the normal state and altered in parkinsonism. J Neurophysiol 95:2120–2133. 10.1152/jn.01013.2005 [DOI] [PubMed] [Google Scholar]
- Wilson CJ (2013) Active decorrelation in the basal ganglia. Neuroscience 250:467–482. 10.1016/j.neuroscience.2013.07.032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson CJ (2017) Predicting the response of striatal spiny neurons to sinusoidal input. J Neurophysiol 118:855–873. 10.1152/jn.00143.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson CJ, Barraza D, Troyer T, Farries MA (2014) Predicting the responses of repetitively firing neurons to current noise. PLoS Comput Biol 10:e1003612. 10.1371/journal.pcbi.1003612 [DOI] [PMC free article] [PubMed] [Google Scholar]