Misconceptions About the Direction of Bias From Nondifferential Misclassification

Abstract

Measurement error is pervasive in epidemiologic research. Epidemiologists often assume that mismeasurement of study variables is nondifferential with respect to other analytical variables and then rely on the heuristic that “nondifferential misclassification will bias estimates towards the null.” However, there are many exceptions to the heuristic for which bias towards the null cannot be assumed. In this paper, we compile and characterize 7 exceptions to this rule and encourage analysts to take a more critical and nuanced approach to evaluating and discussing bias from nondifferential mismeasurement.

Abbreviations

RR

risk ratio

Editor ’s note: An invited commentary on this article appears on page 1496, and the authors’ response appears on page 1498.

Epidemiologic data are rarely collected without errors in measurement, a potentially important source of systematic error in estimates of effect. Rather than quantify the potential impact such errors may have on study results (1–9), epidemiologists often assume that any mismeasurement of study variables is nondifferential with respect to other analytical variables and rely on the heuristic that “nondifferential misclassification biases estimates towards the null.” We suspect that this is one of the most cited heuristics in the Discussion sections of published articles. It is often used to conclude that study findings are “conservative,” so the unbiased estimate of effect would have been further from the null than what was observed. Therefore, a thorough understanding of the limitations of this heuristic is essential to prevent its suboptimal use.

Bias towards the null is not always “conservative.” What is “conservative” depends on the value systems of the interested parties. When an association between air pollution and the health of the local community is biased towards the null by nondifferential mismeasurement of exposure to the pollution, the bias “conserves” the profits of the polluting industry at the expense of the health of the community, which might have otherwise been protected by industry regulation. In this example and others like it, the size of the bias is critically important but is missing completely from the heuristic. Thus, there are fundamental concerns about the widespread use of the heuristic when making inferences from epidemiologic research.

Leaving this aside, however, it is important to realize that there are many exceptions to the heuristic for which bias towards the null cannot be assumed. While these exceptions have been previously documented, they have not (to our knowledge) been compiled in one reference text that allows for a more complete picture of the potential pitfalls of relying on this heuristic. In this paper, we compile and characterize 7 exceptions to this rule and encourage analysts to take a more critical and nuanced approach to evaluating and discussing bias from nondifferential mismeasurement. Our aim is to provide a resource for considering the potential impact of information bias in epidemiologic studies. We do not claim that this list is comprehensive; there may be other exceptions.

INFORMATION BIAS: A BRIEF OVERVIEW

Information bias occurs when there is misclassification of binary or categorical variables or mismeasurement of continuous variables. When we discuss these concepts together, we call them “measurement error.” The mechanism of measurement error can be characterized according to 2 axes: 1) whether the design suggests an expectation of differential or nondifferential measurement error and 2) whether the design suggests an expectation of dependent or independent measurement error. See Hernán and Cole (10) for examples of these misclassification mechanisms presented in causal diagrams.

Taking the case of misclassification of an exposure, differential misclassification occurs when the probability of exposure misclassification is expected by design to depend on the true status of another analytical variable, typically the outcome, whereas nondifferential exposure misclassification occurs when the error is not expected to depend on the true outcome status (i.e., , where E is the true exposure, 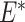is the classified exposure, and D is the true outcome status). Likewise, outcome misclassification can be expected to be nondifferential or differential with respect to other analytical variables, typically the exposure. Misclassification of 2 variables is considered dependent if the factors that predict misclassification of one variable are expected by design to also predict misclassification of the other variable. This misclassification is also referred to as common source bias or correlated errors. If the mechanisms of misclassification of the 2 variables are not related, the misclassification is expected to be independent. That is, misclassification is independent if the probability of joint misclassification is equal to the product of the individual misclassification probabilities: 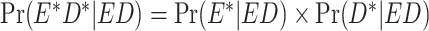, where E^* and D^* are the classified exposure and outcome status, respectively, and E and D are the true exposure and outcome status, respectively.

EXCEPTION 1: DEVIATION OF REALIZED MISCLASSIFICATION FROM EXPECTATION

Estimates of the magnitude and direction of bias represent an expectation under a model of the data that would be generated given the misclassification mechanisms expected by design. The actual study is a single realization of the data obtained by the data-generating mechanism, and so is vulnerable to random deviation from the expectation (11–13). Though information bias is systematic rather than random, the magnitude and direction of bias depends upon the sensitivity and specificity of the misclassified variable and the application of these classification parameters to the individual data records. Sensitivity and specificity are probabilities that pertain to the classification scheme in expectation but operate at an individual level (14). For example, if 100 persons are going to be classified into an exposed category with 70% sensitivity, the expectation is that 70 persons will be classified as exposed. In a single study’s realization of this data-generating mechanism, anywhere between 0 and 100 people will be classified as exposed. It follows that in any given study where the mechanism of misclassification is expected to be nondifferential, the observed errors may not be exactly nondifferential. Even when the expected bias is towards the null, the observed estimate may lie on either side of the unbiased value due to this deviation from expectation. As with any random process, the probability of large deviations from expectation will grow smaller as the sample size increases. Simulation studies have shown that in some scenarios, even slight deviations from the expectation of nondifferentiality can create bias away from the null in a substantial proportion of simulated iterations of the data-generating mechanism (15). Therefore, both the expectation for the direction and amount of bias implied by the bias parameters and design and the probabilistic nature of the application of those parameters must be considered when evaluating the potential impact of misclassification bias on research findings.

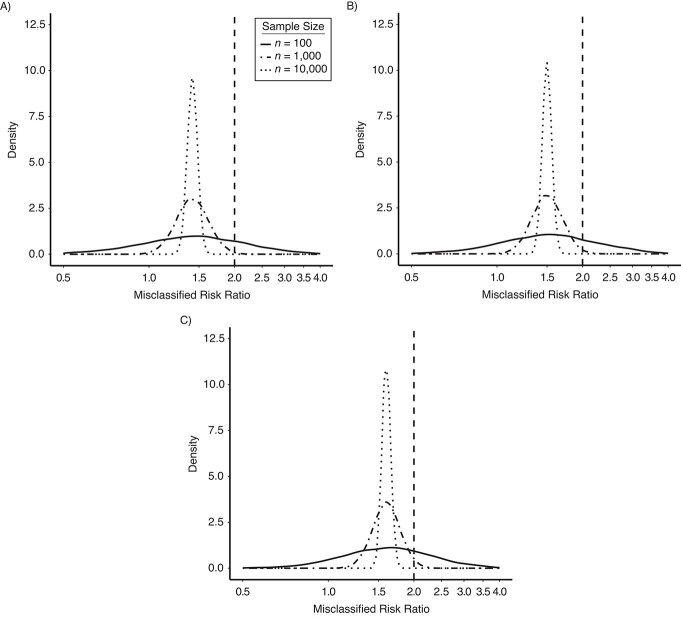
To illustrate random deviations from nondifferentiality, we simulated nondifferential misclassification at the record level (as opposed to using summary-level data), representing 3 hypothetical true data sets of varying sizes, but with the true risk ratio (RR) equal to 2.0 and the same distribution of the exposure and outcome in each, as shown in Table 1.

Table 1.

Hypothetical True Data Sets With Varying Sizes but the Same Distribution of the Exposure (E) and Outcome (D)

	Outcome Status (n)
Data Set	D+	D−	RR
n = 100			2.0
E+	10	40
E−	5	45
n = 1,000			2.0
E+	100	400
E−	50	450
n = 10,000			2.0
E+	1,000	4,000
E−	500	4,500

Abbreviation: RR, risk ratio.

For each data set, we simulated a classified version of the exposure variable as a 0/1 indicator variable with a specificity of 0.9 and a sensitivity of either 0.6, 0.7, or 0.8 (in 3 different simulations). For truly exposed individuals, we classified the exposure by drawing from a binomial distribution with a probability equal to the sensitivity for the simulation (0.6, 0.7, or 0.8). For truly unexposed individuals, we classified the exposure by drawing from a binomial distribution with a probability equal to 1 minus the specificity for the simulation (i.e., the probability of a false-positive exposure status: (1 − 0.9) = 0.1).

We ran each simulation 10,000 times and plotted the densities of the observed, misclassified RRs for each specified sensitivity: 0.8 (Figure 1A), 0.7 (Figure 1B), and 0.6 (Figure 1C). We also visualized the realized sensitivities and specificities in Web Figure 1 (available at https://doi.org/10.1093/aje/kwac035). The specified values for sensitivity and specificity determined the expectation of the observed results, while the sample size determined the spread of the distribution. Taken together, these parameters determined how likely it was that a result would be biased towards or away from the null. The proportion of simulations in which the observed RR was biased away from the null was 21%, 23%, and 27% when sensitivity was 60%, 70%, and 80%, respectively, and the sample size was 100. When the sample size was 1,000, the proportion of simulations biased away from the null was 0.5%, 1.0%, and 2.0%, for sensitivities of 60%, 70%, and 80%, respectively. When the sample size was 10,000, there was no simulation in which the RR was biased away from the null. The plots in Figure 1 demonstrate that when the sample size is smaller and when there is less misclassification (i.e., the center of the distribution of misclassified RRs is closer to the true effect), results are more likely to be biased away from the null because of chance. Other aspects of the simulation will influence the result, including the risk in the unexposed, the strength of association, and exposure prevalence. Note that simulations with smaller sample sizes are more sensitive to the discrete nature of the binomial distribution, which was used to classify exposure. For example, the mode of the density distribution for simulations with 100 participants is slightly shifted in comparison with simulations with 1,000 or 10,000 participants because binomial sampling does not allow for decimal fractions (Figure 1). Similarly, this causes the density distribution of the actualized, disease-specific exposure sensitivity and specificity from simulations with 100 participants to appear bumpy (Web Figure 1).

Figure 1.

Results from an observation-level simulation of nondifferential exposure misclassification, using 3 example data sets of varying sizes (Table 1) and a range of sensitivities. The figure shows density plots of the misclassified risk ratios (RRs) from 10,000 simulations. We simulated the classified version of exposure by drawing from binomial distributions with probabilities equal to the specified specificity and sensitivity. Each analysis was repeated at 3 different sample sizes but with the true RR equal to 2.0 and the same distribution of the exposure and outcome in each. A) Exposure specificity = 90%; exposure sensitivity = 80%; true RR = 2.0. B) Exposure specificity = 90%; exposure sensitivity = 70%; true RR = 2.0. C) Exposure specificity = 90%; exposure sensitivity = 60%; true RR = 2.0. The vertical dashed line denotes the true RR (RR = 2.0) in each panel. The mode of the density distribution for simulations with 100 participants is slightly shifted compared with simulations with 1,000 or 10,000 participants because binomial sampling does not allow for decimal fractions; smaller sample sizes are more sensitive to the discrete nature of the binomial distribution.

Note that the bias in these examples is towards the null, because the direction of bias is described in terms of its expectation. However, any one study is a single realization of the data-generating mechanism and may deviate from expectation.

EXCEPTION 2: NONDIFFERENTIAL MISCLASSIFICATION OF A MULTILEVEL EXPOSURE VARIABLE

Nondifferential misclassification of a categorical exposure variable with more than 2 levels can result in an expectation of bias away from the null in at least 1 of the middle category comparisons with the reference group by mixing risk across levels (16), and it can result in no bias in the highest exposure category if there is no mixing of other exposure categories with it. These bias patterns depend on the location of the misclassification (i.e., across adjacent and/or nonadjacent categories), the size of the true effects, the dose-response pattern, and the degree of misclassification. Consider a hypothetical study in which data on smoking are collected as never smoker (reference category), former smoker, and current smoker. Misclassification of current smokers as former smokers (i.e., across adjacent categories) results in bias away from the null when examining the risk of lung cancer in former smokers compared with never smokers. Because the only mixing is of current smokers with former smokers, the estimate comparing current smokers with never smokers is unbiased. When misclassification occurs across nonadjacent categories (a situation that may be uncommon), the bias can cause the estimate to cross the null. In Table 2, we present example data to demonstrate the impact of nondifferential miclassification across adjacent and nonadjacent exposure categories with both high and moderate amounts of misclassification.

Table 2.

Example of Nondifferential Misclassification Across Adjacent and Nonadjacent Categories of a Multilevel Exposure Variable

	Outcome Status (n)
Exposure Status	D+	D−	Total (n)	Risk a	RR
Correctly classified data
High	300	4,700	5,000	0.06	6.00
Low	100	4,900	5,000	0.02	2.00
None	50	4,950	5,000	0.01	1.00b
30% exposure misclassification across adjacent categories (high to low)c
High	210	3,290	3,500	0.06	6.00
Low	190	6,310	6,500	0.03	2.92
None	50	4,950	5,000	0.01	1.00b
15% exposure misclassification across adjacent categories (high to low)d
High	255	3,995	4,250	0.06	6.00
Low	145	5,605	5,750	0.03	2.52
None	50	4,950	5,000	0.01	1.00b
30% exposure misclassification across nonadjacent categories (high to none)e
High	210	3,290	3,500	0.06	2.79
Low	100	4,900	5,000	0.02	0.93
None	140	6,360	6,500	0.02	1.00b
5% exposure misclassification across nonadjacent categories (high to none)f
High	285	4,465	4,750	0.06	4.85
Low	100	4,900	5,000	0.02	1.62
None	65	5,185	5,250	0.01	1.00b

Abbreviation: RR, risk ratio.

^a Risk = number in D+/total number.

^b Referent.

^c 30% of people with truly high exposure are misclassified as having low exposure. In this example, the RR for high exposure versus no exposure is unchanged, but the RR for low exposure versus no exposure is biased away from the null.

^d 15% of people with truly high exposure are misclassified as having low exposure. In this example, the RR for high exposure versus no exposure is unchanged, but the RR for low exposure versus no exposure is biased away from the null.

^e 30% of people with truly high exposure are misclassified as having no exposure. In this example, the RR for high exposure versus no exposure is biased towards the null, and the RR for low exposure versus no exposure crosses the null.

^f 5% of people with truly high exposure are misclassified as having no exposure. In this example, the RRs for both high exposure versus no exposure and low exposure versus no exposure are biased towards the null.

In the presence of a true strictly monotonically increasing dose-response association between exposure and outcome, misclassification occurring in both directions can result in a spurious inverse dose-response relationship. For example, if never smokers are misclassified as current smokers and current smokers are misclassified as never smokers, the observed risk of lung cancer in the reference group would be greater than the truth, whereas the observed risk among current smokers would be less than the truth. However, in most cases, a high degree of misclassification (e.g., >50%) is necessary for this inverse dose-response relationship to appear. Example data for this scenario are presented in Web Table 1.

In each of these examples, the expected magnitude of bias depends partially on how much the risk of disease differs across exposure groups. Typically, if the true effects comparing current and former smokers with never smokers are large, the potential extent of bias away from the null will be greater than if the true effects were small. In addition, as the proportion of misclassified subjects increases, the expected extent of bias will increase.

It is also possible to induce bias away from the null by collapsing 2 or more exposure categories that are nondifferentially misclassified. In this case, collapsing exposure categories can induce differential misclassification, resulting in bias away from the null or even a reversal of the association (17). For example, if smoking affects the outcome risk, if current smokers are nondifferentially misclassified as never smokers, and if current and former smoking are collapsed to “ever smoking,” there could be differential misclassification of ever smoking versus never smoking with respect to the outcome. In Table 3, we present data where 30% of individuals with truly high exposure are misclassified as having low exposure. After collapsing the exposure categories to any (low or high) versus none, the sensitivity of exposure classification was 77% in the D+ group and 83% in the D− group. This deviation from nondifferentiality caused the RR to cross the null, from 1.86 (true) to 0.95 (observed). Note that using these hypothetical data, the effect estimate crossed the null only when there was at least 25% misclassification.

Table 3.

Example of a Reversal of Association When Nondifferentially Misclassified Exposure Categories Are Collapsed

	Outcome Status (n)
Exposure Status	D+	D−	Total (n)	Risk a	RR
Correctly classified data
High	200	7,800	8,000	0.03	2.50
Low	60	5,940	6,000	0.01	1.00
None	20	1,980	2,000	0.01	1.00b
Low or high	260	13,740	14,000	0.02	1.86
30% exposure misclassified across adjacent categories (high to low)c
High	140	5,460	5,600	0.03	1.38
Low	60	5,940	6,000	0.01	0.55
None	80	4,320	4,400	0.02	1.00b
Low or high	200	11,400	11,600	0.02	0.95

Abbreviation: RR, risk ratio.

^a Risk = number in D+/total number.

^b Referent.

^c 30% of people with truly high exposure are misclassified as having low exposure. In this example, the RR for any exposure versus no exposure crosses the null (the direction of the association is reversed).

EXCEPTION 3: NONDIFFERENTIAL BUT DEPENDENT MISCLASSIFICATION OF EXPOSURE

Dependent misclassification occurs when the rate at which subjects who are misclassified with respect to 2 key variables differs from what would be expected based on the rates of misclassification of each variable alone (18–20). In most cases, the focus is on dependency between exposure and outcome. In this scenario, the probability of being doubly misclassified is not equal to the product of the probabilities of being singly misclassified with respect to exposure and outcome. Even small amounts of dependent nondifferential misclassification of exposure and outcome can create strong bias away from the null, depending on the exposure and outcome distribution (18). However, bias arising from dependent misclassification is challenging to predict. Quantifying the potential extent of dependent misclassification requires specification of the individual probabilities of misclassification in every possible direction (i.e., 12 probabilities, each corresponding to the arrows in Figure 2 (18)).

Figure 2.

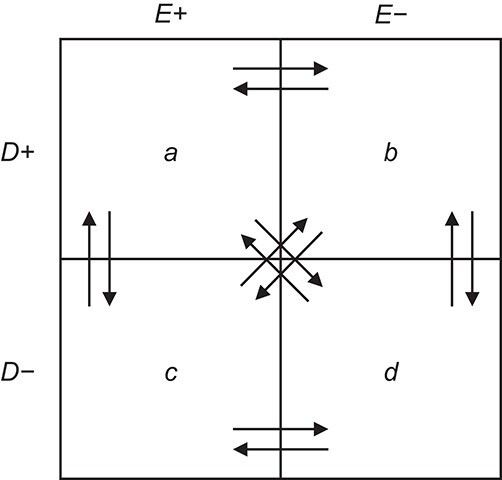
Rearrangement of exposure and outcome classification in a 2 × 2 table resulting from both exposure and outcome misclassification. Adapted from Kristensen (18).

Lash and Fink (21) presented a motivating example of dependent nondifferential misclassification using data from a study by Balfour and Kaplan (22). In that study, data on neighborhood environment (exposure) were collected using a survey administered to older adults, and self-reported decline in physical function (outcome) was ascertained after 1 year of follow-up. The observed crude RR was 2.8 for the association between neighborhood problems and reporting a decline in overall function. Lash and Fink hypothesized that dependent misclassification could arise if individuals had varying “thresholds” for reporting their exposure and outcome status. For example, some participants may be more likely to overstate their neighborhood problems as well as their declining physical function. Using equations presented by Kristensen (18), Lash and Fink quantified the degree of dependent misclassification that would be necessary to completely explain away the observed RR. Under a truly null association, a spurious RR of 2.8 could be observed if only 1.6% of participants systematically over- or understated their exposure and outcome.

We demonstrate this with a different example, in which a true null association is biased upwards due to dependent misclassifcation of exposure and outcome (Table 4). With only 1% dependent error, we observe a spurious RR equal to 1.2. The movement between each cell, depicted graphically in a general sense in Figure 2, is described numerically in Table 5.

Table 4.

Example of Upwards Bias Due to Nondifferential, Dependent Exposure Misclassification

	Outcome Status (n)
Exposure Status	D+	D−	Total (n)	Risk a	RR
Correctly classified data
Exposed	20	180	200	0.10	1.00
Unexposed	60	540	600	0.10	1.00b
Exposure and outcome misclassified with 1% dependent errors
Exposed	25	180	205	0.12	1.22
Unexposed	60	535	595	0.10	1.00b

Abbreviation: RR, risk ratio.

^a Risk = number in D+/total number.

^b Referent.

Table 5.

Expected Movement Between True and Classified Data Cells to Produce the Hypothetical Data in Table 4^a

True Status	No. of Persons Truly in   Each E/D Combination	Classification	Expected No. of Persons Classified   in Each E/D Combination
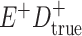
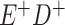
	20		19.8
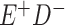
			0.0
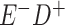
			0.0
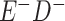
			0.2
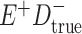
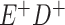
	180		0.0
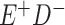
			180.0
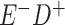
			0.0
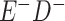
			0.0
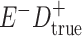
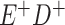
	60		0.0
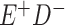
			0.0
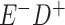
			60.0
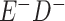
			0.0
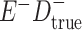
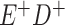
	540		5.4
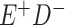
			0.0
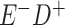
			0.0
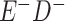
			534.6

^a In this example, there is only movement between the 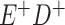and 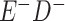cells. The number classified as 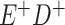is equal to 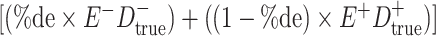, where 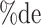is the percentage of dependent error. The number classified as 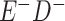is equal to .

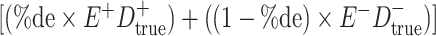Dependent misclassification is most likely to occur when the same instrument is used to measure the exposure and the outcome, particuarly when the exposure and outcome are subjective. If both exposure and outcome are perceived to be harmful, the exposed-diseased and unexposed-nondiseased cells will be inflated at the expense of the exposed-nondiseased and unexposed-diseased cells. This pattern can result in large amounts of bias, particularly when the true prevalence of exposure and outcome are low. However, dependent error can be avoided during the design phase of a study by collecting exposure and outcome information using separate methods. In the example of neighborhood function and physical function, data were collected using different questionnaires, but both exposure and outcome collection relied on self-report. Use of separate and different instruments (e.g., questionnaire and registry, or biomarker and medical record data) would, in most cases, remove the dependency in the misclassifiation. However, it is unrealistic to expect researchers to collect data on every important study variable (including confounders and effect modifiers) using separate instruments. In particular, exposure and confounder information are often collected jointly via questionnaires (3, 19, 23, 24). Thus, investigators should consider the potential influence of both exposure-outcome and exposure-covariate dependent misclassification on their results.

EXCEPTION 4: NONDIFFERENTIAL MISCLASSIFICATION OF ECOLOGICALLY MEASURED EXPOSURE

Though epidemiologists are typically cautioned against making individual-level inferences using ecological data (i.e., the “ecological fallacy”), it is possible to infer individual-level rate ratios under certain assumptions (25). Consider an ecological study of the risk of death from an exposure using mortality rates and exposure prevalences in 2 distinct populations. The ratio of the predicted mortality rates for the extreme cases (i.e., everyone is exposed vs. everyone is unexposed) will be equivalent to the individual-level rate ratio estimating the exposure-outcome association, assuming that 1) the background mortality rate and the exposure effect do not vary across the populations and 2) there is no confounding of the exposure-outcome relationship within the populations. In an ecological study, nondifferential misclassification of exposure occurs when the observed population-specific exposure prevalences differ from the true exposure prevalences. Unlike the case in individual-level studies, nondifferential exposure misclassification in ecological studies induces an expected bias away from the null for both rate ratios and rate differences (26). This bias can occur even at relatively small deviations from perfect sensitivity and specificity, and generally is worse with larger true effects.

EXCEPTION 5: OUTCOME MISCLASSIFICATION

When outcome specificity is perfect and sensitivity is nondifferentially misclassified with respect to the exposure, the RR will be unbiased and the risk difference will be biased towards the null by a factor equal to the sensitivity. This pattern arises because the observed incidence of the outcome (I_obs) in the absence of false-positive outcomes is equal to the true incidence (I_true) multipled by the sensitivity (Se), such that 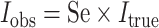. If the sensitivity of outcome classification is the same in the exposed and unexposed, then the observed RR is equal to the true RR 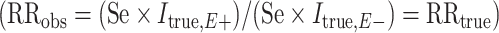while the observed risk difference is equal to 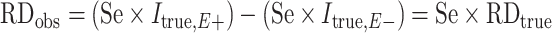. For example, if 50% of individuals who have the outcome in the exposed group are misclassified as disease-negative and 50% of individuals who have the outcome in the unexposed group are misclassified as disease-negative, then the observed risk of disease at each level of exposure will be halved relative to the true risks. The RR will remain unchanged, but the risk difference will be halved. We demonstrate this using example data in Table 6.

Table 6.

Example of Outcome Misclassification Yielding an Unbiased Risk Ratio

	Outcome Status (n)
Exposure Status	D+	D−	Total (n)	Risk a	RR	RD
Correctly classified data
Exposed	100	400	500	0.20	2.00	0.10
Unexposed	50	450	500	0.10	1.00b	1.00b
Outcome misclassified with perfect specificity and imperfect 60% sensitivityc
Exposed	60	440	500	0.12	2.00	0.06
Unexposed	30	470	500	0.06	1.00b	1.00b

Abbreviations: RD, risk difference; RR, risk ratio.

^a Risk = number in D+/total number.

^b Referent.

^c 40% of individuals with the disease are misclassified as not having the disease, in both the exposed and unexposed groups. In this example, the RR for exposed versus unexposed is unchanged, but the RD is biased towards the null by 40%.

The potential impact of outcome misclassification is particularly relevant for hospital-based case-control studies, in which misclassification of cases can affect both precision and validity. For example, low sensitivity due to a very restrictive case definition with high specificity may lead to reduced precision if few cases are identified (27). However, especially with rare outcomes, losses in specificity tend to have a more substantial impact on validity than losses in sensitivity, which will bias the odds ratio only when specificity is also imperfect. Given that investigators must often prioritize either sensitivity or specificity, specificity should be favored to optimize validity. Near-perfect outcome specificity with nondifferential sensitivity will yield only negligible bias in ratio measures. See Jurek et al. (28) for important caveats for bias adjustment of misclassified case and control status.

EXCEPTION 6: COVARIATE MISCLASSIFICATION

Nondifferential misclassification of a confounder biases the expected relative risk due to confounding (the ratio of the crude to the adjusted estimate) towards the null, resulting in incomplete control for confounding (3). Thus, the effect estimate will be biased in the direction of the original confounding. For example, nondifferential misclassification of a confounder whose lack of control results in bias away from the null will result in a bias away from the null. The reverse is true for a confounder that acts in the opposite direction. The magnitude of this bias will depend on the strength of the confounder and the degree of misclassification: typically, a stronger and more heavily misclassified confounder will result in a greater degree of residual confounding in the effect estimate.

When evaluating potential effect modification, nondifferential misclassification of the stratification variable results in an unpredictable bias. This misclassification can create a spurious appearance of effect modification or mask true effect modification, on either the relative or absolute scale (3). In Table 7, we present an example where the covariate C is a confounder of the exposure-disease relationship, but it is not an important effect-measure modifier on the relative scale (RR_C+ = 0.70 and RR_C− = 0.69). Misclassification of C that is nondifferential with respect to the exposure and outcome results in an adjusted effect estimate (RR = 1.13) that is between the true (RR = 0.70) and crude (RR = 1.23) estimates, and it also induces spurious heterogeneity across strata of C (RR_C+ = 1.21 and RR_C− = 1.03).

Table 7.

Example of Incomplete Confounding Adjustment and Spurious Effect Modification on the Relative Scale Due to Covariate Misclassification

	Outcome Status (n)		Total (n)	Risk a	RR	Adjusted   RR (SMR)
Data Set	D+	D−
Correctly Classified Data
Total						0.70
E+	60	270	330	0.18	1.23
E−	130	750	880	0.15	1.00b
C+
E+	45	70	115	0.39	0.70
E−	50	40	90	0.56	1.00b
C−
E+	15	200	215	0.07	0.69
E−	80	710	790	0.10	1.00b
Covariate Misclassified With 80% Specificity and 70% Sensitivity c
Total						1.13
E+	60	270	330	0.18	1.23
E−	130	750	880	0.15	1.00b
C+
E+	34.5	89	123.5	0.28	1.21
E−	51	170	221	0.23	1.00b
C−
E+	25.5	181	206.5	0.12	1.03
E−	79	580	659	0.12	1.00b

Abbreviations: RR, risk ratio; SMR, standardized mortality ratio.

^a Risk = number in D+/total number.

^b Referent.

^c Misclassification of the confounder, C, is nondifferential with respect to both the exposure and the outcome, with 80% specificity and 70% sensitivity. In this example, the true unbiased RR is 0.70, the crude RR is 1.23, and the RR adjusted for the misclassified variable C is 1.13. While there is no evidence of effect modification on the relative scale in the correctly classified data, the stratum-specific RRs in the misclassified data are 1.03 and 1.21, falsely suggesting effect modification by C.

EXCEPTION 7: MISMEASUREMENT OF CONTINUOUS VARIABLES

Mismeasurement of continuous variables, which may be the exposure, the outcome, or a covariate, generally has the same exceptions as described above for misclassification of discrete variables. There are, however, some important additional nuances that lead to additional exceptions to the heuristic. First, for exposures and covariates measured on a continuous scale, the continuous measures are sometimes grouped into categories using boundary cutoffs. For example, body mass index (weight (kg)/height (m)²) is often categorized using boundary cutoffs with labels such as “underweight,” “normal weight,” “overweight,” and “obese.” Nondifferential mismeasurement of a continuous exposure does not ensure nondifferential misclassification when the continuous measure is binned into categories (17, 29). Second, when the continuous measure is an independent variable in a general linear model, when the extent of error is nondifferential with respect to the outcome, and when the mismeasured variable is a function of the true value plus error, the association is expected to be biased towards the null. This is commonly called “classical measurement error.” When the extent of error is nondifferential with respect to the outcome and when the true value is a function of the mismeasured value and a symetrically distributed error term with mean 0, there is no expected bias (although there is additional uncertainty). This is commonly called “Berkson measurement error” (30), and it provides another exception to the heuristic. Likewise, classical measurement error affecting the outcome yields an expectation of no bias, but with additional uncertainty.

CONCLUSION

In this paper, we describe notable exceptions to the heuristic that “nondifferential misclassification biases toward the null.” First, misclassification is stochastic and can deviate from expectation. Even when the mechanism of misclassification of a binary exposure variable is nondifferential and independent and there are no other sources of bias, the observed estimate may be biased away from the null simply due to chance. This deviation from expectation is more likely in studies with sparse data than in more statistically efficient analyses. Second, nondifferential misclassification of a multilevel exposure variable can result in bias away from the null in the middle dose categories, no bias in the highest dose category or, in some extreme cases, a spurious inverse dose-response relationship. Collapsing nondifferentially misclassified exposure categories can also induce the appearance of differential misclassification, and thus lead to unpredictable bias. Third, nondifferential but dependent misclassification of an exposure variable can create unpredictable bias, and even small amounts of dependent misclassification can create strong bias away from the null. Fourth, individual-level rate ratios estimated using ecological data will generally be biased away from the null due to nondifferential misclassification of the exposure variable. Fifth, nondifferential outcome misclassification can yield an unbiased RR when specificity is perfect. Sixth, misclassification of a confounder results in an observed estimate that is somewhere between the true estimate and the crude estimate, and can either induce or mask the presence of heterogenity across stratum-specific estimates. Last, nondifferential mismeasurement of a continuous variable can result in differential misclassification if the continuous variable is binned, nondifferential misclassification of a continuous exposure results in no bias of an exposure-outcome association when the error structure is Berksonian, and nondifferential misclassification of a continuous outcome results in no bias of the exposure-outcome association when the error structure is classical.

Taking these examples into consideration, epidemiologists should not rely on the “nondifferential misclassification” heuristic as justification for why an association is biased towards the null. There are too many exceptions to the heuristic to rely on it for inference about the direction of bias. Instead, we encourage investigators to consider all possible mechanisms of measurement error and to implement quantitative bias analysis whenever possible to better understand the direction, magnitude, and uncertainty resulting from the measurement error.