Abstract
Chronic traumatic encephalopathy (CTE) is a neurodegenerative disease associated with exposure to repetitive head impacts such as those from American football. Our understanding of this association is based on research in autopsied brains, since CTE can only be diagnosed postmortem. Such studies are susceptible to selection bias, which needs to be accounted for to ensure a generalizable estimate of the association between repetitive head impacts and CTE. We evaluated the relationship between level of American football playing and CTE diagnosis after adjusting for selection bias. The sample included 290 deceased male former American football players who donated their brains to the Veterans Affairs–Boston University–Concussion Legacy Foundation (VA-BU-CLF) Brain Bank between 2008 and 2019. After adjustment for selection bias, college-level and professional football players had 2.38 (95% simulation interval (SI): 1.16, 5.94) and 2.47 (95% SI: 1.46, 4.79) times the risk of being diagnosed with CTE as high-school–level players, respectively; these estimates are larger than estimates with no selection bias adjustment. Since CTE is currently diagnosed only postmortem, we additionally provide plausible scenarios for CTE risk ratios for each level of play during the former players’ lifetime. This study provides further evidence to support a dose-response relationship between American football playing and CTE.
Keywords: American football, autopsy, chronic traumatic encephalopathy, football, probabilistic analysis, repetitive head injury, selection bias
Abbreviation
- CTE
chronic traumatic encephalopathy
- NCAA
National Collegiate Athletic Association
- NFL
National Football League
- RHI
repetitive head impacts
- RR
risk ratio
- SI
simulation interval
- UNITE
Understanding Neurologic Injury in Traumatic Encephalopathy
- VA-BU-CLF
Veterans Affairs–Boston University–Concussion Legacy Foundation
Chronic traumatic encephalopathy (CTE) is a neurodegenerative disease associated with exposure to repetitive head impacts (RHI), such as those from contact sport participation, military combat exposure, and other sources (1–6). Millions of individuals participate in contact sports each year, especially in American football, and CTE may thus be a major public health concern (7, 8). Consequently, a growing amount of research has sought to clarify the risk of CTE in American football players. Most recently, Mez et al. (9) reported a dose-response relationship between duration of American football playing and CTE status, with the odds of being diagnosed with CTE doubling with every 2.6 years of football played.
Currently, CTE can only be diagnosed postmortem using established neuropathological diagnostic criteria (10). Our knowledge of the relationship between exposure to RHI from contact sport play and CTE has been derived from persons who donated their brains for autopsy, particularly brain donors who were part of the Veterans Affairs–Boston University–Concussion Legacy Foundation (VA-BU-CLF) Brain Bank (4, 11). In general, autopsy studies suffer from selection bias, which may bias the estimates of association between exposure and outcome. Specifically, brain donation has been shown to be influenced by age, sex, race, marital status, depression, and dementia (12). It has been argued that selection is further amplified in the case of the VA-BU-CLF Brain Bank, since most donors tend to have had cognitive and mood/behavioral symptoms suggestive of CTE (7, 13, 14). Therefore, brain donors with higher levels of RHI exposure who are symptomatic are more likely to donate their brains and perhaps more likely to have CTE.
The validity of research involving CTE has been questioned due to the inherent bias in the selection process of brain donation studies. To respond to such criticism, there is a significant need to adjust for selection bias in the analytical phases of these studies (7, 12). The standard approach to adjusting for selection bias is to make the sample more representative of the population of interest (12). While weighting approaches exist, we extend the methodology of Lash et al. (15) to risk ratios (RRs), which can be used to adjust for selection bias using conditional probabilities of selection. Although these are often unknown, simulation approaches can be used to account for this uncertainty and to model the association across the range of conditional probability estimates.
Besides that of Mez et al. (9), no other study (to our knowledge) has explored whether a dose-response relationship exists between highest level of football played and CTE. Additionally, Mez et al. employed inverse probability weighting to adjust for selection bias, but the ranges of the conditional probabilities of selection were not based on empirical evidence. Although the baseline probability of selection for an individual with neither exposure nor CTE was estimated from a community-based study, the effects of exposure and CTE status on selection were unknown. Therefore, the inverse probability weighting was implemented as a sensitivity analysis, using simulation approaches to vary the effects of exposure and CTE status (9). Here, we expanded on this prior work by using population-level data to estimate the bounds of these conditional probabilities of selection. Furthermore, we consider the situation where CTE is affecting people during their lifetime. Although this is beyond current scientific capabilities, since there are no diagnostic criteria for CTE premortem, we provide plausible scenarios that depend on the unknown mortality risk of different population groups of former football players.
Additionally, the selection processes inherent in brain donation studies may bias estimates of the cumulative CTE incidence (7, 16, 17). To obtain an estimate of the true prevalence of CTE, Binney and Bachynski (16) used the number of deceased American football players who were diagnosed with CTE, as reported in the 2017 study by Mez et al. (4), and a cohort of deceased National Football League (NFL) players who did not participate in that study despite being eligible. Then the lower and upper bounds of the prevalence were estimated by Binney and Bachynski to range from 9.6% to 100% in professional American football players, by first assuming that the eligible cohort did not contain any CTE cases and then assuming it contained only CTE cases (16). In this paper, we update the prevalence bounds for professional football players using the latest data and expand them to other populations, notably high school and college football players, which involve even more persons at risk.
To this end, we performed simulations under various selection criteria using a convenience sample of former American football players from the VA-BU-CLF Brain Bank. We hypothesized that there would be a dose-response association between the level of American football played (i.e., high school, college, or professional) and risk of a neuropathological diagnosis of CTE, even after adjustment for selection bias.
METHODS
VA-BU-CLF Brain Bank
Our convenience sample of donor brains came from the VA-BU-CLF Brain Bank. The VA-BU-CLF Brain Bank was established in 2008 as a partnership between the VA Boston Healthcare System, Boston University School of Medicine, and the Concussion Legacy Foundation (Boston, Massachusetts). All brain donors were part of the Understanding Neurologic Injury in Traumatic Encephalopathy (UNITE) Study (11). The objective of the UNITE Study is to study the long-term consequences of RHI. It is made up of brain donors who have a history of exposure to RHI regardless of whether symptoms were present during life. Next of kin contact the Boston University CTE Center to arrange brain donation near the time of death or following death. Other brain donors are referred by medical examiners, are recruited by the Concussion Legacy Foundation, or agree to brain donation during life. Brain donors are excluded for a prolonged postmortem interval (>72 hours) or poor tissue quality. The outreach and recruitment process and methods of data collection have been described in great detail elsewhere (4, 9, 11). At the time of this study, 85.3% of the brain donors in the UNITE brain bank had played American football at any level. Institutional review board approval was obtained through the Boston University Medical Campus (Boston, Massachusetts) and the Edith Nourse Rogers Memorial Veterans Hospital (Bedford, Massachusetts).
Neuropathological diagnosis of CTE
Neuropathological evaluation occurred with the neuropathologists blinded to clinical data and was reviewed by 4 neuropathologists; discrepancies in the neuropathological diagnosis were resolved by group discussion and consensus. Methods for processing of tissue samples and evaluation in the UNITE Study have been published elsewhere (2, 4, 10, 11, 18, 19) and follow established procedures (20, 21). Twenty-two sections of paraffin-embedded tissue were stained with Luxol fast blue–hematoxylin and eosin and Bielschowsky’s silver for detection of phospho-tau monoclonal antibody (AT8), α-synuclein, amyloid β, and phosphorylated transactive response DNA-binding protein 43. The neuropathological diagnosis of CTE was made using criteria defined by the National Institute of Neurological Disorders and Stroke/National Institute of Biomedical Imaging and Bioengineering consensus panel (10).
Defining the primary (deceased) target population
We chose the deceased target population to reflect the overarching population from which our brain bank participants were presumably sampled. Because CTE currently cannot be diagnosed during life, our deceased target population of interest was American men who died during study recruitment (2008–2019) and had played high school, college, or NFL professional football for at least 1 year. We excluded players whose highest level of play was pre–high school or semiprofessional, because there are no reliable exposure data for these groups. Further, to match our study sample, our target population consisted only of men who were at least 20 years of age at death.
Defining the secondary (living and deceased) target population
Given that CTE cannot be diagnosed during life, our primary target population was deceased. However, conditioning the outcome of our analysis on death would not lend itself well to public health ramifications, since we would not be considering a population that could be intervened upon. To this end, we introduced a secondary target population—the population of all American men (living and deceased) who had played at least 1 year of high school, college, or NFL professional football—to explore the situation where the outcome is affecting players premortem, albeit undiagnosed with the current state of scientific knowledge.
Participant selection
The current sample included male former American football players who played either high school, college, or NFL professional football for at least 1 year. Additionally, only those who died during the study recruitment period, 2008–2019, were included in this analysis. Similar to the study by Mez et al., participants were included only if they were at least 20 years of age at death (9). All donor brains had complete data on CTE status.
There were 538 football players in the brain bank who died within the study enrollment period (2008–2019) and were at least 20 years of age at death. However, we excluded some brain bank participants to ensure that our sample was drawn from our theorized target population. Because the information on our target population was restricted to certain years of play for high school and college players, we excluded brain bank participants who were high school players who did not retire between 1970 and 2015 (n = 22) and college players who did not retire between 1982 and 2015 (n = 117). All professional football players in the brain bank were included, since the information on our professional player target population was not restricted to certain years of play. Additionally, we excluded football players whose highest level of play was pre–high school (n = 11) or semiprofessional (n = 98). The sample ultimately included 290 male former American football players.
Estimating counts in our deceased target population
In order to adjust for selection bias, we needed estimates of the probabilities of selection into the study for each level of football playing. Estimating these probabilities required knowing the number of men in our target population who died during this time frame, by level of play. We obtained data from the National Federation of State High School Associations (Indianapolis, Indiana), which provided the total number of high school students enrolled in a football program each year from 1970 to 2015 (22–29). Missing data (8.7%) were imputed by means of cubic spline regression. Similarly, data on college football participation were obtained from the National Collegiate Athletic Association (NCAA) Sports Sponsorship and Participation Rates Database, which provided the total number of college students enrolled in a football program in each year from 1982 to 2015 (30). Coupling this information with mortality rates from the Centers for Disease Control and Prevention, we estimated the number of former high school and college players who died between 2008 and 2019 (31). In estimating the number who died, we assumed that, on average, 25% of players stopped playing each year, reflecting a uniform rate of stopping play over the approximately 4 years spent in high school and college. Additionally, we assumed that high school football players were aged 18 years when they stopped playing and that college football players were aged 22 years when they stopped playing. Use of mortality rates provided by the Centers for Disease Control and Prevention rested on the assumption that the mortality rates of former high school and college football players were the same as those of same-age males from the general population.
For the professional football players, we used individual-level data on year of birth, year of death, and retirement age, available from Hidden Game Sports (Detroit, Michigan), a private company that produces licensed sports databases. This database showed that 1,549 NFL professionals died during the data collection period of the brain bank (2008–2019). For players who were known to be deceased but had a missing year of death and a nonmissing retirement year (n = 106), the year of death was estimated using the mortality rates and algorithm described above for the high school and college players. Again, this rested on the assumption that professional players have the same mortality rates as the general population. For the players who had missing age at retirement (n = 47), their age at retirement was estimated by adding the number of professional years played to 22, which is assumed to be the average age of entering professional football. After imputation of missing years of death, there were an additional 2 players who died during the brain bank operating period, bringing the estimated number of professionals in our target population to 1,551.
Estimating counts in our living target population
Defining our secondary living target population required knowing the number of living men in our target population who had played football on at least 1 level, by level of play. We utilized the same data sources as we did for the deceased target population—that is, the National Federation of State High School Associations, the NCAA Sports Sponsorship and Participation Rates Database, and Hidden Game Sports. Again, these estimates rested on the aforementioned assumption about when players stopped playing. For high school and college players, we took the number of players who retired each year who did not die within the study enrollment period. For professionals, all players with a nonmissing year of death were known to be alive at the time of data collection (2020).
Statistical analyses
Estimating the minimum cumulative incidence of CTE.
We estimated the minimum cumulative incidence of CTE in the deceased target population for each level of play by dividing the observed number of CTE cases by the total number of men within the deceased target population.
Calculating conventional age-adjusted estimates of association.
To evaluate the association between highest level of football playing and CTE, we fitted a log binomial regression to our brain bank data. Since highest level of football playing had 3 levels, the reference group was those who played at least 1 year of high school football. We thus estimated the RR for CTE for college and professional players. Because neurodegenerative diseases such as CTE are age-dependent, these associations were adjusted for categorical age at death (defined as ≤40 years or >40 years). To account for random error in this estimate, we performed bootstrapping 50,000 times. Each of these estimates was later adjusted for selection bias using the conditional probabilities of selection.
Adjustment for selection bias.
To adjust these age-adjusted RR estimates for selection bias, we multiplied the conventional adjusted analysis RR by the appropriate combination of selection probabilities and 
, and 
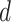, which are the age-adjusted counts from the CTE and exposure 2 × 2 contingency tables. For the derivation of equation 1, we refer the reader to the Web Appendix (available at https://doi.org/10.1093/aje/kwac075). The selection probabilities are conditional on death, as well as CTE and exposure status, where 
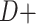and 
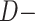denote CTE diagnosis and no CTE diagnosis, respectively, whereas 
and 
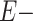denote having the exposure or not, respectively. Moreover, because we are interested in evaluating a potential dose-response relationship, this formula was implemented twice, once comparing the risk of CTE diagnosis in college football players with that of high school players and again comparing the risk of CTE diagnosis in professional football players with that of high school players.
 |
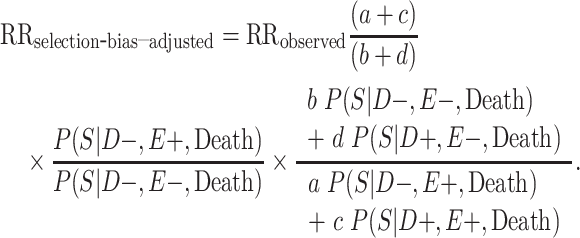(1) |
Estimating the conditional selection probabilities.
In order to adjust the RR for selection bias, the probabilities of selection conditional on the highest level of American football playing, CTE status, and death are required. Because such probabilities are unknown, they were decomposed into estimable components via Bayes’ theorem. More specifically, the probabilities of selection conditional on the highest level of football playing, CTE status, and death can be represented as
 |
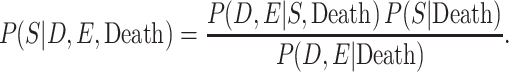The joint probabilities of the highest level of football playing and CTE status, conditional on selection and death, were observed in our brain bank. The probability of selection, conditional on death, was the number of participants included in our brain bank, divided by the total number estimated to be in our deceased target population. The main source of uncertainty in our estimates comes from the joint probabilities of the highest level of football playing and CTE status, conditional on death. We account for the uncertainty due to random sampling error in both the probability of selection given death and the joint probabilities of highest level of football playing and CTE status, conditional on selection and death, by bootstrapping the conventional estimate of association.
The joint probabilities of the highest level of football playing and CTE status, conditional on death, are not known with certainty. To limit the range of plausible probabilities for our simulation, we generated lower and upper bounds based on data at hand. The lower bounds for the joint probabilities of the highest level of football playing and CTE status, conditional on death, were the observed frequencies in our brain bank, divided by the total number estimated in our target population. In other words, we assumed that there were no brains with CTE outside of our brain bank. The upper bounds for the joint probabilities of CTE status and the highest level of play can be estimated using the total number of men in the target population at a given level of play, excluding known non-CTE brains from our study, again divided by the total number estimated to be in our target population. In other words, we assumed that everyone we did not observe had CTE. Similar logic applies for estimating the joint probabilities of being a decedent with no CTE diagnosis and a given highest level of play. This approach to estimating the joint probabilities of the highest level of football playing and CTE status, conditional on death, in turn produces a range of plausible values for each conditional selection probability.
Simulating the sampling distributions of adjusted RRs.
Selection probabilities were conservatively drawn from truncated β(2, 2) distributions, using the prespecified bounds as the support of the truncated β distribution. Untruncated β(2, 2) distributions have support (0, 1), are centered at 0.5, and are bell-shaped. Furthermore, when sampling the selection probabilities, the following restriction was applied:
 |
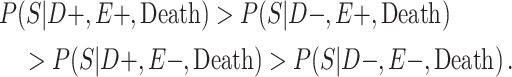This inequality was implemented because it imposes the theorized selection process of the VA-BU-CLF Brain Bank. Specifically, persons who have CTE at the higher level of football playing are more likely to be selected into the study, compared with any other CTE status and exposure combination. Moreover, it implies that having a higher level of exposure is a stronger driver of selection than having CTE pathology. This assumption is based on the experience of our brain bank, where the number of case men who played high school football was small relative to the number of college cases, considering the relative sizes of the target populations.
For the primary analysis, we first sampled each conditional selection probability according to its plausible bounds. Then, to impose the ordering, we kept only the vector of probabilities that satisfied the inequality. The 4 conditional selection probabilities were then used to produce an estimate of the selection-bias–adjusted RR. This process was repeated 50,000 times, for each bootstrapped conventional age-adjusted RR, creating sampling distributions of the selection-bias–adjusted RR. The mean values and 2.5th and 97.5th percentiles of the distributions were computed to obtain point estimates and 95% simulation intervals (SIs), respectively.
Other sampling schemes were implemented as sensitivity analyses: 1) by first sampling the smallest conditional selection probability and iterating upwards; 2) by first sampling the largest conditional selection probability and iterating downwards; 3) by assuming no hierarchical relationship between the probabilities and drawing each from the prespecified bounds, independently of all other probabilities; and 4) by first randomly selecting a conditional selection probability and then sampling according to its plausible bounds, then sampling the remaining conditional selection probabilities in order to maintain the inequality.
Estimating a, b, c, and d, the age-adjusted counts from the CTE and exposure contingency table.
While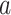 
,
,
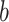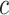, and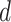 
are observed counts in the 2 × 2 CTE and exposure contingency table, these counts also need to be adjusted for age of death. To do so, we implemented a log-linear model, first for the college versus high school analysis and then again for the professional versus high school analysis. The main effects in the log-linear models included CTE, highest level of exposure, and categorical age of death. The predicted cell counts were obtained from the log-linear model and then collapsed over the age categories to ultimately produce counts 
,
,
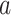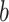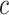, and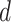 
, for each analysis.
Removing the conditioning on death from the selection-bias–adjusted RR.
In order to extend our inferences to the living population, we implement Bayes’ theorem to produce the following age- and bias-adjusted RR, unconditional on death:
 |
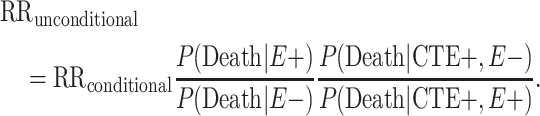The ratio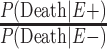 
is not currently known; thus, we assume various scenarios: that it is equal to 0.5, 1.0, and 1.5. The first scenario corresponds to the estimate of the overall mortality of professional players compared with that of the general US population (32). The last 2 scenarios were estimates of a Cox proportional hazards regression from our brain bank, which imply that the mortality risk of the high school group is unlike that of the general population. The quantity 
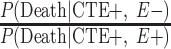is a hazard ratio also estimated from the brain bank, where we used the time from symptom onset (as a proxy for a positive neuropathological diagnosis of CTE) to death. Symptom onset was defined as the minimum of age at diagnosis of cognitive symptoms and age at diagnosis of behavioral symptoms. To account for the uncertainty in the hazard ratio, we bootstrapped the hazard ratio 50,000 times. The 50,000 conditional RRs were multiplied by the quantities 
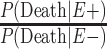and bootstrapped hazard ratios to ultimately produce a distribution of RRs unconditional on death.
RESULTS
The analysis sample from our brain bank included 290 participants who had played at least 1 year of high school, college, or professional American football, 235 of whom had CTE and 55 of whom did not (Table 1). After adjustment for age at death, highest level of football playing was associated with CTE status in a dose-response manner. Conditional on being deceased, men who had played college football had 1.82 (95% CI: 1.23, 2.68) times the risk of being diagnosed with CTE postmortem as high school players, whereas those who played professional football had 2.13 (95% CI: 1.44, 3.08) times the risk of being diagnosed with CTE postmortem, relative to high school players (Table 2).
Table 1.
Demographic Characteristics of Participants According to Highest Level of American Football Played Among Brain Donors From the VA-BU-CLF Brain Bank, 2008–2019
| Highest Level of Play | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| High School (n = 51) | College (n = 60) | Professional (n = 179) | |||||||||||||
| Demographic Characteristic | No. | % | Mean (SD) | Median (IQR a ) | Range | No. | % | Mean (SD) | Median (IQR) | Range | No. | % | Mean (SD) | Median (IQR) | Range |
| CTE status | |||||||||||||||
| CTE diagnosis | 22 | 9.4 | 47 | 20.0 | 166 | 70.6 | |||||||||
| No CTE diagnosis | 29 | 52.7 | 13 | 23.6 | 13 | 23.6 | |||||||||
| Age at death, years | 39 (16.2) | 36 (24–54) | 21–80 | 41 (13.4) | 42 (29–50) | 21–86 | 66 (15.2) | 70 (57–77) | 23–90 | ||||||
| Total duration of play, years | 7 (3.5) | 6 (4–10) | 1–16 | 12 (3.3) | 12 (9–14) | 4–17 | 17 (4.9) | 16 (14–20) | 5–33 | ||||||
Abbreviations: CTE, chronic traumatic encephalopathy, IQR, interquartile range; SD, standard deviation; VA-BU-CLF, Veterans Affairs–Boston University–Concussion Legacy Foundation.
a Quartile 1–quartile 3.
Table 2.
Relationship Between Highest Level of American Football Played and Diagnosis of CTE, Before and After Adjustment for Selection Bias, When CTE Was Conditioned on Death Among Brain Donors From the VA-BU-CLF Brain Bank, 2008–2019
|
Highest Level
of Play |
Adjusted for Age at Death a | Further Adjusted for Selection Bias b | ||||
|---|---|---|---|---|---|---|
| Mean RR | 95% CI | Median RR | Mean RR | 95% SI | Median RR | |
| High school | 1.00 | Referent | 1.00 | Referent | ||
| College | 1.82 | 1.23, 2.68 | 1.77 | 2.38 | 1.16, 5.94 | 2.00 |
| Professional | 2.13 | 1.44, 3.08 | 2.08 | 2.47 | 1.46, 4.79 | 2.25 |
Abbreviations: CI, confidence interval; CTE, chronic traumatic encephalopathy; RR, risk ratio; SI, simulation interval; VA-BU-CLF, Veterans Affairs–Boston University–Concussion Legacy Foundation.
a The RR estimate is the mean (and median) value of the bootstrapped distribution; the 95% CI was constructed from the 2.5th and 97.5th percentiles of the bootstrapped distribution.
b The RR estimate is the mean (and median) value of the sampling distribution; the 95% SI was constructed from the 2.5th and 97.5th percentiles of the sampling distribution.
In our primary target population—American men who died during study recruitment (2008–2019)—it was estimated that there were 433,041 men who played football at the high school level, 12,489 who played at the college level, and 1,551 who played at the professional level. We therefore estimated that high school, college, and professional football players in our target population developed CTE pathology with a cumulative incidence of at least 5.1, 376, and 10,703 CTE cases per 100,000 deaths, respectively (Table 3).
Table 3.
Estimated Minimum Cumulative Incidence of CTE in the Primary Target Populationa During Recruitment for the VA-BU-CLF Brain Bank Study, by Highest Level of Play, 2008–2019
|
Highest Level
of Play |
Estimated No. of Players Who Died | Minimum Cumulative Incidence Proportion |
|---|---|---|
| High school | 433,041 | 0.0000508 |
| College | 12,489 | 0.0037633 |
| Professional | 1,551 | 0.1070277 |
Abbreviations: CTE, chronic traumatic encephalopathy; VA-BU-CLF, Veterans Affairs–Boston University–Concussion Legacy Foundation.
a The primary target population was American men who died during study recruitment (2008–2019) and had played at least 1 year of high school, college, or professional football.
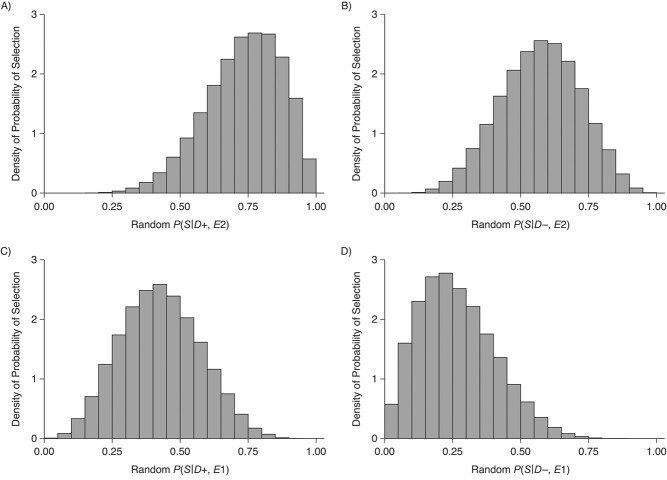
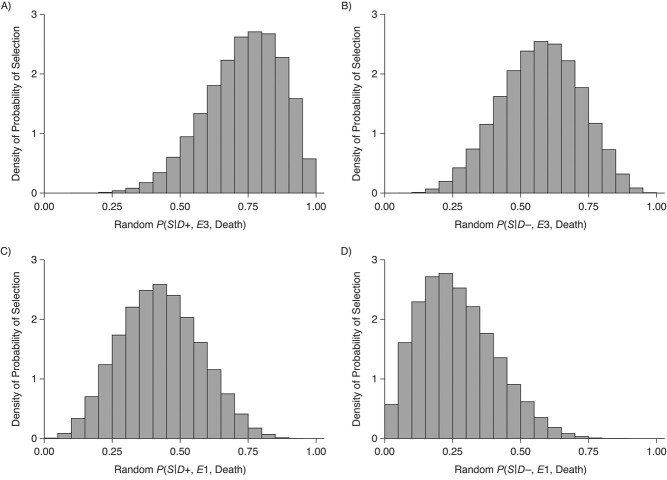
Furthermore, in order to adjust for selection bias in the analytical phase of this study, we estimated the bounds of the unconditional joint probabilities of the highest level of football playing and CTE status (Table 4) and conditional probabilities of selection (Table 5). The distributions of these conditional probabilities of selection are seen in Figures 1 and 2. Conditional on death, the sampling distribution of adjusted RRs for college players, relative to high school players, had a mean RR of 2.38 (95% SI: 1.16, 5.94), whereas the distribution of adjusted RRs for professional players, relative to high school players, had a mean RR of 2.47 (95% SI: 1.46, 4.79) (Table 2). Therefore, after adjustment for selection bias, the dose-response relationship between highest level of football playing and CTE was maintained. Additionally, the selection-adjusted estimates were larger in magnitude than the estimates not adjusted for selection, indicating that the conventional estimates were biased toward the null. Furthermore, the adjusted estimates had wider intervals to reflect the additional uncertainty of accounting for selection bias.
Table 4.
Estimated Bounds of Joint Probabilities of the Highest Level of American Football Played and CTE Status, Conditional on Death, VA-BU-CLF Brain Bank, 2008–2019
| Joint Probabilities a | Lower Bound | Upper Bound |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
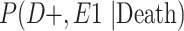
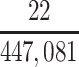
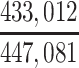
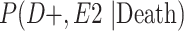
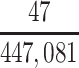
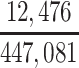
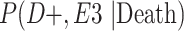
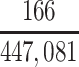
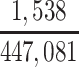
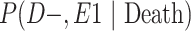
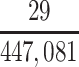
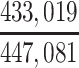
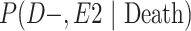
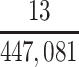
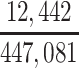
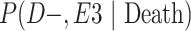
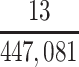
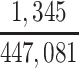
Abbreviations: CTE, chronic traumatic encephalopathy; VA-BU-CLF, Veterans Affairs–Boston University–Concussion Legacy Foundation.
a P(D+, E1|Death) denotes the joint probability of CTE diagnosis and having played high school football; P(D+, E2|Death) denotes the joint probability of CTE diagnosis and having played college football; and P(D+, E3|Death) denotes the joint probability of CTE diagnosis and having played professional football. P(D−, E1|Death) denotes the joint probability of no CTE diagnosis and having played high school football; P(D−, E2|Death) denotes the joint probability of no CTE diagnosis and having played college football; and P(D−, E3|Death) denotes the joint probability of no CTE diagnosis and having played professional football.
Table 5.
Estimated Bounds of the Probabilities of Selection Into the Study Among American Football Players, Conditional on CTE Status, Highest Level of Play, and Death, VA-BU-CLF Brain Bank, 2008–2019
| Conditional Probability of Selection a | Lower Bound | Upper Bound |
|---|---|---|
|
|
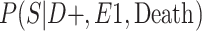
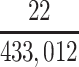
1 |
|
|
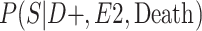
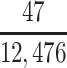
1 |
|
|
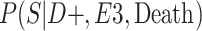
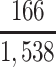
1 |
|
|
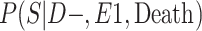
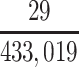
1 |
|
|
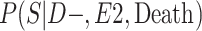
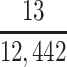
1 |
|
|
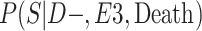
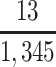
1 |
Abbreviations: CTE, chronic traumatic encephalopathy; VA-BU-CLF, Veterans Affairs–Boston University–Concussion Legacy Foundation.
a P(S|D+, E1, Death) denotes the probability of selection conditional on CTE diagnosis and having played high school football; P(S|D+, E2, Death) denotes the probability of selection conditional on CTE diagnosis and having played college football; and P(S|D+, E3, Death) denotes the probability of selection conditional on CTE diagnosis and having played professional football. P(S|D−, E1, Death) denotes the probability of selection conditional on no CTE diagnosis and having played high school football; P(S|D−, E2, Death) denotes the probability of selection conditional on no CTE diagnosis and having played college football; and P(S|D−, E3, Death) denotes the probability of selection conditional on no CTE diagnosis and having played professional football.
Figure 1.
Distributions of the probabilities of selection into the study, conditional on traumatic encephalopathy (CTE) status, exposure status (highest level of football playing), and death, for an analysis comparing collegiate American football players with high school football players, VA-BU-CLF Brain Bank, 2008–2019. A) P(S|D+, E2, Death) denotes the probability of selection conditional on CTE diagnosis and having played college football. B) P(S|D−, E2, Death) denotes the probability of selection conditional on no CTE diagnosis and having played college football. C) P(S|D+, E1, Death) denotes the probability of selection conditional on CTE diagnosis and having played high school football. D) P(S|D−, E1, Death) denotes the probability of selection conditional on no CTE diagnosis and having played high school football. VA-BU-CLF, Veterans Affairs–Boston University–Concussion Legacy Foundation.
Figure 2.
Distributions of the probabilities of selection into the study, conditional on chronic traumatic encephalopathy (CTE) status, exposure status (highest level of football playing), and death, for an analysis comparing professional American football players with high school football players, VA-BU-CLF Brain Bank, 2008–2019. A) P(S|D+, E3, Death) denotes the probability of selection conditional on CTE diagnosis and having played professional football. B) P(S|D−, E3, Death) denotes the probability of selection conditional on no CTE diagnosis and having played professional football. C) P(S|D+, E1, Death) denotes the probability of selection conditional on CTE diagnosis and having played high school football. D) P(S|D−, E1, Death) denotes the probability of selection conditional on no CTE diagnosis and having played high school football. VA-BU-CLF, Veterans Affairs–Boston University–Concussion Legacy Foundation.
However, if we remove the assumption that the outcome is conditioned on death and consider the quantity 
, then our RRs comparing college players with high school players become 1.49 (95% SI: 0.56, 3.93), 2.45 (95% SI: 1.11, 7.86), and 4.47 (95% SI: 1.67, 11.79), respectively (Table 6). Similarly, our RR estimates comparing professional players with high school players become 1.78 (95% SI: 0.84, 3.84), 3.57 (95% SI: 1.69, 7.68), and 5.35 (95% SI: 2.53, 11.51), respectively.
Table 6.
Relationship Between Highest Level of American Football Played and Diagnosis of CTE, After Adjustment for Selection Bias, When CTE Is Not Conditioned on Death Among Brain Donors From the VA-BU-CLF Brain Bank, 2008–2019
| Selection-Bias–Adjusted Estimate When CTE Is Not Conditioned on Death a | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Highest Level of Play | 0.50 b | 1.00 b | 1.50 b | ||||||
| Mean RR | 95% SI | Median RR | Mean RR | 95% SI | Median RR | Mean RR | 95% SI | Median RR | |
| High school | 1.00 | Referent | 1.00 | Referent | 1.00 | Referent | |||
| College | 1.49 | 0.56, 3.93 | 1.23 | 2.98 | 1.11, 7.86 | 2.45 | 4.47 | 1.67, 11.79 | 3.68 |
| Professional | 1.78 | 0.84, 3.84 | 1.59 | 3.57 | 1.69, 7.68 | 3.17 | 5.35 | 2.53, 11.51 | 4.76 |
Abbreviations: CTE, chronic traumatic encephalopathy; RR, risk ratio; SI, simulation interval; VA-BU-CLF, Veterans Affairs–Boston University–Concussion Legacy Foundation.
a The adjusted RR estimate is the mean (and median) of the sampling distribution; the 95% SI is constructed from the 2.5th and 97.5th percentiles of the sampling distribution.
b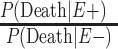 
.
Results of sensitivity analyses are shown in Tables 7 and 8. As expected, the sampling scheme that assumed no relationship between the probabilities of selection produced a relatively wide SI, attenuating significance for the association between college players and CTE, with high school players as the reference group. Lastly, we performed a final sensitivity analysis to relax the assumption that the upper bound of the conditional probabilities of selection was 1. Rather, we assumed that the conditional probabilities of selection were at most 90%. The direction and magnitude of the estimates were consistent between approaches (Tables 9 and 10).
Table 7.
Estimated Relationship Between Highest Level of American Football Played and Diagnosis of CTE, After Adjustment for Selection Bias, When CTE Is Conditioned on Death (Sensitivity Analyses) Among Brain Donors From the VA-BU-CLF Brain Bank, 2008–2019
| Highest Level of Play a | Selection-Bias–Adjusted Estimate b | ||
|---|---|---|---|
| Mean RR | 95% SI | Median RR | |
| Collegec | |||
| Upwards | 2.33 | 1.28, 5.17 | 2.01 |
| Downwards | 1.97 | 0.58, 4.87 | 1.72 |
| No relationship between probabilities | 2.11 | 0.58, 5.50 | 1.77 |
| Initially randomly selecting a probability | 2.25 | 0.84, 5.50 | 1.93 |
| Professionalc | |||
| Upwards | 2.43 | 1.51, 4.33 | 2.25 |
| Downwards | 2.20 | 0.99,4.21 | 2.05 |
| No relationship between probabilities | 2.24 | 1.05, 4.30 | 2.07 |
| Initially randomly selecting a probability | 2.38 | 1.26, 4.52 | 2.19 |
Abbreviations: CTE, chronic traumatic encephalopathy; RR, risk ratio; SI, simulation interval; VA-BU-CLF, Veterans Affairs–Boston University–Concussion Legacy Foundation.
a Sampling schemes were implemented as follows: 1) by first sampling the smallest conditional selection probability in the imposed inequality and iterating upwards; 2) by first sampling the largest conditional selection probability in the imposed inequality and iterating downwards; 3) by assuming no hierarchical relationship between the conditional selection probabilities and drawing each from the prespecified bounds, independently of all other probabilities; and 4) by first randomly selecting a conditional selection probability and then sampling according to its plausible bounds, and then sampling the remaining conditional selection probabilities in order to maintain the inequality.
b The adjusted RR estimate is the sample mean (and median) of the sampling distribution; the 95% SI was constructed from the 2.5th and 97.5th percentiles of the sampling distribution.
c Referent: high school (RR = 1).
Table 8.
Estimated Relationship Between Highest Level of American Football Played and Diagnosis of CTE, After Adjustment for Selection Bias, When CTE Is Not Conditioned on Death (Sensitivity Analyses) Among Brain Donors From the VA-BU-CLF Brain Bank, 2008–2019
| Selection-Bias–Adjusted Estimate When CTE Is Not Conditioned on Death a | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Highest Level of Play | 0.50 b | 1.00 b | 1.50 b | ||||||
| Mean RR | 95% SI | Median RR | Mean RR | 95% SI | Median RR | Mean RR | 95% SI | Median RR | |
| Collegec | |||||||||
| Upwards | 1.46 | 0.60, 3.55 | 1.23 | 2.92 | 1.20, 7.11 | 2.46 | 4.38 | 1.81, 10.66 | 3.69 |
| Downwards | 1.24 | 0.32, 3.38 | 1.03 | 2.48 | 0.63, 6.75 | 2.06 | 3.72 | 0.95, 10.13 | 3.09 |
| No relationship between probabilities | 1.33 | 0.32, 3.75 | 1.07 | 2.65 | 0.63, 7.51 | 2.13 | 3.98 | 0.95, 11.26 | 3.21 |
| Initially randomly selecting a probability | 1.41 | 0.44, 3.73 | 1.17 | 2.83 | 0.88, 7.46 | 2.34 | 4.24 | 1.32, 11.19 | 3.51 |
| Professionalc | |||||||||
| Upwards | 1.76 | 0.87, 3.55 | 1.58 | 3.51 | 1.74, 7.09 | 3.17 | 5.27 | 2.61, 10.64 | 4.75 |
| Downwards | 1.59 | 0.62, 3.43 | 1.42 | 3.17 | 1.25, 6.87 | 2.85 | 4.76 | 1.87, 10.30 | 4.27 |
| No relationship between probabilities | 1.62 | 0.64, 3.50 | 1.45 | 3.23 | 1.29, 7.00 | 2.89 | 4.85 | 1.93, 10.50 | 4.34 |
| Initially randomly selecting a probability | 1.72 | 0.75, 3.66 | 1.54 | 3.44 | 1.51, 7.32 | 3.07 | 5.15 | 2.26, 10.98 | 4.61 |
Abbreviations: CTE, chronic traumatic encephalopathy; RR, risk ratio; SI, simulation interval; VA-BU-CLF, Veterans Affairs–Boston University–Concussion Legacy Foundation.
a The adjusted RR estimate is the mean (and median) of the sampling distribution; the 95% SI was constructed from the 2.5th and 97.5th percentiles of the sampling distribution.
b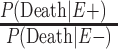 
.
c Referent: high school (RR = 1).
Table 9.
Estimated Relationship Between Highest Level of American Football Played and Diagnosis of CTE, After Adjustment for Selection Bias, Assuming That Conditional Probabilities of Selection Are at Most 90%, When CTE Is Conditioned on Death (Sensitivity Analyses) Among Brain Donors From the VA-BU-CLF Brain Bank, 2008–2019
| Highest Level of Play and Sampling Scheme a | Selection-Bias–Adjusted Estimate b | ||
|---|---|---|---|
| Mean RR | 95% SI | Median RR | |
| Collegec | |||
| Primary analysis | 2.39 | 1.17, 5.94 | 2.00 |
| Upwards | 2.32 | 1.29, 5.13 | 2.01 |
| Downwards | 1.98 | 0.59, 4.87 | 1.72 |
| No relationship between probabilities | 2.11 | 0.59, 5.45 | 1.77 |
| Initially randomly selecting a probability | 2.25 | 0.85, 5.50 | 1.93 |
| Professionalc | |||
| Primary analysis | 2.47 | 1.46, 4.77 | 2.25 |
| Upwards | 2.43 | 1.51, 4.31 | 2.25 |
| Downwards | 2.20 | 1.00, 4.21 | 2.05 |
| No relationship between probabilities | 2.24 | 1.06, 4.28 | 2.07 |
| Initially randomly selecting a probability | 2.38 | 1.27, 4.52 | 2.20 |
Abbreviations: CTE, chronic traumatic encephalopathy; RR, risk ratio; SI, simulation interval; VA-BU-CLF, Veterans Affairs–Boston University–Concussion Legacy Foundation.
a Sampling schemes were implemented as follows: 1) by first sampling the smallest conditional selection probability in the imposed inequality and iterating upwards; 2) by first sampling the largest conditional selection probability in the imposed inequality and iterating downwards; 3) by assuming no hierarchical relationship between the conditional selection probabilities and drawing each from the prespecified bounds, independently of all other probabilities; and 4) by first randomly selecting a conditional selection probability and then sampling according to its plausible bounds, and then sampling the remaining conditional selection probabilities in order to maintain the inequality.
b The adjusted RR estimate is the sample mean (and median) of the sampling distribution; the 95% SI was constructed from the 2.5th and 97.5th percentiles of the sampling distribution.
c Referent: high school (RR = 1).
Table 10.
Estimated Relationship Between Highest Level of American Football Played and Diagnosis of CTE, After Adjustment for Selection Bias, Assuming That Conditional Probabilities of Selection Are at Most 90%, When CTE Is Not Conditioned on Death (Sensitivity Analyses) Among Brain Donors From the VA-BU-CLF Brain Bank, 2008–2019
| Selection-Bias–Adjusted Estimate When CTE Is Not Conditioned on Death a | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Highest Level of Play and Sampling Scheme | 0.50 b | 1.00 b | 1.50 b | ||||||
| Mean RR | 95% SI | Median RR | Mean RR | 95% SI | Median RR | Mean RR | 95% SI | Median RR | |
| Collegec | |||||||||
| Primary analysis | 1.49 | 0.56, 3.93 | 1.23 | 2.99 | 1.12, 7.87 | 2.46 | 4.48 | 1.68, 11.80 | 3.70 |
| Upwards | 1.46 | 0.60, 3.54 | 1.23 | 2.92 | 1.21, 7.08 | 2.46 | 4.37 | 1.81, 10.62 | 3.70 |
| Downwards | 1.24 | 0.32, 3.38 | 1.03 | 2.48 | 0.64, 6.75 | 2.06 | 3.72 | 0.95, 10.13 | 3.10 |
| No relationship between probabilities | 1.32 | 0.32, 3.71 | 1.07 | 2.65 | 0.64, 7.42 | 2.14 | 3.97 | 0.95, 11.13 | 3.21 |
| Initially randomly selecting a probability | 1.41 | 0.44, 3.73 | 1.17 | 2.83 | 0.89, 7.46 | 2.35 | 4.24 | 1.33, 11.18 | 3.52 |
| Professionalc | |||||||||
| Primary analysis | 1.79 | 0.85, 3.88 | 1.59 | 3.57 | 1.69, 7.75 | 3.18 | 5.36 | 2.54, 11.63 | 4.77 |
| Upwards | 1.75 | 0.87, 3.53 | 1.59 | 3.51 | 1.74, 7.06 | 3.17 | 5.26 | 2.61, 10.59 | 4.76 |
| Downwards | 1.59 | 0.63, 3.44 | 1.43 | 3.18 | 1.25, 6.88 | 2.85 | 4.76 | 1.88, 10.31 | 4.28 |
| No relationship between probabilities | 1.61 | 0.64, 3.48 | 1.45 | 3.23 | 1.29, 6.97 | 2.89 | 4.84 | 1.93, 10.45 | 4.34 |
| Initially randomly selecting a probability | 1.72 | 0.75, 3.66 | 1.54 | 3.44 | 1.51, 7.31 | 3.08 | 5.16 | 2.26, 10.97 | 4.62 |
Abbreviations: CTE, chronic traumatic encephalopathy; RR, risk ratio; SI, simulation interval; VA-BU-CLF, Veterans Affairs–Boston University–Concussion Legacy Foundation.
a The adjusted RR estimate is the mean (and median) of the sampling distribution; the 95% SI was constructed from the 2.5th and 97.5th percentiles of the sampling distribution.
b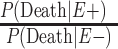 
.
c Referent: high school (RR = 1).
DISCUSSION
Selection bias is a methodological barrier common to all studies that require brain donation. While many methods have been developed to assess the impact of this issue and mitigate it in the analytical phase of the study, many are implemented with some degree of uncertainty (12, 15). In our study, although additional uncertainty was introduced in our estimates of conditional probabilities of selection, our results nonetheless confirmed an association between exposure to football playing and CTE status.
Using our convenience sample of deceased former American football players, the hypothesized dose-response relationship between highest level of football playing and CTE remained significant after adjustment for selection bias. More specifically, we estimated that conditional on CTE being diagnosed postmortem, college players have 2.38 times the risk of CTE as high school players (95% SI: 1.16, 5.94) and professional players have 2.47 times the risk (95% SI: 1.46, 4.79). Moreover, we estimated that high school, college, and professional football players in our target population developed CTE with a cumulative incidence of at least 5.1, 376, and 10,703 CTE cases per 100,000 deaths, respectively.
The estimation of the number of professional players in the primary target population rested on the assumption that professional players have the same all-cause mortality rates as the general population, which may not be the case. In fact, professional athletes tend to have a lower all-cause mortality rate than the rest of the nonathlete population (33, 34). This assumption yields a conservative approach in estimating the cumulative incidence of CTE, since using larger mortality rates will estimate more former players in our target population, which will consequently decrease the minimum cumulative incidence. Additionally, our estimates of the number of college players in the target population relied on data from the NCAA, which does not capture other, non-NCAA college participation. Our estimations also did not take into account the common practice of “redshirting,” leading some college football players to take 5 years to graduate. Lastly, our assumption about uniform dropout rates for high school and college players, albeit noninformative, might not have been accurate.
The main limitation of these results in the primary target population is that they are not generalizable to the living population of American football players, who could be intervened upon. Such restrictions in inference are a result of the caveat that currently CTE can only be diagnosed postmortem and that criteria for diagnosing CTE during life are still under development (10). Although criteria for diagnosing CTE in life have been iteratively proposed and improved upon, assessment of their validity is currently under way (35, 36). To remove the assumption that CTE is conditioned on death, we were limited by the value of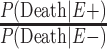 
, which is unknown. The existing studies compared the former only with the general population, and they found that former NFL players have lower overall mortality risk, often attributed to routine physical activity and the healthy worker effect (32–34, 37). To our knowledge, no studies to date have compared the mortality risks of former professional or collegiate players with those of people who played up to the high school level. Athletes are typically perceived as a healthy cohort, with evidence supporting the view that fitness and better access to health care provide protection against the known health risks of obesity and related comorbid conditions, which would result in former high school players also having a lower overall mortality risk than the general population (29, 30). We chose to analyze 3 plausible scenarios for the mortality risk to emphasize the uncertainty of these estimates, as well as to highlight the need for future research in this area.
Our study was also limited in that highest level of American football playing served as a proxy measure for RHI. However, we were unable to consider other measures of exposure, such as frequency of RHI, or even duration of play as Mez et al. did (9), because the methods employed rely on having information on the exposure for the target population. Implementing these analyses would require information on the exposure distribution of the target population, which is not readily available for measures of exposure other than highest level of play.
In their 2020 study, Mez et al. concluded that under their proposed selection conditions, the magnitude of the relationship between duration of football playing and CTE diagnosis remained consistent (9). Here, we presented findings showing that the association was biased toward the null. This discrepancy can be attributed to the differences in the conditional probabilities of selection, as our proposed ranges were wider than those of Mez et al. and based on population-level data. Here, the driving factor for biasing the RR toward the null was that the conditional selection probability for high school players without a CTE diagnosis was much smaller than that proposed by Mez et al. This work was also able to provide an estimate of the minimum cumulative incidence, whereas the prior work was not able to because there were no population-level data available. To our knowledge, no estimates of the minimum cumulative incidence of CTE were available for high school and college football players before this study.
Results from this study provide an increased understanding of the mechanism of selection into brain banks focused on RHI and CTE. Namely, after adjustment for selection bias, our measures of association increased, suggesting that the selection bias was in fact biasing the measures of association toward the null. More specifically, we argue that the factor driving the inflation of the RR after selection bias adjustment was the non-CTE brain donors who played only high school football, as evidenced by the relatively small conditional probabilities (Figures 1 and 2). Thus, we conclude that players at the lowest level of play were disproportionally not selected into our study. These players are also less likely to develop CTE, and hence are less likely to donate their brains, meaning that they need to be up-weighted in adjusted analyses. This is important, and additional efforts to recruit high school football players for CTE studies should be instituted in the future. Furthermore, our analysis, which considers CTE not conditioned on death, provides further impetus for the need to investigate health risks in high school football players.
In conclusion, we have shown that after adjustment for brain bank selection, there is evidence of a dose-response relationship between level of American football playing and risk of CTE. That relationship is also strong in most scenarios when we consider CTE incidence without conditioning on death.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Biostatistics, School of Public Health, Boston University, Boston, Massachusetts, United States (Jessica LeClair, Yorghos Tripodis); Department of Epidemiology, School of Public Health, Boston University, Boston, Massachusetts, United States (Jennifer Weuve, Matthew P. Fox); Department of Global Health, School of Public Health, Boston University, Boston, Massachusetts, United States (Matthew P. Fox); Boston University Alzheimer’s Disease Research Center, Boston, Massachusetts, United States (Jesse Mez, Michael L. Alosco, Chris Nowinski, Ann McKee, Yorghos Tripodis); Boston University CTE Center, Boston, Massachusetts, United States (Jesse Mez, Michael L. Alosco, Chris Nowinski, Ann McKee, Yorghos Tripodis); Department of Neurology, School of Medicine, Boston University, Boston, Massachusetts, United States (Jesse Mez, Michael L. Alosco, Ann McKee); Concussion Legacy Foundation, Boston, Massachusetts, United States (Chris Nowinski, Ann McKee); VA Boston Healthcare System, Boston, Massachusetts, United States (Ann McKee); Department of Veterans Affairs Medical Center, Bedford, Massachusetts, United States (Ann McKee); and Department of Pathology and Laboratory Medicine, School of Medicine, Boston University, Boston, Massachusetts, United States (Ann McKee).
This work was supported by the National Institute of General Medical Sciences (Interdisciplinary Training Grant for Biostatisticians T32 GM74905); the National Institute on Aging (grants AG057902, AG06234, RF1AG054156, and P30AG13846 and supplemental grants 0572063345, R01AG057902, R01AG061028, K23AG046377, R01AG1649, R21HD089088, and F32NS096803); the National Institute of Neurological Disorders and Stroke (grants U54NS115266, U01NS086659, U01NS093334, K23NS102399, R01NS078337, and R56NS078337); the National Institute on Aging/Boston University Alzheimer’s Disease Research Center (grant P30AG13846 and supplemental grant 0572063345-5); the US Department of Veterans Affairs (grants I01 CX001135, CSP 501, and B6796-C); the US Department of Defense (grants W81XWH-13-2-0095, W81XWH-13-2-0064, W81XWH1810580, and PRARP-13267017); the Nick and Lynn Buoniconti CTE Research Fund; and the Boston University Clinical and Translational Science Institute (grant 1UL1TR001430).
The data that support the findings of this study are available upon request from the corresponding author. Some data are not publicly available because they contain information that could compromise the privacy of research participants.
The views, opinions, and/or findings contained in this article are those of the authors and should not be construed as an official US Department of Veterans Affairs or Department of Defense position, policy, or decision, unless so designated by other official documentation. The funders did not play any role in the design and conduct of the study; the collection, management, analysis, and interpretation of the data; the preparation, review, or approval of the manuscript; or the decision to submit the manuscript for publication.
Conflict of interest: none declared.
REFERENCES
- 1. Omalu BI, DeKosky ST, Minster RL, et al. Chronic traumatic encephalopathy in a National Football League player. Neurosurgery. 2005;57(1):128–134. [DOI] [PubMed] [Google Scholar]
- 2. McKee AC, Stein TD, Nowinski CJ, et al. The spectrum of disease in chronic traumatic encephalopathy. Brain. 2013;136(1):43–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Bieniek KF, Ross OA, Cormier KA, et al. Chronic traumatic encephalopathy pathology in a neurodegenerative disorders brain bank. Acta Neuropathol. 2015;130(6):877–889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Mez J, Daneshvar DH, Kiernan PT, et al. Clinicopathological evaluation of chronic traumatic encephalopathy in players of American football. JAMA. 2017;318(4):360–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. McKee AC, Cantu RC, Nowinski CJ, et al. Chronic traumatic encephalopathy in athletes: progressive tauopathy after repetitive head injury. J Neuropathol Exp Neurol. 2009;68(7):709–735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Ling H, Morris HR, Neal JW, et al. Mixed pathologies including chronic traumatic encephalopathy account for dementia in retired association football (soccer) players. Acta Neuropathol. 2017;133(3):337–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Asken BM, Sullan MJ, DeKosky ST, et al. Research gaps and controversies in chronic traumatic encephalopathy: a review. JAMA Neurol. 2017;74(10):1255–1262. [DOI] [PubMed] [Google Scholar]
- 8. Finkel AM, Bieniek KF. A quantitative risk assessment for chronic traumatic encephalopathy (CTE) in football: how public health science evaluates evidence. Hum Ecol Risk Assess. 2018;25(3):564–589. [Google Scholar]
- 9. Mez J, Daneshvar DH, Abdolmohammadi B, et al. Duration of American football play and chronic traumatic encephalopathy. Ann Neurol. 2020;87(1):116–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. McKee AC, Cairns NJ, Dickson DW, et al. The first NINDS/NIBIB consensus meeting to define neuropathological criteria for the diagnosis of chronic traumatic encephalopathy. Acta Neuropathol. 2016;131(1):75–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Mez J, Solomon TM, Daneshvar DH, et al. Assessing clinicopathological correlation in chronic traumatic encephalopathy: rationale and methods for the UNITE Study. Alzheimers Res Ther. 2015;7(1):62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Haneuse S, Schildcrout J, Crane P, et al. Adjustment for selection bias in observational studies with application to the analysis of autopsy data. Neuroepidemiology. 2009;32(3):229–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Schwab N, Hazrati LN. Assessing the limitations and biases in the current understanding of chronic traumatic encephalopathy. J Alzheimers Dis. 2018;64(4):1067–1076. [DOI] [PubMed] [Google Scholar]
- 14. Zuckerman SL, Brett BL, Jeckell A, et al. Chronic traumatic encephalopathy and neurodegeneration in contact sports and American football. J Alzheimers Dis. 2018;66(1):37–55. [DOI] [PubMed] [Google Scholar]
- 15. Lash T, Fox M, Fink A. Applying Quantitative Bias Analysis to Epidemiologic Data. New York, NY: Springer Publishing Company; 2009. [Google Scholar]
- 16. Binney ZO, Bachynski KE. Estimating the prevalence at death of CTE neuropathology among professional football players. Neurology. 2019;92(1):43–45. [DOI] [PubMed] [Google Scholar]
- 17. Tharmaratnam T, Iskandar MA, Tabobondung TC, et al. Chronic traumatic encephalopathy in professional American football players: where are we now? Front Neurol. 2018;9:445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Alosco ML, Stein TD, Tripodis Y, et al. Association of white matter rarefaction, arteriolosclerosis, and tau with dementia in chronic traumatic encephalopathy. JAMA Neurol. 2019;76(11):1298–1308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Alosco ML, Cherry JD, Huber BR, et al. Characterizing tau deposition in chronic traumatic encephalopathy (CTE): utility of the McKee CTE staging scheme. Acta Neuropathol. 2020;140(4):495–512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Vonsattel JP, Aizawa H, Ge P, et al. An improved approach to prepare human brains for research. J Neuropathol Exp Neurol. 1995;54(1):42–56. [DOI] [PubMed] [Google Scholar]
- 21. Vonsattel JPG, Vonsattel JPG, del Amaya MP, et al. Twenty-first century brain banking. Processing brains for research: the Columbia University methods. Acta Neuropathol. 2008;115(5):509–532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. National Federation of State High School Associations . High School Participation Survey Archive. High School Athletics Participation History (1969–2008). https://www.nfhs.org/sports-resource-content/high-school-participation-survey-archive/. Reviewed August 28, 2019. Accessed July 18, 2018.
- 23. National Federation of State High School Associations . High School Participation Survey Archive. 2009–10 High School Athletics Participation Survey. https://www.nfhs.org/sports-resource-content/high-school-participation-survey-archive/. Reviewed August 28, 2019. Accessed July 18, 2018.
- 24. National Federation of State High School Associations . High School Participation Survey Archive. 2010–11 High School Athletics Participation Survey. https://www.nfhs.org/sports-resource-content/high-school-participation-survey-archive/. Reviewed August 28, 2019. Accessed July 18, 2018.
- 25. National Federation of State High School Associations . High School Participation Survey Archive. 2011–12 High School Athletics Participation Survey. https://www.nfhs.org/sports-resource-content/high-school-participation-survey-archive/. Reviewed August 28, 2019. Accessed July 18, 2018.
- 26. National Federation of State High School Associations . High School Participation Survey Archive. 2012–13 High School Athletics Participation Survey. https://www.nfhs.org/sports-resource-content/high-school-participation-survey-archive/. Reviewed August 28, 2019. Accessed July 18, 2018.
- 27. National Federation of State High School Associations . High School Participation Survey Archive. 2013–14 High School Athletics Participation Survey. https://www.nfhs.org/sports-resource-content/high-school-participation-survey-archive/. Reviewed August 28, 2019. Accessed July 18, 2018.
- 28. National Federation of State High School Associations . High School Participation Survey Archive. 2014–15 High School Athletics Participation Survey. https://www.nfhs.org/sports-resource-content/high-school-participation-survey-archive/. Reviewed August 28, 2019. Accessed July 18, 2018.
- 29. National Federation of State High School Associations . High School Participation Survey Archive. 2015–16 High School Athletics Participation Survey. https://www.nfhs.org/sports-resource-content/high-school-participation-survey-archive/. Reviewed August 28, 2019. Accessed July 18, 2018.
- 30. National Collegiate Athletic Association . NCAA Sports Sponsorship and Participation Rates Database. Indianapolis, IN: National Collegiate Athletic Association; 2019. http://www.ncaa.org/about/resources/research/ncaa-sports-sponsorship-and-participation-rates-database. Accessed July 18, 2018. [Google Scholar]
- 31. National Center for Health Statistics . Life tables. https://www.cdc.gov/nchs/products/life_tables.htm. Reviewed April 25, 2022. Accessed June 5, 2018.
- 32. Lehman EJ, Hein Misty J, Baron SL, et al. Neurodegenerative causes of death among retired National Football League players. Neurology. 2012;79(19):1970–1974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Teramoto M, Bungum TJ. Mortality and longevity of elite athletes. J Sci Med Sport. 2009;13(4):410–416. [DOI] [PubMed] [Google Scholar]
- 34. Owora AH, Kmush BL, Walia B, et al. A systematic review of etiological risk factors associated with early mortality among National Football League players. Orthop J Sports Med. 2018;6(12):2325967118813312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Katz DI, Bernick C, Dodick DW, et al. National Institute of Neurological Disorders and Stroke consensus diagnostic criteria for traumatic encephalopathy syndrome. Neurology. 2021;96(18):848–863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Montenigro PH, Baugh CM, Daneshvar DH, et al. Clinical subtypes of chronic traumatic encephalopathy: literature review and proposed research diagnostic criteria for traumatic encephalopathy syndrome. Alzheimers Res Ther. 2014;6(5):68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Nguyen VT, Zafonte RD, Chen JT, et al. Mortality among professional American-style football players and professional American baseball players. JAMA Netw Open. 2019;2(5):e194223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Lee CD, Blair SN, Jackson AS. Cardiorespiratory fitness, body composition, and all-cause and cardiovascular disease mortality in men. Am J Clin Nutr. 1999;69(3):373–380. [DOI] [PubMed] [Google Scholar]
- 39. McHugh C, Hind K, Davey D, et al. Cardiovascular health of retired field-based athletes: a systematic review and meta-analysis. Orthop J Sports Med. 2019;7(8):2325967119862750. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.