An emergent temporal basis set robustly supports cerebellar time-series learning

Abstract

The cerebellum is considered a “learning machine” essential for time interval estimation underlying motor coordination and other behaviors. Theoretical work has proposed that the cerebellum’s input recipient structure, the granule cell layer (GCL), performs pattern separation of inputs that facilitates learning in Purkinje cells (P-cells). However, the relationship between input reformatting and learning has remained debated, with roles emphasized for pattern separation features from sparsification to decorrelation. We took a novel approach by training a minimalist model of the cerebellar cortex to learn complex time-series data from time-varying inputs, typical during movements. The model robustly produced temporal basis sets from these inputs, and the resultant GCL output supported better learning of temporally complex target functions than mossy fibers alone. Learning was optimized at intermediate threshold levels, supporting relatively dense granule cell activity, yet the key statistical features in GCL population activity that drove learning differed from those seen previously for classification tasks. These findings advance testable hypotheses for mechanisms of temporal basis set formation and predict that moderately dense population activity optimizes learning.

NEW & NOTEWORTHY During movement, mossy fiber inputs to the cerebellum relay time-varying information with strong intrinsic relationships to ongoing movement. Are such mossy fibers signals sufficient to support Purkinje signals and learning? In a model, we show how the GCL greatly improves Purkinje learning of complex, temporally dynamic signals relative to mossy fibers alone. Learning-optimized GCL population activity was moderately dense, which retained intrinsic input variance while also performing pattern separation.

INTRODUCTION

The cerebellum refines movement and maintains calibrated sensorimotor transformations by learning to predict outcomes of behaviors through error-based feedback (1–5). A major site of cerebellar learning is in the cerebellar cortex, where Purkinje cells (P-cells) receive sensorimotor information from parallel fibers (6) whose synaptic strengths are modified by the conjunction of presynaptic (parallel fiber) activity and climbing fiber inputs to P-cells thought to convey instructive feedback (7–10). P-cell activity is characterized by rich temporal dynamics during movements, representing putative computations of internal models of the body and the physics of the environment (11, 12). Parallel fibers are the axons of cerebellar granule cells (GCs), a huge neuronal population (comprising roughly half of the neurons in the entire brain; 13), which are the major recipient of extrinsic inputs to the cerebellum. Thus, understanding the output of the GCL is key in determining the encoding capacity and information load of incoming activity projected to the cerebellum. Inputs to GCs arise from mossy fibers (MFs), which convey sensorimotor information for P-cell computations (14–16). There are massively more GCs than MFs and each GC typically receives input from just four MFs (17), such that the information carried by each MF is spread among many GCs, but each GC samples from only a tiny fraction of total MFs (18, 19).

The GCL has been the focus of theoretical work spanning decades, which has explored the computational advantages of the unique feedforward architecture of the structure. Notably, early studies of the cerebellar circuit by Marr (20) and Albus (21) proposed that a key component of the cerebellar algorithm is the sparse representation of MF inputs by GCs. In this view, the cerebellum often must discriminate between overlapping, highly correlated patterns of MF activity with only subtle differences distinguishing them (22). Sparse recoding of MF activity in a much larger population of GCs (“expansion recoding”) increases the dimensionality of population representation and transforms correlated MF activity into independent activity patterns among a subset of GCs (23–25). These decorrelated activity patterns are easier to distinguish by learning algorithms operating in P-cells, leading to better associative learning and credit assignment (23, 26, 27).

The machine learning perspective of the Marr-Albus theory tends to assume that the cerebellum is presented with a series of static input patterns that must be distinguished and categorized. However, during movements, neuronal population dynamics are rarely, if ever, static. Mauk and Buonomano (3) revisited cerebellar expansion recoding in the context of temporal encoding, a necessary computation for the cerebellar-dependent task of delay eyelid conditioning. They proposed that a static activity pattern in MFs could be recoded in the GC layer as a temporally evolving set of distinct activity patterns, termed a temporal basis set (26, 28–31). P-cells could learn to recognize the GC activity pattern present at the correct delay and initiate an eyeblink to avert the “error” signal representing the air puff to the eye. This transformative theory has given rise to an emerging literature exploring mechanisms of basis set formation. A variety of mechanisms have been proposed for how such time-varying population activity might emerge, including local inhibition, short-term synaptic plasticity, diverse unipolar brush cell properties, and varying GC excitability (32–40, 42–49).

Despite these promising avenues, the problem of learning more complex movements presents a distinct set of questions about how the cerebellum processes and uses time-variant inputs to learn complex P-cell signals, a type of time series. Therefore, to test how expansion recoding of time-varying input contributes to learning, we used a simple model of the GCL and a time-series prediction task to explore the effect of putative GCL-filtering mechanisms on expansion recoding and learning. Similar to previous models, this simplified model made GC activity sparser relative to MF inputs (20, 21) and increased the dimensionality of the input activity (25) while preserving information (50). The model greatly enhanced learning accuracy and speed by P-cells on a difficult time-series prediction task when compared with MF inputs alone. Together, these results suggest that the cerebellar GCL provides a rich basis for learning in downstream Purkinje cells, providing a mixture of lossless representation (50) and enhanced spatiotemporal representation (25) that are selected for by associative learning to support the learning of diverse outputs that support adaptive outputs in a variety of tasks (51, 52).

METHODS

Model Construction

The model presented here incorporated only the dominant features of the granule cell layer (GCL) circuit anatomical organization and physiology. The features chosen for the model were the sparse sampling of inputs (GCs have just 4 synaptic input branches in their segregated dendrite complexes on average), which was reflected in the connectivity matrix between the input pool and the GCs, where each GC received four inputs with weights of 1/4th (i.e., 1 divided by the number of inputs; 1/M) of the original input strength, summing to a total weight of 1 across all inputs. The other features were thresholding, representing inhibition from local inhibitory Golgi neurons and intrinsic excitability of the GCs. The degree of inhibition and intrinsic excitability (threshold) was a free parameter of the model, and the dynamics were normalized to the z-score of the summated inputs. This feature reflects the monitoring of inputs by Golgi cells while maintaining simplicity in their mean output to GCs. Although this model simplifies many aspects of previous models of the GCL, it recreated many of the important features of those models, suggesting that the sparse sampling and firing are the main components dictating GCL functionality.

The model, in total, uses the following formulas to determine GC output:

$$G{C}_i(t)={\left[\right(\hspace{0.17em}{\displaystyle \sum }_{k_1}^{k_M}\frac{M{F}_k(t)}{M}\hspace{0.17em})-\hspace{0.17em}\theta \hspace{0.17em}]}_{+}$$ (1)

where k is a random selection of M MFs from the MF population. The inputs are summed and divided by the total number of MF inputs to the GC, M, so that their total weight is equal to 1. Unless noted as a variable, we used M = 4, reflecting the mean connectivity between MFs and GCs, and the optimal ratio for expansion recoding (25), and the point of best input variance retention (Fig. 5). This function is then linearly rectified, i.e., ${[x]}_{+}=x$ if x > 0 and 0 otherwise so that there are no negative rates present in the GC activity. The θ function, which determines the threshold, estimating the effects of intrinsic excitability and feedforward inhibition, was formulated as:

$$\theta \hspace{0.17em}=\hspace{0.17em}\overline{MF}\hspace{0.17em}+\hspace{0.17em}(z\hspace{0.17em}*\hspace{0.17em}\sigma (MF))\hspace{0.17em}$$ (2)

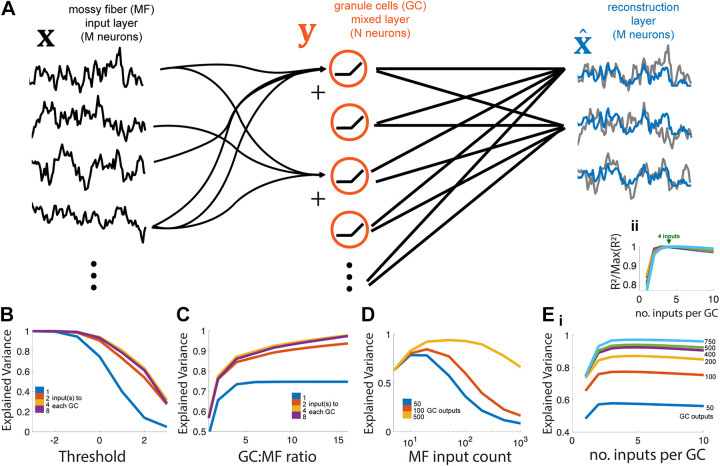
Figure 5.

Recovering inputs with an optimal linear readout. A: network model schematic. Granule cell (GC, red, center) layer thresholds the sum of (4 here) randomly chosen mossy fiber (MF, black, left) inputs, which are then fed into a reconstruction layer which uses the optimal weighting from all N GCs to approximate each of the M inputs (compare blue readouts to gray inputs). B: increasing the threshold of the GC layer (N = 500 outputs) decreases the explained variance (i.e., variance retained) of the best reconstruction layer (M = 50), but the effect is reduced with an intermediate number of MF inputs per GC. C: variance retained increases with the ratio of GCs per MF but gains from increasing the number of inputs to each GC are limited (max at 4 inputs). Here, there are M = 50 MF inputs at the threshold = 0. D: for a fixed number of GC outputs N, there is an optimal number of MF inputs (M) for which the variance retained of the reconstruction layer is maximized. Ei: for a fixed number of GC outputs N and MF inputs M = 50, there is an optimal number of inputs per G (around 4) for maximizing variance retained. ii: same as i, but with each value normalized to its maximum to show maximized values at inputs = 4. MF, mossy fiber.

Here, z sets the number of standard deviations from the MF mean. z is the only free parameter, which determines the minimum value below which granule cell activity is suppressed. Therefore, we report z as the “threshold.” Note that the summated MF inputs are divided by the number of inputs per GC (M) in Eq. 1 such that their received activity relative to θ is proportional to the input size, M. As the input to GCs is Gaussian in our model, the summed activity integrated by the GCs is Gaussian as well. For that reason, we found it convenient to define the GC thresholding term in terms of a z-score. Thus, a GC with a threshold of “zero” has its threshold set at the mean value of its MF inputs; such a GC would be silent 50% of the time on average because the Gaussian presynaptic input would be below the mean value half the time. This makes it possible to discuss functionally similar thresholds across varying network architectures (e.g., a GC with a threshold of zero would discard half of its input on average regardless of whether it received 2 or 8 MF inputs).

OU Input Construction

To provide a range of inputs with physiological-like temporal properties that could be parameterized, we used a class of randomly generated signals called Ornstein-Uhlenbeck processes (OU), defined by the following formula:

$$OU(t)=(\hspace{0.17em}OU(t-\Delta t)\hspace{0.17em}*\hspace{0.17em}{e}^{\left(-\frac{\Delta t}{\tau }\right)})\hspace{0.17em}+\hspace{0.17em}(\sigma \hspace{0.17em}*\hspace{0.17em}\sqrt{1\hspace{0.17em}-\hspace{0.17em}{e}^{-2*\frac{\Delta t}{\tau }}\hspace{0.17em}}*\hspace{0.17em}R)\hspace{0.17em}$$ (3)

Here, t is the time point being calculated, Δt is the time interval (the time base is in ms and Δt is 1 ms). σ is the predetermined standard deviation of the signal, and R is a vector of normally distributed random numbers. This process balances a decay term, the exponential with e raised to −Δt/$\tau$, and an additive term which introduces random fluctuations. Without the additive term, this function decays to zero as time progresses. For all simulations, unless noted otherwise, τ was 100 ms. This resulted in a mean autocorrelation τ of 502 ± 52 ms, which was intermediate between pontine neurons and reach-related electromyograms autocorrelation τ of 351 ± 120 ms and 567 ± 151 ms, used below as model inputs, respectively. After the complete function has been calculated, the desired mean is added to the time series to set the mean to a predetermined value.

The vector R can also be drawn from a matrix of correlated numbers, as was the case in Fig. 7 and Supplemental Fig. S3, B and C. These numbers were produced with the MATLAB functions randn() for normal random numbers, and mvnrnd() for matrices with a predetermined covariance matrix supplied to the function. The covariance matrix used for these experiments was always a 1-diagonal with a constant, predetermined, covariance value on the off-diagonal coordinates.

Figure 7.

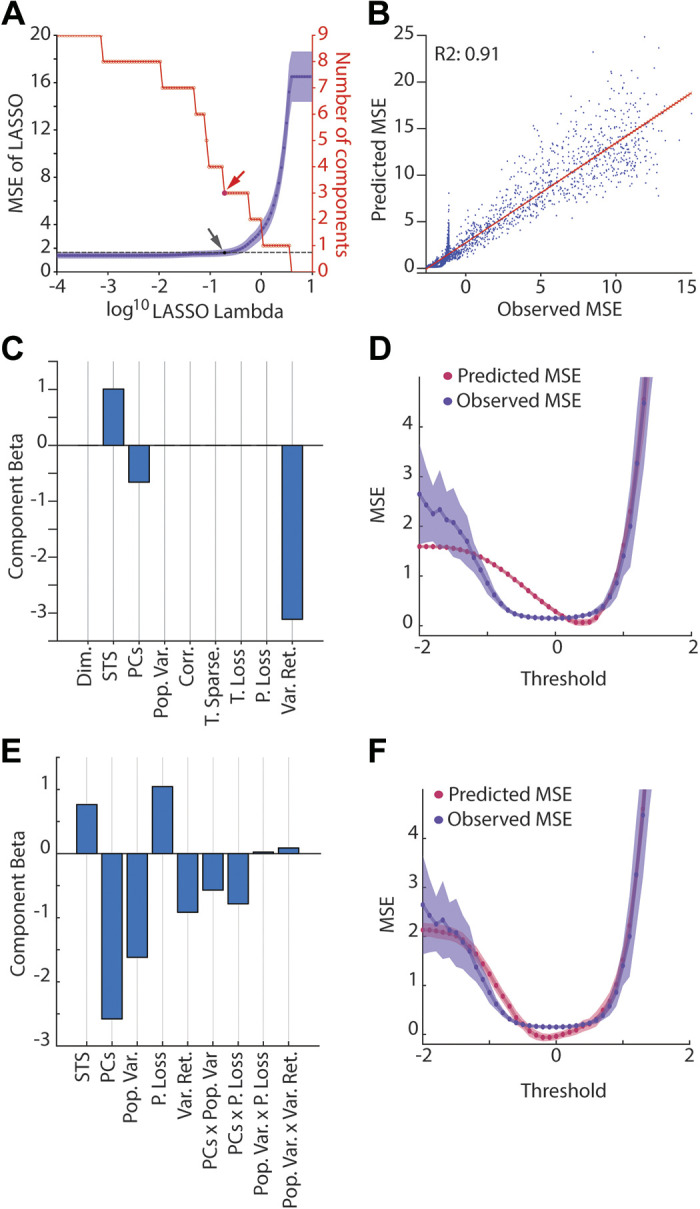
Relationship between GCL population statistics and MSE. A: LASSO regression was used to identify GCL population metrics that predicted learning performance. A: the model selection as a function of progression of the Lambda parameter (which is the penalty applied to each regressor). The following potential regressors were used: dimensionality (Dim.), spatiotemporal sparseness (STS), explanatory principal components of the GC population (PCs), population variability (Pop. Var.), spatial sparseness (S. Sparse.), temporal sparseness (T. Sparse.), temporal lossiness (T. Loss.), population lossiness (P. Loss), and input variance retained (Var. Ret; Fig. 5). Arrow shows selection point of LASSO regression MSE using “1SE” (1 standard error) method (see methods, purple lines, black dot, and arrow indicating the selected model, with red arrow showing selection point in the parameter reduction plot, red). B: relationship between LASSO model (predicted relative MSE) against the observed relative MSE (ratio of GC MSE to MF alone MSE) with fit line and variance explained by regression (R² = 0.91). C: regression slopes of the selected LASSO model from A, showing that STS, PCs, and input variance retained are the selected regressors, with Var. Ret. being the largest contributing factor. All factors normalized to a normal distribution for comparison. D: the output of the selected model and the observed MSE plotted against threshold for a comparison of fits, demonstrating high accuracy in the 0–2 range, but less accuracy in the −2 to 0 range. E and F: similar to C and D except using Bayesian information criteria stepwise regression model to select metrics that explain learning. GCL, granule cell layer; MSE, mean squared error.

Introduction of Noise to Input and GCL Population

To test whether fluctuations riding on input signals influence GCL basis set formation, we introduced Gaussian noise that was recalculated trial to trial and added it to the MF input population. The amplitude of the introduced noise was scaled to the amplitude of the input so that the proportion of the signal that is noise could be described with a percentage: % Noise = 100 × Noise Amp./(Signal Amp. + noise Amp.). For example, if the amplitude of the noise was equal to the amplitude of the input, the % noise would be equivalent to 1/(1 + 1) = 0.5 or 50% noise.

To determine the stability of representations in the MF and GCL populations with introduced noise, we measured the displacement of the temporal location where peak firing occurred between noiseless and noisy activity patterns at threshold 0 (unless noted). This measurement was rectified to obtain the absolute displacement of peak firing time.

Learning Accuracy and Speed Assay

To understand how the GCL contributed to learning, we constructed an artificial Purkinje cell (P-cell) layer. The P-cell unit learned to predict a target function through a gradient descent mechanism, such that the change in weight for each step was:

$$\hspace{0.17em}Err(t)=|P(t)-TF(t)|\hspace{0.17em}$$ (4)

$$\Delta W_i=W_i-(Err(t)*G{C}_i\hspace{0.17em}(t)*\hspace{0.17em}\eta )$$ (5)

where P(t) is the output of the P-cell at time t, TF(t) is the target function at time t, W_i is the weight between the Purkinje cell and the i^th GC, and η is a small scalar termed the “step size.” η was 1E-3 for GCs, and 1E-5 for MF alone in simulations shown in this study where the step size was held fixed, which was chosen to maximize learning accuracy and stability of learning for both populations. Although not strictly physiological because of membrane time constant temporal filtering and variable eligibility windows for plasticity, this form of learning is widely applied in neural models, including cerebellar (e.g., Ref. 53). Physiological equivalents of negative weights found by gradient descent could be achieved by molecular layer interneuron feedforward inhibition to P-cells. The learning process in Eqs. 4 and 5 was repeated for T trials at every time point in the desired signal. The number of trials was chosen so that learning reached asymptotic change across subsequent trials. Typically, 1,000 trials were more than sufficient to reach asymptote, so that value was used for the experiments in this study.

The overall accuracy of this process was determined by calculating the mean squared error between the predicted and desired function:

$$MSE=\frac{1}{T}{\displaystyle \sum }_{t=1\hspace{0.17em}}^T{(P(t)-TF(t))}^2\hspace{0.17em}$$ (6)

The learning speed was determined by fitting an exponential decay function to the MSE across every trial and taking the τ of the decay (see GCL Output Metrics).

GCL Output Metrics

To assay the properties of the GCL output that influence learning, we measured the features of GCL output across a spectrum of metrics that have theoretically been associated with GCL functions like pattern separation or expansion, as well as optimization or cost-related metrics developed for this paper. These included dimensionality, spatiotemporal sparseness, contributing principal components, spatial sparseness (mean population pairwise correlation), temporal sparseness (mean unit autocovariance exponential decay), population variance, temporal lossiness, population lossiness, and temporal cover.

We considered three forms of lossiness here, two related to the dimensions of sparseness considered above, time and space, and one that is a measure of sparseness on the individual GC level. Temporal lossiness is a measure of the percentage of time points that are not encoded by any members of the GCL population, essentially removing the ability of P-cells to learn at that time point and producing no output at that time in the final estimation of the target function. Increases in the value are guaranteed to degrade prediction accuracy for any target function that does not already contain a zero value at the lossy time point.

$$Temp.\hspace{0.17em}Lossiness=\frac{1}{T}\hspace{0.17em}{\displaystyle \sum }_{t=1}^T{x}_t\hspace{0.17em}where\hspace{0.17em}{x}_t\hspace{0.17em}\left\{\begin{array}{c}({\displaystyle \sum }_{i=1}^{N}G{C}_i(t))\hspace{0.17em}\le 0=1\\ else=0\end{array}\right\}$$ (7)

Here, T is the total number of points in the encoding epoch, the bracketed portion of the formula is a summation of inputs from all GCs (N = population size) at that time point. When all GCs are silent, the sum is 0, and the temporal lossiness is calculated as 1, and when all time points are covered by at least one GC, total temporal lossiness is 0.

Spatial lossiness, or population lossiness, is the proportion of GCs in the population that are silent for the entirety of the measured epoch. This is thought to reduce total encoding space and deprive downstream P-cells of potential information channels and could potentially impact learning efficacy. It is defined as

$$Pop.\hspace{0.17em}Lossiness=\frac{1}{N}\hspace{0.17em}{\displaystyle \sum }_{i=1}^N{x}_i\hspace{0.17em}where\hspace{0.17em}{x}_i\hspace{0.17em}\left\{\begin{array}{c}\left({\displaystyle \sum }_{t=1}^{T}G{C}_t\right)\hspace{0.17em}\le 0=1\\ else=0\end{array}\right\}$$ (8)

Here, N is the total population size of the GCL, and the bracketed portion of the formula is a sum of the activity of GCs across all time points, such that if a GC is silent across all time points, x_i is calculated as 1, indicating the “loss” of that GC unit’s contribution. When all GCs are silent, population lossiness is 1, and when all GCs are active for at least one time point, population lossiness is 0.

In addition, we looked at the mean sparseness of activity across the population by measuring the “coverage” or proportion of time points each GC was active during, defined as:

$$Coverage=\frac{1}{N}\hspace{0.17em}{\displaystyle \sum }_{i=1}^N(\frac{1}{T}\hspace{0.17em}{\displaystyle \sum }_{t=1}^T{x}_{i\hspace{0.17em}}\hspace{0.17em}where\hspace{0.17em}{x}_i\hspace{0.17em}\left\{\begin{array}{c}{GC}_i(t)>0=1\\ else=0\end{array}\right\}\hspace{0.17em})\hspace{0.17em}$$ (9)

As before, N is the number of cells in the population and T is the total length of the epoch. The bracketed function counts the number of time points where GC_i is active and divides that by the total time period length to get the proportion of time active. This value is summed across all GCs and divided by N to calculate the average coverage in the population. This value has strong synonymy with population variance, so it was not used for fitting assays in later experiments (Fig. 6), but reflects the effect of thresholding on average activity in the GCL population.

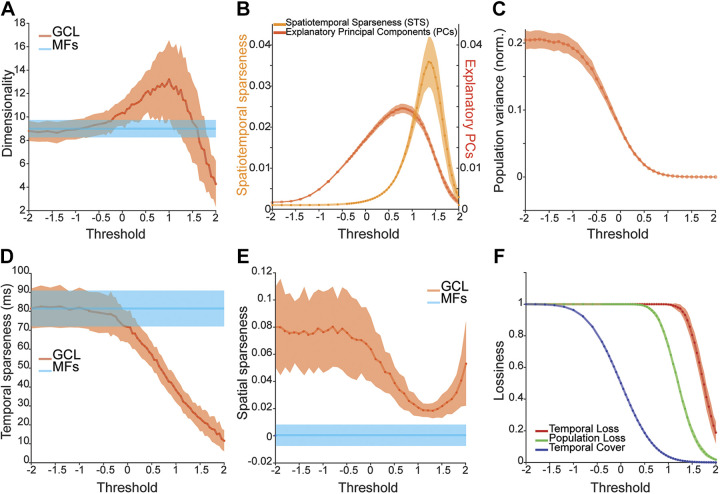
Figure 6.

Statistical features of GCL output. A: GCL dimensionality (red) and MF dimensionality (blue) as a function of threshold. Note peak near a threshold of 1 for the GCL. B: two metrics of pattern separation in GCL output—STS (light orange) and PCs (dark orange)—as a function of threshold. Note peaks near 1.5 and 0.5, respectively. C: the sum of GCL variance produced by the model as a function of threshold. Note monotonic decrease with threshold. D: temporal sparseness as a function of thresholding. Note monotonic decrease in GCL with thresholding. E: mean pairwise correlation of the population plotted as a function of threshold. Note trough near 1. F: three forms of lossiness in GCL output as a function of threshold. Each metric had differential sensitivity to thresholding but note that all decrease with increasing threshold. Across metrics, function maxima and minima ranged widely and were not obviously related to thresholds of optimized learning. GCL, granule cell layer; MF, mossy fiber; PC, principal component; STS, spatiotemporal sparseness.

Dimensionality is a measure of the number of independent dimensions needed to describe a set of signals, similar in concept to the principal components of a set of signals. This measure is primarily influenced by the covariance between signals, and when dimensionality approaches the number of signals included in the calculation (n), the signals become progressively independent. The GCL has previously been shown to enhance the dimensionality of input sets and does so in the model presented here too. Dimensionality is calculated with

$$Dim\hspace{0.17em}={\left({\displaystyle \sum }_{i=1\hspace{0.17em}}^n{\lambda }_i\right)}^2/\left({\displaystyle \sum }_{i=1\hspace{0.17em}}^n{\lambda }_i{}^2\right)\hspace{0.17em}$$ (10)

provided by Litwin-Kumar et al. (25). This is the ratio of the squared sum of the eigenvalues to the sum of the squared eigenvalues of the covariance matrix of the signals.

Spatiotemporal sparseness (STS) was a calculated cost function meant to measure the divergence of GC population encoding from a “perfect” diagonal function where each GC represents one point in time and does not overlap in representation with other units. This form of representation is guaranteed to produce perfect learning, and transformations between the diagonal and any target function can be achieved in a single learning step, making this form of representation an intriguing form of GCL representation, if it is indeed feasible. We calculated the cost as

$$STS\hspace{0.17em}=(1-L_t\hspace{0.17em})*\left(\frac{1}{T}\right)*\left(\frac{W}{G{C}_w}\right)$$ (11)

where (1 – L_t) is the cost of temporal lossiness, defined above (Eq. 7), and T is the total length of the epoch. W is the number of unique combinations (termed “words,” akin to a barcode of activity across the population) of GCs across the epoch at each point of discrete time, and GC_w is the average number of words that each GC’s activity contributes to. The intuition used here is that when there is no temporal lossiness, all points in time are represented, leading the 1 – L_t term to have no effect on the STS equation, and when W, the number of unique combinations of GC activities is equal to T, then each point in time has a unique “word” associated with it. Finally, when GC_w is 1, W/GC_w is equal to W, which only occurs when each GC contributes to a single word. When these conditions are met, STS = 1, otherwise when GCs contribute to more than one word, GC_w increases and W is divided by a number larger than 1, decreasing STS. Alternately, when there are not many unique combinations, such as when every GC has the exact same output, W/GC_w is equal to (1/T), decreasing STS. Finally, because lossiness causes the occurrence of a “special,” but nonassociable word, we multiplied the above calculations by (1 – L_t) to account for the effect of the unique nonencoding word (i.e., all GCs inactive) on distance from the ideal diagonal matrix.

Mean temporal decay, i.e., temporal sparseness, is a measure of variance across time for individual signals, where a low value would indicate that the signal’s coherence across time is weak, meaning that the signal varies quickly, whereas a high value would mean that trends in the signal persist for long periods. This value is extracted by fitting an exponential decay function to the autocovariance of each unit’s signal and measuring the τ of decay in the function

$$y=a\hspace{0.17em}*\hspace{0.17em}{e}^{(-x/\tau )}$$ (12)

This is converted to the ms form by taking the ratio of 1,000/τ. y here τ is a description of the autocovariance of the activity of a MF or GC signal, so when the descriptor τ is a large number, the decay in autocovariance is longer, or slower, when τ is a small number, the autocovariance across time decays more quickly, making the change in activity faster.

Although dimensionality and STS are metrics rooted in a principled understanding of potentially desirable properties of population encoding, the gradient descent algorithm can extract utility from population statistics that are much noisier and correlated than the ideal populations that dimensionality and STS account for. To measure a more general pattern separation feature in GCL output that could still be associated with the complex target function, we turned to principal component analysis (PCA) with the intuition that components that explain variance in the GCL output could be used by the downstream Purkinje cell units to extract useful features from the input they receive (54). We parameterized the utility of this measure by taking the proportion of the PCs derived from the GCL output which explained variance (of the GCL output) in that population by more than or equal to 1/N, where N is the number of GCs, suggesting that they explain more variance than would be expected from chance.

Population correlation was measured by taking the mean correlation between all pairwise combinations of GCs using the corr() function in MATLAB and excluding the diagonal and top half of the resultant matrix.

Population aggregate variance is a measure related to the expansion or collapse of total space covered by the encoding done by a population, and higher or expanded values in this metric are thought to assist in pattern separation and classification learning.

$$\hspace{0.17em}\text{Pop}.\text{ Var}={\displaystyle \sum }_{n=1\hspace{0.17em}}^N{(x_n-\mathit{\mu })}^2\hspace{0.17em}$$ (13)

As shown in Cayco-Gajic et al. (23), here, x is the activity of one of N cells across a measured epoch, and μ is the mean of that activity. This value is reported relative to the number of GC units, such that Pop. Var reported in Fig. 6 is normalized to Pop. Var/N.

Variance Retained Assay

To test the recovery of inputs by a feedforward network with a granule cell layer (GCL), we used explained variance, R², to quantify the quality of recovery of a sequence of normal random variables (Fig. 5) across N_w = 1,000 numerical experiments. To distinguish this metric from the MSE and R² metrics to evaluate other models in the study, we rename this “variance retained.” Within each numerical experiment i, at each time point, a vector of inputs x_t of length M (representing the mossy fiber, MF, inputs) was drawn from an M-dimensional normal distribution with no correlations, ${\mathit{x}}_{\mathit{t}}\sim \mathcal{N}(0,{\mathit{I}}_{\mathit{M}})$. This vector is then left-multiplied by a random binary matrix W with N rows and M columns with n 1’s per row and the rest zeros, followed by a threshold linearization to obtain the GCL output, ${\mathit{y}}_{\mathit{t}}={[W{\mathit{x}}_{\mathit{t}}-\mathit{z}]}_{+}$ with threshold. This process is then repeated T = 1,000 times and a downstream linear readout was fit to optimally recover x_t from y_t. It can be shown that multivariate linear regression [MATLAB’s regress() function, employing least squares to minimize mean squared error] solves this problem, identifying for each MF input stream ${\mathit{x}}_{1:\mathit{T}}^{\mathit{j}}$, the optimal weighting $B_{1:T}$ from the GCL to estimate ${\widehat{\mathit{x}}}_{1:\mathit{T}}^{\mathit{j}}=B_{j,1:N}{\mathit{y}}_{1:\mathit{T}}$. Across time t = 1:T, we then computed the squared error across the vector, $MS{E}_i=\sum _{t=1}^T\sum _{j=1}^M{({\widehat{\mathit{x}}}_{\mathit{t}}^{\mathit{j}}-{\mathit{x}}_{\mathit{t}}^{\mathit{j}})}^2$, as well as the summed variance of the actual input, $Va{r}_i=\frac{1}{MT}\sum _{j=1}^M\sum _{t=1}^T{({\mathit{x}}_{\mathit{t}}^{\mathit{j}}-{\overline{\mathit{x}}}^{\mathit{j}})}^2$, where ${\overline{\mathit{x}}}^{\mathit{j}}=\frac{1}{\mathit{T}}\sum _{\mathit{t}=1}^{\mathit{T}}{\mathit{x}}_{\mathit{t}}^{\mathit{j}}$ is the mean of the jth MF input stream. Lastly, to compute variance explained, we take $R^2=1-\frac{{\sum }_{i=1}^{N_w}MS{E}_i}{{\sum }_{i=1}^{N_w}Va{r}_i}$, so the higher the relative mean-squared error is, the lower the variance explained will be. To generate the panels in Fig. 5, we always kept the number of time points and experiments the same, but varied the threshold along the axis and the number of inputs n per GC output (Fig. 5B), the total number of GC outputs N and input per output n (Fig. 5C), number of inputs M and outputs N (Fig. 5D), and finally the number of inputs per GC output n along with the total number of outputs N (Fig. 5E).

Generation of GCL Output with Defined Statistical Structure

To determine if the sparseness measures had inherent benefits for learning, we supplemented the GCL output with OU processes with known temporal and correlational properties to examine their effect on learning accuracy (Fig. 7; Supplemental Fig. S3). We varied the temporal properties by systematically varying the τ value in the exponential decay function. To vary population correlation, the random draw function in the OU process was replaced with a MATLAB function, mvnrnd(), which allowed for preset covariance values to direct the overall covariance between random samples. We used a square matrix with 1 s on the diagonal and the desired covariance on all off-diagonal locations for this process and varied the covariance to alter the correlation between signals. The OU outputs from this controlled process were then fed into model P cells with randomized OU targets, as per the normal learning condition described in Eqs. 4 and 5. To vary the effect of the input population size, the size of the supplemented population varied from 10 to 3,000 using a τ of 10 and drawing from normal random numbers.

To measure the effects of STS on learning, a diagonal matrix was used at the input to a Purkinje unit, which represented population activity with an STS of 1 (see Eq. 11 under GCL Output Metrics). To degrade the STS metric, additional overlapping activity was injected either by expanding temporal representation or at random, for example, adding an additional point of activity causes inherent overlap in the diagonal matrix, increasing the GC_w denominator of Eq. 11 to (1 + 2/N) because the overlapping and overlapped units now each contribute to 1 additional neural word. This process was varied by increasing the amount of overlap to sample STS from 0 to 1.

Statistics of GCL Output Metrics and Learning

To estimate the properties of GCL output that contribute to enhanced learning of time series, we used multiple linear regression to find the fit between measures of GCL population activity and observed MSE in learning. Because there are large inherent correlations between the metrics used (dimensionality, spatiotemporal sparseness, explanatory principal components of the GC population, population variability, mean pairwise GC correlation, temporal sparseness, temporal lossiness, population lossiness, and input variance retained), we used two linear regression normalization techniques: LASSO and RIDGE regression. For Fig. 7, LASSO was used to isolate the “top” regressors, whereas RIDGE was used in Fig. 8 to preserve small contributions from regressors. The RIDGE regression method was then used to compare resultant regression slopes (β coefficients) to changes in task parameters (see methods, Simulation of Cerebellar Tasks).

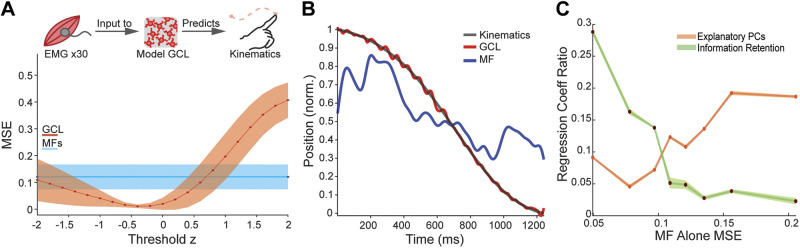
Figure 8.

Relationship of MF input to learned output influences how GCL supports learning. A, top: schematic of model task, using recorded EMGs as an input to the model GCL to predict kinematics. Bottom: MSE of model as a function of threshold when using EMG alone (MFs; blue) or GCL (red) as input to model P-cell. At a range of thresholds, P-cells that receive GCL input outperform P-cells receiving MFs alone. B: example of learned kinematic position after training for MF alone (blue line) and GCL network (red) showing good metric fit by the GCL model. C: plot showing the strength of different GCL population statistical features driving learning that vary as a function of how well MFs intrinsically support learned P-cell output (MF alone MSE). When MFs are already excellent predictors, information retention (variance retained) has a high regression slope (RIDGE regression method). When MFs are poorer intrinsic predictors, the number of explanatory PCs (a pattern separation metric) emerges as a stronger driver of learning performance. Goodness of fit (R²) was between 0.83 and 0.95 across all MF- alone MSEs used. GCL, granule cell layer; MF, mossy fiber; P-cell; Purkinje cells.

Regressions were performed using the fitrlinear() function in MATLAB, with LASSO selected by using the “SpaRSA” (sparse reconstruction by separable approximation; 55) solver, and RIDGE selected with the “lbfgs” (limited-memory BFGS; 56) solver techniques. The potential spread of MSE in the models was determined using a K-fold validation technique, with 10 “folds” used, as well as for determining the range of absolute slopes shown in Fig. 8C, of which the mean and standard deviation of cross-validation trials are plotted with solid lines and shaded polygons, respectively. Models were selected by choosing the model with the least complex fitting parameters (i.e., the model with the highest Lambda) while still falling within the bounds of the model with the minimized MSE plus the standard error (a standard “1SE” method).

We reasoned that interactions between explanatory GCL statistical features might account for observed learning accuracy to some degree. A standard method for selecting potential interactions while constraining the regression model to a reasonable number of parameters is through selection by Bayesian information criteria (BIC) stepwise regression. We used the MATLAB stepwiselm() function with the BIC method to select from our nine statistical features and allowed the regression function to select potential interactions between them. The output of the regression listed which linear and interacting components best fit the model. Although this output also included the β values of the fits, they were not regularized in a way that was intuitively interpretable, so we therefore transferred the BIC-selected parameters to a RIDGE regressor to get the final β values and fit.

To convey the overall contribution of regressors to the above models of MSE, the slope relative to the magnitude of all slopes were used as plotted metrics (Fig. 8C).

Pontine Neuron Activity Patterns

To investigate the properties of GCL filtering on physiological inputs to the cerebellar cortex, we extracted recordings of pontine neurons, a primary source of mossy fibers, from the work of Guo et al. (41) during a reaching task in mice. We used the first 50 neurons for the recording to keep MF counts similar to the modeled OU population and applied a 100-ms Gaussian filter to the raw spiking data, aligned to reach onset, to obtain the estimated firing rate. The firing rate values were range normalized for display and filtering (Fig. 1, B and E) and are shown in order of their peak firing rate time.

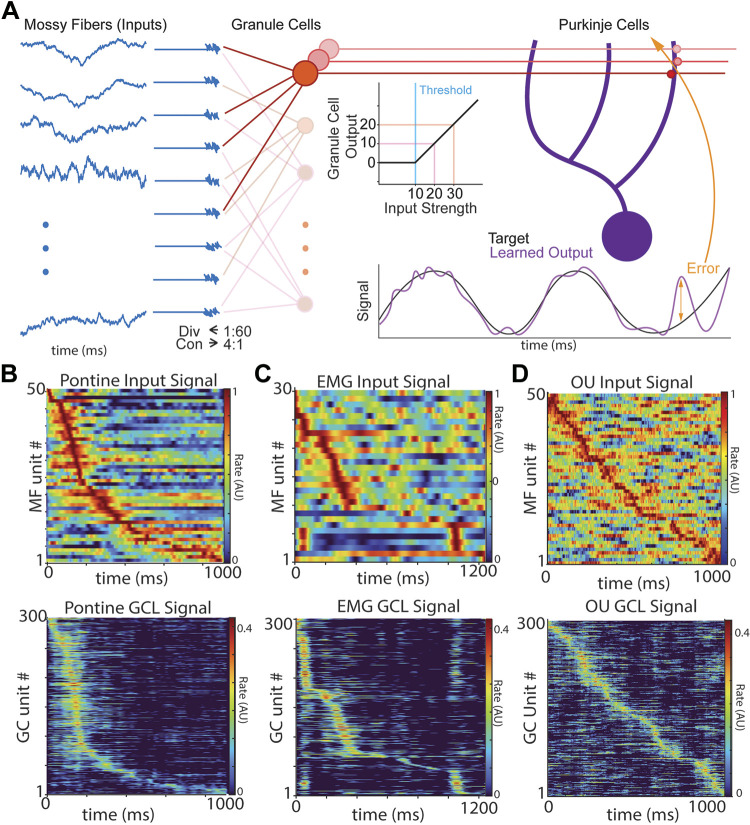
Figure 1.

Model architecture and effects of thresholding on GCL population activity. A: diagram of algorithm implementation. Left shows Ornstein-Uhlenbeck (OU) processes (see methods) as proxies for mossy fiber (MF, blue) inputs to granule cell units (GCs, red), with convergence and divergence of MFs to GCs noted beneath MFs. GCs employ threshold-linear filtering shown beneath the red parallel fibers. GC outputs are then transmitted to downstream Purkinje cells (P-cells). P-cells learn to predict target functions by reweighting GC inputs. Differences between the prediction and true target are transmitted as an “error,” which updates synaptic weights to P-cells. B–D: examples of MF inputs and GCL outputs. B: emergence of temporal basis sets in model GCLs using inputs derived from pontine neuron recordings. Top: pontine recordings in mice during pellet reaching task, aligned to reach onset at 0 ms. Bottom: model GCL output using PN activity as input. C: same as B, but using EMGs as MF inputs. Top: electromyogram (EMG) recordings from human subject in point-to-point reaching task (EMG). Bottom: model GCL output using EMG as input. D: same as B, but using OU functions as MF inputs. Bottom: model GCL output using OU processes as inputs. The model GCL enhanced spatiotemporal representation for all three input types (B–D). GCL, granule cell layer.

Simulation of Cerebellar Tasks

To simulate the transformation between motor commands and kinematic predictions, we used human EMG as a proxy for a motor command-like input signal to the GCL. Thirty muscles from 15 bilateral target muscles were used (57, 58). The target function was a kinematic trajectory recorded simultaneously with the recordings of EMG used for the study. Although many body parts and coordinate dimensions were recorded of the kinematics, we opted to use the kinematic signal with the largest variance to simplify the experiment to a single target function.

Code Availability

All computer code and simulation data is freely available at https://github.com/jesse-gilmer/2022-GCL-Paper. Supplemental Figures are available at https://doi.org/10.6084/m9.figshare.21763943.v1.

RESULTS

Temporal Basis Set Formation as Emergent Property of GCL Filtering of Time-Varying Inputs

In many motor tasks, both mossy fibers and P-cells show highly temporally dynamic activity patterns, raising the question of how GCL output supports time-series learning using time-varying inputs, a divergence from traditional classification tasks used in most cerebellar models (Fig. 1; 59).

We used a simple model, similar to previously published architectures (23, 25, 50), capturing the dominant circuit features of the GCL; sparse sampling of mossy fiber (MF) inputs by postsynaptic granule cells (GCs) and coincidence detection regulated by cellular excitability and local feedforward inhibition (Fig. 1A; Eqs. 1 and 2; 17, 20, 21, 34, 60). GC output is generated by summing MF inputs and thresholding the resultant sum; anything below threshold is set to zero while suprathreshold summed activity is passed on as GC output (Fig. 1A, middle). The GC threshold level represents both intrinsic excitability and the effect of local inhibition on regulating GC activity.

We fed two naturalistic sources of cerebellar inputs to the model: recordings from the mouse pontine nucleus (PN, Fig. 1B, reanalyzed data previously published in Ref. 41) and electromyograms measured during reaching tasks (EMG, Fig. 1C, reanalyzed data from Ref. 57). In both cases, the GCL enhanced the spatiotemporal representation of input activity. To parameterize such time-varying inputs, we next generated artificial MF activity using Ornstein-Uhlenbeck (OU) stochastic processes. These signals provide a statistically tractable ensemble that was rich enough to capture the dynamic nature of naturalistic inputs while remaining analytically tractable and easily parameterized, fully characterized by just three parameters: correlation time, mean, and standard deviation. Example OU input functions are shown in Fig. 1D (top). Importantly, OU functions preserve autocorrelations typical of physiological signals, such that they are not random from moment-to-moment (Fig. 1D, τ of 100 ms). All OU MFs had the same τ and were not correlated with one another. As with the naturalistic inputs, the model GCL spatiotemporally diversified OU processes Fig. 1D (explored more thoroughly below). The emergence of sparse spatiotemporal representation under the simplistic constraints of the model suggests that the cerebellum’s intrinsic circuitry is sufficient to produce spatiotemporal separation when given sufficiently time-varying inputs. Below, we refer to the transformation of information between GCL inputs and outputs as “GCL filtering.”

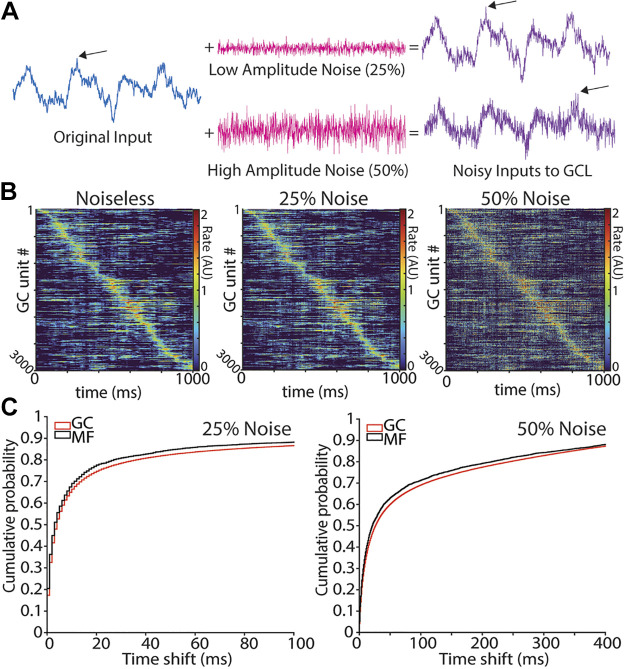
GCL Temporal Basis Is Robust to Noise

By relying on coincident peaks in time-varying mossy fibers, this mechanism of spatiotemporal sparsening raised the question of whether such temporal basis sets were robust to noise. To address whether noise degrades spatiotemporal representation, we ran repeated simulations, adding Gaussian noise that changed from trial to trial to fixed OU functions, and compared the resultant GCL basis sets (Fig. 2). We modeled trial-over-trial noise variance by superimposing a Gaussian fluctuation such that the overall proportion of the total signal was noise ranged from 25%–50%.

Figure 2.

Effect of increased input noise on GCL peak activity timing. A: example MF input modeled as an OU process without noise (left) and with (right). B: example of a GCL population with stable OU process as input (noiseless; left), and the population with addition of noise (middle and right). The granule cell (GC) population is ordered by timing of peak rate in the noiseless condition. C: cumulative distribution of peak rate time shift between “no noise” and 25% noise (left) or 50% noise (right), with MFs in black and GCs in red. x-axis is bounded to capture ∼85% of population. CDF step length is 1 ms. GCL, granule cell layer; MF, mossy fiber; OU, Ornstein-Uhlenbeck.

GCL population activity was generally stable across noise levels (Fig. 2B). To quantify stability, we measured the shift in the time of peak rate for each GC over 100 trials at threshold of 0. Fifty percent of granule cells shifted 10 ms or less in the 25% noise condition (Fig. 2C, left) and 50% shifted less than 30 ms when 50% of the signal was unstable noise (Fig. 2C, right). Thus, although the basis set structure is not perfectly resistant to noise, the primary temporally correlated OU signal dominates the population’s temporal structure. The effect of high noise on the stability of the temporal basis was dependent on threshold; higher thresholds coupled with higher noise degraded temporal stability. At a threshold of 0, the mean time shift was 136 ms. While at a threshold of 1, the mean time shift was 305 ms.

GCL Improves Time-Series Learning Accuracy

If mossy fiber activity is naturally time-varying, it raises the question of whether it, by itself, is intrinsically suited to support time-series learning, obviating a role for the GCL (61, Supplemental Fig. S1). To address this question, we tested whether GCL population activity assisted learning beyond the temporal representations inherent in the mossy fibers. We devised a task where P-cells learned to generate specific time-varying signals (OU process with 10 ms autocorrelation time) using gradient descent (Eqs. 4 and 5, methods). Inputs to P-cells were either MFs or GCL populations. Initially, P-cell output was distinct from the target function, but over repeated trials, P-cell output converged toward the target function (Fig. 4A). We quantified the convergence of the P-cell output to the target function and compared performance to instances when MF activity was sent directly to P-cells (“MFs alone”). GCL activity was used as P-cell input. Finally, we examined performance of these learning simulations across different thresholds, expressed in terms of a z-score, such that a threshold of “zero” indicates the threshold is at the mean of MF input.

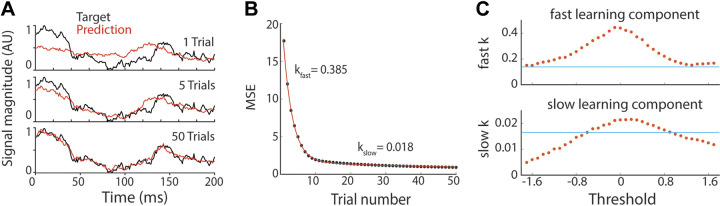
Figure 4.

Learning speed increases with GCL. A: example of learned predictions after 1, 5, and 50 trials of learning, with predictions in red and target function in black. B: example learning trajectory of MSE fit with a double exponential. Black circles: MSE of network output on each trial. Red line: double exponential fit MSE during learning. Here, step size was 10⁻⁶ and z-scored GCL threshold was 0. We use the exponents k from the exponential fit to measure learning speed. C: learning speed as a function of GCL threshold (red dots). Blue line: learning speed in networks lacking GCL, i.e., mossy fibers directly innervate output Purkinje unit, gradient descent step size was 10⁻⁶. GCL, granule cell layer; MSE, mean squared error.

The model achieved excellent learning with either MFs or GCL inputs. Notably, the GCL markedly enhanced the convergence to a target function at thresholds between –1 and 1 (Fig. 3A), achieving a minimized mean-squared error (MSE) of roughly 0.005, outperforming learning using MFs alone (MSE 0.02; normalized to a range of [0,1]). To establish an intuition into the practical difference of the range of MSEs achieved with GCL or MFs alone, we tasked the model with learning a time series which could be rendered as a recognizable image to human viewers (Fig. 3B). This function had an identical range of target function values ([0,1], Fig. 3B). GCL inputs facilitated P-cell time-series learning that recapitulated the recognizable image (Fig. 3B, bottom; MSE 0.002). By contrast, P-cells that received MFs alone generated a time series that rendered an unrecognizable image, despite the seemingly excellent MSE of 0.02. Thus, the small errors of MF-driven output accumulated along the time series to degrade performance, while GCL-driven P-cell output yielded an easily recognizable image (Fig. 3B, top right vs. three thresholds, bottom). Importantly, this was not a consequence of the large population expansion between MFs and GCs, as increasing the number of MFs alone did not improve performance to the levels observed in the model GCL (Supplemental Fig. S1, A and B). Nevertheless, a sufficiently large GCL population is required to improve learning (Supplemental Fig. S1B).

Figure 3.

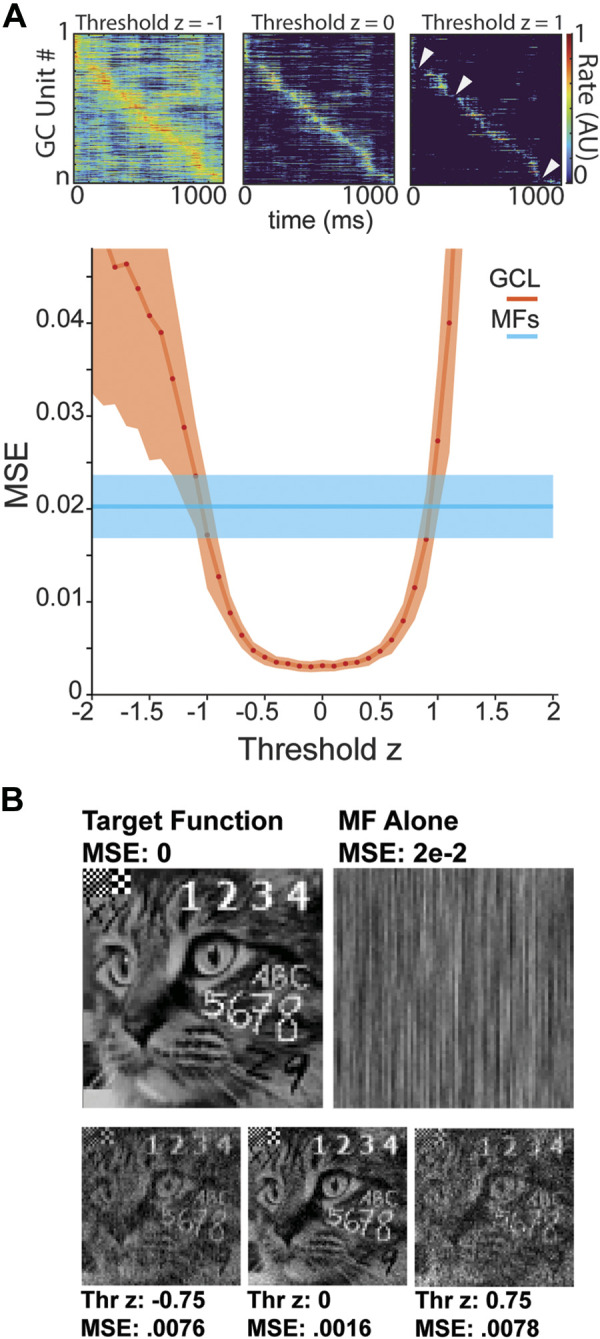
Enhanced time-series learning using GCL model. A, top: GCL output at different threshold levels. Bottom: relationship of threshold level to learning accuracy (MSE) for Purkinje (P) cells fed MFs directly (blue) or the output of the GCL (orange; error, standard deviation). B, top left: P-cells were tasked with learning a complex timeseries that could be rendered as an image recognizable to humans, a cat with superimposed text. Top, right: if P-cells were fed MF input directly, their best learning output was not recognizable as a cat, despite seemingly low MSE of 0.02. Bottom: if P-cells were fed GCL output, they learned timeseries that rendered a matching image, with MSEs dependent on threshold, but varying between 0.0078 and 0.0016. This figure provides an intuitive sense of the practical difference between MSE of 0.02 and 0.0016, achieved with P-cells learning using MFs directly or with the support of GCL preprocessing. GC, granule cell; GCL, granule cell layer; MF, mossy fiber; MSE, mean squared error.

GCL Model Speeds Time-Series Learning

Having found that the GCL improves the match between predicted output and target output over a range of thresholds, we next examined whether the GCL also increased the speed of convergence. We examined the MSE between the model output and the target function on each trial as training progressed (Fig. 4C, red circles) and found that output usually converged rapidly at first then more slowly in later stages of training (Fig. 4A). The reduction in MSE over training in our model was reasonably well fit by a double exponential (Fig. 4B, red curve) of the form

$$MSE(n)=A_1\hspace{0.17em}{e}^{(-k_1\hspace{0.17em}n)}+A_2\hspace{0.17em}{e}^{(-k_2\hspace{0.17em}n)}+C$$

where n is the trial number. We measured the convergence speed of a simulation by the rate constants k₁ and k₂. In the vast majority cases, one of these rate constants was 5–50 times larger than the other; we denote the larger constant k_fast and the other k_slow. For most parameter values, k_fast accounts for more than 80% of learning.

We next examined the influence of several key model parameters on convergence speed, such as threshold and gradient descent steps size. First, we looked at the effect of the GC threshold. Learning was fastest for GCL thresholds near a z-score of zero (Fig. 4C, red circles), the level that filters out half of the input received by a GC. Convergence in networks that lack a GCL (MFs directly innervating P-cells) was consistently slower (Fig. 4C, blue line) than networks with a GCL. Convergence was also sped up by increasing the size of the parameter jumps in synaptic weight space during gradient descent (the “step size”), but only to a limited degree (Supplemental Fig. S2). Indeed, at a GCL threshold of 0, convergence speed decreased as the step size increased beyond ∼10⁻⁶ (au). We speculated that this trade-off was a consequence of a failure to converge in a subset of simulations. To test this, we looked at the fraction of simulations that converged toward a low MSE as a function of the update magnitude. We found that the fraction of simulations that converged (“fraction successful”) decreased with increasing step size (Supplemental Fig. S3B); in simulations that did not converge, the MSE increased explosively and synaptic weights diverged. In such cases, we assume the large weight updates made it impossible to descend the MSE gradient; each network weight update drastically changed the cost function such that local MSE minima were overshot. When larger step sizes did permit convergence, progress was nevertheless slowed, likely because the relatively large learning rates led to inefficient progress toward the MSE minimum.

Although larger step sizes eventually cause learning to slow and then fail entirely at a given GCL threshold, higher thresholds permitted larger step sizes before failures predominated (Supplemental Fig. S2). Since higher thresholds permit larger step sizes before convergence failure sets in, convergence speed might be maximized by jointly optimizing step size and GCL threshold. We tested this by systematically raising step sizes at each threshold until convergence success fell to 50%. We defined the “maximum convergence rate” for a given threshold as the maximum convergence rate (derived from fitting the MSE trajectory with a double exponential) yielding successful convergence at least 50% of the time. We found that the threshold giving the fastest convergence was indeed higher when step size was also optimized (Supplemental Fig. S2) than when step size was fixed (Fig. 4C). Thus, increased GCL thresholding can allow the network to trade learning accuracy for increased speed of learning.

Recovering GCL Input from GCL Output

Having established a framework for studying GCL processing of time-varying inputs, we wanted to understand to what extent thresholding GCL activity led to the loss of information supplied by MF inputs, which potentially contains useful features for learning. In other words, would Purkinje neurons be deprived of behaviorally relevant mossy fiber information if these inputs are severely filtered by the GCL? To assess this issue, we used a metric of information preservation called explained variance (62); however, in this special case, we use the term “variance retained,” because this metric represents the preservation of information about the input after being subjected to filtering in the GCL layer and we wanted to avoid confusing when describing linear regression results below. Let x_t denote the MF input at time t. If the GCL activity preserves the information present in x_t, then it should be possible to reconstruct the activity of MFs from GCL activity (see methods for details on how this reconstruction was performed). The variance retained is then the mean-squared error between the actual MF input x_t and the reconstructed input, normalized by the MF input variance:

$$R^2=1-\frac{{{\displaystyle \sum }}_{t=1}^T{({\widehat{x}}_t-x_t)}^2}{{{\displaystyle \sum }}_{t=1}^{T}Var[x_t]}$$

Our primary finding is that the GCL transmits nearly all of the information present in the MF inputs even at fairly high thresholds, but only if the GCL is sufficiently large relative to the MF population. The threshold, feedforward architecture, and relative balance of MF inputs and GC outputs all affect the quality of the reconstruction. Variance retained by the reconstruction layer decreased with the GC layer threshold, since it masked some subthreshold input values (Fig. 5B). Allowing more MF inputs per GC recovered some of this masked information, since some subthreshold values are revealed through summing with sufficiently suprathreshold values. However, these gains cease beyond a few MF inputs per GC, since the exponential growth of MF combinations rapidly exceeds the number that the GCs can represent (20, 63).

To disentangle the information contained in the summed inputs, many different combinations of inputs must be represented to disambiguate the contributions of each MF input. Increasing the number of GCs generally increases the variance retained, since more combinations of MF inputs are represented and reveal subthreshold input values (Fig. 5C). Interestingly, variance retained by the network varied nonmonotonically with the number of MF inputs (M) when the number of GCs (N) was fixed. This is because having too few MF inputs means there may not be a sufficient number of combinations so that subthreshold values can be revealed (by summing them with suprathreshold inputs), but having too many saturates the information load of the GC layer (Fig. 5D). Lastly, when fixing the number of MF inputs and GCs, there is an optimal number of MF inputs to each GC, which aligns with the anatomical convergence factor of 4 MF/GC (Fig. 5E), related to previous findings that suggest the best way to maximize dimensionality in the GC output layer is to provide sparse input from the mossy fibers (23, 25). Thus, there are two key features that shape the information transferred to the GCL from the MF inputs. First, the way in which MF inputs are combined to form the total input to each GC determines how much information about subthreshold inputs can be transferred through the nonlinearity. Second, the total number of GC outputs determines how many MF input combinations can be represented, so that, ultimately, the random sums of MFs can be disentangled by the downstream reconstruction layer. Together, information transfer requires a combined summation and downstream decorrelation process accomplished by the three-layer feedforward network.

General Statistical Features of GCL Population Activity

We were ultimately interested in which features of GCL signal processing account for learning. As a first step, we examined a variety of population metrics across threshold levels, which had previously been proposed to support perceptron learning. The first set of metrics related to pattern separation are 1) dimensionality (Dim), 2) the number of explanatory principal components (PCs), 3) spatiotemporal sparseness (STS), and 4) population variability (See methods for details). Most of these pattern separation metrics, (Dim, PCs, and STS) showed nonmonotonic relationships with threshold and peaked at thresholds ranging between 0.5 and 1.5 (Fig. 6, A and B). Population variability, however, decreased with increasing thresholds (Fig. 6C). Intuitively, this relationship captures the effect of low thresholds allowing GC activity to relay the mean input, with no pattern separation occurring. With increasing threshold, GC activity is driven by coincidence detection, leading to higher dimensional population output. At high thresholds, inputs rarely summate to threshold, leading to lost representation that drives a roll-off in pattern separation within the population. Notably, Dim, PCs, and STS peaked at higher thresholds than peak learning performance, which was best at threshold zero, thus none of these three pattern separation metrics alone map directly to learning performance. Population variability (i.e., GCL variance per unit) is thought to aid classification and separability of GCL output (23). This metric’s decrease with increasing threshold was likely due to the decrease in overall representation by each unit due to sparsening and diminishing the dynamic range of GC rates due to threshold subtraction (Figs. 2A, top, and 6C).

The second set of metrics are related to sparseness that include 1) temporal sparseness and 2) spatial sparseness. Temporal sparseness is defined by the exponential decay of GC autocovariance, where smaller values typify signals that change quickly with time decreased as a function of threshold because of sparsened representation at higher thresholds (Fig. 6D). Spatial sparseness is defined as the mean pairwise GC correlation shared a drop-off after a threshold of 0, but increased again at high thresholds because only a few MF signals were retained at high threshold and thus were highly correlated (Fig. 6E). By experimental design, decorrelation was already maximized in OU inputs. Similar to the pattern separation metrics, these sparseness metrics did not show an obvious relationship to the U-shaped learning performance seen in Fig. 3A, bottom.

Finally, we examined three metrics of lossiness defined to quantify 1) the fraction of the total epoch with no activity in any GC unit (e.g., with “temporal lossiness” of 0.1, 10% of the total epoch has no activity in any GCs), 2) the proportion of granule cells with any activity over the entire epoch (“population lossiness”), and 3) the mean fraction of the epoch in which each granule cell is active (“temporal cover”). Not surprisingly, each lossiness metric increased with high thresholds (Fig. 6F). However, despite diminishing activity in individual GCs with increasing threshold (the blue curve Fig. 6F), each GC was resistant to becoming completely silent (green curve drop, Fig. 6F), owing to a few dominant inputs.

Notably, none of these metrics alone obviously tracked the U-shaped learning performance (Fig. 3A). However, collectively, these descriptive statistics of model GCL population activity set the stage for analyzing how information preprocessing by the basic GCL architecture relates to learning time series, explored below.

Improved Learning with GCL Transformations

With the knowledge that thresholding drives changes both in learning time series (Figs. 3 and 4) and in GC population metrics that are theorized to modulate learning (Figs. 5 and 6), we next directly investigated the relationships of these metrics to learning performance. To test this, we used LASSO regression to identify variables driving learning performance, taken from the metrics described in Figs. 5 and 6 (Fig. 7, A and C). We found that a three-term model using the most explanatory variables, STS, the number of explanatory PCs, and variance retained (Fig. 7, B, C, and D), accounted for 91% of learning variance. The three-term model performance is plotted against the observed MSE over a range of thresholds in Fig. 7D, showing strong similarity.

Although this model accounted for most learning, its performance was notably poorer at threshold ranges where the GCL-based learning was best. We reasoned that interactions between GCL statistical metrics might account for this deviation. To select potential metric interactions while constraining a regression model, we used Bayesian information criteria (BIC) stepwise regression to identify variables that accounted for learning (See methods for normalization methods; Fig. 7E). This model produced a better approximation of learning (Fig. 7F). We found that a handful of competing variables (i.e., pattern separation competing with retention of lossless representation) provided a small but crucial representation of learning, which offset the poor learning between thresholds of −1 to 1 in the purely linear model (Fig. 7D vs. Fig. 7F). Although these interaction components were necessary to produce the best fitting model for learning, the interactions were not the dominant regressors, as indicated by their relatively small β values, and PCs and population variance remained top features explaining learning, similar to the linear model.

These results were somewhat surprising given prior studies showing benefits of population sparseness or decorrelation to learning. We noted that with the GCL filter model we could not clamp specific population metrics to determine their contribution to learning, thus to interrogate this seeming disparity, we constructed fictive GCL population activity that had specific statistical features and used these as inputs to P-cells. Consistent with previous reports, decorrelation and temporal sparseness improved learning accuracy, with complete decorrelation and temporally sparse supporting the best performance (Supplemental Fig. S3; 64). Thus, on their own, population, temporal, and idealized spatiotemporal sparseness do modulate learning when their contribution is independent. Nevertheless, these features did not emerge as features driving learning using GCL output from OU inputs to learn time series. This discrepancy raises the possibility that the pattern separation metrics that drive learning may be dependent on MF input statistics.

GCL Properties That Enhance Learning in Naturalistic Tasks

Together, these models suggest that the GCL can reformat inputs in ways that support rapid and accurate time-series learning. We next asked whether the GCL metrics that drive best learning change when inputs were inherently matched to outputs. This question is motivated by the topographical modules that characterize the real cerebellum, each with associated specialized afferents (65, 66). Might these specialized afferents with specific statistical structure be especially suited to support P-cell tuning for specific behaviors?

To examine whether statistical features that drive learning are sensitive to intrinsic input-output relationships, we tested whether model inputs with naturalistic, behaviorally correlated statistics, derived from electromyogram (EMG) signaling could support learning movement kinematics. In this assay, “MF inputs” were EMG signals from human subjects performing a point-to-point reaching task. We tested whether the model could learn associated limb kinematics from this input (Fig. 8, A and B; 12, 57, 67, 68).

Consistent with our previous observations, model P-cell output better learned kinematic target functions when EMG inputs were preprocessed by the model GCL rather than fed directly to P-cells (Fig. 8A). Moreover, thresholds that supported best learning were comparable to those using OU functions as inputs (Fig. 8A vs. Fig. 3A) and the accuracy of the learned outputs strongly resembled the recorded kinematic positions (Fig. 8B). We observed a slight negative shift in thresholds supporting best performance using EMG, suggesting that GCL population statistics that retain more of their inherent relationship to kinematics (i.e., that the EMG alone predicted kinematics well), facilitated by lower threshold, might be beneficial to learning kinematics. However, some EMG-kinematic pairings had stronger intrinsic relationships than others. We used this variability to assay whether the strength of the intrinsic relationship influenced which population metrics supported best learning. We first identified which population statistics drove learning using RIDGE regression, which preserves even small contributions of regressor variables to the model. We then looked at the slope of regressors that predicted learning as a function of the MSE of MFs alone. We found that when the P-cell MSE was already low with direct MF inputs, the information retention (Fig. 5) emerged as a key predictor of learning (i.e., GCL MSE, Fig. 8C, green). Conversely, when MF-based learning was poor (high MSE), a pattern separation metric, number of explanatory PCs, became a more important driver of learning (Fig. 8C, orange). This observation is captured in the metric “Regression Coeff. Ratio” in Fig. 8C, which quantifies the coefficient of the variance retained or explanatory PC regressor divided by the sum of all regressor coefficients computed in the RIDGE regression. In effect, this method shows the normalized size of their impact on the regression. Together this suggests that different population statistical features of GCL reformatting may serve learning under different conditions. When intrinsic relationships are strong, the GCL’s preservation of MF input variance (variance retained) is an important population statistical feature; when MF activity is more arbitrary relative to what the P-cell needs to encode, explanatory PCs (a pattern separation feature) are more valuable for learning. Thus, “pattern separation” by the GCL is not one universal transform that has broad utility. This observation raises the possibility that regional circuit specializations within the cerebellar cortex, such as density of unipolar brush cells (37, 40), Golgi cells, or neuromodulators could bias GCL information reformatting to be more suitable for learning of different tasks.

DISCUSSION

Here, we asked a simple question: how does the cerebellar granule layer support temporal learning? The question of the function of GCL architecture has captivated theorists for decades, leading to a hypothesis of cerebellar learning that posits that the GCL reformats information to best suit associative learning in Purkinje cells. Recent work has called many of these foundational ideas into question, including the sparseness and dimensionality of GCL activity and what properties of pattern separation best support learning (23, 63, 69–71). To reconcile empirical observations with theory, we hypothesized that input statistics and task structures influence how the GCL supports learning. Here, we used naturalistic and artificial time-varying inputs to a model GCL and identified pattern-separation features that supported learning time series, with an arbitrary but temporally linked input-output mapping, recapitulating important features of physiological cerebellar learning tasks (33, 43, 72). Here, we attempt to bridge these findings by examining naturalistic challenges faced by the real circuit. Several important observations stemmed from these simulations: 1) with naturalistic input statistics, the GCL produces temporal basis sets akin to those hypothesized to support learned timing with minimal assumptions; 2) this reformatting is highly beneficial to learning at intermediate thresholds; 3) maximal pattern separation does not support the best learning; 4) rather, trade-offs between loss of information and reformatting favored best learning at intermediate network thresholds; and finally 5) different learning tasks are differentially supported by diverse GCL population statistical features. Together these findings provide insight into the granule cell layer as performing pattern separation of inputs that transform information valuable for gradient descent-like learning.

Emergence of Spatiotemporal Representation and Contribution to Learning

A perennial question in cerebellar physiology is how the granule cell layer produces temporally varied outputs that could support learned timing (3). Although cellular and synaptic properties have been shown to contribute (32–36, 38–40, 42, 44–49), we observed that with naturalistic inputs, temporal basis set formation is a robust emergent property of the feedforward architecture of the cerebellum coupled with a threshold-linear input-output function of granule cells receiving multiple independent time-varying inputs (Fig. 1, B–D). But is this reformatting beneficial to learning? We addressed this question by comparing learning of a complex time-series in model Purkinje cells receiving either mossy fibers alone or reformatted output from the GCL. We found that indeed the GCL outperformed MFs alone in all tasks (Figs. 3, 4, and 7). Nevertheless, we wondered what features of the population activity accounted for this improved learning. Although sparseness, decorrelation, dimensionality, and lossless encoding have been put forward as preprocessing steps supporting learning, we found that none of these alone accounted for the goodness of model performance. Rather, disparate pattern-separation metrics appear to strike a balance between maximizing sparseness without trespassing into lossy encoding space that severely, and necessarily, degrades learning of time series.

These observations are interesting in light of a long history of work on granule layer function. Marr, Albus, and others proposed that the granule cell layer performs pattern separation useful for classification tasks. In this framework, sparseness is the key driver of performance and could account for the vast number of granule cells. Nevertheless, large-scale GCL recordings unexpectedly showed high levels of correlation and relatively nonsparse activity (69–71). Despite methodological caveats, alternate recording methods seem to support the general conclusion that sparseness is not as high as originally thought (54, 73, 74). Indeed, subsequent theoretical work showed that sparseness has deleterious properties (23, 50), also observed in the present study, that may explain dense firing patterns seen in vivo. Here, we found that the best learning occurred when individual granule cell activity occupied around half of the observed epoch (Fig. 6F, blue trace), achieved with intermediate thresholding levels. We also observed temporal organization that is consistent with the firing patterns observed in vivo. Although these findings seem to suggest that sparseness is not the “goal” of GCL processing, our findings and others (23, 25) suggest that pattern separation broadly is a positive modulator of GCL support of learning processes.

Previous work proposed that time-series prediction was possible with access to a diverse set of geometric functions represented in the GC population (27). However, that study left open the question of how such a diverse collection of basis functions would emerge. The GCL model used here minimized free parameters by incorporating very few independent circuit elements, suggesting that a single transform is sufficient to produce a basis set which is universally able to learn arbitrary target functions. We used a simple threshold-linear filter with a singular global threshold that relied on sparse sampling to produce spatiotemporally varied population outputs. This simple function worked to support learning at a broad range of inputs and thresholding values, ultimately allowing the Purkinje cells downstream to associate the spatiotemporally sparser inputs with feedback to learn arbitrary and complex target functions. The emergence of this basis set is remarkable given the very simple assumptions applied, but is also physiologically realistic, given the simple and well characterized anatomical properties of the MF divergence and convergence patterns onto GCs, which are among the simplest neurons in the brain (17, 19, 75). Although we suggest that the key regulator of thresholding in the system is the feedforward inhibition from Golgi cells, many factors may regulate the transformation between input and GC output in the network, allowing for multiple levels and degrees of control over the tuning of the filter or real mechanism that controls the outcomes of GCL transformations. Golgi cell dynamics may prove critical for enforcing the balance between pattern-separation metrics and lossy encoding (76) and thus are critical players in mean thresholding found here to optimize learning. Additional mechanistic considerations may also play a role, including short-term synaptic plasticity (34, 77), network recurrence (78–81), and unipolar brush cells (37), allowing for a more nuanced and dynamic regulatory system than the one shown here.

Recapturing Input Information in the Filtered GCL Output

Two schools of thought surround what information is relayed to Purkinje cells through GCs. Various models assume that Purkinje cells inherit virtually untransformed MF information capable of explaining kinematic tuning in P-cells (61, 82, 83). This view is in contrast to suggestions of Marr and Albus, where the GCL sparsens information to such a degree that Purkinje cells receive only a small remnant of the sensorimotor information present in mossy fiber signals. These divergent views have never been reconciled to our knowledge. We addressed this disconnect by determining the fraction of MF input variance recoverable in GCL output. Interestingly, the GCL population retains sufficient information to recover more than 90% the input variance despite filtering out 50% or more of the original signal (Fig. 5). This information recovery is achieved at the population level and thus requires sufficient numbers of granule cells so that the subset of signals that are subthreshold are also superthreshold in other subsets of GCs through probabilistic integration with other active inputs. Although variance recovery is not a true measure of mutual information, it is indicative of the utility of the intersectional filtering performed by the GCL. The expansion of representations in the GCL population achieved by capturing the coincidence of features in the input population creates a flexible representation in the GCL output that has many beneficial properties, including the preservation of information through some degree of preserved mutual information between the GCL and its inputs. Yet despite this retention of input variance by the GCL, its transformations nevertheless greatly improve learning.

Faster Learning

Our model not only improved learning accuracy but also speed, compared with MFs alone (Fig. 4). Both learning speed and accuracy progressed in tandem; threshold parameter ranges that enhanced overall learning speed also minimized mean-squared error, suggesting that speed and accuracy are enhanced by similar features in GCL output. Learning speed was well described by a double exponential function with a slow and fast component. This dual time course in the model with only one learning rule is interesting in light of observations of behavioral adaptation that also follow dual time courses (1, 84). Some behavioral studies have postulated that these time courses suggest multiple underlying learning processes (10). Our model indicates that even with a single learning rule and site of plasticity, multiple time courses can emerge, presumably because when error becomes low, update rates also slow down.

Another observation stemming from simulations studying learning speed was that the behavior of the model varied as a function of the learning “step size” parameter of the gradient descent method (Supplemental Fig. S2). The step size, i.e., the typically small, scalar regulating change in the weights between GCs and P-cells following an error, determined the likelihood of catastrophically poor learning. When the step size was too large, it led to extremely poor learning because the total output “explodes” and fails to converge on a stable output. Nevertheless, the model tolerated large steps and faster learning under some conditions, since the threshold also influenced the likelihood of catastrophic learning. Generally, higher thresholds prevented large weight changes from exploding, suggesting that sparse outputs may have an additional role in speeding learning by supporting larger weight changes in Purkinje cells. Indeed, appreciable changes in simple spike rates occur on a trial-by-trial basis, gated by the theorized update signals that Purkinje cells receive, climbing fiber-mediated complex spikes. These plastic changes in rate could reflect large weight updates associated with error. Moreover, graded complex spike amplitudes that alter the size of trial-over-trial simple spike rate changes suggest that update sizes are not fixed (82, 85, 86). Thus, although gradient descent is not wholly physiological, this finding predicts that the amplitude of synaptic weight changes following a complex spike might be set by tunable circuitry in the molecular layer to optimize learning speed relative to the statistics of the GCL output.

Together, this study advances our understanding of how the GCL may diversify time-varying inputs and informs interpretation of empirical results. For instance, the time course of learning varies widely across tasks. Eyeblink conditioning (EBC) paradigms require hundreds of trials to learn (87–89), whereas saccade adaptation and visuomotor adaptation of reaches (90, 91), require just tens of trials (11, 68, 92, 93). A prediction from our study is that the temporal diversity of the GCL basis set during a behavior influences learning speed. Time-invariant cues such as those seen in EBC would be difficult, if not impossible, for our model GCL to reformat and sparsen, as they are incompatible with thresholding-based filtering of input signals. Supportive of this view, recent work showed that EBC learning was faster if the animal is locomoting during training (94). We hypothesize that naturalistic time-variant signals associated with ongoing movements entering the cerebellum support robust temporal pattern separation in the GCL, enhancing learning accuracy and speed, whereas time-invariant associative signals used in typical classical conditioning paradigms result in an impoverished “basis,” making learning more difficult, despite other circuit elements that may contribute to the GCL basis formation.

DATA AVAILABILITY

All computer code and simulation data is freely available at https://github.com/jesse-gilmer/2022-GCL-Paper.

SUPPLEMENTAL DATA

Supplemental Figs. S1–S3: https://doi.org/10.6084/m9.figshare.21763943.v1.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke (NINDS) NRSA NS113409 Grant to J. I. Gilmer; National Institute of Biomedical and Bioengineering (NIBIB) Grant R01EB029847 to Z.K.; and NINDS Grant NS114430, NSF CAREER grant 1749568, and the Simons Foundation as part of the Simons-Emory International Consortium on Motor Control to A. L. Person.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.I.G., M.A.F., Z.K., and A.L.P. conceived and designed research; J.I.G., M.A.F., Z.K., I.D., and J.D.C. performed experiments; J.I.G., M.A.F., Z.K., and I.D. analyzed data; J.I.G., M.A.F., Z.K., and A.L.P. interpreted results of experiments; J.I.G., M.A.F., and Z.K. prepared figures; J.I.G. M.A.F., Z.K, and A.L.P. drafted manuscript; J.I.G., M.A.F., Z.K., and A.L.P. edited and revised manuscript; J.I.G., M.A.F., Z.K., I.D., J.D.C., and A.L.P. approved final version of manuscript.