Abstract
Genetic sequences collected over time provide an exciting opportunity to study natural selection. In such studies, it is important to account for linkage disequilibrium to accurately measure selection and to distinguish between selection and other effects that can cause changes in allele frequencies, such as genetic hitchhiking or clonal interference. However, most high-throughput sequencing methods cannot directly measure linkage due to short-read lengths. Here we develop a simple method to estimate linkage disequilibrium from time-series allele frequencies. This reconstructed linkage information can then be combined with other inference methods to infer the fitness effects of individual mutations. Simulations show that our approach reliably outperforms inference that ignores linkage disequilibrium and, with sufficient sampling, performs similarly to inference using the true linkage information. We also introduce two regularization methods derived from random matrix theory that help to preserve its performance under limited sampling effects. Overall, our method enables the use of linkage-aware inference methods even for data sets where only allele frequency time series are available.
Keywords: statistical inference, selection coefficients, genetic linkage, short-read data, allele frequency time series, covariance estimation
Introduction
Identifying molecular causes of population adaptation is a key problem in evolutionary biology. Examples include identifying cancer driver mutations that confer growth advantages to tumor cells (Bignell et al. 2010; Burrell et al. 2013; Landau et al. 2013), detecting mutations that help viruses like HIV-1 evade immune control (Phillips et al. 1991; Rambaut et al. 2004; Allen et al. 2005), and characterizing mutations that enable drug resistance in pathogens (Wu and Wilson 2017). A better understanding of such evolutionary processes can also aid in the development of new therapies to prevent or treat disease (McMichael et al. 2010; Neher et al. 2016; Łuksza et al. 2017; Lee et al. 2018). For example, understanding effects of adaptive mutations in the seasonal human influenza virus helps predict the evolution of the viral population from one year to the next, which can improve vaccine selection (Luksza and Lässig 2014).
Recent advances in genetic sequencing technologies have provided a wealth of new data for evolutionary studies. Genetic time-series data (i.e. sequences sampled over time from a population), in particular, directly interrogates evolutionary histories and offers a powerful window into the dynamics of evolution. Genetic time-series data can be collected from time-resolved global evolutionary records (Bao et al. 2008; Lee et al. 2022), sampled from naturally infected hosts (Zanini et al. 2015; Xue et al. 2017), or generated in the lab through evolve-and-resequence (E&R) experiments in which samples from a population are repeatedly sequenced over time under controlled conditions (Barrick et al. 2009; Long et al. 2015).
However, it is difficult to infer which specific alleles have the largest effects on fitness. Genetic linkage (i.e. the correlation between alleles at different locations on the genome due to shared inheritance) makes it challenging to sort out the individual effects of alleles that are linked or correlated. Inferences that ignore linkage disequilibrium (LD) can be misleading because they do not account for the effects of the genetic background. For example, when a neutral or deleterious allele occurs together with other strongly beneficial ones, their net effect can still be beneficial. In such cases, the neutral or deleterious allele can rise to a high frequency in the population, known as hitchhiking (Smith and Haigh 1974). Genetic linkage can also result in clonal interference (Gerrish and Lenski 1998), where subpopulations with different beneficial genetic alleles compete, and background selection (Charlesworth 1994), where neutral alleles are purged by negative selection on other deleterious alleles on the same genetic background. It is therefore important to account for LD in order to accurately quantify fitness contributions from individual alleles in complex evolving populations.
Inference methods that account for genetic linkage have been developed (Illingworth and Mustonen 2011; Illingworth et al. 2014; Terhorst et al. 2015; Sohail et al. 2021). However, these methods require the knowledge of how different alleles are linked, or even full haplotype frequencies, which may be unavailable due to sequencing constraints. To identify haplotypes present in the population, single cells would need to be sequenced individually, which would be of low throughput due to high costs. An alternative high-throughput and cost-effective approach is to sequence DNA/RNA from pools of individuals using next generation sequencing (NGS) techniques (Anand et al. 2016). To achieve high throughput, NGS technology generally involves randomly breaking genomes into smaller sizes (<1,000 bases) and sequencing a massive amount of these fragments in parallel (Metzker 2010). The generated short reads are then mapped to the genome, providing estimates for all individual allele frequencies in a population. However, it is not generally possible to unambiguously identify full haplotypes or even complete maps of LD from short reads (Lynch et al. 2014).
Given that limited information in genetic data is common, efforts have been made to reconstruct linkage patterns or haplotype frequencies from the available data. Various methods have been developed to reconstruct haplotype sequences and estimate their relative frequencies from short-read sequence data generated by NGS techniques (Beerenwinkel et al. 2012). However, they typically rely on linkage preserved within each short read and overlaps among the reads to assemble them into haplotype sequences that span the entire genomic region of interest. For example, read graph-based methods for haplotype reconstruction involve aggregating the reads in a read graph and subsequently identifying haplotypes as paths in this graph (Bansal and Bafna 2008; Eriksson et al. 2008; Zagordi et al. 2011). The LDx method uses an approximate maximum likelihood approach to estimate the measure (Hill and Robertson 1968) of LD between pairs of single nucleotide polymorphisms (SNPs) that are observed within and among single reads with sufficient read depth (Feder et al. 2012).
Other methods do not rely on read data and take only allele frequencies as input. However, the linkage/haplotype reconstruction problem is impossible to solve with only allele frequencies taken from a single time point. Hence, they typically require time-series data which encode dynamics of the evolution. For example, haploSep uses time-series allele frequency data to infer haplotype information and is computationally faster than methods that rely on read data (Pelizzola et al. 2021). However, it is designed to infer stable haplotype structures that do not change much over time. The haploReconstruct method (Franssen et al. 2017; Barghi et al. 2019) targets haplotype reconstruction problems in experimental evolution during which variants present in founder population are selected to rise in frequency. Another method, Evoracle, is a machine learning method that reconstructs full-length haplotype frequencies, trajectories, and fitness from time-series allele frequency data (Shen et al. 2021). However, it is designed for data generated from directed evolution campaigns, which feature strong selection and low haplotype diversity.
Here we present a simple, generic method to estimate time-varying LD statistics from time-series allele frequencies. By studying how allele frequencies change in time, we can detect correlations between different alleles. Alleles that have correlated changes in frequency are likely to be on the same genetic background, while anticorrelated alleles are likely to compete with each other on different backgrounds. We use these relationships to estimate the allele frequency covariance matrix, commonly expressed as the LD matrix (Hedrick 1987). Our reconstruction approach can then be combined with inference methods such as marginal path likelihood (MPL) (Sohail et al. 2021) to infer fitness effects of individual alleles. Our method thus fills the gap between the lack of covariance information from pool-sequenced data and inference methods that use covariance to accurately estimate the fitness effects of mutations.
Simulations show that our method successfully reconstructs patterns of LD from limited data. This reconstruction leads to accurate inferences that can nearly match the performance of estimators that use complete, true linkage information. Reconstruction is more difficult when data are sampled infrequently in time, but this difficulty can be overcome with novel regularization methods and by combining data from multiple replicates. Overall, our method provides a way to extend the excellent performance of fitness estimation methods that rely on complete sequence data to short-read data, even in cases where no linkage information is preserved.
Methods
Estimating LD
Given time-series allele frequency data taken from an evolving population, we aim to reconstruct pairwise LD statistics among all alleles. Specifically, our goal is to estimate the allele frequency covariance matrix throughout the evolution.
To explore the connection between allele frequencies and covariance in a quantitative manner, we consider the Wright–Fisher (WF) model with mutation, selection, and recombination for a population consisting of individuals (Ewens 2012). The WF dynamics models an evolving population as a discrete-time Markov chain where haplotype frequencies, , in generation are derived by sampling with replacement from haplotypes in generation , i.e.
| (1) |
where is the probability of observing haplotype at generation , including the effects of selection, mutation, and recombination. For clarity, we use to refer to locus indices and to refer to haplotype indices. For simplicity, we assume that alleles are binary, taking on values of either 0 (wild-type (WT)) or 1 (mutant) at a particular locus, and that selection is additive. We further assume that the population size is large, and that selection coefficients, mutation rates, and recombination rates (per site per generation) are small (). Expanding to leading order in , one can then show that the expected product of changes of two allele frequencies and at loci and at time is proportional to the covariance of the allele frequencies and the population size (Supplementary File):
| (2) |
where
| (3) |
| (4) |
Here is the frequency of haplotypes in the population with mutant alleles at sites and at time . Given the connection between covariances and changes in allele frequencies demonstrated in equation (2), we explored whether empirical changes in allele frequencies could be used to estimate the unknown covariance matrix . This is equivalent to the LD measure (Hedrick 1987).
In a given data set, we only have one realization of for each time point and each pair of alleles. Therefore, it is not possible to compute the expectation directly. However, if we assume that the covariance does not change dramatically in a short time, it is plausible to use the mean value of in a time window around time as an estimate of its expectation at time . Multiplied by , this gives an estimate of . This estimate can be expressed as
| (5) |
where the time window, denoted as , includes a total of time points. Intuitively, a trade-off is expected when tuning the time window. A larger window includes more values of at neighboring time points, hence more reliably yields a mean closer to the expectation value. However, covariance can change on short time scales as recombination and/or mutation break down LD, or as selection drives alleles to fixation or extinction. Past work has shown that covariances in allele frequency changes can decay over the course of tens of generations (Buffalo and Coop 2020). Therefore, by including time points far away from the time currently considered, the expectation value will deviate from .
In principle, variance terms could be estimated following equation (5), but they can also be readily calculated from the observed allele frequencies. We use the difference between estimated and calculated variances to normalize the current estimate for improved accuracy. Specifically, we rescale the estimated covariance matrix with an anisotropic scaling matrix . After rescaling, estimates of variances are equal to calculated ones, and estimates of covariances are adjusted by
| (6) |
By normalizing the initial estimates with calculated variances, this step also makes it unnecessary to know the population size , which may be difficult to obtain or estimate in real data.
MPL inference
MPL (Sohail et al. 2021) is a framework for statistical inference of selection from evolutionary histories. While originally developed in the context of population genetics, this framework has also been recently applied to study disease transmission in epidemiological models (Lee et al. 2022). The main idea of this approach is to estimate a set of selection coefficients for individual alleles that best explain an observed evolutionary history, in the sense that these selection coefficients maximize the posterior probability of the data. Even for the WF model, the complexity of the likelihood makes this a difficult problem to solve exactly. However, following the assumptions above (additive and weak selection, mutation, and recombination), under the diffusion approximation (Ewens 2012), the probability of an evolutionary history or “path” is straightforward to write down. While this probability is a complicated function of the haplotype frequencies, it is a simple Gaussian function of the selection coefficients.
Applying Bayes’ theorem then leads to an analytical expression for the maximum a posteriori (MAP) estimate of selection coefficients. For time-series genetic data sampled at times , the MAP solution provided by MPL is
| (7) |
where , is the mutation rate, is the vector of mutant allele frequencies at time , is the mutant frequency covariance matrix at time , and is a multiple of the identity matrix serving as a regularization term. In a Bayesian sense, the regularization term can be interpreted as a Gaussian prior distribution over the selection coefficients with zero mean and variance. A prior of strength is applied by default, which slightly constrains magnitudes of inferred selection coefficients and helps to ensure that the matrix term is invertible. A more detailed introduction to MPL can be found in the Supplementary File.
Regularization
Ideally, in equation (7) should be the allele frequency covariance matrix computed from all individuals in the population at time . However, in real data sets we only have the sample covariance matrix, which is computed from a subsample of the whole population. Performance is therefore limited by finite sampling effects. Regularization is often used to alleviate the influence of noisy input in inference algorithms. Below, we examine methods for covariance estimation originally developed for high-dimensional statistics.
Estimation of population covariance matrices is a fundamental problem in statistics (Ledoit and Wolf 2020). In classical statistical settings, with a limited number of variables and a large sample size , the sample covariance matrix is a good estimator of the population covariance matrix. However, it will be insufficient or misleading in the high-dimensional limit, when is of the same order of magnitude as . An extreme case is that if , the sample covariance matrix will be singular. Genetic data may often fall into this limit, because when data are limited, the number of sequences observed can be of the same order of magnitude as the number of mutant alleles. Various “shrinkage estimators” (i.e. estimators that reduce the effects of sampling noise) have been proposed aiming for better estimation of the population covariance matrix (Ledoit and Wolf 2020). Given the similarity of both contexts, we applied two methods, linear shrinkage and nonlinear shrinkage, to regularize our estimate of the sample covariance matrix in order to improve inference results with finitely sampled data.
Linear shrinkage on the covariance matrix
Ledoit and Wolf proposed a shrinkage estimator for covariance estimation which asymptotically minimizes the mean-squared error between the inferred and true covariance in the high-dimensional limit (Ledoit and Wolf 2004). It has a simple form, a linear combination of the sample covariance matrix with the identity matrix, and behaves well with finite sampling as shown in simulations (Ledoit and Wolf 2004). We refer to this method as linear shrinkage hereafter. Linear shrinkage coincides with the regularization term in equation (7). As noted before, we use a value of by default. A stronger prior (i.e. larger ) can help suppress improbably large magnitudes of inferred selection coefficients caused by noise from finite sampling and our estimation process.
Nonlinear shrinkage on the correlation matrix
A common model to analyze covariance in the high-dimensional limit is the spiked covariance model (Johnstone 2001), which assumes the population covariance has a fixed number, say , of eigenvalues larger than 1 (spikes) and all other eigenvalues equal to 1. In the null case where , the population covariance matrix becomes the identity matrix. However, the empirical distribution of the sample eigenvalues converges as to a nondegenerate absolutely continuous distribution, the Marčenko–Pastur law (Marčenko and Pastur 1967). The distribution, or bulk, is supported on a single interval, whose limiting bulk edges are given by
| (8) |
where is the asymptotic ratio between number of variables and number of samples when they both go to infinity, i.e. as . Donoho et al. showed that in this model, the optimal estimation of the population covariance matrix from a sample covariance matrix relies on the design of an optimal shrinker that acts elementwise on the sample eigenvalues (Donoho et al. 2018). The strength of each shrinker is tuned by the asymptotic ratio . The shape of the optimal shrinker is determined by the choice of a loss function, which measures similarity between the population covariance and sample covariance. Optimal shrinkers have been derived for a number of loss functions, including the Frobenius norm and nuclear norm (defined in Supplementary Equation S4) of , , , , and (Donoho et al. 2018).
The integrated population covariance matrix ( in equation (7)), in our case, does not directly resemble the spiked covariance model. At the least, alleles do not share the same variance, so that even if all sites evolved independently, the eigenvalues of our population covariance matrix would not all be equal. However, the corresponding correlation matrix could fit into this model. When data are limited, we assume that most correlation signals are indistinguishable from correlation induced by noise from random sampling and other sources, so that only a few prominent signals reflecting the spike eigenvalues of the population correlation matrix can be picked up on top of noise. We apply the optimal shrinkers proposed in Donoho et al. (2018) to our correlation matrix, which we denote by to distinguish it from the covariance matrix, then adjusting our estimate of the sample covariance matrix accordingly. In our context of shrinking eigenvalues of the estimated correlation matrix, neither the selection of the optimal loss function nor the regularization strength are obvious. We therefore tested a variety of possibilities.
In summary, we considered the following steps for nonlinear regularization:
Compute our estimate of the mutant allele correlation matrix from the estimate of covariance matrix . , where is a matrix with only sample variances on the diagonals, for .
Choose a loss function and a regularization strength , and apply the corresponding optimal shrinker as proposed in Donoho et al. (2018) on our estimate of the correlation matrix , yielding a shrunk estimate .
Transform the shrunk estimate back to an estimate of the covariance matrix, .
Results
We first describe the simulated data used to benchmark performance of our method. We then present its performance with complete or finitely sampled data. We further test how two kinds of regularization methods can help preserve the method’s performance when data are limited. We also show that inference can be greatly improved by combining observations from multiple replicates. Finally, we present an example application to a real experimental evolution data set.
Evolutionary simulations
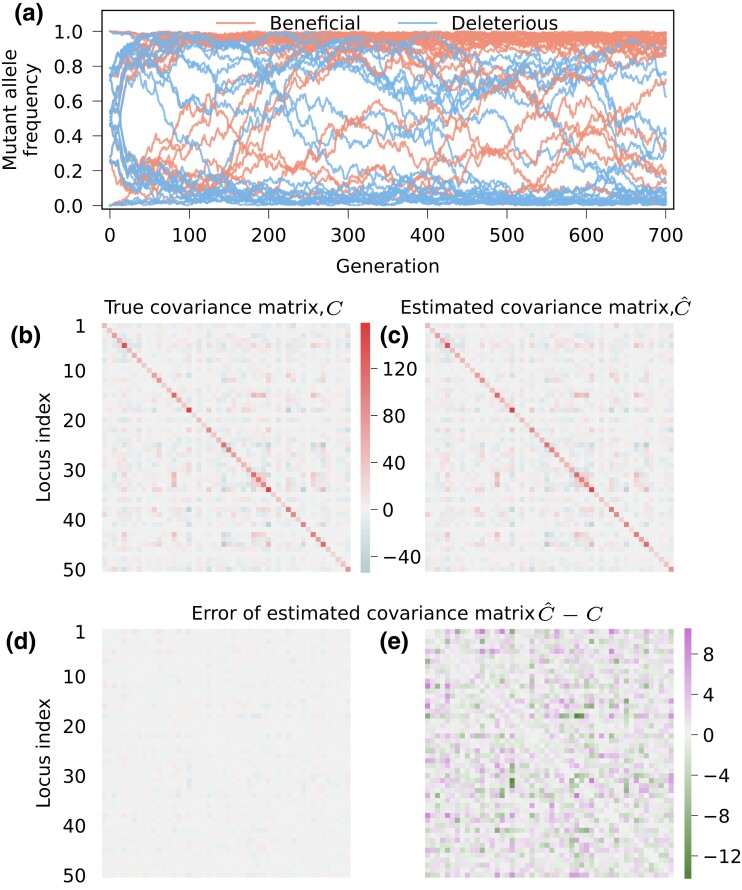
To benchmark the performance of our method, we generated artificial time series sequence data by simulating evolution as a WF process. We considered an evolving population of 1000 sequences with 50 bi-allelic (WT or mutant) loci. We used 10 different sets of selection coefficients (see Supplementary Fig. S1) and simulate 20 replicates of data for each set, totaling 200 simulations. In each simulation, the population started from a composition of four haplotypes and evolved for 700 generations. The mutation rate was set as per locus per generation, which generated around mutation events for each simulation. Figure 1a shows an example of simulated mutant allele frequency trajectories. To test the effect of recombination, we performed another 200 simulations with the same setup as above with a recombination probability of per site per generation. More detailed settings of the simulations can be found in Supplementary File.
Fig. 1.
Linkage information is accurately recovered from trajectories of mutant allele frequencies exhibiting complex dynamics in a WF simulation. (a) A population of 1,000 individuals was simulated to evolve for 700 generations under WF dynamics, starting from a mixed population of four haplotypes. The sequences have 50 sites where the loci were assumed to be bi-allelic (WT or mutant). Mutation rate was set as per locus per generation. The simulation plotted here used the fifth set of selection coefficients, which are drawn from a trimodal distribution, a combination of three Gaussian distributions with standard deviation of 0.01, centered at 0.03, 0, and 0.03, respectively (see Supplementary Fig. S1). For this simulation, we show (b) the true covariance matrix, (c) our estimate of it, and (d) error of our estimation integrated over 700 generations throughout the simulation. Error of estimation is shown on a smaller scale in (e). The estimated covariance matrix was calculated following equation (5) using a window of , and then normalized by equation (6). Terms of the error matrix have much smaller magnitude than those of true and estimated ones, indicating that the linkage information is accurately recovered.
Recovery of linkage information
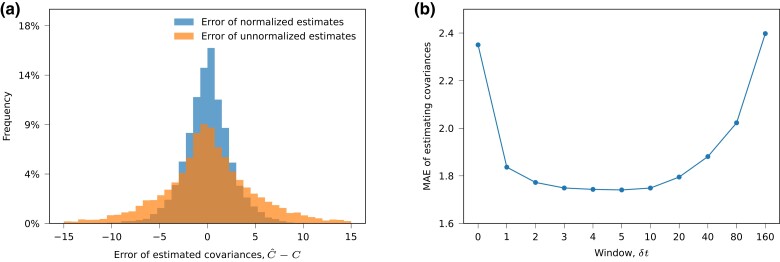
As shown in Fig. 1, our method is typically able to accurately reconstruct linkage information from allele frequency trajectories. In general, we find that normalizing estimates of the covariance matrix (see equation (6)) is important to reduce errors (Fig. 2a). We also find that there exists a wide range of time windows () over which the mean absolute error (MAE) in the estimated covariances is low, showing that estimation of linkage information is not very sensitive to the choice of the window size (Fig. 2b).
Fig. 2.
Normalization and choosing a proper time window are important for the accurate estimation of linkage information. (a) Plots the distribution of error of estimated covariance with and without normalization (see equation (6)). (b) Shows MAE of normalized estimation with different time windows. The data used in these plots are collected from 10 simulations, each with a different set of selection coefficients.
Recovery of linkage information is more challenging with finitely sampled data. Real data contain only reads from a small portion of all individuals in a population and are not typically sampled at every generation. With shallower sampling and larger time intervals between samples, noise becomes more dominant in the estimated covariance matrix. We use two regularization methods, linear shrinkage and nonlinear shrinkage, to alleviate the influence of noise. Supplementary Fig. S2a compares the true covariance matrix with the estimated covariance matrices with and without regularization for the simulation in Fig. 1a, using data sampled every 10 generations with 100 sequences per sample. Although both regularization methods have minor effects on off-diagonal terms of the estimated covariance matrix, they greatly reduce the magnitudes of entries of the inverse of the estimated covariance matrix (Supplementary Fig. S2b). In the MPL framework (equation (7)), the inverse of the covariance matrix is critical for the inference of the underlying selection coefficients. The noisy covariance matrices have larger entries when inverted, which leads to the inference of improbably large selection coefficients. Regularization helps to control this issue. We explore factors affecting successful inference of selection coefficients in the next section below.
Recovery of underlying selection coefficients
Here we investigate the degree to which the estimated linkage information be used to improve the inference of selection. To test the inference of selection, we first infer allele frequency covariance matrices as described above. We then use the estimated allele frequency covariance matrices in equation (7) to infer selection coefficients.
Normalization and choice of window size
As for the estimation of linkage, we find that normalization of the estimated covariance matrices leads to better inferred selection coefficients (Supplementary Fig. S3). We also found a wide range of window sizes that lead to good performance for inferred selection coefficients (Supplementary Fig. S4). Unsurprisingly, larger window sizes were more helpful when data were sparse. However, unlike the direct estimation of linkage information, we found that the accuracy of inferred selection coefficients did not decline for very large window sizes, up to the maximum value of that we tested. Considering the effects of the window size on both estimating linkage and inferring selection coefficients, we chose as a default value of the window size with uniformly good performance.
Benchmarking against alternative models
To test our ability to use estimated covariance information to improve selection inferences, we compared our method against two extreme limits. All three methods use MPL’s inference framework, but with different covariance matrices in equation (7). Our (naive) method, referred to as Est, uses the normalized estimate of the covariance matrix with the time window set to and the regularization strength . Later, we consider modified versions of this method using additional linear or nonlinear regularization. One comparison method, referred to as MPL, uses the true population matrix , which is not available in real pool-sequenced data and can be viewed as an ideal limit for perfect performance. The other comparison method, referred to as single locus (SL), assumes no LD and uses a matrix with only variance information, with for . Performance of SL serves as a lower bound: when Est performs worse than SL, it is better to simply ignore LD than to try to estimate it with our approach.
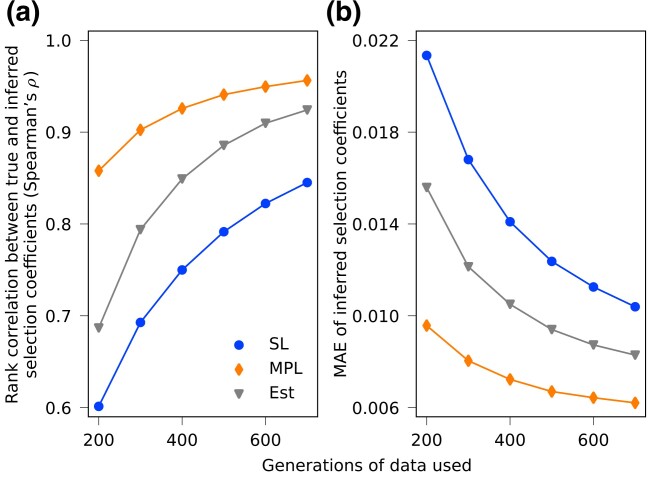
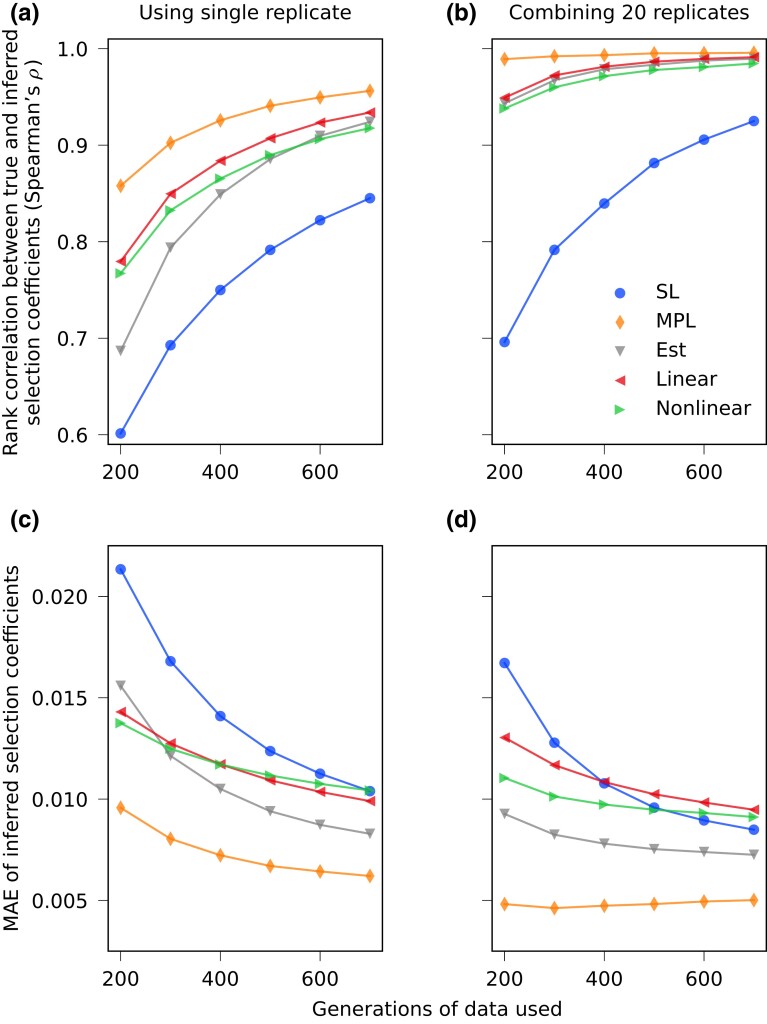
We first applied the three methods to complete simulated data using all 1,000 sequences at each generation. Figure 3 shows the performance of these methods using evolutionary trajectories of different lengths. When all data are available, our method reliably outperforms SL, which demonstrates the potential benefit of incorporating estimated covariance information to account for LD. In these tests, and throughout the paper, we do not assume that there is prior knowledge about which alleles are under selection. All alleles are treated equivalently. Supplementary Fig. S5 compares inferred selection coefficients with the true values for the simulation example plotted in Fig. 1a, including those inferred by regularized methods (introduced in later sections).
Fig. 3.
Estimated covariance can improve inference of selection coefficients with ample data. (a) Spearman’s rank correlation coefficients and (b) MAE between inferred and true selection coefficients are shown, using different lengths of data, averaged over 200 simulations with same setup as shown in Fig. 1a. With ample data, the Est method performs reliably better than the SL method at all lengths, demonstrating that inference can be improved with estimated linkage information.
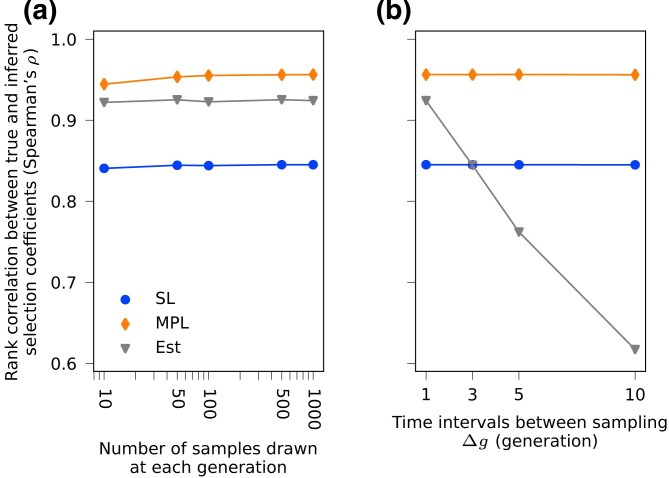
Selection inference with finitely sampled data
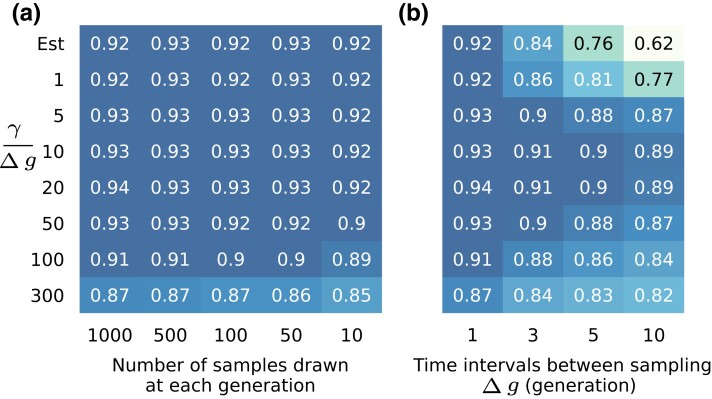
To test its robustness against finite sampling effects, we applied our method on data with different sampling depths and sampling time intervals (Fig. 4). We find our method to be generally robust against sampling with small numbers of sequences. Performance remains robust even with only samples from 10 individuals per generation. However, naive inference with estimated linkage information is quite sensitive to the time interval between samples. For the data sets considered here, performance of Est becomes worse than SL when samples are taken five or more generations apart. As we show below, this sensitivity to sampling times can be alleviated with different forms of regularization or by combining data from multiple replicates.
Fig. 4.
Performance is robust to sampling depth but sensitive to sampling time interval. (a) Spearman’s rank correlation coefficients between inferred and true selection coefficients averaged over 200 simulations with same setup as shown in Fig. 1a are compared with different sampling depths. The sampling time interval is 1 generation here. All three methods are robust against shallower sampling depths. (b) The same metrics (Spearman’s ) compared with different sampling time intervals. At each sampling time point all 1,000 samples in the population are used here. The Est method is more sensitive to larger sampling time intervals compared to the MPL and SL methods, and performs worse than the SL method as time interval increases to five generations and above.
Regularization improves selection inference
Figure 5 shows that appropriately chosen linear regularization (also equivalent to a Gaussian prior on the selection coefficients) can lead to significantly better inferred selection coefficients. Even when the time between samples becomes larger, regularization results in better recovery of inferred selection coefficients than SL. In general, stronger regularization is needed when sampling is more limited, especially when becomes large. We found that a regularization strength of yields consistently good performance across data sets and different levels of sampling.
Fig. 5.
Linear shrinkage can improve performance under limited sampling. Spearman’s rank correlation coefficients between inferred and true selection coefficients, averaged over 200 simulations with the same setup as shown in Fig. 1a, are shown using different strengths of linear shrinkage, with (a) different sampling depths and (b) different sampling time intervals. Linear shrinkage of a proper strength improves inference results of our method. When the sampling time interval gets larger, the optimal strength increases as well, which is why we choose the -axis to be , the linear shrinkage strength divided by the sampling time interval. We find that a strength of 10 times time interval, , yields the highest Spearman’s consistently.
We also tested a wide range of nonlinear regularization methods (i.e. those derived using loss functions for the Frobenius norm or nuclear norm of , , , , and ) as well as values of the regularization strength , ranging from to . Performance is compared in detail in Supplementary Fig. S6. While different choices for the loss function tend to yield very similar results, we find that the loss function of the Frobenius norm of combined with a small regularization strength yields near-optimal results across all sampling variations. Like the linear case, nonlinear regularization also improves upon SL even with longer gaps between samples.
Performance of the linear and nonlinear regularization methods is compared in detail in Supplementary Figs. S7 and S8. While the naive Est method could suffer from limited sampling, the two regularization methods stably preserve performance in terms of Spearman’s . Both SL and regularization methods have larger MAE for inferred coefficients. However, the causes are different. For methods that employ regularization, the regularization can systematically shrink selection coefficients toward zero, although the relative magnitudes of the inferred coefficients are roughly correct. Here we accept underestimation of magnitudes of selection coefficients as a trade-off in order to alleviate finite sampling effects that would otherwise make it difficult to correctly infer the relative order of selection coefficients. Supplementary Fig. S5 provides an example showing the typical extent to which inferred selection coefficients are shrunk toward zero. This depends on the strength of the regularization, with stronger regularization resulting in more shrinkage. For SL, large errors are typically due to noise, where the inferred coefficients may not be properly ranked.
On average, linear shrinkage tends to perform very slightly better than nonlinear methods when the time interval between samples is small. However, the regularization strength for the linear method needs to be tuned for optimal performance. For large sampling intervals, the linear regularization strength needed to achieve optimal rank correlation between the true and inferred selection coefficients increases in proportion to , which results in extremely small magnitudes for inferred selection coefficients, reflected in the large MAE at larger time intervals (Supplementary Fig. S8e). For these reasons, nonlinear regularization is likely the best choice for arbitrary inference problems. Here we found that one loss function and regularization strength yields near-optimal performance for nonlinear regularization across all data sets and sampling variations.
Effect of recombination on inference
In the tests described above, we assumed no recombination. To test the potential influence of recombination, we performed another 200 simulations with recombination. In these simulations, we used a recombination probability of per locus per generation, while all other parameters remained the same. Thus, each simulation had around mutation events and around recombination events. More details are described in Supplementary File. Recombination acts to break up linkage, slightly improving performance for all approaches. However, the overall relative performance of various methods on selection inference is consistent with those evaluated on simulated data without recombination (Supplementary Figs. S9 and S10).
Combining multiple replicate data
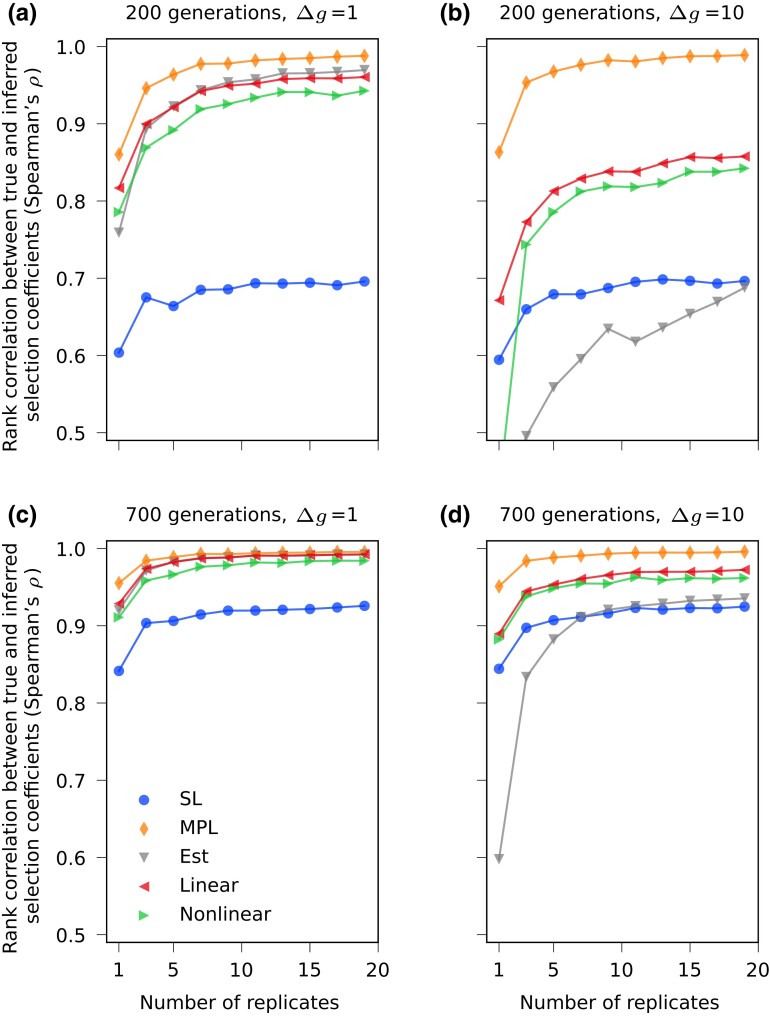
We define replicates as multiple instances of time-series data of an evolving population driven by the same set of selection coefficients. Here we perform 20 WF simulations for each set of selection coefficients with the same initial distribution of four founder haplotypes, yielding 20 replicates. In real data, multiple replicates could represent, for example, data from evolutionary experiments performed under the same conditions, or the history of pathogen evolution during different isolated outbreaks. We find that our ability to recover selection coefficients can be greatly boosted by combining data from multiple replicates. Figure 6 compares the accuracy of inferred selection coefficients using either a single replicate or multiple ones. When 20 replicates are combined, our method achieves virtually the same performance as using true covariance information even without additional regularization. Figure 7 shows how performance improves as we gradually increase the number of combined replicates. We find that the performance of regularized methods (linear-cov and nonlinear-corr) generally converges with 5–10 replicates. More replicates are needed when the length of data is shorter and when the sampling time interval becomes larger.
Fig. 6.
Performance can be greatly improved by combining data from multiple replicates. Spearman’s rank correlation coefficients and MAE between inferred and true selection coefficients, averaged over 200 simulations with same setup as shown in Fig. 1a, are shown (a,c) when using a single replicate, and (b,d) when combining 20 replicates. The inference using true covariance, and using our estimated covariance (with or without regularization), are dramatically improved when combining multiple replicates’ observations. In contrast, the performance of SL does substantially improve with additional replicates.
Fig. 7.
Performance improves as the number of combined replicates increases. Spearman’s rank correlation coefficients between inferred and true selection coefficients averaged over 200 simulations with same setup as shown in Fig. 1a are shown as we increase the number of combined replicates under different limited sampling effects. The performance of regularized methods (linear-cov and nonlinear-corr) generally converges with 5–10 replicates. More replicates are needed when the length of data is shorter and when the sampling time interval is larger.
We also tested effects of combining multiple replicate data with the same selection coefficients but different founder haplotypes, shown in Supplementary Fig. S11. For each set of selection coefficients, 20 replicate simulations are combined, each starting with four random founder haplotypes. Individuals in the initial population are randomly distributed across founder haplotypes. Consistently, we find that performance on selection inference is improved. In contrast to what we found in cases with the same initial population, SL can also benefit substantially from combining multiple replicates. This is reasonable because variation in initial populations weakens the LD induced by a specific set of founder haplotypes and alleviates the need to disentangle the selective effects of individual mutations.
Benchmarking against haplotype reconstruction methods on simulated data
Methods that reconstruct haplotypes and time-series haplotype frequencies from short-read data can also provide covariance information that can be used for selection inference. For comparison with our method, we tested two haplotype reconstruction methods that take allele frequency time series as input, haploSep (Pelizzola et al. 2021) and Evoracle (Shen et al. 2021), on the simulated data. Compared to these approaches, our method more accurately recovers true LD statistics (Supplementary Fig. S12). We also find that our approach yields more accurate inferred selection coefficients from these data (using the inferred LD statistics in equation (7); Supplementary Fig. S12). These results may be due in part to the complexity of our simulation setup, which makes the haplotype reconstruction problem more challenging.
Application to experimental directed evolution data
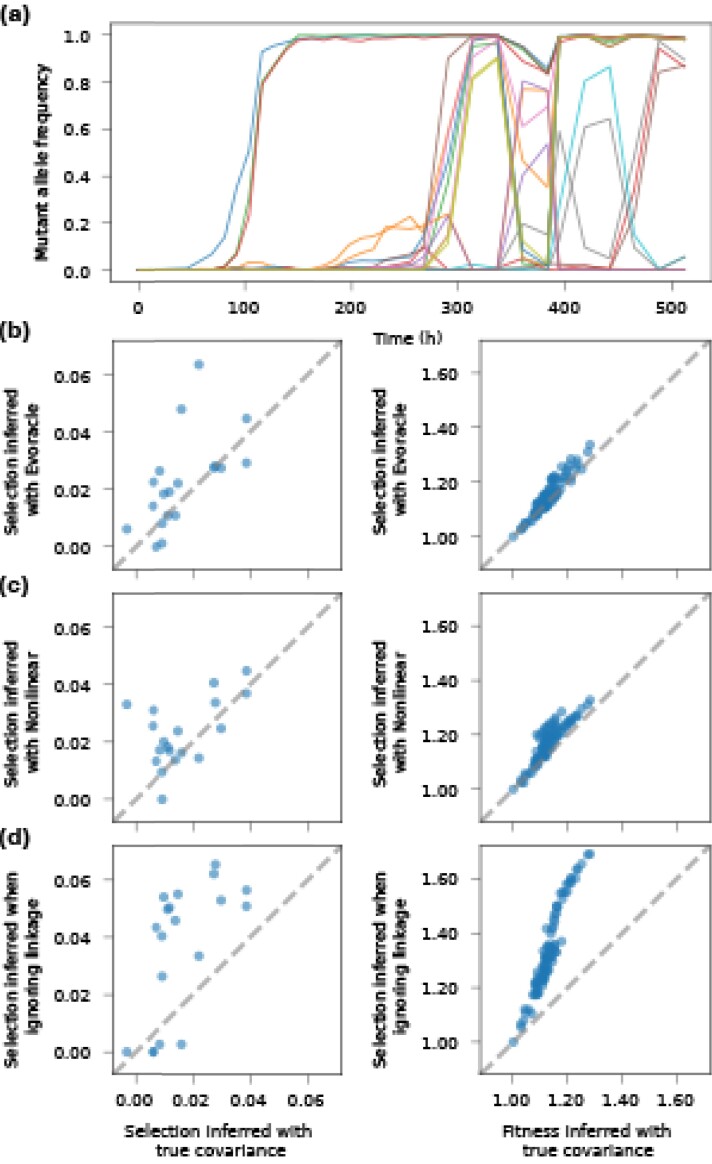
Badran et al. evolved the Cry1Ac gene for 528 hr using phage-assisted continuous evolution (PACE), a system that enables effective continuous directed evolution of gene-encoded molecules that can be linked to protein production in Escherichia coli (Esvelt et al. 2011; Badran et al. 2016). The Cry1Ac gene (2,138 nt) encodes an insecticidal Bacillus thuringiensis-endotoxin (Bt toxin) that is widely used in agriculture for pest control (Badran et al. 2016). During PACE, samples were collected and sequenced with long-read (2,138 nt) PacBio sequencing to an average depth of 500 reads every 12 hr or 24 hr for 528 hr, totaling 34 time points. Shen et al. developed and applied the haplotype reconstruction method, Evoracle, on 100-nt reads truncated from PacBio reads that incorporate 19 commonly evolved nonsynonymous amino acid mutations (Shen et al. 2021). Evoracle is shown to accurately reconstruct the 100-nt haplotype frequency trajectories (Shen et al. 2021).
We tested the ability of our method to improve selection inference on this dataset. We obtained selection coefficients inferred with SL, and nonlinear-norm methods, and compared them with selection coefficients inferred with true covariance information computed from the full-length (100nt) sequences. We also compared our results with the selection coefficients inferred using the haplotypes inferred by Evoracle. Our method yields inferred selection coefficients that are substantially closer to those inferred using true covariance information than SL, and comparable to ones based on haplotypes inferred by Evoracle (Fig. 8). The same observation holds when we study the inferred fitness values for observed haplotypes. Here, the SL approach, which ignores LD, substantially overestimates selection because groups of beneficial alleles arise and sweep together during the experiment (Fig. 8a). SL treats each mutant independently, hence it infers all alleles that rise together to be highly beneficial. Our method accounts for the LD among these co-rising mutations and hence provides more accurate inference results.
Fig. 8.
Performance on Cry1Ac dataset. (a) Mutant allele frequency trajectories over directed evolution for 528 hr. Performance on selection and fitness inference are plotted for methods (b) Evoracle, (c) nonlinear, and (d) SL, against inference results using true covariance information computed from sequences. The Evoracle result denotes selection inferred with covariance matrix computed from haplotype frequencies reconstructed by Evoracle. Evoracle and nonlinear methods provide more accurate inference for both selection and fitness than SL.
Discussion
Here we proposed a simple method to estimate genetic linkage from time-series allele frequencies, and we evaluated its performance when used together with MPL to infer the fitness effects of individual mutations. Our simulations showed that inference using properly regularized estimates of the allele frequency covariance matrix outperforms methods that ignore genetic linkages in most cases.
Our method is general and should be applicable to investigate selection in evolving populations when combined with inference methods that use covariance information. However, it is limited by the quantity and extent of data available. Our approach is especially sensitive to the temporal sampling interval of data, though this sensitivity can be mitigated with regularization and by combining data from multiple replicates. Remarkably, when multiple replicates of evolutionary data are combined, selection can be estimated using only allele frequencies just as accurately as if complete haplotype information were available. This benefit is further magnified when the starting populations for different replicates are distinct.
Methods that aim to recover haplotypes and their frequencies, such as those developed for viruses (Beerenwinkel et al. 2012), can also aid inference of selection from pool-sequenced data. Pelizzola et al. (2021) showed that reconstructed haplotype information could improve the accuracy of allele frequency estimation because haplotype frequency estimates combine information across many SNPs and are less noisy than allele frequencies from pool sequencing. Similarly reconstructed haplotype information could potentially improve covariance estimation. They can also be used to directly infer selection coefficients with inference methods taking haplotype frequencies as input. Higher order covariance information (i.e. beyond pairwise allele frequency covariances) is also necessary to estimate epistatic interactions from data (Sohail et al. 2022), further emphasizing the importance of this reconstruction problem.
Prior work has also examined the time dependence of allele frequency changes and exploited them for inference. In a recent series of papers, Buffalo and Coop (2019, 2020) developed detailed analytical expressions for the temporal autocovariance of allele frequency changes for a neutral site, including the influence of factors such as linked selection, recombination, and genetic drift. As in our work, they use these expressions for inference by equating theoretical expectations with measurements from data, which they used to estimate parameters including effective population sizes and time-varying selection (Buffalo and Coop 2019). Their approach also identifies the fraction of allele frequency change attributable to linked selection, which was estimated between 17 and 37% in the analysis of three experimental evolve-and-resequence data sets (Buffalo and Coop 2020). In other work, Franssen et al. (2015) combined temporal changes in allele frequencies with haplotype data from initial populations to identify and follow selected regions (haplotype blocks). Subsequently, the haploReconstruct method was developed to automatically identify selected haplotype blocks from temporal allele frequency data (Franssen et al. 2017; Barghi et al. 2019). This approach works by normalizing frequency trajectories of selected alleles that start at low frequencies but rise in later generations, and then using the linear correlation coefficients between normalized trajectories as a measure of their linkage. Strongly linked alleles are then clustered into selected haplotypes.
Substantial effort in computational biology is dedicated to extracting knowledge on selection from genetic data. However, pool-sequenced data lack crucial information needed to account for genetic linkage that frequently occurs in nature. Our method provides a tool to augment pool-sequenced data by estimating covariance solely from allele frequencies. The estimated covariance can then be used with inference methods like MPL to resolve genetic linkage and infer selection coefficients. Our results demonstrate that such approaches yield substantially better performance than ignoring linkage.
Supplementary Material
Acknowledgments
We thank two anonymous reviewers for their constructive comments, which have helped to strengthen the paper.
Contributor Information
Yunxiao Li, Department of Physics and Astronomy, University of California, Riverside, CA 92521, USA.
John P Barton, Department of Physics and Astronomy, University of California, Riverside, CA 92521, USA; Department of Computational and Systems Biology, University of Pittsburgh School of Medicine, Pittsburgh, PA 15260, USA.
Data availability
Data and code used in our analysis are available in the GitHub repository at https://github.com/bartonlab/paper-covariance-estimation. This repository also contains Jupyter notebooks that can be run to reproduce these results. Supplemental material is available at GENETICS online.
Funding
The work of YL and JPB reported in this publication was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award Number R35GM138233.
Conflicts of interest
None declared.
Author contributions
All authors contributed to methods development, data analysis, interpretation of results, and writing the paper.
Literature cited
- Allen TM, Altfeld M, Geer SC, Kalife ET, Moore C, O’sullivan KM, DeSouza I, Feeney ME, Eldridge RL, Maier EL, et al. Selective escape from CD8+ t-cell responses represents a major driving force of human immunodeficiency virus type 1 (HIV-1) sequence diversity and reveals constraints on HIV-1 evolution. J Virol. 2005;79:13239–13249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anand S, Mangano E, Barizzone N, Bordoni R, Sorosina M, Clarelli F, Corrado L, Martinelli Boneschi F, D’Alfonso S, De Bellis G. Next generation sequencing of pooled samples: guideline for variants’ filtering. Sci Rep. 2016;6:33735. [DOI] [PMC free article] [PubMed]
- Badran AH, Guzov VM, Huai Q, Kemp MM, Vishwanath P, Kain W, Nance AM, Evdokimov A, Moshiri F, Turner KH, et al. Continuous evolution of Bacillus thuringiensis toxins overcomes insect resistance. Nature. 2016;533:58–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bansal V, Bafna V. HapCUT: an efficient and accurate algorithm for the haplotype assembly problem. Bioinformatics. 2008;24:i153–i159. [DOI] [PubMed] [Google Scholar]
- Bao Y, Bolotov P, Dernovoy D, Kiryutin B, Zaslavsky L, Tatusova T, Ostell J, Lipman D. The influenza virus resource at the national center for biotechnology information. J Virol. 2008;82:596–601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barghi N, Tobler R, Nolte V, Jakšić AM, Mallard F, Otte KA, Dolezal M, Taus T, Kofler R, Schlötterer C. Genetic redundancy fuels polygenic adaptation in drosophila. PLoS Biol. 2019;17:e3000128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrick JE, Yu DS, Yoon SH, Jeong H, Oh TK, Schneider D, Lenski RE, Kim JF. Genome evolution and adaptation in a long-term experiment with Escherichia coli. Nature. 2009;461:1243–1247. [DOI] [PubMed] [Google Scholar]
- Beerenwinkel N, Günthard HF, Roth V, Metzner KJ. Challenges and opportunities in estimating viral genetic diversity from next-generation sequencing data. Front Microbiol. 2012;3:329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bignell GR, Greenman CD, Davies H, Butler AP, Edkins S, Andrews JM, Buck G, Chen L, Beare D, Latimer C, et al. Signatures of mutation and selection in the cancer genome. Nature. 2010;463:893–898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buffalo V, Coop G. The linked selection signature of rapid adaptation in temporal genomic data. Genetics. 2019;213:1007–1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buffalo V, Coop G. Estimating the genome-wide contribution of selection to temporal allele frequency change. Proc Natl Acad Sci USA. 2020;117:20672–20680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burrell RA, McGranahan N, Bartek J, Swanton C. The causes and consequences of genetic heterogeneity in cancer evolution. Nature. 2013;501:338–345. [DOI] [PubMed] [Google Scholar]
- Charlesworth B. The effect of background selection against deleterious mutations on weakly selected, linked variants. Genet Res. 1994;63:213–227. [DOI] [PubMed] [Google Scholar]
- Donoho DL, Gavish M, Johnstone IM. Optimal shrinkage of eigenvalues in the spiked covariance model. Ann Stat. 2018;46:1742–1778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eriksson N, Pachter L, Mitsuya Y, Rhee SY, Wang C, Gharizadeh B, Ronaghi M, Shafer RW, Beerenwinkel N. Viral population estimation using pyrosequencing. PLoS Comput Biol. 2008;4:e1000074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esvelt KM, Carlson JC, Liu DR. A system for the continuous directed evolution of biomolecules. Nature. 2011;472:499–503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewens WJ. Mathematical Population Genetics 1: Theoretical Introduction. New York, NY: Springer Science & Business Media; 2012. [Google Scholar]
- Feder AF, Petrov DA, Bergland AO. LDx: estimation of linkage disequilibrium from high-throughput pooled resequencing data. PLoS ONE. 2012;7:e48588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franssen SU, Barton NH, Schlötterer C. Reconstruction of haplotype-blocks selected during experimental evolution. Mol Biol Evol. 2017;34:174–184. [DOI] [PubMed] [Google Scholar]
- Franssen SU, Nolte V, Tobler R, Schlötterer C. Patterns of linkage disequilibrium and long range hitchhiking in evolving experimental Drosophila melanogaster populations. Mol Biol Evol. 2015;32:495–509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerrish PJ, Lenski RE. The fate of competing beneficial mutations in an asexual population. Genetica. 1998;102–103:127–144. [PubMed] [Google Scholar]
- Hedrick PW. Gametic disequilibrium measures: proceed with caution. Genetics. 1987;117:331–341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill WG, Robertson A. Linkage disequilibrium in finite populations. Theor Appl Genet. 1968;38:226–231. [DOI] [PubMed] [Google Scholar]
- Illingworth CJR, Fischer A, Mustonen V. Identifying selection in the within-host evolution of influenza using viral sequence data. PLoS Comput Biol. 2014;10:e1003755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Illingworth CJR, Mustonen V. Distinguishing driver and passenger mutations in an evolutionary history categorized by interference. Genetics. 2011;189:989–1000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnstone IM. On the distribution of the largest eigenvalue in principal components analysis. Ann Stat. 2001;29:295–327. [Google Scholar]
- Landau DA, Carter SL, Stojanov P, McKenna A, Stevenson K, Lawrence MS, Sougnez C, Stewart C, Sivachenko A, Wang L, et al. Evolution and impact of subclonal mutations in chronic lymphocytic leukemia. Cell. 2013;152:714–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ledoit O, Wolf M. A well-conditioned estimator for large-dimensional covariance matrices. J Multivar Anal. 2004;88:365–411. [Google Scholar]
- Ledoit O, Wolf M. The power of (non-)linear shrinking: a review and guide to covariance matrix estimation. J Financ Econ. 2020;20:187–218. [Google Scholar]
- Lee B, Sohail MS, Finney E, Ahmed SF, Quadeer AA, McKay MR, Barton JP. Inferring effects of mutations on sars-cov-2 transmission from genomic surveillance data. medRxiv. 2022; 2021-12.
- Lee JM, Huddleston J, Doud MB, Hooper KA, Wu NC, Bedford T, Bloom JD. Deep mutational scanning of hemagglutinin helps predict evolutionary fates of human H3N2 influenza variants. Proc Natl Acad Sci USA. 2018;115:E8276–E8285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long A, Liti G, Luptak A, Tenaillon O. Elucidating the molecular architecture of adaptation via evolve and resequence experiments. Nat Rev Genet. 2015;16:567–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luksza M, Lässig M. A predictive fitness model for influenza. Nature. 2014;507:57–61. [DOI] [PubMed] [Google Scholar]
- Łuksza M, Riaz N, Makarov V, Balachandran VP, Hellmann MD, Solovyov A, Rizvi NA, Merghoub T, Levine AJ, Chan TA, et al. A neoantigen fitness model predicts tumour response to checkpoint blockade immunotherapy. Nature. 2017;551:517–520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Bost D, Wilson S, Maruki T, Harrison S. Population-genetic inference from pooled-sequencing data. Genome Biol Evol. 2014;6:1210–1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marčenko VA, Pastur LA. Distribution of eigenvalues for some sets of random matrices. Mathematics of the USSR-Sbornik. 1967;1:457.
- McMichael AJ, Borrow P, Tomaras GD, Goonetilleke N, Haynes BF. The immune response during acute HIV-1 infection: clues for vaccine development. Nat Rev Immunol. 2010;10:11–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metzker ML. Sequencing technologies—the next generation. Nat Rev Genet. 2010;11:31–46. [DOI] [PubMed] [Google Scholar]
- Neher RA, Bedford T, Daniels RS, Russell CA, Shraiman BI. Prediction, dynamics, and visualization of antigenic phenotypes of seasonal influenza viruses. Proc Natl Acad Sci USA. 2016;113:E1701–E1709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelizzola M, Behr M, Li H, Munk A, Futschik A. Multiple haplotype reconstruction from allele frequency data. Nat Comput Sci. 2021;1:262–271. [DOI] [PubMed] [Google Scholar]
- Phillips RE, Rowland-Jones S, Nixon DF, Gotch FM, Edwards JP, Ogunlesi AO, Elvin JG, Rothbard JA, Bangham CR, Rizza CR. Human immunodeficiency virus genetic variation that can escape cytotoxic T cell recognition. Nature. 1991;354:453–459. [DOI] [PubMed] [Google Scholar]
- Rambaut A, Posada D, Crandall KA, Holmes EC. The causes and consequences of HIV evolution. Nat Rev Genet. 2004;5:52–61. [DOI] [PubMed] [Google Scholar]
- Shen MW, Zhao KT, Liu DR. Reconstruction of evolving gene variants and fitness from short sequencing reads. Nat Chem Biol. 2021;17:1188–1198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith JM, Haigh J. The hitch-hiking effect of a favourable gene. Genet Res. 1974;23:23–35. [PubMed] [Google Scholar]
- Sohail MS, Louie RHY, Hong Z, Barton JP, McKay MR. Inferring epistasis from genetic time-series data. Mol Biol Evol. 2022;39:sac199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohail MS, Louie RHY, McKay MR, Barton JP. MPL resolves genetic linkage in fitness inference from complex evolutionary histories. Nat Biotechnol. 2021;39:472–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terhorst J, Schlötterer C, Song YS. Multi-locus analysis of genomic time series data from experimental evolution. PLoS Genet. 2015;11:e1005069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu NC, Wilson IA. A perspective on the structural and functional constraints for immune evasion: insights from influenza virus. J Mol Biol. 2017;429:2694–2709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue KS, Stevens-Ayers T, Campbell AP, Englund JA, Pergam SA, Boeckh M, Bloom JD. Parallel evolution of influenza across multiple spatiotemporal scales. Elife. 2017;6:e26875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zagordi O, Bhattacharya A, Eriksson N, Beerenwinkel N. ShoRAH: estimating the genetic diversity of a mixed sample from next-generation sequencing data. BMC Bioinform. 2011;12:119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanini F, Brodin J, Thebo L, Lanz C, Bratt G, Albert J, Neher RA. Population genomics of intrapatient HIV-1 evolution. Elife. 2015;4:e11282. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data and code used in our analysis are available in the GitHub repository at https://github.com/bartonlab/paper-covariance-estimation. This repository also contains Jupyter notebooks that can be run to reproduce these results. Supplemental material is available at GENETICS online.