DCI: learning causal differences between gene regulatory networks

Abstract

Summary

Designing interventions to control gene regulation necessitates modeling a gene regulatory network by a causal graph. Currently, large-scale gene expression datasets from different conditions, cell types, disease states, and developmental time points are being collected. However, application of classical causal inference algorithms to infer gene regulatory networks based on such data is still challenging, requiring high sample sizes and computational resources. Here, we describe an algorithm that efficiently learns the differences in gene regulatory mechanisms between different conditions. Our difference causal inference (DCI) algorithm infers changes (i.e. edges that appeared, disappeared, or changed weight) between two causal graphs given gene expression data from the two conditions. This algorithm is efficient in its use of samples and computation since it infers the differences between causal graphs directly without estimating each possibly large causal graph separately. We provide a user-friendly Python implementation of DCI and also enable the user to learn the most robust difference causal graph across different tuning parameters via stability selection. Finally, we show how to apply DCI to single-cell RNA-seq data from different conditions and cell states, and we also validate our algorithm by predicting the effects of interventions.

Availability and implementation

Python package freely available at http://uhlerlab.github.io/causaldag/dci.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Biological processes from differentiation to disease progression are governed by gene regulatory networks. Various methods have been developed for inferring such networks from gene expression data (Wang and Huang, 2014), the majority by learning undirected graphs using correlations (Langfelder and Horvath, 2008), Gaussian graphical models to capture partial correlations (Friedman et al., 2008), or mutual information (Reshef et al., 2011). However, the ultimate goal is often to use gene regulatory networks to predict the effect of an intervention (small molecule, overexpression of a transcription factor, knock-out of a gene, etc.). This cannot be done using an undirected graph and necessitates modeling a gene regulatory network by a causal (directed) graph.

Causal relationships are commonly represented by a directed acyclic graph (DAG) and a variety of methods have been developed for learning causal graphs from observational data (Glymour et al., 2019). These methods have been successfully applied to learning (directed) gene regulatory networks on a small number of genes, starting with the pioneering study by Friedman et al. (2000). However, applying these methods at the whole genome-level is still challenging due to high sample size and computational requirements of the algorithms.

We address this problem by noting that it is often of interest to learn changes in causal (regulatory) relationships between two related gene regulatory networks corresponding to different conditions, disease states, cell types or developmental time points, as opposed to learning the full gene regulatory network for each condition. This can reduce the high sample and computational requirements of current causal inference algorithms, since while the full regulatory network is often large and dense, the difference between two related regulatory networks is often small and sparse. As of now, this problem has only been addressed in the undirected setting, namely by KLIEP (Liu et al., 2017), DPM (Zhao et al., 2014) and others (Fukushima, 2013; Lichtblau et al., 2017) that estimate differences between undirected graphs; for a recent review see Shojaie (2020). In this article, we describe the difference causal inference (DCI) algorithm and present an easy to use Python package for the direct estimation of the difference between two causal graphs based on observational data from two conditions (for the theoretical properties of this algorithm see Wang et al., 2018). In particular, we show how to apply DCI to gene expression data from different conditions and demonstrate the algorithm’s performance on predicting the effects of interventions on single-cell RNA-seq data. Importantly, our DCI implementation also allows selecting the most robust difference gene regulatory network based on a collection of tuning parameters via stability selection. To seamlessly integrate DCI with other causal inference methods, it is incorporated in the causaldag package.

2 Difference causal inference (DCI) package

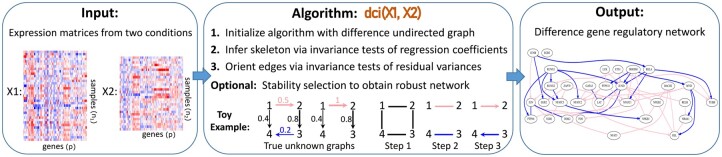
DCI takes as input two matrices ${\widehat{X}}^{(1)}$ and ${\widehat{X}}^{(2)}$ of size $n_1\times p$ and $n_2\times p$, where n₁, n₂ are the number of samples in each dataset and p is the number of genes. These matrices contain the RNA-seq values corresponding to two different conditions. DCI outputs the difference causal graph between the two conditions, i.e. the edges in the gene regulatory networks that appeared, disappeared or changed weight between the two conditions (Fig. 1).

Fig. 1.

Overview of DCI algorithm: DCI takes as input two gene expression matrices X1 and X2, representing two different conditions of interest. The function dci(X1, X2) outputs the difference gene regulatory network consisting of the causal relationships that appeared, disappeared or changed weight between the two conditions

The data for each condition is assumed to be generated by a linear structural equation model with Gaussian noise. More precisely, let ${\mathcal{G}}^{(1)}$ and ${\mathcal{G}}^{(2)}$ denote two DAGs on p nodes with weighted adjacency matrices $B^{(1)}$ and $B^{(2)}$. Each node $j\in \{1,\dots ,p\}$ in the two graphs ${\mathcal{G}}^{(k)},\hspace{0.17em}k\in \{1,2\}$, is associated with a random variable $X_j^{(k)}$, which is given by a weighted sum of its parents and independent Gaussian noise ${ϵ}^{(k)}$, i.e. $X_j^{(k)}=\sum _{i=1}^p{B}_{ij}^{(k)}{X}_i+{ϵ}_j^{(k)}$. Given data ${\widehat{X}}^{(1)}$ and ${\widehat{X}}^{(2)}$ from two unknown causal graphs ${\mathcal{G}}^{(1)}$ and ${\mathcal{G}}^{(2)}$, DCI determines their difference, i.e. edges $i\to j$ for which $B_{ij}^{(1)}\ne B_{ij}^{(2)}$. DCI consists of three steps described below; for further details see Supplementary Materials. These steps are implemented in the dci function of the causaldag package.

Step 1: Initialization with a difference undirected graph. Instead of starting in the complete graph, computation time can be reduced by initializing DCI with an undirected graph, which represents changes of conditional dependencies among genes between the two conditions. This can be obtained using previous methods such as KLIEP (Liu et al., 2017) or a constraint-based method as described in Supplementary Materials.

Step 2: Estimation of the skeleton of the difference causal graph. Edges are removed from the difference undirected graph by testing for invariance of regression coefficients using an F-test. Since each entry B_ij corresponds to a regression coefficient ${\beta }_{ij|S}$ obtained by regressing X_j on X_i given the parents of node j in $\mathcal{G}$, testing whether $B_{ij}^{(1)}=B_{ij}^{(2)}$, is equivalent to testing whether there exists a set of nodes S such that ${\beta }_{i,j|S}^{(1)}={\beta }_{i,j|S}^{(2)}$.

Step 3: Orienting edges in the difference causal graph. All edge directions that are identifiable from observational data are obtained by testing for invariance of residual variances. For any edge i—j in the undirected graph obtained in Step 2, if there exists a set of nodes S such that the residual variances satisfy ${\sigma }_{j|S}^{(1)}={\sigma }_{j|S}^{(2)}$, then the edge is directed as $i\to j$ if $i\in S$ and $j\to i$ otherwise (see Supplementary Materials).

Stability selection to obtain robust difference gene regulatory network. DCI requires choosing hyperparameters for each step, namely the ${\ell }_1$ regularization parameter for KLIEP or the significance level for the constraint-based method in step 1 and the significance levels for the F-tests in steps 2 and 3. To overcome this difficulty, we implemented DCI with stability selection, which achieves family-wise error rate control (Meinshausen et al., 2016; Meinshausen and Bühlmann, 2010). For this, DCI is run across a grid of tuning parameters and bootstrap samples of the data, the results are aggregated, and only edges with a stability score above a predefined threshold are output in the difference causal graph (Supplementary Fig. S1).

3 Applications and conclusions

We applied DCI to two single-cell RNA-seq datasets: CROP-seq (Datlinger et al., 2017) and Perturb-seq (Dixit et al., 2016). Both also contain interventional gene expression data from knockouts. We applied DCI to the observational single-cell data and evaluated it using an ROC curve based on the interventional data (see Supplementary Materials). The resulting difference gene regulatory networks between naive and activated T cells as well as between pre- and post-stimulation of dendritic cells with LPS are shown in Supplementary Fig. S2–S7. In both cases, DCI outperforms the naive approach of estimating two causal graphs separately and can provide valuable mechanistic insights into the underlying biological processes. The naive approach of estimating a separate graph for each condition suffers from the fact that each gene regulatory network may be large with many high degree nodes, which poses a challenge for many causal inference algorithms. Since the difference gene regulatory network is likely sparse, DCI can result in significantly better performance.

We developed the DCI package for learning differences between gene regulatory networks based on gene expression data from two different conditions of interest, such as healthy and diseased, different cell types or developmental time points. Our package is implemented in Python for ease-of-use, is scalable (Supplementary Fig. S8, S9), and also includes functionality to ensure that the output difference gene regulatory network is stable and robust across different hyperparameters and data subsampling.

Financial Support

A. B. was supported by J-WAFS and J-Clinic for Machine Learning and Health at MIT. C. S. was partially supported by an NSF Graduate Fellowship (Grant No. 1745302), MIT J-Clinic for Machine Learning and Health, and the MIT-IBM Watson AI Lab. C.U. was partially supported by NSF (DMS-1651995), ONR (N00014-17-1-2147 and N00014-18-1-2765), and a Simons Investigator Award.

Conflict of Interest: none declared.

Data availability

All datasets used in this work are publicly available. CROP-seq data was obtained from GSE92872 and Perturb-seq data was obtained from GSE90063.