Surface crossing and energy flow in many-dimensional quantum systems

Significance

Quantum scrambling and energy redistribution are important in many problems ranging from photosynthetic energy flow to charge transfer at electrodes and in quantum dots. In mesoscopic systems such as large molecules, a transition from coherent organized quantum behavior to chaotic behavior can be found. Two of the key scrambling mechanisms, electronic surface crossing and vibrational anharmonic resonance, have usually been treated separately. Here, we develop a unified theory providing a transition criterion from localized to scrambled regimes. The criterion is easy to compute even for very complicated systems, and we test it by comparisons with numerical quantum dynamics simulations for a model inspired by bacteriochlorophyll dimers involved in photosynthesis.

Abstract

Energy flow in molecules, like the dynamics of other many-dimensional finite systems, involves quantum transport across a dense network of near-resonant states. For molecules in their electronic ground state, the network is ordinarily provided by anharmonic vibrational Fermi resonances. Surface crossing between different electronic states provides another route to chaotic motion and energy redistribution. We show that nonadiabatic coupling between electronic energy surfaces facilitates vibrational energy flow and, conversely, anharmonic vibrational couplings facilitate nonadiabatic electronic state mixing. A generalization of the Logan–Wolynes theory of quantum energy flow in many-dimensional Fermi resonance systems to the two-surface case gives a phase diagram describing the boundary between localized quantum dynamics and global energy flow. We explore these predictions and test them using a model inspired by the problem of electronic excitation energy transfer in the photosynthetic reaction center. Using an explicit numerical solution of the time-dependent Schrödinger equation for this ten-dimensional model, we find quite good agreement with the expectations from the approximate analytical theory.

In macroscopic systems, a variety of elementary processes (collisions, nonlinear resonances, isomerization, etc.) eventually lead to the sharing of energy among the various parts of the system and to the scrambling of quantum information. In individual molecules and designed macroscopic quantum systems, such energy flow can be slow or even incomplete. Many theories of chemical reaction dynamics rely on making the assumption of rapid energy flow and phase scrambling. In contrast, useful quantum computers will need to be able to minimize these effects. It has been established that the transition to facile energy flow in moderate-sized organic molecules due to anharmonic (e.g., Fermi) resonance occurs at an energy threshold close to the typical activation energies needed for conformational barrier crossing (1–5) and thus, energy flow can modify kinetics. At energies above the threshold, a quantum transport network between vibrational states interacting through anharmonic Fermi resonance couplings becomes sufficiently well connected to explore much of the state space, allowing statistical treatment. Using an analogy to Anderson localization (6), Logan and Wolynes constructed a theory of the quantum energy flow transition for local random matrix models of the vibrational state space that provides a criterion involving the anharmonic couplings and the local density of connected states and predicts the threshold for free vibrational energy flow (7). Their model has been elaborated in many ways (8–10). Gruebele and collaborators developed a way to map organic molecules with known vibrational spectra onto this abstract model (11, 12). This mapping has allowed simple prediction of the energy flow threshold for specific molecules. These estimates appear to be accurate when compared to experiments (13). A distinct fully quantum mechanical mechanism that leads to quantum number scrambling was identified by Heller (14) and by Cederbaum and coworkers (15) long ago: the (near) crossing of Born–Oppenheimer surfaces corresponding to different electronic states. Far from being a spectroscopic curiosity, such crossings are an essential feature of electronic energy transport in condensed phases and in biological systems (16). Surface crossing also features in nonadiabatic electron transfer reactions that occur throughout electrochemistry and biology (17, 18). Qubits in quantum computing devices based on cold atoms in near-harmonic optical traps also can be described in a similar fashion (19). In this paper, we explore the simultaneous effects of Fermi resonances and surface crossing mechanics on quantum energy flow and state mixing.

We first extend the Logan–Wolynes treatment of the many-Fermi resonance problem on a single potential energy surface to the situation where there are two electronic surfaces. In the simplest case where the two crossing surfaces are displaced from each other but have the same shape (e.g., exciton transfer between homodimers), we exploit the analogical structure of Feenberg’s perturbation expansion describing vibrational anharmonic coupling and the perturbation theory for nonadiabaticity to obtain a simple expression for the joint transition criterion where both mechanisms of scrambling play a role. The transition depends jointly on the strength of the anharmonic vibrational couplings, the nonadiabatic coupling strength between the potential surfaces, and the Frank–Condon factors for the nonadiabatic surface crossing. These quantities are weighted by appropriate local densities of states and can be obtained by the method of Leitner and Wolynes (20). We find that the two mechanisms of scrambling mutually reinforce each other in a simple summation form.

To test the analytic theory, we computationally study a model inspired by electronic excitation transfer in photosynthesis. We set up a two-surface model of the bacteriochlorophyll (BChl) homodimer with a truncated but realistic vibrational frequency spectrum. We then use the scaling model of the vibrational couplings from Madsen et al. (21) to compute the anharmonic couplings between states and compute the threshold between the restricted and free quantum energy flow regimes, illustrating the energy dependence of quantum scrambling.

We further explore the physics by varying the electronic couplings over a wide range around realistic values for the photosynthetic system. By limiting ourselves to the five strongest coupled modes in each monomer, the simplified model has a low enough dimensionality so that the time-dependent Schrödinger equation can be directly solved numerically for many different initial states. In this way, we develop a computational phase diagram that compares quite well with the analytical theory’s predictions. For realistic values of the parameters relevant for the photosynthetic system, we find that both mechanisms of energy flow contribute above the surface crossing energy. Clearly, the balance between the two mechanisms of scrambling will be system dependent.

The organization of the paper is as follows. In Section 1, we introduce the model Hamiltonian. In Section 2, the Logan–Wolynes theory for the transition is briefly reviewed and its extension to the nonadiabatic case is sketched based on the analogous structure of the vibrational and nonadiabatic contributions to the self-energy of a state computed in self-consistent perturbation theory. In Section 3, the numerical results for the phase diagram of the model are compared with the expectations from analytical theory. In Section 4, we discuss the general consequences of simultaneous anharmonic resonance and nonadiabatic surface crossing-induced quantum scrambling and its relevance to energy transport in photosynthesis.

1. Model Hamiltonian

In our model Hamiltonian, the two potential energy surfaces are each described by a vibrational Hamiltonian $H_{\mathit{vib}}$ that couples vibrations anharmonically. For modeling the surface crossing, we choose a constant nonadiabatic coupling $V_t$ between the two potential energy surfaces. We assume that the two potential energy surfaces share the same set of normal mode vibrational frequencies, but that the minima of the 0th-order harmonic oscillators on each surface are displaced with respect to each other.

$$\begin{array}{l}\widehat{H}={\widehat{H}}_{vib}^{\left(0\right)}\left|0\right.〉\left.〈0\right|+{\widehat{H}}_{vib}^{\left(1\right)}\left|1\right.〉\left.〈1\right|+V_t(\left|0\right.〉\left.〈1\right|+\left|1\right.〉\left.〈(0\right|)+ \delta E\left|1\right.〉\left.〈1\right|\\ {\widehat{H}}_{vib}^{\left(0\right)} ={\widehat{H}}_{vib,0}^{(0)} + {\widehat{H}}_{\text{a}}^{(0)}\\ \begin{array}{c}{\widehat{H}}_{vib,0}^{\left(0\right)} = {\displaystyle {\sum }_{i = 1}^N\left(\frac{1}{2}{p}_i^2+\frac{1}{2}{\omega }_i^2{q}_i^2\right)}\\ {\widehat{H}}_{vib}^{\left(1\right)} = {\widehat{H}}_{vib,0}^{\left(1\right)} + {\widehat{H}}_{\text{a}}^{\left(1\right)}\\ {\widehat{H}}_{vib,0}^{\left(1\right)} ={\displaystyle {\sum }_{i = 1}^N\left(\frac{1}{2}{p}_i^2+\frac{1}{2}{\omega }_i^2{\left(q_i-c_i/{\omega }_i^2\right)}^2\right)} \\ {\widehat{H}}_{\text{a}} = {\displaystyle \sum _m{\displaystyle \prod }_{\alpha }{V}_m{\left(b_{\alpha }^{†}\right)}^{m_{\alpha }^{+}}{b}_{\alpha }^{m_{\alpha }^{-}}.}\end{array}\text{}\end{array}$$ [1]

Here, the states s = 0,1 represent different potential energy surfaces, $N$ is the number of vibrational modes, $V_t$ is the nonadiabatic coupling between potential energy surfaces (which is assumed constant presently), $\delta E$ is the ground state potential energy difference between the two potential energy surfaces. ${\widehat{H}}_{\mathit{vib}}^{\left(0\right)}$ and ${\widehat{H}}_{\mathit{vib}}^{\left(1\right)}$ represent the vibrational Hamiltonians of each potential energy surface, ${\widehat{H}}_{vib,0}^{(0)}$ and ${\widehat{H}}_{vib,0}^{(1)}$ represent their zeroth-order Harmonic oscillator parts, while ${\widehat{H}}_{\mathrm{a}}$ is the anharmonic vibrational coupling operator. The $\mathit{m}=$ {m_α} are integers that describe the order of the anharmonic vibrational couplings, e.g., $m_1^{+}$ = 2 and $m_2^{-}$ = 1 would be a Fermi (cubic) resonance between modes 1 and 2. The dominant nonlinear coupling is generally cubic, and was first identified by Fermi in explaining the carbon dioxide infrared spectrum where there is a 2:1 near-resonance between the doubly degenerate bending and symmetric stretching modes (22). The cubic term also provides the nonlinearity in the famous Fermi–Pasta–Ulam–Tsingou study (23, 24).

We chose the anharmonic scaling model from refs. 11, and 21 for the anharmonic vibrational Hamiltonian ${\widehat{H}}_{\mathrm{a}}$ , which includes higher-order resonances as well. By defining $m={\Sigma }_{\alpha }\left(m_{\alpha }^{+}+m_{\alpha }^{-}\right)$ , the model assumes that the anharmonic coupling decays exponentially with $m$ as

$$V_m=V_3{a}^{m-3},$$ [2]

as follows from smooth molecular potentials of well-bonded systems (21). The cubic Fermi coupling strength $V_3$ for molecules typically has values of the order of 0.1 to 10 cm^–1, while the factor a ranges between 0.1 and 0.3 (21, 25), right in the range where higher-order couplings can facilitate energy transfer (26, 27). In summary, the overall vibrational Hamiltonian for each electronic surface is described by the vibrational frequencies ${\omega }_i$ , anharmonic coupling strengths $V_3$ , and the anharmonic scaling factor $a$ (Fig. 1).

Fig. 1.

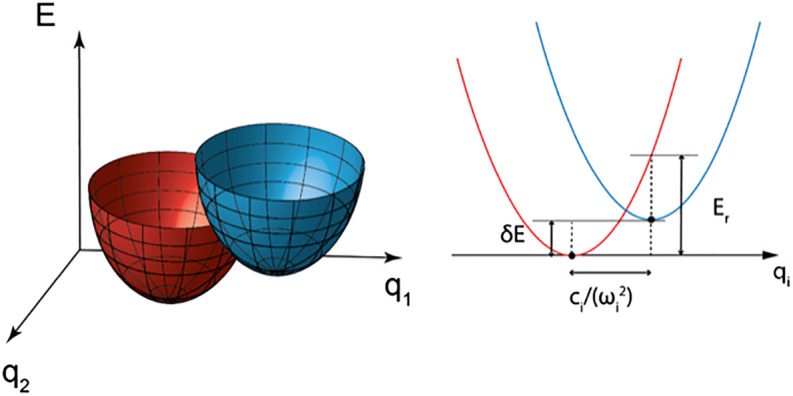
Potential energy surfaces of two electronic states with multiple vibrational degrees of freedom in each state. Left: Two multidimensional potential energy surfaces (red and blue) intersect one another, with two vibrational coordinates q₁ and q₂ shown. Right: A cut through the two potential energy surfaces along coordinate $q_i$ . The center of the potential energy surface 2 is displaced by $c_i/\left({{\omega }_{\mathrm{i}}}^2\right)$ from the center of the potential energy surface 1 in each coordinate. The zero point energy difference δE and the reorganization energy E_r are drawn schematically, and may not lie in the plane of one of the coordinates q_i.

The vibrational eigenstates on the displaced energy surfaces are denoted as $\left|\right\{{\text{α}}_i\};n⟩$ . These basis sets depend on the displacement of each mode and their frequencies through the parameter

$${\text{α}}_i=\sqrt{ \frac{{\text{ω}}_i}{2\hslash }} \frac{c_i}{{\text{ω}}_i^2},$$ [3]

which measures the strength of the electron-vibrational coupling that induces the shift in the minimum location from one potential surface to the other. This coupling is related to the so-called Huang–Rhys factor for each mode “i” by the relation ${\alpha }_i=\sqrt{{\mathrm{S}}_i}$ . The nonadiabatic couplings between specific basis states on the two different surfaces are denoted as $V_t^{n,n^{\prime }}=V_t⟨n\left|\right\{{\alpha }_i\};n^{\prime }⟩$ between vibrational state n on one surface and state n′ on the displaced surface. For harmonic surfaces, the Franck–Condon factors $⟨n\left|\right\{{\alpha }_i\};n^{\prime }⟩$ can be evaluated using associated Laguerre polynomials $L_n^{\left(n^{\prime }\right)}\left(x\right),$ see the work of Cahill and Glauber (28) and SI Appendix, Section A. We do not include a possible Duschinsky rotation (29) of the vibrational modes between the two surfaces in the present calculation.

2. Nonadiabatic Energy Flow Transition Theory

We now formulate and discuss the nonadiabatic generalization of the Logan–Wolynes self-consistent theory to two potential surfaces (7). We outline both the threshold criteria from the one surface theory $T_{\mathit{FR}},$ and the criterion $T_{\mathit{NA}}$ for energy flow coming from surface crossing events alone. When both Fermi resonant couplings and surface crossing effects are present, the theory gives a transition criterion for vibrational energy flow in the nonadiabatic quantum system for a vibrational state “j” in electronic state “s” at total energy E, which now depends on a sum of the two couplings appropriately weighted by local densities of coupled states. We only sketch here the essential ideas by making use of the previous work (7) to simplify the derivation.

The approach we use to determine the transition to facile energy flow in a nonadiabatic quantum system follows from the statistical mean field theory developed by Logan and Wolynes (7), who were inspired by the procedure of Abou-Chacra, Anderson, and Thouless (6) for the Anderson problem of single-particle quantum transport on a disordered Cayley tree. The aim of the Logan–Wolynes analysis was to determine whether eigenstates of a many-oscillator Fermi-resonant Hamiltonians (having only cubic couplings as in the Fermi model) at a given energy are localized on a few vibrational basis states or are extended to connect most of the energetically accessible phase space, thus determining the transition energy between localized and ergodic behavior. By self-consistently solving only for the most probable value of the energy flow rate ${\mathrm{\Delta }}_j(E)$ rather than by making self-consistent the full distribution of self-energies as was done by Abou-Chacra et al., a dimensionless factor depending on the anharmonic couplings which we call $T_{\mathit{FR}}$ was derived describing when vibrational states are localized ( $T_{\mathit{FR}}$ < 1) and when they become extended over many of the original vibrational states ( $T_{\mathit{FR}}$ ≥ 1). The FR subscript stands for “Fermi resonance,” but higher-order terms are included here as well. The theory was further developed to include higher-order couplings, predicting a bimodal distribution of dilution factors (i.e., some vibrational states remain localized while others are delocalized as energy increases) (20). The bimodal distribution has been found to be quite accurate by comparison with numerical models based on experimental data (13, 30, 31). The approach of Logan and Wolynes has also been used to study many-body localization of systems of interacting fermions and spins (32–34) and an analogous approach is used to study the ergodic transition of single quantum dots (35). In this section, we extend the theory to describe the energy flow transition in single systems with two potential surfaces. The theory leads to a dimensionless factor $T_{\mathit{NA}}$ that would characterize the energy flow threshold arising from nonadiabatic coupling between the surfaces alone, in addition to the quantity $T_{\mathit{FR}}$ , which accounts for anharmonic Fermi-resonant coupling in the Logan–Wolynes single-surface theory.

We begin by summarizing the statistical mean field theory on a single surface developed by Logan and Wolynes (7), so we can exploit the similarities between vibrational and electronic mixing. The vibrational Hamiltonian $H$ on each potential energy surface consists of an unperturbed portion $H_0$ which is diagonal and an anharmonic coupling $V$ , which can be written in the tight-binding form in the vibrational Fock space:

$$\begin{array}{c}H=H_0+V={\displaystyle \sum _i{\epsilon }_i\left|i\right.〉\left.〈i\right|}+{\displaystyle \sum _{i\ne j}{V}_{ij}\left|i\right.〉\left.〈j\right|}\end{array}$$ [4]

Here, each zeroth-order state $\left|i\right.\mathrm{\rangle }=\left|\right\{n_{\alpha }\}\mathrm{\rangle }$ is described by a set of quantum numbers indicating the level of excitation in each of the individual oscillators. This molecular vibrational Hamiltonian is a specific realization of models termed local random matrix models (4, 13, 36–39). In local random matrix models, sites which are closer together in state space are more strongly coupled than sites which are further away in the state spaces, but otherwise the specific couplings are characterized by a random variable drawn from an uncorrelated distribution. The tight-binding description in the vibrational Fock space suggests the analogy with the single-particle Anderson problem.

State space site Green functions $G_{\mathit{kj}}\left(t\right)$ and $G_{\mathit{kj}}\left(E\right)$ play central roles in describing how state space is explored:

$$\begin{array}{c}{\mathrm{G}}_{kj}\left(\mathrm{t}\right)=-\frac{\mathrm{i}}{\mathrm{\hslash }} \mathrm{⟨}\mathrm{k}\left|{\mathrm{e}}^{-\mathit{itH}/\mathrm{\hslash }}\right|\mathrm{j}\mathrm{⟩}\hfill \\ G_{kj}\left(E\right)=\underset{\eta \to 0^{+}}{\lim }{\int }_0^{\infty }dt{e}^{it(E+i\eta )/\hslash }{G}_{kj}\left(t\right)\\ =\underset{\eta \to 0^{+}}{\lim }\mathrm{⟨}\mathrm{k}|{\left(E + i\eta - H\right)}^{-1}j\mathrm{⟩},\end{array}$$ [5]

from which the self-energy $S_j\left(E\right)$ can be introduced:

$$\begin{array}{l}{G}_{jj}\left(E\right)={\left(g_{jj}{\left(E\right)}^{-1}-S_j\left(E\right)\right)}^{-1}\hfill \\ g_{jj}\left(E\right)=〈j\left|{\left(E-H_0+i\eta \right)}^{-1}\right|j〉={\left[E-{\epsilon }_j+i\eta \right]}^{-1}.\hfill \end{array}$$ [6]

Here, H₀ which gives rise to the zero-order Green functions is the uncoupled oscillator Hamiltonian.

The asymptotic value of the survival probability ${\overline{P}}_{\mathit{jj}}\left(t,=,\infty \right)$ , also known as the “dilution factor” σ (13, 40), is related to imaginary part of the site self-energy ${\mathrm{\Delta }}_j\left(E\right)=-\mathrm{I}\mathrm{m}\left[S_j\left(E\right)\right]$ :

$$\begin{array}{c}{\overline{\mathrm{P}}}_{jj}\left(t \to \infty \right)=\underset{t\to \infty }{\lim }\frac{1}{t}{{\displaystyle \int }}_0^{t}d{t}^{\prime }{\left| 〈j\left|e^{-i{t}^{\prime }H/\hslash }\right|j〉\right|}^2\\ =\underset{\eta \to 0}{\lim }{\displaystyle \sum _{\lambda }{\left(1+{\text{Δ}}_j\left(E_{\lambda }\right)/\eta \right)}^{-2}}\end{array},$$ [7]

where $\lambda$ is the index for eigenstates and $E_{\lambda }$ is the exact eigenenergy. ${\mathrm{\Delta }}_j$ is proportional to $\eta$ for localized states $j$ , and thus vanishes for an isolated system. When states are extended, ${\mathrm{\Delta }}_j$ yields the rate of energy flow out of state $|j\mathrm{\rangle }$ and can be finite at $\eta =0$ for an infinite system, strictly speaking. Thus, this expression is to be understood here with the caveat that molecules always have a finite, albeit possibly large, global density of states, and will be represented that way in our computational models in Section 3.

The local random matrix model is implemented as follows. To simplify the analysis of the self-energy $S_j\left(E\right)$ , the states are assumed to be coupled having the topology of a Cayley tree with connectivity $K$ between tiers. One site $j$ is coupled to K states in a Cayley tree at the distribution of the coupling strength $P\left(V\right)$ . The energies of $K$ local states $|k\rangle$ to which the state $|j\rangle$ is directly connected are taken to be distributed randomly with the distribution $P(\xi ={\epsilon }_k-{\epsilon }_j)$ . Of course, in a given molecule, which is a specific realization of such a random model, these distributions are specific fixed sums of frequencies, once the original spectrum of vibrations is specified.

The self-energy ${\mathrm{S}}_j$ of each site on the Cayley tree depends on the self-energies of the states further down the Cayley tree. Therefore, the distribution of self-energies on a particular site depends not only on distribution of coupled state energy difference $P\left(\xi \right)$ and the anharmonic coupling strength distribution $P\left(V\right)$ , but also on the distribution of the self-energies of the states locally coupled to the original site which then must be solved for self-consistently. The central object of the self-consistent probabilistic analysis is the Feenberg second-order renormalized perturbation series for the self-energy $S_j\left(E\right)$ which is a random variable in the local random matrix description (41):

$$\begin{array}{c}{S}_j\left(E\right)={{\displaystyle \sum }}_{k\ne j}^{ }{\left|V_{jk}\right|}^2{\left(E+i\eta -{\epsilon }_k-S_k\left(E\right)\right)}^{-1}\\ =E_j\left(E\right)-i{\text{Δ}}_j\left(E\right).\end{array}$$ [8]

A nonlinear integral equation for the joint probability of the self-energy $F(E_j,{\mathrm{\Delta }}_j)$ can be obtained from the renormalized perturbation series as was done by Abou-Chacra et al. for the Anderson problem. In the localized regime, by setting ${\mathrm{\Delta }}_j\left(E\right)=0$ , the simplified integral equation for $F(E_j,{\mathrm{\Delta }}_j)$ can be solved and the mobility-edge boundary can be located. In the extended regime, analyzing the full form of the integral equation has proved quite intractable (6).

Logan and Wolynes simplified the problem of probabilistic self-consistency by replacing the ${\mathrm{\Delta }}_k\left(E\right)$ of site $|k\mathrm{\rangle }$ with its most probable value ${\mathrm{\Delta }}_{\mathit{mp}}$ , and then by requiring only self-consistency of this most probable value ${\mathrm{\Delta }}_{\mathit{mp}}$ instead of the full joint distribution $F(E_j,{\mathrm{\Delta }}_j)$ (7, 42–44). The resulting algebraic equations are much simpler than the analysis of the nonlinear integral equations for $F(E_j,{\mathrm{\Delta }}_j)$ but yield fruitful results in both the localized and the extended regimes (1, 9, 10, 20, 45, 46). In this approximation, it is also straightforward to explicitly explore the effect of dephasing by external degrees of freedom (7, 42).

We now extend the theory to describe the energy flow transition on two surfaces including contributions from surface crossing. The renormalized perturbation series at the leading (second) order level is the sum of the contributions from Fermi resonances and surface crossing transitions:

$$\begin{array}{c}{S}_j\left(E\right)={{\displaystyle \sum }}_{l\ne j}^{ }\frac{{\left|V_{jl}^{\left(s\text{,}s\right)}\right|}^2}{E + i\eta - {\epsilon }_{l,s} - S_{l,s}\left(E\right)} \\ + {{\displaystyle \sum }}_k^{ }\frac{{\left|t_{jk}^{\left(-1,1\right)}\right|}^2}{E + i\eta - {\epsilon }_{k, -s} - S_{k, -s}\left(E\right)}.\end{array}$$ [9]

here, the labels s = −1,1 reflect the two surfaces. The self-energy has contributions from both the anharmonic couplings on each surface and the nonadiabatic couplings between the two surfaces. The assumption of the Cayley tree topology is a stronger one for the surface crossing resonance part especially when the two surfaces are energetically symmetric, as we presently will assume.

We denote the conditional probability distribution for ${\mathrm{\Delta }}_j$ , if we were to consider only the anharmonic couplings $V_{\mathit{jk}}^{(s,s)}$ , as $f_V\left({\mathrm{\Delta }}_j\right)$ . Likewise, we will denote the distribution we would find if we were only to consider nonadiabatic couplings $t_{\mathit{jk}}^{(-1,1)}$ between the surfaces as $f_t\left({\mathrm{\Delta }}_j\right)$ . The probability distribution $f\left({\mathrm{\Delta }}_j\right)$ when accounting for both $V_{\mathit{jk}}^{(s,s)}$ and $t_{\mathit{jk}}^{(-1,1)}$ then is the convolution of $f_V\left({\mathrm{\Delta }}_j\right)$ and $f_t\left({\mathrm{\Delta }}_j\right)$ , assuming that the local topologies are independent of each other:

$$f\left(\mathrm{\Delta }\right)=\int d{\mathrm{\Delta }}^{\prime }{f}_V\left({\mathrm{\Delta }}^{\prime }\right)f_t(\mathrm{\Delta }-{\mathrm{\Delta }}^{\prime }).$$ [10]

For the distribution $f_{\alpha }\left({\mathrm{\Delta }}_j\right)$ ( $\alpha =$ V or t), we denote ${\mathrm{\Delta }}_{mp,\alpha }^{\mathrm{s}}$ (s = −1,1) as the most probable value on two surfaces. In the symmetric case considered here, ${\mathrm{\Delta }}_{mp, \alpha }^{\left(-1\right)} = {\mathrm{\Delta }}_{mp, \alpha }^{\left(1\right)} = {\mathrm{\Delta }}_{mp, \alpha }$ . We therefore introduce ${\mathrm{\Delta }}_{\mathit{mp}}$ as the most probable value for the distribution $f\left({\mathrm{\Delta }}_j\right)$.

In the limit of weak coupling when only a localized eigenstate of energy $E$ will overlap site $j$ , $f_V\left({\mathrm{\Delta }}_j\right)$ and $f_t\left({\mathrm{\Delta }}_j\right)$ can be obtained straightforwardly following previous work (7):

$$\begin{array}{c}{f}_{\alpha }\left({\mathrm{\Delta }}_j\right)={\left(\frac{3{\mathrm{\Delta }}_{mp,\alpha }}{2\pi }\right)}^{1/2}{{\mathrm{\Delta }}_j}^{-3/2}\exp \left(\frac{-3{\mathrm{\Delta }}_{mp,\alpha }}{2{\mathrm{\Delta }}_j}\right),\hfill \end{array}$$ [11]

where $\alpha$ = V or t, and ${\mathrm{\Delta }}_{mp,V}$ and ${\mathrm{\Delta }}_{mp,t}$ are given by:

$$\begin{array}{c}\sqrt{{\mathrm{\Delta }}_{mp,V}}=\sqrt{{\mathrm{\Delta }}_{mp}+\eta }{T}_{FR}(E;{\epsilon }_j)\hfill \\ \sqrt{{\mathrm{\Delta }}_{mp,t}}=\sqrt{{\mathrm{\Delta }}_{mp}+\eta }{T}_{NA}(E;{\epsilon }_j)\\ T_{FR}(E;{\epsilon }_{js})=\sqrt{\frac{2\pi }{3}}K\langle \left|{\mathrm{V}}^{(\mathrm{s},\mathrm{s})}\right|\rangle D_L^{FR}(E;{\epsilon }_{js})\\ T_{NA}(E;{\epsilon }_{js})=\sqrt{\frac{2\pi }{3}}{K}_t\langle \left|{\mathrm{t}}^{(-1,1)}\right|\rangle D_L^{NA}(E;{\epsilon }_{js})\end{array},$$ [12]

$T_{\mathit{FR}}(E;{\epsilon }_{\mathit{js}})$ is the transition parameter measuring whether the anharmonic coupling $V_{\mathit{jl}}^{(s,s)}$ has a significant probability to connect vibrational Fock states into resonance, $K$ is the number of anharmonically coupled states, and $D_L^{\mathit{FR}}(E;{\epsilon }_{\mathit{js}})$ is the local density of states thus coupled. $T_{\mathit{NA}}(E;{\epsilon }_{\mathit{js}})$ is the transition parameter measuring whether the nonadiabatic coupling $t_{\mathit{jk}}^{(-1,1)}$ can bring two states on the two distinct electronic surfaces into resonance, $K_t$ is the number of nonadiabatically coupled states, and $D_L^{\mathit{NA}}(E;{\epsilon }_{\mathit{js}})$ is the local density of states for nonadiabatic couplings.

The distributions $f_V\left({\mathrm{\Delta }}_j\right)$ and $f_t\left({\mathrm{\Delta }}_j\right)$ are Lévy distributions, and we can now exploit the fact that the convolution of two Lévy distributions as in Eq. 10 is also a Lévy distribution. The probability distribution $f\left({\mathrm{\Delta }}_j\right)$ also obeys a Lévy distribution:

$$\begin{array}{l}f\left(\text{Δ}\right)={\left(\frac{3{\text{Δ}}_{mp}}{2\text{π}}\right)}^{1/2}{\text{Δ}}^{-3/2}\exp \left(\frac{-\text{}3{\text{Δ}}_{mp}}{2\text{Δ}}\right)\\ f\left(k\right) = \mathcal{F}\left(f\left(\text{Δ}\right)\right) = \exp \left(-(1-\text{i}){\left(3k{\text{Δ}}_{mp}\right)}^{1/2}\right).\\ {\text{Δ}}_{mp}^{1/2} = {\left({\text{Δ}}_{mp,V}\right)}^{1/2} + {\left({\text{Δ}}_{mp,t}\right)}^{1/2}\end{array}$$ [13]

Solving for ${\mathrm{\Delta }}_{\mathit{mp}}$ self-consistently with the following equations:

$$\begin{array}{c}{\text{Δ}}_{mp} = \left(\eta +{\text{Δ}}_{mp}\right){\left[T_{FR}\left(E;{\epsilon }_{js}\right)+T_{NA}\left(E;{\epsilon }_{js}\right)\right]}^2,\end{array}$$ [14]

our simple expression for the transition criterion obtained by considering the breakdown of the stability of localized states is therefore:

$$T_{\mathit{FR}}(E;{\epsilon }_{\mathit{js}}) + T_{\mathit{NA}}(E;{\epsilon }_{\mathit{js}}) = 1.$$ [15]

By construction, T_FR and T_NA are positive. The theory thus predicts that the surface crossing assists delocalization of the vibrational states, and provides a quantitative description for the shift of the transition boundary between localized and extended regime when two quantum surfaces are coupled nonadiabatically. In the section below, we provide numerical results from a family of models inspired by a specific biophysically interesting system to support the predictions here.

3. Numerical Simulation for the BChl Dimer Exciton Transfer

Exciton transfer in BChl assemblies has been studied extensively both experimentally and computationally (47). Therefore, good estimates of the values of about 50 of the most relevant vibrational frequencies and the Huang–Rhys factors involved in excitation transfer as described in Section 1 are available for this system (48). To analyze the validity of the transition criterion $T_{\mathit{FR}}$ +$T_{\mathit{NA}}$ >1 for energy flow, we study a model inspired by the BChl dimer. Five modes in each monomer have been found to have particularly large Huang Rhys factors, and we include these in our model, together with the literature value of the nonadiabatic electronic coupling $V_t$ = 363 cm⁻¹ (49), which allows the electronic excitation to hop from one monomer to the other. The parameters of the system we use are shown in Table 1.

Table 1.

Five vibrational frequencies of the BChl monomer, with Huang–Rhys factors S_i and displacement factors αi

$f_i$	890	727	345	1,117	1,158
$S_i$	0.028	0.0266	0.0161	0.0103	0.0103
${\alpha }_i=\sqrt{S_i}$	0.169	0.163	0.127	0.101	0.101
V3	4.1	3.0	1.0	5.8	6.1
a	0.110	0.100	0.069	0.124	0.126

Data are taken from Table 2 in ref. 48. Below are shown the anharmonic constants and scaling parameters used for each mode, calculated using Eq. 5 in Ref. 13.

For this model, we can examine a large number of initial states “$i$” that span a range of vibrational excitation energies, and we can estimate both the $T_{\mathit{FR}}$ value for vibrational energy flow and the $T_{\mathit{NA}}$ value for the nonadiabatic surface crossing. To calculate the parameter describing intramolecular energy flow on a single surface, $T_{\mathit{FR}}$ , we proceeded as in Section 2.3.2 of ref. 50, and Section 4.A. of ref. 20. The calculation of $T_{\mathit{NA}}$ in terms of frequencies {${\omega }_i$}, vibrational quantum numbers $\{n_j$}, electronic vibration coupling strengths {${\alpha }_i$}, and nonadiabatic couplings $V_t$ is described in SI Appendix, Part C.

For all initial states in the vibrational Fock space, we explicitly integrate the time-dependent Schrödinger equation using a filtered basis set as was done in ref. 26 to determine whether a state is localized or delocalized. SI Appendix, section B shows the computed survival probability P(t) for specific example states, from which we obtain dilution factors as the long-time average of P(t) (Eq. 7). These calculations cover a time span $\tau =5ps,$ sufficiently long for P(t) to decay to its baseline in all the cases we have studied. For the 10-mode dimer model, which has fewer modes than the full BChl system, we studied higher-than-room temperature “thermal” vibrational energies so that the effect of vibrational anharmonicity and T_FR is evident. As we will see below, the energy flow threshold actually appears at an energy comparable to thermal energy for the natural system, which, owing to the size of its vibrational Fock space, can currently be treated only using the extended Logan–Wolynes analysis.

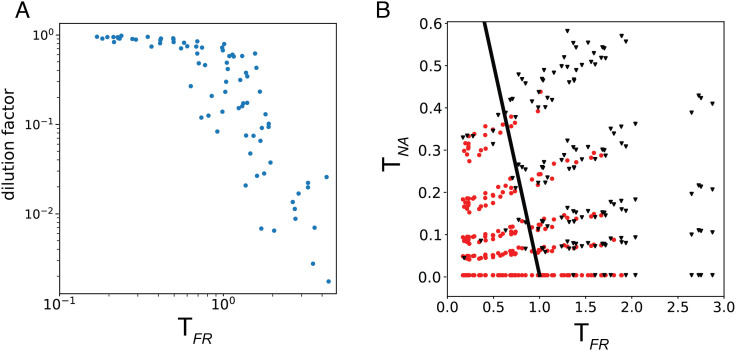
We can then compare the predicted dilution factors with the anharmonic threshold criterion $T_{\mathit{FR}}$ =1 for a sample of 80 vibrational states at different energies when $V_t=0$ . As can be seen in Fig. 2A, a sudden drop in the majority of the dilution factors coincides with the approach of T_FR to 1, the facile energy flow threshold of the local random matrix model. For practical purposes, we define a dilution factor ${\sigma }_c$ that corresponds to the geometric mean between the maximum value (1) and the minimum value, which is nonzero due to the finite size of our state space (51). For the distribution of σ values in Fig. 2A, we obtain ${\sigma }_c$ = 0.04.

Fig. 2.

Phase diagram for the 10-mode dimer model calculation. Each monomer has five modes with frequencies and Huang–Rhys factors given in Table 1. In this computation, we keep the vibrational couplings the same as in the natural system and vary the nonadiabatic coupling $V_{\mathrm{t}}$ with values $[0,50,100,200,363] {\mathrm{cm}}^{-1}$ . This is a realistic range for exciton transfer, as $V_t$ =363 cm⁻¹ is the value obtained from first-principles calculation (48). (A) Dilution factor $\sigma =⟨P(t\to \infty )⟩$ and $T_{\mathit{FR}}$ for 80 states when there is only anharmonic coupling V₃ with the scaling factors a shown in Table 1. (B) Scatter plot for the dilution factors in the plane of $T_{\mathit{FR}}$ vs. $T_{\mathit{NA}}$ . We choose the criterion ${\sigma }_c=0.04$ to classify states as localized or extended; this value is the square root of the minimum dilution factor that can be obtained on the single surface without nonadiabatic coupling in our simulation. Here, the red dotted data represent states with dilution factor $\sigma >{\sigma }_{\mathrm{c}}$ , and black inverted triangle data represent states with dilution factor $\sigma <{\sigma }_c$ . The solid black line is the theoretical prediction for the combined threshold $T_{\mathit{FR}}$ = 1 – $T_{\mathit{NA}}.$ The initial states have similar levels of vibrational excitation in both monomers; setting the excitation energy of one monomer to zero yields a very similar phase diagram (SI Appendix, Part B and Fig. S2). See SI Appendix, Part C for the procedure we used to estimate $T_{\mathit{FR}}$ and $T_{\mathit{NA}}.$

We then scanned the value of the nonadiabatic coupling strength $V_t$ over the range from zero up to the estimated value of 363 cm⁻¹ for the BChl dimer (49). While doing this, we keep the anharmonic couplings V₃ and scaling factors a constant, to study how the dilution factor varies separately with $T_{\mathit{FR}}$ and $T_{\mathit{NA}}$ . In Fig. 2B, we plot the resulting phase diagram in the plane of $T_{\mathit{FR}}$ and $T_{\mathit{NA}}$ for 80 states in a vibrational energy window between 5,000 and 40,000 cm⁻¹, allowing the nonadiabatic coupling to take on five values. The black line represents the boundary $T_{\mathit{FR}}$ =1− $T_{\mathit{NA}}$ , which is the transition boundary between localized and extended states obtained from the theory described in Section 2. As can be seen, the numerically determined transition regime corresponds well with the simple theoretical prediction of the threshold. The actual boundary is not sharp: Some localized states intermingle with extended states above the threshold and an occasional extended state is found below the threshold. The sources of this fuzziness include edge states that concentrate the energy in a single mode (11), the random character of resonances as expected in the local random matrix theory (36), and localization above the threshold that may signal the presence of quantum “scars” (52–55) that are remnants of classical trajectories or reflect the symmetry of the Hamiltonian when $\delta E=0$ (8).

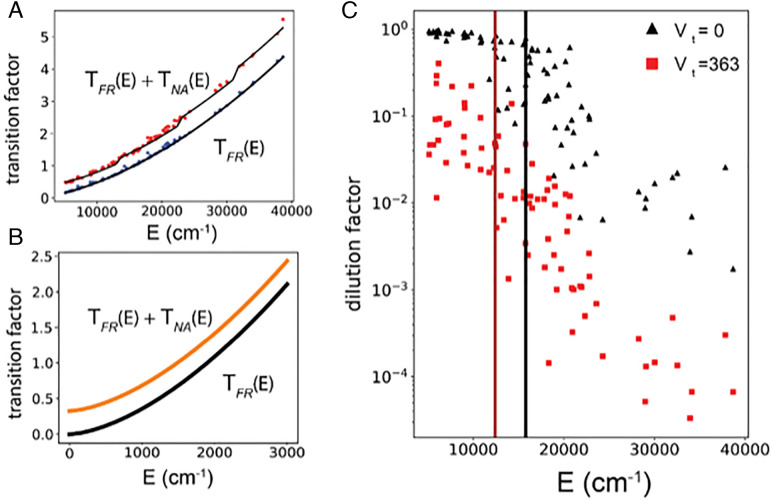
It now becomes possible to compare the effect of nonadiabatic couplings reflected in $T_{\mathit{NA}}$ on the energy flow threshold relative to the purely anharmonic vibrational couplings case. For the 10-mode dimer model, Fig. 3A plots $T_{\mathit{FR}}\left(E\right)$ vs. dimer energy $E$ for the electronically uncoupled molecules and $T_{\mathit{FR}}\left(E\right)+T_{\mathit{NA}}\left(E\right)$ for the two monomers coupled by $V_t$ = 363 cm⁻¹. In the 10-mode model, the threshold occurs at about 15,000 cm⁻¹ and shifts down in energy by about 25% when the electronic coupling is turned on, allowing surface hopping. While our anharmonic Hamiltonian numerical simulation cannot be used to study molecules with more degrees of freedom by exact quantum dynamics, the analysis in Section 2 allows us to calculate the thresholds for much larger systems that are still more realistic. In Fig. 3B, we show the calculated $T_{\mathit{FR}}\left(E\right)$ and $T_{\mathit{FR}}\left(E\right)+T_{\mathit{NA}}\left(E\right)$ for the 100-mode model of the BChl dimer system (50 modes from ref. 48 in each monomer). As expected, the threshold for facile energy flow is now much lower, around 2,000 cm⁻¹, and the downward shift of the threshold due to the additional nonadiabatic coupling still amounts to 25% of the energy. The thermal energy at room temperature of the 100-mode system is $3,632 \mathrm{c}{\mathrm{m}}^{-1}$ , which lies somewhat above the threshold of Fig. 3B. The dilution factor σ vs. the dimer energy $E$ for the 10-mode dimer model is shown in Fig. 3C. We can see that the predicted shift of the quantum ergodic transition energy $E_c$ (vertical lines) agrees well with the numerical computation. SI Appendix, Fig. S3 also shows how the dilution factor depends on $T_{\mathit{FR}}$ +$T_{\mathit{NA}}$ for different values of the nonadiabatic coupling.

Fig. 3.

(A) The transition factor $T_{\mathit{FR}}\left(E\right)$ for the single surface, and the transition factor $T_{\mathit{FR}}\left(E\right)+T_{\mathit{NA}}\left(E\right)$ for the two surface systems (surface crossing amplitude $V_t=363c{m}^{-1}$ ) vs. the dimer vibrational energy E (cm⁻¹) for the 10-mode dimer model (five modes in each monomer). The anharmonic constants and scaling factors $a_i$ for each mode “$i$” used in the computation are listed in Table 1. To estimate $T_{\mathit{FR}}$ , the geometric mean value of the typical scaling factors: $a$ = 0.10 was used. By assuming equal vibrational energy in each monomer, we can estimate $T_{\mathit{FR}}\left(E\right)$ and $T_{\mathit{FR}}\left(E\right)+T_{\mathit{NA}}\left(E\right)$ vs. the dimer energy E (cm⁻¹) (black curve). $T_{\mathit{FR}}\left(E\right)$ (blue) and $T_{\mathit{FR}}\left(E\right)+T_{\mathit{NA}}\left(E\right)$ (red) for the 80 states simulated in Fig. 2 are also shown. (B) $T_{\mathit{FR}}\left(E\right)$ (black) and $T_{\mathit{FR}}\left(E\right)+T_{\mathit{NA}}\left(E\right)$ (orange) for the two surface systems ( $V_t=363c{m}^{-1}$ ) vs. the dimer vibrational energy E (cm⁻¹) for 100-mode BChl dimer (50 modes in each monomer). We assume that the energy is statistically shared between monomers in making the estimates of $T_{\mathit{FR}}$ and $T_{\mathit{NA}}$ . We estimate anharmonic scaling factor $a$ as described in ref. (13). (C) The dilution factor $\sigma$ vs. the dimer energy $E$ for the 10-mode dimer model. The dilution factor for the case $V_t=0$ (black, triangle) is shown with the transition energy $E_c=15,900 \mathrm{c}{\mathrm{m}}^{-1}$ ( $T_{\mathit{FR}}\left(E\right)=1$ ) for the single surface (black vertical line). The dilution factors for the case $V_t=363\mathrm{c}{\mathrm{m}}^{-1}$ (red, square) are shown with the transition energy $E_c=12,300 \mathrm{c}{\mathrm{m}}^{-1}\left(T_{FR}\left(E\right) +T_{NA}\left(E\right) =1\right)$ for the two surface systems (brown vertical curve).

We also analyzed the model with only nonadiabatic surface crossings on the many-dimensional surface (V₃ = 0). We compute the survival probability P(t) = |<t = 0|t>|² of initial zero-order vibrational states |t = 0> using the Huang–Rhys factors shown in Table 1. The numerical results for the survival probability are shown in SI Appendix, Fig. S1. We find that energy flow indeed can occur between two multidimensional harmonic vibrational manifolds solely through the nonadiabatic electronic coupling as envisioned by Heller (14).

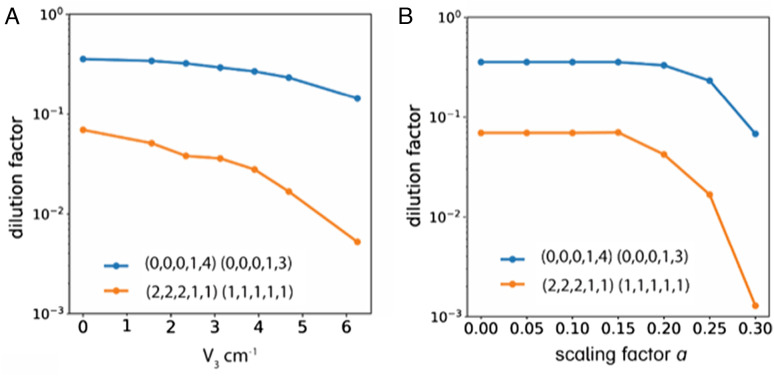
Finally, we examined how quickly increased anharmonicity turns on facile energy flow by varying both the cubic coupling strength V₃ and the scaling parameter a that determine how rapidly couplings of quartic and higher order decrease with $m$ . As shown in Fig. 4A, the near-edge state (where most vibrations are not excited) has a larger dilution factor and requires a stronger anharmonic coupling to mix with other states than does the interior state (where all modes are excited), although both states have a similar energy (11, 56). As shown in Fig. 4B, there is a threshold value of a required for the dilution factor to decrease as observed previously for a purely vibrational model system (26), indicating that higher-order couplings are important for the transition to free energy flow. The predicted dependence of energy flow on anharmonicity as a parameter could be tested in future simulations of the present Hamiltonian using ion trap quantum simulators (57, 58), where the nearly harmonic wells containing the ions could be detuned to introduce anharmonicity purposely.

Fig. 4.

Dependence of the dilution factor $\sigma$ on the anharmonic coupling strength V₃ and the scaling factor a. $V_t$ is held constant at 363 cm⁻¹. In both cases, the state close to the edge of state space mixes less even though both states are at similar total energy. (A) Dilution factor for a near-edge state (blue) and an interior state (orange) as a function of cubic coupling strength V₃ with a = 0.25 (B) Dilution factor for a near-edge state (blue) and an interior state (orange) as a function of scaling factor a when there is a threshold between a = 0.2 and 0.3 where the dilution factor begins to decrease rapidly.

4. Discussion

Using analytical theory and exact quantum dynamics, we have explored the interplay between energy flow through intramolecular Fermi resonances and electronic surface crossing. The simple theory based on the Logan–Wolynes treatment of local random matrix models turns out to locate reasonably well the transition from localized behavior to facile energy flow.

These ideas were explored in the context of a simplified model inspired by exciton transfer in the BChl dimer. The full implications of the present analysis for actual photosystems and other biological processes that involve surface crossing (such as electron and coupled proton–electron transfer) will require further investigation, but some qualitative ideas that have emerged are worth describing already.

The threshold for quantum energy flow is determined by both nonadiabatic surface crossing and by Fermi resonances in the range of thermal excitation energies for chromophores such as BChl. The Fermi-resonant contribution is dominant, even though such nonlinear resonances are not explicitly considered in most current models; instead, their effect is subsumed through the introduction of “dephasing” in relaxation theory treatments (59–64) or by broadening the bath spectrum in path integral treatments (65–68).

Above the threshold for facile energy flow, most quantum states in the complex chromophores are delocalized over many modes, but a few states appear to remain localized over a few vibrational motions. This coexistence of specifically regular and more chaotic behavior, while familiar in finite dimensional quantum systems, (52) is generally thought to disappear in the infinite system limit (54, 69–71). This phenomenon of coexisting regular and quantum chaotic behavior may be part of the origin of the controversy concerning the amount of quantum entanglement and coherence in natural photosynthetic systems (72–77) as manifested in ultrafast nonlinear optical experiments. In such experiments, one of course must also account for the initial excitation event, as well as the energy and coherence transfer process (73). In much of the discussion of these experiments, it is assumed that vibrational and electronic excitations are clearly separable, but our argument suggests that they can be intimately mixed together.

The models discussed here have far fewer modes than most real biological systems which in addition have enormous numbers of protein vibrational modes and solvent modes, although most of these will be rather weakly coupled. The dephasing effect of such modes can be treated by Logan–Wolynes self-consistent analysis which shows that such dephasing would further smear the transition (7). In the vicinity of the localization transition, their analysis suggests that external dephasing also can act to speed quantum transport as has recently been highlighted (75). While ultimately increased dephasing will lead to incoherent hopping, the present model calculations, showing coexistence of localized and extended states in natural systems, suggest that both of these effects of external dephasing may be simultaneously manifested.

In the light-gathering apparatus, typically many more than two chromophores will be coupled together. It will be interesting to see how the Fermi resonance mechanism can play a role for those more extended systems. In addition, the static disorder of the basic chromophore energies from the protein environment must be superimposed on the effects in the present model.

While the nonadiabatic couplings are quite large for the exciton transfer problem, they are smaller for electron transfer between redox centers embedded in proteins. Nonetheless, the issue of the interplay of reaction kinetics, resonances, and internal quantum energy flow can be important (60). It may be especially relevant for strongly exothermic reactions which are usually assigned to the so-called abnormal regime of Marcus theory. We hope to address that problem using a generalization of the present treatment for strongly asymmetric wells in the future.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.