The Growth Dependent Design Constraints of Transcription-Factor-Based Metabolite Biosensors

Abstract

Metabolite biosensors based on metabolite-responsive transcription factors are key synthetic biology components for sensing and precisely controlling cellular metabolism. Biosensors are often designed under laboratory conditions but are deployed in applications where cellular growth rate differs drastically from its initial characterization. Here we asked how growth rate impacts the minimum and maximum biosensor outputs and the dynamic range, which are key metrics of biosensor performance. Using LacI, TetR, and FadR-based biosensors in Escherichia coli as models, we find that the dynamic range of different biosensors have different growth rate dependencies. We developed a kinetic model to explore how tuning biosensor parameters impact the dynamic range growth rate dependence. Our modeling and experimental results revealed that the effects to dynamic range and its growth rate dependence are often coupled, and the metabolite transport mechanisms shape the dynamic range-growth rate response. This work provides systematic understanding on biosensor’s performance under different growth rates, which will be useful for predicting biosensor’s behavior in broad synthetic biology and metabolic engineering applications.

Introduction

Metabolite-responsive transcription factor (MRTF)-based biosensors have broad applications in synthetic biology and metabolic engineering, ranging from metabolic detection^1–4 screening and selecting for high-metabolite-producing strains^5–7, dynamic metabolic control^8–13, to strain functional evolution^14,15. Nature has evolved various MRTFs that can be harnessed to create biosensors for a wide range of metabolites^16–20. Protein engineering and directed evolution of MRTF have further expanded the range of compounds which can be detected^21–23. Additionally, promoters regulated by MRTFs can be engineered to tune sensitivity and dynamic range^24,25, enabling precise control of biosensor’s performance^26,27. These biosensors can be further layered to create complex circuits^28,29, which require a well-defined performance for correct operation³⁰.

Most MRTF-based biosensors were designed and tested in well-defined laboratory conditions using rich growth media. These biosensors were often characterized using fluorescent proteins whose expression has little burden to growth and other cellular processes. However, during applications, biosensors are often deployed in different growth environments and used to control burdensome genes that affect cell growth rate. Changes in cell growth rate has been shown to impact several cellular parameters including plasmid copy numbers³¹, ribosome concentration and mass fraction³², transcription factor abundance and concentration³³, gene expression rate^34,35, and average cellular volume^36,37. Biosensor operation relies on these shared cellular resources, so changes in cell growth rate will unavoidably affect the expression of MRTF and its regulated genes. Additionally, cell growth dilutes all molecular components as the volume of the cell increases (Fig. 1A), so faster growth may lead to a net reduction in the concentration of molecules needed for biosensor operation^34,38. Thus, when cell growth rate changes, it may significantly alter a sensor’s behavior, leading to undesirable performance. For example, in two-stage dynamic metabolic control, engineered microbial cells need to shift from a high-growth phase to a low-growth production phase¹². Biosensors used in two-stage dynamic metabolic control have to be optimized to perform under both growth conditions^39,40.

Figure 1. Molecular components contributing to the operation of a metabolite-responsive transcription factor (MRTF)-based biosensor.

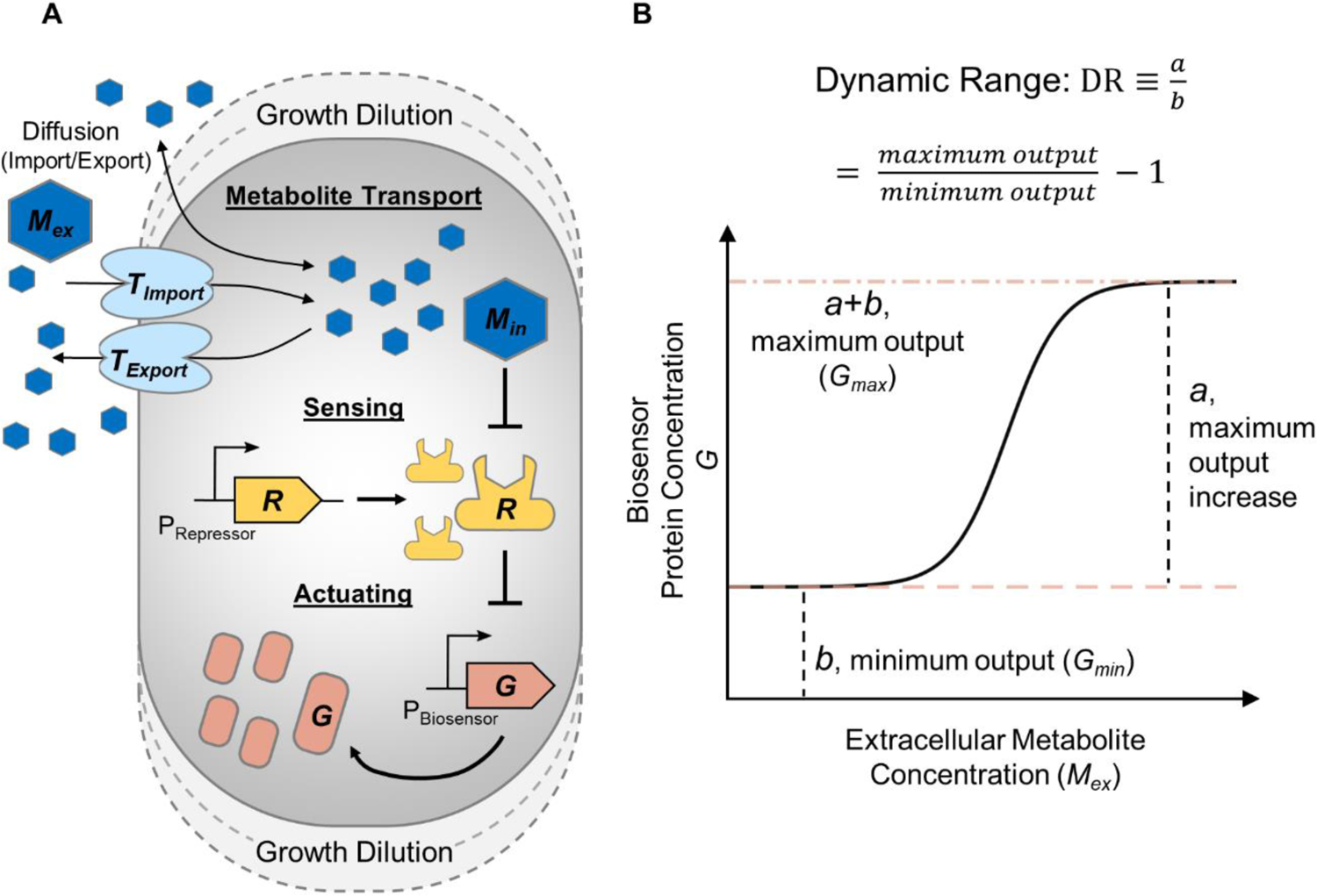
(A) Schematic of general components contributing to overall biosensor response. Extracellular metabolite enters the cell, becoming intracellular metabolite. Intracellular metabolite represses the DNA-binding activity of the MRTF. The MRTF represses the biosensor’s promoter, which controls the expression of a reporter protein. All components are universally affected by growth rate through dilution as the cell volume expands. B) Minimum output, maximum output, and dynamic range (DR) are critical parameters characterizing the dose-response curve of a MRTF-based biosensor.

Many MRTF-based biosensors use a repressed-repressor architecture^41,42. In this architecture, the MRTF represses gene expression from its cognate promoter in the absence of its target metabolite, but its expression repression activity is antagonized by the presence of a specific intracellular metabolite (Fig. 1A). The output of a biosensor is the steady-state expression level of the controlled gene at a particular target metabolite concentration (Fig. 1B). A sensor’s behavior can be characterized by its minimum output in the absence of target metabolite, its maximum output under a saturating concentration of extracellular target metabolite, and its dynamic range (DR) which is defined as the ratio of the maximal increase in biosensor output relative to the its minimum output (Fig. 1B)²⁶. In real applications, it is often desirable to keep a low minimum output to prevent unwanted gene expression in the absence of target metabolite⁴³, a high maximum output to reach high signal-to-noise ratios⁴⁴, and a large DR. Previous studies have shown how TF-repressed gene expression varies under different cell growth rates³⁴, yet, little is known about how growth rate affects a biosensor’s behavior. Experimentally characterizing biosensor’s behavior under a wide range of growth rates, for example by growing the biosensor in medium with different nutrient conditions both with and without the target metabolite, is labor intensive. Thus, it would be beneficial to develop quantitative models to understand how biosensor operation is impacted by growth rate to avoid undesirable sensor performance due to the change of growth rate.

In this work, we use three repressed-repressor type of biosensors to explore the effect of growth rate to sensor behavior. Interestingly, we found that while all sensors displayed both decreasing minimum and maximum outputs, the DR could have either a positive or negative growth rate dependence. By integrating experimental data with kinetic modeling, we provide a mathematical framework to reveal biosensor’s behavior under changing growth conditions. We show how different parameters of the biosensor promoter and TF expression can lead to either a positive or negative dynamic range-growth rate (DR-μ) dependence. Additionally, our results show how growth rate-dependent membrane transport mechanisms of the target metabolite shape the overall DR-μ dependence. Our model and experimental results demonstrate a coupling between DR and sensitivity of DR to changes in growth rate for most biosensor designs, which implies a trade-off between high DR and low sensitivity objectives. Altogether our work provides a framework for tuning or predicting a biosensor’s behavior under varying growth conditions, which will be useful for a wide range of biosensor applications in synthetic biology.

Results

Growth Rate Dependence of Biosensor Dynamic Range

To study the relationship between sensor DR and cell growth rate of MRTF-based biosensors, we first tested three TF-promoter systems with a repressed-repressor architecture, TetR-P_tet (Fig. 2A), LacI-P_LacUV5⁴² (Fig. 2B), and FadR-P_AR (Fig. 2C)^45–47 that sense extracellular chemicals anhydrotetracycline (aTc), isopropyl β-D-1-thiogalactopyranoside (IPTG), and fatty acid (FA), respectively. All these three sensors have been commonly used for various applications^42,45. For each biosensor, we used a red fluorescent protein (RFP) as a reporter. Each biosensor construct was cloned into plasmids with the stringently regulated SC101 origin of replication to reduce copy number variation due to changes in growth rate^31,48. Additionally, for the FA-sensor, native regulations of the fadR and fadD genes were removed, and fadE was knocked-out to prevent FA from being used as a carbon source for growth through β-oxidation⁴⁷. Thus, all three target metabolites are primarily non-metabolizable activators of the biosensor output gene.

Figure 2. Minimum output, maximum output, and dynamic range of P_Tet, P_LacUV5, and P_AR biosensors at different growth rates.

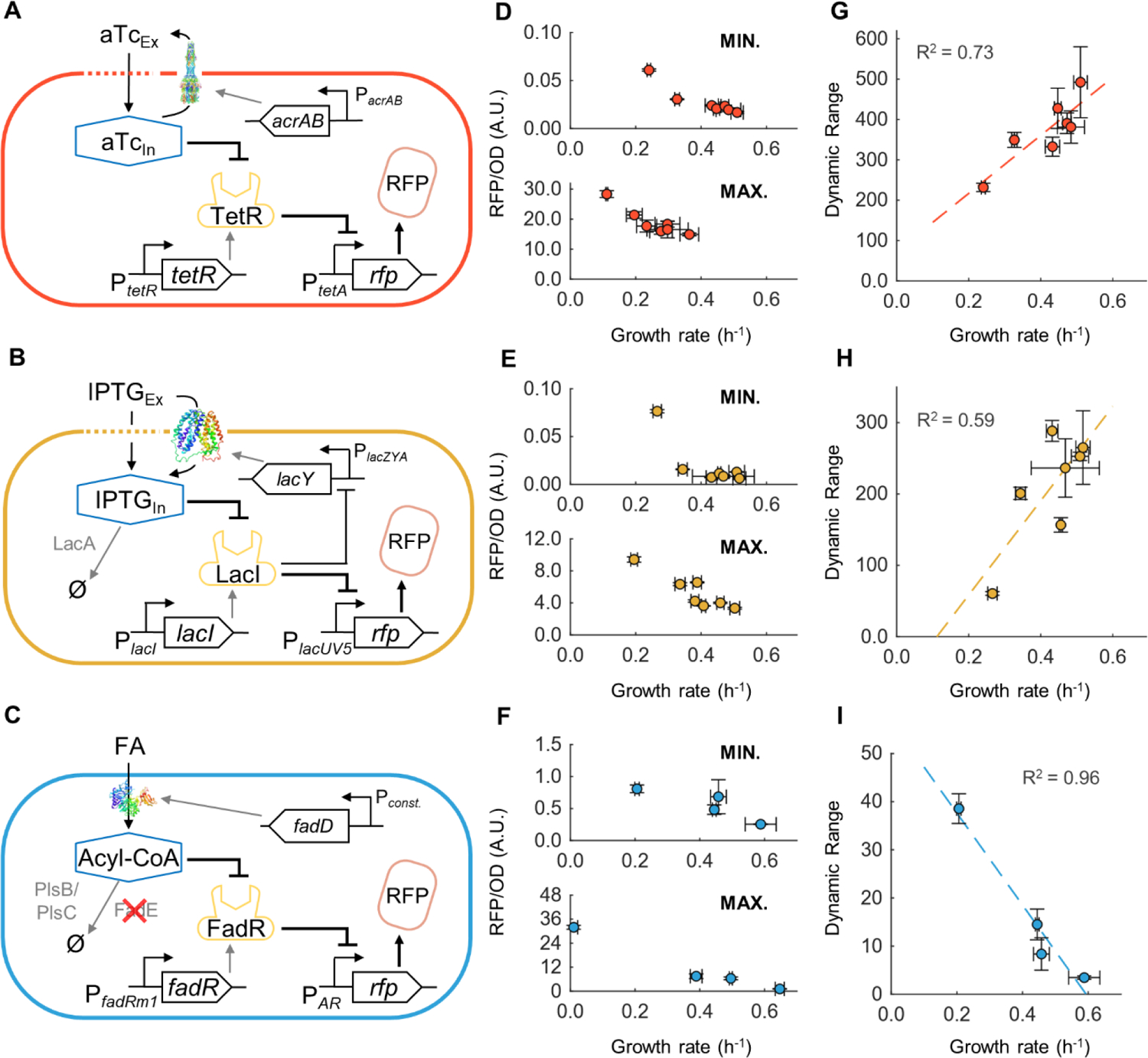
(A-C) Schematic of cellular interactions for the (A) TetR-based biosensor, (B) LacI-based biosensor and (C) FadR-based biosensor. (D-F) Minimum (top) and maximum (bottom) output of the biosensor at different growth rates for (D) TetR, (E) LacI, and (F) FadR-based biosensors. (G-I) Calculated dynamic range of biosensor at different growth rates for (G) TetR, (H) LacI, and (I) FadR-based biosensors. Error bars are S.D. of biological replicates, n=3. Dashed line: Line of best fit.

To manipulate cellular growth rate, biosensor cells were grown in minimal medium supplemented with different commonly-used carbon sources⁴⁹ including acetate, pyruvate, glycerol, sorbitol, succinate, glycerol with amino acids, and xylose. These differing media conditions supported a range of growth rates from 0.24–0.51 h⁻¹ (see Supplemental Table S3 for a summary of media conditions and growth rates). To quantify the effect of growth rate on DR, sensor minimum and maximum outputs were measured under exponential growth phase under different media conditions either without or with high concentrations of the target metabolites, respectively. The target metabolite concentrations used for aTc (1000 nM)⁴², IPTG (1 mM)²⁶, and FA (4 mM)⁴⁵ were previously shown to saturate the output of these biosensors. Our results show that both minimum and maximum outputs decreased with increasing growth rate for all three sensors (Fig. 2D, 2E, 2F). At a saturated target metabolite concentration (i.e. maximum output) a sensor’s promoter is equivalent to a strong constitutive promoter, while in the absence of the target metabolite (i.e. minimum output), a sensor’s promoter is equivalent to a repressor repressed promoter. Previous studies have shown that protein concentration under the control of either a constitutive promoter or a repressor controlled promoter decreases with increasing growth rates³⁴. Thus, our observations are consistent with previous studies. Additionally, we observe that cell growth rates in maximum output are always lower than in minimum output (Fig. 2D, 2E, 2F), suggesting growth burden from activation of these sensors, even when they were only used to express an RFP reporter protein. These observations clearly demonstrated the influence of cell growth rate to sensor output as well as the effect of sensor’s function to cell growth, which cannot be ignored during biotechnology applications^50,51.

We next calculated the DR of each biosensor under different growth rates. Interestingly, the aTc and IPTG sensors displayed an increasing DR with increasing growth rate (Fig. 2G, 2H), while the FA sensor showed a decreased DR with increasing growth rate. Our results showed that for aTc and IPTG sensors, although both the minimum and maximum outputs decreased with growth rate, the minimum output decreased more rapidly than the maximum output, thus leading to a relative increase in the ratio of the two, as quantified by the DR. In contrast, the FA strain has a negative DR trend with increasing growth rate (Fig. 2I) because the maximum output decreased more rapidly than the minimum output for this system. One major difference between the aTc/IPTG biosensors, and the FA biosensors is that FA transport requires the protein FadD to enter the intracellular space, whereas aTc and IPTG can diffuse into the cell (Fig. 2A, 2B, 2C). The concentration of these transport proteins is growth-dependent, particularly since FadD is expressed from a constitutive promoter³⁴, which may contribute to the rapid decline in maximum biosensor output at higher growth rates. Thus, these results suggest that although all three biosensors have the same general architecture, their DR-μ dependency are different and may be a tunable property of biosensors.

To gain further insights into the different DR-μ dependencies, we developed a kinetic model to describe the intracellular concentration of the biosensor’s output protein (G) and the intracellular concentrations of TF repressor (R) and target metabolite (M_In) at different growth rates. The volumetric production rate of each species is balanced by dilution due to cellular volume expansion during cell growth. Additionally, transport of the target metabolite across cell membrane via either passive transport by diffusion or enzyme-facilitated active transport were also considered. For active transport, the concentration of protein transporters can also be affected by dilution due to cell growth. For a detailed description of the model, see Supplemental Note 1.1.

In the absence of the target metabolite, an analytical solution can be derived to describe the minimum output (G_min) at steady state (see Supplemental Note 1.2 for details):

$$G_{\mathit{\text{min}}}=\frac{1}{\mu }\left(b_G+\frac{a_G}{1+\frac{b_R}{K_G\mu }}\right)$$ (1)

where μ represents cell growth rate. Parameters b_G, a_G, and K_G are intrinsic to the biosensor and describe the basal expression level, the strength of activated expression, and the MRTF-promoter dissociation constant, respectively (Fig. 1B). b_R describes the constitutive expression rate of MRTF. While the production rate of the MRTF is constant with growth, the total concentration of MRTF (R = b_R / μ) is decreasing due to dilution by cell growth (see Supplemental Note 1.1 and 1.2 for details). Because both the biosensor output protein (G) and its repressor (R) are being diluted by growth, we calculate the dependence of G_min on μ to understand the combined effect:

$$\frac{d}{d\mu }\left(G_{\mathit{\text{min}}}\right)=\frac{-1}{{\mu }^2}\left(b_G+\frac{a_G}{{\left(1+\frac{b_R}{K_G\mu }\right)}^2}\right)$$ (2)

The dependence of G_min on μ is negative for all parameter values. Thus, G_min always decreases with growth rate, and is consistent with our experimental observation for all three biosensors (Fig. 2D, 2E, 2F). The dependence of maximum output and DR on growth rate depend on sensor parameters and are not monotonic. A biosensor’s DR can be described as:

$$DR=\frac{a_G{b}_R}{K_G\mu }\frac{M_{in}}{\left(a_G+b_G+\frac{b_G{b}_R}{K_G\mu }\right)\left(K_R+M_{In}+\frac{b_R{K}_R}{K_G\mu }\right)}$$ (3)

where K_R represents the dissociation constant between the target metabolite and MRTF. Finally, M_in describes the intracellular target metabolite concentration which can also be a function of the growth rate, depending on the target metabolite’s transport kinetics. To understand how the model parameters affect the DR-μ dependency, we next calculate the derivative of DR with respect to growth rate μ (dDR/dμ):

$$\frac{d}{d\mu }\left(DR\right)=\frac{a_G{b}_R}{K_G}\frac{{\text{M}}_{in}\left(\frac{b_G{K}_R{b}_R{}^2}{K_G{}^2{\mu }^2}-\left(a_G+b_G\right)\left(K_R+M_{in}\right)\right)+K_R\frac{d{M}_{in}}{d\mu }\left(a_G+b_G+\frac{b_G{b}_R}{K_G\mu }\right)\left(\mu +\frac{b_R}{K_G}\right)}{{\mu }^2{\left(a_G+b_G+\frac{b_G{b}_R}{K_G\mu }\right)}^2{\left(K_R+M_{in}+\frac{b_R{K}_R}{K_G\mu }\right)}^2}$$ (4)

Our modeling result suggests that depending on the parameter values of a biosensor and its intracellular target metabolite concentration, dDR/dμ can be either positive (increasing with growth rate) or negative (decreasing with growth rate), depending on the sign of S:

$$S=M_{in}\left(\frac{b_G{K}_R{b}_R{}^2}{K_G{}^2{\mu }^2}-\left(a_G+b_G\right)\left(K_R+M_{in}\right)\right)+K_R\frac{d{M}_{in}}{d\mu }\left(a_G+b_G+\frac{b_G{b}_R}{K_G\mu }\right)\left(\mu +\frac{b_R}{K_G}\right)$$ (5)

Tuning DR-μ Dependence Through TF Expression

To understand how sensor parameters affect the growth dependence of G_min, G_max, and of the biosensor’s DR (i.e. dDR/dμ), we first targeted to the aTc-inducible sensor and tuned the production rate of the MRTF repressor TetR (i.e. b_R). According to our model, both G_min and G_max should decrease with increasing b_R at a fixed growth rate, regardless of other parameters (see Equation (1) and (S12)). Experimentally, we placed TetR under the control of a constitutive promoter and a library of RBS with different strengths to vary the TetR production rate (Fig. 3A), while not changing the promoter or RBS sequence of the biosensor output gene. When growing the library of cells at a fixed growth rate (in glycerol minimal medium), both G_min and G_maxdecreased with increasing TetR levels for 3.7- and 1.2-fold change across the library, respectively (Fig. 3B, 3C), which matches our analytical model predictions (Fig. 3E, 3F). Our model also shows that G_min is sensitive to changes in TetR production rate at low levels of TetR, while it becomes less sensitive at higher TetR levels (Fig. 3E), which matches our observation of high sensitivity in G_min to TetR expression when TetR is low (Fig. 3B). We further observe that under our experimental parameter regime, G_min is more sensitive to changes in TetR production rate than G_max (Fig. 3B, 3C), thus affecting DR mostly by lowering the leaky expression level and leading to an increasing DR (Fig. 3D), consistent with model prediction (Fig. 3G). Additionally, we fit our model to the experimentally measured TetR expression, G_min and G_max (see Supplemental Note 2.2 for details). From the fitted model, we calculated the DR and observed a good agreement between the model and the observed DR-TetR expression trend (R² = 0.49). Overall, these experimental observations are qualitatively consistent with numerical simulations with increasing b_R values and with model fitting, thus validating our model.

Figure 3. Tuning biosensor DR through changing TetR expression level at a constant growth rate.

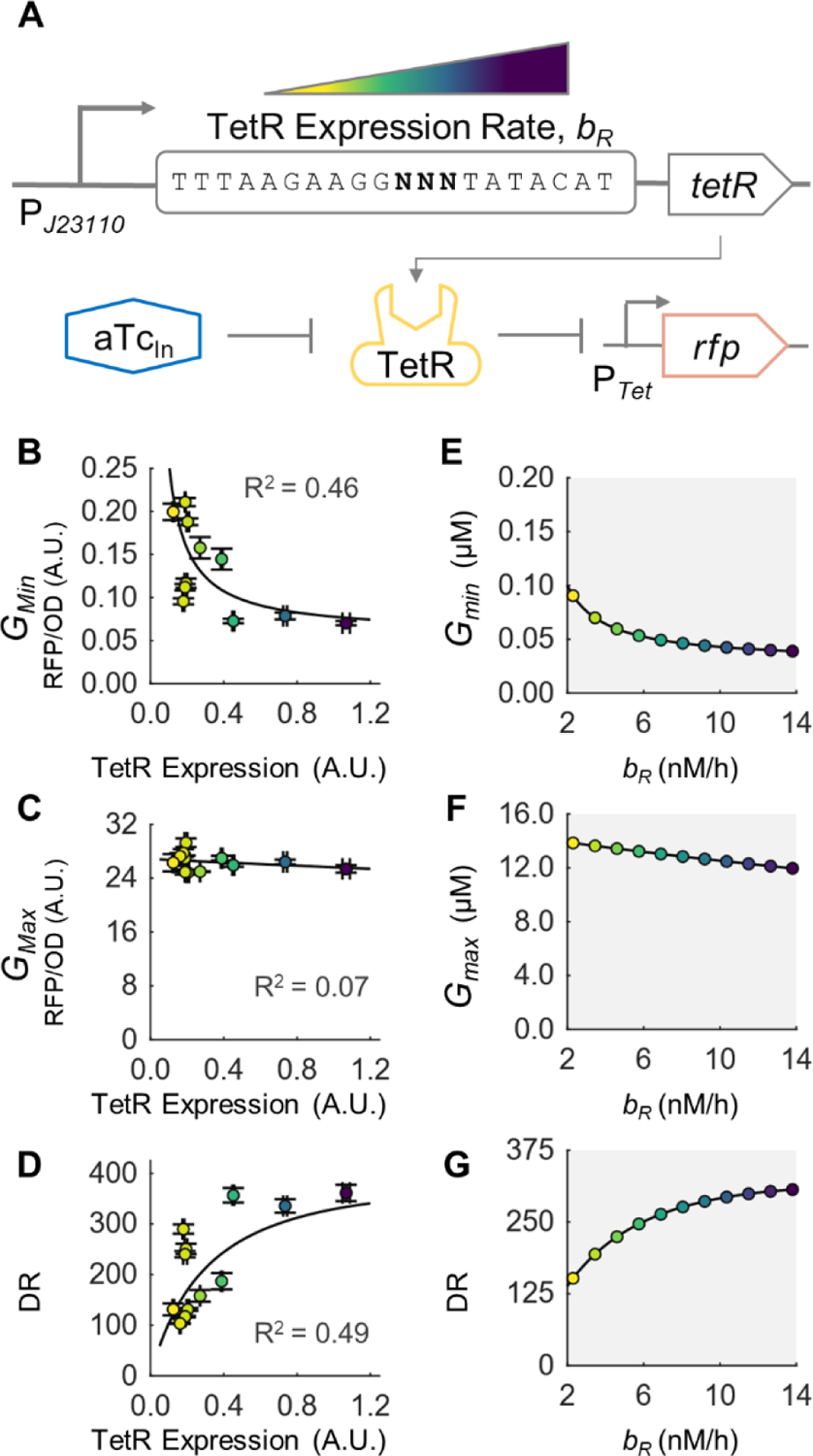
(A) Schematic of the TetR gene used to tune TetR expression level (b_R). The TetR level was varied by using a library of TetR genes with different RBS strength. (B-D) Experimentally measured (B) minimum biosensor output, G_min, (C) maximum biosensor output, G_max, and (D) dynamic range of TetR RBS library members with varying TetR expression levels. Error bars represent S.D., n=3. RBS sequences and their corresponding TetR expression levels, G_min, G_max, and DR are given in Supplemental Table S6. Solid line is fit of model to the experimental data (details in Supplemental Note 2.2) (E-F) Numerical model simulations of (E) minimum output, (F) maximum output, and (G) DR for different values of b_R. Parameter values and ranges are given in Supplemental Table S1.

We next measured how G_min, G_max, and DR change with growth rate under different TetR production rate (Fig. 4A). According to Equation (2), as b_R increases, the dependence of G_min on μ is expected to be less negative. Experimentally, we indeed observed a less negative slope on the G_min- μ plot with a higher TetR expression (Fig. 4B). This result indicates that when TetR production is insufficient (low TetR production), leaky expression becomes worse at lower growth rates, while a high TetR production rate can make the sensor less leaky across a wide growth rate range. The dependence of G_max on growth rate was negative and had similar slope for low and medium TetR production rates and a reduced slope at high TetR production rates (Fig. 4C). This result indicates that at high TetR expression, maximal induction may not be achieved at lower growth rates. Finally, Equation (5) predicts that lowering the TetR production rate b_R should reduce the DR-μ dependence, changing it towards a negative regime. Our experimental results indeed showed a less positive dDR/dμ value at a lower TetR production rate (Fig. 4D). Overall, our result showed that for the aTc biosensor, a high TetR production rate provides high DR, however at a cost of higher growth dependence.

Figure 4. The growth rate dependence of DR for TetR-based biosensors with varying TetR production rates.

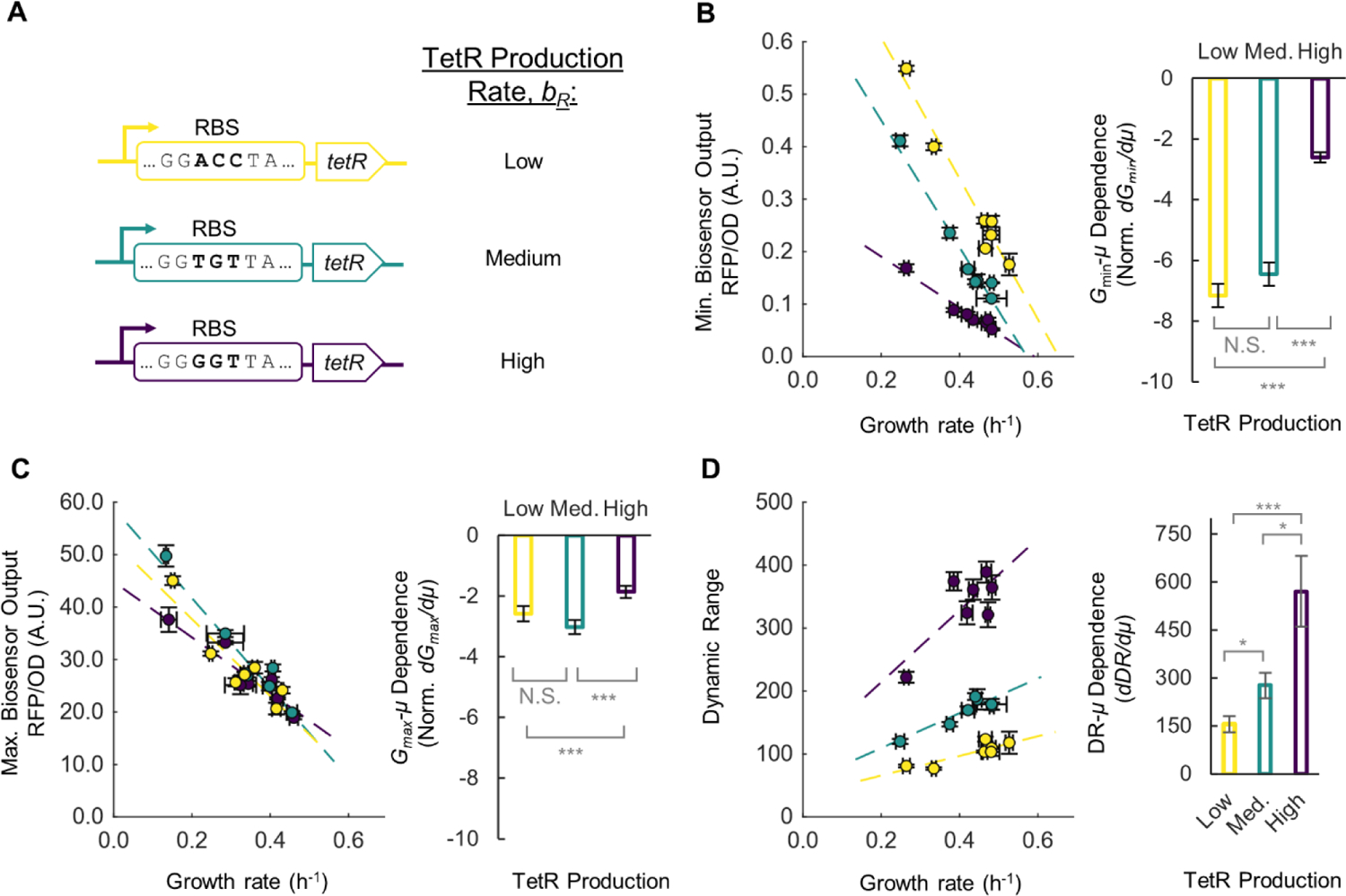
(A) Three tetR genes with different RBS strength to produce TetR at low (yellow), medium (green), and high (purple) levels. (B) Minimum biosensor output at varying growth rate for each library member (left) and the dependence of minimum output on growth rate (right). (C) Maximum biosensor output at varying growth rate for each library member (left) and the dependence of the maximum output on growth rate (right). (D) DR at varying growth rate for each library member (left) and the dependence of DR on growth rate (right). dG_min/dμ and dG_max/dμ are normalized to the average G_min and G_max, respectively, from all data. Error bars of individual data points are S.D., n=3. Error bars for G_min, G_max, and DR-μ dependence are standard error of the slope. A Student’s t-test was conducted between each pair of growth rate dependence data, stars indicate significant difference (N.S., not significant; * p < 0.05; ** p < 0.01; *** p < 0.001).

Metabolite Transport Affects DR-μ Dependence

Our experimental results on the aTc sensor showed that DR increased with both growth rate and TetR production rate. We next examine which parameter space can simultaneously support these trends and whether such trends can inform us on the parameters of the target metabolite transport mechanism. An extracellular target metabolite can enter or exit a cell via either passive transport (metabolite concentration gradient related) or protein-facilitated active transport (growth rate related), or a combination of both mechanisms. If passive transport is the only mechanism, the intracellular target metabolite concentration is mostly determined by extracellular target metabolite concentration and has little influence from growth rate. In this case, our mathematical analysis indicates that sensor DR cannot increase with both growth rate and MRTF production rate (see Supplemental Note 1.3). On the other hand, DR can increase with growth rate and MRTF production rate if intracellular aTc concentrations are also increasing with growth rate (see Supplemental Note 1.3). One way this could occur is when aTc membrane transport involves proteins whose steady state concentration is regulated by growth rate via cell dilution. Indeed, previous studies demonstrated that aTc can be exported by the AcrAB-TolC multi-drug efflux pump⁵², and demonstrate that the expression of acrAB is elevated at lower growth rates⁵³. Together, this may lead to reduced aTc concentrations at low growth rates due to elevated efflux. To elucidate this mechanism, we incorporated both passive transport and active export to our model (Fig. 5A) and explored the parameter space that provides positive dependence of DR on both growth rate and TetR production rate. When active export is incorporated in the model, intracellular target metabolite becomes growth-dependent, which causes the gradient-dependent passive export to also be growth-dependent (Fig. S1A). Both passive and active transport rates were varied over 4-orders of magnitude to explore a large parameter space, starting from parameter settings where the target metabolite’s passive and active export rates are equal and considering different target metabolite concentration regimes (M_in » K_M,ex, M_in = K_M,ex, or M_in « K_M,ex, Fig. S1A). Our parameter space covers three modes of target metabolite export, where metabolite export is primarily through the active pathway, the passive pathway, or a mix of both active and passive pathways (Fig 5B). Modeling results show that sensor DR increased as passive transport rate increased and active export decreased (Fig. 5C). This is because intracellular target metabolite concentration is high when the passive transport rate is higher than the active export rate (Fig. S1B). Interestingly, when active export rate is similar to or higher than passive transport rate, DR is more likely to positively correlate with growth (Fig. 5D). And when active export rate is lower than passive transport rate, DR is more likely to positively correlate with TetR production rate (Fig. 5E). As a result, DR can positively correlate with both cell growth and TetR production rate only when active export rate is similar to passive import (Fig. 5F). Our modeling results further show that dM_in/dμ strongly increases when active export rate is similar to passive import (Fig. S1C), which is a necessary condition to observe simultaneous positive correlation for DR with cell growth and TetR production rate (see Supplemental Note 1.3). Thus, the aTc biosensor used in our experiments likely fall into this parameter range.

Figure 5. Modeling the impact of passive and active transport mechanism on DR-growth rate dependence for aTc-type biosensors.

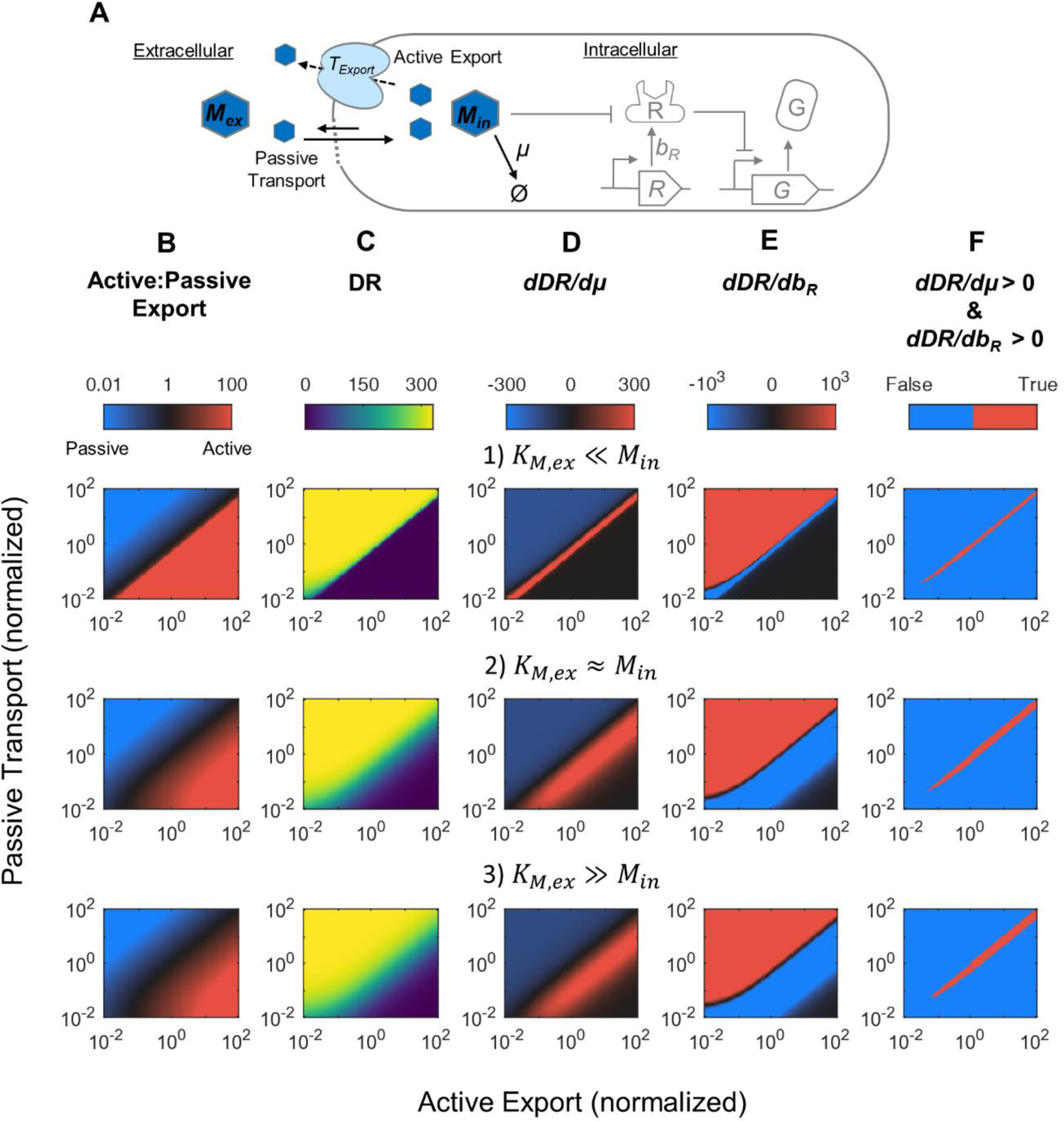
(A) Diagram of transport reactions including passive import of metabolite by diffusion and active export facilitated by a protein transporter. (B) Ratio of active to passive export rates, (C) Calculated DR, (D) dDR/dμ, (E) dDR/db_R, and (F) Parameter region where both dDR/dμ and dDR/db_R are increasing, under different parameter space. The parameters k_diff and k_cat,ex were increased to increase passive and active transport rate, respectively. K_M,ex was varied to represent three scenarios where its value is either greater, similar, or smaller than the intracellular target metabolite concentration (M_in). See Supplemental Fig. S1 and Supplemental Note 2.1 for details. Parameters values are given in Supplemental Table S1.

In contrast to the aTc sensor, many chemicals cannot diffuse across cell membrane passively, but solely rely to protein transporters and enzyme conversion to turn on the sensor. For example, the FA sensor requires a membrane-associated acyl-CoA synthase to convert extracellular FA into intracellular acyl-CoA, which binds to FadR, the MRTF, to turn on reporter expression. Thus, to understand the FA sensor, we modified our model to include both enzyme-based import and export mechanisms without passive transport (Fig. 6A). Similar to the aTc model, DR increases when the active import rate is higher than export rate (Fig. 6B), leading to higher intracellular target metabolite (acyl-CoA) concentration (Fig. 6C). In contrast to aTc-type of sensors, the DR of FA-type of sensors has a negative dependence on cell growth when import rate is higher than export rate, which should occur under most cases since faster target metabolite import is necessary for high biosensor induction (Fig. 6D). Thus, these modeling results are consistent with our experimental results. Additionally, when import is higher than export, the intracellular target metabolite growth dependence (dM_in/dμ) is strongly negative (Fig. 6E) indicating a large potential drop in the maximum biosensor output at higher growth rates, which is also consistent with experiments.

Figure 6. Modeling the impact of active transport mechanism on GR-growth rate dependence for FA-type biosensors.

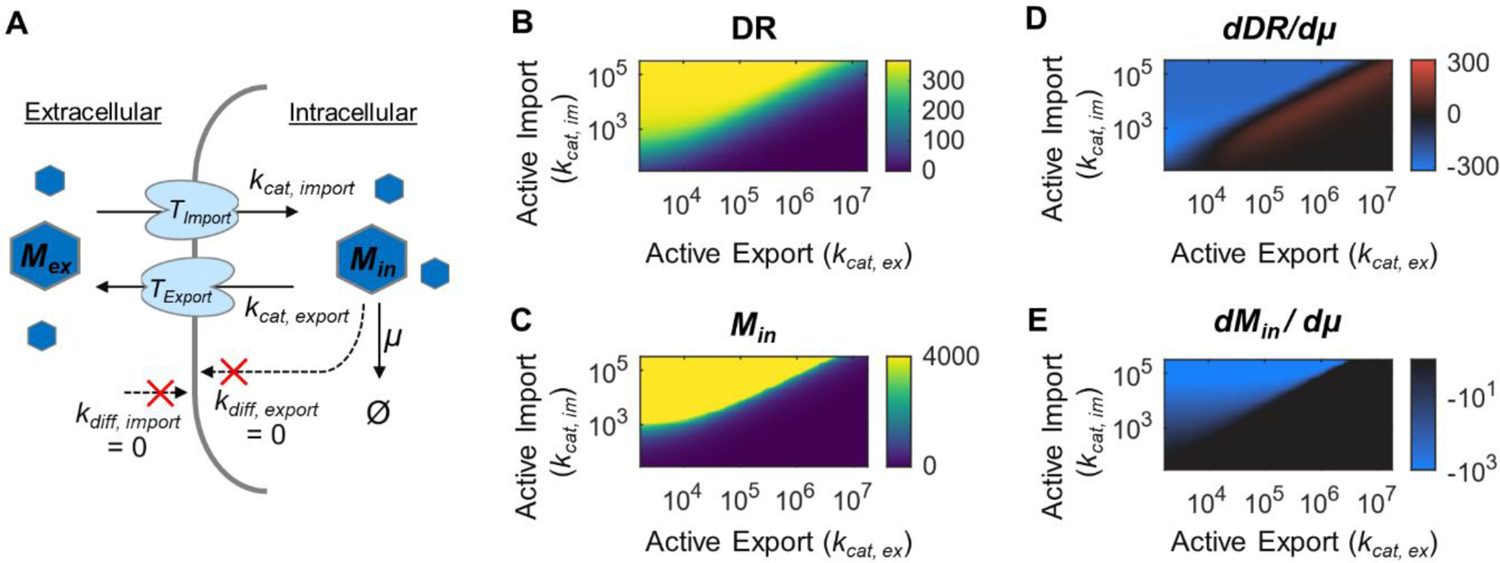
(A) Diagram of transport reactions. Target metabolite transport only occurs by protein-facilitated active mechanisms. (B) Model simulated DR under different import and export rates. All other parameters are held constant and are given in Supplemental Table S1. (C) Intracellular target metabolite concentration (M_in), (D) DR-μ dependence, and (E) Intracellular metabolite-μ dependence, under different parameter space.

DR and DR-μ Are Sensitive to Similar Parameters

Thus far, our modeling and experimental results have shown good qualitative agreement and have predicted the effects of b_R and transport mechanisms on both DR and DR-μ dependence. In order to gain a deeper understanding of the other parameters effects on DR and DR-μ dependence, we conducted a global parameter sensitivity analysis, for a transport mechanism with both passive and active transport (Supplemental Note 3). Our results show that both the DR (Fig. S2A) and dDR/dμ (Fig. S2B) are most sensitive to parameters intrinsic to the biosensor (a_G, b_G, and K_G), the MRTF expression level, and parameters in MRTF-metabolite interaction (b_R, k_sr, k_sf). The similarity in parameter sets which strongly affect DR and dDR/dμ suggest both are tightly coupled. These results are consistent with our observation of the TetR system where increasing TetR production rate tuned both the DR and the DR-μ dependence in the same direction.

Discussion

Change in cellular growth rate often affects the performance of biosensors and cause problems when using biosensors in a different nutrient or environment⁵⁴. In this work, we characterized the growth-rate dependent behavior of three commonly-used MRTF-based biosensors through changing the growth medium of the biosensors. Our results show that DR of the aTc-TetR and IPTG-LacI sensors have positive correlations with cell growth rate. In industrial-scale bioreactor settings where growth rates are typically lower than that in rich medium of lab settings, these sensors will have lower DRs and leakier expression before induction (Fig. 2D, 2E)^55,56. Thus, these sensors may not be suitable for controlling toxic genes or burdensome pathways whose leaky expression can cause undesirable mutations to deactivate the strain’s function. In contrast, DR of the FA-FadR biosensor has a negative correlation with cell growth rates. A higher DR at lower growth rate can benefit the sensor’s application, although its leaky expression was also high at lower growth rate (Fig. 2F).

In this work we used a simplified kinetic model for understanding the DR-μ dependency. The core modeling approach expands upon previous phenomenological models which were successful in capturing design constraints between various tunable molecular interactions and biosensor dose-response parameters²⁶. We extended these phenological models with kinetic interactions between TF and intracellular target metabolite, as well as metabolite transport, which have been shown to capture key dynamic features of bacterial response to external metabolites⁴⁷. Many of the model parameters are related to key biological processes that can be tuned experimentally to optimize a sensor’s performance, such as the TF-operator interactions^57,58 and the presence of exporters^59,60. Our model captures new design constraints for tuning DR across growth rates. For example, while the DR can be increased by reducing the minimum output through a stronger binding of the MRTF to the biosensor promoter, our model predicts this can result in a reduction of the maximum output at some growth rates, because there is a limit to how much the sensor promoter can be activated by the intracellular target metabolite. Thus, once model parameters are characterized at a single growth rate, the model can be used to predict the change in DR under different medium compositions by measuring the growth rate, allowing engineers to check for a potential loss of sensor performance without the need for lengthy experimental re-characterization of the biosensor at different growth rates or under different growth mediums. Additionally, while our results focus on biosensor’s with a repressed-repressor architecture, previous phenomenological models²⁶ can be similarly extended following our procedures to identify growth-dependent design constraints for other biosensor architectures, such as the commonly used activated-activator architecture.

Importantly, our model also highlights some fundamental couplings in biosensor’s performance across varying growth rates, which are important when engineering a MRTF-based sensor. For both types of sensors explored in this study, strategies in increasing the DR always led to stronger growth rate dependence of DR (regardless of whether the dependence is positive or negative), thus making the DR more sensitive to changes in growth (Fig. 4D, Fig. 5, Fig. 6). Therefore, there is a trade-off between high DR and low DR-μ sensitivity, which is important in applications when the value of the DR itself is critical. As an example, MRTF-based biosensors used for high-throughput screening usually require high DRs to reduce the identification of false-positive and false-negative strains^25,61. However, a sensor with too high of a DR also has high DR-μ sensitivity, which will lead to a high false-hit rate when screening under different conditions. Thus, reducing DR in exchange for a less sensitive DR-μ dependence may present a better strategy in sensor design.

Additionally, our model suggests that transport of the target metabolite plays important roles in the growth rate dependence of DR. Different biosensors with similar underlying parameters can show different DR-μ dependencies. For biosensors where the target metabolite’s transport is controlled by passive diffusion and active export (e.g. aTc), there is a narrow parameter region where increasing TF expression can improve DR while also maintaining a positive DR-μ dependence (Fig. 5E). In contrast, for biosensors where intracellular target metabolite levels are controlled solely by enzymes (e.g. FA), the metabolite-μ dependence is negative over a large parameters space, so DR cannot be improved by increasing TF levels without leading to a more negative DR-μ dependence under these conditions. Thus, our model highlights metabolite transport or production as an important consideration for understanding the impact of growth on a sensor’s DR.

MRTF-based biosensors are key components of synthetic biology systems and enable a diverse range of sensing applications. These applications require sensors with robust and predictable operation under a wide range of nutrient conditions and growth environments. Our work has uncovered new design considerations and trade-offs for metabolite biosensors under changing growth conditions, which will be found useful for a wide range of metabolic engineering and synthetic biology applications.

Methods

Materials.

Phusion polymerase, restriction enzymes, and T4 ligase were purchased from Thermo Fisher Scientific (Waltham, MA, U.S.A.). DNA primers were synthesized by Integrated DNA Technologies (Coralville, IA, U.S.A.). DNA plasmid miniprep kits were purchased from iNtRON Biotechnology (Burlington, MA, U.S.A). All other reagents were purchased from Sigma-Aldrich (St. Louis, MO, U.S.A.)

Plasmids and Strains.

E. coli MDS42pdu⁶² was used to clone and isolate plasmids. E. coli MG1655 was used to host biosensor plasmids. All plasmids were constructed through PCR amplification and standard Golden-Gate DNA assembly techniques. Plasmids were transformed into electro-competent strains by electroporation and selected on LB agar plates with corresponding antibiotics (ampicillin, 100 mg/L; kanamycin, 50 mg/L; streptomycin 100 mg/L). Plasmids (Table S4), strains (Table S5), and sequences of constructed plasmids are given in the supplementary information (Supplemental Note 5).

FA biosensor construction.

The FA-FadR biosensor was created in E. coli strain MG1655 by modifying a previous FA sensor⁴⁷. These modifications include the deletion of fadE, replacement of fadD’s native promoter with a constitutive promoter P_pro4 to deactivate the positive feedback loop in FA transport⁴⁷, and deletion of the negative autoregulation of FadR⁶³. These genome modifications were performed using CRISPR-Cas9 following previous methods^64,65 using pTargetF plasmids as listed in Table S4. The sequence of P_pro4 was taken from a library of insulated constitutive promoters⁶⁶ and constructed from PCR of overlapping primers. Deletion of the negative autoregulation of FadR was done by replacing fadR’s native promoter with the constitutive P_fadRm1 (Supplemental Note 5.1). Additionally, the constitutively controlled fadR was cloned to the pA6a BglBrick plasmid, resulting in plasmid pAfadRm1a-fadR (Supplemental Note 5.1 for full sequence).

TetR RBS library construction.

A library of plasmids with varying TetR RBS strength (namely pSk-P_Tet-rfp-P_J23110-RBSLibrary-tetR) was constructed by introducing a terminator, followed by the constitutive Bba_J23110 promoter, followed by an RBS 3’ of pTetR promoter and 5’ of the TetR coding sequence on a pS2k-rfp plasmid. Terminator and promoter were constructed from overlapping primers. The RBS library was then introduced by primers with degenerate nucleotide sequences. To evaluate the RBS strength, we constructed another plasmid library, namely pSk-P_J23110-RBSLibrary-rfp, by replacing the tetR gene of pSk-P_J23110-RBSLibrary-tetR with rfp. This library was constructed by individually amplifying the promoter, RBS sequence and first 30 codons of the TetR coding sequence from aTc-biosensor-TetR-RBS-library members which had characterized minimum and maximum outputs. These sequences were then individually cloned 5’ of rfp and introduced to a BglBrick backbone with SC101 origin and kanamycin resistance. The final constructed sequences are shown in Supplemental Note 5.1. A list of the tested RBS sequences is given in Supplemental Table S6.

Cell Growth and Induction Conditions.

Cells were cultivated in different growth media following previous protocols^67,68. Specifically, single colonies from an overnight Luria-Bertani (LB) plate were cultivated for 3–5 hours in LB medium (225 rpm, 37 °C) supplemented with appropriate antibiotic. Cells were then washed twice by centrifugation (4500 rcf, 3 minutes) into M9 minimal medium supplemented with 1% (w/v) glycerol and diluted to OD₆₀₀ ~0.04 and grown overnight. Overnight cultures were again washed in M9 media without supplemented carbon. To achieve different growth rates, washed cells were transferred to M9 media supplemented with the following nutrient sources: 75 mM sodium acetate, 20 mM sodium pyruvate, 1% Glycerol, 20 mM sorbitol, 15 mM sodium succinate, 1% glycerol + 7 amino acids (0.8 mM Glycine, 0.2 mM Histidine, 0.4 mM isoleucine, 0.8 mM leucine, 0.4 mM lysine, 0.2 mM methionine, 0.4 mM phenylalanine), 20 mM xylose. For the FadR-based biosensor only, media was supplemented with 0.5% Tergitol NP-40 and the following nutrient sources were used: 75 mM sodium acetate, 1% glycerol, 1% glycerol+7 amino acids, and 0.4% glucose. A summary of growth rates achieved for each media condition is given in Supplemental Table S3. To induce biosensor activity, 1000 nM anhydrotetracycline (aTc), 1 mM isopropyl β-D-1-thiogalactopyranoside (IPTG), and 4 mM of sodium oleate, were added to the media for the aTc, IPTG, and FA sensors, respectively.

Biosensor Growth Rate, Minimum, Maximum, and Dynamic Range Assays.

Cells growing in different carbon sources, with or without the target metabolite were diluted to OD₆₀₀ at ~0.0007. Exponentially growing cells were transferred to a Falcon 96-Well Imaging Microplate (Corning, NY, U.S.A.). An Infinite F200PRO plate reader (TECAN, Männedorf, Switzerland) was used to take automated OD₆₀₀ and red fluorescence measurements (Excitation: 584±9 nm, Emission: 620±20 nm) every 15 minutes with constant shaking at 37°C. Following previously established procedures for calculating growth rate^67,68 and biosensor output²⁶, growth rate was calculated as the slope of natural log(OD₆₀₀) from OD₆₀₀ 0.1 to 0.4. RFP values were normalized by the OD₆₀₀, and the minimum and maximum RFP/OD values were calculated as the average of RFP/OD measurements over the same OD₆₀₀ range (0.1–0.4). The dynamic range was calculated from the minimum and maximum outputs measured from the same biological replicate (colony).

TetR RBS library characterization.

Colonies of freshly transformed aTc-biosensor-TetR-RBS-library members were picked and grown following the cell growth and induction methods in M9 media supplemented with 1% glycerol. The minimum, maximum, and dynamic range of several colonies were measured, and colonies with different dynamic range were chosen for further characterization. The RBS sequence was determined by Sanger sequencing to confirm uniqueness of tested library members and duplicate members were combined. The minimum, maximum, and DR of the sequence verified library members were then re-measured with biological triplicates in 1% glycerol medium. To get the TetR expression level, TetR expression library members were individually constructed, and then also grown in M9 with 1% glycerol, and the growth rate and steady state RFP/OD were measured by plate reader. A summary of the RBS sequences characterized, and their TetR expression level, minimum and maximum outputs is provided in Supplemental Table S6.

Dynamic Range Modeling and Simulations.

Details of the model development and parameterizations are given in Supplemental Note 2.1. Kinetic model simulations were performed using MATLAB 2020b ode15s (The Mathworks, Natick, MA, U.S.A.) from initial conditions where the concentration each species is zero. Simulations were run for 10⁹ seconds to reach steady state, and the end point of each simulation was used as the model output. To obtain the model minimum and maximum outputs, the model was run with either 0 μM or 4000 μM external target metabolite (M_ex), respectively. dDR/db_R was calculated directly from the simulations using Equation (S21), dDR/dμ was calculated numerically using a 5-point central difference formula by running 5 simulations at nearby μ (equally spaced on the range μ ± 0.0039).

Abbreviations

aTc

anhydrotetracycline

DR

dynamic range

DR-μ

Dynamic range-growth rate

FA

fatty acid

IPTG

isopropyl β-D-1-thiogalactopyranoside

MRTF

metabolite-responsive transcription factor