Abstract
The forests of central Europe have undergone remarkable transitions in the past 40 years as air quality has improved dramatically. Retrospective analysis of Norway spruce (Picea abies) tree rings in the Czech Republic shows that air pollution (e.g. SO2 concentrations, high acidic deposition to the forest canopy) plays a dominant role in driving forest health. Extensive soil acidification occurred in the highly polluted "Black Triangle" in Central Europe, and upper mineral soils are still acidified. In contrast, acidic atmospheric deposition declined by 80% and atmospheric SO2 concentration by 90% between the late 1980s and 2010s. In this study we oserved that annual tree ring width (TRW) declined in the 1970s and subsequently recovered in the 1990s, tracking SO2 concentrations closely. Furthermore, recovery of TRW was similar in unlimed and limed stands. Despite large increases in soil base saturation, as well as soil pH, as a result of repeated liming starting in 1981, TRW growth was similar in limed and unlimed plots. TRW recovery was interrupted in 1996 when highly acidic rime (originating from more pronounced decline of alkaline dust than SO2 from local power plants) injured the spruce canopy, but recovered soon to the pre-episode growth. Across the long-term site history, changes in soil chemistry (pH, base saturation, Bc/Al soil solution ratio) cannot explain observed changes in TRW at the two study sites where we tracked soil chemistry. Instead, statistically significant recovery in TRW is linked to the trajectory of annual SO2 concentrations or sulfur deposition at all three stands.
1. Introduction
Central Europe was heavily polluted by SO2 originating from the burning of high sulfur lignite for electricity generation [1, 2]. In the Czech Republic coal mining started in the mid 19th century, but accelerated significantly after Word War II. It peaked in the 1980s (129 MT in 1983) and has declined [2] significantly since the early 1990s (30.7 Mt in 2019). In the so-called "Black Triangle" region on the border of Germany (former DDR), Poland and the Czech Republic (former Czechoslovakia), massive forest dieback occurred starting in the 1960s with a peak in the 1970s and 1980s. In the Czech Republic alone, 1.5 million ha of forest were heavily damaged and about 40 000 ha of mainly Norway spruce (Picea abies) stands died or were salvage logged due to air pollution [3], which represents ca. 9.5 million cubic meters of wood [2]. The decline in SO2 emission during the 1990s was one of the great "success stories" in environmental protection worldwide [4, 5]. Czech SO2 emissions declined from 3 150 Mkg (1985) of SO2 to 86.6 Mkg in 2017 [2], representing a decline of more than 97%. Annual ambient SO2 concentration in the Czech part of the Black Triangle has declined from a peak of 130 μg·m-3 measured in the 1970s to less than 10 μg·m-3 at present [2]. The estimated median total deposition of S in the current Czech Republic peaked in 1979 (41 kg S ha−1·yr−1) and then declined to 7.3 kg S ha−1·yr−1 in 2012 [6]. Recent estimates show that S deposition had fallen even further by 2017 (5.4 kg S ha−1·yr−1).
Acid deposition results in elevated inorganic Al and H+ in soil solution, especially in soils with low base saturation (<20%). For forests, where the toxicity of aluminium to tree roots is considered to be critical, the Al3+ to Ca2+ ratio in soil water is a good predictor of damage to roots [7, 8] or crown defoliation and transformation. High inorganic Al in soil solution can also impact tree fine root growth and functioning [9].
Foliar injury by air pollutants has also been identified as a potential reason for forest dieback in highly polluted areas such as the Black Triangle [10], and high concentrations of SO2 and ozone result in canopy damage [11]. Deterioration of cuticular waxes and leaching of nutrients from the canopy [12] leading to chlorosis and a decline in photosynthesis is thought to drive the canopy decline and contribute to forest dieback. Widespread and rapid declines of Norway spruce in the Black Triangle in the 1970s were usually also connected with climatic episodes when highly acidic fog or rime during winter inversions seriously damaged the spruce canopy [1]. Understanding the relative importance of these two potential drivers of tree health–acidification of forest soils, and exposure of forest canopies to atmospheric pollution–is central to effective management and mitigation of the past effects of environmental degradation in this highly impacted region. Mitigation strategies such as liming would be warranted if the dominant effects are associated with soil acidification, whereas continued efforts to reduce air pollution loads would be warranted if direct foliar exposure to pollutants is most closely associated with forest health.
Now, approximatelly two decades after a significant decline of SO2 emissions in the region [2], data from long-term measurements of soils, atmospheric deposition and air quality allow us to distinguish between these two mechanisms. One of the best opportunities for evaluating the future growth capacity of individual species is a retrospective analysis of past growth responses to climate and pollution [13, 14]. High-resolution long-term proxies, where annual changes can be delineated, are needed to describe previous environmental variability [15]. Annual rings produced by temperate tree species provide such a retrospective record of tree growth in response to past environmental conditions [16–18].
In this paper, we examine the hypothesis that observed declines in growth of Norway spruce (Picea abies) were caused by some combination of (i) long-term air pollution by SO2 gas that directly damaged foliage; (ii) deposition of acidic precipitation that damaged foliage; or (iii) soil acidification that altered base cation and Al concentrations. Using study sites in the Ore Mts. in the northern Czech Republic that were extremely polluted in previous decades, we assess drivers of tree health by comparing annual tree ring width (TRW) with temporal trends of airborne SO2, acidic deposition and soil chemistry to determine the most important factors affecting forest vitality during the past 50 years.
2. Site description
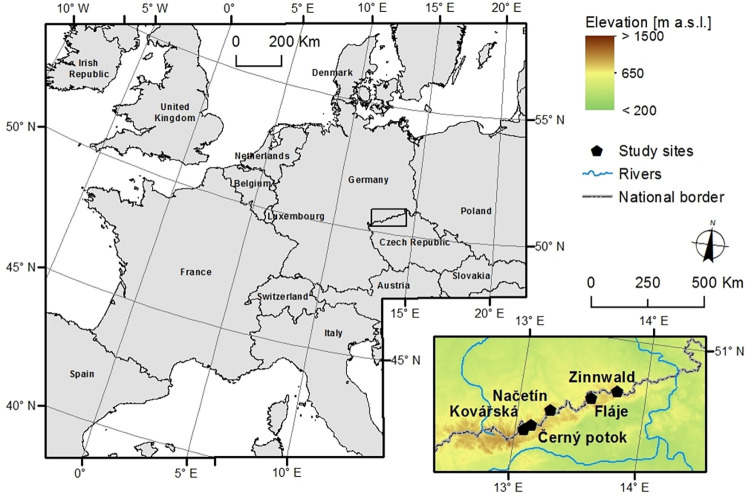
The study sites are spruce stands located in the Ore Mountains (Krušné hory in Czech, Erzgebirge in German), northwestern Czech Republic (Fig 1). All Norway spruce (Picea abies) stands are at a similar altitude (Table 1) and are exposed to similar climatic conditions. The average annual temperature in the region is 7.1°C, and the average annual precipitation is 1110 mm (2005–2017). Most of the Norway spruce stands were salvage logged in the 1970s to 1980s [3]. Only a few adult stands suitable for dendrochronological analyses have survived until present. As the region was extensively limed several times (Table 1) all stands (except those of the Načetín experimental forest) were on limed soils and selection of unlimed control plots was not possible.
Fig 1. Study site locations in Ore Mts., Czech Republic.
The maps are based on data from OpenStreetMap and OpenStreetMap Foundation publicly available without special privileges under a CC BY-SA 2.0 licence from the OpenStreetMap contributors (https://www.openstreetmap.org/copyright/en) available from www.openstreetmap.org.
Table 1. Characteristics of studied plots in Ore Mts., Czech Republic.
| Site | Coordinates | Bedrock | Soil | Altitude (m a.s.l.) | Forest age (years)* | Liming (year, dose in tons.ha-1) |
|---|---|---|---|---|---|---|
| Načetín | 50° 33´23´´ 13°15´12´´ | Gneiss | Dystric cambisol | 775 | 95 | 2007**, 3.0 |
| Kovářská | 50° 29´53´´ 13° 07´20´´ | Gneiss | Dystric cambisol | 786 | 116 | 1981, 1.5 |
| 1988, 2.0 | ||||||
| 1997, 3.0 | ||||||
| Černý potok | 50° 28´09´´ 13° 03´54´´ | Gneiss | Dystric cambisol | 768 | 69 | 1981, 1.5 |
| 1988, 2.0 | ||||||
| 1997, 3.0 | ||||||
| Fláje | 50° 40´ 48´´ 13° 34´ 12´´ | Basalt | Hyperskeletic Leptosol | 860 | 69 | 1981, 1.5 |
| 1988, 2.0 | ||||||
| 1997, 3.0 |
*first identified tree ring +10 years
**Načetín limed only
The Načetín experimental forest stand has been studied since the late 1980s as part of research into the phenomenon of acid rain [19–21]. Experimental liming by 3 tons per hectare of dolomitic limestone occurred in an experimental plot at the Načetín site in 2007, thus "Načetín control" and "Načetín liming" will be used to identify the different subplots.
Tree rings were sampled at each plot, although soil chemistry was not analysed at Černý potok as the site position, bedrock, and soils were almost identical with the nearby Kovářská site. Field sampling was approved by Lesy České republiky, státní podnik (State Forest of the Czech Republic).
3. Methods
3.1. Tree-ring sampling and chronology development
We randomly selected and sampled 15 dominant spruce trees at each forest site. Considering the lack of direction-specific effects on variability in tree radial growth [22], one core per tree was extracted using a Pressler borer (Haglof Company Group) at breast height (1.3 m). To avoid wood compression, the cores were sampled in a direction parallel to the slope. All samples were measured using a VIAS TimeTable device with a measuring length of 78 cm and resolution <1/100 mm (©SCIEM, Vienna, Austria). The TRW series were measured (accuracy of 0.01 mm) and cross-dated using PAST4 [23]. Missing and false rings were corrected using both PAST4 [23] and COFECHA [24].
To remove non-climatic, age-related growth trends from the raw tree ring width (TRW) series as well as other non-climatic factors (e.g., competition), we applied cubic smoothing splines with a 50% frequency cutoff at 100 years [25] using ARSTAN software [26]. We used this method to preserve interannual to multi-decadal growth variations [27]. TRW indices were calculated as residuals after applying an adaptive power transformation to the raw measurement series [28]. The site chronologies were calculated using bi-weight robust means. Similarities among the site TRW chronologies were assessed using statistical criteria (correlation coefficient; Gleichläufigkeit [29]) and visual comparison. Negative extremes were defined by years in which the standardised TRW chronology (period replicated >20 TRWi series) exceeded the -1.0 multiple of a standard deviation (SD).
3.2. Soil analyses
Soils were sampled in 2018 by excavating four 0.5 m2 quantitative pits using the method described by Huntington et al. [30]. The Ol (litter) and Of+Oh (fermented + humified) horizons were sampled together. Mineral soil was collected for the depths of 0–10, 10–20 and 20–40 cm. The soil samples were weighed and then sieved after air-drying (mesh size of 5 mm for organic horizons and 2 mm for mineral horizons). Soil moisture was determined gravimetrically by drying at 105°C. Soil pH was measured using a glass combination electrode in a water extract. Exchangeable cations were analysed in 0.1 M BaCl2 extracts by flame atomic absorption spectrometry (FAAS). Cation exchange capacity (CEC) was calculated as the sum of exchangeable Ca, Mg, Na, K and total exchangeable acidity (TEA). Base saturation (BS) was determined as the fraction of CEC associated with base cations. Total carbon (C) and total nitrogen were determined using an elemental analyser. Soil water chemistry at Načetín was sampled monthly since 1994 using quartz and Teflon suction lysimeters (Prenart) from the depth of -30 cm of mineral soil.
3.3. MAGIC model
MAGIC (Model of Acidification of Groundwater in Catchments) was designed to reconstruct past and predict future drainage water and soil chemistry [31–33]. MAGIC is a lumped-parameter model of intermediate complexity which calculates for annual time steps the concentration of major ions under the assumption of simultaneous reactions involving SO4 adsorption, cation exchange, dissolution-precipitation-speciation of aluminium and dissolution-speciation of inorganic and organic C. MAGIC accounts for the mass balance of major ions in the soil by bookkeeping the fluxes from atmospheric inputs, chemical weathering, net uptake in biomass and loss to runoff.
Water fluxes, wet and dry atmospheric deposition, net vegetation uptake, weathering, and a description of organic acids are required as external inputs to MAGIC. The “verification” or “validation” of a biogeochemical model of a natural system is problematic as natural systems are never closed, model results are non-unique, and “true” values cannot be proved absolutely. Model evaluation is, however, feasible when the model is tested against observations from a range of ecosystems at multiple sites, and confidence in the models is increased if it is found to produce satisfactory results [34]. This was the premise of the current study. For calibration procedures of the MAGIC model related to this study, see S1 Annex.
3.4. Atmospheric deposition and chemistry
Atmospherice deposition (bulk precipitation and spruce throughfall) was measured at Načetín experimental forest since 1994 [20]. The historical record of atmospheric deposition was estimated during MAGIC model calibration (S1 Annex) using the record of coal mining in the region [2]. Atmospheric chemistry (annual SO2 concentrations) was measured at Zinwald station, Germany [35]. Dust emissions were derived from the database of the Czech Hydrometeorological Institute [2].
3.5. Climatic variables
Complementary to air pollution data, climatic data series were reconstructed for all sites. Climate data covering the period from the early 1920s to 2017 were derived through interpolation from the three most representative weather stations in the vicinity of each sampling area. Selection has been based both on quality control results as well as detailed review of the metadata records. All observations of weather variables were tested for outliers and breaks through a detailed homogenisation sequence, and gaps in missing data were filled [36]. The database for each site included the daily average, minimum and maximum temperatures (Tavg, Tmin and Tmax, respectively), the daily sum of global radiation or duration of sunshine, mean daily wind speed, mean daily relative humidity and the daily sum of precipitation. The sum of global radiation was corrected based on the site aspect and slope. The SoilClim [37] model was employed to estimate the daily values of the relative soil water content (AWR) for the top 1.3 m, which was used to generate a water availability proxy (self-calibrated Palmer Drought Severity Index or PDSI [38].
3.6. Statistical analysis
Besides site-specific correlation (Pearson) of TRW with the environmental factors S deposition, air SO2 emissions, soil pH, soil base saturation and soil Bc/Al, we also applied a general linear models (GLM) using R package stats [39] to identify which environmental factors, including climatic variables and forest age, were linked to observed changes in TRW over the 1979–2017 period. The climatic factors in GLM analysis included mean (May-August) air temperature, total (May-August) precipitation and mean (May-August) Palmer drought severity index (PDSI). We allowed interaction between forest age and all environmental factors. All explanatory variables were standardized, so they have a mean of zero and standard deviation of one. The dredge function from the MuMln R package [40] was used to identify the best candidate model according to the lowest Akaike information criterion. Complemetary to our final glm model, we examined independent effects of fixed factors through hierarchical partitioning (HP) using the R package hier.part [41].
4. Results and discussion
4.1. Atmospheric chemistry and deposition
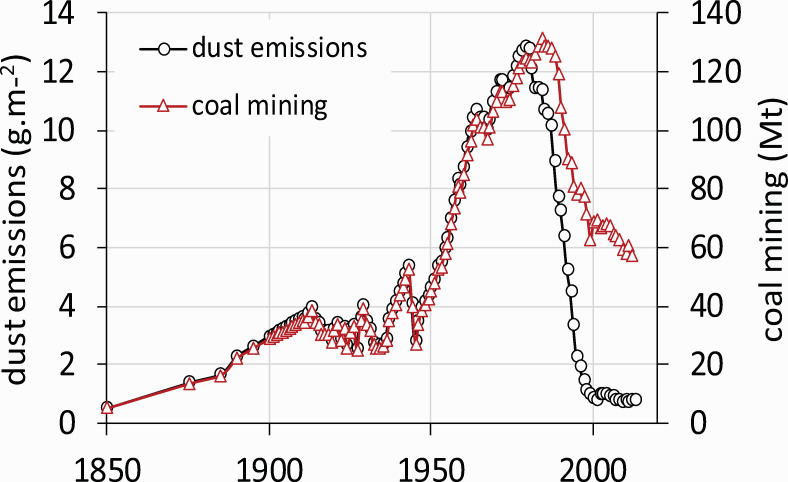
Historically, sulfur emission and deposition were associated with mining and burning brown coal (lignite) from the nearby Bohemian coal basin (Fig 2) since the second half of the 19th century. The period after World War II was accompanied by a massive production of energy by burning this high-S content lignite in local power plants. Coal mining, as well as SO2 emissions (Fig 3), peaked in the 1980s. The decrease since then can be attributed in part to the declining volume of coal mined after 1989, when the extensive industrial activity in former Czechoslovakia declined with a change in political structure.
Fig 2. Coal mining and dust emissions in the Czech Republic between 1850–2017.
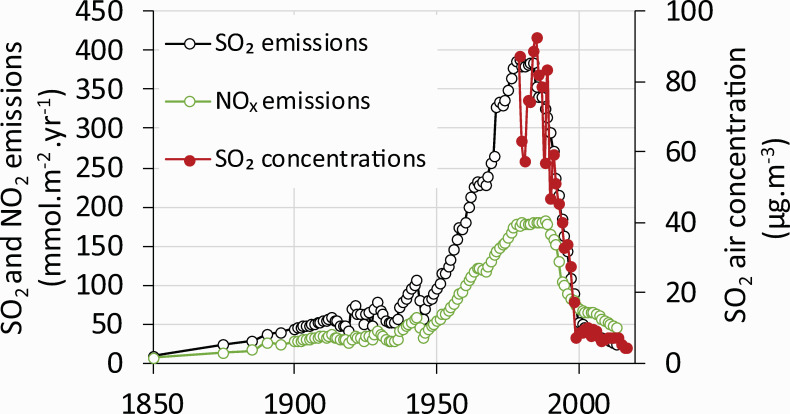
Fig 3. SO2 emissions (Czech Republic) between 1850–2017 and ambient annual SO2 concentrations measured at Cínovec (Zinwald) at the Czech/German border between 1979–2017.
There was a distinct break in SO2 emissions in 1993 when the first power plants in the Czech Republic were equipped with flue-gas desulfurization (Fig 3). This process was completed in 1999. As a result, SO2 emissions In the Czech Republic declined from a peak of 395 mmol·m-2·yr-2 in 1982 to 25 mmol·m-2·yr-2 in 1999. Since then, it fell to 10 mmol·m-2·yr-2 in 2017 (Fig 3) due to the continuous decline in coal mining (Fig 2). Modelled S emissions coincide very well with measured ambient SO2 concentrations. The longest record in the region is available from Zinwald station [35] on the Czech-German border on the ridge of the Ore Mts. (Fig 1). Annual concentrations peaked in the mid-1980s at 93 μg·m-3 (Fig 3). As SO2 emissions declined, ambient SO2 concentrations declined proportionally to ca. 10 μg·m-3 in the late 1990s and 4 μg·m-3 in 2017.
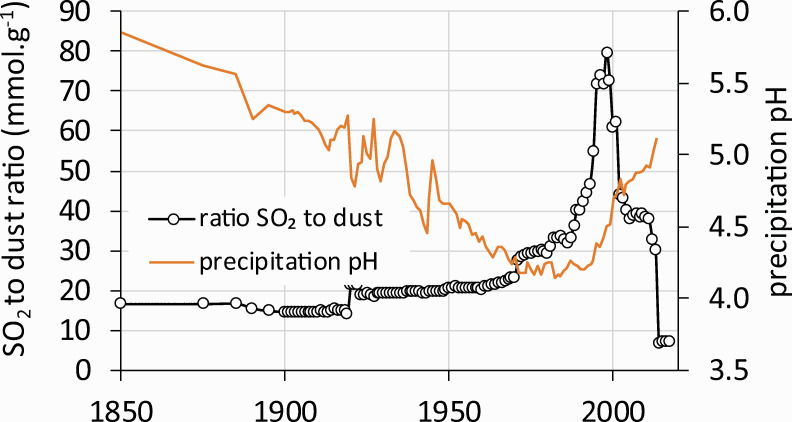
Dust emissions (Fig 2) increased similarly to coal mining activities [6]. Dust was rich in base cations (primarily Ca) and partly neutralized precipitation acidity (Fig 4). Despite this neutralization, precipitation pH was about 4.2 during the 1970s and 1980s [42] (Fig 4) and has risen slowly since the 1990s to values >5.0 in recent years. Electrostatic removal of dust from power plants started in the 1980s when it peaked at around 12 g·m-2. It declined sharply to <1 g·m-2 until the late 1990s (Fig 2). As dust removal was effective earlier than SO2 removal (Fig 3), the ratio of SO2/dust in the atmosphere peaked in the 1990s (Fig 4). This peak in SO2/dust was accompanied by highly acidic episodes like the formation of acidic rime ice in the winter of 1995/1996. The acidity of the rime developed on the spruce canopy at Načetín was measured to be pH<3 (lowest pH = 2.33 was recorded in January/February 1996). Ambient SO2 concentration was 2 300 μg·m-3 at Rudolice, 20 km east of Načetín (February 2nd 1996) as a result of repeated inversions occurring on the ridge of the Ore Mts. [43].
Fig 4. Modelled and measured annual precipitation pH and SO2/dust ratio (1850–2017) for the Czech Republic.
Modelled values from 1850 to 2013 for pH, 1850 to 2013 for SO2/dust ratio.
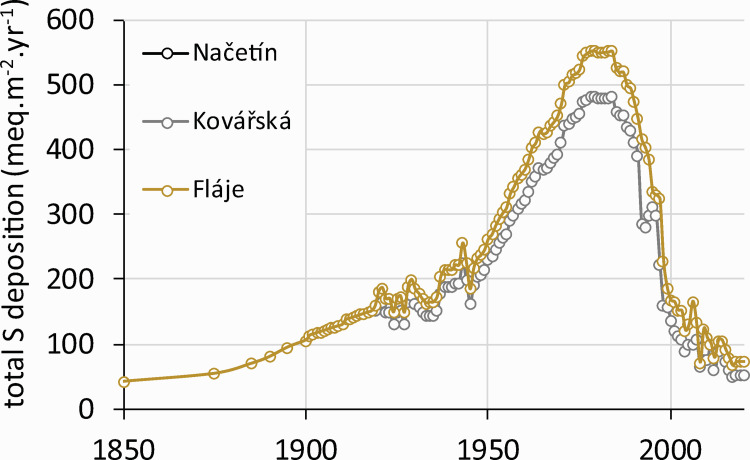
Based on the coal mining and measured sulfur deposition data between the 1990s and 2010s from the Czech Republic, Germany and Poland [6], we constructed a simple statistical model for reconstructing and predicting historic S deposition. This model estimated the deposition of S in throughfall for sites in the Ore Mts (Fig 5) for the period 1850–2017. All sites showed synchronous patterns, with the highest deposition estimated for Fláje (ca. 550 meq·m-2·yr-1 in the 1980s), but other sites (Kovářská and Načetín) also received very high loads (ca. 480 meq·m-2·yr-1). Present deposition (60–70 meq·m-2·yr-1) is equal to the historical values estimated for the second half of the 19th century and represents an 80–90% decline (Fig 5).
Fig 5. Modelled (1850–1993) and measured (1994–2017) annual sulfur deposition at study sites in the Ore Mts.
4.2. Soil chemistry
4.2.1. Long-term changes at Načetín
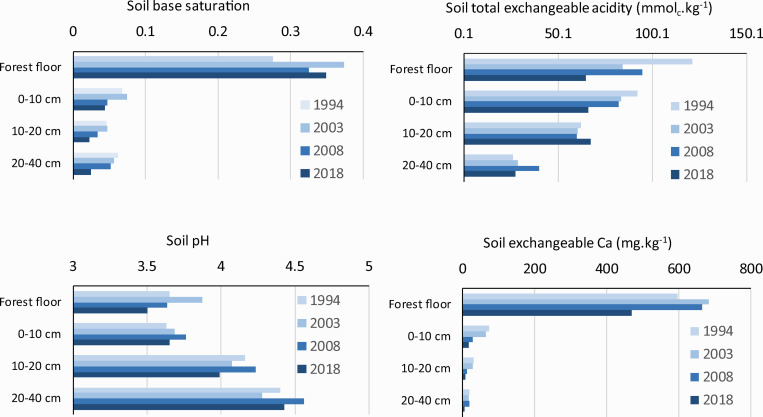
Since 1994, four soil sampling campaigns were undertaken at the Načetín control site. Despite a significant decrease in atmospheric deposition of sulfur (Fig 5), soil chemistry exhibited only limited changes. Soil base saturation (BS) has increased only in the organic layer between 1994 and 2003 and has stayed at a similar level of 33–37% since 2003 (Fig 6). Mineral soil BS did not change significantly between 1994 and 2008, but declined in 2018 to the lowest measured levels, with values of only 3% of saturation at a depth of 20–40 cm compared to the initial value of 6% at that depth in 1994 (Fig 6). Total exchangeable acidity (TEA) declined markedly in the humus horizon (from 125 mmolc·kg-1 in 1994 to 67 mmolc·kg-1 in 2018). It also decreased markedly in the upper mineral soil (0–10 cm) but did not change in deeper mineral soil (Fig 6). Soil pH did not exhibit consistent trends over time and increased from 3.6 in the forest floor up to 4.4 in the B horizon (20–40 cm). Exchangeable calcium has declined similarly to TEA, with substantial declines in the humus horizon (from 600–700 mg·kg-1 in 1994 to about 450 in 2018) and in the upper mineral soil (from 70 to 15 mg·kg-1). Similar sharp declines were observed in deeper mineral horizons, with exchangeable Ca dropping from about 30 to 7 mg·kg-1 at 10–20 cm and from 20 to 4 mg·kg-1 at 20–30 cm (Fig 6). Patterns for exchangeable Mg were similar to those of Ca.
Fig 6. Long-term changes of soil chemistry at the Načetín control research site (1994–2018).
4.2.2. Variation in soil chemistry among sites
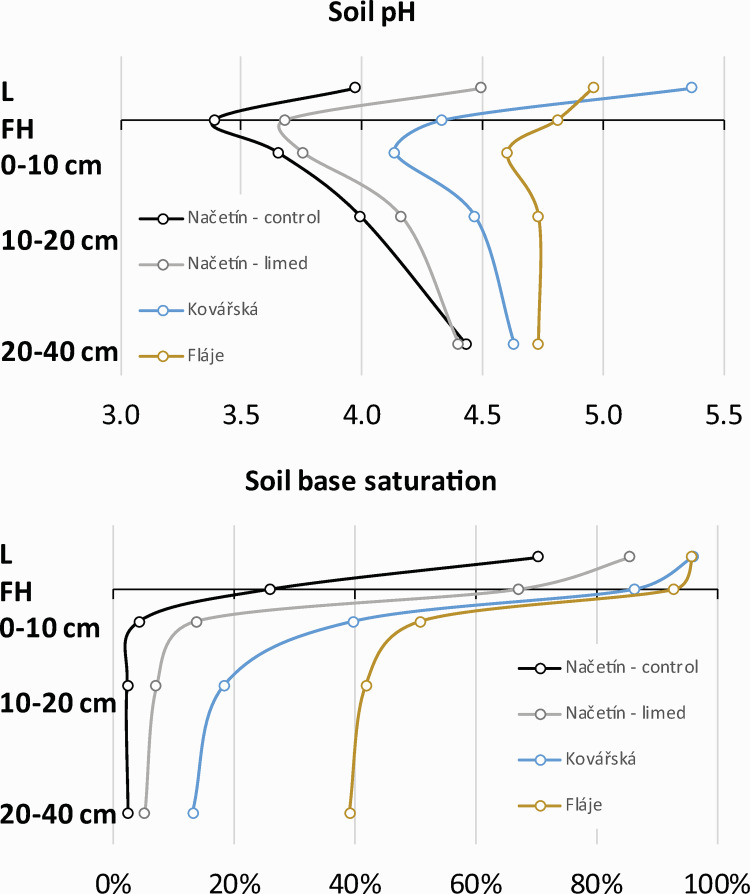
Among our study sites, the most acidic was the Načetín control plot (exchangeable pH = 3.4 at FH horizon) followed by Načetín limed plot, Kovářská and Fláje (4.7 at FH horizon, Fig 7). Soil pH showed the typical pattern being most acidic in the organic FH horizons and the highest exchangeable pH was observed in the deeper mineral soil. Soil base saturation has declined at all sites from the L horizon down to mineral at 20–40 cm. The lowest BS was observed for the Načetín control plot (70% in L horizon and 3% in 20–40 cm) and highest at Fláje (95% in L and 39% in 20–40 cm, respectively).
Fig 7. Soil pH and base saturation in 2018.
Soil base saturation follows liming history as well as geological settings. The second most acidic site (Načetín limed, underlain by gneiss) was experimentally limed in 2007 (Table 1). Other sites Kovářská (gneiss) and Fláje (basalt) were limed three times (Table 1) between 1981 and 1997 [44, 45] resulting in a cumulative dose of 6.5 t.ha-1. As a result, soil pools of Ca were 8x higher, and the Mg pool was 11x enriched (Table 2) at Kovářská, even though it is underlain by similar bedrock (gneiss) as Načetín. Similar levels of enrichment were observed at Fláje, which is underlain by basalt. As Načetín was limed in 2007 by a lower dose (3 t·ha-1), Ca enrichment was only 3x and Mg 4x (Table 2), reflecting the slow kinetics of limestone dissolution (S1 Annex).
Table 2. Soil pH, fine earth mass,pools of base cations, carbon and nitrogen (means and standard deviations) measured in 2018 in 5 depths at investigated sites in Ore Mts.
| Site | Soil horizon | Fine earth | pH (H2O) | pH (KCl) | Ca | Mg | Na | K | exchangeable acidity Al + H | exchangeable Al | cation exchange capacity (CEC) | Sum of base cations | Base saturation | C | N | C/N | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| kg/m2 | mg/kg | mmolc/kg | % | g/g | ||||||||||||||||||||||||||||||||||||||||||
| Načetín—control | L | 2.1 | ± | 1.0 | 3.97 | ± | 0.2 | 3.11 | ± | 0.2 | 572 | ± | 180 | 99 | ± | 16 | 8.6 | ± | 3.3 | 317 | ± | 79 | 19 | ± | 4.4 | 0.10 | ± | 0.0 | 64 | ± | 7.8 | 45 | ± | 8.8 | 70% | ± | 7.2% | 47% | ± | 0.8% | 1.6% | ± | 0.1% | 29 | ± | 2.9 |
| Načetín—control | FH | 8.5 | ± | 2.0 | 3.39 | ± | 0.2 | 2.43 | ± | 0.1 | 315 | ± | 141 | 92 | ± | 11 | 15 | ± | 2.8 | 124 | ± | 19 | 77 | ± | 6.2 | 34 | ± | 5.0 | 104 | ± | 9.7 | 27 | ± | 7.9 | 26% | ± | 5.9% | 36% | ± | 2.5% | 1.7% | ± | 0.1% | 22 | ± | 1.7 |
| Načetín—control | 0–10 | 54 | ± | 7.0 | 3.65 | ± | 0.1 | 2.83 | ± | 0.1 | 16 | ± | 7.3 | 16 | ± | 7.6 | 5.2 | ± | 0.6 | 25 | ± | 5.2 | 66 | ± | 4.3 | 42 | ± | 5.2 | 69 | ± | 4.2 | 3.0 | ± | 1.1 | 4.3% | ± | 1.6% | 8.4% | ± | 0.6% | 0.4% | ± | 0.03% | 22 | ± | 0.1 |
| Načetín—control | 10–20 | 51 | ± | 6.5 | 3.99 | ± | 0.2 | 3.29 | ± | 0.2 | 7.4 | ± | 1.9 | 8.0 | ± | 3.2 | 4.4 | ± | 0.6 | 14 | ± | 3.8 | 67 | ± | 9.9 | 42 | ± | 6.6 | 69 | ± | 10 | 1.6 | ± | 0.4 | 2.3% | ± | 0.6% | 4.5% | ± | 0.7% | 0.2% | ± | 0.03% | 19 | ± | 1.7 |
| Načetín—control | 20–40 | 103 | ± | 14.0 | 4.43 | ± | 0.1 | 3.90 | ± | 0.1 | 4.4 | ± | 0.7 | 1.7 | ± | 0.5 | 3.2 | ± | 0.9 | 7.2 | ± | 2.4 | 27 | ± | 7.0 | 18 | ± | 4.9 | 28 | ± | 7.2 | 0.7 | ± | 0.2 | 2.5% | ± | 0.2% | 2.8% | ± | 0.3% | 0.1% | ± | 0.02% | 20 | ± | 1.3 |
| Soil mean/sum | 219 | ± | 1.9 | 4.09 | ± | 0.09 | 3.43 | ± | 0.10 | 26 | ± | 12 | 11 | ± | 3.6 | 4.5 | ± | 0.8 | 21 | ± | 3.5 | 48 | ± | 3.5 | 30 | ± | 2.9 | 51 | ± | 3.5 | 2.9 | ± | 1.0 | 5.8% | ± | 1.9% | 6.3% | ± | 0.3% | 0.30% | ± | 0.01% | 20 | ± | 1.0 | |
| Načetín—limed | L | 1.8 | ± | 0.7 | 4.50 | ± | 0.4 | 3.35 | ± | 0.2 | 1076 | ± | 181 | 205 | ± | 25 | 11 | ± | 2.3 | 379 | ± | 57 | 13 | ± | 1.9 | 0.10 | ± | 0.0 | 94 | ± | 11 | 81 | ± | 12 | 86% | ± | 3.1% | 46% | ± | 0.6% | 1.7% | ± | 0.1% | 28 | ± | 2.0 |
| Načetín—limed | FH | 8.3 | ± | 1.0 | 3.68 | ± | 0.3 | 2.79 | ± | 0.3 | 1117 | ± | 553 | 322 | ± | 176 | 11 | ± | 6.8 | 113 | ± | 58 | 36 | ± | 12 | 11 | ± | 6.9 | 121 | ± | 27 | 86 | ± | 38 | 67% | ± | 21% | 39% | ± | 1.9% | 1.8% | ± | 0.03% | 22 | ± | 1.4 |
| Načetín—limed | 0–10 | 54 | ± | 7.0 | 3.76 | ± | 0.1 | 2.90 | ± | 0.1 | 48 | ± | 24 | 92 | ± | 46 | 8.1 | ± | 0.5 | 37 | ± | 7.8 | 70 | ± | 3.1 | 47 | ± | 4.6 | 81 | ± | 7.2 | 11 | ± | 5.0 | 14% | ± | 5.5% | 10% | ± | 1.7% | 0.4% | ± | 0.06% | 22 | ± | 2.5 |
| Načetín—limed | 10–20 | 51 | ± | 6.5 | 4.16 | ± | 0.3 | 3.45 | ± | 0.3 | 9.3 | ± | 2.4 | 30 | ± | 17 | 5.3 | ± | 0.6 | 16 | ± | 3.9 | 48 | ± | 14 | 38 | ± | 8.9 | 52 | ± | 14 | 3.6 | ± | 1.4 | 7% | ± | 2.3% | 4% | ± | 1.6% | 0.2% | ± | 0.06% | 22 | ± | 2.8 |
| Načetín—limed | 20–40 | 103 | ± | 14.0 | 4.40 | ± | 0.2 | 3.92 | ± | 0.2 | 5.0 | ± | 2.1 | 5.4 | ± | 2.2 | 4.1 | ± | 0.7 | 8.7 | ± | 3.0 | 23 | ± | 12 | 19 | ± | 12 | 25 | ± | 12 | 1.1 | ± | 0.2 | 5% | ± | 1.9% | 2% | ± | 1.0% | 0.1% | ± | 0.04% | 21 | ± | 2.3 |
| Soil mean/sum | 218 | ± | 1.1 | 4.16 | ± | 0.18 | 3.51 | ± | 0.17 | 69 | ± | 29 | 46 | ± | 20 | 5.7 | ± | 0.6 | 24 | ± | 3.9 | 41 | ± | 8.6 | 30 | ± | 7.7 | 49 | ± | 6.5 | 8.1 | ± | 3.0 | 17% | ± | 7.1% | 6.4% | ± | 1.3% | 0.28% | ± | 0.04% | 22 | ± | 1.6 | |
| Kovářská | L | 1.1 | ± | 0.5 | 5.37 | ± | 0.4 | 4.85 | ± | 0.5 | 1556 | ± | 263 | 766 | ± | 146 | 11 | ± | 4.0 | 584 | ± | 272 | 6.4 | ± | 0.8 | 0.10 | ± | 0.0 | 163 | ± | 26 | 156 | ± | 27 | 96% | ± | 0.8% | 40% | ± | 3.0% | 1.2% | ± | 0.1% | 33 | ± | 5.3 |
| Kovářská | FH | 10 | ± | 1.7 | 4.33 | ± | 0.4 | 3.43 | ± | 0.4 | 1862 | ± | 590 | 749 | ± | 258 | 13 | ± | 0.8 | 109 | ± | 16 | 22 | ± | 14 | 5.1 | ± | 5.9 | 180 | ± | 38 | 158 | ± | 51 | 86% | ± | 10% | 28% | ± | 2.3% | 1.2% | ± | 0.1% | 24 | ± | 1.0 |
| Kovářská | 0–10 | 54 | ± | 8.7 | 4.13 | ± | 0.2 | 3.14 | ± | 0.1 | 326 | ± | 122 | 240 | ± | 115 | 6.6 | ± | 0.6 | 32 | ± | 3.7 | 54 | ± | 8.3 | 34 | ± | 6.9 | 92 | ± | 7.7 | 37 | ± | 15 | 40% | ± | 13% | 7.1% | ± | 0.9% | 0.3% | ± | 0.04% | 22 | ± | 0.3 |
| Kovářská | 10–20 | 63 | ± | 5.1 | 4.47 | ± | 0.1 | 3.74 | ± | 0.04 | 64 | ± | 33 | 52 | ± | 22 | 3.6 | ± | 1.2 | 14 | ± | 3.5 | 35 | ± | 4.2 | 24 | ± | 2.7 | 43 | ± | 4.6 | 8.0 | ± | 3.0 | 18% | ± | 6.4% | 2.8% | ± | 0.3% | 0.2% | ± | 0.01% | 18 | ± | 1.7 |
| Kovářská | 20–40 | 114 | ± | 12 | 4.63 | ± | 0.1 | 4.08 | ± | 0.04 | 24 | ± | 12 | 14 | ± | 8.7 | 2.6 | ± | 1.8 | 11 | ± | 1.6 | 18 | ± | 1.7 | 9.1 | ± | 1.5 | 21 | ± | 2.2 | 2.8 | ± | 1.2 | 13% | ± | 5.0% | 1.7% | ± | 0.2% | 0.1% | ± | 0.01% | 17 | ± | 1.2 |
| Soil mean/sum | 243 | ± | 7.0 | 4.47 | ± | 0.07 | 3.76 | ± | 0.04 | 189 | ± | 61 | 112 | ± | 49 | 4.2 | ± | 1.0 | 23 | ± | 2.8 | 31 | ± | 2.3 | 18 | ± | 1.5 | 50 | ± | 4.9 | 19 | ± | 6.9 | 38% | ± | 10% | 4.5% | ± | 0.2% | 0.22% | ± | 0.01% | 19 | ± | 0.9 | |
| Fláje | L | 1.2 | ± | 0.3 | 4.96 | ± | 0.1 | 4.25 | ± | 0.1 | 2596 | ± | 264 | 388 | ± | 28 | 7.2 | ± | 2.8 | 292 | ± | 28 | 7.4 | ± | 0.7 | 0.10 | ± | 0.0 | 177 | ± | 16 | 169 | ± | 16 | 96% | ± | 0.6% | 44% | ± | 1.6% | 1.5% | ± | 0.1% | 29 | ± | 2.5 |
| Fláje | FH | 12 | ± | 5.3 | 4.81 | ± | 0.2 | 3.99 | ± | 0.3 | 2517 | ± | 629 | 755 | ± | 107 | 9.0 | ± | 1.8 | 135 | ± | 22 | 13 | ± | 9.2 | 3.2 | ± | 4.6 | 205 | ± | 30 | 192 | ± | 39 | 93% | ± | 5.8% | 29% | ± | 4.0% | 1.5% | ± | 0.2% | 19 | ± | 1.2 |
| Fláje | 0–10 | 17 | ± | 9.5 | 4.60 | ± | 0.1 | 3.68 | ± | 0.1 | 466 | ± | 97 | 293 | ± | 80 | 8.3 | ± | 1.2 | 69 | ± | 13 | 47 | ± | 5.7 | 31 | ± | 5.1 | 97 | ± | 10 | 50 | ± | 11 | 51% | ± | 7.4% | 15% | ± | 2.9% | 1.0% | ± | 0.1% | 15 | ± | 1.4 |
| Fláje | 10–20 | 12 | ± | 7.7 | 4.73 | ± | 0.1 | 3.89 | ± | 0.1 | 287 | ± | 53 | 141 | ± | 59 | 7.0 | ± | 2.1 | 45 | ± | 10 | 37 | ± | 5.6 | 24 | ± | 4.3 | 65 | ± | 12 | 27 | ± | 7.5 | 42% | ± | 4.4% | 10% | ± | 1.8% | 0.7% | ± | 0.1% | 14 | ± | 1.8 |
| Fláje | 20–40 | 33 | ± | 26 | 4.73 | ± | 0.1 | 3.99 | ± | 0.1 | 250 | ± | 71 | 89 | ± | 25 | 7.6 | ± | 1.3 | 30 | ± | 7.6 | 32 | ± | 2.4 | 21 | ± | 2.1 | 53 | ± | 6.1 | 21 | ± | 5.3 | 39% | ± | 6.2% | 7.5% | ± | 1.9% | 0.5% | ± | 0.1% | 14 | ± | 2.1 |
| Soil mean/sum | 75 | ± | 29 | 4.72 | ± | 0.07 | 3.89 | ± | 0.07 | 730 | ± | 267 | 260 | ± | 67 | 7.6 | ± | 0.9 | 65 | ± | 19 | 32 | ± | 3.1 | 20 | ± | 3.0 | 92 | ± | 16.5 | 60 | ± | 19.3 | 64% | ± | 8.4% | 14% | ± | 2.9% | 0.84% | ± | 0.10% | 15 | ± | 2.1 | |
4.2.3. Estimate of historical soil chemistry development
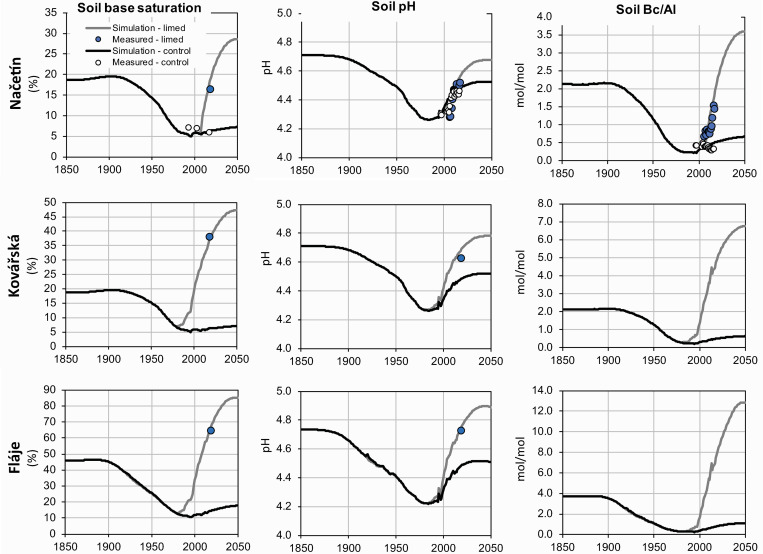
As tree rings reflected forest damage and the physiological stress in the past, retrospective assessment of soil chemistry was needed for disentangling the effects of ambient air chemistry, atmospheric deposition and soil chemistry on tree growth. According to the MAGIC model estimates (S1 Annex), soil base saturation declined during the 19th and most of the 20th century due to increasing acidic deposition (Fig 5) at all of our study sites (Fig 8), indicating an ongoing depletion of the soil pool of exchangeable base cations. At Načetín control, where liming was not applied, the MAGIC simulations showed substantial depletion, from an estimated base saturation of 19% in 1850 to 6% in 2018. The projected recovery, with acid deposition assumed to be unchanged from levels in 2018, revealed only minor increases in soil base saturation (7% in 2050). Such small increases resulted from nearly equal base cations inputs (weathering + deposition) and outputs (uptake + leaching), resulting in only a small increase in base saturation in future decades.
Fig 8.
Modelled and measured (a) soil base saturation, (b) soil solution pH and (c) soil solution Bc/Al ratio (1850–2050) for all investigated sites.
Other limed sites exhibited similar patterns until liming when base saturation increased markedly (Fig 8). Načetín limed revealed current BS of 16.5%, not far from the preindustrial estimate (19%). Future scenarios predict base saturation of 27% in 2050. A more pronounced liming effect was observed and modelled for Kovářská where the preindustrial estimate was 19% but measured BS was 38.5% in 2018. This high base saturation was due to earlier liming (beginning in 1981) and a higher cumulative dose (Table 1). More alkaline bedrock with a high weathering rate (see S1 Annex) at Fláje resulted in preindustrial base saturation of 45% (Fig 8). Acid deposition lowered BS to 15% in 1981 and subsequent liming raised BS to 64% in 2018, significantly higher than the preindustrial estimate.
Preindustrial soil water pH was estimated to be 4.7 (Fig 8) at Načetín, and the lowest pH (4.25) was modelled for the 1980s. pH started to rise soon after the decline in deposition in the 1990s (Fig 5). A pH of 4.45 was reached at the naturally regenerated control plot by 2018 (Table 2). The limed plot’s pH increased to 4.55 between 2007 and 2018. Modelled pH was 4.7 for the limed plot and 4.5 for the control plot. Almost identical preindustrial (4.7) and minimum pH (4.25) pH values were estimated for Kovářská. Liming since 1981 resulted in measured and modelled pH of 4.65 in 2018 and an estimated pH of 4.8 in 2050. Highly weathered basaltic and limed Fláje showed very similar patterns as Kovářská (Fig 8)–preindustrial pH = 4.75, minimum 4.25 and present pH = 4.7. The estimated pH for 2050 (4.9) was higher than the preindustrial estimate.
The molar Bc/Al ratio ((Ca + Mg + K)/Al) in soil solution for Načetín was estimated to be around two as a preindustrial value (Fig 8) and it declined to as low as 0.2 in the 1980s. In contrast to pH, it increased only slightly and stayed around 0.4 between 1994–2018. At the limed plot, Bc/Al increased significantly to 1.5 in 2018 and future predictions are that Bc/Al will rise to 3.5 in 2050. A similar pattern was modelled for Kovářská, where Bc/Al was estimated at 4.5 in 2018 (from a minimum of 0.2 in the 1980s before liming) and almost 7.0 was predicted for 2050 after liming. At the base-rich and limed Fláje site, preindustrial Bc/Al was estimated at 3.9, with a minimum of 0.2 for the beginning of the 1980s, 8.0 for 2018 and 13 for 2050.
4.3. TRW chronologies and climatic effects
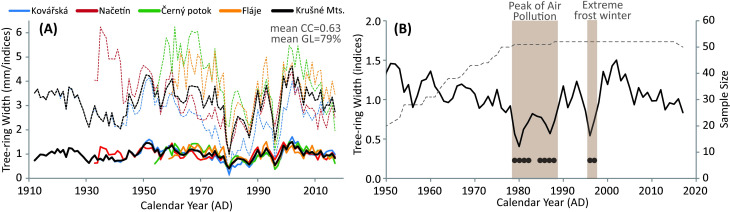
The site TRW chronologies from the four sites vary in length from 59 to 106 tree rings. The high reliability of all site chronologies was confirmed by the Rbar (>0.48) and EPS (>0.92) values, which remained above the threshold of 0.85 [46] for the entire study period. The high similarity among TRW chronologies at each site allows compilation of the mean TRW chronology (Rbar = 0.40, EPS = 0.97), covering the period from 1912 to 2017 (Fig 9A). Replication of the mean chronology decreased backwards and dropped below the 20 TRW series before 1950 (Fig 9B). The mean chronology with an average annual growth rate of 2.75 mm shows a considerable decrease in annual growth starting in the 1950s.The three most significant growth reductions were revealed by analysis of negative extremes in the periods 1979–1982, 1985–1988, and 1996–1997 when average tree-ring widths drop to 1.42, 1.67, and 1.49 mm, respectively. Additionally, we detect seven missing rings between 1979–1982 and five in 1996–1997. The interval of the most pronounced growth reduction (1979–1988), likely initiated by the extremely cold and harsh winter of 1978/1979 [47], corresponds also to one of the highest concentrations of SO2 (Fig 3).
Fig 9.
(A) Raw (dotted line) and standardised (full line) TRW chronologies of all individual sites as well as Ore (Krušné) Mts. Mean correlation coefficient (CC) and mean GL (Gleichläufgkeit; Eckstein, Bauch 1969) indicate similarity among the site chronologies. (B) Indexed mean TRW chronology for Ore Mts. truncated for sample size (dotted line) of at least 20 TRW series. Black dots indicated negative extremes.
Radial growth of conifers at high altitudes is primarily driven by growing season temperature and global radiation [48]. However, the strong growth–temperature relationship was significantly reduced in the second half of the 20th century when mountain forests of Central Europe experienced widespread and long-lasting effects related to acid deposition [49]. The coincidence of freezing temperatures in winter 1978/1979 and high concentrations of SO2 led to tree-ring width fluctuations and the weakening of the climate signal. In the 1980s, the radial growth of Norway spruce in the "Black Triangle" was not controlled by summer temperature at all. Extremely narrow tree-ring widths or even missing rings were detected under exceptionally unfavourable environmental conditions [14].
During the time of the highest sulfur emissions, the TRW reached its lowest values (Fig 9). The TRW indices were reduced by >40% during the 1980s compared with their long-term mean (1950–2018). After the decline in sulfur deposition, the mean TRW indices increased, and soon exceeded values from the period before the extreme emission load.
General linear model (GLM) and Hierarchical Partitioning (HP) analyses applied on TRW 1979–2017 (Table 3) showed that climatic effects have had a minor effect on TRW compared to atmospheric pollution. SO2 concentration was the dominant negative factor driving decline of TRW in GLM,explaining 57% of variance for all sites taken together. TRW was influenced negatively by Palmer drought severity index (PDSIV-VIII), despite the positive effects of summer air temperature on TRW. Neither parameter was able to explain more than 8.2% and 24% of total variance, respectively (Table 3). Forest age itself was able to explain only 6% of observed variance (declines in TRW with forest age), but forest age and PDSIV-VIII together showed a positive correlation with TRW as well as with soil base saturation (Table 3)
Table 3. Assessment of the best (lowest AIC criterion) general linear model (GLM) with Hierarchical Partitioning (HP) analysis applied to annual tree-ring width index for the period 1979–2017.
Asterisks in HP analysis dentote p<0.05.
| GLM analysis | All sites | Načetín | Kovářská | Fláje | ||||
|---|---|---|---|---|---|---|---|---|
| Predictors | Estimates | p value | Estimates | p value | Estimates | p value | Estimates | p value |
| SO2 concentration | -0.20 | <0.001 | -0.12 | <0.001 | -0.18 | <0.001 | -0.08 | 0.023 |
| PDSIV-VIII | -0.07 | 0.008 | -0.09 | 0.013 | -0.11 | 0.017 | ||
| Air temperatureV-VIII | 0.05 | 0.093 | 0.10 | 0.029 | ||||
| Soil BS | -0.05 | 0.082 | -4.30 | 0.007 | ||||
| Forest age | -0.09 | 0.004 | ||||||
| Forest age: PDSIV-VIII | 0.04 | 0.046 | ||||||
| Forest age:Soil BS | 0.08 | 0.031 | ||||||
| HP analysis | Z scorep value | Explained variance (%) | Z scorep value | Explained variance (%) | Z scorep value | Explained variance (%) | Z scorep value | Explained variance (%) |
| SO2 concentration | 20.9* | 57 | 6.7* | 56 | 10.4* | 65 | 3.73* | 48 |
| PDSIV-VIII | 2.29* | 8.2 | 1.7* | 19 | 4.0* | 52 | ||
| Air temperatureV-VIII | 7.67* | 24 | 5.5* | 35 | ||||
| Soil BS | 1.48 | 5.7 | 2.5* | 24 | ||||
| Forest age | 1.4 | 6.0 | ||||||
4.4. Relationships between forest growth and acidification
Periods of low TRW were observed throught the record, but were most commin in in years 1980s (Fig 9). Both direct (SO2 concentrations, atmospheric deposition) and indirect (soil chemistry represented by soil pH, Bc/Al and soil base saturation) factors were evaluated to judge the likely importance of various factors in driving the observed periods of low TRW.
4.4.1. Atmospheric deposition and SO2 concentrations
Atmospheric deposition of sulfur was identified as the most critical factor controlling reduced TRW for the period of tree lifetimes (Table 4) for gneiss underlain Načetín (since 1933) and Kovářská (since 1912). S deposition was not identified to be important for reduced growth at basalt-underlain Fláje (since 1959). S deposition was the only relevant explanatory parameter when the whole tree lifetime was analysed. TRW was reduced from 1979–1999 (Fig 9) and has been fully recovered since 2000. During this period of reduced tree growth deposition was about 300–350 meq·m-2·yr-1 in 1979 and ca. 250 at the end of the period of reduced TRW (S1 Annex, S5 Fig).
Table 4. Correlation coeficients between the individual parameters and TRW.
Correlation was assessed during two intervals: (i) modelled annual atmospheric deposition and soil chemistry for the life span of trees and (ii) modelled annual soil chemistry, deposition and measured annual airborne SO2 concentrations for the period 1979–2017. Statistically significant (p<0.05) values are displayed in bold.
| 1850–2017 | 1979–2017 | |||
|---|---|---|---|---|
| Načetín | R | p | R | p |
| Total S deposition | -0.40 | <0.001 | -0.49 | 0.001 |
| Air SO2 concentrations | -0.50 | 0.001 | ||
| Soil pH | 0.23 | 0.030 | 0.18 | 0.260 |
| Soil base saturation | 0.13 | 0.220 | -0.30 | 0.070 |
| Soil Bc/Al | 0.14 | 0.180 | 0.06 | 0.700 |
| Kovářská | ||||
| Total S deposition | -0.38 | <0.001 | -0.72 | <0.001 |
| Air SO2 concentrations | -0.69 | <0.001 | ||
| Soil pH | 0.28 | 0.003 | 0.56 | <0.001 |
| Soil base saturation | 0.34 | <0.001 | 0.59 | <0.001 |
| Soil Bc/Al | 0.26 | 0.008 | 0.49 | 0.002 |
| Fláje | ||||
| Total S deposition | -0.14 | 0.290 | -0.45 | 0.005 |
| Air SO2 concentrations | -0.50 | 0.001 | ||
| Soil pH | 0.07 | 0.580 | 0.30 | 0.060 |
| Soil base saturation | 0.07 | 0.620 | 0.34 | 0.040 |
| Soil Bc/Al | 0.02 | 0.910 | 0.23 | 0.160 |
| Černý potok | ||||
| Total S deposition | -0.27 | 0.031 | -0.61 | <0.001 |
| Air SO2 concentrations | -0.62 | <0.001 | ||
TRW was additionally and deeply reduced in the years 1996–1997. Acid rime with extremely low pH was recorded during winter 1995/1996 [43]. It resulted in significant defoliation in spring 1996 and a subsequent decrease of TRW for two years. Trees fully recovered their radial growth in 1998. The acid rime episode was caused by an asymmetrical reduction of dust and SO2 emissions (Fig 2). Dust from power plants was reduced earlier and more effectively than SO2 (Fig 2). Thus precipitation and rime were extremely acidic in this short period in the mid-1990s. TRW reduction was observed at all sites (Fig 9). Still, the most pronounced reduction was observed at the oldest stand at Kovářská and the lowest reduction was observed at the youngest stand, Fláje, underpinning the role of the vitality associated with young stands.
SO2 concentrations in the air were available for the period 1979–2017 from the Zinwald station (German-Czech border). This station has the longest record in the region and documents the level of air pollution in the "Black triangle" region where Czech, as well as German and Polish power plants, contributed to the extreme local pollution [2]. Analyzing relationships for 1979–2017 only, SO2 concentrations and sulfur deposition explained forest decline equally and were statistically significant at all sites (p<0.05, Table 4). The role of S deposition in driving the TRW trends was highlighted in the linear mixed effect model analysis. Fitted linear model highlighted the pivotal role of SO2 emissions in driving the TRW trends in the full datasets and in analysis for each site separately. Among all environmental factors retained in the final GLM model, SO2 emissions explained 57% of variance, followed by climatic factors which contributed by 32% to the explained variance (Table 3). A significant interaction of forest age with PDSI and soil base saturation suggested higher sensitivity of older trees to drought and to the adverse soil chemistry. Althought the weather conditions certainly influenced the TRW dynamics across our sites, acidic air pollution was identified as a principal driver of observed TRW changes.
4.4.2 Soil chemistry
Soil chemistry did not show a statistically significant correlation with TRW for the lifetime of trees at any site (Table 4). It also did not explain changes in tree growth during shorter periods that experienced rapid changes in pollution (1979–2017) for Načetín control and Fláje. The only site where soil chemistry, as well as air pollution, explains TRW is Kovářská. This site is naturally acidic (gneiss in bedrock), and was first limed in 1981 (Table 1), during the most profound TRW depression (Fig 9B). Thus soil solution pH, Bc/Al and base saturation increased significantly and monotonically (Fig 8) from low values (BS of 6% in 40 cm) to very high saturation (38% in 2018), significantly higher than the preindustrial estimate of 20%. Such artificial soil treatment makes soil chemistry "recovery" very robust, linear and coincident with a declining level of air pollution. At acidic and unlimed Načetín, as well as at naturally alkaline and limed Fláje, TRW did not correlate with modelled soil chemistry.
5. Synthesis
Long-term changes in soil chemistry (soil pH, base saturation and Bc/Al ratio) as well as climatic factors (Table 3) did not explain the observed decline in TRW at two of three sites for which data are available (Table 4) despite the depletion of nutrient cations and enhanced concentration of potentially toxic Al in the soil solution that has frequently been hypothesized to lead to deterioration of forest health. The molar Bc/Al ratio ((Ca + Mg + K)/Al) has been widely used as a criterion for the risk of tree damage [50–52]. Experiments with seedlings by Sverdrup et al. [50] showed that increased mortality occurred if the Bc/Al ratio was lower than 1. Field data from the Czech Republic [52] suggested that increasing tree damage occurred with decreasing Bc/Al in soil solution of the rooting zone in Norway spruce stands. On the other hand, this concept’s limitation was shown by De Wit et al. [53]. They found that of the base cations, only reduction of Mg uptake occurred after long-term experimental addition of AlCl3 to the rooting zone of Norway spruce in southern Norway. Our observations support the hypothesis that direct injury of the needlesis more important for tree damage, at least in the areas where extremely high SO2 concentrations, as well as S deposition, occurred in the past [e. g. 1, 14, 49].
If the shorter period 1979–2017 is examined (Table 3), statistically significant correlations for soil pH, base saturation, and Bc/Al were observed for Kovářská only (Table 4). This plot was limed three times since 1981 (Fig 8), and soil chemistry became less acidic and more base-rich than the unlimed Načetín control (the same bedrock), where no correlation was observed. The magnitude of soil chemistry change at Kovářská was very pronounced in comparison to Načetín control (Fig 8), but TRW changes were similar and no statistical difference between TRW recovery after 1979 was detected (Fig 9).
The minor role of soil chemistry was also manifested at naturally well buffered and also massively limed Fláje. Very high base saturation before the liming and supersaturation after that (Fig 8) did not eliminate TRW decline in the 1970s and 1980s (Fig 9).
Similar findings from Krkonoše Mts. National Park (ca. 150 km east of our sites) were published by Kolář et al. [14]. They found that TRW of Norway spruce declined significantly at high altitudes since the 1970s and recovered fully around 2000 when acidic deposition declined. One plot from five investigated was limed by 5 t·ha-1 of dolomitic limestone in the mid-1980s. Liming did not affect TRW, and all five sites recovered synchronously as the acid deposition declined.
The fact that canopy injury was the most important predictor for TRW reduction was well documented during the frost/acid rime episode (Fig 4) in the winter of 1995/1996 (Fig 9) when spruce trees at Načetín lost the two youngest years of needles [43]. It was followed by a short but deep depression in tree ring width, even though soil chemistry did not show any deviation from long-term trends (Figs 6 and 8).
Our results suggest that the direct impact of acidic deposition from high SO2 concentrations and/or sulfur deposition was the main driver of forest decline. Soil chemistry to a depth of 40 cm most probably did not play a crucial role in the observed forest dieback in the heavily polluted so-called "Black Triangle" of Central Europe, formerly one of the most SO2-polluted areas in the world. Soil liming did not appear to help recover tree growth from chronic stress, despite the fact that this argument has often been made to justify repeated liming [44]. Liming may help reduce soil acidity and increase the availability of base cations (Ca and Mg). Nonetheless, our study showed no visible effects of liming on tree growth measured as changes in TRW. Other authors [e. g. 54] have also found that enhanced radial growth of trees did not occur after dolomitic limestone application.
We cannot reject altogether the hypothesis that forest growth might be negatively affected by soil chemistry, as the uppermost organic and mineral soil down to 10 cm slightly recovered at the long-term Načetín control plot (Fig 6). In contrast, deeper mineral soil down to 40 cm became even more acidic during the last few decades (Fig 6). Very acidic forest soils (down to 30 cm) were detected at 31% of 1599 semi-randomly selected soil samples taken between 2006–2009 in the Czech Republic [55], but significant forest decline which can be attributed to soil acidification was not observed during the same time period [56]. As roots of Norway spruce are located mainly in the organic layer and upper mineral soil, more favorable conditions (less Al, slightly higher soil base saturation) were created in the 1990s. But the uppermost layers responded quickly to the steep decline of acidic deposition (Fig 5). Thus it is difficult to disentangle the effects of atmospheric chemistry and rapid but limited soil recovery in the uppermost rooting zone.
As has been shown in this paper and many papers and reviews previously [e. g. 45, 57, 58], acidic deposition caused a deterioration in soil chemistry that might have some effects on Norway spruce, but increases in Norway spruce growth during periods of improved air quality are not clearly linked to changes in soil chemistry. In contrast, direct effects on foliage from sulfur gas and sulfur deposition appear to be the most critical factors driving increased growth rates of Norway spruce during the recovery of environmental health in the infamous “Black Triangle” region of central Europe.
Supporting information
(DOCX)
(XLSX)
(TIF)
(TIF)
(TIF)
(TIF)
(TIF)
Acknowledgments
Pavla Holečková from Czech Geological Survey is thanked for editorial assistence.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
This study was supported by the Czech Science Foundation in the form of grants to JH [No. 20-19471S] and FO [No. 21-22810J], and by the Czech Ministry of Education, Youth and Sport in the form of funding to MT [CZ.02.1.01/0.0/0.0/16_019/0000797].
References
- 1.Moldan B, Schnoor JL. Czechoslovakia: examining a critically ill environment. Environ. Sci. Technol. 1992; 26(1): 14–21. doi: 10.1021/es00025a001 [DOI] [Google Scholar]
- 2.Hůnová I. Ambient Air Quality in the Czech Republic: Past and Present. Atmosphere. 2020; 11(2): 214. doi: 10.3390/atmos11020214 [DOI] [Google Scholar]
- 3.Kubíková J. Forest dieback in Czechoslovakia. Vegetatio. 1991; 93: 101–108. [Google Scholar]
- 4.Sullivan TJ, Driscoll CT, Beier CM, Burtraw D, Fernandez IJ, Galloway JN, et al. Air pollution success stories in the United States: the value of long-term observations. Environ Sci Policy. 2018; 84: 69–73. doi: 10.1016/j.envsci.2018.02.016 [DOI] [Google Scholar]
- 5.Grennfelt P, Engleryd A, Forsius M, Hov Ø, Rodhe H, Cowling E. Acid rain and air pollution– 50 years of progress in environmental science and policy. Ambio. 2020; 49: 849–864. doi: 10.1007/s13280-019-01244-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Oulehle F, Kopáček J, Chuman T, Černohous V, Hůnová I, Hruška J, et al. Predicting sulphur and nitrogen deposition using a simple statistical method. Atmospheric Environ. 2016; 140: 456–468. doi: 10.1016/j.atmosenv.2016.06.028 [DOI] [Google Scholar]
- 7.Sverdrup H, de Vries W, Henriksen A. Mapping critical loads. Copenhagen: Nordic Council of Ministers. Nord. 1990; 98. [Google Scholar]
- 8.De Vries W, Reinds GJ, Posch M. Assessment of critical loads and their exceedance on European forests using a one-layer steady-state model. Water, Air, and Soil Pollut. 1994; 72: 357–394. [Google Scholar]
- 9.Godbold DL, Fritz H‐ W, Jentschke G, Meesenburg H, Rademacher P. Root turnover and root necromass accumulation of Norway spruce (Picea abies) are affected by soil acidity. Tree Physiol. 2003; 23: 915–921. doi: 10.1093/treephys/23.13.915 [DOI] [PubMed] [Google Scholar]
- 10.Kandler O, Innes JL. Air pollution and forest decline in Central Europe: Environ. Pollut. 1995; 90(2): 171–180. doi: 10.1016/0269-7491(95)00006-d [DOI] [PubMed] [Google Scholar]
- 11.Schulze E-D. Air Pollution and Forest Decline in a Spruce (Picea abies) Forest. Science. 1989; 244 (4906): 776–783. doi: 10.1126/science.244.4906.776 [DOI] [PubMed] [Google Scholar]
- 12.Krause GMH. Impact of air pollution on above-ground plant parts of forest trees. In: Mathy p (ed) Air Pollution and ecosystems. Riedel Publ. Co. Dordrecht; 1988. pp. 168–216. [Google Scholar]
- 13.Büntgen U. Urban O. Krusic PJ. et al. Recent European drought extremes beyond Common Era background variability. Nat. Geosci. 2021; 14: 190–196. 10.1038/s41561-021-00698-0 [DOI] [Google Scholar]
- 14.Kolář T, Čermák P, Oulehle F, Trnka M, Štěpánek P, Cudlín P, et al. Pollution control enhanced spruce growth in the “Black Triangle” near the Czech–Polish border. Sci Total Environ. 2015; 538: 703–711. doi: 10.1016/j.scitotenv.2015.08.105 [DOI] [PubMed] [Google Scholar]
- 15.Black BA, Griffin D, van der Sleen P, Wanamaker AD Jr, Speer JH, Frank DC, et al. The value of crossdating to retain high-frequency variability, climate signals, and extreme events in environmental proxies. Glob Change Biol. 2016; 22(7): 2582–2595. doi: 10.1111/gcb.13256 [DOI] [PubMed] [Google Scholar]
- 16.Altman J, Fibich P, Leps J, Uemura S, Hara T, Dolezal J. Linking spatiotemporal disturbance history with tree regeneration and diversity in an old-growth forest in northern Japan. Perspect. Plant Ecol. Evol. Syst. 2016; 21: 1–131. [Google Scholar]
- 17.Sohar K, Altman J, Leheckova E, Dolezal J. Growth–climate relationships of Himalayan conifers along elevational and latitudinal gradients. Int J Climatol. 2017; 37(5): 2593–26051. [Google Scholar]
- 18.Rybníček M, Kolář T, Ač A, Balek J, Koňasová E, Trnka M, et al. Non-pooled oak (Quercus spp.) stable isotopes reveal enhanced climate sensitivity compared to ring widths. Clim Res. 2021; 83: 27–41. 10.3354/cr01632 [DOI] [Google Scholar]
- 19.Dambrine E, Kinkor V, Jehlička J, Gelhaye D. Fluxes of dissolved mineral elements through a forest ecosystem submitted to extremely high atmopsheric pollution inputs (Czech Republic). Ann Sci For. 1993; 50: 147–157. [Google Scholar]
- 20.Oulehle F, Evans CD, Hofmeister J, Krejčí R, Tahovská K, Persson T, et al. Major changes in forest carbon and nitrogen cycling caused by declining sulphur deposition. Glob Change Biol. 2011; 17: 3115–3129. [Google Scholar]
- 21.Růžek M, Tahovská K, Guggenberger G, Oulehle F. Litter decomposition in European coniferous and broadleaf forests under experimentally elevated acidity and nitrogen addition. Plant Soil. 2021; 463: 471–485. doi: 10.1007/s11104-021-04926-9 [DOI] [Google Scholar]
- 22.Gut U, Árvai M, Bijak S, Camarero JJ, Cedro A, Cruz-García R, et al. No systematic effects of sampling direction on climate-growth relationships in a large-scale, multi-species tree-ring data set. Dendrochronologia. 2019; 57: 125624. [Google Scholar]
- 23.Knibbe B. PAST4—Personal Analysis System for Treering Research Version 4. Instruction Manual. Vienna: SCIEM/Bernhard Knibbe; 2004. [Google Scholar]
- 24.Grissino-Mayer HD. Evaluating crossdating accuracy: a manual and tutorial for the computer program COFECHA. Tree Ring Res. 2001; 57 (2): 205–221. [Google Scholar]
- 25.Cook ER, Peters K. The smoothing spline: a new approach to standardizing forest interior tree-ring width series for dendroclimatic studies. Tree Ring Bull. 1981; 41: 45–53. [Google Scholar]
- 26.Cook ER, Krusic PJ. ARSTAN v. 41d: a Tree-ring Standardization Program Based on Detrending and Autoregressive Time Series Modeling, with Interactive Graphics. Palisades; New York; USA: Tree-Ring Laboratory: Lamont-Doherty Earth Observatory of Columbia University; 2005. [Google Scholar]
- 27.Büntgen U, Frank DC, Wilson R, Carrer M, Urbinati C, Esper J. Testing for tree-ring divergence in the European Alps. Glob Chang Biol 2008; 14: 2443–2453. [Google Scholar]
- 28.Cook ER, Peters K. Calculating unbiased tree-ring indices for the study ofclimatic and environmental change. Holocene. 1997; 7: 361–370. [Google Scholar]
- 29.Eckstein D, Bauch J. Beitrag zur Rationalisierung eines dendrochronologischen Verfahrens und zur Analyse seiner Aussagesicherheit. Forstwissenschaftliches Zentralblatt. 1969; 88: 230–250. [Google Scholar]
- 30.Huntington TG, Ryan DF, Hamburg SP. Estimating soil-nitrogen and carbon pools in northern hardwood forest ecosystem. Soil Sci Soc Am J. 1988; 52: 1162–1167. [Google Scholar]
- 31.Cosby BJ, Hornberger GM, Galloway JN, Wright RF. Time scales of catchment acidification: a quantitative model for estimating freshwater acidification. Environ Sci Technol. 1985; 19: 1144–1149. [DOI] [PubMed] [Google Scholar]
- 32.Cosby BJ, Ferrier RC, Jenkins A, Wright RF. Modelling the effects of acid deposition: refinements, adjustments and inclusion of nitrogen dynamics in the MAGIC model. Hydrol Earth Syst Sci. 2001; 5: 499–518. [Google Scholar]
- 33.Oulehle F, Cosby BJ, Wright RF, Hruska J, Kopacek J, Kram P, et al. Modeling soil nitrogen: the MAGIC model with nitrogen retention linked to carbon turnover using decomposer dynamics. Environ Pollut. 2012; 165: 158–166. doi: 10.1016/j.envpol.2012.02.021 [DOI] [PubMed] [Google Scholar]
- 34.Heliwell RC, Wright RF, Jackson-Blake LA, Ferrier RC, Aherne J, Cosby BJ, et al. Assesing recovery from acidification of European surface waters in the year 2010: Evaluation of projections made with the MAGIC model in 1995. Environ Sci Technol. 2014, 48: 13280−13288. [DOI] [PubMed] [Google Scholar]
- 35.Sächsisches Landesamt für Umwelt, Landwirtschaft und Geologie [cited 17 July 2021]. Available from: https://www.lfulg.sachsen.de/.
- 36.Štěpánek P, Zahradníček P, Huth R.) Interpolation techniques used for data quality control and calculation of technical series: An example of a Central European daily time series. Idojaras. 2011, 115: 87–98. [Google Scholar]
- 37.Hlavinka P, Trnka M, Balek J, et al. Development and evaluation of the SoilClim model for water balance and soil climate estimates. Agric Water Manag. 2011, 98: 1249–1261. doi: 10.1016/J.AGWAT.2011.03.011 [DOI] [Google Scholar]
- 38.Wells N, Goddard S, Hayes MJ. A Self-Calibrating Palmer Drought Severity Index. J Clim. 2004, 17: 2335–2351. doi: [DOI] [Google Scholar]
- 39.Pinheiro J, Bates D, DebRoy S, Sarkar DR, Core Team. nlme: Linear and nonlinear mixed effect models. R package, Version 3.1–155, 2022. https://cran.r-project.org/web/packages/nlme/nlme.pdf.
- 40.Barton K. MuMln: Multi-Model Inference. R package, Version 1.43.17, 2020. https://cran.r-project.org/web/packages/MuMIn/MuMIn.pdf.
- 41.Mac Nally R, Walsh CJ. Hierarchical Partitioning Public-domain Software. Biodivers. Conserv. 2004, 13, 659–660. [Google Scholar]
- 42.Kopáček J, Hejzlar J, Krám P, Oulehle F, Posch M. Effect of industrial dust on precipitation chemistry in the Czech Republic (Central Europe) from 1850 to 2013. Water Res. 2016; 103: 30–37. doi: 10.1016/j.watres.2016.07.017 [DOI] [PubMed] [Google Scholar]
- 43.Krejčí R. Poškození smrkového lesa v Krušných horách. Vesmír. 2001; 10: 576–80. [Google Scholar]
- 44.Kubelka L, Karásek A, Rybář V, Badalík V, Slodičák M. Obnova lesa v imisemi poškozované oblasti severovýchodního Krušnohoří. Praha: Ministerstvo zemědělství České republiky; 1992. [Google Scholar]
- 45.Hruška J, Cienciala E. Long-term acidification and nutrient degradation of forest soils—limiting factors of forestry today. Praha: Ministry of the Environmet of the Czech Republic; 2003. ISBN 80-7212-190-1. [Google Scholar]
- 46.Wigley TML, Briffa KR, Jones PD. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J Clim Appl Meteorol. 1984; 23: 201–213. [Google Scholar]
- 47.Rein F, Štekl J. The extremeness of the cold front of Dec. 31, 1978 over the CSR. Trav Géophys. 1981; 29: 379–404. [Google Scholar]
- 48.Kolář T, Čermák P, Trnka M, Žid T, Rybníček M. Temporal changes in the climate sensitivity of Norway spruce and European beech along an elevation gradient in Central Europe. Agric For Meteorol. 2017; 239: 24–33. doi: 10.1016/j.agrformet.2017.02.028 [DOI] [Google Scholar]
- 49.Rydval M, Wilson R. The impact of industrial SO2 pollution on North Bohemia conifers. Water Air Soil Pollut. 2012; 223 (9): 5727–5744. doi: 10.1007/s11270-012-1310-6 [DOI] [Google Scholar]
- 50.Sverdrup H, Warfvinge P, Rosén K. A model for the impact of soil solution Ca:Al ratio, soil moisture and temperature on tree base cation uptake. Water Soil Air Pollut. 1992; 61: 365–373. [Google Scholar]
- 51.Cronan CS, Grigal DF. Use of calcium/aluminum ratios as indicators of stress in forest ecosystems. J Environ Qual. 1995; 24: 209–216. [Google Scholar]
- 52.Hruška J, Cudlín P, Krám P. Relationship between Norway spruce status and soil water base cations/aluminum ratios in the Czech Republic. Water Air Soil Pollut. 2001; 130: 983–988. [Google Scholar]
- 53.de Wit HA, Eldhuset TD, Mulder J. Dissolved Al reduces Mg uptake in Norway spruce forest: Results from a long‐term field manipulation experiment in Norway. For Ecol Manage. 2010; 259: 2072–2082. doi: 10.1016/j.foreco.2010.02.018 [DOI] [Google Scholar]
- 54.Schaaf W. Evaluation of different magnesium fertilization strategies. In: Hüttl RF, Schaff WW, editors. Magnesium deficiency in Forest Ecosystems. Kluwer Academic Publishers; 1997. pp. 333–355. [Google Scholar]
- 55.Šantrůčková H, Cienciala E, Kaňa J, Kopáček J. The chemical composition of forest soils and their degree of acidity in Central Europe. Sci Total Environ. 2019; 687: 96–103. doi: 10.1016/j.scitotenv.2019.06.078 [DOI] [PubMed] [Google Scholar]
- 56.Cienciala E, Russ R, Šantrůčková H, Altman J, Kopáček J, Hůnová I, et al. Discerning environmental factors affecting current tree growth in Central Europe. Sci Total Environ. 2016; 573: 541–554. doi: 10.1016/j.scitotenv.2016.08.115 [DOI] [PubMed] [Google Scholar]
- 57.de Vries W, Dobbertin HH, Solberg SH, van Dobben HF, Schau F. Impacts of acid deposition, ozone exposure and weatherconditions on forest ecosystems in Europe: an overview. Plant Soil. 2014; 380: 1–45, doi: 10.1007/s11104-014-2056-2 [DOI] [Google Scholar]
- 58.Oulehle F, Hofmeister J, Cudlín P, Hruška J. The effect of reduced atmospheric deposition on soil and soil solution chemistry at a site subjected to long‐term acidification, Načetín, Czech Republic. Sci Total Environ. 2006; 370: 532–544. doi: 10.1016/j.scitotenv.2006.07.031 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX)
(XLSX)
(TIF)
(TIF)
(TIF)
(TIF)
(TIF)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.