Investigating the temporal pattern of neuroimaging-based brain age estimation as a biomarker for Alzheimer’s Disease related neurodegeneration

Abstract

Neuroimaging-based brain-age estimation via machine learning has emerged as an important new approach for studying brain aging. The difference between one’s estimated brain age and chronological age, the brain age gap (BAG), has been proposed as an Alzheimer’s Disease (AD) biomarker. However, most past studies on the BAG have been cross-sectional. Quantifying longitudinal changes in an individual’s BAG temporal pattern would likely improve prediction of AD progression and clinical outcome based on neurophysiological changes. To fill this gap, our study conducted predictive modeling using a large neuroimaging dataset with up to 8 years of follow-up to examine the temporal patterns of the BAG’s trajectory and how it varies by subject-level characteristics (sex, APOEε4 carriership) and disease status. Specifically, we explored the pattern and rate of change in BAG over time in individuals who remain stable with normal cognition or mild cognitive impairment (MCI), as well as individuals who progress to clinical AD. Combining multimodal imaging data in a support vector regression model to estimate brain age yielded improved performance over single modality. Multilevel modeling results showed the BAG followed a linear increasing trajectory with a significantly faster rate in individuals with MCI who progressed to AD compared to cognitively normal or MCI individuals who did not progress. The dynamic changes in the BAG during AD progression were further moderated by sex and APOEε4 carriership. Our findings demonstrate the BAG as a potential biomarker for understanding individual specific temporal patterns related to AD progression.

1. Introduction

Alzheimer’s Disease (AD) is the 6th leading cause of death in the U.S., affecting 1 in 9, or 6.2 million Americans over the age of 65 as of 2021 (Alzheimer’s Association, 2021). Crucially, AD-related brain changes precede clinical symptoms, making treatment difficult to implement (Jack et al., 2013; Singh-Manoux et al., 2012; Wilson et al., 2011). Thus, exploring the trajectory of AD-related brain changes may lead to improved treatment through early detection and future outcome prediction. While aging in cognitively normal (CN) individuals ultimately leads to some structural brain atrophy (Anderton, 1997), neurodegenerative diseases such as AD show rapid deviation from the normal aging trajectory (Anderson et al., 2012). To understand the temporal pattern of these AD-related deviations from normal aging, predictive models using large longitudinal neuroimaging datasets can be leveraged.

To accomplish this, machine-learning methods using neuroimaging features as input have been used to estimate a person’s chronological age (Baecker et al., 2021; Cole and Franke, 2017; Franke et al., 2010; Niu et al., 2020; Wang et al., 2019). This estimated age is also called brain age and allows the difference of this estimated brain age to the participant’s chronological age to be compared. This difference, referred to as the brain age gap (BAG), has been used to examine brain aging in major depressive disorder (Han et al., 2020), Parkinson’s disease (Eickhoff et al., 2021), schizophrenia (Chung et al., 2018), as well as non-disease related differences in cognitive maintenance (Anatürk et al., 2021) and lifestyle behaviors (Bittner et al., 2021). In AD, a positive BAG value (where the estimated brain age is greater than the chronological age) has been associated with increased risk of dementia onset using unimodal (Franke et al., 2010; Gaser et al., 2013; Wang et al., 2019) and multimodal neuroimaging measures (Liem et al., 2017), suggesting its potential as a personalized AD biomarker. Furthermore, individuals at an intermediate stage of AD-related brain changes, known as mild cognitive impairment (MCI), exhibit spatially distinct patterns of gray matter loss consistent with AD related neuropathology (Driscoll et al., 2009). Studies showing significantly greater BAG at later stages of AD and association with clinical symptom severity reflect this (Franke and Gaser, 2012; Löwe et al., 2016), suggesting the BAG may follow a nonlinear trajectory. While pinpointing the exact biological differences quantified by the BAG remains a challenge, its association with brain diseases warrants further investigation.

However, literature relating the BAG to AD progression is sparse. Most studies used cross-sectional designs (Liem et al., 2017), which are inadequate in describing trajectories and do not simultaneously consider intra- (i.e., within subject neurophysiological changes) or inter- (i.e., between subject variance) individual differences (Thompson et al., 2011; Ziegler et al., 2012). The misleading notion of describing greater BAG values in cross-sectional studies as an acceleration of brain aging was recently recognized by Vidal-Pineiro et al. (2021), though they did not explore the BAG in the context of AD. There have been remarkably few studies investigating the BAG with a longitudinal design (Bjørnebekk et al., 2021; Egorova et al., 2019; McWhinney et al., 2021; Wrigglesworth et al., 2022), and fewer still related AD. Two notable BAG studies using longitudinal data to explore AD compared study time-points only to baseline assessment (Franke and Gaser, 2012; Löwe et al., 2016), but this approach does not fully investigate potential non-linear trajectories of the BAG. For example, these studies found BAG scores compared between baseline and a follow up time in several years were significantly greater in progressive MCI and AD individuals compared to earlier or stable groups, though whether this remains significant after considering variation across multiple timepoints is unclear. Identifying how an individual’s BAG temporal pattern changes over time (i.e., linear or non-linear) would enable improved prediction of clinical outcome based on neurophysiological changes.

Together, this data requires consideration of the covariance structure among repeated measures across individuals and groups to account for the heterogeneity common in longitudinal datasets and in particular, AD patient data (Noh et al., 2014; Sun et al., 2019). The appropriate analytical design would then suggest either a linear or non-linear fit to the data. Extant literature on brain and cognitive aging have shown both linear and non-linear changes across age groups, brain structures, and cognitive abilities (Raz et al., 2005; Raz and Lindenberger, 2011). One other study of note examined longitudinal patterns of brain atrophy between CN and MCI subjects using magnetic resonance imaging (MRI) data and found accelerating brain aging for older CN and MCI individuals, though the results were based on a small sample size and did not distinguish between those with stable or progressive diagnoses, and in addition did not explore the moderating effects of covariates (Davatzikos et al., 2009).

Choice of neuroimaging modality has also been relatively homogenous in the BAG literature. Typically, structural T1-weighted MRI has been used to estimate BAG. While MRI derived cortical thickness inform structural brain changes and have been used in AD prediction (Dickerson and Wolk, 2012), fluorodeoxyglucose positron emission tomography (FDG-PET) provides complementary functional information through an indirect measure of metabolic function via glucose consumption (Benvenutto et al., 2018; Dukart et al., 2011). Studies using this modality have shown neuronal dysfunction can precede gray matter atrophy (Jack et al., 2010; Landau et al., 2011), and has been used to measure neurodegeneration (Jack et al., 2018). However, FDG-PET’s use in BAG prediction and understanding its temporal pattern has not been extensively studied (Beheshti et al., 2019), despite its utility in predicting AD (Frisoni et al., 2017). Importantly, it has been suggested to show more consistent functional changes at earlier AD stages compared to the structural-related MRI modality (Dukart et al., 2011), making FDG-PET an ideal method for tracking biological changes preceding clinical symptoms of AD. This presents an opportunity to utilize both modalities for understanding the BAG trajectory. A recent article by Lee et al. (2022) compared brain age prediction models when using either FDG-PET- or MRI-alone, finding the FDG-PET-only model had better performance than the latter. Literature on combining these modalities for predicting brain age is considerably scarcer. Extant literature unrelated to brain age prediction has shown the combination of MRI and FDG-PET data improves discrimination prediction performance of AD (Lu et al., 2018) and MCI (Xu et al., 2016). Given multimodal datasets improve brain age prediction performance (Liem et al., 2017; Niu et al., 2020), the use of both FDG-PET and MRI images is warranted.

In the current study, we explored the use of structural MRI and FDG-PET for a brain age prediction model and tested the hypothesis that the BAG’s temporal pattern would be non-linear, increasing at a faster rate in individuals who were initially diagnosed as MCI but progressed to AD, vs. those who remained diagnosed as CN or MCI. To study the temporal pattern, we utilized longitudinal data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (http://adni.loni.usc.edu/) from individuals with up to 8 years of follow-up. Further, as BAG has been shown to be moderated by factors such as sex (Franke and Gaser, 2019; Wrigglesworth et al., 2022) and carriership of the apolipoprotein E ε4 (APOEε4) allele (Löwe et al., 2016), we also examined their influence on the BAG temporal patterns. Importantly, this study uses a longitudinal design to investigate the pattern (linear vs. non-linear) and rate of change in BAG over time in individuals who progress from MCI to clinical AD. With further validation, BAG as a biomarker for AD has clinical application in assessing brain health and providing insight into a patient’s brain age trajectory (Baecker et al., 2021).

2. Methods

2.1. Participants

Data were downloaded from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database that included ADNI1, ADNI-GO, ADNI2, and ADNI3 (adni.loni.usc.edu/). The primary goal of ADNI has been to test whether neuroimaging, clinical, neuropsychological, or other biological markers can be combined to measure the progression of MCI and early AD.

ADNI participants were stratified into three groups: stable CN (sCN), stable MCI (sMCI), or progressive MCI (pMCI). Stable individuals maintained the same diagnosis, either CN or MCI, for the duration of ADNI. Progressive individuals changed from a baseline assessment of MCI diagnosis to an assessment diagnosis of AD for the duration of ADNI without reverting to MCI. The full sCN sample consisted of N = 227 who had at least baseline data. This full sCN sample was further divided into a training (n = 170) and test (n = 57) set as described in the ‘Brain Age Estimation’ section. To prevent leakage between model training and future statistical comparisons, only the sCN test sample was used in the later longitudinal analyses.

To enable longitudinal analyses, each group was further filtered since the total number of assessment time points varied across subjects. Participants were only included if they had two or more assessments (including baseline) and had both MRI and PET scans. With these filters, the final study sample for longitudinal analyses included 45 sCN, 217 sMCI, and 108 pMCI individuals. Participant sex, age, years of education, race, mini-mental state exam (MMSE) score, and APOEε4 allele carriership were provided from the ADNI dataset.

Demographic and clinical measurements were documented and available for each assessment point for all individuals. APOEε4 carriership was determined at the initial enrollment of that individual. Baseline data from participants in the three groups were compared in reported sex, age, years of education, race, MMSE score, and APOEε4 carriership. One-way ANOVA between groups was carried out for variables age and education, while MMSE scores were compared using a permutation-based ANOVA. Categorical data of sex and APOEε4 were compared using Chi-Square tests. The variable race was analyzed using Fisher’s Exact test.

2.2. Imaging data

Structural MRI and FDG-PET imaging measures used for brain age estimation were provided by Popuri et al. (2018). In that study, structural MRI data were processed through FreeSurfer v5.3 (Fischl, 2012), generating 85 cortical and subcortical gray matter regions of interest (ROI) (Table S4). In the present study, structural MRI mean cortical thickness values were used in subsequent analysis for brain age estimation. Popuri et al. (2018) also parcellated each cortical ROI into equal-size patches, using a previously described adaptive surface patch generation method where vertices within individual ROIs were k-means clustered to reduce dimensionality in an anatomically meaningful way (Raamana et al., 2015). With this method, each ROI could be subdivided into potentially multiple patches depending on the patch size parameter (m) used, where a smaller m would result in a fine resolution (e.g., larger ROIs being parcellated into multiple patches with the same label), and a larger m would result in a coarser resolution. The goal of this method was to create a uniform patch density (i.e., patches in ROI / voxels in ROI) of the cortical surface. 16 patch-size levels were used to obtain this fine to coarse signal representation: 100 voxels per patch, 150, 200, 250, 300, 350, 400, 450, 500, 1000, 1500, 2000, 3000, 4000, 5000, and 10,000. FDG-PET images were co-registered with structural MRI, and patch-wise standardized uptake value ratios (SUVRs) of FDG-PET were provided for ROIs at each patch-size level. To reduce computation time, we evaluated 5 of these 16 patch-size levels (500, 1000, 2000, 5000, and 10,000) in the training step of the brain age estimation analysis (explained in the following section below) and selected the patch size of 2000 voxels/patch based on it returning the lowest root mean squared error (Table S1). This 2000 voxels/patch size resulted in 66 and 65 left and right hemisphere MRI features, respectively, and 343 FDG-PET whole brain features (cortical and sub-cortical). Subsequent brain age estimation analyses were based on SUVRs at this patch size.

2.3. Brain age estimation

Data preparation and analysis were carried out using R (v3.6.2, R Core Team, 2019). Brain age estimation was accomplished using a support vector regression (SVR) model (e1071 package (v1.7–3) within R) (Smola and Schölkopf, 2004), given that the dependent variable of age was continuous, and that this method has been frequently used in brain age prediction literature (Dosenbach et al., 2010; Erus et al., 2015; Franke et al., 2010; Liem et al., 2017; Niu et al., 2020). Briefly, SVR transforms a training set of data into high-dimensional feature space and attempts to fit the data by not penalizing error less than a threshold while minimizing model complexity through its hyperparameters. To observe deviations from healthy brains, the SVR was trained using baseline sCN data, then applied to data at all other time points in each analysis group (i.e., sCN test set, sMCI, pMCI).

SVR model selection procedures are visualized in Fig. 1. The full sCN sample was randomly split (without replacement) into a training set (75% of the data) and test set (remaining 25%). The training set (n = 170) had an age range of 59.8 – 85.9 years (mean = 73.86, sd = 5.59, median = 73.4), and the test set (n = 57) had an age range of 62.8 – 86.2 years (mean = 72.92, sd = 6.14, median = 72.6). All subjects had neuroimaging data at 5 patch-size levels (500, 1000, 2000, 5000, 10,000 voxels/patch). In short, a different SVR trained with baseline neuroimaging data at each patch size was used to predict age, and the resulting prediction performances were compared to select the best model and patch size.

Fig. 1.

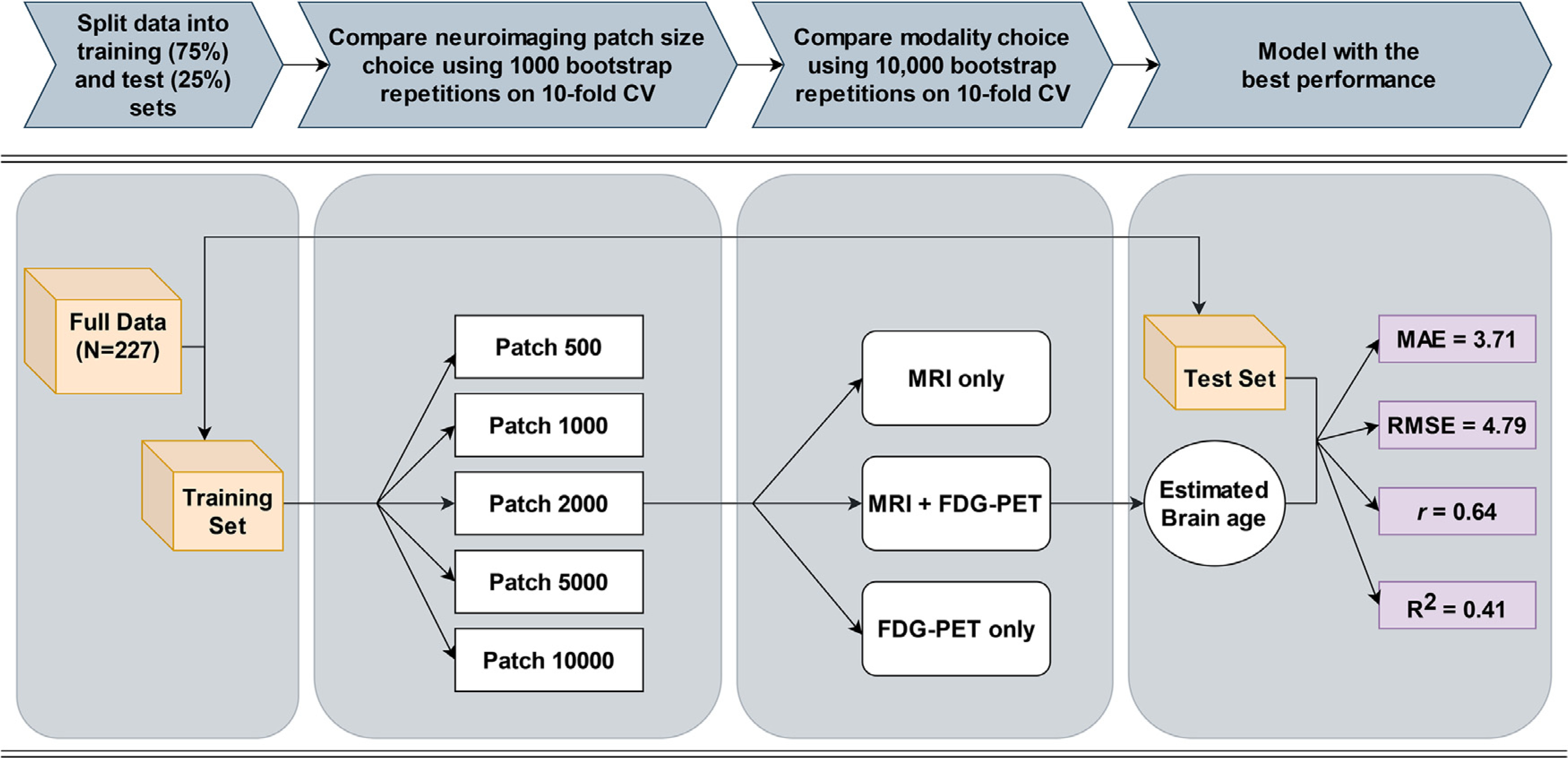
Model selection pipeline. 227 stable cognitively normal (sCN) participants were split into a training set (75% of the sample) and test set (25%), where each participant had baseline neuroimaging data at 5 different patch sizes (500, 1000, 2000, 5000, 10,000 voxels/patch). A separate support vector regression (SVR) was trained and tested with each patch size to predict age. Hyperparameters of each SVR were optimized using 10-fold cross-validation with either linear or polynomial kernel. Patch size and modality comparisons were assessed against the same test set. Training data from the patch size that resulted in the lowest root mean squared error (RMSE) was then used to compare multimodal and unimodal models. The model with the best brain age estimation performance against the test set, or the lowest mean absolute error (MAE), RMSE, and highest correlation coefficient (r) and coefficient of determination (R²), is shown. This best performing model and associated neuroimaging data were then used for all future analyses.

Using either a linear or polynomial (to identify non-linear relationships) kernel, hyperparameters (i.e., cost parameter for both kernels, and gamma, degree, and constant term for polynomial kernel) of each SVR were optimized using 10-fold cross-validation. Briefly, this commonly used procedure splits the training data into 10 partitions, where 9 partitions are used to fit the model, and the remaining partition is used as a validation set to estimate the sample error. This is repeated 10 times such that each partition is used as a validation set once and the sample error is averaged across validation sets. Crucially, only data from the validation sample is used to estimate error during this procedure. Following 10-fold cross-validation, each SVR then predicted age on the test set, which contained participants unseen during model training to produce a valid estimate of prediction performance. Thus, the best performing model was chosen as the one with the lowest root mean squared error (RMSE). This model and the neuroimaging data from the associated patch size were then used for all future analyses. Additionally, performance metrics mean absolute error (MAE), Pearson correlation coefficient (r), and coefficient of determination (R²) were computed.

Finally, each metric was compared between models using both MRI and FDG-PET data (i.e., multimodal) and only MRI or only FDG-PET (i.e., unimodal) from the prespecified patch size. To assess the differences in data modality for brain age prediction, 95% confidence intervals were generated by bootstrapping (10,000 repetitions) on the 10-fold cross-validation of the multimodal and unimodal models. The modality with the best performance on average (i.e., highest MAE and RMSE, and lowest r and R²) was chosen, and the estimation of brain age by this best performing model is subsequently referred to as estimated brain age.

This best performing model was then applied to all individuals in each analysis group (i.e., sCN test set, sMCI, and pMCI) to obtain individualized estimated brain ages at each available assessment time point (not just baseline). The BAG was calculated as the difference between the individual’s estimated brain age and actual chronological age, where a positive BAG represents greater than expected brain aging. Similar procedures of SVR model training and testing were also conducted using single modality MRI or FDG-PET data.

Finally, a well-documented observation in brain age prediction is the bias towards overestimating the BAG for younger subjects and underestimating it for older subjects, likely due to regression towards the mean (Le et al., 2018; Liang et al., 2019; Smith et al., 2019). To overcome this bias, BAGs should be further corrected for the confounding effects of chronological age. We evaluated a linear regression model on the full sCN baseline data (see Liang et al., 2019 for further description of this procedure) to remove this known bias. Given the BAG is estimated using cognitively healthy data at baseline, the expected age-regression in sCN should be centered around 0. Fig. 2 (bottom left graph) shows this procedure was effective in greatly reducing the bias when visualizing the entire sCN sample. When examining the sCN test set sample used for longitudinal analyses (n = 45), this trend is more difficult to observe with the smaller sample size. However, one-sample t-test suggests the sCN test set sample’s bias corrected BAG scores were not significantly different from zero (t = 1.321, p = .193), after assuming a normal distribution using the Shapiro-Wilk test (W = 0.968, p = .247). Notably, the bias is not eliminated in the sMCI and pMCI panels, suggesting especially for pMCI that the unbiased BAG is positive. It is important to note that correction for age-bias was done only for values in subsequent analysis of BAG trajectory, and not done during SVR training to avoid artificially boosting the model’s performance (Butler et al., 2021).

Fig. 2.

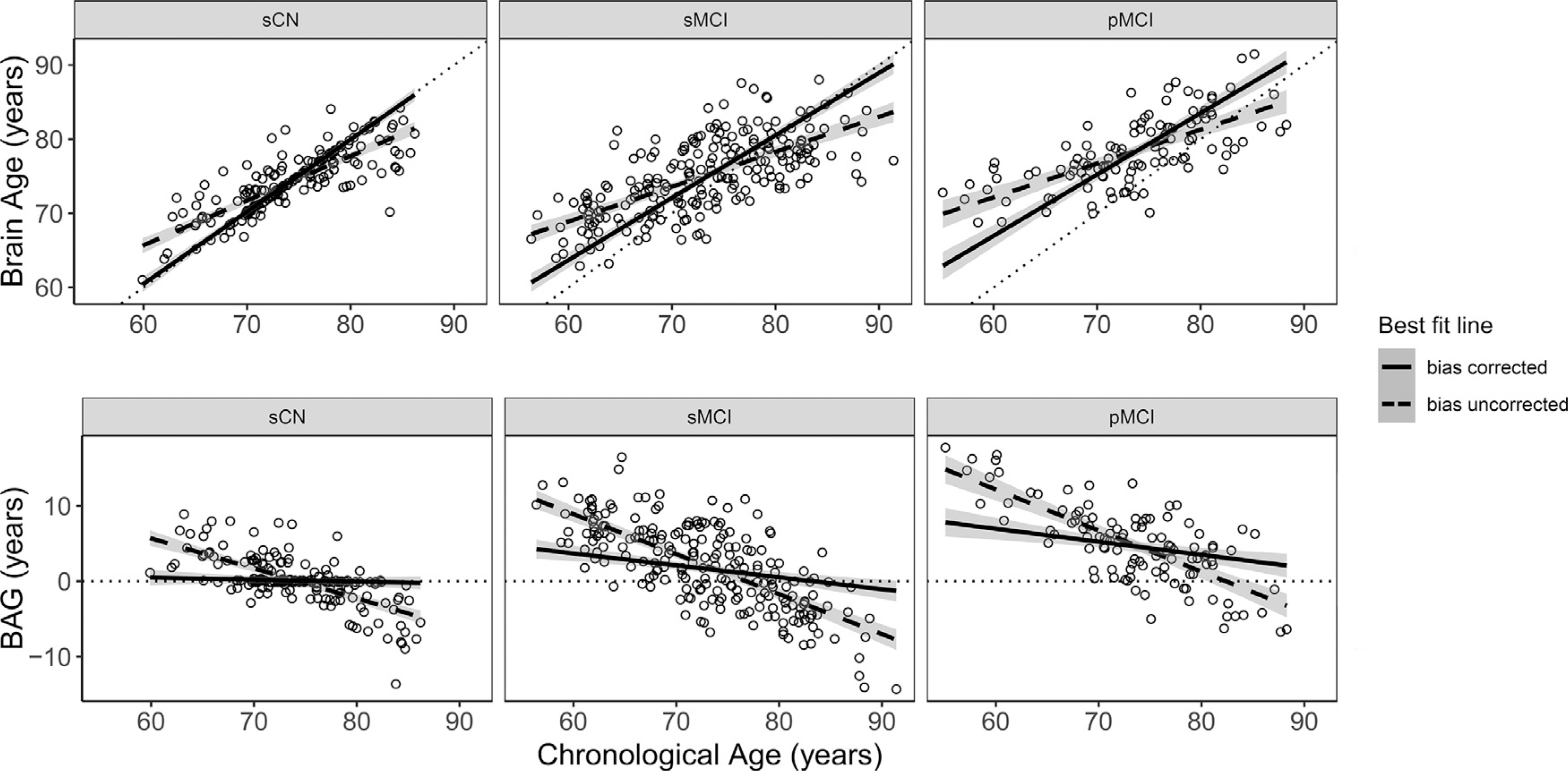
Comparison of best fit line for data before (dashed line) and after (complete line) bias correction is applied for each group. Groups are given as stable cognitively normal (sCN), stable mild cognitive impairment (sMCI), and progressive mild cognitive impairment (pMCI). To show the effect of bias correction, the full sCN sample (N = 227) is plotted here. For all plots, shaded area around each line indicates the 95% confidence interval. Individual points represent baseline data prior to bias correction. Dotted identity y = x and horizontal lines are given as reference. Top: Baseline estimated brain age as a function of chronological age for all individuals in each group. Bottom: Baseline brain age gap (BAG) as a function of chronological age for all individuals in each group.

2.4. Feature visualization

To aid interpretability between modalities, MRI and FDG-PET features were quantitatively labeled depending on their importance for SVR prediction performance. For instance, if the removal of a feature results in model performance of greater MAE value compared to the MAE of a model when using all features, that removed feature would be considered “important” for predicting brain age in that dataset. Thus, the importance of each feature was gauged by removing one feature at a time and calculating the resulting model’s MAE. An importance score for each feature was calculated as the ratio of MAE after removing a feature, over the original MAE, where a higher positive ratio indicated greater importance for normal brain age prediction. Features were then min/max scaled, and any features that were divided into multiple patches (during preprocessing) were averaged together to create single overall importance values for each ROI. Top features were identified as being at least 1 standard deviation from the mean (Table S5). Cortical surface features were visualized using SurfStat (Fig. S1) (Worsley et al., 2009). Of note, this method of feature importance assessment is done using only sCN data during the model training/testing phase, and thus are interpreted in the context of normal brain aging and not disease-related aging.

2.5. Longitudinal analysis of BAG trajectory

Comparisons in BAG trajectory among groups were performed using multilevel modeling with the lme4 package (v.1.1–21) in R. Multilevel modeling allows simultaneous quantification of inter- and intra-individual level patterns in the data, while taking advantage of the regression framework to examine effects of different covariates (Raudenbush and Bryk, 2002). All models assessed the random effects of individuals by allowing their slopes and intercepts to vary across time. The time variable was defined as the assessment time point, coded as the number of months following baseline. Restricted maximum likelihood was used to estimate model parameters and to test the significance of random effects. The basic formation of multilevel models examined time as linear. Higher-order quadratic time or orthogonal polynomial effects were also examined separately, and subsequent model comparisons were conducted based on likelihood ratio testing and the model selection criterion Akaike Information Criterion (AIC). Following this determination, fixed effects of group type and its interaction term with time (either between sCN and pMCI, or sMCI and pMCI, where the pMCI factor was always compared against the sCN or sMCI reference factors) were added to the model. Additional covariates of sex and APOEε4 were tested separately as a fixed effect in the model to determine if they significantly moderated the effect of group type on the BAG trajectory.

2.6. Analysis of pMCI BAG trajectory

To investigate whether the BAG trajectory pattern for pMCI individuals followed a non-linear pattern, piecewise linear segments centered around the assessment of AD diagnosis were used. The segment containing assessments from baseline until the assessment before the AD diagnosis was labeled preAD, and the segment containing assessment times for and following AD diagnosis was labeled postAD. To examine the rate of BAG change, only pMCI individuals with at least two assessments before and two assessments after the initial AD diagnosis assessment were included (N = 24). Multilevel modeling was used estimate the rate of change in BAG for each segment, where segments preAD and postAD were used as separate fixed effects, and the random effect structure varied the slope and intercept of all pMCI subjects across preAD and postAD time segments.

However, the above analysis only allowed us to estimate the preAD and postAD slopes separately and compare the slopes numerically. To establish whether the difference in BAG slopes for the preAD and postAD segments (i.e., interaction between preAD and postAD) was statistically significant, an additional variable centered on the AD diagnosis (1 = assessment with AD diagnosis, 0 = assessment with MCI diagnosis) was created to indicate the individual’s AD conversion status. This conversion variable was added as a fixed effect to the multilevel model to interact with the time effect. A significant positive estimate of this interaction would indicate whether the difference in BAG slope between the segment following the initial AD diagnosis (i.e., postAD) and segment before the diagnosis (i.e., preAD) was actually greater. If the postAD segment was significantly greater than the preAD segment, this would suggest brain aging accelerates after diagnosis in this sample.

3. Results

3.1. Participants

Age, sex, years of education, and race were not significantly different between the three groups (all p > .05), suggesting these variables would not confound later analyses. Differences in group MMSE (p < .001) and APOEε4 (p < .001) were significant, though this was expected as CN individuals categorized as such due to lack of cognitive impairment and are less likely to be APOEε4 carriers compared to AD individuals. Full demographic characteristics can be found in Table 1.

Table 1.

Demographic information for each group. Stable cognitively normal (sCN) and stable mild cognitive impairment (sMCI) maintain the same diagnosis across assessments, while the group with progressive mild cognitive impairment (pMCI) progresses from MCI to at least a final diagnosis of Alzheimer’s Disease. Bold p-values are <0.05.

	sCN (n = 45)	sMCI (n = 217)	pMCI (n = 108)	P-value
Female (%)	15 (33.3%)	86 (39.6%)	42 (38.9%)	0.731
Mean Age (SD)	73.9 (±6.22)	73 (±7.55)	73.5 (±7.14)	0.711
Mean MMSE (SD)	29.0 (±1.12)	27.9 (±1.75)	27 (±1.66)	<0.001
APOEε4 carriers (%)	10(22.2%)	83 (38.2%)	71 (65.7%)	<0.001
Mean years of education (SD)	16.8 (±2.44)	15.9 (±2.83)	16.2 (±2.61)	0.131
% White	91.1%	91.7%	96.3%	0.493

3.2. SVR performance

The SVR model was trained using baseline MRI and FDG-PET data from sCN individuals. The model with the best performance (e.g., lowest RMSE) was achieved using a linear kernel compared to polynomial. Estimation performance of the multimodal model on the test set found an overall performance of r = 0.64, R² = 0.41, MAE = 3.71 years, and RMSE = 4.79 years. Compared to unimodal models (e.g., MRI only, FDG-PET only), the multimodal model yielded on average lower MAE and RMSE, and higher r and R² (Fig. 3). Almost all bootstrapped confidence intervals overlapped, indicating the differences were numerically different but not statistically significant. The exception was for the MAE metric, where the intervals did not overlap between the multimodal and MRI only model, suggesting the multimodal model achieved significantly lower MAE compared to the MRI only model. Performance values are also given in Table 2.

Fig. 3.

Comparison of model performances across modalities of magnetic resonance imaging (MRI) and fluorodeoxyglucose positron emission tomography (FDG-PET), including mean absolute error (MAE), root mean squared error (RMSE), correlation coefficient (r) and coefficient of determination (R²). Error bars represent the adjusted bootstrap percentile 95% confidence intervals, computed over 10,000 bootstrap repetitions.

Table 2.

Model performances across modalities of magnetic resonance imaging (MRI) and fluorodeoxyglucose positron emission tomography (FDG-PET), including mean absolute error (MAE), root mean squared error (RMSE), correlation coefficient (r) and coefficient of determination (R²). Adjusted bootstrap percentile 95% confidence intervals, indicated in square brackets, were computed over 10,000 bootstrap repetitions.

Metric	MRI & FDG-PET	MRI only	FDG-PET only
MAE	3.710 [3.24 3.86]	4.500 [4.05 4.84]	3.784 [3.44 3.89]
RMSE	4.790 [4.30 4.93]	5.294 [4.81 5.51]	5.008 [4.69 5.14]
r	0.640 [0.61 0.71]	0.542 [0.51 0.62]	0.590 [0.55 0.67]
R2	0.410 [0.37 0.51]	0.294 [0.26 0.38]	0.348 [0.31 0.45]

3.3. Group BAG trajectory comparisons

Brain age prediction and bias correction models were then applied to all available assessment time points for each subject within each analysis group. Mean BAG for the pMCI group was greater than the stable groups at every level of assessment (Fig. 4), while a visual assessment shows sMCI and sCN maintained relatively stable BAG trajectories. Notably, the estimated variance in Fig. 4 is minimal up until the final two assessment points, m84 and m96, where each group contained only several observations. Removal of these final assessment points did not drastically change the significance or slopes of the following results.

Fig. 4.

Individual and group brain age gap (BAG) values at each assessment month following baseline. Thick lines represent BAG of all subjects for each group across assessments, fitted by loess curve. Shaded area along each curve indicates the 95% confidence interval. Individual dots and lines represent individual subjects for each group. Groups are given as stable cognitively normal (sCN), stable mild cognitive impairment (sMCI), and progressive mild cognitive impairment (pMCI). Assessment time represents the months following the baseline (initial) assessment.

Multilevel modeling was used to assess the temporal trajectory of BAG over time (linear vs. nonlinear) across all individuals regardless of their group type. Given the large amount of variance among subjects in each group, a random effects structure varying subjects over assessment time was necessary to improve model fit (X² (2) = 160.96, p < .001). The pattern of change in BAG for all individuals was found to be linear over time (b = 0.123, p < .001). Inclusion of the fixed and random effects of quadratic or orthogonal assessment time did not significantly improve the model fit.

In addition, we examined whether the rate of change in BAG over time was different for each group by including the 2-way interaction between assessment and group type. Comparing pMCI against the stable groups found the BAG of the pMCI group increased at a faster rate than the sCN group (b = 0.372, p < .001), and sMCI group (b = 0.310, p < .001). Results for all models are reported in Table 3 for sCN, and Table 4 for sMCI.

Table 3.

Multilevel modeling results for group type stable cognitively normal (sCN) compared to progressive mild cognitive impairment (pMCI). Bold p-values are <0.05.

Estimate		Std. Error	CI (95%)	Statistic	P-value
Assessment, Group type
Intercept	0.740	0.556	[−0.351, 1.831]	1.331	0.184
Assessment	−0.034	0.082	[−0.195, 0.126]	−0.422	0.673
pMCI group	3.918	0.659	[2.625. 5.212]	5.950	<0.001
Assessment * pMCI group	0.372	0.095	[0.186, 0.558]	3.930	<0.001
Assessment, Group type, Sex
Intercept	0.815	0.969	[−1.088, 2.719]	0.841	0.401
Assessment time	−0.037	0.125	[−0.282, 0.208]	−0.299	0.765
pMCI group	4.053	1.126	[1.842, 6.265]	3.599	<0.001
Males	−0.108	1.190	[−2.445, 2.229]	−0.091	0.928
Assessment * pMCI group	0.607	0.143	[0.327, 0.888]	4.254	<0.001
Assessment * Males	−0.000	0.158	[−0.310, 0.310]	−0.001	1.000
pMCI diagnosis * Males	−0.212	1.398	[−2.957, 2.533]	−0.152	0.879
Assessment * pMCI group * Males	−0.397	0.182	[−0.754, −0.040]	−2.186	0.029
Assessment, Group type, APOEε4
Intercept	0.585	0.576	[−0.546, 1.716]	1.015	0.310
Assessment	−0.010	0.093	[−0.193, 0.173]	−0.109	0.913
pMCI group	3.612	0.717	[2.203, 5.020]	5.036	<0.001
APOEε4 carrier	0.672	0.651	[−0.607, 1.950]	1.032	0.303
Assessment * pMCI group	0.136	0.119	[−0.098, 0.371]	1.142	0.254
Assessment * APOEε4 carrier	−0.092	0.182	[−0.449, 0.264]	−0.509	0.611
Assessment * pMCI group * APOEε4 carrier	0.435	0.205	[0.033, 0.837]	2.123	0.034

Table 4.

Multilevel modeling results for group type stable mild cognitive impairment (sMCI) compared to progressive mild cognitive impairment (pMCI). Bold p-values are <0.05.

	Estimate	Std. Error	CI (95%)	Statistic	P-value
Assessment, Group type
Intercept	1.611	0.270	[1.083, 2.140]	5.977	<0.001
Assessment	0.023	0.039	[−0.054, 0.099]	0.582	0.560
pMCI group	3.052	0.462	[2.145, 3.958]	6.599	<0.001
Assessment * pMCI group	0.310	0.060	[0.192, 0.427]	5.150	<0.001
Assessment, Group type, Sex
Intercept	1.005	0.431	[0.161, 1.849]	2.333	0.020
Assessment	0.054	0.062	[−0.067, 0.175]	0.880	0.379
pMCI group	3.867	0.741	[2.414, 5.320]	5.216	<0.001
Males	0.995	0.553	[−0.089, 2.079]	1.800	0.072
Assessment * pMCI group	0.513	0.092	[0.333, 0.694]	5.579	<0.001
Assessment * Males	−0.049	0.078	[−0.201, 0.104]	−0.629	0.529
pMCI group * Males	−1.312	0.950	[−3.173, 0.549]	−1.382	0.167
Assessment * pMCI group * Males	−0.351	0.118	[−0.583, −0.120]	−2.982	0.003

Given the significant interaction of group type and assessment on the BAG, additional subject-level covariates were included in the multilevel models to test whether the difference in rate of BAG change over assessment across groups (i.e., the 2-way interaction effect) depended on subject-specific characteristics. These models examined the influence of sex (male or female) using the 3-way interaction of assessment, group type, and sex. Comparing pMCI to sCN found the difference in BAG rate of change was stronger for females compared to males (b = 0.397, p = .029), and similarly for pMCI compared to sMCI (b = 0.351, p = .003). Visualizing the trajectory of each group over assessments shows a slight increasing BAG trajectory for pMCI females compared to males across groups (Fig. 5).

Fig. 5.

Individual and group brain age gap (BAG) values at each assessment month following baseline for females (top) and males (bottom). Thick lines represent BAG of all subjects for each group across assessments, fitted by loess curve. Shaded area along each curve indicates the 95% confidence interval. Individual dots and lines represent individual subjects for each group. Groups are given as stable cognitively normal (sCN), stable mild cognitive impairment (sMCI), and progressive mild cognitive impairment (pMCI). Assessment time represents the months following the baseline (initial) assessment.

APOEε4 carriership was examined similarly (i.e., comparing carriers to non-carriers). The respective 3-way interaction was significant when comparing pMCI to sCN (b = 0.435, p = .034), but not when comparing pMCI to sMCI (b = 0.184, p = .128) (Fig. 6).

Fig. 6.

Individual and group brain age gap (BAG) values at each assessment month following baseline for APOE4 carriers (top) and non-carriers (bottom). Thick lines represent BAG of all subjects for each group across assessments, fitted by loess curve. Shaded area along each curve indicates the 95% confidence interval. Individual dots and lines represent individual subjects for each group. Groups are given as stable cognitively normal (sCN), and progressive mild cognitive impairment (pMCI). Assessment time represents the months following the baseline (initial) assessment.

3.4. Trajectory analysis of pMCI

The increasing change in BAG for the pMCI group was further examined using piecewise linear segments to assess whether the rate of increase in BAG was greater following the diagnosis of AD. Piecewise linear segments of preAD and postAD as fixed effects were best modeled when varying individuals over the preAD and postAD assessments in the random effects, compared to using only preAD (X²(3) = 19.544, p < .001) or only postAD (X²(3) = 11.399, p = .010). Using this random effect structure, the rate of increase in BAG was numerically greater for the postAD segment (b = 0.425, p < .001) compared to the preAD segment (b = 0.327, p = .031).

To examine whether the difference in rates of BAG change were statistically significant before and after AD diagnosis, multilevel modeling of the 2-way interaction of assessment and conversion variable (i.e., a binary variable indicating whether assessments were before and after AD) was conducted. This interaction was non-significant (b = 0.170, p = .415), suggesting that while the preceding analysis identified a greater slope for the postAD segment, the rate of increase in BAG did not differ significantly before and after conversion.

3.5. Feature importance

Top neuroimaging features at least one standard deviation above the average feature importance value were considered to contribute positively to the prediction of the BAG (Table S5). Top MRI features of cortical thickness were the left inferior parietal cortex, inferior temporal gyrus, lingual gyrus, pars triangularis, precuneus cortex, rostral middle frontal gyrus, superior temporal gyrus, and right entorhinal cortex, lateral orbital frontal cortex, middle temporal gyrus, postcentral gyrus, superior frontal gyrus, and supramarginal gyrus. Top cortical FDG-PET features were bilateral fusiform gyrus, precuneus cortex, rostral middle frontal gyrus, and pars opercularis, as well as left caudal anterior-cingulate cortex, lingual gyrus, postcentral gyrus, superior temporal gyrus, transverse temporal cortex, and finally right inferior parietal cortex, lateral occipital cortex, pericalcarine cortex, superior parietal cortex, supramarginal gyrus, and insula. Top subcortical FDG-PET features included bilateral cerebellum cortex, left thalamus, and right pallidum and accumbens area. Cortical features are visualized in Fig. S1.

4. Discussion

The present study adds to the growing number of longitudinal BAG studies through an investigation into the temporal pattern of the BAG in the context of AD. We found that the difference between brain age and chronological age (i.e., estimated BAG) values were not only consistently higher in MCI participants who progressed to AD compared to CN or MCI individuals who did not progress, but they also increased at a faster rate, given multiple timepoints were considered. Furthermore, this difference was moderated by sex, where the increase was larger in female participants. Additionally, the difference in BAG increase between MCI individuals who progressed and sCN was moderated by APOEε4 carriership where the increase was larger in APOEε4 carriers. Finally, investigation of the increasing rate of BAG for the pMCI group showed a greater slope across assessments following the diagnosis of AD compared to assessments preceding the AD diagnosis, however this increasing rate overall was not significantly moderated by timepoint of AD conversion. While the specific cause for the increasing rate of BAG change is unclear, these results demonstrate the utility of the BAG as a biomarker for understanding group specific temporal patterns related to AD progression.

4.1. Modality choice and model performance

Compared to past studies using similar older age cohorts to ours (between 63 and 86 years with a mean of 73 years), the present study achieved a reasonable prediction performance with a MAE = 3.71, RMSE = 4.79, r = 0.64, and R² = 0.41 (Table S3) (Anatürk et al., 2021; Aycheh et al., 2018; Bittner et al., 2021; Ly et al., 2020; Vidal-Pineiro et al., 2021; Wang et al., 2019). Sample age range must be considered when contextualizing these results in the broader brain age literature. For example, a number of brain aging studies boast impressive correlation coefficient metrics (e.g., r > 0.9), and similarly high R² values, but use wider sample age ranges across entire adulthood (Bellantuono et al., 2021; Cole and Franke, 2017; Liem et al., 2017). When using a sample with an older age range (and similarly greater mean age), r and R² tend to be smaller (Table S3). It’s possible that the wider age range represents a more morphologically diverse dataset than one with a narrower age range, and with a large enough sample size, would afford the model improved performance. To properly compare model performances to other studies the current study would need to be replicated using a larger sample size with an age range spanning the entire adult lifespan. Nevertheless, training a superior brain age model compared to the current literature was not the goal of this study.

Importantly, this is one of the few brain aging studies to combine both MRI and FDG-PET modalities. The majority of literature uses MRI alone, with only a handful using FDG-PET alone (Goyal et al., 2019; Lee et al., 2022). Our model results (Fig. 3) align with recent findings by Lee et al. (2022), who showed that a brain age model based on FDG-PET data alone performed better than MRI alone. Notably, this past study did not explore a multimodal model, whereas we found the combination of both MRI and FDG-PET gave the best performance. This suggests FDG-PET data provides additional information on normal age-related patterns beyond MRI alone. However, the requirement of having both MRI and FDG-PET data limited our sample size. The performance of our brain age prediction model is likely to be further improved with more subjects.

A potential caveat is that our MRI features reflect only cortical thickness. Previous brain age studies used a variety of MRI measures, including FreeSurfer derived cortical thickness, volume, and surface area, or simply raw MRI images (Bellantuono et al., 2021; Cole and Franke, 2017). A few of these studies found better brain age prediction performance when using cortical thickness alone compared to other MRI measures (Liem et al., 2017; Wang et al., 2014), though high performance has also been found using volumetric data alone (Rokicki et al., 2021). As compared to recent studies utilizing elderly cohorts, our model performance using cortical thickness MRI features alone was relatively comparable to a study also using only cortical thickness (Aycheh et al., 2018), as well as to studies using multiple measures (Anatürk et al., 2021; Bittner et al., 2021; Vidal-Pineiro et al., 2021). Future research should explore other MRI measures (e.g. volume and surface area), but a direct comparison of FDG-PET to a single MRI measure (i.e. cortical thickness) still furthers our understanding of brain aging.

The improved prediction performance following addition of FDG-PET data into the model supports the current understanding of FDG-PET as a measure of neurodegeneration distinct from MRI, providing additional information critical to improved brain age prediction (Benvenutto et al., 2018; Ou et al., 2019), and perhaps more broadly throughout brain networks (Stocks et al., 2022). While MRI cortical thickness values reflect structural related neurodegeneration, FDG-PET broadly measures functional information, and particularly neuronal dysfunction signaled by hypometabolism. The relative importance of each FDG-PET and MRI feature was explored by comparing the performance of the original model to a model with that feature removed. Since the model is trained and validated using 75% of the sCN baseline data, relative importance calculated this way must be interpreted in the context of normal aging, and not aging under disease stages. Thus, calculated importance values represent the association between improved prediction performance and aging in an older, cognitively healthy sample and not necessarily the effect of AD-related changes.

Given this, it is not surprising that the hippocampus, a region typically associated with AD while also exhibiting minimal metabolic impairment during normal aging (Kalpouzos et al., 2009), was not among the top importance values in the present model. Subregions that make up the hippocampus, including the dentate gyrus, are less resistant to normal aging effects, but are typically combined with other subregions when considering the hippocampus as a whole (Small et al., 2011). So, while parts of the hippocampus are associated with normal aging, a lack of variability in thickness or metabolic values may prevent the model from identifying the hippocampus as an ‘important’ region for healthy brain age prediction. Relatedly, another explanation is how the ‘importance’ of a feature was defined. Our label of ‘top importance’ for a feature was given when its absence in the model resulted in an MAE at least 1 standard deviation from the mean. Relative to the last subcortical features that met this arbitrary threshold (the left cerebellum cortex with a scaled importance of 0.381), the importance value of the left hippocampus was 0.231, and 0.246 for the right hippocampus. While the definition of ‘top importance’ in this study is meant to guide feature interpretation, it is not a definitive list.

However, we did not expect the right entorhinal and left precuneus to be labeled as highly important MRI features. Cortical thickness reduction in both regions have previously been related to increased MCI risk (Thambisetty et al., 2010). It is possible that while still cognitively intact, this older cohort has larger variability in cortical thickness and metabolic activity for these sensitive regions as compared to a younger cohort. Given reduced metabolic activity typically precedes gray matter atrophy, FDG-PET features likely capture initial risk information in this elderly but still symptomatically healthy cohort. Further, as the entorhinal cortex is one of the first regions to show signs of AD related pathology (Braak and Del Tredici, 2015), and age is a major risk factor for AD, this would lend support to the idea of AD as a continuum, rather than one with discrete disease stages (Aisen et al., 2017).

In support of this idea, other regions rated as highly important including the thalamus, middle frontal gyrus, and precuneus have previously been suggested to exhibit increased glucose uptake as a compensatory mechanism for the decline in superior temporal gyrus or frontal lobe regions due to normal (i.e. CN) aging (Shen et al., 2012). Thus, by measuring metabolism alongside structural measures, we can directly explore both changes in functional and structural connectivity, providing additional information beyond MRI alone which may not capture the full picture of underlying disease processes. Interestingly, many FDG-PET regions rated highly in importance, including superior temporal gyrus and several frontal and parietal lobe regions, were similarly rated as important MRI regions. Since our multimodal data improves model performance, finding similar important regions in both modalities lends support to the notion that both FDG-PET and MRI provide complementary information. While the specificity of FDG-PET findings in the current model above and beyond MRI is not entirely clear given these results, the findings may relate simply to the greater diversity in data provided in a multimodal model, which affords a higher sensitivity to disease processes.

4.2. Longitudinal analysis of BAG

Interestingly, the non-linear assessment time effect was not significant, though this is likely due to the test considering data from all groups. When comparing group effects, the BAG was observed to increase at a significantly faster rate for MCI individual who progressed compared to the stable individuals. Several cross-sectional studies have observed larger BAG in MCI individuals who progressed to AD (Franke and Gaser, 2012; Liem et al., 2017). However, these did not account for individual variances, which were considered in our multi-level models. Accounting for individual differences is important given expected differences in genetic and environmental effects across aging (Ziegler et al., 2012).

Within pMCI, we also found that BAG increased at a numerically greater rate after conversion to AD compared to before conversion, however this increase was not statistically significant. This is likely due to the small sample size for pMCI after filtering for individuals with at least two assessment points before and after the initial AD diagnosis (N = 24). Our findings suggest that, although the progression of AD-related brain changes likely precede clinical diagnosis, there may be a change point for when the BAG begins to accelerate. Identifying this change point could potentially create a more personalized prediction of AD progression. Future studies with larger longitudinal samples are warranted.

How the BAG trajectory is moderated by AD progression-related covariates also yielded interesting results. In a healthy control population, a recent brain aging study found weak but accelerated brain aging in men compared to women in an older population (Wrigglesworth et al., 2022). When stratifying our sample by disease status (i.e. sCN, sMCI, pMCI) however, we found the opposite in pMCI individuals, where women showed an increasing trajectory compared to males. In AD populations, women are afflicted at a greater rate than men after accounting for greater life expectancy (Li and Singh, 2014), and may show a greater rate of decline if afflicted (Buckley et al., 2019; Holland et al., 2013). This may result from neurological consequences of menopause triggering pathological protein aggregation in women (Barnes et al., 2005; Hua et al., 2010; Skup et al., 2011), or differential effects of APOEε4 (Yi et al., 2014). Interestingly, another study by Goyal et al. (2019) using similar machine learning techniques to predict metabolic brain age with solely PET measures found a persistently lower metabolic brain age for female adults compared to male adults, suggesting female brains had increased youthfulness. Though, this is not necessarily in contradiction with the current study, since our findings relate to an increased rate of BAG change over time for female participants.

Similarly, we found rates of BAG increase were greater for pMCI APOEε4 carriers than for non-carriers, which is in line with a recent study (unrelated to the BAG) which found carriers of APOEε4 were associated with faster progression of AD-related dementia (Chen et al., 2021). Taken together with results from the model including sex, these results are particularly interesting as volume in the hippocampus, a region implicated in AD pathology (Mu and Gage, 2011), has previously been found to be significantly reduced in female APOEε4 carriers with MCI, compared to female non- APOEε4 carriers with MCI (Fleisher et al., 2005). Further, APOEε4 has been shown to improve accuracy for predicting AD conversion (Löwe et al., 2016) and interact with race and sex. White and black adult APOEε4 carriers were shown to have overlapping but differential cognitive resilience factors (Kaup et al., 2015), a predictor for AD risk (though our sample size limited an investigation into race). Amyloid-β deposition may also have moderating effects on the BAG trajectory, given frequent associations between amyloid and AD (Jack et al., 2013). Indeed, a recent study has shown the brain age prediction framework can be used to distinguish between amyloid- β negative or positive status (Ly et al., 2020). The present study did not consider this covariate due to sample size constraints, but importantly, the mentioned study could only significantly distinguish between the two statuses when increasing the sample size beyond only ADNI, which introduces potential variability in site effects (Fortin et al., 2018). Clearly, the moderating effects of covariates such as sex, race, Amyloid-β, and APOEε4 (among others) on the BAG trajectory is complex but necessary to evaluate. Future studies using a longitudinal design to study the BAG’s temporal pattern should consider these covariates.

Taken together, our results are line with the larger literature of AD-related changes in the brain suggesting accelerated aging, such as gray matter and cortical thickness atrophy (Anderson et al., 2012; Chan et al., 2003; Driscoll et al., 2009). While normal aging is associated with gray matter atrophy between 0.2–0.5% annually, longitudinal MRI studies have shown annual atrophy rates of 2–3% in AD patients (Fox and Schott, 2004). However, reports of differential cortical thickness changes across regions of the brain (Storsve et al., 2014) suggests the utility of the BAG as a biomarker of brain changes could be enhanced through improved brain parcellation (Niu et al., 2022). Nevertheless, the results of the present study have potential clinical relevance. Previous studies have already demonstrated not only an association between a positive BAG and increased likelihood of AD, but also a number of other neurological conditions (Baecker et al., 2021). Our findings expand on these studies by considering a longitudinal design and how related covariates may influence the trajectory of the BAG. Longitudinal designs are critical for early detection of neurodegenerative diseases.

4.3. Limitations & future directions

The SVR model using MRI and FDG-PET data should be further explored using a sample with a wider age range. While our use of an elderly cohort allowed longitudinal comparisons of age-matched groups, future models trained using a CN sample with age ranging across the adult lifespan would allow direct comparisons to the latest high performing brain age prediction models. Similarly, importance values based on our model are not conclusive and would need to be explored in a sample with a wider age range.

Further, the SVR model was trained using only the ADNI dataset and does not necessarily generalize to other datasets with different racial or socioeconomic distributions, or methodological differences. For example, the study’s sample is predominantly Caucasian and male. The advantage of a single, homogenous-leaning dataset is that the results can be directly compared to other studies working with the ADNI, and differences would be less attributable to dataset or methodology variations. Related to all PET imaging data (including from ADNI) are partial volume effects due to low resolution, which may cause the activity from small ROIs to be underestimated (Thomas et al., 2011). On the other hand, whether correction methods for these effects are reliable or have a noticeable impact on results are controversial (Malpas B et al., 2015; Samper-González et al., 2018; Yang et al., 2017). Future brain aging studies using FDG-PET may wish to consider these effects.

Additionally, other choice of brain age prediction methods should be considered. Our SVR model yielded superior performances to two other commonly used methods, including relevance vector regression (RVR) (Franke et al., 2010) and LASSO (Tishbirani, 1996) (Table S2). Although optimization in the SVR lead to more accurate representation of the BAG trajectories, its computational cost was high. RVR has the potential for clinical adoption because of its low computational cost from not requiring parameter optimization. Other methods such as deep neural networks have also demonstrated improved brain age prediction accuracies, representing an exciting future direction (Jonsson et al., 2019; Lee et al., 2022; Levakov et al., 2020; Niu et al., 2020). Relatedly, recent efforts using deep-learning methods (Hepp et al., 2021) or Gaussian process regression (Gutierrez Becker et al., 2018) have argued brain aging methodology requires a measure of uncertainty given the natural noise associated with CN data and their chronological age. Future studies improving upon the current study should account for this uncertainty in the brain age model perhaps through Bayesian methods.

5. Conclusion

Our study contributes to the existing literature by taking a multimodal, longitudinal approach to examine the temporal patterns of brain aging and found that brain aging occurs at an accelerated rate for those with pMCI compared to stable individuals. It further suggests that there may be a point of acceleration, although this finding needs replication in a larger longitudinal sample. These dynamic changes as subjects progress from MCI to AD are further moderated by both sex and APOEε4 status. Describing the temporal trajectory for brain aging is particularly valuable for understanding AD progression and improving early detection through predictive models. Additionally, BAG prediction performance was improved using both MRI and FDG-PET data, suggesting complementary neuroimaging measures should be considered in BAG studies. Future studies should expand the generalizability of the BAG machine learning models through use of diverse samples, as well as examine the influence of other covariates on the BAG and explore individualized change points in pMCI trajectory.

DATA availability statement

Data used in this study are publicly available through the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). Data access requires acceptance of the ADNI Data Use Agreement (https://adni.loni.usc.edu/wp-content/uploads/how_to_apply/ADNI_Data_Use_Agreement.pdf) and online application form (https://adni.loni.usc.edu/data-samples/access-data/). R codes for analysis are available upon request.