Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2023 Feb 22;8(9):8448–8460. doi: 10.1021/acsomega.2c07497

Development of Yttrium-Doped BaTiO3 for Next-Generation Multilayer Ceramic Capacitors

Mohammed Tihtih †,*, Jamal Eldin F M Ibrahim †, Mohamed A Basyooni ‡,§,∥, Redouane En-nadir ⊥, Walid Belaid #, Irina Hussainova , István Kocserha †
PMCID: PMC9996788  PMID: 36910924

Abstract

graphic file with name ao2c07497_0012.jpg

The use of electronic devices that incorporate multilayer ceramic capacitors (MLCCs) is on the rise, requiring materials with good electrical properties and a narrow band gap. This study synthesized yttrium-substituted barium titanate (Ba1–xYxTiO3, BYT) using a sol–gel process at 950 °C with varying concentrations of yttrium (0 ≤ x ≤ 0.3). X-ray diffraction analysis showed that the tetragonal phase became less pronounced as the yttrium content increased. The samples had varying grain sizes and porosity, with the BY30%T sample having the narrowest band gap at 2.21 eV. The BYT ceramic with 30% yttrium had a thermal conductivity of up to 7 W/m K and an electrical conductivity down to 0.002 (Ω cm)−1 at 180 °C. The current–voltage characteristics of the BYT MLCC were also studied, showing potential use in next-generation high-capacity MLCCs. This work presents BYT as a promising material for these types of capacitors.

1. Introduction

Barium titanate (BT) is a type of material that is often used in the electrical and electronic industries due to its various desirable properties, such as its ability to exhibit ferroelectricity, pyroelectricity, and piezoelectricity, as well as having a high dielectric permittivity and a positive temperature coefficient of resistivity. It is abbreviated as BT and is written as BaTiO3 in chemical notation.1,2 Perovskite materials that are derived from BT have a wide range of applications, including use in devices that have a positive temperature coefficient, devices that generate pulses, infrared detectors, microwave electronics that can be voltage-tuned, multilayer ceramic capacitors (MLCCs), piezoelectric and ultrasonic actuators, thermal sensors and controllers, and microwave devices that utilize piezoelectric transducers and charge storage devices3−5 and so forth. In order to produce MLCCs using BT material, the formulation of the BT must be carefully designed to control its electrical properties, particularly at high temperatures and under high electric fields.6 To improve the reliability of MLCCs made with BT, various additives and dopants, such as yttria (Y2O3), are substituted to the BaTiO3. These dopants create compensation mechanisms that help to enhance the reliability of the capacitors.

Yttrium (Y) is added to BT to improve the reliability of MLCCs. The Y3+ ion has an ionic radius that is intermediate in size between the Ba2+ and Ti4+ ions, which allows it to occupy either the Ba2+ or Ti4+ site in the BT lattice.7 This means that the Y3+ ion can act as an acceptor or donor depending on its position in the lattice, and its inclusion in the BT structure is influenced by kinetic and thermodynamic factors.8,9 It is reported that the formation energy of YBa + VBa″ is 7.23 eV, whereas it is only 4.35 eV to form a YBa + VBa defect.10 The oxygen partial pressure and sintering temperature can create vacancies in the BT lattice for the Ba2+ or Ti4+ ions. These vacancies can then be filled by Y3+ ions, which may occupy either both or one of the sites.11 The solubility of yttrium ions in the BT lattice, and therefore their ability to occupy the vacancies created by the Ba2+ or Ti4+ ions, is influenced by the Ba/Ti ratio, the dopant concentration, and its solubility. The solubility of Y ions can vary depending on whether they are occupying the Ba-site or the Ti-site in the lattice. According to a study by Wang et al.,12 the solubility of Y3+ ions in the BT lattice can vary depending on the sintering conditions and the site in the lattice that the ions are occupying. For example, the solubility of Y3+ ions at the Ba-site is approximately 1.5% when sintered in air at 1440–1470 °C, but it increases to 4% when sintered under reducing conditions. The solubility of Y3+ ions at the Ti-site is higher, at approximately 12.2% when sintered in air at 1515 °C. In addition, the introduction of Y3+ ions into the BT lattice can cause structural changes, such as a phase transformation from tetragonal to cubic. The amount of yttrium ions added to BT can be consumed by various processes during the processing of the ceramic material. A study by Belous et al.13 found that the dopant could be consumed in processes such as the exchange of paramagnetic impurities that occupy Ti-sites, charge compensation mechanisms, and the formation of secondary phases such as Ba6Ti17O40 and Y2Ti2O7. These secondary phases can form when the solid solubility of the dopant in the BT is exceeded. The yttrium ions can also influence the charge compensation mechanisms in the BT lattice.

It is possible to improve the structural, optical, and thermoelectric properties of a BT system by adding the appropriate amount of dopants.14,15 The formation of secondary phases such as Ba2TiSi2O8, Ba6Ti17O40, Y2TiO5, and pyrochlore-type phases like R2Ti2O7 (where R is a rare-earth element such as Dy, Er, Ho, or Y)16−18 has been observed when BT is doped with rare-earth elements.19 These secondary phases are usually formed when the amount of dopant exceeds its solubility limit in the BT lattice and reacts with other free ions in the system, like Ti4+. The formation of these phases depends on factors such as the sintering conditions and the concentration of the dopant. The presence of these secondary phases can adversely affect the structural and dielectric properties of BT, which is of concern for industrial applications. Among the pyrochlore-type phases that have been reported, Y2Ti2O7 has been suspected to have a negative impact on the reliability of BT-based MLCCs.20,21 This phase is believed to have a highly conductive nature and to cause resistance degradation in BT through the acceleration of oxygen vacancy electromigration.22 The effects of Y2Ti2O7 and other secondary phases on the structural and dielectric properties of BT are of high interest for industrial applications, as several studies have reported negative impacts on the major properties of BT.21,22 The investigation of the parameters that influence the formation of Y2Ti2O7 and its potential effects on BT is of interest in both the academic and industrial fields, as Y2O3 is a commonly used dopant in the production of MLCCs.

The electrical conductivity of a material can be measured to study the properties related to defects in non-stoichiometric compounds.23 The advantage of measuring electrical conductivity is that it allows us to examine the properties of materials at high temperatures and monitor these properties during the materials’ processing. However, interpreting electrical conductivity data, especially for polycrystalline materials, can be difficult due to the complexity of the physical sense of electrical conductivity.

Thermal management is important for ensuring the reliability and integrity of electronics in a variety of applications. To optimize the performance and device design of electronics in challenging thermal environments, it is essential to understand the thermal properties of BT. These properties, including thermal conductivity and heat capacity, play a significant role in the design and efficiency of many applications, particularly in thermal management in the optoelectronic industries and phase transition materials.24,25 In addition, evaluating the mechanical properties, such as compressive strength of MLCCs is necessary to understand the internal stresses imposed on the MLCCs26 and to extend their lifetime. BaTiO3 has also been used in a range of electro-optic systems due to its excellent optical characteristics, including highly sensitive photodetectors, second harmonic generators, light sensors, and optical signal processing.27,28 By altering the content of yttrium (Y) in Ba1–xYxTiO3 ceramic materials, it is possible to modify the physical characteristics and energy band gap of the material, potentially expanding its potential technological applications.

Several methods have been used to synthesize BaTiO3 for electrical device applications, including conventional solid-state reactions, hydrothermal techniques, and co-precipitation.29−31 However, the sol–gel method is particularly useful for fabricating new compositions because it allows for control of the stoichiometry and homogeneity of the material and can be performed at lower temperatures using simple laboratory equipment. In this research, the authors used the sol–gel method to prepare yttrium-doped BaTiO3 at different doping concentrations and sintered the materials in air. The resulting materials were analyzed to study the structural, microstructural, thermoelectrical, and optical properties, with a focus on the stoichiometric ratio of BaTiO3 and its semiconducting nature in relation to its use in MLCCs.

2. Experimental Procedure

2.1. Samples Preparation

BYxT; x = 0–30% ceramic samples were prepared via the sol–gel method and outlined in Figure 1. The process involves using three precursors: barium acetate trihydrate [Ba (CH3CO2)2·3H2O ≥ 99% Aldrich], yttrium acetate hydrate III [C6H11O7Y ≥ 99% Aldrich], and titanium isopropoxide [Ti[OCH(CH3)2]4 ≥ 97% Aldrich]. Lactic acid [CH3CH(OH)CO2H] and acetic acid CH3COOH were used as stabilizing agents, while distilled water was employed as a substance for dissolving the barium and yttrium acetates. The first step involves dissolving a specific amount of titanium isopropoxide in water and acetic acid while stirring continuously at 70 °C. The previous solution was stabilized using lactic acid as a chelating agent to form a stable Ti-solution and to avoid premature precipitation. A transparent TiO2 with adequate proportions was obtained. In the second step, barium acetate and yttrium acetate are dissolved in distilled water at 90 °C for 15 min and then added to the TiO2 mixture. Initially, white precipitates are formed and the solution becomes cloudy for 10 min, which then will be converted to a clear Ba–Ti–Y solution at 80 °C. The sol was converted into a viscous gel at 80 °C for 1 h. The gel was dried at 120 °C overnight and turned into a white dried gel. To avoid the agglomeration of the powders and improve reactivity, the resultant xerogel is processed in an agate mortar. Finally, the raw powders were calcined at the temperature of 950 °C for 3 h to obtain BYT powders. The calcined powders were pressed into pellets and sintered at 1200 °C for 6 h in air with a heating/cooling step size of 5 °C/min.

Figure 1.

Figure 1

Open in a new tab

Synthesis flowchart of the ceramic materials.

2.2. Characterization

The crystallinity and phases of the powders were examined using an X-ray diffractometer (XRD) with Cu Kα (λ = 1.5405 Å) radiation. The vibration bands were identified using FTIR spectroscopy (4500–400 cm–1, Hitachi 3140 spectrophotometer FT-IR). The ceramic samples’ morphological characteristics were analyzed using scanning electron microscopies (SEM, Thermo Helios G4-PFIB CXe Dual-Beam), fitted with a Bruker microprobe, and running at a voltage of 20 kV. Before FESEM imaging, the ceramic samples and the fractured samples were coated with multi-layers of gold utilizing coating spray devices to enhance conductivity. The images were captured under different magnifications using ES-BSD mode. An energy-dispersive X-ray spectrometer EDAX Octane Elect-Plus was used to provide quantitative and qualitative analyses of the elemental composition of the samples. The optical properties were measured using an Ocean Optics UV–vis spectrophotometer-QE65Pro. Thermal conductivity’s behavior was determined through a combination of two methods: modified transient plane source (MTPS) and adjusted transient plane source (MTPS). Keithley-2400 source meter was used to study the V–I polarization of the prepared ceramic pellets.

3. Results and Discussion

3.1. Structural Analysis Using XRD

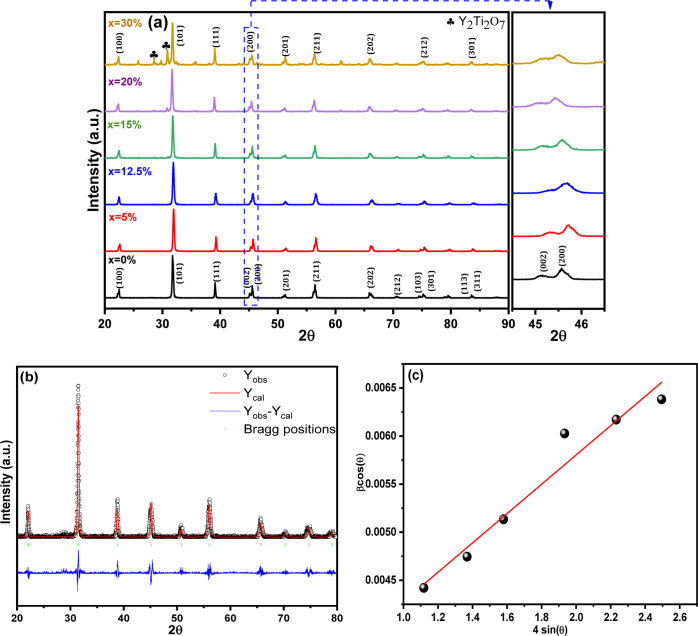
The XRD analysis was conducted to determine the phase purity and crystallinity of yttrium-doped BT (Ba1–xYxTiO3) at various doping concentrations (x = 0.00, 0.05, 0.125, 0.15, 0.2, and 0.3). The study used XRD spectra between 20 and 90° scan angles, and the samples were heated to 950 °C. The results showed that the powdered samples had a perovskite structure, as indicated by the diffraction pattern in Figure 2a. The diffraction peaks observed at 2θ° = 22.23, 31.41, 38.74, 44.96, 45.42, and 50.79° matched with those reported in the previous studies.15,32 The XRD analysis revealed that the average diffraction peaks of the samples were consistent with JCPDS card no. 00-005-0626, which indicates a tetragonal formation of BaTiO3 ceramic for all the samples except x = 0.03, which shows a pseudocubic structure. This is likely due to the fact that yttrium is dissolved up to a certain depth in the BT particles,6 which leads to a reduction in tetragonality. A similar outcome was reported by Kim et al., who found that the ferroelectricity of BT decreases significantly when the grain size is below 7 μm and the structure changes from tetragonal to pseudocubic.33 The phase changes observed in the samples are a combination of tetragonal and cubic phases, which are presented as a pseudocubic phase. The XRD pattern of BT powder shows a pure tetragonal phase, but as the concentration of Y2O3 increases, there is a decrease in tetragonality. This result is consistent with our previous studies.14,34,35 The XRD diffractogram revealed a double peak at around 2θ ≈ 45°, as shown in Figure 2a, which indicates the presence of a tetragonal ferroelectric phase with (002) and (200) planes. The peaks at (002) and (200) show a minor distortion and shift toward a higher angle, as well as an increase in lattice parameters. This is believed to be caused by the incorporation of Y3+ ions at the Ba sites, which leads to an enlargement of the crystal cell volume. The structural properties can be inferred from the characteristic peaks (002, 200) at around 45°.

Figure 2.

Figure 2

Open in a new tab

(a) XRD patterns of Y–BaTiO3 ceramics, (b) Rietveld refinement plot of BY20%T, and (c) W–H plot of BY20%T.

To obtain more accurate structural parameters, the Rietveld refinement was conducted using the FullProf software on the XRD data of the synthesized samples. Figure 2b presents a comparison of the experimental and fitted XRD patterns for the BY20%T composition.

The variation of the crystallite size (D) was determined using the Debye-Scherrer formula36

3.1. 1

The Rietveld refinement was used to determine various parameters such as the lattice parameters (a, b, and c), tetragonality (c/a), and crystallite size from the XRD data of the synthesized samples. The Rietveld refinement was performed using eq 1 and the X-ray wavelength (λ), Bragg diffraction angle (θ), and the full width at half-maximum (fwhm) of the XRD peak were taken into account. Table 1 shows the results of these calculations.

Table 1. Structural Parameters of BYxT, x = 0, 5, 12.5, 15, 20, and 30% Samples.

            crystalline size, D (nm)
 strain, ε
sample Ba1–xYxTiO3 a = b (Å) c (Å) c/a V (Å3) space group Debye–Shearer Williamson–Hall method Debye–Shearer (×103) Williamson–Hall method (×103)
x = 0.00 3.9988 4.0398 1.0102 64.598 P4mm 30.146 29.36 5.287 1.27
x = 0.05 3.9911 4.0293 1.0102 64.182 P4mm 27.52 28.2 4.356 1.35
x = 0.125 3.9989 4.0291 1.0075 64.43 P4mm 29.89 29.99 5.0154 1.25
x = 0.15 3.9901 4.0185 1.0071 63.978 P4mm 34.78 33.53 7.581 3.47
x = 0.2 3.9976 4.0021 1.0011 63.956 P4mm 33.12 31.41 6.125 1.52
x = 0.3 4.0027 4.0051 1.0005 64.168 P4mm 25.03 23.16 4.03 2.24
Open in a new tab

The crystalline size of BT decreases initially for a doping concentration of x = 5% wt of yttrium, but then increases with further doping; for x = 0.125 wt, the cell volume also increases. The tetragonality or grain lattice parameters can be affected37 by defects and impurities when sintering at a low temperature of 1200 °C. The XRD analysis suggests the formation of a perovskite phase with improved crystallinity in BYT. The change in the lattice parameter c values shows the incorporation of the dopant metal Y3+ into the Ba-site. However, it is also possible that the yttrium is integrated into the titanium site, as it can occupy either the Ba or Ti site.14 The formation of oxygen vacancies, grain growth, and grain boundary diffusion can depend on the sintering temperature and can also be influenced by temperature, impurities, and crystal orientation. The volume of the unit cell was calculated by multiplying a2 × c, and the results are presented in Table 1. The addition of Y3+ significantly enhances the tetragonal matrix of BYT, increasing the unit cell volume from 64.598 Å3 (x = 0.0) to 63.956 Å3 (x = 0.07). The lattice parameters (a, c) of the samples increase as the yttrium content increases, as a result of the variation in electronic density and ionic radii of Y3+. This type of enlargement has also been observed for zirconium doping in a tetragonal matrix of BaTiO3.38

The broadening of diffraction peaks in a material is mainly caused by lattice-strain that is initiated by crystallite defects and distortions, according to the suggestion of Williamson and Hall (W–H).38

3.1. 2

The W–H method states that the full width at half maxima intensity (Whkl) is related to the lattice strain and crystalline sizes. The broadening that is attributed to the lattice strain can be denoted as Wstrain, which is calculated using the following equation39

3.1. 3

Rearranging W–H eq 2 we get

3.1. 4

The W–H method plots the Whkl cos θ versus 4 sin θ for Y-BT samples, as shown in Figure 2c. The lattice strain and the average crystalline size can be determined from the slope and the y-intercept of the linear line. These values are obtained using eqs 3 and 4 and are presented in Table 1. Both the Debye–Scherrer and W–H analyses indicate that the crystalline size and strain of all the samples follow the same trend.39

The perovskite (ABO3) structure is relatively stable due to the large difference in ionic radius between the A-site and B-site ions, which makes it difficult for them to jump positions and produce corresponding resistance drift. The most prominent feature of the perovskite structure is that it has strong doping ability on both the A-site and the B-site, and other elements are often doped in experiments to enhance their original properties. The tolerance factor t of the perovskite structure was proposed by Goldschmidt in 1926, and the expression for ABO3 is as follows40

3.1. 5

where rA is the ionic radius of the A-site cation, rO is the ionic radius of the oxygen ion, and rB is the ionic radius of the B-site cation, which is a semi-empirical formula, which can roughly explain the stability of perovskite materials, and the tolerance factor of stable perovskite is between 0.77 < t < 1.10.

The tolerance factor for pure BT ceramic is t = 1.07, which suggests a slight deformation of the crystal structure, where rA(Ba2+) = 1.61 Å, rB(Ti4+) = 0.605 Å, and rO(O2–) = 1.4 Å. The incorporation of Y3+ [r (Y3+) = 0.9 Å] into BT causes a reduction in Goldschmidt’s tolerance factor. The values of t for Ba1–xYxTiO3 samples are calculated and presented in Table 2, which range from 1.07 to 1.051, similar to the results in ref (41). Here, it is expected that the A-site and B-site will be occupied by large and small ions, respectively, and both the A and B sites with different partitioning for each ion will be occupied by intermediate ions. However, using tolerance factors to assess the ions in different sites is simply a qualitative measure.41

Table 2. Tolerance Factor (t), Bulk Density (ρb), X-ray Density (ρx), and Porosity (P) of BYT.

sample Ba1–xYxTiO3 tolerance factor (t) bulk density, ρb (g cm–3) X-ray density, ρx (g cm–3) porosity, P (%)
x = 0.00 1.07 2.490 6.033 58.72
x = 0.05 1.068 2.398 6.175 54.52
x = 0.125 1.061 1.229 5.879 40.15
x = 0.15 1.056 2.783 5.778 40.08
x = 0.2 1.055 1.691 5.745 39.25
x = 0.3 1.051 1.613 5.695 35.9
Open in a new tab

The X-ray density of the synthesized samples have determined by the equation

3.1. 6

where Z is the number of atoms per unit cell, M is the molar mass, NA is Avogadro’s number, and a is the lattice constant of the samples, respectively. The bulk density has been calculated by the following formula.42

3.1. 7

where m is the mass, t is the thickness, and r is the radius of the prepared pallet samples, respectively. The porosity of synthesized BYT samples was estimated using the following relation.43

3.1. 8

ρx, ρb are the X-ray density and bulk density of the prepared samples, and porosity is measured using eqs 6–8, respectively. The thickness of the BYT pellets was ∼0.50 cm for all studied samples. The calculated values of X-ray density, bulk density, and porosity of the BYT samples are summarized in Table 2. With an increase in doping concentration, the X-ray density, porosity, and bulk density decrease.

3.2. FTIR Spectroscopy

FTIR spectroscopy was used to study the functional groups present in ceramic powders. The results, shown in Figure 3a, demonstrate the FTIR spectra of Y-doped BaTiO3 ceramic materials. The bands at 870 and 1428 cm–1 are attributed to the O–H stretching vibration and deformation vibration, respectively, caused by the hygroscopic nature of the KBr used in the analysis. Two bands at 449 and 479 cm–1 are present in all samples, the band at 438 cm–1 is associated with the Ti–O bending vibration along the polar axis, and the band at 479 cm–1 is assigned to the Ti–O stretching vibration.44 These bands indicate that all of the synthesized samples have a pure tetragonal phase. From Figure 3b, it is clear that the wavenumber position of the Ti–O bond stretching and bending vibrations changes smoothly as the amount of yttrium increases. This is due to the distortion of the unit cell when yttrium atoms are introduced into the BaTiO3 lattice structure. However, the wavenumber position remains constant for the bending vibration as the Y content in the BaTiO3 matrix changes.

Figure 3.

Figure 3

Open in a new tab

(a) FTIR spectra of Y-doped BaTiO3 ceramic powders and (b) absorption frequency of the Ti–O bond as a function of the Y content.

3.3. Surface Structure Measurement Using FESEM

Figure 4a–c shows FESEM micrographs of the BT, BY20%, and BY30%T pellets. The FESEM micrographs of the BT sample reveal an assortment of non-uniform grains with some coalescence. The interiors of the fleshy grains are clearly visible in the BT sample. Noticeable changes in the texture of the grains are observed with yttrium doping. It can be observed that each composition exhibits a dense microstructure, which can provide favorable electrical properties and improve the electrical stability of ceramics.45 Furthermore, the grain size decreases with an increase in yttrium content, accompanied by a transition from surface grains with a porous structure to a nanoporous structure. A closer examination of Figure 4b,c shows that the surface layers of the pellets are covered with a large number of smaller grains as well as larger grains of various shapes. Interestingly, sharp-edged hexagonal-shaped grains are embedded within the matrix of smaller grains in the A-site Y-doped samples. This structure is less pronounced in the simultaneously and B-site doped materials, where sedimentary growth patterns are observed. The irregular surface morphology in Y-doped samples may be attributed to the interaction between granular surfaces facilitated by the dopant cation.

Figure 4.

Figure 4

Open in a new tab

FESEM micrographs of Ba1–xYxTiO3 (where a, b, and c are x = 0.00, 0.2, and 0.3, respectively).

An energy-dispersive X-ray spectrometer EDAX Octane Elect-Plus was used to check the distribution of individual elements within the grains. The EDS investigations show that the obtained ceramics contain only the elements introduced as substrates, with no other impurities detected in the spectrum. The content of barium and titanium elements slightly differs from the theoretical stoichiometry, whereas the content of yttrium is encumbered by a small uncertainty, which is related to their small participation in the whole mass of the sample, smaller than the threshold of device detection (Table 3).

Table 3. Theoretical and Experimental Contents of Elements for BT, BY20%T, and BY30%T Ceramics.

element content of element from EDS (wt%) (measurement) theoretical content (wt%) accuracy (wt%)
BT Ceramics
BaL 50.36 50.21 0.298
TiK 31.26 31.76 1.57
O K 18.38 18.03 1.94
BY20%T Ceramics
BaL 41.63 41.27 0.874
TiK 22.96 23.1 0.6
O K 15.47 15.63 0.88
Y L 19.95 20 0.25
BY30%T Ceramics
BaL 28.71 29.57 2.9
TiK 24.20 23.8 1.67
O K 17.06 16.63 2.58
Y L 30.03 30 0.1
Open in a new tab

The surfaces of the samples were checked in terms of element distribution homogeneity (Figure 5a–c). The presence of each element is shown on the mapping in the form of points, where density informs about its concentration. The obtained results indicate that the element distribution is homogeneous in all samples, with some places characterized by lower concentrations due to the microstructural features of the material.

Figure 5.

Figure 5

Open in a new tab

Mapping images for (a) BT, (b)BY20%T, and (c) BY30%T.

3.4. Optical Properties

The relationship between the crystalline structure and physical properties in perovskite materials is delicate, meaning that small changes in the structure can lead to significant variations in their physical and optical properties. To analyze the optical behavior of the materials, UV–visible absorption spectroscopy was used. The results, shown in Figure 6, display the diffused reflectance UV–vis spectra of pure and Y-doped BT ceramics in the range of 350–800 nm. The doped samples exhibit an interesting behavior by absorbing visible photons in the region above 400 nm, with a maximum absorption of 45% for highly doped BT. This absorption causes a drop in the UV spectra of yttrium-doped samples. Regardless of the Y site occupancy, all doped samples show three distinct peaks in the visible region of the spectra. The preference of Y in the BT lattice has a slight effect on the absorption of photons.

Figure 6.

Figure 6

Open in a new tab

Diffused reflectance spectra of BYxT (x = 0–30%) samples.

The optical band gap energy (Eg) of Ba1–xYxTiO3 (x = 0–0.3) samples was calculated using the Kubelka–Munk (K–M) method. This method was chosen because it allows for accurate extraction of Eg values as well as the stimulation of the measured diffuse reflectance.46 The Kubelka–Munk equation at any given wavelength is represented by the equation

3.4. 9

where K, S, and R parameters represent the absorption coefficient, scattering coefficient, and diffuse reflectance, respectively. The F(R) function, which is proportional to the absorbance coefficient, is proposed by P. Kubelka and F. Munk.46 This function was used to analyze the type of inter-band transitions by applying the McLean analysis.46 The Tauc plot relation was then used to calculate the optical band gap (Eg) as shown in Figure 7

3.4. 10

where F(R) = α(λ) = k/S is the absorption coefficient, and C1 is a constant dependent on the transmittance, called the band tailing parameter. The coefficient ν = c/λ is the light frequency, and h is Plank’s constant h = 6.626 × 10–34 J s. The possible values for the index n are equal to 1/2, 2, 3/2, or 3 and each describes direct allowed, indirect allowed, direct forbidden, and indirect forbidden transition types, respectively. From eq 10, the extrapolation of the tangential line from high photon energy gives the optical band gap value. So, in order to get the optical band gap value, the Tauc functions were used for BYT with the assumption that n = 2. As shown in Figure 7 and listed in Table 4, the for example values of BYxT (x = 0, 5, 12.5, 15, 20, and 30%) obtained by extrapolating the linear part to the horizontal axis are in the range of 3.10–2.21 eV, which are considerably lower than that of the pure BT (3.10 eV). The band gap reduction of BY30%T (Figure 7f) is the most evident, and it is even more significant than those of other photovoltaic perovskite ceramics.47,48 The optical behavior of the materials can be explained by the electronic states of the highest energy band that is occupied by electrons valence band maximum (VBM), and the next highest energy band above the valence band that is unoccupied conduction band minimum (CBM) generated by Y3+ cation doping. In BT, the VBM is around the O 2p orbital, which has a slight interaction with the Ti 3d and Ba 6p orbitals, whereas the CBM is around the Ti 3d orbital.49 The position of the conduction band is affected by the electronegativity of the doping ions; the more electronegative the ions, the lower the conduction band position.50 When a doping element is introduced, the VBM is localized around the Y 3d orbital. As the Y cations are more electronegative than the Ti, the energy of the Y 3d orbital is lower than that of the Ti 3d orbital. This results in a downward shift of the conduction band edge into the band gap, leading to a reduction in the Eg. Moreover, according to a report by Choi and Lee,51 the optical band gap may also be related to the lattice distortion caused by the ion substitution. The lattice distortion increases as the radius of the doping ions decreases, resulting in a rearrangement of the molecular orbitals and a decrease in the band gap. Yttrium is the preferred element to reduce the band gap of BT material, according to the experimental data analysis. These results indicate that the band gap of the BT ceramic can be effectively reduced by Y doping to improve its properties for visible and ultraviolet absorption. Optimizing the doping concentration can further modify the band gap of BT ceramic material. All these results suggest that the optical properties of BYxT (x = 0–30%) ceramics can be regulated, and the synthesized ceramics are good candidates for high-performance MLCCs.

Figure 7.

Figure 7

Open in a new tab

Bandgap energy from Tauc plot of (a) BT, (b) BY5%T, (c) BY12.5%T, (d) BY15%T, (e) BY20%T, and (f) BY30%T.

Table 4. Band Gap Value of Ba1–xYxTiO3 (x = 0–0.3).

sample band gap value (eV) this work band gap value (eV) literature
Ba1–xYxTiO3, x = 0.00 3.10 3.26,52 3.253
Ba1–xYxTiO3, x = 0.05 2.93 3.1154
Ba1–xYxTiO3, x = 0.125 2.85 2.9153
Ba1–xYxTiO3, x = 0.15 2.72  
Ba1–xYxTiO3, x = 0.20 2.31 3.1454
Ba1–xYxTiO3, x = 0.30 2.21  
Open in a new tab

As previously discussed, the band gap estimated from the reflectance results is influenced by both the structure parameters and the composition. The new optical band gap obtained for the compositions is a result of the displacement of the valence and conduction band edges. To visualize this shift, the CBM and the VBM were calculated using the following equation

3.4. 11
3.4. 12

The equation used to calculate the CBM and VBM is where ECB and EVB are the conduction band and the valence band potentials, respectively. Eg is the band gap estimated from the UV–vis results. Ee is equal to 4.5 and represents the energy of the free electrons versus hydrogen. χ is the electronegativity of the semiconductor and can be calculated as follows

3.4. 13

The parameters a, b, c, d, and e are the number of atoms in each composition, and χ(y) is the electronegativity of each element of the compound. The new optical band gap obtained for the compositions is a result of the displacement of the valence and conduction band edges. To visualize this displacement, the CBM and the VBM were calculated using an equation that takes into account the conduction band and valence band potentials, the band gap estimated from the UV–vis results, the energy of free electrons, and the electronegativity of the semiconductor. The equation also includes parameters such as the number of atoms in each composition and the electronegativity of each element of the compound. Figure 8 illustrates the shift of the CBM and VBM which is in line with the shrink of the band gap. Both bands are affected as the amount of substitution increases; a downward shift is observed for the CBM while the VBM shifts upward.

Figure 8.

Figure 8

Open in a new tab

Schematic representations of the calculated CBM and the VBM for the perovskite series Ba1–xYxTiO3 (0 ≤ x ≤ 0.3).

3.5. Thermal and Electrical Properties

The thermal and electrical conductivities of Ba1–xYxTiO3 ceramic samples (BYxT) were examined as a function of yttrium content at room temperature and 180 °C, as illustrated in Figure 9. BaTiO3 has lower thermal and electrical conductivity compared to Y, thus the addition of Y in BaTiO3 system will lead to percolation behavior. As the concentration of Y increases, the thermal and electrical conductivities follow a power law pattern, as demonstrated in eqs 14 and 15.55

3.5. 14
3.5. 15

Figure 9.

Figure 9

Open in a new tab

Thermal conductivity and electrical conductivity of BYT as a function of Y content at (a) room temperature and (b) 180 °C.

The thermal and electrical conductivities of Ba1–xYxTiO3 ceramic samples (BYxT) were studied as a function of yttrium content. Equations 14 and 15 were used to estimate the thermal and electrical conductivities as a function of Y content, and the percolation thresholds (VT and VE) were calculated. When the Y content is low, the heat conduction is mainly dependent on the vibration of phonons, and the electrons play a minor role. The phonon scattering effect makes it difficult to improve thermal conductivity significantly. As the Y content increases, the Y phase becomes interconnected, allowing electrons to move freely and carry heat, resulting in a percolation behavior. The thermal percolation threshold VT is 12.5%, and the electrical conductivity of the compounds increases sharply when Y content increases from 12.5 to 30%. The electrical percolation threshold VE is calculated to be 12.5%. Although VT is very close to VE, BYxT samples with 12.5% of Y content show a high thermal conductivity but a relatively low electrical conductivity. The electrical conductivity of all the samples increases with measurement temperature, which is typical of semiconducting behavior as shown in Figure 9b. The sample 30%Y BT has a notably higher electrical conductivity when compared to other samples. This suggests that the carrier concentration and mobility in this sample are in an ideal doping range. It was also observed that there is a significant improvement in the electrical conductivity of BaTiO3 samples when Y is added in greater than 20%. However, adding more than 30% Y to BaTiO3 may decrease the conductivity because BaTiO3 is a Mott insulator, and in alloy form it reduces the conductivity. The electrical conductivity is directly proportional to carrier concentration and mobility. Although it would be beneficial to use Hall effect measurements to measure carrier concentration and mobility separately, it is not possible for these samples due to their low conductivity. The sample BY5%T has a lower conductivity in comparison to BY30%T, which has the same Y doping. This difference in conductivity is likely due to the presence of nanostructured pores which impede carrier mobility.56 Our research aimed to investigate the impact of yttrium doping on the electrical properties of BaTiO3 for use in MLCCs. Since BaTiO3 is naturally insulating, adding Y in atomic percentage improves the electrical conductivity and converts it into an n-type semiconducting material through electron doping. Other dopants have also been shown to improve the electrical conductivity of BaTiO3 in previous studies.57,58

The thermal conductivity of all the samples increases with temperature, as shown in Figure 9a,b. The sample BY30%T BT has the highest thermal conductivity, which is likely due to the charge compensation of defects in the crystal structure near the Y atoms, which improves the electronic conductivity. Notably, the thermal conductivity of the sample with nanostructured pores (BT sample) is significantly lower compared to the sample BY30%T, which has less nanoporosity. This is likely caused by the phonon boundary scattering by the nanostructured pores of the sample in addition to the phonon defect scattering by the Y atoms.59,60 Multiple theoretical studies have indicated that structures containing pores within the range of a few nanometers to a few tens of nanometers can effectively scatter phonons of various wavelengths.61 The thermal conductivity for the porous sample is less than 2.24 W/K m at room temperature and around 2.02 W/K m at 180 °C. Thermal conductivity can be broken down into two parts: κel, which is the thermal conductivity caused by the movement of electrons or holes, and κph, which is the thermal conduction by lattice vibration, also known as phonon thermal conductivity. The κph can be expressed as κph = 1/3 × CV × V, where the heat capacity (Cv) at constant volume and the phonon velocity (V) are constant, and thus the κph primarily depends on the phonon mean free path (MFP) (l). The MFP of phonons in BaTiO3 is on the order of 10–8 m, which is close to the nanometer scale; thus, it is possible to scatter the phonons with nanoscale pores.62 The MFP of the phonons is increased due to the nanostructured pores in the sample BY30%T, resulting in a low phonon thermal conductivity. To isolate the role of phonon thermal conductivity, the electronic contribution must first be subtracted. According to the Wiedemann–Franz law, κel is directly proportional to the electrical conductivity and temperature, T. κel = LTσ, where L is the proportional constant known as the Lorenz number, which is an experimental value, and σ is the electrical conductivity. Normally, L is treated as a universal factor with the value of 2.44 × 10–8 W Ω K–2 for a degenerate semiconductor. In the samples of Y-doped BaTiO3, the presented data show that the contribution of κel to the total thermal conductivity is insignificant. Furthermore, the increase in thermal conductivity with increasing yttrium content is likely because yttrium is a good heat conductor. Yttrium has a relatively high melting point and a relatively low atomic mass, which can contribute to its ability to conduct heat. Additionally, yttrium has a relatively low lattice thermal conductivity, meaning it does not transfer heat efficiently through the vibrations of the atomic lattice. It is also possible that the increase in thermal conductivity with increasing yttrium content is due to the formation of a solid solution between the yttrium and BaTiO3. When yttrium is added to BaTiO3, it may form a solid solution in which the yttrium atoms are distributed randomly throughout the BaTiO3 lattice. This can lead to an increase in the number of conduction electrons in the material, which can in turn increase its thermal conductivity.

To investigate the electrical behavior of Ba1–xYxTiO3 (x = 0.05–0.3) ceramic samples, an impedance analysis of the prepared sample was conducted at 180 °C. The V–I polarization plots, shown in Figure 10, consisting of three distinct regions: the activation loss (MN), ohmic loss (NP), and concentration loss regions (PQ). The loss that occurs near low values of current is known as the activation loss and is likely caused by the electrostatic potential that overcomes the energy barrier.63,64 The activation energy is the minimum energy required to cross the energy barrier at the interface to initiate a reaction (electrochemical) at electrodes. The region NP indicated in the entire graphs of Figure 10a–e is the ohmic loss, when the energy barrier is crossed, ion transport occurs through the nanopores, which generates appreciable resistance, this is because of the resistance generation while the transport of the ions through the nanopores of the prepared materials towards the electrodes. The Ohmic loss region is a linear region, which is also evident from Figure 10a–e. It is noted that pure BT ceramics have a nearly linear curve, while Y-doped BT ceramics exhibit curves with nonlinear regions. This reveals that Y-doped BT samples have varistor-like nonlinear current–voltage properties. The insufficient ions available for the electrodes in the highly reactive state may be responsible for the concentration loss, as indicated by the PQ region of Figure 10a–d. In the case of BYT, the presence of nanopores can affect the I–V characteristics in several ways. For example, the presence of nanopores may increase the surface area of the material, which can increase the number of charge carriers available to contribute to the current. This leads to an increase in the conductivity of the material (Figure 9a,b) and a corresponding decrease in the resistance. This can be seen as a decrease in the flattening of the I–V curve. The FESEM analysis (Figure 4a–c) of the prepared samples reveals that the pure BT sample has many nanopores, whereas the samples BY20%T and BY30%T have reduced porosity. The samples BY20%T and BY30%T do have some porosity, but less than the BT sample. On average, the porosity of the prepared BT has been reduced with the increase in Y3+ content. The XRD analysis also confirms the reduced porosity of doped samples. The above optical analysis confirms the reduced band gap energy and defect states of the higher doped samples BYxT (x = 5–30 wt %), which indicate the generation of oxygen vacancies and unsaturated surface cations.65 Additionally, the decrease in porosity results in a weak electrostatic potential, which dissociates physisorbed atom bonds to a lesser extent, thereby reducing the offload current and output power. A systematic decrease in offload current and output power has been observed with the increase in Y3+ content. Thus, the present study shows that structural, optical, and voltage–current properties can be tuned using yttrium metal.

Figure 10.

Figure 10

Open in a new tab

V–I characteristics measured at 180 °C of (a) BY5%T, (b) BY12.5%T, (c) BY15%T, (d) BY20%T, and (e) BY30%T.

4. Conclusions

The solid series of perovskite B1–xYxTiO3 (0 ≤ x ≤ 0.3) ceramics have been successfully prepared by sol–gel method. Analysis of XRD data confirms the pure perovskite tetragonal structure of the ceramic samples. However, tetragonality decreases with an increase in yttrium content. The FESEM micrographs reveal a decrease in grain size as the transition occurs from surface grains with a porous structure to nanoporous structures with an increase in Y3+ content. The doping of Y3+ ions led to a decrease of the direct band gap energy and a shift of the band gap edges, namely the CBM and VBM. The optical band gap energy was found in the semiconducting range of 3.1–2.21 eV. The thermal and electrical conductivity of BaTiO3 has been improved by optimizing the doping of yttrium in weight percentages and causing the samples to become semiconductor materials. The electrical conduction mechanism in doped ceramics could be attributed to the passage of free carrier chargers through a material. The work in this paper is fundamental to the understanding of the defects associated with the crystal structure and thermoelectric behavior of Y-doped BaTiO3 ceramics and can provide a reference for their application in the MLCC industry.

Acknowledgments

This research was supported by the Hungarian State in the framework of the RF-2.3.1-21-2022-00014 National Multidisciplinary Laboratory for Climate Change project. This research work was also supported by the Estonian Research Council under the personal research grants PUT1063 (I. Hussainova) and DoRa + program.

The authors declare no competing financial interest.

References

  1. Islam S.; Satter S. A.; Khatun N.; Hossain M. S.; Farhad S. F. U.; Bala P.; Tabassum S.; Siddika A. Investigation of Structural, Dielectric and Electrical Properties of Barium Titanate Ceramics Co-Doped with Bismuth and Yttrium. J. Mol. Eng. Mater. 2019, 07, 1950006. 10.1142/S2251237319500060. [DOI] [Google Scholar]
  2. Slimani Y.; Selmi A.; Hannachi E.; Almessiere M. A.; AlFalah G.; AlOusi L. F.; Yasin G.; Iqbal M. Study on the Addition of SiO2 Nanowires to BaTiO3: Structure, Morphology, Electrical and Dielectric Properties. J. Phys. Chem. Solids 2021, 156, 110183. 10.1016/J.JPCS.2021.110183. [DOI] [Google Scholar]
  3. Zhao C.; Wu H.; Li F.; Cai Y.; Zhang Y.; Song D.; Wu J.; Lyu X.; Yin J.; Xiao D.; Zhu J.; Pennycook S. J. Practical High Piezoelectricity in Barium Titanate Ceramics Utilizing Multiphase Convergence with Broad Structural Flexibility. J. Am. Chem. Soc. 2018, 140, 15252–15260. 10.1021/JACS.8B07844. [DOI] [PubMed] [Google Scholar]
  4. Rathod V. T. A Review of Acoustic Impedance Matching Techniques for Piezoelectric Sensors and Transducers. Sensors 2020, 20, 4051. 10.3390/S20144051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Tihtih M.; Ibrahim J.; Basyooni F. M.; Belaid M. A.; Gömze W.; Kocserha L. A.; Kocserha I. Structural, Optical, and Electronic Properties of Barium Titanate: Experiment Characterisation and First-Principles Study. Mater. Technol. 2022, 37, 2995–3005. 10.1080/10667857.2022.2107473. [DOI] [Google Scholar]
  6. Liu J.; Jin G.; Chen Y.; Xue W. Properties of Yttrium-Doped Barium Titanate Ceramics with Positive Temperature Coefficient of Resistivity and a Novel Method to Evaluate the Depletion Layer Width. Ceram. Int. 2019, 45, 6119–6124. 10.1016/J.CERAMINT.2018.12.086. [DOI] [Google Scholar]
  7. Wang M. J.; Yang H.; Zhang Q. L.; Hu L.; Yu D.; Lin Z. S.; Zhang Z. S. Doping Behaviors of Yttrium, Zinc and Gallium in BaTiO3 Ceramics for AC Capacitor Application. J. Mater. Sci.: Mater. Electron. 2014, 25, 2905–2912. 10.1007/S10854-014-1958-3. [DOI] [Google Scholar]
  8. Makovec D.; Samardžija Z.; Drofenik M. Solid Solubility of Holmium, Yttrium, and Dysprosium in BaTiO3. J. Am. Ceram. Soc. 2004, 87, 1324–1329. 10.1111/J.1151-2916.2004.TB07729.X. [DOI] [Google Scholar]
  9. Tihtih M.; Ibrahim J. E. F. M.; Kurovics E.; Gömze L. A. Study of the Structure, Microstructure and Temperature Dependent Thermal Conductivity Properties of SrTiO3: Via Y3+ Substitution. J. Nano Res. 2021, 69, 33–42. 10.4028/WWW.SCIENTIFIC.NET/JNANOR.69.33. [DOI] [Google Scholar]
  10. Belous A.; V’yunov O.; Kovalenko L.; Makovec D. Redox Processes in Highly Yttrium-Doped Barium Titanate. J. Solid State Chem. 2005, 178, 1367–1375. 10.1016/J.JSSC.2005.01.014. [DOI] [Google Scholar]
  11. Paredes-Olguín M.; Lira-Hernández I. A.; Gómez-Yáñez C.; Espino-Cortés F. P. Compensation Mechanisms at High Temperature in Y-Doped BaTiO3. Phys. B 2013, 410, 157–161. 10.1016/J.PHYSB.2012.11.001. [DOI] [Google Scholar]
  12. Wang X.; Fan Y.; Luo G.; Tu R.; Shen Q.; Zhang L. Effect of Yttrium (Y) Substitution on the Structure and Dielectric Properties of BaTiO3. Ceram. Int. 2023, 49, 9042–9051. 10.1016/j.ceramint.2022.11.060. [DOI] [Google Scholar]
  13. Belous A.; V’yunov O.; Glinchuk M.; Laguta V.; Makovez D. Redox Processes at Grain Boundaries in Barium Titanate-Based Polycrystalline Ferroelectrics Semiconductors. J. Mater. Sci. 2008, 43, 3320–3326. 10.1007/S10853-008-2503-7. [DOI] [Google Scholar]
  14. Tihtih M.; Ibrahim J. E. F. M.; Basyooni M. A.; Kurovics E.; Belaid W.; Hussainova I.; Kocserha I. Role of A-Site (Sr), B-Site (Y), and A, B Sites (Sr, Y) Substitution in Lead-Free BaTiO3 Ceramic Compounds: Structural, Optical, Microstructure, Mechanical, and Thermal Conductivity Properties. Ceram. Int. 2023, 49, 1947–1959. 10.1016/J.CERAMINT.2022.09.160. [DOI] [Google Scholar]
  15. Tihtih M.; Ibrahim J. E. F. M.; Kurovics E.; Gömze L. A. Synthesis of Ba1–xSrxTiO3 (x = 0–0.3) Ceramic Powders via Sol-Gel Method: Structural, Microstructure, Thermal Conductivity, and Compressive Strength Properties. Cryst. Res. Technol. 2022, 57, 2100106. 10.1002/CRAT.202100106. [DOI] [Google Scholar]
  16. Drdlik D.; Marak V.; Maca K.; Drdlikova K. Modification of Barium Titanate Sintering via Rare Earth Oxides Addition: Dilatometric and Microstructural Study. Ceram. Int. 2022, 48, 24599–24608. 10.1016/J.CERAMINT.2022.05.105. [DOI] [Google Scholar]
  17. Zhang K.; Li L.; Wang M.; Luo W. Charge Compensation in Rare Earth Doped BaTiO3-Based Ceramics Sintered in Reducing Atmosphere. Ceram. Int. 2020, 46, 25881–25887. 10.1016/J.CERAMINT.2020.07.072. [DOI] [Google Scholar]
  18. Aslla-Quispe A. P.; Miwa R. H.; Guerra J. D. S. Role of the Rare-Earth Doping on the Multiferroic Properties of BaTiO3: First-Principles Calculation. Phys. B 2021, 615, 413107. 10.1016/J.PHYSB.2021.413107. [DOI] [Google Scholar]
  19. Alkathy M. S.; Hezam A.; Manoja K. S. D.; Wang J.; Cheng C.; Byrappa K.; Raju K. C. J. Effect of Sintering Temperature on Structural, Electrical, and Ferroelectric Properties of Lanthanum and Sodium Co-Substituted Barium Titanate Ceramics. J. Alloys Compd. 2018, 762, 49–61. 10.1016/J.JALLCOM.2018.05.138. [DOI] [Google Scholar]
  20. Luo Y.; Pu Y.; Zhang P.; Zhao J.; Wu Y.; Liu Y. Study on Dielectric Properties of SiO2-Doped BaTiO3 Ceramics. Ferroelectrics 2016, 492, 10–16. 10.1080/00150193.2015.1071594. [DOI] [Google Scholar]
  21. Yoon S. H.; Park Y. S.; Hong J. O.; Sinn D. S. Effect of the Pyrochlore (Y2Ti2O7) Phase on the Resistance Degradation in Yttrium-Doped BaTiO3 Ceramic Capacitors. J. Mater. Res. 2007, 22, 2539–2543. 10.1557/JMR.2007.0326. [DOI] [Google Scholar]
  22. Zhang J.; Hou Y.; Zheng M.; Jia W.; Zhu M.; Yan H. The Occupation Behavior of Y2O3 and Its Effect on the Microstructure and Electric Properties in X7R Dielectrics. J. Am. Ceram. Soc. 2016, 99, 1375–1382. 10.1111/JACE.14100. [DOI] [Google Scholar]
  23. Alkhammash H. I.; Ibrahim A. M.; Fouad S. Enhancement of Dielectric Properties of Borate Glasses Doped BaTiO3 for Energy Storage Devices: Characterization of Optical, Thermal and Electrical Properties. J. Mater. Sci.: Mater. Electron. 2022, 33, 17048–17063. 10.1007/S10854-022-08582-2. [DOI] [Google Scholar]
  24. Xing J.; Radovic M.; Muliana A. Thermal Properties of BaTiO3/Ag Composites at Different Temperatures. Composites, Part B 2016, 90, 287–301. 10.1016/J.COMPOSITESB.2015.12.014. [DOI] [Google Scholar]
  25. Lin Y.; Jia Y.; Alva G.; Fang G. Review on Thermal Conductivity Enhancement, Thermal Properties and Applications of Phase Change Materials in Thermal Energy Storage. Renewable Sustainable Energy Rev. 2018, 82, 2730–2742. 10.1016/J.RSER.2017.10.002. [DOI] [Google Scholar]
  26. Ryu S.-S.; Kim H.-T.; Kim H. J.; Kim S. Characterization of Mechanical Properties of BaTiO3 Ceramic with Different Types of Sintering Aid by Nanoindentation. J. Ceram. Soc. Jpn. 2009, 117, 811–814. 10.2109/JCERSJ2.117.811. [DOI] [Google Scholar]
  27. Chen L.; Wang H.; Zhao P.; Shen Z.; Zhu C.; Cen Z.; Li L.; Wang X. Effect of MnO2 on the Dielectric Properties of Nb-Doped BaTiO3-(Bi0.5Na0.5)TiO3 Ceramics for X9R MLCC Applications. J. Am. Ceram. Soc. 2019, 102, 2781–2790. 10.1111/JACE.16157. [DOI] [Google Scholar]
  28. Tihtih M.; Ibrahim J.; Basyooni F. M.; En-nadir M. A.; Hussainova R.; Kocserha I.; Kocserha I. Functionality and Activity of Sol–Gel-Prepared Co and Fe Co-Doped Lead-Free BTO for Thermo-Optical Applications. ACS Omega 2023, 8, 5003. 10.1021/ACSOMEGA.2C07660. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Goel S.; Tyagi A.; Garg A.; Kumar S.; Baskey H. B.; Gupta R. K.; Tyagi S. Microwave Absorption Study of Composites Based on CQD@BaTiO3 Core Shell and BaFe12O19 Nanoparticles. J. Alloys Compd. 2021, 855, 157411. 10.1016/J.JALLCOM.2020.157411. [DOI] [Google Scholar]
  30. Song E.; Kim D. H.; Jeong E. J.; Choi M.; Kim Y.; Jung H. J.; Choi M. Y. Effects of Particle Size and Polymorph Type of TiO2 on the Properties of BaTiO3 Nanopowder Prepared by Solid-State Reaction. Environ. Res. 2021, 202, 111668. 10.1016/J.ENVRES.2021.111668. [DOI] [PubMed] [Google Scholar]
  31. Habib M.; Munir M.; Akram F.; Lee S.; Song T. K.; Turak A.; Kim M. H.; Hussain A. Structural Evolution and Electromechanical Properties of SrTiO3-Modified Bi0.5Na0.5TiO3–BaTiO3 Ceramics Prepared by Sol-Gel and Hydrothermal Methods. Mater. Chem. Phys. 2021, 266, 124529. 10.1016/J.MATCHEMPHYS.2021.124529. [DOI] [Google Scholar]
  32. Slimani Y.; Selmi A.; Hannachi E.; Almessiere M. A.; Baykal A.; Ercan I. Impact of ZnO Addition on Structural, Morphological, Optical, Dielectric and Electrical Performances of BaTiO3 Ceramics. J. Mater. Sci.: Mater. Electron. 2019, 30, 9520–9530. 10.1007/S10854-019-01284-2. [DOI] [Google Scholar]
  33. Kim C. H.; Park K. J.; Yoon Y. J.; Hong M. H.; Hong J. O.; Hur K. H. Role of Yttrium and Magnesium in the Formation of Core-Shell Structure of BaTiO3 Grains in MLCC. J. Eur. Ceram. Soc. 2008, 28, 1213–1219. 10.1016/J.JEURCERAMSOC.2007.09.042. [DOI] [Google Scholar]
  34. Tihtih M.; Ibrahim J. F. M.; Kurovics E.; Abdelfattah M. Study on the Effect of Bi Dopant on the Structural and Optical Properties of BaTiO3 Nanoceramics Synthesized via Sol-Gel Method. J. Phys.: Conf. Ser. 2020, 1527, 012043. 10.1088/1742-6596/1527/1/012043. [DOI] [Google Scholar]
  35. Tihtih M.; Ibrahim J. E. F. M.; Basyooni M. A.; En-nadir R.; Belaid W.; Abdelfattah M. M.; Hussainova I.; Pszota G.; Kocserha I. Enhanced Optical and Thermal Conductivity Properties of Barium Titanate Ceramic via Strontium Doping for Thermo-Optical Applications. Opt. Quantum Electron. 2023, 55, 226. 10.1007/S11082-022-04516-8. [DOI] [Google Scholar]
  36. Williamson G. K.; Hall W. H. X-Ray Broadening from Filed Aluminium and Tungsten. Acta Metall. 1953, 1, 22–31. 10.1016/0001-6160(53)90006-6. [DOI] [Google Scholar]
  37. Qi J.; Li L.; Wang Y.; Fan Y.; Gui Z. Yttrium Doping Behavior in BaTiO3 Ceramics at Different Sintered Temperature. Mater. Chem. Phys. 2003, 82, 423–427. 10.1016/S0254-0584(03)00264-5. [DOI] [Google Scholar]
  38. Reda M.; El-Dek S. I.; Arman M. M. Improvement of Ferroelectric Properties via Zr Doping in Barium Titanate Nanoparticles. J. Mater. Sci.: Mater. Electron. 2022, 33, 16753–16776. 10.1007/S10854-022-08541-X. [DOI] [Google Scholar]
  39. Hannachi E.; Almessiere M. A.; Slimani Y.; Alshamrani R. B.; Yasin G.; Ben Azzouz F. Preparation and Characterization of High-Tc (YBa2Cu3O7-δ)1-x/(CNTs)x Superconductors with Highly Boosted Superconducting Performances. Ceram. Int. 2021, 47, 23539–23548. 10.1016/J.CERAMINT.2021.05.071. [DOI] [Google Scholar]
  40. Choi W. J.; Yang D.; Jeon S. C.; Moon K. S. Effect of Charge Compensation Change on the Crystal Structure, Grain Growth Behavior, and Dielectric Properties in the La2O3-Doped BaTiO3 System with MnCO3 Addition. J. Alloys Compd. 2022, 916, 165388. 10.1016/J.JALLCOM.2022.165388. [DOI] [Google Scholar]
  41. Hannachi E.; Sayyed M. I.; Mahmoud K. A.; Slimani Y.; Akhtar S.; Albarzan B.; Almuqrin A. H. Impact of Tin Oxide on the Structural Features and Radiation Shielding Response of Some ABO3 Perovskites Ceramics (A = Ca, Sr, Ba; B = Ti). Appl. Phys. A: Mater. Sci. Process. 2021, 127, 970. 10.1007/S00339-021-05092-6. [DOI] [Google Scholar]
  42. Kacem H.; Sassi Z.; Gdaiem M. A.; Dhahri A.; Seveyrat L.; Lebrun L.; Dhahri J. Deep Understanding of Structural and Physical Properties of BaTiO3 over a Broad Temperature Range. Inorg. Chem. Commun. 2022, 144, 109771. 10.1016/J.INOCHE.2022.109771. [DOI] [Google Scholar]
  43. Ruzimuradov O.; Hasegawa G.; Kanamori K.; Nakanishi K. Preparation of Hierarchically Porous Nanocrystalline CaTiO3, SrTiO3 and BaTiO3 Perovskite Monoliths. J. Am. Ceram. Soc. 2011, 94, 3335–3339. 10.1111/J.1551-2916.2011.04613.X. [DOI] [Google Scholar]
  44. Garrido-Hernández A.; García-Murillo A.; de J Carrillo-Romo F.; Cruz-Santiago L. A.; Chadeyron G.; de J Morales-Ramírez A.; Velumani S. Structural Studies of BaTiO3:Er3+ and BaTiO3:Yb3+ Powders Synthesized by Hydrothermal Method. J. Rare Earths 2014, 32, 1016–1021. 10.1016/S1002-0721(14)60176-9. [DOI] [Google Scholar]
  45. Park K. S. Structural and Electrical Properties of FeMg0.7Cr0.6Co0.7–xAlxO4 (0 ≤ x ≤ 0.3) Thick Film NTC Thermistors. J. Eur. Ceram. Soc. 2006, 26, 909–914. 10.1016/J.JEURCERAMSOC.2004.12.021. [DOI] [Google Scholar]
  46. Badapanda T.; Sarangi S.; Behera B.; Parida S.; Saha S.; Sinha T. P.; Ranjan R.; Sahoo P. K. Optical and Dielectric Study of Strontium Modified Barium Zirconium Titanate Ceramic Prepared by High Energy Ball Milling. J. Alloys Compd. 2015, 645, 586–596. 10.1016/J.JALLCOM.2015.05.005. [DOI] [Google Scholar]
  47. Pascual-Gonzalez C.; Schileo G.; Murakami S.; Khesro A.; Wang D.; Reaney I. M.; Feteira A. Continuously Controllable Optical Band Gap in Orthorhombic Ferroelectric KNbO3-BiFeO3 Ceramics. Appl. Phys. Lett. 2017, 110, 172902. 10.1063/1.4982600. [DOI] [Google Scholar]
  48. Pascual-Gonzalez C.; Schileo G.; Khesro A.; Sterianou I.; Wang D.; Reaney I. M.; Feteira A. Band Gap Evolution and a Piezoelectric-to-Electrostrictive Crossover in (1 −x )KNbO 3–x (Ba 0.5 Bi 0.5)(Nb 0.5 Zn 0.5)O 3 Ceramics. J. Mater. Chem. C 2017, 5, 1990–1996. 10.1039/C6TC05515J. [DOI] [Google Scholar]
  49. Zhou W.; Deng H.; Yu L.; Yang P.; Chu J. Magnetism Switching and Band-Gap Narrowing in Ni-Doped PbTiO3 Thin Films. J. Appl. Phys. 2015, 117, 194102. 10.1063/1.4921459. [DOI] [Google Scholar]
  50. Chen X.; Huang F.; Lu Z.; Xue Y.; Min J.; Li J.; Xiao J.; Yang F.; Zeng X. Influence of Transition Metal Doping (X = Mn, Fe, Co, Ni) on the Structure and Bandgap of Ferroelectric Bi3.15Nd0.85Ti2X1O12. J. Phys. D: Appl. Phys. 2017, 50, 105104. 10.1088/1361-6463/AA5624. [DOI] [Google Scholar]
  51. Choi W. S.; Lee H. N. Strain Tuning of Electronic Structure in B I4 T I3 O12-LaCo O3 Epitaxial Thin Films. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 174101. 10.1103/PHYSREVB.91.174101. [DOI] [Google Scholar]
  52. Li G.; Xie J.; Wang J.; Xia L.; Li Y.; Hu W. Nanoscale Surface Disorder for Enhanced Solar Absorption and Superior Visible-Light Photocatalytic Property in Ti-Rich BaTiO3 Nanocrystals. ACS Omega 2019, 4, 9673–9679. 10.1021/ACSOMEGA.9B00739. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Alshoaibi A.; Kanoun M. B.; Ul Haq B.; AlFaify S.; Goumri-Said S. Insights into the Impact of Yttrium Doping at the Ba and Ti Sites of BaTiO3on the Electronic Structures and Optical Properties: A First-Principles Study. ACS Omega 2020, 5, 15502–15509. 10.1021/ACSOMEGA.0C01638. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Madani A.; Alghamdi M.; Alamri B.; Althobaiti S.. Structural and Optical Properties Of Sb-Batio3 and Y- Batio3 Doped Ceramics Prepared by Solid-State Reaction. https://papers.ssrn.com/abstract=4299946 (accessed Jan 05, 2023).
  55. Yin R.; Zhang Y.; Zhao W.; Huang X.; Li X.; Qian L. Graphene Platelets/Aluminium Nitride Metacomposites with Double Percolation Property of Thermal and Electrical Conductivity. J. Eur. Ceram. Soc. 2018, 38, 4701–4706. 10.1016/J.JEURCERAMSOC.2018.06.036. [DOI] [Google Scholar]
  56. Park C.-S.; Han W.; Shim D. I.; Cho H. H.; Park H.-H. The Effect of Mesoporous Structure on the Thermoelectric Properties of Nonstoichiometric La-Doped SrTiO 3. J. Electrochem. Soc. 2016, 163, E155–E158. 10.1149/2.0441606JES. [DOI] [Google Scholar]
  57. Suchanicz J.; Czaja P.; Kluczewska K.; Czternastek H.; Sokolowski M.; Węgrzyn A. The Influence of Pb(Mg1/3Nb2/3)O3-Doping on the Thermoelectric Properties of BaTiO3 Ceramics. Phase Transitions 2018, 91, 1036–1043. 10.1080/01411594.2018.1506880. [DOI] [Google Scholar]
  58. Xiao X.; Widenmeyer M.; Xie W.; Zou T.; Yoon S.; Scavini M.; Checchia S.; Zhong Z.; Hansmann P.; Kilper S.; Kovalevsky A.; Weidenkaff A. Tailoring the Structure and Thermoelectric Properties of BaTiO3via Eu2+ Substitution. Phys. Chem. Chem. Phys. 2017, 19, 13469–13480. 10.1039/C7CP00020K. [DOI] [PubMed] [Google Scholar]
  59. Hudiono Y.; Greenstein A.; Saha-Kuete C.; Olson B.; Graham S.; Nair S. Effects of Composition and Phonon Scattering Mechanisms on Thermal Transport in MFI Zeolite Films. J. Appl. Phys. 2007, 102, 053523. 10.1063/1.2776006. [DOI] [Google Scholar]
  60. Parrish K. D.; Abel J. R.; Jain A.; Malen J. A.; McGaughey A. J. H. Phonon-Boundary Scattering in Nanoporous Silicon Films: Comparison of Monte Carlo Techniques. J. Appl. Phys. 2017, 122, 125101. 10.1063/1.4993601. [DOI] [Google Scholar]
  61. Lee H.; Vashaee D.; Wang D. Z.; Dresselhaus M. S.; Ren Z. F.; Chen G. Effects of Nanoscale Porosity on Thermoelectric Properties of SiGe. J. Appl. Phys. 2010, 107, 094308. 10.1063/1.3388076. [DOI] [Google Scholar]
  62. Obara H.; Yamamoto A.; Lee C. H.; Kobayashi K.; Matsumoto A.; Funahashi R. Thermoelectric Properties of Y-Doped Polycrystalline SrTiO3. Jpn. J. Appl. Phys., Part 2 2004, 43, L540. 10.1143/JJAP.43.L540. [DOI] [Google Scholar]
  63. Saini S.; Shah J.; Kotnala R. K.; Yadav K. L. Nickel Substituted Oxygen Deficient Nanoporous Lithium Ferrite Based Green Energy Device Hydroelectric Cell. J. Alloys Compd. 2020, 827, 154334. 10.1016/J.JALLCOM.2020.154334. [DOI] [Google Scholar]
  64. Shah J.; Shukla A.; Kar M.; Gupta G.; Jain S.; Kotnala R. K. ZnO Nanoflakes Self-Assembled from the Water Splitting Process Using a Hydroelectric Cell. React. Chem. Eng. 2022, 7, 1836–1846. 10.1039/D2RE00094F. [DOI] [Google Scholar]
  65. Li X.; Zhao H.; Shen W.; Gao F.; Huang X.; Li Y.; Zhu Z. Synthesis and Properties of Y-Doped SrTiO3 as an Anode Material for SOFCs. J. Power Sources 2007, 166, 47–52. 10.1016/J.JPOWSOUR.2007.01.008. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES